带传动设计中几个问题的分析
带传动的受力分析和传动时的应力分析
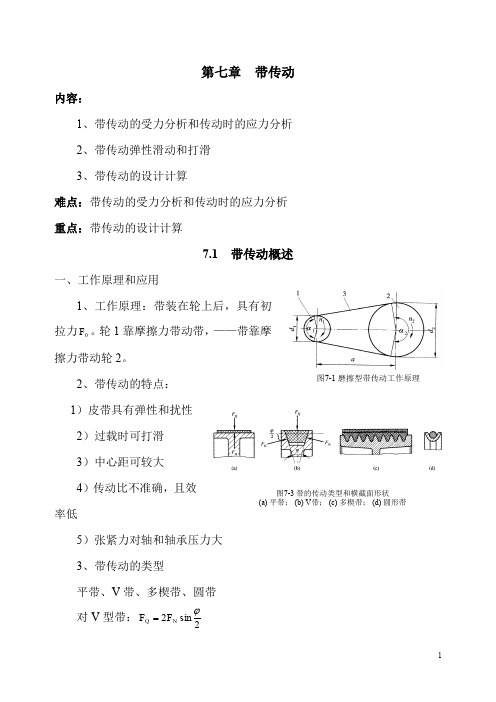
第七章 带传动内容:1、带传动的受力分析和传动时的应力分析2、带传动弹性滑动和打滑3、带传动的设计计算难点:带传动的受力分析和传动时的应力分析 重点:带传动的设计计算7.1 带传动概述一、工作原理和应用1、工作原理:带装在轮上后,具有初拉力0F 。
轮1靠摩擦力带动带,——带靠摩擦力带动轮2。
2、带传动的特点: 1)皮带具有弹性和扰性 2)过载时可打滑 3)中心距可较大 4)传动比不准确,且效率低5)张紧力对轴和轴承压力大 3、带传动的类型平带、V 带、多楔带、圆带 对V 型带:2sin 2ϕN Q F F =图7-1 磨擦型带传动工作原理图7-3 带的传动类型和横截面形状(a) 平带;(b) V 带;(c) 多楔带;(d) 圆形带2sin2ϕQ N F F =Q q N f fvF fF fF F ===2sin2ϕ设2sinϕf f v =当量摩擦系数4、V 带结构 普通V 带5、应用:远距离 二、普通V 带型号和基本尺寸 1、型号:2、尺寸 基准长度尺寸d L7-2带传动工作情况分析一、带传动受力分析不工作时01=T 0F 工作时 01〉T图7-4 V 带的结构表7-2 普通V 带截面基本尺寸摩擦力()圆周力F F F F f =-=21310FVP = P 为功率KW 2001F F F F --= 021F 2F F =+ αf e F F 21=对V 带αfv 21F F e =1e 1e 2F Ff f 0max+-=αα二、带传动的应力分析1、由紧边和松边拉力产生应力A F 11=σ AF 22=σ 2、由离心力产生应力AF A qv cl ==2σ3、由带弯曲产生应力2d ab d h Eh E='=ρσ 121max b σσσσ++=三、带传动的弹性滑动1、含义:由于带的弹性变形而引起带与带轮之间的相对滑动称弹性滑动。
2、后果图7-5带传动的受力分析图7-6 带的弯曲应力图7-7 带工作时应力变化1)传动比不准确,如带不伸长:210V V V == 4111106⨯=n d V d π4222106⨯=n d V d π122112d d d d n n i ==带有伸长:321V V V 〉〉 滑动率ε21V V 〉%%V V V 100n d n d n d 10011d 22d 11d 121πππε--==2)损失能量()ε-==1d d n n i d12d 21()12d 1d 2n 1d d n ε-= 四、失效1、打滑现象1)、含义:当传递的有效圆周力F 大于极限摩擦力αF f v 时带在轮上全面滑动图7-8带传动中的弹性滑动2)、危害:失效2、带的疲劳破坏:脱层、撕裂、断裂7-3 V 带传动选用计算1、设计准则:保证带传动不打滑,不发生疲劳破坏。
带传动设计实验报告

带传动设计实验报告1. 引言带传动是一种用于传递动力的重要机械元件,在工业生产中应用广泛。
本实验旨在通过设计和制作带传动装置来加深对带传动原理的理解,并通过实验来验证设计的可行性。
本报告将详细介绍实验的设计方案、实验过程和结果分析。
2. 设计方案2.1 实验目标本实验的目标是通过设计和制作一个带传动装置,实现两个主工作轴的动力传递。
2.2 实验材料和仪器本实验所需材料和仪器包括带轮、皮带、传动装置、电动机和测量工具等。
2.3 实验步骤1. 根据实验要求和实验目标,确定传动比和传动方式。
2. 选择合适的带轮和皮带,确定传动轴的位置和布局。
3. 安装传动装置和电动机,并调整传动装置的位置和紧度。
4. 运行电动机,测试带传动的性能,如传递效率和传动功率。
3. 实验过程3.1 设计传动比和传动方式根据实验要求,本实验选择使用直线传动方式,并确定传动比为2:1,即带轮1转2圈时,带轮2转1圈。
3.2 选择带轮和皮带根据传动比和轴的转速要求,选择合适的带轮和皮带。
经过计算和比较,我们选择了带轮1的直径为20cm,带轮2的直径为10cm,并选择了适当的皮带。
3.3 安装传动装置和电动机在实验装置上安装和调整传动装置和电动机,确保传动装置和皮带的正常运转。
根据带传动的紧度要求,调节皮带的紧度。
3.4 测试传动性能运行电动机,测试带传动的性能。
使用测量工具测量传动轴的转速,并计算传递效率和传动功率。
4. 结果分析4.1 实验结果通过实验测量,带轮1的转速为1200rpm,带轮2的转速为600rpm。
根据传动比的设计,带轮2应该为带轮1转速的一半。
实验结果与设计值吻合,验证了传动装置的设计可行性。
4.2 计算结果根据实验结果和测量值,计算得到传递效率为80%。
通过测量电动机的功率和传动装置的转速,计算得到传动功率为6kW。
5. 结论通过本实验,我们成功设计和制作了一个带传动装置,并通过实验验证了设计的可行性。
实验结果表明,带传动装置具有较高的传递效率和传动功率,适用于许多实际应用场景。
带传动的受力分析和应力分析

带传动的受力分析和应力分析带传动系统是一种常见的机械传动方式,广泛应用于各个领域。
在带传动系统中,带传递动力和转矩,因此对其受力和应力进行分析非常重要。
本文将详细介绍带传动的受力分析和应力分析的方法和步骤。
1.带传动受力分析带传动受力分析是指确定带传动中各个部件所受到的受力情况,包括带、轮毂和轴承等部件。
带传动中的受力分析主要可以通过以下几个步骤进行。
步骤一:确定带的受力情况。
带的受力主要分为两种情况,一种是张紧侧受到的张紧力,另一种是松弛侧受到的迫近力。
其中,张紧力主要由张紧装置施加,迫近力主要由带与轮毂之间的摩擦力引起。
受力分析时需要根据具体情况确定张紧力和迫近力的大小。
步骤二:确定轮毂受力情况。
轮毂是带传动系统中的受力部件之一,受力分为两种情况,一种是由于带的张紧力和迫近力而引起的轮毂弯曲应力,另一种是由于带的轴向力而引起的轴向压力。
在确定轮毂受力时,需要考虑带的受力情况以及轮毂的刚度和强度等因素。
步骤三:确定轴承受力情况。
轴承是带传动系统中的重要支撑部件,其主要受力情况包括径向力和轴向力。
在进行受力分析时,需要考虑带的张紧力、迫近力以及轮毂的刚度和强度等因素,以确定轴承受力的大小和方向。
2.带传动应力分析带传动应力分析是指对带的受力情况进行应力计算和分析,以确定带的强度和稳定性。
在带传动应力分析中,常用的方法有静态力学分析和有限元分析。
静态力学分析是一种基于力学原理的传统方法,可以通过受力分析和应力分析计算得到带的应力分布和最大应力。
静态力学分析需要考虑带的材料性质、几何形状以及受力情况等因素,通过应力计算和曲线绘制等方法,可以得到带的应力分布和最大应力。
有限元分析是一种数值计算方法,可以模拟和计算带传动系统中复杂的应力场分布。
有限元分析基于有限元法原理,将带传动系统分割为多个小元件,通过求解大量的有限元方程组,可以得到带的应力分布和最大应力。
有限元分析适用于复杂的带传动系统,可以提供更准确和详细的应力分布信息。
带式输送机常见故障原因分析及处理方法

带式输送机常见故障原因分析及处理⽅法·带式输送机常见故障原因分析及处理⽅法带式输送机常见故障原因分析及处理⽅法带式输送机可作为运输机械已⼴泛应⽤于煤炭、粮⾷、⾯粉加⼯⼚等⾏业。
既可运送散装物料,⼜可运送袋装物料。
⽤户在安装及使⽤此类设备时,对常出现⼀些故障原因不太清楚,处理⽅法不多。
本⽂分析说明了此类设备常见故障的原因及处理⽅法。
⼀、输送带的打滑及解决办法输送带在运⾏中,打滑的原因是多⽅⾯的,常见的原因及解决办法有:1、初张⼒太⼩。
输送带离开滚筒处的张⼒不够造成输送带打滑。
这种情况⼀般发⽣在启动时,解决的办法是调整拉紧装置,加⼤初张⼒。
2、传动滚筒与输送带之间的摩擦⼒不够造成打滑。
其不要原因多半是输送带上有⽔或环境潮湿。
解决办法是在滚筒上加些松⾹末。
但要注意不要⽤⼿投加,⽽应⽤⿎风设备吹⼊,以免发⽣⼈⾝事故。
3、尾部滚筒轴承损坏不转或上下托辊轴承损坏不转的太多。
造成损坏的原因是机尾浮沉太多,没有及时检修和更换已经损坏或转动不灵活的部件,使阻⼒增⼤造成打滑。
4、启动速度太快也能形成打滑。
此时可慢速启动。
如使⽤⿏笼电机,可点动两次后再启动,也能有效克服打滑现象。
5、输送带的负荷过⼤,超过电机能⼒也会打滑。
此时打滑有利的⼀⾯是对电机起到了保护作⽤。
否则时间长了电机将被烧毁。
但对于运⾏来说则是打滑事故。
克服输送带打滑现象,⾸先要找到打滑原因,⽅可采取有效解决措施。
⼆、输送带的跑偏及其处理- 带式输送机运⾏时输送带跑偏是最常见的故障之⼀。
跑偏的原因有多种,其主要原因是安装精度低和⽇常的维护保养差。
安装过程中,头尾滚筒、中间托辊之间尽量在同⼀中⼼线上,并且相互平⾏,以确保输送带不偏或少偏。
另外,带⼦接头要正确,两侧周长应相同。
在使⽤过程中,如果出现跑偏,则要作以下检查以确定原因,进⾏进⾏调整。
输送带跑偏时常检查的部位和处理⽅法有:1、检查托辊横向中⼼线与带式输送机纵向中⼼线的不重合度。
如果不重合度值超过3mm,则应利⽤托辊组两侧的长形安装孔对其进⾏调整。
带式输送机常见故障分析及处理方法

带式输送机常见故障分析及处理方法摘要:带式输送机以其运行稳定,物料输送量大,耗能低,而且结构简单便于维护等优点,在钢厂铁前各工序中广泛应用,成为了一种最经济的物流输送设备。
但由于输送物料和运行环境的不同,带式输送机在现场实际使用过程中,经常出现的一些故障,本文简略的谈谈带式输送机几种常见故障的原因分析与处理方法。
关键词:带式输送机;故障分析;处理方法一、带式输送机皮带打滑和断带的分析和处理1.1皮带机打滑皮带出现打滑的问题,主要是由于皮带的张紧力不够、传动滚筒和皮带之间的摩擦力的设定数值和实际的要求误差太大、皮带非工作面表面有水或油污、皮带输送机的超负荷工作和重新启动输送机的时候皮带被物料压死了等多个方面的问题。
通常情况下,如果为了更快速处理皮带打滑异常,通常是调整卡紧滚筒、尾部重锤装置,同时确认尾部小车灵活和滚筒包胶完好、日常生产中禁止超负荷作业、增加皮带的张力值,以及采用吹扫装置等处理的方式。
而一旦发生了皮带被物料压死的情况,在重新启动输送机前,马上组织人员对皮带上的物料进行快速卸料,以便于达到适当的主动滚筒摩擦力。
1.2皮带机断带一般情况下,导致带式输送机发生断带的原因有:(1)皮带打滑不转,驱动滚筒与胶带摩擦发热损坏;(2)胶带发生了严重跑偏的情况,被机架卡住了;(3)输送带超过使用周期,并伴有明显的老化现象;(4)铁料中的铁件和片石等坚硬异物被卡在导料槽处、尾部滚筒及胶带之间,或因皮带跑偏严重或托辊脱掉等故障造成机架尖锐部位刮伤胶带;(5)作用在胶带上的拉紧设备的张紧力度过大。
而要想更高效的防止皮带机发生断带的故障,应该采用如下几种方法:(1)发现后马上停机排查打滑原因并快速排除;(2)增设调校偏角托辊和防止跑偏的防护设备,但一旦发生了胶带被机架卡住的情形,则应立即停机检查并解决;(3)输送带按照使用周期和生产工况变化,及时更换;(4)物料里的大块物件、铁器及时清除,皮带正上方增加除铁器和回程皮带增设挡料器(5)根据输送机各部件的磨损变形,及时调整张紧装置,保持合适的张紧力度。
机械设计基础-7.2带传动的工作情况分析

在各类机械中应用广泛,但摩擦式带传动不适用于对传动比有精确要求的场合。
带传动的工作情况分析是指带传动的受力分析、应力分析、运动分析。
带传动是一种挠性传动,其工作情况具有一定的特点。
一、带传动的受力分析工作拉力带传动尚未工作时,传动带中的预紧力为F0。
带传动工作时,一边拉紧,一边放松,记紧边拉力为F1和松边拉力为F2。
设带的总长度不变,根据线弹性假设(环形带的总长度不变,则可推出紧边拉力的增量应该等于松边拉力的减量):F1-F0=F0-F2;或:F1 +F2=2F0;记传动带与小带轮或大带轮间总摩擦力为Ff ,其值由带传动的功率P 和带速v 决定。
定义由负载所决定的传动带的有效拉力为Fe =P/v ,则显然有Fe =Ff 。
取绕在主动轮或从动轮上的传动带为研究对象 ,有:Fe =Ff =F1-F2;因此有: F1=F0+Fe /2;F2=F0-Fe /2;工作中有效拉力的大小取决于所传递功率的大小。
即:)(1000KW V F P e =显然承载能力的大小取决于带两端的拉力差,而不是某个力的大小。
需要传递的功率越大,需要的有效拉力越大。
二、带传动的最大有效拉力及其影响因素带传动的最大有效拉力Fec 有多大?由欧拉公式确定刚刚打滑时,带两端的拉力关系式为: 欧拉公式给出的是带传动在极限状态下各力之间的关系,或者说是给出了一个具体的带传动所能提供的最大有效拉力Fec 。
由欧拉公式可知:(预紧力F0↑→最大有效拉力Fec ↑(包角α↑→最大有效拉力Fec ↑摩擦系数 f ↑→最大有效拉力Fec ↑可知影响带的承载能力的因素:f 、α、0F 。
但注意各个参数都不能过大或过小。
如:初张力太大,带易断裂,拉应力增大,轴上的受力同时增大;相反,太小,易打滑。
μ太大,带轮就要作得粗糙,带易磨损;一般都采用打蜡,在带轮表面加沥青等方法加大摩擦系数。
包角与中心距有关,包角太大,中心距增大,但太大会使结构庞大。
当已知带传递的载荷时,可根据欧拉公式确定应保证的最小初拉力F0。
带传动分析实验报告

带传动分析实验报告
本次实验旨在通过带传动系统的分析,掌握传动功率、压力角等参数的计算方法,并
通过实验验证和了解齿轮齿条传动的优缺点及其应用领域。
实验装置包括一台带传动试验机和几组不同齿数、不同大小的齿轮齿条传动装置。
首
先进行了传动功率的测量实验,实验中我们选用了两个齿轮轮廓数分别为10和17的齿轮。
通过转速、制动扭矩的测量,利用公式P=Tω 计算出传动功率,实验结果表明:当传动
装置的齿轮轮廓数增加时,传动功率也随之增加。
这是由于齿轮齿条系统中齿轮轮廓数的
增加,可增加齿轮外径,提高齿轮齿条的传动能力,从而提高传动功率。
而当传动装置的
齿数增加时,传动功率也随之增加。
这是因为齿数的增加,减小了单个齿齿面的压力,从
而降低了齿面的损耗。
接着进行了压力角的测量实验。
利用测量仪器可以测量角度,结合公式计算得到压力角,实验结果表明:压力角的大小与齿轮齿条角度有关,当齿轮齿条所对应的压力角逐渐
增大时,齿轮齿条系统的传动效率逐渐降低,同时,齿轮齿条系统的噪音和振动也会逐渐
增大。
最后我们对齿轮齿条传动系统进行了优缺点的比较和探讨。
齿轮齿条传动装置具有带
动方向确定、传动比稳定、重量轻等优点,但也存在着齿面磨损等问题。
相比之下,链条
传动的优点是齿面的磨损较少,但同时存在着拉伸和弯曲等问题。
时键传动则不存在齿面
磨损和拉伸等问题,但在运转时需要增加一定的轴向负载。
带传动的受力分析和传动时的应力分析

带传动的受力分析和传动时的应力分析带传动的受力分析和传动时的应力分析是机械工程中非常重要的内容之一、带传动是一种将动力传递至不同轴线之间的装置,通过带传动可以实现不同轴线之间的转速换算和动力传递。
由于带传动具有结构简单、噪音小等特点,因此在机械传动中被广泛应用。
下面将详细介绍带传动的受力分析和传动时的应力分析。
首先,我们来看带传动的受力分析。
带传动受到两种主要的受力:张力和摩擦力。
带传动的原理是通过两个平行轴之间的带条,使主动轴上的驱动轮通过带条的摩擦与被动轴上的从动轮相连。
在传动过程中,带条会受到相应的张力和摩擦力。
对于带条,其张力的大小是不均匀的,张力最大的地方称为紧侧,张力最小的地方称为松侧。
张力的分布情况与带传动所处的工作状态、受力部位以及传动比等因素有关。
在带传动过程中,紧侧的张力T1以及松侧的张力T2之间会形成一个张力差ΔT,ΔT是带条张力的一个重要参数。
除了张力外,带传动中的摩擦力也是非常重要的受力分析内容。
摩擦力是带条与驱动轮、从动轮之间的相互作用力。
摩擦力的大小不仅受到带条的张力影响,还受到摩擦系数、载荷和转速等因素的影响。
在带传动中,摩擦力不仅决定了传动效率,还对带条的寿命和传动稳定性有着重要影响。
接下来,我们来看带传动的应力分析。
应力是带条在传动过程中所承受的材料内部的力。
带传动中的应力分为两种情况:带条的张应力和剪应力。
对于带条的张应力,其大小与带条的宽度、厚度、张力和倒弯半径等因素有关。
张应力在带传动中十分重要,它会决定带条的受力情况和寿命。
为了保证带条工作在安全的应力范围内,需要根据实际使用情况和材料特性来选择合适的带传动设计参数。
剪应力是带条在传动过程中产生的剪力对带条内部的应力。
剪应力的产生与带条的工作情况、转速和带条的厚度等因素有关。
过大的剪应力不仅会导致带条变形和破坏,还会使传动效率下降。
因此,通过合理的设计和选择适当的带条材料,可以减小带条受到的剪应力。
总之,带传动的受力分析和传动时的应力分析是机械工程中非常重要的内容。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C=
q ! dl ! v 2 q ! r d ! v 2 2 = = qv d r r
( 11) fv
V 带轮轮槽角系列值有 32&, 34&, 36&, 38&, 所以 3f 。因此在相同条件下 , V 带传动能力为平带 的 3 倍 , 在一般机械中 , 多采用 V 带传动。
设该离心力在该微弧段两边引起拉力为 F c , 由 微弧段上各力的平衡得: 2F c sin d 2 = qv d 2 ( 12)
但未加以证明 , 以下为证明过程。 设小带轮 和大 带轮 的基 准直 径分 别为 d 1 和 d 2 , 包角分别为 看出
1 1 2
和
2
0
引言
机械设计是机械类各专业中研究机械共性问题
。从图 1 中的几何关系可以 d1 2 d2 2
= - 2 ,
= + 2 , 带长为 :
1
L = 2 A B + A D + BC = 2 acos +
3
( 5)
弯曲应力的计算公式
带绕过带轮时要引起弯曲应力, 设 y 为带的中
( d2 + d1 ) +
性层到最外层的垂直距离; E 为带的弹性模量 ; d 为 带轮基准直径 ( 如图 3 所示 ) 力的推导过程。
[ 3]
2
柔韧体摩擦的欧拉公式
带传动中, 当带有打滑趋势时 , 摩擦力即达到极
。以下为带的弯曲应
限值 , 亦即带传动的有效拉力达到最大值, 根据柔韧 体摩擦的欧拉公式, 带的紧边拉力 F 1 和松 边拉力 F 2 两者的临界值间的关系为 : F1 = F2 e ( 6) 很多设计资料和教材直接给出了上式, 未提供 证明 , 下面对其进行证明 [ 2] 。 设 f 为带和带轮间的静摩擦系数 ( 对于 V 带 , 用当量摩擦系数 f
( 3) 2 2
2
因 d 很小 , 故 sin 阶微量 d F sin
d 2
d d , cos 2 2
1, 并忽略二
1- 4sin2 2 ( 1- sin
2
cos 2
2
d , 可得 d F N = F sind , f dF N = d F, 从 2
) 12 4
而 dF = f d 。 F 两端积分得 1n +
∀ 机械与电子# 2010( 11)
本身的质量将引起离心力。设 q 为传动带单位长度 的质量 ; A 为带的横截面面积
[ 4]
。由于离心力的作
用 , 带中产生的离心拉力在带的横截面上就要产生 ( 7) ( 8) 离心应力 ! c , 以下为 ! c 的推导过程。 如图 4 所示 , 当带绕过带轮时, 在微弧段 dl 上 产生的离心力为: ! 37 !
7
结束语
对机械设计教材和手册中未详细讨论的一些带 传动的设计计算公式和原理进行了分析、 推导和证 明 , 有助于学生更深入地掌握带传动的工作原理和 设计计算方法, 有利于培养学生的创造性思维, 从而 提高学生综合运用所学知识分析和解决工程实际问 题的能力。 参考文献:
[ 1] 濮良贵 , 纪 名刚 . 机 械设 计 . 7 版 [ M ] . 北京 : 高 等教 育 出版社 , 2003. 朱文坚 , 黄 平 . 机 械设 计 . 2 版 [ M ] . 北京 : 高 等教 育 出版社 , 2008. [ 3] [ 4] [ 5] 许贤泽 , 戴书华 . 精密机械设计基础 [ M ] . 北 京 : 电子 工 业出版社 , 2007. 邱宣怀 . 机械设计 [ M ] . 北京 : 高等教育出版社 , 1997. 莫海军 , 吴上生 , 蓝民华 , 等 . 机械设计教材中几个问 题 的探讨[ J] . 机械设计与研究 , 2009, 25( 3) : 117- 120. 作者简介 : 李 旻 ( 1974- ) , 男 , 江西南昌人 , 讲师 , 博士 , 研
b 用代入法可得弯曲应力 ! 2y E / d 。 若用 h 表示带的高度 , 则对平带, y = h/ 2; 对
V 带, y !b
图 2 带传动的受力分析
h/ 2, 代入弯曲应力公式可得: Eh/ d ( 10)
4
离心拉应力的计算公式
当带以线速度 v 沿带轮轮缘作圆周运动时, 带
角为 d 。设微弧段两端的拉力分别为 F 和 F + d F, 微弧段对带轮的正压力为 d F N , 带与带轮间的最大 静摩擦力为 f d F N 。忽略离心力的影 响, 由法 向和 切向的平衡条件得平衡方程: d d dF N = F sin + ( F + dF) sin 2 2 d d f dF N + F cos 2 = ( F + d F) cos 2
2
) [ 1- (
2
2
) ]=
/2
2
4 ( 4)
∃
1 2
F F
dF = F
∃f d
0
, 从而得 : ( 9)
将式 ( 3) 和式( 4 ) 代入式( 2) , 得 : L 2a( 1= 2a+ 2 2 )+ 2 ( d1 + d2 ) + ( d2 - d1 ) ( d2 - d1 ) 4a
2
F1 = f F2 由式( 9 ) 即可得式 ( 6) 。
究方向为机器人与微机械技术。
图5
平带与 V 带传动的比较
当平带和 V 带受到同样的压紧力 F N 时, 它们 的法向反力 F%N 却不相同。平 带与带轮接触 面上 的摩擦力为 f F%N = f F N 。而对于 V 带 , 由平衡条件 2 ! ( F%N / 2 ) ! sin( # / 2) = F N 可得 : F%N = F N / sin( # / 2) ( 14) ( 15)
摘要 : 针对机械设计教材及手册中 , 对带传动设 计计算的一些公式未加证明而不利于理解的现状 , 对带长和带轮中心距的关系、 柔韧体摩擦的欧拉公 式、 弯曲应力及离心拉应力的计算公式等进行了分 析推导, 对 V 带与平带传动能力的比较 、 带的根数 计算等教材中未阐述透彻的问题进行了补充说明 。 关键词: 机械 设计; 带 传动; 欧拉公式 ; 弯曲 应 力; 离心应力 中图分类号 : T H 122 文献标识码 : A 文章编号: 1001 2257( 2010) 11 0036 03 Abstract: Som e import ant fo rmulas in belt drive desig n are not pro ved in t he t ext books and manuals of m achine design, and t his w ill not help the st udent s t o underst and t he co nt ent s concerned. T o solve t his problem, several f orm ulas are ana l yzed and derived, including t he for mula indicating the relat io nship bet w een belt lengt h and w heel cen t er dist ance, t he Euler s f orm ula of flex ible body frict io n, t he f ormulas t o calculat e bending str ess and cent rif ugal t ensile st ress. T he issues such as drive ability compar ison bet w een V belt and f lat belt , t he calculation o f belt number, w hich ar e not thor oug hly ex plained in t ex t bo oks and m anuals, ar e discussed her e. Key words: machine desig n; bel t drive; Euler s fo rmula; bending st ress; cent rif ug al st ress
6
带的根数计算问题
设 P ca 为计算功率 ; K 为包角系数; K L 为长度
系数; ∃P 0 为单根 V 带额定功率的增量。则根数: P ca ( 17) z= ( P 0 + ∃P 0 ) K K L 设[ ! ] 为许用应力 ; !b1 为紧边拉应力 ; ! c 为离心 应力[ 5] 。单根 V 带的基本额定功率 : ( [ !] - !b1 - ! c ) 1P 0=
v f
代替 f ) ,
为带在带轮 上的包
图3
带的弯曲应力的计截取一微弧段 d l , 对 应的包
设 M 为截面所受的弯矩 ; W 为截 面的抗弯截 面系数。由材料力学可知弯曲应力为 ! b = M/ W 。 设 I 为截面的惯性矩; ∀为中性层曲率半径 , 由 材料力学还可得 M = EI / ∀ , W = I / y 。取 ∀ d/ 2, 使
离心力虽只发生在带作圆周运动的部分, 但由 此引起的拉力却作用于带的全长, 故离心拉应力为 :
2 ! c = F c / A = qv / A
( 13)
5
V 带与平带传动能力的比较
教材中介绍 V 带传动能力比平带强 , 有的书还
提到 V 带传动能力为平带的 3 倍 , 但未加解释。下 面对此进行分析 , 如图 5 所示 , 平带的横截面为扁平 矩形 , 其工作面是与轮面相接触的内表面 , 而 V 带 的横截面为等腰梯形 , V 带靠两侧面工作。
1
带长和带轮中心距的关系
