结构力学课后答案第7章位移法
结构力学位移法题及答案
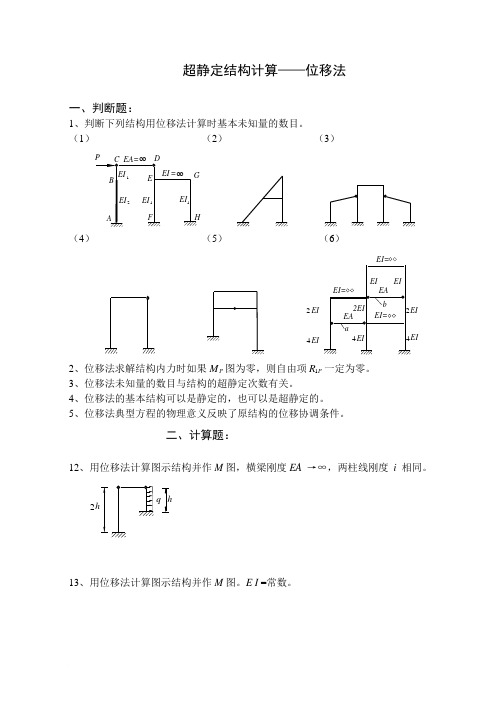
超静定结构计算——位移法一、判断题:1、判断下列结构用位移法计算时基本未知量的数目。
(1) (2) (3)(4) (5) (6)EIEIEIEI 2EI EI EIEIEAEA ab EI=EI=EI=244422、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
3、位移法未知量的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静定的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二、计算题:12、用位移法计算图示结构并作M 图,横梁刚度EA →∞,两柱线刚度 i 相同。
213、用位移法计算图示结构并作M 图。
E I =常数。
—— 41 ——ll /2l /214、求对应的荷载集度q 。
图示结构横梁刚度无限大。
已知柱顶的水平位移为 ()5123/()EI →。
12m12m8mq15、用位移法计算图示结构并作M 图。
EI =常数。
ll ll16、用位移法计算图示结构,求出未知量,各杆EI 相同。
4m19、用位移法计算图示结构并作M 图。
qll20、用位移法计算图示结构并作M 图。
各杆EI =常数,q = 20kN/m 。
6m6m23、用位移法计算图示结构并作M 图。
EI =常数。
ll 224、用位移法计算图示结构并作M 图。
EI =常数。
q29、用位移法计算图示结构并作M 图。
设各杆的EI 相同。
qql l /2/232、用位移法作图示结构M 图。
E I =常数。
—— 43 ——qql l/2l /2l36、用位移法计算图示对称刚架并作M 图。
各杆EI =常数。
l l38、用位移法计算图示结构并作M 图。
EI =常数。
ql l l l42、用位移法计算图示结构并作M 图。
2m 2m43、用位移法计算图示结构并作M 图。
EI =常数。
lllql48、已知B 点的位移∆,求P 。
ll/2/2A∆51、用位移法计算图示结构并作M 图。
超静定结构计算——位移法(参考答案)1、(1)、4; (2)、4; (3)、9; (4)、5; (5)、7;(6)、7。
结构力学-第7章 位移法

第7章位移法一。
教学目的掌握位移法的基本概念;正确的判断位移法基本未知量的个数;熟悉等截面杆件的转角位移方程;熟练掌握用位移法计算荷载作用下的刚架的方法了解位移法基本体系与典型方程的物理概念和解法。
二。
主要章节§7—1 位移法的基本概念§7-2 杆件单元的形常数和载常数-位移法的前期工作§7—3 位移法解无侧移刚架§7-4 位移法解有侧移刚架§7-5 位移法的基本体系§7—6 对称结构的计算*§7—7支座位移和温度改变时的位移法分析(选学内容)§7-8小结§7—9思考与讨论三. 学习指导位移法解超静定结构的基础是确定结构的基本未知量以及各个杆件的转角位移方程,它不仅可以解超静定结构,同时还可以求解静定结构,另外,要注意杆端弯矩的正负号有新规定。
四。
参考资料《结构力学(Ⅰ)—基本教程第3版》P224~P257第六章我们学习了力法,力法和位移法是计算超静定结构的两个基本方法,力法发展较早,位移法稍晚一些。
力法把结构的多余力作为基本未知量,将超静定结构转变为将定结构,按照位移条件建立力法方程求解的;而我们今天开始学的这一章位移法则是以结构的某些位移作为未知量,先设法求出他们,在据以求出结构的内力和其他位移。
由位移法的基本原理可以衍生出其他几种在工程实际中应用十分普遍的计算方法,例如力矩分配法和迭代法等.因此学习本章内容,不仅为了掌握位移法的基本原理,还未以后学习其他的计算方法打下良好的基础。
此外,应用微机计算所用的直接刚度法也是由位移法而来的,所以本章的内容也是学习电算应用的一个基础。
本章讨论位移法的原理和应用位移法计算刚架,取刚架的结点位移做为基本未知量,由结点的平衡条件建立位移法方程.位移法方程有两种表现形式:①直接写平衡返程的形式(便于了解和计算)② 基本体系典型方程的形式(利于与力法及后面的计算机计算为基础的矩阵位移法相对比,加深理解)§7-1 位移法的基本概念1。
结构力学位移法题与答案解析
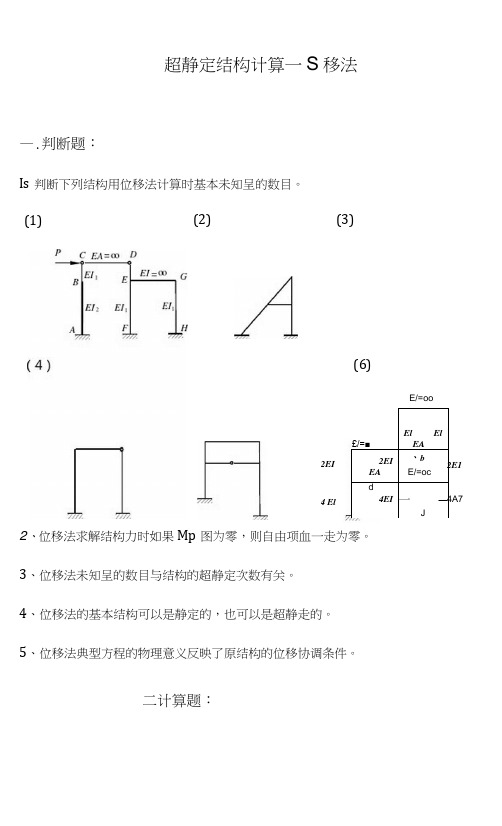
超静定结构计算一S移法—.判断题:Is判断下列结构用位移法计算时基本未知呈的数目。
2、位移法求解结构力时如果Mp图为零,则自由项血一走为零。
3、位移法未知呈的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静走的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二计算题:(2) (3)(1)(6)£/=■El ElEA2EI、bEA E/=ocd4EI一—JE/=oo2E14A72EI4 El12.用位移法计算图示结构并作〃图,横梁刚度EA -8 ,两柱线刚度/相同。
13、用位移法计算图示结构并作〃图。
F/二常数。
14、求对应的荷载集度g。
图示结构横梁刚度无限大。
已知柱顶的水平位移为512/(3 曰)(T)。
15、用位移法计算图示结构州乍M图。
曰=常数。
16、用位移法计算图示结构r求出未知呈,各杆曰相同。
4m4m19、用位移法计算图示结构并作〃图。
-2/ 2fq 二i i20、用位移法计算图示结构并作〃图。
各杆日=営数r q = 20kN/m o6m4 ------- B6m 6mR --- k ----- 123、用位移法计算图示结构州乍M图。
曰=常数。
7T7F24、用位移法计算图示结构州乍M图。
曰=常数。
°^=ZJ週AV 酔辭圍闕¥觀⑨由、充。
回申Z7阴甘县欲 遍如士星與莎竺园蔑44辛觀⑨由、6乙IcnnM M I Z M fc/i in38、用位移法计算图示结构并作〃图。
曰=常数。
42、用位移法计算图示结构州乍〃图。
43、用位移法计算图示结构州乍〃图。
曰=常数。
48、已知0点的位移0,求几51.用位移法计算图示结构并作M 图。
qP M H 1 1 1El---------JIIk —— ------ H超静定结构计算一^移法(参考答案)(617.14、q = 3kN/m1. (11 4 ; (21 4; (31 9; ⑷ 5;(51 7;2、( X )3、( X )< (0)5. (X)12、x qh 2/40 )("/)M图20、24、3236M图(Xql2 n )(X2(//2/33)42912 El----25 I34&。
结构力学第七章位移法

10
§7-3 位移法基本结构与未知量数目
二 位移法基本结构 1 附加刚臂 控制结点转动 2 附加链杆 控制结点线位移
ΔC C θC
ΔD θD
D
基本结构
将原结构结点位移锁住,所得单跨梁的组合体
11
三 位移法基本结构与未知量数目
ΔC
ΔD
Z1
θD
C θC
D
Z2 Z3
基本结构
结点角位移的数目=刚结点的数目=附加刚臂的数目 独立结点线位移的数目=附加链杆的数目
B
15i 16
6
0(2)
位移法方程实质上平衡方程 33
2i
3i/2Z2=1
A
D
2i
k 21
FQ BA
FQ CD
3i 2
B
C k22
FQBA
FQCD
3i
i2
3i/2
k 22
i
3i 4
3i 16
15i 16
B i
0
FQ BA
3i 4
C FQCD i
3i 2
M1
3i 4
A
FQ CD
3i 16
3i/2
D 3i/4 26
4
B
C F2P
3kN/m 3kN/m
16
皮肌炎图片——皮肌炎的症状表现
▪ 皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的, 全身性疾病,而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下:
▪ 1、早期皮肌炎患者,还往往伴 有全身不适症状,如-全身肌肉酸 痛,软弱无力,上楼梯时感觉两 腿费力;举手梳理头发时,举高 手臂很吃力;抬头转头缓慢而费 力。
结构力学习题集-矩阵位移法习题及答案

第七章 矩阵位移法一、是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
6、结 构 刚 度 矩 阵 是 对 称 矩 阵 ,即 有K i j = K j i ,这 可 由 位 移 互 等 定 理 得 到 证 明 。
7、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应满足的变形条件。
8、在直接刚度法的先处理法中,定位向量的物理意义是变形连续条件和位移边界条件。
9、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
10、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
11、矩阵位移法既能计算超静定结构,也能计算静定结构。
二、选择题1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下的单元刚度矩阵[]k 66⨯,就其性质而言,是: A .非对称、奇异矩阵; B .对称、奇异矩阵; C .对称、非奇异矩阵; D .非对称、非奇异矩阵。
3、单元i j 在图示两种坐标系中的刚度矩阵相比:A .完全相同;B .第2、3、5、6行(列)等值异号;C .第2、5行(列)等值异号;D .第3、6行(列)等值异号。
xi4、矩阵位移法中,结构的原始刚度方程是表示下列两组量值之间的相互关系: A .杆端力与结点位移; B .杆端力与结点力; C .结点力与结点位移; D .结点位移与杆端力 。
结构力学位移法题及问题详解
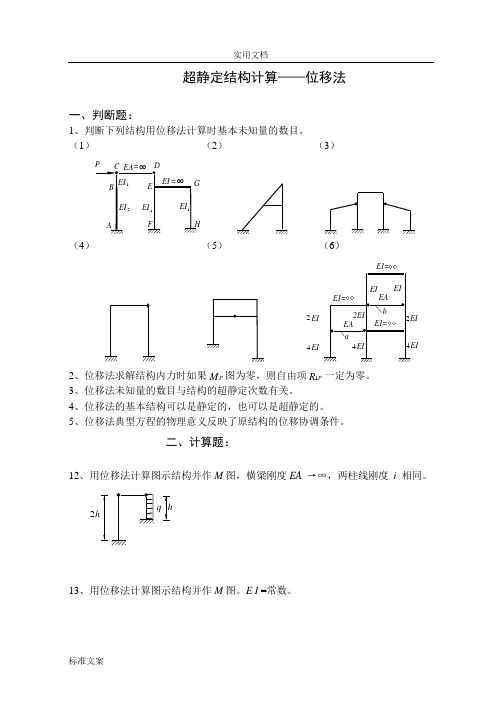
超静定结构计算——位移法一、判断题:1、判断下列结构用位移法计算时基本未知量的数目。
(1) (2) (3)(4) (5) (6)EIEIEIEI 2EI EI EIEIEA EA ab EI=EI=EI=244422、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
3、位移法未知量的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静定的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二、计算题:12、用位移法计算图示结构并作M 图,横梁刚度EA →∞,两柱线刚度 i 相同。
213、用位移法计算图示结构并作M 图。
E I =常数。
lll/2l/214、求对应的荷载集度q。
图示结构横梁刚度无限大。
已知柱顶的水平位移为()5123/()EI→。
12m12m 8mq15、用位移法计算图示结构并作M图。
EI =常数。
ll l l16、用位移法计算图示结构,求出未知量,各杆EI相同。
4m19、用位移法计算图示结构并作M图。
ql l20、用位移法计算图示结构并作M 图。
各杆EI =常数,q = 20kN/m 。
6m6m23、用位移法计算图示结构并作M 图。
EI =常数。
ll 224、用位移法计算图示结构并作M 图。
EI =常数。
q29、用位移法计算图示结构并作M 图。
设各杆的EI 相同。
qql l /2/232、用位移法作图示结构M 图。
E I =常数。
qql l/2l /2l36、用位移法计算图示对称刚架并作M 图。
各杆EI =常数。
l l38、用位移法计算图示结构并作M 图。
EI =常数。
ql l l l42、用位移法计算图示结构并作M 图。
2m 2m43、用位移法计算图示结构并作M 图。
EI =常数。
lll48、已知B 点的位移∆,求P 。
ll/2/2A∆51、用位移法计算图示结构并作M 图。
q超静定结构计算——位移法(参考答案)1、(1)、4; (2)、4; (3)、9; (4)、5; (5)、7;(6)、7。
《结构力学习题集》(下)-矩阵位移法习题及答案 (2)

第七章 矩阵位移法一、就是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间得关系。
2、单元刚度矩阵均具有对称性与奇异性。
3、局部坐标系与整体坐标系之间得坐标变换矩阵T 就是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间得关系。
5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
6、结 构 刚 度 矩 阵 就是 对 称 矩 阵 ,即 有K i j = K j i ,这 可 由 位 移 互 等 定 理 得 到 证 明 。
7、结构刚度方程矩阵形式为:,它就是整个结构所应满足得变形条件。
8、在直接刚度法得先处理法中,定位向量得物理意义就是变形连续条件与位移边界条件。
9、等效结点荷载数值等于汇交于该结点所有固端力得代数与。
10、矩阵位移法中,等效结点荷载得“等效原则”就是指与非结点荷载得结点位移相等。
11、矩阵位移法既能计算超静定结构,也能计算静定结构。
二、选择题1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号就是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下得单元刚度矩阵,就其性质而言,就是:A.非对称、奇异矩阵;B.对称、奇异矩阵;C.对称、非奇异矩阵;D.非对称、非奇异矩阵。
3、单元i j 在图示两种坐标系中得刚度矩阵相比:A.完全相同;B.第2、3、5、6行(列)等值异号;C.第2、5行(列)等值异号;D.第3、6行(列)等值异号。
4、矩阵位移法中,结构得原始刚度方程就是表示下列两组量值之间得相互关系:A.杆端力与结点位移;B.杆端力与结点力;C.结点力与结点位移;D.结点位移与杆端力。
四川大学结构力学第7章

F
F
F
θ3
F
θ1
θ2
Δ2
F M
Δ1
F M
F
A E
C
F M AE A
F
BF
A
E
BF
D
F
F
B
M AE A
D
D
θ1
F
B
D
F
A
B
C
FRB
B
C
F DE
F
G
DE
F RB
M CB C
DE
G
F
G
FRB
M CB C
θ1 DE
F
G
由平衡条件建立位移法方程
16i1
6i l
1
ql 2 8
0
(1)
M CD
FX 0, FQCA 0
M CA
B FQCA
M CA
M AC l
6i l
1
12i l2
1
C
D
6i l
1
12i l2
1
0
例2、用位移法分析图示结构
10kN.m
20kN/m
B 2EI
40kN
E D 2EI
4m EI
EI
C
A
4m
2m
2m
❖ 解:1、确定基本未知量
20kN/m
40kN
10kN.m θ2
E
θ1 B
2i
D
2i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:(1)确定基本未知量
两个位移未知量,各种M图如下
(2)位移法典型方程
(3)确定系数并解方程
代入,解得
(4)求最终弯矩图
(e)
解:(1)确定基本未知量
两个角位移未知量,各种M图如下
(2)位移法典型方程
(3)确定系数并解方程
代入,解得
(4)求最终弯矩图
7-7试分析以下结构内力的特点,并说明原因。若考虑杆件的轴向变形,结构内力有何变化?
(a)
解:(1)利用对称性得:
(2)由图可知:
可得:
(3)求最终弯矩图
(b)
解:(1)利用对称性,可得:
(2)由图可知,各系数分别为:
解得:
(3)求最终弯矩图如下
(c)
解:(1)在D下面加一支座,向上作用1个单位位移,由于BD杆会在压力作用下缩短,所以先分析上半部分,如下图。
D点向上作用1个单位,设B向上移动x个单位,则 ,得 个单位。
习题
7-1试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a)(b) (c)
1个角位移3个角位移,1个线位移4个角位移,3个线位移
位移3个角位移,2个线位移
(g)(h)(i)
一个角位移,一个线位移一个角位移,一个线位移三个角位移,一个线位移
7-2试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?
(a) (b) (c)
(d) (e) (f)
7-8试计算图示具有牵连位移关系的结构,并绘出M图。
(a)
解:(1)画出 图
由图可得:
由图可知:
(2)列方程及解方程组
解得:
(3)最终弯矩图
(b)
解:C点绕D点转动,由Cy=1知,
知
求
知
(c)
解:(1)作出各M图
(2)列出位移法方程
解得:
(3)最终M图
(d)
(3)确定系数并解方程
代入,解得
(4)画最终弯矩图
(b)
解:(1)确定基本未知量
两个位移未知量,各种M图如下
(2)位移法典型方程
(3)确定系数并解方程
代入,解得
(4)画最终弯矩图
(c)
解:(1)确定基本未知量
两个位移未知量,各种M图如下
(2)位移法典型方程
(3)确定系数并解方程
代入,解得
(4)求最终弯矩图
(2)同理可求出Mp图。
可得:
(3)求最终弯矩图
(d)
(e)
解:(1)利用对称性,取左半结构
(2)由图可知:
解得:
(3)求得最终弯矩图
(f)
解:由于Ⅱ不产生弯矩,故不予考虑。只需考虑(Ⅰ)所示情况。对(Ⅰ)又可采用半结构来计算。如下图所示。
(4)画M图
(b)
解:(1)确定基本未知量
1个角位移未知量,各弯矩图如下
(2)位移法典型方程
(3)确定系数并解方程
(4)画M图
(c)
解:(1)确定基本未知量
一个线位移未知量,各种M图如下
(2)位移法典型方程
(3)确定系数并解方程
(4)画M图
(d)
解:(1)确定基本未知量
一个线位移未知量,各种M图如下
7-3试说出位移法方程的物理意义,并说明位移法中是如何运用变形协调条件的。
7-4试回答:若考虑刚架杆件的轴向变形,位移法基本未知量的数目有无变化?如何变化?
7-5试用位移法计算图示结构,并绘出其内力图。
(a)
解:(1)确定基本未知量和基本结构
有一个角位移未知量,基本结构见图。
(2)位移法典型方程
(3)确定系数并解方程
(2)位移法典型方程
(3)确定系数并解方程
(4)画M图
(e)
解:(1)确定基本未知量
两个线位移未知量,各种M图如下
(2)位移法典型方程
(3)确定系数并解方程
代入,解得
(4)画M图
7-6试用位移法计算图示结构,并绘出M图。
(a)
解:(1)确定基本未知量
两个角位移未知量,各种M图如下
(2)位移法典型方程
解:基本结构选取如图所示。
作出 及 图如下。
由位移法方程得出:
作出最终M图
7-9试不经计算迅速画出图示结构的弯矩图形。
(a)
(b)
题7-9图
7-10试计算图示有剪力静定杆的刚架,并绘出M图。
解:(1)画出 图
由图可知,得到各系数:
求解得:
(2)求解最终弯矩图
7-11试利用对称性计算图示刚架,并绘出M图。
