对称振子天线_阵列天线
雷达阵列天线介绍

■开课目的“阵列天线分析与综合”是电子信息工程专业电磁场与微波通信方向的专业选修课程。
课程的任务是使学生掌握阵列天线的基本理论、基本分析与综合方法,掌握单脉冲阵列、相控阵扫描天线的基本理论和概念、以及阵列天线的优化设计思想,培养学生分析问题和解决问题的能力,为今后从事天线理论研究、工程设计和开发工作打下良好的基础。
■课程要求●约有五次作业●考核平时成绩占20%。
包括平时作业,出勤情况。
期末考试成绩占80%(一页纸开卷)雷达阵列天线简介1、“AN/SPY—1”S波段相控阵雷达是海军“宙斯盾”(Aegis)武器系统中的一部分,由RCA公司研制。
它有四个相控阵孔径,提供前方半空间很大的覆盖范围。
接收时它使用带68个子阵的馈电系统,每个子阵包含64个波导辐射器,总共有68×64=4352个单元。
发射时,子阵成对组合,形成32个子阵,每个子阵128个单元,总共32×128=4096辐射单元。
移相器为5位二进制铁氧体移相器,直接向波导辐射器馈电。
为了避免相位量化误差引起的高副瓣电平,后来移相器改为7位二进制移相器,合成的相控阵由强制馈电功分网络馈电,辐射单元也改为4350个,单脉冲的和、差波瓣及发射波束均按最佳化设计。
AN/SPY—1天线正在进行近场测试(RCA公司电子系统部提供)目前该系统安装在导弹巡洋舰上导弹巡洋舰上的AN/SPY—1系统2、爱国者(PATRIOT)多功能相控阵雷达是Raytheon公司为陆军研制的一种多功能相控阵雷达系统。
其天线系统使用光学馈电的透镜阵列形式。
和差波瓣分别通过单脉冲馈源达到最佳。
孔径呈圆形,包含大约5000个单元,采用4位二进制铁氧体移相器和波导型辐射器单元。
它安装在车辆上,并可平叠以便于运输。
爱国者多功能相控阵雷达天线(Raytheon公司提供)3、机载预警和控制系统(AW ACS)世界上第一个具有超低副瓣的作战雷达天线是由西屋电气公司为AWACS 系统研制的。
实验五 对称振子天线的设计与仿真

实验五对称振子天线的设计与仿真一、实验目的1.设计一个对称振子天线2.查看并分析该对称振子天线的反射系数及远场增益方向二、实验设备装有HFSS 13.0软件的笔记本电脑一台三、实验原理1、电流分布对于从中心馈电的偶极子,其两端开路,故电流为零。
工程上通常将其电流分布近似为正弦分布。
假设天线沿z轴放置,其中心坐标位于坐标原点,如图所示,则长度为l的偶极子天线的电流分布为:I(z)=Imsink(l-|z|),其中Im是波腹电流,k波数。
对半波偶极子而言l=λ/4.则半波偶极子的电流分布,可以写成:I(z)=Imsin(π/2-kz)=Imcos(kz)。
首先明白一点:半波偶极子天线就是对称阵子天线。
2、辐射场和方向图已知半波偶极子天线上的电流分布,可以利用叠加原理来计算半波偶极子天线的辐射场。
式中,称为半波偶极子的方向性函数。
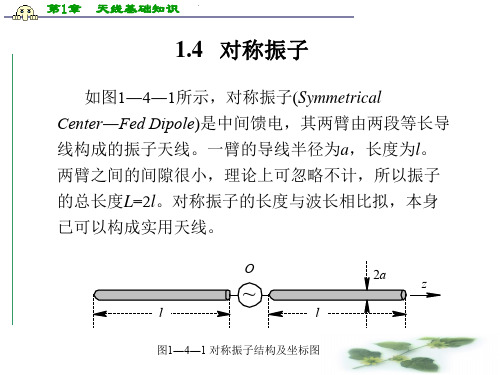
3、方向系数:对称振子是中间馈电,其两臂由两段等长导线构成的振子天线。
一臂的导线半径为,长度为I。
两臂之间的间隙很小,理论上可以忽略不计,所以振子的总长度L=21。
对称振子的长度与波长相比拟,本身己可以构成实用天线。
在计算天线的辐射场时,经过实践证实天线上的电流可以近似认为是按正弦律分布,忽略振子损耗。
根据正弦分布的特点,对称振子的末端为电流的波节点;电流分布关于振子的中心店对称;超过半波长就会出现反相电流。
在分析计算对称振子的辐射场时,可以把对称振子看成是由无数个电流I(z),长度为dz的电流元件串联而成。
利用线性媒介中电磁场的叠加原理,对称振子的辐射场是这些电流元辐射场之矢量和。
四、实验内容利用HFSS软件设计一个近似理想导体平面的UHF 对称振子天线。
中心频率为0.55GHz,采用同轴线馈电,并考虑平衡馈电的巴伦结构。
最后得到反射系数和二维辐射远场仿真结果。
五、实验步骤.建立新工程了方便建立模型,在Tool>Options>HFSS Options中讲Duplicate Boundaries with geometry复选框选中。
微波与天线-对称阵子天线

实例分析:某型号对称阵子天线设计过程展示
馈电方式选择
采用偏心馈电方式,通过微带线 将信号引入阵子中心,实现宽带
匹配。
阵子结构设计
选择半波振子作为阵子结构,阵 子长度为1/4波长,直径为1/50 波长。阵子间距设置为1/2波长
,以获得较好的辐射特性。
设计目标
设计一款工作于2GHz频段,具 有较宽带宽和良好辐射特性的对
提高信号传输效率
对称阵子天线具有较高的辐射效 率和较宽的带宽,能够快速地将 信号辐射到空间中,从而提高信
号的传输效率。
增强信号接收能力
对称阵子天线具有较好的方向性和 增益特性,能够准确地接收来自特 定方向的信号,并增强信号的接收 能力。
降低系统成本
相对于其他类型的天线,对称阵子 天线具有较低的成本和较小的体积, 便于集成到各种通信设备中,从而 降低整个系统的成本。
偶极子天线
由两个相同且平行的半波振子 组成,具有宽频带、中等增益 和方向性可调等特点。
垂直阵子天线
由多个垂直排列的半波振子组 成,具有高增益、窄波束和垂 直面内方向性可调等特点。
环形阵子天线
由多个环形辐射元组成,具有 全向辐射、低剖面和宽频带等 特点。
微带阵子天线
利用微带传输线技术实现阵子 天线的平面化设计,具有低剖 面、轻量化和易于集成等特点 。
雷达系统
雷达系统需要实现远距离的目标探测和定位,对称阵子天线具有较好的方向性和较高的增益,能够提高 雷达系统的探测距离和定位精度。同时,对称阵子天线还能够适应各种复杂环境和气候条件,保证雷达 系统的稳定性和可靠性。
06
未来发展趋势预测与挑战分析
技术创新方向预测
01
02
03
《微波与天线》PPT课件

8.2 阵列天线
多个天线按一定方式排列所构成的系统称为天线阵,分为直线阵(超级链接)、平面阵(超 级链接)、立体阵和园环阵(超级链接)等。目前该技术的最新应用:3G移动通信上的智能 天线和相控阵天线。
1. 二元阵的辐射场
设天线阵是由间距为d并沿x轴排列的两个相同的天线元所组成, 如图下图所示。 假设天线元的电流振幅相等, 但天线元2的电流相位超前天线元1的角度为ζ, 它们 的远区电场是沿θ方向的, 于是有:
z
r′
h dz
z
r
Im h
图 8- 1 细振子的辐射
图 8 – 2 开路传输线与对称振子
令振子沿z轴放置(图 8 - 1), 其上的电流分布为 I(z)=Imsinβ(h-|z|)………………………..(第一章开路线的结论)
式中, β为相移常数, β=k= 的贡献为
在距中心2点为z处取电流元段dz, 则它对远区场 0 c
3) 主瓣宽度 当N很大时, 头两个零点之间的主瓣宽度可近似确定。令ψ01表示
第一个零点, 实际就是令上式中的m=1, 则
01
2 N
4) 旁瓣方位 旁瓣是次极大值, 它们发生在:
sin N 1 处,即
2
N (2m 1) ................(m 1,2,3,...)
2
2
第一旁瓣发生在m=1 即 ψ=±3π/N方向。
RΣ=73.1 (Ω) (与75欧同轴线几乎匹配) 将F(θ)代入式(6 -3 -8)得半波振子的方向系数:
D=1.64
(8 -1 -11)
方向图的主瓣宽度等于方程:
cos( cos )
F( ) 2
1
sin
2
(0°<θ<180°的两个解之间的夹角 )
对称振子天线

z
o sin
y
图8-2a 电流元E面方向图 z
z
y
sin 900 1
x
图8-2b电流元H面方向图
y
x 图8-2c 电流元立体 方向图
实际天线的方向图要比图8-2复杂。图8-3 为某 天线的方向图,它有很多波瓣,分别称为主瓣、副 瓣和后瓣。其中最大辐射方向的波瓣称为主瓣,其 他波瓣统称为副瓣,把位于主瓣正后方的波瓣称为 后瓣。
H 0
(8-22c)
再根据麦克斯韦方程 E 1 H,可得电流环产生
的电场为
j
E
j
I a 2k 2
4π
j
kr
1 (kr) 2
sin
e jkr
Er E 0
(8-23a) (8-23b)
对于电流环感兴趣的是其远区场,因 kr 1 , 由式(8-22)和式(8-23)得
H
I a 2k 2 4πr
方向性天线所需的辐射功率Pr
与被研究天线的辐射
0
功率 Pr 之比,即
D Pr0 Pr Emax E0
(8-10)
对于被研究的天线,其辐射功率
Pr
S
Sav
dS
S
1 2
E( ,) 2 0
dS
1 2
2 0
0
Emax
2 F 2 ( ,) r 2 sin d d 0
Emax 2 r 2
20
2
0
0
F 2 ( ,) sin d d
称为零功率波瓣宽度,用 表示2。0由图8-2可见,
电流元的主瓣宽度
2,0.5零 9功0率波瓣宽
度 2 0 180。
副瓣最大辐射方向上的功率密度与主瓣最大辐 射方向上的功率密度之比的对数值,称为副瓣电平, 用dB表示。通常离主瓣近的副瓣电平要比远的高, 所以副瓣电平通常是指第一副瓣电平。一般要求副 瓣电平尽可能低。
对称振子天线_阵列天线

kd = - b
骣 ççç桫2p
d l
÷÷÷
• 当阵的最大辐射方向在垂直于阵轴的方向上, a m = 90?
称为边射阵或侧射式天线阵。由上式可得b =0。
Emax
9
“1” “2” “3”
“N-1” “N” z
端射阵
cos a m = - b
kd = - b
骣 ççç桫2p
d l
÷÷÷
• 当阵的最大辐射方向在阵
即由相似元所构成的天线阵列的方向性函数farry()等
于各阵元单独存在时的方向性函数F(q )(元因子)和
阵方向函数fa () (阵因子)的乘积。
方向图乘积定理: farray (a) = F (q) fa (a )
应用方向图乘积定理时应注意:
❖阵元为相似元;
❖阵元的方向性函数F(q ) ,其自变量不一定等 于 ,如对称振子,其q为振子轴与射线之间 的夹角, 而为射线与阵轴的夹角;(q 不 一定等于 )
y = b + kd cos a
其阵因子是一等比级数:
å fa (a ) = 1+ e jy
+ e j2y
+ ... + e j(N- 1)y
=
N- 1
e jny
n= 0
=
sin 骣 ççç桫N2y
÷÷÷ j 1 (Ne2
1) y
sin y
2
式中1 (N 1) 为总场强的相位因子,如以阵的 中心2点作为参考点,则此因子为零。
r2 = r1 - d cos a
M
由于两阵元有:
F1(a ) = F2(a ) = F(a )
“1”
“2”
对称阵子天线
1 l 2l Z 0 ( z )dz 120(ln 1) l 0 a
(1―4―10)
z
dz
2a
l z
dz
~
O
D z z l z
~
O
dz 2a
(a )
(b )
第1章 天线基础知识
由上式可知,振子越粗,Z0A就越小。Z0A就是与其
对应的等效传输线的特性阻抗。
前面已经指出,将对称振子的辐射功率看作是一 种欧姆损耗均匀分布在天线的臂上。若设单位长度损
耗电阻为Rl,则振子上的损耗功率为 P l
l
0
1 2 I ( z ) Rl dz 2
,故
1 2 I m Rr ,应等于这个天线的辐射功率 Pr 2
D Z 0 120ln a
Z0 A
1 l 2l Z 0 ( z )dz 120(ln 1) l 0 a
第1章 天线基础知识
臂电长度的变化曲线如图1―4―7所示,对称振子越粗, 平均特性阻抗Z0A越低,对称振子的输入阻抗随 l/λ的变
化越平缓,有利于改善频带宽度。由计算结果还可以
得知,对称振子存在着一系列的谐振点。在这些谐振 点上,输入电抗为零,储存在近区中的电场和磁场无 功能量是相等的。第一个谐振点位于l/λ≈0.48处;第二 个谐振点位于l/λ≈0.8~0.9的范围内,虽然此时的输入电 阻很大,但是频带特性不好。
60 I m sin k (l z )dz jkr (1―4―2) dE j sin e r
由于上式中的r与r′可以看作互相平行,因而以从
坐标原点到观察点的路径r作为参考时,r与r′的关系为
r′≈r-zcosθ
(1―4―3)
一种具有防雷保护功能的对称振子天线设计

一种具有防雷保护功能的对称振子天线设计文章在L频段设计了一个对称振子天线,通过矩量法对天线尺寸进行了推导计算,并设计了一种特殊的馈电方式,使其在满足电性能要求的同时具备了防雷保护的功能。
仿真结果表明,天线电性能与理论设计值相符,满足水平全向的使用要求。
标签:对称振子天线;防雷保护;矩量法1 概述对称振子作为一种历史悠久的经典天线[1],具有结构简单,易于实现等特点,在雷达信标、敌我识别等领域中有着广泛应用。
在实际使用中,为了利用对称振子水平全向辐射特性,往往将对称振子垂直安装于设备平台的最高处,对称振子本身是金属件,暴露在空间中,相当于一个自然的接闪器,容易受到雷击而损坏。
针对这个问题,有文献[2]建议在天线旁架设避雷针,不失为一种有效的办法,但在具体实现中存在一定问题,比如在狭小的安装平台上应该如何处理架设距离和高度,如果避雷针过于靠近,便构成天线的单元,无论是干涉和反射都会对天线的方向性造成一定影响;如果避雷针架设过远,则会影响避雷针的保护范围,天线仍有可能受到雷击而损坏。
还有文献[3]提出为天线设计了自保护功能,从结构上给雷电在天线振子和安装架之间提供一条短接释放路径,由于90%的雷电能量分布在直流和低频,一旦发生雷击,短接释放路径可让雷电流安全入地。
这种做法保护了天线,消除了架设避雷针的不利影响,也提高了天线设计难度,目前还没有适用于对称振子的防雷设计办法,本文将提出一种防雷保护功能结合电性能设计的办法,在保证主要电性能指标的同时,从物理结构上实现对天线的防雷保护功能。
2 设计考虑关于对称振子分析和设计方法较多,最常见是运用矩量法来推导振子长短和粗细对辐射特性的影响。
运用矩量法的推导结论,选取合适的天线振子尺寸,可以保证天线振子的辐射性能,许多文献都有详细的推导,这里不再详述。
而对称振子馈电设计是实现防雷保护功能的重点,本文设计时有以下三点考虑:第一,分离高低频能量的传输路径。
通常采用图1(a)所示的传统馈电方式是不能分离高低频能量的传输路径,雷电流仅有一条传输路径,即通过芯线进入天馈线,会对馈电点或天馈线开路处造成伤害,所以分离高低频能量的传输路径是必需的。
第三讲 对称振子天线

I I m sin (h z )
在距中心点z处取dz段的电流元, 其远区场为
e jr dE j sin I m sin (h z ) dz r 60
选取振子的中心与球坐
h dz z Im h
z
r r
r′ r
r r
标系的原点重合,则
r2 r 2 z 2 2 zr cos
根据对称性,有
h I m 60 e j r E j sin sin (h z )(e j z cos +e j z cos )dz 0 r
South China University of Technology
利用积分公式
ax e ax e sin(bx c)dx a 2 b2 [a sin(bx c) b cos(bx c)]
Research Institute of Antennas & RF Techniques School of Electronic & Information Engineering
3.4 对称振子的辐射参数
对称振子的辐射功率为
South China University of Technology
3.4 对称振子的输入阻抗
近似公式:
South China University of Technology
传统的工程近似计算方法是把振子近似看作是末端 开路的有耗传输线。借助有耗传输线的阻抗公式进 行计算。对于 h 0.4的对称振子,输入阻抗为: R Zin jZ 0 cos h 2 sin h
3.3 对称振子的方向图
令细振子沿z 轴放置, 其上的电
微波技术与天线第6章复习

第6章1、简述天线的功能(概念+4个功能)在无线通信系统中,需要将来自发射机的导波能量转变为无线电波,或将无线电波转变为导波能量,原来辐射和接收无线电波的装装置称为天线。
①天线应能将导波能量尽可能多地转变为电磁波能量.这首先要求天线是一个良好的电磁开放系统, 其次要求天线与发射机或接收机匹配.②天线应使电磁波尽可能集中于确定的方向上, 或对确定方向的来波最大限度的接受, 即天线具有方向性.③天线应能发射或接收规定极化的电磁波, 即天线有适当的极化.④天线应有足够的工作频带.2、名词解释:什么是天线?①作用:在发射部分,将高频导行波转换为空间电波,在接收端,空间电波转换为导行波。
②性能:是能量转换器件、具有定向辐射能力、频率选择特性、极化特性。
③结构:开放。
3、把天线和发射机或接收机连接起来的系统为馈线系统,天线和馈线系统统称天线馈线系统,简称天馈系统。
4、点电基本振子近区场又为准静态场;离天线较远时,近似为0;电场磁场相位差90°,为感应场。
远区场中电基本振子的的远区场是沿着径向外传的横电磁波,远区场又称辐射场。
E/H=120pi,远区场具有与平面波相同的特性。
随着距离增加,辐射场减小。
4、电,磁基本振子具有相同的方向函数,空间相互正交,相位差90°5、天线的电参数有哪些?①主瓣宽度:主瓣宽度是衡量天线的最大辐射区域的尖锐程度的物理量。
在场强方向图中,等于最大场强两点间的宽度,称为半功率波瓣宽度;或将头两个零点之间的角度作为主瓣宽度,即零功率波瓣宽度。
②旁瓣电平: 旁瓣电平是指离主瓣最近且电平最高的第一旁瓣电平, 一般以分贝表示。
③前后比: 前后比是指最大辐射方向(前向)电平与其相反方向(后向)电平之比, 通常以分贝为单位。
④方向系数:方向系数定义为: 在离天线某一距离处, 天线在最大辐射方向上的辐射功率流密度Smax与相同辐射功率的理想无方向性天线在同一距离处的辐射功率流密度S0之比,记为D, 即天线方向系数的一般表达式为6、要使天线方向系数大,不仅要求主瓣窄,还要全空间的旁瓣电平小。
对称振子天线课程设计

对称振子天线课程设计一、课程目标知识目标:1. 学生能理解对称振子天线的概念、原理和应用;2. 学生能掌握对称振子天线的阻抗特性、辐射特性及影响参数;3. 学生能运用相关公式计算对称振子天线的长度及间距。
技能目标:1. 学生能运用所学知识,分析对称振子天线的性能,并进行优化设计;2. 学生能通过实际操作,制作并测试对称振子天线;3. 学生能运用相关软件(如CST、HFSS等)进行对称振子天线的仿真分析。
情感态度价值观目标:1. 学生培养对无线电通信及天线技术的兴趣,增强对物理学科的学习热情;2. 学生通过团队协作,培养沟通、合作能力,增强集体荣誉感;3. 学生在学习过程中,培养严谨、细致的科学态度,提高解决问题的能力。
课程性质:本课程为高二年级物理选修课程,旨在让学生了解对称振子天线的基本原理和实际应用,提高学生的实践能力和创新能力。
学生特点:高二学生对物理学科有一定的基础,具备一定的分析、计算能力,对实际操作和新技术具有浓厚兴趣。
教学要求:结合学生特点,注重理论与实践相结合,充分调动学生的积极性,提高学生的动手能力和创新能力。
在教学过程中,将目标分解为具体的学习成果,便于后续教学设计和评估。
二、教学内容1. 引入对称振子天线的基本概念,介绍其发展历程及应用领域;相关教材章节:第三章第1节“天线的基本概念与发展”2. 讲解对称振子天线的原理、结构特点及分类;相关教材章节:第三章第2节“对称振子天线的基本原理与结构”3. 详细阐述对称振子天线的阻抗特性、辐射特性及影响参数;相关教材章节:第三章第3节“对称振子天线的阻抗与辐射特性”4. 探讨对称振子天线的优化设计方法,包括长度、间距等参数的调整;相关教材章节:第三章第4节“对称振子天线的优化设计”5. 实践操作:指导学生制作对称振子天线,并进行测试;相关教材章节:第三章第5节“对称振子天线的制作与测试”6. 介绍相关软件(如CST、HFSS等)在对称振子天线仿真分析中的应用;相关教材章节:第三章第6节“对称振子天线的计算机仿真”7. 分析实际应用案例,让学生了解对称振子天线在现代通信系统中的作用;相关教材章节:第三章第7节“对称振子天线的应用实例”教学内容安排与进度:1. 第1课时:引入对称振子天线的基本概念、发展历程及应用领域;2. 第2课时:讲解对称振子天线的原理、结构特点及分类;3. 第3课时:详细阐述对称振子天线的阻抗特性、辐射特性及影响参数;4. 第4课时:探讨对称振子天线的优化设计方法;5. 第5课时:实践操作,制作对称振子天线并进行测试;6. 第6课时:介绍相关软件在对称振子天线仿真分析中的应用;7. 第7课时:分析实际应用案例,总结本章节内容。
微波及天线考查报告任务书(第二版)刘学观

《微波与天线技术》课程考查报告任务书专业:通信工程班级:OX姓名:OOXX学号:XXOO二零一三年一月课程内容总结本书共分为十章,包括微波技术、天线与电波传播和微波应用系统三个部分。
第一至五章为微波技术部分,主要讨论了均匀传输线理论、规则金属波导、微波集成传输线、微波网络基础和微波元器件,其中在微波集成传输线部分主要讨论了带状线、微带线、耦合微带线及介质波导的传输特性,并对光纤的传输原理及特性做了介绍;在“微波元器件”一章中,从工程应用的角度出发,重点介绍了具有代表性的几组微波元器件,主要包括连接匹配元件、功率分配元器件、微波谐振元件和微波铁氧体器件。
第六至九章为天线与电波传播部分,主要叙述了天线辐射与接收的基本理论、电波传播概论、线天线及面天线,其中在线天线部分侧重介绍了在工程中常用的鞭天线、电视天线、移动通信基站天线、行波天线、宽频带天线、微带天线等,还对智能天线技术做了简要介绍。
微波应用系统安排在第十章,主要讨论了雷达系统、微波通信系统级微波遥感系统三个典型系统。
上述三部分既相互联系有相互独立,下面将做详细说明。
微波技术部分一、均匀传输线理论1、均匀传输方程及其解(1)均匀传输线方程⎪⎪⎭⎪⎪⎬⎫==++)()_()()_(i u z I z I Γz U z U Γ 对于时谐振电压和电流,可得时谐传输线方程式中,L j R Z ω+= C j G Y ω+= 分别称为传输线单位长串联阻抗和单位长并联导纳。
(2)均匀传输线方程的解z sh Z I z ch U z U γγ011)(+= z sh Z Uz ch I z I γγ011)(+=(3)传输线的工作特性参数特性阻抗0Z ;传播常数γ;相速p ν与波长λ。
2、传输线阻抗与状态参量(1)输入阻抗: 对无耗均匀传输线, 线上各点电压U(z)、 电流I(z)与终端电压U1、终端电流Il 的关系如下:(2)反射系数: 传输线上任意一点z 处的反射波电压(或电流)与入射波电(或电流)之比为电压(或电流)反射系数, 即:(3)输入阻抗与反射系数的关系 )](1[)()()(1z e A z U z U z U z j Γ+=+=-+β )](1[)()()(01_z e Z A z I z I z I zj Γ-=+=+β tt z u C t z Gu z t z i ∂∂+=∂∂),(),(),(t t z i L t z Ri zt z u ∂∂+=∂∂),(),(),()()(z YU dzZ dI =)()(z ZI dzZ dU =⎪⎭⎪⎬⎫+=+=)sin(j )cos()()sin(j )cos()(011011z Z U z I z I z Z I z U z U ββββ3、无线传输线的状态分析无线传输线有以下三种工作状态:①行波状态;②纯驻波状态;③行驻波状态。
各种天线概念解析

螺旋天线是一种具有螺旋形状的天线。
它由导电性能良好的金属螺旋线组成,通常用同轴线馈电,同轴线的心线和螺旋线的一端相连接,同轴线的外导体则和接地的金属网(或板)相连接。
螺旋天线的辐射方向与螺旋线圆周长有关。
当螺旋线的圆周长比一个波长小很多时,辐射最强的方向垂直于螺旋轴;当螺旋线圆周长为一个波长的数量级时,最强辐射出现在螺旋旋轴方向上。
全向天线全向天线,即在水平方向图上表现为360°都均匀辐射,也就是平常所说的无方向性,在垂直方向图上表现为有一定宽度的波束,一般情况下波瓣宽度越小,增益越大。
全向天线在移动通信系统中一般应用与郊县大区制的站型,覆盖范围大。
机械天线所谓机械天线,即指使用机械调整下倾角度的移动天线。
电调天线所谓电调天线,即指使用电子调整下倾角度的移动天线。
施主天线移动基站BTS用的一种收发天线.也就是收发到用户(手机)的天线。
不定向天线在各个方向上均匀辐射或接收电磁波的天线,称为不定向天线,如小型通信机用的鞭状天线等。
V形天线是由彼此成一角度的两条导线组成,形状象英文字母V的一种天线。
其结构如图4所示,它的终端可以开路,也可以接有电阻,其电阻的大小等于天线的特性阻抗。
V形天线具有单向性,最大发射方向在分角线方向的垂直平面内。
它的缺点是效率低、占地面积大。
介质天线介质天线是一根用低损耗高频介质材料(一般用聚苯乙烯)作成的圆棒,它的一端用同轴线或波导馈电。
图15所示的天线是用同轴线馈电的棒状介质天线。
图中1是介质棒;2是同轴线的内导体的延伸部分,形成一个振子,用以激发电磁波;3是同轴线;4是金属套筒。
套筒的作用除夹住介质棒外,更主要的是反射电磁波,从而保证由同轴线的内导体激励电磁波,并向介质棒的自由端传播。
介质天线的优点是体积小,方向性尖锐;缺点是介质有损耗,因而效率不高。
开槽天线在一块大的金属板上开一个或几个狭窄的槽,用同轴线或波导馈电,这样构成的天线叫做开槽天线,也称裂缝天线。
3 对称振子 天线原理

得
式中
60 I m j r E j e F ( ) r
F ( ) cos( h cos ) cos h sin
为对称振子的归一化场强方向图函数。
Research Institute of Antennas & RF Techniques School of Electronic & Information Engineering
根据对称性,有
h I m 60 e j r E j sin sin (h z )(e j z cos +e j z cos )dz 0 r
South China University of Technology
利用积分公式
ax e ax e sin(bx c)dx a 2 b2 [a sin(bx c) b cos(bx c)]
I I m sin (h z )
在距中心点z处取dz段的电流元, 其远区场为
e jr dE j sin I m sin (h z ) dz r 60
选取振子的中
r
r′
标系的原点重合,则
r2 r 2 z 2 2 zr cos
3.1 引言
对称振子(也称偶极子,dipole):两根粗细和
South China University of Technology
长度都相同的导线, 中间为馈电端口。 连接收发机与天线馈电端口的传输线把高频电流 输送到天线上,该传输线称为天线的馈线(feed line) 。 对称振子是一种结构最简单、应用最广泛的基本 线天线,可以看作开路的双导线演变而来:
对于相位因子,取近似
平行线 的程差
HFSS仿真对称阵子天线

基于HFSS 的对称阵子天线仿真一、对称阵子天线概述 对称阵子天线是最基本也是最常用的天线形式。
对于中心点馈电的对称振子天线,其结构可看做是一段开路传输线张开而成。
馈电时,在对称振子两臂产生高频电流,此电流将产生辐射场。
可以将对称振子分成无数小段,每一小段都可以看成电基本振子,则对称振子辐射场就是这些无数小段电基本振子辐射场的总和。
由于结构简单,对称振子广泛应用于雷达、通信、电视和广播等无线电技术设备中。
对称振子的工作频率从短波波段到微波波段。
它既可作为独立的天线使用,也可以作为天线阵基本单元组成线阵或平面阵,还可以作为反射面天线的馈源。
二、天线参数对称阵子天线主要有输入阻抗,反射系数,回波损耗这几个重要参数。
图1为用MATLAB 仿真得出的半波对称阵子的E 面方向图。
输入阻抗in in in jX R Z +=,反射系数00Z Z Z Z in in +-=Γ,回波损耗Γ=lg 20RL 。
图1 理论E面方向图三、仿真过程对称阵子天线模型由几部分组成:两臂、馈电、辐射箱。
对称阵子的两臂为圆柱体,材料为理想导体,半径为变量r,臂长为变量l。
对称阵子一般通过同轴馈电,可以看作在振子的两臂之间施加了及总电压。
在用HFSS仿真时通过一个平面连接两臂,在平面上设置激励源来实现。
通过建立辐射箱,表面设置吸收边界条件来模拟无界空间。
依据这些要点建立了对阵振子天线模型,如图2。
图2 对称阵子天线模型四、结果分析图3为阻抗曲线图,深色为实部,浅色为虚部,模拟情况与理论值接近。
图4为端口2匹配时端口1的反射系数。
条件设定为r=1mm,l=25mm,即半波对称阵子。
比较图3和图4,可以得出在2.6GHz处反射系数最低,端口阻抗值约为50Ω,此为半波对称阵子天线的谐振频率。
图3 阻抗曲线图4 S11曲线图5为对称阵子天线的三维方向图,可以得出对称阵子的辐射场关于天线轴向对称。
图5 三维方向图图6是对称阵子的E面方向图,此方向图画出的是天线总增益的绝对值,与理论值接近。
方向性与方向图,85线天线与天线阵PPT课件

sin
cos
)
sin
二元阵的辐射场
E
E1
E 2
j
60 I1 r1
cos( cos )
2
e- j
r
1
sin
( 1 mej )
其中 d sin cos为点P 处 E和1 E的 2相位差
第8页/共23页
P(r1 , ,)
y
(r1sin
,
2
, )
二元天线阵场强的模:
E
60 I1 r1
cos( cos )
2
sin
1 mej
60 I1 r1
F ( 1
,
)
F12 (
)
元因子
cos( cos )
F1( , )
2
sin
元因子为半波振子天线的归一化方向函数,只与振子本身的结构和
取向有关。
阵因子
F12( , ) 1 mej (1 m2 2mcos )1 2
1 m2 2mcos( dsin cos) 1 2
z
E1
j
60I1 r1
cos( cos 2 sin
) e- j r1
E 2
j
60I2 r2
cos( cos 2 sin
)
e-
j
r 2
1 d 2
r1
r2
x
作近似处理 r2 r1 d sin cos , d sincos: 波程差
则
E
2
j
60m I1e j r1
cos( cos )
2
e-
j
(
r
1
-
d
( )
H () H ()max
汽车收音机天线的参数

汽车收音机天线的参数天线的参数短波通信是指波长100-10米(频率为3-30MHz)的电磁波进行的无线电通信。
短波通信传输信道具有变参特性,电离层易受环境阻碍,处于不断变化当中,因此,其通信质量,不如其它通信方式如卫星、微波、光纤好。
短波通信系统的成效好坏,要紧取决于所使用电台性能的好坏和天线的带宽、增益、驻波比、方向性等因素。
近年来短波电台随着新技术提高进展专门快,实现了数字化、固态化、小型化,但天线技术的进展却较为滞后。
由于短波比超短波、卫星、微波的波长长,因此,短波天线体积较大。
在短波通信中,选用一个性能良好的天线关于改善通信成效极为重要。
下面简单介绍短波天线如何选型和几种常用的天线性能。
一、衡量天线性能因素天线是无线通信系统最差不多部件,决定了通信系统的特性。
不同的天线有不同的辐射类型、极性、增益以及阻抗。
1.辐射类型:决定了辐射能量的分配,是天线所有特性中最重要的因素,它包括全向型和方向型。
2.极性:极性定义了天线最大辐射方向电气矢量的方向。
垂直或单极性天线(鞭天线)具有垂直极性,水平天线具有水平极性。
3.增益:天线的增益是天线的差不多属性,能够衡量天线的优劣。
增益是指定方向上的最大辐射强度与天线最大辐射强度的比值,通常使用半波双极天线作为参考天线,其它类型天线最大方向上的辐射强度能够与参考天线进行比较,得出天线增益。
一样高增益天线的带宽较窄。
4.阻抗和驻波比(VSWR):天线系统的输入阻抗直截了当阻碍天线发射效率。
当驻波比(VSWR)1:1时没有反射波,电压反射比为1。
当VSWR大于1时,反射功率也随之增加。
发射天线给出的驻波比值是最大承诺值。
例如:VSWR为2:1时意味着,反射功率消耗总发射功率的11%,信号缺失0.5dB。
VSWR为1.5:1时,缺失4%功率,信号降低0.18dB。
二、几种常用的短波天线1.八木天线(YagiAntenna)八木天线在短波通信中通常用于大于6MHz以上频段,八木天线在理想情形下增益可达到19dB,八木天线应用于窄带和高增益短波通信,可架设安装在铁塔上具有专门强的方向性。
2.天线的方向图(1)

31
《天线原理与设计》讲稿
王建
这种场称为感应场,所以近场区又称作感应场区。在此区域内无功功率占主导地 位。因 β r 1 ,可令 e − jβ r ≈ 1 ,则该区中的电磁场表示式(1.5a)~(1.5d)与恒定电流 元的场完全相同。
2. 中场区( β r > 1 )
随着 β r 值的逐渐增大, 当其大于 1 时, 式(1.4)中 β r 高次幂的项将逐渐变小, 最后消失。如果要计算该区中的电磁场,则可取式(1.4)中各场量的前两项。为分 析的方便,可取各场量的第一项即可。 β Idz Hϕ j sin θ e − jβ r (1.7a) 4π r β Idz sin θ e − jβ r (1.7b) Eθ jη0 4π r Idz E r η0 cosθ e − jβ r (1.7c) 2 2π r
(1.4)
式中, E 为电场强度; H 为磁场强度;下标 r 、θ 、ϕ 表示球坐标系中的各分量。 自由空间媒质的介电常数为 ε 0 = 8.854 × 10−12 F / m 10−9 / 36π F / m ; 磁导率为 µ0 = 4π × 10−7 H / m ; 相位常数 β = 2π / λ ; λ 为自由空间媒质中的波长; η0 = µ0 / ε 0 为媒质中波阻抗,在自由空间中η0 = 120π Ω ; ˆ 之间的夹角。 θ 为天线轴与矢量 r 由此式,我们可根据场点的距离按场区写出基本振子的电磁场。
点的球面,即相位方向图是一个球面。
(4) 电场 Eθ 分量与磁场 Hϕ 分量的比值等于媒质中的波阻抗。
Eθ = η0 Hϕ
(1.11)
(5) 适当建立坐标系, 使基本振子轴与 z 轴重合, 则其辐射场只与 θ 角有关, 与ϕ 角无关。即基本振子的辐射场是旋转对称的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∵a为场点与z轴的夹角:
cos a = cos q
p (1 + cos q) 1 sin 轾 臌 Farray (a ) = Fa (a ) = N sin 轾 p (1 + cos q) / 4 臌
XOZ面:(f =0゜)
p (1 + cos q) 1 sin 轾 臌 Fa (a ) = 4 sin 轾 p (1 + cos q) / 4 臌
p (1 + cos q) 1 sin 轾 臌 Farray (a ) = Fa (a ) = N sin 轾 p (1 + cos q)/ 4 臌
XOY面:(q =90゜)
Farray (a ) = Fa (a ) = 0
如果阵元为电基本振子且 振子与x轴平行则有
f 0 (q ⅱ ) = sin(q )
M
骣 Ny ÷ 其幅值为: sin ç ÷ ç ç 桫2 ÷ f a (a ) = y sin 2
“1”
“2” d d
“3”
“N-1”
“N”
z
式中:
y = b + kd cos a
Iej0
j2 b Iejb Ie ... Iej(N-2)b
Iej(N-1)b
d
当 =0时,阵元在M点所产生的场同相叠加, 故场强最大。 骣 çNy ÷ 对上式取极限:
D ~ l / l 曲线
D=
120 f max RS
2
D =1.65
§5.5 天线阵列与方向图乘积定理
M
1.方向图乘积定理
二元阵列天线,其阵元的结构及 尺寸相同。两元的距离为d,电流 分别为I1和I2,
“1”
r1
d “2”
r2
z
I 2 = mI1e
jb
二元阵
这里m为两电流振幅比,b 为两电流的相位差。
2l =0.1l
0. 5l
1l
1.25l
1.5l
2l
分析对称振子天线的方向图(E面)可以看出: ① l <0.5l 时,随着振子长度的增加,其方向图波瓣变尖锐, 其最大辐射方向在q =90º ,无副瓣; ②当l >0.5l 时,开始出现副瓣, 但最大辐射方向仍在q =90º 的方向上; ③当l >0.625l 时,最大辐射方向将偏离q =90º 的方向;(当l ④当l =l时,天线上的反向电流与正向电流相同,故在q =90º 上场将完全抵消,其总场为零,但在q =60º 的方向上,由于 场的行程差引起的相位差和电流的相位差互相抵消,从而 形成场的最大值。
其阵因子是一等比级数:
f a (a ) = 1 + e jy + e j 2y + ... + e j ( N - 1) y =
å
e jny
骣 Ny sin ç ç ç 桫2 = y sin 2
÷ ÷ ÷ j 1 ( N - 1) y e 2
式中1 ( N 1) 为总场强的相位因子,如以阵的 2 中心点作为参考点,则此因子为零。
对于距离天线很远的观察点M而言,阵元1和 2到M点的射线相互平行,则:
r2 = r 1 - d cos a
M
由于两阵元有:
F1 (a ) = F2 (a ) = F (a )
对于阵元1在M点产生的场:
“1”
d
“2”
z
E1 = E1m F (a ) = E10 F (a )e
则阵元2在M点所产生的场为:
x x r cos q ¢= = ? R r R cos j sin q
1 2 / 2 e j e j 3 / 2
H面为yoz面 E面为xoz面
j = 90?
FH 1
j = 0?
FE cos q
E面阵列方向性
sin 轾 p (1+ cos q) 臌 f array (a ) = f0 fa = cos(q) sin 轾 p (1+ cos q) / 4 臌
I
对称振子的电流分布
ì I m sin a(l - z ) ï ï Iz = í ï ï î I m sin a(l + z )
l =1l, 2l =2l l =0.6l,2l =1.2l l =0.5l, 2l =1l 全波振子 l =0.25l,2l =0.5l 半波振子 l =0.05l, 2l =0.1l 电小天线
z z
0 0
对称振子的方向图
F (q) =
f (q) f max
=
1 f max
cos(kl cos q) - cos kl sin q
对称振子的方向图随它的电长度而变化,(对于 固定长度的天线,其方向图随频率而变)
0.1l的对称振子 的方向图 0.5l的对称振子 的方向图 l =0.25l 1l的对称振子 2l的对称振子 的方向图 的方向图 l =0.5l l =1l 1.25l的对称振子 的方向图 1.5l的对称振子 l =0.625l 的方向图 l =0.75l
方向图乘积定理:
farry (a) = F (a ) fa (a )
即由相似元所构成的天线阵列的方向性函数farry()等 于各阵元单独存在时的方向性函数F(q )(元因子)和 阵方向函数fa () (阵因子)的乘积。
方向图乘积定理: f array (a) = F (q) f a (a )
应用方向图乘积定理时应注意:
m鬃 E10 F (a )e
jy
e
jb
e
jkd cos a
= mE1m F (a )e
M点的合成场强为
E = E1 + E2 = E1m F (a )(1+ me jy )
式中
y = b + kd cos a
f a (a ) = 1+ me
jy
令
则上式可:
阵因子
E = E1m F (a ) fa (a ) = E1m farry (a )
- jkr 1
与电流成正比
jb
E2 = E2 m F (a ) = E20 F (a )e = mE10 e ?F (a )e = mE1m F (a )e
jb j ( b + kd cos a )
- jkr2
= mE10 e
F (a )e
- jkr1
- jkr2
- jkr1 + jkd cos a
§5.4 对称振子
对称振子:由两根大小相 同的导线或金属棒组成 对于开路线:电流分布 故对称振子的电流分布应有: 1.电流分布应为连续(除馈电点外,连 续),振子终端应为电流节点。 2.由于开路,电流形成驻波分布,为正弦 状态,每个周期的长度为一个波长。 3.电流分布对称。 4.两臂上相对应点的电流方向为同向。
阵元为相似元;
阵元的方向性函数F(q ) ,其自变量不一定等 于 ,如对称振子,其q为振子轴与射线之间 的夹角, 而为射线与阵轴的夹角;(q 不 一定等于 )
方向图乘积定理适用于多元阵;
如果F(q )=1 ,为理想点源,则farry()fa ()
M
2.均匀直线阵
N元均匀直线 阵应满足:
E =
å
N
Ei
i= 1
由于阵元的结构一致,故其场的方向函数一致, 场的振幅可用标量表示:
E=
jy j 2y j ( N - 1) y E = E [1 + e + e + ... + e ] = E1 邋i 1 i= 1 N N- 1 n= 0
e jny
式中:
y = b + kd cos a
N- 1 n= 0
“1” “2” “3” “N-1” “N” z
Iej0
Ie
d
jb
Ie
d
j2 b
... Iej(N-2)b
d
Ie
j(N-1)b
① N个阵元排列在一直线上; ② 各元的电流幅度相等(I1=I2=…=In=I); ③ 相邻元的间距相等(d); ④ 电流的相位依次递增(相邻元相位相差b )
由叠加定理:
p
[cos(kl cos q) - cos kl ]
sin q
2
0
dq
RS m = 73.1(W )
RS m 籛200( )
RS 0 » 20(kl )2
l < 0.1 l
对称振子 RS m ~ l / l 曲线
辐射阻抗
半波对称振子: ZS m = 73.1+ j 42.5(W )
方向系数
半波振子天线:
f ma =
lim
y®0
sin ç ÷ ç 桫2 ÷ = N y sin 2
则均匀线阵的归一 化方向函数为:
Fa (a ) =
骣 Ny ÷ sin ç ÷ ç ç f a (a ) 1 桫2 ÷ = y f max N sin 2
Fa (a )
骣 Ny ÷ sin ç ÷ ç ç 桫2 ÷ 1 Fa (a ) = N sin y 2
N=2 N=10 N=20 N=3 N=4 N=5
均匀线阵的归 一化方向图
若要求均匀直线阵在 =m方向产生最大辐射 由 y = b + kd cos a = 0 Emax
b = - kd cos a m
相位差 阵元间距的电长度
骣 d÷ cos a m = - b kd = - b ç 2p ÷ ç ç 桫 l ÷
b =0
b =kd
例:四个无方向性点源排列如图,阵子的间距为 d = l / 4
求天线阵的方向性(XOY,XOZ平面的方向图)。 解: d = l / 4;
