第二章 单级平衡过程(化工分离过程)
合集下载
化工分离工程第2章 单级平衡过程
FLGC
• 活度系数法通式
fˆi L
i
xi
fiL
i
xi
is
Pi s
expVi L
(P RT
Pi s
)
yiˆiv
P
i
xiis Pi s
expVi L
(P RT
Pi s
)
i 1,2,, N
低压至中压
expVi
L
(P RT
Pi
s
)
1
yiˆiv P
xi
s
ii
Pi
s
i 1,2,, N
(2-7)
11
FLGC
两种常用的汽液相平衡关系表达式：
(2-5)式和(2-6)式代入（2-4），得 ˆiV yi p ˆiL xi p (2-5)式和(2-7)式代入（2-4），得 ˆiV yi p i xi fiOL
12
FLGC
二、相平衡关系的表示方法：
1. 相图 yi
主要用来表示二元组分体系的相 平衡关系，包括恒压下的t-x图和 y-x图，以及恒温下的p-x图。
i
④判定 | 1 S y | 是否接近0，是，得到Tb=T和Ki；否，按以下方式调整
T。
⑤ S y 1，T偏大，调小； S y 1，T偏小，调大；调整后返回②。
FLGC
一、泡点温度的计算
1. Ki与组成无关： Ki f (T, P)
泡点方程：
f
T
C
Ki xi
1
0
i 1
假定T
已知P 得到Ki 调整T
3
FLGC
• 相平衡，是研究多相平衡体系的状态如何随温度、 压力、组成的变化的科学。
化工分离过程胡大乔第2章单级平衡过程2
b0.08R 6c7 T pc
范围进行比较。
Soave-Redlich-Kwong (SRK or RKS)
p RT a
Vb V(Vb)
0 .5 1 ( 1 T r 0 .5 )0 .4 ( 1 8 .50 7 0 .1 42 7 ) 6
a0.42R 72T 8 c52 pc
b0.08R 6c7 T pc
ˆ iL ˆ Vi
应用状态方程分别计算汽、液两相的逸度系数。
2.1.1 汽液平衡 Vapor-liquid equilibria
At vapor-liquid equilibrium, fˆiV fˆiL
Activity coefficient of i species in a liquid phase is defined by:
equal to its partial pressure, pi yi p .
Dalton’s law
2.1.1 汽液平衡 Vapor-liquid equilibria源自Case 3---真实混合物
用逸度系数或活度系数计算逸度
For a real mixture, partial fugacity coefficients are defined by
Van der waals方程：
V t3 (b R P )V T t2 a p V t a p b 0 1
——a、b为Van der waals常
数
混合物：
纯组分i：
ai 27R2Tc2,i
64Pc,i
bi RTc,i 8Pc,i
c
a ( yi i1
c
b yibi i1
i
fˆi L xi fˆi 0 L
化工分离过程ppt
自由度数与
相律：f c 2 c 2 2 c
组分数相当
计算类型 泡点温度 泡点压力 露点温度 露点压力
规定量（c个）
P, x1, x2 ,xc1 T , x1, x2 ,xc1 P, y1, y2 ,yc1 T , y1, y2 ,yc1
求解量 T , y1, y2,yc P, y1, y2,yc T , x1, x2 ,xc P, x1, x2 ,xc
2. lnPiS=Ai-Bi/(t+Ci)
3. 常压操作 解法1：用试差法计算
Ki Pi S
c
P ; Ki xi 1 i 1
T(设) ∑Kixi
70℃ 0.379
110℃ 1.344
98℃ 0.951
100℃ 1.00
15
2.2.1 泡点温度和压力的计算
解法2：用αiK计算（不试差，适用于完全理想系）
露点温度是在一定压力下降低温度，当出现第一个液滴 时的温度，露点压力是在一定温度下增加压力，当出现 第一个液滴时的压力。
5
泡点和露点的意义
泡点温度:一定组成的液体，在恒压下加热的过程中，出现第一个气泡时的温 度，也就是一定组成的液体在一定压力下与蒸汽达到汽液平衡时的温度。
露点温度:一定组成的汽体，在恒压下冷凝的过程中，出现第一个液滴时的温 度，也就是一定组成的蒸汽在一定压力下与液相达到汽液平衡时的温度。
c
f P Ki xi 1 0 i 1
11
2.2.1 泡点温度和压力的计算
1. 平衡常数与组成无关的泡点温度计算
Ki f (T , P)
泡点方程：
c
f T Ki xi 1 0 i 1
化工分离过程第二章
18
yi yj
2.1.2 相平衡常数的计算
ˆ 计算K——状态方程法 一、根据逸度系数
ˆ V V y P 汽相： f i i i
ˆ L L x P 液相： f i i i
yi iL 相平衡常数： Ki V xi i
(2-14)
关键: 选择一 个既适用于汽 相、又适用于 液相的状态方 程。
式中：fi0V 在系统温度和压力下纯组分i的气相逸度 γiV 组分i的气相活度系数 φi0V在系统温度和压力下，纯组分i的气相逸度系数 φiV 在系统温度和压力下，组分i的气相分逸度系数且
V 0V V ˆ i i i
9
同样，液相逸度与液相组成的关系为：
ˆ L f 0L L x P 0L L x P ˆL x f i i i i i i i i i
式中的逸度系数可从该物质的p-V-T（状态方程）关系或 实测数据计算。逸度系数通过状态方程计算： 此法适用于中压下，液相非理想性不是很强的烃类系统。
19
由热力学原理可以推导出以下表达式：
以V为自变量பைடு நூலகம்
RT 1 P ˆ lni dVt lnZ m v RT ni T ,V ,n Vt j
应用：已知 T，P，xi , yi ( i 1, 2, 求
V i
c)
26
L i
步骤：
输入：T、P、Tc、i、Pc、i，xi、yi
i=1
i） (1)式求V（ t （i） (2)式求Z M ˆ（i） (3)式求 i
i=i+1
i=1
Yes No
V L ˆ ˆ 输出 i 或 i
注意：
● i=1时求汽相逸度系数；i=2时求液相逸度系数。
yi yj
2.1.2 相平衡常数的计算
ˆ 计算K——状态方程法 一、根据逸度系数
ˆ V V y P 汽相： f i i i
ˆ L L x P 液相： f i i i
yi iL 相平衡常数： Ki V xi i
(2-14)
关键: 选择一 个既适用于汽 相、又适用于 液相的状态方 程。
式中：fi0V 在系统温度和压力下纯组分i的气相逸度 γiV 组分i的气相活度系数 φi0V在系统温度和压力下，纯组分i的气相逸度系数 φiV 在系统温度和压力下，组分i的气相分逸度系数且
V 0V V ˆ i i i
9
同样，液相逸度与液相组成的关系为：
ˆ L f 0L L x P 0L L x P ˆL x f i i i i i i i i i
式中的逸度系数可从该物质的p-V-T（状态方程）关系或 实测数据计算。逸度系数通过状态方程计算： 此法适用于中压下，液相非理想性不是很强的烃类系统。
19
由热力学原理可以推导出以下表达式：
以V为自变量பைடு நூலகம்
RT 1 P ˆ lni dVt lnZ m v RT ni T ,V ,n Vt j
应用：已知 T，P，xi , yi ( i 1, 2, 求
V i
c)
26
L i
步骤：
输入：T、P、Tc、i、Pc、i，xi、yi
i=1
i） (1)式求V（ t （i） (2)式求Z M ˆ（i） (3)式求 i
i=i+1
i=1
Yes No
V L ˆ ˆ 输出 i 或 i
注意：
● i=1时求汽相逸度系数；i=2时求液相逸度系数。
化工分离过程
系数 ˆiL
( 7 ) 由 Ki ˆiL ˆiV 求取 Ki
例题
［例2-1］计算乙烯在311K和3444.2kPa下的汽液平衡常数 (实测值KC2=1.726)。
解： （1）理想气体+理想溶液
fˆiV pyi
fˆiL pis xi
Ks C2
yi xi
ps C2 p
9117.0 2.647 3444.2
溶质的活度系数基准态定义为：
xi
0,
* i
1
不对称型 标准化方法
ˆiV
相平衡常数：
Ki
yi xi
i fiOL ˆiV P
？求取液相活度系数
2、液相活度系数 i：
活度系数i由过剩自由焓GE推导得出：
Excess free energy:
c
G E f ( i ) ni RT ln i i 1
设 pA*和 pB*分别为液体A和B在指定温度时的饱和蒸 气压，p为体系的总蒸气压
pA
p* A
xA
pB pB* xB pB* (1 xA )
p pA pB p*AxA pB* (1 xA )
pB* ( p*A pB* )xA
（2）p-x-y 图
这是 p-x 图的一种，把液相组成 x 和气相组成 y 画在 同一张图上。A和B的气相组成 yA 和 yB 的求法如下：
对象： 处于不同相态 分离依据：利用两相平衡组成不等的原理
B、速率控制分离 包括：膜分离（如反渗透 RO、超滤 UF、微滤 MF ）；
场分离（如电泳） ； 对象： 处于同一相态 分离依据：利用各组分传质速度的差异
我们要重点掌握的是传质分离中的平衡分离
三、发展趋势 1）传统分离技术改造：
( 7 ) 由 Ki ˆiL ˆiV 求取 Ki
例题
［例2-1］计算乙烯在311K和3444.2kPa下的汽液平衡常数 (实测值KC2=1.726)。
解： （1）理想气体+理想溶液
fˆiV pyi
fˆiL pis xi
Ks C2
yi xi
ps C2 p
9117.0 2.647 3444.2
溶质的活度系数基准态定义为：
xi
0,
* i
1
不对称型 标准化方法
ˆiV
相平衡常数：
Ki
yi xi
i fiOL ˆiV P
？求取液相活度系数
2、液相活度系数 i：
活度系数i由过剩自由焓GE推导得出：
Excess free energy:
c
G E f ( i ) ni RT ln i i 1
设 pA*和 pB*分别为液体A和B在指定温度时的饱和蒸 气压，p为体系的总蒸气压
pA
p* A
xA
pB pB* xB pB* (1 xA )
p pA pB p*AxA pB* (1 xA )
pB* ( p*A pB* )xA
（2）p-x-y 图
这是 p-x 图的一种，把液相组成 x 和气相组成 y 画在 同一张图上。A和B的气相组成 yA 和 yB 的求法如下：
对象： 处于不同相态 分离依据：利用两相平衡组成不等的原理
B、速率控制分离 包括：膜分离（如反渗透 RO、超滤 UF、微滤 MF ）；
场分离（如电泳） ； 对象： 处于同一相态 分离依据：利用各组分传质速度的差异
我们要重点掌握的是传质分离中的平衡分离
三、发展趋势 1）传统分离技术改造：
2单级平衡分离过程
9
泡点温度与泡点压力计算的难易比较分析 由于系统设计变量指定的不同，泡点温度与泡点压力的计 算在解法上的难易也就有所区别。这是因为不同的变量对 系统状态及其物性参数所产生的影响不同所至。 泡点计算的设计变量为c个，除（c-1）组成已知外，还需 给定温度或压力。T、P这两个变量对共同变量中的物性参 数Ki（或i和Pi等）影响最大，而且，其中有些参数本身的 关联式就很复杂。 当T、P两个参数未预先赋值的话，相应的解法就比较复 杂，尤其是当T为未知时，其解法最难。因为温度与压力相 比，T对物性参数及平衡状态的影响要强得多，特别是在常 压条件下更是如此。也就是说，泡点温度的计算要比泡点 压力的计算复杂。
（2－7）
式中T为系统温度，各项系数为常数，可由各自的K－T 数据用最小二乘法等关联方法确定。而K－T数据可由给定 压力在P－T－K图上读取，也可按适当的汽液平衡模型计 算。
11
2）目标函数的选择
目标子函数又称收敛子函数的选择在计算机运算中是非常重要的一环， 其选择的恰当与否直接关系到运算是否收敛及收敛的速度等问题。在泡 点计算中常用的收敛子函数有如下几种形式：
f (T , P, xi , y i )
对于满足：
y i K i xi
yi 1
1
C
（2－3）
方程组的Ki所对应的温度（或压力）就是泡点，而式 （2－3）就称为泡点方程。
5
由汽液平衡条件式（2－1）可得： 教材：P28-32
Pyi i xi i* Pi* exp Vil ( P Pi* ) / RT
K i Pi* P(T , P) 又如汽相为实际气体的理想溶液时， K i f i0 f iV (T , P)
8
这时的泡点计算可方便地用手算完成。计算步骤如下： ① 根据溶液的组成与沸点，假设泡点初值T； ② 由T，P计算相平衡常数； ③ 计算汽相组成 y i K i xi ，判断 yi 1 是否满足收敛条 件，满足，则所设温度即为泡点温度，否则，重新调整温 度后，从第二步开始进行迭代计算。 温度调整应参照 y i 值进行： 该值大于1，说明平衡常数值偏大，所设温度偏高，应调低 温度，温度调整的幅度应根据与1的差值大小确定。 该值小于1，所设温度偏低。 如果物系的非理想性极强，平衡常数与组成密切相关，计算 相当繁复，需运用计算机进行计算，此时，温度的调整是否合 理有效，将决定泡点温度的计算能否收敛和收敛的速度。这在 后面目标函数的选择中还要讨论。
泡点温度与泡点压力计算的难易比较分析 由于系统设计变量指定的不同，泡点温度与泡点压力的计 算在解法上的难易也就有所区别。这是因为不同的变量对 系统状态及其物性参数所产生的影响不同所至。 泡点计算的设计变量为c个，除（c-1）组成已知外，还需 给定温度或压力。T、P这两个变量对共同变量中的物性参 数Ki（或i和Pi等）影响最大，而且，其中有些参数本身的 关联式就很复杂。 当T、P两个参数未预先赋值的话，相应的解法就比较复 杂，尤其是当T为未知时，其解法最难。因为温度与压力相 比，T对物性参数及平衡状态的影响要强得多，特别是在常 压条件下更是如此。也就是说，泡点温度的计算要比泡点 压力的计算复杂。
（2－7）
式中T为系统温度，各项系数为常数，可由各自的K－T 数据用最小二乘法等关联方法确定。而K－T数据可由给定 压力在P－T－K图上读取，也可按适当的汽液平衡模型计 算。
11
2）目标函数的选择
目标子函数又称收敛子函数的选择在计算机运算中是非常重要的一环， 其选择的恰当与否直接关系到运算是否收敛及收敛的速度等问题。在泡 点计算中常用的收敛子函数有如下几种形式：
f (T , P, xi , y i )
对于满足：
y i K i xi
yi 1
1
C
（2－3）
方程组的Ki所对应的温度（或压力）就是泡点，而式 （2－3）就称为泡点方程。
5
由汽液平衡条件式（2－1）可得： 教材：P28-32
Pyi i xi i* Pi* exp Vil ( P Pi* ) / RT
K i Pi* P(T , P) 又如汽相为实际气体的理想溶液时， K i f i0 f iV (T , P)
8
这时的泡点计算可方便地用手算完成。计算步骤如下： ① 根据溶液的组成与沸点，假设泡点初值T； ② 由T，P计算相平衡常数； ③ 计算汽相组成 y i K i xi ，判断 yi 1 是否满足收敛条 件，满足，则所设温度即为泡点温度，否则，重新调整温 度后，从第二步开始进行迭代计算。 温度调整应参照 y i 值进行： 该值大于1，说明平衡常数值偏大，所设温度偏高，应调低 温度，温度调整的幅度应根据与1的差值大小确定。 该值小于1，所设温度偏低。 如果物系的非理想性极强，平衡常数与组成密切相关，计算 相当繁复，需运用计算机进行计算，此时，温度的调整是否合 理有效，将决定泡点温度的计算能否收敛和收敛的速度。这在 后面目标函数的选择中还要讨论。
《化工分离工程》PPT课件-第4讲分离过程
(k )
f T (k ) − f ′ T (k )
( ) ( )
f (T ) = ∑ K i xi − 1
2. Ki与组成有关： 与组成有关：
已知： 已知： x 、p 计算： 计算： y 、T 已知： 已知： x 、T 计算： y 、p 计算： 泡点方程： 泡点方程：
f (T ) =
பைடு நூலகம்泡点温度计算 泡点压力计算
pb = ∑ pis xi
y i = K i xi
C
i = 1,2,..., C
C
（2）摩尔分率加和方程： 2个 摩尔分率加和方程：
∑x
i =1
i
= 1 .0
∑y
i =1
i
= 1.0
2C＋ 2C＋2 C个
（3）汽液平衡常数关联式： 汽液平衡常数关联式：
Ki = f (T , P, x, y)
i = 1,2,...,C
变量数： 变量数：
∑K
i =1
C
i
xi − 1 = 0
K i = f T , P , x, y
(
)
由状态方程法或活度系数法求取K 由状态方程法或活度系数法求取 i ：
K
i
φˆ i L = φˆ iV
K
i
yi γ i Pi sφ = = xi φˆ iV P
s i
v iL ( P − P i s ) exp RT
已知条件
开始
输入p 及有关参数 输入 ，x及有关参数
活 度 系 数 法 计 算 泡 点 温 度 的 框 图
设T并令φiV＝1，作第一次迭代 并令 ，
L Vm,i p − pis pisϕis Ki = )V exp RT ϕi p
化工分离第二章1
i 1 c
纯组分i：
yi
2 2 a i 27 R Tc ,i 64 Pc ,i bi RTc ,i 8 Pc ,i
、
ai )2
b y i bi
i 1
c
( 3 ) 由状态方程求取混合物的体积 Vt 及压缩因子 Z m ;
RT a ab 2 V (b )Vm Vm 0 P p p
ln 1 ln
ln 2 ln
1
x1
T21 Z r1 T12 q1 ln 1 2 l l q ln T q 1 2 21 2 1 1 r 2 1 2 1 T T 2 2 1 12 1 2 21
G21 exp( 21 ) b12 RT b 21 21 RT
12
优点：适用于二元和多元气液平衡和液液 平衡体系（特别是含水体系）。 缺点：需要三个参数。
, b12, b21 are specific to a pair of species
2014-9-9
• UNIQUAC（two-constant）:
难以在临界区内应用201732244烃类系统相平衡常数的近似估计烃类系统相平衡常数的近似估计烃类系统相平衡常数的近似估计ptk列线图烃类系统的汽液两相均较接近于理想溶液ptk列线图是deprister以bwr状态方程为基准绘制而成见图21及汽液组成ptk图适用于081mpa绝压以下的较低压区域注意tp的影响2017322由图21p21atm21273kpa2017322例21
yi i f i Ki V ˆ P xi i
？求取基准态逸度、液相活度系数和汽相逸度系数。
纯组分i：
yi
2 2 a i 27 R Tc ,i 64 Pc ,i bi RTc ,i 8 Pc ,i
、
ai )2
b y i bi
i 1
c
( 3 ) 由状态方程求取混合物的体积 Vt 及压缩因子 Z m ;
RT a ab 2 V (b )Vm Vm 0 P p p
ln 1 ln
ln 2 ln
1
x1
T21 Z r1 T12 q1 ln 1 2 l l q ln T q 1 2 21 2 1 1 r 2 1 2 1 T T 2 2 1 12 1 2 21
G21 exp( 21 ) b12 RT b 21 21 RT
12
优点：适用于二元和多元气液平衡和液液 平衡体系（特别是含水体系）。 缺点：需要三个参数。
, b12, b21 are specific to a pair of species
2014-9-9
• UNIQUAC（two-constant）:
难以在临界区内应用201732244烃类系统相平衡常数的近似估计烃类系统相平衡常数的近似估计烃类系统相平衡常数的近似估计ptk列线图烃类系统的汽液两相均较接近于理想溶液ptk列线图是deprister以bwr状态方程为基准绘制而成见图21及汽液组成ptk图适用于081mpa绝压以下的较低压区域注意tp的影响2017322由图21p21atm21273kpa2017322例21
yi i f i Ki V ˆ P xi i
？求取基准态逸度、液相活度系数和汽相逸度系数。
化工分离过程第二章
(2) 逸度与组成的关系 气相逸度与气相组成yi的关系为：
fˆiV
fi0V
V i
yi
Pi0V
V i
yi
PˆiV yi
式中：fi0V 在系统温度和压力下纯组分i的气相逸度 γiV 组分i的气相活度系数 φi0V在系统温度和压力下，纯组分i的气相逸度系数 φiV 在系统温度和压力下，组分i的气相分逸度系数且
ˆiL
i0L
L i
平衡时，汽液两相逸度相等，通过平衡常数Ki的定义式可求 出相平衡常数。
10
1. 汽液平衡关系（Vapor-liquid phase equilibrium）
fˆiV fˆi L
(2-4)
引入逸度系数 ：
ˆ i
，汽相中组分i的逸度系数 ˆ Vi 定义为
ˆ iV fˆiV / yiP
ZM
PVt RT
RT (Vt b
a Vt2
)Vt
RT
Vt Vt
b
a RTVt
2
④计算汽相逸度系数
将（2—15）积分后代入以上结果：
ln
) i
bi Vt b
ln[ZM
(1
b Vt
)]
2 aai RTVt
3
25
⑤用xi代替yi，按照②～④步骤求各组分的液相逸度 系数
⑥由式（2-14）求Ki值。
fi L
Pi S iS
exp[ViL (P PiS )] RT
（2-21）
33
由式（2—21）可知，纯液体i在T、P下的逸度等于饱和 蒸汽压乘以两个校正系数。
S i
为校正处于饱和蒸汽压下的蒸汽对理想气体的偏离，
而指数校正项也称普瓦廷（Poynting）因子，是校正压
第二章_单级平衡过程
组分的相平衡常数Ki 是平衡物系的温度、压力及组成的函数，根据 物系所处的温度、压力和溶液性质，可分为五种情况。
1) 低压下，组分的物理性质比较接近的物系，称为完全理想物系。
此时
is 1
il 1
ˆ iV 1
pis ki f (T , P) p
K仅与温度、压力有关而与溶液组成无关。这类物质的特点：汽相服从
yi Ki xi
（3）分离因子或相对挥发度α
Ki ij Kj 组分i对组分j的相对挥发度定义为：
1、气液相平衡
• 汽液平衡时，组分 i 在汽、液两相的逸度相等
ˆV f L ˆ fi i
对于纯组分，逸度等于纯组分的逸度， 对于理想气体混合物，逸度等于组分的分压， 对于真实混合物，用逸度系数或活度系数计算逸度
2.2.2 求取K的两条途径
一、根据逸度系数计算K——状态方程法
ˆ ˆ 汽相： f iV iV yi P
ˆ ˆ 液相： f i L iL xi P
ˆ y i iL Ki V xi i ˆ
相平衡常数：
关键: 选择 一个既适用 于汽相、又 适用于液相 的状态方程。
式中的逸度系数可从该物质的p-V-T（状态方程）关系或
ˆ iL i0L iL
。 平衡时，汽液两相逸度相等，通过平衡常数Ki的定义式可求出相平衡常数
由此可得
对应着计算相平衡常数的两种途径：状态方程 法和活度系数法。
小节
相平衡常数Ki的计算
• 理想体系的吸收过程 亨利定律
• 理想体系的精馏过程
拉乌尔定律
• 非理想体系
气相逸度或液相活度系数来计算
ij
Ki
y i / xi yi x j Kj y /x y j xi j j
分离过程-第2章单级平衡过程
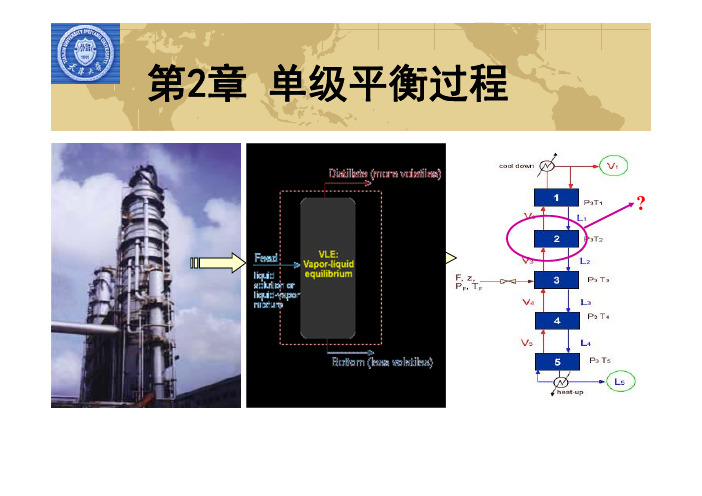
⎟⎞dP ⎠
（2-20）
对气、液、固组分均适用。
纯液体组分i的逸度：
∫ ∫ ln fiL P
=
1 RT
⎡ ⎢⎣
Pis 0
⎜⎛ ⎝
vi
−
RT P
⎟⎞dP ⎠
+
P pis
⎜⎛ ⎝
vi
−
RT P
⎟⎠⎞dP⎥⎦⎤
=
ln φis
+
viL (P − RT
Pis )
−
ln
P Pi s
纯组分i在一定温度的饱 纯液体组分i在系统温度下
第2章 单级平衡过程
?
2.1 相平衡
所谓相平衡指的是混合物或溶液形成若干相，这 些相之间保持着物理平衡而共存的状态。 从热力学上看，整个物系的自由焓处于最小状态。 从动力学来看，相间表观传递速率为零。
2.1.1 相平衡关系
一、相平衡条件（准则）： 各相的温度、压力相同，各相组分的逸度也相等。
T ′ = T ′′ = T ′′′ = ...... P′ = P′′ = P′′′ = ......
泡点方程：
C
f (T ) = ∑ Ki xi
−1= 0
i =1
假定T 已知P 得到Ki 调整T
ΣKixi
f(T)=|ΣKixi-1 |<ε
no yes
T，yi
（1）温度T初值的选定
取纯物质的沸点作为温度的迭代初值。
（2） Ki值的获得
1）p-T-K图（烃类物系） 2）简化表达式： K i = Pis / P 3）经验关系式
⎣
viL
(
P− RT
Pi
s
)
⎤ ⎥ ⎦
《化工分离工程》PPT课件-第3讲分离过程
描述系统的独立变量数可以由进出系统的物流和系统与 环境进行能量交换的情况确定具体的原则为： 环境进行能量交换的情况确定具体的原则为： 对一单相物流，其独立变量为： 对一单相物流，其独立变量为：
NV = C + 2
如果系统与环境有能量交换， 如果系统与环境有能量交换，则独立变量应该加上描述 能量交换的变量数， 一股热交换，又有一股功交换， 能量交换的变量数，如有 一股热交换，又有一股功交换， 则应该再加上两个设计变量， 则应该再加上两个设计变量，即：
1
确定装置变量郭氏原则
按每一股单相物流有（ 按每一股单相物流有（C+2）个变量， ）个变量， 计算进料物流所确定的固定设计变量。 计算进料物流所确定的固定设计变量。 确定装置中具有的不同压力的数目。 确定装置中具有的不同压力的数目。 上述之和既为为装置的固定设计变量。 上述之和既为为装置的固定设计变量。 将串级单元数，分配器数， 将串级单元数，分配器数，侧线采出单 元数以及传热单元的数目相加为装置的 可调设计变量数。 可调设计变量数。
简单吸收塔的设计变量
N
设计变量 可以规定为: 可以规定为 固定设计变 量: 两股进 2C+4 料 每级压力 N 可调设计变 量 理论级数 1
该装置由N个绝热操作的简单平衡级构 该装置由 个绝热操作的简单平衡级构 因此有: 成,因此有 e 因此有
i
VN=D
LN+1=S
= 2c + 5
Nr = 1
N N-1 N-2 N-3
N V = C + 2 + 能量交换增加的变量数
独立变量之间约束关系
独立变量之间的约束关系包括： 独立变量之间的约束关系包括： 1 物料平衡关系（对C组分体系有 个） 组分体系有C个 组分体系有 2 能量平衡关系（对一个体系只有一个） 对一个体系只有一个） 3 相平衡关系（对C组分 相体系有 （ π+1）个） 组分π相体系有C（ 组分 ） 4 化学平衡关系（分离过程只考虑无化学反应的体系，不考虑该约束条件） 分离过程只考虑无化学反应的体系，不考虑该约束条件） 5 内在关系 （指约定的关系，如物流之间温度，压力降之间的关系等） 指约定的关系，如物流之间温度，压力降之间的关系等）
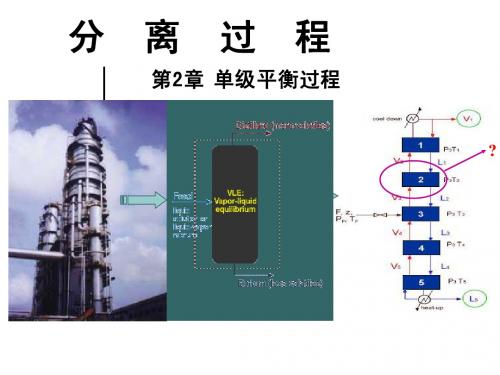
NV = C + 2
如果系统与环境有能量交换， 如果系统与环境有能量交换，则独立变量应该加上描述 能量交换的变量数， 一股热交换，又有一股功交换， 能量交换的变量数，如有 一股热交换，又有一股功交换， 则应该再加上两个设计变量， 则应该再加上两个设计变量，即：
1
确定装置变量郭氏原则
按每一股单相物流有（ 按每一股单相物流有（C+2）个变量， ）个变量， 计算进料物流所确定的固定设计变量。 计算进料物流所确定的固定设计变量。 确定装置中具有的不同压力的数目。 确定装置中具有的不同压力的数目。 上述之和既为为装置的固定设计变量。 上述之和既为为装置的固定设计变量。 将串级单元数，分配器数， 将串级单元数，分配器数，侧线采出单 元数以及传热单元的数目相加为装置的 可调设计变量数。 可调设计变量数。
简单吸收塔的设计变量
N
设计变量 可以规定为: 可以规定为 固定设计变 量: 两股进 2C+4 料 每级压力 N 可调设计变 量 理论级数 1
该装置由N个绝热操作的简单平衡级构 该装置由 个绝热操作的简单平衡级构 因此有: 成,因此有 e 因此有
i
VN=D
LN+1=S
= 2c + 5
Nr = 1
N N-1 N-2 N-3
N V = C + 2 + 能量交换增加的变量数
独立变量之间约束关系
独立变量之间的约束关系包括： 独立变量之间的约束关系包括： 1 物料平衡关系（对C组分体系有 个） 组分体系有C个 组分体系有 2 能量平衡关系（对一个体系只有一个） 对一个体系只有一个） 3 相平衡关系（对C组分 相体系有 （ π+1）个） 组分π相体系有C（ 组分 ） 4 化学平衡关系（分离过程只考虑无化学反应的体系，不考虑该约束条件） 分离过程只考虑无化学反应的体系，不考虑该约束条件） 5 内在关系 （指约定的关系，如物流之间温度，压力降之间的关系等） 指约定的关系，如物流之间温度，压力降之间的关系等）
第2章 单级平衡过程 化学分离工程讲解
yi
ij
yj xj
xi
Ki Kj
(2-13)
8
END
2.1.2 汽液平衡常数的计算
一、状态方程法
由2-8式得方法模型：k i 其中：
yi
xi
ˆL i
ˆ V (2-14) i
L ˆ i
和
V ˆ i
由状态方程计算。
ˆL 和 ˆV 表达式： 由P-V-T关系计算 i i
i i
f ioI iII xiII f ioII
(2-12)
２、相平衡常数法 相平衡常数的定义式：
Ｋi yi x i
对精馏、吸收而言， Ki 称为汽液平衡常数； 对萃取而言， Ki 称为液液平衡常数（分配系数）。 ３、分离因子法
定义：
s ij
xi 1 x j 1 xi 2 x j 2
26
2.2 Calculation about Bubble-point and
(2-15) 计算 逸度 系数 的普 遍化 公式
9
(2-16)
2.1.2 汽液平衡常数的计算
只要知道状态方程，代入（2-15、2-16）就可以 ˆ 求逸度系数 i 不同的状态方程或同一状态方程采用不同的混合规
则，逸度系数的表达式不同！
状态方程选择原则：
选择既适用于汽相又适用于液相的状态方程。 常用方程：RK、SRK、PR、BWRS等方程。 适用条件：中压、液相非理想性不是很强的烃类系统。
(2-35)
(1)汽相为理想气体，液相为理想溶液（完全理想系） 活度系数、逸度系数为1，指数因子近似为1，所以 Ki = PiS/P (2-36) Ki=f(T,P) 适用物系：P<200kPa、分子结构相似的物系 (苯-甲苯) (2)汽相为理想气体，液相为非理想溶液 逸度系数为1，指数因子近似为1，所以 Ki=γi PiS/P (2-38) Ki=f(T,P,xi) 适用物系：低压下，分子结构相差不大组分溶液（醇、醛、 22
化工分离过程(2单级平衡过程)(第4讲)
28
2.3.1等温闪蒸和部分冷凝过程
④ 计算汽、液相产量V和L： V=ΨF=202.5kmol/h，L=(1-Ψ)F=297.5kmol/h ⑤ 利用下式计算汽、液相组成y和x：
yi
成分 汽相组成yi 液相组成xi
K i zi ( K i 1) 1
乙烷(1) 0.1512 0.0315
c个 2c＋3
i 1, 2 ,... c
（3）摩尔分率加和式—S方程： 2个
c
xi 1
i 1
c
yi 1
i 1
（4）热量平衡式— H方程： 1个
FH
F
Q VH
V
LH
L
10
2.3 闪蒸过程的计算
闪蒸过程的设计变量
变量数： 3c+8个 （F,TF ,PF ,T,P,V,L,Q,zi ,yi ,xi）
z 1 0 . 08
z 2 0 . 22
z 3 0 . 53
z 4 0 . 17
试计算汽、液相产品的流率和组成。
26
2.3.1等温闪蒸和部分冷凝过程
① 利用P-T-K图查得： K1=4.80，K2=1.96，K3=0.80，K4=0.33
② 验证料液的泡点和露点： 泡点验证：
K
i 1
约束方程总数：
2c+3个
需规定变量数(设计变量)：c＋5个
其中进料变量数 (固定设计变量)：
(可调设计变量)：
c+3个 2个
（F,TF ,PF ,zi ）
11
2.3 闪蒸过程的计算
根据2个可调设计变量的规定方法可将闪蒸计算 分为如下五类： 规定变量
P,T P,Q=0 P,Q≠0 P,L(或ψ)
2.3.1等温闪蒸和部分冷凝过程
④ 计算汽、液相产量V和L： V=ΨF=202.5kmol/h，L=(1-Ψ)F=297.5kmol/h ⑤ 利用下式计算汽、液相组成y和x：
yi
成分 汽相组成yi 液相组成xi
K i zi ( K i 1) 1
乙烷(1) 0.1512 0.0315
c个 2c＋3
i 1, 2 ,... c
（3）摩尔分率加和式—S方程： 2个
c
xi 1
i 1
c
yi 1
i 1
（4）热量平衡式— H方程： 1个
FH
F
Q VH
V
LH
L
10
2.3 闪蒸过程的计算
闪蒸过程的设计变量
变量数： 3c+8个 （F,TF ,PF ,T,P,V,L,Q,zi ,yi ,xi）
z 1 0 . 08
z 2 0 . 22
z 3 0 . 53
z 4 0 . 17
试计算汽、液相产品的流率和组成。
26
2.3.1等温闪蒸和部分冷凝过程
① 利用P-T-K图查得： K1=4.80，K2=1.96，K3=0.80，K4=0.33
② 验证料液的泡点和露点： 泡点验证：
K
i 1
约束方程总数：
2c+3个
需规定变量数(设计变量)：c＋5个
其中进料变量数 (固定设计变量)：
(可调设计变量)：
c+3个 2个
（F,TF ,PF ,zi ）
11
2.3 闪蒸过程的计算
根据2个可调设计变量的规定方法可将闪蒸计算 分为如下五类： 规定变量
P,T P,Q=0 P,Q≠0 P,L(或ψ)
第二章 单级平衡过程
（1）二元溶液的活度系数
A、Van-Laar Equation
A12 A21 A
A12 A21 0
A12 0, A21 0
单参数的对称方程
2 2 lg 1 A12 x 2 Ax2
i 1
理想体系 负偏差非理想体系 正偏差非理想体系
i 1
i 1
A12 0, A21 0
xi
L ˆ i
V ˆ i
（2）活度系数法
yi i fi ki V ˆ xi Pi
0L
③
k i 与 ij 的关系
相对挥发度的定义 i，j两组分的相平衡常数之比
yi y j ki yi xi ij k j y j x j xi x j ij xi ij yi ki x x ij i ij i yi x yi ij ki ij i yi ij
比较不变 调整T（P）
计算框图见P37
[例3] 某厂氯化法合成甘油车间，氯丙烯精馏塔的釜液 组成为：3-氯丙烯0.0145, 1,2-二氯丙烷0.3090， 1,3-二氯丙烯0.6765（摩尔分率）。塔釜压力为常 压，试求塔釜温度。各组分的饱和蒸汽压数据为： （ P s : kPa; ℃ t :） 3- 氯丙烯
2 2
x A13 2x1 ( A31 A13 )
2 3
x2 x3[ A21 A13 A32 2x1 ( A31 A13 )
A21 A12 A23 A32 A31 A13 C 2
2x3 ( A32 A23 ) C(1 2 x1 )]
ki f (T , P)
（1）手算
第二章 单级平衡过程(化工分离过程)
第二章单级平衡过程?1.相平衡常数计算：状态方程法，活度系数法2. 泡点、露点计算（1）泡点计算：在一定p （或T）下，已知x i ，确定T b （或P b ）和y i 。
（2）露点计算3. 等温闪蒸计算：给定物料的量与组成，计算在一定p 和T下闪蒸得到的汽相量与组成，以及剩余的液相量与组成。
本章主要内容及要求第二章单级平衡过程• 2.1 相平衡√• 2.2 多组分物系的泡点和露点计算√• 2.3 闪蒸过程的计算√• 2.4 液液平衡过程的计算• 2.5 多相平衡过程第二章单级平衡过程•2.1 相平衡•2.2 多组分物系的泡点和露点计算•2.3 闪蒸过程的计算2.1 相平衡2.1.1 相平衡关系√2.1.2 相平衡常数的计算√2.1.3 液液平衡2.1.1 相平衡关系2.1.1.1 相平衡条件（准则）：各相的温度、压力相同，各相组分的逸度(Fugacity)也相等。
......=′′′=′′=′T T T ''''''......p p p ===ˆˆˆ......i i i f f f ′″′′′===状态方程法计算汽液平衡常数时，关键在于选择一个适用于汽、液两相的状态方程。
思考题：对常用的状态方程（范德华方程、RK方程、SRK方程、PR方程、BWRS方程）的优缺点和应用范围进行比较。
小节：对于由一种溶质（不凝性组分）和一种溶剂（可凝性组分）构成的两组分溶液，通常:→1，γi→1定义基准态；溶剂的活度系数按xi→0，γi＊→1定义基准态。
溶质的活度系数按xi由于两组分的基准态不同，称为不对称型标准化方法。
思考题：对常用的活度系数方程：Margules-Van laar方程、Margules方程、Wilson 方程、NRTL方程、UNIQUAC方程、UNIFAC方程的优缺点和应用范围进行比较。
活度系数法计算KiOL基准态逸度---fi液相活度系数---γiV 汽相逸度系数---Φi第二章单级平衡过程•2.1 相平衡•2.2 多组分物系的泡点和露点计算•2.3 闪蒸过程的计算2.2 多组分物系的泡点和露点计算2.2.1 泡点温度和压力的计算√2.2.2 露点温度和压力的计算√方程总数：2C+2个变量数：3C+2个p ）T K x （y i i i ,,,,已知变量数：C 个未知变量数：2C+2个唯一解计算复杂程度取决于K i 。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章单级平衡过程
?
1.相平衡常数计算：状态方程法，活度系数法
2. 泡点、露点计算
（1）泡点计算：在一定p （或T）下，已知x i ，确定T b （或P b ）和y i 。
（2）露点计算
3. 等温闪蒸计算：给定物料的量与组成，计算在一
定p 和T下闪蒸得到的汽相量与组成，以及剩余的液相量与组成。
本章主要内容及要求
第二章单级平衡过程• 2.1 相平衡√
• 2.2 多组分物系的泡点和露点计算√• 2.3 闪蒸过程的计算√
• 2.4 液液平衡过程的计算
• 2.5 多相平衡过程
第二章单级平衡过程•2.1 相平衡
•2.2 多组分物系的泡点和露点计算•2.3 闪蒸过程的计算
2.1 相平衡
2.1.1 相平衡关系√
2.1.2 相平衡常数的计算√2.1.3 液液平衡
2.1.1 相平衡关系2.1.1.1 相平衡条件（准则）：
各相的温度、压力相同，各相组分的逸度(Fugacity)也相等。
......
=′′′=′′=′T T T ''''''......
p p p ===ˆˆˆ......
i i i f f f ′″′′′===
状态方程法计算汽液平衡常数时，关键在于选择一个适用于汽、液两相的状态方程。
思考题：
对常用的状态方程（范德华方程、RK方程、SRK方程、PR方程、BWRS方程）的优缺点和应用范围进行比较。
小节：
对于由一种溶质（不凝性组分）和一种溶剂（可凝性组分）构成的两组分溶液，通常:
→1，γi→1定义基准态；
溶剂的活度系数按x
i
→0，γi＊→1定义基准态。
溶质的活度系数按x
i
由于两组分的基准态不同，称为不对称型标准化方法。
思考题：
对常用的活度系数方程：
Margules-Van laar方程、Margules方程、Wilson 方程、NRTL方程、UNIQUAC方程、UNIFAC方程的优缺点和应用范围进行比较。
活度系数法计算K
i
OL
基准态逸度---f
i
液相活度系数---γ
i
V 汽相逸度系数---Φ
i
第二章单级平衡过程•2.1 相平衡
•2.2 多组分物系的泡点和露点计算•2.3 闪蒸过程的计算
2.2 多组分物系的泡点和露点计算
2.2.1 泡点温度和压力的计算√
2.2.2 露点温度和压力的计算√
方程总数：2C+2个
变量数：3C+2个p ）T K x （y i i i ,,,,已知变量数：C 个未知变量数：2C+2个唯一解
计算复杂程度取决于K i 。
（1）温度T 初值的选定
取纯物质的沸点作为温度的迭代初值。
（2）K i 值的获得
1）p-T-K 图（烃类物系）2）简化表达式：P P K s i i /=3）经验关系式。