物理化学第二章总结
物理化学主要公式及使用条件总结

物理化学主要公式及使用条件第二章 热力学第一定律1. 热力学第一定律的数学表示式W Q U +=∆ 或 'ambδδδd δdU Q W Q p V W =+=-+规定系统吸热为正,放热为负。
系统得功为正,对环境作功为负。
式中 pamb 为环境的压力,W’为非体积功。
上式适用于封闭体系的一切过程。
2. 焓的定义式 3. 焓变(1) )(pV U H ∆+∆=∆式中)(pV ∆为pV 乘积的增量,只有在恒压下)()(12V V p pV -=∆在数值上等于体积功。
(2) 2,m 1d p H nC T ∆=⎰此式适用于理想气体单纯pVT 变化的一切过程,或真实气体的恒压变温过程,或纯的液体、固体物质压力变化不大的变温过程。
4. 热力学能(又称内能)变此式适用于理想气体单纯pVT 变化的一切过程。
5. 恒容热和恒压热V Q U =∆ (d 0,'0V W == p Q H =∆(d 0,'0)p W ==6. 热容的定义式 (1)定压热容和定容热容δ/d (/)p p p C Q T H T ==∂∂δ/d (/)V V V C Q T U T ==∂∂(2)摩尔定压热容和摩尔定容热容,m m /(/)p p p C C n H T ==∂∂ ,m m /(/)V V V C C n U T ==∂∂上式分别适用于无相变变化、无化学变化、非体积功为零的恒压和恒容过程。
(3)质量定压热容(比定压热容),m //p p p c C m C M==pVU H +=2,m 1d V U nC T∆=⎰BB /νξn ∆=式中m 和M 分别为物质的质量和摩尔质量。
(4) ,m ,mp VC C R -= 只适用于理想气体。
(5)摩尔定压热容与温度的关系 23,m p C a bT cT dT =+++式中a , b , c 及d 对指定气体皆为常数。
(6)平均摩尔定压热容21,m ,m 21d /()Tp p T C T T T C =-⎰7. 摩尔蒸发焓与温度的关系21vap m 2vap m 1vap ,m ()()d T p TH T H T C T ∆=∆+∆⎰或 v a p m v a p (/)p p H T C ∂∆∂=∆式中 vap ,m p C ∆ = ,m p C (g) —,m p C (l),上式适用于恒压蒸发过程。
物理化学第二章总结

第二章 主要公式及适用条件热力学第一定律dU = δQ + δW 或 ∆U = Q + W一.体积功WdV p W amb -=⎰或 dV p W amb -=δ 适用于任何系统、任何过程的体积功的计算。
1.自由膨胀过程(向真空膨胀): W = 02.恒外压过程: )(12V V p W amb --=3.恒容过程:4. 恒压过程: )(12V V p W --= 一定量理想气体恒压过程 T nR W ∆-=5.一定量理想气体恒温可逆过程:1221ln ln p p nRT V V nRT W ==6.一定量理想气体绝热可逆过程W = ΔU = n C v.m (T 2-T 1) 或)11(1111211----=γγγγV V V p W(其中 γ = C p.m / C v.m 称为绝热指数 也称热容商。
)7.恒温恒压相变过程: W = - p (V β-V α )若β相为理想气体: W = - p V g = -nRT8.恒温恒压化学反应;且气体视为理想气体W = - R T(g ) (式中为反应计量系数,反应物为“-”,产物为“+”。
)二.热容热容定义 C = Q / ΔT = δQ / d TC v. m = δQ v / d T = (әU m / әT )vC p. m =δQ p / d T = (әH m /әT )p对理想气体 C p.m – C v.m = R单原子分子 C v.m = 3R /2 , C p.m = 5R / 2双原子分子 C v.m = 5R/2, C p.m =7R /2多原子分子 C v.m = 3 R , C p.m = 4 R三. 热1.封闭体系无非体积功恒容变温过程:dT nC Q T T m V V ⎰=21, 若常数=m V C ,,则)(12,T T nC Q m V V -=2.封闭体系无非体积功恒压变温过程: dT nC Q T T m p V ⎰=21,若常数=m p C ,,则)(12,T T nC Q m p p -=3.绝热过程及理想气体自由膨胀过程:Q = 04.恒温恒压无非体积功的相变过程:Q p = n ΔH m5.恒温恒压与恒温恒容化学反应 Q p 与Q v 关系:Q p –Q v = Δr H – Δr U = R T Δn或Q p.m –Q v.m = Δr H m – Δr U m = R T四.热力学能(内能):ΔU = Q + W1.一定量理想气体恒温过程或隔离体系任何过程 ΔU = 02.封闭体系无非体积功恒容变化或一定量理想气体任何过程dT nC U T T m V ⎰=∆21, 3.绝热过程:ΔU = W (Q =0)五.焓:定义: H = U + p V1. 封闭体系任何过程ΔH = ΔU + Δ(p V ) = ΔU + (p 2V 2 – p 2V 2 )2.封闭体系无非体积功的恒压变化或一定量理想气体任何状态变化过程dT nC H T T m p ⎰=∆21, 3.一定量理想气体恒温、实际气体节流膨胀及恒压无非体积功的绝热化学反应过程 ΔH = 0 。
物理化学(第二章)

系统在恒 且非体积功为零的过程中与环境交换的热量 的过程中与环境交换的热量。 系统在恒压,且非体积功为零的过程中与环境交换的热量。
Q= ∆U −W ∆U =Q+W
W = −p环(V −V ) 2 1
= − p 系 (V 2 − V1 )
= − ( p 2V 2 − p1V1 )
U2
Q+W
dU =δQ+δW
第一类永动机 是不可能造成的。 是不可能造成的。 永远在做功,却不消耗能量。 永远在做功,却不消耗能量。
∆U =Q+W = 0
若 <0 则 >0. W , Q
W < 0,
Q= 0
∆ = Q+W U
推论: 、 推论: 1、隔离系统 内能守恒
W = 0 Q= 0
∆ =0 U
4、热和功的分类 、 显热 热 相变热(潜热) 相变热(潜热) 化学反应热 功 非体积功( ) 非体积功(W’) 体积功
5、体积功的计算 、
dV = Asdl
截面 As
环 境
δW = Fd l
热 源
系统
Q F = p环 As
V=As l l dl
p环
∴δW = p环 Asdl
= p环d( Asl ) = p环dV
x = f ( y, z)
∂x dy+ ∂x dz dx = ∂y ∂z y z
(2)广度性质 ) 摩尔热力学能: 摩尔热力学能: (3)绝对值未知 ) 始态
U Um = n
∆ U
强度性质
末态
U1
U2
物理化学第二章热力学第一定律

第二章热力学第一定律一.基本要求1.掌握热力学的一些基本概念,如:各种系统、环境、热力学状态、系统性质、功、热、状态函数、可逆过程、过程和途径等。
2.能熟练运用热力学第一定律,掌握功与热的取号,会计算常见过程中的Q,W, U和 H的值。
3.了解为什么要定义焓,记住公式U Q V , H Q p的适用条件。
4.掌握理想气体的热力学能和焓仅是温度的函数,能熟练地运用热力学第一定律计算理想气体在可逆或不可逆的等温、等压和绝热等过程中,U, H, W, Q的计算。
二.把握学习要点的建议学好热力学第一定律是学好化学热力学的基础。
热力学第一定律解决了在恒定组成的封闭系统中,能量守恒与转换的问题,所以一开始就要掌握热力学的一些基本概念。
这不是一蹴而就的事,要通过听老师讲解、看例题、做选择题和做习题等反反复复地加深印象,才能建立热力学的概念,并能准确运用这些概念。
例如,功和热,它们都是系统与环境之间被传递的能量,要强调“传递”这个概念,还要强调是系统与环境之间发生的传递过程。
功和热的计算一定要与变化的过程联系在一起。
譬如,什么叫雨?雨就是从天而降的水,水在天上称为云,降到地上称为雨水,水只有在从天上降落到地面的过程中才被称为雨,也就是说,“雨”是一个与过程联系的名词。
在自然界中,还可以列举出其他与过程有关的名词,如风、瀑布等。
功和热都只是能量的一种形式,但是,它们一定要与传递的过程相联系。
在系统与环境之间因温度不同而被传递的能量称为热,除热以外,其余在系统与环境之间被传递的能量称为功。
传递过程必须发生在系统与环境之间,系统内部传递的能量既不能称为功,也不能称为热,仅仅是热力学能从一种形式变为另一种形式。
同样,在环境内部传递的能量,也是不能称为功(或热)的。
例如在不考虑非膨胀功的前提下,在一个绝热、刚性容器中发生化学反应、燃烧甚至爆炸等剧烈变化,由于与环境之间没有热的交换,也没有功的交换,所以 Q 0, W 0, U 0 。
物理化学第二章

③状态函数的环路积分为零(始末同归,状变为零)即 ∫ dz = 0 .
4,过程与途径 , 1)定义:物系状态发生的一切变化叫过程,完成某一过程所经历 定义: 定义 的具体步骤叫途径 2)分类:单纯状态变化,化学变化(化学组成变化),相变化(化学 分类: 分类 组成不变而聚集态变化) ①定温过程:T始 = T终 = T环 (中间有波动). ②定压过程: P = P = P (中间有波动). 环 始 终 ③定容过程:V始 = V终 = 常数 (过程中物系体积始终不变). ④绝热过程; δQ = 0 (系统与环境间无热交换)的过程. ⑤循环过程:物系经一系列变化又回到始态的过程. ⑥可逆过程:循原过程的逆过程,能使物系与环境均复原者,则 原过程与逆过程互为可逆过程.
1 B
数及t=0时反应进度(为0)及B的摩尔数). 当ξ=1mol时发生单位反应. 注意:方程式一定的反应,以任意反应物计算ξ均相同,但νB ,ξ均 与方程式书写有关,ξ只表示反应程度,与转化率无关. (3)反应的摩尔焓变 反应的摩尔焓变:△rHm(kJ/mol)=△rH(kJ)/△ξ(mol) 反应的摩尔焓变 2,化学反应热效应(反应热 ,化学反应热效应 反应热 反应热) (1)定义:当产物与反应物温度相同且在反应过程中只做体积功的化 定义:衡 , 1)定义:物系各种性质不随时间而变化的平衡状态. )定义: 2)分类: )分类: ①热平衡—物系各部分温度相同. ②力学平衡—在略去重力场情况下,物系各部分压力相等(物 系各部分间及物系与环境间无不平衡力存在). ③相平衡—物质在各相间分布达平衡. ④化学平衡—物系组成不随时间而变化. 6,热力学能(U)或内能 ,热力学能( ) 物系内部一切形式能量总和(包括平动,转动,振动,核 能,电子运动,化学键,分子间作用能等)只能求相对值,不 能求绝对值,具有能量单位:J,kJ(atml or atmm3 or cal or kcal etc)是容量(广度)性质的状态函数.
大学课程《物理化学》第二章(热力学第二定律)知识点汇总

VB ,m
V nB T , p ,n jB
H nB T , p ,n jB G nB T , p ,n jB
U B ,m
U nB T , p ,n jB
S nB T , p ,n jB
T2 p1 dT S S '1 S '2 nR ln C p p2 T1 T
dU TdS pdV
T p V S S V
dH TdS Vdp
( U )V T S
T V p S S p
S系统 S B S A
Qr
T
S孤立=S系统 S环境 0
A
熵变的计算
总则
S环境
Q实际 T环境
理想气体等温过程的熵变
S S B S A
B
Qr
A
Q ( )r T T
Wmax Qr S T T
可逆相变过程的熵变
V2
V1
dG SdT Vdp B dnB
B
dU TdS pdV B dnB
B
U dU TdS pdV dnB nB S ,V ,n j B
B
U H F G nB S ,V ,n j B nB S , p ,n j B nB T ,V ,n j B B nB T , p ,n j B
B
dG SdT Vdp B dnB
B
纯理想气体的化学势
Gm Vm p T p T
物理化学知识点归纳

第二章热力学第一定律一、热力学基本概念1.状态函数状态函数,是指状态所持有的、描述系统状态的宏观物理量,也称为状态性质或状态变量.系统有确定的状态,状态函数就有定值;系统始、终态确定后,状态函数的改变为定值;系统恢复原来状态,状态函数亦恢复到原值。
2.热力学平衡态在指定外界条件下,无论系统与环境是否完全隔离,系统各个相的宏观性质均不随时间发生变化,则称系统处于热力学平衡态。
热力学平衡须同时满足平衡(△T=0)、力平衡(△p=0)、相平衡(△μ=0)和化学平衡(△G=0)4个条件.二、热力学第一定律的数学表达式1.△U=Q+W或dU=ΔQ+δW=δQ—p amb dV+δW`规定系统吸热为正,放热为负.系统得功为正,对环境做功为负。
式中p amb为环境的压力,W`为非体积功。
上式适用于封闭系统的一切过程.2.体积功的定义和计算系统体积的变化而引起的系统和环境交换的功称为体积功.其定义式为:δW=-p amb dV(1) 气体向真空膨胀时体积功所的计算 W=0(2) 恒外压过程体积功 W=p amb (V 1—V 2)=-p amb △V 对于理想气体恒压变温过程 W=—p △V=—nR △T (3) 可逆过程体积功 W r =⎰21p V V dV(4)理想气体恒温可逆过程体积功W r =⎰21p V V dV =—nRTln(V 1/V 2)=—nRTln (p 1/p 2)(5)可逆相变体积功 W=-pdV三、恒热容、恒压热,焓 1.焓的定义式H def U + p V 2.焓变(1)△H=△U+△(pV)式中△(pV)为p V 乘积的增量,只有在恒压下△(pV)=p(V 2—V 1)在数值上等于体积功。
(2)△H=⎰21,T T m p dT nC此式适用于理想气体单纯p VT 变化的一切过程,或真实气体的恒压变温过程,或纯的液、固态物质压力变化不大的变温过程。
3. 内能变 (1)△U=Qv式中Qv 为恒热容.此式适用于封闭系统,W`=0、dV=0的过程。
02-物理化学第二章 热力学第一定律
H
m
298
K
H1
H
2
r
H
m
298
K
298K
T
eCP,E fC P,F dT
T
298K gCP,G hCP,H dT
X = f(T,P)o=rf(T,V)… 双变量坐标
强度性质—— 与量n无关
整体 = 部分 (T、P)
广延性质—— 与量n成正比 整体 = ∑部分
强度量 = 广延量/广延量
本章任务:
计算能量变化:
状态函数 U、H + 过程量 Q、W 理想气体,纯物质的 U、H 性质
步骤: ㈠ 不需第一定律即能计算的Q和W ㈡ 第一定律及内能 ㈢ 用于计算过程热及焓 ㈣ 用于绝热功的计算
§2-1
热和功
过程量——计算时一定要看具体过程 2·1·1 热Q
显热的计算
用热容
QB n CB,mdT
利用手册中数据,只能计算恒压或恒容热
QP or V
n
C dT T2
T1
P or V ,m
2·1·2 功W
体积功的计算
2
W 1 PexdV
eg. 恒容过程 W = 0
等外压过程 Pex=constant
Ⅱ:192.5kPa
298.15K
352.15K
求:Q、W、△U、△H
解: Q=0
U n CV ,mdT
nCV ,m T2 T1 1.366kJ
H n CP,mdT
n CV ,m R T2 T1 1.814kJ
W U Q 1.366kJ
例2·5·2 1mol双原子理想气体于27℃, 101.325 kPa 状态下,受某恒定外压恒温 压缩到平衡,再由该状态恒容升温至 97 ℃,则压力升到 1013.25 kPa。求整个过 程的W、Q、 △U及△H。
物理化学第二章

(2.2.1) )
对一微小变化
dS ≡
δ QR
T
(2.2.2) )
2.2.2 熵函数
对一可逆循环
∫ dS ≡ ∫
δQR
T
=0
(2.2.2) )
熵的定义式。 式(2.2.1)和(2.2.2)均为熵的定义式。 ) )均为熵的定义式 注意: 注意: 1) 熵是体系的状态函数。 是体系的状态函数 状态函数。 2) 熵与热温商不能混淆。Q/T的数值与过程有关, 热温商不能混淆 不能混淆。 的数值与过程有关, 的数值与过程有关 式中T 为环境温度。 式中 为环境温度 。 只有在可逆过程中两者才 发生联系。 为体系温度。 发生联系。 S = Q 可逆过程 的T 为体系温度。 ∆
2.2.4 熵增加原理 实际体系: 实际体系: —— 体系 环境 = 大孤立体系 体系+环境
环境视为无限大,其微小变化可当作可逆过程: 环境视为无限大,其微小变化可当作可逆过程: 可当作可逆过程
dS 环 = −
δQ
T环
dS −
δQ
T环
= dS 体系 + dS 环境 = dS 孤立 ≥ 0
>0 自发,不可逆 自发, =0 平衡,可逆 平衡,
δQ可逆
T
dS −
−
δQ实际
T
≥0
δQ实际
T环
≥0 或
dS −
δQ
T环
≥0
> 0 不可逆过程 = 0 可逆过程 < 0 不可能发生
δQ
T环 )→ II ≥ 0 I
或
∆S I → II − ∑ (
I
II
——克劳修斯不等式 克劳修斯不等式
2.2 热力学第二定律
物理化学第二章全解

第二章:热力学第一定律一.基本概念体系与环境体系:在科学研究时必须先确定研究对象,把一部分物质与其余分开,这种分离可以是实际的,也可以是想象的。
这种被划定的研究对象称为体系,亦称为物系或系统。
环境:与体系密切相关、有相互作用或影响所能及的部分称为环境。
体系的分类:(1)敞开体系:体系与环境之间既有物质交换,又有能量交换(2)封闭体系:体系与环境之间无物质交换,但有能量交换(3)孤立体系:体系与环境之间既无物质交换,又无能量交换,故又称为隔离体系。
有时把封闭体系和体系影响所及的环境一起作为孤立体系来考虑体系的性质:广度性质:又称为容量性质,它的数值与体系的物质的量成正比,如体积、质量、熵等。
这种性质有加和性,在数学上是一次齐函数。
强度性质:它的数值取决于体系自身的特点,与体系的数量无关,不具有加和性,如温度、压力等。
它在数学上是零次齐函数。
指定了物质的量的容量性质即成为强度性质,如摩尔热容热力学平衡态热平衡:体系各部分温度相等。
力学平衡体系各部的压力都相等,边界不再移动。
如有刚壁存在,虽双方压力不等,但也能保持力学平衡。
相平衡:多相共存时,各相的组成和数量不随时间而改变。
化学平衡:反应体系中各物的数量不再随时间而改变。
状态函数:体系的一些性质,其数值仅取决于体系所处的状态,而与体系的历史无关;它的变化值仅取决于体系的始态和终态,而与变化的途径无关。
具有这种特性的物理量称为状态函数状态函数的特性可描述为:异途同归,值变相等;周而复始,数值还原。
状态函数在数学上具有全微分的性质。
状态方程体系状态函数之间的定量关系式称为状态方程对于一定量的单组分均匀体系,状态函数T,p,V 之间有一定量的联系。
经验证明,只有两个是独立的,它们的函数关系可表示为:T=f(p,V)p=f(T,V)V=f(p,T)热和功热:体系与环境之间因温差而传递的能量称为热,用符号Q表示。
Q的取号:体系吸热,Q>0;体系放热,Q<0 。
物理化学第二章总结

第二章 主要公式及适用条件热力学第一定律dU = δQ + δW 或 ∆U = Q + W一.体积功WdV p W amb -=⎰或 dV p W amb -=δ 适用于任何系统、任何过程的体积功的计算。
1.自由膨胀过程(向真空膨胀): W = 02.恒外压过程: )(12V V p W amb --=3.恒容过程:4. 恒压过程: )(12V V p W --= 一定量理想气体恒压过程 T nR W ∆-=5.一定量理想气体恒温可逆过程:1221ln ln p p nRT V V nRT W ==6.一定量理想气体绝热可逆过程W = ΔU = n C v.m (T 2-T 1) 或)11(1111211----=γγγγV V V p W(其中 γ = C p.m / C v.m 称为绝热指数 也称热容商。
)7.恒温恒压相变过程: W = - p (V β-V α )若β相为理想气体: W = - p V g = -nRT8.恒温恒压化学反应;且气体视为理想气体W = - R T(g ) (式中为反应计量系数,反应物为“-”,产物为“+”。
)二.热容热容定义 C = Q / ΔT = δQ / d TC v. m = δQ v / d T = (әU m / әT )vC p. m =δQ p / d T = (әH m /әT )p对理想气体 C p.m – C v.m = R单原子分子 C v.m = 3R /2 , C p.m = 5R / 2双原子分子 C v.m = 5R/2, C p.m =7R /2多原子分子 C v.m = 3 R , C p.m = 4 R三. 热1.封闭体系无非体积功恒容变温过程:dT nC Q T T m V V ⎰=21, 若常数=m V C ,,则)(12,T T nC Q m V V -=2.封闭体系无非体积功恒压变温过程: dT nC Q T T m p V ⎰=21,若常数=m p C ,,则)(12,T T nC Q m p p -=3.绝热过程及理想气体自由膨胀过程:Q = 04.恒温恒压无非体积功的相变过程:Q p = n ΔH m5.恒温恒压与恒温恒容化学反应 Q p 与Q v 关系:Q p –Q v = Δr H – Δr U = R T Δn或Q p.m –Q v.m = Δr H m – Δr U m = R T四.热力学能(内能):ΔU = Q + W1.一定量理想气体恒温过程或隔离体系任何过程 ΔU = 02.封闭体系无非体积功恒容变化或一定量理想气体任何过程dT nC U T T m V ⎰=∆21, 3.绝热过程:ΔU = W (Q =0)五.焓:定义: H = U + p V1. 封闭体系任何过程ΔH = ΔU + Δ(p V ) = ΔU + (p 2V 2 – p 2V 2 )2.封闭体系无非体积功的恒压变化或一定量理想气体任何状态变化过程dT nC H T T m p ⎰=∆21, 3.一定量理想气体恒温、实际气体节流膨胀及恒压无非体积功的绝热化学反应过程 ΔH = 0 。
物理化学第二章(第一定律)

热力学
8
系统的性质具有如下特点: 1.系统的性质只决定于它现在所处的状态,而与其过
去的历史无关。 2. 系统的状态发生变化时,它的一系列性质也随之而改
变,改变多少,只决定于系统的开始状态和终了状态, 而与变化的途径无关。
热力学把具有这种特征的系统性质称为状态函数。
或不能使一个自然发生的过程完全复原。
第一类永动机 (能量不守衡)
热源 Q W
第二类永动机
2
根据大量的实验结果和自然现象,得出热力学第一、 二定律。
热力学定律的特点: (1) 大量分子系统
(2)不管物质的微观结构 (3)不管过程的机理
优点:结论绝对可靠, 如从热力学导出纯液体 饱和蒸汽压与温度的关系:
(3) 热分为: 显热(Sensible heat)系统做单纯的pVT变化(没有相 变化),如: 25C水75C水时,系统与环境交换的热量。 潜热(Latent heat)系统发生相变化时,如:
100C水100C水汽时,系统与环境交换的热量。
27
§2-2 热力学第一定律 The First Law of Thermodynamics
活塞
p1 dV
pe
汽缸
如果p1>pe(外压),气体膨胀dV,
则系统对环境做体积功为:dWe= pedV
21
(1) 自由膨胀(Free expansion) 为外压等于零的膨胀,即 pe=0,所以:
We,1 0
(2) 恒外压膨胀pe=const.
We,2
V2
-
pedV
-pe (V2
V1 )
第二章 热力学第一定律及其应用
物理化学第2章热力学第一定律

第二章热力学第一定律2.1 热力学的理论基础与方法1.热力学的理论基础热力学涉及由热所产生的力学作用的领域,是研究热、功及其相互转换关系的一门自然科学。
热力学的根据是三件事实:①不能制成永动机。
②不能使一个自然发生的过程完全复原。
③不能达到绝对零度。
热力学的理论基础是热力学第一、第二、第三定律。
这两个定律是人们生活实践、生产实践和科学实验的经验总结。
它们既不涉及物质的微观结构,也不能用数学加以推导和证明。
但它的正确性已被无数次的实验结果所证实。
而且从热力学严格地导出的结论都是非常精确和可靠的。
不过这都是指的在统计意义上的精确性和可靠性。
热力学第一定律是有关能量守恒的规律,即能量既不能创造,亦不能消灭,仅能由一种形式转化为另一种形式,它是定量研究各种形式能量(热、功—机械功、电功、表面功等)相互转化的理论基础。
热力学第二定律是有关热和功等能量形式相互转化的方向与限度的规律,进而推广到有关物质变化过程的方向与限度的普遍规律。
利用热力学第三定律来确定规定熵的数值,再结合其他热力学数据从而解决有关化学平衡的计算问题。
2.热力学的研究方法热力学方法是:从热力学第一和第二定律出发,通过总结、提高、归纳,引出或定义出热力学能U,焓H,熵S,亥姆霍茨函数A,吉布斯函数G;再加上可由实验直接测定的p,V,T等共八个最基本的热力学函数。
再应用演绎法,经过逻辑推理,导出一系列的热力学公式或结论。
进而用以解决物质的p,V,T变化、相变化和化学变化等过程的能量效应(功与热)及过程的方向与限度,即平衡问题。
这一方法也叫状态函数法。
热力学方法的特点是:(i)只研究物质变化过程中各宏观性质的关系,不考虑物质的微观结构;(ii)只研究物质变化过程的始态和终态,而不追究变化过程中的中间细节,也不研究变化过程的速率和完成过程所需要的时间。
因此,热力学方法属于宏观方法。
2.2 热力学的基本概念1.系统与环境系统:作为某热力学问题研究对象的部分;环境:与系统相关的周围部分;按系统与环境交换内容分为:(1)敞开系统(open system) :体系与环境间既有物质交换又有能量交换的体系。
物理化学第二章 小结

第二章热力学第一定律 小 结一、热力学基本概念 二、主要公式及使用条件2009-12-22 1一、热力学基本概念1、系统和环境 系统: 即研究的对象。
环境: 是系统以外,与之相联系的那部分物质。
系统分为三类: 隔离系统:孤立体系,环境与体系间即无能量交换又无物 质交换 封闭系统:体系与环境无物质交换但有能量交换。
敞开系统:体系与环境即有能量交换又有物质交换。
2009-12-2222、系统的宏观性质 热力学系统是大量分子、原子、离子等微观粒子组成的宏观 集合体。
这个集合体所表现出来的集体行为,如p,V, T,U,H,S,A,G 等叫热力学系统的宏观性质。
分为两类: 强度性质--系统的性质参数数值与物质的量无关,不具 有加和性。
如:p, T 等 广度性质--系统的性质参数数值与物质的量成正比,有 加和性,如:V, S, U, H, G 等一种广度性质 V m =强度性质, 如 Vm = , ρ = 等 另一种广度性质 n V2009-12-22 33、相的定义 系统中物理性质及化学性质均匀的部分。
均相系统;非均相系统 4、系统的状态和状态函数 系统的状态是指系统所处的样子。
系统的宏观性质称为系统的状态函数。
当系统的状态变化时,状态函数的改变量只决定于系统 的始态和终态,而与变化的过程或途径无关。
2009-12-2245、热力学平衡态 当体系的诸性质不随时间而改变,则体系就处于热力学平衡 态,它包括下列几个平衡: 热平衡; 力学平衡; 相平衡; 化学平衡。
6、系统的变化过程与途径 ①、过程与途径 过程--在一定环境条件下,系统由始态变化到终态的经过。
途径--系统由始态变化到终态所经历的过程的总和。
系统的变化过程分pVT变化过程,相变化过程,化学变化过程2009-12-22 5可逆过程--物系内部与环境间在无限接近于平衡时所进行的 过程 可逆过程的特点: (i) 在整个过程中系统内部无限接近于平衡; (ii) 在整个过程中,系统与环境的相互作用无限接近于平衡, 因此过程进展无限缓慢;环境的温度、压力与系统的温度、 压力相差甚微,可看做相等; (iii) 系统和环境能够由终态沿着原来的途径从相反方向步步回 复,直到都恢复到原来状态。
物理化学 2第二章 热力学第二定律

第二章 热力学第二定律内容提要一、自发过程及其不可逆性(1)自发过程(spontaneous process ):不靠外力就能自动进行的过程。
自发过程都有确定的方向,它的逆过程绝不会自发进行。
若靠外力干涉,使原过程逆相进行,体系恢复原状,则在环境中会留下无论如何也不能消除的后果。
这种不能消除的后果就是自发过程的不可逆性。
即一切自发过程都是不可逆的。
(2)可逆过程(reversible process):可逆过程是由一连串近平衡态的微小变化组成的。
变化的动力与阻力相差无限小,因而可逆变化进行的无限缓慢。
循原过程相反方向无限缓慢变化,可使体系与环境同时恢复原状,可逆过程的后果是可以消除的。
可逆过程中,体系对环境做功最大,环境对体系做功最小。
过程在热力学上是否可逆,最终归结为过程热功的转换问题。
由于热不能完全变为功,所以凡是涉及热的过程都是不可逆的。
二、热力学第二定律的表述及公式1、Kelvin 表述:“不可能从单一热源取热使之完全变为功而不产生其它变化”。
单一热源取热使之完全变为功虽不违背热力学第一定律,但涉及热功转换现象。
此表述也可说成“第二类永动机不可能制成”。
2、Clausius 表述:“热不能自动地由低温热源传到高温热源而不发生其它变化”。
两种表述都断言:一切实际过程都是不可逆的。
3、Clausius (克劳修斯)不等式(Clausius ineauality ):d S ≥δQ/T 或 T d S ≥δQ“=”适用于可逆过程,“>”适用于不可逆过程。
该不等式表示:可逆过程的热温商δQ/T 等于过程的熵变d S ;不可逆过程的热温商δQ/T 小于过程的熵变d S 。
三、熵(entropy )的定义及计算1、熵(entropy )的定义熵是体系的性质,状态函数,以符号S 表示。
⎰=∆BA R T Q S 式中,Q 为可逆过程的热,T 是可逆过程体系的温度。
2、熵的微观解释:体系任一平衡的宏观状态都与一定的微观状态数,即称混乱度相对应。
物理化学 第二章 热力学第二定律

卡诺定理的意义:
(1)引入了一个不等号 i r ,原则上解决了热机 效率的极限值问题。 (2)证实了热不能完全转化为功,因为T1 /T2 = 0 是 不可能的。
卡诺定理(1)的证明: i r 证明:反证法 假设: i 热机效率大于 r :
高温 T2
Q’2 Q2
i
W Q
' 2
r
上式的意义:系统由状态 A 到状态 B,S有唯一的值, 等于从 A 到B 可逆过程的热温商之和。
熵的特别提醒:
(1)熵(S)是状态函数;热温商(Qr/T)是与途径 相关的概念; (2)可逆过程热温商(Qr/T)不是熵(S) ;它只 是过程熵变(ΔS)的一种量度,一种测定方法; (3)熵(S)是广度性质,具有加和性;但 Sm 是强 度性质。
这个设计就相当于热从低温热源传到高温热源而 没有发生其它变化 ---违背热力学第二定律
因此 B A
卡诺定理(2)的证明:
2. 如果A带动B,使B倒转:
高温 T2
Q’2
Q2
假设A可逆热机效率大于B
A
W
Q
' 2
B
W
Q2
A®
W W
' Q2 Q2
B®
Q2 W
Q ’2 W
卡诺定理(2)的证明:
证明: 1. 如果B带动A,使A倒转:
高温T2
Q’2
Q2
假设B可逆热机效率大于A
B
W Q
' 2
A
W Q2
B®
W W
' Q2 Q2
A®
Q2 W
Q ’2 W
低温T1
循环净结果为: 1. 两热机均恢复原态 2. 高温热源得热: Q2 Q2 3. 低温热源失热:
《物理化学》第2章

实际过程的热温商:
2.热由高温物体传向低温物体:
高温热源T2 Q’=Q1+W Q=W 做功W 吸热Q1 低温热源T1 冷冻机做功后,系统(两个热源)恢复原状,… 传热Q1
结果环境失去功W,得到热Q ,环境是否能恢复原状, 决定于热Q能否全部转化为功W而不引起任何其它变化 ?
3.化学反应:
Cd(s)+PbCl2(aq)=CdCl2(aq)+Pb(s)
用一闭合曲线代表任意可逆循环。在曲线上任 意取A,B两点,把循环分成AB和BA两个可逆过 程,即: A B A
根据任意可逆循环热温商的公式:
B
Qr
Qr Qr 0 T T B T A
B A
p T
Qr
热力学第二定律的提出
19世纪初,资本主义工业生产已经很发达,迫切需要解
决动力问题。当时人们已经认识到能量守恒原理,试图制
造第一类永动机已宣告失败,然而人们也认识到能量是可 以转换的。于是,人们就想到空气和大海都含有大量的能
量,应该是取之不尽的。有人计算若从大海中取热做功,
使大海温度下降1℃,其能量可供全世界使用100年…。于 是人们围绕这一设想,设计种种机器,结果都失败了。这 个问题的实质可归结为热只能从高温物体自动传向低温物 体,没有温差就取不出热来(即从单一热源吸热)。
环境中吸热全部变为功,但体积变大了,压力变小了。
3.“第二类永动机不可能造成”可用来判断过程的方
向。
热力学第二定律的提出是起源于热功转化的研究,寻找相
应的热力学函数需从进一步分析热功转化入手(热机效率)。
物理化学2、3章公式整理
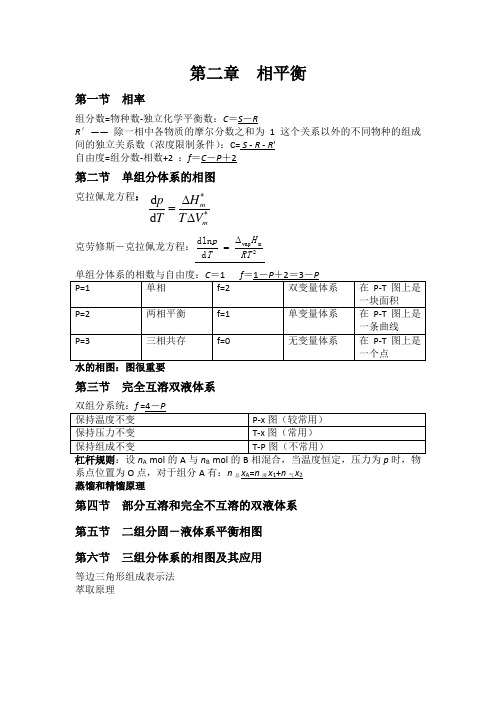
第二章 相平衡第一节 相率组分数=物种数-独立化学平衡数:C =S -RR ′—— 除一相中各物质的摩尔分数之和为1这个关系以外的不同物种的组成间的独立关系数(浓度限制条件):C= S - R - R ′ 自由度=组分数-相数+2 :f =C -P +2第二节 单组分体系的相图克拉佩龙方程:克劳修斯-克拉佩龙方程:2m vap d dln RTH T p∆=第三节 完全互溶双液体系A B 系点位置为O 点,对于组分A 有:n 总x A =n 液x 1+n 气x 2 蒸馏和精馏原理第四节 部分互溶和完全不互溶的双液体系 第五节 二组分固-液体系平衡相图 第六节 三组分体系的相图及其应用等边三角形组成表示法 萃取原理d d m mH p T T V **∆=∆第三章 多组分第一节 多组分系统热力学基本概念1、物质的量分数浓度(摩尔分数浓度):∑=BBB n n x 2、质量分数浓度(质量百分比浓度):3、物质的量浓度(体积摩尔浓度):Vn c BB =4、质量摩尔浓度:mn b BB =第二节 偏摩尔量XB ,m 称为物质B 的某种广度性质X 的偏摩尔量:)B (C ,,B m B,C ≠⎪⎪⎭⎫⎝⎛∂∂=n p T n X X B 物质的偏摩尔体积:B n p T B m B C nVV ≠⎪⎪⎭⎫ ⎝⎛∂∂=,,, B 物质的偏摩尔内能:Bn p T B m B C nUU ≠⎪⎪⎭⎫ ⎝⎛∂∂=,,, B 物质的偏摩尔焓:B n p T B m B C nHH ≠⎪⎪⎭⎫ ⎝⎛∂∂=,,, B 物质的偏摩尔熵:Bn p T Bm B C nSS ≠⎪⎪⎭⎫ ⎝⎛∂∂=,,, B 物质的偏摩尔吉布斯能:Bn p T Bm B C nGG ≠⎪⎪⎭⎫ ⎝⎛∂∂=,,, 偏摩尔量的集合公式:X ∑==iBm B B X n 1,Gibbs -Duhem 公式:0d 1B ,B =∑=im B X n偏摩尔量之间的关系:在热力学关系式中,如果将其中的容量性质都改为某个组B B Bm m ω=∑分B 的偏摩尔量,这些等式仍然成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 主要公式及适用条件热力学第一定律dU = δQ + δW 或 ∆U = Q + W一.体积功WdV p W amb -=⎰或 dV p W amb -=δ 适用于任何系统、任何过程的体积功的计算。
1.自由膨胀过程(向真空膨胀): W = 02.恒外压过程: )(12V V p W amb --=3.恒容过程:4. 恒压过程: )(12V V p W --= 一定量理想气体恒压过程 T nR W ∆-=5.一定量理想气体恒温可逆过程:1221lnln p p nRT V V nRT W ==6.一定量理想气体绝热可逆过程W = ΔU = n C v.m (T 2-T 1) 或)11(1111211----=γγγγV V V p W(其中 γ = C p.m / C v.m 称为绝热指数 也称热容商。
)7.恒温恒压相变过程: W = - p (V β-V α )若β相为理想气体: W = - p V g = -nRT8.恒温恒压化学反应;且气体视为理想气体W = - R T(g ) (式中为反应计量系数,反应物为“-”,产物为“+”。
)二.热容热容定义 C = Q / ΔT = δQ / d TC v. m = δQ v / d T = (әU m / әT )vC p. m =δQ p / d T = (әH m /әT )p对理想气体 C p.m – C v.m = R单原子分子 C v.m = 3R /2 , C p.m = 5R / 2双原子分子 C v.m = 5R/2, C p.m =7R /2多原子分子 C v.m = 3 R , C p.m = 4 R三. 热1.封闭体系无非体积功恒容变温过程:dT nC Q T T m V V ⎰=21, 若常数=m V C ,,则)(12,T T nC Q m V V -=2.封闭体系无非体积功恒压变温过程: dT nC Q T T m p V ⎰=21,若常数=m p C ,,则)(12,T T nC Q m p p -=3.绝热过程及理想气体自由膨胀过程:Q = 04.恒温恒压无非体积功的相变过程:Q p = n ΔH m5.恒温恒压与恒温恒容化学反应 Q p 与Q v 关系:Q p –Q v = Δr H – Δr U = R T Δn或Q p.m –Q v.m = Δr H m – Δr U m = R T四.热力学能(内能):ΔU = Q + W1.一定量理想气体恒温过程或隔离体系任何过程 ΔU = 02.封闭体系无非体积功恒容变化或一定量理想气体任何过程dT nC U T T m V ⎰=∆21, 3.绝热过程:ΔU = W (Q =0)五.焓:定义: H = U + p V1. 封闭体系任何过程ΔH = ΔU + Δ(p V ) = ΔU + (p 2V 2 – p 2V 2 )2.封闭体系无非体积功的恒压变化或一定量理想气体任何状态变化过程dT nC H T T m p ⎰=∆21, 3.一定量理想气体恒温、实际气体节流膨胀及恒压无非体积功的绝热化学反应过程 ΔH = 0 。
4.相变过程:ΔH=n ΔH m=Q p5.在298K—T 之间各物质无相变的化学反应:Δr H(T ) =Δr H(298K ) +此式称为基尔霍夫定律,其中Δr H(298K )可从标准摩尔生成焓或标准摩尔燃烧焓求出。
Δr H(298K ) =Δr H(298K ) = -六.理想气体绝热可逆过程方程式p Vγ= 常数T Vγ-1 = 常数Tγpγ-1=常数(其中γ = C p.m / C v.m)七.节流膨胀1.恒焓过程Δ H= 02.节流膨胀系数μJ-T= (әT / әp )H练习题一、选择题1.下列对于焓变的描述,正确的是( )A.系统的焓等于等压热B.气体的焓只是温度的函数C.理想气体在节流膨胀中,它的温度不变D.因为)(pV U H ∆+∆=∆,所以任何过程都有0>∆H 的结论2.热力学第一定律表达式为U Q W ∆=+,其只适用于( )A.敞开系统B.理想气体系统C.封闭系统D.孤立系统3.在一个恒容的绝热箱内有一绝热隔板,其两侧分别放有,,n T p 皆不相同的2N (g),若该气体可视为理想气体,则抽去隔板达到平衡,则混合过程的U ∆( ),W ( ),Q ( ),H ∆( )。
A. > 0B. < 0C. =0D.无法确定4.从焓的定义H U pV =+出发,判断下列说法中正确的是( )A.焓是能量,它遵守热力学第一定律B.焓是系统内含的热C.焓的增量只与系统的始末状态有关D.系统的焓等于系统的热力学能与体积功之和5.公式,d d m V m U C T=的适用条件是( )A.恒容过程;B.等容过程;C.组成不变均相系统的等容过程D.无化学变化、无相变化且非体积功为零的恒容过程6.理想气体等温自由膨胀过程中( ) (A)W = 0,Q>0,∆U>0,∆H=0(B)W>0,Q=0,∆U>0,∆H>0(C)W<0,Q>0,∆U=0,∆H=0(D)W = 0,Q = 0,∆U = 0,∆H = 07.273K, θp时,冰融化为水的过程中,下列关系式正确的有( ) (A)W<0(B)∆H = Q P(C)∆H<0 (D)∆U<08. 凡是在孤立体系中进行的变化,其△U 和△H 的值一定是( )(A) △U > 0 , △H > 0(B) △U = 0 , △H = 0(C) △U < 0 , △H < 0(D) △U = 0 , △H 大于、小于或等于零不确定9. 苯在一个刚性的绝热容器中燃烧,C6H6(l) + (15/2)O2(g) = 6CO2(g)+ 3H2O(g) ,则()(A) △U = 0 , △H < 0 , Q = 0(B) △U = 0 , △H > 0 , W = 0(C) Q = 0 , △U = 0 , △H = 0(D) Q = 0 , △U≠0 , △H≠010. 下列诸过程可应用公式 dU = ( C p- nR )dT 进行计算的是: ( )(A) 实际气体等压可逆冷却(B) 恒容搅拌某液体以升高温度(C) 理想气体绝热可逆膨胀(D) 量热弹中的燃烧过程11. 当以 5mol H2气与 4mol Cl2气混合,最后生成 2mol HCl 气。
若以下式为基本单元,H2(g) + Cl2(g) → 2HCl(g),则反应进度ξ应是: ( )(A) 1 mol (B) 2 mol (C) 4 mol (D) 5 mol12. 对于理想气体下述结论中正确的是 ( )(A) (∂H/∂T)v = 0; (∂H/∂V)T = 0(B) (∂H/∂T)p = 0; (∂H/∂P)T= 0(C) (∂H/∂T)p = 0; (∂H/∂V)T = 0(D) (∂H/∂V)T = 0; (∂H/∂P)T= 013.当理想气体反抗一定的外压做绝热膨胀时,则 .A. 焓总是不变的 B.热力学能总是不变的C.焓总是增加的 D.热力学能总是减小的14.在隔离系统发生某化学反应,使系统的温度明显升高,则该系统的U ∆( ),H ∆( )A. >0B.=0C. <0D.无法确定15. 功的计算公式为)(12,T T nC W m V -=,下列过程中不能用此式的是( )A. 理想气体的可逆绝热过程B. 理想气体的绝热恒外压过程C. 实际气体的绝热过程D. 凝聚系统的绝热过程16.对于非理想气体进行绝热自由膨胀时,下述表达式中不正确的是( )A.0Q =B.0W =C.0U ∆=D. 0H ∆=17.下列表述中正确的有( )A.理想气体的焦尔-汤姆逊系数不一定等于零B.真实气体的焦尔-汤姆逊系数一定不为零C.理想气体不能作为制冷机的工作介质D.真实气体的焦尔-汤姆逊系数为零时对应一组p 和T 值二、计算题1. 1mol O 2(理想气体)C p,m =29.355 J·K -1·mol -1,处于293K,采用不同途径升温至586K,求过程的Q、W、∆H、∆U。
(1)定容过程;(2)定压过程;(3)绝热过程。
2.有1mol双原子理想气体,自始态273K、200KPa 经p/V= K (常数)的过程可逆地变化至终态400KPa,求该过程的Q、W、ΔU及ΔH 。
解:V1 = n R T1/ p1 == 1.135 10-2 m3因p1/ V1 = p2 / V2, 所以V2 =V1p2 / p 1 =1.13510-2400/200=2.27010-2m3T2 ==(4003 2.27010-2 )/ (18.314)= 1092KΔU = nC v.m (T2–T1 ) =15/28.314(1092-273)= 1.702104 JΔH = n C p.m (T2–T1 )=17/28.314(1092 - 273)= 2.383104 JW = = =- K (V- V)/ 2= - p1(V– V) / 2V1=- [200 103 / (20.01135)](0.022702– 0.011352)= - 3.405 103JQ = ΔU – W =1.702104 –(-3.405103)=2.043104 J3.有5mol双原子理想气体,自始态410dm3、0.1MPa 经pT= K (常数)的过程可逆地压缩至终态0.2MPa,求该过程的Q、W、ΔU及ΔH 。
4. 已知冰在00C 、100KPa 下的摩尔熔化焓为5858J·mol -1,冰和水的平均摩尔热容分别为37.6和75.3J· K–1·mol -1,计算1mol 、–100C 100KPa 的过冷水在等温等压下凝结为-100C、100KPa 冰时系统的ΔU和ΔH。
解:此过程为不可逆相变,设计下列可逆过程 263K, 100KPa H2O(l) 263K, 100KPa H2O(s )(1) (3)273K, 100KPa H2O(l) 273K,100KPa H2O(s ) ΔH=ΔH1+ ΔH2+ΔH3=n C p. m (l)ΔT +nΔH m +n C p.m(s )ΔT= 1 + 1+ 1=-5481JΔU= ΔH = -5481 J5. 计算20℃,101.325kPa,1mol液态水蒸发为水蒸汽的汽化热。
(已知,100℃,101.325kPa时,水的∆r Hθm=4067 kJ·mol-1,水的C p,m=75.3 J·K-1·mol-1,水蒸汽的C p,m= 33.2 J·K-1·mol-1)。
