流体力学与叶栅理论
流体力学习题及答案

流体力学与叶栅理论 课程考试试题一、 选择题(每小题1分,共10分)1、在括号内填上“表面力”或“质量力”:摩擦力( ); 重力( ); 离心力( ); 浮力( ); 压力( )。
2、判断下列叙述是否正确(对者画√,错者画╳):(a) 基准面可以任意选取。
( )(b) 流体在水平圆管内流动,如果流量增大一倍而其它条件不变的话,沿程阻力也将增大一倍。
( )(c) 因为并联管路中各并联支路的水力损失相等,所以其能量损失也一定相等。
( )(d) 定常流动时,流线与迹线重合。
( )(e) 沿程阻力系数λ的大小只取决于流体的流动状态。
( )二、 回答下列各题(1—2题每题5分,3题10分,共20分)1、什么是流体的连续介质模型?它在流体力学中有何作用?2、用工程单位制表示流体的速度、管径、运动粘性系数时,管流的雷诺数410Re ,问采用国际单位制时,该条件下的雷诺数是多少?为什么?3、常见的流量的测量方法有哪些?各有何特点?三、计算题(70分)1、如图所示,一油缸及其中滑动栓塞,尺寸D =120.2mm ,d =119.8mm ,L =160mm ,间隙内充满μ=·S的润滑油,若施加活塞以F=10N的拉力,试问活塞匀速运动时的速度是多少?(10分)题1图2、如图所示一盛水容器,已知平壁AB=CD=2.5m,BC及AD为半个圆柱体,半径R=1m,自由表面处压强为一个大气压,高度H=3m,试分别计算作用在单位长度上AB面、BC面和CD面所受到的静水总压力。
(10分)题2图3、原型流动中油的运动粘性系数υp=15×10-5m2/s,其几何尺度为模型的5倍,如确定佛汝德数和雷诺数作为决定性相似准数,试问模型中流体运动粘性系数υm=?(10分)4、如图所示,变直径圆管在水平面内以α=30。
弯曲,直径分别为d1=0.2m,d2=0.15m,过水流量若为Q=0.1m3/s,P1=1000N/m2时,不计损失的情况下,求水流对圆管的作用力及作用力的位置。
流体动力学及叶栅理论.

流体动力学及叶栅理论课程小结《流体动力学及叶栅理论》下篇课程主要包括流体动力学和叶栅理论两部分。
其中流体动力学的主要内容是:流体力学性质及概念、流体运动的基本方程、平面有势流动、势流叠加、旋涡理论等。
叶栅理论主要内容是:机翼及翼型特性、茹科夫斯基翼型、薄翼绕流及有限机翼理论、叶栅及叶栅特性方程、平面叶栅绕流求解方法等。
一、流体动力学流体力学是研究流体平衡和运动的规律以及它与固体间的相互作用的科学。
流体力学性质及概念:包括流体的流动性和粘滞性(相互运动时的内摩擦力产生的)、迹线(流体为团运动的轨迹线)、流线(指某时刻t时,连接流场中各点流体微团运动方向的光滑曲线)、微团分析(流体微团具有平移、旋转及变形的特征)等。
流体运动的基本方程:包括连续性方程、动量方程与动量矩方程、纳维-斯托克斯方程、欧拉方程(粘度为零的方程)、能量方程等。
平面有势流动:包括均匀流(流动过程中运动要素不随坐标位置(流程)而变化)、平面源、汇(与平面源的流向相反)、点涡(环流)、偶极子等基本概念,速度势函数和流函数,简单平面势流、偶极流、有环量绕流和无环量绕流(两者相差一个点窝)等。
势流叠加:包括源流和均匀流叠加、等强度源和汇流与直线流叠加、偶极流、圆柱绕流、汇流和环流的叠加、以及其他由两种或两种或以上的基本势流叠加等。
旋涡理论:包括涡线、涡管、涡束、涡通量(旋涡强度)等基本概念,开尔文-汤姆逊定理、斯托克斯定理(当封闭周线内有涡束时,则沿封闭轴线的速度环量等于该封闭周线内所有涡束的涡通量之和),亥姆兹定理(包括第一定律、第二定律和第三定律),二元旋涡内外压力分布等。
二、叶栅理论1、机翼及翼型机翼的外形以椭圆形状最为有利,但由于制造上的困难难,实际多采用与椭圆相近的形状。
翼型指的是顺着来流方向切下来的剖面。
翼型通常都具有流线型外形,头部圆滑,尾巴尖瘦,背(上弧)稍拱曲,腹(下弧)的形状则有凹的、凸的、半凹半凸的及平的。
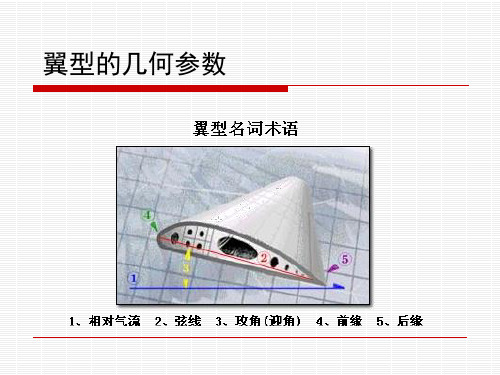
机翼几何参数:机翼翼展b、机翼面积A、平均翼弦lm(A/b)、展翼比 (b/lm)、翼弦l、翼型厚度d(最大的叫翼型最大厚度dmax)、翼型弯度f、前、后缘圆角半径。
流体动力学及叶栅理论课程作业—河海大学

流体动力学及叶栅理论(下篇)一、课程内容小结1.机翼及翼型特性机翼的几何特性:翼型几何参数(翼弦、翼型厚度、翼型弯度、前、后缘圆角半径和后缘角),机翼几何参数(机翼翼展、机翼面积、平均翼弦、展弦比)。
机翼的气动力特性:机翼与绕流流体相互作用的力学特性,叫做机翼的气动力特性。
机翼绕流:正问题和反问题。
机翼分类:无限翼展机翼和有限翼展机翼。
翼型绕流的实验结果:介绍翼型气动方性能,随冲角及翼型几何形状变化的实验结果。
冲角对翼型气动力性能的影响翼型的升力和助力:升、阻力系数曲线,升、阻力极曲线。
压力沿翼型表面的分布:工程上不仅很重视翼型上的总作用力,而且对压力沿翼型表面如何分布也很关心,特别是在水利机械中,压力沿叶片的分布情况,关系到叶轮汽蚀性能的好坏。
翼型几何形状对动力性能的影响:弯度的影响,厚度的影响,前缘抬高度的影响,表面粗糙度的影响,雷诺数的影响。
常见翼型:NACA四位数字翼型,NACA五位数字翼族,以及其他翼型。
2.茹可夫斯基翼型对于翼型绕流的理论分析,分别介绍翼型绕流的保角变换与点奇点分布两种解法。
茹可夫斯基变换变换图解。
变换图形:圆心在原点的圆,圆心在坐标轴上的圆,圆心在第二象限的圆。
圆柱绕流。
圆柱绕流的来流速度。
圆柱绕流的来流环量。
绕流翼型流动的复势绕翼型流动的速度场。
翼型气动力特性。
翼型上的作用力:在理想流体的条件下,翼型将不受阻力,翼型上只作用者升力。
升力的大小,可以类似于圆柱绕流那样求出,结果也和圆柱绕流时一样。
升力系数。
3.薄翼绕流及有限翼展机翼理论当流体绕流翼型时,由于翼型的存在产生对来流的扰动,改变了来流的性态。
它一方面使流动顺翼型表面偏折,并形成一条流线;另一方面使流速值在翼型两侧产生跃变,出现了速度差和压力差,并进而产生了升力。
由于翼型对来流的扰动的作用,可以用沿翼型适当分布的涡、源(奇点)来代替,把这种计算绕翼型流场的方法,称为奇点分布法。
薄翼绕流。
薄翼绕流的特点:翼型厚度很薄,翼型中弧线微弯,在小冲角之下被绕流。
《流体力学与叶栅理论》课程思政优秀案例

《流体力学与叶栅理论》课程思政优秀案例一、课程介绍《流体力学与叶栅理论》课程40学时,2.5学分,秋季学期开课,面向我校能源与动力工程专业大三学生,是能源与动力工程专业基础课与核心课程。
课程主要涵盖3个单元的内容:理想流体动力学、粘性流体动力学基础和机翼理论与叶栅理论基础,其中理想流体动力学和粘性流体动力学基础是基础理论部分,机翼理论与叶栅理论基础是前两个部分在机翼和叶栅中的应用。
从课程知识结构可以看出本课程是一门面向工程实际应用的课程,在课程学习过程中需要与工程实际紧密结合,是一门从理论学习到实际应用全覆盖的课程。
二、课程思政育人目标课程以知识掌握、创新能力培养和价值观树立为育人目标。
(1)在知识掌握层面,不仅使学生掌握流体力学知识,还应掌握课程所涉及的数学、物理和流动测量等方面的综合知识。
(2)在创新能力培养方面,利用流体力学课程面向工程实际应用的特点,训练学生综合运用所学知识识别、表达、并通过文献研究等分析问题和解决问题的能力,在此过程中激发学生的创新意识,培养学生的创新能力。
(3)在价值观树立方面,利用流体力学课程前沿属性和在卡脖子领域中的应用,激发学生爱国和服务建设祖国的热情,形成社会主义核心价值观,并坚定成为社会主义建设者和接班人的理想信念。
三、经典课程思政案例设计和展示在育人大纲制定方面,秉承以学生为中心和以学为核心的教育理念,将立德树人教育和创新能力培养融入教育教学全过程。
在以学生为中心方面,将课程内容知识点化,让学生选择自己感兴趣的知识点进行准备和课堂讲解,采用这种知识点学生讲的翻转课堂形式,激发学生学习兴趣和主动性,配合学生互评、过程评价的课程成绩评价体系,融合教与学,达到以学生为中心、以学为核心的教学效果。
在立德树人教育方面,结合流体力学在国防和航空航天领域的应用案例讲解,分享国家在科技封锁的严峻条件下自主研发所取得的成就,激发学生的爱国和服务建设祖国的社会主义价值观。
在创新能力培养方面,结合流体力学课程面向工程实际应用的特点,结合教师自身的科研工作,在教学过程中融入相关课程领域的前沿知识和应用,通过已有的一些前沿应用实例讲解,激发学生的创新意识,培养学生的创新能力。
流体力学第十一章 翼型与叶栅理论

儒可夫斯基假设最简单的敘述是:在实际流动中无限大的 速度是不允许的。
库塔---儒可夫斯基定理描述了升力与环量的关系,没有环 量,就没有升力。而且升力方向垂直于来流速度;如果绕物体 的流动为势流并且不发生分离,平行于来流方向上没有力(阻力), 阻力仅由边界层内表面摩擦产生。
第十一章 翼型与叶栅理论
翼型的几何参数 翼型的气动参数 儒可夫斯基变换 库塔—儒可夫斯基原理 叶栅理论 二维叶栅流动理论 离心泵及内流图例
翼型的几何参数
翼型的气动参数
升力 阻力 俯仰力矩
儒可夫斯基变换
z
1 2
b2
儒可夫斯基变换在平板绕流问题中的应用
叶栅理论
按照一定规律排列起来的相同机翼,叫做翼栅。 翼栅理论是研究翼栅绕流规律的,是单个翼型绕流的推广。 在叶片式流体机械方面应用极广泛,故翼栅也称叶栅,组成它 的机翼也因此称为叶片。
叶栅的几何参数: 列线:叶栅中叶片上对应点连线(直线和圆周线)。 栅轴:与列线垂直的直线。 叶型:叶片与过列线之流面相交所得截面。 栅距:同一列线上,两相邻的对应点间线段长度。 安放角:弦与列线的夹角。 疏密度:弦长与栅距之比,倒数为相对栅距。
(b)
Ry wx (w'y' w'y )t
在上下游断面AD与BC处列出伯努利方程:
p' 1 2
wx2 w'y2
p''
1 2
(wx2
w'y' 2 )
从而:
p' p'' 1 2
流体力学习题及答案

1. 连续介质假设意味着
(A)流体分子互相紧连
(D)
5.温度为20r,压强为105Pa的空气密度为
kg/m3。
(A)341
(B)17.42
(C)1.19
(D)0.041
6. 水的体积弹性模数
空气的弹性模数。
(A)小于(B)近似等于(C)大于
7. 静止流体剪切应力。
(A)不能承受(B)可以承受(C)能承受很小的(D)具有粘性时可承受 8. 温度升高时,空气的粘性系数
回答下列各题(
1、什么是流体的连续介质模型?它在流体力学中有何作用?
2、用工程单位制表示流体的速度、管径、运动粘性系数时,管流的雷诺数Re104, 问采用国际单位制时,该条件下的雷诺数是多少?为什么?
3、常见的流量的测量方法有哪些?各有何特点?
三、计算题(
1、如图所示,一油缸及其中滑动栓塞,尺寸D=120.2mm, d=119.8mm, L=160mm,
流体力学与叶栅理论
课程考试试题
压力(
(a)基准面可以任意选取。(
(b)流体在水平圆管内流动,如果流量增大一倍而其它条路的水力损失相等,所以其能量损失也一定相 等。()
(d)定常流动时,流线与迹线重合。()
(e)沿程阻力系数入的大小只取决于流体的流动状态。()
确定佛汝德数和雷诺数作为决定性相似准数,试问模型中流体运动粘性系数u=?(10分)
4、如图所示,变直径圆管在水平面内以a=30。弯曲,直径分别为d1=0.2m,
叶栅理论

2.空间叶栅 流经叶栅流道的流动是空间流动。如:混流式水轮机、水泵、风机的叶轮。 3.直列叶栅 流面上列线成一无限长直线,为直列叶栅,如:轴流式叶轮叶栅。 4.环列叶栅 流面上列线为圆周线,为环列叶栅。如:离心式叶轮叶栅为环列叶栅。 5.不动叶栅 叶栅本身不运动为不动叶栅。如:导叶。 6.运动叶栅 叶栅本身运动,为运动叶栅。又可以分为移动和转动叶栅。
对控制体内的流体列动量方程( ∑ Fx , ∑ Fy 为对流体的作用力) :
∑ Fx = ρ Q( β 2v2 x β1v1x ) ∑ Fy = ρ Q( β 2v2 y β1v1 y )
(1)
对理想流体: β1 , β 2 = 1,另外 Q = w2 xt = w1xt = wxt ,所以 w2 x = w1x = wx p1t p2t Rx = ρwxt ( w2 x w1x ) (2) Ry = ρwxt ( w2 y w1 y ) 将 w2 x = w1x = wx 代入并整理可得:
根据栅前、栅后速度的变化,可将叶栅分成: 1.收敛叶栅 叶栅进口到出口断面是减少的(收敛) ,因而流动是加速的,压力下降, 如水轮机转轮叶栅。 2.扩压叶栅 叶栅流道断面是扩张的,此时流速下降而压力上升,如轴流式水泵。 3.冲击叶栅 叶栅前后速度、压力大小相等,但方向发生改变,如冲击式水轮机叶栅。 二 、 栅中翼型的受力 无穷空间单个翼型的受力为:
K:
设有二个流量相等、绕同一叶栅的不同流动,对这二个流动列它们的特 征方程:
Γ2 1 = K Γ1 1 + (1 K ) i0 q Γ2 2 = K Γ1 2 + (1 K ) i0 q
两式相减:
Γ2 2 Γ2 1 = K (Γ1 2 Γ1 1 ) Γ2 = K Γ1 K= Γ2 Γ1
微尺度射流、平板边界层及叶栅流动实验研究

南京航空航天大学硕士学位论文微尺度射流、平板边界层及叶栅流动实验研究姓名:***申请学位级别:硕士专业:航空宇航推进理论与工程指导教师:梁德旺;黄国平20060101南京航空航天大学硕士学位论文摘要本文以某型微型涡轮喷气发动机研制为背景,以认识微尺度下粘性流体流动状态及其机理和微涡轮叶栅通道内部流动特性为目的,设计并搭建了除本实验外还可供其他流体力学实验使用的微型风洞,并在该微型风洞基础上进行了微尺度射流实验、微尺度壁面边界层实验和微尺度涡轮叶栅实验。
微射流实验在出口宽度固定为20mm情况下,选取了3种不同出口高度:2mm,3mm和5mm,并通过改变速度使出口高度雷诺数在约20000到约55000之间改变,实验得到了流动图谱和微射流数学模型。
实验发现微射流中内外层流体微团之间的动量交换较常规大尺度下减弱,掺混变得相对缓慢,射流特征半厚度相对减小,从而初始段扩张角和基本段极角都有所减小。
该实验还同时研究了下游较远处射流流动情形,发现其掺混强度在微尺度二维平面射流和常规三维射流之间。
微尺度平板边界层实验选取从总长度为15mm的微平板前缘8mm到14mm之间的7个站位,4种马赫数,13个不同雷诺数(从35000到150000)的实验状态,发现了该尺度下边界层流动的一些新的特点,如形状因子比常规大尺寸下充分发展湍流状态的形状因子更小等。
微尺度叶栅实验使用弦长5.64mm的VKI-1叶型,选取了4种安装角度,3种叶尖间隙,4种出口主流马赫数状态的实验,得到了叶栅出口的总损失分布云图,发现微尺度叶栅栅后高损失区域与栅距的比例较常规大尺度下明显增大;同时对叶栅出口流动损失进行了分析,发现为了提高涡轮的效率,需要尽可能减小叶尖间隙并选择合适的安装角度(针对本实验中叶栅,最佳安装角为45~50度)。
关键词微流动微射流平板边界层流动涡轮叶栅Experimental Research on Micro Jet Flow , Flat Plate Boundary Layer Flow & Turbine Cascades FlowAbstractThis dissertation has on the research and design of a Micro Turbine Engine as background and it is for the purpose of comprehending viscous flow behaviors in micro scaled conditions and that in the mini-turbine cascades. A mini wind tunnel is designed and set up which also can be used in other micro flow experiments. On the basis of this mini wind tunnel, three mini flow experiments, including micro jet experiment, micro boundary layer experiment and mini-turbine cascades experiment, have been carried out.The micro jet experiment is under conditions of 3 different heights, 2mm, 3mm and 5mm of 2D (2 dimensional) rectangle jet outlet and the width of each is same, 20mm. 5 Reynolds numbers vary from 20,000 to 55,000.The experiment characters tell that compared with that of the normal scaled jet flow, the dilution power of this micro jet becomes weaker. Furthermore, the flow in the far down stream are also researched. The diluting power of the flow within this area is between that of 2D micro jets and normal scale 3D jets.The micro boundary layer experiment is carried out from 8mm to 14mm of a 15mm-long micro plane. Re numbers vary from 35,000 to 150,000 and 4 different Mach numbers are selected. Some new characters are discovered, such as velocity curve factor is smaller than that of well developed normal scale turbulence Boundary Layer.VKI-1 cascade with 5.64mm chord is adopted in mini-turbine cascades experiment. 4 assembly angles, 3 different blade tip clearances and 4 Mach number statuses are chosed as status variables. From 12 total pressure distribution maps, a conclusion is formed that ratio of high-loss area to full width of cascades period is large that that of normal scaled cascedes. Based on effiociency analysis,it has been found that narrower blade tip clearance and right assembly angle lead to utmost efficience. (e.g. 45~50 degree for this micro VKI-1 cascades)Keywords: Micro Flow, Micro Fluid, Micro jet(s), Flat Plate Boundary Layer Flow, Turbinary Cascades.承诺书本人郑重声明:所呈交的学位论文,是本人在导师的指导下,独立进行研究工作所取得的成果。
第十一章翼型与叶栅理论
)
1
2
z
a2
1
2 1
2 z 1
a2
0
1 z z2 a2
取”+”,取板外区 域
得:
W (z) 2iv z2 a2
由条件:
dW
dz
i v0
z
dW dz
z
2iv
z z2 a2
z
2iv
速度关系: v0 2v W i v0 z2 a2
儒可夫斯基翼型绕流
无环量时:
W(
非定常速度的演化-旋转框架下
2 Ri
解得:
2 Rv0 sin( )
有时称 ( ) 为绝对攻角
二元机翼中:
CL
FL
b • v02
2
对于儒可夫斯基翼型:
b 4R
故升力系数为:
CL
v0 2 Rv0 sin( 4Rv02 / 2
)
(
)
对于小的绝对攻角,升力系数随绝对攻角线性增加,迫近 失 速角时,升力会急剧下降。
库塔—儒可夫斯基原理
2) 同一叶型单独绕流和置于叶栅中在同一攻角下被绕流时,其动力 特性也不同。加速叶栅中叶型,其升力系数大于单独叶型的升力系 数,但减速叶栅中叶型升力系数恒小于单独叶型的升力系数。
离心泵及内流图例
绝对速度分布的变化
压强分布的变化
初始场的非定常模拟
某一时刻的流动
非定常速度的演化-固定框架下
静止流场中有一翼型,翼型起动前,整个流场无旋; 翼型起动并达到图示速度,此时后缘点处速度达到很大的值,压力 很低,机翼下侧面流体绕过后缘点流向驻点,流体同低压流向高压,流 动产生分离,产生逆时针旋涡随流体向尾部移动,在尾部脱落; 总环量为零,在翼型上同时产生一个脱落涡强度相同而方向相反的 涡,这个涡的作用使驻点向后缘点移动,在沿未达到后缘点时,不断有 逆时针旋涡产生并脱落,而在翼型上涡的强度也将继续加强。 不断脱落流向下游的涡称为起动涡,附在翼型上的涡称为附着涡; 驻点移至后缘点后,上下两股流动在后缘汇合,不再有涡脱落,附着涡 的强度也不再变化,机翼环量值对应均匀直线来流情况下翼型绕流的环 量值。
流体动力学及叶栅理论

CR
R 1 2 v l 2
式中 R 为合力,而且此直线与横轴夹角就等于合力与来流的夹角; (3)上述直线斜率为
Cy Cx FY FX
即为在该点冲角下工作时的翼型升阻比;
(4)通过极曲线很容易确定翼型的最佳冲角——与ε最大值对应的冲角。过原点作极曲线的切线,其 切点所对应的冲角,就是最佳冲角。
5
5.2 翼型绕流的实验结果
在这一节里,介绍翼型气动方性能,随冲角及翼型几何形状变化的实验结果。
5.2.1 冲角对翼型气动力性能的影响
5.2.1.1 翼型的升力与阻力 在单翼型绕流情况下,由于沿翼展取为单位长,从而机翼面积:
A l 1 l
升、阻力公式(5-1)对翼型可写成:
2 v
FY C y FX C x
2
录
第5章
5.1 概 述
机翼及翼型特性
机翼一词,最早出现于航空工程,指的是飞机翅膀。如今它可用以泛指相对于流体运动的各种升 力装置。因此,流体机械中的工作轮叶片也可视为一个机翼。
5.1.1 机翼的几何特性
工程上引用机翼主要是为了获取升力,但由于在流体中运动的物体,不可避免地会遭受到流体阻 力的作用,因此对机翼性能的要求,首先就是尽可能大的升力 Fy 和尽量小的阻力 Fx,也就是希望具有 这就要求机翼采取适当的几何形状, 图 5-1 是一个低速机翼的一般外形图。 最佳的、 阻力比值ε=Fy/Fx。
f max
xf f max , xf l l
像厚度一样,这些相对值习惯上常用百分数表示:
f max xf
f max 100% l xf l 100%
(4)前、后缘圆角半径和后缘角 翼型前,后缘的曲率半径,叫做翼型的圆角半径,分别以 RL、RT 记之。它们的相对值 RL=RL/l、
《流体力学与流体机械》教学课件—10机翼与叶栅理论

中弧线的y坐标
局部厚度的一半
NACA翼型
NACA翼型是美国国家航空资讯委员会(National Advisory Committee for Aeronautics)所发表的 翼型系列,有以下常用的系列翼型:
(1)NACA四位数字翼型
厚度方程为: 最大厚度
1
2i
C
f (z) z z0
dz
0, z0在C外
f
(
z
0
),
z
0
在C内
第四节 儒可夫斯基翼型 与保角变换法
一、保角变换法求解平面势流
利用解析的复变函数 z =f(ζ)将ζ平面上的圆域变换
成z平面上的实用域。
Z
y
z
Cz
ζ
η
Cζ
o
V∞z αz
x
V∞ζ
o
αζ
ξ
注意:
保角变换过程中,同一点两个线段的夹角在变换过 程中保持不变。
机翼一部分是由流过上表面的空气把它吸 起来的,且上表面产生的负压对全部升力的 贡献大于下表面的贡献。
吸力
压力系数分布曲线
压力
较大攻角翼型绕流
翼型表面压强的分布
大攻角翼型绕流
流体绕过翼型时要产生升力,是由于翼型 上下表面速度不同造成压强分布的不同。 将上下翼面速度分布的差异视为均匀的无 穷远来流与由翼型形成的有一定环量的环 流两者叠加而成。 升力的大小与流体绕流翼型的环量Γ成正比, 即
f (z)
f
(z0
)
(z
z0
)
f
'(z0
)
(z
z0 n!
)n
叶栅流动特性数值计算

《叶栅流动特性数值计算》实验指导书航空航天学部动力系2012年12月实验一 亚声速叶栅流动特性数值计算实验Numerical Experiment of Flow Characteristic of Subsonic Cascade一、实验目的1、初步学习计算流体力学理论知识,加深对叶栅流动理论的认识;2、初步掌握计算流体力学相关软件;3、掌握亚声速叶栅流动的数值模拟方法;4、掌握对数值计算结果的分析与处理方法。
二、实验内容本实验内容包括以下三个部分:1、初步学习计算流体力学理论知识,包括N-S 方程、离散方法和湍流模型。
2、学习相关流体力学软件:GAMBIT 和 FLUENT ;3、掌握亚声速叶栅流动的数值模拟方法,其中包括以下部分:1)计算域的建立与网格划分;2)亚声速叶栅流动的数值求解,;3)数值计算结果的处理与分析。
三、计算流体力学理论知识1、N-S 方程Navier-Stocks 方程是描述粘性流体方程,简称N-S 方程。
其中,ρ是流体密度;p 是压力;u ,v ,w 是流体在t 时刻,在点(x ,y ,z )处的速度分量。
常数μ依赖于流体的性质,叫做粘性系数。
S 为源项。
连续方程 ()0ρρ∂+=∂div u t动量方程 ()()()ρρμ∂∂+=-++∂∂Mx u p div uu div grad u S t x()()()ρρμ∂∂+=-++∂∂My v p div vu div grad v S t y()()()ρρμ∂∂+=-++∂∂Mz w p div wu div grad w S t z能量方程 ()()()ρρρ∂+=-++Φ+∂i i div iu p divu div k grad T S t状态方程(),ρ=p p T (),ρ=i i T2、离散方法1)有限差分法 有限差分法是数值解法中最经典的方法。
它是将求解域划分为差分网格,用有限个网格节点代替连续的求解域,然后将偏微分方程(控制方程)的导数用差商代替,推导出含有离散点上有限个未知数的差分方程组。
流体力学与流体机械——第10章(机翼与叶栅理论6-7)

满足条件:
(1)平板叶栅与原叶栅的栅距t相等;
(2)安放角等于原叶栅的无环量绕流角β0(即
零升力方向);
升力系数
(3)弦长满足:b (Clz / Cl )bz
五、叶栅绕流问题的解法
叶栅绕流的求解分为正命题和反命题。
基本思想是应用保角变换,把给定的叶栅平面 变换到某一辅助平面,使在辅助平面上的绕流 是已知的或容易求解的。这样,在叶栅平面上 的流动就可以逆变换关系求出。
3. 奇点法 用来解任意叶栅正、反命题的现代方法之一。 其实质是在有势流场中置入的点源系与点涡 系替代叶栅中的翼型,以确定流场受叶栅干 扰后的流动。
第六节 叶栅及叶栅特征方程
叶片式水力机械的转轮、导叶轮都由若干 个相同的叶片或翼型按相互等距离排列组 成,叶片或翼型之间将彼此相互影响。 按 照一定规律排列起来而又相互影响的叶片 或翼型的组合,叫做翼栅或叶栅。
叶栅理论的目的在于寻找叶栅与流体之间 相互作用的运动学和动力学规律,以及影 响这些规律的各种因素,是叶片式水力机 械水动力学计算的理论基础。
v1xv2 y 'v2 xv1 y '
v1xv2 y 'v2 xv1 y '
引入新的系数i0
i0
m 1 K
式(3)可写成
v y '' Kv y '(1 K )i0v x (4)
上式两端同时乘以列线长度2πr, r为展 开成平面叶栅的圆柱流面的半径,有
2rv y '' 2rKv y '2r(1 K )i0v x
4. 安放角 翼型的弦线与列线之间的夹角称为安放角, 用βs表示。中弧线在前缘点处的切线与列 线的夹角叫进口安放角,用βs1表示。同样可 定义出口安放角βs2 。
第四章叶栅理论

第四章 叶栅理论 §4—1 概 论把按照一定规律排列起来的相同机翼之系列,叫做翼栅。
翼栅问题是单个机翼问题的推广。
翼栅理论在工程上得到广泛应用,特别是在叶片式流体机械方面。
因此,翼栅常被称为叶栅,组成它的机翼也就叫做叶片了。
一、叶栅几何参数表征一个叶栅的几何特征的参数,叫做叶栅的几何参数。
叶栅的几何参数主要有下列几个:(一)列线栅中诸叶片上各相应点的联结线,称为叶栅的列线。
通常都以叶片前后缘点的联线表示之。
实际上所遇到的列线,其形状有两种:一为无限长直线;另(见图4一1)。
(二)栅轴垂直于列线的直线叫栅轴。
但对圆周列线的叶栅,把旋转轴定义为其栅轴。
有些文献中,把上述列线叫做栅轴,而不再引用列线这一名词。
(三)叶型叶片与过列线的流面交截出来的剖面形,叫叶栅的叶型。
其一几何参数见翼型。
图4—1直列叶栅与环列叶栅(四)栅距列线上二相邻的相应点间的线段长度,叫叶栅的栅距或栅隔,用字母t 记之。
对圆列线叶栅,不引用此参数,而用角距nπ2(n ——叶片数)代替它。
(五)安放角叶型的弦与列线间之夹角e β,称为叶型在叶栅中之安放角。
叶型中线在前、后缘之切线与列线之夹角'e β、''e β分别叫作叶型的进、出口安放角。
对圆列线叶栅,只引用后二个参数。
(六)疏密度栅中叶型弦长l 与栅距t 之比值t l /,叫做叶栅的疏密度。
而把其倒数l t /,称为相对栅距。
圆列线叶栅不引用此参数。
二、叶栅分类在工程实际当中所遇到叶栅多种多样,为便于分析和讨论问题,可以给这些叶型加以分 类。
但从不同角度又可得出不同的分类,这里仅就水力机械中常用到的分类法,介绍两种。
(一)根据绕流流面分类叶栅1.平面叶栅如能将绕叶栅液流分成若干等厚度流层,这些流层本身为平面或这些流层虽为曲而,但若沿流线切开后,能铺展成一平面者,称这类叶栅为平面叶栅。
绕这类叶栅的流动为平面流动。
例如水轮机的导叶叶栅,低比速水轮机和水泵的转轮叶栅等,绕流这些叶栅的流面本身就是平面;而轴流式水轮机、水泵和风机等转轮叶栅之流面,虽为圆柱面,但顺流线切开后可展成平面。
流体动力学及叶栅理论.

流体动力学及叶栅理论课程小结《流体动力学及叶栅理论》下篇课程主要包括流体动力学和叶栅理论两部分。
其中流体动力学的主要内容是:流体力学性质及概念、流体运动的基本方程、平面有势流动、势流叠加、旋涡理论等。
叶栅理论主要内容是:机翼及翼型特性、茹科夫斯基翼型、薄翼绕流及有限机翼理论、叶栅及叶栅特性方程、平面叶栅绕流求解方法等。
一、流体动力学流体力学是研究流体平衡和运动的规律以及它与固体间的相互作用的科学。
流体力学性质及概念:包括流体的流动性和粘滞性(相互运动时的内摩擦力产生的)、迹线(流体为团运动的轨迹线)、流线(指某时刻t时,连接流场中各点流体微团运动方向的光滑曲线)、微团分析(流体微团具有平移、旋转及变形的特征)等。
流体运动的基本方程:包括连续性方程、动量方程与动量矩方程、纳维-斯托克斯方程、欧拉方程(粘度为零的方程)、能量方程等。
平面有势流动:包括均匀流(流动过程中运动要素不随坐标位置(流程)而变化)、平面源、汇(与平面源的流向相反)、点涡(环流)、偶极子等基本概念,速度势函数和流函数,简单平面势流、偶极流、有环量绕流和无环量绕流(两者相差一个点窝)等。
势流叠加:包括源流和均匀流叠加、等强度源和汇流与直线流叠加、偶极流、圆柱绕流、汇流和环流的叠加、以及其他由两种或两种或以上的基本势流叠加等。
旋涡理论:包括涡线、涡管、涡束、涡通量(旋涡强度)等基本概念,开尔文-汤姆逊定理、斯托克斯定理(当封闭周线内有涡束时,则沿封闭轴线的速度环量等于该封闭周线内所有涡束的涡通量之和),亥姆兹定理(包括第一定律、第二定律和第三定律),二元旋涡内外压力分布等。
二、叶栅理论1、机翼及翼型机翼的外形以椭圆形状最为有利,但由于制造上的困难难,实际多采用与椭圆相近的形状。
翼型指的是顺着来流方向切下来的剖面。
翼型通常都具有流线型外形,头部圆滑,尾巴尖瘦,背(上弧)稍拱曲,腹(下弧)的形状则有凹的、凸的、半凹半凸的及平的。
机翼几何参数:机翼翼展b、机翼面积A、平均翼弦lm(A/b)、展翼比 (b/lm)、翼弦l、翼型厚度d(最大的叫翼型最大厚度dmax)、翼型弯度f、前、后缘圆角半径。
第四章叶栅理论

第四章 叶栅理论 §4—1 概 论把按照一定规律排列起来的相同机翼之系列,叫做翼栅。
翼栅问题是单个机翼问题的推广。
翼栅理论在工程上得到广泛应用,特别是在叶片式流体机械方面。
因此,翼栅常被称为叶栅,组成它的机翼也就叫做叶片了。
一、叶栅几何参数表征一个叶栅的几何特征的参数,叫做叶栅的几何参数。
叶栅的几何参数主要有下列几个:(一)列线栅中诸叶片上各相应点的联结线,称为叶栅的列线。
通常都以叶片前后缘点的联线表示之。
实际上所遇到的列线,其形状有两种:一为无限长直线;另(见图4一1)。
(二)栅轴垂直于列线的直线叫栅轴。
但对圆周列线的叶栅,把旋转轴定义为其栅轴。
有些文献中,把上述列线叫做栅轴,而不再引用列线这一名词。
(三)叶型叶片与过列线的流面交截出来的剖面形,叫叶栅的叶型。
其一几何参数见翼型。
图4—1直列叶栅与环列叶栅(四)栅距列线上二相邻的相应点间的线段长度,叫叶栅的栅距或栅隔,用字母t 记之。
对圆列线叶栅,不引用此参数,而用角距nπ2(n ——叶片数)代替它。
(五)安放角叶型的弦与列线间之夹角e β,称为叶型在叶栅中之安放角。
叶型中线在前、后缘之切线与列线之夹角'e β、''e β分别叫作叶型的进、出口安放角。
对圆列线叶栅,只引用后二个参数。
(六)疏密度栅中叶型弦长l 与栅距t 之比值t l /,叫做叶栅的疏密度。
而把其倒数l t /,称为相对栅距。
圆列线叶栅不引用此参数。
二、叶栅分类在工程实际当中所遇到叶栅多种多样,为便于分析和讨论问题,可以给这些叶型加以分 类。
但从不同角度又可得出不同的分类,这里仅就水力机械中常用到的分类法,介绍两种。
(一)根据绕流流面分类叶栅1.平面叶栅如能将绕叶栅液流分成若干等厚度流层,这些流层本身为平面或这些流层虽为曲而,但若沿流线切开后,能铺展成一平面者,称这类叶栅为平面叶栅。
绕这类叶栅的流动为平面流动。
例如水轮机的导叶叶栅,低比速水轮机和水泵的转轮叶栅等,绕流这些叶栅的流面本身就是平面;而轴流式水轮机、水泵和风机等转轮叶栅之流面,虽为圆柱面,但顺流线切开后可展成平面。
科学方法与流体动力学叶栅

科学方法与流体动力学叶栅作者:李沛工作单位成都卓伦动力科技有限责任公司[摘要]本文通过对流体学各个领域的哲学思考,详细的阐述了自然辩证法三大组成部分之一的科学认识方法论对流体动力学的深刻影响,说明了计算机、科学认识系统、科学问题、科学观察、科学实验等要素在流体力学研究、流体机械生产发挥的重要作用。
[关键词]科学方法叶栅计算机水轮机流体力学随着科学技术的迅猛发展,最大限度地利用最先进的现代科技对传统的理论领域进行深刻的剖析、研究,已在各个学科广泛的展开,流体力学是一门古老的学科,“科学是生产的另一个可变要素,而且不仅是科学不断变化、完善、发展等方面而言。
科学的这种过程或科学的这种运动本身,可以看作积累过程的因素之一。
”[1]流体力学也随着人类的进步,不断的发展、完善,现在已进入用计算机进行三维流场模拟、分析的计算流体力学阶段(CFD),牵涉领域之广、考虑因素之复杂都是空前的,是对许许多多未知对象的探索,科学方法作为认识客观对象的途径和手段,对于科学研究有着十分重要的作用。
良好的方法能使我们更好地发挥运用天赋的才能,而拙劣的方法则可能阻碍才能的发挥,以水轮机为例,长期以来人们对水力设计的方法和理论进行了大量的研究,各过流部件的设计方法为:1、传统的蜗壳设计方法有两种:等速度矩法和等周向平均速度法2、导水机构由固定导叶和活动导叶组成,活动导叶很少进行专门设计,一般都套用现行的标准导叶。
固定导叶的设计常采用一维方法,认为固定导叶不改变环量。
3、混流式转轮的水力设计采用叶片数为无穷多、叶片厚度为无限薄的轴对称假定。
4、轴流式转轮的水力设计中采用圆柱层无关假设,常用的方法有:升力法和奇点分布法。
5、尾水管也很少专门设计,常采用标准尾水管。
这些方法和理论曾对我国的国民经济建设作出过巨大的贡献,但现已远远落后于世界先进水平,掌握和应用先进的方法,是每一个科学工作者和工程技术人员都必须认真面对的问题,而获得良好方法的前提是清晰地了解科学技术认识系统。
流体力学与叶栅理论

4.旋涡泵、液环泵、射流泵
5.水轮机与叶片泵结构
6.流体力学
7.工业用离心泵设计与应用
8.计算流体力学
9.水力机械流动理论
10.工程流体力学
11.流体机械原理(上下册)
