开关电源环路补偿概述
其中 f =
1 ， Re 为等效电阻， C e 为等效电容。 2πRe C e
上式分子中对应的频率 fZ 为零点频率，分母中对应的频率 fP 为极点频率，f0 称为初始极点频率。
-2-
一个零点会在其零点频率处将斜率增加+1（20dB） 。零点会引起相位超前，由 fZ 处的零点， 引起在频率 f 处超前的相位是 θ ld = arctan f 。如下图示。 fZ
1 + j 2πfR2 C1 j 2πfR1 (C1 + C 2 )(1 + j 2πfR2 C1C 2 ) C1 + C 2
∠D ( f ) ⋅ 180 o π 幅频特性如右图上，相频特性如右图下。 θ1 ( f ) =
-7-
补偿后系统总开环传递函数如下 TV ( f ) = D( f )G ( f ) 幅频及相频特性曲线如右图。 从右边的曲线中，我们可以计算 出电压环的穿越频率： f C = 1.944 × 10 4 然后还可以计算出电压环的相位 裕量： θ 2 (1.944 × 10 4 ) + 180 = 66.427
斜率-1
斜率+1 斜率 0
fZ
fZ
斜率 0
一个极点会在其极点频率处将斜率增加-1（-20dB） 。极点会引起相位滞后，由 fP 处的极点， 引起在频率 f 处滞后的相位是 θ lag = arctan f 。如下图示。 fP fP
斜率+1 斜率 0
斜率 0
fP
斜率-1
四．常用补偿器分析 下面是 TypeII 型补偿器的电路原理图
-8-
dB
Hz 1 f2 = = 1 × 10 5 。 C1C 2 2πR2 C1 + C 2 计算实际的电阻电容参数： Rbias = 1 × 10 3 ，则 R1 = VO − VREF Rbias = 1.64 × 10 3 VREF 0o − 30o
− 60o − 90o
Hz
开环传递函数在穿越频率处增益为 0dB， 又 20 lg(| G (20 × 10 3 ) |) = −14.973 ， 则 20 lg( R2 ) = 14.973 ， R1
-6-
选择补偿器的零点 f 1 = 0.75 f P 0 = 1.40 × 10 3 ， 选择补偿器的极点 f 2 = 则 f1 = fS = 1 × 10 5 ， 2
20 lg
1 = 1.40 × 10 3 ， 2πR2 C1
R2 R1
1 1 CC 1 2πR1C2 2πR2 1 2 C1 + C2 2πR2C1
由输出电容 RSR 引起的零点： fZ0 = 幅频和相频特性曲线如下 1 = 4.019 × 10 3 2π ⋅ ESR ⋅ C OUT
-5-
从上面的曲线中，我们可以计算出电压环的穿越频率为 f C = 5.016 × 10 3 ，相位裕度 65.415。 （问题：到目前为止开环系统已经是稳定的，还需要设计环路吗？） 根据采样定理， 穿越频率(fc)必须小于开关频率的 1/2， 但实际上穿越频率必须远小于开关 频率的 1/2，否则在输出中将会有很大的开关纹波。这里开关频率为 200KHz，我们选择穿越频 率 20KHz（1/10 开关频率） 。 因为 fP0<fZ0<fC<fS/2，所以选择 Type II 型补偿器。如下图所示
阻抗用复变量 S=jω=2πf，电阻复阻抗为 R，电容 C 复阻抗为 递函数为
1 ，电感 L 复阻抗为 SL。则传 SC
VOUT ( S ) Z 2 ( S ) = 。如果输入和反馈支路是由不同的电阻和电容构成的，则幅频和相频 VIN ( S ) Z1 ( S )
曲线将会有许多种形式。把阻抗 Z1 和 Z2 用复变量 S(S=jω)表示，经过一系列的数学运算，将 会得到传递函数。由传递函数就可以绘制增益/相位曲线。 通过代数运算，把 G(S)表示为 G ( S ) = N (S ) ，其分子和分母都是 S 的函数，然后将分子和 D( S )
20 lg
R2 R1
1 1 CC 1 2πR1C2 2πR2 1 2 C1 + C2 2πR2C1
dB
其传递函数为 VOUT ( S ) = VIN ( S ) 1 + SR2 C1 SR1 (C1 + C 2 )(1 + SR2 C1C 2 ) C1 + C 2 0o − 30o
− 60o − 90o
VIN ( S )→ 0
lim [1 + H (S )G( S ) V
G(S )
IN
( S )]
| H ( S )G ( S ) |= 1 = 0dB 由此可得 1 + H ( S )G ( S ) = 0 → o ∠H ( S )G ( S ) = −180 实际中的环路是不允许出现上述情况的。 二．波特图及相关概念 波 特 图是线性非时变系统的传递函数对频率的对数坐标图，其横轴频率以对 数尺 度 （20lg[A(jω)]，单位 dB）表示，利用波特图可以看出系统的频率响应。波特图一般是由两张 图组合而成，一张幅频图表示频率响应增益的分贝值对频率的变化，另一张相频图则是频率响 应的相位对频率的变化。波特图示如下。
开关电源环路补偿概述
一．环路基本结构 VIN ( S ) +
_
G(S) H(S)
VOUT ( S )
上图中代表了最普遍的电压环路结构，由图上可得 [VIN ( S ) − H ( S )VOUT ( S )]G ( S ) = VOUT ( S ) 由上式可得传递函数 VOUT ( S ) G(S ) = VIN ( S ) 1 + H ( S )G ( S ) 其中 H(S)G(S)被称为开环增益。 在环路发生自激振荡时，即 VIN(S)=0 时，VOUT(S)不为零，则可得下式 VOUT =
分母进行因式分解，表示成多个因式的乘积，即 N (S ) = D( S ) (1 + S 2πf P 0 S S S )(1 + )(1 + ) 2πf Z 1 2πf Z 2 2πf Z 3 ， S S S (1 + )(1 + )(1 + ) 2πf P1 2πf P 2 2πf P 3
G(S ) =
20 lg
零点 f Z 1 =
极点 f P1 =
1 RRC 2π 1 3 2 R1 + R3 1 2πR2C1
1 CC 2πR2 1 2 C1 + C2 1 2π ( R1 + R3 )C3
20 lg
R2 R1
90 o
0o
− 90o
环路补偿设计步骤： 1．收集系统参数，例如输入电压，输出电压，滤波参数等，并确定开关频率； 2．确定功率级的零极点； 3．确定穿越频率和补偿器的类型； 4．确定所需要的补偿器的零极点； 5．计算实际的电阻电容参数。
20dB
| A( jω ) |= 0dB
0dB
− 20dB 0o − 90
o
Hz ∠A( jω )
− 180o
100
1000
10 4
-1-
105
106
穿 越 频 率 （ crossover frequency ） ： 增益 曲 线 穿越 0dB 线 的频 率 点 ， 即上 图 标 出 的 “A(jω)=0dB”中的ω。 相位裕量（phase margin） ：相位曲线在穿越频率处的相位和-180 度之间的相位差，即上图 中 ∠A( jω ) + 180 o 所得角度。 增益裕量(Gain margin)：增益曲线在相位曲线达到-180 度的频率处对应的增益。 三．系统稳定性判据 根据奈奎斯特稳定性判据，当系统的相位裕量大于 0 度时，此系统是稳定的。 准则 1：在穿越频率处，总开环系统要有大于 30 度的相位裕量。 准则 2：为防止-2 增益斜率的电路相位快速变化，系统的开环增益曲线在穿越频率附近的 增益斜率应为-1（-20dB/10 倍频程)。 准则 3：增益裕量是开环系统的模的度量，该变化可能导致曲线刚好通过-1 点。一般需要 6dB 的增益裕量。 （备注：应当注意，并不是绝对要求开环增益曲线在穿越频率附近的增益斜率为必须为-1，但 是由于-1 增益斜率对应的相位曲线相位延迟较小，且变化相对缓慢，因此它能够保证当某些环 节的相位变化被忽略时，相位曲线仍将具有足够的相位裕量，使系统保持稳定。 ） 要满足上述的 3 个准则，需要知道开环系统所有环节的增益和相位情况，引入传递函数的 零极点概念可以很好的分析这个问题。 下图的误差放大器中
下面是同步降压 buck 电路控制系统框图
功率级传递函数 G ( S ) =
1 + S ⋅ ESR ⋅ C OUT 1+ S( L RLOAD + ESR ⋅ C OUT ) + S 2 LC OUT
⋅ VIN ⋅
1 VOSC
由输出滤波电感和电容引起的双极点：
f P0 = 1 2π LC OUT = 1 . 868 × 10 3
14.973 20
R2 = R1 × 10 则 C1 =
= 9.194 × 10 3 ，
1 = 1.236 × 10 −8 ， f1 ⋅ 2πR2 C1 + C 2 2πR2 C1C 2
再由 f 2 =
解得 C 2 = 175.57 × 10 −12 。
补偿电路传递函数如下： D( S ) = 1 + SR2 C1 SR1 (C1 + C 2 )(1 + SR2 D( f ) = C1C 2 ) C1 + C 2
dB
R2 ( R1 + R3 ) R1 R3
Hz
Hz
-4-
五．电路实例分析 下面是同步降压 buck 电路原理图 电路参数： 输入电压 VIN=5v； 输出电压 VO=3.3v； 输出电流 IO=10A； 开关频率 fS=200KHz； 输出滤波电感 L=3.3μH； 输出滤波电容 COUT=2200μF； 输出滤波电容 ESR=0.018Ω； 负载电阻 RLOAD=0.33Ω； 调制器峰峰值 VOSC=1.25。
开关电源环路设计与计算_ON-Bright
On-Bright confidential
23
零1234....极左右左右负系在系所位点半半半半反统f统有增l平平平平馈的y稳负益对b面面面面系环a定载带c环极极零零统路k性和宽O系路点点点点D补n产所为C统-::：:固偿B生有1稳中/r有必i影电6g，-定h增不增增1须响压18为t/性益稳益益0使。输1C度了0衰定增增系o入f的相减sn减，大大统的(f移小开影id，导，，满情，右关e响引致引引足形n半频起系起起系稳t。及i平a率-统9-统定l909面)环t0震度0的性o度度零路荡相剩条T相相点e移下件n带移移影p的，响a宽零而o，选极且可点要择取将考单标对虑准
On-B开riOg关hn-tB电Erigleh源cttCr环oonnif路icdse设(nStiha计al tno与gThea计nip) aC算oo. Ltd
On-Bright confidential
1
开 开 开 一 讨关关关个论电电电基源源源于OO的环简nB-环路介B2r2i路分g6h3补析t的C偿(1以o2(内nW以反fid电容反激e源n激变ti环a变换l 路t换器o设器为Te计为例np实例)a例o)
18
DCvMvFB(ΛΛs(模s)O) ≈n式V-VBF0Br下ig⋅ 11h++PtRRoCoo12wCCooon11eSsfridSetnat由平对Figalye于面于lbtaoP零Cc小owwCkTw点zp系eM==e信(n1r统而RR/pSoHR2C更言t号aoao1PC1go容，Zoe1传)易D，无C补所函右M偿以半！相
On-Bright confidential
19
电流模式与电压模式的直观a理o 解 电压模式是占空比直接调制，变压器电感是开环状态，在外围电压回路 np 中引入一个DC极点(s=0) Te 电流模式是占空比间接调制，变压器电感是闭环状态。 l to 反激变换器类似于buck-boost架构，以buck-boost为例分析。 tia 无论是电压还是电流模式，CCM中RHZ始终存在，且频率相同。
开关电源环路中的TL431
开关电源环路中的TL431作者：安森美半导体产品线应用工程总监Christophe Basso 来源:电子设计应用2009年第4期通过极点和零点创建相位提升环路补偿的原理，在于当转换器工作在闭环时，确保所有工作条件下都有安全的相位和增益裕量。
相位增益意指在交越频率fc下环路增益T(s)的总相位旋转小于-360°，相反，总相位旋转是-360°时，相位增益容许环路增益模块与0dB轴之间存在距离。
为确保顾及这些设计条件，必须插入一个补偿电路G(s)，其任务是在选定频率下改变环路增益，使其穿越0dB轴，以及在所考虑到的频率下具备足够的相位和增益裕量。
应该如何选择交越频率呢？举例来说，有的设计人员武断地选择开关频率的1/5作为交越频率。
更好的方法是根据规范表中列出的最大下冲值来分析获得0dB轴上的交越点。
参考文献1中介绍了获得0dB交越点的一个合适方法。
为方便起见，可假定交越频率为1kHz，并以此为例展开讨论。
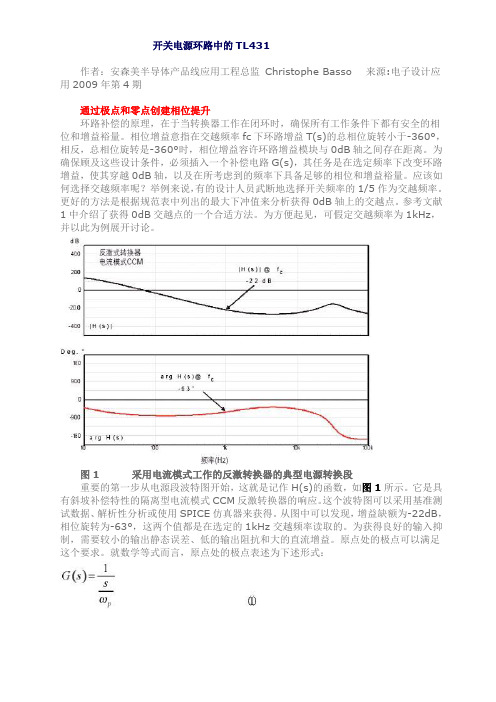
图1 采用电流模式工作的反激转换器的典型电源转换段重要的第一步从电源段波特图开始，这就是记作H(s)的函数，如图1所示。
它是具有斜坡补偿特性的隔离型电流模式CCM反激转换器的响应。
这个波特图可以采用基准测试数据、解析性分析或使用SPICE仿真器来获得。
从图中可以发现，增益缺额为-22dB，相位旋转为-63°，这两个值都是在选定的1kHz交越频率读取的。
为获得良好的输入抑制，需要较小的输出静态误差、低的输出阻抗和大的直流增益。
原点处的极点可以满足这个要求。
就数学等式而言，原点处的极点表述为下述形式：遗憾的是，将极点恰当置于原点会导致永久的相位旋转。
而且，由于使用运放或采用反向配置接线的TL431，总相位旋转将达到-270°。
因此，如果将这-270°的相位旋转与电源段-63°的相位旋转相加，最后会得到-333°的总环路相位旋转。
这就为设计提供了27°的裕量，避免冲击到-360°的限制。
开关电源环路补偿设计
开关电源环路补偿设计开关电源环路补偿设计在开关电源设计中，环路补偿是至关重要的一步。
环路补偿的正确设计可以提高电源的稳定性和效率，从而提供更为可靠的电源输出。
本文将针对开关电源的环路补偿设计，从三个方面进行阐述。
一、开关电源环路补偿的基本原理开关电源的环路补偿，是指将部分输出信号回馈到反馈端口，通过正反馈作用来改善系统的动态性能。
补偿的目的，是使电源输出稳定，对负载的响应性更好。
为了实现这一目的，设计师需要对开关电源的基本原理有深入的理解。
在开关电源中，电容、电感和频率之间的相互影响是至关重要的。
通过合理的组合设计，可以提高电源的效率，降低功耗。
二、开关电源环路补偿的设计方法开关电源的环路补偿设计方法，需要综合考虑多个参数，如响应时间、阻尼稳定性、相位裕度等。
其中，响应时间涉及到电路响应时间、电源传输函数以及负载条件，需要根据具体情况予以调整。
阻尼稳定性关系到系统的稳态稳定性，需要根据不同负载条件下的阻尼因素予以设计。
相位裕度涉及到极点间距，可以通过更改反馈回路的增益稳定性来达到较好的效果。
三、开关电源环路补偿的优化在实际电路中，由于电容、电感和负载等多种因素的影响，开关电源环路补偿存在一定的误差。
优化环路补偿，可以通过在电路中加入滤波电容、降低负载电感等措施，提高电源输出的稳定性。
此外，在滤波器的选型方面，选择与系统肖特基二极管参数相匹配的器件，可以较为有效地降低噪声和振荡。
总之，开关电源环路补偿对整个系统的性能至关重要。
一个合理的补偿设计将使电源输出变得更加稳定、高效，具有更好的响应性。
因此，在开发开关电源的过程中，我们应该时刻保持对环路补偿原理的理解，并综合考虑各种参数和因素，以达到最优的设计效果。
开关电源环路补偿概述
开关电源环路补偿概述开关电源环路补偿是一种通过在开关电源回路中引入补偿元件，来提高开关电源输出性能的技术手段。
它的目标是通过合理设计和安排补偿电路，减小开关电源输出电压的波动、提高输出电流稳定性，从而满足电源对电压和电流稳定性的要求，降低系统的噪声，提高系统的可靠性和稳定性。
首先，反馈电路是开关电源中最基本的补偿措施。
它通过对输出电压或输出电流进行采样，并与期望值进行比较得到误差信号，再经过比例放大、积分等处理，通过对控制信号进行调整，实现对输出电压和电流的精确控制。
其次，补偿元件的作用是对开关电源中的非线性元件进行补偿。
例如，开关管的开关过程会引起电压和电流的突变，补偿元件可以通过电容、电感等元件对这些突变进行分解和平滑处理。
同时，补偿元件还可以对开关电源中的功率因素进行补偿，提高电源的功率因数。
最后，滤波元件的作用是对开关电源的输出信号进行滤波处理，消除高频噪声和干扰，使得输出信号更加平稳和稳定。
总体来说，开关电源环路补偿技术可以提高开关电源的稳定性和可靠性，降低噪声和干扰，满足电源对电压和电流稳定性的要求。
在实际应用中，需要根据具体的开关电源工作条件和要求，选择合适的补偿措施和元件，并进行合理的设计和优化。
同时，还需要考虑补偿元件的稳定性、成本和占用空间等因素，使得补偿方案具有实用性和经济性。
开关电源环路补偿技术在电源领域有着广泛的应用。
它可以应用于各种类型的开关电源中，例如交流-直流开关电源、直流-直流开关电源以及交流-交流开关电源等。
同时，它还可以适用于不同的电源输出要求，包括电压型和电流型等。
在一些特殊应用中，例如高精度仪器设备、通信设备、医疗设备等，对电源输出稳定性和噪声要求非常高的场合，开关电源环路补偿技术更是不可或缺的。
总结起来，开关电源环路补偿技术能够通过合理的补偿措施和元件设计，提高开关电源的输出性能，使得其在输入电压和负载变化时能够稳定输出所需的电压和电流。
它有着广泛的应用前景，可以提高电源系统的可靠性和稳定性，降低系统噪声和干扰，满足各种应用领域的需求。
开关电源环路分析
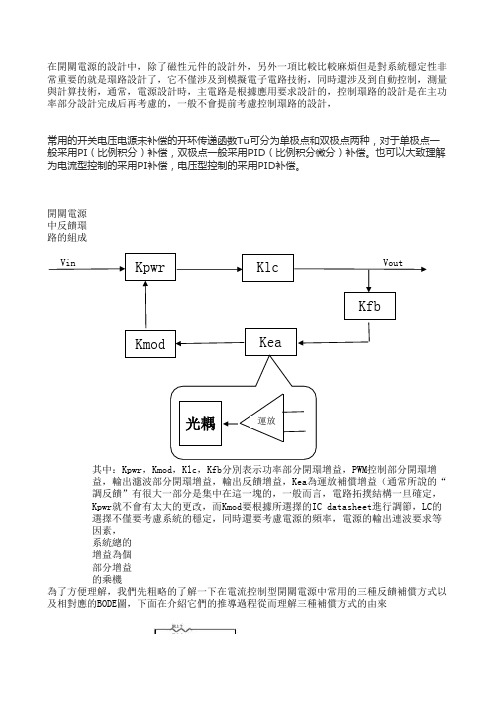
開關電源中反饋環路的組成Vin Vout系統總的增益為個部分增益的乘機常用的开关电压电源未补偿的开环传递函数Tu 可分为单极点和双极点两种，对于单极点一般采用PI （比例积分）补偿，双极点一般采用PID （比例积分微分）补偿。
也可以大致理解为电流型控制的采用PI 补偿，电压型控制的采用PID 补偿。
在開關電源的設計中，除了磁性元件的設計外，另外一項比較比較麻煩但是對系統穩定性非常重要的就是環路設計了，它不僅涉及到模擬電子電路技術，同時還涉及到自動控制，測量與計算技術，通常，電源設計時，主電路是根據應用要求設計的，控制環路的設計是在主功率部分設計完成后再考慮的，一般不會提前考慮控制環路的設計，其中：Kpwr，Kmod，Klc，Kfb分別表示功率部分開環增益，PWM控制部分開環增益，輸出濾波部分開環增益，輸出反饋增益，Kea為運放補償增益（通常所說的“調反饋”有很大一部分是集中在這一塊的，一般而言，電路拓撲結構一旦確定，Kpwr就不會有太大的更改，而Kmod要根據所選擇的IC datasheet進行調節，LC的選擇不僅要考慮系統的穩定，同時還要考慮電源的頻率，電源的輸出連波要求等因素，為了方便理解，我們先粗略的了解一下在電流控制型開關電源中常用的三種反饋補償方式以及相對應的BODE圖，下面在介紹它們的推導過程從而理解三種補償方式的由來Kpwr KlcKmod KeaKfb 光耦運放圖一：反激開關電源中常用的實際反饋補償電路其傳遞函數Kea=Iopto=(Vo-V1)/Rb補償方式一：單極點補償適用條件：補償方式二：極點零點補償適用條件：補償方式三：雙極點單零點補償電流型控制和DCM（斷續電流模式）並且電容的ESR零點頻率較低的電源系統，其主要作用是把環路中第一個極點和其餘的極點距離拉開，使相位達到180以前將增益降到0DB，結果會使補償后的最大帶寬小於補償前第一個極點的帶寬和主極點補償的條件近似，其極點相當于主極點中的極點，零點則是把第一個極點抵消，這時的帶寬可以達到第二個極點的帶寬，帶寬最大，這樣既達到可主極點補償的效果又增加了帶寬適用條件：補償方式四：三极点,双零点补偿（在反激拓撲中很少使用）適用條件：注：C1和R2串联是用来抑制低频时的100HZ 纹波的,在介紹補償方式的推導過程之前，先介紹一下幾個基本概念三：穿越頻率，相位裕量和增益裕量（如下圖所示）相位裕度是指环路增益为 0dB 的频率处的环路相位，增益裕度则是指环路相位为 360o 的频率处的环路增益穿越頻率是指增益曲綫穿越0dB線時對應的頻率適用於傳遞函數有雙極點的補償，輸出帶LC諧振的拓撲結構，如所有沒用電流型控制的電感電流連續方式拓撲結構中（公式中的傳遞函數進行了適當的工程近似）一：BODE圖：根據頻率特性繪製出的一種對數頻率特性曲綫，有兩部分組成，幅頻特性和相頻特性二：零點和極點 表示的是增益斜率變化的拐點，其中零點使增益斜率變化+1，極點使增益斜率變化-1適用於功率部分只有一個極點的補償，如所有電流型控制和非連續性電壓型控制，（公式中的傳遞函數進行了適當的工程近似）如圖所示，虛短：虛斷五：捲積 卷积的过程就是相当于把信号分解为无穷多的冲击信号，然后进行冲击响应的叠加。
开关电源环路补偿概述
开关电源环路补偿概述开关电源环路补偿是一种电子电路设计技术，用于提高开关电源的负载能力、精度和稳定性。
随着电子设备的不断发展，开关电源已经成为广泛使用的电源类型，应用于各种领域，如计算机、通信、工业控制、汽车电子等。
然而，开关电源在输出电流波形、输出电压稳定性以及负载适应能力上存在一些问题，通过使用环路补偿技术可以有效解决这些问题，提高开关电源的性能。
首先，我们来了解一下开关电源的基本工作原理。
开关电源主要由开关器件、变压器、整流滤波电路和控制电路组成。
输入电压经过整流滤波电路和开关器件的切换，最终输出变压器的二次侧，形成输出电压。
控制电路通过监测输出电压并调整开关器件的工作状态，来稳定输出电压。
然而，开关电源存在输出电流波形不理想、输出电压精度不高以及负载变化响应较慢等问题，这些问题可以通过环路补偿技术来解决。
在开关电源中，输出电流波形的不理想会导致输出电压的纹波增大，给其他电路造成干扰。
环路补偿技术可以通过对开关电源的控制电路进行补偿，使输出电流波形接近理想的直流信号。
具体来说，环路补偿技术包括两个主要方面，一个是在控制回路中引入一个外部补偿网络，另一个是在采样过程中加入一个额外的测量回路。
在控制回路中引入外部补偿网络可以改变系统的传递函数，从而减小输出电流的纹波。
补偿网络一般包括串联电感和并联电容，通过调整它们的数值可以改变控制环节的频率响应，从而达到减小输出电流纹波的目的。
此外，还可以通过控制补偿网络中的电感、电容的数值和连接方式，对系统的相位特性进行调整，以进一步提高系统的稳定性和攻角余量。
在采样过程中加入额外的测量回路可以提供准确的输出电流信息，从而使控制电路更好地调整开关器件的工作状态，进一步提高输出电压的精度和稳定性。
具体来说，额外的测量回路可以通过采样电阻、电流传感器或者其他测量设备获取输出电流信息，并反馈给控制电路，以校正开关器件的工作状态。
通过不断调整开关器件的工作状态，可以使输出电压尽量接近设定值，提高开关电源的稳定性和精度。
【干货分享】开关电源环路补偿设计步骤讲解
【干货分享】开关电源环路补偿设计步骤讲解1.对于硬件工程师来说，开关电源和运放的信号处理电路是最常遇到的，都是典型的带负反馈的闭环控制系统。
因此，这两类电路设计的稳定性和控制理论密切相关。
简化的闭环控制系统框图如图1所示，被控对象的传递函数为H，反馈部分的传递函数为G。
图1以上各式中的GH一般称为系统的环路增益或者开环增益。
根据式（2）可知，当1+GH=0，即GH=-1时，意味着环路增益为1，相位滞后180°，系统不稳定发生自激振荡。
当然也可以从另一个角度进行理解，系统发生自激振荡时，不需要输入量Xi，即净输入量，可得GH=-1，即反馈量Xf和输出量Xo形成彼此互相维持的关系。
从稳定性条件出发，我们可以知道环路增益小于1时系统可以稳定，相位滞后不到180°时系统可以稳定。
这表明左半平面的极点和零点都在某一方面提升稳定性，另一方面降低稳定性。
比如左半平面极点可以使增益降低，这能提升稳定性；但是极点增加了相位滞后，这降低了稳定性。
比如左半平面零点使相位超前，这能提升稳定性；但是零点使增益增加，这降低了稳定性。
只有右半平面零点是最特殊的，增加增益的同时相位滞后，这会加剧系统不稳定。
根据控制理论的稳定性条件可知，相位裕量至少为45°，转化为伯德图的话，就是要求在增益为0dB时的穿越频率处，斜率应该为-20dB/decade，即负20dB每十倍频，或斜率为，两者等价。
根据式（3）可知，当GH>>1时，即引入深度负反馈后，Xf=Xi。
这就是为什么运放的虚短需要在引入深度负反馈时才成立的原因。
由于运放本身的开环放大倍数H已经非常大，引入负反馈后一般都能满足深度负反馈的要求。
根据式（4）可知，如果想要直流稳态误差为0，则应满足。
这就是为什么控制系统的低频环路增益（开环增益）要尽量大的原因，这点在开关电源环路设计中很重要。
对于一般的运放电路而言，图1即是其控制系统框图。
而开关电源的系统框图则较为复杂，如图2所示，可以将PWM调制器，开关管和LC滤波器合并统称为功率级，用H表示，误差补偿器用G表示，反馈分压系数用k表示，实际设计中我们经常将k和G合并在一起称为G，则简化后的框图和图1类似，环路增益为GH。
开关电源控制环路分析
开关电源控制环路分析摘 要开关电源被誉为高效节能型电源，它代表着稳压电源的发展方向，现已成为稳压电源的主流产品。
同时，开关电源也是反馈回路控制系统，所谓电路反馈，就是指将放大电路的输出量(电压或电流信号)的部分或全部，通过一定方式(元件或网络)返送到输入回路的过程，完成输出量向输入端回送的电路称为反馈元件或反馈网络。
关键词 零极点 幅值裕度 相位裕度1 引言稳定的反馈环路对开关电源来说是非常重要的，如果没有足够的相位裕度和幅值裕度，电源的动态性能就会很差或者出现输出振荡。
下面先介绍三种控制方式的各种零，极点的幅频和相频特性，再对最常用的反馈调整器TL431的零、极点及特性进行分析。
Topswitch是市场上广泛应用的反激式电源的智能芯片，它的控制方式是比较复杂的电压型控制，内部集成了一部分补偿功能，最后分析一个Topswitch设计的电源，对它的环路进行解剖。
2 环路补偿方式及TL431特性2.1 单极点补偿适用于电流型控制和工作在DCM方式并且滤波电容的ESR零点频率较低的电源。
其主要作用原理是把控制带宽拉低，在功率部分或加有其他补偿的部分的相位达到180度以前使其增益降到0dB。
图12.2 双极点，单零点补偿适用于功率部分只有一个极点的补偿，例如所有电流型控制和非连续方式电压型控制。
图22.3 三极点、双零点补偿适用于输出带LC谐振的拓扑，例如所有没有用电流型控制的电感电流连续方式拓扑。
图32.4 TL431输出供电时的零极点特性TL431是开关电源次级反馈最常用的基准和误差放大器件，其供电方式不同对它的传递函数有很大的影响。
图4其中：（1）（2）将(2)代入(1)得到：从上面的公式可以看到，在输出直接给431供电的情况下，零点的位置在1/[2π(R+R1)C]处，而不是1/(2πRC)。
即使没有R，只接一个C的情况下，零点还是存在，如果R1远大于R，零点的位置主要有反馈网络的上分压电阻决定。
开关电源环路补偿
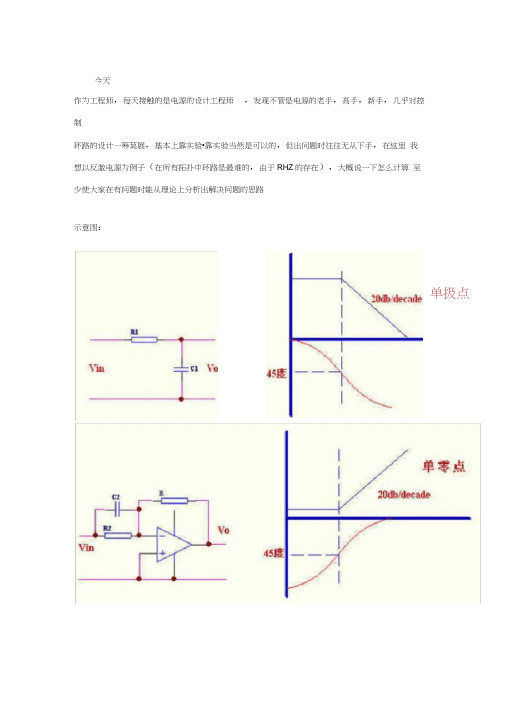
今天作为工程师，每天接触的是电源的设计工程师，发现不管是电源的老手，高手，新手，几乎对控制环路的设计一筹莫展，基本上靠实验•靠实验当然是可以的，但出问题时往往无从下手，在这里我想以反激电源为例子（在所有拓扑中环路是最难的，由于RHZ的存在），大概说一下怎么计算至少使大家在有问题时能从理论上分析出解决问题的思路示意图：单扱点递函数自己写吧，正好锻炼一下，把输出电压除以输入电压就是传递函数•bode 图可以简单的判定电路的稳定性，甚至可以确定电路的闭环响应，就向我下面的图中表 示的•零，极点说明了增益和相位的变化度以前使其增益降到 0dB.也叫主极点补偿这里给出了右半平面零点的原理表示，这对用PSPICE 做仿真很有用，可以直接套用此图单极点补偿，适用于电流型控制和工作在 DCM 方式并且滤波电容的 ESR 零点频率较低的电源.其主要作用原理是把控制带宽拉低，在功率部分或加有其他补偿的部分的相位达到180双极点，单零点补偿，适用于功率部分只有一个极点的补偿•如:所有电流型控制和非连续方式电压型控制适用「传遥曲数为单极点的补弦R2/B1_______ 、I 2plR2C21 2piR2Cl14SR2C1G(i)=S R1C1(1^S R2C2)三极点，双零点补偿•适用于输出带LC谐振的拓扑，如所有没有用电流型控制的电感电流连续方式拓扑。
C1的主要作用是和R2提升相位的•当然提高了低频增益•在保证稳定的情况下是越小越好C2增加了一个高频极点，降低开关躁声干扰串聯C1實質是增加一個零點，零點的作用是減小峰值時間，使系統響應加快，并且閉環越接近虛軸，這种效果越好•所以理論上講,C1是越大越好•但要考慮，超調量和調節時間，因爲零點越距离虛軸越近，閉環零點修正系數Q越大，而Q與超調量和調節時間成正比，所以又不能大總之，考慮閉環零點要折衷考慮.并聯C2實質是增加一個及點，級點的作用是增大峰值時間，使系統響應變慢.所以理論上講，C2也是越大越好.但要考慮到，當零級點彼此接近時，系統響應速度相互抵消.從這一點就可以說明，我們要及時響應的系統C1大,至少比C2大三：环路稳定的标准.只要在增益为1时（OdB）整个环路的相移小于360度，环路就是稳定的.但如果相移接近360度，会产生两个问题：1）相移可能因为温度，负载及分布参数的变化而达到360度而产生震荡；2）接近360度，电源的阶跃响应（瞬时加减载）表现为强烈震荡，使输出达到稳定的时间加长，超调量增加.如下图所示具体关系1 2plR2C2 I 2plR5C ivR2/RVI 2piR?( I l ?piRK 3G(AsRlCUI si<2Cli(l+sR3C3)氐*丨丄伽叩htpp 尉川 pJwM' iri.irgm 妙-i ，n4 L krscd kjc )p pcdluwQU NL wp ntspom# 禎 ihc wra (Mjn )cT lyuem.阴 ^9.26) and 丹 TT\.險 vtncu 诃晌 of Q所以环路要留一定的相位裕量，如图Q=1时输出是表现最好的，所以相位裕量的最佳值为度左右，工程上一般取45度以上•如下图所示52%■0-0T5G-at Q ・<nQ m Q >0 03 .0.001这里要注意一点，就是补偿放大器工作在负反馈状态，本身就有180度相移,所以留给功率部分和补偿网络的只有180度•幅值裕度不管用上面哪种补偿方式都是自动满足的，所以设计时一般不用特别考虑•由于增益曲线为-20dB/decade时此曲线引起的最大相移为90度，尚有90度裕量,所以一般最后合成的整个增益曲线应该为-20dB/decade部分穿过OdB.在低于OdB带宽后,曲线最好为-40dB/decade,这样增益会迅速上升，低频部分增益很高，使电源输出的直流部分误差非常小，既电源有很好的负载和线路调整率•四，如何设计控制环路？经常主电路是根据应用要求设计的，设计时一般不会提前考虑控制环路的设计•我们的前提就是假设主功率部分已经全部设计完成，然后来探讨环路设计•环路设计一般由下面几过程组1）画出已知部分的频响曲线2）根据实际要求和各限制条件确定带宽频率，既增益曲线的OdB频率.3）根据步骤2）确定的带宽频率决定补偿放大器的类型和各频率点.使带宽处的曲线斜率为20dB/decade,画出整个电路的频响曲线.上述过程也可利用相关软件来设计：如pspice,POWER-4-5-6•—些解释：|----- s| | ------------------------|已知部分的频响曲线是指除Kea（补偿放大器）外的所有部分的乘积，在波得图上是相加•环路带宽当然希望越高越好，但受到几方面的限制：a）香农采样定理决定了不可能大于1/2Fs;b）右半平面零点（RHZ）的影响，RHZ随输入电压，负载，电感量大小而变化，几乎无法补偿，我们只有把带宽设计的远离它，一般取其1/4-1/5;c）补偿放大器的带宽不是无穷大，当把环路带宽设的很高时会受到补偿放大器无法提供增益的限制，及电容零点受温度影响等•所以一般实际带宽取开关频率的1/6-1/10五,反激设计实例条件:输入85-265V交流，整流后直流100-375V输出12V/5A初级电感量370uH初级匝数：40T,次级:5T次级滤波电容1000uFX3=3000uF震荡三角波幅度•开关频率100K电流型控制时，取样电阻取欧姆下面分电压型和峰值电流型控制来设计此电源环路•所有设计取样点在输出小LC前面•如果取样点在小LC后面，由于受LC谐振频率限制，带宽不能很高.1）电流型控制假设用3842,传递函数如下th Kmitd*'KpWr*klr)a Kn» 1* ■】Rteuv*(l^D)1，tCRcrfi------- = -------------- 1 ___________"X•艮心Mm * t* | * 「* TL Tl+uU W I'inU C为■出电容Hu I収电111此图为补偿放大部分原理图.RHZ 的频率为33K,为了避免其引起过多的相移，一般取带宽为其 频率的1/4-1/5,我们取1/4为8K.分两种情况：I Hiiiin I I mini I I limn i i mini …TTmin 广怖「…T …rmii 『… I i u I mi l l limn i I iiiim I I ii mu100400(1+s 1225)*(1 s/$3K)G(s)= 194* -----------------------------1000uF/16V ESR=130m 欧姆输出滤波电容的内阻比较大，自身阻容形成的零点比较低 ，这样在8K 处的相位滞后比较小Phanseangle=arctan (弘arctan(8/-arctan(8 /33)=--22 度.另外可看到在 8K 处增益曲线为水平，所以可以直接用单极点补偿，这样可满足-20dB/decade1 (1)肚…UU uni ….…1 rSiWllll 1 1 IIIL —L 丄血电1丄Ljr.VIn Hill _____A)输出电容ESR 较大…丄.广口 TWi 「…厂TTmi 】「…T …「ITH1II I IIIIIIII I I lllllll I llllllll niniul 广r 仃涮…「门TIIII 「…I" I I I I I 川 II miniI44UI limnI III I 11(1 Qil)+出卅卜…44卄怖卜…上I I HI mi I I II mu I I iiimi i i limn …十计卄付卅…一卜.十卄”卅.-…卜-十忡时卅…十计卄卅卜…的曲线形状•省掉补偿部分的 R2,C1.设Rb 为,则R 仁[/]*Rb=.8K 处功率部分的增益为 -20*log(1225/33)+20*=因为带宽8K,即8K 处OdB所以8K 处补偿放大器增益应为，*log(Fo/8)=0Fo 为补偿放大器OdB 增益频率Fo=1/(2*pi*R1C2)=C2=1/(2*pi*R1*=1 /(2***=相位裕度：180-22-90=68 度仿真團* *空为功率都分，绿色光4偿祁分，红色为整个开环増益.008060402002040®D 刼 -100 -1 50 -200 -250 -300 -350 -400100 1000 1 0000 1 00000 1 000000Frequency (Hr)B)馨£哋9 ESRfrK •(1 ^s/5*3K)*(l-s/3SK)G(s)= 19.4* -----------------------------1000uF/25V ESR=30mgt^输出滤波电容的内阻比较大，自身阻容形成的零点比较高，这样在8K 处的相位滞后比较大Phanseangle=arctan(&-arctan(8 /-arctan(8/33)=-47 度.如果还用单极点补偿，则带宽处相位裕量为180-90-47=43度.偏小用2型补偿来提升.三个点的选取，第一个极点在原点，第一的零点一般取在带宽的 1/5左右,这样在带宽处提升相 位78度左右，此零点越低，相位提升越明显 但太低了就降低了低频增益 ，使输出调整率降低 此处我们取.第二个极点的选取一般是用来抵消ESR 零点或RHZ 零点引起的增益升高，保证增muJ I f I ITI111I llllll in iii i ujji 11HII1 1 11 1 1L…riiir^111miniIIIIIII■ » 1^ ■ ■I flllll 1UJJJI IIIIIU L±i Hft IInTiiin 11IIIIIInTIllli lHlUJlHill urn111川I ］耐毗I IIIIIII I I I lllira^l llllll \m …卜4出川 i i IIIIIII L 十卄 Hlft …十I ilium i iiiHiii i T-r ittmr …"r-tt+twt ■ t-ritmit ……! I lilllllI —r i riiiii TT f r ii F100(}imo益裕度•我们用它来抵消ESR零点，使带宽处保持-20db/10decade的形状，我们取ESR零点频率数值计算:8K 处功率部分的增益为-20*log(5300/ 33)+20*=-18dB因为带宽8K,即最后合成增益曲线8K处0dB所以8K处补偿放大器增益应为18dB,处增益=18+20log(8/=水平部分增益=20logR2R仁推出R2=12*R1=233Kfp2=1/2*pi*R2C2推出C2=1/(2**233K*==1 /2*pi*R2C1推出6= 1(2**233K*=.相位际电路中Q 值几乎不可能大于 4— 5.Phanse angle = 47 - 90+arttar^ 8/16 baictam 8/5.3)— 115 度 相位珞度* 180415=€5度*V 于=* ■3 V V ■■卢 F \L仿真图，2. ffe 压型控制・•武门同林设计帮宽药呂忆传谨鲂如下・禹频 MDX 电容的 ESR r Rc-iam Kfii. ■10 ^99(2*pi> 605Hxfo 为LC 谐振频率，注意Q 值并不是用的计算值，而是经验值，因为计算的Q 无法考虑LC 串联 回路的损耗（相当于电阻）,包括电容ESR 二极管等效内阻，漏感和绕组电阻及趋附效应等 •在实Gu V » Vc hin.d»ik F mr*Kl« ^klK --------------Vfi*tn X*U Df S1 !< Rd*|l*W“ <Vht - \X»)K«^4!*E&RS*I1 In -------- ------- --G<4)- \(i Vr = 16*0 J -50 - -100 -3 -150 r* -200 * | -250 - f -300 - -350 - *400 -110 1OT 1000 100001OT000 1000000Frequency 血工)11 1>^*KR«G^iia dB由于输出有LC 谐振，在谐振点相位变动很剧烈，会很快接近180度，所以需要用3型补偿放大 器来提升相位•其零，极点放置原则是这样的，在原点有一极点来提升低频增益，在双极点处放 置两个零点，这样在谐振点的相位为-90+(-90)+45+45=-90.在输出电容的ESR 处放一极点，来抵 消ESR 的影响，在RHZ 处放一极点来抵消 RHZ 引起的高频增益上升•元件数值计算，为方便我们把3型补偿的图在重画一下3 Lt 2|dR2C2 1 2piR3( 3k j ^—I ^SjRMUx^l/2plR2Cl USplRlC3适用于箱递函數 有敢楼皮的补偿90 —-— ■*. 卜—.・・・「y Z ・“一・ ・i■■■J i n^>・— 90 ---先计8S 功率部分瞅处的厝益’ 亦5】K,R1F94K 、26- 4010^5.3/0^05）-血啦的 3>15 3dB 尸靈緡到毗带宽，补翩吠98在磁处.麻平顶朗分的増益应15.3dB 収歩恵处増益为’- 15 3 JOto0（53/O dO5>3i^dBv从J 卜偿图上可远 此处増苕淘2血0国冰0-订①#t±jt R2-1 51*Rl-29 3K 1 贞 2，pTRl ・C ：3）-6Q5 一£>口上成卩 l^2*pt*R3*C3）-33K R3-355 欧姆* l/f2*pi*R2*Cl ）-«a5 CHftnFA l<2*fn*R2-C2>-5 3K OlnF.SR 8K 处葡相仏 卜］80+越如8/5.齐a （如8/33）1 时-90+2*5^8/0 605>3£j9g （8«_3p 議监翩（的了）］・亠12丘》 担位番加 180-116-54 $- “ 仿鼻结負如尺“兰色为功率部分，绿色为补偿部分，红色为整个开环增益如果相位裕量不够时，可适当把两个零点位置提前，也可把第一可极点位置放后一点同样假设光耦CTR=1如果用CTR 大的光耦，或加有其他放大时，如同时用IC 的内部运放，只需 要在波得图上加一个直流增益后，再设计补偿部分即可•这时要求把IC 内部运放配置为比例放(ltsR2Cl)(l UMC) ^R1C1(I- KR2C2H1 -»R3C3)大器，如果再在内部运放加补偿，就稍微麻烦一点，在图上再加一条补偿线结束我想大家看完后即使不会计算,出问题时也应该知道改哪里。
uc3842反激式开关电源环路补偿计算书
UC3842反激式开关电源环路补偿计算书一、介绍1.1 UC3842简介UC3842是一款具有反激式开关电源功能的控制IC，它被广泛应用于交换电源、逆变器和其他开关电源中。
UC3842具有工作频率可调的特点，典型应用中通常工作在50kHz至500kHz的范围内。
它内部集成有高压开关管，用于控制开关管的导通和关断，从而实现输出电压的稳定控制。
1.2 反激式开关电源环路补偿的重要性反激式开关电源的环路补偿是影响其稳定性和性能的关键因素之一。
正确的环路补偿设计可以有效地提高电源的动态响应和稳态精度，在保证系统稳定性的还能够提高系统的动态性能和抗干扰能力。
进行反激式开关电源环路补偿的计算十分重要。
二、环路补偿计算2.1 反激式开关电源的环路补偿原理反激式开关电源的环路补偿主要通过在控制回路中引入补偿网络来实现。
在设计中需要考虑控制回路的开环增益、相位裕度、带宽等参数，以及输出环路特性和负载特性等因素。
通常使用频率补偿网络和振荡器来实现环路补偿。
2.2 环路补偿计算步骤进行环路补偿计算时，需要依次进行以下步骤：步骤一：根据设计要求确定系统的带宽和相位裕度。
步骤二：选择合适的频率补偿网络和振荡器。
步骤三：计算补偿网络的元件参数。
步骤四：进行仿真验证和实际电路测试。
三、计算实例3.1 设计要求假设需要设计一个输出电压为12V、输出电流为2A的反激式开关电源，工作频率为100kHz。
系统要求带anWh (abolt-Var) 。
宽3dB，相位裕度为45°。
现进行环路补偿的计算和元件选择。
3.2 计算过程步骤一：根据设计要求计算系统的带宽和相位裕度。
设计带宽=100kHz，相位裕度=45°。
步骤二：选择频率补偿网络和振荡器。
选择一个合适的频率补偿网络和振荡器，比如R-C振荡器和阻容型频率补偿网络。
步骤三：计算补偿网络的元件参数。
根据选择的频率补偿网络，计算出所需的元件参数。
步骤四：进行仿真验证和实际电路测试。