实验12缉私艇追赶走私船模型实验
数学实验期末作业(缉私艇问题)
问题:缉私艇问题续。
(1)在本问题的求解过程中,假定了走私艇的逃跑方向是正北方向,而初始缉私艇的位置在x 轴正向。
如果放宽这个假定,也就是当这个夹角是任意角度时,如何建立方程进行求解。
以下面数值为例进行求解:b=40,a=20,c=15,其中坐标系如课件上所述,走私船的方向为45°。
(2)如果有多个走私艇在一个位置上进行交易,而缉私艇向该方向追赶。
这些走私艇向不同方向四散逃走,问如何安排追赶路线? (假定缉私艇追上一个立刻掉头追赶另外一个,中间没有时间停留)。
以下面数值为例进行求解:b=40,a1=20, a2=25, a3=30,c=15,三个角度分别为45°,90°和-60°。
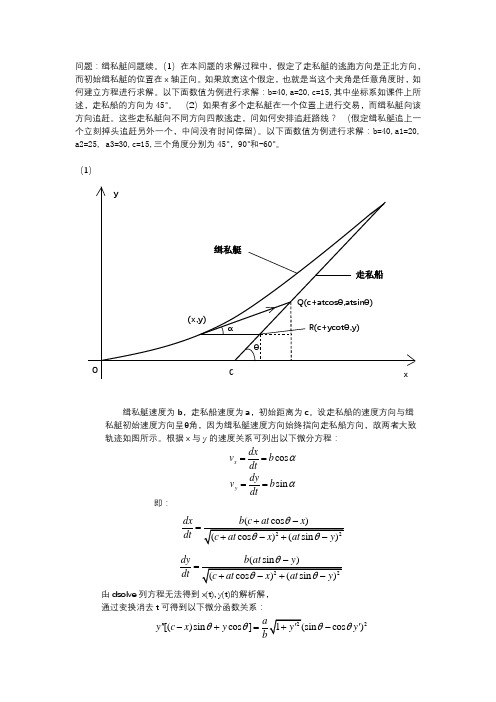
(1)缉私艇速度为b ,走私船速度为a ,初始距离为c 。
设走私船的速度方向与缉私艇初始速度方向呈θ角,因为缉私艇速度方向始终指向走私船方向,故两者大致轨迹如图所示。
根据x 与y 的速度关系可列出以下微分方程:cos x dxv b dt α== sin y dy v b dt α==即:22(cos )(cos )(sin )dx b c at x dt c at x at y θθθ+-=+-+-22(sin )(cos )(sin )dy b at y dt c at x at y θθθ-=+-+-由dsolve 列方程无法得到x(t), y(t)的解析解,通过变换消去t 可得到以下微分函数关系:22[()sin cos ]1(sin cos )ay c x y y y b θθθθ''''-+=+-αθC(x,y)Q(c+atcos θ,atsinθ)R(c+ycot θ,y)yx走私船缉私艇再通过dsolve函数求解,仍无法得到y(x)的解析解。
因此只能用数值解法求其解。
给定初值:a=20,b=40,c=15,θ=45°。
使用MATLAB求解可得:轨迹图由图和数据初步判断大约在t=0.5到t=1之间缉私艇追上走私船。
10-缉私艇追走私船模型实验

最简单的使用格式为
ode23('fname',[xs,xe],sv)
其中用单引号引起的是存储微分方程的函数文件名, xs表示自变量的初始值,xe表示自变量的终止值,sv 表示迭代初始向量值。该命令执行后自动画出微分方 程数值解曲线。
[xb,yb]=ode23('fname',[xs,xe],sv)
解:(1)直接在命令窗执行命令
dsolve('Dy=3/x*y+x^3*(exp(x)+cos(x))-2*x', 'y(pi)=(exp(pi)+2/pi)*pi^3','x') ans= x^3*exp(x)+x^3*sin(x)+2*x^2
(2) 取步长0.1,用欧拉公式求数值解
clc;clf; szy_eu=[]; y=(exp(pi)+2/pi)*pi^3; for x=pi:0.1:2*pi y=y+0.1*(3/x*y+x^3*(exp(x)+cos(x))-2*x); szy_eu=[szy_eu,y]; end szy_eu t=pi:0.1:2*pi; f=t.^3.*exp(t)+t.^3.*sin(t)+2*t.^2; plot(t,f,'b*--') hold on plot(t,szy_eu,'r-','linewidth',2)
海上边防缉私艇发现距c公里处有一走私船正以匀 速a沿直线行驶,缉私艇立即以最大速度b追赶,在雷 达的引导下,缉私艇的方向始终指向走私船。问缉 私艇何时追赶上走私船?并求出缉私艇追赶的路线 方程。 y
o
上机实验(微分与差分方程)

实验一一、实验名称:微分方程数值解二、实验内容一天,缉私舰雷达(A)发现,距离10公里处的海面上有一艘走私船(B)正以匀速25公里/小时沿垂直于AB的直线行驶,缉私舰立即以最大速度(匀速40公里/小时)追赶。
若用雷达进行跟踪,保持船的瞬时速度方向始终指向走私船。
(1) 缉私舰的运动轨迹是怎样的?是否能够追上走私船?如果能追上,需要用多长时间?(2)若缉私舰在走私船2公里处,被走私船发现,走私船立刻加速逃窜(匀速30公里/小时)。
假设走私船沿任意方向逃离,此时是否能够追上走私船?如果能追上,最多需要用多长时间?走私船沿哪个方向逃离时被追上所花的时间最长?(3)如果走私船发现缉私舰后,在逃离的过程中,随时都可能改变方向,此时缉私舰是否能够追上走私船?如果能追上,最多需要用多长时间?三、实验目的熟悉matlab的符号运算环境,掌握微分方程建立、求解方法四、实验原理建立相应的微分方程,并用所掌握的求解方法进行求解与分析.六、实验结果及分析七、实验结论和注记实验二一、实验名称:动态系统模拟二、实验内容一小超级市场有4个付款柜,每个柜台为一位顾客计算货款数的时间与顾客所购商品件数成正比(大约每件费时2s),20%的顾客用支票或信用卡支付,这需要1.5min,其余的顾客付现金则仅需0.5min。
有人倡议设一个快速服务台专为购买8个或8个以下商品的顾客服务,指定另外两个为“现金支付柜”。
请你建立一个模拟模型,用于比较现有系统和倡议的系统的运转。
假设顾客到达平均间隔时间是15秒,顾客购买商品件数按如下频率表分布。
三、实验目的熟悉matlab的统计工具箱,掌握随机数的生成、固定时间增量法与面向事件法的动态模拟方法.四、实验原理把该问题抽象为多队列、多服务台的排队系统,应用动态模拟方法得到模拟数据,分析平均队列长度、平均等待时间等指标。
六、实验结果及分析七、实验结论和注记。
数学建模综合实验缉私艇走私艇

数学建模综合实验缉私艇走私艇
为了保护国家利益和维护边境安全,海关和边境巡逻部门需要对走私活动进行严格监
控和打击。
因此,他们需要一艘高效的缉私艇,该艇不仅可以确保有效的监控和追缉走私
船只,而且还需要具备良好的性能和稳定性,以适应不同的海上环境。
为了设计这样一艘缉私艇,我们需要考虑以下因素:
1. 尺寸和外形:缉私艇需要足够大,以容纳所需的设备和人员。
同时,它需要具有
高度流线型的外形,以减少水阻和提高速度。
2. 推进系统:缉私艇需要一种高效的推进系统,以确保它可以快速移动和灵活操作。
通常,这种推进系统使用柴油发动机和水下推进器。
3. 船体材料和结构:缉私艇需要使用轻质但坚固的材料来构建船体。
同时,船体的
结构应该经过设计和测试,以确保它能在恶劣的海上环境下保持稳定性。
4. 船载设备和传感器:缉私艇需要搭载各种设备,如雷达、红外线探测器、声纳和
高清摄像头等,以帮助监测和追踪走私船只。
5. 操控系统:为了使船员能够更容易地操作缉私艇,需要科学地设计操控系统,包
括方向盘、油门控制器、仪表板和导航系统等。
6. 安全性和稳定性:缉私艇需要具备良好的安全性和稳定性,以应对各种潜在威胁,例如海浪和风浪。
通过考虑这些因素,我们可以设计出一艘高效的缉私艇,该艇可以帮助海关和边境巡
逻部门有效地打击走私活动,保障国家利益和边境安全。
常微分方程模型及其数值解

Q(c,at)
P(x,y)
R(c,y )
0
y
x
c
例2 弱肉强食
问题 自然界中在同一环境下的两个种群之间存在着几种不同的生存方式,比如相互竞争,即争夺同样的食物资源,造成一个种群趋于灭绝,而另一个趋向环境资源容许的最大容量;或者相互依存,即彼此提供部分食物资源,二者和平共处,趋于一种平衡状态;再有一种关系可称之为弱肉强食,即某个种群甲靠丰富的自然资源生存,而另一种群乙靠捕食种群甲为生,种群甲称为食饵(Prey),种群乙为捕食者(Predator),二者组成食饵-捕食者系统。海洋中的食用鱼和软骨鱼(鲨鱼等)、美洲兔和山猫、落叶松和蚜虫等都是这种生存方式的典型。这样两个种群的数量是如何演变的呢?近百年来许多数学家和生态学家对这一系统进行了深入的研究,建立了一系列数学模型,本节介绍的是最初的、最简单的一个模型,它是意大利数学家Volterra在上个世纪20年代建立的。
0.00 0.40 0.80 1.20 1.60 2.00
0.00000 0.36085 0.51371 0.50961 0.45872 0.40419
0.00000 0.34483 0.48780 0.49180 0.44944 0.40000
0.00000 -0.01603 -0.02590 -0.01781 -0.00928 -0.00419
而
从而有: y(xn+1)-yn+1=O(h3)
2.4 Taylor展开方法
设y(x)是初值问题(4)的精确解, 利用Taylor展开式可得
称之为p阶Taylor展开方法. …… …… …… 因此,可建立节点处近似值yn满足的差分公式 其中
所以,此差分公式是p阶方法.
02
2-数学实验举例:缉私艇追击走私船

matlab
5 结果分析
用求解析解的方法算得的解是最为精确的;用数值方法计算的结果 依赖于迭代终值的设定,减小迭代终值可以提高计算精度;用计算机仿 真法计算的结果依赖于时间迭代步长的选取和程序终止条件的设定,修 改终止条件的设定和减小时间迭代步长可以提高计算精度,减小误差。
6 实验任务
1. 有一只猎狗在B点位置发现了一只兔子在正东北方距离它200米的地 方O处,此时兔子开始以8米/秒的速度向正西北方距离为120米的洞口A全 速跑去,假设猎狗在追赶兔子的时候始终朝着兔子的方向全速奔跑,用计 算机仿真法等多种方法完成下面的实验: (1) (2) (3) (4) 问猎狗能追上兔子的最小速度是多少? 在猎狗能追上兔子的情况下,猎狗跑过的路程是多少? 画出猎狗追赶兔子奔跑的曲线图。 假设在追赶过程中,当猎狗与兔子之间的距离为30米时,兔子由于 害怕, 奔跑的速度每秒减半,而猎狗却由于兴奋奔跑的速度每秒增 加0.1倍,在这种情况下,再按前面的(1)—(3)完成实验任务。
⎧ dy 1 ⎡⎛ x ⎞ r ⎛ c ⎞ r ⎤ ⎪ = ⎢⎜ ⎟ − ⎜ ⎟ ⎥ ⎨ dx 2 ⎢⎝ c ⎠ ⎝ x ⎠ ⎥ ⎣ ⎦ ⎪ ⎩ y (c ) = 0
3) r
=1
1 ⎛ x2 − c2 x⎞ ⎜ ⎟ , y = 2 ⎜ 2c − c ln c ⎟ ⎝ ⎠
y → +∞ ,缉私艇不可能追赶上走私船。
2 ⎧ d2y ⎛ dy ⎞ ⎪x 2 = r 1 + ⎜ ⎟ ⎨ dx ⎝ dx ⎠ ⎪ ⎩ y (c ) = 0, y ′(c ) = 0
微分方程模型缉私艇追击走私船问题
ans=1/2*exp(-r*(log(c)-log(x)))*c^r*(1/c)^r/(r+1)*x+ 1/2*exp(r*(log(c)-log(x)))/(-1+r)*x1/2*c*(-(1/c)^r*c^r+c^r*(1/c)^r*r+r+1)/(r^2-1)
微分方程模型实例2——缉私艇追击走私船问题
y(c) 0
微分方程模型实例2——缉私艇追击走私船问题
1)
r a 1 b
y
c 2
1 1 r
x c
1 r
1 1 r
x
1
r
c
cr 1 r2
dy
1
x r
c
r
dx 2 c x
y(c) 0
当 x = 0 时,
y cr 1 r2
,
t y cr bc a a(1 r 2 ) (b2 a 2 )
dx
又 ds b dt
s表示弧长
dt dt ds 1 1 ( dy )2 (2)
dx ds dx b
dx
结合(1)、(2)得到如下微分方程:
d2y
x
dx 2
r
1 ( dy )2 dx
y(c) 0, y'(c) 0
其中r a b
问题:是否存在解析解?
微分方程模型实例2——缉私艇追击走私船问题
matlab
若想看图中“o”点的坐标可执行下面的命令: [t,y]=ode23('zx',3,0.0005,0) plot(t,y)
此时缉私艇的位置坐标是(0.00050000000000,1.96013657712118)
MATLAB缉私艇追击走私船_数学建模汇总

p(c)
0
p 1 p2 x r c
p
1
p2
c
r
x
x
d
2y
r
dx2
1 dy 2 dx
y(c)
0,
y(c)
0
r a/b
dy
1
x
r
c
r
dx 2 c x
y(c) 0
1)r a 1, b
y
c 2
1 1 r
x
1 r
c
1 1 r
x c
1r
cr 1 r2
t=t+dt;
jstx=jstx-b*dt*jstx/sqrt(jstx^2+(a*t-jsty)^2);
jsty=jsty+b*dt*(a*t-jsty)/sqrt(jstx^2+(a*t-jsty)^2);
zscy=a*t;
penadupsleo(t0(j.2st)x,jsty,'ro',zscx,zscy,'b*')艇:(0历.0时00:04219,6秒1.9,7)
1
t=9,5,2.8125(分钟)
0.5
0
0
0.5
1
1.5
2
2.5
3
3.5
2) r a 1, b
y
c 2
1
1
r
x c
1 r
r
1 1
c r1
x
cr r2 1
dy
1
x
r
c
r
dx 2 c x
y(c) 0
当 x 0 时, y ,缉私艇不可能追赶上走私船。
追击问题

追赶时间分别为: 追赶时间分别为: 9.0000 5.0000 2.8125
2):当r=1时 ):当r=1时 即走私船的速度a等于缉私艇的速度b 即走私船的速度a等于缉私艇的速度b时, 方程的解为: 方程的解为:
1 x −c x y= ( − c ln ) 2 2c c
2 2
式中当x 式中当x(0)时,y(inf)说明这种情 inf) 况下,缉私艇不可能追上走私船。 况下,缉私艇不可能追上走私船。
3)当r>1时 r>1时 此时走私船的速度a大于缉私艇的速度b 此时走私船的速度a大于缉私艇的速度b 方程的解为: 方程的解为:
c 1 x 1 c y= + 2 1+ r c r −1 x
1+r
r−1
cr Байду номын сангаас 2 r −1
式中当x(0)时 式中当x(0)时,y(inf)这种情况下缉 x(0) inf) 私艇不可能追上走私船。 私艇不可能追上走私船。
MATLAB软件求解 3 用MATLAB软件求解 对降阶的微分方程
jstxb=[jstxb,jstx]; jsty=jsty+b*dt*(a*tsqrt(jstx^2+(a*tjsty=jsty+b*dt*(a*t-jsty)/ sqrt(jstx^2+(a*t-jsty)^2); jstyb=[jstyb,jsty]; zscy=a*t; zscyb=[zscyb,zscy];
应用、 追击问题, 应用、思考和练习(追击问题,如果雷达失效)
当缉私舰雷达发现d处有一走私船后, 当缉私舰雷达发现d处有一走私船后,雷 达突然损坏 若假定走私船作匀速直线运动( 但不知 若假定走私船作匀速直线运动 ( 方向) 且缉私舰艇速度v 方向),且缉私舰艇速度v大于走私船速 度a, 则缉私舰应采用什么样的航行路线, 则缉私舰应采用什么样的航行路线 , 不 管走私船从哪个方向逃跑, 都能追捕上 管走私船从哪个方向逃跑 , 它?
海上缉私模型论文数学建模MATLAB.

.海上缉私问题建模题目二组别:第五组组长:练佳翔组员:邵*组员:***海上缉私问题摘要针对海上缉私问题,要求出缉私船是否能追上走私船,或着是求缉私艇追上走私船的位置和时间,就需要知道走私船和缉私艇的位置坐标、大概的行驶路线、及二者的速度。
对于走私船和缉私艇的位置坐标,可以由二者的行驶路线 、速度、行驶时间之间的关系得到。
而走私船和缉私艇的位置坐标,可用三角函数、坐标关系、圆的位置关系求解。
当缉私船追上走私船时,走私船和缉私艇的位置坐标相同,即二者的横坐标相等,纵坐标相等。
在此期间,再加以MATLAB 软件进行求解。
关键字: 海上缉私 位置坐标 速度 MATLAB 软件问题重述分别对以下情况建立缉私船的位置和航线的数学模型,自己设定速度等参数,求数值解:(1) 走私船向正向非匀速直线行驶,其速度()a t 按正弦规律变化,如图1.已知缉私船以速度b 匀速追击, 1.5b d =(d 为常数),两船初始距离2c d =.图1(2) 两船速度大小都不变,走私船以速度a 沿着与正向成θ角的直线行驶,如图2.已知缉私船的速度 1.6b a =,两船初始距离c a =.取25θ=与65θ=,求数值解,并说明走私船按哪个角度逃跑较快?图2(3) 两船速度大小都不变,走私船以速度a 沿半径为r 的圆弧向P 点逃跑,现有两种方案,如图3.问两种方案是否都能到达P 点?已知圆弧半径r a =,缉私船的速度 1.4b a =,两船初始距离0.8c a =.方案1 方案2图3(4)两船速度都大小不变,走私船以速度a 先向正向直线行驶,一段时间(设尚未被缉私船追上)后改变方向,沿着与正向成θ角(90180)θ<≤的直线行驶,如图4.已知缉私船的速度 1.2b a =,两船初始距离 1.5c a =.取170θ=,求数值解.图4(4)(5) 开始两船速度大小都不变,走私船以速度a 向正向沿直线行驶,但当两船距离小于r 时,缉私船会发现被人追击,将沿正北方向以速度g 加速逃跑,如图5.已知0.5r a =, 1.5g a =,缉私船的速度 1.8b a =,两船初始距离3c a =,求数值解.图5(6) 实际在追击时,缉私船速度方向的改变并不连续,每隔时间t∆变换一次角度,在两次变换之间,缉私船按直线运动.若两船速度大小都不变,走私船以速度a向正向沿直线行驶,30b=(海里/小时),两船初始距离25c= a=(海里/小时),缉私船的速度50(海里),60t∆=(秒).试画出缉私船的航线图,建立此时的追击模型,比较与之前模型有何不同,并求数值解.问题分析问题一:要确定缉私船追上走私船的位置及时间,就必须确定缉私船、走私船的坐标。
实验缉私艇追赶走私船模型实验

11
实例1:海上缉私
• 模型建立: • 建立直角坐标系 :t=0时,艇在(0,0)
船在(0,c);船速a,艇速b (b>a); 时刻t,艇在P(x,y), 船在Q(c, at)。 模型:
x(t)、y(t) 无解析解!
12
常微分方程初值问题的提法
f对y满足李普希茨(Lipschitz)条件,
44
图形结果
16
10
14
9
8
12
x(t)
7
10 6
8
5
6
y(t)
4
3 4
2
2
1
0
0
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
0
2
4
6
8
10
12
14
16
x(t),y(t)图形
y=y(x)图形
45
模型数据分析
• 先固定b,c,而走私船的速度a变大为 30,35,…接近40,观察解的变化。修改a的输 入,并相应地延长t的终点。设a=35,t的终 点经试探,调整为1.6合适。
向前、后欧拉公式 梯形、改进欧拉公式
差商 代替 导数
龙格——库塔方法的基本思想
25
龙格——库塔方法的形式
龙格——库塔方法的一般形式:(参看P111) 龙格——库塔方法的经典形式:4级4阶公式
26
常微分方程组和高阶方程 初值问题的数值方法
1、常微分方程组初值问题的数值方法 欧拉方法可直接推广
龙格——库塔方法也有类似的推广形式
②编写主程序 ts=0:3000; x0=[2;0]; [t,y]=ode15s(@vdp1000,ts,x0); plot(t,y(:,1),'r-')
缉私船路线的微分方程模型(周东海、熊潘、文跃忠)

缉私船路线的微分方程模型队员:周东海 20087610熊潘 20087618文越忠 20087622摘要:对缉私船追上走私船的问题,为了便于分析,我们用数值法模拟,然后用MATLAB求解。
对模型1根据定义的参数2,m i l en 60,20,10πθ====d kn v kn a ,用MATLAB 解得运动轨迹见附录1,在(60,40)处缉私船追上走私船,所耗时间小时4,4010==t t 。
对模型2根据定义的参数4,mile n 50,30,15πθ====d kn v kn a ,用MATLAB解得运动轨迹见附录2,在(81.13,31.13)处缉私船追上走私船。
此时935.2,13.314sin 15==t t π,即在2.935小时后缉私船追上走私船对模型3根据定义的参数32,mile n 40,40,20πθ====d kn v kn a ,用MATLAB 解得运动轨迹见附录3,在(29.41,18.34)处缉私船追上走私船。
此时059.1,34.1832sin 20==t t π,即在1.059小时后缉私船追上走私船 对模型1进行稳定性分析,在2πθ=的条件时,由水平位移的时间等于垂直位移的时间,va v da y t /)(22-==将第3组数据代入,t=0.917,误差134.0059.1917.0059.1=-=∆,只相差几分钟,说明模型还是可信。
关键词:MATLAB 微分方程 数值模拟 数值稳定性一、问题的重述我缉私船雷达发现,距离d处有一走私船正以匀速a沿直线行驶,缉私船立即以最大速度(匀速v)追赶。
若用雷达进行跟踪,保持船的瞬时速度方向始终指向走私船,则缉私船的运动轨迹是怎样的?是否能够追上走私船?如果能够追上,需用多少时间?试用数值方法进行模拟。
【思考】当缉私船雷达发现d处有一走私船后雷达突然损坏,无法跟踪走私船逃窜的位置。
若假定走私船作匀速直线运动(但不知方向),且缉私船速度v大于走私船速度a,则缉私船应采用什么策略才能确保追上走私船?二、问题分析、假设与符号说明假设1 走私船正以匀速a沿直线行驶假设2 缉私船的速度方向始终指向走私船并立即以最大速度(匀速v)追赶假设3 不考虑风浪的影响涉及常量:a走私船的速度(kn)n )d 走私船与缉私船之间的距离(milev缉私船的速度(kn)涉及变量:θ走私船与x轴的夹角以缉私船与走私船初始位置的连线为x轴,以走私船为坐标原点,垂直两船连线为y轴建立直角坐标系图1设缉私船航行的曲线方程为)(x f y =,在时刻t 时缉私船位于(,)P x y ,走私船位于Q , Q 点坐标为()θθsin ,cos at at ,直线PQ 与缉私船的路线相切,缉私船的方向始终指向走私船可得到:)sin ()sin ()cos ()cos ()sin ()cos (2222y at y at x d at vdt dy x d at y at x d at v dt dx --+-+=-+-+-+=θθθθθθ(1)为了便于求解及分析,我们用数值法进行模拟。
数学建模综合实验缉私艇走私艇

一.实验目的本综合实验旨在考察及训练学生对微分方程建模及Matlb 编程的灵活运用。
通过本实验了解数学建模的基本思想,并熟练掌握用数学软件解决数学问题的方法。
提高学生的综合能力。
二.实验内容1、已知微分方程组⎪⎪⎩⎪⎪⎨⎧=-+=++00y x dtdy y x dtdx满足初始条件0|,1|00====t t y x . (1)求上述微分方程组初值问题的特解(解析解),并画出解函数()y f x =的图形.(2) 分别用ode23、ode45求上述微分方程组初值问题数值解(近似解),求解区间为[0,0.5]t ∈.利用画图比较两种求解器之间的差异.2、分别用 Euler 折线法和四阶 Runge-Kutta 法求解微分方程初值问题⎩⎨⎧=-=1)0(,cos 'y x e y y x 的数值解(步长h 取0.1),求解范围为区间[0,3] .3、海防某部缉私艇上的雷达发现正东方向15海里处有一艘走私船正以20海里/小时的速度向正北方向行驶,缉私艇立即以40 海里/小时的速度前往拦截。
用雷达进行跟踪时,可保持缉私艇的速度方向始终指向走私船。
建立任意时刻缉私艇的位置和缉私艇航线的数学模型,确定缉私艇追上走私船的位置,求出追上的时间,画出航线图形,并通过改变速度等参数进行讨论。
三. 实验方案(程序设计说明)第1题:使用 dsolve 函数、ode23、ode45求解器编程求解;第2题:利用 Euler 折线法和四阶 Runge-Kutta 法的递推公式编程求解; 第3题:实验方案如下: (一)建立模型以0=t 时刻缉私艇位置为原点,正东方向为正x 轴方向,正北方向为正y 轴方向建立直角坐标系,则缉私艇与走私船的初始距离15=a ,设缉私艇行驶的路程为s ,缉私艇航线任一点切线与x 轴正向夹角为θ,则有缉私艇:速度40=V j ,初始位置()0,0,t 时刻位置()y x , 走私艇:速度20=V z ,初始位置()0,15,t 时刻位置()t a z V ,。
海上缉私模型论文数学建模MATLAB

.海上缉私问题建模题目二摘要针对海上缉私问题,要求出缉私船是否能追上走私船,或着是求缉私艇追上走私船的位置和时间,就需要知道走私船和缉私艇的位置坐标、大概的行驶路线、及二者的速度。
对于走私船和缉私艇的位置坐标,可以由二者的行驶路线 、速度、行驶时间之间的关系得到。
而走私船和缉私艇的位置坐标,可用三角函数、坐标关系、圆的位置关系求解。
当缉私船追上走私船时,走私船和缉私艇的位置坐标相同,即二者的横坐标相等,纵坐标相等。
在此期间,再加以MATLAB 软件进行求解。
关键字: 海上缉私 位置坐标 速度 MATLAB 软件问题重述分别对以下情况建立缉私船的位置和航线的数学模型,自己设定速度等参数,求数值解:(1) 走私船向正东方向非匀速直线行驶,其速度()a t 按正弦规律变化,如图1.已知缉私船以速度b 匀速追击, 1.5b d =(d 为常数),两船初始距离2c d =.图1(2) 两船速度大小都不变,走私船以速度a 沿着与正东方向成θ角的直线行驶,如图2.已知缉私船的速度 1.6b a =,两船初始距离c a =.取25θ=o 与65θ=o ,求数值解,并说明走私船按哪个角度逃跑较快?图2(3) 两船速度大小都不变,走私船以速度a 沿半径为r 的圆弧向P 点逃跑,现有两种方案,如图3.问两种方案是否都能到达P 点?已知圆弧半径r a =,缉私船的速度 1.4b a =,两船初始距离0.8c a =.方案1 方案2图3(4)两船速度都大小不变,走私船以速度a 先向正东方向直线行驶,一段时间(设尚未被缉私船追上)后改变方向,沿着与正东方向成θ角(90180)θ<≤o o的直线行驶,如图4.已知缉私船的速度 1.2b a =,两船初始距离 1.5c a =.取170θ=o ,求数值解.图4(4)(5) 开始两船速度大小都不变,走私船以速度a 向正东方向沿直线行驶,但当两船距离小于r 时,缉私船会发现被人追击,将沿正北方向以速度g 加速逃跑,如图5.已知0.5r a =, 1.5g a =,缉私船的速度 1.8b a =,两船初始距离3c a =,求数值解.图5(6) 实际在追击时,缉私船速度方向的改变并不连续,每隔时间t ∆变换一次角度,在两次变换之间,缉私船按直线运动.若两船速度大小都不变,走私船以速度a 向正东方向沿直线行驶,30a =(海里/小时),缉私船的速度50b =(海里/小时),两船初始距离25c =(海里),60t ∆=(秒).试画出缉私船的航线图,建立此时的追击模型,比较与之前模型有何不同,并求数值解.问题分析问题一:要确定缉私船追上走私船的位置及时间,就必须确定缉私船、走私船的坐标。
缉私艇追击走私船问题论文

基于微分模型下的缉私问题摘 要为了研究缉私艇追击走私船问题,我们通过对缉私船以及走私船之间的运动轨迹关系进行讨论,通过结合两者之间的相互关系,建立相应微分方程模型。
首先,对问题一,我们建立缉私船与走私船之间的坐标系,得出缉私船及走私船之间的关系并得到其微分方程。
然后将得到的微分方程方程简化,得到微分模型的方程⎪⎩⎪⎨⎧='==⎪⎭⎫ ⎝⎛+=,0)(,0)(1222c y c y b ar dx dy r dx y d x , 对bar =与1之间的关系进行讨论,得到: 当1<=b a r 时,方程的解析解为211111112rcr c x r c x r c y rr -+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=-+ 即当0=x 时, 缉私船能追上走私船,此时21r cr y -=,)()1(222a b bcr a cr a y t -=-== 当1≥=bar 时,缉私船不能追上走私船。
其次,对问题二,根据题设给出的条件c=3千米,a=0.4千米/秒,b=0.8千米/秒结合问题一建立的微分方程模型,通过matlab 软件绘制出缉私艇追赶走私船运动轨迹的图形。
然后我们利用计算机仿真算法,模拟缉私艇追击走私船的动态过程。
从而实现对缉私艇整个追击过程的完美拟合。
关键字:微分方程模型;matlab 仿真法;缉私艇追击过程AbstractTo study the anti-smuggling smuggling boat chase, we trajectory through the relationship between anti-smuggling boats and smuggling boat to discuss, through a combination of mutual relations between the two differential equations to model appropriate.First, a problem, we have established smuggling coordinate between the ship and the smuggling boat, draw anti-smuggling and smuggling boat relationship between ship and get their equations. The differential equation is then simplified to give the differential equation model⎪⎩⎪⎨⎧='==⎪⎭⎫ ⎝⎛+=,0)(,0)(1222c y c y b ar dx dy r dx y d x , The relationship between a discussion, we get: At that 1<=bar time, the analytical solution for the equation 211111112rcr c x r c x r c y rr-+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=-+ That 0=x time, the anti-smuggling boats can catch smugglers, then21r cr y -=,)()1(222a b bc r a cr a y t -=-== At that 1≥=bar time, the anti-smuggling boats can not catch smugglers. Secondly, the question two, according to the title given conditions set c = 3 one thousand meters, a = 0.4 km / s, b = differential equation model 0.8 km / sec combined with a problem created by matlab software to map out anti-smuggling catch smugglers trajectory graphics. Then we use computer simulation algorithms, simulated anti-smuggling smuggling boat chase dynamic process. Anti-smuggling in order to achieve the perfect fit throughout the course of the pursuit.Keywords: differential equation model; matlab simulation method; anti-smuggling chase procedure一、问题重述1.1问题的提出缉私艇追击走私船问题:海上边防缉私艇发现距c公里处有一走私船正以匀速a沿直线行驶, 缉私艇立即以最大速度b追赶, 在雷达的引导下,缉私艇的方向始终指向走私船。
追击船只-信息-郝爱虎

数学建模上机实验实验目的:求追击船只所用的时间及轨迹学院:理学院专业:信息与计算科学01班姓名:郝爱虎学号:40808010123实验题目如下:海上边防缉私艇发现距c 公里处有一走私船正以匀速a 沿直线行驶,缉私艇立即以最大速度b 追赶,在雷达的引导下,缉私艇的方向始终指向走私船。
问缉私艇何时追赶上走私船?并求出缉私艇追赶的路线。
2=b 问题分析:建立坐标系如图: t =0 艇在(0, 0), 船在(c, 0); 船速a , 艇速b, 时刻 t 艇位于P (x, y ), 船到达 Q (c, at ),cos αb dt dx = ,sin αb dtdy = dt dx = 22)()()(y at x c c b b -+-- (1)dt dy = 22)()()(y at x c y at b -+-- (2)x(0)=0, y(0)=0假设数值:a=30 b=40 c=25求出追上时的位置和所走的轨迹.用MATLAB 编写程序:function dx=ting(t,x)a=30;b=40;c=25;s=sqrt((c-x(1))^2+(a*t-x(2))^2);dx=[b*(c-x(1))/s;b*(a*t-x(2))/s];将文件保存之后再回到commandwidow 的界面中输入程序: ts=0:0.05:0.5x0=[0 0];[t,x]=ode45(@ting,ts,x0);[t,x]plot(t,x),grid,gtext('x(t)'), gtext('y(t)'),pauseplot(x(:,1),x(:,2)),gridgtext('x'), gtext('y')则结果为:ans =0 0 00.0500 1.9987 0.06160.1000 3.9892 0.25290.1500 5.9612 0.58330.2000 7.9027 1.06160.2500 9.7990 1.69540.3000 11.6337 2.48990.3500 13.3890 3.44700.4000 15.0463 4.56520.4500 16.5881 5.83790.5000 17.9989 7.25440.5500 19.2672 8.79980.6000 20.3862 10.45670.6500 21.3548 12.20580.7000 22.1764 14.02870.7500 22.8598 15.90790.8000 23.4159 17.82870.8500 23.8591 19.77880.9000 24.2032 21.74880.9500 24.4641 23.73161.0000 24.6547 25.7225图像为:00.10.20.30.40.50.60.70.80.91051015202530。
2.4 舰艇追击问题

舰艇追击问题某缉私舰位于走私船以东d=10km,走私船以匀速u=8km/h向北沿直线行驶,缉私舰立即以速度v=12km/h追赶,若用雷达进行跟踪,保持船的瞬时速度方向始终指向走私船,试求缉私舰追逐路线和追上的时间。
我们采用理论求解和计算机模拟两种方法。
1.、理论求解该问题采用微分方程建模求解。
图1 追击坐标示意图二、计算机模拟仿真Matlab程序:dt=0.01;n=151;d=10;u=8;v=12;T=d*v/(v*v-u*u); %理论时间x1=zeros(n,1); y1=zeros(n,1);x2=zeros(n,1); y2=zeros(n,1);x1(1)=0; y1(1)=0; %走私船开始位置 x2(1)=d; y2(1)=0; %缉私舰开始位置%仿真曲线for j=1:n-1x1(j+1)=0; %走私船横坐标y1(j+1)=(j+1)*dt*u; %走私船纵坐标ct=(x1(j)-x2(j))/sqrt((x1(j)-x2(j))^2+(y1(j)-y2(j))^2);st=(y1(j)-y2(j))/sqrt((x1(j)-x2(j))^2+(y1(j)-y2(j))^2);x2(j+1)=x2(j)+v*dt*ct; %缉私舰横坐标y2(j+1)=y2(j)+v*dt*st; %缉私舰纵坐标end%理论曲线x=d:-0.01:0;k=u/v;y=d/2*((x/d).^(1+k)/(1+k)-(x/d).^(1-k)/(1-k))+d*k/(1-k^2); plot(x1,y1,'r',x2,y2,'-r',x,y,'b');图2 仿真曲线与理论曲线比较图谢谢!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/9/20
为什么要学习微分方程数值解?
微分方程是研究函数变化规律的有力工具, 有着广泛的应用。 如:
物体的运动、电路的电压、 人口增长的预测、种群数量的演变…… 许多微分方程没有解析解,比如:
2020/9/20
一、微分方程的解析解的Matlab的实现
y(pi/2)=2','Dy(pi/2)=-2/pi','x')
结果为:y=2^(1/2)*pi^(1/2)/x^(1/2)*sin(x)
2020/9/20
思考:若程序这样写行吗?为什么? 》n=1/2; 》y=dsolve('x^2*D2y+x*Dy+(x^2-n^2)*y' , …
y(pi/2)=2','Dy(pi/2)=-2/pi','x')
2020/9/20
常微分方程初值问题的提法
f对y满足李普希茨(Lipschitz)条件,
即存在L使
2020/9/20
什么是数值解?
离散点通常取等步长h xn= x0+nh
2020/9/20
欧拉方法及其基本思想
基本 思路
基本 公式
x取不同,得到不同的欧拉公式
2020/9/20
向前欧拉公式
x取左端点xn
校正
2020/9/20
编程求微分方程的数值解?
解:(1)解析解的求解 》 y=dsolve('Dy=y-2*x/y','y(0)=1','x')
2020/9/20
(2)数值解的求解
2020/9/20
数值解的求解程序
x=0:0.1:1; y=sqrt(1+2*x); y1(1)=1;y2(1)=1; h=0.1; m=length(x)-1; for n=1:m
2020/9/20
》 y=dsolve('Dy=x^2+y^2','x') 无解析解
2020/9/20
实例1:海上缉私
海防某部缉私艇上的雷达发现正东方向c海里处 有一艘走私船正以一定速度a向正北方向行驶, 缉私艇立即以最大速度b前往拦截(b>a)。用 雷达进行跟踪时,可保持缉私艇的速度方向始终 以指向走私船。
建立任意时刻缉私艇的位置和缉私艇航线 的数学模型,并求解;
求出缉私艇追上走私船的时间。
2020/9/20
实例1:海上缉私
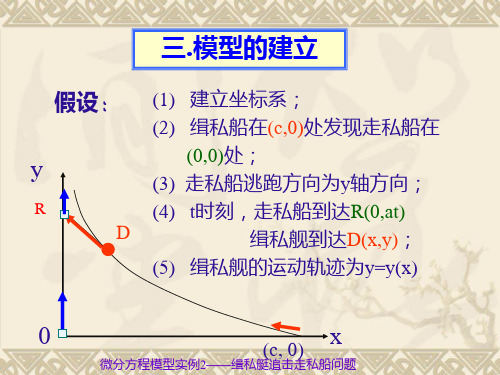
• 模型建立:
•
建立直角坐标系 :t=0时,艇在
(0,0)
船在(0,c);船速a,艇速b (b>a);
模时型刻:t,艇在P(x,y), 船在Q(c, at)。
x(t)、y(t) 无解析解!
dsolve
2020/9/20
2、调用格式:
dsolve('eqn1','eqn2', ...)
其中:eqn1,eqn2,…表示方程;用单引号引 起来,默认自变量为‘t’,如果不采用‘t’,必须 申明。
2020/9/20
3、简单应用
例 1、求 dy 解 1y2的通y(解 0)1及 时的 dx
通解: 》y=dsolve('Dy=1+y^2','x')
1、怎么用Matlab命令求微分方程的符号解呢 ? 借助Matlab7.0帮助文件Help—— Matlab help——Symbolic Math Toolbox——Solving Equations——Single Differential Equation or Several Differential Equations——
%向前欧拉法; y1(n+1)=y1(n)+h*(y1(n)-2*x(n)/y1(n));
2020/9/20
数值解的求解程序(续)
%改进欧拉法; k1=y2(n)-2*x(n)/y2(n); k2=y2(n)+h*k1-2*x(n+1)/(y2(n)+h*k1); y2(n+1)=y2(n)+h/2*(k1+k2); end disp([x;y;y1;y2]) plot(x,y,'bo',x,y1,'r*',x,y2,'k+')
实验12 缉私艇追赶走私船模型实验
实验目的
1、学会用Matlab软件求解微分方程的初值问题 2、了解微分方程数值解思想、掌握两种简单的 微分方程数值解求法; 3、学会根据实际问题建立简单的微分方程数学 模型。
实验内容
[1]用Matlab的dsolve命令求微分方程解析解; [2]编程用向前欧拉公式和改进欧拉公式求微分方程的数值解;
结果为:y=tan(x+c1)
特解: 》y=dsolve('Dy=1+y^2','y(0)=1','x') 结果为:y=tan(x+1/4*pi)
2020/9/20
ห้องสมุดไป่ตู้
例2、求解二阶微分方程
x2 y xy (x2 n2)y 0,
y( ) 2, y( ) 2 ,n 1.
2
2
2
》y=dsolve('x^2*D2y+x*Dy+(x^2-(1/2)^2)*y' , …
2020/9/20
数值解的图形结果
1.8
1.7
1.6
1.5
1.4
1.3
1.2
value
qeuler
1.1
geuler
1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
改进欧拉公式计算的结果与精确解非常接近; 向前欧拉公式计算的结果累计误差大。
2020/9/20
龙格——库塔方法
2020/9/20
例3、求方程 dddyxt组 xxyy,x(0)1,y(0)2的特解 dt
》[x,y]=dsolve('Dx=x+y','Dy=-x+y',…
'x(0)=1','y(0)=2') 结果为: x=exp(t)*(cos(t)+2*sin(t))
y=exp(t)*(-sin(t)+2*cos(t))
几何意义 求解步骤
2020/9/20
向前欧拉公式 显式公式
向后欧拉公式
x取右端点xn+1
向后欧拉公式 隐式公式
2020/9/20
欧拉梯形公式
向前欧拉公式
向后欧拉公式
二者平均得到梯形公式
仍为隐式公式, 需迭代求解
2020/9/20
改进欧拉公式
改进欧 拉公式
将梯形公式的迭代过程简化为两步
预测
改进欧拉公式
欧拉 方法 思想
向前、后欧拉公式 梯形、改进欧拉公式
差商 代替 导数
龙格——库塔方法的基本思想
2020/9/20
龙格——库塔方法的形式
龙格——库塔方法的一般形式:(参看P111) 龙格——库塔方法的经典形式:4级4阶公式
2020/9/20
常微分方程组和高阶方程 初值问题的数值方法
