北师大版八年级数学下册同步练习题一元一次不等式

合集下载

(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析)

(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析) ⋯⋯⋯⋯⋯⋯⋯⋯⋯○装⋯○⋯⋯⋯⋯_____⋯⋯____⋯⋯：号装考_○__⋯____⋯_⋯__：⋯⋯班__⋯__⋯__○___⋯：⋯名姓_外⋯____⋯_⋯___⋯：校⋯学内⋯⋯⋯⋯⋯○⋯⋯○⋯⋯⋯⋯⋯(完整word 版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析)优来文化培训中心数学八下第一章一元一次不等式和一元一次不等式组练习题分卷 I分卷 I 注卷人得分一、 ( 注 )1、关于 x 、y 的二元一次方程的解足不等式＞ 0，的取范是〔〕A ．＜ -1B ．＜ 1C ．＞ -1D ．＞ 12、如果 a ＜ 0，以下式子的是A ． 5+a ＞3+aB ． 5 a ＞ 3 aC ． 5a ＞3aD ．3、不等式的解集在数上表示A ．B ．C ．D ．4、数 a 、 b 在数上的位置如所示，以下各式成立的是A ．B ． a b ＞0C ． ab ＞ 0D ． a+b ＞05、点P 〔〕在第一象限， a 的取范在数上表示正确的选项是A ．B ．C ．D ．6、把不等式的解集在数上表示出来，正确的选项是A ．B ．C ．D ．7、假设〔 m+1〕 x |m| +2＞0 是关于 x 的一元一次不等式， m=〔〕 A ． ± 1B ． 1C ． 1D ． 0试卷第 1 页，总 19 页(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析) ⋯⋯⋯⋯⋯⋯⋯⋯⋯○装⋯○⋯⋯⋯⋯_____⋯⋯____⋯⋯：号装考_○__⋯____⋯_⋯__：⋯⋯班__⋯__⋯__○___⋯：⋯名姓_外⋯____⋯_⋯___⋯：校⋯学内⋯⋯⋯⋯⋯○⋯⋯○⋯⋯⋯⋯⋯(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析)16、假设 a<b，以下各式中一定正确的选项是A． ab<0B． ab>0C． a－ b>0D．－ a>－ b优来文化培训中心数学八下试卷第 2 页，总 19 页8、由 a＞ b 得到 am＞ bm 的条件是〔〕A． m＞ 0B． m＜0C． m≥0D． m≤O9、如果关于x 的不等式 (a+1)x>a+1 的解集x<1， a 的取范是〔〕A． a<0B． a<-1C． a>1D． a>-110、不等式的解集在数上表示A．B．C．D．11、如天平右中的每个砝的量都是1g，物体 A 的量 m(g)的取范在数上可表示 ( )12、不等式的解集在数上表示〔〕13、假设关于 x的一元一次不等式有解，m 的取范A．B．C．D．14、以下命正确的选项是A．假设 a＞ b， b ＜c， a＞ c B．假设 a＞ b， ac＞ bcC．假设 a＞ b， ac2＞ bc2D．假设 ac2＞ bc2， a＞ b15、一个不等式的解集在数上的表示如下，个不等式的解集是A． x<3B． x≥－1C．－ 1<x ≤3D．－ 1≤ x<3(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析) ⋯⋯⋯⋯⋯⋯⋯⋯⋯○装⋯○⋯⋯⋯⋯_____⋯⋯____⋯⋯：号装考_○__⋯____⋯_⋯__：⋯⋯班__⋯__⋯__○___⋯：⋯名姓_外⋯____⋯_⋯___⋯：校⋯学内⋯⋯⋯⋯⋯○⋯⋯○⋯⋯⋯⋯⋯(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析)试卷第 3 页，总 19 页优来文化培训中心数学八下17、 a<b，以下不等式一定成立的是A． a+5>b+5B． -2a<-2b C．D． 7a-7b<018、在数上表示不等式的解集，正确的选项是19、 a、 b 均 a>b，以下不正确的选项是〔〕A． a+3>b+3B． a-3>b-3C． 3a>3b D．20、不等式的解集，〔〕A． 2021B．C．D． 1(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析) ⋯⋯⋯⋯⋯⋯⋯⋯⋯○装⋯○⋯⋯⋯⋯_____⋯⋯____⋯⋯：号装考_○__⋯____⋯_⋯__：⋯⋯班__⋯__⋯__○___⋯：⋯名姓_外⋯____⋯_⋯___⋯：校⋯学内⋯⋯⋯⋯⋯○⋯⋯○⋯⋯⋯⋯⋯(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析) 优来文化培训中心数学八下31、解不等式．分卷II分卷 II注卷人试卷第 4 页，总 19 页得分二、填空(注)21、某采石爆破，点燃火的甲工人要在爆破前移到400 米以外的平安区域．甲工人在移程中，前40 米只能步行，之后自行．火燃的速度米 / 秒，步行的速度 1米 / 秒，的速度 4 米 / 秒．了确保甲工人的平安，火的要大于米．22、不等式和x+3〔x1〕＜ 1 的解集的公共局部是．23、关于 x 的方程 kx 1=2x 的解正数，k 的取范是．24、当 x，代数式的不小于的．25、假设关于 x的不等式的解集是x＞ 2， m 的取范是．26、足不等式 5＜ 6 2x＜3 的所有整数解的和是．27、不等式 1 2x＜6 的整数解是．28、 3x+4 ≤ 6+2〔 x 2〕， |x+1|的最小等于．29、不等式x＜1 的正整数解是．30、不等式的解集是；卷人得分三、算 ( 注 )(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析) ⋯⋯⋯⋯⋯⋯⋯⋯⋯○装⋯○⋯⋯⋯⋯_____⋯⋯____⋯⋯：号装考_○__⋯____⋯_⋯__：⋯⋯班__⋯__⋯__○___⋯：⋯名姓_外⋯____⋯_⋯___⋯：校⋯学内⋯⋯⋯⋯⋯○⋯⋯○⋯⋯⋯⋯⋯(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析)试卷第 5 页，总 19 页优来文化培训中心数学八下32、〔 1〕解方程：〔2〕解不等式：．33、解不等式〔8 分〕34、解方程：〔 1〕〔2〕35、因式分解：〔 1〕 m3－ 4m〔2〕36、先化：再从不等式的整数解中一个恰当的x 代入并求．(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析) ⋯⋯⋯⋯⋯⋯⋯⋯⋯○装⋯○⋯⋯⋯⋯_____⋯⋯____⋯⋯：号装考_○__⋯____⋯_⋯__：⋯⋯班__⋯__⋯__○___⋯：⋯名姓_外⋯____⋯_⋯___⋯：校⋯学内⋯⋯⋯⋯⋯○⋯⋯○⋯⋯⋯⋯⋯(完整word 版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析)优来文化培训中心数学八下37、解不等式，并把解集在数上表示出来．38、解不等式，并把它的解集在数上表示出来.(1)〔 2〕39、解不等式 ≥ ，将解集在数上表示出来，且写出它的正整数解。

2021-2022学年度初中数学北师大版八年级下册第二章第六节一元一次不等式组同步练习

初中数学北师大版八年级下册第二章第六节一元一次不等式组同步练习一、单选题1．下列不等式组中，无解的是（）A．{x<2x<−3B．{x<2x>−3C．{x>2x>−3D．{x>2x<−32．已知关于x的不等式组的{x−a≥b2x−a<2b+1解集为3≤x＜5，则ba的值为（）A．﹣2B．−12C．﹣4D．﹣143．若不等式组{x<1x<m的解为x＜m，则m的取值范围为（）A．m≤1B．m=1C．m≥1D．m＜14．定义：对于实数a，符号[a]表示不大于a的最大整数.例如：[3.2]=3，[2]=2，[-2.3]=-3.如果[x−12]=2，则x的取值范围是（）A．5≤x≤7B．5<x≤7C．5<x<7D．5≤x<75．定义一种运算：a∗b={a,a≥bb,a<b，则不等式(2x+1)∗(2−x)>3的解集是（）A．x>1或x<13B．−1<x<13C．x>1或x<−1D．x>13或x<−16．已知某程序如图所示，规定：从“输入实数x”到“结果是否大于95”为一次操作，如果该程序进行了两次操作停止，那么实数x的取值范围是()A．x>23B．11≤x≤23C．23<x≤47D．x≤477．若关于x的一元次不等式组{−2x+3m4≤2x2x+7≤4(x+1)的解集为x≥32，且关于y的方程3y−2=2m−(5−3y)2的解为非负整数，则符合条件的所有整数m的积为（）A．2B．7C．11D．108．目前，我国已获批上市4款自主研发的新冠疫苗．某生物制药公司计划生产制造A、B两种疫苗共40万支，已知生产每支A疫苗需甲种原料8mg，乙种原料5mg；生产每支B疫苗需甲种原料4mg，乙种原料9mg．公司现有甲种原料4kg，乙种原料3kg，设计划生产A疫苗x支，下列符合题意的不等式组是（）A ．{8x +5(400000−x)≤40000004x +9(400000−x)≤3000000B ．{5x +9(400000−x)≤40000008x +4(400000−x)≤3000000C ．{8x +4(400000−x)≤40000005x +9(400000−x)≤3000000D ．{8x +9(400000−x)≤40000005x +4(400000−x)≤3000000二、填空题9．不等式组 {5x +4>3xx−12≤2x−15 的解是 .10．已知关于 x 的不等式组 {5−3x ≥−1,a −2x <0无解，则 a 的取值范围是． 11．三个数3， 1-a ，1-2a 在数轴上从左到右依次排列，且以这三个数为边长能构成三角形，则a 的取值范围为12．在某种药品的说明书上的部分内容是“用法用量：每天 30~60mg ，分2~3次服用”.则一次服用这种药品的剂量 x 的范围是 mg .13．对于任意实数，m ，n ，定义一种运算： m※n =mn −m −n +72 ，请根据上述定义解决问题：若关于x 的不等式 a <(12※x)<7 的解集中只有一个整数解，则实数a 的取值范围是 .14．若点 P 的坐标为 (x−15,2x −10) ，其中 x 满足不等式组 {5x −10≥2(x +1)12x −1≤7−32x ，则点 P 在第象限.15．令 a 、b 两数中较大的数记作 max|a ，b|，如 max|2，3|=3，已知 k 为正整数且使不等式 max|2k+1，﹣k+5|≤5 成立，则 k 的值是 .16． 12月是成都奶油巧克力草莓大丰收的季节，重庆渝北海领开展“水果一带一路”活动，成都顺丰快递公司出动所有车辆分12月25，26日两批往重庆运输现摘草莓.该公司共有A ，B ，C 三种车型，其中A 型车数量占公司车辆总数的一半，B 型车数量与C 型车数量相等.25日安排A 型车数量的一半，B 型车数量的 13 ，C 型车数量的 34 进行运输，且25日A ，B ，C 三种车型每辆车载货量分别为10吨，15吨，20吨，则25日刚好运完所有草莓重量的一半.26日安排剩下的所有车辆完成剩下的所有草莓的运输，且26日A ，B ，C 三种车型每辆载货量分别不超过14吨，27吨，24吨.26日B 型车实际载货量为26日A 型车每辆实际载货量的 32.已知同型货车每辆的实际载货量相等，A ，B ，C 三种车型每辆车26日运输成本分别为100元/吨，200元/吨，75元/吨，则26日运输时，一辆A 型车、一辆B 型车，一辆C 型车总的运输成本至多为元.三、解答题17．解不等式组： {6(23x −2)<x −31−x2−2⩽x 并把解集在数轴上表示出来．18．已知a ，b ，c 是△ABC 的三边长，若b ＝2a ﹣1，c ＝a+5，且△ABC 的周长不超过20cm ，求a 的范围.19．x 取哪些正整数值时，不等式 5x +2>3(x −1) 与 2x−13≤3x+16 都成立?20．已知关于x ，y 的方程满足方程组 {3x +2y =m +1 ①2x +y =m −1 ② ，（Ⅰ）若 x-y=2 ，求m 的值；（Ⅱ）若x ，y ，m 均为非负数，求m 的取值范围，并化简式子|m −3|+|m −5| ；（Ⅲ）在（Ⅱ）的条件下求 s =2x −3y +m 的最小值及最大值．四、综合题21．疫情期间，为满足市民的防护需求，某医药公司想要购买A 、B 两种口罩．在进行市场调研时发现：A 型口罩比B 型口罩每件进价多了10元．用68000元购买A 型口罩的件数是用32000元购买B 型口罩件数的2倍．（1）A 、B 型口罩进价分别为每件多少元？（2）若该公司计划购买A 、B 型口罩共200件，其中A 型口罩的件数不大于B 型口罩的件数，且用于购买A 型口罩的钱数多于购买B 型口罩的钱数．设购买A 型口罩x 件，则符合条件的进货方案共多少种？（件数均为整数，不用列出方案）22．2010年6月5日是第38个世界环境日，世界环境日的主题为“多个物种、一颗星球、一个未来”.为了响应节能减排的号召，某品牌汽车4S 店准备购进A 型（电动汽车）和B 型（太阳能汽车）两种不同型号的汽车共16辆，以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息：（1）若经营者的购买资金不少于576万元且不多于600万元，则有哪几种进车方案？（2）在（1）的前提下，如果你是经营者，并且所进的汽车能全部售出，你会选择哪种进车方案才能使获得的利润最大？最大利润是多少？（3）假设每台电动汽车每公里的用电费用为0.65元，且两种汽车最大行驶里程均为30万公里，那么从节约资金的角度，你做为一名购车者，将会选购哪一种型号的汽车？并说明理由.23．对实数x 、y ，我们定义一种新运算：F （x ，y ） =ax +by （其中a ，b 为常数）.例如：F （2，3） =2a +3b ，F （2， −3 ） =2a −3b .已知F （1，1）=2，F （1， −1 ）=0. （1）则 a = ， b = ；（2）若方程组 {F(x,−y)=4m −3F(x,2y)=−5m 的解中，x 是非正数，y 是负数： ①求m 的取值范围；②若 2x ⋅4y =2n ，求n 的最小值；（3）若关于x 的不等式组 {F(3x,0)>−2cF(−2x,0)≥−3c恰好有3个整数解，求c 的取值范围.24．某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒，乙品牌的进货单价是甲品牌进货单价的2倍，考虑各种因素，预计购进乙品牌文具盒的数量y （个）与甲品牌文具盒的数量x （个）之间的函数关系如图所示．当购进的甲、乙品牌的文具盒中，甲有120个时，购进甲、乙品牌文具盒共需7200元．（1）根据图象，求y与x之间的函数关系式；（2）求甲、乙两种品牌的文具盒进货单价；（3）若该超市每销售1个甲种品牌的文具盒可获利4元，每销售1个乙种品牌的文具盒可获利9元，根据学生需求，超市老板决定，准备用不超过6300元购进甲、乙两种品牌的文具盒，且这两种品牌的文具盒全部售出后获利不低于1795元，问该超市有几种进货方案？哪种方案能使获利最大？最大获利为多少元？答案解析部分1．D2．A3．A4．D5．C6．C7．D8．C9．-2＜x≤310．a≥411．−3<a<−212．10≤x≤3013．6≤a＜13214．四15．2或116．540017．解：解不等式①，得：x＜3，解不等式②，得：x≥﹣1，则不等式组的解集为﹣1≤x＜3，将不等式组的解集表示在数轴上如下：18．解：由题意得：{a+5<2a−1+aa+5+a+2a−1≤20，解得3＜a≤4.∴a的取值范围为3＜a≤419．解：解不等式5x+2>3(x−1)得：5x+2>3x−3x >−52解不等式 2x−13≤3x+16得：2(2x −1)≤3x +1 4x −2≤3x +1x ≤3∴ −52<x ≤3∴符合条件的正整数值有1、2、3 20．解：（Ⅰ） {3x +2y =m +1 ①2x +y =m −1 ②①－②×2得： −x =−m +3 得： x =m −3 2m −6+y =m −1③ 把③代入②2m-6+y=m-1 y =−m +5④把③和④代入 x −y =2 ， m-3+m-5=2, m =5 ， ∴ 的值为5．（Ⅱ）∵x ，y ，m 均为非负数，{m −3≥0−m +5≥0m ≥0∴3≤m ≤5∴|m −3|+|m −5| ． =m-3+5-m ， =2．（Ⅲ）把 x=m-3 y=-m+5， x −y =2 代入 s =2x −3y +m ， ∴ s=2x-3y+m ， =2(m-3 )-3(-m+5)+m =6m-21 ∵ 3≤m≤5 ， ∴-3≤6m -21≤9∴−3≤s ≤9 ．答： s =2x −3y +m 的最小值为－3，最大值为9．21．（1）解：设B 型口罩每件的进价为y 元，则A 型口罩每件的进价为（y+10）元依题意得： 68000y+10 ＝2×32000y 解得：y ＝160经检验，y ＝160是原方程的解，且符合题意∴y+10＝170．答：A 型口罩每件的进价为170元，B 型口罩每件的进价为160元；（2）解：设购买A 型口罩x 件，则购买B 型口罩（200﹣x ）件依题意得： {x ≤200−x170x >160(200−x) 解得：963233＜x≤100又∵x 为正整数，∴x 可以取97，98，99，100， ∴符合条件的进货方案共4种．22．（1）解：设A 型汽车购进x 辆，则B 型汽车购进（16﹣x ）辆.根据题意得： {30x +42(16−x)≤60030x +42(16−x)≥576 ，解得：6≤x≤8. ∵x 为整数， ∴x 取6、7、8. ∴有三种购进方案：（2）解：设总利润为w 万元.根据题意得：W ＝（32﹣30）x+（45﹣42）（16﹣x ）＝﹣x+48. ∵﹣1＜0，∴w 随x 的增大而减小，∴当x ＝6时，w 有最大值，W 最大＝﹣6+48＝42（万元）.∴当购进A 型车6辆，B 型车10辆时，可获得最大利润，最大利润是42万元. （3）解：设电动汽车行驶的里程为a 万公里.当32+0.65a ＝45时，解得：a ＝20＜30. ∴选购太阳能汽车比较合算.23．（1）1；1（2）解：①原式= {x −y =4m −3x +2y =−5m ，解得： {x =m −2y =1−3m ， ∵x 是非正数，y 是负数，∴{m −2≤01−3m <0，解得： 13<m ≤2 ；②原式整理为： 2x ⋅22y =2n ，∴x +2y =n ，即 m −2+2(1−3m)=n ，整理得： n =−5m ，∴当 m 取最大值2时，此时 n 的值最小，最小值为： n =−5×2=−10 ；（3）解：不等式组整理为： {3x >−2c−2x ≥−3c，解得： −23c <x ≤32c ，∵不等式组恰好有3个整数解，∴2<32c −(23c)≤3 ，解得：1213<c ≤1813.24．（1）解：设y 与x 之间的函数关系式为y=kx+b ，由函数图象，得 {50k +b =250200k +b =100，解得： {k =−1b =300. ∴y 与x 之间的函数关系式为y=﹣x+300. （2）解：∵y=﹣x+300，∴当x=120时，y=180.设甲品牌进货单价是a 元，则乙品牌的进货单价是2a 元，由题意，得 120a+180×2a=7200，解得：a=15， ∴乙品牌的进货单价是30元.答：甲、乙两种品牌的文具盒进货单价分别为15元，30元.（3）解：设甲品牌进货m 个，则乙品牌的进货（﹣m+300）个，由题意，得{15m +30(−m +300)≤63004m +9(−m +300)≥1795，解得：180≤m≤181.∵m 为整数，∴m=180，181. ∴共有两种进货方案：方案1：甲品牌进货180个，则乙品牌的进货120个；方案2：甲品牌进货181个，则乙品牌的进货119个.设两种品牌的文具盒全部售出后获得的利润为W元，由题意，得W=4m+9（﹣m+300）=﹣5m+2700.∵k=﹣5＜0，∴W随m的增大而减小.∴m=180时，W最大=1800元.。

八年级下册数学北师大版同步课时作业 2.6一元一次不等式组(有答案)

八年级下册数学北师大版同步课时作业2.6一元一次不等式组一、单选题1.下列不等式组：20324x xx x>->⎧⎧⎨⎨<+>⎩⎩①②22130724x x xxx⎧+<+>⎧⎪⎨⎨<-+>⎪⎩⎩③④1010xy+>⎧⎨-<⎩⑤其中一元一次不等式组的个数是（）A.2 B.3 C.4 D.52.不等式组2030xx-⎧⎨+>⎩的解集是( )A.32x-<≤ B.32x-≤< C.2x≥ D.3x<-3.不等式组2(1)3112x xxx+>⎧⎪⎨+-⎪⎩的解集在数轴上表示正确的是( )A. B.C. D.4.小明去商店购买A B，两种玩具，共用了10元钱，A种玩具每件1元，B种玩具每件2元若每种玩具至少买一件，且A种玩具的数量多于B种玩具的数量，则小明的购买方案有( )A.5种B.4种C.3种D.2种5.已知关于x的不等式组321123x xx a--⎧-⎪⎨⎪-<⎩恰有3个整数解，则a的取值范围为( )A.12a<≤ B.12a<< C.12a≤< D.12a≤≤6.不等式组2342x xx>⎧⎨+>⎩的整数解是( )A.0B.1-C.2-D.17.若关于x的不等式组2(1)2xa x->⎧⎨-<⎩的解集是x a>，则a的取值范围是( )A.2a< B.2a≤ C.2a> D.2a≥8.已知关于x的不等式组2323(2)5x ax x>-⎧⎨≥-+⎩仅有三个整数解，则a的取值范围是( )A.112a< B.112a C.112a< D.1a<9.一宾馆有二人间，三人间，四人间三种客房供游客租住，某旅行团20人准备同时租用这三种客房共7间，如果每个房间都住满，租房方案有（）A．4种B．3种C．2种D．1种二、填空题10.某班级从文化用品市场购买了签字笔和圆珠笔共15支，所付金额大于26元，但小于27元.已知签字笔每支2元，圆珠笔每支1.5元，则签字笔购买了_________支.11.若关于x的不等式组10,2420x ax⎧->⎪⎨⎪-⎩无解，则a的取值范围为_______.12.关于x的不等式组240,1xa x->⎧⎨->-⎩的解集是24x<<，则a的值为__________.三、解答题13.2020年6月，国务院总理李克强表示：“地摊经济、小店经济是就业岗位的重要来源，是人间的烟火，是中国的生机”一时间，地摊兴起.小邱决定采购甲、乙两种文具到学校附近的地摊经营，采购甲种文具8件，乙种文具3件，需要95元；采购甲种文具5件，乙种文具6件，需要80元.（1）求甲、乙两种文具每件各多少元；（2）小邱想采购两种文具共100件，考虑到市场需求和资金周转，用于采购这100件文具的资金多于750元，但不超过765元，那么小邱共有哪几种进货方案？请列举出来.参考答案1.答案：B解析：根据一元一次不等式组的定义，①②④是一元一次不等式组;③中未知数的最高次数是2,⑤含有两个未知数，所以③⑤都不是一元一次不等式组.故有①②④三个一元一次不等式组.故选B.2.答案：A解析：求出每个不等式的解集分别为23x x≤>-，，所以不等式组的解集为32x-<≤.3.答案：A解析：2(1)3112x xxx+>⎧⎪⎨+-⎪⎩①②解不等式①得2x<，解不等式②得1x≥-，则不等式组的解集为12x-≤<，在数轴上表示如下故选A4.答案：C解析：设小明购买了A 种玩具x 件，则购买的B 种玩具为102x -件，根据题意得1012102x x x -⎧⎪⎪⎨-⎪<⎪⎩解得1383x < x 为整数，102x -也为整数，4x ∴=或6或8 ∴有3种购买方案5.答案：A 解析：解321123x x ---得12x ≥- 解0x a -<得x a <，不等式组的整数解有3个，∴不等式组的整数解为1-、0、1，则12a <≤6.答案：B解析：2342x x x >⎧⎨+>⎩①② 解不等式①得0x <，解不等式②得2x >-不等式组的解集为20x -<<，不等式组2342x x x >⎧⎨+>⎩的整数解是1-，故选B 7.答案：D解析：解()212x ->得2x >，解0a x -<得x a >，关于x 的不等式组2(1)20x a x ->⎧⎨-<⎩的解集是x a >，2a ∴≥ 8.答案：A解析：解不等式()2325x x ≥-+得1x ≤，因为不等式组仅有三个整数解，所以这三个整数解为1，0，1-，所以2231a -≤-<-，解得112a ≤<，故选A. 9.答案：C解析：设租二人间x 间，租三人间y 间，则四人间客房7x y --．依题意得：234(7)70x y x y x y ++--⎧⎨-->⎩，解得：1x >．28070x y y x y +=>-->，，，2,4,71;x y x y ∴==--=3,2,72x y x y ==--=．故有2种租房方案．故选：C ．10.答案：8解析：设签字笔购买了x 支，则圆珠笔购买了()15x -支，根据题意2 1.5(15)272 1.5(15)26x x x x +-<⎧⎨+->⎩解不等式组得79x << x 是整数，8x ∴=11.答案：1a解析：本题考查解不等式组.解不等式102x a ->得2x a >，解不等式420x -得 2.x 不等式组无解，22a ∴，解得1a .12.答案：3 解析：解不等式240x ->，得2x >.解不等式1a x ->，得1x a <+.不等式组的解集为2414x a <<∴+=，，即3a =.故答案为3.13.答案：（1）设甲种文具每件x 元，乙种文具每件y 元，则83955680x y x y +=⎧⎨+=⎩解得105x y =⎧⎨=⎩答：甲种文具每件10元，乙种文具每件5元.（2）设小邱采购甲种文具t 件，则采购乙种文具()100t -件，则()750105100765t t <+-≤，解得5053t <≤. t 为正整数，515253∴=，，，即有三种方案第一种方案：采购甲种文具51件，乙种文具49件；第二种方案：采购甲种文具52件，乙种文具48件；第三种方案：采购甲种文具53件，乙种文具47件.。

北师大版八年级数学下册 2 (1)

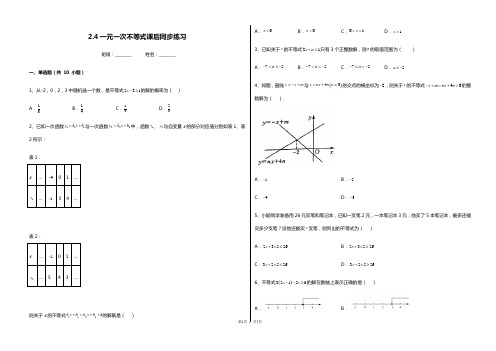
2.4一元一次不等式课后同步练习班级：________ 姓名：________一、单选题（共 10 小题）1、从-2，0，2，3中随机选一个数，是不等式231x -≥的解的概率为（）A ．13B ．14C ．12D ．232、已知一次函数111y k x b =+与一次函数222y k x b =+中，函数1y 、2y 与自变量x 的部分对应值分别如表1、表2所示：表1：x… 4- 0 1 …1y … 1- 3 4 …表2：x … 1- 0 1 …2y (5)4 3 …则关于x 的不等式11221k x b k x b +>++的解集是（）A ．0x <B ．0x >C ．01x <<D ．1x >3、已知关于x 的不等式21x a +≤只有3个正整数解，则a 的取值范围为（）A ．75a -<≤-B ．75a -<<-C ．75a -≤<-D ．5a ≤-4、如图，直线y x m =-+与()40y nx n n =+≠的交点的横坐标为2-，则关于x 的不等式40x m nx n -+>+>的整数解为（）.A ．1-B ．5-C ．4-D ．3-5、小颖同学准备用26元买笔和笔记本，已知一支笔2元，一本笔记本3元，他买了5本笔记本，最多还能买多少支笔？设他还能买x 支笔，则列出的不等式为（）A ．23526x +⨯≤B ．23526x +⨯≥C ．32526x +⨯≤D ．32526x +⨯≥6、不等式()32150x x --≥的解在数轴上表示正确的是（）A ．B ．C ．D ．7、若|3x －2|＝2－3x ，则( )A ．x ＝23B ．x ＞23C ．x ≤23D ．x ≥238、若实数3是不等式2x –a –2<0的一个解，则a 可取的最小正整数为（）A ．2B ．3C ．4D ．59、不等式12x +＞223x +﹣1的正整数解的个数是( ) A ．1个B ．2个C ．3个D ．4个10、不等式131722x x -≤-的解集在数轴上表示为（）A ．B ．C ．D ．二、填空题（共 10 小题）1、2018年国内航空公司规定：旅客乘机时，免费携带行李箱的长，宽，高三者之和不超过115cm ．某厂家生产符合该规定的行李箱．已知行李箱的宽为20cm ，长与高的比为8：11，则符合此规定的行李箱的高的最大值为 cm ．2、已知关于x 的不等式x ﹣a ﹥0的最小整数解为2a －6，则a ＝__________．3、某超市现有n 个人在收银台排队等候结账．设结账人数按固定的速度增加，收银员结账的速度也是固定的．若同时开放2个收银台，需要20分钟可使排队等候人数为0；若同时开放3个收银台，需要12分钟可使排队等候人数为0．为减少顾客等待结账的时间，需要6分钟内使排队等候人数为0，则需要至少同时开放_______个收银台．4、定义：[x]表示不大于x 的最大整数，例如：[2.3]＝2，[1]＝1．有以下结论：①[﹣1.2]＝﹣2；②[a ﹣1]＝[a]﹣1；③[2a]＜[2a]+1；④存在唯一非零实数a ，使得a 2＝2[a]．其中正确的是_____．（写出所有正确结论的序号）5、某学校为落实“五项管理”工作，促进学生健康和全面发展，丰富学生的体育活动，准备从体育用品商店购买一些排球、足球和篮球，排球和足球的单价相同，买一个足球需要50元，买一个篮球需要80元．根据实际需要，该学校从体育用品商店一次性购买了三种球共100个，且购买三种球的总费用不超过6000元，则这所中学最多可购买篮球________个．6、某商品的成本为60元，标价为90元，如果商店打折销售但要保证利润不低于5%，则最多可以打_______折出售．7、甲工厂将生产的I 号、II 号两种产品共打包成5个不同的包裹，编号分别为A ，B ，C ，D ，E ，每个包裹的重量及包裹中I 号、II 号产品的重量如下：包裹编号I号产品重量/吨II号产品重量/吨包裹的重量/吨A 5 1 6B 3 2 5C 2 3 5D 4 3 7E 3 5 8甲工厂准备用一辆载重不超过19.5吨的货车将部分包裹一次运送到乙工厂．（1）如果装运的I号产品不少于9吨，且不多于11吨，写出一种满足条件的装运方案________（写出要装运包裹的编号）；（2）如果装运的I号产品不少于9吨，且不多于11吨，同时装运的II号产品最多，写出满足条件的装运方案________（写出要装运包裹的编号）．8、若一次函数y＝kx＋b的图像如图所示，则关于kx＋32b＞0的不等式的解集为________．9、已知关于x的方程2132x m xm+--=的解是非正数，则m的取值范围是___．10、若不等式30x a-≤的正整数解是1,2,3，则a的取值范围是____．三、解答题（共6 小题）1、解下列不等式，并将解集在数轴上表示出来．(1)173x x->-+(2)()21132x x+-≥+(3)2192136x x-+-≤2、近两年，共享经济快速崛起，共享汽车、共享单车、共享雨伞、共享KTV，共享充电宝等等．现南宁市计划在城区再投放一批“共享新能源汽车”，这批汽车分为A，B两种不同款型，其中A型车单价5万元，B型车单价3万元．(1)今年年初，“共享新能源汽车”再投放在城区正式启动．投放A，B两种款型的汽车共80辆，总价值340万元．试问本次试点投放的A型车与B型车各多少辆？(2)为鼓励市民绿色出行，特推出以下优惠活动：①优惠卡：保证金2500元（还车可退回），每小时内（含1小时）18元②VIP卡：会员费1680元（不退还），每小时内（含1小时）12元．若市民出行每次用车均不超过1小时，如何选择才能使一年内租用共享汽车最合算．3、如图，为了节省空间，家里的饭碗一般是摞起来存放的．如果6只饭碗(注:饭碗的大小形状都一样)摞起来的高度为15cm，9只饭碗摞起来的高度为21cm．(1)求出一个碗的高度是多少？(2)李老师家的碗柜每格的高度为36cm，求李老师一摞碗最多只能放多少只？4、抗击疫情，我们在行动．某药店销售A型和B型两种型号的口罩，销售一箱A型口罩可获利100元，销售一箱B型口罩可获利120元．该药店计划一次购进两种型号的口罩共80箱，其中B型口罩的进货量不超过A型口罩的3倍．设购进A型口罩x箱，这80箱口罩的销售总利润为y元．(1)求y与x的函数关系式；(2)该商店购进A型、B型口罩各多少箱，才能使销售利润最大？最大利润是多少？5、甲、乙两商场以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购买100元后，超出100元的部分按90%收费；在乙商场累计购买超过50元后，超过50元的部分按95%收费．设累计购物x元．(1)若x＝80，顾客到______商场购物花费少．（填“甲”或“乙”）(2)当x＞100时．①顾客到甲商场购物，花费______元，到乙商场购物，花费______元．（用含x的式子表示）②顾客到哪家商场购物花费少？6、某乒乓球馆将买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍，乒乓球拍每副定价200元，乒乓球每盒定价40元．经洽谈后，甲商店每买一副球拍赠一盒乒乓球；乙商店全部按定价的9折优惠．该球馆需买球拍5副，乒乓球若干盒（大于5盒）．(1)如果购买5副球拍和6盒乒乓球，则在甲商店购买需花费元，在乙商店购买需花费元；(2)当购买乒乓球多少盒时，在两家商店花费金额一样；(3)当购买乒乓球多少盒时，在乙商店购买划算．。

北师大版八年级下册 2.5一元一次不等式与一次函数同步练习题

2.5一元一次不等式与一次函数同步练习题一.选择题1. 如图，直线y=kx+b 与坐标轴的两交点分别为A （2，0）和B （0，﹣3），则不等式kx+b+3≤0的解为（）A ．x≤0B ．x≥0C ．x≥2D ．x≤22.一次函数y=kx +b 的图象如图，则当0＜x ≤1时，y 的范围是（）A ．y ＞0B ．﹣2＜y ≤0C ．﹣2＜y ≤1D ．无法判断3. 已知关于x 的不等式1ax +＞0（a ≠0）的解集是x ＜1，则直线1y ax =+与x 轴的交点是（）A ．（0，1）B ．（－1，0）C ．（0，－1）D ．（1，0）4. 如图，已知函数3y x b =+和3y ax =-的图象交于点P （－2，－5），则根据图象可得不等式3x b +＞3ax -的解集在数轴上表示正确的是（）A ．B ．C ．D ．5. 如图，1l 反映了某公司的销售收入与销售量的关系，2l 反映了该公司产品的销售成本与销售量的关系，当该公司赢利（收入大于成本）时，销售量（）A ．小于3吨B ．大于3吨C ．小于4吨D ．大于4吨6. 如图，已知函数13y x b =+和23y ax =-的图象交于点P （－2，－5），则下列结论正确的是（）A ．x ＜－2时，1y ＜2yB ．x ＜－2时，1y ＞2yC ．a ＜0D ．b ＜0二.填空题7. 不等式2x －6＜x ＋6的解集，表示对于同一个x 的值，函数26y x =-的图象上的点在6y x =+的图象上的点的_______方.8. 已知直线121y x =-和21y x =--的图象如图所示，根据图象填空．当x ______时，1y ＝2y ；当x _______时，1y ＜2y ；方程组211y x y x =-⎧⎨=--⎩的解是______.9. 一次函数1y kx b =+与2y x a =+的图象如图，则下列结论①0k <；②0a >；③当3x <时，12y y <中，正确的是______．10. 一次函数111y k x b =+与222y k x b =+的图象如图所示，则当x ______时，1y ＜2y ；当x ______时，1y ＝2y ；当x ______时，1y ＞2y ．11.如图，直线y=kx+b 经过A （﹣1，1）和B （﹣，0）两点，则不等式组0＜kx+b ＜1的解集为．12. 已知不等式5x -+＞33x -的解集是x ＜2，则直线5y x =-+与33y x =-的交点坐标是_______.三.解答题13. 在同一直角坐标系中（1）作出函数2y x =-+和24y x =-的图象．（2）用图象法求不等式2x -+＞24x -的解集.14.某移动通信公司开展两种业务：“全球通”使用者缴30元月租费，然后每通话一分钟再付费0.25元；“神州行”不缴月租费，每通话一分钟付话费0.40元．若一个月内通话x 分钟．（1）用代数式表示两种方式的费用各是多少？（2）若某人估计一个月内通话200分钟，应选择哪一种方式合算些？15.如图，已知直线y1=﹣x+1与x轴交于点A，与直线y2=﹣x交于点B．（1）求△AOB的面积；（2）求y1＞y2时x的取值范围．参考答案一.选择题1. 【答案】A ；【解析】解：由kx+b+3≤0得kx+b≤﹣3，直线y=kx+b 与y 轴的交点为B （0，﹣3），即当x=0时，y=﹣3，由图象可看出，不等式kx+b+3≤0的解集是x≤0．故选A ．2. 【答案】B ；【解析】因为一次函数y=kx +b 的图象与两坐标轴的交点分别为（1，0）、（0，﹣2），所以当0＜x ≤1，函数y 的取值范围是：﹣2＜y ≤0，故选B.3. 【答案】D ；【解析】由于关于x 的不等式1ax +＞0（a ≠0）的解集是x ＜1，即当x ＝1时，函数的值为0，故可得到直线1y ax =+与x 轴的交点坐标．4. 【答案】C ；【解析】从图象得到，当x ＞－2时，3y x b =+的图象对应的点在函数3y ax =-的图象上面，∴不等式3x b +＞3ax -的解集为x ＞－2．5. 【答案】D ；【解析】当x ＞4时，1l ＞2l ．6. 【答案】A ；【解析】A 、由图象可知x ＜－2时，1y ＜2y ，故正确；B 、由图象可知x ＜－2时，1y＜2y ，故错误；C 、由23y ax =-经过一、三象限是a ＜0，经过四象限是a ＞0，故错误；D 、由函数13y x b =+一、二、三象限，可知b ＞0，故错误．二.填空题7. 【答案】下；8. 【答案】＝0；＜0；01x y =⎧⎨=-⎩； 9. 【答案】① ；【解析】由图象可知，k ＜0，a ＜0，当3x <时，1y 的图象在2y 的上方，所以12y y >，所以只有①正确.10.【答案】＞1；＝1；＜1；11.【答案】﹣＜x ＜1；【解析】解：由题意可得：一次函数图象在y=1的下方时x ＜﹣1，在y=0的上方时x ＞﹣，∴关于x 的不等式0＜kx+b ＜1的解集是﹣＜x ＜﹣1．12.【答案】（2，3）；【解析】已知不等式5x -+＞33x -的解集是x ＜2，则当x ＝2时，－x ＋5＝3x －3；即当x ＝2时，函数5y x =-+与33y x =-的函数值相等；因而直线5y x =-+与33y x =-的交点坐标是：（2，3）．三.解答题13.【解析】解：（1）对于2y x =-+，当x ＝0时，y ＝2；当y ＝0时，x ＝2，即2y x =-+过点（0，2）和点（2，0），过这两点作直线即为2y x =-+的图象；对于24y x =-，当x ＝0时，y ＝－4；当y ＝0时，x ＝2，即24y x =-过点（0，－4）和点（2，0），过这两点作直线即为24y x =-的图象．图象如下图：（2）从图象得出，当x ＜2时，函数2y x =-+的图象在函数24y x =-的上方，∴不等式2x -+＞24x -的解集为：x ＜2．14.【解析】解：（1）设两种费用分别为：y 1，y 2，依题意可得：y 1=30+0.25x ，y 2=0.4x ；（2）当x=200时，y 1=80，y 2=80，两种方式一样．15.【解析】解：（1）由y 1=﹣x +1，可知当y=0时，x=2，∴点A 的坐标是（2，0），∴AO=2，∵y 1=﹣x +1与直线y 2=﹣x 交于点B ，∴B 点的坐标是（﹣1，1.5），∴△AOB 的面积=×2×1.5=1.5；（2）由（1）可知交点B 的坐标是（﹣1，1.5），由函数图象可知y1＞y2时，x＞﹣1．。

八年级数学北师大版下册第二章一元一次不等式与一元一次不等式组同步单元训练卷(含答案)

北师大版八年级数学下册第二章一元一次不等式与一元一次不等式组同步单元训练卷一、选择题（共10小题，3*10=30）1．若2a ＋6的值是正数，则a 的取值范围是( ) A ．a ＞0 B ．a ＞3 C ．a ＞－3 D ．a ＜－32．若关于x 的一元一次方程x －m ＋2＝0的解是负数，则m 的取值范围是( ) A ．m≥2 B ．m ＞2 C ．m ＜2 D ．m≤23．把某不等式组中两个不等式的解集表示在数轴上，如图所示，则这个不等式组可能是( )A.⎩⎪⎨⎪⎧x ＞－1，x≤2B.⎩⎪⎨⎪⎧x≥－1，x ＜2 C.⎩⎪⎨⎪⎧x≥－1，x≤2 D.⎩⎪⎨⎪⎧x ＜－1，x≥2 4．在数轴上到原点的距离大于2的点对应的x 满足( ) A ．x>2 B ．x<2C ．x>2或x<－2D ．－2<x<25．若函数y ＝kx ＋b 的图象如图所示，则关于x 的不等式kx ＋2b ＜0的解集为( )A ．x ＜3B ．x ＞3C ．x ＜6D ．x ＞66. 不等式组⎩⎪⎨⎪⎧2－x ＞1，①x ＋52≥1②中，不等式①和②的解集在数轴上表示正确的是( )7．三个连续正整数的和小于39，这样的正整数中，最大一组的和是( ) A ．39 B ．36 C ．35 D ．348．关于x 的不等式2x ＋a ≤1只有2个正整数解，则a 的取值范围为( ) A.－5＜a ＜－3 B.－5≤a ＜－3 C.－5＜a ≤－3 D.－5≤a ≤－39．若不等式2x<4的解都能使关于x 的不等式(a －1)x<a ＋5成立，则a 的取值范围是( ) A ．1<a≤7 B ．a≤710．某镇有甲，乙两家液化气站，它们每罐液化气的价格，质地和重量都相同．为了促销，甲站的液化气每罐降价25%销售；每个用户购买乙站的液化气，第1罐按照原价销售，若用户继续购买，则从第2罐开始以7折优惠，促销活动都是一年．若小明家每年需购买8罐液化气，则购买液化气最省钱的方法是( ) A ．买甲站的 B ．买乙站的 C ．买两站的都一样D ．先买甲站的1罐，以后买乙站的二．填空题（共8小题，3*8=24） 11．不等式 2x －1>3的解集是________．12. 已知“x 的3倍大于5，且x 的一半与1的差不大于2”，则x 的取值范围是__________. 13．不等式组⎩⎪⎨⎪⎧x －3（x －2）≤8，5－12x ＞2x 的整数解是________．14．已知关于x 的不等式(a －1)x ＞4的解集是x ＜4a －1，则a 的取值范围是____________．15．若|5－10x|＝10x －5, 则x 的取值范围是________．16．某商场推出一种购物“金卡”，凭卡在该商场购物可按商品价格的八折优惠，但办理金卡时每张要收100元购卡费，设按标价累计购物金额为x(元)，当x___________时，办理金卡购物省钱． 17．某中学举办了“汉字听写大会”，准备为获奖的40名同学颁奖(每人一个书包或一本词典)，已知每个书包28元，每本词典20元，学校计划用不超过900元钱购买奖品，则最多可以购买________个书包．18．已知实数x ，y 满足2x －3y ＝4，并且x≥－1，y ＜2，现有k ＝x －y ，则k 的取值范围是____________．三．解答题（7小题，共66分）19．(8分) 解不等式，并把它们的解集在数轴上表示出来：15－9y ＜10－4y ；20．(8分) 已知不等式3x －a≤0的正整数解是1，2，3.求a 的取值范围．21．(8分) 根据题意列出不等式：(1)某市化工厂现有甲原料290千克，计划用这种原料与另一种足够多的原料配合生产A，B两种产品共50件．已知生产一件A型产品需甲种原料15千克，生产一件B型产品需甲种原料2.5千克，若该化工厂现有的原料能保证生产，试写出满足生产A型产品x(件)的关系式；(2)某厂生产一种机械零件，固定成本为2万元，每件零件成本为3元，零售价为5元，应纳税款为总销售额的10%.若要使该厂盈利，则该零件至少要生产销售x个，试写出x应满足的不等式．22．(10分) 如图，一次函数y1＝kx－2和y2＝－3x＋b的图象相交于点A(2，－1)．(1)求k，b的值；(2)利用图象求出：当x取何值时，y1≥y2?(3)利用图象求出：当x取何值时，y1＞0且y2＜0?23．(10分) 某校九年级有三个班，其中九(一)班和九(二)班共有105名学生，在期末体育测试中，这两个班级共有79名学生满分，其中九(一)班的满分率为70%，九(二)班的满分率为80%.(1)求九(一)班和九(二)班各有多少名学生；(2)该校九(三)班有45名学生，若九年级体育成绩的总满分率超过75%，求九(三)班至少有多少名学生体育成绩是满分．24．(10分) 如图，一次函数y1＝kx－2和y2＝－3x＋b的图象相交于点A(2，－1)．(1)求k，b的值．(2)利用图象求出：当x取何值时，y1≥y2.(3)利用图象求出：当x取何值时，y1>0且y2＜0.25．(12分) 某区为绿化行车道，计划购买甲、乙两种树苗共计n棵．设买甲种树苗x棵．有关甲、乙两种树苗的信息如图所示．(1)当n＝500时．①根据信息填表(用含x的代数式表示)：②如果购买甲、乙两种树苗共用25600元，那么甲、乙两种树苗各买了多少棵？参考答案1-5CCACD 6-10BBCAB11. x>2 12．53＜x≤6 13．－1，0，1 14．a ＜1 15. x≥1216．>500 17. 12 18．1≤k ＜319.解：移项，得－9y ＋4y ＜10－15.合并同类项，得－5y ＜－5.系数化为1，得y ＞1.不等式的解集在数轴上表示如图所示．20. 解：3x －a≤0，解得x≤a 3，因为它的正整数解为1，2，3，当a 3＝3时，a ＝9；当a3＝4时，a ＝12.当a ＝12时，x≤4，有4个正整数，舍去，∴9≤a<1221. 解：(1)生产A 型产品x 件，则生产B 型产品(50－x)件，根据题意，得15x ＋2.5(50－x)≤290. (2)5x －3x －5x×10%－20 000＞0.22. 解：(1)k ＝12，b ＝5.(2)当x≥2时，y 1≥y 2.(3)当x ＞4时，y 1＞0且y 2＜0.⎩⎪⎨⎪⎧x ＝50，y ＝55.答：九(一)班有50名学生，九(二)班有55名学生 (2)设九(三)班有m 名学生体育成绩满分，根据题意得79＋m ＞(105＋45)×75%，解得m ＞33.5，∵m 为整数，∴m 的最小值为34.答：九(三)班至少有34名学生体育成绩是满分24. 解：(1)将A 点的坐标代入y 1＝kx －2，得2k －2＝－1，即k ＝12. 将A 点的坐标代入y 2＝－3x ＋b ，得－6＋b ＝－1，即b ＝5.(2)从图象可以看出：当x≥2时，y 1≥y 2.(3)直线y 1＝12x －2与x 轴的交点坐标为(4，0)，直线y 2＝－3x ＋5与x 轴的交点坐标为⎝⎛⎭⎫53，0.从图象可以看出：当x ＞4时，y 1＞0；当x ＞53时，y 2＜0，∴当x ＞4时，y 1＞0且y 2＜0.25. 解：(1)①500－x 50x 80(500－x)②由题意得50x ＋80(500－x)＝25600，解得x ＝480，500－x ＝20.答：甲种树苗买了480棵，乙种树苗买了20棵(2)由题意得90%x ＋95%(n －x)≥92%×n ，解得x≤35n ，50x ＋80(n －x)＝26000，解得x ＝8n －26003.∵8n －26003≤35n ，∴n≤4191131.∵n 为正整数，x 为正整数，当n 为419时，x ＝7523≈250.7不是整数；当n 为418时，x ＝248，∴n 的最大值为418。

【数学八年级下】北师大版八年级下册一元一次不等式_2.5一元一次不等式与一次函数同步练习

三、解答题（共 6 题；共 30 解．
16、已知函数 y=ax+b，y 随 x 增大而减少，且交 x 轴于 A（3，0），求不等式（a﹣b）x﹣2b ＜0 的解集．
2
17、如图，函数 y=2x 和 y= x+4 的图象相交于点 A，
3
（1）求点 A 的坐标；
二、填空题 9、（﹣3，0）解：解关于 x 的不等式 kx﹣2＞0，移项得到；kx＞2，而不等式 kx﹣2＞0（k≠0）的解集是：x＜﹣3，
∴ =﹣3，
解得：k=﹣ ，
∴直线 y=﹣kx+2 的解析式是：y= x+2，在这个式子中令 y=0，解得：x=﹣3，因而直线 y=﹣kx+2 与 x 轴的交点是（﹣3，0）．故本题答案为：（﹣3，0）． 10、x≥ 解：∵直线 y=2x+b 经过点（3，5）， ∴5=2×3+b，解得：b=﹣1， ∴不等式 2x+b≥0 变为不等式 2x﹣1≥0，解得：x≥ ，
（2）根据图象，直接写出不等式 2x≥ 2 x+4 的解集． 3
18、如图是一次函数 y=2x﹣5 的图象，请根据给出的图象写出一个一元一次方程和一个一元一次不等式，并用图象求解所写出的方程和不等式．
19、函数 y=2x 与 y=ax+4 的图象相交于点 A（m，2），求不等式 2x＜ax+4 的解集．
b1 b2
的解是
x
y
2 3
，你认为小华写正确（
）
A、0 个 B、1 个 C、2 个 D、3 个 7、若一次函数 y=ax+b 的图象经过第一、二、四象限，则下列不等式中总是成立的是（） A、ab＞0 B、a﹣b＞0 C、a2+b＞0 D、a+b＞0 8、直线 l1：y=k1x+b 与直线 l2：y=k2x 在同一平面直角坐标系中的图象如图所示，则关于 x

北师大版八年级下册数学第二章一元一次不等式与一元一次不等式组同步课时练习题(含答案)

北师大版八年级下册数学第二章一元一次不等式与一元一次不等式组同步课时练习题2．1不等关系01基础题知识点1不等式的意义1．(2017·太原期中)学校组织同学们春游，租用45座和30座两种型号的客车，若租用45座客车x辆，租用30座客车y辆，则不等式“45x＋30y≥500”表示的实际意义是(A)A．两种客车总的载客量不少于500 人B．两种客车总的载客量不超过500 人C．两种客车总的载客量不足500人D．两种客车总的载客量恰好等于500人2．有下列数学表达式：①3<0；②4x＋5>0；③x＝3；④x＋x；⑤x≠－4；⑥x＋2>x＋1.其中是不等式的有4 个．2知识点2列不等式3．某电梯标明“载客不超过13人”，若载客人数为x，x 为自然数，则“载客不超过13人”用不等式表示为(C)A．x＜13 C．x≤13 B．x＞13 D．x≥134．如图为一隧道入口处的指示标志牌，图1 表示汽车的高度不能超过3.5 m，由此可知图2 表示汽车的宽度l(m)应满足的关系为l≤3．限制高度限制宽度图1 图25．用适当符号表示下列关系：(1)x的绝对值是非负数；解：|x|≥0.15(2)a的3倍与b的的和不大于3；1解：3a＋b≤3.5(3)x与17的和比它的5 倍小．解：x＋17<5x.02中档题6．小新买了一罐八宝粥，看到外包装标明：净含量为330±10 g，那么这罐八宝粥的净含量x 的范围是(D)A．320＜x＜340 C．320＜x≤340 B．320≤x＜340 D．320≤x≤3407．下列叙述：①a是非负数，则a≥0；②“a减去10不大于2”可表示为a－10＜2；③“x 的倒数超过10”可表2 21x示为＞10；④“a，b两数的平方和为正数”可表示为a2＋b2＞0.其中正确的个数是(C)A．1 C．3 B．2 D．48．在数轴上，点A 表示2，点B 表示－0.6，点C 在线段A B 上，点C 表示的数为a，则用不等关系表示为－0.6≤a≤2．9．某次知识竞赛共有20道题，每一题答对得10分，答错或不答都扣5 分，娜娜得分要超过90分，设她答对了n 道题，则根据题意可列不等式为10n－5(20－n)＞90．03 综合题10．请设计不同的实际背景来表示下列不等式：(1)x>y ；(2)2.0≤x ≤2.6；(3)3a ＋4b ≤560.解：答案不唯一，如：(1)八年级(1)班的男生比女生多，其中男生 x 人，女生 y 人．(2)某班级男生立定跳远成绩 x 在 2.0 米到 2.6 米之间．(3)3 条长裤和 4 件上衣的总价不超过 560 元，其中长裤单价 a 元，上衣单价 b 元．2.2 不等式的基本性质01 基础题知识点 1 不等式的基本性质1．若 a<b ，则下列各式中一定成立的是(B)A ．－3a<－3b C ．a ＋c>b ＋cB ．a －3<b －3D ．2a>2b2．(2017·成都期末)若 x>y ，则下列式子中错误的是(D)x y A ．x －3>y －3 C ．x ＋3>y ＋3B. > 3 3D ．－3x>－3y 3．(2017·株洲)已知实数 a ，b 满足 a ＋1＞b ＋1，则下列选项错误的为(D)A ．a ＞bB ．a ＋2＞b ＋2D ．2a ＞3bC ．－a ＜－b 4．下列说法不一定成立的是(C)A ．若 a ＞b ，则 a ＋c ＞b ＋cB ．若 a ＋c ＞b ＋c ，则 a ＞bC ．若 a ＞b ，则 ac ＞bc 2 2D ．若 ac ＞bc 则 a ＞b2 2， 5．由不等式 a ＞b 得到 am ＜b m 的条件是 m ＜0.6．已知 m ＜n ，下列关于 m ，n 的命题：①6m ＞6n ；②－3m ＜－3n ；③m －5＜n －5；④2m ＋5＞2n ＋5.其中正确命题的序号是③．7．小燕子竟然推导出了 0＞5 的错误结论．请你仔细阅读她的推导过程，指出问题到底出在哪里．已知 x ＞y ，两边都乘 5，得 5x ＞5y .①两边都减去 5x ，得 0＞5y －5x .②即 0＞5(y －x)．③两边都除以(y －x)，得 0＞5.④解：错在第④步．∵x ＞y ，∴y －x ＜0.不等式两边同时除以负数(y －x)，不等号应改变方向才能成立．知识点 2 将不等式化为“x ＞a ”或“x ＜a ”的形式8．(2017·太原期中)下列不等式的变形过程中，正确的是(D)A ．不等式－2x ＞4 的两边同时除以－2，得 x ＞2B ．不等式 1－x ＞3 的两边同时减去 1，得 x ＞2C ．不等式 4x －2＜3－x 移项，得 4x ＋x ＜3－2x 3 x 2D ．不等式＜1－去分母，得 2x ＜6－3x 9．将下列不等式化成“x>a”或“x<a”的形式．(1)x －5<1； (2)2x>x －2；解：x<6. 解：x>－2.12(3)x>－3;(4)－5x<－2.2解：x>－6.解：x>.502中档题10．若点P(x－2，y－2)在第二象限，则x与y的关系正确的是(D)A．x≥y C．x≤y B．x＞y D．x＜y11．设“▲”“●”“■”分别表示三种不同的物体，现用天平称两次，情况如图所示，那么▲，●，■这三种物体按质量从大到小排列应为(C)A．■●▲C．■▲●B．▲■●D．●▲■12．若实数a，b，c在数轴上对应点的位置如图所示，则下列不等式成立的是(B)A．a－c＞b－c C．ac＞bc B．a＋c＜b＋c a cD.＜b b13．已知x－y＝3，若y＜1，则x的取值范围是x＜4．14．下列变形是怎样得到的？1 21 2(1)由x＞y，得x－3＞y－3；1 21 2解：两边都除以2，得x＞y.1 21 2两边都减去3，得x－3＞y－3.1 21 2(2)由x＞y，得(x－3)＞(y－3)；解：两边都减去3，得x－3＞y－3.1 21 2两边都除以2，得(x－3)＞(y－3)．(3)由x＞y，得2(3－x)＜2(3－y)．解：两边都除以－1，得－x＜－y.两边都加上3，得3－x＜3－y.两边都乘2，得2(3－x)＜2(3－y)．15．阅读下面的解题过程，再解题．已知 a ＞b ，试比较－2 018a ＋1 与－2 018b ＋1 的大小．解：因为 a ＞b ，①所以－2 018a ＞－2 018b .②故－2 018a ＋1＞－2 018b ＋1.③问：(1)上述解题过程中，从第②步开始出现错误；(2)错误的原因是什么？(3)请写出正确的解题过程．解：(2)错误地运用了不等式的基本性质 3，即不等式两边都乘同一个负数，不等号的方向没有改变．(3)因为 a ＞b ，所以－2 018a ＜－2 018b .故－2 018a ＋1＜－2 018b ＋1.03 综合题16．比较大小：(1)如果 a －1>b ＋2，那么 a>b ；(2)试比较 2a 与 3a 的大小：①当 a>0 时，2a<3a ；②当 a ＝0 时，2a ＝3a ；③当 a<0 时，2a>3a ；(3)试比较 a ＋b 与 a 的大小；(4)试判断 x －3x ＋1 与－3x ＋1 的大小．2 解：(3)当 b>0 时，a ＋b>a ；当 b ＝0 时，a ＋b ＝a ；当 b<0 时，a ＋b<a .(4)∵x ≥0，2 ∴x 2－3x ＋1≥－3x ＋1.2.3 不等式的解集01 知识点 1 不等式的解和解集1．下列数值中不是不等式 5x ≥2x ＋9 的解的是(D)A ．5B ．4C ．32．下列说法中，错误的是(C)基础题D ．2A ．不等式 x ＜2 的正整数解只有一个B ．－2 是不等式 2x －1＜0 的一个解C ．不等式－3x ＞9 的解集是 x ＞－3D ．不等式 x ＜10 的整数解有无数个3．(2016·安徽)不等式 x －2≥1 的解集是 x ≥3．知识点 2 用数轴表示不等式的解集4．用不等式表示如图所示的解集，其中正确的是(C) A ．x ＞－2 C ．x ≥－2 B ．x ＜－2D ．x ≤－25．在数轴上表示不等式 x －1＜0 的解集，正确的是(B)6．将下列不等式的解集分别表示在数轴上：(1)x ≤2；解：如图所示：(2)x>－2.解：如图所示：02 中档题7．(2017·太原期末)若一个不等式的正整数解为 1，2，则该不等式的解集在数轴上的表示可能是(D)8．如果关于 x 的不等式 ax ＋4＜0 的解集在数轴上表示如图，那么(C)A ．a ＞0B ．a ＜0D ．a ＝2C ．a ＝－2 9．(2017·西安期中)若关于 x 的不等式(a ＋1)x ＞a ＋1 的解集为 x ＞1，则 a 的取值范围是 a ＞－1．10．不等式 2x ≥－9 有多少个负整数解？请全部写出来．解：由题意，得 x ≥－9，2 所以不等式有 4 个负整数解：－1，－2，－3，－4.03 综合题11．小华在解不等式 x ＞2x －1 时，发现所有的负数都满足不等式，于是他有理有据地说：“如果x<0，那么 x>2x ，而 2x>2x －1，所以 x>2x －1 成立．”小华得到了这样的结论：x>2x －1 的解集是 x<0.小华说得对吗？说说你的观点．1 2解：小华前面说明负数是不等式 x ＞2x －1 的解是对的，但结论不对．因为解集包含所有的解，如 x ＝是不等式 x 1 2 ＞2x －1 的解，但＞0，所以 x<0 不是 x>2x －1 的解集．15．阅读下面的解题过程，再解题．已知 a ＞b ，试比较－2 018a ＋1 与－2 018b ＋1 的大小．解：因为 a ＞b ，①所以－2 018a ＞－2 018b .②故－2 018a ＋1＞－2 018b ＋1.③问：(1)上述解题过程中，从第②步开始出现错误；(2)错误的原因是什么？(3)请写出正确的解题过程．解：(2)错误地运用了不等式的基本性质 3，即不等式两边都乘同一个负数，不等号的方向没有改变．(3)因为 a ＞b ，所以－2 018a ＜－2 018b .故－2 018a ＋1＜－2 018b ＋1.03 综合题16．比较大小：(1)如果 a －1>b ＋2，那么 a>b ；(2)试比较 2a 与 3a 的大小：①当 a>0 时，2a<3a ；②当 a ＝0 时，2a ＝3a ；③当 a<0 时，2a>3a ；(3)试比较 a ＋b 与 a 的大小；(4)试判断 x －3x ＋1 与－3x ＋1 的大小．2 解：(3)当 b>0 时，a ＋b>a ；当 b ＝0 时，a ＋b ＝a ；当 b<0 时，a ＋b<a .(4)∵x ≥0，2 ∴x 2－3x ＋1≥－3x ＋1.2.3 不等式的解集01 知识点 1 不等式的解和解集1．下列数值中不是不等式 5x ≥2x ＋9 的解的是(D)A ．5B ．4C ．32．下列说法中，错误的是(C)基础题D ．2A ．不等式 x ＜2 的正整数解只有一个B ．－2 是不等式 2x －1＜0 的一个解C ．不等式－3x ＞9 的解集是 x ＞－3D ．不等式 x ＜10 的整数解有无数个3．(2016·安徽)不等式 x －2≥1 的解集是 x ≥3．知识点 2 用数轴表示不等式的解集4．用不等式表示如图所示的解集，其中正确的是(C) A ．x ＞－2 C ．x ≥－2 B ．x ＜－2D ．x ≤－25．在数轴上表示不等式 x －1＜0 的解集，正确的是(B)6．将下列不等式的解集分别表示在数轴上：(1)x ≤2；解：如图所示：(2)x>－2.解：如图所示：02 中档题7．(2017·太原期末)若一个不等式的正整数解为 1，2，则该不等式的解集在数轴上的表示可能是(D)8．如果关于 x 的不等式 ax ＋4＜0 的解集在数轴上表示如图，那么(C)A ．a ＞0B ．a ＜0D ．a ＝2C ．a ＝－2 9．(2017·西安期中)若关于 x 的不等式(a ＋1)x ＞a ＋1 的解集为 x ＞1，则 a 的取值范围是 a ＞－1．10．不等式 2x ≥－9 有多少个负整数解？请全部写出来．解：由题意，得 x ≥－9，2 所以不等式有 4 个负整数解：－1，－2，－3，－4.03 综合题11．小华在解不等式 x ＞2x －1 时，发现所有的负数都满足不等式，于是他有理有据地说：“如果x<0，那么 x>2x ，而 2x>2x －1，所以 x>2x －1 成立．”小华得到了这样的结论：x>2x －1 的解集是 x<0.小华说得对吗？说说你的观点．1 2解：小华前面说明负数是不等式 x ＞2x －1 的解是对的，但结论不对．因为解集包含所有的解，如 x ＝是不等式 x 1 2 ＞2x －1 的解，但＞0，所以 x<0 不是 x>2x －1 的解集．15．阅读下面的解题过程，再解题．已知 a ＞b ，试比较－2 018a ＋1 与－2 018b ＋1 的大小．解：因为 a ＞b ，①所以－2 018a ＞－2 018b .②故－2 018a ＋1＞－2 018b ＋1.③问：(1)上述解题过程中，从第②步开始出现错误；(2)错误的原因是什么？(3)请写出正确的解题过程．解：(2)错误地运用了不等式的基本性质 3，即不等式两边都乘同一个负数，不等号的方向没有改变．(3)因为 a ＞b ，所以－2 018a ＜－2 018b .故－2 018a ＋1＜－2 018b ＋1.03 综合题16．比较大小：(1)如果 a －1>b ＋2，那么 a>b ；(2)试比较 2a 与 3a 的大小：①当 a>0 时，2a<3a ；②当 a ＝0 时，2a ＝3a ；③当 a<0 时，2a>3a ；(3)试比较 a ＋b 与 a 的大小；(4)试判断 x －3x ＋1 与－3x ＋1 的大小．2 解：(3)当 b>0 时，a ＋b>a ；当 b ＝0 时，a ＋b ＝a ；当 b<0 时，a ＋b<a .(4)∵x ≥0，2 ∴x 2－3x ＋1≥－3x ＋1.2.3 不等式的解集01 知识点 1 不等式的解和解集1．下列数值中不是不等式 5x ≥2x ＋9 的解的是(D)A ．5B ．4C ．32．下列说法中，错误的是(C)基础题D ．2A ．不等式 x ＜2 的正整数解只有一个B ．－2 是不等式 2x －1＜0 的一个解C ．不等式－3x ＞9 的解集是 x ＞－3D ．不等式 x ＜10 的整数解有无数个3．(2016·安徽)不等式 x －2≥1 的解集是 x ≥3．知识点 2 用数轴表示不等式的解集4．用不等式表示如图所示的解集，其中正确的是(C) A ．x ＞－2 C ．x ≥－2 B ．x ＜－2D ．x ≤－25．在数轴上表示不等式 x －1＜0 的解集，正确的是(B)6．将下列不等式的解集分别表示在数轴上：(1)x ≤2；解：如图所示：(2)x>－2.解：如图所示：02 中档题7．(2017·太原期末)若一个不等式的正整数解为 1，2，则该不等式的解集在数轴上的表示可能是(D)8．如果关于 x 的不等式 ax ＋4＜0 的解集在数轴上表示如图，那么(C)A ．a ＞0B ．a ＜0D ．a ＝2C ．a ＝－2 9．(2017·西安期中)若关于 x 的不等式(a ＋1)x ＞a ＋1 的解集为 x ＞1，则 a 的取值范围是 a ＞－1．10．不等式 2x ≥－9 有多少个负整数解？请全部写出来．解：由题意，得 x ≥－9，2 所以不等式有 4 个负整数解：－1，－2，－3，－4.03 综合题11．小华在解不等式 x ＞2x －1 时，发现所有的负数都满足不等式，于是他有理有据地说：“如果x<0，那么 x>2x ，而 2x>2x －1，所以 x>2x －1 成立．”小华得到了这样的结论：x>2x －1 的解集是 x<0.小华说得对吗？说说你的观点．1 2解：小华前面说明负数是不等式 x ＞2x －1 的解是对的，但结论不对．因为解集包含所有的解，如 x ＝是不等式 x 1 2 ＞2x －1 的解，但＞0，所以 x<0 不是 x>2x －1 的解集．。

(完整word版)北师大版八年级数学下第二章一元一次不等式测试含,文档

北师大版八年级数学下第二章一元一次不等式测试含答案一、选择题〔每题 5 分，共 25 分〕1. 如图，数轴上表示的是某个不等式组的解集，那么该不等式组可能是〔〕x 1≤ 0B ．x1≤ 0A ．2 ≥ 0x 0 x2x 1≥ 0D ．x 1≥ 0-2-1012C ．x 0x2 ≥ 022. 假设关于 x 的不等式 mx n 的解集为 xn〕，那么 m 的取值范围是〔mA ． m ≥ 0B ． m 0C ． m ≤ 0D ． m 03. 假设 a b ，且 c ≠ 0，那么以下关系必然成立的是〔〕A ． ac bca1C ． c a c babB ． bD ．c 2c 24. 不等式5x 6( x 3) ≥x〕6的正整数解是〔2A ．不存在B ． 1， 2，3C ． 0， 1，2D ． 0， 1，2， 35.假设关于 x 的不等式组x 8 4x 13 ，那么 m 的取值范围是〔x ≤ m的解集为 x〕A ． m ≥ 3B ． m ≤ 3C ． m 3D ． m 3二、填空题〔每题 5 分，共 25 分〕6.假设关于 x 的不等式组2x n 3 的解集是 1x 2 ，那么 m n __________ ．x 1m 17. 某校将假设干间宿舍分配给八年级〔 1〕班女生住宿，该班女生少于35 人，假设每个房间住 5 人，那么剩下5人没处住；假设每个房间住8 人，那么空一间房，且有一间住不满．那么该班有 ____________ 名女生．8. 如图，直线y kx b 经过点 A(3， 1)和点 B(6， 0)，那么不等式组 0 kxb1x 的解集为 ________________ ．y3AOBx2x 1 1无解，那么化简 39.假设关于 x 的不等式组3 aa 2 的结果为 _________________ ．x ax 15x 3210.假设关于 x 的不等式组的整数解只有两个，那么 a 的取值范围是 __________．2x 2≤xa3111. 〔 8 分〕下面是小明解不等式x 53x221的过程：2①去分母，得 x 5 1 3x 2 ，②移项、合并同类项，得 2x 2 ，③两边都除以 2 ，得 x1．先阅读以上解题过程，尔后解答以下问题．〔 1〕小明的解题过程从哪一步开始出现错误？请写出该步的代号 __________；（ 2〕错误的原因是 __________________________________________________________ ；（ 3〕第③步的依据是 ________________________________________________________ ；（ 4〕该不等式的解集应该是 ________________ ．12. 〔 8 分〕解以下不等式〔组〕，并把它们的解集分别表示在数轴上．〔 1〕x 69 2x ≤ 5x 1 ；〔2〕 12x 1 1 ． 3323213. 〔 10 分〕某工厂现有甲种布料70 米，乙种布料 52 米，方案利用这两种布料生产 A ， B 两种型号的时装共80 套．生产一套A 型号的时装需甲种布料 0.6 米，乙种布料 0.9 米；生产一套B 型号的时装需甲种布料 1.1 米，乙种布料 0.4 米．利用现有布料，工厂能否完成任务？假设能，请设计出所有可能的生产方案；假设不能够，请说明原因．14. 〔 12 分〕某公司在 A ，B 两地分别有同型号的机器17 台和 15 台，现要运往甲地 18 台，乙地 14 台，从 A ， B 两地运往甲、乙两地的花销以下表：甲地〔元 /台〕乙地〔元/台〕A 地600500B 地400800〔 1〕假设从 A 地运往甲地 x 台，完成以上调运所需总花销为y 元，求 y 与 x 之间的函数关系式，并写出x 的取值范围．〔 2〕请你为该公司设计出使总花销最少的调运方案，并求出最少的总花销．15.〔 12 分〕某农村方案建筑 A，B 两种型号的沼气池共 20 个，以解决该村所有农户的燃料问题．两种型号沼气池的占地面积和可供使用农户数见下表：占地面积可供使用农户数型号〔单位： m2/个〕〔单位：户 /个〕A1518B2030可供建筑沼气池的占地面积不高出365m2，该村农户共有492 户．（1〕如何合理分配建筑 A ， B 型号“沼气池〞的个数才能满足条件？满足条件的方案有几种？经过计算分别写出各种方案．〔 2〕假设 A 型号“沼气池〞每个造价 2 万元， B 型号“沼气池〞每个造价 3 万元，试说明在〔1〕中的各种建筑方案中，哪一种建筑方案最省钱，最少的花销需要多少万元？参照答案一、选择题1．C2．D3． D4． B5．A 二、填空题6．17． 308．3x69．52a810． 3 ≤ a3三、解答题11．〔 1〕①；（2〕不等式的两边同时乘以2时，1没有乘以 2；（3〕不等式的根本性质 3；〔 4〕x 1．212．〔 1〕x≥15x 1．解集在数轴上的表示略．；〔 2〕413．工厂能完成任务，共有 5 种生产方案．方案一，生产 A 型号时装36 套， B 型号时装44 套；方案二，生产 A 型号时装37 套， B 型号时装43 套；方案三，生产 A 型号时装38 套， B 型号时装42 套；方案四，生产 A 型号时装39 套， B 型号时装41 套；方案五，生产 A 型号时装40 套， B 型号时装40 套．14．〔 1〕y500x13 300 〔 3 ≤ x ≤ 17 ，且x为整数〕〔 2〕总花销最少的调运方案为，从 A 地运往甲地 3 台，运往乙地14 台；从 B 地运往甲地15 台，运往乙地0 台．最少的总花销为14 800 元．15．〔 1〕满足条件的方案有 3 种．方案一，建筑7 个 A 型号沼气池，13 个 B 型号沼气池．方案二，建筑8 个 A 型号沼气池，12 个 B 型号沼气池．方案三，建筑9 个 A 型号沼气池，11 个 B 型号沼气池．〔 2〕在〔 1〕中的各种建筑方案中，方案三最省钱，最少的花销需要51 万元．。

2022-2023学年北师大版八年级数学下册《2-6一元一次不等式组》同步自主提升练习题(附答案)

2022-2023学年北师大版八年级数学下册《2.6一元一次不等式组》同步自主提升练习题（附答案）一．选择题2．下列选项中是一元一次不等式组的是（）A．B．C．D．1．关于x，y的方程组，若2＜k＜4，则x﹣y的取值范围是（）A．﹣1＜x﹣y＜0B．0＜x﹣y＜1C．﹣3＜x﹣y＜﹣1D．﹣1＜x﹣y＜1 2．不等式组的解集是（）A．无解B．x＜﹣1C．x≥D．﹣1＜x≤3．已知点P（1﹣a，2a+6）在第四象限，则a的取值范围是（）A．a＜﹣3B．﹣3＜a＜1C．a＞﹣3D．a＞15．已知关于x的不等式组的整数解共有5个，则a的取值范围是（）A．﹣4＜a＜﹣3B．﹣4≤a＜﹣3C．a＜﹣3D．﹣4＜a＜6．关于x的不等式组的所有整数解的积为2，则m的取值范围为（）A．m＞﹣3B．m＜﹣2C．﹣3≤m＜﹣2D．﹣3＜m≤﹣2 7．八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1名同学植树的棵数不到8棵．若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是（）A．7x+9﹣9（x﹣1）＞0B．7x+9﹣9（x﹣1）＜8C．D．8．“a与5的和是正数且a的一半不大于3”用不等式组表示，正确的是（）A．B．C．D．9．某企业决定购买A，B两种型号的污水处理设备共8台，具体情况如下表：A型B型价格（万元/台）1210月污水处理能力（吨/月）200160经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低1380吨，该企业有哪些购买方案呢？为解决这个问题，设购买A型污水处理设备x台，所列不等式组正确的是（）A．B．C．D．10．运行程序如图所示，规定：从“输入一个值x”到“结果是否＞95”为一次程序操作，如果程序操作进行了两次才停止，那么x的取值范围是（）A．x＞23B．23＜x≤47C．11≤x＜23D．x≤47二．填空题11．写出一个无解的一元一次不等式组为．12．不等式组的解集为．13．不等式组有3个整数解，则a的取值范围是．14．某种植物生长的适宜温度不能低于18℃．也不能高于22℃．如果该植物生长的适宜温度为x℃．则有不等式．15．一个矩形，两边长分别为xcm和10cm，如果它的周长小于80cm，面积大于100cm2，则x的取值范围是．三．解答题16．解不等式组，并把解集表示在数轴上．17．解不等式组，并把解集在数轴上表示出来．18．已知关于x、y的方程组的解满足，求整数k的值．19．求不等式组的正整数解．20．已知两个语句：①式子2x﹣1的值在1（含1）与3（含3）之间；②式子2x﹣1的值不小于1且不大于3．请回答以下问题：（1）两个语句表达的意思是否一样（不用说明理由）？（2）把两个语句分别用数学式子表示出来．参考答案一．选择题1．解：A、含有三个未知数，不符合题意；B、未知数的最高次数是2，不符合题意；C、含有两个未知数，不符合题意；D、符合一元一次不等式组的定义，符合题意；故选：D．2．解：，解得：，x﹣y＝，∵2＜k＜4，∴0＜x﹣y＜1，故选：B．3．解：解不等式3﹣2x＜5，得：x＞﹣1，解不等式2（x﹣2）≤1，得：x≤，则不等式组的解集为﹣1＜x≤，故选：D．4．解：∵点P（1﹣a，2a+6）在第四象限，∴，解得a＜﹣3．故选：A．5．解：解不等式x﹣a＞0，得：x＞a，解不等式3﹣2x＞0，得：x＜1.5，∵不等式组的整数解有5个，∴﹣4≤a＜﹣3．故选：B．6．解：由x≤﹣且不等式组的所有整数解的积为2知整数解为﹣1、﹣2这2个，所以﹣3≤m＜﹣2，故选：C．7．解：（x﹣1）位同学植树棵树为9×（x﹣1），∵有1位同学植树的棵数不到8棵．植树的棵数为（7x+9）棵，∴可列不等式组为：，即．故选：C．8．解：由题意可得：．故选：A．9．解：设购买污水处理设备A型号x台，则购买B型号（8﹣x）台，根据题意，得，故选：A．10．解：由题意得，，解不等式①得，x≤47，解不等式②得，x＞23，∴23＜x≤47，故选：B．二．填空题11．解：根据不等式组解集的口诀：大大小小找不到（无解），可写x≤2，x≥3，即．12．解：解不等式x﹣1≤2，得：x≤3，解不等式3﹣4x＜﹣5，得：x＞2，则不等式组的解集为2＜x≤3，故答案为：2＜x≤3．13．解：不等式组，由﹣x＜﹣1，解得：x＞4，由4（x﹣1）≤2（x﹣a），解得：x≤2﹣a，故不等式组的解集为：4＜x≤2﹣a，由关于x的不等式组有3个整数解，解得：7≤2﹣a＜8，解得：﹣6＜a≤﹣5．故答案为：﹣6＜a≤﹣514．解：根据题意温度不能低于18℃可得x≥18，根据不能高于22℃可得x≤22，故18≤x≤22．故答案为：18≤x≤22．15．解：矩形的周长是2（x+10）cm，面积是10xcm2，根据题意，得，解不等式：2（x+10）＜80，解得：x＜30，解不等式：10x＞100，解得：x＞10，所以x的取值范围是：10＜x＜30．故答案为：10＜x＜30．三．解答题16．解：．解不等式①，得：x≥﹣3；解不等式②，得：x＜2．∴不等式组的解集为：﹣3≤x＜2．将其表示在数轴上，如图所示．17．解：解不等式x﹣3（x﹣2）≥4，得：x≤1，解不等式＞x﹣1，得：x＜4，则不等式组的解集为x≤1，将不等式组的解集表示在数轴上如下：18．解：两方程分别相加和相减可得，∴，解得，∴整数k的值为1、2．19．解：解不等式5x﹣12≤2（4x﹣3），得：x≥﹣2，解不等式＜5，得：x＜3，则不等式组的解集为﹣2≤x＜3，所以不等式组的正整数解为1、2．20．解：（1）一样；（2）①式子2x﹣1的值在1（含1）与3（含3）之间可得1≤2x﹣1≤3；②式子2x﹣1的值不小于1且不大于3可得．。

北师大版八年级下册数学一元一次不等式练习题

1.已知关于x的不等式kx-2>0(k≠0)的解集是x<-3,则直线y=-kx+2与x轴的交点是:解kx-2>0 , kx>2, 因为解是x<-3, 则k<0所以x<2/k=-3, 所以k=-2/3所以直线为y=(2/3)x+2与x轴交点令y=0得x=-3所以(-3,0)2.已知|2a-4|+（4a-b-2m）2=0,则(1)当b<0时求m的取值范围.(2)当b>0时求m的取值范围.(3)当b=0时求m的取值范围.解：2a-4=0 a=24a-b-2m=0 b=8-2m(1)b<0 即8-2m<0 m>4(2)b>0 即8-2m>0 m<4(3)b=0 即8-2m=0 m=43.不等式组x>2,x>a的解集为x>2，则a的取值范围是分析：不等式组的解集是使每个不等式都成立的x的取值范围，即它们解的公共部分，你可以借助于数轴来分析。

解：因为不等式组x>2,x>a的解集为x>2，所以所以它们解的公共部分是x>2，所以a≤2.4.为了保护环境，某企业决定购买10台污水处理设备，现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗费如下表：A型B型价格（万元/台）12 10处理污水量（吨/月）240 200年消耗费（万元/台） 1 1经预算，该企业购买设备的资金不高于105万元。

（1）请你设计该企业共有几种购买方案（2）若企业每月生产的污水量为2040吨，为了节约资金，应选择哪种购买方案（3）在第（2）问的条件下，若每台设备的使用年限为10年，污水厂处理污水的费用为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）解：（1）设购买污水处理设备A型x台，则B型(10－x)台。

北师大版八年级下册数学一元一次不等式组同步练习题

北师大版数学八年级下册一元一次不等式组课时练习一、选择题1.关于x 的不等式组314(1x x x m--⎧⎨⎩＞）＜的解集为x ＜3，那么m 的取值范围为（）A ．m =3B ．m ＞3C ．m ＜3D ．m ≥3 2. 不等式组1321x x x+⎧⎨-⎩＜＞的解集是（）A ．x ＞1B ．x ＜2C ．1≤x ≤2D ．1＜x ＜2 ．3．使不等式x -1≥2与3x -7＜8同时成立的x 的整数值是（） A ．3，4 B ．4，5 C ．3，4，5 D ．不存在4．若不等式组1x x m ⎧⎨-⎩＜1＞恰有两个整数解，则m 的取值范围是（）A ．-1≤m ＜0B ．-1＜m ≤0C ．-1≤m ≤0D ．-1＜m ＜06．若不等式组01x a x +⎧⎨+⎩≥≥0无解，则实数a 的取值范围是（）A ．a ≥-1B ．a ＜-1C ．a ≤1D ．a ≤-17．把一些笔记本分给几个学生，如果每人分3本，那么余8本；如果前面的每个学生分5本，那么最后一人就分不到3本．则共有学生（） A ．4人 B ．5人 C ．6人 D ．5或6人8. 有数颗等重的糖果和数个大、小砝码，其中大砝码皆为5克、小砝码皆为1克，且图是将糖果与砝码放在等臂天平上的两种情形．判断下列哪一种情形是正确的（）A ．B ．C ．D ．9. 不等式组23a x a x +⎧⎨⎩-1＜＜＜＜5的解集是3＜x ＜a +2，则a 的取值范围是（）A ．a ＞1B ．a ≤3C ．a ＜1或a ＞3D ．1＜a ≤310．若关于x 的不等式组5133x ax x a +⎧-⎪⎨⎪-⎩＜（）＞12的其中一个整数解为x =2，则a 的值可能为（）A ．-3B ．-2C ．-1D ．0 11. 若不等式组x a x b ⎧⎨⎩＞＜无解（a ≠b ），则不等式组22x ax b-⎧⎨-⎩＞＜的解集是（） A ．2-b ＜x ＜2-a B ．b -2＜x ＜a -2 C ．2-a ＜x ＜2-b D ．无解 12. 一宾馆有二人间，三人间，四人间三种客房供游客租住，某旅行团20人准备同时租用这三种客房共7间，如果每个房间都住满，租房方案有（） A ．4种 B ．3种 C ．2种 D ．1种13. 已知实数x 、y 同时满足三个条件：①3x -2y =4-p ，②4x -3y =2+p ，③x ＞y ，那么实数p 的取值范围是（） A ．p ＞-1 B ．p ＜1 C ．p ＜-1 D ．p ＞1 二、填空题16．关于x 的不等式组213x a x +⎧⎨-⎩＞＞1的解集为1＜x ＜3，则a 的值为 _________．17. 不等式组x x x ⎧⎨⎩2-4＞03(-1)≤4的解集为________18．若点P（x，y）在平面直角坐标系x O y中第四象限内的一点，且满足2x-y=4，x+y=m，则m 的取值范围是__________ ．19. 已知关于x的不等式x ax-⎧⎨⎩≥05-2＞1只有四个整数解，则实数a的取值范是__________20.对于任意实数m、n，定义一种运运算m※n=mn-m-n+3，等式的右边是通常的加减和乘法运算，例如：3※5=3×5-3-5+3=10．请根据上述定义解决问题：若a＜2※x＜7，且解集中有两个整数解，则a的取值范围是_________．三、解答题21. 解不等式组21xx x+⎧⎨⎩＞5+1＞4（-2）22．解不等式组12xx⎧⎪⎨⎪⎩＞1①1-≥-3②请结合题意，完成本题解答．（Ⅰ）解不等式①，得_______（Ⅱ）解不等式②，得_______（Ⅲ）把不等式①和②的解集在数轴上表示出来：（Ⅳ）原不等式组的解集为_______23．某中学为了绿化校园，计划购买一批榕树和香樟树，经市场调查榕树的单价比香樟树少20元，购买3棵榕树和2棵香樟树共需340元．（1）请问榕树和香樟树的单价各多少？（2）根据学校实际情况，需购买两种树苗共150棵，总费用不超过10840元，且购买香樟树的棵树不少于榕树的1.5倍，请你算算，该校本次购买榕树和香樟树共有哪几种方案．340元两个等量关系列出二元一次方程组，求解即可；（2）设购买榕树a棵，则香樟树为（150-a）棵，然后根据总费用和两种树的棵数关系列出不等式组，求出a的取值范围，在根据a是正整数确定出购买方案．24．为了鼓励城区居民节约用水，某市规定用水收费标准如下：每户每月的用水量不超过20度时（1度=1米3），水费为a元/度；超过20度时，不超过部分仍为a元/度，超过部分为b元/度．已知某用户四份用水15度，交水费22.5元，五月份用水30度，交水费50元．（1）求a，b的值；（2）若估计该用户六月份的水费支出不少于60元，但不超过90元，求该用户六月份的用水量x的取值范围．25．某汽车制造厂开发了一款新式电动汽车，计划一年生产安装240辆．由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人；他们经过培训后上岗，也能独立进行电动汽车的安装．生产开始后，调研部门发现：1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车．（1）每名熟练工和新工人每月分别可以安装多少辆电动汽车？（2）如果工厂招聘n（0＜n＜10）名新工人，使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务，那么工厂有哪几种新工人的招聘方案？（3）在（2）的条件下，工厂给安装电动汽车的每名熟练工每月发2000元的工资，给每名新工人每月发1200元的工资，那么工厂应招聘多少名新工人，使新工人的数量多于熟练工，同时工厂每月支出的工资总额W（元）尽可能地少？。

北师大版八年级数学下册 同步练习题一元一次不等式

(完整word版)北师大版八年级下册数学第一章_一元一次不等式和一元一次不等式组练习题(带解析)

2021-2022学年度初中数学北师大版八年级下册第二章第六节 一元一次不等式组 同步练习