北京市中学生数学竞赛高一级复赛参考解答Word版
北京市中学生数学竞赛高一级复赛参考解答

2020年北京市中学生数学竞赛高一年级复赛参考解答一、选择题(总分值40分,每题8分,将答案写在下面相应的空格中)1.二次三项式x 2+ax +b 的根是实数,其中a 、b 是自然数,且ab =22020,那么如此的二次三项式共有 个.答:1341.咱们发觉,事实上,数a 和b 是2的非负整数指数的幂,即,a =2k ,b =22020–k ,那么判别式Δ=a 2– 4b =22k – 422020–k =22k – 22021–k ≥0,得2k ≥2021–k ,因此k ≥32013=671,但k ≤2020,因此k 能够取2020–671+1=1341个不同的整数值.每一个k 恰对应一个所求的二次三项式,因此如此的二次三项式共有1341个.2.如右图,在半径为1的圆O 中内接有锐角三角形ABC ,H 是△ABC 的垂心,角平分线AL 垂直于OH ,那么BC = .解:易知,圆心O 及垂心H 都在锐角三角形ABC 的内部,延长AO 交圆于N ,连接AH 并延长至H 1与BC 相交,连接CN ,在Rt △CAN 和Rt △AH 1B 中,∠ANC =∠ABC ,于是有∠CAN =∠BAH 1,再由AL 是△ABC 的角平分线,得∠1=∠2.由条件AP ⊥OH ,得AH=AO=1.连接BO 交圆于M ,连接AM 、CM 、CH ,可知AMCH 为平行四边形,因此CM=AH=AO =1,BM =2,因为△MBC 是直角三角形,由勾股定理得BC ==3.已知概念在R 上的函数f (x )=x 2和g (x )=2x +2m ,假设F (x )=f (g (x )) – g (f (x ))的最小值为14,那么m = .答:14-.解:由f (x )=x 2和g (x )=2x +2m ,得F (x )= f (g (x )) – g (f (x ))=(2x +2m )2–(2x 2+2m )=2x 2+8mx +4m 2–2m ,F (x )=2x 2+8mx +4m 2–2m 的最小值为其图像极点的纵坐标()2222242(42)84284242m m m m m m m m ⨯⨯--=--=--⨯.由已知,21424m m --=,得21202m ⎛⎫+= ⎪⎝⎭,因此1.4m =-4.tan 37.5= . 答:6232-+-.解1:作Rt △ADB ,使得∠ADB =90º,AD =1,AB =2,那么∠B =30º,BD =3.延长BD 到C ,使BC =2,那么DC =23-.连接AC ,那么∠ACB =(180º–30º)÷2=75º.作∠ACD 的平分线交AD 于E ,那么∠ECD =º. 由于AC 2=AD 2+DC 2=1+(2–3)2=8–43,因此 ()2843621226262AC =-=-+=-=-.由三角形的角平分线定理,得AE AC ED DC=,于是AE ED AC DCED DC ++=,即()()()()322162233221ED AD DC AC CD ====-++-+-+-,因此()()tan 37.53221EDDC==-+6232=-+-.解2:作等腰直角三角形ABC ,使∠C =90º,AC =BC =1,那么AB =2. 作∠CAD =30º,那么CD =33,AD =233,那么∠DAB =15º. 作∠BAD 的平分线AE ,记CE =x ,那么BE =1–x ,DE =x –3. 因此33232x -=,整理得 ()()213221623 2.3232x +-+===-+--+tan 37.562321CE xAC ===-+-. 5.设f (x ) =113xx+-,概念f 1(x ) = f (f (x )),f n (x )=f (f n –1(x )) (n =2, 3,…),f 2020(2020)= . 答:10053017.A21 30º解:记01()()13x f x f x x +==-,那么()111113()()1131313xx x f x f f x x x x++--===--+-⋅-; ()211113()()11313xx f x f f x x x x--+===-+⋅+;()3201()()()()13x f x f f x f x f x x +====-; 接下来有41()()f x f x =,52()()f x f x =,63()()f x f x =,…,f n (x )的表达式是循环重复的,以3项为一周期.因此,20113670111()()()13x f x f x f x x ⨯+-===+,20112011120101005(2011)13201160343017f -===+⨯.二、(总分值15分)D 是正△ABC 的边BC 上一点,设△ABD 与△ACD 的内心别离为I 1,I 2,外心别离为O 1,O 2,求证:(I 1O 1)2+(I 2O 2)2=(I 1I 2)2. 证明:作以A 为中心、逆时针旋转60的变换(,60)R A ,使△ABD 到△ACD 1,由于∠ADC +∠AD 1C =∠ADC +∠ADB =180º,因此A 、D 、C 、D 1共圆,因此2O 是△AD 1C 的外心,也确实是(,60)12R A O O −−−−→,因此AO 1=DO 1=AO 2=DO 2=O 1O 2,因此∠O 1AO 2=∠O 1DO 2=60º.由∠AO 1O 2+∠ACB =120º+60º=180º,O 1在△ACD 的外接圆⊙O 2上.由于111(180)6012012022AI D ABD ABD ∠=∠+-∠=+⨯=,因此I 1在⊙O 2上,因此11118018030150O I D O AD ∠=-∠=-=,111118015030I O D I DO ∠+∠=-=.同理可证,I 2在△ABD 的外接圆⊙O 1上,因此22150DI O ∠=.由于12118090,2I DI ∠=⨯=而22111212906030I DO I DO I DI O DO ∠+∠=∠-=-=,比较可得1122I O D I DO ∠=∠.在△O 1I 1D 与△DI 2O 2中,因为已证O 1D=DO 2,1122150,O I D DI O ∠=∠=又1122.I O D I DO ∠=∠因此 △O 1I 1D ≌△DI 2O 2.因此,I 1O 1=DI 2,DI 1= I 2O 2.由于1290,I DI ∠=△I 1DI 2是直角三角形.依照勾股定理,有()()()2221212,DI DI I I +=而I 1O 1=DI 2,DI 1=I 2O 2. 因此()()()222112212.I O I O I I +=三、(总分值15分)n 是正整数,记n !=1×2×3×…×n ,如1!=1,2!=1×2=2,3!= 1×2×3=6,又记[a ]表示不超过a 的最大整数,求方程120111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的所有正整数解.解1:由于当x 是正整数时,[]1!x x ⎡⎤=⎢⎥⎣⎦,2!2x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦≥12x -,3!6x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦>6x –1,因此1126x x x -++-<2020即53x <120122,得方程的正整数解x 知足0<x <. 由于6!=720,7!=5040,因此方程的正整数解x <7!,即07!8!9!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦. 因此,方程20111!2!3!4!5!6!x x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的解与原方程的解是一样的.设小于7!的正整数x 为上述方程的解,咱们写出(1,2,3,4,5,6)!xk k =的带余除法表达式:设16!6!r x a =+,0≤r 1<6!,(0≤a ≤6,a ∈N );因此.6!x a ⎡⎤=⎢⎥⎣⎦① 12665!5!5!r r x a a b =+=++,0≤r 2<5!,(0≤b ≤5,b ∈N ),因此65!x a b ⎡⎤=+⎢⎥⎣⎦. ② 323053054!4!4!r r xa b a b c =++=+++,0≤r 3<4!,(0≤c ≤4,c ∈N ), 因此3054!x a b c ⎡⎤=++⎢⎥⎣⎦. ③341202*********!3!3!r r xa b c a b c d =+++=++++,0≤r 4<3!,(0≤d ≤3,d ∈N ); 因此1202043!x a b c d ⎡⎤=+++⎢⎥⎣⎦. ④5436060123360601232!2!2!r r xa b c d a b c d e =++++=+++++,0≤r 5<2, (e =0,1,2);因此360601232!x a b c d e ⎡⎤=++++⎢⎥⎣⎦. ⑤5720120246272012024621!1!r xa b c d e a b c d e f =+++++=+++++,(f =0,1); 因此72012024621!x a b c d e f ⎡⎤=+++++⎢⎥⎣⎦. ⑥①~⑥相加得1237a +206b +41c +10d +3e +f =2020. 显然a =1,因此206b +41c +10d +3e +f =2020–1237=774; 易知b =3,因此41c +10d +3e +f =774–206×3=156; 易知c =3,于是10d +3e +f =156–41×3=33;类似求得d =3,e =1,f =0.所求的x =1×720+3×120+3×24+3×6+1×2+0×1=1172.x =1172是方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的唯一正整数解. 解2:设f (x )=1!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,因为关于所有的正整数k ,!x k ⎡⎤⎢⎥⎣⎦都是单调增的,其和f (x )确实是增函数;又因为关于正整数x ,11!x +⎡⎤⎢⎥⎣⎦=1!x ⎡⎤⎢⎥⎣⎦+1,因此f (x )是严格单调的.经估数,将x =1172带入,求f (1172)的值,得f (1172)=2020,因此,x =1172是方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的唯一正整数解.四、(总分值15分)平面上的n 个点,假设其中任3个点中必有2个点的距离不大于1,那么称如此的n 个点为“标准n 点组”.要使一个半径为1的圆纸片,对任意“标准n 点组”都能至少盖住其中的25个点,试求n 的最小值. 答案:49.解:第一证明,n min >48.在平面上画长为5的线段AB ,别离以A 、B 为圆心,画半径为的两个圆,在每一个圆内,取24个点,那么平面上有48个点满足题设条件(其中任意3点中必有2点的距离不大于1),显然,不可能画出一个半径为1的圆,其包括有25个所选的点,因此n >48.下面证明n min =49.若49=n ,设A 是其中的一点,作以A 为圆心半径为1的⊙A ,假设所有的点都在圆A 中,那么就知足题设条件.假设不是所有的点都在圆A 中,那么至少有一点B 不在圆A 中,再作以B 为圆心、半径为1的⊙B ,那么A 、B 的距离大于1(如右图),除A ,B 外,余下的47个点中每一点P 都与A 、B 组成3点组,必有两个点的距离不大于1,因此要么P A ≤1,要么PB ≤1,即点P 要么在⊙A 中,要么在⊙B 中,依照抽屉原理,必有一个圆至少包括了这47个点中的24个点,不妨设那个圆确实是⊙A ,再加上圆心A 点,就有很多于25个点在那个半径为1的⊙A 中(圆内或圆周上).因此n 的最小值是49.五、(总分值15分)已知函数f :R →R ,使得对任意实数x y z ,,都有11()()()()22f xy f xz f x f yz +-≥14, 求[1×f (1)]+[2×f (2)]+[3×f (3)]+…+[2020×f (2020)]的值.其中关于实数a ,[a ]表示不超过a 的最大整数.解:由于已知函数f R R →:,使得对任意实数x y z ,,都知足11()()()()22f xy f xz f x f yz +-≥14,可令0x y z ===,有 ()211(0)(0)(0)22f f f +-≥14,即21(0)2f ⎛⎫- ⎪⎝⎭≤0, 由于f (0)是一个实数,因此1(0).2f =再令1x y z ===,有()211(1)(1)(1)22f f f +-≥14,即21(1)2f ⎛⎫- ⎪⎝⎭≤0, 由于f (1)是一个实数,因此1(1).2f =又令0y z ==,有11(0)(0)()(0)22f f f x f +-≥14,代入1(0)2f =得对任意实数x ,都有()f x ≤12. ①又令1y z ==,有11()()()(1)22f x f x f x f +-≥14,代入1(1)2f =得对任意实数x ,都有()f x ≥12. ②综合①、②可得,对任意实数x ,都有1()2f x =.验证:函数1()2f x =知足题设条件,取的是等号,因此知足题设条件的函数的唯一解为1()2f x =.于是[][][][]1(1)2(2)3(3)2011(2011)f f f f ⨯+⨯+⨯++⨯1234201122222⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦011223310051005=+++++++++()21231005=⨯++++(11005)1005=+⨯.1011030。
2016年北京市中学生数学竞赛高一年级复赛试题及解答_

圆 O1,半 圆 O2,形 成 的 阴
图5
影图形称作“皮匠刀形”,过 C 的AB 的垂线交大
半圆于 D,两个小 半 圆 的 外 公 切 线 是 EF.求 证:
CD=EF.
证 明 如 图 6,设 O1C=a,CO2 =b,则 AB
=2a+2b.
知 CD2=AC×CB,
图6
所 以,CD2 =2a×2b
=4ab
①
连接 O1E,O2F,过 O2 作 EF 的 平 行 线 交
O1E 于P,易知△O1O2P 中,∠O2PO1=90°,O1P
=a-b,O1O2=a+b,
故 EF2=O2P2=O1O22-O1P2 = (a+b)2 -
(a-b)2=4ab
②
由①、②得 CD2=EF2,所以 CD=EF.
三、(满分10分)在黑板 上 写 有 方 程 x2+2x
答 10108.
解 构 造 一 个 函 数 g(x)=x f(x)-1, 则 g(1)=g(2)= … =g(2015)=0. 所 以 g(x)=a(x-1)(x-2)… (x-2015), 其中g(x)中的系数a 是一个待定常数. 由f(x)=g(xx)+1=a(x-1)(x-2)x…(x-2015)+1
于点 B、C,PO 交 ⊙O 于
点 D,AE⊥PO 于 E,联
结 BE 并 延 长 交 ⊙O 于
图3
点F,联 结 OC、OF、AD、
AF.若∠BCO=30°,∠BFO=20°.确 定 ∠DAF
的度数.
答 115°.
解 如 图 4,连 结
OA,CD,CF,因 为 PA 切
⊙O 于 点 P,所 以 OA ⊥
答 {1980}. 解 显然x<2016,不 难 见 到,小 于 2016 的 自然数中数字和最 大 为 28,如 S(1999)=28,这 意味着S(x)≤28,进 一 步 S(S(x))≤S(19)= 10,最 后 S(S(S(x)))≤9. 由 方 程 得 出 x=2016-S(x)-S(S(x))-S (S(S(x)))≥2016-28-10-9=1969, 所 以 x∈ {1969,1970,…,2015};另 外,x, S(x),S(S(x)),S(S(S(x)))被 9 除 的 余 数 相 同,而2016被9除 的 余 数 为 0,所 以 每 个 数 被 9 除 的 余 数 为 0.因 此 x 只 可 能 在 1971,1980, 1989,1998 和 2007 中.经 检 验 得 只 有 1980+18 +9+9=2016,所 以 方 程 的 解 集 为 {1980}. 2.如图 1 所 示,⊙O 与 正 方 形 ABCD 的 边 AB 和AD 分别切于点L 和 K ,交边 BC 于点 M 和P,BM=8厘米,MC=17厘米.问⊙O 的 面 积 是多少平方厘米? 答 1 的 半 径 OK ,OL 和
2020年北京市中学生数学竞赛高一年级试题(含答案)

2020年北京市中学生数学竞赛高一年级试题2020年6月 27日8:30~10:30一、填空题(满分40分,每小题8分)1.已知实函数f (x )满足f (x +y )=f (x )+f (y )+4xy ,且f (−1)·f (1)≥4.则293f ⎛⎫-= ⎪⎝⎭______. 2.等腰梯形ABCD (AB =CD )的内切圆与腰CD 的切点为M ,与AM 、BM 的交点分别为K 和L .则AM BM AK BL+的值等于______. 3.四位数abcd 比它的各位数字的平方和大2020,在所有这样的四位数中最大的一个是______.4.已知点O 在△ABC 内部,且2021202020193AB BC CA AO ++=,记△ABC 的面积为S 1,△OBC 的面积为S 2,则12S S =______. 5.有4个不同的质数a , b , c , d ,满足a +b +c +d 是质数,且a 2+bc 、a 2+bd 都是完全平方数,那么a +b +c +d = ______.二、(满分15分)面积为S 1,S 2,S 3,S 4,S 5,S 6的正方形位置如右图所示.求证:S 4+S 5+S 6=3(S 1+S 2+S 3).三、(满分15分)存在2020个不是整数的有理数,它们中任意两个的乘积都是整数四、(满分15分)如右图,已知D 为等腰△ABC BC 上任一点,⊙I 1、⊙I 2分别为△ABD 、△ACD 内切圆,M 为BC 的中点.求证:I 1M ⊥I 2M .五、(满分15分)将集合I ={1, 2, 3, 4, 5, 6, 7, 8, 9}B ={w , x , y , z },使得A ∪B =I ,A ∩B =Ø,且A 与B 的元素至少有一种排列组成的正整数满足2wxyz abcde ,则称A 与B 为集合I 的一个“两倍型2分划”.(1)写出集合I 的所有“两倍型2分划”,并给出理由;(2)写出集合I 的每个“两倍型2分划”对应的所有可能的2wxyz abcde .2020年北京市中学生数学竞赛(邀请)高一年级试题及参考解答2020年6月 27日8:30~10:30一、填空题(满分40分,每小题8分)1.已知实函数f (x )满足f (x +y )=f (x )+f (y )+4xy ,且f (−1)·f (1)≥4.则29()3f -=______. 解:令x =y =0得f (0)=0,令x =−1,y =1,得f (1)+f (−1)=4.平方得f 2(1)+2f (1)·f (−1)+f 2(−1)=16,又因为f (−1)·f (1)≥4,所以f 2(1)+2f (1)·f (−1)+f 2(−1)≤4f (1)·f (−1).即(f (1)−f (−1))2≤0.所以f (1)=f (−1)=2. 因为)32)(31(4)32()31()32(31)1(--⋅+-+-=⎪⎭⎫ ⎝⎛-+-=-f f f f 1118=3()4()()3339f , 所以 .234)31(3=+-f 因此.92)31(=-f 所以.9894)31(2)32(=+-=-f f 于是29()3f -=8.2.等腰梯形ABCD (AB =CD )的内切圆与腰CD 的切点为M ,与AM 、BM 的交点分别为K 和L .则AM BM AK BL+的值等于______. 解:设N 是边AD 的中点,a =AN ,x =AK ,y =AM ,α=∠ADM ,(如图).则ND=DM=a ,且根据余弦定理,对于△ADM ,有y 2=4a 2+a 2−4a 2cos α=a 2(5−4cos α). 另一方面,根据切割线定理,有xy=a 2,所以 2AM y y AK x xy ===5−4cos α. 类似地对于△BCM ,得到54cos .BM BLα=+ 因此,10.AM BM AK BL+= C BD A LK a y αMx3.四位数abcd 比它的各位数字的平方和大2020,在所有这样的四位数中最大的一个是______.解: 设abcd 为所求的自然数,则根据条件1000a +100b +10c +d =a 2+b 2+c 2+d 2+2020.考虑到 2000<a 2+b 2+c 2+d 2+2020≤92+92+92+92+2020=2344,可以断定a =2,于是100b +10c +d =b 2+c 2+d 2+24.即 b (100−b )+c (10−c )=d (d −1)+24 (*)由于c (10−c )>0,当b ≥1时,b (100−b )≥99,所以(*)式左边大于99,而(*)式右边小于9×8+24=96,因此要(*)式成立,必须b =0.当b =0时,(*)式变为 d 2−d =10c −c 2−24. 由于四位数abcd 中a =2,b =0,要使20cd 最大,必需数字c 最大.若c =9,c 2−c −24=90−92−24<0,而d 2−d ≥0故(*)式不能成立.同理,c =8和c =7时,(*)式均不能成立.当c =6时,c 2−c −24=60−62−24=0,这时,d =0及d =1,均有d 2−d =0,即(*)式均成立. 于是abcd =2060或2061.所以满足题设条件的四位数中最大的一个是2061.4.已知点O 在△ABC 内部,且2021202020193AB BC CA AO ++=,记△ABC的面积为S 1,△OBC 的面积为S 2,则12S S =______. 解:由2021202020193AB BC CA AO ++=,得22019()3AB BC AB BC CA AO ++++=,因为0AB BC CA ++=,所以23AB BC AO +=,故23AB AC AB AO +-=. 所以3AB AC AO +=,取BC 的中点D ,则23AD AO =.于是A 、D 、O 三点共线,且3AD OD =.所以123S AD S OD==.5.有4个不同的质数a , b , c , d ,满足a +b +c +d 是质数,且a 2+bc 、a 2+bd 都是完全平方数,那么a +b +c +d = ______.解:由a +b +c +d 是质数,可知a , b , c , d 中有2.如果a ≠2,那么b , c , d 中有2,从而a 2+bc 、a 2+bd 中有一个模4余3,不是完全平方数.故a =2.假设22+bc =m 2,那么bc =(m −2)(m +2).如果m −2=1,那么m =3,bc =5,与已知矛盾.故不妨设b =m −2,c =m +2,则c =b +4.同理d =b −4,所以{a , b , c , d }={a , b , b +4, b −4}.而b −4, b , b +4中有一个是3的倍数,又是质数,所以只能是b −4=3,此时a +b +c +d =2+3+7+11=23.二、(满分15分)面积为S 1,S 2,S 3,S 4,S 5,S 6的正方形位置如图所示.求证:S 4+S 5+S 6=3(S 1+S 2+S 3).证明:见右图:AKLB ,BMNC ,ACPQ 都是正方形,对应的面积为S 1、S 2和S 3.设,,βα=∠=∠ABC BAC .γ=∠ACB 因为,,,321S AC S BC S AB === 则根据余弦定理,有αcos 232321S S S S S -+=βcos 231312S S S S S -+=γcos 221213S S S S S -+= 由此,.cos 2cos 2cos 2321213132S S S S S S S S S ++=++γβα ①又因为 ,180,180,180γβα-=∠-=∠-=∠ NCP LBM QAK 以及,,,465S NP S LM S QK === 则有αcos 231315S S S S S ++= ②βcos 221216S S S S S ++= ③ γcos 232324S S S S S ++= ④由等式①~④得 S 4+S 5+S 6=3(S 1+S 2+S 3).三、(满分15分)存在2020个不是整数的有理数,它们中任意两个的乘积都是整数吗?如果存在,请给出例证,如果不存在,请说明理由.解:存在. 例证如下:因为质数有无限多个,所以任选2020个两两不同的质数122020,,,p p p ,构造2020个两两不同的数: 1220202ii p p p x p ,i =1, 2, 3, …, 2020. 易知,因为122020,,,x x x 的分子不被分母整除,皆为不是整数的有理数.而任意两个数的乘积 12202012202022i i i j p p p p p p x x p p 2222222222122020121111202022ii j j i j p p p p p p p p p p p p . 这2018个质数平方的乘积是整数,满足题意要求.A B C I 1 I 2 • • F 四、(满分15分)如图,已知D 为等腰△ABC 底边BC 上任一点,⊙I 1、⊙I 2分别为△ABD 、△ACD 的内切圆,M 为BC 的中点.求证:I 1M ⊥I 2M .证明: (1)当D 与M 重合时,显然有∠I 1MI 2=90°,即I 1M ⊥I 2M .(2)当D 不与M 重合时,不妨设BD >DC , 过I 1作I 1E ⊥BC 于点E ,过I 2作I 2F ⊥BC 于点F ,连结I 1D ,I 2D ,I 1I 2.因为⊙I 1为△ABD 的内切圆,⊙I 2为△ACD 的内切圆,所以 2AB BD AD BE +-=,2DC AD AC DF +-= 所以,EM =BM −BE=22BC AB BD AD +--()2BC BD AD AB -+-=.2DF AC AD DC =-+= 进而有 ED=MF .因为I 1、I 2分别为△ABD 、△ACD 的内心,易知∠I 1DI 2=90°. 由勾股定理得I 1D 2+I 2D 2=I 1I 22.(*)在Rt △I 1DE 与Rt △DI 2F 中,由勾 股定理得I 1E 2+ED 2=I 1D 2,I 2F 2+DF 2=I 2D 2,代入(*)式,得(I 1E 2+ED 2)+(I 2F 2+DF 2)= I 1I 22.注意EM=DF ,ED=MF 代换得(I 1E 2+MF 2)+(I 2F 2+EM 2)= I 1I 22.即 (I 1E 2+EM 2)+(I 2F 2+MF 2)= I 1I 22.所以 I 1M 2+I 2M 2=I 1I 22.根据勾股定理的逆定理,有△I 1MI 2为直角三角形,∠I 1MI 2=90°,即I 1M ⊥I 2M .五、(满分15分)将集合I ={1, 2, 3, 4, 5, 6, 7, 8, 9}划分为两个子集A ={a , b , c , d , e }和B ={w , x , y , z },使得A ∪B =I ,A ∩B =Ø,且A 与B 的元素至少有一种排列组成的正整数满足2wxyz abcde ,则称A 与B 为集合I 的一个“两倍型2分划”.(1)写出集合I 的所有“两倍型2分划”,并给出理由;(2)写出集合I 的每个“两倍型2分划”对应的所有可能的2wxyz abcde . 解:(1)集合I 共有2个“两倍型2分划”:A ={1, 3, 4, 5, 8},B ={2, 6, 7, 9}及A ={1, 4, 5, 6, 8},B ={2, 3, 7, 9}.理由简述如下:1° 由易知,a =1,所以a ∈A . A B C I 1 I 2 • •2° 由0∉ I ={1, 2, 3, 4, 5, 6, 7, 8, 9}=A ∪B ,而5×2=10,所以5∈A .3° 试验知,a , b , c , d , e 均不能等于9,所以9∈B ,进而有8∈A .4° 因为数wxyz abcde 和的9个数字和恰为1+2+3+4+5+6+7+8+9=45是9的倍数,可判知+abcde wxyz 是9的倍数,即+abcde wxyz ≡0(mod9). 又2wxyz abcde ,所以3wxyz ≡0(mod9).于是wxyz ≡0(mod3).所以)(wxyz S 是3的倍数,进而推得)(abcde S 也是3的倍数.5° 同样试验可判定7∈B .此时分配剩下的4个元素:2, 3, 4, 6.由于A 中的1+5+8=14,被3除余2,所以从2, 3, 4, 6中选出的两个数之和被3除余1.于是只能选3, 4或4, 6属于A ,对应剩下的2, 6或2, 3归属于B .因此,找到集合I 的两个“两倍型2分划”:A ={1, 3, 4, 5, 8},B ={2, 6, 7, 9}及A ={1, 4, 5, 6, 8},B ={2, 3, 7, 9}.(2)集合I 的“两倍型2分划”满足的不同的2wxyz abcde 共12个.1° 当B={2, 6, 7, 9}时,得到6个不同的式子:6729×2=13458, 6792×2=13584, 6927×2=13854,7269×2=14538, 7692×2=15384, 9267×2=18534.2° 当B={2, 3, 7, 9}时,得到6个不同的式子:7293×2=14586, 7329×2=14658, 7923×2=15846,7932×2=15864, 9273×2=18546, 9327×2=18654.。
北京市中学生数学竞赛高一级复赛参考解答

2011年北京市中学生数学竞赛高一年级复赛参考解答一、选择题(满分40分,每小题8分,将答案写在下面相应的空格中)题 号 1 234 5答 案1341314- 623 2.-+-100530171.二次三项式x 2+ax +b 的根是实数,其中a 、b 是自然数,且ab =22011,则这样的二次三项式共有 个.答:1341.我们发现,实际上,数a 和b 是2的非负整数指数的幂,即,a =2k ,b =22011–k ,则判别式Δ=a 2– 4b =22k – 422011–k =22k – 22013–k ≥0,得2k ≥2013–k ,因此k ≥32013=671,但k ≤2011,所以k 能够取2011–671+1=1341个不同的整数值.每个k 恰对应一个所求的二次三项式,所以这样的二次三项式共有1341个.2.如右图,在半径为1的圆O 中内接有锐角三角形ABC ,H 是△ABC 的垂心,角平分线AL 垂直于OH ,则BC = . 答:3.解:易知,圆心O 及垂心H 都在锐角三角形ABC 的内部,延长AO 交圆于N ,连接AH 并延长至H 1与BC 相交,连接CN ,在Rt △CAN 和Rt △AH 1B 中,∠ANC =∠ABC ,于是有∠CAN =∠BAH 1,再由AL 是△ABC 的角平分线,得∠1=∠2.由条件AP ⊥OH ,得AH=AO=1.连接BO 交圆于M ,连接AM 、CM 、CH ,可知AMCH 为平行四边形,所以CM=AH=AO =1,BM =2,因为△MBC 是直角三角形,由勾股定理得2221 3.BC =-=3.已知定义在R 上的函数f (x )=x 2和g (x )=2x +2m ,若F (x )=f (g (x )) – g (f (x ))的最小值为14,则m = .答:14-.解:由f (x )=x 2和g (x )=2x +2m ,得F (x )= f (g (x )) – g (f (x ))=(2x +2m )2–(2x 2+2m )=2x 2+8mx +4m 2–2m ,F (x )=2x 2+8mx +4m 2–2m 的最小值为其图像顶点的纵坐标ABCOHL MPNH 1 1 2()2222242(42)84284242m m m m m m m m ⨯⨯--=--=--⨯.由已知,21424m m --=,得21202m ⎛⎫+= ⎪⎝⎭,所以1.4m =-4.tan 37.5= . 答:6232-+-.解1:作Rt △ADB ,使得∠ADB =90º,AD =1,AB =2,则∠B =30º,BD =3.延长BD 到C ,使BC =2,则DC =23-.连接AC ,则∠ACB =(180º–30º)÷2=75º.作∠ACD 的平分线交AD 于E ,则∠ECD =37.5º.由于AC 2=AD 2+DC 2=1+(2–3)2=8–43,所以 ()2843621226262AC =-=-+=-=-.由三角形的角平分线定理,得AE AC ED DC=,于是AE ED AC DCED DC ++=,即()()()()1322162233221ED AD AD DC AC CD ====-++-+-+-,所以()()tan 37.53221EDDC==-+6232=-+-.解2:作等腰直角三角形ABC ,使∠C =90º,AC =BC =1,则AB =2. 作∠CAD =30º,则CD =33,AD =233,则∠DAB =15º. 作∠BAD 的平分线AE ,记CE =x ,则BE =1–x ,DE =x –33. 所以3132323x x --=,整理得 ()()213221623 2.3232x +-+===-+--+tan 37.562321CE xAC ===-+-. 5.设f (x ) =113xx+-,定义f 1(x ) = f (f (x )),f n (x )=f (f n –1(x )) (n =2, 3,…),f 2011(2011)= .答:10053017.AC D E B21 30º解:记01()()13x f x f x x +==-,则()111113()()1131313xx x f x f f x x x x++--===--+-⋅-; ()211113()()11313xx f x f f x x x x--+===-+⋅+;()3201()()()()13x f x f f x f x f x x +====-; 接下来有41()()f x f x =,52()()f x f x =,63()()f x f x =,…,f n (x )的表达式是循环重复的,以3项为一周期.所以,20113670111()()()13x f x f x f x x ⨯+-===+,20112011120101005(2011)13201160343017f -===+⨯.二、(满分15分)D 是正△ABC 的边BC 上一点,设△ABD 与△ACD 的内心分别为I 1,I 2,外心分别为O 1,O 2,求证:(I 1O 1)2+(I 2O 2)2=(I 1I 2)2. 证明:作以A 为中心、逆时针旋转60的变换(,60)R A ,使△ABD 到△ACD 1,由于∠ADC +∠AD 1C =∠ADC +∠ADB =180º,所以A 、D 、C 、D 1共圆,因此2O 是△AD 1C 的外心,也就是(,60)12R A O O −−−−→,因此AO 1=DO 1=AO 2=DO 2=O 1O 2,所以∠O 1AO 2=∠O 1DO 2=60º.由∠AO 1O 2+∠ACB =120º+60º=180º,O 1在△ACD 的外接圆⊙O 2上.由于111(180)6012012022AI D ABD ABD ∠=∠+-∠=+⨯=,所以I 1在⊙O 2上,因此11118018030150O I D O AD ∠=-∠=-=,111118015030I O D I DO ∠+∠=-=.同理可证,I 2在△ABD 的外接圆⊙O 1上,所以22150DI O ∠=.由于12118090,2I DI ∠=⨯=而22111212906030I DO I DO I DI O DO ∠+∠=∠-=-=,比较可得1122I O D I DO ∠=∠.在△O 1I 1D 与△DI 2O 2中,因为已证O 1D=DO 2,1122150,O I D DI O ∠=∠=又1122.I O D I DO ∠=∠因此 △O 1I 1D ≌△DI 2O 2.所以,I 1O 1=DI 2,DI 1= I 2O 2.由于1290,I DI ∠=△I 1DI 2是直角三角形.根据勾股定理,有()()()2221212,DI DI I I +=而I 1O 1=DI 2,DI 1=I 2O 2. 因此()()()222112212.I O I O I I +=三、(满分15分)n 是正整数,记n !=1×2×3×…×n ,如1!=1,2!=1×2=2, 3!= 1×2×3=6,又记[a ]表示不超过a 的最大整数,求方程ABCDO 1I 2I 1D 1O 220111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的所有正整数解.解1:由于当x 是正整数时,[]1!x x ⎡⎤=⎢⎥⎣⎦,2!2x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦≥12x -,3!6x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦>6x –1,所以1126x x x -++-<2011即53x <120122,得方程的正整数解x 满足0<x <1207.5. 由于6!=720,7!=5040,所以方程的正整数解x <7!,即07!8!9!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦. 因此,方程20111!2!3!4!5!6!x x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的解与原方程的解是一样的.设小于7!的正整数x 为上述方程的解,我们写出(1,2,3,4,5,6)!xk k =的带余除法表达式:设16!6!r x a =+,0≤r 1<6!,(0≤a ≤6,a ∈N );因此.6!x a ⎡⎤=⎢⎥⎣⎦① 12665!5!5!r r x a a b =+=++,0≤r 2<5!,(0≤b ≤5,b ∈N ),因此65!x a b ⎡⎤=+⎢⎥⎣⎦. ② 323053054!4!4!r r xa b a b c =++=+++,0≤r 3<4!,(0≤c ≤4,c ∈N ), 因此3054!x a b c ⎡⎤=++⎢⎥⎣⎦. ③341202*********!3!3!r r xa b c a b c d =+++=++++,0≤r 4<3!,(0≤d ≤3,d ∈N ); 因此1202043!x a b c d ⎡⎤=+++⎢⎥⎣⎦. ④5436060123360601232!2!2!r r xa b c d a b c d e =++++=+++++,0≤r 5<2, (e =0,1,2);因此360601232!x a b c d e ⎡⎤=++++⎢⎥⎣⎦. ⑤5720120246272012024621!1!r xa b c d e a b c d e f =+++++=+++++,(f =0,1); 因此72012024621!x a b c d e f ⎡⎤=+++++⎢⎥⎣⎦. ⑥①~⑥相加得1237a +206b +41c +10d +3e +f =2011. 显然a =1,因此206b +41c +10d +3e +f =2011–1237=774; 易知b =3,因此41c +10d +3e +f =774–206×3=156; 易知c =3,于是10d +3e +f =156–41×3=33;类似求得d =3,e =1,f =0.所求的x =1×720+3×120+3×24+3×6+1×2+0×1=1172.x =1172是方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的唯一正整数解. 解2:设f (x )=1!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,因为对于所有的正整数k ,!x k ⎡⎤⎢⎥⎣⎦都是单调增的,其和f (x )就是增函数;又因为对于正整数x ,11!x +⎡⎤⎢⎥⎣⎦=1!x ⎡⎤⎢⎥⎣⎦+1,所以f (x )是严格单调的.经估数,将x =1172带入,求f (1172)的值,得f (1172)=2011,所以,x =1172是方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的唯一正整数解.四、(满分15分)平面上的n 个点,若其中任3个点中必有2个点的距离不大于1,则称这样的n 个点为“标准n 点组”.要使一个半径为1的圆纸片,对任意“标准n 点组”都能至少盖住其中的25个点,试求n 的最小值. 答案:49.解:首先证明,n min >48.在平面上画长为5的线段AB ,分别以A 、B 为圆心,画半径为0.5的两个圆,在每一个圆内,取24个点,则平面上有48个点满足题设条件(其中任意3点中必有2点的距离不大于1),显然,不可能画出一个半径为1的圆,其包含有25个所选的点,所以n >48.下面证明n min =49.若49=n ,设A 是其中的一点,作以A 为圆心半径为1的⊙A ,若所有的点都在圆A 中,那么就满足题设条件.若不是所有的点都在圆A 中,则至少有一点B 不在圆A 中,再作以B 为圆心、半径为1的⊙B ,则A 、B 的距离大于1(如右图),除A ,B 外,余下的47个点中每一点P 都与A 、B 组成3点组,必有两个点的距离不大于1,所以要么P A ≤1,要么PB ≤1,即 点P 要么在⊙A 中,要么在⊙B 中,根据抽屉原理,必有一个圆至少包含了这47个点中的24个点,不妨设这个圆就是⊙A ,再加上圆心A 点,就有不少于25个点在这个半径为1的⊙A 中(圆内或圆周上).所以n 的最小值是49.五、(满分15分)已知函数f :R →R ,使得对任意实数x y z ,,都有11()()()()22f xy f xz f x f yz +-≥14, 求[1×f (1)]+[2×f (2)]+[3×f (3)]+…+[2011×f (2011)]的值.其中对于实数a ,[a ]表示不超过a 的最大整数.解:由于已知函数f R R →:,使得对任意实数x y z ,,都满足11()()()()22f xy f xz f x f yz +-≥14,可令0x y z ===,有 ()211(0)(0)(0)22f f f +-≥14,即21(0)2f ⎛⎫- ⎪⎝⎭≤0, 由于f (0)是一个实数,所以1(0).2f =再令1x y z ===,有()211(1)(1)(1)22f f f +-≥14,即21(1)2f ⎛⎫- ⎪⎝⎭≤0, 由于f (1)是一个实数,所以1(1).2f =又令0y z ==,有11(0)(0)()(0)22f f f x f +-≥14,代入1(0)2f =得对任意实数x ,都有()f x ≤12. ①又令1y z ==,有11()()()(1)22f x f x f x f +-≥14,代入1(1)2f =得对任意实数x ,都有()f x ≥12. ②综合①、②可得,对任意实数x ,都有1()2f x =.验证:函数1()2f x =满足题设条件,取的是等号,所以满足题设条件的函数的唯一解为1()2f x =.于是[][][][]1(1)2(2)3(3)2011(2011)f ff f ⨯+⨯+⨯++⨯ 1234201122222⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦011223310051005=+++++++++()21231005=⨯++++(11005)1005=+⨯1011030=.。
2017年北京市中学生数学竞赛复赛(高一)

记 中的 最 小 数 =0 :…a ,
△2=p 一4g2
S(n)=口l+02+… +0f. 若 的个位数字 a ≠9,则
又三条边长 的平方 分别为 ( ) =2 ,(2x:) =4 ,( 。) =6 , 于是 ,长 为 2 2 、2 ,的三条线段 所构成 的 三角形 为直角三角形. 设该 直角三角形面积为 Js.则
5 :( ×2 ×2 :) = =4
= 1 lp2.
由 以上 两 式 得 11(P1-p2)=9k一1. 对于最小 的 ,有最小 的 自然数 k,使得 11 I(9k一1). 经检验 ,k=1,2,3,4不符合题意. 当 k=5时 ,9×5—1=44为 11的倍 数 , 此 时 ,P1-p2=4.
且 厂(1)=2.
(1)证 明 :_厂( )为奇 函数 ;
(2)求八_厂(2 017))的值.
四、(15分 )如 图 1,在 △ ABC中 ,AB=
AC,AD上 BC于点 D,DE上 AC于点 E,c为
参 考 答 案
一 1-24. 、
由点 P 向 AB所 在 的直线 引垂 线 ,垂 足 为 H 则
P1=5,P2= 1
= S(n)=55,S(n+1):11. 由 口1+Ⅱ2+… +。f一 十9×5=55,得
a l + a2 + … + n =10 >9 : t一 ≥2.
一
又 k=5,于是 ,最小 的 n为七位数 ,前两
位数字和为 10.
当 0:2,b=一1, =0时 ,取得最大值 2.
一
为 3的 平 行 线 与 o 0 交 于 点 P、P , 联 结 4尸、BP.则 在
、、
//
、~ 一
2016年北京市中学生数学竞赛复赛高一

一2k一1
注意到,小于2 016的自然数中的数字 和最大为28,例如,S(1 999)=28,这表明,
|s(菇)≤28.
所以,对于任意的k E Z+,均有
[竿】+[警】=72k-1-1
--7(一1)扣1—1(mod 50). 贝0 A-7(1—1+1—1+…+1—1)一1 -42(mod 50).
X
由以戈):d丛旦
一堡(兰二!)(兰二圣):::i查二竺Q!主2±!
为2 014次的多项式,得 a(x一1)(菇一2)…(菇一2 015)+1 的常数项必为0. 故一2
015
3(b+c)
I>4(/7,2—3(n一1+n一2)) =4(//,2—6n+9)=4(n一3)2i>0. 从而,方程①有实根. 因此,任意三个两两不同的整数,只要以 j 其中最大的一个放在左边第一个★的位置, 其余两个放在后两个★的位置,所得的方程 就有实根. 四、记((//,2+n)2一(T/,2一//,)2)(n6—1) 为M 则N=4(r/,3—1)/i,3(17,3+1). 而2
4.115。. 008
进一步,S(.s(菇))≤5(19)=10. 最后,Js(S(S(戈)))≤9. 由方程得
菇=2
016一Js(菇)一.s(S(戈))-s(s(S(x)))
969,1 970,…,2
≥2 016—28—10—9=1 969.
联结OA、CD、CF.
故戈E{1
015}.
因为尉与00切于点A,所以,以上以.
016=25
X
1¨1_0
0。而裔・
因此,f(2
016)=揣=志.
二、如图6,设01C=a,C02=b.
32
X
2013年北京市中学生数学竞赛高一年级复赛试题及解答

( ) 解得 另一根槡 a=槡 2-1, 2+2 舍! ) 因此b=1- a=1- ( 2-1 =2-槡 2. 槡
2 ) ( SABCD = ( a- a b- a) =1 7 2-2 4. 槡 函 数 f: 使 对 一 切 n ∈ N, 有 3. N → N,
2.如 图 1,菱 形 A B C D 的 顶 点 D、 C在 直 线 y =x 上 , 且顶点
2 上, A、 B 在 曲 线y =x 则菱 DA 平 行 于 y 轴 ,
B、 A C 于点 ⊙O 分别交 A 若弦 E E、 F, F 长度的最
小 值 为 2, 此时 A B 的长 为
图1 图2
形 A B C D 的面积 = . 答: 1 7 2-2 4. 槡
数 学 竞 赛 之 窗
) 且 f( 则 n) +f ( n) =2 n +3, 0) =1, f( f( ) ) ) ) ) 6 7 8 9 1 0 f( f( f( f( f( 的值等于 ) ) ) ) ) 1 +f( 2 +f( 3 +f( 4 +f( 5 f( . 答: 2 7 7 2. 解 以 n=0 代入 ) n) +f( n) =2 n+3 f( f( ( ( ) ) ( ) 得 f f 0 +f 0 =2×0+3, ( *)
4 2 2 2 ห้องสมุดไป่ตู้ 2 2 + z - 2 x z x =2 4 的全部整数解 y -2 yz -2 ( ) 的集合是. x, z y,
) ) 得 f( 即 f( 1 +1=3, 1 =2. ) 进一步 , 令 n=1, 由( 式得 同 2) =3, * f( 所 理得 f( n) =n+1, n=3, 4, 5, 6, 7, 8, 9, 1 0, ) ) ) ) ) 6 7 8 9 1 0 f( f( f( f( f( 以 =2 7 7 2. ( ) ( ) ( ) ( ) ) 1 + 2 + 3 + 4 + 5 f f f f f( 如 图 2, 在 △A 4. B C , 中, 0 ° C B= ∠B =6 ∠A , 点 D 是B 7 5 ° C 边上的 动 点, 以 AD 为 直 径 作
2018年北京市中学生数学竞赛复赛(高一)

不共 线 ,且 每个 点均 标注 了数 1、2、3中的一
个 ,将标有 不 同数 的所有点对均用线段 联结 ,
每条线段 上 均标 注 一 个数 1、2或 3,此 数 与
该线段 端点标 注 的数不 同 ,结果 呈现 出写在 平 面上 的三个数 1、2或 3中的每一个 均恰有
n次.则 n的值为— — .
中至少有一个为偶数.
又 + =一a 为偶数 ,则 ¨、Xk2均 ,
为偶数.
从 而 ,4I b .
注意到 ,十个 连续 的偶数 中只有 五个 被
4整除 ,另五个被 4除余 2.
因为 b ,b ,… ,b 中 的每一 个均 被 4整
除 ,所 以 ,a ,a:,… ,a 中的每一个 均被 4除
二 、(15分 )能否选 出 10个连续 的偶数 ,
且将其分为五个对子 (0 ,b )(k=l,2,…,5),
使得方程
+akx+b =0(k=1,2,… ,5)
均具有 整数根?若能 ,试举一例 ;若不 能 ,请 说
明理 由.
三 、(15分 )如 图 2,D为 锐 角△ ABC内
一 点 ,使得 ADB= ACB+9O。,且 AC·BD = AD·BC,延 长 AD、BD、CD,分 别 与 △ ABC 的外接 圆 厂交 于点 G、E、F.
于是 ,a+b+C=200,且标 注数 1、2、3的
线段的数量分别为 bc、ca、ab.
贝0 n=a+bc=b+ca=c+r上6.
故 (n+6c)一(b+ca)=(a一6)(1一C)=0.
类fI 地 ,(b—c)(1一a)=(c—a)(1—6)=0.
若 a、b、C中 至 少 有 两 个 数 不 为 1,则 a=b=C,这与 3十200矛盾 ,也不可能 a=b=
最新北京市高中数学竞赛高一年级复赛试题资料

高一年级试题(120分钟)一、填空题(满分40分,每小题8分,将答案写在下面相应的空格中)1.函数f(x)=23x x-+-的值域是______.2.方程x2−31x+220=2x(31−2x−2x)所有实根的平方和等于______.3.边长等于10厘米的正六边形ABCDEF中,H为DE的中点,G为BC边上一点,且满足∠AGB=∠CGH,如图所示,则五边形AFEHG的面积是______平方厘米.4.已知甲、乙两个施工队各有若干工人,如果甲队借调给乙队90名工人,则乙队的工人总数将是甲队的2倍;如果乙队借调给甲队若干工人,则甲队的工人总数将是乙队的6倍.甲施工队原来最少有______名工人.5.在平面上有200个点,任何三个点都不共线,且每个点都标注了数1, 2, 3中的一个数,将标有不同数的所有点对都用线段连接,每条线段上都标注一个数1, 2或3,这个数与该线段端点标注的数不同,结果呈现出写在平面上的三个数1, 2或3中的每一个均恰有n次,则n的值是______.二、(满分15分)能够选出10个连续的偶数,且分它们为5个对子:(a1, b1), (a2, b2), (a3,b3), (a4, b4), (a5, b5),使得方程x2+a1x+b1=0, x2+a2x+b2=0, x2+a3x+b3=0, x2+a4x+b4=0,x2+a5x+b5=0都具有整数根吗?如果能,试举一例;如果不能,请说明理由.三、(满分15分)D为锐角三角形ABC内一点,使得∠ADB=∠ACB+90°且AC·BD=AD·BC.延长AD,BD,CD分别交三角形ABC的外接圆于点G,E,F,如图所示.求证:(1)EF=FG;(2)1=EFGABCπ三角形的面积三角形外接圆的面积.四、(满分15分)(1)证明:2018可以表示为两个正整数的平方和.(2)证明:存在这样的三角形,可以把它分割为2018个全等的三角形.五、(满分15分)已知n元正整数集A={a1, a2,…, a n},对任意一个i {1, 2, …, n},由集合A去掉元素a i后得到的集合A i可以分成两个不交的子集之并,且两子集元素之和相等,我们称这样的数集A为“好数集”.(1)求证:“好数集”的元素个数n是奇数;(2)求“好数集”的元素个数n的最小值.。
09年高一北京数学竞赛复赛参考解答
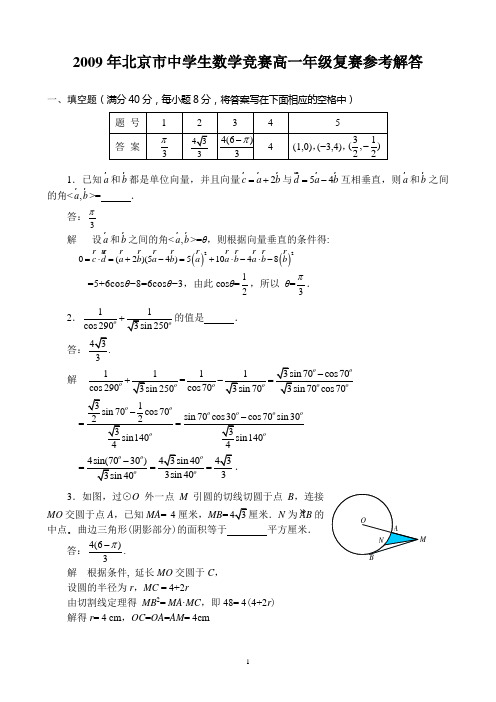
2009年北京市中学生数学竞赛高一年级复赛参考解答一、填空题(满分40分,每小题8分,将答案写在下面相应的空格中)1.已知a 和b 都是单位向量,并且向量2c a b =+ 与54d a b =- 互相垂直,则a 和b之间的角<,a b>= .答:3π解 设a 和b 之间的角<,a b>=θ,则根据向量垂直的条件得: ()()220(2)(54)51048c d a b a b a a b a b b =⋅=+-=+⋅-⋅-=5+6cos θ−8=6cos θ−3,由此cos θ=12,所以 θ=3π. 2.1cos 290的值是.答:3解 1cos 290+1cos70= 170cos 70-==s 0433= 3.如图,过⊙O 外一点M 引圆的切线切圆于点B ,连接MO交圆于点A ,已知MA = 4厘米,MB =N 为 AB的中点.曲边三角形(阴影部分)的面积等于 平方厘米.答:4(6)3π-.解 根据条件, 延长MO 交圆于C , 设圆的半径为r ,MC = 4+2r 由切割线定理得 MB 2= MA ·MC ,即48= 4(4+2r ) 解得r = 4 cm ,OC =OA =AM = 4cm连接OB ,在直角△OBM 中,sin MB MOB OM ∠===所以∠MOB =60°,因此 AB 为60°,而N 为 AB 的中点, 30AN = ,连接ON ,则∠MON =30°,所以111sin 30848222MON S OM ON ∆=⋅⋅⋅=⨯⨯⨯= (cm 2).而扇形AON 的面积230443603ππ=⨯=(cm 2),所以阴影图形的面积42444(6)8333πππ--=-==(cm 2). 4.的值是 . 答:4解 设x =则x 3=2020++-= 40+6x即 36400x x --= 观察之,4为方程的一个根,所以2(4)(410)0x x x -++= 由24410240∆=-⨯=-<,方程2410x x ++= 0无实根. 所以 方程36400x x --=只有唯一的实根4x = 即得证4x ==.5.在平面直角坐标系中,不论m 取何值时,抛物线y =mx 2+(2m +1)x −(3m +2)都不通过的直线y =−x +1上的点的坐标是 .(写出全部符合条件点的坐标)答:(1,0),(−3,4),41(,33- 解 由 y =mx 2+(2m +1)x −(3m +2)=m (x +3)(x −1)+(x −2)可知抛物线一定过点A (1, −1),B (−3, −5).过点A 、B 分别作y 轴的平行线交直线y =−x +1于点C (1, 0),D (−3, 4).过A 、B 两点的直线与直线y =−x +1交于点E 31(,22-. 则C 、D 、E 三点满足条件. 二、(满分15分)直角△ABC 内切圆的半径为r ,直角的平分线的长为t .求证:直角△ABC的两条直角边的长a 和b 是关于x 的一元二次方程222()20t x x tr -+-=的根.证明 设直角△ABC 中,∠C =90°,边长AB =c ,AC =b ,CB =a ,∠C 的平分线CD =t ,内切圆的圆心为O ,内切圆半径为r .连接OA ,OB ,OC ,S △ABC =12ab (1)又 S △ABC = S △ADC + S △BDC =12bt sin45°+12at sin45°t (a +b )所以, ab(a +b ) (2)……………………(5分)又 S △ABC = S △OBC + S △OAC + S △OAB =12r (a +b +c )=12r (a +b +a +b −2r )= r (a +b −r )= (a +b )r −r 2,与(1)比较得 ab =2(a +b )r −2r 2 (3)……………………(8分) 联立(2)与(3)解得a +b ,ab 得22a b ab +==……………………………(10分) 所以根据韦达定理,以a 和b 为根的一元二次方程为22x x =即方程 222()220t x r x t r -+-=.……………………………………………(15分) 三、(满分15分)求函数f :Z +→Z +,使得① f (1)=1;② 对于所有x , y ∈ Z +,()()()f x y f x f y xy +=++都成立.解 设函数f :Z +→Z +,满足① f (1)=1;② 对于所有x , y ∈ Z +,()()()f x y f x f y xy +=++ 对于正整数,n m ,下列的等式成立2(2)2()f n f n n =+2(3)()(2)2f n f n f n n =++, 2(4)()(3)3f n f n f n n =++, …… …… …… ……()2()()(1)(1)f mn f n f m n m n =+-+- 将上面的等式相加,得()2()()123(1)f mn mf n m n =+++++-由于(1)123(1)2m m m -++++-=, 所以2(1)()()2m m f mn mf n n -=+,对所有的正整数m 和n 都成立.………………(8分) 特别是,当n =1时(1)()2m m f m += (*)……………………………………(10分)等式(*)定义了在正整数集合上的函数f .因为1(11)(1)12f +== 22()(1)()()2()22x y x y x x y y xyf x y ++++++++==(1)(1)()()22x x y y xy f x f y xy ++=++=++所以(1)()2m m f m +=是问题的唯一解.…………………………………………… (15分)四、(满分15分)如图所示,在平行四边形ABCD 中,∠BAD 的平分线交BC 于点M ,交DC 的延长线于点N ,△CMN 的外心为O ,△CMN 的外接圆与△CBD 的外接圆的另一交点为K .证明:(1) 点O 在△CBD 的外接圆上; (2) ∠AKC =90°.证明 (1)由于平行四边形ABCD 中,∠BAD 的平分线交BC 于点M ,交DC 的延长线于点N ,所以∠BMA =∠MAD =∠BAM ,因此BA=BM ,同理可得MC=CN .连接OC ,则OC 平分∠NCM .连接OB ,OM ,OD ,设∠BAD = θ,则∠OCD =∠BCD +∠OCM = θ +12(180°−θ) = 90°+2θ∠BMO =180°−∠OMC =180°−∠OCM =90°+2θ,所以 ∠BMO =∠OCD .因此,△OBM ≌△ODC ,所以∠OBC =∠ODC .于是B ,O ,C ,D 四点共圆,也就是点O 在△CBD 的外接圆上.…(8分)(2) 由(1)知 BO=OD ,又KO=OC ,因为B ,K ,O ,C 和D 都在同一个圆上,则K ,C 关于BD 的中垂线对称,BK=CD=AB ,又∠KBD =∠CDB =∠ABD ,所以点K 与点A 是关于BD 的对称点,即AK ⊥BD ,而KC//BD ,所以AK ⊥KC ,即∠AKC =90°. ………………………………………………………………………………………………(15分) 五、(满分15分)证明,在任意给出的7个实数中,一定能找到两个实数x ,y ,使得 0≤1x y xy -+ 证明 设任意给出的7个实数为1234567,,,,,,a a a a a a a ,在,22ππ⎛⎫- ⎪⎝⎭内存在7个实数1234567,,,,,,θθθθθθθ,使得tan i i a θ= 其中(1,2,3,4,5,6,7)i =.…………………………(5分)将,22ππ⎛⎫- ⎪⎝⎭等分为6个长为6π的区间:,,,,0,0,,,,,2336666332ππππππππππ⎛⎫⎡⎤⎛⎫⎡⎤⎛⎤⎛⎫----- ⎪ ⎪ ⎪⎢⎥⎢⎥⎥⎝⎭⎣⎦⎝⎭⎣⎦⎝⎦⎝⎭, 根据抽屉原理,必存在,i j θθ属于同一个长为6π的小区间,………………………………(8分)不妨设i j θθ≥,则 06i j πθθ≤-≤,因此0t a n ()t a n 6ij πθθ≤-≤ …………………………………………(12分)即 t a n t a n 01t a n t a n3i j ij θθθθ-≤≤+令x =a i ,y =aj ,这样,我们从任意给出的7个实数中,找到了两实数x ,y ,使得 0≤1x y xy -+≤3.……………………………………………………………………………(15分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年北京市中学生数学竞赛高一年级复赛参考解答一、选择题(满分40分,每小题8分,将答案写在下面相应的空格中)1.二次三项式x 2+ax +b 的根是实数,其中a 、b 是自然数,且ab =22011,则这样的二次三项式共有个.答:1341.我们发现,实际上,数a 和b 是2的非负整数指数的幂,即,a =2k,b =22011–k,则判别式Δ=a 2– 4b =22k – 422011–k =22k – 22013–k ≥0,得2k ≥2013–k ,因此k ≥32013=671,但k ≤2011,所以k 能够取2011–671+1=1341个不同的整数值.每个k 恰对应一个所求的二次三项式,所以这样的二次三项式共有1341个.2.如右图,在半径为1的圆O 中内接有锐角三角形ABC ,H 是△ABC 的垂心,角平分线AL 垂直于OH ,则BC = .解:易知,圆心O 及垂心H 都在锐角三角形ABC 的内部,延长AO 交圆于N ,连接AH 并延长至H 1与BC 相交,连接CN ,在Rt △CAN 和Rt △AH 1B 中,∠ANC =∠ABC ,于是有∠CAN =∠BAH 1,再由AL 是△ABC 的角平分线,得∠1=∠2.由条件AP ⊥OH ,得AH=AO=1.连接BO 交圆于M ,连接AM 、CM 、CH ,可知AMCH 为平行四边形,所以CM=AH=AO =1,BM =2,因为△MBC 是直角三角形,由勾股定理得BC == 3.已知定义在R 上的函数f (x )=x 2和g (x )=2x +2m ,若F (x )=f (g (x )) – g (f (x ))的最小值为14,则m = .答:14-.解:由f (x )=x 2和g (x )=2x +2m ,得F (x )= f (g (x )) –g (f (x ))=(2x +2m )2–(2x 2+2m )=2x 2+8mx +4m 2–2m ,F (x )=2x 2+8mx +4m 2–2m 的最小值为其图像顶点的纵坐标()2222242(42)84284242m m m m m m m m ⨯⨯--=--=--⨯.由已知,21424m m --=,得21202m ⎛⎫+= ⎪⎝⎭,所以1.4m =-4.tan 37.5= . 答:6232-+-.解1:作Rt △ADB ,使得∠ADB =90º,AD =1,AB =2,则∠B =30º,BD =3.延长BD 到C ,使BC =2,则DC =23-.连接AC ,则∠ACB =(180º–30º)÷2=75º.作∠ACD 的平分线交AD 于E ,则∠ECD =37.5º.由于AC 2=AD 2+DC 2=1+(2–3)2=8–43,所以 ()2843621226262AC =-=-+=-=-.由三角形的角平分线定理,得AE AC ED DC=,于是AE ED AC DCED DC ++=,即()()()()322162233221ED AD DC AC CD ====-++-+-+-,所以()()tan 37.53221EDDC==-+6232=-+-.解2:作等腰直角三角形ABC ,使∠C =90º,AC =BC =1,则AB =2. 作∠CAD =30º,则CD =3,AD =23,则∠DAB =15º. 作∠BAD 的平分线AE ,记CE =x ,则BE =1–x ,DE =x –33. 所以33232x -=,整理得 ()()213221623 2.3232x +-+===-+--+tan 37.562321CE xAC ===-+-. 5.设f (x ) =113xx+-,定义f 1(x ) = f (f (x )),f n (x )=f (f n –1(x )) (n =2, 3,…),f 2011(2011)= . 答:10053017.A21 30º解:记01()()13x f x f x x +==-,则()111113()()1131313xx x f x f f x x x x++--===--+-⋅-; ()211113()()11313xx f x f f x x x x--+===-+⋅+;()3201()()()()13x f x f f x f x f x x +====-; 接下来有41()()f x f x =,52()()f x f x =,63()()f x f x =,…,f n (x )的表达式是循环重复的,以3项为一周期.所以,20113670111()()()13x f x f x f x x ⨯+-===+,20112011120101005(2011)13201160343017f -===+⨯.二、(满分15分)D 是正△ABC 的边BC 上一点,设△ABD 与△ACD 的内心分别为I 1,I 2,外心分别为O 1,O 2,求证:(I 1O 1)2+(I 2O 2)2=(I 1I 2)2. 证明:作以A 为中心、逆时针旋转60的变换(,60)R A ,使△ABD 到△ACD 1,由于∠ADC +∠AD 1C =∠ADC +∠ADB =180º,所以A 、D 、C 、D 1共圆,因此2O 是△AD 1C 的外心,也就是(,60)12R A O O −−−−→,因此AO 1=DO 1=AO 2=DO 2=O 1O 2,所以∠O 1AO 2=∠O 1DO 2=60º.由∠AO 1O 2+∠ACB =120º+60º=180º,O 1在△ACD 的外接圆⊙O 2上.由于111(180)6012012022AI D ABD ABD ∠=∠+-∠=+⨯=,所以I 1在⊙O 2上,因此11118018030150O I D O AD ∠=-∠=-=,111118015030I O D I DO ∠+∠=-=.同理可证,I 2在△ABD 的外接圆⊙O 1上,所以22150DI O ∠=.由于12118090,2I DI ∠=⨯=而22111212906030I DO I DO I DI O DO ∠+∠=∠-=-=,比较可得1122I O D I DO ∠=∠.在△O 1I 1D 与△DI 2O 2中,因为已证O 1D=DO 2,1122150,O I D DI O ∠=∠=又1122.I O D I DO ∠=∠因此 △O 1I 1D ≌△DI 2O 2.所以,I 1O 1=DI 2,DI 1= I 2O 2.由于1290,I DI ∠=△I 1DI 2是直角三角形.根据勾股定理,有()()()2221212,DI DI I I +=而I 1O 1=DI 2,DI 1=I 2O 2. 因此()()()222112212.I O I O I I +=1三、(满分15分)n 是正整数,记n !=1×2×3×…×n ,如1!=1,2!=1×2=2,3!= 1×2×3=6,又记[a ]表示不超过a 的最大整数,求方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的所有正整数解.解1:由于当x 是正整数时,[]1!x x ⎡⎤=⎢⎥⎣⎦,2!2x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦≥12x -,3!6x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦>6x –1,所以1126x x x -++-<2011即53x <120122,得方程的正整数解x 满足0<x <1207.5. 由于6!=720,7!=5040,所以方程的正整数解x <7!,即07!8!9!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦. 因此,方程20111!2!3!4!5!6!x x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的解与原方程的解是一样的.设小于7!的正整数x 为上述方程的解,我们写出(1,2,3,4,5,6)!xk k =的带余除法表达式:设16!6!r x a =+,0≤r 1<6!,(0≤a ≤6,a ÎN );因此.6!x a ⎡⎤=⎢⎥⎣⎦① 12665!5!5!r r x a a b =+=++,0≤r 2<5!,(0≤b ≤5,b ÎN ),因此65!x a b ⎡⎤=+⎢⎥⎣⎦. ② 323053054!4!4!r r xa b a b c =++=+++,0≤r 3<4!,(0≤c ≤4,c ÎN ), 因此3054!x a b c ⎡⎤=++⎢⎥⎣⎦. ③341202*********!3!3!r r xa b c a b c d =+++=++++,0≤r 4<3!,(0≤d ≤3,d ÎN ); 因此1202043!x a b c d ⎡⎤=+++⎢⎥⎣⎦. ④5436060123360601232!2!2!r r xa b c d a b c d e =++++=+++++,0≤r 5<2, (e =0,1,2);因此360601232!x a b c d e ⎡⎤=++++⎢⎥⎣⎦. ⑤5720120246272012024621!1!r xa b c d e a b c d e f =+++++=+++++,(f =0,1); 因此72012024621!x a b c d e f ⎡⎤=+++++⎢⎥⎣⎦. ⑥①~⑥相加得1237a +206b +41c +10d +3e +f =2011.显然a =1,因此206b +41c +10d +3e +f =2011–1237=774; 易知b =3,因此41c +10d +3e +f =774–206×3=156; 易知c =3,于是10d +3e +f =156–41×3=33; 类似求得d =3,e =1,f =0.所求的x =1×720+3×120+3×24+3×6+1×2+0×1=1172.x =1172是方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的唯一正整数解. 解2:设f (x )=1!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,因为对于所有的正整数k ,!x k ⎡⎤⎢⎥⎣⎦都是单调增的,其和f (x )就是增函数;又因为对于正整数x ,11!x +⎡⎤⎢⎥⎣⎦=1!x ⎡⎤⎢⎥⎣⎦+1,所以f (x )是严格单调的.经估数,将x =1172带入,求f (1172)的值,得f (1172)=2011,所以,x =1172是方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的唯一正整数解.四、(满分15分)平面上的n 个点,若其中任3个点中必有2个点的距离不大于1,则称这样的n 个点为“标准n 点组”.要使一个半径为1的圆纸片,对任意“标准n 点组”都能至少盖住其中的25个点,试求n 的最小值. 答案:49.解:首先证明,n min >48.在平面上画长为5的线段AB ,分别以A 、B 为圆心,画半径为0.5的两个圆,在每一个圆内,取24个点,则平面上有48个点满足题设条件(其中任意3点中必有2点的距离不大于1),显然,不可能画出一个半径为1的圆,其包含有25个所选的点,所以n >48.下面证明n min =49.若49=n ,设A 是其中的一点,作以A 为圆心半径为1的⊙A ,若所有的点都在圆A 中,那么就满足题设条件.若不是所有的点都在圆A 中,则至少有一点B 不在圆A 中,再作以B 为圆心、半径为1的⊙B ,则A 、B 的距离大于1(如右图),除A ,B 外,余下的47个点中每一点P 都与A 、B 组成3点组,必有两个点的距离不大于1,所以要么PA ≤1,要么PB ≤1,即 点P 要么在⊙A 中,要么在⊙B 中,根据抽屉原理,必有一个圆至少包含了这47个点中的24个点,不妨设这个圆就是⊙A ,再加上圆心A点,就有不少于25个点在这个半径为1的⊙A 中(圆内或圆周上).所以n 的最小值是49.五、(满分15分)已知函数f :R →R ,使得对任意实数x y z ,,都有11()()()()22f xy f xz f x f yz +-≥14, 求[1×f (1)]+[2×f (2)]+[3×f (3)]+…+[2011×f (2011)]的值.其中对于实数a ,[a ]表示不超过a 的最大整数.解:由于已知函数f R R →:,使得对任意实数x y z ,,都满足11()()()()22f xy f xz f x f yz +-≥14,可令0x y z ===,有 ()211(0)(0)(0)22f f f +-≥14,即21(0)2f ⎛⎫- ⎪⎝⎭≤0, 由于f (0)是一个实数,所以1(0).2f =再令1x y z ===,有()211(1)(1)(1)22f f f +-≥14,即21(1)2f ⎛⎫- ⎪⎝⎭≤0, 由于f (1)是一个实数,所以1(1).2f =又令0y z ==,有11(0)(0)()(0)22f f f x f +-≥14,代入1(0)2f =得对任意实数x ,都有()f x ≤12. ①又令1y z ==,有11()()()(1)22f x f x f x f +-≥14,代入1(1)2f =得对任意实数x ,都有()f x ≥12. ②综合①、②可得,对任意实数x ,都有1()2f x =.验证:函数1()2f x =满足题设条件,取的是等号,所以满足题设条件的函数的唯一解为1()2f x =.于是[][][][]1(1)2(2)3(3)2011(2011)f f f f ⨯+⨯+⨯++⨯1234201122222⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦011223310051005=+++++++++()=⨯++++21231005=+⨯(11005)10051011030=.(注:可编辑下载,若有不当之处,请指正,谢谢!)。
