考研数学线代知识框架
线性代数知识点全归纳

线性代数知识点全归纳线性代数是数学的一个重要分支,研究向量空间及其上的线性映射。
它广泛应用于物理、工程、计算机科学等领域。
下面将对线性代数的主要知识点进行全面归纳。
1.矩阵及其运算:矩阵是线性代数的基本概念之一,由若干行和列组成的方阵。
常见的矩阵运算有加法、减法、数乘、矩阵乘法和转置等。
2.向量及其运算:向量是一个有序数组,具有大小和方向。
常见的向量运算有加法、减法、数乘、点乘和叉乘等。
3.线性方程组:线性方程组是线性代数的核心内容之一、包括齐次线性方程组和非齐次线性方程组。
解线性方程组的方法有高斯消元法、克莱姆法则和矩阵求逆等。
4.向量空间与线性变换:向量空间是线性代数的基本概念之一,包含零向量、加法和数乘运算。
线性变换是一种保持向量空间结构的映射。
5.基与维度:基是向量空间的一组线性无关向量,可以由基线性组合得到向量空间中的任意向量。
维度是向量空间中基的数量。
6.线性相关与线性无关:向量组中的向量线性相关指存在非零的线性组合,其系数不全为零。
如果向量组中的向量线性无关,则任何线性组合的系数都为零。
7.线性变换与矩阵:线性变换可以用矩阵表示,矩阵的列向量表示线性变换作用于基向量上后的结果。
矩阵乘法可以将多个线性变换组合为一个线性变换。
8.特征值与特征向量:对于一个线性变换,如果存在一个非零向量,使得它在该线性变换下只发生伸缩而不发生旋转,那么这个向量称为该线性变换的特征向量,对应的伸缩比例为特征值。
9.二次型与正定矩阵:二次型是线性代数中的重要概念,是一个关于变量的二次函数。
正定矩阵是指二次型在所有非零向量上的取值都大于零。
10.内积与正交性:内积是向量空间中的一种运算,它满足线性性、对称性和正定性。
正交性是指两个向量的内积为零,表示两个向量互相垂直。
11.正交变换与正交矩阵:正交变换是指保持向量长度和向量之间夹角的变换。
正交矩阵是一种特殊的方阵,它的行向量和列向量两两正交,并且长度为112.奇异值分解与特征值分解:奇异值分解将一个矩阵分解为三个矩阵的乘积,其中一个是正交矩阵,另外两个是对角矩阵。
线性代数基础知识

线性代数基础知识导言:线性代数是现代数学的重要分支之一,广泛应用于数学、物理、工程、计算机科学等领域。
本文将介绍线性代数的基本概念、运算规律和应用,以帮助读者建立对线性代数的基础知识。
一、向量与向量空间1.1 向量的定义与性质向量是具有大小和方向的量,可以用有序数对或矩阵形式表示。
向量的加法与数量乘法满足交换律、结合律和分配律等基本性质。
1.2 向量空间的定义与性质向量空间是由一组向量和运算规则构成的数学结构,包括加法和数量乘法运算。
向量空间满足加法和数量乘法的封闭性、结合律、分配律以及零向量和负向量的存在等性质。
二、矩阵与线性方程组2.1 矩阵的定义与性质矩阵是由一组数按照矩形排列组成的数学对象,可以表示为一个二维数组。
矩阵的加法与数量乘法满足交换律、结合律和分配律等基本性质。
2.2 线性方程组的表示与求解线性方程组可以用矩阵和向量表示,形式为Ax=b。
其中,A为系数矩阵,x为未知向量,b为常数向量。
线性方程组的解可以通过消元法、矩阵的逆或行列式等方法求得。
三、线性变换与特征值特征向量3.1 线性变换的定义与性质线性变换是指一个向量空间到另一个向量空间的映射,保持向量加法和数量乘法运算。
线性变换满足加法封闭性、乘法封闭性和保持零向量不变等性质。
3.2 特征值与特征向量线性变换的特征值和特征向量是线性变换的重要性质。
特征值为标量,特征向量为非零向量,满足Av=λv。
其中,A为线性变换的矩阵表示,λ为特征值,v为对应的特征向量。
四、内积空间与正交性4.1 内积空间的定义与性质内积空间是一个向量空间,具有额外定义的内积运算。
内积满足对称性、线性性、正定性和共轭对称性等性质。
4.2 正交性与正交基在内积空间中,若两个向量的内积为零,则它们互为正交。
正交基是一个向量空间中的基,其中任意两个基向量互相正交。
五、特殊矩阵与特殊向量5.1 对称矩阵与正定矩阵对称矩阵是满足A^T=A的矩阵,其中A^T为A的转置矩阵。
线性代数知识结构框架

第一章:行列式考试内容:行列式的概念和基本性质行列式按行(列)展开定理考试要求:1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.第二章:矩阵考试内容:矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵等价分块矩阵及其运算考试要求:1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件,理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.理解矩阵的初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.第三章:向量考试内容:向量的概念向量的线性组合和线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量空间以及相关概念n维向量空间的基变换和坐标变换过渡矩阵向量的内积线性无关向量组的正交规范化方法规范正交基正交矩阵及其性质考试要求:1.理解n维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.理解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.理解向量组等价的概念,理解矩阵的秩与其行(列)向量组的秩之间的关系5.了解n维向星空间、子空间、基底、维数、坐标等概念.6.了解基变换和坐标变换公式,会求过渡矩阵.7.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.8.了解规范正交基、正交矩阵的概念以及它们的性质.第四章:线性方程组考试内容:线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解解空间非齐次线性方程组的通解考试要求l.会用克莱姆法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系、通解及解空间的概念,掌握齐次线性方程组的基础解系和通解的求法.4.理解非齐次线性方程组解的结构及通解的概念.5.掌握用初等行变换求解线性方程组的方法.第五章:矩阵的特征值及特征向量考试内容:矩阵的特征值和特征向量的概念、性质相似变换、相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值、特征向量及相似对角矩阵考试要求:1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵的特征值和特征向量. 2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,掌握将矩阵化为相似对角矩阵的方法.3.掌握实对称矩阵的特征值和特征向量的性质.第六章:二次型考试内容:二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求:1.掌握二次型及其矩阵表示,了解二次型秩的概念,了解合同变化和合同矩阵的概念了解二次型的标准形、规范形的概念以及惯性定理.2.掌握用正交变换化二次型为标准形的方法,会用配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法概率与统计第一章:随机事件和概率考试内容:随机事件与样本空间事件的关系与运算完备事件组概率的概念概率的基本性质古典型概率几何型概率条件概率概率的基本公式事件的独立性独立重复试验考试要求:1.了解样本空间(基本事件空间)的概念,理解随机事件的概念,掌握事件的关系与运算.2.理解概率、条件概率的概念,掌握概率的基本性质,会计算古典型概率和几何型概率,掌握概率的加法公式、减法公式、乘法公式、全概率公式,以及贝叶斯(Bayes)公式.3.理解事件的独立性的概念,掌握用事件独立性进行概率计算;理解独立重复试验的概念,掌握计算有关事件概率的方法.第二章:随机变量及其分布考试内容:随机变量随机变量的分布函数的概念及其性质离散型随机变量的概率分布连续型随机变量的概率密度常见随机变量的分布随机变量函数的分布考试要求:1.理解随机变量的概念.理解分布函数的概念及性质.会计算与随机变量相联系的事件的概率.2.理解离散型随机变量及其概率分布的概念,掌握0-1分布、二项分布、几何分布、超几何分布、泊松(Poisson)分布及其应用.3.了解泊松定理的结论和应用条件,会用泊松分布近似表示二项分布.4.理解连续型随机变量及其概率密度的概念,掌握均匀分布、正态分布、指数分布及其应用,其中参数为λ(λ>0)的指数分布的概率密度为5.会求随机变量函数的分布.第三章:多维随机变量及其分布考试内容:多维随机变量及其分布二维离散型随机变量的概率分布、边缘分布和条件分布二维连续性随机变量的概率密度、边缘概率密度和条件密度随机变量的独立性和不相关性常用二维随机变量的分布两个及两个以上随机变量简单函数的分布考试要求:1.理解多维随机变量的概念,理解多维随机变量的分布的概念和性质. 理解二维离散型随机变量的概率分布、边缘分布和条件分布;理解二维连续型随机变量的概率密度、边缘密度和条件密度.会求与二维随机变量相关事件的概率.2.理解随机变量的独立性及不相关性的概念,掌握随机变量相互独立的条件. 3.掌握二维均匀分布,了解二维正态分布的概率密度,理解其中参数的概率意义.4.会求两个随机变量简单函数的分布,会求多个相互独立随机变量简单函数的分布。
考研线性代数知识点全面总结

《线性代数》复习提纲第一章、行列式(值,不是矩阵)1.行列式的定义:用2n 个元素ija 组成的记号称为n 阶行列式。
(1)它表示所有可能的取自不同行不同列的n 个元素乘积的代数和; (2)展开式共有n!项,其中符号正负各半; 2.行列式的计算一阶|α|=α行列式,二、三阶行列式有对角线法则; N 阶(n ≥3)行列式的计算:降阶法定理:n 阶行列式的值等于它的任意一行(列)的各元素与其对应的代数余子式乘积的和。
方法:选取比较简单的一行(列),保保留一个非零元素,其余元素化为0,利用定理展开降阶。
特殊情况:上、下三角形行列式、对角形行列式的值等于主对角线上元素的乘积;◊行列式值为0的几种情况:Ⅰ 行列式某行(列)元素全为0; Ⅱ 行列式某行(列)的对应元素相同;Ⅲ 行列式某行(列)的元素对应成比例; Ⅳ 奇数阶的反对称行列式。
3.概念:全排列、排列的逆序数、奇排列、偶排列、余子式ijM 、代数余子式ijj i ijM A+-=)1(定理:一个排列中任意两个元素对换,改变排列的奇偶性。
奇排列变为标准排列的对换次数为基数,偶排列为偶数。
n 阶行列式也可定义:nq q q n a aa⋯=∑21t211-D )(,t 为nq q q ⋯21的逆序数4.行列式性质:1、行列式与其转置行列式相等。
2、互换行列式两行或两列,行列式变号。
若有两行(列)相等或成比例,则为行列式0。
3、行列式某行(列)乘数k,等于k 乘此行列式。
行列式某行(列)的公因子可提到外面。
4、行列式某行(列)的元素都是两数之和,则此行列式等于两个行列式之和。
5、行列式某行(列)乘一个数加到另一行(列)上,行列式不变。
6、行列式等于他的任一行(列)的各元素与其对应代数余子式的乘积之和。
(按行、列展开法则)7、行列式某一行(列)与另一行(列)的对应元素的代数余子式乘积之和为0.5.克拉默法则::若线性方程组的系数行列式0D ≠,则方程有且仅有唯一解DD D Dx D D n =⋯==n 2211x ,x,,。
线代必备资料:线性代数知识框架(word版)

分块对角阵相乘: A
A11
B11 , B A22
*
B22 AB*
A B AB 11 11
A22 B22
A BA* 分块对角阵的伴随矩阵: B
√ 矩阵方程的解法( A 0 ):设法化成(I)AX B
1 , 2 , , s 线性无关; 1 , 2 , , s 都是 Ax 0 的解;
③ s n r ( A) 每个解向量中自由未知量的个数 .
5
√ 一个齐次线性方程组的基础解系不唯一.
1 2 3 4 5
零向量是任何向量的线性组合,零向量与任何同维实向量正交. 单个零向量线性相关;单个非零向量线性无关. 部分相关,整体必相关;整体无关,部分必无关. 原向量组无关,接长向量组无关;接长向量组相关,原向量组相关. 两个向量线性相关 对应元素成比例;两两正交的非零向量组线性无关 p教材114 . 向量组 1 , 2 , , n 中任一向量 i (1 ≤ i ≤ n) 都是此向量组的线性组合. 向量组 1 , 2 , , n 线性相关 向量组中至少有一个向量可由其余 n 1 个向量线性表示. 向量组 1 , 2 , , n 线性无关 向量组中每一个向量 i 都不能由其余 n 1 个向量线性表示.
T
CT Dห้องสมุดไป่ตู้
A1 A 分块矩阵的逆矩阵: B A1 A C O B O
1
1
1 B A1CB 1 B
B
A 1 A
1
1
B 1
A1 O A O 1 1 B C B B CA
考研线代知识点

考研线性代数知识点是考研数学科目中的重要内容之一。
线性代数是数学的一个分支,主要研究向量空间、线性变换、矩阵等概念和性质。
在考研中,线性代数的知识点有一定的难度,需要考生们进行系统的学习和掌握。
下面将介绍考研线性代数知识点的学习思路,帮助考生们更好地理解和掌握这一门学科。
第一步:基础知识的学习线性代数的基础知识包括向量、矩阵、行列式等概念。
首先,我们需要了解向量的定义和性质。
向量是具有大小和方向的量,可以用有序数对或有序数组来表示。
在学习向量的过程中,我们要掌握向量的加法、减法、数量乘法等基本运算规则。
其次,矩阵是线性代数中的重要概念。
我们需要学习矩阵的定义、矩阵的加法、减法、乘法等运算规则,并理解矩阵转置、逆矩阵等重要概念。
同时,还要学习矩阵的行列式和特征值、特征向量等性质。
第二步:线性方程组的求解线性方程组是线性代数中的基本问题之一。
我们需要学习如何解线性方程组。
首先,要学习高斯消元法、克拉默法则等常用的线性方程组求解方法。
通过这些方法,可以求解二元一次方程组、三元一次方程组等简单的线性方程组。
此外,我们还需要学习矩阵的初等变换和矩阵的秩的概念。
通过初等变换,可以将线性方程组化为阶梯形或行简化阶梯形,从而求解线性方程组。
而矩阵的秩则可以帮助我们判断线性方程组是否有解,以及求解线性方程组的解的个数。
第三步:线性空间和线性变换线性空间是线性代数的核心概念之一。
我们需要学习什么是线性空间,线性空间的性质以及线性空间的基和维数等重要概念。
此外,还需要掌握线性空间的子空间和线性相关、线性无关等概念。
线性变换是线性代数中的另一个重要概念。
我们需要学习线性变换的定义和性质,以及线性变换的矩阵表示和标准基下的矩阵形式等内容。
同时,还要学习线性变换的核和像的概念,以及线性变换的特征值和特征向量等内容。
第四步:特征值和特征向量的应用特征值和特征向量是线性代数中的重要概念,具有广泛的应用。
我们需要学习如何计算矩阵的特征值和特征向量,并理解它们的几何意义。
考研数学线性代数重点整理

考研数学线性代数重点整理一、矢量空间矢量空间是线性代数的基础概念,它描述了一组对象(称为矢量)的性质及其之间的运算规则。
以下是矢量空间的一些重要性质和定义:1. 定义:矢量空间是满足以下8个条件的集合V,其中两个运算(加法和乘法)满足特定的性质。
2. 加法:对于任意的矢量u和v,它们的和u+v也是V中的一个矢量。
3. 加法交换律:对于任意的矢量u和v,有u+v = v+u。
4. 加法结合律:对于任意的矢量u、v和w,有(u+v)+w = u+(v+w)。
5. 加法单位元:存在一个称为零矢量的特殊矢量0,对于任意的矢量v,有v+0 = 0+v = v。
6. 加法逆元:对于任意的矢量v,存在一个称为负矢量的特殊矢量-u,使得v+(-u) = (-u)+v = 0。
7. 乘法定义:对于任意的矢量v和实数c,cv也是V中的一个矢量。
8. 乘法分配律:对于任意的矢量v和实数c和d,有c(dv) = (cd)v。
9. 乘法单位元:对于任意的矢量v,有1v = v。
二、矩阵与线性方程组矩阵是线性代数中另一个重要的概念,它可以用来表示线性方程组和线性变换。
以下是与矩阵和线性方程组相关的一些重要内容:1. 矩阵定义:将数按矩形排列成的矩形数表称为矩阵,其中行数和列数分别称为矩阵的行数和列数。
2. 矩阵运算:矩阵之间可以进行加法和乘法的运算,具体规则如下:- 矩阵加法:对应位置元素相加。
- 矩阵乘法:设A是一个m×n矩阵,B是一个n×p矩阵,那么它们的乘积AB是一个m×p矩阵,乘法规则为A的行乘以B的列。
3. 线性方程组:线性方程组是一组线性方程的集合,矩阵可以用来表示和求解线性方程组。
对于一个m×n矩阵A、一个n×1矩阵X和一个m×1矩阵B,线性方程组可以表示为AX=B。
4. 线性方程组的解:根据矩阵的性质,可以通过高斯消元法、矩阵求逆等方法求解线性方程组。
考研数学之线性代数讲义(考点知识点+概念定理总结)

考研数学之线性代数讲义(考点知识点+概念定理总结)线性代数讲义目录第一讲基本概念矩阵的初等变换与线性矩阵方程的消去完全展开式化零降阶法其它性质克莱姆法则第三讲矩阵乘积矩阵的列向量和行向量矩阵分解矩阵方程逆矩阵伴随矩阵第4讲向量组线性表示向量组的线性相关性向量组的极大无关组和秩矩阵的秩第五讲方程组解的性质解的判别基本解系统和通解第6讲特征向量和特征值的相似性和对角化特征向量与特征值―概念,计算与应用相似对角化―判断与实现附录一内积正交矩阵施密特正交化实对称矩阵的对角化第七讲二次型二次型及其矩阵可逆线性变量取代了实对称矩阵惯性指数正定二次型与正定矩阵的合同标准化与规范化附录二向量空间及其子空间附录III两个线性方程组的解集之间的关系附录四06,07年考题一第一讲基本概念1.线性方程组的基本概念。
线性方程组的一般形式是:a11x1+a12x2++a1nxn=b1,a21x1+a22x2+?+a2nxn=b2,????am1x1+am2x2+?+amnxn=bm,其中未知数的个数n和方程式的个数m不必相等.线性方程组的解是一个n维向量(k1,k2,k,kn)(称为解向量),它满足当每个方程中的未知数席被Ki替换时,它变成一个方程。
线性方程组的解的情况有三种:无解,唯一解,无穷多解.在线性方程组的讨论中有两个主要问题:(1)判断解(2)求解,特别是当存在无穷多个连接时求通解b1=b2=?=bm=0的线性方程组称为齐次线性方程组.n维零向量总是齐次线性方程组的解,称为零解。
因此,齐次线性方程组只有两种解:唯一解(即只要零解)和无限解(即非零解)把一个非齐次线性方程组的每个方程的常数项都换成0,所得到的齐次线性方程组称为原方程组的导出齐次线性方程组,简称导出组.2.矩阵和向量(1)基本概念矩阵和向量都是描写事物形态的数量形式的发展.是M吗?一张表有M行和N列,以N个数字排列,两边用括号或方括号括起来,就变成了M?例如N型矩阵2-101111102254-29333-18是4吗?5矩阵对于上述线性方程组,它被称为矩阵a11a12?a1na11a12?a1nb1a=a21a22?a2n和(a|?)=a21a22?a2nb2??????? am1am2?amnam1am2?amnbm为其系数矩阵和增广矩阵.增广矩阵体现了方程组的全部信息,而齐次方程组只用系数矩阵就体现其全部信息.矩阵中的数字称为其元素,第I行和第J列中的数字称为(I,J)位元素所有元素为0的矩阵称为零矩阵,通常记录为0两个矩阵a和b相等(记作a=b),是指它的行数相等,列数也相等(即它们的类型相同),并且对应的元素都相等.N个数的有序数组称为N维向量,这些数称为其分量书写中可用矩阵的形式来表示向量,例如分量依次是a1,a2,?,an的向量可表示成二a1(a1,a2,?,an)或a2,┆an请注意,作为向量它们并没有区别,但是作为矩阵,它们不一样(左边是1?n矩阵,右边是n?1矩阵).习惯上把它们分别称为行向量和列向量.(请注意与下面规定的矩阵的行向量和列向量概念的区别.)一个M?n的矩阵的每一行是一个n维向量,称为其行向量;每一列都是一个m维向量,称为它的列向量。
考研数学线代主要考点及要求

考研数学线性代数主要考点及要求前言线性代数是数学中的重要分支学科,几乎存在于所有数学应用领域。
在考研中,线性代数占有相当的比重,因此无论是对于数学专业考生还是非数学专业考生,都需要充分了解这一学科的主要考点与要求。
本文将详细介绍考研数学线性代数的主要考点以及历年考研数学中线性代数的考察情况,旨在为考生提供参考。
主要考点考研数学线性代数的主要考点如下:1.向量空间2.矩阵论3.行列式理论4.线性方程组5.特征值与特征向量6.内积空间下面将分别进行介绍。
向量空间向量空间是线性代数的核心概念,它是定义了向量加法和数乘运算的集合。
在考研中,需要掌握向量空间的基本定义及其相关概念,例如:•向量空间的基本性质•子空间的定义及判定•线性无关、极大线性无关子集、基的定义及其定理•维数的概念及相应的判别定理矩阵论矩阵论是线性代数中的一个重要组成部分,它主要涉及矩阵的定义、运算规则与性质,以及相关的定理。
在考研中,需要掌握以下几个方面的知识:•矩阵的基本概念与运算规则•行、列、秩、行列式的概念与计算方法•矩阵的逆、转置与伴随矩阵的定义及其计算方法•利用矩阵的运算规则与性质简化计算行列式理论行列式是矩阵论中的一个重要概念,它具有很多重要的性质与应用,例如:•行列式的定义与计算方法•行列式的性质,如交换性、性质、加减性等•Cramer法则及其应用线性方程组线性方程组是线性代数中的重要内容,它应用广泛,是解决实际问题中常用的一种数学方法。
在考研中,需要掌握以下几个方面的知识:•线性方程组的一般形式与矩阵形式•线性方程组的基本概念,如解的存在唯一性等•系数矩阵、增广矩阵与阶梯形矩阵间的关系及计算方法•利用初等变换化简线性方程组特征值与特征向量特征值与特征向量是线性代数中的核心概念,它们在科学工程、金融数学、信息学等领域中有广泛的应用。
在考研中,需要掌握以下几个方面的知识:•特征值与特征向量的概念及其性质•特征值与特征向量的计算方法•矩阵的相似与对角化•求解线性微分方程组内积空间内积空间是线性代数中的一个重要概念,它是定义了两个向量之间的乘积。
(完整版)线代知识点总结-数学一

线性代数知识点、难点1、n 阶行列式的定义 对于n 阶行列式的定义,重点应把握两点:一是每一项的构成,二是每一项的符号。
每一项的构成是不同行不同列的n 个元素构成,一个n 阶行列式共有!n 项。
乘积项为1212...n j j nj a a a 的符号取决于12,,...n j j j 的逆序数,即当12,,...n j j j 为偶排列时取正号,当12,,...n j j j 为奇排列时取负。
例1 行列式 3122D =为二阶行列式,每一项由2个元素构成,第一项为3*2,符号为正,第二项为1*2,符号为负。
2、余子式和代数余子式余子式和代数余子式的概念容易出错,在计算中应注意。
代数余子式(1)i j ij ij A M +=-,其中ij M 为余子式。
一般这类题,重点考察对代数余子式的理解和其基本性质的应用,所以考生一定要灵活掌握,掌握基本思想。
下面请看一例: 例2 设行列式3040222207005322D =--则第4行元素余子式之和的值为__________ 【分析】4142434441424344M M M M A A A A +++=-+-+3230403402222(7)(1)22228071111111+==--=------部分考生答案为0。
原因是将余子式和代数余子式混淆了。
本题中第四行元素的代数余子式之和为0。
因为41424344414243441(2222)02A A A A A A A A +++=+++=。
3、行列式按一行(列)展开设()ij n n A a ⨯=,则1122||,...0,i j i j in jn A i ja A a A a A i j=⎧+++=⎨≠⎩ 或1122||,...0,i j i j ni nj A i ja A a A a A i j =⎧+++=⎨≠⎩注意:公式中使用的是代数余子式,而不是余子式。
4、行列式的计算 行列式的基本计算方法有三个:例21 归化 利用行列式的性质将行列式化成较简单且易于计算的行列式(如三角行列式等);例22 降阶 利用行列式的展开定理,将高阶行列式化成低阶行列式进行计算。
考研线代知识点总结

考研线代知识点总结摘要:一、考研线性代数知识点概述二、矩阵与线性方程组三、向量空间与线性变换四、特征值与特征向量五、二次型与矩阵的对称性六、复习与拓展建议正文:一、考研线性代数知识点概述考研线性代数作为数学一门重要学科,主要包括矩阵、线性方程组、向量空间、线性变换、特征值与特征向量、二次型与矩阵的对称性等内容。
这些知识点在考研数学中占有很大比重,因此,对于线性代数的掌握程度直接影响到考研成绩。
本文将对这些知识点进行总结,以帮助考生更好地复习和掌握线性代数。
二、矩阵与线性方程组1.矩阵的运算:加法、减法、数乘、矩阵乘法、逆矩阵、行列式等。
2.线性方程组的解法:高斯消元法、克莱姆法则、齐次线性方程组、非齐次线性方程组等。
3.矩阵的秩、行阶梯形式、简化阶梯形式等。
三、向量空间与线性变换1.向量空间的概念、基、维数、向量模等。
2.线性变换的概念、性质、矩阵表示、不变量等。
四、特征值与特征向量1.特征值、特征向量的概念及求解方法。
2.矩阵的对角化、相似矩阵等。
五、二次型与矩阵的对称性1.二次型的概念、标准型、正定二次型、负定二次型、半正定二次型、半负定二次型等。
2.矩阵的对称性:对称矩阵、反对称矩阵、正交矩阵、对称分量等。
六、复习与拓展建议1.熟练掌握考研线性代数大纲要求的知识点,做到深入理解、熟练应用。
2.针对自己的薄弱环节进行有针对性的练习,提高解题能力。
3.学习线性代数相关的拓展知识,如奇异值分解、广义逆矩阵、线性空间论等。
4.注重理论联系实际,熟练运用线性代数知识解决实际问题。
总之,考研线性代数知识点繁多,要想在考试中取得好成绩,就需要扎实掌握这些知识点,并不断提高自己的解题能力。
考研数学一详细知识点总结

考研数学一详细知识点总结一、线性代数1. 行列式行列式是线性代数中的一个重要概念,它是一个具有特定数学性质的标量函数,它可以对矩阵进行某种代数计算,得到一个数。
通过行列式的性质和运算法则,我们可以求解线性方程组的解,判断矩阵的逆矩阵是否存在等。
行列式的基本定义、性质和运算法则是线性代数中的重要基础知识点。
2. 矩阵与向量空间矩阵是线性代数中的另一个重要概念,它是一个矩形数组,它是向量空间的一种表达形式。
矩阵的定义、运算法则、转置矩阵、伴随矩阵、特征值和特征向量等都是线性代数中的重要知识点。
3. 线性变换与矩阵的相似变换线性变换是线性代数中的一个重要概念,它是定义在向量空间上的一个运算,将一个向量空间中的一个向量映射到另一个向量空间中的一个向量。
线性变换与矩阵的相似变换在数学和工程中有着广泛的应用,对于理解线性代数的基本概念和运用都具有重要意义。
4. 线性方程组线性方程组是线性代数中的一个重要概念,它是由一系列线性方程构成的方程组。
通过行列式和矩阵的知识可以求解线性方程组的解,判断矩阵的逆矩阵是否存在等。
5. 向量的线性相关性向量的线性相关性是线性代数中的另一个重要概念,它是判断向量空间中向量之间的线性组合是否有零解的一个关键概念。
向量的线性相关性的性质、判断方法和应用是线性代数中的重要知识点之一。
6. 最小二乘法最小二乘法是线性代数中的另一个重要概念,它是一种用于数据拟合和参数估计的数学方法。
通过最小二乘法可以得到一个最优的拟合曲线或者参数估计,它在数学、统计学和工程领域中都有着广泛的应用。
二、概率统计1. 随机事件与概率随机事件是概率统计中的一个重要概念,它是指在一定条件下,结果是不确定的事件。
概率是描述随机事件发生可能性的一种数学方法,它是随机事件发生可能性的度量标准。
随机事件的基本性质和概率的基本性质是概率统计中的基础知识点。
2. 条件概率与独立性条件概率是指在已知一件事情发生的情况下,另一件事情发生的可能性。
考研数学《线性代数》考点知识点总结

n
aki Akj
k 1
Dij
D, 0,
当i 当i
j, n
j;
或
k 1
aik
Ajk
Dij
D, 0,
当i 当i
j, j; 其中ij
1, 0,
当i j, 当i j.
1 1 1 1
范德蒙德 行列式:
x1 Dn x12
x2 x22
x3 x32
x n 1 1
x n 1 2
x n 1 3
xn xn2 = (xi x j ) .证明用数学归纳法.
A
0
A2
0
A11
,若
A
0 ,则 A1
As
0
A
1 2
0
A
1 s
性质: A A1 A2 As ,且 Ai 0 (i 1,2, , s) ,则 A 0 .
行向量:
α1T
A mn
α
T 2
,
α
T m
αiT (ai1, ai2, , ain )
列向量:
A (a1, a2 , , an )
线性方程组有解,称它相容;无解,就称 它不相容.
(iii)有无限多解的充分必要条件是 R( A) R( A, b) n .
线性方程组 Ax b 有解的充要条件是 R(A) R(A, b) .
n 元齐次线性方程组 Ax 0 有非零解的充要条件是 R(A) n .
矩阵方程 AX B 有解的充要条件是 R(A) R(A, B) .
定理 2: n 阶行列式可定义为 D (1)t a a p11 p2 2 apnn = (1)t a1p1 a2 p2 anpn .
1.D=DT,DT 为 D 转置行列式.(沿副对角线翻转,行列式同样不变)
考研数学线性代数必考的知识点

考研数学线性代数必考的知识点一、行列式与矩阵第一章《行列式》、第二章《矩阵》是线性代数中的基础章节,有必要熟练掌握。
行列式的核心内容是求行列式,包括具体行列式的计算和抽象行列式的计算二、向量与线性方程组三、特征值与特征向量相对于前两章来说,本章不是线性代数这门课的理论重点,但却是一个考试重点。
其原因是解决相关题目要用到线代中的大量内容,既有行列式、矩阵又有线性方程组和线性相关,“牵一发而动全身”。
四、二次型本章所讲的内容从根本上讲是第五章《特征值和特征向量》的一个延伸,因为化二次型为标准型的核心知识为“对于实对称矩阵A存在正交矩阵Q使得A可以相似对角化”,其过程就是上一章相似对角化在为实对称矩阵时的应用。
考研数学概率以大纲为本夯实基础从考试的角度,大家看看历年真题就发现比较明显的规律:概率的题型相对固定,哪考大题哪考小题非常清楚。
概率常考大题的地方是:随机变量函数的分布,多维分布(边缘分布和条件分布),矩估计和极大似然估计。
其它知识点考小题,如随机事件与概率,数字特征等。
从学科的角度,概率的知识结构与线性代数不同,不是网状知识结构,而是躺倒的树形结构。
第一章随机事件与概率是基础知识,在此基础上可以讨论随机变量,这就是第二章的内容。
随机变量之于概率正如矩阵之于线性代数。
考生也可以看看考研真题,数一、数三概率考五道题,这五题的第一句话为“设随机变量X……”,“设总体X……”,“设X1,X2,…,Xn为来自X的简单随机样本”,无论“随机变量”、“总体”和“样本”本质上都是随机变量。
所以随机变量的理解至关重要。
讨论完随机变量之后,讨论其描述方式。
分布即为描述随机变量的方式。
分布包括三种:分布函数、分布律和概率密度。
其中分布函数是通用的描述工具,适用于所有随机变量,分布律只针对离散型随机变量而概率密度只针对连续型随机变量。
之后讨论常见的离散型和连续性随机变量,考研范围内需要考生掌握七种常见分布。
介绍完一维随机变量之后,推广一下就得到了多维随机变量。
2022考研线性代数强化讲义(知识体系+重点题型解析)
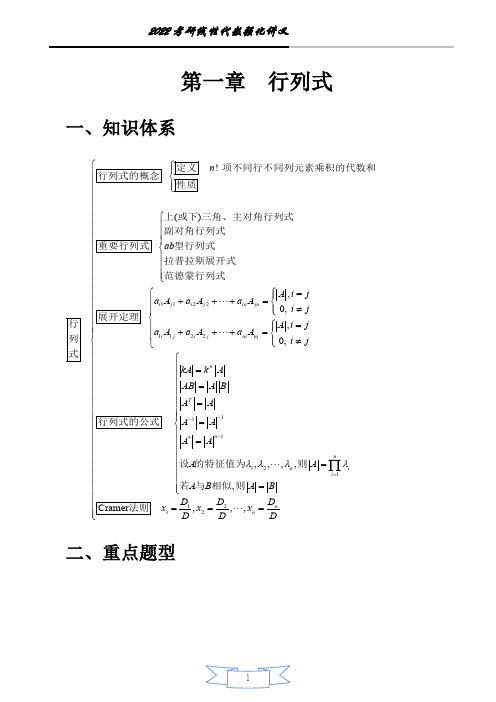
第一章行列式一、知识体系 1122,,A i j i j A i j i j =a A a A a A ≠ i j i j 1122 +++= 0,= a A a A a A i j i j +++= ≠ 0, in jnn ! 项不同行不同列元素乘积的代数 定 ni nj 义和 性质 上()或下三角、主对角行列式 副对角行列式ab 型行列式 拉普拉斯展开式 范德蒙行列式行列式12,,,,12,,,T n kA k A A A D n D D x x x −D D D1−1n −1i =1 行列式的概念重要行列式展开定理=nAB A B ==A A= 行列式的公式 * =A A=12=== = ∏ n i 设 n A A 的特征值为λλλλ则 若A B A B 与相似,则Cramer 法则二、重点题型重点题型一数字行列式的计算【方法】【例1.1】设212322212223333245354435743x x x x x x x x x x x x −−−−−−−− f x ()=−−−−x x x x −−− 则方程f x ()0 =根的个数为【】(B )2(C )3(A )1【详解(D )4】【例1.2】利用范德蒙行列式计算222a a bcb bac cc ab=.【详解】【例1.3】设x x x x 1234≠0,则11121314212223243132333441424344x a a a a a a a a a x a a a a a a a a a x a a a +a a a a a a x a 2+2=+2+2.【详解】【例1.4】计算三对角线行列式000000000000αβαβαβαβαββαβ+++D n =++αβα【详解】重点题型二代数余子式求和【方法】【例1.5】已知1234522211312451112243150A=27,则A A A 414243=++=,A A 4445+=.【详解】010000200001n 000【例1.6】设A =n −,则A 的所有代数余子式的和为.【详解】重点题型三抽象行列式的计算【方法】【例1.7】(2005,数一、二)设α1,α2,α3均为3维列向量,A =(α1,α2,α3),(,24,39)B ααααααααα=++++++123123123.若A =1,则=B .【详解】【例1.8】设A 为n 阶矩阵,αβ,为n 维列向量.若A a =,TAαb=0,β则TA β【详解】(2)(2)A A O −O A 1*−【例1.9】设A 为2阶矩阵,B =2 .若A =−1,则=B .【详解】【例1.10】设n 阶矩阵A 满足A A 2=,A E ≠,证明A =0.【详解】第二章矩阵一、知识体系 ()AB A A Ax +A B kAAT⇔≠||0 ⇔=r A n ⇔ ⇔=⇔=定 义 性质 定义法 初等变换 求法伴 随矩法阵法 分块矩阵法的列(或行)向量组线性无关 充要条件齐次线性方0 程组只有零解 非齐次线性方程组Ax b 有唯一解 ⇔A 的特征值均不为零 定义矩性质阵求法基本运算逆 秩定 义 伴随矩阵性质 定义 性质 求矩阵的逆初等变换与初等矩阵 求矩阵的秩线性 应用求表极大示线性无关组 解线性方程组 求二次型的标准形分块矩阵二、重点题型重点题型一求高次幂【方法】2131【例2.1】设46A a b c − =,B 为3阶矩阵,满足BA O=,且r B ()1>,则A n =.【详解】200412 【例2.2】设A =−320,则A n=.【详解】−−121 【例2.3】设A =−− −−363 121,P 为3阶可逆矩阵,B P AP =−12022B E ,则()+=.【详解】重点题型二逆的判定与计算【方法】 【例2.4】设n 阶矩阵A 满足A 2=2A ,则下列结论不正确的是【】 (B )A E (C )−可逆A E(D )+可逆A E −3可逆 (A )A 可逆【详解】,为n 阶矩阵,【例2.5】设A B a b ,为非零常数.证明: I )若(AB aA bB ,则=+AB BA =2+=,则(II )若A aAB E AB BA ;=.【详解】11a 0110a 【例2.6】(2015,数二、三)设A a =−,满足A O 3=. (I )求a 的值;(II )若矩阵X 满足22X XA AX AXA E ,求X −−+=.【详解】重点题型三秩的计算与证明 【方法】秩的性质(1)设A 为m ×n 阶矩阵,则()min ,r A m n {}≤; 2)(()()()r A B r A r B +≤+; ({3)()min (),()r AB r A r B }≤;({4)max (),()()()()r A r B r A B r A r B }≤≤+;5)r A r kA k (()()(0)=≠;(6)设A 为m ×n 阶矩阵,P 为m 阶可逆矩阵,Q 为n 阶可逆矩阵,则()()()()r A r PA r AQ r PAQ ===;7)设A 为m ×n 阶矩阵,若(r A n ()=,则()()r AB r B ;若=r A m ()=,则()()r CA r C =;===TTT8)(()()()()r A r A r AA r AA ;(9)设A 为m ×n 阶矩阵,B 为n ×s 阶矩阵,AB O =,则r A r B n ()()+≤.,为n 阶矩阵,【例2.7】(2018,数一、二、三)设A B () X Y 表示分块矩阵,则【】 (A )( )()r A AB r A (B )=( )()r A BA r A ={ }(C )( )max (),()r A B r A r B =T T(D )r A B r A B ( )( )=【详解】 【例2.8】设A 为n 阶矩阵.证明:I )若A 2=A ,则(r A r A E n ()()+−=;2=,则(II )若A E r A E r A E n ()()++−=.【详解】重点题型四关于伴随矩阵【伴随矩阵的性质】||01**11(1),AA A AA E A A A A AA A≠**−−== →==; (*1*=n 2)()kA k A −; 3)()AB B A (***=(4;)*A A n −1=;(** A A 5)()()T T=;( 6)()()A 1**1A A A−−==;( n −7)()A A A 2**=; ,()8)r A r A n (()1,()1=n r A n *==−r A n <−0,()1.【例2.9】设n 阶矩阵A 的各列元素之和均为2,且A =6,则A ∗的各列元素之和均为【】(B )31(C )3 (A )2【详解(D )6】ij 为n n 【例2.10】设A a =()(3)阶非零矩阵,A ij 为a ij 的代数余子式,≥证明:(*(,1,2,,)TTI )a A i j n A A AA E ij ij ==⇔=⇔= 且A =1;*(,1,2,,)TT(II )a A i j n A A AA E ij ij =−=⇔=−⇔= 且A =−1.【详解】重点题型五初等变换与初等矩阵【初等变换与初等矩阵的性质】(1)E i j (,)1=−,(())E i k k =,E ij k (())1=; T2)((,)(,)E i j E i j =T,E ij k E ji k T ,E i k E i k (())(())=(())(())=;−13)((,)(,)E i j E i j =1,E i k E i k(())−1=−1,(())(())E ij k E ij k =−;(4)初等行(或列)变换相当于左(或右)乘相应的初等矩阵;(5)可逆矩阵可以写成有限个初等矩阵的乘积.【例2.11】(2005,数一、二)设A 为n (n ≥2)阶可逆矩阵,交换A 的第1行与第2行得到矩阵B ,则【】(A )交换A *的第1列与第2列,得B *(B )交换A *的第1行与第2行,得B *(C )交换A *的第1列与第2列,得−B *(D )交换A *的第1行与第2行,得−B *【详解】123012001 【例2.12】设A = 001010100,P =110010001 ,Q = ,则()()T −P A Q 120212022=__________.【详解】第三章向量一、知识体系212(,,,)(,,,) (,,,)s k k k x 1x x r r βαααααααααβ αααβαβ+ k α [αβ,] =+++ ⇔= ⇔= →1122 s s 12 s 12 s s 12 s 定初等行变换义非齐次线性方程组(,,,)αααβ有解 充要条件 充分条件 求法行最简形矩阵向线性相关量 1 22 (,,,)0(,,,)x x x s r s x 1x x s ααα 定ααα义 ⇔=⇔< ⇔= 12s 12 s 12s ⇔至少有一个向量可由其余向量线性表 示齐次线性方程组充要条件ααα有非零解 充分条件齐次线性方程组充要条件(,,,)0只有零解 (,,,)ααα基本运算线性表示定义⇔任意向量均不能由其余向量线性表示线性无 关αs =s ⇔r (,,αα12,)12 s → 充分条初等行变换件定义极大线性无关组与向量组的秩求法行阶梯形矩阵二、重点题型重点题型一线性表示的判定与计算 【方法】,,与数【例3.1】设向量组αβγk l m ,,满足k l m km αβγ++=≠0(0),则【】,与(A )αβαγ ,等价 ,与(B )αββγ,等价(D )α与γ,,与(C )αγβγ等价等价【详解】【例3.2】(123(1,2,0),(1,2,3),(1,2,2)T T T2004,数三)设αααa ab a b ==+−=−−−+,β=−(1,3,3)T .当a ,b 为何值时, ,,线性表示I )β不能由ααα(123;,,唯一地线性表示,并求出表示式(II )β可由ααα123;,,线性表示,但表示式不唯一,并求出表示式(III )β可由ααα123. 【详解】【例3.3】(2019,数二、三)设向量组(123(1,1,4),(1,0,4),(1,2,3)T TT a 2I )ααα===+;向量组2a a a 123(1,1,3),(0,2,1),(1,3,3)T T T (II )βββ=+=−=+I )与(II )等价,求a 的.若向量组(值,,,线性表示并将β3由ααα123.【详解】重点题型二线性相关与线性无关的判定【方法】【例3.4】(2014,数一、二、三)设ααα123,,均为3维列向量,则对任意常数k l,,1323,αααα ++k l ,,线性无关的【线性无关是ααα123】(B )充分非必要条件(C )充分必要条件(A )必要非充分条件【详解(D )既非充分又非必要条件】【例3.5】设A 为n 阶矩阵,ααα123,,均为n 维列向量,满足A A 2αα11=≠0,212A A2ααα=+, 2323A A ααα=+ ,,线性无关,证明ααα123.【详解】,,线性无关,与4维列向量β1,β2两两正交,证明β1,β2线性相关【例3.6】设4维列向量ααα123.【详解】重点题型三极大线性无关组的计算与证明【方法】 1234(1,1,1,3),(1,3,5,1),(3,2,1,2),(2,6,10,)TTTT【例3.7】设ααααa a ==−−=−+=−−.(I )当a 为何值时,该向量组线性相关,并求其一个极大线性无关组;(II )当a 为何值时,该向量组线性无关,并将α=(4,1,6,10)T 由其线性表示.【详解】,为I )设A B m n ×矩阵,则()()()r A B r A r B +≤+;×矩阵,B 为n s {×矩阵,则()min (),()r AB r A r B 【例3.8】证明:((II )设A 为m n 【详解}≤.】重点题型四向量空间(数一专题)【方法】过渡矩阵12,,,n 到基β1,β2, ,βn 的过渡矩阵为由基ααα(,,,)(,,,)=βββααα12C 12 n n ,−12αααβββ1C =(,,,)(,,,) 12 n n .12坐标变换公式,,, n 下的坐标为设向量γ在基αααx x x x12 n T,在基β1,β2, ,βn 下=(,,,)的坐标为y y y y 12 n T,则坐标变换公式为x =Cy =(,,,).2015,数一)设向量组ααα【例3.9】(123,,为R 3的一个基,113βαα=+22k ,βα22=2,313k=++βαα(1).,,为R 3的一个基I )证明向量组βββ(123;(II )当k 为何值时,存在非零向量ξ在基ααα123,,下的坐标相同,并求所有的ξ,,与基βββ123.I 【详解】()3123201(,,)(22,2,(1))(,,)020201k k βββαααααααα1231321=+++= k k +201020201令C =k k +,则,,为R 3的一个基,,线性无关,故βββ=≠40,从而βββC 123123.(II )设ξ在基ααα123,,下的坐标为x ,,与基βββ123,则 123123123Cx x=ξαααβββααα(,,)(,,)(,,)=x =C E x −=得()0.对C E −作初等行变换,1011010100102000k k kC E −=→当k =0时,方程组()00−C E x −=有非零解,所有非零解为1x c 1=,在两个基下坐标相同的所有非零向量为1231231xc −ξαααααααα1=(,,)(,,)0()==−c 31,其中c 为非零常数第四章线性方程组一、知识体系11220 () 0() ()()()()1 ()()()()r A n Ax r A n r A r A n r A r A n k k k ξξξ−− =⇔= Ax =0Ax =⇔<Ax b r A r A r A r A =⇔<⇔=− Ax b Ax b ==⇔== Ax b =⇔=< +++ 性 n r n r 质只有零解有非零解无解 判定有唯一解有无穷多解的通解线性方程组 1122()()()()()()()AX BAX B r A r A B n r A r A B n ξξξη−− Ax =0 ++++ Ax b k k k = =⇔< AX B r A r A B =⇔== AX B =⇔=< A B → n r n r =的通初等行变换解 定义无解矩阵方程判定有唯一解有无穷多解 求法行最简形矩阵 定义 求法,的行向量组等价()()A ⇔r A r r B B 解的性质与判定解的结构公共解定义公共解与同解 ⇔ A B 同解充要条 件==二、重点题型重点题型一解的判定【方法】【例4.1】(0TA2001,数三)设A 为n 阶矩阵,α为n 维列向量,且r r A α α=(),则线性方程组(A )Ax =α有无穷多解(B )Ax =α有唯一解A x α (C )αT0y =0只 有零解Ax α(D ) αT 0y =0有 非零解 【详解】 ×阶矩阵,且【例4.2】设A 为m n r A m n ()=<,则下列结论不正确的是【】T =0(A )线性方程组A x 只有零解 T (B )线性方程组A Ax =0有非零解 (C )∀b ,线性方程组A x b(D )∀b ,线性方程组T =有唯一解Ax b =有无穷多解【详解】重点题型二求齐次线性方程组的基础解系与通解【方法】1234为4阶矩阵,(1,0,1,0)T为线性方程组Ax =0【例4.3】(2011,数一、二)设A =αααα(,,,)的 *=0的基础解系可为【基础解系,则A x 】 , (A )αα12,(B )αα13,,(C )ααα123,,(D )ααα234【详解】a b c ,【例4.4】(2005,数一、二)设3阶矩阵A 的第1行为(,,)a b c 12324636k ,,不全为零,B =,满足AB O=,求线性方程组Ax =0的通解.【详解】【例4.5】(2002,数三)设线性方程组n 0n 0n 0 123n 0++++=ax bx bx bx bx ax bx bx 123++++=123++++=bx bx ax bx123++++=bx bx bx ax其中a ≠0,b ≠0,n ≥2. 当a b 求其通解,为何值时,方程组只有零解、有非零解,当方程组有非零解时,.【详解】重点题型三求非齐次线性方程组的通解【方法】,,为非齐次线性方程组【例4.6】设A 为4阶矩阵,k 为任意常数,ηηη123Ax b =的三个解,满足124ηη12+=23245 3,ηη23+==,则.若r A ()3Ax b =的通解为【】11203142− (A ) +k (B )21324051 +k (C )01102132− +k (D )11121011 +k【详解】2017,数一、二、三)设3阶矩阵A =【例4.7】((,,)=+2ααα123有三个不同的特征值,其中312ααα. I )证明r A (()2=;(II )若βααα=++123,求线性方程组Ax =β的通解.【详解】1101011λλλ 【例4.8】(2010,数一、二、三)设A =−11a ,b =,线性方程组 Ax b=有两个不同的解.(I )求λ,a 的值;(II )求方程组Ax b =的通解.【详解】【例4.9】设A 为m n ×阶矩阵,且r A r 12,,,()=.若ξξξ−为齐次线性方程组Ax =0的 n r 基础解系,η为非齐次线性方程组Ax =b 的特解,证明:(,,,,I )ηξξξ12 n r −线性无关;,,,,(II )ηηξηξηξ+++12 n r −线性无关;,,,,(III )ηηξηξηξ+++n r −为Ax =b 所有解的极大线性无关组12 .【详解】重点题型四解矩阵方程【方法】矩阵方程解的判定AX B=无解⇔<()()r A r A B AX B ()()r Ar A B n =有唯一解⇔==AX B ()()r Ar A B n =有无穷多解⇔=<矩阵方程的求法对()AB 作初等行变换,化为行最简形矩阵,得矩阵X .101−202101【例4.10】设A =−−,矩阵X 满足AX E A X 20222,求矩阵X +=+.【详解】【例4.11】(123401111203−−2014,数一、二、三)设A =− −.(I )求线性方程组Ax =0的一个基础解系;(II )求满足AB E =的所有矩阵B .【详解】重点题型五公共解的判定与计算【方法】【例4.12】(2007,数一、二、三)设线性方程组(+ +=++=001321x x I )x x 1+4x 2+a 2x 3=0ax 2x 32x 与方程(II )x 1+2x 2+x 3=a −1有公共解,求a 的值及所有公共解.【详解】【例4.13】设齐次线性方程组(123420x x x 123+−=230I )x x x x ++−= 12(2,1,2,1),(1,2,4,8)齐次线性方程组(II )的一个基础解系为ααa a T T =−+=−+.(1)求方程组(I )的一个基础解系;(2)当a 为何值时,方程组(I )与(II )有非零公共解,并求所有非零公共解.【详解】重点题型六同解的判定与计算【方法】【例4.14】(2005,数三)设线性方程组( =+=++ I )202132+321 x 35 x 1+x 2+ax 3=0x x x x 3x +=++0 12+321 2(1)x 3=0c x 0与(II ) x cx b x +bx 2同解,求a ,b ,c 的值.【详解】第五章特征值与特征向量一、知识体系 (0)0()0A E B P AP P AP A n A λλA αλαα−1=≠ −= A E x −= =−1=Λ ⇔ ⇔k k A n 定义性质 特征方程法 定义 性质特征值与特 定义征有个线性无关的特征向量 充要条件重特征值有个线性无关的向特征向量量有个不同的特征值 充分条件为实对称矩阵 T k k 特征值与特征向量相似矩阵相似对角化==Λ特征值均为实数不同特征值的特征向量正交实对称矩阵重特征值有个线性 无关的特征向量,使得− A 可正交相似对角化,即存在正交矩阵Q Q AQ Q AQ 1二、重点题型重点题型一特征值与特征向量的计算【方法】特征值与特征向量的性质 (1)不同特征值的特征向量线性无关;(2)不同特征值的特征向量之和不是特征向量;(3)k 重特征值最多有k 个线性无关的特征向量;4)设A 的特征值为12(,,,λλλnn ,则i =1∑nA λi=tr A (),λi i =1=∏;=,即A =αβT,其中5)若r A (()1αβ,为n 维非零列向量,则A 的特征值为TT tr A ()λαββαn1===0 ,λλ2===(6)设α为矩阵A 属于特征值λ的特征向量,则【例5.1】设1111111111111111−−A = −− −−求A 的特征值与特征向量.【详解】322 223010001【例5.2】(2003,数一)设A = 232 ,P = 101 ,B =P −1A *P ,求B +2E 的特征值与特征向量.【详解】12214212a 【例5.3】设A = −−− 的特征方程有一个二重根,求A 的特征值与特征向量. 【详解】 2【例5.4】设3阶非零矩阵A 满足A O = ,则A 的线性无关的特征向量的个数是【】(B )1(C )2(A )0【详解(D )3】【例5.5】设A =+αββαTT,其中αβ 1,为3维单位列向量,且αβT 3=,证明:(I )0为A 的特征值; ,(II )αβαβ为A +−的特征向量;(III )A 可相似对角化.【详解】重点题型二相似的判定与计算【相似的性质】(1)若A B ,则A B ,有相同的行列式、秩、特征方程、特征值、迹;2)若(A B ,则()()f A f B ,A B −− 11 ,(0)AB BA A ≠,A B T T ,A B ** ;3)若(A B ,B C,则A C .【例5.6】设1000030000110022 A =矩阵B 与A 相似,则r B E r B E ()(3)−+−=.【详解】【例5.7】设n 阶矩阵A 与B 相似,满足A E 2=2,则 AB A B E +−−=. 【详解】【例5.8】(22−−002221 2019,数一、二、三)设A x =−−21001000y与B =−相似.I )求(x y ,的值;−(II )求可逆矩阵P ,使得P AP B 1=.【详解】重点题型三相似对角化的判定与计算【方法】【例5.9】设3阶矩阵A 的特征值为1,3,−2,对应的特征向量分别为ααα123,,.若P =−ααα(,2,)−1*=【132,则P A P 】12 (A )−1− 36 (B )−2 −36 (C ) −2 13(D ) −2【详解】【例5.10】设n 阶方阵A 满足32A A E O ,证明A 可相似对角化2−+=.【详解】【例5.11】(2020,数一、二、三)设A 为2阶矩阵,P A =(,)αα,其中α为非零向量且不是A 的特征向量.(I )证明P 为可逆矩阵; 2ααα+−=60,求II )若(A A P AP−1,并判断A 是否相似于对角矩阵.【详解】重点题型四实对称矩阵的计算【方法】2+=,n 阶矩阵B 满足【例5.12】设n 阶实对称矩阵A 满足A A O B B E 2+=,且r AB ()2=,则A +【详解】01413【例5.13】(2010,数二、三)设40A a a −=−T,正交矩阵Q 使得Q AQ 为对角矩阵.若Q的第12,1)T ,求a Q ,.【详解】 2=,【例5.14】设3阶实对称矩阵A 满足A E A E+的各行元素之和均为零,且r A E ()2+=.(I )求A 的特征值与特征向量;(II )求矩阵A .【详解】第六章二次型一、知识体系0,0T T f x Ax B C AC x Ax x Bx =x x Ax T =T ⇔ ⇔ 定∀≠>义 拉格朗日配方法 合同变换 标准形的求法法正交变换法 定义与有相同的正、负惯性指数 充要条件A B ,有相同的正、负特征值的个数 充分条件A B 与相似必要条件二次A B 与等价型有T 0(1,,)0A E A A 二次型与标准形合同矩阵定义 性质 ⇔f n ⇔ 正定矩阵 ⇔ii >= a i n > 的正惯性指数为与合同充要条件的特征 值均大于零⇔A 的顺序主子式均大于零必要条件二、重点题型重点题型一求二次型的标准形【方法】222【例6.1】(2016,数二、三)设二次型123123122313(,,)()222f x x x a x x x x x x x x x=+++++ 的正、负惯性指数分别为1,2,则【】(B )a <−2 a (A )a >1【详解(D )a =1或−(C )−<<212】 =−+++++222【例6.2】(2018,数一、二、三)设二次型1231232313(,,)()()()f x x x x x x x x x ax .I )求f x x x ((,,)0 123=的解;(II )求f x x x (,,)123的规范形.【详解】【例6.3】(2020,数一、三)设二次型121122(,)44f x x x x x x 1122x y =−+22经正交变换x y =Q化为二=++22,其中次型(,)4121122g y y ay y y by a b ≥.I )求(a b ,的值;(II )求正交矩阵Q .【详解】重点题型二合同的判定【方法】 12【例6.4】(2008,数二、三)设A =21,与A 合同的矩阵是【】−1221 (A )− 21− (B ) −12 21 12(C )12− (D )−21 【详解】【例6.5】设A B ,为n 阶实对称可逆矩阵,则存在n 阶可逆矩阵P ,使得 ①PA B −;②=P ABP BA 1−;③=P AP B 122T =;④P A P B =. 成立的个数是【 】 (A )1 (B )2(C )3 (D )4【详解】重点题型三二次型正定与正定矩阵的判定【方法】【例6.6】设A 为m n ×阶矩阵,且r A m ()=,则下列结论 ①AA T 与单位矩阵等价;③AA T 与单位矩阵合同;②AA T 与对角矩阵相似;④AA T 正定. 正确的个数是【 】(B )2(C )3 (A )1【详解(D )4】 I )设A 为n 阶正定矩阵,B 为n 阶反对称矩阵,则【例6.7】证明:(A B −2为正定矩阵;,为n 阶矩阵,且(II )设A B r A B n TT()+=,则A A B B +为正定矩阵.【详解】。
数学一线代知识点

考研数学一《线性代数》知识点总结第一部分行列式一、本部分内容重点1.了解行列式的概念,掌握行列式的性质。
2.会用行列式的性质和行列式按行(列)展开法则计算行列式。
二、考点分析1.行列式是基础,它与后续要学的内容——方阵构成的行列式、逆矩阵、向量组的线性相关性、矩阵的秩、线性方程组、特征值、正定二次型与正定矩阵等问题中都有重要应用。
所以必须要弄清楚行列式在处理有关问题中的功能与作用,熟练掌握行列式的性质和计算方法,为应用行列式处理有关问题打下良好的基础。
2.计算行列式的常用方法:1)用定义法计算行列式中含某一项的系数;2)应用行列式的性质化简行列式(例如化为三角形行列式就是一个常用方法);3)将各行(列)加到某一行(列),提取公因式;4)按行(列)展开行列式——降阶法(在此基础上,有些题可用数学归纳法、有些题可用递推关系式法来计算行列式)。
5)逐行(列)相加减;6)拆项法——将一个行列式分成几个较简单的行列式进行计算;7)公式法——如对角行列式、范德蒙德行列式等;8)升阶法。
在实际计算过程中,常常将上述方法交替使用。
第二部分矩阵一、本部分内容重点1.理解矩阵的概念。
2.了解单位矩阵、数量矩阵、对角矩阵、对称矩阵和反对称矩阵,以及它们的性质。
3.掌握矩阵的线性运算、乘法、转置,以及它们的运算律,了解方阵的幂,掌握方阵乘积的行列式。
4.理解逆矩阵的概念,掌握逆矩阵的性质,以及矩阵可逆的充分必要条件,理解伴随矩阵的概念,会用伴随矩阵求逆矩阵。
5.掌握矩阵的初等变换,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法。
6.了解分块矩阵及其运算。
二、考点分析1.矩阵的运算(含逆矩阵)是矩阵考试内容中的重点,其中,又以矩阵乘法和逆矩阵最为重要。
要掌握矩阵运算,除了要理解各种运算的定义外,还要熟练掌握各种运算的运算律和运算性质。
在作矩阵运算时,一般要先利用运算法则通过“字母”运算进行化简。
考研数学线代定理公式总结

考研数学线代定理公式总结√ 关于:①称为的标准基,中的自然基,单位坐标向量;②线性无关;③;④;⑤任意一个维向量都可以用线性表示、行列式的定义√ 行列式的计算:①行列式按行(列)展开定理:行列式等于它的任一行(列)的各元素与其对应的代数余子式的乘积之和、推论:行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零、②若都是方阵(不必同阶),则(拉普拉斯展开式)③上三角、下三角、主对角行列式等于主对角线上元素的乘积、④关于副对角线:(即:所有取自不同行不同列的个元素的乘积的代数和)⑤范德蒙德行列式:矩阵的定义由个数排成的行列的表称为矩阵、记作:或伴随矩阵,为中各个元素的代数余子式、√ 逆矩阵的求法:① :②③ √ 方阵的幂的性质:√ 设的列向量为,的列向量为,则,为的解可由线性表示、即:的列向量能由的列向量线性表示,为系数矩阵、同理:的行向量能由的行向量线性表示,为系数矩阵、即:√ 用对角矩阵乘一个矩阵,相当于用的对角线上的各元素依次乘此矩阵的向量;用对角矩阵乘一个矩阵,相当于用的对角线上的各元素依次乘此矩阵的向量、√ 两个同阶对角矩阵相乘只用把对角线上的对应元素相乘、√分块矩阵的转置矩阵:分块矩阵的逆矩阵:分块对角阵相乘:,分块对角阵的伴随矩阵:√ 矩阵方程的解法():设法化成① 零向量是任何向量的线性组合,零向量与任何同维实向量正交、② 单个零向量线性相关;单个非零向量线性无关、③ 部分相关,整体必相关;整体无关,部分必无关、(向量个数变动)④ 原向量组无关,接长向量组无关;接长向量组相关,原向量组相关、(向量维数变动)⑤ 两个向量线性相关对应元素成比例;两两正交的非零向量组线性无关、⑥ 向量组中任一向量≤≤都是此向量组的线性组合、⑦ 向量组线性相关向量组中至少有一个向量可由其余个向量线性表示、向量组线性无关向量组中每一个向量都不能由其余个向量线性表示、⑧ 维列向量组线性相关;维列向量组线性无关、⑨ 若线性无关,而线性相关,则可由线性表示,且表示法唯一、⑩ 矩阵的行向量组的秩列向量组的秩矩阵的秩、行阶梯形矩阵的秩等于它的非零行的个数、行阶梯形矩阵可画出一条阶梯线,线的下方全为;每个台阶只有一行,台阶数即是非零行的行数,阶梯线的竖线后面的第一个元素非零、当非零行的第一个非零元为1,且这些非零元所在列的其他元素都是时,称为行最简形矩阵⑪矩阵的行初等变换不改变矩阵的秩,且不改变列向量间的线性关系;矩阵的列初等变换不改变矩阵的秩,且不改变行向量间的线性关系、即:矩阵的初等变换不改变矩阵的秩、√ 矩阵的初等变换和初等矩阵的关系:对施行一次初等变换得到的矩阵,等于用相应的初等矩阵乘;对施行一次初等变换得到的矩阵,等于用相应的初等矩阵乘、矩阵的秩如果矩阵存在不为零的阶子式,且任意阶子式均为零,则称矩阵的秩为、记作向量组的秩向量组的极大无关组所含向量的个数,称为这个向量组的秩、记作矩阵等价经过有限次初等变换化为、记作:向量组等价和可以相互线性表示、记作:⑫矩阵与等价,可逆作为向量组等价,即:秩相等的向量组不一定等价、矩阵与作为向量组等价矩阵与等价、⑬向量组可由向量组线性表示有解≤、⑭向量组可由向量组线性表示,且,则线性相关、向量组线性无关,且可由线性表示,则≤、⑮向量组可由向量组线性表示,且,则两向量组等价;⑯任一向量组和它的极大无关组等价、向量组的任意两个极大无关组等价、⑰向量组的极大无关组不唯一,但极大无关组所含向量个数唯一确定、⑱若两个线性无关的向量组等价,则它们包含的向量个数相等、⑲设是矩阵,若,的行向量线性无关;若,的列向量线性无关,即:线性无关、√ 矩阵的秩的性质:①≥ ≤≤ ② ③ ④ ⑤≤⑥ 即:可逆矩阵不影响矩阵的秩、⑦若;若⑧等价标准型、⑨≤ ≤≤ ⑩ :线性方程组的矩阵式向量式矩阵转置的性质:矩阵可逆的性质:伴随矩阵的性质:(无条件恒成立)线性方程组解的性质:√ 设为矩阵,若一定有解,当时,一定不是唯一解,则该向量组线性相关、是的上限、√ 判断是的基础解系的条件:① 线性无关;② 都是的解;③ 、√ 一个齐次线性方程组的基础解系不唯一、√ 若是的一个解,是的一个解线性无关√ 与同解(列向量个数相同),则:① 它们的极大无关组相对应,从而秩相等;② 它们对应的部分组有一样的线性相关性;③ 它们有相同的内在线性关系、√ 两个齐次线性线性方程组与同解、√ 两个非齐次线性方程组与都有解,并且同解、√ 矩阵与的行向量组等价齐次方程组与同解(左乘可逆矩阵);矩阵与的列向量组等价(右乘可逆矩阵)、√ 关于公共解的三中处理办法:① 把(I)与(II)联立起来求解;② 通过(I)与(II)各自的通解,找出公共解;当(I)与(II)都是齐次线性方程组时,设是(I)的基础解系, 是(II)的基础解系,则 (I)与(II)有公共解基础解系个数少的通解可由另一个方程组的基础解系线性表示、即:当(I)与(II)都是非齐次线性方程组时,设是(I)的通解,是(II)的通解,两方程组有公共解可由线性表示、即:③ 设(I)的通解已知,把该通解代入(II)中,找出(I)的通解中的任意常数所应满足(II)的关系式而求出公共解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考研数学线代知识框架[摘要]不仅专业课需要知识框架,数学也是如此。
一个优秀而全面的知识框架有助于厘清整体的解题思路。
下面分享的是凯程考研老师精心整理的线代知识点框架。
线性代数的学习切入点:线性方程组。
换言之,可以把线性代数看作是在研究线性方程组这一对象的过程中建立起来的学科。
线性方程组的特点:方程是未知数的一次齐次式,方程组的数目s和未知数的个数n可以相同,也可以不同。
关于线性方程组的解,有三个问题值得讨论:(1)、方程组是否有解,即解的存在性问题;(2)、方程组如何求解,有多少个解;(3)、方程组有不止一个解时,这些不同的解之间有无内在联系,即解的结构问题。
高斯消元法,最基础和最直接的求解线性方程组的方法,其中涉及到三种对方程的同解变换:(1)、把某个方程的k倍加到另外一个方程上去;(2)、交换某两个方程的位置;(3)、用某个常数k乘以某个方程。
我们把这三种变换统称为线性方程组的初等变换。
任意的线性方程组都可以通过初等变换化为阶梯形方程组。
由具体例子可看出,化为阶梯形方程组后,就可以依次解出每个未知数的值,从而求得方程组的解。
对方程组的解起决定性作用的是未知数的系数及其相对位置,所以可以把方程组的所有系数及常数项按原来的位置提取出来,形成一张表,通过研究这张表,就可以判断解的情况。
我们把这样一张由若干个数按某种方式构成的表称为矩阵。
可以用矩阵的形式来表示一个线性方程组,这至少在书写和表达上都更加简洁。
系数矩阵和增广矩阵。
高斯消元法中对线性方程组的初等变换,就对应的是矩阵的初等行变换。
阶梯形方程组,对应的是阶梯形矩阵。
换言之,任意的线性方程组,都可以通过对其增广矩阵做初等行变换化为阶梯形矩阵,求得解。
阶梯形矩阵的特点:左下方的元素全为零,每一行的第一个不为零的元素称为该行的主元。
对不同的线性方程组的具体求解结果进行归纳总结(有唯一解、无解、有无穷多解),再经过严格证明,可得到关于线性方程组解的判别定理:首先是通过初等变换将方程组化为阶梯形,若得到的阶梯形方程组中出现0=d这一项,则方程组无解,若未出现0=d一项,则方程组有解;在方程组有解的情况下,若阶梯形的非零行数目r等于未知量数目n,方程组有唯一解,若r在利用初等变换得到阶梯型后,还可进一步得到最简形,使用最简形,最简形的特点是主元上方的元素也全为零,这对于求解未知量的值更加方便,但代价是之前需要经过更多的初等变换。
在求解过程中,选择阶梯形还是最简形,取决于个人习惯。
常数项全为零的线性方程称为齐次方程组,齐次方程组必有零解。
齐次方程组的方程组个数若小于未知量个数,则方程组一定有非零解。
利用高斯消元法和解的判别定理,以及能够回答前述的基本问题(1)解的存在性问题和(2)如何求解的问题,这是以线性方程组为出发点建立起来的最基本理论。
对于n个方程n个未知数的特殊情形,我们发现可以利用系数的某种组合来表示其解,这种按特定规则表示的系数组合称为一个线性方程组(或矩阵)的行列式。
行列式的特点:有n!项,每项的符号由角标排列的逆序数决定,是一个数。
通过对行列式进行研究,得到了行列式具有的一些性质(如交换某两行其值反号、有两行对应成比例其值为零、可按行展开等等),这些性质都有助于我们更方便的计算行列式。
用系数行列式可以判断n个方程的n元线性方程组的解的情况,这就是克莱姆法则。
总而言之,可把行列式看作是为了研究方程数目与未知量数目相等的特殊情形时引出的一部分内容。
[摘要]以下是凯程考研辅导名师特为大家整理总结的一些有趣的数学小题目,供大家参考!祝愿各位考生都能在强化复习阶段顺利,考研成功!微积分如果用心去学你会发现很多乐趣,然后在解题的过程享受这些小小的成就感,何乐而不为呢。
快来看看这位朋友分享的一些小乐趣吧。
▶被积函数是连续函数f(x)的积分上限函数F(x)可导,且导数就是f(x)。
逆向思维,这就用“构造法”证明了:连续函数一定有原函数。
把“作上限函数”视为一种变换方式,从条件角度看,相当于通过变换将连续函数提升为可导函数。
《广义函数》理论中,在不光滑点(连续不可导点)微局部地实施这样的变换,就好象是用“沙轮”把曲线“尖点”给磨光了。
故称之为“磨光变换”。
当年武汉X中有个学生入选中国中学生奥数代表队。
在清华北大的集训中,他将这套技术学得很精。
正式参加世界大赛时,决赛卷上最后的坡度题恰好用“磨光变换”最简单。
这个小子设计了“磨光变换”逼近列,很快地完成了解答。
自信无误之际,竟在草稿上画卜克游戏玩。
新华社电讯稿报道中学生奥数代表队夺金时,记者把“磨光变换”写成了“魔光变换”,好不吓人哦。
这里有一个有趣的联想。
如果f(x)仅有第一类间断,那么相应的上限函数是否一定连续呢?结论是,“相应的上限函数一定连续。
”(画外音:考研题中出现过一次。
)在《概率统计》中,连续型随机变量X的分布函数就是密度函数的上限函数。
它一定连续。
由于密度函数非负,证明这个结论,用连续的增量定义最简明。
要注意的是,设f(x)有跳跃间断点a,相应的上限函数在点a虽然连续,却一定不可导。
即改善是有一定限度的。
要证明这个结论正好用上我的“有意思(4)右导数与导函数的右极限”。
实际上,设点a左側,f(x)=初等函数φ(x),右侧f(x)=ψ(x),φ(x-0)≠ψ(x+0)形成跳跃间断。
记f(x)相应的上限函数为F(x),则F(x)在点a连续,但是左側求导F′(x)=φ(x),右側求导F′(x)=ψ(x),φ(x-0)≠ψ(x+0)F(x)在点a不可导。
在点a的邻域内,F(x)不是f(x)的原函数。
相当一些“模拟卷”上有这样的题目。
可以算是“擦边球”。
▶《概率统计》不是第一层次基础课程。
学习《概率》需要你有较好的《高等数学》基础。
比如,计算D(卡方(1))就是个大综合练习。
(潜台词:D(卡方(n))=2n)预备1——我们知道,exp(x2)是四个“典型不可积”中最为露脸的一个。
正态分布的密度函数与它同为一家,但是密度函数在全直线积分为1。
在历史上,人们曾利用这个特点及定积分技巧来计算一些无穷积分。
计算D(卡方(1)),最尾端就要用到它。
预备2——我在“讲座”中逐讲给大家建立一个“材料库”。
最早在(5)中有一条“x趋于+∞时,指数函数exp(x)是比任意高次方的幂函数都还要高阶的无穷大。
”或者说,“x趋于+∞时,函数exp(-x)是任意高阶的无穷小。
”预备3——分部积分的要点是“变化”∫甲·乙dx=(甲的一个原函数)·(乙)-∫(甲的这个原函数)·(乙的导数)dx设X服从标准正态分布,我们计算D(X2),即证明D(卡方(1))=2鉴于输入问题,我写出步骤,大家在纸上划一下(1)用平方关系来算D(X2),得先算均值E(X四次方)设f(x)是N(0,1)的密度函数,求E(X四次方),被积函数x四次方f(x)在全直线积分分x四次方f(x)=x3·xf(x),注意xf(x)的原函数恰是-f(x)分部积分一次,求极限知第一部分答案为0,(运用预备2)第二部分是3x2f(x)在全直线积分再分x2f(x)=x·xf(x),又分部积分,同样求极限知第一部分答案为0,第二部分已是3倍密度函数f(x)在全直线积分,当然为3(2)用平方关系来算我常常开玩笑把平方关系E(X2)=μ2+σ2称为“概率勾股定理”。
D(X2)=E(X四次方)-(E(X2))2=3-1=2怎么样,有点意思吧。
▶如果你作了一个假设,你就建立了逻辑推理的一个基本点。
如果你还要作第二个假设,那得小心思考,新的假设是否与第一个假设独立。
一个同学在论坛上发贴,先设“对任意x,总有f(x)>x”,推出“f(f(x))>f(x)”,突然又假设“f(x)单减”,然后就不明白,“为什么会矛盾”。
这就是没考虑逻辑,随意作第二个假设造成的。
数学历史上,正当人们陶醉于“集合理论”与“勒贝格积分”等成果的完美之际,“悖论”的出现给大家当头一棒,砸得人晕头转向。
仿佛有世界末日来临的感觉。
以至于对很多成功的“公理化假设”也提出怀疑:“是否在筑好篱笆之时,已经圈进了狼?”思考“第二假设是否与第一个假设独立”,有时的确较为困难。
看一个线性代数问题。
(讲座(40))例15设n维行向量组a1,a2,---,ak线性无关,k向量组a1,a2,---,ak,β线性无关。
例15是原数学四的考题。
它可以深化为,*例“设向量组β1,β2,---,βr线性无关,向量组ξ1,ξ2,---,ξk线性无关。
若前一向量组的每一个向量都与后一向量组的各向量正交。
则两向量组的合并组线性无关。
(暂时不写一个条件)证明设有一组数C1,……,Cr,Cr+1,……,Cr+k,使得C1β1+……+Crβr+Cr+1ξ1+……+C(r+k)ξk=0用β1对等式两边作内积,得β1ˊβ1C1+……+β1ˊβrCr=0用β2对等式两边作内积,得β2ˊβ1C1+……+β2ˊβrCr=0…………用βr对等式两边作内积,得βrˊβ1C1+……+βrˊβrCr=0现在,问题归结为,证明这个齐次方程组仅有零解。
问题延伸1,若记A=(β1,β2,---,βr),则系数矩阵恰为AˊA(潜台词:矩阵乘法,“左行右列作内积”)问题延伸2,秩R(A)=秩R(A′A)证明作齐次线性方程组AX=0和A′AX=0,AX=0的解显然都是A′AX=0的解。
如果列向量β是A′AX=0的解,则内积(Aβ)′(Aβ)=β′A′Aβ=β′(A′Aβ)=0这说明Aβ=0(向量),即A′AX=0的解也都是AX=0的解。
两方程组同解。
解集秩n-R(A)=n-R(A′A)故秩R(A)=秩R(A′A)前述关于C1,……,Cr的齐次方程组仅有零解。
带回假设式,由后一向量组的线性无关性知,其余系数也全为零。
故两向量组的合并组线性无关。
(画外音:这是一个可以记住的结论。
请体会证明的特色。
)好象什么问题都没有?!?!?!联想“n+1个n维向量线性相关”,这里还有向量个数问题。
在没有限定向量个数时,第二个假设,“前一向量组的每一个向量都与后一向量组的各向量正交”,不一定成立。
必须先说“k+r≤n”这个条件不影响证明。
凯程教育:凯程考研成立于2005年,国内首家全日制集训机构考研,一直从事高端全日制辅导,由李海洋教授、张鑫教授、卢营教授、王洋教授、杨武金教授、张释然教授、索玉柱教授、方浩教授等一批高级考研教研队伍组成,为学员全程高质量授课、答疑、测试、督导、报考指导、方法指导、联系导师、复试等全方位的考研服务。
凯程考研的宗旨:让学习成为一种习惯;凯程考研的价值观口号:凯旋归来,前程万里;信念:让每个学员都有好最好的归宿;使命:完善全新的教育模式,做中国最专业的考研辅导机构;激情:永不言弃,乐观向上;敬业:以专业的态度做非凡的事业;服务:以学员的前途为已任,为学员提供高效、专业的服务,团队合作,为学员服务,为学员引路。
