磁场,感应计算题
磁场强度、磁通量及磁感应强度的相互关系及计算

磁场强度、磁通量及磁感应强度的相互关系及计算1. 磁场强度磁场强度(H)是指单位长度上的磁力线数目,用来描述磁场的强弱。
磁场强度是一个矢量量,具有大小和方向。
在国际单位制中,磁场强度的单位是安培/米(A/m)。
磁场强度的计算公式为:[ H = ]其中,N 表示单位长度上的磁极数目,I 表示通过每个磁极的电流,L 表示磁极之间的距离。
2. 磁通量磁通量(Φ)是指磁场穿过某个面积的总量。
磁通量也是一个矢量量,具有大小和方向。
在国际单位制中,磁通量的单位是韦伯(Wb)。
磁通量的计算公式为:[ = B A () ]其中,B 表示磁场强度,A 表示面积,θ 表示磁场线与法线之间的夹角。
3. 磁感应强度磁感应强度(B)是指单位面积上的磁通量。
磁感应强度用来描述磁场在某一点上的分布情况。
在国际单位制中,磁感应强度的单位是特斯拉(T)。
磁感应强度的计算公式为:[ B = ]其中,Φ 表示磁通量,A 表示面积。
4. 相互关系磁场强度、磁通量和磁感应强度之间存在紧密的相互关系。
根据法拉第电磁感应定律,磁通量的变化会产生电动势,从而产生电流。
因此,磁场强度和磁感应强度可以相互转化。
当电流通过导体时,会产生磁场。
这个磁场的磁感应强度与电流强度成正比,与导线的长度成正比,与导线之间的距离成反比。
因此,磁场强度、磁感应强度和电流之间也存在相互关系。
5. 计算实例假设有一个长直导线,长度为 1 米,电流为 2 安培。
求该导线产生的磁场强度和磁感应强度。
首先,根据磁场强度的计算公式,可以求出导线产生的磁场强度:[ H = = = 2 ]然后,假设在导线附近有一个平面,面积为 1 平方米。
根据磁感应强度的计算公式,可以求出该平面上的磁感应强度:[ B = = = 2 ]因此,该导线产生的磁场强度为 2 A/m,磁感应强度为 2 T。
6. 总结磁场强度、磁通量和磁感应强度是描述磁场的基本物理量。
它们之间存在相互关系,可以通过相应的计算公式进行计算。
磁场,感应计算题有详细答案(快考试了,希望对同学们有所帮助)

稳恒磁场计算题144.稳恒磁学计算题144、如下图所示,AB 、CD 为长直导线BC 为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O点的磁感应强度.解:如图所示,O 点磁场由DC 、CB 、BA 三部分电流产生,其中:DC 产生 )21(4)2sin 4(sin45cos 40001-=-=RI R IB πμπππμ 方向向里 CB 产生 RIR I B 16224002μμππ== 方向向里 BA 产生 03=BRIR I B B B B O 16)12(400321μπμ+-=++= 方向向里145、如图所示,一载流导线中间部分被弯成半圆弧状,其圆心点为O ,圆弧半径为R 。
若导线的流过电流I ,求圆心O 处的磁感应强度。
解:两段直电流部分在O 点产生的磁场01=B弧线电流在O 点产生的磁场 RIB 2202μπα=RI R I B B B O παμπαμ42220021==+=∴146、载流体如图所示,求两半圆的圆心点P 处的磁感应强度。
解:水平直电流产生01=B大半圆 产生1024R IB μ=方向向里小半圆 产生2034R IB μ=方向向里竖直直电流产生2044R I B πμ=方向向外4321B B B B B O +++=∴ )111(44442210202010R R R I R I R IR IB O πμπμμμ-+=-+=方向向里147、在真空中,有两根互相平行的无限长直导线相距0.1m ,通有方向相反的电流,I 1=20A,I 2=10A ,如图所示.试求空间磁感应强度分布,指明方向和磁感应强度为零的点的位置.、解:取垂直纸面向里为正,如图设X 轴。
)1.0(102102)(2272010x x xx d I x I B --⨯=-+=-πμπμ 在电流1I 左侧,B方向垂直纸面向外在电流1I 、2I 之间,B方向垂直纸面向里在电流2I 右侧,当m x 2.0<时,B方向垂直纸面向外当m x 2.0>时,B方向垂直纸面向里当0=B 时,即0)1.0(1021027=--⨯-x x x则 m x 2.0=处的B为0。
14磁场
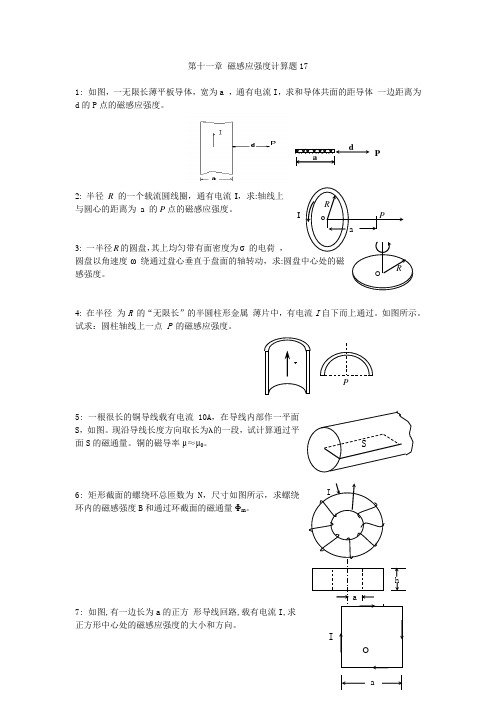
第十一章 磁感应强度计算题171: 如图,一无限长薄平板导体,宽为a ,通有电流I ,求和导体共面的距导体 一边距离为d 的P 点的磁感应强度。
2: 半径 R 的一个载流圆线圈,通有电流I ,求:轴线上与圆心的距离为 a 的P 点的磁感应强度。
3: 一半径R 的圆盘,其上均匀带有面密度为σ 的电荷 ,圆盘以角速度ω 绕通过盘心垂直于盘面的轴转动,求:感强度。
4: 在半径为R 的“无限长”的半圆柱形金属 薄片中,有电流I 自下而上通过。
如图所示。
试求:圆柱轴线上一点 P 的磁感应强度。
5: 一根很长的铜导线载有电流10A ,在导线内部作一平面S ,如图。
现沿导线长度方向取长为 的一段,试计算通过平面S 的磁通量。
铜的磁导率μ≈μ0。
6: 矩形截面的螺绕环总匝数为N ,尺寸如图所示,求螺绕环内的磁感强度B 和通过环截面的磁通量Φm 。
7: 如图,有一边长为a 的正方 形导线回路,载有电流I,求正方形中心处的磁感应强度的大小和方向。
× × a × × × × × d P I P8: 将通有电流I 的导线弯成如图所示的形状, 求O 点处的磁感强度B 。
9: 在半径为2a 的无限长金属圆柱体内挖去一半径为 a 无限长圆柱体 ,两圆柱体的轴线平行,相距为 a ,如图所示。
今有电流沿空心柱体的的轴线方向流动,电流均匀分布在空心柱体的横截面上,设电流密度为δ 。
求 P 点及O 点的磁感应强度。
10: 将通有电流I 的导线弯成如图所示的形状, 求O 点处的磁感强度B 。
11: 如图所示,电荷Q 均匀分布在长为b 的细杆上,杆以角速度ω绕垂直于纸面过 O 点的轴转动 。
O 点在杆的延长线上,与杆的一端距离为a ,求O 点处的磁感应强度B 的大小。
12: 将通有电流I 的导线弯成如图所示的形状, 求O 点处的磁感强度矢量B的大小和方向。
13:如图,两段共心圆弧与半径构成一闭合载流回路,对应的圆心角为θ(rad),电流强度为I 。
电磁感应一解答

回路旋转时,OC、OD段交替切割磁场线,二者产生的E大小相等、方向相反。E的大小为
OC切割时UO>UC
OD切割时UO>UD
3.如图,导体棒AB在均匀磁场B中绕通过C点的垂直于棒长且沿磁场方向的轴OO’转动(角速度w与B同方向),BC的长度为棒长的1/3,则 (A) A点比B点电势高. (B) A点与B点电势相等. (C) A点比B点电势低. (D) 有稳恒电流从A点流向B点.
一、选择题
1. 一无限长直导体薄板宽为 l,板面与 z 轴垂直,板的长度方向沿 y 轴,板的两侧与一个伏特计相接,如图.整个系统放在磁感强度为 B 的均匀磁场中,B 的方向沿z 轴正方向.如果伏特计与导体平板均以速度 u 向 y 轴正方向移动,则伏特计指示的电压值为
(A) 0
(B) uBl/2
(C) uBl
无感应电流
无感应电流
无磁通量变化.
a>>r时,圆环中心的磁场可视为均匀的
2.如图,一半径为r的很小的金属圆环,在初始时刻与一半径为a(a>>r)的大金属圆环共面且同心.在大圆环中通以恒定的电流I,方向如图.如果小圆环以匀角速度w绕其任一方向的直径转动,并设小圆环的电阻为R,则任一时刻 t 通过小圆环的磁通量F =______.小圆环中的感应电流 i =_____________________.
z轴正方向
1.如图,一根长为L的金属细杆ab绕竖直轴O1O2以角速度w在水平面内旋转,O1O2在离细杆a端L/5处.若已知地磁场在竖直方向的分量为B .求ab两端间的电势差Ua-Ub.
解: 由右手螺旋法则知,a端、b端的电位均高于O点
由法拉第电磁感应定律有
三、计算题
2.长为L、质量为m的均匀金属细棒,以棒端O为中心在水平面内旋转,棒的另一端在半径为L的金属环上滑动,棒端O和金属环之间接一电阻R,整个环面处于均匀磁场B中,B的方向垂直于纸面向外,如图.设t=0时初角速度为w0 .忽略摩擦力及金属棒、导线和圆环的电阻.求(1)当角速度为w时金属棒内的动生电动势的大小.(2)棒的角速度随时间变化表达式.
磁学中的磁感应强度和磁场强度计算题

磁学中的磁感应强度和磁场强度计算题磁学是物理学的一个重要分支,研究磁场的发生、性质和变化规律。
在磁学中,磁感应强度和磁场强度是两个重要的物理量。
本文将介绍磁感应强度和磁场强度的概念以及如何计算这两个物理量。
一、磁感应强度(B)的概念和计算方法磁感应强度是一个表示磁场强度大小的物理量,用字母B表示。
它与电流元、磁化强度和磁路的面积有关。
磁感应强度的单位是特斯拉(T)。
磁感应强度的计算公式为:B = μ0 * μr * (H + M)其中,μ0是真空中的磁导率,μr是相对磁导率,H是磁场强度,M是磁化强度。
例如,某个磁体中的磁场强度为0.05A/m,磁化强度为100A/m,真空中的磁导率为4π * 10^-7 H/m,相对磁导率为1。
那么该磁体中的磁感应强度可以通过以下计算得到:B = (4π * 10^-7) * 1 * (0.05 + 100) = 0.05π * 10^-5 T二、磁场强度(H)的概念和计算方法磁场强度是一个表示磁场的物理量,用字母H表示。
它与磁铁磁化强度、电流元和磁路的长度有关。
磁场强度的单位是安培/米(A/m)。
磁场强度的计算公式为:H = (N * I) / l其中,N是电流元的匝数,I是电流元的电流,l是磁路的长度。
举例来说,一个长直导线通有电流为3A,导线的长度为4m,那么该导线周围的磁场强度可以通过以下计算得到:H = (1 * 3) / 4 = 0.75 A/m三、磁感应强度和磁场强度的关系在一定条件下,磁感应强度和磁场强度之间存在线性关系。
当磁场强度为零时,磁感应强度也为零;当磁场强度不为零时,磁感应强度也不为零。
通过调整磁化强度和磁场强度,可以改变磁感应强度的大小。
四、磁感应强度和磁场强度的应用磁感应强度和磁场强度在许多领域有着广泛的应用。
在电动机、变压器、磁共振成像等设备中,磁感应强度和磁场强度都扮演着重要角色。
通过合理计算磁感应强度和磁场强度,可以为这些设备的设计和运行提供依据。
磁场的感应和磁通量练习题

磁场的感应和磁通量练习题1. 简答题(1) 什么是磁感应强度?(2) 什么是磁通量?(3) 什么是法拉第电磁感应定律?(4) 描述磁通量守恒定律的原理。
(5) 什么是楞次定律?2. 计算题(1) 一个匀强磁场的磁感应强度为2T,某垂直于磁场方向上的圆线圈的面积为0.5平方米,当线圈轴线的法向速度为10m/s时,计算在这个过程中感应在圆线圈上的电动势。
(2) 一根长为10cm的导线以匀速1m/s在垂直于磁感应强度为0.5T的磁场中直线运动,求此导线两端之间的电势差。
(3) 一个电感为2H的电感线圈,当通过电流变化的速率为0.2A/s 时,计算感应在电感线圈上的电动势。
(4) 某导体在垂直于磁感应强度为0.8T的磁场中以速率5m/s运动,导体的长度为10cm,导体两端之间的电势差为多少伏特?3. 综合题一根长度为20cm的导线以匀速2m/s向左运动,同时垂直于导线的方向有一个磁场,磁感应强度大小为1T,方向指向纸面内。
导线两端之间的电势差为U。
求:(1) 导线两端之间的电势差U的大小;(2) 当导线长度变为40cm时,导线两端之间的电势差U'的大小。
4. 应用题(1) 在一个长度为10cm的导线周围,空间内有一个与导线平面垂直的匀强磁场,当磁感应强度为0.5T时,导线中通过的电流为2A。
求导线两端之间的电势差。
(2) 一台发电机的磁感应强度为0.2T,由发电机产生的电动势为12V,发电机旋转一周的时间为1s。
求发电机的匝数。
通过以上的练习题,你能够更好地理解和应用磁场的感应和磁通量的相关概念和定律。
希望这些题目能够帮助你巩固相关知识,提高解题能力。
磁场与电磁感应习题及答案

一 选择题 (共36分)1. (本题 3分)(2734) 两根平行的金属线载有沿同一方向流动的电流.这两根导线将: (A) 互相吸引. (B) 互相排斥.(C) 先排斥后吸引. (D) 先吸引后排斥. [ ]2. (本题 3分)(2595) 有一N 匝细导线绕成的平面正三角形线圈,边长为a ,通有电流I ,置于均匀外磁场B v中,当线圈平面的法向与外磁场同向时,该线圈所受的磁力矩M m 值为 (A) 2/32IB Na . (B) 4/32IB Na .(C) °60sin 32IB Na . (D) 0. [ ]3. (本题 3分)(2657) 若一平面载流线圈在磁场中既不受力,也不受力矩作用,这说明: (A) 该磁场一定均匀,且线圈的磁矩方向一定与磁场方向平行. (B) 该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向平行. (C) 该磁场一定均匀,且线圈的磁矩方向一定与磁场方向垂直.(D) 该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向垂直.[ ]4. (本题 3分)(2404) 一导体圆线圈在均匀磁场中运动,能使其中产生感应电流的一种情况是 (A) 线圈绕自身直径轴转动,轴与磁场方向平行. (B) 线圈绕自身直径轴转动,轴与磁场方向垂直. (C) 线圈平面垂直于磁场并沿垂直磁场方向平移.(D) 线圈平面平行于磁场并沿垂直磁场方向平移. [ ]5. (本题 3分)(5137) 尺寸相同的铁环与铜环所包围的面积中,通以相同变化率的磁通量,当不计环的自感时,环中(A) 感应电动势不同. (B) 感应电动势相同,感应电流相同. (C) 感应电动势不同,感应电流相同.(D) 感应电动势相同,感应电流不同. [ ]6. (本题 3分)(1932) 如图所示,一矩形金属线框,以速度vv从无场空间进入一均匀磁场中,然后又从磁场中出来,到无场空间中.不计线圈的自感,下面哪一条图线正确地表示了线圈中的感应电流对时间的函数关系?(从线圈刚进入磁场时刻开始计时,I 以顺时针方向为正)[ ] BvIO(D)IO (C)O (B)I7. (本题 3分)(2417) 对于单匝线圈取自感系数的定义式为L =Φ /I .当线圈的几何形状、大小及周围磁介质分布不变,且无铁磁性物质时,若线圈中的电流强度变小,则线圈的自感系数L(A) 变大,与电流成反比关系. (B) 变小. (C) 不变.(D) 变大,但与电流不成反比关系. [ ]8. (本题 3分)(2752) 在真空中一个通有电流的线圈a 所产生的磁场内有另一个线圈b ,a 和b 相对位置固定.若线圈b 中电流为零(断路),则线圈b 与a 间的互感系数: (A) 一定为零. (B)一定不为零.(C) 可为零也可不为零, 与线圈b 中电流无关. (D) 是不可能确定的.[ ]9. (本题 3分)(2421) 已知一螺绕环的自感系数为L .若将该螺绕环锯成两个半环式的螺线管,则两个半环螺线管的自感系数(A) 都等于L 21. (B) 有一个大于L 21,另一个小于L 21.(C) 都大于L 21. (D) 都小于L 21. [ ]对于单匝线圈取自感系数的定义式为L =Φ /I .当线圈的几何形状、大小及周围磁介质分布不变,且无铁磁性物质时,若线圈中的电流强度变小,则线圈的自感系数L(A) 变大,与电流成反比关系. (B) 变小. (C) 不变.(D) 变大,但与电流不成反比关系. [ ]11. (本题 3分)(5675) 真空中一根无限长直细导线上通电流I ,则距导线垂直距离为a 的空间某点处的磁能密度为(A) 2002(21a I πµµ (B) 2002(21aI πµµ (C) 20)2(21I a µπ (D)2002(21aI µµ [ ]12. (本题 3分)(2415) 用导线围成如图所示的回路(以O 点为心的圆,加一直径),放在轴线通过O 点垂直于图面的圆柱形均匀磁场中,如磁场方向垂直图面向里,其大小随时间减小,则感应电流的流向为[ ]二 填空题 (共76分)13. (本题 3分)(5303) 一平面试验线圈的磁矩大小p m 为1×10-8 A ·m 2,把它放入待测磁场中的A 处,试验线圈如此之小,以致可以认为它所占据的空间内场是均匀的.当此线圈的p m 与z 轴平行时,所受磁力矩大小为M =5×10-9 N ·m ,方向沿x 轴负方向;当此线圈的p m 与y 轴平行时,所受磁力矩为零.则空间A 点处的磁感强度B v的大小为____________,方向为______________.14. (本题 5分)(2066) 一带电粒子平行磁感线射入匀强磁场,则它作________________运动.一带电粒子垂直磁感线射入匀强磁场,则它作________________运动. 一带电粒子与磁感线成任意交角射入匀强磁场,则它作______________运动.如图所示,一半径为R ,通有电流为I 的圆形回路,位于Oxy 平面内,圆心为O .一带正电荷为q 的粒子,以速度v v沿z 轴向上运动,当带正电荷的粒子恰好通过O 点时,作用于圆形回路上的力为________,作用在带电粒子上的力为________.16. (本题 5分)(2070) 截面积为S ,截面形状为矩形的直的金属条中通有电流I .金属条放在磁感强度为B v 的匀强磁场中,B v的方向垂直于金属条的左、右侧面(如图所示).在图示情况下金属条的上侧面将积累____________电荷,载流子所受的洛伦兹力f m =______________.(注:金属中单位体积内载流子数为n )17. (本题 5分)(2580) 电子质量m ,电荷e ,以速度v 飞入磁感强度为B 的匀强磁场中,v v与B v 的夹角为θ ,电子作螺旋运动,螺旋线的螺距h =________________________,半径R =______________________.18. (本题 3分)(2387) 已知面积相等的载流圆线圈与载流正方形线圈的磁矩之比为2∶1,圆线圈在其中心处产生的磁感强度为B 0,那么正方形线圈(边长为a )在磁感强度为B v的均匀外磁场中所受最大磁力矩为______________________.19. (本题 3分)(2096) 在磁场中某点放一很小的试验线圈.若线圈的面积增大一倍,且其中电流也增大一倍,该线圈所受的最大磁力矩将是原来的______________倍.20. (本题 5分)(2603) A 、B 、C 为三根共面的长直导线,各通有10 A 的同方向电流,导线间距d =10 cm ,那么每根导线每厘米所受的力的大小为=l F Ad d ______________________, =l F Bd d ______________________, =lF Cd d ______________________. (µ0 =4π×10-7 N/A 2) I半径为a 的无限长密绕螺线管,单位长度上的匝数为n ,通以交变电流i =I m sin ωt ,则围在管外的同轴圆形回路(半径为r )上的感生电动势为_____________________________.22. (本题 5分)(2702) 如图所示,一直角三角形abc 回路放在一磁感强度为B 的均匀磁场中,磁场的方向与直角边ab 平行 ,回路绕ab 边以匀角速度ω旋转 ,则ac 边中的动生电动势为__________________________,整个回路产生的动生电动势为____________________________.v23. (本题 3分)(2692) 有一根无限长直导线绝缘地紧贴在矩形线圈的中心轴OO ′上,则直导线与矩形线圈间的互感系数为_________________.24. (本题 3分)(2525) 一自感线圈中,电流强度在 0.002 s 内均匀地由10 A 增加到12 A ,此过程中线圈内自感电动势为 400V ,则线圈的自感系数为L =____________.25. (本题 4分)(2619) 位于空气中的长为l ,横截面半径为a ,用N匝导线绕成的直螺线管,当符合________和____________________的条件时,其自感系数可表成V I N L 20)/(µ=,其中V 是螺线管的体积.26. (本题 3分)(2624) 一个中空的螺绕环上每厘米绕有20匝导线,当通以电流I =3 A 时,环中磁场能量密度w =_____________ .(µ 0 =4π×10-7 N/A 2)27. (本题 3分)(5678) 真空中一根无限长直导线中通有电流I ,则距导线垂直距离为a 的某点的磁能密度w m =________________.有两个长度相同,匝数相同,截面积不同的长直螺线管,通以相同大小的电流.现在将小螺线管完全放入大螺线管里(两者轴线重合),且使两者产生的磁场方向一致,则小螺线管内的磁能密度是原来的__________倍;若使两螺线管产生的磁场方向相反,则小螺线管中的磁能密度为____________(忽略边缘效应).29. (本题 4分)(2180) 写出麦克斯韦方程组的积分形式:_____________________________,_____________________________, _____________________________,_____________________________.30. (本题 3分)(2198) 坡印廷矢量S v的物理意义是:_____________________________________________________________; 其定义式为 _____________________ .31. (本题 3分)(2339) 反映电磁场基本性质和规律的积分形式的麦克斯韦方程组为∫∫⋅=VSV S D d d ρv v, ① ∫∫⋅⋅∂∂−=SL S t B l E v vv v d d , ②0d =∫⋅S S B vv , ③ ∫⋅∫⋅∂∂+=SL S t DJ l H v vv v v d )(d . ④试判断下列结论是包含于或等效于哪一个麦克斯韦方程式的.将你确定的方程式用代号填在相应结论后的空白处.(1) 变化的磁场一定伴随有电场;__________________(2) 磁感线是无头无尾的;________________________ (3) 电荷总伴随有电场.__________________________在没有自由电荷与传导电流的变化电磁场中, 沿闭合环路l (设环路包围的面积为S )=∫⋅ll H vv d __________________________________________.=∫⋅ll E vv d __________________________________________.三 计算题 (共46分)33. (本题10分)(2737) 两根平行无限长直导线相距为d ,载有大小相等方向相反的电流I ,电流变化率d I /d t =α >0.一个边长为d 的正方形线圈位于导线平面内与一根导线相距d ,如图所示.求线圈中的感应电动势E ,并说明线圈中的感应电流是顺时针还是逆时针方向.34. (本题10分)(2409) 如图所示,一半径为r 2电荷线密度为λ的均匀带电圆环,里边有一半径为r 1总电阻为R 的导体环,两环共面同心(r 2 >> r 1),当大环以变角速度ω =ω(t )绕垂直于环面的中心轴旋转时,求小环中的感应电流.其方向如何?35. (本题10分)(2410) 一内外半径分别为R 1, R 2的均匀带电平面圆环,电荷面密度为σ,其中心有一半径为r 的导体小环(R 1 >>r ),二者同心共面如图.设带电圆环以变角速度ω =ω(t )绕垂直于环面的中心轴旋转,导体小环中的感应电流i 等于多少?方向如何(已知小环的电阻为R ')?36. (本题 8分)(2138) 求长度为L 的金属杆在均匀磁场B v中绕平行于磁场方向的定轴OO '转动时的动生电动势.已知杆相对于均匀磁场B v的方位角为θ,杆的角速度为ω,转向如图所示.O无限长直导线旁有一与其共面的矩形线圈,直导线中通有恒定电流I ,将此直导线及线圈共同置于随时间变化的而空间分布均匀的磁场B v 中.设0>∂∂tB,当线圈以速度v v垂直长直导线向右运动时,求线圈在如图所示位置时的感应电动势.一 选择题 (共36分)1. (本题 3分)(2734) (A)2. (本题 3分)(2595) (D)3. (本题 3分)(2657) (A)4. (本题 3分)(2404) (B)5. (本题 3分)(5137) (D)6. (本题 3分)(1932) (C)7. (本题 3分)(2417) (C)8. (本题 3分)(2752) (C)9. (本题 3分)(2421) (D)10. (本题 3分)(2417) (C)11. (本题 3分)(5675) (B)12. (本题 3分)(2415) (B)二 填空题 (共76分)13. (本题 3分)(5303) 0.5 T 2分y 轴正方向 1分参考解:B p M m v v v ×=,由m p v平行y 轴时M = 0可知B v 必与y 轴平行,m p v沿z 轴时M 最大,故有 5.0==mp M B T由B p M m v v v ×=定出B v沿y 轴正方向.14. (本题 5分)(2066) 匀速直线 1分 匀速率圆周 2分 等距螺旋线 2分15. (本题 4分)(0361) 0 2分 0 2分16. (本题 5分)(2070) 负 2分 IB / (nS ) 3分17. (本题 5分)(2580) )/(cos 2eB m θv π 3分 )/(sin eB m θv 2分3分19. (本题 3分)(2096) 4 3分20. (本题 5分)(2603) 3×10-6N/cm 2分 0 2分3×10-6N/cm 1分21. (本题 3分)(2615) t a nI m ωωµcos 20π− 3分22. (本题 5分)(2702) 8/2B l ω 3分 0 2分23. (本题 3分)(2692) 0 3分24. (本题 3分)(2525) 0.400 H 3分25. (本题 4分)(2619) l >>a 2分 细导线均匀密绕 2分26. (本题 3分)(2624) 22.6 J ·m -3 3分27. (本题 3分)(5678) )8/(2220a I πµ 3分28. (本题 5分)(2425) 4 3分 0 2分29. (本题 4分)(2180) ∫∫⋅=V S V S D d d ρv v 1分 ∫∫⋅⋅∂∂−=S L S t B l E v v v v d d 1分 0d =∫⋅SS B v v 1分∫⋅∫⋅∂∂+=SL S t D J l H v v v v v d )(d 1分 30. (本题 3分)(2198) 电磁波能流密度矢量 2分 H E S v v v ×= 1分31. (本题 3分)(2339) ② 1分 ③ 1分 ① 1分32. (本题 4分)(5160) ∫∫⋅∂∂S S D t v v d 或 t D /d d Φ 2分 ∫∫⋅∂∂−S S B t v v d 或 t m /d d Φ− 2分三 计算题 (共46分)33. (本题10分)(2737) 解:(1) 载流为I 的无限长直导线在与其相距为r 处产生的磁感强度为: )2/(0r I B π=µ 2分以顺时针绕向为线圈回路的正方向,与线圈相距较远的导线在线圈中产生的磁通量为: 23ln 2d 203201π=π⋅=∫Id r r I d d dµµΦ 与线圈相距较近的导线对线圈的磁通量为:2ln 2d 20202π−=π⋅−=∫Id r r I d d dµµΦ 总磁通量 34ln 2021π−=+=Id µΦΦΦ 4分感应电动势为: 34ln 2d d )34(ln 2d d 00αµµπ=π=−=d t I d t ΦE 2分由E >0和回路正方向为顺时针,所以E 的绕向为顺时针方向,线圈中的感应电流 亦是顺时针方向. 2分解:大环中相当于有电流 2)(r t I λω⋅=2分这电流在O 点处产生的磁感应强度大小λωµµ)(21)2/(020t r I B == 2分以逆时针方向为小环回路的正方向,210)(21r t π≈λωµΦ 2分∴ tt r t i d )(d 21d d 210ωλµΦπ−=−=E tt R r R i i d )(d 2210ωλµ⋅π−==E 2分方向:d ω(t ) /d t >0时,i 为负值,即i 为顺时针方向.1分 d ω(t ) /d t <0时,i 为正值,即i 为逆时针方向.1分35. (本题10分)(2410) 解:带电平面圆环的旋转相当于圆环中通有电流I .在R 1与R 2之间取半径为R 、宽度为d R 的环带,环带内有电流R t R I d )(d ωσ= 2分d I 在圆心O 点处产生的磁场R t R I B d )(21/.d 21d 00σωµµ== 2分由于整个带电环面旋转,在中心产生的磁感应强度的大小为))((21120R R t B −=σωµ 1分选逆时针方向为小环回路的正方向,则小环中2120))((21r R R t π−≈σωµΦ 1分tt R R r t i d )(d )(2d d 1220ωσµΦ−π−=−=E tt R R R r R i i d )(d 2)( 1220ωσµ⋅′−−=′=E 2分方向:当d ω (t ) /d t >0时,i 与选定的正方向相反.1分 当d ω (t ) /d t <0时,i 与选定的正方向相同.1分36. (本题 8分)(2138) 解:在距O 点为l 处的d l 线元中的动生电动势为d E l B v v v d )(⋅×=v 2分θωsin l =v 2分∴ E ∫∫⋅π=×=Ld cos )21sin(v d )v (l B l B L αv v v ∫∫==ΛθωθθωL l l B l lB 02d sin sin d sin θω22sin 21BL = 3分 E 的方向沿着杆指向上端.1分 O B v v ×v解:取顺时针方向回路正向.设动生电动势和感生电动势分别用E 1和E 2表示,则总电动势EE = E 1 + E 2 l B l B 211v v −=E ))(22(00b a I a I l +π−π=µµv )(20b a a lIb +π=v µ 4分 ∫∂∂−=⋅∂∂−=S t B bl S t B v v d 2E 3分∴ bl tB b a a I ])(2[0∂∂−+π=vµE 1分。
大学物理磁场试题及答案

大学物理磁场试题及答案一、选择题(每题2分,共10分)1. 磁场的基本特性是()。
A. 有方向性B. 有大小和方向C. 只有方向性D. 只有大小答案:B2. 根据安培环路定理,穿过闭合回路的磁通量与()。
A. 回路的面积成正比B. 回路的面积成反比C. 回路的面积无关D. 回路的面积的平方成正比答案:C3. 磁感应强度的方向是()。
A. 电流方向B. 电流方向的相反方向C. 垂直于电流方向D. 与电流方向成任意角度答案:C4. 磁通量的大小由()决定。
A. 磁场的强度B. 面积的大小C. 磁场与面积的夹角D. 以上所有因素答案:D5. 磁感应强度的单位是()。
A. 特斯拉B. 高斯C. 安培/米D. 以上都是答案:D二、填空题(每题2分,共10分)1. 一个长直导线产生的磁场,其磁感应强度与导线距离的平方成______。
答案:反比2. 地球的磁场可以近似看作是一个______。
答案:条形磁铁3. 根据洛伦兹力公式,一个带电粒子在磁场中运动时受到的力的方向与______。
答案:磁场方向和粒子速度方向都垂直4. 磁通量的基本单位是______。
答案:韦伯5. 磁感应强度的定义式为______。
答案:B = F/IL三、计算题(每题10分,共30分)1. 一个长为L的直导线,通有电流I,求在距离导线r处的磁感应强度。
答案:B = (μ₀I)/(2πr)2. 一个半径为R的圆形线圈,通有电流I,求其轴线上距离线圈中心d处的磁感应强度。
答案:B = (μ₀I)/(2R² + d²)^(3/2)3. 一个长为L的直导线,通有电流I,求在距离导线r处的磁通量,假设导线上方有一面积为A的平面与磁场垂直。
答案:Φ = B * A = (μ₀I * A)/(2πr)四、简答题(每题5分,共10分)1. 简述磁感应强度和磁通量的区别。
答案:磁感应强度是描述磁场强弱和方向的物理量,其大小和方向由磁场本身决定,与测试电荷无关。
电工基础第4章磁场与电磁感应题库(可编辑修改word版)

四、计算题
1.有一环状铁心线圈,流过的电流为5A,要使磁动势达到2000A,试求线圈的匝数。
2.有一圆环形螺旋线圈,外径为60cm,内径为40c:m,线圈匝数为1200匝,通有5A的电流,求线圈内分别为空气隙和软铁时的磁通(设软铁的相对磁导率为700H/m)。
3.磁感应强度和磁场强度有哪些异同?
4—3 磁场对电流的作用一、填空题
1.通常把通电导体在磁场中受到的力称为,也称,通电直导体在磁场内的受力方向可用定则来判断。
2.把一段通电导线放人磁场中,当电流方向与磁场方向时,导线所受到的电磁力最大;当电流方向与磁场方向时,导线所受的电磁力最小。
3.两条相距较远且相互平行的直导线,当通以相同方向的电流时,它们;当通以相反方向的电流时,它们。
第四章磁场与电磁感应
一、填空题(每空 1 分)
[问题]
某些物体能够的性质称为磁性。具有的物体称为磁体,磁体分为和两大类。
[答案]
吸引铁、镍、钴等物质磁性天然磁体人造磁体
[问题]
磁体两端的部分称磁极。当两个磁极靠近时,它们之间也会产生相互作用力,即同名磁极相互,异名磁极相互。
[答案]
磁性最强排斥吸引
[问题]
2.在一自感线圈中通人如图所示电流,前2s内产生的自感电动势为1V,则线圈的自感系数是多少?
第 3s、第 4s 内线圈产生的自感电动势是多少?第 5s 内线圈产生的自感电动势是多少?
54—7 互感一、填空题
1.由于一个线圈中的电流产生变化而在中产生电磁感应的现象叫互感现象。
2.当两个线圈相互时,互感系数最大;当两个线圈相互时,互感系数最小。
1.当线圈中通入()时,就会引起自感现象。A.不变的电流
初中电磁感应专题练习(含详细答案)

初中电磁感应专题练习(含详细答案)
一、选择题
1. 一个导线在磁场中匀速向右移动,感应电动势的方向如何?
A. 由左向右
B. 由右向左
C. 没有感应电动势
D. 无法确定
答案:B
2. 带电粒子在磁场中匀速运动,运动轨迹如何?
A. 直线运动
B. 圆形运动
C. 抛物线运动
D. 双曲线运动
答案:B
二、计算题
1. 一个弯曲的导线长为10cm,导线中有一个电流I=2A,若在
导线处有一个磁感应强度为B=3T的磁场,求电动势的大小为多少?
解答:
$\mathcal{E}=Blv=\frac{1}{2}Blv=\frac{1}{2}Blsin\theta=\frac{1}{2} \times 3 \times 0.1 \times 2=\frac{3}{20}$V。
三、简答题
1. 什么是电磁感应?
电磁感应是指导体中的电子受到磁场的作用从而在导体两端产
生的电动势。
2. 什么是法拉第电磁感应定律?
法拉第电磁感应定律指出,当导体中的磁力线发生变化时,沿
着导体的任意闭合回路中就会产生感应电动势,其大小与磁通量的
变化率成正比,方向满足楞次定律。
3. 什么是楞次定律?
楞次定律指出,当导体内有感应电流时,该电流所发出的磁场的方向是这样的,即它所引起的磁通量的变化总是阻碍引起这种变化的原因。
4. 什么情况下会产生感应电流?
当导体在磁场中发生运动或被磁场线穿过而发生变化时,就会在导体中产生感应电流。
电磁感应计算题及解答

电磁感应一、选择题1、如图所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且垂直纸面,MN、PQ为其边界,OO’为其对称轴。
一导线折成变长为的正方形闭合回路abcd,回路在纸面内以恒定速度v o向右运动,当运动到关于OO’对称的位置时A.穿过回路的磁通量为零B.回路中感应电动势大小为C.回路中感应电流的方向为顺时针方向D.回路中ab边与cd边所受安培力方向相同2、如图8,在O点下方有一个具有理想边界的磁场,铜环在A点由静止释放向右摆至最高点B,不考虑空气阻力,则下列说法正确的是()A.A、B两点在同一水平线B.A点高于B点C.A点低于B点D.铜环将做等幅摆动二、计算题3、如图所示,两根质量均为m=2kg的金属棒垂直地放在光滑的水平导轨上,左右两部分导轨间距之比为1∶2,导轨间有大小相等但左右两部分方向相反的匀强磁场,CD棒电阻为AB棒电阻的两倍,不计导轨电阻,今用250N的水平力F向右拉CD棒,在CD棒运动0.5m的过程中,两棒上产生的焦耳热共为45J,此时CD棒速率为8m/s,立即撤去拉力F,设导轨足够长且两棒始终在不同磁场中运动,求:(1)撤去拉力F瞬间AB棒速度v A;(2)两棒最终匀速运动的速度v A′和v C′。
4、如图所示,光滑矩形斜面ABCD的倾角为,在其上放置一矩形金属线框,的边长,的边长,线框的质量,电阻,线框通过细线绕过定滑轮与重物相连,细线与斜面平行且靠近。
重物质量,离地面的高度为。
斜面上区域是有界匀强磁场,方向垂直于斜面向上,已知AB到的距离为,到的距离为,到CD的距离为,取。
现让线框从静止开始运动(开始时刻与AB边重合),发现线框匀速穿过匀强磁场区域,求:(1)区域内匀强磁场的磁感应强度B(2)线框在通过磁场区域过程中产生的焦耳热Q(3)通过计算分析画出线框从开始运动到边与CD边重合过程中线框的图象5、如图所示,半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于导线框所在平面,导线框的左端通过导线接一对水平放置的平行的金属板,两极间的距离为d,板长为L。
高中物理磁场经典计算题训练(有答案)

高中物理磁场经典计算题训练(有答案)1.弹性挡板围成边长为L = 100cm 的正方形abcd ,固定在光滑的水平面上,匀强磁场竖直向下,磁感应强度为B = 0。
5T ,如图所示。
质量为m =2×10-4kg 、带电量为q =4×10-3C 的小球,从cd 边中点的小孔P 处以某一速度v 垂直于cd 边和磁场方向射入,以后小球与挡板的碰撞过程中没有能量损失。
(1)为使小球在最短的时间内从P 点垂直于dc 射出来,小球入射的速度v 1是多少? (2)若小球以v 2 = 1 m/s 的速度入射,则需经过多少时间才能由P 点出来?2。
如图所示, 在区域足够大空间中充满磁感应强度大小为B 的匀强磁场,其方向垂直于纸面向里。
在纸面内固定放置一绝缘材料制成的边长为L 的等边三角形框架DEF , DE 中点S 处有一粒子发射源,发射粒子的方向皆在图中截面内且垂直于DE 边向下,如图(a )所示.发射粒子的电量为+q ,质量为m ,但速度v 有各种不同的数值.若这些粒子与三角形框架碰撞时均无能量损失,并要求每一次碰撞时速度方向垂直于被碰的边。
试求: (1)带电粒子的速度v 为多大时,能够打到E 点? (2)为使S 点发出的粒子最终又回到S 点,且运动时间最短,v 应为多大?最短时间为多少? (3)若磁场是半径为a 的圆柱形区域,如图(b )所示(图中圆为其横截面),圆柱的轴线通过等边三角形的中心O ,且a =)10133( L 。
要使S 点发出的粒子最终又回到S 点,带电粒子速度v 的大小应取哪些数值?3。
在直径为d 的圆形区域内存在匀强磁场,磁场方向垂直于圆面指向纸外.一电荷量为q ,质量为m 的粒子,从磁场区域的一条直径AC 上的A 点射入磁场,其速度大小为v 0,方向与AC 成α.若此粒子恰好能打在磁场区域圆周上D 点,AD 与AC 的夹角为β,如图所示.求该匀强磁场的磁感强度B 的大小.a b cdACFD(a )(b )4。
带电粒子在匀强磁场中的运动计算题含答案

带电粒子在匀强磁场中的运动计算题1.如图,空间存在方向垂直于纸面(xOy平面)向里的磁场。
在x≥0区域,磁感应强度的大小为B0;x<0区域,磁感应强度的大小为λB0(常数λ>1)。
一质量为m、电荷量为q(q>0)的带电粒子以速度v0从坐标原点O沿x轴正向射入磁场,此时开始计时,当粒子的速度方向再次沿x轴正向时,求(不计重力)(1)粒子运动的时间;(2)粒子与O点间的距离。
2.平面直角坐标系xOy中,第Ⅰ象限存在垂直于平面向里的匀强磁场,第Ⅲ象限存在沿y轴负方向的匀强电场,如图所示。
一带负电的粒子从电场中的Q点以速度v0沿x轴正方向开始运动,Q点到y轴的距离为到x轴距离的2倍。
粒子从坐标原点O离开电场进入磁场,最终从x轴上的P点射出磁场,P点到y轴距离与Q点到y轴距离相等。
不计粒子重力,求:(1)粒子到达O点时速度的大小和方向;(2)电场强度和磁感应强度的大小之比。
3.如图,在y>0的区域存在方向沿y轴负方向的匀强电场,场强大小为E,在y<0的区域存在方向垂直于xOy 平面向外的匀强磁场。
一个氕核11H和一个氘核12H先后从y轴上y=h点以相同的动能射出,速度方向沿x 轴正方向。
已知11H进入磁场时,速度方向与x轴正方向的夹角为60°,并从坐标原点O处第一次射出磁场。
1H的质量为m,电荷量为q,不计重力。
求1(1)11H第一次进入磁场的位置到原点O的距离;(2)磁场的磁感应强度大小;(3)12H第一次离开磁场的位置到原点O的距离。
4.如图甲,空间存在﹣范围足够大的垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.让质量为m,电量为q(q>0)的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向入射到该磁场中。
不计重力和粒子间的影响。
(1)若粒子以初速度v1沿y轴正向入射,恰好能经过x轴上的A(a,0)点,求v1的大小;(2)已知一粒子的初速度大小为v(v>v1),为使该粒子能经过A(a,0)点,其入射角θ(粒子初速度与x 轴正向的夹角)有几个?并求出对应的sinθ值;(3)如图乙,若在此空间再加入沿y轴正向、大小为E的匀强电场,一粒子从O点以初速度v0沿y轴正向发射。
磁场+电磁感应-题干

1. 【推题】如图,长为2l的直导线拆成边长相等,夹角为60o的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在该导线中通以电流强度为I的电流时,该V形通电导线受到的安培力大小为()A.0 B.0.5BIl C.BIl D.2BIl2. 【推题】电磁感应发射装置的简易模型如图所示,质量为m,电阻为R,边长为L的正方形金属线框abcd竖直静止放置在水平面上,垂直于线框平面存在有界匀强磁场,线框cd边在磁场外侧且紧靠磁场边界。
在某次成功发射过程中,磁感应强度B随时间t的变化规律为B=B0+kt(k是大于零的常数),线框能穿过磁场继续上升,上升的最大高度为h。
重力加速度为g,空气阻力不计,线框平面在运动过程中不旋转始终保持竖直。
下列说法错误的是()A.t=0时刻,线框中的电流大小I=kL2RB.t=0时刻,线框ab边受到安培力F=B0kL3RC.线框从静止到最高点的过程中安培力所做的功等于mghD.线框从最高点下落,再次经过磁场的过程中磁感应强度大小为B′且保持恒定,使线框最终以速度v安全着陆。
则线框下落过程运动总时间t=B ´2L3mgR3. 【推题】如图所示,金属线框abcd 置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度。
金属线框以速度v0开始向右运动最终穿过磁场区域,ab边始终保持与磁场边界平行,则在线框进入磁场区域和离开磁场区域过程()A.线框受到的安培力方向相同B.线框受到的安培力大小相同C.通过线框导体横截面的电量相同D.线框中产生的热量相同4. 【推题】如图所示,在光滑的水平面上方有两个磁感应强度大小均为B、方向相反的水平匀强磁场区域,磁场宽度均为L。
一个边长为L、电阻为R的单匝正方形金属线框,在水平外力作用下沿垂直磁场方向运动,从如图实线位置Ⅰ进入磁场开始到线框运动到分别有一半面积在两个磁场中的位置Ⅱ时,线框的速度始终为v ,则下列说法正确的是( )A .在位置Ⅱ时外力F 为22B L vRB .在位置Ⅱ时线框中的电功率为2224B L v RC .此过程中回路产生的电能为233B L vRD .此过程中通过导线横截面的电荷量为2BL R5. 【推题】如图甲所示,等离子气流(由高温高压的等电量的正、负离子组成)由左方连续不断地以速度v 0 射入P 1 和P 2 两极板间的匀强磁场中,ab 直导线与P 1 、P 2 相连接,线圈A 与直导线cd 相连接,线圈A 内存在如图乙所示的变化磁场,且磁感应强度B 的正方向规定为向左,则下列叙述正确的是( )A .0~1s 内ab 、cd 导线互相排斥B .1~2s 内ab 、cd 导线互相吸引C .2~3s 内ab 、cd 导线互相排斥D .3~4s 内ab 、cd 导线互相吸引6. 【推题】如图3-6所示的等臂天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽为l ,共N 匝,线圈的下部悬在匀强磁场中,磁场方向垂直纸面.当线圈中通有电流I (方向如图)时,在天平左、右两边加上质量各为m 1、m 2的砝码,天平平衡.当电流反向(大小不变)时,右边再加上质量为m 的砝码后,天平重新平衡.由此可知( )A .磁感应强度的方向垂直纸面向外B .磁感应强度的方向垂直纸面向里C .磁感应强度的大小为12()m m gNIlD .磁感应强度的大小为2mgNIl7. 【推题】如图所示,边长为L 的正方形abcd 为两个匀强磁场的边界,正方形内磁场的方向垂直纸面向外。
物理练习题电磁感应练习题

物理练习题电磁感应练习题物理练习题:电磁感应一、单选题1. 电磁感应的基本定律是:A. 荷塞定律B. 法拉第定律C. 伏特定律D. 麦克斯韦定律正确答案:B2. 在匀强磁场中,一根导线长度为L,导线移动的速度为v,两段导线之间的电势差为U,磁感应强度为B。
根据法拉第定律,电势差U与导线的长度L、速度v、磁感应强度B之间的关系是:A. U ∝ LB. U ∝ vC. U ∝ BD. U ∝ Lvb正确答案:D3. 远离电流的一侧把右手握成半握拳,拇指指向电流方向,其他四指所指方向即为:A. 磁场方向B. 电流方向C. 电势方向D. 导线方向正确答案:A4. 在磁场中,当一个导体切割磁感线运动时,导体两端会产生:A. 电动势B. 电流C. 磁化D. 弹性正确答案:A5. 变压器的原理是基于:A. 磁化原理B. 法拉第定律C. 电动势产生D. 电磁感应现象正确答案:D二、填空题1. 电磁感应现象最早由_______发现。
正确答案:法拉第2. 变压器的工作原理是基于_______现象。
正确答案:电磁感应3. 根据电磁感应现象,当导体运动时,导线两端产生的电势差与速度的关系为_______。
正确答案:正比例4. 在匀强磁场中,导线的运动方向与磁感应线的方向______。
正确答案:垂直5. 根据法拉第定律,当闭合回路中的磁链发生变化时,产生的感应电动势会阻止_______变化。
正确答案:磁链三、解答题1. 一个导体沿着磁场方向运动,运动方向与磁感应线方向垂直,当导体速度为v,磁感应强度为B时,求导体受到的安培力大小。
解答:根据洛仑兹力公式,安培力的大小可以通过公式F = BIL计算得到。
在本题中,导体的速度与磁感应线方向垂直,所以磁感应线与导体的角度为90°,导体的长度为L。
根据公式,可得到F = BLv。
2. 一个电阻为R的闭合回路中,磁感应强度为B,在t时刻磁通量发生了变化Φ = Φ0 + αt,其中Φ0和α为常数。
法拉第电磁感应定律典型练习题40道 附答案

姓名:_______________班级:_______________考号:_______________题号一、选择题二、填空题三、计算题四、多项选择总分得分一、选择题(每空?分,共?分)1、彼此绝缘、相互垂直的两根通电直导线与闭合线圈共面,下图中穿过线圈的磁通量可能为零的是2、伟大的物理学家法拉第是电磁学的奠基人,在化学、电化学、电磁学等领域都做出过杰出贡献,下列陈述中不符合历史事实的是()A.法拉第首先引入“场”的概念来研究电和磁的现象B.法拉第首先引入电场线和磁感线来描述电场和磁场C.法拉第首先发现了电流的磁效应现象D.法拉第首先发现电磁感应现象并给出了电磁感应定律3、如图所示,两个同心放置的共面金属圆环a和b,一条形磁铁穿过圆心且与环面垂直,则穿过两环的磁通量Φa和Φb大小关系为:A.Φa>ΦbB.Φa<ΦbC.Φa=ΦbD.无法比较4、关于感应电动势大小的下列说法中,正确的是()A.线圈中磁通量变化越大,线圈中产生的感应电动势一定越大评卷人得分B.线圈中磁通量越大,产生的感应电动势一定越大C.线圈放在磁感强度越强的地方,产生的感应电动势一定越大D.线圈中磁通量变化越快,产生的感应电动势越大5、对于法拉第电磁感应定律,下面理解正确的是A.穿过线圈的磁通量越大,感应电动势越大B.穿过线圈的磁通量为零,感应电动势一定为零C.穿过线圈的磁通量变化越大,感应电动势越大D.穿过线圈的磁通量变化越快,感应电动势越大6、如图所示,均匀的金属长方形线框从匀强磁场中以匀速V拉出,它的两边固定有带金属滑轮的导电机构,金属框向右运动时能总是与两边良好接触,一理想电压表跨接在PQ两导电机构上,当金属框向右匀速拉出的过程中,电压表的读数:(金属框的长为a,宽为b,磁感应强度为B)A.恒定不变,读数为BbV B.恒定不变,读数为BaVC.读数变大 D.读数变小7、如图所示,平行于y轴的导体棒以速度v向右匀速直线运动,经过半径为R、磁感应强度为B的圆形匀强磁场区域,导体棒中的感应电动势ε与导体棒位置x关系的图像是8、如图所示,一个高度为L的矩形线框无初速地从高处落下,设线框下落过程中,下边保持水平向下平动。
高中磁场试题及答案

高中磁场试题及答案一、选择题1. 磁场的基本性质是什么?A. 磁场对放入其中的电流有力的作用B. 磁场对放入其中的电荷有力的作用C. 磁场对放入其中的物体有力的作用D. 磁场对放入其中的金属有力的作用答案:A2. 根据安培环路定理,磁场线是闭合的,那么以下哪个选项是错误的?A. 磁场线是闭合的B. 磁场线不相交C. 磁场线可以是直线D. 磁场线总是从磁北极指向磁南极答案:D3. 一个带正电的粒子以一定速度进入磁场,如果磁场方向垂直于粒子运动的方向,那么粒子的运动轨迹是什么形状?A. 直线B. 圆C. 螺旋D. 抛物线答案:B二、填空题4. 根据洛伦兹力公式,一个带电粒子在磁场中的受力大小为 \[ F = q \times v \times B \],其中 \( q \) 表示______,\( v \) 表示______,\( B \) 表示______。
答案:电荷量;速度;磁感应强度5. 磁通量是穿过一个闭合表面的磁场线的总数,其单位是______。
答案:韦伯(Weber)三、简答题6. 请简述法拉第电磁感应定律的主要内容。
答案:法拉第电磁感应定律指出,当磁场中的磁通量发生变化时,会在闭合电路中产生感应电动势。
感应电动势的大小与磁通量变化的速率成正比。
四、计算题7. 一个长为 \( L \) 的导线,以速度 \( v \) 在垂直于磁场 \( B \) 的方向上运动,求导线两端的感应电动势。
答案:根据法拉第电磁感应定律,导线两端的感应电动势 \( E \) 可以通过公式 \( E = B \times L \times v \) 计算得出。
五、论述题8. 论述磁场对带电粒子运动的影响,并给出一个实际应用的例子。
答案:磁场对带电粒子的影响主要体现在洛伦兹力的作用上。
当带电粒子以一定速度进入磁场时,如果其速度方向与磁场方向不平行,粒子将受到一个垂直于速度和磁场方向的力,导致粒子做圆周运动。
一个实际应用的例子是质谱仪,它利用磁场使带电粒子在磁场中做圆周运动,通过测量粒子的轨迹半径来确定粒子的质量和电荷比。
磁场、电磁感应

一、 选择题:(每小题3分,共6)磁场1 一个带电粒子以速度v 垂直进入匀强磁场B 中,其运动轨迹是一半径为R 的圆。
要使半径变为 2R ,磁感应强度B 应变为:( )(A) 2B (B) B/2 (C)2 B (D) 2 B/22. 磁场的高斯定理说明了稳恒磁场的某些性质。
下列说法正确的是 ( )(A) 磁场力是保守力;(B) 磁场是无源场;(C) 磁场是非保守力场;(D) 磁感应线不相交。
3 如图所示,1/4圆弧导线 ab,半径为r,电流为I ,均匀磁场为B, 方向垂直ab 向上,求圆弧ab 受的安培力的大小和方向()(A 2BIr 垂直纸面向外 (B 2BIr 垂直纸面向里(C )2BIrπ 垂直纸面向外 (D )2BIrπ垂直纸面向里4. 如图所示,圆型回路L 内有电流1I 、2I ,回路外有电流3I ,均在真空中,P 为L 上的点,则( )得分(A )012()L d I I μ•=-+⎰B l (B )0123()L d I I I μ•=++⎰B l(C )0123()L d I I I μ•=+-⎰B l (D )012()L d I I μ•=+⎰B l5 匀强磁场B 中有一半径为r ,高为L 的圆柱面,B 方向与柱轴平行,则穿过圆柱面的磁通量为:()(A) B R 2π(B) 0(C) B R 22π (D) BR 221π6 载有电流I 的导线如图放置,在圆心O 处的磁感应强度B 为:( )(A)µ0I/4R+µ0I/4πR (B)µ0I/2πR+ 3µ0I/8R(C) µ0I/4πR -3µ0I/8R (D) µ0I/4R+ µ0I/2πR7 如图所示,共面放置一根无限长的载流导线和一矩形线圈,在磁场力的作用下,线圈将在该平面内如何运动?()(A) 向上(B) 向下(C) 向左(D)向右8 下列说法正确的是()(A)闭合回路上各点磁感强度都为零时,回路内一定没有电流穿过(B)闭合回路上各点磁感强度都为零时,回路内穿过电流的代数和必定为零(C)磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度必定为零(D)磁感强度沿闭合回路的积分不为零时,回路上任意一点的磁感强度都不可能为零9 如图所示,在无限长载流直导线附近作一球形闭合曲面S,当曲面S向长直导线靠近时,穿过曲面S的磁通量Φ和面上各点的磁感应强度B将如何变化?()(A)Φ增大,B也增大;(B)Φ不变,B也不变;(C)Φ增大,B不变;(D)Φ不变,B增大。
大学物理D-05稳恒磁场、电磁感应定律-参考答案

0i ,选回路的绕行方向为顺时针方向, 2r
dr r
Bds
0 I ldr 2 r
当矩形线圈距离长直导线为 R 时,通过矩形线圈的磁通量为
d
Ra
R
0 I I Ra ldr 0 l ln R 2 r 2
d I
l
4
a
Ra d ln 1 dR 0 R 1 d lI n n 0 l I 则: n dt 2 2 dt R R a dt
2 B2 lv
0 Ilv 得 2 ( d a )
n( 1 2)
0 Ilvn 1 1 ( ) d d a 2
1
2
5
a点电势高于O点.∴ U a U b 2 1
1 16 15 3 BL2 BL2 BL2 BL2 50 50 50 10
如果金属细杆绕杆中央旋转,则ab两端电势差为0. 5.2.5 如图所示,一无限长直导线通有电流 I=5.0A,一矩形单匝线圈与此长直导线共面。设矩形线圈 以 v=2.0m/s 的速度垂直于长直导线向右运动。已知:l=0.40m, a=0.20m, d=0.20m,求矩形线圈中的感应电 动势。 (不计线圈的自感) 解:方法(一)如图,距离长直导线为 r 处的磁感应强度为: B 则通过窄条面积 ds 的磁通量为: d
B dS 0 说明了下面的哪些叙述是正确的?
(
A )
穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数; 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数; 一根磁感应线可以终止在闭合曲面内; 一根磁感应线可以完全处于闭合曲面内。
(A)ad; (B)ac; (C)cd; (D)ab。 5.2.3. 如图,无限长直载流导线与正三角形载流线圈在同一平面内,若长直导 线固定不动,则载流三角形线圈将 (A) 向着长直导线平移; (B) 离开长直导线平移; (C) 转动; (D) 不动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
稳恒磁场计算题144.稳恒磁学计算题144、如下图所示,AB 、CD 为长直导线BC 为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如图所示,O 点磁场由DC 、CB 、BA 三部分电流产生,其中:DC 产生 )21(4)2sin 4(sin45cos 40001-=-=RI R IB πμπππμ 方向向里 CB 产生 RIR I B 16224002μμππ== 方向向里 BA 产生 03=BRIR I B B B B O 16)12(400321μπμ+-=++= 方向向里145、如图所示,一载流导线中间部分被弯成半圆弧状,其圆心点为O ,圆弧半径为R 。
若导线的流过电流I ,求圆心O 处的磁感应强度。
解:两段直电流部分在O 点产生的磁场 01=B弧线电流在O 点产生的磁场 RIB 2202μπα=RI R I B B B O παμπαμ42220021==+=∴146、载流体如图所示,求两半圆的圆心点P 处的磁感应强度。
解:水平直电流产生 01=B大半圆 产生 1024R IB μ=方向向里小半圆 产生 2034R IB μ=方向向里竖直直电流产生 2044R I B πμ=方向向外4321B B B B B O +++=∴)111(44442210202010R R R I R I R IR IB O πμπμμμ-+=-+=方向向里147、在真空中,有两根互相平行的无限长直导线相距0.1m ,通有方向相反的电流,I 1=20A,I 2=10A ,如图所示.试求、解:取垂直纸面向里为正,如图设X 轴。
)1.0(102102)(2272010x x xx d I x I B --⨯=-+=-πμπμ 在电流1I 左侧,B方向垂直纸面向外在电流1I 、2I 之间,B方向垂直纸面向里在电流2I 右侧,当m x 2.0<时,B方向垂直纸面向外 当m x 2.0>时,B方向垂直纸面向里当0=B 时,即0)1.0(1021027=--⨯-x x x则 m x 2.0=处的B为0。
148、图中所示是一根很长的长直圆管形导体的横截面,内、外半径分别为a 、b ,导体内载有沿轴线方向的电流I ,电流均匀地分布在管的横截面上.设导体的磁导率μ0,试计算导体空间各点的磁感应强度。
解:取以截面轴线点为心,r 为半径的圆形回路根据安培环路定理:∑⎰=∙i LI l d B 0μ(1)当a r <时 02=r B π 0=B(2)当b ra <<时 )(222202a r ab Ir B ππππμπ--=)()(222220a b a r r I B --=πμ (3)当b r>时 I r B o μπ=2 rI B πμ20=149、 如图所示,一根无限长直导线,通有电流I ,中部一段弯成圆弧形,求图中O 点磁感应强度的大小。
解:两段直线电流在O 点产生的磁场==21B B )sin 1(cos 4)sin 2(sincos 400ααπμαπαπμ-=-R IR I方向垂直纸面向里弧线电流在O 点 απμμπαRIR I B 2222003==方向垂直纸面向里)tan cos 1(22)sin 1(cos 2000321αααπμαπμααπμ+-=+-=++=∴R I RIR IB B B B O 方向垂直纸面向里150、一根同轴电缆由半径为R 1的长圆柱形导线和套在它外面的内半径为R 2、外半径为R 3的同轴导体圆筒组成,如图所示,传导电流I 沿导线向上流去,由圆筒向下流回,在它们的截面上电流都是均匀分布的,求同轴电缆内外各处的磁感应强度的大小。
解: 根据:∑⎰=∙i LI l d B 0μ(1)当1R r <时 2212r R I r B ππμπ= r R I B 2102πμ= (2)当21R r R <<时 I r B 02μπ= rI B πμ20=(3)当32R r R <<时 [])(222222302R r R R II rB ππππμπ---=)()(222232230R R r R r I B --=πμ(4)当3R r >时 02=rB π 0=B151、有电流I 的无限长导线折成如图的形状,已知圆弧部分的半径为R ,试求导线在圆心O 处的磁感应强度矢量B 的大小和方向?解:竖直直电流在O 点RI B πμ401=方向垂直纸面向里水平直电流在O 点 RIB πμ402=方向垂直纸面向外 弧线形电流在O 点 RIR I B 83243003μμ==方向垂直纸面向外321B B B B O++=∴RIB B B B O 830321μ=++-= 方向垂直纸面向外152、长直载流导线通以电流I ,其旁置一长为m 、宽为n 的导体矩形线圈。
矩形线圈与载流导线共面,且其长边与载流导线平行(两者相距为a),(1)求该线圈所包围面积内的磁通量;(2)若线圈中也通以电流I ,求此载流线圈所受的合力。
解:(1)取面元mdr ds =an a mI mdr r I Bmdrs d B n a am +===∙=⎰⎰⎰+ln 2200πμπμφ(2)根据 ⎰⨯=B l Id F左边 amI m a I I IBdl F πμπμ222001===⎰ 方向向左 右边 )(2Im 202n a mI B F +==πμ 方向向右上边 an a I dr r I I F na a+==⎰+ln 222003πμπμ 方向向上 下边 an a I F +=ln 2204πμ 方向向下4321F F F F F+++=合)(2)11(2202021n a a mn I n a a m I F F F +=+-=-=πμπμ合 方向向左153、无限长载流导线I 1与直线电流I 2共面,几何位置如图所示.试求载流导线I 2受到电流I 1磁场的作用力.解:取 l d I 2 B l d I F d⨯=2dl I r I dF 2102πμ= ab a I I dr r I I F ba a+==⎰+ln60cos 22100210πμπμ 方向垂直2I 向上154、无限长载流导线I 1与直线电流I 2共面且垂直,几何位置如图所示.计算载流导线I 2受到电流I 1磁场的作用力和关于O 点的力矩;试分析I 2施加到I 1上的作用力.解: 在l 上取dr , 它与长直导线距离为r ,1I 在此产生的磁场方向垂直纸面向里,大小为rI B πμ210= dr I 2受力B r d I F d ⨯=2dr rI I dF πμ2210= 方向向上ab 导线受力dld I I dr r I I dF F ld d+===⎰⎰+ln22210210πμπμ 方向向上 F d 对O 点力矩 F d r M d⨯=其大小 dr I I rdF dM πμ2210== 方向垂直纸面向外 l II dr I I dM M ld dπμπμ22210210===∴⎰⎰+ 方向向外 从对称角度分析,直电流2I 在无限长载流导线1I 上产生的磁场以O 点对称,即O 点上下对称点的B大小相等,方向相反,所以2I 在1I 对称点上所施加的安培力也应大小相等,方向相反,具有对称性,则2I 施加在1I 上的合外力为零。
155、长直载流导线I 1附近有一等腰直角三角形线框,通以电流I 2,二者共面.求△ABC 的各边所受的磁力.解:B l d I F BAAB ⨯=⎰2daI I dl d I I F BAAB πμπμ22210102==⎰ 方向垂直AB 向左 B l d I F CAAC ⨯=⎰2dad I I dr r I I F ad dAC +==⎰+ln 22210102πμπμ 方向垂直AC 向下 同理 rI dlI F BC πμ2102⎰=45cos drdl =d ad I I dr r I I F ad dBC +==∴⎰+ln245cos 22102210πμπμ 方向垂直BC 向上156、边长为l =0.1m 的正三角形线圈放在磁感应强度B =1T 的均匀磁场中,线圈平面与磁场方向平行.如图所示,使线圈通以电流I =10A ,求:线圈每边所受的安培力;对OO /轴的磁力矩大小;(3)从所在位置转到线圈平面与磁场垂直时磁力所作的功.解:(1)B l I F ab ⨯= N IlB F ab 866.0120sin 0== 方向垂直纸面向外0=⨯=B l I F bcB l I F ca⨯= N IlB F ca 866.0120sin 0== 方向垂直纸面向里(2)n m e IS P= B P M M ⨯=m N ISB B P M M ∙⨯===-201033.490sin 方向沿'O O 方向(3)磁力功 )(12φφ-=I A01=φ B l BS 2243==φ J B l IA 221033.443-⨯==∴157、一平面塑料圆盘,半径为R ,表面带有面密度为σ剩余电荷.假定圆盘绕其轴线A A '以角速度ω (rad ·s -1)转动,磁场B 的方向垂直于转轴A A '.试证磁场作用于圆盘的力矩的大小为44BR M πσω=.(提示:将圆盘分成许多同心圆环来考虑.)解 :“取圆环rdr ds π2=,其中rdr rdr Tdq dI σωωππσ===22磁矩 dr r dI r dP M 32πσωπ==B P d M d M⨯= 方向垂直纸面向里大小为rB r B P M m d d d 3πωσ=⨯=4d d 403B R r r B M M Rπσωπωσ===⎰⎰158、在磁感应强度为B 的均匀磁场中,垂直于磁场方向的平面内有一段载流弯曲导线,电流为I ,如图所示.建立适当的坐标系,求其所受的安培力.解:在曲线上取l d ,则⎰⨯=baab B l Id Fl d 与B 夹角都是2π不变,B 是均匀的B b Ia B l d I B l Id F b ab aab⨯=⨯=⨯=∴⎰⎰)(其大小BIab F ab = 方向垂直ab 向上159、如图所示,在长直导线内通以电流I 1=20A ,在矩形线圈中通有电流I 2=10 A , 两者共面,且矩形线圈之纵边与长直导线平行.已知a=9.0cm, b=20.0cm, d=1.0 cm ,求:(1)(2)矩形线圈所受合力和合力矩.解:(1)CD F方向垂直CD 向左,大小4102100.82-⨯==dI bI F CD πμ N同理FE F方向垂直FE 向右,大小5102100.8)(2-⨯=+=a d I bI F FE πμ NCF F方向垂直CF 向上,大小为⎰+-⨯=+πμ=πμ=ad dCF dad I I r r I I F 5210210102.9ln 2d 2 N ED F方向垂直ED 向下,大小为5102.9-⨯==CF ED F F N(2)合力ED CF FE CD F F F F F+++=方向向左,大小为4102.7-⨯=F N合力矩B P M m⨯=∵ 线圈与导线共面∴ B P m//0=M.电磁感应计算题160、两相互平行无限长的直导线,流有大小和方向如图所示的电流,金属杆CD 与两导线保持共面,相对位置如图。
