机械优化设计上机报告
机械优化设计实验报告

《机械优化设计》课程实验报告M a t l a b优化工具箱一、实验目的和要求熟悉Matlab7.0软件的界面和基本功能,了解Matlab优化工具箱的常用算法;使用Matlab优化工具箱的f m i n u n c/f m i n s e a r c h函数求解多变量非线性无约束优化问题;使用Matlab优化工具箱的f m i n c o n函数求解多变量非线性约束优化问题。
二、实验设备和软件台式计算机,Matlab7.0软件。
三、实验内容求解下列优化问题的最优解。
要求:(1)编写求解优化问题的M文件,(2)在命令窗口输入求解优化问题的命令,并得出计算结果。
1、标量优化问题1) f=x2-10x+362) f=x4-5x3+4x2-6x+603) f=(x+1)(x-2)22、多变量非线性无约束优化问题1) f=4(x1-5) 2+( x2-6) 2初始点:x0=[8,9]T;2) f=(x12+x2-11)2+( x1+ x22-7)2初始点:x0=[1,1]T;3) f=[1.5- x1(1- x2)]2+[2.25- x1(1- x22)]2+[2.625- x1(1- x23)]2初始点:x0=[2,0.2]T;4) f=( x12+12 x2-1)2+(49 x1+49 x2+84 x1+2324 x2-681)2初始点:x0=[1,1]T;5) f=( x1+10 x2)2+5(x3- x4)2+( x2-2 x3)4+10(x1- x4)4初始点:x0=[3,-1,0,1]T;3、多变量非线性约束优化问题1) f=( x1-2)2+( x2-1)2g1= x12-x2≤0g2= x1+x2-2≤0初始点:x0=[3,3]T;2) f= x23[( x1-3)2-9]/273≤0g1=x2-x1/3≤0g2=-x1+x2/3≤0g3=x1+x2/3-6≤0g4=-x1≤0g5=-x2≤0初始点:x0=[1,5]T;3) f=1000- x12-2x2 2-x32-x1x2-x1x3g1=-x1≤0g2=-x2≤0g3=-x3≤0g4=x12+x22+x3 2-25=0g5=8x1+14x2+7x3-56=0初始点:x0=[2,2,2]T4)f=100(x2-x12)2+(1-x1)2+90(x4-x32)2+(1-x3)2+10[(x2-1)2+(x4-1)2]+19.8(x2-1)(x4-1)-10≤x1≤10-10≤x2≤10-10≤x3≤10-10≤0x4≤10初始点:x0=[-3,-1,-3,-1]T;四、M文件、在命令窗口输入的求解命令清单及计算结果记录>>1、(1)目标函数的M文件function f=fun1(x)f=x^2-10*x+36调用求解命令x0=0;options=optimset('LargeScale','off');lb=-10;ub=10;[x,fval]=fminbnd(@fun1,lb,ub,options)或{ x0=0; [x,fval]=fminbnd(@fun1,-10,10)} x =5.0000fval =11.00002、(2)目标函数的M文件function f=fun2(x)f=x^4-5*x^3+4*x^2-6*x+60调用求解命令x0=0;options=optimset('LargeScale','off');lb=0;ub=10;[x,fval]=fminbnd(@fun2,lb,ub,options)x =3.2796fval =22.65902、(3)目标函数的M文件function f=fun3(x)f=(x+1)*(x-2)^2调用求解命令> x0=0;options=optimset('LargeScale','off');lb=0;ub=10;[x,fval]=fminbnd(@fun3,lb,ub,options)x =2.0000fval =1.9953e-0113(1)目标函数的M文件function f=fun4(x)f=4*(x(1)-5)^2+(x(2)-6)^2调用求解命令x0=[8,9];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun4,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun. x =5.00006.0000fval =1.7876e-0123(2)目标函数的M文件function f=fun5(x)f=(x(1)^2+x(2)-11)^2+(x(1)+x(2)^2-7)^2调用求解命令>> x0=[1,1];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun5,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun. x =3.0000 2.0000fval =5.2125e-0123(3)目标函数的M文件function f=fun6(x)f=[1.5-x(1)*(1-x(2))]^2+[2.25-x(1)*(1-x(2)^2)]^2+[2.625-x(1)*(1-x(2)^3)]^2调用求解命令x0=[2,0.2];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun6,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun. x =3.0000 0.5000fval =3.9195e-0143(4)目标函数的M文件function f=fun7(x)f=(x(1)^2+12*x(2)-1)^2+(49*x(1)+49*x(2)+84*x(1)+2324*x(2)-681)^2调用求解命令x0=[1,1];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun7,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun. x =0.9570 0.2333fval =7.37643(5)目标函数的M文件function f=fun8(x)f=(x(1)+10*x(2))^2+5*(x(3)-x(4))^2+(x(2)-2*x(3))^4+10*(x(1)-x(4))^4调用求解命令>> x0=[3,-1,0,1];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun8,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun.x =0.0015 -0.0002 -0.0031 -0.0031fval =6.3890e-009三、3、(1)目标函数的M文件function f=fun9(x)f=(x(1)-2)^2+(x(2)-1)^2约束函数的M文件function [c,cep]=con1(x)c=[x(1)^2-x(2);x(1)+x(2)-2];cep=[]当前窗口条用求解命令x0=[3,3];options=optimset('LargeScale','off');[x,fval]=fmincon(@fun9,x0,[],[],[],[],[],[],@con1,options)Optimization terminated: first-order optimality measure less than options.TolFun and maximum constraint violation is less than options.TolCon.Active inequalities (to within options.TolCon = 1e-006):lower upper ineqlin ineqnonlin12x =1.0000 1.0000fval =1.00003、(2)目标函数的M文件function f=fun10(x)f=x(2)^3*[(x(1)-3)^2-9]/27*3^(1/2)约束函数的M文件function [c,cep]=con2(x)c=[x(2)-x(1)/3^(1/2);-x(1)+x(2)/3^(1/2);x(1)+x(2)/3^(1/2)-6];cep=[]当前窗口条用求解命令x0=[1,5];lb=[0,0];options=optimset('LargeScale','off');[x,fval]=fmincon(@fun10,x0,[],[],[],[],lb,ub,@con2,options)Optimization terminated: first-order optimality measure lessthan options.TolFun and maximum constraint violation is lessthan options.TolCon.Active inequalities (to within options.TolCon = 1e-006):lower upper ineqlin ineqnonlin13x =4.5000 2.5981fval =-7.59383、(3)目标函数的M文件function f=fun11(x)f=1000-x(1)^2-2*x(2)^2-x(3)^2-x(1)*x(2)-x(1)*x(3)约束函数的M文件function [c,cep]=con3(x)c=[];cep=[x(1)^2+x(2)^2+x(3)^2-25;8*x(1)+14*x(2)+7*x(3)-56];当前窗口条用求解命令x0=[2,2,2];lb=[0,0,0];ub=[];options=optimset('LargeScale','off');[x,fval]=fmincon(@fun11,x0,[],[],[],[],lb,ub,@con3,options)Optimization terminated: first-order optimality measure lessthan options.TolFun and maximum constraint violation is lessthan options.TolCon.No active inequalitiesx =3.5121 0.2170 3.5522fval =961.71523、(4)目标函数的M文件function f=fun12(x)f=100*(x(2)-x(1)^2)^2+(1-x(1))^2+90*(x(4)-x(3)^2)^2+(1-x(3))^2+10*[(x(2)-1) ^2+(x(4)-1)^2]+19.8*(x(2)-1)*(x(4)-1)约束函数的M文件function [c,cep]=con4(x)cep=[];当前窗口条用求解命令x0=[-3,-1,-3,-1,];lb=[-10,-10,-10,-10];ub=[10,10,10,10];options=optimset('LargeScale','off');[x,fval]=fmincon(@fun12,x0,[],[],[],[],lb,ub,@con4,options)Optimization terminated: Magnitude of directional derivative in searchdirection less than 2*options.TolFun and maximum constraint violationis less than options.TolCon.No active inequalitiesx =1.0001 1.0002 0.9999 0.9997fval =2.3989e-007五、质疑和建议对于一维标量优化问题搜索,在当前窗口中调用求解命令时,[x,fval]=fminbnd(@fun1,lb,ub,options)可以改成[x,fval]=fminbnd(@fun1,-10,10)如下:function f=fun1(x)f=x^2-10*x+36调用求解命令x0=0;options=optimset('LargeScale','off');lb=-10;ub=10;[x,fval]=fminbnd(@fun1,lb,ub,options)或{ x0=0; [x,fval]=fminbnd(@fun1,-10,10)}x =5.0000fval =11.0000。
机械优化设计上机实践报告【精编版】

机械优化设计上机实践报告【精编版】机械优化设计上机实践报告班级:机械(茅以升)101姓名:学号: 1004010510成绩:指导教师: 张迎辉日期: 2013.11.201 《一维搜索方法》上机实践报告1、写出所选择的一维搜索算法的基本过程、原理(可附流程图说明)。
(一)进退法1. 算法原理进退法是用来确定搜索区间(包含极小值点的区间)的算法,其理论依据是:()f x 为单谷函数(只有一个极值点),且[,]a b 为其极小值点的一个搜索区间,对于任意12,[,]x x a b ∈,如果()()12f x f x <,则2[,]a x 为极小值的搜索区间,如果()()12f x f x >,则1[,]x b 为极小值的搜索区间。
因此,在给定初始点0x ,及初始搜索步长h 的情况下,首先以初始步长向前搜索一步,计算()0f x h +。
(1) 如果()()00f x f x h <+则可知搜索区间为0[,]xx h +%,其中x %待求,为确定x %,后退一步计算0()f x h λ-,λ为缩小系数,且01λ<<,直接找到合适的*λ,使得()*00()f x h f x λ->,从而确定搜索区间*00[,]x h x h λ-+。
(2) 如果()()00f x f x h >+则可知搜索区间为0[,]x x %,其中x %待求,为确定x %,前进一步计算0()f x h λ+,λ为放大系数,且1λ>,知道找到合适的*λ,使得()*00()f x h f x h λ+<+,从而确定搜索区间*00[,]x x h λ+。
2. 算法步骤用进退法求一维无约束问题min (),f x x R ∈的搜索区间(包含极小值点的区间)的基本算法步骤如下:(1) 给定初始点(0)x ,初始步长0h ,令0h h =,(1)(0)x x =,0k =;(2) 令(4)(1)x x h =+,置1k k =+;(3) 若()()(4)(1)f x f x <,则转步骤(4),否则转步骤(5);(4) 令(2)(1)(1)(4),x x x x ==,()()(2)(1)f x f x =,()()(1)(4)f x f x =,令2h h =,转步骤(2);(5) 若1k =,则转步骤(6)否则转步骤(7);(6) 令h h =-,(2)(4)x x =,()()(2)(4)f x f x =,转步骤(2);(7) 令(3)(2)(2)(1)(1)(4),,x x x x x x ===,停止计算,极小值点包含于区间(1)(3)(3)(1)[,][,]x x x x 或(二)黄金分割法1、黄金分割法基本思路:黄金分割法适用于[a ,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
机械优化设计上机实践报告

机械优化设计上机实践报告本次机械优化设计上机实践报告是由学生在机械专业课程的学习中所完成的一项任务,旨在通过实践操作提高学生的机械设计和优化能力。
本次实践任务分为两个部分,第一部分是机械零件的设计,第二部分是该零件的优化设计。
一、机械零件设计在机械零件设计的部分,我们需要使用软件来实现。
首先,我们需要通过建立一个零部件的三维模型,然后通过在模型上进行绘制,来完成机械零件的设计。
在实践过程中,我们学习了许多机械零件设计的基本操作。
比如,怎样用不同的工具来创建不同的几何形状的零件。
同时我们还学习了常用的切削工具和块状建模工具。
这些工具让我们能够在短时间内完成复杂的机械零件的建模操作。
我们也学会了如何使用装配工具,通过将不同的零部件组合成装配体,从而使业主更直观地看到最终的产品形态。
二、机械优化设计经过机械零件设计的部分后,我们就开始了机械零件的优化设计。
因为在设计过程中,我们不仅需要考虑性能问题,还要考虑到材料成本和制造工艺等实际因素。
机械优化设计就是在保证零部件符合需要的功能的前提下,通过对材料和几何形状的优化,提高了零部件的机械性能和制造效率。
在实践过程中,我们首先需要了解机械零件的功能和作用,然后参考相关的设计标准和规范,确定重点优化对象。
我们还需要收集和分析机械零件在使用中的各种受力情况,然后确定机械零件的性能参数和指标,然后对机械零件的机械性能和材料利用率进行计算和分析。
经过机械优化设计的部分后,我们已经对完成的机械零件进行了大量的优化操作。
我们优化了零部件的材料选取、几何形状、工艺流程等方面,使机械零件的机械性能得到进一步提升,同时也降低了制造成本,实现了性价比的优化。
总结通过本次机械优化设计研讨实践,我们更好地理解和掌握了机械零件的设计和优化方法。
我们学会了如何使用专业设计软件,更好地了解了机械零件的实际构造和特性。
我们也学会了机械优化设计的思维方式,明确了优化设计需要考虑的各方面因素,能够更好地满足机械零件使用的实际要求。
机械优化设计实验
§1 综合性编程的上机实验一实验目的无约束坐标轮换优化方法调用一维最优化方法,一维最优化方法(0。
618法)又调用区间搜索法(进退法),综合性编制程序的上机实验。
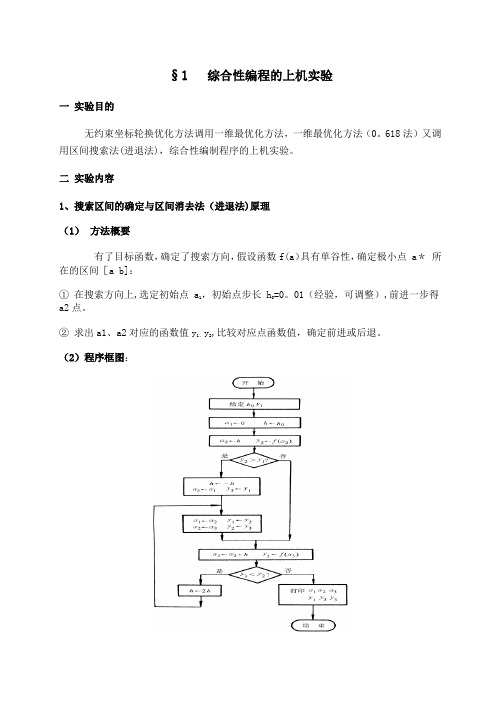
二实验内容1、搜索区间的确定与区间消去法(进退法)原理(1)方法概要有了目标函数,确定了搜索方向,假设函数f(a)具有单谷性,确定极小点 a*所在的区间[a b]:①在搜索方向上,选定初始点 a1,初始点步长 h=0。
01(经验,可调整),前进一步得a2点。
②求出a1、a2对应的函数值y1、y2,比较对应点函数值,确定前进或后退。
(2)程序框图:3、一维搜索黄金分割法(0.618法)(1)基本思想前提:已通过进退法确定了符合函数值高低高规律的搜索区间[a,b]即,函数的极小点必在[a,b]内.所以要调用搜索区间的进退法(2)程序框图①初始区间[a,b],由进退法确定。
收敛精度ε(ε=10—4~ 10-5),缩短率λ=0。
618②计算a1、a2,f (a1)、 f (a2),③根据区间消去法原理缩短区间,进行区间名称的代换,并保留区间中计算的一个新试验点及函数值。
④检查区间是否短到足够小和函数值收敛到足够近。
若条件不满足,则返回到②⑤若条件满足,则取最后两个试验点的平均值作为极小点数值的近似解。
4、多维无约束坐标轮换法(1)基本思想把多维问题转化为一系列一维搜索问题.沿设计变量的各个分量形成的坐标轴依次进行一维搜索(固定其它分量,仅对一个分量优选,轮番搜索),即调用一维最优化方法(0.618法),而一维最优化方法(0。
618法)又调用区间搜索法(进退法)。
重复进行,直至找出满足精度的极小点。
(2)程序框图(3)具体要求①注意数组的应用,便于设计过程中沿各坐标轴迭代时的数据处理;②注意子程序和子函数的调用,简化设计过程,便于数据的计算机处理;③设计结果在界面上显示,并进行数据分析。
④写出上机实验报告§2有约束优化方法应用编制程序的上机实验一、实验目的使学生能用有约束优化设计方法解决简单工程问题的优化设计,对所设计的问题建立数学模型,并确定设计变量、目标函数和约束条件;调用有约束问题的最优化方法(惩罚函数法)编制程序,进而在计算机上求解并对优化的计算结果进行正确的分析和处理。
机械优化设计上机实践报告书

机械优化设计上机实践报告班级:机械(茅以升)101姓名:学号: 1004010510成绩:指导教师: 张迎辉日期: 2013.11.201 《一维搜索方法》上机实践报告1、写出所选择的一维搜索算法的基本过程、原理(可附流程图说明)。
(一)进退法1.算法原理进退法是用来确定搜索区间(包含极小值点的区间)的算法,其理论依据是:()f x 为单谷函数(只有一个极值点),且[,]a b 为其极小值点的一个搜索区间,对于任意12,[,]x x a b ∈,如果()()12f x f x <,则2[,]a x 为极小值的搜索区间,如果()()12f x f x >,则1[,]x b 为极小值的搜索区间。
因此,在给定初始点0x ,及初始搜索步长h 的情况下,首先以初始步长向前搜索一步,计算()0f x h +。
(1) 如果()()00f x f x h <+则可知搜索区间为0[,]x x h +,其中x 待求,为确定x ,后退一步计算0()f x h λ-,λ为缩小系数,且01λ<<,直接找到合适的*λ,使得()*00()f x h f x λ->,从而确定搜索区间*00[,]x h x h λ-+。
(2) 如果()()00f x f x h >+则可知搜索区间为0[,]x x ,其中x 待求,为确定x ,前进一步计算0()f x h λ+,λ为放大系数,且1λ>,知道找到合适的*λ,使得()*00()f x h f x h λ+<+,从而确定搜索区间*00[,]x x h λ+。
2. 算法步骤用进退法求一维无约束问题min (),f x x R ∈的搜索区间(包含极小值点的区间)的基本算法步骤如下:(1) 给定初始点(0)x ,初始步长0h ,令0h h =,(1)(0)x x =,0k =; (2) 令(4)(1)x x h =+,置1k k =+;(3) 若()()(4)(1)f x f x <,则转步骤(4),否则转步骤(5);(4) 令(2)(1)(1)(4),x x x x ==,()()(2)(1)f x f x =,()()(1)(4)f x f x =,令2h h =,转步骤(2); (5) 若1k =,则转步骤(6)否则转步骤(7);(6) 令h h =-,(2)(4)x x =,()()(2)(4)f x f x =,转步骤(2);(7) 令(3)(2)(2)(1)(1)(4),,x x x x x x ===,停止计算,极小值点包含于区间(1)(3)(3)(1)或x x x x[,][,](二)黄金分割法1、黄金分割法基本思路:黄金分割法适用于[a,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
机械优化设计上机报告

机械优化设计上机实践报告班级:机械(茅以升)101姓名 :学号 : 1004010510成绩 :指导教师 : 迎辉日期 : 2013.11.201 《一维搜索方法》上机实践报告1、写出所选择的一维搜索算法的基本过程、原理(可附流程图说明)。
(一)进退法 1. 算法原理进退法是用来确定搜索区间(包含极小值点的区间)的算法,其理论依据是:()f x 为单谷函数(只有一个极值点),且[,]a b 为其极小值点的一个搜索区间,对于任意12,[,]x x a b ∈,如果()()12f x f x <,则2[,]a x 为极小值的搜索区间,如果()()12f x f x >,则1[,]x b 为极小值的搜索区间。
因此,在给定初始点0x ,及初始搜索步长h 的情况下,首先以初始步长向前搜索一步,计算()0f x h +。
(1) 如果()()00f x f x h <+则可知搜索区间为0[,]x x h +%,其中x %待求,为确定x %,后退一步计算0()f x h λ-,λ为缩小系数,且01λ<<,直接找到合适的*λ,使得()*00()f x h f x λ->,从而确定搜索区间*00[,]x h x h λ-+。
(2) 如果()()00f x f x h >+则可知搜索区间为0[,]x x %,其中x %待求,为确定x %,前进一步计算0()f x h λ+,λ为放大系数,且1λ>,知道找到合适的*λ,使得()*00()f x h f x h λ+<+,从而确定搜索区间*00[,]x x h λ+。
2. 算法步骤用进退法求一维无约束问题min (),f x x R ∈的搜索区间(包含极小值点的区间)的基本算法步骤如下:(1) 给定初始点(0)x ,初始步长0h ,令0h h =,(1)(0)x x =,0k =; (2) 令(4)(1)x x h =+,置1k k =+;(3) 若()()(4)(1)f x f x <,则转步骤(4),否则转步骤(5);(4) 令(2)(1)(1)(4),x x x x ==,()()(2)(1)f x f x =,()()(1)(4)f x f x =,令2h h =,转步骤(2); (5) 若1k =,则转步骤(6)否则转步骤(7);(6) 令h h =-,(2)(4)x x =,()()(2)(4)f x f x =,转步骤(2);(7) 令(3)(2)(2)(1)(1)(4),,x x x x x x ===,停止计算,极小值点包含于区间(1)(3)(3)(1)[,][,]x x x x 或(二)黄金分割法1、黄金分割法基本思路:黄金分割法适用于[a ,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
机械优化设计上机实践报告

机械优化设计上机实践报告1. 引言机械优化设计是利用计算机辅助设计与优化方法,对机械结构进行改进和优化,以提高机械设计的性能和效率。
本实践报告基于团队在机械优化设计课程中的上机实践,探讨了机械优化设计的基本原理、方法和实践过程,并对优化后的设计进行了验证和评估。
2. 方法与流程2.1 问题定义本实践中,我们选择了一个简化的机械结构问题:求解一根长度为L的钢杆在两个支点上的最大挠度。
这个问题可以抽象为一个优化问题:寻找一个合适的杆件横截面形状,使得钢杆的挠度最小。
2.2 初始设计我们首先需要设计一个初始杆件形状作为优化的起点。
根据经验和初步分析,我们选择了一个圆形横截面作为初始设计。
通过计算机辅助设计软件绘制出了该初始设计的三维模型,并进行了有限元分析,得到了初始设计的挠度。
2.3 优化算法为了寻找更优的杆件形状,我们采用了一种遗传算法作为优化方法。
遗传算法模拟了自然界中的进化过程,通过选择、交叉和变异等操作对初始设计进行优化。
具体的算法流程如下:1.初始化种群:随机生成一定数量的个体作为种群。
2.评估适应度:利用有限元分析对每个个体进行挠度计算,并评估其适应度。
3.选择操作:根据适应度选择一部分个体作为父代,用于繁殖下一代。
4.交叉操作:对选中的父代进行交叉操作,产生新的个体。
5.变异操作:对新产生的个体进行变异操作,引入新的基因。
6.更新种群:用新产生的个体替换原有种群中的部分个体。
7.终止条件判断:如果满足终止条件,则结束优化过程;否则返回第2步。
2.4 优化结果与分析经过多轮迭代,我们得到了优化后的设计结果。
通过有限元分析对优化后的设计进行挠度计算,发现挠度明显减小。
此外,我们还对优化前后的设计进行了对比测试,结果显示优化后的设计在挠度方面有明显的改进。
3. 结果与讨论本次机械优化设计实践取得了良好的效果。
通过遗传算法优化,我们成功改进了钢杆的横截面形状,使得其挠度显著减小。
这表明机械优化设计在提高机械结构性能方面具有很大的潜力。
(机械制造行业)机械优化设计上机报告

机械优化设计上机实践报告班级:机械(茅以升)101姓名:学号: 1004010510成绩:指导教师: 张迎辉日期: 2013.11.201 《一维搜索方法》上机实践报告1、写出所选择的一维搜索算法的基本过程、原理(可附流程图说明)。
(一)进退法 1. 算法原理进退法是用来确定搜索区间(包含极小值点的区间)的算法,其理论依据是:()f x 为单谷函数(只有一个极值点),且[,]a b 为其极小值点的一个搜索区间,对于任意12,[,]x x a b ∈,如果()()12f x f x <,则2[,]a x 为极小值的搜索区间,如果()()12f x f x >,则1[,]x b 为极小值的搜索区间。
因此,在给定初始点0x ,及初始搜索步长h 的情况下,首先以初始步长向前搜索一步,计算()0f x h +。
(1) 如果()()00f x f x h <+则可知搜索区间为0[,]x x h +%,其中x %待求,为确定x %,后退一步计算0()f x h λ-,λ为缩小系数,且01λ<<,直接找到合适的*λ,使得()*00()f x h f x λ->,从而确定搜索区间*00[,]x h x h λ-+。
(2) 如果()()00f x f x h >+则可知搜索区间为0[,]x x %,其中x %待求,为确定x %,前进一步计算0()f x h λ+,λ为放大系数,且1λ>,知道找到合适的*λ,使得()*00()f x h f x h λ+<+,从而确定搜索区间*00[,]x x h λ+。
2. 算法步骤用进退法求一维无约束问题min (),f x x R ∈的搜索区间(包含极小值点的区间)的基本算法步骤如下:(1) 给定初始点(0)x ,初始步长0h ,令0h h =,(1)(0)x x =,0k =; (2) 令(4)(1)x x h =+,置1k k =+;(3) 若()()(4)(1)f x f x <,则转步骤(4),否则转步骤(5);(4) 令(2)(1)(1)(4),x x x x ==,()()(2)(1)f x f x =,()()(1)(4)f x f x =,令2h h =,转步骤(2); (5) 若1k =,则转步骤(6)否则转步骤(7);(6) 令h h =-,(2)(4)x x =,()()(2)(4)f x f x =,转步骤(2);(7) 令(3)(2)(2)(1)(1)(4),,x x x x x x ===,停止计算,极小值点包含于区间(1)(3)(3)(1)[,][,]x x x x 或(二)黄金分割法1、黄金分割法基本思路:黄金分割法适用于[a ,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械优化设计上机实践报告班级:机械(茅以升)101姓名:学号: 1004010510成绩:指导教师: 张迎辉日期: 2013.11.201 《一维搜索方法》上机实践报告1、写出所选择的一维搜索算法的基本过程、原理(可附流程图说明)。
(一)进退法 1. 算法原理进退法是用来确定搜索区间(包含极小值点的区间)的算法,其理论依据是:()f x 为单谷函数(只有一个极值点),且[,]a b 为其极小值点的一个搜索区间,对于任意12,[,]x x a b ∈,如果()()12f x f x <,则2[,]a x 为极小值的搜索区间,如果()()12f x f x >,则1[,]x b 为极小值的搜索区间。
因此,在给定初始点0x ,及初始搜索步长h 的情况下,首先以初始步长向前搜索一步,计算()0f x h +。
(1) 如果()()00f x f x h <+则可知搜索区间为0[,]x x h +,其中x 待求,为确定x ,后退一步计算0()f x h λ-,λ为缩小系数,且01λ<<,直接找到合适的*λ,使得()*00()f x h f x λ->,从而确定搜索区间*00[,]x h x h λ-+。
(2) 如果()()00f x f x h >+则可知搜索区间为0[,]x x ,其中x 待求,为确定x ,前进一步计算0()f x h λ+,λ为放大系数,且1λ>,知道找到合适的*λ,使得()*00()f x h f x h λ+<+,从而确定搜索区间*00[,]x x h λ+。
2. 算法步骤用进退法求一维无约束问题min (),f x x R ∈的搜索区间(包含极小值点的区间)的基本算法步骤如下:(1) 给定初始点(0)x ,初始步长0h ,令0h h =,(1)(0)x x =,0k =; (2) 令(4)(1)x x h =+,置1k k =+;(3) 若()()(4)(1)f x f x <,则转步骤(4),否则转步骤(5);(4) 令(2)(1)(1)(4),x x x x ==,()()(2)(1)f x f x =,()()(1)(4)f x f x =,令2h h =,转步骤(2); (5) 若1k =,则转步骤(6)否则转步骤(7);(6) 令h h =-,(2)(4)x x =,()()(2)(4)f x f x =,转步骤(2);(7) 令(3)(2)(2)(1)(1)(4),,x x x x x x ===,停止计算,极小值点包含于区间(1)(3)(3)(1)[,][,]x x x x 或(二)黄金分割法1、黄金分割法基本思路:黄金分割法适用于[a ,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
因此,这种方法的适应面非常广。
黄金分割法也是建立在区间消去法原理基础上的试探方法,即在搜索区间[a ,b]内适当插入两点a1,a2,并计算其函数值。
a1,a2将区间分成三段,应用函数的单谷性质,通过函数值大小的比较,删去其中一段,是搜索区间得以缩小。
然后再在保留下来的区间上作同样的处理,如此迭代下去,是搜索区间无限缩小,从而得到极小点的数值近似解。
2 黄金分割法的基本原理一维搜索是解函数极小值的方法之一,其解法思想为沿某一已知方向求目标函数的极小值点。
一维搜索的解法很多,这里主要采用黄金分割法(0.618法)。
该方法用不变的区间缩短率0.618代替斐波那契法每次不同的缩短率,从而可以看成是斐波那契法的近似,实现起来比较容易,也易于人们所接受。
图1黄金分割法是用于一元函数f(x)在给定初始区间[a,b]内搜索极小点α*的一种方法。
它是优化计算中的经典算法,以算法简单、收敛速度均匀、效果较好而著称,是许多优化算法的基础,但它只适用于一维区间上的凸函数[6],即只在单峰区间内才能进行一维寻优,其收敛效率较低。
其基本原理是:依照“去劣存优”原则、对称原则、以及等比收缩原则来逐步缩小搜索区间[7]。
具体步骤是:在区间[a,b]内取点:a1 ,a2 把[a,b]分为三段。
如果f(a1)>f(a2),令a=a1,a1=a2,a2=a+r*(b-a);如果f(a1)<f(a2) ,令b=a2,a2=a1,a1=b-r*(b-a),如果|(b-a)/b|和|(y1-y2)/y2|都大于收敛精度ε重新开始。
因为[a,b]为单峰区间,这样每次可将搜索区间缩小0.618倍或0.382倍,处理后的区间都将包含极小点的区间缩小,然后在保留下来的区间上作同样的处理,如此迭代下去,将使搜索区[a,b]逐步缩小,直到满足预先给定的精度时,即获得一维优化问题的近似最优解。
黄金分割法原理如图1所示,3 程序流程如下:4 实验所编程序框图否算例1:min f(x)= x*x+2*x(1)C++程序如下:#include <math.h>#include <stdio.h>#define f(x) x*x+2*xdouble calc(double *a,double *b,double e,int *n){ double x1,x2,s;if(fabs(*b-*a)<=e)s=f((*b+*a)/2);else{ x1=*b-0.618*(*b-*a);x2=*a+0.618*(*b-*a);if(f(x1)>f(x2))*a=x1;else*b=x2;*n=*n+1;s=calc(a,b,e,n);}return s;}main(){ double s,a,b,e;int n=0;scanf("%lf %lf %lf",&a,&b,&e);s=calc(&a,&b,e,&n);printf("a=%lf,b=%lf,s=%lf,n=%d\n",a,b,s,n);}2、程序运行结果:算例2:min f=x^2-10*x+36理论最优解:x*=5.0,f(x*)=11.0(1)MATLAB程序清单:function f=myfun_yi(x)f=x^2-10*x+36>> fminbnd(@myfun_yi,1,12)(2)运行结果:>> fminbnd(@myfun_yi,1,12)f =11.0407f =18.8309f =12.9691f =11f =11.000011.0000ans =5(3)结果分析:由迭代程序f=11.0,ans=5,与理论结果相等算例3:minf=x^4-5*x^3+4*x^2-6*x+60理论最优解:x*=3.2796,f(x*)=22.6590(1)MATLAB程序清单:function f=myfun_yi(x)f=x^4-5*x^3+4*x^2-6*x+60>> fminbnd(@myfun_yi,1,12)(2)运行结果:>> fminbnd(@myfun_yi,1,12)f =165.3948f =1.5836e+03f =24.8730f =35.9194f =23.9089f =22.7621f =31.7507f =22.6673f =22.6594f =22.6590f =22.6590f =22.6590f =22.6590 ans =3.2796(3)结果分析:由迭代程序得f =22.659,ans =3.2796,与理论最优解相等2 《无约束优化搜索方法》上机实践报告1、写出所选择的无约束优化搜索算法的基本过程、原理(可附流程图说明)。
鲍威尔改进方法鲍威尔(Powell)法是直接利用函数值来构造共轭方向的一种方法在鲍威尔基本算法中,每一轮迭代都用连结始点和终点所产生出的搜索方向去替换原向量组中的第一个向量,而不管它的“好坏”,这是产生向量组线性相关的原因所在。
在改进的算法中首先判断原向量组是否需要替换。
如果需要替换,还要进一步判断原向量组中哪个向量最坏,然后再用新产生的向量替换这个最坏的向量,以保证逐次生成共轭方向。
2、程序计算结果分析:中间各步骤的结果分析及与理论计算结果分析对比。
算例1:min f=4*(x(1)-5)^2+(x(2)-6)^2初始点:x0=[8;9],f(x0)=45最优解:x*=[5;6],f(x*)=0(1)MATLAB程序清单:function f=myfun_wuyueshu(x)f=4*(x(1)-5)^2+(x(2)-6)^2>> [x,fval]=fminunc(@myfun_wuyueshu,x0)(2)运行结果:f =45Warning: Gradient must be provided for trust-region algorithm;using line-search algorithm instead.> In fminunc at 367f =45.0000f =45.0000f =f =23.5625f =23.5625f =2.6958f =2.6958f =2.6958f =1.3788f =1.3788f =1.3788f =0.00540.0054f =0.0054f =6.4975e-05f =6.4973e-05f =6.4975e-05f =6.1579e-09f =6.1522e-09f =6.1443e-09f =1.7876e-121.8627e-12f =1.5586e-12Local minimum found.Optimization completed because the size of the gradient is less thanthe default value of the function tolerance.<stopping criteria details>x =5.00006.0000fval =1.7876e-12(3)结果分析:由迭代程序得x =[ 5.0000;6.0000],fval =1.7876e-12,与理论最优解相等。
算例2:min f=(x(1)^2+x(2)-11)^2+(x(1)+x(2)^2-7)^2初始点:x0=[1;1],f(x0)=106最优解:x*=[3;2],f(x*)=0(1)MATLAB程序清单:function f=myfun_wuyueshu(x)f=(x(1)^2+x(2)-11)^2+(x(1)+x(2)^2-7)^2>> [x,fval]=fminunc(@myfun_wuyueshu,x0)(2)运行结果:>> x0=[1;1]11>> [x,fval]=fminunc(@myfun_wuyueshu,x0)f =106Warning: Gradient must be provided for trust-region algorithm; using line-search algorithm instead.> In fminunc at 367f =106.0000f =106.0000f =29.5430f =29.5430f =29.5430f =1.7450e+041.7450e+04f =1.7450e+04f =90.3661f =90.3661f =90.3661f =0.3575f =0.3575f =0.3575f =0.0179f =0.0179f =0.0179f =0.0064f =0.0064f =0.0064f =1.0048e-06f =1.0044e-06f =1.0049e-06f =4.8639e-09f =f =4.8781e-09f =5.2125e-12f =5.8703e-12f =5.7870e-12Local minimum found.Optimization completed because the size of the gradient is less thanthe default value of the function tolerance.<stopping criteria details>x =3.00002.0000fval =5.2125e-12(3)结果分析:由迭代程序得x=[3;2],fval = 5.2125e-12,与理论最优解相等算例3:ff=x[0]*x[0]+2*x[1]*x[1]-4*x[0]-2*x[0]*x[1];(1)鲍威尔改进算法C++程序清单:#include "stdio.h"#include "stdlib.h"#include "math.h"double objf(double x[]){double ff;ff=x[0]*x[0]+2*x[1]*x[1]-4*x[0]-2*x[0]*x[1];return(ff);}void jtf(double x0[ ],double h0,double s[ ],int n,double a[ ],double b[ ]) {int i;double *x[3],h,f1,f2,f3;for (i=0;i<3;i++)x[i]=(double *)malloc (n*sizeof(double));h=h0;for(i=0;i<n;i++)*(x[0]+i)=x0[i];f1=objf(x[0]);for(i=0;i<n;i++)*(x[1]+i)=*(x[0]+i)+h*s[i];f2=objf(x[1]);if(f2>=f1){h= -h0;for (i=0;i<n;i++)*(x[2]+i)=*(x[0]+i);f3=f1;for(i=0;i<n;i++){*(x[0]+i)= *(x[1]+i);*(x[1]+i)= *(x[2]+i);}f1=f2;f2=f3;}for(;;){h=2. *h;for(i=0;i<n;i++)*(x[2]+i)=* (x[1]+i) +h*s[i];f3= objf(x[2]);if(f2<f3)break;else{ for(i=0;i<n;i++){*(x[0]+i)= *(x[1]+i);*(x[1]+i)= *(x[2]+i);}f2=f3;}}if(h<0. )for(i=0;i<n;i++){a[i]=*(x[2]+i);b[i]=*(x[0]+i);}elsefor(i=0;i<n;i++){a[i]=*(x[0]+i);b[i]=*(x[2]+i);}for(i=0;i<3;i++)free(x[i]);}double gold(double a[],double b[],double eps,int n,double xx[]) {int i;double f1,f2,*x[2],ff,q,w;for(i=0;i<2;i++)x[i]=(double*)malloc (n*sizeof(double));for(i=0;i<n;i++){*(x[0]+i)=a[i]+0.618*(b[i]-a[i]);*(x[1]+i)=a[i]+0.382*(b[i]-a[i]);}f1=objf(x[0]);f2=objf(x[1]);do{if(f1>f2){for(i=0;i<n;i++){b[i]=*(x[0]+i);*(x[0]+i)=*(x[1]+i);}f1=f2;for(i=0;i<n;i++)*(x[1]+i)=a[i]+0.382*(b[i]-a[i]);f2=objf(x[1]);}else{for(i=0;i<n;i++){a[i]=*(x[1]+i);*(x[1]+i)=*(x[0]+i);f2=f1;for(i=0;i<n;i++)*(x[0]+i)=a[i]+0.618*(b[i]-a[i]);f1=objf(x[0]);}q=0;for(i=0;i<n;i++)q=q+(b[i]-a[i])*(b[i]-a[i]);w=sqrt(q);}while(w>eps);for(i=0;i<n;i++)xx[i]=0.5*(a[i]+b[i]);ff=objf(xx);for(i=0;i<2;i++)free(x[i]);return(ff);}double oneoptim(double x0[],double s[],double h0,double epsg,int n,double x[]) {double *a,*b,ff;a=(double *)malloc(n*sizeof(double));b=(double *)malloc(n*sizeof(double));jtf(x0,h0,s,n,a,b);ff=gold(a,b,epsg,n,x);free(a);free(b);return(ff);}double powell(double p[],double h0,double eps,double epsg,int n,double x[]) {int i,j,m;double *xx[4],*ss,*s;double f,f0,f1,f2,f3,fx,dlt,df,sdx,q,d;ss=(double *)malloc(n*(n+1)*sizeof(double));s=(double *)malloc(n*sizeof(double));for (i=0;i<n;i++){for (j=0;j<=n;j++)*(ss+i*(n+1)+j)=0;*(ss+i*(n+1)+i)=1;}for (i=0;i<4;i++)xx[i]=(double *)malloc(n*sizeof(double));for (i=0;i<n;i++)*(xx[0]+i)=p[i];for(;;){for (i=0;i<n;i++){*(xx[1]+i)=*(xx[0]+i);}f0=f1=objf(x);dlt=-1;for (j=0;j<n;j++){for (i=0;i<n;i++){*(xx[0]+i)=x[i];*(s+i)=*(ss+i*(n+1)+j);}f=oneoptim(xx[0],s,h0,epsg,n,x);df=f0-f;if(df>dlt){dlt=df;m=j;}}sdx=0.;for (i=0;i<n;i++)sdx=sdx+fabs(x[i]-(*(xx[1]+i)));if(sdx<eps){free(ss);free(s);for (i=0;i<4;i++)free(xx[i]);return(f);}for (i=0;i<n;i++)*(xx[2]+i)=x[i];f2=f;for (i=0;i<n;i++){*(xx[3]+i)=2.*(*(xx[2]+i)-(*(xx[1]+i))); x[i]=*(xx[3]+i);}fx=objf(x);f3=fx;q=(f1-2*f2+f3)*(f1-f2-dlt)*(f1-f2-dlt);d=0.5*dlt*(f1-f3)*(f1-f3);if((f3<f1)||(q<d)){if(f2<=f3)for (i=0;i<n;i++)*(xx[0]+i)=*(xx[2]+i);elsefor (i=0;i<n;i++)*(xx[0]+i)=*(xx[3]+i);}else{*(ss+(i+1)*(n+1))=x[i]-(*(xx[1]+i)); *(s+i)=*(ss+(i+1)*(n+1));}f=oneoptim(xx[0],s,h0,epsg,n,x);for(i=0;i<n;i++)*(xx[0]+i)=x[i];for (j=m+1;j<=n;j++)for (i=0;i<n;i++)*(ss+i*(n+1)+j-1)=*(ss+i*(n+1)+j);}}}void main(){double p[]={1,1};double ff,x[2],x1,x2,f;ff=powell(p,0.3,0.001,0.0001,2,x); printf("shuchuzuiyoujie:\n");x1=x[1];x2=x[2];f=ff;printf("x1=%f,x2=%f,f=%f\n",x1,x2,f); getchar();}(2)运行结果为:3《约束优化搜索方法》上机实践报告1、写出所选择的约束优化搜索算法的基本过程、原理(可附流程图说明)。
