第二章 原子的玻尔—索末菲理论 (4)
索末菲原子模型

索末菲原子模型著名理论物理学家阿诺德·索末菲(Arnold Sommerfeld ,1868~1951),是德国慕尼黑大学理论物理研究院院长,他对玻尔原子理论的扩充和他所著的《原子结构和光谱线》这部深具影响的教科书,被他的学生誉为“原子物理学的圣经”。
在量子力学史上,他赢得量子力学三大重要学派领袖之一的声誉,他在培养人才方面是无与伦比的,他有能把像海森伯、泡利这样的毛头小伙子精雕细琢成杰出科学家的神奇本领。
爱因斯坦1922年很赞赏地说道:“我特别欣赏您培养出了如此众多的青年才俊。
”3、1 索末菲的生平1868年12月5日,索末菲生于东普鲁士的柯尼斯堡(Königsberg )(今俄罗斯的加里宁格勒),是中欧理论物理的发源地,德国成立的第一个数学和物理研究班就诞生在这里。
中学时代索未菲和德国实验物理学家维恩是同学,1886年进入柯尼斯堡大学数学教授林德曼(C .Lindemann )指导的数学——物理研究班主修数学,同当时许多别的数学家一样,索未菲运用开尔文勋爵的数学物理理论对麦克斯韦电磁场方程的进行了概述,并对应用数学产生了浓厚的兴趣。
于是,他从林德曼的数论领域转变到开尔文勋爵的数学对物理学的应用研究,他研究过电子波的物理特性和关于旋转陀螺的理论,对于应用复变函数理论解决边界问题颇有造诣。
1891年,他在康尼斯堡的数学物理教授沃尔克曼(P .V olkmann )的指导下,完成了数学物理方面的博士学位论文。
1893~1894年在哥廷根的矿物研究所担任数学家克莱因(F .Klein )的助手。
1897年任克劳斯塔尔矿业学校的数学教授。
1900年由克莱因推荐,在亚琛工业大学任工程力学教授。
在此期间,他致力于把数学和工程力学联系起来,使工程力学有坚实的数学基础;这是克莱因一贯的主张。
1906年起任慕尼黑大学理论物理学教授,不久主持建立了理论物理研究院并任院长。
1905年爱因斯坦(A .Einstein )的关于狭义相对论的论著发表以后,在1907年德国自然研究者大会上,索末菲曾为爱因斯坦的理论辩护,而且他在这个领域所做的工作,为后来的轫致辐射理论提供了理论基础。
第二章 原子的玻尔—索末菲理论 (4)
之比。
这即意味着,当n相同nφ不同时,在不同轨道中运动的体系会具有相同的 能量,这种情况称为简并(或退化)。例如对同一n,由于nφ=1,2,…, n,便有n个可能的轨道,我们说它有n个状态,但这n个状态的能量是相 同的,故这种情况就被称为n度简并(或退化)。下图所示的是氢原子能 级简并(或退化)的情况。
n 4 n
在上面的简单推导过程中,我们不难看出相对论效应是如何被考虑进去的。显 而易见,上式中第一项就是玻尔理论原来给出的,第二基则是考虑了相对论效 应后增加的修正项。虽然这一简单推导只对圆轨道才成立,但是,它已包含了 相对论修正引起的主要效果。
值得指出,在作上述展开时,认为β<< 1,至少是β<1,那么当β=αZ/n>1,
T
m
m0
c
2
m0c
2
1
1
2
1
与经典公式不同,当v << c ,即β很小时,对上式右
边第一项作级数展开,且略去高阶无穷小量,就得到了动 能的经典表述形式。
下面将用相对论对圆周轨道进行修正。让我们从能量 角度看,能量可写成动能与势能之和,即
E
T
V
m
m0
c
2
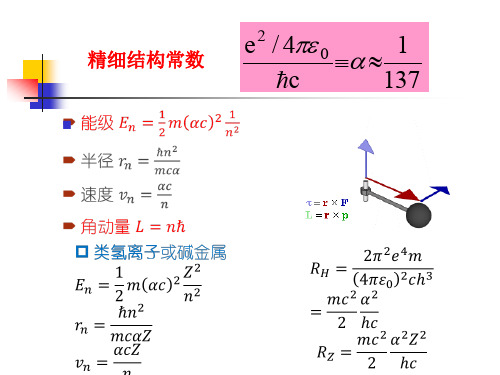
精细结构常数
e2 / 4 0 1
c
137
光谱
类氢离子,毕克林系 折合质量,里德堡常数随不同类氢离子变化
Franck-Hertz实验
广义量子化条件和索末菲理论
A. 广义量子化条件
玻尔在氢原子理论中得出,只有满足角动量量子化条件
Ln,n1,2,3,
的电子轨道运动才是实际上可能存在的,将上式改写一下,即
量子力学中的玻尔索末菲模型

量子力学中的玻尔索末菲模型玻尔索末菲模型是量子力学中一个重要的模型,描述了原子的电子运动特性。
本文将从量子力学的历史背景、玻尔索末菲模型的提出与原理以及该模型的应用等方面进行探讨,并讨论该模型在现代物理研究中的一些局限性。
一、量子力学的历史背景量子力学是20世纪初兴起的一门重要的物理学分支,它的发展与经典力学中的一些难题密切相关。
例如,在经典力学中,描述电子在原子内运动的理论与实验结果存在着严重的矛盾,无法解释原子光谱的特征。
为了解决这个问题,玻尔于1913年提出了玻尔氢原子模型,即玻尔索末菲模型。
二、玻尔索末菲模型的提出与原理玻尔索末菲模型是基于一些假设和实验结果得出的,它主要包括以下几个要点:1. 电子在原子中绕核运动的轨道是定量化的,即只允许存在特定能量的轨道,这些能量被称为能级。
2. 电子跃迁时吸收或放出特定能量的光子,这些能量与电子所在的能级差有关,从而解释了原子光谱的特征。
3. 电子在特定轨道上具有固定的能量和角动量,能量和角动量的量子化条件为玻尔量子条件。
基于这些假设和理论,玻尔索末菲模型成功地解释了氢原子光谱的一系列实验结果,为量子力学的发展奠定了基础。
这一模型的简洁性和可解性使得它成为教学中常用的模型之一。
三、玻尔索末菲模型的应用玻尔索末菲模型不仅被应用于氢原子的研究,也适用于其他原子系统的简化描述。
通过计算电子在不同能级之间的跃迁,可以预测不同原子的光谱特征,从而与实验结果进行对比,验证模型的可靠性。
此外,玻尔索末菲模型也为其他研究领域提供了启示。
例如,在凝聚态物理中,可以将晶体中的电子视为类似原子的粒子,利用类似的思想进行能带结构的研究。
然而,随着科学技术的发展,人们对原子结构和电子运动的认识逐渐深入,一些玻尔索末菲模型无法解释的现象也逐渐被发现。
这些局限性包括不能解释更复杂的原子系统、忽略了电子的波动性以及无法描述原子核结构等。
四、小结玻尔索末菲模型作为量子力学中的一个经典模型,为我们理解原子的电子结构和光谱特性提供了重要的参考。
第2章 原子的量子态:玻尔模型

第二章 原子的量子态:玻尔模型§2-1背景知识普朗克于1900年提出量子假说,但人们并不很理解它,他曾试图将量子假说纳入经典理论中。
在爱因斯坦发表狭义相对论后还认为爱因斯坦“迷失了方向”。
但当时年仅28岁的玻尔(丹麦)却将量子概念用于卢瑟福原子模型,成功地解释了近30年的光谱之谜。
一、 量子假说的根据之一:黑体辐射物体都有热辐射,这其实是发射一定频率的电磁波。
从理论上分析,黑体腔壁可认为是由大量作谐振动的谐振子(作谐振动的电偶极矩)组成,振动的固有频率可从(∞→0)连续分布,谐振子通过发射与吸收电磁波,与腔中辐射场不断交换能量。
1859年,基尔霍夫证明:黑体辐射达平衡时,辐射能量密度νE 随频率的变化曲线只与黑体的绝对温度T 有关,而与空腔的形状及组成材料无关。
1893年,维恩发现黑体辐射的位移律:辐射能量密度最大值所对应的频率m ν与平衡时黑体的绝对温度T 成正比,即c.Tm 28980=ν。
由此得维恩位移律公式(m λ为最大波长,m m c λν=)辐射本领)T ,(R ν:在单位时间内黑体单位面积在单位频率内(频率ν附近)辐射的能量。
(即能量随ν的变化规律) 设黑体内腔达热平衡时的辐射场的能量密度为νE ,则其辐射本领),(4),(T E c T R νν=。
黑体总的辐射本领为ννλλd )T ,(E c d )T ,(R )T (R ⎰⎰∞∞==004由此可得等式:ννλλd )T ,(E c d )T ,(R 4=维恩经验公式:频率在),(νννd +相符,但在低频部分与实验有显著偏差。
瑞利-1899年据经典电动力学和统计物理学导出,此公式在低频部分与实验相符,但在高频部分与实验的偏差很大。
当∞→ν时, ∞→νE ,即在高频时是发散的,这就是当时有名的“紫外灾难”。
1904年开尔文勋爵(英,物理学家)在总结物理学几百年成果时谈到“物理学晴朗天空的远处有两朵令人不安的乌云”:黑体辐射的引发的“紫外灾难”和迈克尔逊-莫雷实验(1887年)的“零结果”。
第二章 原子的玻尔—索末菲理论

这表明,1m2的钠金属板上,每个原子每秒钟接受到的 能量约为0.1μeV,既使每个原子中只有一个电子接受能量, 要使这个电子获得1eV的能量,还需要107s≈1/3a!这与实验 事实发生严重的矛盾。光电效应的响应时间快(T<10-9s), 是经典物理最难理解的。 另外,依照经典理论,决定电子能量的是光强,而不 是光的频率。但实验事实却是:暗淡的蓝光照出的电子的 能量居然比强烈的红光照出的电子的能量大。这种电子能 量与光频率的关系是经典物理所无法解释的。
普朗克发表的常数
h=6.55×10-34J· S
只比现代值低1%;同时导出的玻耳兹曼常数
k=1.346×10-23J/K
比现代值低约2.5%。由此可相当精确地算出阿伏伽德 罗常数N0及电子的电荷e,而在实验上只是在近二十年 之后才独立地把N0和e测量到这样精确的水平。 普朗克常数在1986年的推荐值为:
§2.2 光谱
光谱是光的 频率(或波长) 成分和强度分 布的关系图, 它是研究原子 结构的重要途 径之一。
若要了解物质 的内部情况, 只要看其光谱 就可以了。
光谱是用光谱仪测量的。光谱仪的种类繁多,但其基 本结构原理却几乎都一样,大致由三部分组成:光源;分光 器(棱镜,或光栅);记录仪(把分出的不同成分的光强记 录下来)。 光源:研究光谱所用的光源,除自然光外,可有各种类 型,有火焰、高温炉、电弧、火花放电、气体放电、化学发 光、荧光等。
A、黑体辐射
什么叫黑体辐射?记得有时在评论某人物时(例如, 莎士比亚的喜剧《威尼斯商人》中的高利贷者夏洛克),人 们会贬称他‚黑心‛,就是说这个人对什么东西都贪得无厌。 与此相比,若一物体对什么光都吸收而无反射,我们就称这 种物体为‚绝对黑体‛,简称‚黑体‛。事实上当然不存在 ‚绝对黑体‛,不过有些物体可以近似地作为‚黑体‛来处 理,如一束光一旦从狭缝射入某一空腔后,就很难再通过狭 缝反射出来,这个空腔的开口就可以被看作是黑体。
索末菲理论课件ppt

解:粒子所受的力:F
U r
r2
m v2 r
2
mr
粒子的总能量为:E 1 m 2 即 r
2
r 2r r 2r
2E
由量子化通则: mvrd
m 2 d nh
2E
即: m 2 2 nh
2E
E
2 2m 2
n2h2
将
Ze2
4 0
索末菲理论课件
玻尔理论得成功:
(1)指出了原子能级得存在。
(2)提
出了定态得概念,事实表明,这一结论对于各种原
子也就是普遍正确得。
(3)角动量量子化条件L=nh/2,引出了角动量量子化这
一普遍正确得结论。
(4)解释氢原子及类氢离子得光谱现象。
玻尔理论得局限性:
没有完全解决原子问题,只能解释氢原子与类氢离子光谱,无法 解释复杂原子得光谱现象。量子通则不具备有普遍性。
q为广义坐标, dq为广义位移, p为广义动量。
i就是自由度个数,有几个自由度就有几个相应得量子化条件。
例1:设粒子得质量为m,在具有无限高势垒、宽度为a得一维 直角势阱里运动。试根据索末菲量子化通则对上述情况求出 这粒子能量得允许值。
解:根据量子化通则:
a
0
pdx 0 (mv)dx a (mv)dx 2mva nh
2
40 r 2
40 r
由量子化通则可得以下结果
a n2 a1 Z
b
nn
a1 Z
a :半长轴,b:半短轴
En
2 2me4 (40 )2 h2
Z2 n2
Rhc
Z2 n2
主量子数
n nr n
浅谈原子核物理的发展

浅谈原子核物理的发展院系:理学院年级:09 级专业:物理学姓名:学号:教师:浅谈原子核物理的发展(理学院 2009物理学 20090205011)摘要:远在公元前4世纪,希腊哲学家留基伯和他的学生德漠克利特已经提出"原子"的概念。
他们认为万物都是由大量不可分割的微小质点所组成,他们把这样的微小质点叫做"原子"。
原子除有大小、形状和位置的差异外,没有区别。
原子遵照一定的规律在"虚空"中不断运动。
它们集合在一起时便形成物体,分离时物体便消失。
在当时这仅是一种猜想而已,无法用实验证实。
但是这个说法跟一切物体都能粉碎的事实是相吻合的。
原子说在中世纪受到宗教和神学的压制,没有得到发展。
到了17世纪,随着化学的发展,这种观点又重新传播起来了。
关键字:原子、原子模型、原子核放射性、中子、核素引言:原子核物理是物理学的一个分支,主要研究物质结构的一个层次;这个层次介于原子和粒子物理两层次之间,称之为原子核。
原子核物理是本世纪初开始形成的一门学科,它随着近代物理学的发展,随社会对核技术应用的需要发展起来。
一、原子模型的提出1.1“原子”一词来自希腊文,含义是“不可分割的”。
公元前四世纪,古希腊哲学家德谟克利特(Democritus)提出了这一概念,并把它当作物质的最小单元。
17世纪,通过卡文迪许和拉瓦锡等许多化学家的工作,发现了水可分解为氧和氢两种元素;空气是由氧、氢和氮等元素混合而成的,燃烧只不过是元素和氧起激烈反应等等。
随着几十种元素的发现,英国化学家道尔顿提出了新的原子学说。
他认为物质是由许多种类不同的元素所组成,元素又由非常微小的,不可再分的、不能毁灭又不能创生的原子所组成。
1807年,英国科学家约翰·道尔顿(John Dalton)提出原子论。
他认为原子类似于刚性的小球,它们是物质世界的基本结构单元,是不可分割的。
道尔顿用他的学说说明了化学中的物质不灭定律等。
§2.4 波尔模型的推广——索末菲模型(PPT-YBY)

n 1 a r1 ① n 1 b r1
n 2 a 4r1 n 1 b a / 2 ② n 2 b a
n 3 n 1 ③ n 2 n 3 a 9r1 b a/3 b 2a / 3 b a 9r1
§2.4 波尔模型的推广——索末菲模型 索末菲(A.Sommerfeld,1868-1951德国物理学家) 1916年提出 了椭圆轨道理论。 其一、提出了广义量子化条件(即量子化通则),把玻尔的圆 轨道推广为椭圆轨道。 其二、引入了相对论修正。 一、量子化通则及椭圆轨道 1、量子化通则
L mrV n
现在我们进一步了解到原子内部运动复杂性,同一n还有不同 形状的轨道,而每种轨道具有不同的能量。
第 1 、 2 章 卢 瑟 福 玻 尔 模 型 小 结
2 2 Z 2 2 E c c 1 n (n2 2 Z 2 )1/2 2 r
2 m0 z e
2
2 4
2 4
2
(8)
1 4 0 c 137
这种不同量子态具有相等能量的情况成为简并。 简并度
e2
二、相对论修正
1、相对论动能 质速关系为:
m
m0 1
2
v/c
2 2
(9)
1 1 动能表达式: EK (m m0 )c m0c 2 1 用级数展开式:
(10)
这就是经典表达式。
2、圆轨道的能量修正 (1)求电子运动的速度。利用(8)式的经典能量表达式
1 1 z En Ek U Ek U m0 c 2 2 n
人教版高中物理选修3-5 2.4第二章第4节 玻尔的原子模型 能级

• [例1] 氢原子基态的能量为E1=-13.6 eV。
大量氢原子处于某一激发态。由这些氢原子
可能发出的所有的光子中,频率最大的光子
能量为-0.96E1,频率最小的光子的能量为 ________eV(保留两位有效数字),这些光子
解析
可具有________种不同的频率。
频率最大的光子能量为- 0.96E1 ,即 En - E1 =-
判天地之美,析万物之理
当我一看到巴尔末公式,整个事情就豁然 开朗了。
————玻尔
4
玻尔的原子模型
能级
活动一
玻尔对原子结构的研究
1900年普朗克提出了能量量子化的概念, 认为电磁波的能量不是连续变化的,而是 只能取一些分立的值。 1905年爱因斯坦为了解释光电效应的实验 规律提出了光量子假说,认为光子的能量 也是不连续的。 1885年巴尔末分析了可见光区的四条谱线, 说明了原子光谱波长的分立特性。
一、玻尔提出原子模型的背景:
卢瑟福的原子核式结构学说很好地解释了a粒子 的散射实验,初步建立了原子结构的正确图景,但 跟经典的电磁理论发生了矛盾。 1、原来,电子没有被库仑力吸引到核上,它 一定是以很大的速度绕核运动,就象行星绕着太阳 运动那样。按照经典理论,绕核运动的电子应该辐 射出电磁波,因此它的能量要逐渐减少。随着能量 的减少,电子绕核运行的轨道半径也要减小,于是电 子将沿着螺旋线的轨道落入原子核,就像绕地球运 动的人造卫星受到上层大气阻力不断损失能量后要 落到地面上一样。 这样看来,原子应当是不稳定的, 然而实际上并不是这样。
一、玻尔的原子模型 围绕原子核运动的电子轨道半径只 1.轨道量子化假设::
能是某些不连续(分立)的数值。 (1)如氢原子电子的可能轨道r半经: …) r = n 2r ( n = 1, 2 , 3 1 n r = 0.053nm r = 0.212nm 2 1
原子物理第2章

原子物理第2章第三节:玻尔模型从理论上导出里德伯常数:结束目录nextback 氢光谱的解释玻尔假设电子的运动第二章:原子的能级与辐射:玻尔理论第三节:玻尔模型氢原子轨道半径与谱系结束目录nextback氢光谱的解释玻尔假设电子的运动赖曼系n=1n=2n=3n=4n=5r04r09r016r025r0布喇开系巴耳末系帕邢系第二章:原子的能级与辐射:玻尔理论第三节:玻尔模型结束目录nextback氢光谱的解释玻尔假设电子的运动第二章:原子的能级与辐射:玻尔理论第四节:类氢离子光谱结束目录nextback第二章:原子的能级与辐射:玻尔理论毕克林系起初以为是星体上的一种特殊氢,后在实验室中加氦后的氢光谱中观察到,得以确认是氦离子的光谱。
氢光谱类氢光谱第四节:类氢离子光谱结束目录nextba ck第二章:原子的能级与辐射:玻尔理论如果套用玻尔理论,只需要将氢原子理论中的Z改为2,就可得到氦离子的光谱理论公式上式中n1取4,n2取5、6、7、….就与毕克林系规律相同第四节:类氢离子光谱结束目录nextback第二章:原子的能级与辐射:玻尔理论尽管上述结果与观察结果非常一致,但还有一个明显的差别:类氢离子光谱与氢光谱并不完全重合。
这一差别后来被认为是里德伯常数的变化引起的。
考虑原子核的运动,推导出修正后的里德伯常数核的质量有关。
修正后的里德伯常数与观测结果非常一致第四节:类氢离子光谱结束目录nextback第二章:原子的能级与辐射:玻尔理论里德伯常数受核的质量影响的理论曾被用来证实氢的同位素-氘-的存在。
起初有人从原子质量测定估计有原子量为2的氢存在,但如存在,含量应很低,一时难以确认。
1932年尤雷(HCUre y),观察到类氢光谱,通过质量修正,能很好得到解释。
从而确认氘-的存在。
第四节:类氢离子光谱结束目录nextback第二章:原子的能级与辐射:玻尔理论玻尔理论非常成功地解释了氢、类氢离子光谱的规律,一度被人们广泛接受。
原子结构知识:原子的玻尔-索末菲模型

原子结构知识:原子的玻尔-索末菲模型原子结构是物质世界的基础,理解原子结构的本质对于探索物质结构和物理现象都有着重要的意义。
20世纪初,玻尔和索末菲提出了原子的玻尔-索末菲模型,为原子结构研究开辟了新的道路。
本文将从原子的结构特点、能级理论、碳原子及其化学属性等方面加深对玻尔-索末菲模型的理解。
玻尔-索末菲模型是基于电子在原子中的运动性质提出的,它认为原子大小有限,电子绕原子核做周期性运动,每个环节代表一个能级。
它说明原子有稳定的电子能级,电子在这些能级之间跃迁时,会放出或吸收能量,这种跃迁过程被称为光谱现象。
这个模型概述了原子的最基本结构、相互作用以及放射和吸收光子中的角色。
玻尔-索末菲模型最主要的特点是能级理论。
在这个模型中,原子核被假设为定点,而电子则呈现出某些特定的轨道。
其中,电子在轨道上运动一周的能量是一定的。
这个能量被称为“量子”,它依赖于电子能级的数量和它的位置。
能级跨度越大,能量就越大。
这一概念非常重要,因为它解释了为什么物质对电磁辐射具有非均匀性的响应。
玻尔-索末菲模型的核心思想是量子理论。
电子在原子轨道中运动,而电子的轨道有一个基本的微观建模方式,这就是量子力学。
量子力学跟经典物理学不同,经典物理学认为任何物理量都可以是连续的,而量子力学则认为物理量取决于微观量子机制的规律性。
例如,对于一枚旋转的羽毛,根据量子力学理论,要想精确地判断它的位置和动量,我们就需要用波函数来表述。
那么,玻尔-索末菲模型能够对物质的性质产生什么样的贡献呢?在化学中,有趣的现象很多都是由原子的结构特点所造成的。
熵增原理和化学平衡原理都来源于能量的描述。
例如水分子H2O和氨分子NH3,能够正确解释原子的相对还原性。
而对于碳原子,特别是碳原子手性的描述和其中化学能量变化中的巨大差异,都是从玻尔-索末菲模型中进一步细化得到的。
换句话说,玻尔-索末菲模型就是能够通过强大的量子力学理论来描述原子在化学过程中的相对能量影响。
量子纠缠背后的故事(11):索末菲的原子

量子纠缠背后的故事(11):索末菲的原子作者:程鹗玻尔“关于原子和分子的构成”的论文在英国《哲学杂志》上发表之后,没多久他就接到卢瑟福的来信。
卢瑟福在信中告诉玻尔,达尔文(提出进化论的达尔文的孙子)要离开了,他们在登广告招新人,但都不尽人意。
他希望能找到一个具备独创能力的年轻人。
这时的玻尔在哥本哈根大学担任讲师,主要是给医科学生上普通物理课。
他觉得很无聊,想争取一个教授席位。
虽然有卢瑟福的强力推荐信和本校同行的一致支持,但这机会一时半载还是可望不可即。
玻尔看了导师的来信,立刻领会了他的言下之意。
于是,他请假一年,在1914年9月携妻再度来到曼切斯特,继续在卢瑟福实验室任职。
实验室已经物是人非。
半年前,卢瑟福获得英国国王晋封的骑士爵位。
一战开始后,他的精力集中在用声纳探测潜水艇的绝密项目上,无暇顾及纯科学研究。
实验室来自各地的年轻人全部失去踪影。
其中盖革正在为德国的毒气战效力;达尔文已经参军,在物理学家布拉格(Lawrence Bragg)领导下研究如何监听敌方开炮噪音确定其火炮阵地的方位;莫斯利辞去已得到的牛津大学职位,在一战爆发后“插队”入伍担任通讯兵(1915年8月10日死于战场)。
丹麦是中立国,玻尔得以继续研究他的原子。
他的新模型问世之后,卢瑟福、索末菲等人都感到好奇,同时也期待着他再向前跨一步,解释光谱中更深的奥秘,即所谓的“精细结构(fine structure)”。
早在1887年,通过精密测量否定以太存在的迈克尔逊和莫雷,他们还报告了利用仪器精度能看到氢原子的光谱线并非仅仅是一条条的线,仔细地分辨,可以看到一条谱线其实是由两条挤在一起的细线组成。
随后,荷兰的塞曼(Pieter Zeeman)又有了新发现:在磁场中测量,一些原子的光谱线会“分裂”成两条或更多的细线,即后来所谓的“塞曼效应”。
他的导师洛伦兹很快根据经典电子理论做出了解释。
洛伦兹的理论只适用于磁场的作用,无法解释氢原子谱线本身的精细结构。
第二章 玻尔氢原子理论

第二章 原子的能级和辐射一、学习要点:1.氢原子光谱:线状谱、五个线系(记住名称、顺序)、广义巴尔末公式)11(~22nm R -=ν、 光谱项()2nR n T =、并合原则:)()(~n T m T -=ν 2.玻尔氢原子理论:(1)玻尔三条基本假设的实验基础和内容(记熟)(2)圆轨道理论(会推导):氢原子中假设原子核静止,电子绕核作匀速率圆周运动02200202220A 529,04,Z Z 4≈===e m a n a n e m r e e n πεπε;13714,Z Z 40202≈===c e n c n e c e n πεααπευ; ()n hcT n hc R n e m E e n --=-=∞22224220Z 2Z )41( πε,n =1.2.3……(3)实验验证:(a )氢原子五个线系的形成)11(Z ~,)4(222232042n m R c h e m R e -==∞∞νπεπ (会推导)非量子化轨道跃迁 )(212n E E mv h -+=∞ν (b )夫-赫实验:装置、.结果及分析;原子的电离电势、激发电势3.类氢离子(+++Li ,He ,正电子偶素.-μ原子等) (1) He +光谱:毕克林系的发现、波数公式、与氢原子巴耳末系的异同等(2)理论处理(会推导):计及原子核的运动,电子和原子核绕共同质心作匀速率圆周运动e e m M m M +⋅=μ, 正负电荷中心之距Ze n r n 22204μπε =. 能量2242202Z )41(n e E n μπε-=,里德伯常数变化Mm R R e A +=∞11 重氢(氘)的发现4.椭圆轨道理论 索末菲量子化条件q q n h n pdq ,⎰=为整数a n nb n e m a n e m E n p e n ϕϕϕπεπε==-==,Z 4,2Z )41(,2220224220 ,n n n ,,3,2,1;,3,2,1 ==ϕn 一定,n E 一定,长半轴一定,有n 个短半轴,有n 个椭圆轨道(状态),即n E 为n 度简并。
第二章 原子的玻尔—索末菲理论 小结

Bohr模型
处理原子结构的方法:对于电子绕原子核运 动,用经典力学处理;对于电子轨道半径, 则用量子条件来处理。也就是所谓的半经典 的量子论。只对电子的径向运动采取量子理 论,而对其角向运动采取量子理论。
之所以先量子化径向运动,由于卢瑟福模型 电子塌缩就是与轨道半径有关。只要量子化 而不收缩,塌缩问题就解决了。 解释了近30年的巴尔末公式之谜。 解释了类氢离子光谱。
光谱
光谱是用光谱仪测量的。光谱仪的种类繁多,但其基 本结构原理却几乎都一样,大致由三部分组成:光源;分光 器;记录仪。 连续光谱 固体热辐射 线状光谱 带状光谱 发射光谱
样品光源 分光器 纪录仪
原子发光 分子发光
I
吸收光谱
连续光源 样品 分光器 纪录仪
I
氢原子光谱及其经验规律
巴耳末公式
2n 2 Rc Rc 4 与经典比较 n n3
2Rc e 3 2 n 1 40 mr 3
e2 2 rn 3 n 40 16 2 R 2 c 2 m 1
2 e m R 2 40 ch 3
2 4
h 2
4 0 2 2 h rn n ; 2 2 me
原子实极化和轨道贯穿
电偶极子
碱金属原子光谱的精细结构
me 4 1 En 2 2 2 4 0 2 n
原子中电子的四个量子数

第40卷第5期大 学 物 理Vol.40No.52021年5月COLLEGE PHYSICSMay2021 收稿日期:2020-06-13;修回日期:2014-02-14 基金项目:西安交通大学“名师、名课、名教材”建设工程项目(校2018);西安交通大学第二批“课程思政”示范课项目(校2019)资助 作者简介:黄永义(1978—),男,安徽阜阳人,西安交通大学物理学院副教授,博士,主要从事原子物理教学和研究工作.原子中电子的四个量子数黄永义(西安交通大学物理学院,陕西西安 710049)摘要:较详细地阐述了原子中电子的4个量子数的来源,简要介绍了原子的电子壳层结构和泡利不相容原理.关键词:玻尔-索末菲理论;4个量子数;原子壳层结构;泡利不相容原理中图分类号:O4-1 文献标识码:A 文章编号:1000 0712(2021)05 0008 05【DOI】10.16854/j.cnki.1000 0712.200272原子中电子的4个量子数是大家熟知的,它们的引入过程也是很熟悉的.通过求解氢原子的定态薛定谔方程得到电子的3个量子数,分别是主量子数n,轨道角动量量子数l,轨道磁量子数ml,它们的取值为n=1,2,…;l=0,1,2,…,n-1;ml=0,±1,±2,…,±l,再加上乌伦贝克和哥德斯密特引入的自旋磁量子数ms=±1/2,共4个量子数(n,l,ml,ms).如果考虑到自旋轨道相互作用,需要使用新的4个量子数(n,l,j,mj),其中j为总角动量量子数,mj为总磁量子数.实际上原子中电子的4个量子数在1922年已经提出了,比1926年的波动力学早了好几年,本文就来谈谈4个量子数是怎样提出的,简要介绍它们的应用:原子的电子壳层结构和泡利不相容原理.1 4个量子数1913年玻尔在定态假设和跃迁假设的基础上利用对应原理提出了氢原子理论,给出了氢原子的能级公式En=-hcRZ2n2(1)式中Z为类氢离子的核电荷数,n是取自然数的主量子数,它决定了原子的主要能量,是原子中电子的第一个量子数[1].1916年索末菲就将玻尔的圆轨道推广到椭圆轨道,进一步又考虑电子运动的相对论效应给出了氢原子能级的精细结构[2].如图1所示.电子绕核在一个平面上作椭圆运动是二自由度的运动,极坐标零点在核的位置,坐标是r和φ,对应的动量为沿矢径r方向为pr=mr·和垂直于r方向图1 电子绕核运动的椭圆轨道的角动量pφ=mr2φ·.对极角动量和极径动量分别使用量子化通则∮pφdφ=k1h,∮prdr=nrh,由有心力作用下的角动量守恒可得pφ=k1,ba=k1nr+k1≡k1n,式中 =h/2π()为约化普朗克常量,a为椭圆半长轴,b为椭圆半短轴,n即为主量子数,nr=0,1,2,3,…n-1,k1=1,2,3,…n被称为方位角量子数,它决定了椭圆的形状.nr最小值可以为零,表示没有径向运动,但k1最小值只能为1,如果为0,则电子没有轨道运动,这种情况不会出现.进一步考虑到电子运动的相对论效应,利用量子化通则可得氢原子的能级E=-hcRZ2n2-hcRZ4α2n4nk1-34()+…(2)式中α≈1/137为精细结构常数,而氢原子的能级依赖于主量子数n,还依赖于方位角量子数k1,因此方位角量子数k1是原子中电子的第二个量子数[3].对比碱金属原子的光谱线系的跑动项,k1=1,2,3,…n第5期黄永义:原子中电子的四个量子数9 也可以用英文字母为s、p、d、f、g…,其中前4个字母有确切的含义,为sharp(锐线系),principal(主线系),diffuse(漫线系),fundamental(基线系)的首个字母.如果原子处于磁场中,电子的轨道运动不再是平面,而是三维空间的曲线.磁场不是很强,它对电子运动的影响不是很大,电子的运动仍可以近似地看作是一个平面上的运动,轨道平面绕着磁场方向缓慢旋进,此时三维运动实际上是研究在磁场下电子轨迹的取向问题.如图2所示,Ze表示原子核,-e表示电子,电子的位置可以用3个球坐标r,θ,ψ()表示,对应的线动量角动量分别为pr,pθ,pψ(),它们满足的量子化条件为∮prdr=nrh,∮pθdφ=nθh,∮pψdψ=nψh,量子数nr、nθ、nψ都取整数.图2 有磁场时电子做三维运动,摘自[4]显然角动量pψ为上文极角动量的分量pψ=pφcosα(3)由于电子运动的哈密顿量H=12m(p2r+1r2p2θ+1r2sin2θp2ψ)-Ze24πε0r不含ψ,由正则方程p·ψ=- H/ ψ=0得pψ=常量.考虑到量子化条件∮pψdψ=nψh,得pψ=nψ[4].将此结果代入(3)式:cosα=nψ/k1(4)式中k1=nθ+nψ,由-1≤cosα≤1,得nψ=-k1,-k1+1,…, ,…,k1-1,k1(5)nψ共有2k1+1个取值.nψ=0时电子轨道平面包含了磁场方向,1918年玻尔认为这种情况电子轨道平面不稳定,nψ=0被禁止,因此nψ共有2k1个取值[5].极角动量pφ在磁场方向的分量pψ=nψ 取2k1分立的值的现象被称为角动量的空间量子化.而玻尔的主张也十分重要,后文会看到四个量子数的取值如果不考虑玻尔的意见就得不到正确的结果.基态银原子束的施特恩-盖拉赫实验结果也能得到巧合的解释,基态银原子两个量子数n=5,k1=1,则nψ=±1,银原子束在非均匀磁场中受力Fz= B zμz=B znψμB=± BzμB,μB=e /2me()为玻尔磁子,银原子束就经过非均匀磁场后分裂为两束.由实验参数测量的玻尔磁子和理论预测的一致,这使得一度怀疑玻尔氢原子理论的施特恩也不得不承认玻尔理论的正确.1916年 拜和索末菲使用玻尔-索末菲理论引入磁量子数成功解释了正常塞曼效应,这个磁量子数恰好就是nψ[6,7].磁量子数的引入使得人们认识到仅有两个量子数还不能完全描述电子的状态,碱金属原子的光谱更能说明这一点.到1922年通过高分辨率光谱仪观察到光谱人们已经很清楚知道了元素原子的能级重数,如碱金属原子是双重态,碱土金属原子是单态和三重态,第三列元素原子是双重态和四重态等等.光谱证据表明并不是所有的光谱线都满足频率的里兹组合定律,如碱金属原子的漫线系光谱项d向光谱项p跃迁,应该有4条光谱,而实验只观察到3条谱线.而这些未出现的谱线给索末菲提供了重要的线索:应该还存在某种选择定则禁止了那些未出现的光谱线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
principal
diffuse
fundament al
(next in alphabet after f)
g
4
18
5th shell and higher (theoretically)
原子实极化和轨道贯穿
碱金属原子的光谱可以用类似氢原子的公式表示。这些原 子的能级,当n较大时,非常近氢原子的能级,只有当 n较小 时差别较大。如果考虑到碱金属原子化学上是一价的,它们 容易电离成为带一个单位电荷的离子等情况,可以设想上节 讨论过的那些光谱也是由于单电子的活动产生的。
此式中第一项就是玻尔理论的结果,第二项起则是相对论效 应的修正。显然,对同一n不同nφ,第二项的数值是不同的。 由此可见,同一n而nφ不同的那些轨道运动具有不同的能量。 这样,原来的能级简并在考虑了相对论修正后就消除了。不 过,第二项代表的数值比第一项小得多,所以分裂的能级只 有微小的差别。这个差别被称为能级的精细结构,与它相联 系的常数α称为精细结构常数。索末菲的功绩之一就是引入了 这一十分重要的常数。
n nr n 1,2,3,; n 1,2,3,,n.
上式所表达的是索末菲推广到椭圆轨道后得到的结果,把 它们与玻尔的圆运动情况相比较,不难看出:能量的表达 式没变,但轨道的半径有了长、短半轴之分,且出现了两 个量子数n和nφ。这个结果所包含的物理意义是:轨道的 长半轴和体系的能量只决定于主量子数 n,而与nφ无关; 轨道角动量决定于角量子数nφ,形状取决于 之比。
①椭圆轨道推广 索末菲认为电子绕原子核在一个平面上作椭圆运动,是一 个二维的运动。描述椭圆运动中电子的位置,可用平面极坐 标中的坐标φ和r,与这两个坐标对应的广义动量就是角动量 L 和动量Pr。这体系的能量可表示为
2 1 2 Ze 2 1 Ze 2 2 r 2 E mv mr 2 4 0 r 2 4 0 r
C.量子数的变化
如果利用量子力学严格地进行上面的推导,则上式应为
2 2 2 m0 c Z Z n 3 n 3 Z Z En, Rhc 1 1 1 1 2 n n 4 4 n n 2 2
2 2
其中用 代替nφ,表示核外电子轨道运动角动量量子数,其 取值范围有所变化,
( 1); L m ; L mr 2 Z n 1,2,3,4,; 0,1,2,3,(n 1); m 0,1,2,,.
m 取(2 +1)个值,在量子力 其中LZ为L在Z方向上的投影, m)表示核外电子的运动状态。 学中,一般用量子数组(n, ,
在上面的简单推导过程中,我们不难看出相对论效应是如何 被考虑进去的。显而易见,上式中第一项就是玻尔理论原来 给出的,第二基则是考虑了相对论效应后增加的修正项。虽 然这一简单推导只对圆轨道才成立,但是,它已包含了相对 论修正引起的主要效果。
值得指出,在作上述展开时,认为β<< 1,至少是β<1, 那么当 β=αZ/n>1 ,即在 n=1 ,而 Z> 137 时会出现什么情况 呢?尽管目前还没有出现这个问题,因实际上现在人工能 制造的最重的核素还只是Z=114,并且,在考虑了核的大小 而作出理论修正后表明,在Z<172 时,还不会出现β>1的情 况。但是,重离子加速器将有可能制造Z=184的原子核,一 旦这个尝试成功,将会给我们带来什么影响?那时,对今 天的理论又能作出什么样的裁决呢?这正是当前在原子物 理中的一个活跃的研究领域。
按照玻尔 — 索末菲理论 Hα 线应为n=3到n=2的跃迁,n=3为 三条能级, n=2 为二条能级,考 虑能级跃迁的选择定则 △ =±1,就得到了三条Hα 线,与实验完全符合,但这完全 是巧合,有人称索末菲理论是物 理学中最值得纪念的失败。
图中的s,p,d,f,g,…等字母代表 4,…等值。
=0,1,2,3,
碱金属元素 Li 3=2×12+1, Na 11=2×(12+22)+1, K 19=2×(12+22+22)+1, Rb 37=2×(12+22+32+22)+1, Cs 55=2×(12+22+32+32+22)+1, Fr 87=2×(12+22+32+42+32+22)+1。
用摄谱仪把光谱摄成相片时,不同线系会同时出现。例如 采用对可见光和紫外光灵敏的相片,可以把主线系和两个辅 线系一次摄在一张相片,他们重迭在一起。从谱线的粗细和 强弱并参考它们的间隔,可以把属于不同线系的谱线分辨出 来。从图我们可以想象摄得的光谱相片上的形象。
根据表中锂的数据可以画成能级图。主要特征归结为 如下四条: A、四组谱线(每一组的初始位置是不同的,即表明 有四套动项)。 B、有三个终端(即有三套固定项)。 是角动量量子数)。 C、两个量子数(n 和 , D、一条规则(图中画出的虚线表示在实验中不存在 这样的跃迁,因原子能级之间的跃迁有一个选择规则,即 △ =±1)。 对这个选择规则,我们可以这样解释: 的差别就是 角动量的差别,由于光子的角动量是1,要在跃迁时放出 一个光子,角动量就只能差1。根据这个选择规则,我们 就可以画成能级跃迁图。
③相对论对椭圆轨道的修正
将相对论对圆周轨道的修正推广到椭圆轨道,可以得到体 系的能量表达式
m0 c 2 Z En,n 2 n
2 2 2 2 n 3 Z n 3 Z Z 1 Rhc 1 n n 4 n n n 4
作这样一个二维运动的体系应满足两个量子化条件,其中 nr 和 nφ 都是整数,分别称为角量子数和径量子数,它们之和称 为主量子数,即n=nr+nφ。 由上述式子出发,经过演算推导,索末菲给出了椭圆轨道 的长半轴Байду номын сангаас、短半轴b以及能量的表达式,即
a
a1 2 a n ; b 1 nn ; Z Z Z2 1 cZ 2 E n Rhc 2 m( ) 2 n n
2 2 2 2 2
m0 c 2 1
2
1 m c 1
2 0 2
2
1
En m0 c 2 1 2 1
1 1 1 1 1 1 m0 c 2 1 2 1 4 1 m0 c 2 2 4 2! 2 2 8 2 2 2 2 2 2 m0 c 2 Z 1 Z Z 1 Z 1 Rhc 1 2 n 4 n n 4 n
Subshell label s
ℓ 0
Max electrons 2
Shells containing it Every shell
Historical name sharp
p
d f
1
2 3
6
10 14
2nd shell and higher
3rd shell and higher 4th shell and higher
精细结构常数
e / 40 1 c 137
2
光谱
类氢离子,毕克林系 折合质量,里德堡常数随不同类氢离子变化
Franck-Hertz实验
广义量子化条件和索末菲理论
A. 广义量子化条件
玻尔在氢原子理论中得出,只有满足角动量量子化条件
L n,n1,2,3,
的电子轨道运动才是实际上可能存在的,将上式改写一下, 即
这里是dq角移或位移, pq是与q对应的动量,即角动量或线 动量。积分指经一周期的积分。显然,这个一般表达式包 括了玻尔的圆周运动的轨道角动量量子化条件。
•
B. 玻尔-索末菲模型
在玻尔理论发表不久,索末菲便于 1916 年提出了椭圆 轨道的理论。索末菲主要做了两件事,其一是把玻尔的圆 形轨道推广为椭圆轨道,其二是引入了相对论修正。 索末菲目的是解释在实验观察到的氢光谱的精细结构 ,迈克尔逊和莫雷在1896年就发现氢的Hα线是双线,后在 高分辨率谱仪中呈现出三条线。玻尔猜测可能是由于电子 在椭圆轨道上运动时作进动所引起的。按此想法索末菲作 了计算。在考虑椭圆轨道并引入相对论修正后,原来由玻 尔模型得到的能级发生分裂,根据选择定则,定量计算出 了三条Hα线,与实验完全符合。但这一“完全符合”纯粹 是一种巧合。实际上一条Hα将呈现出七条精细结构谱线。 对此,玻尔-索末菲模型就完全无能为力了。
几种碱金属元素的原子具有相仿的结构。光谱线也明显地 构成几个线系。一般观察到的四个线系称为主线系、第一辅 线系(又称漫线系)、第二辅线系 ( 又称锐线系 ) 和柏格曼线 系 ( 又称基线系 ) 。下图显示了锂原子的这四个线系,是按波 数的均匀标尺作图的,图中也附了波长标尺,从图中可以看 到主线系的波长范围最广,第一条线是红色的,其余诸线在 紫外。主线系的系限的波数是 43484.4 厘米 - 1 ,相当于波长 2299.7Å 。第一辅线系在可见部分。第二辅线系的第一条线 在红外。
碱金属原子的光谱
玻尔理论已经成功讨论和解释了氢原子和类氢离子的结 构和光谱,这里要讨论的是另一类与氢原子类似结构的原 子——碱金属原子,包括锂Li、钠Na、钾K、铷Rb、铯Cs和 钫Fr,原子序数分别为3、11、19、37、55和87。这些元素 在周期表中属同一族,有相仿的化学性质,都是一价的。它 们的电离电势都比较小,易被电离,具有金属的一般性质。 对与氢原子类似结构的两大类原子来说,在谁更像氢原子的 问题上各有所长。从核外只有一个电子 e 这个角度看,显然类氢离子优于碱金 e 属原子,但从最外层那个电子所感受 到的那个“原子实”的作用来说,碱金 属原子中原子实的净电荷Z是1,在这 一点上又优于类氢离子。
