三角形中位线常见类型题培优讲义
三角形中位线培优复习上课讲义

三角形中位线培优复习课题三角形中位线培优F M E C B A P F E D C B A F N M E C B A例题2:BE 、CF 是△ABC 的角平分线,AN ⊥BE 于N ,AM ⊥CF 于M 。
求证:MN ∥BC练习:如图,在∆ABC 中,AB=BC ,∠ABC=90°,F 为BC 上一点,M 为AF 的中点,BE 平分∠ABC ,且EF ⊥BE ,求证:CF=2ME 。
方法二、【取中点构造中位线】例题1:如图,在四边形ABCD 中,AD=BC ,∠CBD=20°,∠BDA=110°,E 、F 、P 分别为AB 、CD 、BD 的中点,探索PF 与EF 的数量关系.练习:如图,在∆ABC 中,∠C=90°,CA=CB ,E ,F 分别为CA ,CB 上一点,CE=CF ,M ,N 分别为AF ,BE 的中点,求证:AE=2MNNM D C B A 例题2:如图,四边形ABCD 中,M ,N 分别为AD ,BC 的中点,边BD ,若AB=10,CD=8,求MN 的取值范围。
练习:已知:如图,在四边形ABCD 中,AD =BC ,E 、F 分别是DC 、AB 边的中点,FE的延长线分别与AD 、BC 的延长线交于H 、G 点.求证:∠AHF =∠BGF .方法三、【借助平行四边形的性质】例题:如图,(1)E 、F 为△ABC 的中点,G 、H 为AC 的两个三等分点,连接EG 、FH 并延长交于D , 连接AD 、CD. 求证:四边形ABCD 是平行四边形.练习:已知:如图,在□ABCD 中,E 是CD 的中点,F 是AE 的中点,FC 与BE 交于G .求证:GF =GC .课后作业1.如图,在△ABC 中,AB=10,BC=7,BE 平分∠ABC ,AE ⊥BE ,点F 为AC 的中点,连接EF ,求EF 的长度.3.如图,AD 是△ABC 的中线,E 是AD 的中点,F 是BE 延长线与AC 的交点。
专题22 三角形中位线定理应用问题(解析版)

专题22 三角形中位线定理应用问题1.三角形中位线的定义:连接三角形两边中点的线段叫做三角形的中位线。
2.三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
3.对三角形中位线的深刻理解(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的,每个小三角形的面积为原三角形面积的. (3)三角形的中位线不同于三角形的中线.【例题1】(2020•福建)如图,面积为1的等边三角形ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,则△DEF 的面积是( )A .1B .12C .13D .14 【答案】D【解析】根据三角形的中位线定理和相似三角形的判定和性质定理即可得到结论.∵D ,E ,F 分别是AB ,BC ,CA 的中点,1214∴DE =12AC ,DF =12BC ,EF =12AB ,∴DF BC =EF AB =DE AC =12,∴△DEF ∽△ABC ,∴S △DEFS △ABC =(DE AC )2=(12)2=14, ∵等边三角形ABC 的面积为1,∴△DEF 的面积是14.【对点练习】(2019内蒙古赤峰)如图,菱形ABCD 周长为20,对角线AC 、BD 相交于点O ,E 是CD 的中点,则OE 的长是( )A .2.5B .3C .4D .5【答案】A .【解析】∵四边形ABCD 为菱形,∴CD =BC ==5,且O 为BD 的中点, ∵E 为CD 的中点,∴OE 为△BCD 的中位线,∴OE =CB =2.5。
【点拨】掌握菱形特点,根据三角形中位线定理解决问题。
【例题2】(2020•临沂)如图,在△ABC 中,D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,H 为AF 与DG 的交点.若AC =6,则DH = .【解析】1.【分析】由三等分点的定义与平行线的性质得出BE =DE =AD ,BF =GF =CG ,AH =HF ,DH 是△AEF 的中位线,易证△BEF ∽△BAC ,得EF AC =BE AB ,解得EF =2,则DH =12EF =1. 【解析】∵D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,∴BE =DE =AD ,BF =GF =CG ,AH =HF ,∴AB =3BE ,DH 是△AEF 的中位线,∴DH =12EF ,∵EF ∥AC ,∴△BEF ∽△BAC ,∴EF AC =BE AB ,即EF 6=BE 3BE ,解得:EF =2,∴DH =12EF =12×2=1,【对点练习】(2019广西梧州)如图,已知在△ABC 中,D 、E 分别是AB 、AC 的中点,F 、G 分别是AD 、AE 的中点,且FG =2cm ,则BC 的长度是 cm .【答案】8.【解析】利用三角形中位线定理求得FG=DE,DE=BC.如图,∵△ADE中,F、G分别是AD、AE的中点,∴DE=2FG=4cm,∵D,E分别是AB,AC的中点,∴DE是△ABC的中位线,∴BC=2DE=8cm【点拨】连续两次应用三角形中位线定理处理本题,是关键。
三角形的中位线习题精讲精析PPT课件
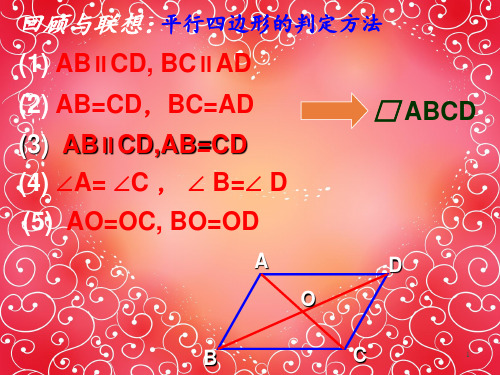
(1) AB∥CD, BC∥AD
(2) AB=CD,BC=AD (3) AB∥CD,AB=CD (4) ∠A= ∠C , ∠ B=∠ D
□ ABCD
(5) AO=OC, BO=OD
A
D
O
B.
C
1
A、B两点被池塘隔开,现在要测量出A、B两 点间的距离 ,但又无法直接去测量,怎么办?
⑶若四边形EFGH是正方形,AC与BD C 应满足什么条件?
.
27
作业
.
28
9 1. 如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则BC= ———
A
F3G
D 4.5 1.5 E P
B
C
9
.
29
2. 已知:如图 E、F把四边形ABCD的对角线BD三等分, CE、CF的延长线分别平分AB、AD .
A
D
A’
D’
O
B’
C’
B
C
.
23
4. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
A。
D。
40
20
C。
。
。B
E
.
学随
们着
解 决 这 个 问 题
将 会 有 更 多 的 办
如果 DE. 是△ABC的中位线
A
那么 ⑴ DE∥BC,
D
⑵ DE=1/2BC E 定理的主要用途:
B
C
① 证明平行
② 证明一条线段是另一条线段
9.13 三角形的中位线知识讲解20202021学年八年级数学下册基础知识专项讲练苏科版

专题9.13 三角形的中位线(知识讲解)【学习目标】4. 理解三角形的中位线的概念,掌握三角形的中位线定理.【要点梳理】要点一、三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的,每个小三角形的面积为原三角形面积的.=4;(2).S S S S ABC DEF ADF CEF BDE DEF ABC D E F AB BC AC DE EF DF ABC ∆∆∆∆∆∆∆∆===如图:在中,、、分别为、、三边的中点,则、、为中位线,则有如下结论:(1).S S(3)三角形的中位线不同于三角形的中线.1214【典型例题】类型一、三角形中位线有关的求解问题1.如图,Rt ABC V 中,90ACB Ð=°,点D ,E 分别是,AB AC 的中点,点F 在BC 的延长线上,且CEF A Ð=Ð.(1)求证:四边形DCFE 是平行四边形;(2)若26,==BC AB ,求四边形DCFE 的周长.【解析】(1)利用两组对边分别平行的四边形是平行四边形证明即可;(2)分别利用中位线定理和直角三角形斜边中线性质得到DE 和CD ,从而计算结果.(1)证明:∵∠ACB=90°,AD=DB ,∴CD=DA=DB ,∴∠DAC=∠DCA ,∵∠CEF=∠A ,∴∠CEF=∠DCE ,∴CD ∥EF ,∵AD=DB ,AE=EC ,∴DE ∥CF ,∴四边形DCEF 是平行四边形.(2)∵D 、E 分别是AB 、AC 的中点,26,==BC AB ,∴DE=12BC=1,CD=12AB=3,∴四边形DCFE 的周长为(1+3)×2=8.【点拨】本题考查平行四边形的判定和性质,直角三角形斜边中线的性质和中位线定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.举一反三【变式】已知,如图,CD 是Rt △FBE 的中位线,A 是EB 延长线上一点,且AB=12BE . (1)证明:四边形ABCD 是平行四边形;(2)若∠E=60°,AD=3cm ,求BE 的长.(1)证明:∵CD 是Rt △FBE 的中位线,∴CD ∥BE ,CD=12BE ,∴AB=12BE ,∴AB=CD ,∴四边形ABCD 是平行四边形;(2)解:∵四边形ABCD 是平行四边形,∴BC=AD=3cm ,∵CD 是Rt △FBE 的中位线,∴BC=CE=12EF ,∵∠E=60°,∴△BCE 是等边三角形,∴BE=BC=3cm .【点拨】此题考查了平行四边形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及三角形中位线的性质.注意利用三角形中位线的性质,证得CD ∥AB ,CD=AB 是解此题的关键.类型二、三角形中位线与面积问题2.如图,AD 为ABC ∆的中线,BE 为ABD ∆的中线.(1)15ABE Ð=°,40BAD Ð=°,求 BED Ð的度数;(2)若ABC ∆的面积为40,5BD =,则E 到BC 边的距离为多少.【答案】(1)55°;(2)4.【分析】(1)根据三角形内角与外角的性质解答即可;(2)过E 作BC 边的垂线即可得:E 到BC 边的距离为EF 的长,然后过A 作BC 边的垂线AG ,再根据三角形中位线定理求解即可.解:(1)BED ÐQ 是ABE ∆的外角,154055BED ABE BAD \Ð=Ð+Ð=°+°=°;(2)过E 作BC 边的垂线,F 为垂足,则EF 为所求的E 到BC 边的距离,过A 作BC 边的垂线AG ,AD ∴为ABC ∆的中线,5BD =,22510BC BD ∴==´=,ABC ∆Q 的面积为40,∴1402BC AG =g ,即110402AG ´=g ,解得8AG =,∵AD 为ABC ∆的中线,∴11402022ABD ABC S S D D ==´=,又∵BE 为ABD ∆的中线,∴11201022EBD ABD S S D D ==´=,则有:1151022BD EF EF =´=g 4EF ∴=.即E 到BC 边的距离为4.【点拨】本题考查了三角形外角的性质、三角形中位线的性质及三角形的面积公式,添加适当的辅助线是解题的关键.举一反三【变式】如图,等腰三角形ABC 中,AB=AC ,点E 、F 分别是AB 、AC 的中点,CE ⊥BF 于点O .(1)求证:四边形EBCF 是等腰梯形;(2)EF=1,求四边形EBCF 的面积.(1)证明:∵点E 、F 分别是AB 、AC 的中点,∴EF//BC ,BE=12AB=12AC=CF ,∴四边形EBCF 是等腰梯形;(2)如图,延长BC 至点G ,使CG=EF ,连接FG ,∵EF//BC ,即EF//CG ,且CG=EF ,∴四边形EFGC 是平行四边形,又∵四边形EBCF 是等腰梯形,∴FG=EC=BF ,∵EF=CG ,FC=BE ,∴△EFB ≌△CGF (SSS ),∴BFG EBCF S S V 四边形,∵GC=EF=1,且EF=12 BC,∴BC=2,∴BG=BC+CG=1+2=3.∵FG//EC,∴∠GFB=∠BOC=90°,∴FH=12BG=32,∴BFGEBCF 1393224S S==´´=V四边形.【点拨】本题考查了等腰梯形的判定,全等三角形的判定和性质,平行四边形的性质,正确的作出辅助线是解题的关键.类型三、与三角形有关的证明3.已知:如图AB=AC,AB⊥AC,AD=AE,AD⊥AE,点M为CD的中点求证:2AM=BE【分析】作CN∥AM,交DA延长线于N,根据AM∥CN,点M是CD的中点,得到AM是△DCN的中位线,推出CN=2AM,AE=AN,根据∠BAC=∠DAE=90°证出∠CAN=∠BAE,证得△BAE≌△CAN,推出BE=CN,由此得到结论.证明:如图,作CN∥AM,交DA延长线于N,∵AM∥CN,点M是CD的中点,∴AM是△DCN的中位线,∴CN=2AM,AD=AN,∴AE=AN,∵AD⊥AE,AB⊥AC,∴∠BAC=∠DAE=90°∴∠EAN=90°,∴∠CAE+∠EAN=∠BAC+∠CAE,∴∠CAN=∠BAE,∵AB=AC,AE=AN,∴△BAE≌△CAN,∴BE=CN,∴2AM=BE..【点拨】此题考查全等三角形的判定及性质,三角形中位线的性质,题中辅助线的引出是解题的关键,在三角形中,已知一边中点时,通常是利用中点构造全等三角形解决问题.举一反三【变式】如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并证明你的结论.证明:四边形EFGH是平行四边形,理由如下连接AC,如图.∵E ,F 分别是AB ,BC 的中点,∴EF 是△ABC 的中位线,∴EF ∥AC ,且EF=12AC ,同理HG ∥AC ,且HG=12AC ,∴EF ∥HG ,且EF=HG .∴四边形EFGH 是平行四边形.【点拨】本题主要考查平行四边形的判定,解题的关键是灵活应用三角形中位线定理,学会添加常用辅助线.类型四、三角形中位线的应用4.在Rt ABC ∆中,90BAC Ð=o ,,E F 分别是,AB AC 上的点,且//EF BC ,作EG 平分AEF Ð交于点G ,在EF 上取点D ,使ED EA =,连接DG 并延长,交BA 的延长线于点P ,连接PF .(1)求证:PD EF ^;(2)若ED DF =,求B Ð的大小(3)在(2)的条件下,若四边形AEDG 的面积为S ,请直接写出PEF ∆的面积(用含S 的式子表示)【分析】(1)由已知证明AEG DEG ∆@∆可得出GAE GDE Ð=Ð=90°,即PD EF^(2)根据已知由中垂线性质可得GE GF =,即GEF GFE AEG Ð=Ð=Ð,由//EF BC 即可得出60B AEF Ð=Ð=o .(3)由已知可推出3PEF S S ∆=.(1)证明:EG Q 平分AEF Ð,AEG DEG ∴Ð=Ð,在AEG ∆和DEG ∆中,ED EA AEG DEGEG EG =ìïÐ=Ðíï=î()AEG DEG SAS ∴∆@∆GAE GDE∴Ð=Ð90EAG Ð=oQ 90GDE ∴Ð=o ,即PD EF ^;(2),ED DF PD EF =^Q ,∴由中垂线性质得:GE GF =,GEF GFE AEG∴Ð=Ð=Ð∴在Rt AEF ∆中,30,60GEF GFE AEG AEF Ð=Ð=Ð=Ð=o o ,又//EF BC Q ,60B AEF ∴Ð=Ð=o(3)由已知可得:3PEF S S ∆=.【点拨】本题考查三角形中位线定理,熟练掌握三角形中位线定理的性质及判定是解题关键.举一反三【变式】如图,直线1:3l y x =-+与x 轴相交于点A ,直线2:l y kx b =+经过点31-(,),与x 轴交于点()6,0B ,与y 轴交于点C ,与直线1l 相交于点D .()1求直线2l 的函数关系式;()2点P 是2l 上的一点,若ABP △的面积等于ABD △的面积的2倍,求点P 的坐标.()3设点Q 的坐标为3m (,) ,是否存在m 的值使得QA QB +最小?若存在,请求出点Q 的坐标;若不存在,请说明理由.【答案】(1)y=13x-2;(2)(212 ,32)或(32,−32 );(3)(92,3).【分析】(1)把点(3,-1),点B (6,0)代入直线l 2,求出k 、b 的值即可;(2)设点P 的坐标为(t ,13t-2),求出D 点坐标,再由S △ABP =2S △ABD 求出t 的值即可;(3)作直线y=3,作点A 关于直线y=3的对称点A′,连结A′B ,利用待定系数法求出其解析式,根据点Q (m ,3)在直线A′B 上求出m 的值,进而可得出结论.解:(1)由题知:1306k b k b-+ìí+î== 解得:213b k -ìïíïî==,故直线l 2的函数关系式为:y=13x-2;(2)由题及(1)可设点P 的坐标为(t ,13 t-2).解方程组1233y x y x ì-ïíï-+î== ,得15434x y ìïïíï-ïî== ,∴点D 的坐标为(154,-34).∵S △ABP =2S △ABD ,∴12AB•|13t-2|=2×12AB•|-34|,即|13t-2|=32,解得:t=212或t=32,∴点P 的坐标为(212 ,32)或(32,−32 );(3)作直线y=3(如图),再作点A 关于直线y=3的对称点A′,连结A′B .由几何知识可知:A′B与直线y=3的交点即为QA+QB最小时的点Q.∵点A(3,0),∴A′(3,6)∵点B(6,0),∴直线A′B的函数表达式为y=-2x+12.∵点Q(m,3)在直线A′B上,∴3=-2m+12解得:m=92,故存在m的值使得QA+QB最小,此时点Q的坐标为(92,3).【点拨】此题考查一次函数综合题,涉及到一次函数图象上点的坐标特点,轴对称最短路线问题,三角形的面积公式,解题关键在于在解答(3)时要注意作出辅助线,利用轴对称的性质求解.。
三角形中位线讲义2023-2024学年北师大版八年级数学下册

三角形中位线讲义【要点梳理】要点一、三角形的中位线1.定义:连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.特别说明:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的,每个小三角形的面积为原三角形面积的. (3)三角形的中位线不同于三角形的中线.要点二、中点三角形 定义:中点三角形就是把一个三角形的三边中点顺次连接起来的一个新三角形.性质:(1)这个新三角形的各个边长分别是原来三角形三边长的一半且分别平行,角的度数与原三角形分别相等,4个三角形都全等(2)中点三角形周长是原三角形的周长一半。
(3)中点三角形面积是原三角形面积的四分之一。
补充:中点三角形与原三角形不仅相似,而且位似。
要点三、中点四边形 定义:依次连接任意四边形各边中点所得的四边形称为中点四边形。
中点四边形的形状与原四边形的对角线的数量和位置关系有关。
性质(1)不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形。
题型一:与三角形中位线有关的线段求解问题【例1】如图,ABCD 中,对角线AC 、BD 相交于点O ,点 E , F ,G ,H 分别是OA 、OB 、OC 、OD 的中点,顺次连接EFGH .(1)求证:四边形EFGH 是平行四边形(2)若ABCD 的周长为2(AB +BC )=32,则四边形EFGH 的周长为__________【解答】 (1)证明:∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD , ∵点 E 、 F 、G 、H 分别是OA 、OB 、OC 、OD 的中点,∴1111,,,2222OE OA OF OB OG OC OH OD ====, ∴OE =OG ,OF =OH ,1214∴四边形EFGH 是平行四边形;(2)∵点 E 、 F 、G 、H 分别是OA 、OB 、OC 、OD 的中点, ∴11,22EF AB FG BC ==, ∴()12EF FG AB BC +=+ , ∵ABCD 的周长为2(AB +BC )=32,∴16AB BC += ,∴8EF FG += ,由(1)知:四边形EFGH 是平行四边形, ∴四边形EFGH 的周长为()22816EF FG +=⨯= .【变式1-1】如图,在△ABC 中,AB =AC ,AD ⊥BC 于点D .(1)若DE ∥AB 交AC 于点E ,证明:△ADE 是等腰三角形;(2)若BC =12,DE =5,且E 为AC 中点,求AD 的值.【解答】 (1)证明:∵在△ABC 中,AB =AC ,∴△ABC 为等腰三角形,∵AD ⊥BC 于点D ,∴由“三线合一”知:∠BAD=∠CAD ,∵DE ∥AB 交AC 于点E ,∴∠BAD=∠ADE ,∴∠CAD=∠ADE ,即:∠ADE=∠EAD ,∴AE=DE ,∴△ADE 是等腰三角形;(2)解:由“三线合一”知:BD=CD ,∵BC=12,∴DC=6,∵E 为AC 中点,∴DE 为△ABC 的中位线,∴AB=2DE ,∴AC=AB=2DE=10,在Rt △ADC 中,22221068AD AC DC =−−=,∴AD=8.【变式1-2】如图,四边形ABCD 中,∠A =90°,AB =12,AD =5,点M 、N 分别为线段BC 、AB 上的动点(含端点,但点M 不与点B 重合),点E 、F 分别为DM 、MN 的中点,则EF 长度的可能为( )A .2B .5C .7D .9 【解答】解:连接DN ,∵ED =EM ,MF =FN ,∴EF =12DN ,∴DN 最大时,EF 最大,DN 最小时,EF 最小,∵N 与B 重合时DN 最大,此时DN =DB =√AD 2+BD 2=√52+122=13,∴EF 的最大值为6.5.∵∠A =90°,AD =5,∴DN ≥5,∴EF ≥2.5,∴EF 长度的可能为5;故选:B .【变式1-3】如图,在△ABC 中,AB =CB =6,BD ⊥AC 于点D ,F 在BC 上且BF =2,连接AF ,E 为AF 的中点,连接DE ,则DE 的长为( )A .1B .2C .3D .4【解答】解:∵CB =6,BF =2,∴FC =6﹣2=4,∵BA =BC ,BD ⊥AC ,∴AD =DC ,∵AE =EF ,∴DE 是△AFC 的中位线,∴DE =12FC =12×4=2,故选:B . 题型二、与三角形中位线有关的面积问题【例2】如图,在ABC 中,D ,E 分别为AB ,AC 的中点,延长BC 至点F ,使12CF BC =,连接CD 和EF .(1)求证:四边形DCFE 是平行四边形.(2)若四边形DCFE 的面积为4,求ABC 的面积.【解答】()1证明:∵D ,E 分别为AB ,AC 的中点,∴DE 为ABC 的中位线,∴//DE BC ,12DE BC =. ∵12CF BC =,∴DE CF =.∵//DE CF , ∴四边形DCFE 是平行四边形; ()2解:∵四边形DCFE 是平行四边形,∴DEC 的面积ECF =的面积2=.∵E 是AC 的中点,∴ADE 的面积DEC =的面积2=.∵D 是AB 的中点,∴BDC 的面积ADC =的面积4=,∴ABC 的面积4228=++=.【变式2-1】如图1,在四边形ABCD 中,E 、F 、G 、H 分别是AD 、BC 、BD 、AC 的中点. (1)求证:四边形EGFH 是平行四边形;(2)如图2,延长BA 、CD 相交于点P ,连接PG 、PH 、GH ,若1PGH S =△,求四边形ABCD 的面积.【解答】 证明:(1),E G 分别是,AD BD 的中点,1,//2EG AB EG AB ∴=,同理可得:1,//2FH AB FH AB =, ,//EG FH EG FH ∴=,∴四边形EGFH 是平行四边形;(2)如图,连接,,,PE AG BH DH ,,E G 分别是,AD BD 的中点,//EG AB ∴,AEG PEG S S ∴=(同底等高),同理可得:DEH PEH S S =,1AEG EGH DEH PEG EGH PEH PGH AGHD S S S S S S S S ∴=++=++==四边形,又G 是BD 的中点,BG DG ∴=,,ABG ADG HBG HDG SS S S ∴==(等底同高), 2()22ABG ADG HBG HDG ADG HDG ABHD AGHD S S S S S S S S ∴=+++=+==四边形四边形,同理可得:2224ABCD ABHD S S ==⨯=四边形四边形,即四边形ABCD 的面积为4.【变式2-2】如图所示,在△ABC 中,D 是BC 边上任一点,F,G,E 分别是AD,BF,CF 的中点,连结GE ,若△FGE 的面积为6,则ABC 的面积为( )A.32B.48C.64D.72【变式2-3】如图,已知在△ABC 中,点D 、E 分别是边AB 、AC 的中点。
三角形中位线定理知识点-例题-习题

第二十三讲三角形中位线定理【要点梳理】要点一、三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于第三边,并且等于第三边的一半.要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.要点二、顺次连接任意四边形各边中点得到的四边形的形状顺次连接任意四边形各边中点得到的四边形是平行四边形.【典型例题】类型一、三角形的中位线例1、如图,已知P、R分别是长方形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P 在BC上从B向C移动,点R不动,那么下列结论成立的是()A.线段EF的长逐渐增大B.线段EF的长逐渐变小C.线段EF的长不变D.无法确定【答案】C;【解析】连AR,由E、F分别为PA,PR的中点知EF为△PAR的中位线, 则12EF AR,而AR长不变,故EF大小不变.【总结升华】当条件中含有中点的时候,要将它与中位线联系起来,进行联想,必要时添加辅助线,构造中位线图形.举一反三:【变式】在△ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.【答案】5;解:四边形MNEF是平行四边形.理由如下:∵BE、CF是中线,∴E、F分别是AC、AB的中点,∴EF是△ABC的中位线,∴EF∥BC且EF=BC,∵M、N分别是BO、CO中点,∴MN是△OBC的中位线,∴MN∥BC且MN=BC,∴EF∥MN且EF=MN,∴四边形MNEF是平行四边形.例2、如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是()A.2 B.3 C.52D.4【思路点拨】利用中位线定理,得到DE∥AB,根据平行线的性质,可得∠EDC=∠ABC,再利用角平分线的性质和三角形内角外角的关系,得到DF=DB,进而求出DF的长.【答案解析】解:在△ABC中,D、E分别是BC、AC的中点∴DE∥AB∴∠EDC=∠ABC∵BF平分∠ABC∴∠EDC=2∠FBD在△BDF中,∠EDC=∠FBD+∠BFD∴∠DBF=∠DFB∴FD=BD=12BC=12×6=3.【总结升华】三角形的中位线平行于第三边,当出现角平分线,平行线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.例3、如图所示,在△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D,AB=12,AC =18,求MD的长.【思路点拨】本题中所求线段MD 与已知线段AB 、AC 之间没有什么联系,但由M 为BC 的中点联想到中位线,另有AD 为角平分线和垂线,根据等腰三角形“三线合一”构造等腰三角形ABN ,D 为BN 的中点,DM 即为中位线,不难求出MD 的长度.【答案与解析】解:延长BD 交AC 于点N .∵ AD 为∠BAC 的角平分线,且AD ⊥BN ,∴ ∠BAD =∠NAD ,∠ADB =∠ADN =90°,在△ABD 和△AND 中,BAD NAD AD =ADADB ADN ∠∠⎧⎪⎨⎪∠∠⎩== ∴ △ABD ≌△AND(ASA)∴ AN =AB =12,BD =DN .∵ AC =18,∴ NC =AC -AN =18-12=6,∵ D 、M 分别为BN 、BC 的中点,∴ DM =12CN =162⨯=3. 【总结升华】当条件中含有中点的时候,可以将它与等腰三角形的“三线合一”、三角形的中线、中位线等联系起来,进行联想,必要时添加辅助线,构造中位线等图形.举一反三:【变式】(2015春•泗洪县校级期中)如图,BE ,CF 是△ABC 的角平分线,AN ⊥BE 于N ,AM ⊥CF 于M ,求证:MN ∥BC .【答案】证明:延长AN 、AM 分别交BC 于点D 、G .∵BE 为∠ABC 的角平分线,BE ⊥AG ,∴∠BAG=∠BGA ,∴△ABG 为等腰三角形,∴BN也为等腰三角形的中线,即AN=GN.同理AM=DM,∴MN为△ADG的中位线,∴MN∥BC.例4、(1)如图1,在四边形ABCD中,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD.(提示取BD的中点H,连接FH,HE 作辅助线)(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA 的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.【思路点拨】(1)连结BD,取DB的中点H,连结EH、FH,证明出EH∥AB,EH=AB,FH∥CD,FH=CD,证出HE=HF,进而证出AB=CD;(2)连结BD,取DB的中点H,连结EH、OH,证明出EH=OH,可证明证出△OEH是等边三角形,进而求出OE=.【答案与解析】(1)证明:连结BD,取DB的中点H,连结EH、FH.∵E、F分别是BC、AD的中点,∴EH∥AB,EH=AB,FH∥CD,FH=CD,∵∠BME=∠CNE,∴HE=HF,∴AB=CD;(2)解:连结BD,取DB的中点H,连结EH、OH,∵AB=CD,∴HO=HE,∴∠HOE=∠HEO,∵∠OEC=60°,∴∠HEO=∠AGO=60°,∴△OEH是等边三角形,∵AB=DC=5,∴OE=.【总结升华】本题考查了三角形的中位线定理、全等三角形的判定与性质,解答本题的关键是参考题目给出的思路,作出辅助线,有一定难度.举一反三:【变式】如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是()A.4 B.3 C.2 D.1【答案】D;解:连接DE并延长交AB于H,∵CD∥AB,∴∠C=∠A,∠CDE=∠AHE,∵E是AC中点,∴AE=CE,∴△DCE≌△HAE,∴DE=HE,DC=AH,∵F是BD中点,∴EF是△DHB的中位线,∴EF=12 BH,∴BH=AB-AH=AB-DC=2,∴EF=1.类型二、中点四边形例5、如图,点O是△ABC外一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G,连接DE、EF、FG、GD.(1)判断四边形DEFG的形状,并说明理由;(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段DG的长.【答案与解析】解:(1)四边形DEFG是平行四边形,理由是:∵线段AB、OB、OC、AC的中点分别为D、E、F、G,∴EF∥BC,EF=BC,DG=BC,DG∥BC,∴EF∥DG,EF=DG,∴四边形DEFG是平行四边形;(2)∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,∴∠BOC=180°﹣90°=90°,∵M为EF的中点,OM=2,∴EF=2OA=4,∵EF=DG,∴DG=4.【总结升华】本题考查了中点四边形形状的判定,主要是利用中位线定理得出一组对边平行且相等,从而判定是平行四边形.【巩固练习】一.选择题1.已知△ABC 的各边长度分别为3cm ,4cm ,5cm ,则连结各边中点的三角形的周长为( )A .2cmB .7cmC .5cmD .6cm2. 如图,点D 、E 、F 分别为△ABC 三边的中点,若△DEF 的周长为10,则△ABC 的周长为( )A .5B .10C .20D .403. 在△ABC 中,AB=3,BC=4,AC=2,D 、E 、F 分别为AB 、BC 、AC 中点,连接DF 、FE ,则四边形DBEF 的周长是( )A .5B .7C .9D .114.如图,△ABC 的中线BD 、CE 交于点O ,连接OA ,点G 、F 分别为OC 、OB 的中点,BC=8,AO=6,则四边形DEFG 的周长为( )A .12B .14C .16D .185. 如图所示,在△ABC 中,AB =AC ,M ,N 分别是AB ,AC 的中点,D ,E 为BC 上的点,连接DN 、EM ,若AB =5cm ,BC =8cm ,DE =4cm ,则图中阴影部分的面积为( )A .12cmB .1.52cmC .22cmD .32cm(第5题) (第6题)6. 如图,在四边形ABCD 中,AB ∥CD ,点E 、F 、G 分别是BD 、AC 、DC 的中点.已知两底的差是6,两腰的和是12,则△EFG 的周长是( )A.8B.9C.10D.12二.填空题7. 顺次连接一个四边形各边中点得到的四边形是_________________.8. 如图, E 、F 分别是口ABCD 的两边AB 、CD 的中点, AF 交DE 于P, BF 交CE 于Q,则PQ 与AB 的关系是 .9. 如图,E 、F 、G 、H 分别是四边形ABCD 各边的中点,对角线AC 、BD 的长分别为7和9,则四边形EFGH 的周长是______.第8题第9题 第10题 10.如图,四边形ABCD 中,∠A=90°,AB=3,AD=3,点M ,N 分别为线段BC ,AB 上的动点(含端点,但点M 不与点B 重合),点E ,F 分别为DM ,MN 的中点,则EF 长度的最大值为 .11.如图,△ABC 的周长为26,点D ,E 都在边BC 上,∠ABC 的平分线垂直于AE ,垂足为Q ,∠ACB的平分线垂直于AD ,垂足为P ,若BC=10,则PQ 的长 .第11题 第12题12.如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,过点O 作EF ∥BC 交AB 于E ,交AC 于F ,过点O 作OD ⊥AC 于D .下列三个结论:①∠BOC =90°+12∠A ;②设OD =m ,AE +AF =n ,则AEF S mn △;③EF 不能成为△ABC 的中位线.其中正确的结论是_______.三.解答题13.如图,四边形ABCD 中,AD ∥BC ,M 、N 、P 、Q 分别为AD 、BC 、BD 、AC 的中点.求证:MN 和PQ 互相平分.14.已知:在△ABC 中,BC >AC ,动点D 绕△ABC 的顶点A 逆时针旋转,且AD =BC ,连接DC .过AB 、DC 的中点E 、F 作直线,直线EF 与直线AD 、BC 分别相交于点M 、N .(1)如图1,当点D 旋转到BC 的延长线上时,点N 恰好与点F 重合,取AC 的中点H ,连接HE 、HF ,根据三角形中位线定理和平行线的性质,可得结论∠AMF =∠BNE (不需证明);(2)当点D 旋转到图2或图3中的位置时,∠AMF 与∠BNE 有何数量关系?请分别写出猜想,并任选一种情况证明.15.已知,如图,在Rt△ABC中,∠ACB=90°,点D为AB中点,连接CD.点E为边AC上一点,过点E作EF∥AB,交CD于点F,连接EB,取EB的中点G,连接DG、FG.(1)求证:EF=CF;(2)求证:FG⊥DG.【答案与解析】一.选择题1.【答案】D ;【解析】由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半,即可求其周长.2.【答案】C ;【解析】根据中位线定理可得BC =2DF ,AC =2DE ,AB =2EF ,继而结合△DEF 的周长为10,可得出△ABC 的周长.3.【答案】B ;【解析】∵D 、E 、F 分别为AB 、BC 、AC 中点,∴DF=12BC=2,DF ∥BC ,EF=12AB=32,EF ∥AB , ∴四边形DBEF 为平行四边形, ∴四边形DBEF 的周长=2(DF+EF )=2×(2+32)=7. 故选B .4.【答案】B ;【解析】解:∵BD ,CE 是△ABC 的中线,∴ED ∥BC 且ED=BC ,∵F 是BO 的中点,G 是CO 的中点,∴FG ∥BC 且FG=BC ,∴ED=FG=BC=4,同理GD=EF=AO=3,∴四边形DEFG 的周长为3+4+3+4=14.故选B .5.【答案】B ;【解析】连接MN ,作AF ⊥BC 于F .∵AB =AC ,∴BF =CF =12BC =12×8=4,在Rt △ABF 中,AF =22AB BF -=2254-=3,∵M 、N 分别是AB ,AC 的中点,∴MN 是中位线,即平分三角形的高且MN =8÷2=4,∴NM =12BC =DE ,∴△MNO ≌△EDO ,O 也是ME ,ND 的中点,∴阴影三角形的高是12AF÷2=1.5÷2=0.75,∴S 阴影=4×0.75÷2=1.5.6.【答案】B;【解析】连接AE,延长交CD于H,可证AB=DH,CH=两底的差,EF是△AHC的中位线,EF=1 2两底的差,EG+FG=12两腰的和,故△EFG的周长是9.二.填空题7.【答案】平行四边形;8.【答案】PQ∥AB,PQ=12 AB;【解析】P,Q分别是AF,BF的中点.9.【答案】16;【解析】根据三角形中位线的性质得出HG 12AC,EF12AC,HE12DB,GF12BD,进而得出HE=GF=12BD,HG=FE=12AC,即可得出答案.10.【答案】3;【解析】解:∵ED=EM,MF=FN,∴EF=DN,∴DN最大时,EF最大,∵N与B重合时DN最大,此时DN=DB==6,∴EF的最大值为3.故答案为3.11.【答案】3;【解析】∵△ABC的周长是26,BC=10,∴AB+AC=26﹣10=16,∵∠ABC的平分线垂直于AE,∴在△ABQ和△EBQ中,,∴△ABQ≌△EBQ,∴AQ=EQ,AB=BE,同理,AP=DP,AC=CD,∴DE=BE+CD﹣BC=AB+AC﹣BC=16﹣10=6,∵AQ=DP,AP=DP,∴PQ是△ADE的中位线,∴PQ=12DE=3.故答案是:3.12.【答案】①,③;【解析】①根据三角形内角和定理求解;②根据△AEF的面积=△AOE的面积+△AOF的面积求解;③若此三角形为等边三角形,则EF即为中位线.三.解答题13.【解析】证明:连接MP,PN,NQ,QM,∵AM=MD,BP=PD,∴PM是△ABD的中位线,∴PM∥AB,PM=12 AB;同理NQ=12AB,NQ∥AB,∴PM=NQ,且PM∥NQ.∴四边形MPNQ是平行四边形.∴MN与PQ互相平分.14.【解析】解:图1:∠AMF=∠ENB;图2:∠AMF=∠ENB;图3:∠AMF+∠ENB=180°.证明:如图2,取AC的中点H,连接HE、HF.∵F是DC的中点,H是AC的中点,∴HF∥AD,HF=12 AD,∴∠AMF=∠HFE,同理,HE∥CB,HE=12 CB,∴∠ENB=∠HEF.∵AD=BC,∴HF=HE,∴∠HEF=∠HFE,∴∠ENB=∠AMF.如图3:取AC的中点H,连接HE、HF.∵F是DC的中点,H是AC的中点,∴HF∥AD,HF=12 AD,∴∠AMF+∠HFE=180°,同理,HE∥CB,HE=12 CB,∴∠ENB=∠HEF.∵AD=BC,∴HF=HE,∴∠HEF=∠HFE,∴∠AMF+∠ENB=180°.15.【解析】证明:(1)如图,∵在Rt△ABC中,∠ACB=90°,点D为AB中点,∴CD是斜边AB上的中线,∴CD=AD=BD=AB.又EF∥AB,∴=,∴==1,∴EF=CF;(2)如图,延长EF交BC于点M,连接GM.∵EF∥AB,∴∠CMF=∠CBD.又∵AD=BD=AB,∴∠DCM=∠CBD,即∠FCM=∠CBD,∴∠CMF=∠FCM,∴CF=MF.又由(1)知,EF=CF,∴EF=FM,即点F是EM的中点,又∵EF∥AB,则FM∥AB∴EM是△ABC的中位线,则点M是BC的中点,∵点G是BE的中点,∴DG是△AEB的中位线,GM是△BEC的中位线,∴GD∥AE,GM∥EC,∴点D、G、M三点共线,∴FG是△CDM的中位线,∴FG∥CM.又∵MC⊥EC,∴FG⊥DG.。
北师大版八年级数学下册6.4《三角形的中位线》知识点精讲
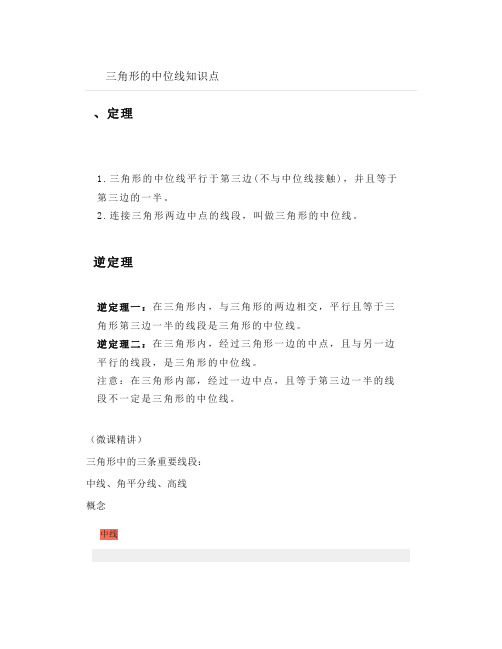
、定理1.三角形的中位线平行于第三边(不与中位线接触),并且等于第三边的一半。
2.连接三角形两边中点的线段,叫做三角形的中位线。
逆定理逆定理一:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
注意:在三角形内部,经过一边中点,且等于第三边一半的线段不一定是三角形的中位线。
(微课精讲)三角形中的三条重要线段:中线、角平分线、高线概念中线在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线(median)。
三角形的三条中线交于一点,这点称为三角形的重心。
如图,AD是边BC上的中线,BE是边AC上的中线,CF是边AB上的中线三条中线交于点O,点O称为△A BC的重心角平分线在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
如图,AD平分∠BAC,BE平分∠ABC,CF平分∠ACB,三角形三条角平分线交于点O点O称为△ABC的内心高线从三角形的一个顶点向它的对边所在直线作垂线,定点和垂足之间的线段叫做三角形的高线,简称三角形的高。
如图,AD⊥BC,BE⊥AC,CF⊥AB三角形三条高线交于点O点O称为△ABC的垂心以上是我们在初一时所学的三角形三条重要线段,今天,我们将学习三角形中第四条重要的线段——中位线(知识点精讲)中位线概念:连接三角形两边中点的线段叫做三角形的中位线性质:三角形的中位线平行于第三边,且等于第三边的一半。
如图,E、F分别是三角形AB、AC边上的中点,所以,EF是三角形BC 边所对的中位线,则EF∥BC且EF=1/2BC三角形的中位线衍生出很多重要的图形,其中最重要的就是中点四边形(微课堂精讲)中点四边形任意画一个四边形,以四边形的中点为顶点组成一个新四边形,这个新四边形称为——中点四边形中点四边形一定是平行四边形证明:连接AC因为E、F分别为AB、BC的中点,所以EF平行且等于AC的一半同理,GH平行且等于AC的一半因此,EF∥HG,EF=HG所以,四边形EFGH是平行四边形思考:四边形ABCD满足什么条件时,四边形EFGH是菱形?矩形?正方形?三角形中位线的解题策略三角形的中位线定理,既有线段的位置关系,又有线段的数量关系,它是一个在三角形中遇到中点,必须联想到的重要定理之一。
三角形中位线课件

三角形中位线的定理
• 定理:三角形的中位线定理是指三角形的中位线长度等于 第三边长度的一半,并且平行于第三边。
三角形中位线的性质定理
01
02
03
性质定理1
三角形的中位线将相对边 分为两段,且这两段长度 相等。
性质定理2
三角形的中位线与第三边 平行,且长度为第三边的 一半。
性质定理3
三角形的中位线将相对顶 点与对边中点连接,且该 连线长度为中位线长度的 一半。
电路设计
在电路设计中,三角形中位线可以用来平衡电流,防止电流过大导致设备损坏或 火灾等安全事故。
05 总结与思考
三角形中位线的重要性和意义
几何构造的基础
在实际生活中的应用
三角形中位线是几何学中的基础概念 ,对于理解几何图形的构造和性质至 关重要。
在建筑、工程和设计等领域,三角形 中位线的应用广泛,例如在测量、绘 图和计算面积等方面。
02 三角形中位线的 性质与判定
三角形中位线的性质
三角形中位线平行于第三边
01
三角形中位线与第三边平行,这是三角形中位线的基本性质。
三角形中位线长度为第三边的一半
02
三角形中位线的长度是第三边长度的一半,这是三角形中位线
的长度性质。
三角形中位线将相对边等分
03
三角形中位线将相对边等分,这是三角形中位线的等分性质。
在解题中的应用
解题辅助
在解决一些几何问题时,三角形中位线可以作为一个重要的解题工具,帮助我 们找到解题的突破口。
证明定理
通过三角形中位线,我们可以证明一些重要的几何定理,如“三角形中位线定 理”等。
在生活中的实际应用
建筑测量
在建筑行业中,三角形中位线被广泛应用于测量和计算角度、长度等参数,决几何证明问题
