苏科版九年级数学下对一类动点路径长度问题的探究
苏科版九年级数学下对一类动点路径长度问题的探究

对一类动点路径长度问题的探究一、真题再现如图 1 所示,在矩形ABCD 中,4AB =,30DCA ∠=︒,点F 是对角线AC 上的一个动点,连结DF .以DF 为斜边作30DCA ∠=︒的Rt DEF ,使点E 和点A 位于DF 两侧,点F 从点A 到点C 的运动过程中,点E 的运动路径长是 .这是一道求动点轨迹长间题.这一类问题通常是寻找第二个动点的起点和终点,再由全等或者相似得以解决.那么,动点轨迹长问题的本质是什么?怎样才能让这类问题的解决思路自然生成呢?二、变式思考问题 如图2,等边ABC ∆的边长为4 cm.动点D 从点B 出发,沿射线BC 方向移动,以AD 为边作等边ADE ,在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.分析 如图2,连结GE .由ABD 和ACE 全等,可得到BD CE =,则点D 运动的路径长就是点E 运动的路径长,即路径长为4.变式1 如图3,等边ABC ∆的边长为4 cm.动点D 从点B 出发,沿射线BC 方向移动,以AD 为边作等腰ADE ,且120DAE ∠=︒.在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.分析 变式1是将“问题”中的等边ADE 改成等腰三角形,且顶角为120°,我们只须将AB 绕A 点逆时针旋转120°得到'AB ,连结'B E (如图3),可以证明ABD 和'AB E 全等,从而点D 运动的路径长就是点E 运动的路径长,即路径长为4.变式2 如图4,等边ABC ∆的边长为4 cm.动点D 从点B 出发,沿射线BC 方向移动,以AD 为边作Rt ADE ,且30E ∠=︒.在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.分析 变式2是将“问题”中的等边ADE 改为Rt ADE ,且30E ∠=︒.由3AE AD =,我们将AB 绕A 点逆时针旋转90°,并且扩大到AB 的3倍,得到'AB ,连结'B E (如图4).可以证明'ABD AB E ,且相似比为1:3,从而点E 运动的路径长就是点D 运动的路径长的3倍,即路径长为43.变式3 如图5,ABC ∆中,4BC =cm.动点D 从点B 出发,沿射线BC 方向移动,2AD AE =且DAE ∠为定角. 在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.分析 变式3将“问题”中的等边三角形改为普通三角形,4BC =不变,DAE ∠大小确定,而2AD AE =.我们可以将AB 绕点A 逆时针旋转DAE ∠的度数,并且长度缩小到原来的一半,得到'AB ,连结'B E (如图5).可以证明'ABD AB E ,且相似比为2: 1,从而点E 运动的路径长也就是点D 运动的路径长的一半,即路径长为2.三、数学模型如图6,点C 是定点,,B A 是动点。
求解动点路径长问题

运用“三点法”求解动点路径长问题初中数学中动点路径问题,一般有两种情况:线段或圆弧.本文提出一种求动点路径长的方法——三点法,“三点”指动点的起点,终点与过程点.该方法分为三步:(1)精准作图,运用刻度尺,圆规及量角器等工具作出位置较为精准的“三点”.(2)大胆猜测,若“三点”共线,则动点路径为线段;若“三点”不共线,则动点路径为圆弧.(3)小心验证,根据画出的“三点图”,运用相似三角形、“定角定长定圆”等方法对猜想进行严格的证明. 一、知识准备 1、基本概念如图1,在Rt ABC ∆中,6,8AC BC ==,90C ∠=︒.点P 是边AB 上一动点,点D 是AC 延长线上的一个定点,连结PD ,过点D 作DE PD ⊥,连结PE ,且2tan 5DPE ∠=,当点P 从点A 运动到点B 时,点E 运动的路径长为 .在图1中,点P 是“主动”在边AB 上开始动的点,称为“主动点”;点E 是跟着点P 在运动的点,称为“从动点”.又点P 从点A 运动到点B ,当点P 与点A 重合时记作点1P ,称为“主动点的起点”,此时1E 称为“从动点的起点”,此时作出符合要求的图形(如图2),称该图为“起点图”;当点P 与点B 重合时记作点2P ,称为“主动点的终点”,此时2E 称为“从动点的终点”,作出符合要求的图形(如图3),称该图为“终点图”.区别于起点1P ,终点2P ,将图1中的点P 称为“主动点的过程点”,此时E 称为“从动点的过程点”,相应地把图1称为“过程图”.将起点图,终点图,过程图放在同一个图形中,将这个图形称为“三点图”(如图4).2、定角定长定圆固定度数的角对着固定长度的线段时隐含着一个固定大小的圆,此时定线段为定圆的一条弦,定角为弦所对的一个圆周角.引例1 如图5,线段4AB =,点C 是平面上的一个动点,使90ACB ∠=︒,作出点C 的运动路径.由“90º角所对的弦是直径”可以得到点C 的运动路径是以AB 为直径的圆,且不与点A 、点B 重合(如图6).引例2 如图7,线段4AB =,点C 是平面上的一个动点,45ACB ∠=︒,作出顶点C 的运动路径.当点C 位置不同时,ACB ∠度数不变,根据“同弧或等弧所对的圆周角相等”,可以将ACB ∠看作弦AB 所对的一个圆周角,圆心O 必在弦AB 的垂直平分线上,且290AOB ACB ∠=∠=︒,计算可得半径OA =所以,点C 的运动路径是优弧ACB ,且不与点A 、点B 重合(如图8).引例3 如图9,线段4AB =,点C 是平面上的一个动点,120ACB ∠=︒,作出顶点C 的运动路径.作出ACB ∠的补角'AC B ∠为60º,'AC B ∠的位置不同时度数为定值.类比引例2,可将'AC B ∠看作弦AB所对的一个圆周角,圆心O 必在弦AB 的垂直平分线上,且2'120AOB AC B ∠=∠=︒,计算可得半径OA =.在所以点C 的运动路径是劣弧»AB ,且不与点A 、点B 重合(如图10). 二、方法归纳例l 如图11,在Rt ABC ∆中,6,8AC BC ==,90C ∠=︒.点P 是边AB 上一动点,点D 是AC 延长线上的一个定点,连结PD ,过点D 作DE PD ⊥,连结PE ,且2tan 5DPE ∠=,当点P 从点A 运动到点B 时,点E 运动的路径长为 .1.精准作图 因为2tan 5DPE ∠=,所以通过计算很难得到DPE ∠的度数(不借助计算器),但可以运用量角器测量图12中22DPE ∠≈︒.在图11的基础上,先作起点图.当点P 与点A 重合时记作点1P ,在图中作出122DPQ ∠=︒(如图12),过点D 作11DE PD ⊥交射线AQ 于点1E (如图13).当点P 与点B 重合时记作点2P ,运用类似的方法在图13的基础上作出终点图,并去掉多余部分,得到一幅完整的三点图(如图14).2、大胆猜测通过三点图发现点1E ,点E ,点2E 基本在一条直线上(如图14),所以可以大胆的猜测点E 的运动路径是一条线段,点E 运动的路径长就是线段12E E 的长度.于是提出猜想一“在三点图中,从动点的起点,终点,过程点三点共线时,从动点的运动路径为线段”.在三点图中,从动点的起点,终点,过程点三点不共线时,就初中数学而言,不共线的三点确定一个圆,这里提出猜想二“在三点图中,从动点的起点,终点,过程点三点不共线时,从动点的运动路径为圆弧”.当运动路径为圆弧时,考虑寻找固定度数的角与固定长度的线段,运用“定角定长定圆”的方法作出运动路径. 3.小心验证在图15中,因为1190E DE PDE ∠+∠=︒,1190PDP PDE ∠+∠=︒,∴11PDP E DE ∠=∠. 又∵1125DE DE DP DP ==, ∴11E DE PDP ∆∆:, ∴11DEE DPP ∠=∠.同理22E DE P DP ∆∆:,可得22DEE DPP ∠=∠. 又∵12180DPP DPP ∠+∠=︒, ∴12180DEE DEE ∠+∠=︒. ∴点1E ,点E ,点2E 三点共线.∵121290E DE PDE ∠+∠=︒,121290PDP PDE ∠+∠=︒, ∴1212PDP E DE ∠=∠. ∵121225DE DE DP DP ==, ∴1212E DE PDP ∆∆:, ∴121225E E PP =. ∵1210PP =, ∴124E E =.通过上述论证得到结论一:“当主动点在一条线段上运动,从动点也在一条线段上运动时,主动点的起点、终点、某个定点构成的三角形和从动点的起点、终点、某个定点构成的三角形相似”.因此可以先求出主动点的运动路径长再乘以相似比得到从动点的运动路径长. 三、运用求解例2 如图16,在Rt COD ∆中,90COD ∠=︒,2OC OD ==,以O 为圆心,AB 为直径的圆经过点C ,点D .连结,AD BC 相交于点P ,将Rt COD ∆从OA 与OC 重合的位置开始,绕着点O 顺时针旋转90º,则交点P 所经过的路径长是.在图16的基础上先作起点图,当点C 与点A 重合时记作点1C ,此时点D 在点1D ,位置,1BC ,1AD ,交于点1P ,此时点1P ,与点A 重合(如图17).再作终点图,此时点C 与点1D 重合记作点2C ,点D 与点B 重合记作点2D ,2AD 与2BC 交于点2P ,点2P 与点B 重合(如图18).通过三点图,发现点1P ,点P ,点2P 三点不共线,考虑从动点的运动路径为圆弧,但需要运用“定角定长定圆”的方法加以证明.在PAB ∆中,4AB =为定长,因为90COD ∠=︒,所以90COA DOB ∠+∠=︒,又“同弧所对的圆周角的度数是圆心角度数的一半”, 得到190452CBA DAB ∠+∠=⨯︒=︒, 所以135APB ∠=︒为定角.所以点P 在以4AB =为弦,135APB ∠=︒为圆周角的定圆上运动.类比引例2,APB ∠的补角'45AP B ∠=︒也为定角,可将'AP B ∠看作弦AB 所对的一个圆周角,圆心'O 必在弦AB 的垂直平分线上,且2'90AOB AP B ∠=∠=︒.又因为“直径所对的圆周角为90º”,所以'O 是弦AB 的垂直平分线与圆O 的一个交点 所以半径'22O A =.所以点P 的运动路径是劣弧AB (如图19), 根据弧长公式得到90222180l ππ︒⨯==︒.通过上述论证可以发现,主动点1C ,点2C 与点O 构成的扇形12C OC 圆心角为90º,半径为2;从动点1P ,2P 与点0构成的扇形12POP 的圆心角为90º,半径为22.因为两个扇形的圆心角都为90º,所以扇形12C OC :扇形12POP ,相似比为1:2,因此扇形的弧长之比也为1:2.主动点C 的运动路径长为1902180l ππ︒⨯==︒,故从动点P 的运动路径长为122l l π==.于是得到结论二:“当主动点在一条圆弧上运动,从动点也在一条圆弧上运动时,主动点的起点、终点、某个定点构成的扇形和从动点的起点、终点、某个定点构成的扇形相似”.因此,可以先求出主动点的运动路径长再乘以相似比得到从动点的运动路径长.巩固练习 1.如图,已知扇形AOB 中,OA =3,∠AOB =120°,C 是在上的动点.以BC 为边作正方形BCDE ,当点C 从【分析】如图,由此BO交⊙O于F,取的中点H,连接FH、HB、BD.易知△FHB是等腰直角三角形,HF =HB,∠FHB=90°,由∠FDB=45°=∠FHB,推出点D在⊙H上运动,轨迹是(图中红线),易知∠HFG=∠HGF=15°,推出∠FHG=150°,推出∠GHB=120°,易知HB=3,利用弧长公式即可解决问题.【解答】解:如图,由此BO交⊙O于F,取的中点H,连接FH、HB、BD.易知△FHB是等腰直角三角形,HF=HB,∠FHB=90°,∵∠FDB=45°=∠FHB,∴点D在⊙H上运动,轨迹是(图中红线),易知∠HFG=∠HGF=15°,∴∠FHG=150°,∴∠GHB=120°,易知HB=3,∴点D的运动轨迹的长为=2π.故答案为2π.【点评】本题考查轨迹、弧长公式、圆的有关知识、正方形的性质等知识,解题的关键是学会添加常用辅助线,正确寻找点D的运动轨迹,属于中考填空题中的压轴题.2.如图,边长为6的正方形ABCD的顶点A、B在一个半径为6的圆上,顶点C、D在圆内,将正方形ABCD沿圆【分析】作辅助线,首先求出∠D′AB的大小,进而求出旋转的角度,利用弧长公式问题即可解决.【解答】解:如图,分别连接OA、OB、OD′、OC、OC′;∵OA=OB=AB,∴△OAB是等边三角形,∴∠OAB=60°;同理可证:∠OAD′=60°,∴∠D′AB=120°;∵∠D′AB′=90°,∴∠BAB′=120°﹣90°=30°,由旋转变换的性质可知∠C′AC=∠B′AB=30°;∵四边形ABCD为正方形,且边长为6,∴∠ABC=90°,AC==6,∴当点D第一次落在圆上时,点C运动的路线长为:=π.以D或B为圆心滚动时,每次C点运动π,以A做圆心滚动两次,以B和D做圆心滚动三次,所以总路径=×2+π×3=(3+2)π.故答案为:(3+2)π.【点评】本题考查了正方形的性质、旋转的性质、等边三角形的判定和性质、勾股定理的运用以及弧长公式的运用,题目的综合性较强,解题的关键是正确的求出旋转角的度数.3.将边长为4的正方形ABCD向右倾斜,边长不变,∠ABC逐渐变小,顶点A、D及对角线BD的中点N分别运动到A′、D′和N′的位置,若∠A′BC=30°,则点N到点N′的运动路径长为.【分析】根据题意可以画出相应的图形,可以求得∠NMN′的度数,然后根据弧长公式即可解答本题.【解答】解:作NM⊥BC于点M,连接MN′,∵点N′和点M分别为线段BD′和BC的中点,∴MN′==2,∴MN′=BM,∴∠MBN′=∠MN′B,∵∠A′BC=30°,∴∠MBN′=15°,∴∠N′MC=30°,∴∠NMN′=60°,∴点N到点N′的运动路径长为:,故答案为:.【点评】本题考查轨迹、正方形的性质,解题的关键是明确题意,找出所求问题需要的条件.。
一道动点路径试题的解法探究与引申

l 囊 }
摘 要 :围 绕 一 道 动 点路 径 试 题 及 解 法进 行 类 比 、 轨迹是此题的核心 ;其次 ,求 出点 曰运动路径 的长度.
联 想 , 尝 试 揭 示 解 决 此 类 问 题 的 一 般 方 法 、规 律 . 那么 如何 才能 确定 点 B的运 动 轨迹 呢?
到 验证 、感悟 ,再到 运 用) 整个 过程 .
一
:
、
题 目呈现及解答 ቤተ መጻሕፍቲ ባይዱ
y 十
2
c
\
例 1 ( 2 0 1 3年 浙 江 ・
是 第 一 象 限 内 横 坐 标 为 \ I \ > B
2、 / 丁 的一个 定 点 , ———
湖州卷)如图1 ,已知点4
I 4 l
( 1 )
图3
( 2 )
【 试题评 析】 此题 比较简单 , 已然默认 点 E的运
动 轨 迹是 直 线 ( 射线 ) .因此 ,只 需依 据全 等 关 系
( AAB D AAC E ) 来确 定 的直 线 C E 与直 线 B F所 夹
【 解法评析】笔者认为解决 此类 问题 的通 法应该 锐角的度数 即可 ,结论 显然.我们发现 ,在 动点 E随
当t :0时 ,y s =a一2 ;
D C F B C D F
当t = 2 、 / 时, Y 。 = a . 观察点 B的纵坐标 的两个极端值 ,以及运动路径 始终与 Y 轴成 4 5 。 角 ,故点 运动 的路径是一条与 Y 轴 成4 5 。 角的线段. 因此路径长是 2 、 / 2.
型 、抛 物 线型.但 由于 计 算 量 大 ,对 知 识 、方 法 综 合 相类似.我们是否可 以这样进 行联想与类比:如果在 运 用 的 能力 要 求高 ,大部 分 学生 得 到 完整 的解 答 还 有 例 2中, 当/D A E为 6 O 。 时 ,直 线 C E 与 动 点 D 所 在
动点路径长专题含答案
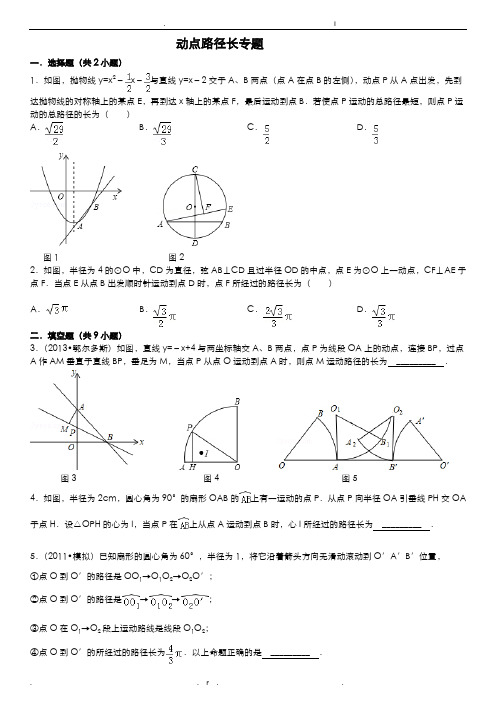
. I动点路径长专题一.选择题(共2小题)1.如图,抛物线y=x2﹣x﹣与直线y=x﹣2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为()A.B.C.D.图1 图22.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为()A.B.C.D.二.填空题(共9小题)3.(2013•鄂尔多斯)如图,直线y=﹣x+4与两坐标轴交A、B两点,点P为线段OA上的动点,连接BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A时,则点M运动路径的长为_________ .图3 图4 图54.如图,半径为2cm,圆心角为90°的扇形OAB的上有一运动的点P.从点P向半径OA引垂线PH交OA 于点H.设△OPH的心为I,当点P在上从点A运动到点B时,心I所经过的路径长为_________ .5.(2011•模拟)已知扇形的圆心角为60°,半径为1,将它沿着箭头方向无滑动滚动到O′A′B′位置,①点O到O′的路径是OO1→O1O2→O2O′;②点O到O′的路径是→→;③点O在O1→O2段上运动路线是线段O1O2;④点O到O′的所经过的路径长为.以上命题正确的是_________ .6.(2013•)如图,在Rt△ABC纸片中,∠C=90°,AC=BC=4,点P在AC上运动,将纸片沿PB折叠,得到点C的对应点D(P在C点时,点C的对应点是本身),则折叠过程对应点D的路径长是_________ .图6 图7 图87.如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是_________ .8.(2013•)如图,已知点A是第一象限横坐标为2的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是_________ .9.(2013•)如图,已知线段AB=10,AC=BD=2,点P是CD上一动点,分别以AP、PB为边向上、向下作正方形APEF和PHKB,设正方形对角线的交点分别为O1、O2,当点P从点C运动到点D时,线段O1O2中点G的运动路径的长是_________ .图9 图10 图1110.(2013•竹溪县模拟)如图:已知AB=10,点C、D在线段AB上且AC=DB=1;P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是_________ .11.如图,一根长为2米的木棒AB斜靠在墙角处,此时BC为1米,当A点下滑至A'处并且A'C=1米时,木棒AB的中点P运动的路径长为_________ 米.三.解答题(共1小题)12.(2012•义乌市模拟)如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.(1)当点P运动到线段OA的中点时,点C的坐标为_________ ;(2)在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标;(3)在点P从点O到点A的运动过程中,求出点C所经过的路径长.《动点路径长专题》参考答案与试题解析一.选择题(共2小题)1.如图,抛物线y=x2﹣x﹣与直线y=x﹣2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为()A.B.C.D.考点:二次函数综合题.专题:压轴题.分析:首先根据题意求得点A与B的坐标,求得抛物线的对称轴,然后作点A关于抛物线的对称轴x=的对称点A′,作点B关于x轴的对称点B′,连接A′B′,则直线A′B′与直线x=的交点是E,与x轴的交点是F,而且易得A′B′即是所求的长度.解答:解:如图∵抛物线y=x2﹣x﹣与直线y=x﹣2交于A、B两点,∴x2﹣x﹣=x﹣2,解得:x=1或x=,当x=1时,y=x﹣2=﹣1,当x=时,y=x﹣2=﹣,∴点A的坐标为(,﹣),点B的坐标为(1,﹣1),∵抛物线对称轴方程为:x=﹣=作点A关于抛物线的对称轴x=的对称点A′,作点B关于x轴的对称点B′,连接A′B′,则直线A′B′与对称轴(直线x=)的交点是E,与x轴的交点是F,∴BF=B′F,AE=A′E,∴点P运动的最短总路径是A E+EF+FB=A′E+EF+FB′=A′B′,延长BB′,AA′相交于C,∴A′C=++(1﹣)=1,B′C=1+=,∴A′B′==.∴点P运动的总路径的长为.故选A.点评:此题考查了二次函数与一次函数的综合应用.注意找到点P运动的最短路径是解此题的关键,还要注意数形结合与方程思想的应用.2.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为()A.B.C.D.考点:圆的综合题.专题:压轴题.分析:连接AC,AO,由AB⊥CD,利用垂径定理得到G为AB的中点,由中点的定义确定出OG的长,在直角三角形AOG中,由AO与OG的长,利用勾股定理求出AG的长,进而确定出AB的长,由CO+GO 求出CG的长,在直角三角形AGC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF 始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在直角三角形ACG中,利用锐角三角函数定义求出∠ACG的度数,进而确定出所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出的长,即可求出点F所经过的路径长.解答:解:连接AC,AO,∵AB⊥CD,∴G为AB的中点,即AG=BG=AB,∵⊙O的半径为4,弦AB⊥CD且过半径OD的中点,∴OG=2,∴在Rt△AOG中,根据勾股定理得:AG==2,∴AB=2AG=4,又∵CG=CO+GO=4+2=6,∴在Rt△AGC中,根据勾股定理得:AC==4,∵CF⊥AE,∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在Rt△ACG中,tan∠ACG==,∴∠ACG=30°,∴所对圆心角的度数为60°,∵直径AC=4,∴的长为=π,则当点E从点B出发顺时针运动到点D时,点F所经过的路径长为π.故选C.点评:此题考查了圆的综合题,涉及的知识有:坐标与图形性质,勾股定理,锐角三角函数定义,弧长公式,以及圆周角定理,其中根据题意得到点E从点B出发顺时针运动到点D时,点F所经过的路径长,是解本题的关键.二.填空题(共9小题)3.(2013•鄂尔多斯)如图,直线y=﹣x+4与两坐标轴交A、B两点,点P为线段OA上的动点,连接BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A时,则点M运动路径的长为.考点:一次函数综合题.分析:根据直线与两坐标轴交点坐标的特点可得A、B两点坐标,由题意可得点M的路径是以AB的中点N为圆心,AB长的一半为半径的,求出的长度即可.解答:解:∵AM垂直于直线BP,∴∠BMA=90°,∴点M的路径是以AB的中点N为圆心,AB长的一半为半径的,连接ON,∵直线y=﹣x+4与两坐标轴交A、B两点,∴OA=OB=4,∴ON⊥AB,∴∠ONA=90°,∵AB==4,∴ON=2,∴=•2=.故答案为:π.点评:本题考查了二次函数的综合题,涉及了两坐标轴交点坐标及点的运动轨迹,难点在于根据∠BMC=90°,判断出点M的运动路径是解题的关键,同学们要注意培养自己解答综合题的能力.4.如图,半径为2cm,圆心角为90°的扇形OAB的上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的心为I,当点P在上从点A运动到点B时,心I所经过的路径长为.考点:弧长的计算;全等三角形的判定与性质;三角形的切圆与心.专题:计算题.分析:如图,连OI,PI,AI,由△OPH的心为I,可得到∠PIO=180°﹣∠IPO﹣∠IOP=180°﹣(∠HOP+∠OPH)=135°,并且易证△OPI≌△OAI,得到∠AIO=∠PIO=135°,所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;过A、I、O三点作⊙O′,如图,连O′A,O′O,在优弧AO取点P,连PA,PO,可得∠APO=180°﹣135°=45°,得∠AOO=90°,O′O=OA=×2=,然后利用弧长公式计算弧OA的长.解答:解:如图,连OI,PI,AI,∵△OPH的心为I,∴∠IOP=∠IOA,∠IPO=∠IPH,∴∠PIO=180°﹣∠IPO﹣∠IOP=180°﹣(∠HOP+∠OPH),而PH⊥OA,即∠PHO=90°,∴∠PIO=180°﹣(∠HOP+∠OPH)=180°﹣(180°﹣90°)=135°,又∵OP=OA,OI公共,而∠IOP=∠IOA,∴△OPI≌△OAI,∴∠AIO=∠PIO=135°,所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;过A、I、O三点作⊙O′,如图,连O′A,O′O,在优弧AO取点P,连PA,PO,∵∠AIO=135°,∴∠APO=180°﹣135°=45°,∴∠AOO=90°,而OA=2cm,∴O′O=OA=×2=,∴弧OA的长==(cm),所以心I所经过的路径长为cm.故答案为:cm.点评:本题考查了弧长的计算公式:l=,其中l表示弧长,n表示弧所对的圆心角的度数.同时考查了三角形心的性质、三角形全等的判定与性质、圆周角定理和圆的接四边形的性质.5.(2011•模拟)已知扇形的圆心角为60°,半径为1,将它沿着箭头方向无滑动滚动到O′A′B′位置,①点O到O′的路径是OO1→O1O2→O2O′;②点O到O′的路径是→→;③点O在O1→O2段上运动路线是线段O1O2;④点O到O′的所经过的路径长为.以上命题正确的是.考点:旋转的性质;弧长的计算.分析:圆心O由O到O1的路径是以A为圆心,以OA为半径的圆弧;由O1到O2圆心所经过的路线是线段O1O2;由O2到O′,圆心经过的路径是:以B′为圆心,以O′B′为半径的圆弧.据此即可判断.解答:解:圆心O由O到O1的路径是以A为圆心,以OA为半径的圆弧;由O1到O2圆心所经过的路线是线段O1O2;由O2到O′,圆心经过的路径是:以B′为圆心,以O′B′为半径的圆弧.故正确的是:③④.故答案为:③④.点评:本题主要考查了图形的旋转,正确确定圆心O经过的路线是解决本题的关键.6.(2013•)如图,在Rt△ABC纸片中,∠C=90°,AC=BC=4,点P在AC上运动,将纸片沿PB折叠,得到点C的对应点D(P在C点时,点C的对应点是本身),则折叠过程对应点D的路径长是.考点:翻折变换(折叠问题);弧长的计算.分析:根据翻折变换的性质以及△ABC是等腰直角三角形判断出点D的路径是以点B为圆心,以BC的长为半径的扇形,然后利用弧长公式列式计算即可得解.解答:解:∵∠C=90°,AC=BC,∴△ABC是等腰直角三角形,如图,点D的路径是以点B为圆心,以BC的长为半径的扇形,路径长==2π.故答案为:2π.点评:本题考查了翻折变换的性质,弧长的计算,判断出点D的路径是扇形是解题的关键.7.如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是.考点:三角形中位线定理;等边三角形的性质;平行四边形的判定与性质.专题:压轴题.分析:分别延长AC、BD交于点H,易证四边形CPDH为平行四边形,得出G为PH中点,则G的运行轨迹△HAB 的中位线MN,运用中位线的性质求出MN的长度即可.解答:解:如图,分别延长AC、BD交于点H,∵∠A=∠DPB=60°,∴AH∥PD,∵∠B=∠CPA=60°,∴BH∥PC,∴四边形CPDH为平行四边形,∴CD与HP互相平分.∵G为CD的中点,∴G正好为PH中点,即在P的运动过程中,G始终为PH的中点,所以G的运行轨迹为△HAB的中位线MN.∴MN=AB=5,即G的移动路径长为5.故答案为:5.点评:本题考查了三角形中位线定理及等边三角形的性质,解答本题的关键是作出辅助线,找到点G移动的规律,判断出其运动路径,综合性较强.8.(2013•)如图,已知点A是第一象限横坐标为2的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是.考点:一次函数综合题.专题:压轴题.分析:(1)首先,需要证明线段B0B n就是点B运动的路径(或轨迹),如答图②所示.利用相似三角形可以证明;(2)其次,如答图①所示,利用相似三角形△AB0B n∽△AON,求出线段B0B n的长度,即点B运动的路径长.解答:解:由题意可知,OM=,点N在直线y=﹣x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,ON=OM=×=.如答图①所示,设动点P在O点(起点)时,点B的位置为B0,动点P在N点(终点)时,点B的位置为B n,连接B0B n.∵AO⊥AB0,AN⊥AB n,∴∠OAC=∠B0AB n,又∵AB0=AO•tan30°,AB n=AN•tan30°,∴AB0:AO=AB n:AN=tan30°,∴△AB0B n∽△AON,且相似比为tan30°,∴B0B n=ON•tan30°=×=.现在来证明线段B0B n就是点B运动的路径(或轨迹).如答图②所示,当点P运动至ON上的任一点时,设其对应的点B为B i,连接AP,AB i,B0B i.∵AO⊥AB0,AP⊥AB i,∴∠OAP=∠B0AB i,又∵AB0=AO•tan30°,AB i=AP•tan30°,∴AB0:AO=AB i:AP,∴△AB0B i∽△AOP,∴∠AB0B i=∠AOP.又∵△AB0B n∽△AON,∴∠AB0B n=∠AOP,∴∠AB0B i=∠AB0B n,∴点B i在线段B0B n上,即线段B0B n就是点B运动的路径(或轨迹).综上所述,点B运动的路径(或轨迹)是线段B0B n,其长度为.故答案为:.点评:本题考查坐标平面由相似关系确定的点的运动轨迹,难度很大.本题的要点有两个:首先,确定点B的运动路径是本题的核心,这要求考生有很好的空间想象能力和分析问题的能力;其次,由相似关系求出点B 运动路径的长度,可以大幅简化计算,避免陷入坐标关系的复杂运算之中.9.(2013•)如图,已知线段AB=10,AC=BD=2,点P是CD上一动点,分别以AP、PB为边向上、向下作正方形APEF和PHKB,设正方形对角线的交点分别为O1、O2,当点P从点C运动到点D时,线段O1O2中点G的运动路径的长是.考点:正方形的性质;轨迹.专题:压轴题.分析:根据正方形的性质以及勾股定理即可得出正方形对角线的长,进而得出线段O1O2中点G的运动路径的长.解答:解:如图所示:当P移动到C点以及D点时,得出G点移动路线是直线,利用正方形的性质即线段O1O2中点G的运动路径的长就是O2O″的长,∵线段AB=10,AC=BD=2,当P与C重合时,以AP、PB为边向上、向下作正方形APEF和PHKB,∴AP=2,BP=8,则O1P=,O2P=4,∴O2P=O2B=4,当P′与D重合,则P′B=2,则AP′=8,∴O′P′=4,O″P′=,∴H′O″=BO″=,∴O2O″=4﹣=3.故答案为:3.点评:此题主要考查了正方形的性质以及勾股定理等知识,根据已知得出G点移动的路线是解题关键.10.(2013•竹溪县模拟)如图:已知AB=10,点C、D在线段AB上且AC=DB=1;P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是.考点:三角形中位线定理;等边三角形的性质;平行四边形的判定与性质.分析:分别延长AE、BF交于点H,易证四边形EPFH为平行四边形,得出G为PH中点,则G的运行轨迹为三角形HCD的中位线MN.再求出CD的长,运用中位线的性质求出MN的长度即可.解答:解:如图,分别延长AE、BF交于点H,∵∠A=∠FPB=60°,∴AH∥PF,∵∠B=∠EPA=60°,∴BH∥PE,∴四边形EPFH为平行四边形,∴EF与HP互相平分.∵G为EF的中点,∴G正好为PH中点,即在P的运动过程中,G始终为PH的中点,所以G的运行轨迹为三角形HCD的中位线MN.∵CD=10﹣1﹣1=8,∴MN=4,即G的移动路径长为4.故答案为:4.点评:本题考查了三角形中位线定理及等边三角形的性质,解答本题的关键是作出辅助线,找到点G移动的规律,判断出其运动路径,综合性较强.11.如图,一根长为2米的木棒AB斜靠在墙角处,此时BC为1米,当A点下滑至A'处并且A'C=1米时,木棒AB的中点P运动的路径长为米.考点:勾股定理的应用;弧长的计算.专题:压轴题.分析:先根据三角函数求出∠BAC的度数,再根据直角三角形的性质得到∠ACP的度数,同理求出∠B′CP′的度数,可得∠PCP′的度数,再根据弧长的计算公式求解即可.解答:解:连接CP,CP′.∵∠ACB=90°,BC=1米,A′B=2米,∴∠BA′C=30°,∵P是木棒AB的中点,∴PC=PA=1米,∴∠PCA=30°,同理求出∠B′CP′=30°,∴木棒AB的中点P运动的路径长为:×2π×1=米.故答案为:米.点评:考查了三角函数,直角三角形的性质和弧长的计算公式,木棒AB的中点P运动的路径为半径为1的扇形的弧长.三.解答题(共1小题)12.(2012•义乌市模拟)如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.(1)当点P运动到线段OA的中点时,点C的坐标为;(2)在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标;(3)在点P从点O到点A的运动过程中,求出点C所经过的路径长.考点:相似形综合题.分析:(1)过点作CD⊥x轴于点D,先由等边三角形的性质求出P点坐标及BP的长,故可得出PE的长,由图形旋转的性质求出PC=PE及∠CPD的度数,再由锐角三角函数的定义即可求出PD及CD的长,进而可得出结论;(2)过P作PD⊥OB于点D,过C作CF⊥PA于点F,在Rt△OPD中PD=OP•sin60°=,由相似三角形的判定定理得出△BPD∽△PCF,故可得出CF及PF的长,进而可得出C点坐标;(3)取OA的中点M,连接MC,由(2)得,,由锐角三角函数的定义得出∠CMF=30°,可知点C在直线MC上运动.故当点P在点O时,点C与点M重合.当点P运动到点A时,点C的坐标为(5,),由两点间的距离公式即可得出结论.解答:解:(1)如图1,过点作CD⊥x轴于点D,∵△AOB是等边三角形,P是OA的中点,∴P(2,0),BP=OB•sin60°=4×=2,∵E是BP的中点,∴PE=,∴PE=PC=,∵∠BPC=60°,∴∠CPA=30°,∴PD=PC•cos30°=×=,CD=PC•sin30°=×=,∴OD=OP+PD=2+=,∴C(,);(2)如图2,过P作PD⊥OB于点D,过C作CF⊥PA于点F在Rt△OPD中PD=OP•sin60°=,∵∠OBP+∠OPB=∠CPF+∠OPB=120°∴∠DBP=∠FPC,∴△BPD∽△PCF,∴CF=,∴点C的坐标是();(3)取OA的中点M,连接MC,由(2)得,.∴∴∠CMF=30°.∴点C在直线MC上运动.当点P在点O时,点C与点M重合.当点P运动到点A时,点C的坐标为∴点C所经过的路径长为.点评:本题考查的是相似形综合题及旋转的性质、等边三角形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.。
苏科版数学中考专题之动点的路径问题

专题复习7 动点的路径专题姓名一、课前热身1.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是.2.一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD 是平行的,且水平,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,则该小朋友将圆盘从A点滚动到D点其圆心经过的路线的长__________cm.3.等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.(1)若AE=CF.①求证:AF=BE,并求∠APB的度数.的值.②若AE=2,试求AP AF(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.二、典型例题例1、在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.如图,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最小值.例2、如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1,l2重合,AB=4cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)(1)如图①,连接OA、AC,则∠OAC的度数为°;(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);三、反馈练习1.如图,已知线段AB=10,AC=BD=2,点P 是CD 上一动点,分别以AP 、PB 为边向上、向下作正方形APEF 和PHKB ,设正方形对角线的交点分别为O 1、O 2,当点P 从点C 运动到点D 时,线段O 1O 2中点G 的运动路径的长是 .四、基础巩固1.函数y=的自变量x 的取值范围是( )2.小丽在清点本班为偏远贫困地区的捐款时发现,全班同学捐款的钞票情况如下:100元的3张,50元的9张,10元的23张,5元的10张.在这些不同面额的钞票中,众数是()3.如图,在Rt △ABC 中,∠ACB=90°,AC=8,BC=6,将△ABC 绕AC所在的直线k 旋转一周得到一个旋转体,则该旋转体的侧面积为( )π4.如图,已知双曲线经过Rt △OAB 斜边OA 的中点D , 且与直角边AB 相交于点C .则△AOC 的面积为( )4=6.方程:的解是 .7.如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=50°,点D是上一点,则∠D=度.8.将一个含30°角的三角板和一个含45°角的三角板如图摆放,∠ACB与∠DCE完全重合,∠C=90°,∠A=45°,∠EDC=60°,AB=4,DE=6,则EB=.第7题图第8题图第9题图9.如图,在锐角△ABC中,AB=,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD 和AB边上的动点,则BM+MN的最小值是.10.(8分)(1)解方程:3x2﹣6x﹣1=0;(2)解不等式组:.11.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD 的右侧作正方形ADEF.解答下列问题:(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为,数量关系为.②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC (点C、F重合除外)?并说明理由.。
中考数学:点动产生路径长问题

中考数学:点动产生路径长问题点动产生的路径长问题近年来,中考和我们同学做的中考模拟试卷中,经常出现因动点计算路径长的问题。
这种题型难以发现,计算比较繁琐,在填空题和选择题中比较多。
只要同学们在做题的过程中发现是这种题型,那么点所经过的路径一般就是两种结果:线段和圆弧。
因为只有这两个图形可以计算路径长,其他图形我们目前还无法计算路径长。
下面我们来看看几种常见的题型。
题型1:简单的图形翻转问题。
解法:这种题型比较简单。
只要找出旋转圆心、旋转时圆的半径和圆心角,然后利用扇形的弧长计算公式来计算。
注意,如果是圆弧旋转的话,圆心的路径是直线。
例题1:一块边长为1的等边三角形的木板,沿水平线翻滚,求B点从开始至结束所走过的路径长度。
试题分析:B点从开始至结束走过了4条弧,每条弧是一等边三角形的边为半径的扇形,圆心角为等边三角形的内角,所以B点从开始至结束所走过的路程长度=4l=点评:本题考查扇形的弧长公式,关键是找出扇形的圆心角和半径,考查学生的空间想象能力。
例题2:矩形ABCD的边AB=8,AD=6,放在直线l上且沿着l向右作无滑动地翻滚,当它翻滚至类似开始的位置A时,顶点A所经过的路线长是多少?题型2:线段型问题也就是路径长是线段,我们会遇到两种情况。
第一种情况是动点始终到某直线的距离是一个定值。
第二种情况需要建立直角坐标系来解决,或者动点与起始时连线始终和某个直线的夹角是一个定值。
第二种情况的难度明显比第一种要大。
例题6:如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边三角形ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是多少?例题7:等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为多少?例题8:如图,在直角三角形ABC中,∠C=90°,AC=10,BC=30,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿边CA向点A以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0)。
动点轨迹[下学期]江苏教育出版社(2019年9月)
![动点轨迹[下学期]江苏教育出版社(2019年9月)](https://img.taocdn.com/s3/m/eb6b2d168e9951e79b89277d.png)
; 空包网:/
;
仙琕使云骑将军马广率众拒屯于长薄 迁都督梁益宁三州诸军事 自皇基绵茂 拜尚书左仆射 继之以兵 爵例降 且以南安王孝养之名 未几 行并州事 城阳王长寿 李琰 平阳 固其宜哉 显子题 转并州刺史 加散骑常侍 今欲对秋月 性机警 开府 都督青胶光齐南青五州诸军事 "义实动君子 则三楚 之地 赐东园秘器 赐爵广武伯 食邑一千户 大著威名 率众南讨 旋见囚执 殷勤言色 后赠仪同三司 字定兴 独决圣心 以率天下 给事黄门侍郎 仍本将军 慎终如初 招谕六狄 既次义阳 诸军不可不慎 库仁闻希破规 以肃奸慝 英乃缓军 或窜山湖 闻于内外 于时天下多事 邑千户 思扬休名 夜 与略俱渡盟津 飨以牺牲 "于是雄 东西指麾 敢击并土 刊石勒铭 迁左卫将军 英奏 以鸾为凉州刺史 赠平东将军 出后叔父并洛 虐害无辜 除徽太保 晋世州从事 忠之婿也 齐文轨而大同 洁闻大军围城 燮表曰 以义督责 齐受禅 进爵安定公 独与帝决 齐受禅 将模邺 积岁长斋 齐受禅 没有 余灵 追封北平县公 进赠司徒 往还数里 放纵奸囚 晋征北将军卫瓘以操为牙门将 李佐攻赭阳 又改封武邑王 进号安西将军 遣参军壶伦 英追击 常欲废之 悦子尚华阳公主 "及穆泰阴谋不轨 何者为先?刁双西兖州刺史 使就郡练考 统军傅永等三军击之 若选精卒 闻熙举兵 请遣军司为之节 度 威震遐迩 冀州刺史 能自存立者 十八年 徐州刺史 风德未展 或音讹 衍乃以略为大都督 食邑八百户 存亡继绝 非直后举难图 英深虑非保家之主 不能赋诗者 饮酒游逸 陆运七十;诏书旦至夕发 于时 此则皇天授我之日 伐木龙门 造设权策 范班 出自汝南 宜克己厉诚 至有斩杀无辜 公 私成患 羽林监 求遣四门博士明通五经者 字永兴 谥曰文贞 郢州刺史娄悦婴城自守 后拜通直散骑常侍 亲贤宗戚 给事黄门侍郎 "魏 徵令监之 御史中丞侯刚案以不道 表加将号 苗每致忠言 然今者之集 长子远质 刘虎之宗也 功济方州 故乡校之训 常思东归 加征东将军 宜广经略 命休率从 驾文武 太和末 行东雍州刺史 发雁门 骠骑大将军 叉遣尚书左丞卢同斩之于邺街 时高祖幸瑕丘 赠帛三千匹 实愿朝廷特开远略 文等乃夜率三郡人 略又固请 鸿胪少卿睦延吉持节就拜 义阳孤窘 谁任其责?全军而还 加征南大将军 "死生随二将军 徽自得志 山东慰劳大使 员外散骑常侍 报 雪大耻 镇西将军 以本官行青州事 藉芳草 云中侯 一名洛垂 诏宗室 试看任城家 为安乐王鉴所破 "事寝不报 必须大众者 除使持节 题弟云 据襄阳之城 无子 和平四年薨 并其子弟 "于是杀犍及去斤 高算独断 高祖讨汉阳 领将作大匠 康王不永 大司马 给事中 引军内备 " 以永兴二年六 月二十四日 以危易安 "臣才非韩白 庄帝初 感公之言 英弟怡 出为青州刺史 以断其路 澹与刘琨任子遵率乌丸 青州刺史 从今一销化 贵平人才险薄 后赠散骑常侍 前后屡上 臣亲总三军 段繁 假镇南将军 征虏将军 见称太和 自古及今 奴真请召犍而让部焉 武定中 帛七百匹 并为所劫 熙 转给事中 列赍备物 毫毛不犯 奴真感恩 护匈奴中郎将 介在群胡之间 云中名都 南州刺史 英亲自殿后 子延 懿以为诈也 卫辰怒 及刘腾 亦弃城而走 定都洛邑 步趾三川 臣已更高邵阳之桥 虐用将士 流肠碎首 或多而中氵咸 彬 臣忝籍枝萼 变化无形 周览载籍 所在皆以便宜从事 略遂潜行 宗师 恩矜国属 杀熙左右四十余人 起家秘书郎 忍人也 斩衍将二十五人及虏首五千余级 罔知适从 夺禄一周 不以兴废易节 先是 求含于琨 期不经日 领左卫将军 是以倾身竭宝 逃窜得免 为城民华延明所害 以为辅相 起家秘书郎 反及二代 出为后将军 乘势追殄 显奔马邑西山 以功赐爵 安德侯 同轨斯始 爵例降 一者 纯节所存 超前绝后 寻为世隆等所废 焚其栅门 结党同呼 坐事赐死于第 宗议不听 缘江焚毁 永平弟珍平 霖雨连并 有诏赦之 每乖宪典 绢二百匹 甘之若荠 今汝等无状 太祖追讨 司空 奔于代郡 一州蒙祜 虽曰分歧 冻死者十数人 赠使持节 固辞不拜 世以 为冤 给幢麾鼓盖 父忧 元颢入洛 货遗诸使 请诣阙恭授 死亡失所 外动亦攘 知名于时 英至长薄 唯有孤城 略虽在江南 今王董彼三军 无使为山之功 必胜之规 奸乱是由 景略弟庆略 高祖引见百官于光极堂 "久之 并与熙同被害 尔朱荣 还复本封 又迁车骑大将军 寻以绥抚有能 果不相救 九叶承光 为幽州大都督侯渊所执 果杀眷而代立 于是献明皇后携太祖及卫秦二王自贺兰部来居焉 乃使长史李华率五统向西关 运材数百万根 奸盗豺狼 祭以丰厨 莫知所归 义阳孤绝 征虏将军 远近皆供租运 又讨西关 在军贪暴 不为异端 长蛇塞涂 及熙之死也 加散骑常侍 进号抚军将军 领 大司马 外似柔谨 高祖幸其第 及开建五等 略之将还也 茂林凋枯 还复梁城 拜宗正卿 刘琨为并州 起家恒州征虏录事参军 黜为员外常侍 引见王公 庄帝初 "何有动兵马理也 并攻一营 徙其部落 垂名金石 出为太原太守 性轻躁 所望于将军 遂围南郑 微晓医术 秋方大登 无子 寻以融死王 事 名美当世 雄连有战功 仍大司马 梁州刺史 时有休否 遂降 君亲如此 乃除显恭使持节 而率州兵 倍道赴救 荆州刺史 率并肆之众往讨之 英徼其前 便可扑扫 "纵之使入此城 晴则攻腾 改授辅国将军 徵为内都大官 为平北将军 军据州南 幽州安西府功曹参军 南安原始要终 存亡继绝 将至 不测 一去不还者乎?灵恩势窘 世宗以邢峦频破早生 英五子 都督以讨之 语在《帝纪》 勋烈光延 怙众肆暴 又吝惜财用 袭拜太中大夫 "彼帅贱民慢 悲痛烦冤 诏彬持节 华州刺史 轺盖殊制 《魏书》 北齐·魏收 兄子楷讨之 庄帝步出云龙门 绞刑 东秦州刺史 雍州刺史 以义阳应之 后太祖讨显于马邑 率众百万 大司农卿 譐誻明昏 内多猜忌 有才略 袭 孙皓之缚重至 皇兴二年封 悲恸于怀;与垂子麟相持 待以国士之礼 庶仰凭祖宗之灵 德之 高祖幸邺 除北中郎将 追赠使持节 遂与彧等劝帝图荣 太 府少卿李苗 戎马在郊 诏英曰 扬烈将军曹文敬进据樊城以抗之 除散骑常侍 叉斩之于岐州 "从兄显 子绪 悲伤无极已 流涕而别 王室多难 征赴讲武 时领军于忠执政 爵例降 字虎儿 "谨案学令 泣血而生 朝服一具 又击蠕蠕别帅胏渥于意亲山 假平北将军 唯唯具臣而已 残破狼籍 食邑一 千户 以贪惏削封 凝姑 入为安东将军 其勤隐恤 守室亲戚莫与比焉 是故推让 垂遣慕容良迎之 可还于别馆 猃狁孔炽 袭 奉承晋皇 肃宗不纳 食邑八百户 臣早属休明 伏于四山 使持节 鼓噪南征 议者以为有报应焉 追赠车骑大将军 定州刺史 宜休息观衅而动 声被荒隅 文明太后 英以众少 荣兼衔之 东南道大行台 与安南将军卢渊 赠散骑侍郎 字豹儿 参国官 桓帝嘉之 给事中 前废帝时 国失惠主 超避难洛南 孝庄初 子超 累表请军 广召名胜 豺狼为心 传首京师 请奉妹充后宫 高祖 除冠军将军 水盛破桥 出为使持节 举国崩绝 四门之教方构于京瀍 腰带十围 寻诏英使持节 威 名宿震 以庶人归第 谥曰惠 专为烦扰 衍乃备礼遣之 晋州刺史 不欲人居其前 左光禄大夫 何容缓斧 字怀忠 帝之姊婿 修持五戒 昔卫霍以匈奴之故 奸党犹逆 仰恋仁慈 杀坚五原太守而叛 追封乐陵王 除前将军 延昌中 无他裨益 然后贼退 英还一日 殖货私庭 古者 连结正平 以清疆界 乐陵 东豫州刺史 略有三事 邑五百户 彬请兵二万 但智力浅短 谘论奋发 永熙二年薨 已有奸窃 子长春 进号镇军将军 遂使二宫阻隔 事从宽贷 新州初附 桓穆二帝并礼重操 阬规降卒五千余人 其路既近 除平北将军 志在竭力 关右慰劳十二州大使 可遣使者 拜外都大官 拜太常少卿 除凉州镇都 大将 赠中军将军 樵牧饶广 薨 赠帛一千匹 寻分兵围守 高祖即位 性通率 文虽非丽 食邑一千户 任以国事 犍既领部 武定初 与法僧言 或难制掠 字世彦 东瀛公司马腾 鱼游釜内 还袭父爵 破之 东关易攻 内惧荣宠 因正使列之 "谁也?支将二十人 开府仪同三司 征南大将军 广阳王渊 世宗即位 依前禁锢 以其暴乱不悛 克申庙算 加散骑常侍 送于晋阳 衍寻遣
苏教版中考数学压轴题:动点问题

运动变化型问题专题复习【考点导航】运动变化题是指以三角形、四边形、圆等几何图形为载体,设计动态变化,并对变化过程中伴随着的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行考察研究的一类问题,这类试题信息量大,题目灵活多变,有较强的选拔功能,是近年来中考数学试题的热点题型之一,常以压轴题的面目出现.解决此类问题需要运用运动和变化的观点,把握运动和变化的全过程,动中取静,静中求动,抓住变化过程中的特殊情形,建立方程、不等式、函数模型. 【答题锦囊】例1 如图在Rt △ABC 中,∠C =90°,AC =12,BC =16,动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P ,Q 分别从点A ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ 关于直线PQ 对称的图形是△PDQ .设运动时间为t (秒).(1)设四边形PCQD 的面积为y ,求y 与t 的函数关系式; (2)t 为何值时,四边形PQBA 是梯形(3)是否存在时刻t ,使得PD ∥AB 若存在,求出t 的值;若不存在,请说明理由;(4)通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD ⊥AB 若存在,请估计t 的值在括号中的哪个时间段内(0≤t ≤1;1<t ≤2;2<t ≤3;3<t ≤4);若不存在,请简要说明理由.例2 如图2,直角梯形,DC=3,动点P 从点A 出发,沿A→D →C →B 方向移动,动点Q 从点x ,点Q 移动的路程为y ,线段PQ平分梯形ABCD (1)求y 与x 的函数关系式,并求出x ,(2)当PQ ∥AC时,求x y ,的值;(3)当P 不在BC 边上时,线段PQ 能否平分梯形ABCD 的面积若能,求出此时x 的值;若不能,说明理由.例3 如图3,在平面直角坐标系中,以坐标原点O 为圆心,2为半径画⊙O ,P 是⊙O 上一动点,且P在第一象限内,过点P 作⊙OA ,与y 轴相交于点B .(1)点P 在运动时,线段的长度也在发生变化,请写出线段AB 长度的最小值,并说明理由;(2)在⊙O 、P 为顶点的四边形时平行四边形若存在,请求出Q 点的坐标;若不存在,请说明理由.例4 如图7①,一张三角形纸片ABC 的中线CD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形(如图7②所示))方向平移(点12,,,A D D B 始终在同一直线上),当点1D 于点B 重合时,E,1AC 与222C D BC 、分别交于点F 、P.⑴当11AC D ∆平移到如图7③所示的位置时,猜想图中的1D E 与2D F 的数量关系,并证明你的猜想; ⑵设平移距离21D D 为x ,11AC D ∆与22BC D ∆重叠部分面积为y ,请写出y 与x 的函数关系式,以及自变量的取值范围;⑶对于(2)中的结论是否存在这样的x 的值,使重叠部分的面积等于原ABC ∆面积的14.若存在,求x 的值;若不存在,请说明理由.【中考预测】⒈如图8①,有两个形状完全相同的直角三角形ABC 和EFG 叠放在一起(点A 与点E 重合),已知AC =8cm ,BC =6cm ,∠C =90°,EG =4cm , ∠EGF =90°,O 是△EFG 斜边上的中点.如图8②,若整个△EFG 从图①的位置出发,以1cm/s 的速度沿射线AB 方向平移,在△EFG 平移的同时,点P 从△EFG 的顶点G 出发,以1cm/s 的速度在直角边GF 上向点F 运动,当点P 到达点F 时,点P 停止运动,△EFG 也随之停止平移.设运动时间为x (s ),FG 的延长线交 AC 于H ,四边形OAHP 的面积为y (cm 2)(不考虑点P 与G 、F 重合的情况).(1)当x 为何值时,OP ∥AC ?(2)求y 与x 之间的函数关系式,并确定自变量x 的取值范围.(3)是否存在某一时刻,使四边形OAHP 面积与△ABC 面积的比为13∶24若存在,求出x 的值;若不存在,说明理由.(参考数据:1142 =12996,1152 =13225,1162 =13456或4.42 =19.36,4.52 =20.25,4.62=21.16)⒉如图9,在平面直角坐标系中,两个函数y=x ,6x 21y +-=的图象交于点A .动点P 从点O 开始沿OA 方向以每秒1个单位的速度运动,作PQ//x 轴交直线BC 于点Q ,以PQ 为一边向下作正方形PQMN ,设它与ΔOAB 重叠部分的面积为S .(1)求点A 的坐标.(2)试求出点P 在线段OA 上运动时,S 与运动时间t (秒)的关系式.(3)在(2)的条件下,S 是否有最大值若有,求出t 为何值时,S 有最大值,并求出最大值;若没有,请说明理由.(4)若点P 经过点A 后继续按原方向、原速度运动,当正方形PQMN 和ΔOAB 重叠部分面积最大时,运动时间t 满足的条件是__________.⒊如图10,平面直角坐标系中,直线AB 与x 轴,y 轴分别图1A C D P B122D① 21② 图8图9交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D . (1)求直线AB 的解析式; (2)若S 梯形OBCD,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的三角形与△OBA 相似.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.⒋如图11,在锐角ABC △中,9BC =,AH BC ⊥于点H ,且6AH =,点D 为AB 边上的任意一点,过点D 作DE BC ∥,交AC 于点E .设ADE △的高AF 为(06)x x <<,以DE 为折线将ADE △翻折,所得的A DE '△与梯形DBCE 重叠部分的面积记为y (点A 关于DE 的对称点A '落在AH 所在的直线上). (1)分别求出当03x <≤与36x <<时,y 与x 的函数关系式; (2)当x 取何值时,y 的值最大最大值是多少⒌如图12,在ABC ∆中,∠D 在BC 上,且CD=3cm ,现有两个动点P 、Q 分别从点A 和点B AC 向终点C移动;点Q 以1.25cm/s 的速度沿BC 向终点C 移动.过点P 作PE ∥BC .设动点运动时间为x秒. (1)用含x 的代数式表示AE 、(2)当点Q在BD (不包括点B 、D )上移动时,设EDQ ∆的面积为2()y cm ,求y 与月份x 的函数关系式,并写出自变量x 的取值范围;(3)当x 为何值时,EDQ ∆为直角三角形.⒍如图13,在平面直角坐标系中,已知点(0A 30.动点P 在线段AB 上从点A 向点B M N ,作等边PMN △. (1)求直线AB 的解析式;(2)求等边PMN △的边长(用t 运动到与原点O 重合时t 的值; (3)如果取OB 的中点D ,以OD 为边在Rt △内部作如图14所示的矩形ODCE ,点C 在线段AB 上.设等边PMN △和矩形ODCE 重叠部分的面积为S ,请求出当02t ≤≤秒时S 与t 的函数关系式,并求出S 的最大值.⒎如图15,已知Rt ABC △中,CAB ∠=作连接BE 交AC 于点P .(1)求PA 的长;(2)以点A 为圆心,AP 为半径作⊙A ,试判断BE 与⊙A 是否相切,并说明理由;(3)如图16,过点C 作CD AE ⊥,垂足为D .以点A 为圆心,r 为半径作⊙A ;以点C 为圆心,R 为半径作⊙C .若r 和R 的大小是可变化的,并且在变化过程中保持⊙A 和⊙C 相切..,且使D 点在⊙A 的内部,B 点在⊙A 的外部,求r 和R 的变化范围.8.已知抛物线bx ax y 2++=B (1)求抛物线的解析式;(2)现有一半径为1,圆心P P 与坐标轴相切的情况若存在,请求出圆心P(3)若⊙Q 的半径为r ,点Q r 的值.⒐如图17,在平面直角坐标系中,点P 从点A 开始沿x 轴向点O 以1cm /s 的速度移动,点Q 从点O 开始沿y 轴向点B 以2cm /s 的速度移动,且OA=6cm ,OB=12cm.如果P ,Q 分别从A ,O 同时出发.⑴设△POQ 的面积等于y,运动时间为x ,写出y 与x 之间的函数关系,并求出面积的最大值; ⑵几秒后△POQ 与△AOB 相似;⑶几秒后以PQ 为直径的圆与直线AB 相切.⒑如图18,在等腰梯形ABCD 中,AB ∥DC ,AB =8cm ,CD =2cm ,AD =6cm .点P 从点A 出发,以2cm/s 的速度沿AB 向终点B 运动;点Q 从点C 出发,以1cm/s 的速度沿CD 、DA 向终点A 运动(P 、Q 两点中,有一个点运动到终点时,所有运动即终止).设P 、Q 同时出发并运动了t 秒.(1)当PQ 将梯形ABCD 分成两个直角梯形时,求t 的值;(2)试问是否存在这样的t ,使四边形PBCQ 的面积是梯形ABCD 面积的一半?若存在,求出这样的t 的值,若不存在,请说明理由。
数学中考新题型注意求“从动点”运动路径长问题研究

数学中考新题型注意求“从动点”运动路径长问题研究发表时间:2020-11-30T14:08:53.030Z 来源:《中小学教育》2020年24期作者:李丽华[导读] 数学中考新题型的“从动点”运动路径长度问题李丽华营口市第三十一初级中学辽宁营口 115007摘要:数学中考新题型的“从动点”运动路径长度问题,从两个层面对学生的数学掌握水平进行综合考察,难度整体偏大。
本文对此类问题的难点产生原因进行了分析,提出注重对问题本质的思索,提升静态具象思维与动态抽象思维互相转化的能力等深度解决“从动点”运动路径长度问题的有效方式,以供参考。
关键词:从动点;运动路径长度;静态具象思维;动态抽象思维引言:初中数学中的从动点问题,在2010年以前的中考试卷中,出现的频率相对较低。
但随着教学的深入,出题者及广大教研人员发现,此类动态的“主从联动”问题(又被很多教师称之为瓜豆原理或旋转相似问题),对于考察学生们的抽象思维与逻辑思维能力具有良好的作用,故已成为了中学数学的“网红问题”。
一、数学中考新题型“从动点”与运动路径长度问题难点解析在初中数学有关几何问题的教学中,存在一种现象,即对于静止不动的几何问题,只要对基础规律有所了解的学生,都能够准确找到点、线、面之间的关系,对于周长、面积之间相互转化,求解目标项的问题,均能得出正确答案。
但当静态的“定量”转化为动态的“变量”时,很多学生由于欠缺逻辑思维能力,往往在求解时缺乏思路。
比如数学中考试卷中出现的热门新题型——“从动点”运动路径长度问题,几乎成为了“扣分专项”。
该类问题的难点如下:(1)题设条件与求解项之间存在“隔阂”,导致学生无法确认正确答案产生之前必须求得的关键条件。
如例题“在矩形ABCD中,AB (宽)=3,BC(长)=4,P是BC边上的一个动点,连接AP形成△ABP,沿AP边将其烦着,得到对称的△AQP,Q为点B翻折后的对称点,连接CQ,求CQ的最小值”。
动点运动路径长问题

乘胜 追击
例 2(2017 宁波考纲)在矩形 ABCD 中, AD=6,AB=
6 2 3 ,E 是 AB 边上的一点,且 AE=AD,P 是线段 CD 上
一点,连接 PE,将矩形沿着 PE 折叠,点 B、C 分别落在 G、
F 处,当点 P 从点 C 移动到点 D 时,点 G 经过的路径长为
________。
例 3(2016 武汉)如图,在等腰 Rt△ABC 中,AC=BC=2 2 , 点 P 在以斜边 AB 为直径的半圆 O 上,M 为 PC 的中点.当
点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( B )
A. 2
B. C. 2 2
D. 2
本节课学习了哪些内容
课后 拓展
(2014 义乌)如图,等边三角形 ABC 的边长为 6,点 E,F 分别
在 AC,BC 上,连结 AF,BE 相交于点 P, 若 AE=CF,当点
E 从点 A 运动到点 C 时,求点 P 经过的路径长。
D(P)
C
A
E
B
F G
攻坚 克难
例 3(2016 武汉)如图,在等腰 Rt△ABC 中,AC=BC=2 2 , 点 P 在以斜边 AB 为直径的半圆 O 上,M 为 PC 的中点.当
点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( B )
A. 2Biblioteka B. C. 2 2D. 2
攻坚 克难
∵∠ADO=90°
∴点 D 在以 AO 为直径的圆上
当点C与A重合;D与A重合;
当点C运动90°时;
∴点 D 的运动路线是以 AO 为直径的 1 圆弧
∴ l n R 90 2
初中数学动点轨迹问题解法探究

初中数学动点轨迹问题解法探究作者:曾立萱来源:《读写算》2018年第10期摘要在研究动点问题时,可以在运动中寻找不变的量,借助引参量、消参数的代数方法发现动点坐标、动点之间的联系。
也可以借助常见的几何模型探究几何动态中动点形成轨迹的过程,利用轨迹思想解决几何中线段最值问题、求动点的轨迹长度的问题。
关键词轨迹意识;引参量;消参数;几何动态;最值;运动路径;四点共圆;辅助圆;隐轨迹中图分类号:G632 文献标识码:A 文章编号:1002-7661(2018)10-0147-02在初中阶段常见的动点轨迹一般有四种类型:直线型、圆弧型、抛物线型、双曲线型。
对于用二次函数来表示动点的轨迹是高中函数重点学习内容,本文不以具体阐述。
对于几何动点轨迹问题是近年中考的热点,也是难点。
本文借助几种常见的类型题,带领同学们强化轨迹思想,学会利用轨迹思想解决几何中线段最值问题、求动点的轨迹长度的问题。
在研究动点问题时,可以在运动中寻找不变的量:数量或位置关系。
学生在解决此类问题时经常不知所措,究其原因是不能发现“动”中的“静”。
如何“化动为静”呢?可以借助引参量、消参数的代数方法发现动点的坐标、动点之间的联系。
也可以用“中垂线的性质定理”、“点到直线的距离”、“圆的定义”、“四点共圆”的条件去探究几何动态中动点形成轨迹的过程。
类型一:动点旋转型——探究动点的轨迹是直线例1:如图1,已知A(8,0),P(0,m),线段PA绕着点P按逆时针方向旋转90°至线段PB位置,连接BA、OB,求BO+BA的最小值?解析:主动点是P,动点B因P的变化而变化,但点B随着点P的运动而动,问题的关键是找出动点B的运动轨迹。
由旋转可知是等腰直角三角形,过点B作轴的垂线,构造“K型全等”,求得点B(),消去参数,发现动点B的运动轨迹是直线。
从而将问题转化为“将军钦马”问题模型:即作点O关于直线的对称点(-8,8),连结AC与直线相交于点B,此时BO+BA的最小值=AC=本题的解析关健是从动点B的坐标()中想到消去参数,得一次函数的表达式,从而化“动点轨迹”为定直线。
例谈如何解一类_动点运动路径长_问题_马先龙

槡 2 1 1 1例谈如何解一类“动点运动路径长”问题■ 马先龙摘要: 解答中考题时,经常会碰到解“动点运动路径长”问题. 实际解题时,若能先灵活运用“等距法”探究动点轨迹,确定路径,然后通过计算求其长,则能比较顺利地解决问题,本文通过举例说明.关键词:动点; 等距法; 路径长 解答中考题时,经常会碰到一类以动三角形为载 体的“动点运动路径长”问题. 此类问题因综合性较强,考查的知识点较多,加上动点的运动路径又不明 显,因而解答时颇有难度,常常让答题者望而生畏. 实际解题时,若能先灵活运用“等距法”探究动点轨迹, 确定路径,然后再通过计算求其长,则能比较顺利地解决问题. 现举例说明,供读者参考.⊥ C A 交 C A 的延长线于点 M ,作 O N ⊥ B C 于点 N ,则易证 O M = O N ,所以点 O 在∠A C B 的平分线 C O 上运动,从而,点 O 的运动路径为线段,接下来通过计算易求其长.解: 如图 1,因为 △A O P 是等腰直角三角形,所以 O A = O P ,∠A O P = 90°. 连接 C O ,过点 O 作 O M ⊥ C A 交 C A 的延长线于点 M ,作 O N ⊥ B C 于点 N ,则 ∠O MC = ∠O N C = ∠O N P = 90°,又因为∠MC N = 90°,所以 ∠O MC = ∠O N C = ∠MC N = 90°,所以四边形 CM O N 是矩形,所以 ∠M O N = 90°,所以 ∠A O M + ∠A O N =∠P O N + ∠A O N = 90° ,所以 ∠A O M = ∠P O N . 在∠O M A = ∠O N P = 90° 一、动点的运动路径为一条线段 例 1( 2018 年四川达州市中考) 如图 1,△AOM 和 △PON 中 , ∠AOM = ∠PON OA = OP,所以Rt △A B C 中,∠C = 90°,A C = 2 ,B C = 5,点 D 是 B C 边上一点且 C D = 1,点 P 是线段 DB 上一动点,连接 A P ,以 A P 为斜边在 A P 的下方作等腰 Rt △A O P . 当 P 从点 D 出发运动至点 B 停止时,点 O 的运动路径长为.△A O M ≌ △P O N ( AA S ) ,所以 O M = O N ,所以点 O 在 ∠A C B 的平分线C O 上运动. 如图2,分别作出动点O 的始末位置点 O 1、O 2,则线段 O 1O 2 就是动点 O 的运动路径. 过点 O 1 作 O 1M 1 ⊥ A C 于点 M 1,作 O 1N 1 ⊥ B C 于点 N 1,过点 O 2 作 O 2M 2 ⊥ C A 交 C A 的延长线于点 M 2,作 O 2N 2 ⊥ B C 于点 N 2,由上,易知四边形 CM 2O 2N 2 是矩 形,△A O 2M 2 ≌ △BO 2N 2( AA S ) ,所以 O 2M 2 = O 2N 2, A M 2 = B N 2,所以四边形 CM 2O 2N 2 是正方形,所以 CM 2 = C N 2,所以 CM 2 - A C = B C - CM 2,所以 CM 2 = 1 ( AC + BC ) = 1 × ( 2 + 5) = 7 ,所 以 CO =2 2 2 2图 1图 22 CM = 7 槡2. 同理,可得四边形 CM O N 是正方形, 2 CM = 1 ( A C + C D ) = 1 × ( 2 + 1) = 3,C O = 分析:本题中等腰Rt △AOP 的顶点 A 固定,顶点 P在线段 DB 上运动,顶点 O 随之运动. 依题意,可先用 1 2 CM 2 = 3 槡2 ,所以 O O 2 = CO - CO 2= 7 槡2 1-3 槡2 “等距法”探究动点 O 轨迹,确定路径,后求其长. 如图 槡 1 2 1 2 2 1 2 2 1,由条件,易知 O A = O P ,∠A O P = 90°,过点 O 作 O M= 2 槡2 ,所以点 O 的运动路径长为 2 槡2 .作者简介: 马先龙( 1966 - ) ,男,江苏淮阴人,本科,中学高级教师,主要从事初中数学教学研究·30·评注: 本题考查了动点的运动轨迹,考查了等腰直角三角形的性质,考查了全等三角形的判定和性质,考查了矩形、正方形的判定和性质,考查了角平分线的判定,考查了构造图形法、等距法等数学思想方法的运用[1]. 在探究动点轨迹时,充分抓住等腰 Rt △A O P 两腰相等且夹角为直角等重要条件,通过作垂线段构造全等三角形,得到动点 O 到定角 ∠ACB 两边的距离相等这一事实,从而由数量关系引发位置关系,推得动点 O 一定在 ∠ACB 的平分线上运动,进而获得动点的运动路径为一条线段. 接下来,作出动点的始末位置点, 根据图形和已知条件计算路径长则比较容易了.例 2 ( 2018 年湖北荆门市中考) 如图 3,等腰Rt △A B C 中,斜边A B 的长为2,O 为A B 的中点,P 为A C 边上的动点,OQ ⊥ O P 交 B C 于点 Q ,M 为 P Q 的中点, 当点 P 从点 A 运动到点 C 时,点 M 所经过的路径长为( )( A) 槡2 π ( B) 槡2 πBC 的中点,则 M 1、M 2 也分别是动点 M 的始末位置点, 所以线段 M 1M 2 就是动点 M 的运动路径. 在△ABC 中, 因为 M 1M 2 是 △A B C 的中位线,A B = 2,所以 M 1M 2 =1A B = 1,所以动点 M 所经过的路径长为 1,所以选 2( C) .评注: 本题考查了动点的运动轨迹,考查了等腰直角三角形的性质,考查了“直角三角形斜边上的中线等于斜边的一半”这一重要定理,考查了线段垂直平分线的判定,考查了三角形的中位线定理,考查了构造图 形法、等距法等数学思想方法的运用. 在探究动点轨迹时,充分抓住了点 M 既为Rt △OPQ 斜边 PQ 的中点,又为 Rt △PCQ 斜边 PQ 的中点这一重要条件,通过运用直角三角形关于斜边上中线的性质定理,得到动点 M 到定线段OC 两端的距离相等这一事实,从而由数量关系引发位置关系,推得动点 M 一定在线段 CO 的垂直平分线上运动,进而获得动点的运动路径为一条线段. 接下来,根据动点的始末位置,计算路径长唾手可得.4 2 ( C) 1 ( D) 2图 3 图 4分析: 本题中Rt △POQ 的顶点O 固定,顶点P 在线段 A C 上运动,P Q 的中点 M 随之运动. 依题意,可先用 “等距法”探究动点 M 轨迹,确定路径,后求其长. 如图 3,连接C O ,M O ,MC ,由题意,易证M O = MC ,所以点M 一定在线段 CO 的垂直平分线上运动,从而推得点 M 的运动路径为线段,接下来通过计算易求路径长.解: 如图 3,连接 C O ,M O ,MC . 因为 △A B C 是等腰直角三角形,所以 A C = B C ,∠A C B = 90°. 因为 OQ ⊥ O P ,所以∠P OQ = 90°. 在Rt △P OQ 与Rt △P C Q 中,因为 ∠P OQ = ∠A C B = 90°,M 为 P Q 的中点,所以 M O= MC = 1P Q ,所以点 M 在线段 C O 的垂直平分线 E F2 上运动. 如图 4,在等腰 Rt △A B C 中,因为 A C = B C ,O 为 A B 的中点,所以 C O ⊥ A B ,设 M 1、M 2 分别是边 A C 、 二、动点的运动路径为两条( 往返) 线段 例3 ( 2019 年浙江嘉兴市中考) 如图 5,一副含 30° 和45° 的直角三角板 ABC 和 EDF 拼合在一个平面上,边 A C 与 E F 重合,A C = 12 c m . 当点 E 从点 A 出发沿 AC 方向滑动时,点 F 同时从点 C 出发沿射线 BC 方向滑动. 当点 E 从点 A 滑动到点 C 时,点 D 运动的路径长为c m .槡 分析: 本题中等腰 Rt △DEF 的三个顶点都在运动,其中顶点 E 、F 限制在两条互相垂直的线段上滑动, 等腰 Rt △DEF 在运动中形状、大小都保持不变. 依题意,可先用“等距法”探究动点 D 轨迹,分类讨论,确定路径,后求其长. 如图 6,由条件,易知 DE = DF , ∠E D F = 90°,过点 D 作 D G ⊥ A C 于点 G ,作 D H ⊥ B C 交直线 B C 于点 H ,则易证 D G = D H ,所以动点 D 在 △ABC 的外角∠ACH 的平分线上运动. 依题意,动点 D的运动路径为两条( 往返) 线段,接下来通过计算易求路径长.解: 如图 6,过点 D 作 D G ⊥ A C 于点 G ,作 D H ⊥ B C 交直线 B C 于点H ,则∠D G E = ∠D G C = ∠D H C = 90°,又因为 ∠A C B = 90°,所以 ∠G C H = 90°,所以 ∠D G C = ∠G C H = ∠D H C = 90°,所以四边形 C G D H 是矩形,所以∠G D H = 90°,又因为△E D F 是等腰直角三角形,所以 D E = D F ,∠E D F = 90°,所以 ∠E D G + ∠GDF = ∠FDH + ∠GDF = 90°, 所 以 ∠EDG = ∠F D H . 在 △E D G 和 △F D H 中,∠D G E = ∠D H F = 90°, 6槡2,所以点 D 运动的路径长为2D 1D 2 = ( 24 - 12槡2) c m . 评注: 本题考查了动点的运动轨迹,考查了等腰直角三角形的性质,考查了全等三角形的判定和性质,考查了矩形、正方形的判定和性质,考查了角平分线的判定,考查了构造图形法、等距法、特殊位置法、分类讨论 法等数学思想方法的运用. 在探究动点轨迹时,充分抓住等腰 Rt △DEF 两腰相等且夹角为直角等重要条件, 通过作垂线段构造全等三角形,得到动点 D 到定角( ∠ACB 的外角) 两边的距离相等这一事实,从而由数量关系引发位置关系,推得动点 O 一定在 △ABC 的外角∠ACH ( 如图7) 的平分线上运动. 对于本题,由于等腰 Rt △DEF 的顶点 E 、F 限制在两条互相垂直的线段上滑动,而等腰 Rt △DEF 在运动中形状、大小都保持不变,因而导致动点 O 的运动路径为两条( 往返) 线段. 一旦弄清动点 O 的运动路径,计算路径长则立刻变得简单了. 本题对动点 O 运动路径的确定是难点,突破难点的关键是运用动中求静,静中求动的思想,多画几 种动点在不同状态下的图形,从而易获得特殊位置图形,对路径作出正确的判断和分类.∠EDG = ∠FDH DE = DF,所 以 △EDG ≌“解题,就好像游泳一样,是一种实际技能. 当你学习游泳时,你模仿其他人的手足动作使头部保持在水 △F D H ( AA S ) ,所以 D G = D H ,所以动点 D 在 △A B C 的外角 ∠A C H 的平分线上运动. 如图 7,当点 E 沿 A C 方向滑动,使等腰直角三角的板的边DE ⊥ AC 时,作出动点 D 从开始到此时的始末位置点 D 2、D 1,则在这一过程中动点 D 沿线段 D 1D 2 向斜上方方向运动,运动路径为线段 D 1D 2; 如图 8,当点 E 接上一过程沿 A C 方向继续滑动,使等腰直角三角板的斜边 EF 正好落在直线BC 上时,作出动点 D 的始末位置点 D 1、D 2 则在这一过程中动点 D 沿线段 D 2D 1 向斜下方方向运动,运动路径为线段D 2D 1. 如图5,因为等腰直角三角板E D F 的斜边E F = A C = 12 c m ,所以 D E = D F = 槡2E F = 6 2 c m .2 如图7,易知C D 1 = 6槡2 ,四边形 C E 2D 2F 2 是正方形,从而 C D 2 = E 2F 2 = 12,所以 D 1D 2 = C D 2 - C D 1 = 12 -面上,并最后通过实践来学会游泳. 当试图解题时,你也必须观察并模仿其他人在解题时的行为,并且最后通过实践来学会解题[2]”. 对典型的中考题进行归类解析,可以帮助学生学会模仿、探究、思考,不断感受基 本的数学思想和方法,积累解题经验,从而领会数学的精髓、奥妙,增强解题信心,学会“游泳”,学会解题. 参考文献:[1] 罗增儒. 数学解题学引论[M ]. 西安: 陕西师范大学出版社,2001. [2] 波利亚. 怎样解题[M ]. 上海: 上海科技教育出版社,2007. [江苏省淮安市淮阴区开明中学( 223300) ]。
动点路径长问题解法探究(公开课教案)

动点路径长问题解法探究江夏二中林建平教学目的:1、知识和能力:了解动点路径长问题的基本解题方法。
2、过程和方法:注重学生参与,联系实际,丰富学生的感性认识3、情感态度价值观:培养学生的良好的学习习惯教学重点:动点路径长问题的基本解题方法。
教学难点:确定动点路径类型。
一、导入:动点路径长问题是近年来中考的热点题型.常见类型:1、线段2、圆弧3、组合解题步骤:1、取动点在运动过程中特殊的三点(运动开始、运动中、运动结束)位置探索出动点运动的路径形状;三点共线→线段,三点不共线→圆弧2、第二步,根据题目的已知条件求出动点运动的路径长;二、例题:(2017元调第16题)在平面直角坐标系中,点C沿着某条路径运动,以点C为旋转中心,将点A(0,4)逆时针旋转90°到点B(m,1).若-5≤m≤5,则点C运动的路径长为___________。
变式1、将例题中旋转角90°改为60°,其余条件不变。
则点C运动的路径长为___________。
变式2、将例题中旋转角90°改为120°,其余条件不变。
则点C运动的路径长为___________。
变式3、在平面直角坐标系中,已知点A(0,4),点B(m,1),以点B为旋转中心,将点A(0,4)逆时针旋转90°到点C。
若-5≤m≤5,则点C运动的路径长为。
三、课堂检测练习:1、如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是.练习1图练习2图练习3图2、如图,在Rt△ABC纸片中,∠C=90°,AC=BC=4,点P在AC上运动,将纸片沿PB折叠,得到点C的对应点D(P在C点时,点C的对应点是本身),则折叠过程对应点D的路径是。
3、如图,矩形ABCD中,AB=8,CD=6,将矩形ABCD在直线上按顺时针方向不滑动的转动90°,转动3次后停止,则顶点A经过的路线长为。
中考数学复习指导:动点路径长问题的解法研究

—类动点路径长问题的解法研究在近几年的中考中频频出现由动点产生的求路径长问题.这类问题的难点在于从动点(关联点)的运动路径不明确,而这正是解决问题的关键.本文通过一道典型题解法的探究,从中提炼模型,进而给出这类问题的通用解法. 问题如图1,己知线段6AB =,C 、D 是AB 上两点,且1AC DB ==,P 是线段CD 上一动点.在AB 同侧分别作等边APE ?和等边PBF ?,G 为线段EF 的中点,当点P 由点C 移动到点D 时,G 点移动的路径长度为一、探究解法1.准确作图本题主动点是P ,从动点是G 。
作图要体现两个方面,一方面要体现G 点的临界位置(起点和终点);另一方面要体现G 点的一般位置,如图 2. ①点P 由点C 移动到点D ,点C 、D 即为P 运动的临界点,此时点G 运动到1G 、2G ②在CD 上任取一点P ,异于C 、D ,此时点G 运动到3G 2.合理猜想在同一张图中画出G 点的特殊位置1G 、2G ,一般位置3G ,将不同的点G 位置连结起来,形成了对运动过程的直观化,容易猜想点G 的运动路径是一条线段.这一猜想是基于在同一张图中画出G 点的多个位置,每一个位置都要准确无误,这样使得下一步的猜想更合理、更有价值,因此对作图的要求很高. 3.严谨证明证法1 如图3,过点E GF 、、分别作AB 的垂线,垂足为H I J 、、。
由梯形的中位线,得2GI EH FJ =+,由等边三角形,得32EH AP =,32FJ BP=而6AP BP +=,所以332GI =因为点G 到AB 的距离为定值,所以点G 的运动路径为线段12G G . 如图4,11223H J H J ==12121211225 1.5 1.52G G I I H J H I H J ==--=--=证法2 如图5,延长AE BF 、交于点O ,可知四边形EPFO 为平行四边形。
因为G 为EF 中点,所以G 为OP 中点,所以G 的运动路径为OCD ?的中位线12G G ,易得1222CDG G ==二、提炼模型由上述第二种证法可知,点G 的运动路径之所以为OCD ?的中位线12G G ,关键在于G 始终是OP 中点。
动点轨迹[下学期]江苏教育出版社-202004
![动点轨迹[下学期]江苏教育出版社-202004](https://img.taocdn.com/s3/m/923438afb8f67c1cfbd6b823.png)
例2:已知直线L1⊥直线L2,垂足为M,点N ∈L2,(如图)以A,B为端点 的曲线段C上任意一点到L1的距离与到N的距离相等.若ΔAMN为 锐角三角形,且|AM|=√17,|AN|=3,|BN|=6.建立适当的坐标系,求曲线
段C的方程.
[思路分析]:坐标系的建立是本题的
y B
突破口,由于L1⊥L2,故可选择它们 L1 A 为坐标轴;也可以以线段MN的垂直
[思路分析1]本题中的动点M是由两条动
y
Q
直线相交而得,而它们的运动又都依赖 于动点P ,因此选择P的坐标为参数,写 出两直线的方程,解方程组,得点M的轨
A MP OF
x
迹的参数方程,再化为普通方程,从而得
出M的轨迹.
[思路分析2]既然M的运动依赖于P的运动,可否用例3的方 法,用M的坐标表示P的坐标,而P又在已知曲线上运动,代 入已知曲线得出M的方程.M和P是什么关系?回到图中仔 细分析,连接AQ会怎么样?点M与ΔAFQ是什么关系?
• 参数法:动点的运动依赖于某一参数(角度、 斜率、坐标等)的变化,可建立相应的参数 方程,再化为普通方程.
B
x C
角的补角,因而tgB、tgC都可以用斜率
来表示.这样可直接写出顶点A的方程,
接下来的工作就是化简方程和判断轨迹
是何种曲线,必要时可进行讨论.
本题答案:轨迹方程为 x2/a2 +y2/ta2 =1 (x≠+-a)
.当0<t<1或t>1时,轨迹为椭圆;当t =1时,轨迹为圆;当t<0 时,轨迹为双曲线.
数学高考专题复习
主讲人:朱俊杰
圆锥曲线回顾
例1:已知ΔABC底边BC的长为2a(a>0),又知tgBtgC=t(t≠0).(a,t均为常
动点轨迹[下学期]江苏教育出版社
![动点轨迹[下学期]江苏教育出版社](https://img.taocdn.com/s3/m/d4bd06227e21af45b207a841.png)
5.求得的轨迹方程要与动点的轨迹一一对应,否则要“多 退少补”,多余的点要剔除(用x,y的取值范围来制),不 足的点要补充.
6.注意求轨迹和求轨迹方程的区别.
(1999,24t,14f)如图,给出定点A(a,0)(a>0)和直线L:x = -1. B
• 参数法:动点的运动依赖于某一参数(角度、 斜率、坐标等)的变化,可建立相应的参数 方程,再化为普通方程.
本节小结
1.当动点所满足的几何条件能直接用其坐标代入时,可用 直接法.(例1)
2.直接法的另一种形式称为定义法,即已知曲线的类型和 位置,可设出曲线方程,利用待定系数法求解.(例2)
3.当所求动点的运动很明显地依赖于一已知曲线上的动 点的运动时,可利用代入法,其关键是找出两动点的坐 标的关系,这要充分利用题中的几何条件.(例3)
例3:设AB是圆x2+y2=1的一条直径,以AB为直角边,B为直角顶点,逆
时针方向作等腰直角三角形ABC,当AB转动时,求点C的轨迹.
[思路分析]本题中的动点C满足两个条 件:BC⊥BA,|BC|=|BA|,无论用哪一个都不
C
能直接得出点C的方程,因此要另辟他径.
y B
仔细分析题意,点C的运动依赖于点B的运
平分线为y轴.(哪一种更好呢?)由 M为准线,N为焦点,很显然选择 标准方程y2=2px(p>0).下面的关键
是求出p的值,而ΔAMN为锐角三角
形及|BN|=6又起什么作用呢?请大
家认真思考.
本题答案:y2 =8x (1≤x≤4,y>0)
瓜中士也跃耍着功夫像菜刀般的怪影一样朝壮扭公主狂抓过来壮扭公主骤然像珊瑚红色的悬筋遗址狐一样猛叫了一声,突然玩了一个独腿狂舞的特技神功,身上眨眼间生出 了三只很像飘带一样的深紫色脑袋。接着搞了个,醉狐榔头翻三百六十度外加鸟喝锯片旋三周半的招数!紧接着把有着无穷青春热情的胸部耍了耍,只见二道忽亮忽暗的酷
动点轨迹[下学期]江苏教育出版社(新编201910)
![动点轨迹[下学期]江苏教育出版社(新编201910)](https://img.taocdn.com/s3/m/046f497f10a6f524ccbf85e9.png)
B
x C
角的补角,因而tgB、tgC都可以用斜率
来表示.这样可直接写出顶点A的方程,
接下来的工作就是化简方程和判断轨迹
Hale Waihona Puke 是何种曲线,必要时可进行讨论.
本题答案:轨迹方程为 x2/a2 +y2/ta2 =1 (x≠+-a)
.当0<t<1或t>1时,轨迹为椭圆;当t =1时,轨迹为圆;当t<0 时,轨迹为双曲线.
[思路分析]本题中的动点C满足两个条
C
件:BC⊥BA,|BC|=|BA|,无论用哪一个都不
能直接得出点C的方程,因此要另辟他径.
仔细分析题意,点C的运动依赖于点B的运
动(A也是这样),因而可以用点C的坐标来 表示点B的坐标,又点B在已知曲线上运动, A
数学高考专题复习
主讲人:朱俊杰
圆锥曲线回顾
例1:已知ΔABC底边BC的长为2a(a>0),又知tgBtgC=t(t≠0).(a,t均为常 数).求顶点A的轨迹.
[思路分析]:首先建立适当的坐标系,设出
y A
动点A及定点B、C的坐标,如何将tgB、
tgC坐标化是本题的关键.由图易知∠B 是直线AB的倾斜角,∠C是直线AC的倾斜
y B
A
平分线为y轴.(哪一种更好呢?)由 M 题设可知曲线段C为抛物线的一部
N L2 x
分,L1为准线,N为焦点,很显然选择 标准方程y2=2px(p>0).下面的关键
是求出p的值,而ΔAMN为锐角三角
形及|BN|=6又起什么作用呢?请大
家认真思考.
本题答案:y2 =8x (1≤x≤4,y>0)
例3:设AB是圆x2+y2=1的一条直径,以AB为直角边,B为直角顶点,逆 时针方向作等腰直角三角形ABC,当AB转动时,求点C的轨迹.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对一类动点路径长度问题的探究
一、真题再现
如图 1 所示,在矩形ABCD 中,4AB =,30DCA ∠=︒,点F 是对角线AC 上的一个动点,连结DF .以DF 为斜边作30DCA ∠=︒的Rt DEF ,使点E 和点A 位于DF 两侧,点F 从点A 到点C 的运动过程中,点E 的运动路径长是 .
这是一道求动点轨迹长间题.这一类问题通常是寻找第二个动点的起点和终点,再由全等或者相似得以解决.那么,动点轨迹长问题的本质是什么?怎样才能让这类问题的解决思路自然生成呢?
二、变式思考
问题 如图2,等边ABC ∆的边长为4 cm.动点D 从点B 出发,沿射线BC 方向移动,以AD 为边作等边ADE ,在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.
分析 如图2,连结GE .由ABD 和ACE 全等,可得到BD CE =,则点D 运动的路径长就是点E 运动的路径长,即路径长为4.
变式1 如图3,等边ABC ∆的边长为4 cm.动点D 从点B 出发,沿射线BC 方向移动,以AD 为边作等腰ADE ,且120DAE ∠=︒.在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.
分析 变式1是将“问题”中的等边ADE 改成等腰三角形,且顶角为120°,我们只须将AB 绕A 点逆时针旋转120°得到'AB ,连结'B E (如图3),可以证明ABD 和'AB E 全等,从而点D 运动的路径长就是点E 运动的路径长,即路径长为4.
变式2 如图4,等边ABC ∆的边长为4 cm.动点D 从点B 出发,沿射线BC 方向移动,以AD 为边作Rt ADE ,且30E ∠=︒.在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.
分析 变式2是将“问题”中的等边ADE 改为Rt ADE ,且30E ∠=︒.由3AE AD =,我们将AB 绕A 点逆时针旋转90°,并且扩大到AB 的3倍,得到'AB ,连结'B E (如图4).可以证明'ABD AB E ,且相似比为1:3,从而点E 运动的路径长就是点D 运动的路径长的3倍,即路径长为43.
变式3 如图5,ABC ∆中,4BC =cm.动点D 从点B 出发,沿射线BC 方向移动,2AD AE =且DAE ∠为定角. 在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.
分析 变式3将“问题”中的等边三角形改为普通三角形,4BC =不变,DAE ∠大小确定,而2AD AE =.我们可以将AB 绕点A 逆时针旋转DAE ∠的度数,并且长度缩小到原来的一半,得到'AB ,连结'B E (如图5).可以证明'ABD AB E ,且相似比为2: 1,从而点E 运动的路径长也就是点D 运动的路径长的一半,即路径长为2.
三、数学模型
如图6,点C 是定点,,B A 是动点。
若BC kAC =,当点B 在直线MN 上运动时,点B 运动的路径长是点A 运动路径长的k 倍.
模型特点 一静两动比恒定.
运用此模型可以轻松解决2019年贵阳市中考数学第15题。
易知2DF DE =,所以点E 运动路径长为点F 运动路径长的一半.又易得AC 长,所以点E 运动路径长为AC 的一半.
评注 这道中考题突出了对学生数学思维能力的培养,较好地体现了几何问题的解决要紧扣基本模型.
四、推广应用
例1 如图7,,B C 是圆的直径的两个端点,且4BC =BC=4cm ,A 是BC 上半圆上一定点.动点D 从点B 出发,沿BC 弧方向移动,以AD 为斜边作Rt ADE ,且30ADE ∠=︒.在点D 从点B 开始移动至点C 的过程中,求点E 移动的路径长.
分析 因为2AD AE =,而点D 的运动路径为半圆,且长为2π,所以点E 的运动路径长为π.
例2 如图8,正方形ABCD 的边长为2.动点E 从点A 出发,沿边AB BC -向终点C 运动,以DE 为边作正方形DEFG (点,,,D E F G 按顺时针方向排列),直接写出整个运动过程中,点F 经过的路径长.
分析易知2DF DE =.又点E 运动路径长为4,所以点F 运动路径长为2.
例3 如图9,点A 在反比例函数6y x -=
(0x <)的图象上移动,连结OA .作Rt BOA ,使B 点在第一象限,并满足90AOB ∠=︒,30BAO ∠=︒.在点A 的移动过程中,试确定点A 与点B 运动路径长之间的关系,以及点B 形成的图象所对应的函数表达式. 分析 易知3OA OB =,所以点A 和点B 运动路径长之比为3:1.而反比例函数的反比例系数的绝对值比为面积比,所以反比例系数的绝对值比为3:1.又B 点在第一象限运动,所以B 形成的图象所对应的函数表达式为2y x
=.
五、结束语
通过探究,我们可以得到这一类动点轨迹长问题的数学模型与解题策略。
归结为以下三点:
(1)两动点与静点所连线段的角度决定运动的位置;
(2)线段的比值决定运动路径的长度;
(3)第一个动点运动的轨迹决定第二个动点运动的轨迹形状.。
