物流管理定量分析方法练习题
精编国家开放大学电大专科《物流管理定量分析方法》2021期末试题及答案(试卷号:2320)

家开放大学电大专科《物流管理定量分析方法》2021期末试题及答案(试卷号:2320 )一、单项选择题(每小题4分,共20分)1. ________________________ 若某物资的总供应量 ______________ 总需求量,则可增设一个虚 ,其供应量取总供应量与总需求量的差额,并取各产地到该销地的运价为0,可将供不应求运输问题化为供求平 衡运输问题。
( )A.大于,销地B.小于,产地C.等于,产销地D.不等于,产销地2. 某物流公司下属企业生产甲、乙两种产品,要用A,B,C 三种不同的原料,已知每生产 一件产品甲,需用三种原料分别为1,1,0单位;生产一件产品乙,需用三种原料分别为1,2,1 单位。
每天A,B,C 三种原料供应的能力分别为6,8,3单位。
又知,销售一件产品甲,企业可 得利润3万元;销售一件产品乙,企业可得利润4万元。
原料B 的限制条件是( )。
A ・HI +2O :2<8B. JCI + X 2^6D. 3xi +4Z 2<17fl -213. 设人= ,根据逆矩阵的定义,判断逆矩阵A-】=()o0 1 ■ ■ ri _2] A. 0 1■ 一「1 °1 D.一2 14. 设函数/(z )在z 。
的某个邻域内有定义,如果对于该邻域内任何异于z 。
的1都有/(x )</(x 0)成立,则称f (工。
)为/愆)的( )。
A.极大值点B.极小值点C.极小值D.极大值5.某物品运输量为q 单位时的边际成本为MC (q ) = 2q + 3(单位:万元/单位),已知固定 成本为2万元,则运输量从1单位增加到2单位时成本的增量()。
A. (2q + 3)dq J 2D.j :MC(g)dq + C(0)C. 了2<3ri (T B.2 1ri 2] c. 0 1B. (2q + 3)dqC ・ j :(2g + 3)dq6. 已知矩阵人= 0 2,求:AB T .1 07. 设了 =&3 +4)(e x — lax),求:/。
《物流管理定量分析方法》复习练习

《物流管理定量分析方法》复习练习————————————————————————————————作者:————————————————————————————————日期:《物流管理定量分析方法》复习练习一、单项选择题(每小题4分,共20分)1. 若某物资的总供应量小于总需求量,则可增设一个( ),其供应量取总需求量与总供应量的差额,并取该产地到各销地的单位运价为0,可将供不应求运输问题化为供求平衡运输问题。
(A ) 虚产地(B ) 虚销地(C) 需求量(D) 供应量2.某物流企业计划生产A ,B 两种产品,已知生产A 产品1公斤需要劳动力7工时,原料甲3公斤,电力2度;生产B 产品1公斤需要劳动力10工时,原料甲2公斤,电力5度。
在一个生产周期内,企业能够使用的劳动力最多6300工时,原料甲2124公斤,电力2700度。
又已知生产1公斤A ,B 产品的利润分别为10元和9元.为建立能获得最大利润的线性规划模型,设生产A 产品1x 公斤,生产B 产品2x 公斤,则对于原料甲,有如下约束条件( ).(A) 31x +22x =2124 (B) 31x +22x ≤2124 (C ) 31x +22x ≥2124(D) 31x +22x ≤63003.设⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=413021,430421B A ,则 B A T +=( ).(A) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--831650(B ) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡412314 (C)⎥⎦⎤⎢⎣⎡--815360(D)⎥⎦⎤⎢⎣⎡1344214。
设某公司运输某物品的总成本(单位:百元)函数为C (q)=500+2q +2q ,则运输量为100单位时的边际成本为( )百元/单位。
(A ) 202(B ) 107(C ) 10700(D ) 7025. 已知运输某物品q 吨的边际收入函数(单位:元/吨)为MR (q )=100-2q,则运输该物品从100吨到200吨时收入的增加量为( )。
精编国家开放大学电大专科《物流管理定量分析方法》2022期末试题及答案(试卷号:2320)

国家开放大学电大专科《物流管理定量分析方法》2022期末试题及答案(试卷号:2320)盗传必究一、单项选择题(每小JS 4分.共20分)1.若某物贵的®供应崎大于拄需求fit .可增设一个虚钥地,箕需求U 取忌供应lit 与总需 求SJ 的差额.井取各产地到虽辑电的单位运价为。
,则可将( )运输问题化为供求平街运输A. 供不戍求 C ・供过于求2. 某物流公诃有三种化学原14八|・A,.A,.每公斤他料A,含B,.B, , B,三种化学成分 的含量分别为0.?公斤、0.2公斤和O ・I 公斤i 每公斤原料A,含B, ,玮的含ift 分别为0.1 公斤・0.3公斤和0.6公斤,每公斤原料A,含B L K.B,的含if 分别为。
・3公斤・0.4公斤和 。
3公斤.何公斤原料A ),A,・A,的成本分别为50。
元.300元和400元.今需要改成份至 少100公斤成份至少50公斤.B,成份至少80公斤.为列出使成本最小的线性规划模型. 设需要原料A,,A,・A,的数fit 分别为与公斤、⑥公斤和工,公斤.则化苏成分出应漪足的约 束条件为( ).A. 0. 2xi + 0. 3x s + 0. 4xi < 100B. 0. 2xi + 0. 3x, + 0. 4x> > 100C. 0. 2jr, + 0. 3x« +。
. 4x t = 100D. 0. 2x> +0. 3x t + 0.4x> < 100 3. 下列矩阵中,《)是单位矩阵.4.设某公司运输某物品的怠收入(单位,千元)函数为R (g )= IOOy-0. I 矿.则运输信为 100革位时的边际收入为(。
千元/箪位.D. 89005.由曲我.宜线i=1与工=2.以及h 轴围成的曲边榔形的面根表示为().评卷人a 供需乎衡 n.供求平衡二,计>!■(*小・9分.共27分)冲卷人.牝 A + ”7. tft +8. H 神定机分J"l+3/ + e ・)dr三.M«M (9小BI9分.共27分)•试国出用MATLAB 软件计算短牌淼速式人-'+%『的命令.2,伏号出用MATl.ABttfUl W*ft >-a\ln (9 + yZT4 )的二阶导数的命令讷句.11. 试乌出JU MATLAB 牧件H 岸不定枳分的j : 3・《/ + L )<Lr 翁令谓句.衍分评幼人四,应用■(第I^ K "分.第13 ■ 8分.共26分)12,某公司从A.B >C 三个产地置输基物费MI dl.ni 三个M 地.各产地的供应■(第位I 晚),缶tn 地的需求欢(熊位I 吨)及各产业到汨。
物流管理定量分析方法试卷(答案)

1. 若某物资的总供应量大于总需求量,则可增设一个( A ),其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问题。
(A) 虚销地 (B) 虚产地 (C) 需求量 (D) 供应量2.某物流企业用甲、乙两种原材料生产A ,B ,C 三种产品。
企业现有甲原料30吨,乙原料50吨。
每吨A 产品需要甲原料2吨;每吨B 产品需要甲原料1吨,乙原料2吨;每吨C 产品需要乙原料4吨。
又知每吨A ,B ,C 产品的利润分别为3万元、2万元和0.5万元。
为列出获得最大利润的线性规划问题,设生产A ,B ,C 三种产品的产量分别为x 1吨、x 2吨和x 3吨,则目标函数为( D )。
(A) max S =30x 1+50x 2 (B) min S =3x 1+2x 2+0.5x 3 (C) min S =30x 1+50x 2 (D) max S =3x 1+2x 2+0.5x 33. 设⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=721,7421x B x A ,并且A =B ,则x =( B )。
(A) 1 (B) 2(C) 3 (D) 44. 设某公司运输某物品的总成本(单位:百元)函数为C (q )=500+2q +q 2,则运输量为100单位时的总成本为( C )百元。
(A) 202 (B) 107 (C) 10700 (D) 7025. 已知运输某物品q 吨的边际成本函数(单位:元/吨)为MC(q )=200+5q ,则运输该物品从100吨到300吨时成本的增加量为( D )。
(A) 100300(2005)d q q +⎰ (B) (2005)d q q +⎰(C)300100(2005)d (0)q q C ++⎰(D)300100(2005)d q q +⎰6. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=101201 , 4321B A ,求:AB T ⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=41032411100214321T AB7. 设5e xy x =,求:y '5545()e (e )(5)e x x x y x x x x '''=⋅+⋅=+8. 计算定积分:311(e )d x x x-⎰333111(e )d (e ln ||)e e ln3|x xx x x -=-=--⎰ 9. 试写出用MA TLAB软件计算函数y = >>clear;>>syms x y;>>y=(3+sqrt(x))/log(x); >>dy=diff(y)10. 试写出用MATLAB 软件计算定积分21||e d x x x -⎰的命令语句。
物流管理定量分析方法练习题

4.设线性方程组 ⎨x 2 + x 3 = 2 ,则下列( )为其解。
⎩ ⎢x ⎥ = ⎢ 0 ⎥ ⎢x ⎥ = ⎢ 1 ⎥ ⎢x ⎥ = ⎢1⎥ ⎢x ⎥ = ⎢ 1 ⎥⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦物流管理定量分析方法 练习题一、单项选择题1.某物流公司有三种化学原料 A1,A2,A3。
每公斤原料 A1 含 B1,B2,B3 三种化学成分 的含量分别为 0.7 公斤、0.2 公斤和 0.1 公斤;每公斤原料 A2 含 B1,B2,B3 的含量分别 为 0.1 公斤、0.3 公斤和 0.6 公斤;每公斤原料 A3 含 B1,B2,B3 的含量分别为 0.3 公斤、 0.4 公斤和 0.3 公斤。
每公斤原料 A1,A2,A3 的成本分别为 500 元、300 元和 400 元。
今 需要 B1 成分至少 100 公斤,B2 成分至少 50 公斤,B3 成分至少 80 公斤。
为列出使总成本 最小的线性规划模型,设原料 A1,A2,A3 的用量分别为 x1 公斤、x2 公斤和 x3 公斤,则 目标函数为()。
A .min S =500x1+300x2+400x3B .min S =100x1+50x2+80x3C .maxS =100x1+50x2+80x3 D .max S =500x1+300x2+400x32.用 MATLAB 软件计算方阵 A 的逆矩阵的命令函数为()。
A . int(a)B . int(A)C .inv(a)D .inv(A)3.设 A 是 5 ⨯ 4 矩阵, I 是单位矩阵,满足 AI = A ,则 I 为()阶矩阵。
A .2B .3C .4D .5⎧x 1 + x 2 = -1 ⎪ ⎪x 1 + x 3 = -1A .C . ⎡ x 1 ⎤ ⎡ 1 ⎤ ⎢ 2⎥ ⎢ ⎥ ⎢ x 3 ⎥ ⎢- 2⎥⎡ x 1 ⎤ ⎡0⎤ ⎢ 2 ⎥ ⎢ ⎥⎢ x 3 ⎥ ⎢1⎥B .D . ⎥⎢ 2 ⎥ ⎢ ⎥ ⎢ x 3 ⎥ ⎢ 0 ⎥⎡x1⎤⎡-2⎤⎡x1⎤⎡-2⎤5.设运输某物品的成本函数为C(q)=q2+50q+2000,则运输量为100单位时的成本为()。
物流管理定量分析方法试题答案

物流管理定量分析⽅法试题答案《物流管理定量分析⽅法》期末复习题⼀、线性规划法 1. 设??-=?---=011101,132031B A ,求:AB T .解:??--=-?---=1121011011132031T AB2.已知矩阵-=??--=?-=2101111412210101C B A ,,,求:AB +C.解:??-=??-+??-=-+---=+3702210116012101111412210101C AB 3.已知矩阵??--=--=131211203012011B A ,,求:AB.解:??--=??--??--=531421131211203012011AB 4. 已知矩阵=--=600540321201110011B A ,,求:B T A. 解:--=????--????=1723 422011201110011653042001T A B 5.设110012212601A B ??-==-,,求:(1) 2B T -A ;(2) AB .解:12000122121126TBA --=--240001241242126164-??=-=??---??6. 已知矩阵??=??--=600540321201110011B A ,,求:AB.解: ??--=600540321201110011AB7. 已知矩阵=-=321212113101012111B A ,,求:AB . 解:=??-=434014646321212113101012111AB ⼆、导数⽅法1.设y =(x 2-3) ln x ,求:y '解:xx x x x x x x y 3ln 2)(ln )3(ln )3(22-+='?-+?'-=' 2.设y =(1+x 3) ln x ,求:y '解:22331ln 3)(ln )1(ln )1(x xx x x x x x y ++='?++?'+=' 3.设y =(1+x 2)ln x ,求:y '解:xx x x x x x x y 2221ln 2))(ln 1(ln )1(++='++'+='4.设xx y e 4=,求:y '解:x x x x x x x y )e 4()e (e )(4344+='?+?'=' 5.设31ln xxy +=,求:y ' 解:23232333)1(ln 31)1()1()(ln )1()(ln x x x x x x x x x x y +-+=+'+?-+?'=' 6.设xy x+=1e ,求:y '解:22)1(e )1()1(e )1()e (x x x x x y xx x +=+'+-+'='7.设y =x 3ln x ,求:y ' 解:2233ln 3)(ln ln )(x x x x x x x y +='?+?'='三、微元变化累积1.计算定积分:解:25e 3)e 321(d )e 3(|10210-=+=+?x xx x x 2.计算定积分:+312d )2(x xx解:3ln 2326|)|ln 231(d )2(|313312+=+=+?x x x x x3.计算定积分:?+103d )e 24(x x x解:1e 2)e 2(d )e 24(|14103-=+=+?x x x x x4.计算定积分:?+13d )e 2(x x x解:47e 2)e 241(d )e 2(|104103-=+=+?x x x x x 5.计算定积分:?+2x解:2ln 3|)|ln (d )12(|21221+=+=+?x x x xx6..计算定积分:?+21d )1e (x xx解:2ln e e |)|ln e (d )1e (22121|+-=+=+?x x x xx7.计算定积分:?+212d )1(x xx解:2ln 37|)|ln 31(d )1(|213212+=+=+?x x x x x四、表上作业法1.某公司从三个产地A 1,A 2,A 3运输某物资到三个销地B 1,B 2,B 3,各产地的供应量(单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表所⽰:运输平衡表与运价表(1)在下表中写出⽤最⼩元素法编制的初始调运⽅案:运输平衡表与运价表(2)检验上述初始调运⽅案是否最优,若⾮最优,求最优调运⽅案,并计算最低运输总费⽤。
物流管理定量分析方法练习题

物流管理定量分析方法练习题物流管理定量分析方法是一种通过对物流相关数据进行统计分析,以评估和优化物流过程的方法。
这种方法可以帮助企业更好地理解物流活动的成本、效率和质量,从而制定出更加有效的物流策略。
本练习题将介绍几种常见的物流管理定量分析方法,并通过案例形式进行实际操作。
某电商企业计划对仓库布局进行调整,希望通过定量分析方法评估不同布局方案的优劣。
该企业提供了以下资料:仓库布局方案:现有两种布局方案,分别为直线型和L型。
库存数据:过去一年内,库存总量为100万件,其中畅销商品占60%,滞销商品占20%,一般商品占20%。
仓储成本数据:现有仓储成本为每月10万元,希望通过调整布局降低成本。
客户需求数据:客户对不同商品的订单数量有一定差异,平均每个订单需要10件商品。
线性回归分析:使用线性回归模型分析库存数据和仓储成本之间的关系,预测不同布局方案下的仓储成本。
聚类分析:根据商品销售量和仓储成本等指标,对商品进行聚类分析,确定不同类别的商品对仓储成本的影响程度。
模拟分析:根据客户需求数据和不同商品的订单数量,模拟不同布局方案下的库存周转情况,评估库存积压和缺货情况。
(1)收集和整理数据:收集过去一年的库存数据和仓储成本数据,整理成适合线性回归分析的格式。
(2)构建线性回归模型:以仓储成本为因变量,以库存量为自变量,构建线性回归模型。
(3)模型拟合和检验:使用统计软件进行模型拟合和检验,分析模型是否具有统计学意义和实际意义。
(4)预测未来成本:根据模型预测不同布局方案下的仓储成本。
(1)数据预处理:对商品销售量和仓储成本等指标进行数据清洗和标准化处理。
(2)聚类分析:使用K-means聚类算法将商品分为不同的类别,根据聚类结果分析不同类别商品对仓储成本的影响程度。
(1)建立模拟模型:根据客户需求数据和不同商品的订单数量,建立模拟模型。
(2)模拟不同布局方案:根据不同布局方案,模拟库存周转情况。
(3)评估库存积压和缺货情况:比较不同布局方案的库存积压和缺货情况,评估不同方案的优劣。
#《物流管理定量分析方法》复习练习(11春)

《物流管理定量分析方法》复习练习一、单项选择题(每小题4分,共20分)1. 若某物资的总供应量小于总需求量,则可增设一个( ),其供应量取总需求量和总供应量的差额,并取该产地到各销地的单位运价为0,可将供不应求运输问题化为供求平衡运输问题。
(A) 虚产地(B) 虚销地(C) 需求量(D) 供应量2.某物流企业计划生产A ,B 两种产品,已知生产A 产品1公斤需要劳动力7工时,原料甲3公斤,电力2度;生产B 产品1公斤需要劳动力10工时,原料甲2公斤,电力5度。
在一个生产周期内,企业能够使用的劳动力最多6300工时,原料甲2124公斤,电力2700度。
又已知生产1公斤A ,B 产品的利润分别为10元和9元。
为建立能获得最大利润的线性规划模型,设生产A 产品1x 公斤,生产B 产品2x 公斤,则对于原料甲,有如下约束条件( )。
(A) 31x +22x =2124 (B) 31x +22x ≤2124 (C) 31x +22x ≥2124(D) 31x +22x ≤63003.设⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=413021,430421B A ,则B A T +=( )。
(A) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--831650(B) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡412314 (C)⎥⎦⎤⎢⎣⎡--815360(D)⎥⎦⎤⎢⎣⎡1344214. 设某公司运输某物品的总成本(单位:百元)函数为C (q)=500+2q +2q ,则运输量为100单位时的边际成本为( )百元/单位。
(A) 202(B) 107(C) 10700(D) 7025. 已知运输某物品q 吨的边际收入函数(单位:元/吨)为MR (q)=100-2q ,则运输该物品从100吨到200吨时收入的增加量为( )。
(A)⎰-200100d )2100(qq (B) ⎰-100200d )2100(q q(C) ⎰-qq d )2100( (D) ⎰-200100d )1002(qq6. 若某物资的总供应量( )总需求量,则可增设一个虚产地,其供应量取总需求量和总供应量的差额,并取该产地到各销地的单位运价为0,可将供不应求运输问题化为供求平衡运输问题。
2021国家开放大学电大专科《物流管理定量分析方法》期末试题及答案(试卷号:2320)

2021国家开放大学电大专科《物流管理定量分析方法》期末试题及答案(试卷号:2320)盗传必究一、单项选择题(每小题4分,共20分)1.若某物资的总供应量()总需求量,可增设一个虚销地,其需求量取总需求量与总供应量的差 额,并取各产地到该虚销地的单位运价为0,则可将供过于求运输问题化为供求平衡运输问题。
A.小于B.等于C.大于D.近似等于2. 某物流公司经过对近期销售资料分析及市场预测得知,该公司生产的甲、乙、丙三种产品,均为市场 紧俏产品,销售量一直持续上升、经久不衰。
今已知上述三种产品的单位产品原材料消耗定额分别为4公 斤、4公斤和5公斤;三种产品的单位产品所需工时分别为6台时、3台时和6台时。
另外,三种产品的利 润分别为400元/件、250元/件和300元/件。
由于生产该三种产品的原材料和工时的供应有一定限制,原 材料每天只能供应180公斤,工时每天只有150台时。
为列出使利润最大的线性规划模型,设生产产品甲、 乙、丙的产量分别为XM 牛、X 】件和X3件,则目标函数为()。
A. maxS = 400x1+250x2 + 300羽3. 设 A =A-1 C -2 D. 44.设某公司运输某物品q 吨的收入(单位,目元)滴数为.则运输量为 100单位时的边际收入为(〉百元/吨.A<800080 C. 20D. 一 205. 已知运输某物品?吨的边际收入函数〈单位:元,'吨>为,俩运输该将品从100吨到200吨时收入的塔加量为(•wo A. (3* — 100)d<7. C (10()—却)dq二、计算题(每小题9分,共27分)B. minS =400xi + 250x2+300x3C. maxS =4xi +4x2 + 5x3D. maxS =6xi +3X 2+6X 3,且 A)•ri»oB. (100 — 3q)dq J2QQ D .「二 1。
一:柯 gJ「一2 一5 3,B= .求:足一2打14 2 7.设 v = (4 + 2.r' )lw •求 1 B.计算定积分:p (3.r J 4-eO (Lz«三、编程题(每小题9分,共27分)X=BV 的命令语句.10. 试写出用MATLAB 软件什冒函数-=h )M + /l+H )的二阶导数的命令涪•如 11. 试与出用MATLAB 软件计•算不定积分x :e u dx 的命令沿句.,四、应用题(第12题8分,第13题18分,共26分)12. i 殳某公司平均位年需要某材料10000件.诙材料单价为10元/件.每件该材料每年的 库存捞为材群的价的20%.为减少库存费,分期分批进货.每次订货资为400元,假定该材料 的使用最均匀的•求该材料的轻济批量.13. 臬公司从三个产地A,B.CE 输某物资到三个销地1,11,01,各产地的供应量(单位'吨)・各精地的需求单位'吨〉及各产地到各销地的单位运价(单位:元/吨)如下表所示*运输平衡衰与运价表、、、销地I供应站IB |in A200 610 4 B600 II 14 8 16 C700 | 1028400 500 6001500《1〉在上表中写出用最小元素法编制的初始询运方案《用其它方法不计成绩),(2)检脸上述初始调运方案是否最优•若非最优,求最优调运方案.并计算最低运输总 贾用.试题答案及评分标准(仅供参考),Y =.4。
物流管理定量分析方法期末复习题

一、单项选择题单项选择题有5小题,每小题4分,共20分。
其中第1章、第3章、第4章各1题,第2章2题。
二、计算题计算题有3小题,每小题7分,共21分。
其中第2章、第3章、第4章各1题。
三、编程题编程题有2小题,每小题6分,共12分。
其中第3章、第4章各1题。
四、应用题应用题共47分。
其中第1章、第2章、第3章各1题。
模拟试题一、单项选择题(每小题4分,共20分)1. 若某物资的总供应量小于总需求量,则可增设一个( ),其供应量取总需求量与总供应量的差额,并取该产地到各销地的单位运价为0,可将供不应求运输问题化为供求平衡运输问题。
(A) 虚产地 (B) 虚销地 (C) 需求量 (D) 供应量因为总供应量小于总需求量,即供不应求,应增设一个虚产地,该虚产地的供应量取总需求量与总供应量的差额,该虚产地到各销地的单位运价为0,便可将该不平衡运输问题化为平衡运输问题,故应选A 。
2.某物流企业计划生产A ,B 两种产品,已知生产A 产品1公斤需要劳动力7工时,原料甲3公斤,电力2度;生产B 产品1公斤需要劳动力10工时,原料甲2公斤,电力5度。
在一个生产周期内,企业能够使用的劳动力最多6300工时,原料甲2124公斤,电力2700度。
又已知生产1公斤A ,B 产品的利润分别为10元和9元。
为建立能获得最大利润的线性规划模型,设生产A 产品公斤,生产B 产品公斤,则对于原料甲,有如下约束条件( )。
(A) 3+2=2124 (B) 3+2≤2124 (C) 3+2≥2124 (D) 3+2≤6300生产A 产品x1公斤,需要原料甲3x1公斤;同时,生产B 产品x2公斤,需要原料甲2x2公斤;一个周期内,原料甲能够使用的数量最多为2124公斤。
因此,原料甲应满足:3x1+2x2≤2124,故B 正确。
3.设⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=413021,430421B A ,则 B A T +=( )。
电大《物流管理定量分析方法》国家开放大学历届试题含答案

1
、 ‘ ,
0
, ,
B
同r I
M
25叫 u‘ n h u
l i l -」
r j
仁 } (
3ZT
求
FZ
求
qJA 十 BT
0
0
算 积分
b d,
三、编程题{每小题 9 分,共 27 分)
,2
9. 设 A=11
•1
1 3 -1
,2
20i , B= 卜 1
2 - 2J
L3
算 X=YB 的命令语句。
II
01 , Y = A~l ,试写出用 MATLAB 软件计
12 分 14 分
已出现负检验数,方案需要调整,调整量为 8=500 吨。 调整后的第二个调运方案如下表所示:
运输平衡表与运价表
二♂变 I
E
皿
供应量
I
EE
A
700
200
900
6
9 10
B
500 100
600
7
3
8
C
需求量
500 700 500 800
500 2000
4
6
5
求第二个调运方案的检验数:
=3x 2 1nx 十三 +X2 Z
J: I: 8. (eI 一川x = (eX - x 2)
2019 年 1 月
5. C
9分 5分 9分 5分
=e2 - 5
三、编程题(每小题 9 分,共 27 分) 9. >>cl 巳 ar
>>A=[2 3 -1;1 2 0; 一 1 2 -2J; >>B=[2 1; 一 1 0;3 1J; >>Y=inv(A);
物流管理定量分析方法试题答案

物流管理定量分析方法试题答案IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】《物流管理定量分析方法》期末复习题一、线性规划法 1. 设⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=011101,132031B A ,求:AB T . 解:⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡---=1121011011132031T AB 2.已知矩阵⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-=2101111412210101C B A ,,,求:AB +C. 解:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡-=+3702210116012101111412210101C AB 3.已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=131211203012011B A ,,求:AB. 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=531421131211203012011AB 4. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011B A ,,求:B T A. 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1723422011201110011653042001T A B 5.设110012212601A B ⎡⎤-⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,,求:(1) 2B T -A ;(2) AB . 解:12000122121126TB A -⎡⎤⎡⎤-=-⎢⎥⎢⎥-⎣⎦⎣⎦240001241242126164-⎡⎤⎡⎤⎡⎤=-=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦6. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011B A ,,求:AB. 解: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011AB 7. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=321212113101012111B A ,,求:AB .解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=434014646321212113101012111AB 二、导数方法1.设y =(x 2-3) ln x ,求:y '解:xx x x x x x x y 3ln 2)(ln )3(ln )3(22-+='⋅-+⋅'-=' 2.设y =(1+x 3) ln x ,求:y '解:22331ln 3)(ln )1(ln )1(x xx x x x x x y ++='⋅++⋅'+=' 3.设y =(1+x 2)ln x ,求:y '解:xx x x x x x x y 2221ln 2))(ln 1(ln )1(++='++'+='4. 设xx y e 4=,求:y '解:x x x x x x x y )e 4()e (e )(4344+='⋅+⋅'=' 5.设31ln xxy +=,求:y ' 解:23232333)1(ln 31)1()1()(ln )1()(ln x x x x x x x x x x y +-+=+'+⋅-+⋅'='6.设xy x+=1e ,求:y '解:22)1(e )1()1(e )1()e (x x x x x y xx x +=+'+-+'='7.设y =x 3ln x ,求:y '解:2233ln 3)(ln ln )(x x x x x x x y +='⋅+⋅'='三、微元变化累积 1.计算定积分:⎰+1d )e 3(x x x解:25e 3)e 321(d )e 3(|1021-=+=+⎰x x x x x 2.计算定积分:⎰+312d )2(x xx解:3ln 2326|)|ln 231(d )2(|313312+=+=+⎰x x x x x3.计算定积分:⎰+103d )e 24(x x x 解: 1e 2)e 2(d )e 24(|1413-=+=+⎰x x x x x4.计算定积分:⎰+13d )e 2(x x x解:47e 2)e 241(d )e 2(|1413-=+=+⎰x x x x x5.计算定积分:⎰+21d )12(x xx解:2ln 3|)|ln (d )12(|21221+=+=+⎰x x x xx6..计算定积分:⎰+21d )1e (x xx解:2ln e e |)|ln e (d )1e (22121|+-=+=+⎰x x xx x7.计算定积分:⎰+212d )1(x xx解:2ln 37|)|ln 31(d )1(|213212+=+=+⎰x x x x x 四、表上作业法1.某公司从三个产地A1,A2,A3运输某物资到三个销地B1,B2,B3,各产地的供应量(单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表所示:(1)在下表中写出用最小元素法编制的初始调运方案:(2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总费用。
《物流管理定量分析方法》模拟试题

4.设A=⎢⎣4-x7⎦B=⎢⎣x7⎦《物流管理定量分析方法》模拟试题一、单项选择题(每小题3分,共18分)1.若某物资的总供应量()总需求量,可增设一个虚销地,其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,则可将该不平衡运输问题化为平衡运输问题。
(A)等于(B)小于(C)大于(D)不超过2.某物资调运问题,在用最小元素法编制初始调运方案过程中,第一步安排了运输量后,其运输平衡表(单位:吨)与运价表(单位:百元/吨)如下表所示:运输平衡表与运价表销地产地B1B2B3供应量B1B2B3A113243A278128A38151812需求量8171035第二步所选的最小元素为()。
(A)1(B)2(C)3(D)43.某物流公司有三种化学原料A1,A2,A3。
每斤原料A1含B1,B2,B3三种化学成分的含量分别为0.7斤、0.2斤和0.1斤;每斤原料A2含B1,B2,B3的含量分别为0.1斤、0.3斤和0.6斤;每斤原料A3含B1,B2,B3的含量分别为0.3斤、0.4斤和0.3斤。
每斤原料A1,A2,A3的成本分别为500元、300元和400元。
今需要B1成分至少100斤,B2成分至少50斤,B3成分至少80斤。
为列出使总成本最小的线性规划模型,设原料A1,A2,A3的用量分别为x1斤、x2斤和x3斤,则化学成分B2应满足的约束条件为()。
(A)0.2x1+0.3x2+0.4x3≥50(B)0.2x1+0.3x2+0.4x3≤50(C)0.2x1+0.3x2+0.4x3=50(D)min S=500x1+300x2+400x3⎡12⎤⎥,⎡12⎤⎥,并且A=B,则x=()。
(A)4(B)3(C)2(D)15.设运输某物品的成本函数为C(q)=q2+50q+2000,则运输量为100单位时的成本为()。
(A)17000(B)1700(C)170(D)250C '(q )d q - C (0) ⎢0 A − →⎢1 ⎥⎥⎥6. 某产品的成本函数、收入函数、利润函数分别为 C (q ),R (q ),L (q ),则下列等式成 立的是( )。
2021国开大学电大专科《物流管理定量分析方法》期末试题及答案

国家开放大学电大专科《物流管理定量分析方法》期末试题及答案(试卷号:2320)2022盗传必究一、单项选择题(每小题4分,共20分)I .若某物资的也供应量小于总需求届.可增设一个虚产地,其()取总供应依与4需求量的差额.并取该产地到各销地的单位运价为。
.则可将供不应求运输同聘化为供求平衡运队虚产地C.虚情地2 .某桁流公司F 属企业欲制定生产AfOR 两种产品的生产计划.已知生产一件A 产品 需要原材料1吨、动力I 机位•生产设备3工时;生产一件R 产品需赛晚材料2吨、动力1单 位,生产设务I 丁•时.在-个生产周期内,可用原材料16吨,动力10中位、生产设备24 11时・ 每件A 产品利润3 "兀.每件B 产品利润4千元.为列出使利润最大的线悝规划模型,役牛 产A.B 的产默分别为工,和件,则生产设备应满足的约束条件为( 1.A. 3工(+工,<24 EL 3丁|+工:<24 C. 3士}+了*}24 D. 3J T| =243.下列《)是时称短阵.设某公司运输臬物品的总收入(单位,千元)函数为氏区)=1009—0.3矿・则运输量为100单位时的边际收入为(,千元/单位.A. 40D. 70005.已知运输某物品"吨的边际收入函数(单位:元/吨)为MR (g ) = IOO-3q •则送输该物 船从100吨到200吨时收入的增加量为().D.供应SIR. 60二.计算■(每小・9分.共27分)6.已知矩阵A =•牝 M + HA.(100 — 3q 〉心评卷入(100 — 3q)dg 100IOO)dgX-YB 的他令沿句.II.仗理出用 MATLAB分]'I x I b<Lr 的命今ift 句.四、应用■(第12 ■ 8分,11 13 ■ 18分,共26分)12.没烘公4V 均每年雷要菜材料<oooon.»«w*价为10元/件•符件成材#旬年的序存使为的网革价的2。
《物流管理定量分析方法》考试题

当前文档修改密码:8362839物流治理定量分析方法?重难点导学对?物流治理定量分析方法?课程重、难点内容的教学要求分为理解和熟练掌握、了解和掌握、明白和会三个层次。
教学建议:一、理解和熟练掌握:教师重点讲授,并指导学生在课上练习 二、了解和掌握:教师重点讲授,要求学生课后练习 三、明白和会:教师概括讲授,以学生自学为主第一章物资调运方案优化的表上作业法 1.熟练掌握用最小元素法编制的初始调运方案,并求出最优调运方案和最低运输总费用。
2.了解物资调运咨询题。
〔包括供求平衡运输咨询题、供过于求运输咨询题、供不应求运输咨询题〕第二章物资合理配置的线性 法 1.熟练掌握建立线性 模型的方法;熟练掌握线性 模型的标准形式以及矩阵表示;熟练掌握用MATLAB 软件求解线性 的编程咨询题。
2.熟练掌握矩阵的加减法、数乘、转置及乘法等运算。
3.掌握行简化阶梯形矩阵、二阶矩阵的逆和线性方程组一般解的概念。
第三章库存治理中优化的导数方法1.明白函数的概念;了解库存函数、总本钞票和平均函数、利润函数; 2.明白极限、连续的概念;了解导数的概念3.熟练掌握利用导数公式和导数四那么运算法那么计算导数的方法;4.熟练掌握用MA TLAB 软件计算导数,特别是计算二阶导数的编程咨询题; 5.了解边际的概念;熟练掌握求经济批量和最大利润的最值咨询题;第四章物流经济量的微元变化累积1.了解定积分的定义;了解微积分全然定理;了解原函数和不定积分的概念; 2.熟练掌握用积分全然公式和积分性质计算积分的直截了当积分法;要紧掌握积分性质及以下三个积分公式:c x a x x a a ++=+⎰111d 〔a ≠-1〕;c x x x+=⎰||ln d 1;c x x x +=⎰e d e ;3.熟练掌握用MA TLAB 软件计算积分的编程咨询题; 4.掌握求经济函数增量的咨询题。
典型例题例1设某物资要从产地A 1,A 2,A 3调往销地B 1,B 2,B 3,B 4,运输平衡表〔单位:吨〕和运价表〔单位:百元/吨〕如下表所示:运输平衡表与运价表〔1〕用最小元素法编制的初始调运方案,〔2〕检验上述初始调运方案是否最优,假设非最优,求最优调运方案,并计算最低运输总费用。
《物流管理定量分析方法》形考作业(第三版B5)
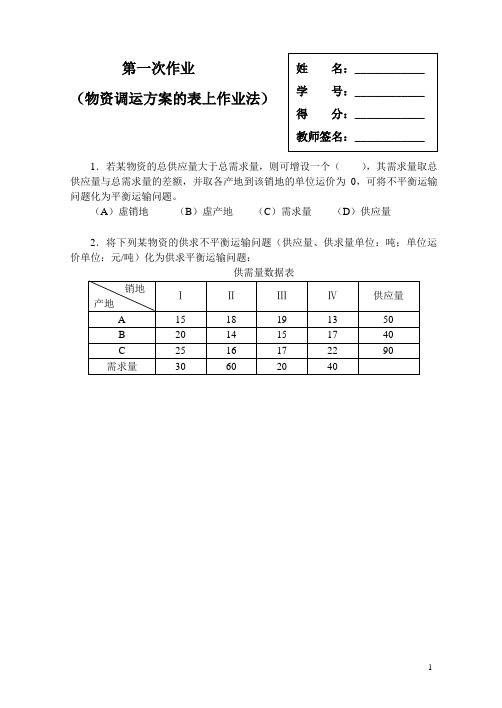
(物资调运方案的表上作业法)1.若某物资的总供应量大于总需求量,则可增设一个(),其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问题。
(A)虚销地(B)虚产地(C)需求量(D)供应量2.将下列某物资的供求不平衡运输问题(供应量、供求量单位:吨;单位运价单位:元/吨)化为供求平衡运输问题:3.若某物资的总供应量()总需求量,则可增设一个虚产地,其供应量取总需求量与总供应量的差额,并取该产地到各销地的单位运价为0,可将供不应求运输问题化为供求平衡运输问题。
(A)大于(B)小于(C)等于(D)大于等于4.将下列某物资的供求不平衡运输问题(供应量、供求量单位:吨;运价单位:元/吨)化为供求平衡运输问题:5.甲、乙两产地分别要运出物资1100吨和2000吨,这批物资分别送到A、B、C、D四个仓库中收存,四仓库收进的数量分别为100吨、1500吨、400吨和1100吨,仓库和发货点之间的单位运价如下表所示:运价表单位:元/吨费用最小。
运价表(单位:元/吨)如下表所示:试用最小元素法编制初始调运方案,并求最优调运方案。
{与旧版不同}吨)与运价表(单位:元/吨)如下表所示:试问应怎样调运才能使总运费最省?{与旧版不同}8.有一运输问题,涉及三个起始点A1、A2、A3和4个目的点B1、B2、B3、B4,三个起始点的供应量分别为50吨、50吨、75吨,4个目的点的需求量分别为40吨、55吨、60吨、20吨。
运输平衡表及各起始点与目的点之间的距离(单位:公里)如下所示:假设每次装车的额外费用不计,运输成本与所行驶的距离成正比,试求最优的调运方案,并求最小吨公里数。
{与旧版不同}第二次作业(资源合理配置的线性规划法)(一) 填空题1.设⎥⎦⎤⎢⎣⎡-=7321x A ,⎥⎦⎤⎢⎣⎡=721x B ,并且B A =,则=x _______________。
2.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=430421A ,⎥⎦⎤⎢⎣⎡--=413021B ,则=+B A T_______________。
物流管理定量分析方法试题答案

《物流管理定量分析方法》期末复习题一、线性规划法 1. 设⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=011101,132031B A ,求:AB T . 解:⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡---=1121011011132031T AB2.已知矩阵⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-=2101111412210101C B A ,,,求:AB +C.解:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡-=+3702210116012101111412210101C AB3.已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=131211203012011B A ,,求:AB.解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=531421131211203012011AB4. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011B A ,,求:B TA. 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1723422011201110011653042001T A B 5.设110012212601A B ⎡⎤-⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,,求:(1) 2B T -A ;(2) AB .解:12000122121126TBA -⎡⎤⎡⎤-=-⎢⎥⎢⎥-⎣⎦⎣⎦240001241242126164-⎡⎤⎡⎤⎡⎤=-=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦6. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011B A ,,求:AB.解: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011AB7. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=321212113101012111B A ,,求:AB . 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=434014646321212113101012111AB 二、导数方法1.设y =(x 2-3) ln x ,求:y '解:xx x x x x x x y 3ln 2)(ln )3(ln )3(22-+='⋅-+⋅'-=' 2.设y =(1+x 3) ln x ,求:y '解:22331ln 3)(ln )1(ln )1(x xx x x x x x y ++='⋅++⋅'+=' 3.设y =(1+x 2)ln x ,求:y '解:xx x x x x x x y 2221ln 2))(ln 1(ln )1(++='++'+='4. 设xx y e 4=,求:y '解:xx x x x x x y )e 4()e (e )(4344+='⋅+⋅'='5.设31ln xxy +=,求:y ' 解:23232333)1(ln 31)1()1()(ln )1()(ln x x x x x x x x x x y +-+=+'+⋅-+⋅'=' 6.设xy x+=1e ,求:y '解:22)1(e )1()1(e )1()e (x x x x x y xx x +=+'+-+'='7.设y =x 3ln x ,求:y ' 解:2233ln 3)(ln ln )(x x x x x x x y +='⋅+⋅'='三、微元变化累积1.计算定积分:⎰+10d )e3(x x x解:25e 3)e 321(d )e 3(|10210-=+=+⎰x x x x x 2.计算定积分:⎰+312d )2(x xx解:3ln 2326|)|ln 231(d )2(|313312+=+=+⎰x x x x x3.计算定积分:⎰+103d )e 24(x x x解:1e 2)e 2(d )e 24(|1413-=+=+⎰xxx x x4.计算定积分:⎰+103d )e 2(x xx解:47e 2)e 241(d )e 2(|104103-=+=+⎰x x x x x 5.计算定积分:⎰+21d )12(x xx解:2ln 3|)|ln (d )12(|21221+=+=+⎰x x x xx6..计算定积分:⎰+21d )1e (x xx解:2ln e e |)|ln e (d )1e (22121|+-=+=+⎰x x x xx7.计算定积分:⎰+212d )1(x xx解:2ln 37|)|ln 31(d )1(|213212+=+=+⎰x x x x x四、表上作业法1.某公司从三个产地A 1,A 2,A 3运输某物资到三个销地B 1,B 2,B 3,各产地的供应量(单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表所示:运输平衡表与运价表(1)在下表中写出用最小元素法编制的初始调运方案:运输平衡表与运价表(2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总费用。
2017年电大春物流管理定量分析方法

2017年电⼤春物流管理定量分析⽅法《物流管理定量分析⽅法》知识点:1. e =2.718281828459 2. 对x 求导,()1x '=3. 对q 求导,()1q '=4. 任何数的0次⽅等于15. ln(1) = 06.n =⼀、单项选择题1.下列问题(供应量、需求量单位:吨;单位运价单位:元/吨)是(供不应求)运输问题。
1.1.若某物资的总供应量(⼩于)总需求量,则可增设⼀个(虚产地),其供应量取总需求量与总供应量的差额,并取该产地到各销地的单位运价为0,可将供不应求运输问题化为供求平衡运输问题。
1.若某物资的总供应量(⼤于)总需求量,则可增设⼀个(虚销地),其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,可将供不应求运输问题化为供求平衡运输问题。
1.某供求平衡运输问题有四个产地和六个销地,按最⼩元素法编制的初始调运⽅案中填数字的格⼦数为(9个)。
2.某物流公司有三种化学原料A 1,A 2,A 3。
每公⽄原料A 1含B 1,B 2,B 3三种化学成分的含量分别为0.7公⽄、0.2公⽄和0.1公⽄;每公⽄原料A 2含B 1,B 2,B 3的含量分别为0.1公⽄、0.3公⽄和0.6公⽄;每公⽄原料A 3含B 1,B 2,B 3的含量分别为0.3公⽄、0.4公⽄和0.3公⽄。
每公⽄原料A 1,A 2,A 3的成本分别为500元、300元和400元。
今需要B 1成分⾄少100公⽄,B 2成分⾄少50公⽄,B 3成分⾄少80公⽄。
为列出使总成本最⼩的线性规划模型,设原料A 1,A 2,A 3的⽤量分别为x 1公⽄、x 2公⽄和x 3公⽄,则⽬标函数为(min S =500x 1+300x 2+400x 3)。
则化学成分B 1应满⾜的约束条件为(0.7x 1+0.1x 2+0.3x 3≥100)。
则化学成分B 2应满⾜的约束条件为(0.2x 1+0.3x 2+0.4x 3≥50)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物流管理定量分析方法 练习题
一、单项选择题
1.某物流公司有三种化学原料A1,A2,A3。
每公斤原料A1含B1,B2,B3三种化学成分的含量分别为公斤、公斤和公斤;每公斤原料A2含B1,B2,B3的含量分别为公斤、公斤和公斤;每公斤原料A3含B1,B2,B3的含量分别为公斤、公斤和公斤。
每公斤原料A1,A2,A3的成本分别为500元、300元和400元。
今需要B1成分至少100公斤,B2成分至少50公斤,B3成分至少80公斤。
为列出使总成本最小的线性规划模型,设原料A1,A2,A3的用量分别为x1公斤、x2公斤和x3公斤,则目标函数为( )。
A .min S =500x1+300x2+400x3 B .min S =100x1+50x2+80x3 C .max S =100x1+50x2+80x3 D .max S =500x1+300x2+400x3
2.用MATLAB 软件计算方阵A 的逆矩阵的命令函数为( )。
A . int(a) B . int(A) C .inv(a) D .inv(A) 3.设A 是45⨯矩阵,I 是单位矩阵,满足A AI
=,则I 为( )阶矩阵。
A .2
B .3
C .4
D .5
4.设线性方程组⎪⎩⎪
⎨⎧-=+=+-=+1
21
31
3221x x x x x x ,则下列( )为其解。
A .⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡201321x x x
B .⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡112321x x x C .⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110321x x x
D .⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡012321x x x 5.设运输某物品的成本函数为C (q )=q 2
+50q +2000,则运输量为100单位时的成本为(??? )。
A .17000
B .1700
C .170
D .250
6.下列函数中为奇函数的是( )。
A .)1ln(2
x y += B .x
e
y -=
C .3
x x y +=
D .13
-=x y
7.满足方程0)(='x f 的点,一定是函数)(x f y =的( )。
A .极值点
B .最值点
C .不可导点
D .驻点
8.某产品的成本函数、收入函数、利润函数分别为C (q ),R (q ),L (q ),则下列等式成立的是(??? )。
A .
⎰+'=q
C dq q L q L 0)0()()(
B .⎰-''=q
C dq q C q C 0)0()()
(
C .⎰'=q dq q R q R 0
)()(
D .⎰-'=q L dq q L q L 0
)0()()(
9.
dx x ⎰
-2
1=( )。
A . dx x ⎰
-2
)1(
B .dx x ⎰-1
0)1(+dx x ⎰-2
1
)1(
C .
dx x ⎰
-20
)1(
D .
dx x ⎰
-1
)1(+dx x ⎰-2
1
)1(
10.某商品的边际收入为q 220-,则收入函数=)(q R ( )。
A . c q q +-2
20 B .2- C .220q q -
D .2
q -
二、应用题
1.将下列某物资的不平衡运输问题转化为平衡运输问题(供应量、需求量单位:吨;运价单位:元/吨): 供需量数据表
2.制造某种产品,每瓶重量为1000克,它是由甲、乙两种原料混合而成,要求每瓶中甲种材料最多不能超过800克,乙种原料至少不少于400克。
而甲种原料的成本是每克5元,乙种原料每克8元。
问每瓶产品中甲、乙两种原料的配比如何,才能使成本最小? 三、简答题
1.简述运输合理化的影响因素。
2.简述流通加工的主要类型。
物流管理定量分析方法 练习题参考答案
一、单项选择题
1.A 2.D 3.C 4.B 5.A 6.C 7.D 8.C 9.B 10.A
二、应用题 1.
2.设每瓶产品中甲、乙两种原料含量分别为21,x x 克。
本问题的线性规划模型为: 写出矩阵形式,选主元,并计算:
321,,x x x 为基变量,4x 为非基变量,得到最优值:2.20min max -=-='S S
最优解:0,6.2,2.3,1.24321====x x x x 本问题的最优值:2.20min =S ,最优解:2.3,1.221==x x
三、简答题
1.答:(1)运输距离。
缩短运输距离对于降低物流费用意义很大。
(2)运输环节。
每增加一个运输环节,不但会增加起运的运费和总费用,而且必然要增加运输的附属活动。
(3)运输工具。
各种运输工具都有各自的优势领域,必须综合考虑。
(4)运输时间。
运输时间的缩短对于整个流通时间的缩短有决定性的作用。
(5)运输费用。
运输费用的降低,是合理化的一个重要目标。
2.答:(1)保护性加工。
延长商品的使用寿命,减少在物流作业中的损失。
(2)满足多样化的消费需要的加工。
(3)为消费方便省力的加工。
(4)提高物品利用率的加工。
(5)衔接不同运输方式,使物流更加合理的流通加工。
