下学期第三章考点练习

合集下载

浙教版七年级下第三章3.3-3.5节练习及答案解析

浙教版七年级下第三章3.3-3.5节练习以及答案解析一、单选题1.小刚同学用力踢一下草坪上静止的足球，足球滚动起来，滚动一段距离后会停下来．关于这个过程，下列描述中正确的是（）A. 以足球为参照物，草坪和它是同向运动的B. 踢一下静止的足球，足球滚动起来，说明力是使物体运动的原因C. 足球最终会停下来，说明力可以改变物体的运动状态D. 足球最终会停下来，是因为足球具有惯性2.今年五一假期，小江一家开车到开化钱江源游玩。

下列是小江对游玩场景的描写，其中符合科学道理的是( )A. 早上冲出家门，由于受到惯性的作用，跑到车边很难停下B. 上车后系上安全带可以减小行车时的惯性，从而减少意外伤害C. 上山过程中惯性越来越大，导致爬山越来越慢D. 爬上山顶抛出太阳帽，太阳帽离手前后惯性不变3.如图所示，质量相同的甲、乙两人所用绳子相同，甲拉住绳子悬在空中处于静止状态；乙拉住绷紧绳子的中点把绳子拉断了．则（）A. 绳子对甲的拉力小于甲受到的重力B. 绳子对甲的拉力大于甲对绳子的拉力C. 乙拉断绳子前瞬间，绳受到的拉力一定小于乙受到的重力D. 乙拉断绳子前瞬间，绳受到的拉力一定大于乙受到的重力4.静止在水平桌面的科学书，与科学书受到的重力相互平衡的力是( )A. 桌面对书的支持力B. 书对桌面的压力C. 桌子的重力D. 地面对桌子的支持力5.用测力计两次拉着重为G的物体竖直向上运动，两次运动的s-t图象，如图所示，其对应的测力计示数分别为F1，F2，则F1和F2的关系是（）A. F1＞F2B. F1=F2C. F1＜F2D. 以上三种情况都有可能6.在科学活动课中，同学们以“假如没有……”为主题展开讨论。

以下是由四位同学提出的具有代表性的观点，你认为正确的是（）A. 假如物体没有受到力的作用，物体就不会运动B. 假如没有了空气，光将无法传播C. 假如没有了惯性，离开喷泉口的水就不会继续向上运动D. 假如没有了重力，弹簧测力计就不能再用来测量物体受到的力7.如图，在一辆放在水平地面上的表面光滑的小车上，静止放置质量为m1、m2的两个小球(m2>m1)．当车从静止状态突然水平向右启动时，则两个小球（）A. 一起向左运动，且m2的速度大于m1的速度B. 一起向右运动，且m2的速度大于m1的速度C. 一起向左运动，且m2的速度等于m1的速度D. 对地面仍保持静止8.运输机参加抗震救灾，在沿水平向右作匀速直线运动过程中，间隔相同时间从飞机上静止释放四个相同的物资．如图能正确表示物资着地位置的是（地面水平，空气阻力不计）（）A. B.C. D.9.关于惯性，下列说法正确的是（）A. 物体在阻力相同的情况下，速度大的不容易停下来，所以速度大的物体惯性大B. 推动地面上静止的物体比维持这个物体做匀速运动所需的力大，所以静止的物体惯性大C. 在月球上举重比在地球上容易，所以同一个物体在月球上比在地球上惯性小D. 物体的惯性与物体运动速度的大小、物体运动状态的改变、物体所处的位置无关10.李明同学在学习运动和力的知识后，对下列问题认识正确的是（）A. 两个力方向相同，大小相等则作用效果一定相同B. 两个力大小相同，方向相反则一定是一对平衡力C. 运动物体突然不受力则它将永远运动下去D. 物体受力越大则惯性也越大11.下列说法正确的是（）A. 作用在物体上的几个力一定是同时产生、同时存在、同时消失B. 两个不接触的物体之间一定没有力的作用C. 足球离脚后还能继续向前运动是由于受到惯性的作用D. 竖直向上抛出的石子上升到最高点时处于非平衡状态（不计空气阻力）12.如图所示，吊在天花板下面的电灯处于静止状态，如果某一天，吊线突然间断开的同时，所受外力全部消失，则电灯将( )A. 保持原来的静止状态B. 竖直向下加速运动C. 竖直向下匀速运动D. 竖直向上匀速运动13.关于“运动和力”的关系，下列说法中正确的是（）A. 力是使物体产生运动的原因B. 力是维持物体运动的原因C. 力是改变物体运动状态的原因D. 物体受到力的作用，运动状态一定改变14.关于牛顿第一定律，下列说法正确的是( )A. 该定律是通过斜面小车实验直接得到的B. 该定律不能用实验证明，只是一种猜想C. 该定律可以用实验证明，因为它是力学的一个基本定律D. 该定律是在可靠的事实基础上，通过科学推理概括出来的，虽然不能用实验证明，但能经受住实践的检验15.对于汤姆如图所示的多项活动解释合理的是（）A. 快速拉出桌布茶具在惯性力作用下留在桌面B. 图中人受到的重力和地面对人的支持力是一对平衡力C. 经过努力没提起杠铃说明杠铃所受拉力小于等于重力D. 划船时船桨对水的作用力大于水对船桨的作用力16.探究“推断物体不受力时运动”(如图)时，同学们得到如下结论，错误的是（）A. 控制小车从斜面同一高度滑下是为了让小车滑到水平面时的初速度相同B. 通过（a）（b）（c）三次实验，可直接验证牛顿第一定律C. 由于惯性，小车到达水平面后继续向前运动D. 实验中主要运用了控制变量和理想实验法17.如图，在车厢中的a是用绳拴在底部上的氢气球，b是用绳挂在车厢顶的金属球，开始时它们和车一起向右作匀速直线运动，若忽然刹车使车厢作匀减速运动，则下列几个图能正确表示刹车期间车内的情况是（）A. B. C. D.18.关于重力，下列说法中错误的是（）A. 重力是由于地球对物体吸引而产生的B. 重力是物体本身的固有属性C. 重力的大小跟物体的质量成正比D. 重力的方向总是竖直向下19.静止在水平桌面上的文具盒，受到的平衡力是（）A. 文具盒受到的重力和文具盒对桌面的压力B. 文具盒受到的重力和桌面对文具盒的支持力C. 文具盒对桌面的压力和桌面对文具盒的支持力D. 文具盒对桌面的压力和文具盒对地球的吸引力TV科教频道曾报道：有一辆小车载人后停在水平放置的地磅上时，左前轮、右前轮、左后轮、右后轮对地磅的压力分别为4750N、4980N、4040N、3960N。

浙教版七年级科学下第三章运动和力测试及答案

七年级科学〔下〕第三章运动和力测试题一、选择题1．2001年9月11日，恐惊分子利用劫持一架质量为104吨，约载35吨燃油波音757飞机，程度撞击世贸大楼北部塔楼爆炸，使世贸大楼受重创宏大能量是〔〕A．飞机重力势能B．飞机动能C．飞机热能D．燃油燃烧产生热能2．敦煌曲子词中有这样词句：“满眼风波多闪灼，看山恰似走来迎，细致看山山不动，是船行。

〞其中“看山恰似走来迎〞和“是船行〞所选参照物分别是〔〕A．船和山B．山和船C．地面和山D．河岸和流水3．如图是投掷实心球场景。

以下状况中实心球受到平衡力作用是〔〕A．实心球在空中上升B．实心球从空中下落C．实心球在地上越滚越慢D．实心球停在地面上4．以下哪幅图中箭头能正确表示球受到重力方向〔〕5．如图，分别用大小相等力拉和压同一弹簧。

该试验说明，弹簧受力产生效果与力〔〕A．大小有关 B．作用点有关C．方向有关 D．大小、方向、作用点都有关6．如下图，使一薄钢条下端固定，现分别用不同力去推它，使其发生甲、乙、丙、丁各图所示形变。

假如F1=F3=F4>F2，则说明力作用效果跟力作用点有关图是( )A．图甲和图乙B．图甲和图丙C．图甲和图丁D．图乙和图丁7．a图是一个铅球刚脱离运发动手，b图是撑杆跳高一瞬间，以下说法正确是〔〕A．脱离运发动手后铅球受到重力和一个向前推力a图b图B．撑杆跳高运发动此时受到重力、杆作用力和一个向上推力C．脱离运发动手后铅球是在推力下向前运动，说明运动物体肯定受到了推力D．b图杆被撑杆跳高运发动压弯了说明力能使物体发生形变8．运用弹簧秤前，应先调整指针指在零刻度线上，再视察其量程。

假设指针指在零刻度线上方而没有刚好调整就开始测重力，则所测得重力大小与真实值相比将是〔〕A．偏小 B．偏大 C．一样 D．不能确定9．F1和F2大小如下图，在比较F1和F2大小时，以下说法中正确是〔〕A．F1<F2，因为F2有六个单位长度B．F1=F2，因为F1和F2长度相等C．不能比较，因为图中没有标明一个单位长度表示多大力D．以上说法均不对10．如下图，某同学试验时在弹簧涮力计两侧沿程度方向各加6牛拉力。

北师版九年级下册数学第3章全章热门考点整合专训

A．50°B．48°C．45°D．36°
【点拨】如图，连接AD.∵BC与⊙A相切于点D， ∴AD⊥BC.∴∠ADB＝∠ADC＝90°. ∵AB＝6，AG＝AD＝3，∴AD＝ AB，
1 2
∴∠B＝30°，∴∠GAD＝60°. ∵∠CDE＝18°，∴∠ADE＝90°－18°＝72°. ∵AD＝AE，∴∠AED＝∠ADE＝72°. ∴∠DAE＝180°－∠ADE－∠AED＝180°－72°－72°＝36°. ∴∠GAE＝∠GAD＋∠DAE＝60°＋36°＝96°. ∴∠GFE＝ ∠GAE＝ ×96°＝48°.
3 足为G，OG＝a.连接OB，OE，OF.
(1)若BF＝2a，试判断△BOF的形状，并说明理由．
解：△BOF为等腰直角三角形．理由如下：∵OG⊥BC， ∴BG＝FG＝ BF＝a. ∵OG＝a，∴BG＝OG，FG＝OG.
1 ∴△BOG和△OFG都是等腰直角三角形． 2 ∴∠BOG＝∠FOG＝45°.∴∠BOF＝90°，
1
1
2
2
【答案】B
8．【中考·广州】平面内，⊙O的半径为1，点P到O的距离为2，过点P可作⊙O的切
线的条数为( )Βιβλιοθήκη A．0条 B．1条C
C．2条 D．无数条
9．【2020·宜昌】如图，在四边形ABCD中，AD∥BC，AB＝2a，∠ABC ＝60°，过点B的⊙O与边AB，BC分别交于E，F两点．OG⊥BC，垂
3
OH sin 60° ∴A︵M的长＝601·8π0×4＝43π.
16．【中考·齐齐哈尔】如图，以△ABC的边BC为直径作⊙O，点A在⊙O上，点D在线段BC的延长线上，AD＝AB，∠D＝30°.
(1)求证：直线AD是⊙O的切线；
证明：连接OA，∵OA＝OB，∴∠OAB＝∠B. 又∵∠COA＝∠OAB＋∠B，∴∠COA＝2∠B. ∵AD＝AB，∠D＝30°， ∴∠B＝∠D＝30°.∴∠COA＝60°. ∴∠OAD＝180°－60°－30°＝90°. ∴OA⊥AD. ∴直线AD是⊙O的切线．

(完整版)北师版九年级下册第三章圆知识点及习题

九年级下册第三章圆【知识梳理】一、圆的认识1. 圆的定义：描述性定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的圆形叫做圆．；固定的端点O叫做圆心．．；以点O为圆心的圆，记作⊙．．；线段OA叫做半径O，读作“圆O”集合性定义：圆是平面内到定点距离等于定长的点的集合。

其中定点叫做圆心．．．．，圆．．，定长叫做圆的半径心定圆的位置，半径定圆的大小，圆心和半径确定的圆叫做定圆．．。

对圆的定义的理解：①圆是一条封闭曲线，不是圆面；②圆由两个条件唯一确定：一是圆心（即定点），二是半径（即定长）。

2、与圆相关的概念①弦和直径：弦：连接圆上任意两点的线段叫做弦．。

直径：经过圆心的弦叫做直径．．。

②弧、半圆、优弧、劣弧：弧：圆上任意两点间的部分叫做圆弧．．，简称弧．，用符号“⌒”表示，以CD为端点的弧记为“”，读作“圆弧CD”或“弧CD”。

半圆：直径的两个端点分圆成两条弧，每一条弧叫做半圆．．。

优弧：大于半圆的弧叫做优弧．．。

劣弧：小于半圆的弧叫做劣弧．．。

(为了区别优弧和劣弧，优弧用三个字母表示。

)③弓形：弦及所对的弧组成的图形叫做弓形．．。

④同心圆：圆心相同，半径不等的两个圆叫做同心圆．．．。

⑤等圆：能够完全重合的两个圆叫做等圆，半径相等的两个圆是等圆。

⑥等弧：在同圆或等圆中，能够互相重合的弧叫做等弧．．。

⑦圆心角：顶点在圆心的角叫做圆心角．．．.⑧弦心距:从圆心到弦的距离叫做弦心距．．．.3、点与圆的位置关系及其数量特征：如果圆的半径为r，点到圆心的距离为d，则①点在圆上 <===> d=r;②点在圆内 <===> d<r;③点在圆外 <===> d>r.其中点在圆上的数量特征是重点，它可用来证明若干个点共圆，方法就是证明这几个点与一个定点、的距离相等。

二. 圆的对称性:1、圆是轴对称图形，直径所在的直线是它的对称轴，圆有无数条对称轴。

(附答案)人教版初中物理第三章物态变化考点专题训练

（附答案）人教版初中物理第三章物态变化考点专题训练单选题1、下列物体中属于晶体的是（）A．橡胶B．沥青C．冰块D．石蜡2、日光灯用久后，灯管两端会出现黑斑，这些黑斑是灯丝中的钨（）A．汽化而成B．升华而成C．先汽化后液化而成D．先升华后凝华而成3、盛夏，打开冰箱门、会看到“白气”冒出；寒冷的冬天，户外的人也会不断呼出“白气”、对这两种“白气”的分析正确是（）A．前者是汽化现象，是冰箱内的水蒸气汽化形成的B．前者是液化现象，是冰箱外的水蒸气液化形成的C．后者是汽化现象，是口腔内的水蒸气汽化形成的D．后者是液化现象，是口腔外的水蒸气液化形成的4、口罩成为常态防疫“神器”，戴眼镜的人们常因口罩佩戴出现镜片模糊的情况，这是液化现象。

下列实例中与它物态变化相同的是（）A．初春，冰雪消融B．夏天，清晨草叶或树叶上形成露珠C．深秋，屋顶的瓦上结了一层霜D．冬天，室外冰冻的衣服变干了5、下列物体中属于晶体的是（）A．橡胶B．沥青C．冰块D．石蜡6、下列措施中，能使蒸发变快的是（）A．给盛有水的杯子盖好杯盖B．用电热吹风机吹湿头发C．把蔬菜放入塑料袋内保存D．把水果放入冰箱冷藏室内保存7、关于物态变化，下列说法正确的是（）A．灯泡里的灯丝用钨制成是因为钨的沸点高B．盛夏，剥开包装纸后冰棒会冒“白气”是汽化现象C．水在凝固过程中不断放出热量，温度保持不变D．深秋的早晨，地面上经常会出现白色的霜，这是液化现象8、如图所示是粤北某天天气预报的信息图片，关于图片中信息的解释正确的是（）A．雪的形成过程中放出热量B．雨的形成是汽化现象C．雨夹雪时气温一定是0℃以下D．当天夜里的温度最高可达5℃9、如图所示是粤北某天天气预报的信息图片，关于图片中信息的解释正确的是（）A．雪的形成过程中放出热量B．雨的形成是汽化现象C．雨夹雪时气温一定是0℃以下D．当天夜里的温度最高可达5℃10、在“探究蜡烛的熔化特点”和“观察碘锤中的物态变化”两个活动中，采用水浴法加热的主要目的是（）A．都是为了受热均匀B．都是为了控制温度C．前者是为了受热均匀，后者是为了控制温度D．前者是为了控制温度，后者是为了受热均匀11、下图中，正确描述巴中铁路铁轨的铸造过程中凝固阶段温度变化的是（）A．B．C．D．12、冷链储运中常用一种装有制冷装置的冷藏车，用于运输冷冻食品和疫苗药品等，制冷装置通过液态制冷剂汽化将车的“热”搬运到外面，实现制冷。

2022年必考点解析北师大版九年级数学下册第三章圆专项练习试卷(含答案详解)

北师大版九年级数学下册第三章圆专项练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，Rt△ABC中，∠A＝90°，∠B＝30°，AC＝1，将Rt△ABC延直线l由图1的位置按顺时针方向向右作无滑动滚动，当A第一次滚动到图2位置时，顶点A所经过的路径的长为（）B C D．（πA2、如图，O是正方形ABCD的外接圆，若O的半径为4，则正方形ABCD的边长为（）A．4 B．8 C．D．3、如图，⊙O中，半径OC⊥AB于D，且CD＝2，弦AB＝8，则⊙O的半径的长等于（）A ．3B ．4C ．5D ．64、到三角形三个顶点距离相等的点是此三角形（）A ．三条角平分线的交点B ．三条中线的交点C ．三条高的交点D ．三边中垂线的交点5、已知半径为5的圆，直线l 上一点到圆心的距离是5，则直线和圆的位置关系为（）A ．相切B ．相离C ．相切或相交D ．相切或相离6、如图，已知O 中，50AOB ∠=︒，则圆周角ACB ∠的度数是（）A ．50°B ．25°C ．100°D ．30°7、如图，直径AB ＝6的半圆，绕B 点顺时针旋转30°，此时点A 到了点A '，则图中阴影部分的面积是（）A ．3πB ．34πC ．πD ．3π8、下列说法正确的是（）A ．等弧所对的圆周角相等B ．平分弦的直径垂直于弦C ．相等的圆心角所对的弧相等D ．过弦的中点的直线必过圆心9、如图，菱形ABCD 中，60C ∠=°，2AB =．以A 为圆心，AB 长为半径画BD ，点P 为菱形内一点，连PA ，PB ，PD ．若PA PB =，且120APB ∠=︒，则图中阴影部分的面积为（）A ．23y π= B ．23y π= C ．23y π= D ．23y π=10、若正六边形的边长为6，则其外接圆半径与内切圆半径的大小分别为（）A ．6，B ．6，C ． 6D ．6，3第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，已知圆锥的母线AB 长为40 cm ，底面半径OB 长为10 cm ，若将绳子一端固定在点B ，绕圆锥侧面一周，另一端与点B 重合，则这根绳子的最短长度是______________．2、如图，AB 是半圆O 的直径，AB ＝4，点C ，D 在半圆上，OC ⊥AB ，2BD CD =，点P 是OC 上的一个动点，则BP ＋DP 的最小值为______．3、已知正六边形的周长是24，则这个正六边形的半径为_____ ．4、在半径为3的圆中，60°的圆心角所对的劣弧长等于_____．5、如图，五边形ABCDE是⊙O的内接正五边形，则ODC的度数是____．三、解答题（5小题，每小题10分，共计50分）1、如图，射线AB和射线CB相交于点B，∠ABC＝α（0°＜α＜180°），且AB＝CB．点D是射线CB 上的动点（点D不与点C和点B重合），作射线AD，并在射线AD上取一点E，使∠AEC＝α，连接CE，BE．（1）如图①，当点D在线段CB上，α＝90°时，请直接写出∠AEB的度数；（2）如图②，当点D在线段CB上，α＝120°时，请写出线段AE，BE，CE之间的数量关系，并说明理由；（3）当α＝120°，tan∠DAB＝13时，请直接写出CEBE的值．2、如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作O的切线交CE的延长线于点D．（1）求证：DB=DE；（2）若AB=12，BD=5，求AC长．3、如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且：CF是⊙O的切线．（1）求证：∠DCF＝∠CAD．（2）探究线段CF，FD，FA的数量关系并说明理由；（3）若cos B35=，AD＝2，求FD的长．4、在平面直角坐标系xOy中，⊙O的半径为1．对于线段AB，给出如下定义：若线段AB沿着某条直线l对称可以得到⊙O的弦A′B′，则称线段AB 是⊙O的以直线l为对称轴的“反射线段”，直线l称为“反射轴”．（1）如图，线段CD，EF，GH中是⊙O的以直线l为对称轴的“反射线段”有；（2）已知A点坐标为（0，2），B点坐标为（1，1），①若线段AB是⊙O的以直线l为对称轴的“反射线段”，求反射轴l与y轴的交点M的坐标．②若将“反射线段”AB沿直线y＝x的方向向上平移一段距离S，其反射轴l与y轴的交点的纵坐标y M的取值范围为12≤y M136≤，求S．（3）已知点M，N是在以原点为圆心，半径为2的圆上的两个动点，且满足MN＝1，若MN是⊙O的以直线l为对称轴的“反射线段”，当M点在圆上运动一周时，求反射轴l未经过的区域的面积．（4）已知点M，N是在以（2，0MN=MN是⊙O的以直线l为对称轴的“反射线段”，当M点在圆上运动一周时，请直接写出反射轴l与y轴交点的纵坐标的取值范围．5、在平面直角坐标系xOy 中，已知抛物线212y x bx =+．（1）求抛物线顶点Q 的坐标；（用含b 的代数式表示）（2）抛物线与x 轴只有一个公共点，经过点（0，2）的直线与抛物线交于点A ，B ，与x 轴交于点K ．①判断△AOB 的形状，并说明理由；②已知E （2，0），F （4，0），设△AOB 的外心为M ，当点K 在线段EF 上时，求点M 的纵坐标m 的取值范围．-参考答案-一、单选题1、C【分析】根据题意，画出示意图，确定出点A 的运动路径，再根据弧长公式即可求解．【详解】解：根据题意可得，Rt △ABC 的运动示意图，如下：Rt △ABC 中，∠A ＝90°，∠B ＝30°，AC ＝1，∴60ACB ∠=︒，2BC =，AB =由图形可得，点A 的运动路线为，先以C 为中心，顺时针旋转120︒，到达点1A ，经过的路径长为120121803ππ⨯=，再以1B 为中心，顺时针旋转150︒，到达点2A ，顶点A 所经过的路径的长为23π=故选：C【点睛】此题考查了旋转的性质，圆弧弧长的求解，解题的关键是根据题意确定点A 的运动路线．2、D【分析】连接OB ，OC ，过点O 作OE ⊥BC 于点E ，由等腰直角三角形的性质可知OE =BE ，由垂径定理可知BC =2BE ，故可得出结论．【详解】解：连接OB ，OC ，过点O 作OE ⊥BC 于点E ，∴OB =OC ，∠BOC =90°，∴∠OBE =45°，45BOE ∠=︒∴OE =BE ，∵OE 2+BE 2=OB 2，∴BE =∴BC =2BE =ABCD 的边长是故选：D【点睛】本题考查的是圆周角定理、垂径定理及勾股定理，根据题意作出辅助线，构造出等腰直角三角形是解答此题的关键．3、C【分析】根据垂径定理得出AD =BD =118422AB ，设⊙O 的半径的长为x ，根据勾股定理222OB OD BD =+，即()22224x x =-+，解方程即可．【详解】解：∵半径OC ⊥AB 于D ，弦AB ＝8， ∴AD =BD =118422AB ，设⊙O 的半径的长为x ，∴OD =OC -CD =x -2，在Rt△ODB 中，根据勾股定理222OB OD BD =+，即()22224x x =-+，解得x =5，∴⊙O的半径的长为5．故选择C．【点睛】本题考查垂径定理，勾股定理，解拓展一元一次方程，掌握垂径定理，勾股定理，解拓展一元一次方程是解题关键．4、D【分析】由题意根据线段的垂直平分线上的性质，则有三角形三边中垂线的交点到三角形的三个顶点距离相等．【详解】解：∵垂直平分线上任意一点，到线段两端点的距离相等，∴到三角形三个顶点的距离相等的点是三角形三边中垂线的交点．故选：D．【点睛】本题考查了线段的垂直平分线的性质，解题的关键是注意掌握线段的垂直平分线上的点到线段的两个端点的距离相等．5、C【分析】根据若直线上一点到圆心的距离等于圆的半径，则圆心到直线的距离等于或小于圆的半径，此时直线和圆相交或相切．【详解】解：∵半径为5的圆，直线l上一点到圆心的距离是5，∴圆心到直线的距离等于或小于5，∴直线和圆的位置关系为相交或相切，故选：C ．【点睛】本题考查了直线和圆的位置关系，判断的依据是半径和直线到圆心的距离的大小关系：设⊙O 的半径为r ，圆心O 到直线l 的距离为d ，①直线l 和⊙O 相交⇔d ＜r ；②直线l 和⊙O 相切⇔d ＝r ；③直线l 和⊙O 相离⇔d ＞r ．6、B 【分析】根据圆周角定理，即可求解．【详解】解：∵1,502ACB AOB AOB ∠=∠∠=︒ ，∴25ACB ∠=︒ ．故选：B 【点睛】本题主要考查了圆周角定理，熟练掌握同圆（或等圆）中，同弧（或等弧）所对的圆周角等于圆心角的一半是解题的关键． 7、D 【分析】阴影面积为旋转后'A B 为直径的半圆面积加旋转后扇形面积减去旋转前AB 为直径的半圆面积，则阴影面积为旋转后的扇形面积，由扇形面积公式计算即可．【详解】∵直径AB ＝6的半圆，绕B 点顺时针旋转30° ∴A'B ABA'AB S S S S =+-阴影为直径的半圆扇形为直径的半圆又∵'AB A B =∴A'B AB S S =为直径的半圆为直径的半圆∴ABA'S S =阴影扇形 ∵AB =6，∠ABA ’=30° ∴223063360360ABA'n r S S π︒⋅π⋅====π︒︒阴影扇形故答案为：D ．【点睛】本题考查了扇形面积公式的应用，扇形面积公式为2360n r π︒，由旋转的性质得出阴影面积为扇形面积是解题的关键． 8、A 【分析】根据圆周角定理，垂径定理的推论，圆心角、弧、弦的关系，对称轴的定义逐项排查即可．【详解】解：A . 同弧或等弧所对的圆周角相等，所以A 选项正确；B .平分弦（非直径）的直径垂直于弦，并且平分弦所对的弧，所以B 选项错误；C 、在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦相等，所以C 选项错误；D .圆是轴对称图形，任何一条直径所在的直线都是它的对称轴，所以D 选项错误.故选A. 【点睛】本题主要考查了圆心角、弧、弦的关系,轴对称图形，垂径定理，圆周角定理等知识点．灵活运用相关知识成为解答本题的关键． 9、C【分析】过点P 作PM AB ⊥交于点M ，由菱形ABCD 得60DAB C ∠=∠=︒，2AB AD ==，由PA PB =，120APB ∠=︒得112AM AB ==，1602APM APB ∠=∠=︒，故可得30PAM ∠=︒，603030PAD DAB PAM ∠=∠-∠=︒-︒=︒，根据SAS 证明ABP ADP ≅，求出PM =ABPADPABD S S SS=--阴扇形．【详解】如图，过点P 作PM AB ⊥交于点M ， ∵四边形ABCD 是菱形，∴60DAB C ∠=∠=︒，2AB AD ==， ∵PA PB =，120APB ∠=︒， ∴112AM AB ==，1602APM APB ∠=∠=︒， ∴30PAM ∠=︒，603030PAD DAB PAM ∠=∠-∠=︒-︒=︒，在ABP △与ADP △中，AB ADPAB PAD AP AP =⎧⎪∠=∠⎨⎪=⎩， ∴()ABP ADP SAS ≅， ∴ABP ADP S S =△△，在Rt AMP △中，30PAM ∠=︒， ∴2AP PM =，222AP PM AM =+，即2241PM PM =+，解得：PM =∴260211222360223ABP ADPABD S S S Sππ⋅=--=-⨯⨯=阴扇形故选：C ．【点睛】此题主要考查了菱形的性质以及求不规则图形的面积等知识，掌握扇形的面积公式是解答此题的关键． 10、B 【分析】如图1，⊙O 是正六边形的外接圆，连接OA ，OB ，求出∠AOB =60°，即可证明△OAB 是等边三角形，得到OA =AB =6；如图2，⊙O 1是正六边形的内切圆，连接O 1A ，O 1B ，过点O 1作O 1M ⊥AB 于M ，先求出∠AO 1B ＝60°，然后根据等边三角形的性质和勾股定理求解即可．【详解】解：（1）如图1，⊙O 是正六边形的外接圆，连接OA ，OB ， ∵六边形ABCDEF 是正六边形， ∴∠AOB =360°÷6=60°， ∵OA =OB ，∴△OAB 是等边三角形， ∴OA =AB =6；（2）如图2，⊙O1是正六边形的内切圆，连接O1A，O1B，过点O1作O1M⊥AB于M，∵六边形ABCDEF是正六边形，∴∠AO1B＝60°，∵O1A= O1B，∴△O1AB是等边三角形，∴O1A= AB=6，∵O1M⊥AB，∴∠O1MA＝90°，AM＝BM，∵AB＝6，∴AM＝BM，∴O 1M 故选B ．【点睛】本题主要考查了正多边形与圆，等边三角形的性质与判定，勾股定理，熟知正多边形与圆的知识是解题的关键．二、填空题1、【分析】根据底面圆的周长等于扇形的弧长求解扇形的圆心角90,BAB '∠=︒ 再利用勾股定理求解即可. 【详解】解：圆锥的侧面展开图如图所示：设圆锥侧面展开图的圆心角为n °，圆锥底面圆周长为210=20，40=20,180n BB 则n =90，∵40,AB AB224040402,BB即这根绳子的最短长度是，故答案为：【点睛】本题考查的是圆锥的侧面展开图，弧长的计算，掌握“圆锥的底面圆的周长等于展开图的弧长求解圆心角”是解本题的关键.2、【分析】如图，连接AD，PA，PD，OD．首先证明PA=PB，再根据PD+PB=PD+PA≥AD，求出AD即可解决问题．【详解】解：如图，连接AD，PA，PD，OD．∵OC⊥AB，OA=OB，∴PA=PB，∠COB=90°，∵2BD CD，∴∠DOB=23×90°=60°，∵OD=OB，∴△OBD是等边三角形，∴∠ABD=60°∵AB是直径，∴∠ADB=90°，∴AD=AB•sin∠ABD∵PB+PD=PA+PD≥AD，∴PD+PB∴PD+PB的最小值为故答案为：【点睛】本题考查圆周角定理，垂径定理，圆心角，弧，弦之间的关系等知识，解题的关键是学会用转化的思想思考问题．3、4【分析】由于正六边形可以由其半径分为六个全等的正三角形，而三角形的边长就是正六边形的半径，由此即可求解．【详解】解：∵正六边形可以由其半径分为六个全等的正三角形，而三角形的边长就是正六边形的半径，又∵正六边形的周长为24，∴正六边形边长为24÷6=4，∴正六边形的半径等于4．故答案为4．【点睛】此题主要考查正多边形和圆，解题的关键是熟练掌握基本知识，属于中考基础题．4、π【分析】弧长公式为l ＝n 180rπ，把半径和圆心角代入公式计算就可以求出弧长．【详解】解：半径为3的圆中，60°的圆心角所对的劣弧长＝603180π⨯＝π，故答案为：π．【点睛】本题主要考查了弧长计算，关键是掌握弧长计算公式． 5、54︒ 【分析】根据圆内接正五边形的定义求出∠COD ，利用三角形内角和求出答案．【详解】解：∵五边形ABCDE 是⊙O 的内接正五边形， ∴∠COD=360725︒=︒， ∵OC=OD ，∴ODC ∠=(180)5412COD ︒-∠=︒，故答案为：54︒．【点睛】此题考查了圆内接正五边形的性质，三角形内角和定理，同圆的半径相等的性质，熟记圆内接正五边形的性质是解题的关键．三、解答题1、（1）45°；（2）AE +CE ，理由见解析；（3【分析】（1）连接AC，证A、B、E、C四点共圆，由圆周角定理得出∠AEB＝∠ACB，证出△ABC是等腰直角三角形，则∠ACB＝45°，进而得出结论；（2）在AD上截取AF＝CE，连接BF，过点B作BH⊥EF于H，证△ABF≌△CBE（SAS），得出∠ABF＝∠CBE，BF＝BE，由等腰三角形的性质得出FH＝EH，由三角函数定义得出FH＝EH，进而得出结论；（3）分两种情况，由（2）得FH＝EH，由三角函数定义得出AH＝3BH＝32BE，分别表示出CE，进而得出答案．【详解】解：（1）连接AC，如图①所示：∵α＝90°，∠ABC＝α，∠AEC＝α，∴∠ABC＝∠AEC＝90°，∴A、B、E、C四点共圆，∴∠AEB＝∠ACB，∵∠ABC＝90°，AB＝CB，∴△ABC是等腰直角三角形，∴∠ACB＝45°，∴∠AEB＝45°；（2）AE+CE，理由如下：在AD 上截取AF ＝CE ，连接BF ，过点B 作BH ⊥EF 于H ，如图②所示：∵∠ABC ＝∠AEC ，∠ADB ＝∠CDE ，∴180°﹣∠ABC ﹣∠ADB ＝180°﹣∠AEC ﹣∠CDE ，∴∠A ＝∠C ，在△ABF 和△CBE 中，AF CE A C AB CB =⎧⎪∠=∠⎨⎪=⎩， ∴△ABF ≌△CBE （SAS ），∴∠ABF ＝∠CBE ，BF ＝BE ，∴∠ABF +∠FBD ＝∠CBE +∠FBD ，∴∠ABD ＝∠FBE ，∵∠ABC ＝120°，∴∠FBE ＝120°，∵BF ＝BE ，∴∠BFE ＝∠BEF ＝11(180)(180120)3022FBE ︒︒︒︒⨯-∠=⨯-=， ∵BH ⊥EF ，∴∠BHE ＝90°，FH ＝EH ，在Rt△BHE中，1,2BH BE FH EH ====，∴22EF EH ===， ∵AE ＝EF +AF ，AF ＝CE ，∴.AE CE=+；（3）分两种情况：①当点D在线段CB上时，在AD上截取AF＝CE，连接BF，过点B作BH⊥EF于H，如图②所示，由（2）得：FH＝EH，∵tan∠DAB＝13 BHAH=，∴332AH BH BE==，∴32CE AF AH FH BE==-==，∴CEBE=；②当点D在线段CB的延长线上时，在射线AD上截取AF＝CE，连接BF，过点B作BH⊥EF于H，如图③所示，同①得：3,32FH EH AH BH BE ====，∴32CE AF AH FH BE==+==，∴CE BE综上所述，当α＝120°，1tan3DAB∠=时，CEBE【点睛】本题是三角形综合题目，考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质、四点共圆、圆周角定理、三角函数定义等知识；本题综合性强，构造全等三角形是解题的关键．2、（1）见解析；（2）15 2【分析】（1）由切线性质及等量代换推出∠4=∠5，再利用等角对等边可得出结论；（2）由已知条件得出sin∠DEF和sin∠AOE的值，利用对应角的三角函数值相等推出结论. 【详解】（1）如图，∵DC⊥OA，∴∠1+∠3=90°，∵BD为切线，∴OB⊥BD，∴∠2+∠5=90°，∵OA=OB，∴∠1=∠2，∵∠3=∠4，∴∠4=∠5，在△DEB中，∠4=∠5，∴DE=DB.(2)如图，作DF⊥AB于F，连接OE，∵DB=DE，∴EF=12BE=3，在Rt△DEF中，EF=3，DE=BD=5，∴DF4=∴sin∠DEF=DFDE=45，∵∠AOE90A A AEC+∠=︒=∠+∠,AEC DEF∠=∠，∴∠AOE=∠DEF，∴在Rt△AOE 中，sin∠AOE =45AE AO = ， ∵AE =6，∴AO =152. 【点睛】本题考查了圆的性质，切线定理，三角形相似，三角函数等知识，结合图形正确地选择相应的知识点与方法进行解题是关键.3、（1）见解析；（2）2·FC FD FA =，见解析；（3）187【分析】（1）连接OC ，根据直径所对的圆周角为直角及切线的性质和各角之间的等量关系即可证明；（2）根据相似三角形的判定定理可得ΔΔΔΔ~ΔΔΔΔ，依据相似三角形的性质：对应边成比例即可得出；（3）根据同弧所对的圆周角相等可得：B ADC ∠=∠，3cos cos 5ADC B ∠=∠=，在Rt ACD ∆中，利用锐角三角函数可得65CD =，由勾股定理确定85AC =，由此得出34CD AC =，即为（2）中的相似比，设3FD x =，则4FC x =，32AF x =+，将其代入（2）中结论求解即可．【详解】解：（1）连接OC ，如图所示：∵AD 为O 直径，∴90ACD ∠=︒，90CAD ADC ∠+∠=︒，∵CF 为O 的切线，∴90OCF ∠=︒，即90OCD DCF ∠+∠=︒，∵OC OD =，∴OCD ADC ∠=∠，∴DCF CAD ∠=∠；（2）在ΔΔΔΔ与AFC ∆中，∵DCF CAD ∠=∠，F F ∠=∠，∴ΔΔΔΔ~ΔΔΔΔ， ∴FCFDAF FC =，∴2·FC AF FD =；（3）∵B ADC ∠=∠， ∴3cos cos 5ADC B ∠=∠=，在Rt ACD ∆中，2AD =，3cos 5CDADC AD ∠==， ∴6·cos 5CD AD ADC =∠=，∴85AC ==， ∴34CDAC =，由（2）结论可得：ΔΔΔΔ~ΔΔΔΔ，∴34FC FD CD AF FC AC ===，设3FD x =，则4FC x =，32AF x =+，将其代入结论（2）可得：()()24332x x x =+，解得：67x =或0x =（舍去）， ∴1837FD x ==．【点睛】题目主要考查圆周角定理、相似三角形的判定和性质、锐角三角函数解三角形、勾股定理等，理解题意，综合运用这些知识点是解题关键．4、（1）2；（2）①1(0,)2M ；②02S ≤≤；（3）1916π⎛ ⎝⎭;（4）1y >或1y <- 【分析】（1）O 的半径为1，则O 的最长的弦长为2，根据两点的距离可得2,EF CD EF ===而即可求得答案；（2）①根据定义作出图形，根据轴对称的方法求得对称轴，反射线段经过对应圆心的中点，即可求得M 的坐标；②由①可得当0S =时，y M 1=2，设当S 取得最大值时，过点1O 作1O P y ⊥轴，根据题意，122,,O A B 分别为沿直线y ＝x 的方向向上平移一段距离S 后,,O A B '的对应点，则1O P PO '=S =，根据余弦求得11cos cos QO PO MOQ O OP OM OO ∠=∠==进而代入数值列出方程，解方程即可求得S 的最大值，进而求得S 的范围；（3）根据圆的旋转对称性，找到MN 所在的2O 的圆心，如图，以MN 为边在O 内作等边三角形2O MN ，连接2OO ，取2OO 的中点R ,过R 作2OO 的垂线l ，则l 即为反射轴,反射轴l 未经过的区域是以O 为圆心OR 为半径的圆，反射轴l 是该圆的切线，求得半径为1算即可；（4）根据（2）的方法找到MN 所在的圆心3O ,当M 点在圆上运动一周时，如图，取3OO 的中点1A ，OT 的中点S ，即3OO 的中点1A 在以S l 与y 轴交点的纵坐标y 的取值范围【详解】（1）O 的半径为1，则O 的最长的弦长为2根据两点的距离可得2,EF CD EF ===2,2,2EF CD EF ∴<<>故符合题意的“反射线段”有2条；故答案为：2（2）①如图，过点B 作BO y '⊥轴于点O '，连接11A BA 点坐标为（0，2），B 点坐标为（1，1），∴AB ==45BAO '∠=︒，(0,1)O 'O 的半径为1，1190AOB ∠=︒11A B ∴1145B A O =︒线段AB 是⊙O 的以直线l 为对称轴的“反射线段”，()00O ，，(0,1)O ' 1(0,)2M ∴ ②由①可得当0S =时，y M 1=2如图，设当S 取得最大值时，过点1O 作1O P y ⊥轴，根据题意，122,,O A B 分别为沿直线y ＝x 的方向向上平移一段距离S 后,,O A B '的对应点，则1O P PO '=S =， (0,1)O '1(,1)O S S ∴+()222211221OO S S S S ∴=++=++ 过1OO 中点Q ，作直线l 1OO ⊥交y 轴于点M ,则l 即为反射轴1(,)22S S Q +∴ 12≤y M 136≤，136OM ∴= 11cos cos QO PO MOQ O OP OM OO ∠=∠== 即11112136OO S OO += 即()21113126OO S =+⨯ ∴()2113126S S S ++=+ 解得1252,6S S ==-（舍）02S ∴≤≤（3）1MN =∴1M N ''= O 的半径为1，则M N O ''是等边三角形，根据圆的旋转对称性，找到MN 所在的2O 的圆心，如图，以MN 为边在O 内作等边三角形2O MN ，连接2OO ，取2OO 的中点R ,过R 作2OO 的垂线l ，则l 即为反射轴, ∴反射轴l 未经过的区域是以O 为圆心OR 为半径的圆，反射轴l 是该圆的切线222OO ∴==2112OR OO ∴==∴当M 点在圆上运动一周时，求反射轴l 未经过的区域的面积为2191=16ππ⎛⎛ ⎝⎭⎝⎭．（4）如图，根据（2）的方法找到MN 所在的圆心3O ,设(2,0)T则TM =2MN =3O MN 是等腰直角三角形3O L ML ∴,TL ∴==3TO ∴=当M 点在圆上运动一周时，如图，取3OO 的中点1A ，OT 的中点S ，1SA ∴是3OO T 的中位线1312SA O T ∴==,13SA TO ∥即3OO 的中点1A 在以S∴若MN 是⊙O 的以直线l 为对称轴的“反射线段”，则l 为S 的切线设S 与y 轴交于点,C D 112OS OT ==，1SC SA =1OC ∴=同理可得1OD =∴反射轴l 与y 轴交点的纵坐标y 的取值范围为1y >或1y <-【点睛】本题考查了中心对称与轴对称，圆的相关知识，切线的性质，三角形中位线定理，余弦的定义，掌握轴对称与中心对称并根据题意作出图形是解题的关键．5、（1）（-b ，-12b 2）；（2）①直角三角形，见解析；②94≤Δ≤3 【分析】（1）y =12x 2+bx =12（x +b ）2-12b 2，即可求解；（2）①求出抛物线的表达式为y=12x2，联立y=12x2和y=kx+2并整理得：x2-2kx-4=0，证明△ADO∽△OEB，即可求解；②△AOB的外心为M，则点M是AB的中点，MP是梯形BADG的中位线，则m=k2+2，进而求解．【详解】解：（1）∵y=12x2+bx=12（x+b）2-12b2，∴抛物线的顶点Q坐标为（-b，-12b2）；（2）①∵抛物线与x轴只有一个公共点，∴△=b2-4×12×0=0，解得b=0，∴抛物线的表达式为y=12x2，如下图，分别过点A、B作x轴的垂线，垂足分别为D、G，设经过点（0，2）的直线的表达式为y=kx+2，联立y=12x2和y=kx+2并整理得：x2-2kx-4=0，则x1+x2=2k，x1x2=-4，∴y1=12x12，y2=12x22，则y1y2=14x12x22=4=-x1x2，∵AD=y1，DO=-x1，BE=y2，OE=x2，∴AD OD OE BE，∴∠ADO=∠BEO=90°，∴△ADO∽△OEB，∴∠AOD=∠OBE，∵∠OBG+∠BOG=90°，∴∠BOG+∠AOD=90°，即AO⊥BO，∴△AOB为直角三角形；②过点A作x轴的平行线交EB的延长线于点H，过点M作MN与y轴平行，交AH于N，∵△AOB的外心为M，MN∥y轴∥BH，∴点M是AB的中点，MP是梯形ABGD的中位线，∴MP=12（AD+BG）=12（y2+y1），则m=MP=12（y1+y2）=12（kx1+2+kx2+2）=12[k（x1+x2）+4]=k2+2，令y=kx+2=0，解得x=-2k，即点K的坐标为（-2k，0），由题意得：2≤-2k≤4，解得-1≤k≤12且k≠0，∴94≤k2+2≤3，即点M的纵坐标m的取值范围94≤m≤3．【点睛】本题主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．。

浙教版七年级下科学第三章3.1-3.2节练习及答案解析

浙教版七年级下第三章3.1-3.2节练习以及答案解析一、单选题1.如图所示，某同学在弹簧测力计的两侧沿水平方向各施加6牛的拉力，并使其保持静止，此时弹簧测力计的示数为( )A. 0牛B. 3牛C. 6牛D. 12牛2.短跑运动员在某次百米赛跑中测得5秒末的速度为9.0m/s，10秒末到达终点的速度为10.2m/s，则下列说法正确的是（）A. 在前5秒内运动员的平均速度为4.5 m/sB. 在后5秒内运动员的平均速度为9.6m/sC. 在本次百米赛跑中运动员的平均速度为10.0 m/sD. 在本次百米赛跑中运动员的平均速度为9.1 m/s3.观察图中的烟和小旗，关于a、b两车相对于房子的运动情况，下列说法正确的是()A. a、b两车一定向左运动B. a、b两车一定向右运动C. a车可能运动，b车向右运动D. a车可能静止，b车向左运动4.以下是我们生活中可见到的几种现象，在这些现象中，物体因受力而改变运动状态的有( )①用力揉橡皮泥，橡皮泥形状发生改变②篮球撞击在篮板上被弹回③用力握小皮球，球变瘪了④一阵风把地面上的灰尘吹得漫天飞舞A. ①②B. ③④C. ②③D. ②④5.为了监督司机是否遵守限速规定，交管部门在公路上安装了固定测速仪．如图所示，汽车向放置在道路中间的测速仪匀速驶来，测速仪向汽车发出两次短促的超声波信号．第一次发出信号到测速仪接收到经汽车反射回来的信号用时0.5s，第二次发出信号到测速仪接收到经汽车反射回来的信号用时0.3s，若发出两次信号的时间间隔是1.1s，超声波的速度是340m/s．则（）A. 汽车接收到第一次信号时，距测速仪170 mB. 汽车接收到第二次信号时，距侧速仪102 mC. 汽车的速度是34 m/sD. 汽车的速度是30.9 m/s6.甲、乙两同学沿平直路面步行，它们运动的路程随时间变化的规律如图所示，下面说法中错误的是（）A. 8s末甲、乙两同学速度相等B. 第6s乙的速度小于甲的速度C. 0s～8s内，甲、乙两同学运动的路程相等D. 4s～8s内，甲、乙同学都作匀速直线运动7.下列说法正确的是( )A. 在发生力的作用时，一定可以找到此力的施力物体和受力物体B. 力是物体对物体的作用，彼此不直接接触的物体之间没有力的作用C. 没有物体，也可能会有力的作用D. 力作用在物体上，只能使物体从静止变为运动8.用细线将一个金属小球悬挂于匀速上升的电梯中，小球稳定后，剪断悬线，则下列关于小球运动情况的说法中正确的是（）①以电梯为参照物，小球立即下落②以电梯为参照物，小球先上升而下落③以地面为参照物，小球立即下落④以地面为参照物，小球先上升后下落A. ①②B. ③④C. ①④D. ②③9.小明和小华在操场上沿直线跑道跑步，他们通过的路程和时间的关系如图所示，则下列说法正确的是（）A. 两人都做匀速直线运动B. 前2 s内，小明跑得更快C. 8 s内，小明的速度是5 m/sD. 8 s内，小明跑的路程更长10.汽车由西向东匀速行驶，车上的乘客看到窗外的雨是竖直下落的，那么在地面上的人看来，雨滴的下落方向是（）A. 竖直下落B. 斜向东下落C. 斜向西下落D. 斜向南或斜向北下落11.下列的估测中，最接近生活实际的是（）A. 一节物理课的时间约为40sB. 成年人正常步行的C. 一根新铅笔的长约为17cmD. 一份中考物理试卷的质量约为100g12.在以“力”为主题的辩论赛中，正方和反方提出了许多观点，小明把他们的观点归纳整理如下表．你认为正确的观点有（）①两个物体相接触，就一定有力的作用；②两个物体相接触，但不一定有力的作用；③力的产生至少涉及两个物体；④一个物体也可以产生力的作用；⑤力的维持物体运动状态的原因；⑥力是改变物体运动状态的原因．A. ⑥②④B. ②④⑥C. ②③⑥D. ①③⑤13.小船往返于沿河的甲、乙两地．若河水静止时，往返一次需时间为t1，若河水流动，则往返一次需要时间为t2，则（）A. t1=t2B. t1＞t2C. t1＜t2D. 由船速和水速决定14.甲、乙二人各乘一台升降机，甲看见楼房在匀速上升，乙也在匀速上升。

北师大版七年级下册数学第三章知识点详细归纳附第三章测试卷及参考答案

北师大版七年级下册数学第三章知识点详细归纳附第三章测试卷及参考答案第三章变量之间的关系@考点归纳1.自变量一、变量的概念2.因变量变量之间的关系 1. 表格法2. 关系式法二、变量的表达方法（1）.速度时间图象3. 图象法（2）.路程时间图象一、变量、自变量、因变量1、在某一变化过程中，不断变化的量叫做变量。

2、如果一个变量y随另一个变量x的变化而变化，则把x叫做自变量，y叫做因变量。

3、自变量与因变量的确定：（1）自变量是先发生变化的量；因变量是后发生变化的量。

（2）自变量是主动发生变化的量，因变量是随着自变量的变化而发生变化的量。

（3）利用具体情境来体会两者的依存关系。

二、表格1、表格是表达、反映数据的一种重要形式，从中获取信息、研究不同量之间的关系。

（1）首先要明确表格中所列的是哪两个量；（2）分清哪一个量为自变量，哪一个量为因变量；（3）结合实际情境理解它们之间的关系。

2、绘制表格表示两个变量之间关系（1）列表时首先要确定各行、各列的栏目；（2）一般有两行，一行表示自变量，第二行表示因变量；（3）写出栏目名称，有时还根据问题内容写上单位；（4）在一行列出自变量的各个变化取值；第二行对应列出因变量的各个变化取值。

（5）一般情况下，自变量的取值从左到右应按由小到大的顺序排列，这样便于反映因变量与自变量之间的关系。

三、关系式1、用关系式表示因变量与自变量之间的关系时，通常是用含有自变量（用字母表示）的代数式表示因变量（也用字母表示），这样的数学式子（等式）叫做关系式。

2、关系式的写法不同于方程，必须将因变量单独写在等号的左边。

3、求两个变量之间关系式的途径：（1）将自变量和因变量看作两个未知数，根据题意列出关于未知数的方程，并写成关系式的形式。

（2）根据表格中所列的数据写出变量之间的关系式；（3）根据实际问题中的基本数量关系写出变量之间的关系式；（4）根据图象写出与之对应的变量之间的关系式。

4、关系式的应用：（1）利用关系式能根据任何一个自变量的值求出相应的因变量的值；（2）同样也可以根据任何一个因变量的值求出相应的自变量的值；（3）根据关系式求值的实质就是解一元一次方程（求自变量的值）或求代数式的值（求因变量的值）。

九年级科学下册第3章人的降章末复习课练习新版浙教版.doc

章末复习课（见A本91页）知识点1传染病的流行与防治1 .肺结核是一种经呼吸道传播的常见传染病，由结核杆菌引起。

目前控制该病的主要方法有：①发现和治疗结核病患者；②新生儿接种卡介苗。

根据以上信息下列说法正确的是（A ）A.结核杆菌是病原体B.电镜观察结核杆菌，可发现成形的细胞核C.给新生儿接种卡介苗，这一措施属于控制传染源D.将肺结核患者隔离治疗属于保护易感人群2.为了防止禽流感在人类中蔓延，专家建议：一旦发现感染上禽流感的家禽应立即灭杀；人类要远离家禽的分泌物，尽量避免触摸活的鸡、鸭等家禽及鸟类；吃禽肉要煮熟煮透;阻止人类随意进入己感染禽流感的养鸡场。

以上措施分别属于（D ）%1控制传染源②保护易感人群③切断传播途径A.①①③②B.③③C.①②③②D.①③③②3.对传染病我们要及时发现、确诊，充分认识其危害性，针对传染病流行的三个基本环节，采取积极有效的预防措施，确保自身安全°下列疾病中属于传染病的是（A ）①血吸虫病②艾滋病③近视眼④蛔虫病⑤糖尿病⑥肺结核⑦佝偻病⑧ 脊髓灰质炎A.①②④⑥⑧B.①②③⑤⑦C.②④⑥⑦⑧D.①③⑤⑥⑦4.阅读下列资料并回答问题。

中东呼吸综合征（MERS）是由一种新型冠状病毒（MERS-CoV）引起的病毒性呼吸道疾病，该病毒于2012年在沙特阿拉伯首次被发现，能引起人发生从普通感冒到严重呼吸综合征的多种疾病。

（1）该病毒和其他病毒一样，结构十分简单，仅由核酸和蛋白质组成。

（2）己康复的患者体内产生了相应的抗体，不会再患该病，这属于特旻（填“特异” 或“非特异”）性免疫。

（3）对患者采取单独隔离属于传染病预防措施中的控制传染源,引起该病的病毒（MERS-CoV）是病原体（填“病原体”或“传染源”）。

知识点2人体的免疫5.人体具有保卫自身的三道防线，第一道防线是（A ）A.皮肤和黏膜B.免疫器官C.体液中的杀菌物质和吞噬细胞D.免疫细胞6.吃饭时口腔内壁不慎被牙齿咬破，但这种伤口一般不会感染发炎，这是因为唾液中含（D ）A.抗原B.抗体C.消化酶D.溶菌酶7.如图是有关免疫的漫画，能形象表示人体第三道防线的是（B ）第7题图A. 御敌于国门之外B.定点清除C.扫地出门D.城市巷战8. 产生肿瘤和引起花粉过敏的原因分别是（B ）A. 免疫功能过强、免疫功能过强B. 免疫监视出现异常、免疫防御功能过强C. 免疫功能较弱、免疫监视出现异常D. 免疫清除出现异常、免疫功能过弱9. 从现代免疫的概念来看，下列不属于抗原物质的是（D ）A. 癌细胞B. 因强烈打击而破裂的红细胞C. 移植的器官D. 自身血液中的红细胞10. 得了 “尿毒症”的病人如果要根治，现在最常用的方法就是进行“换肾”手术。

浙教版八年级下科学第三章3.1-3.2练习及答案解析

浙教版八年级下科学第三章 3.1-3.2练习以及答案解析一、单选题1.燃烧是人类最早利用的化学反应之一，人类已有几十万年的利用燃烧反应的历史。

燃烧需要具备的条件是（）①可燃物②氧气或空气③温度达到着火点A. ①②B. ②③C. ①③D. ①②③2.下列各图所示的实验操作中，正确的是（）A. 检查装置的气密性B. 点燃酒精灯C. 制取氧气D. 用滴管滴加液体3.对下列实验指定容器中的水，其解释没有体现水的主要作用的是（）实验装置解释A 集气瓶中的水：吸收放出的热量B 烧杯中的水：加热铜片，隔绝空气C 集气瓶中的水：冷却溅落熔融物，防止集气瓶炸裂D 集气瓶中的水：水先将集气瓶内的空气排尽，后便于观察O2何时收集满A. AB. BC. CD. D4.下列做法正确的是( )A. 厨房煤气管道漏气，马上打开抽风机B. 冬天关闭门窗用煤炉取暖C. 实验桌上少量酒精着火，迅速用湿布盖灭D. 家用电器着火，立即浇水灭火5.下列关于氧气性质的叙述中，不属于氧气物理性质的是( )A. 在通常情况下，氧气是无色无味的气体B. 氧气具有助燃性，可以支持燃烧C. 在标准状况下，氧气的密度是 1.429克/升D. 氧气不易溶于水6.下列实验操作中，“先”与“后”的顺序正确的是（）A. 制取气体时，先装药品，后检查装置的气密性B. 做氧气的助燃性实验时，先检查氧气的纯度，后点火C. 用排水法收集氧气结束时，先把导管移离水面，后停止加热D. 给试管里的液体加热时先加热，后预热7.实验室用如图所示装置制取氧气，下列有关说法不正确的是（）A. 试管中加入的药品是二氧化锰和过氧化氢B. 实验前应检查装置的气密性C. 待导管口产生连续均匀的气泡时才开始收集氧气D. 实验结束时应先从水槽中取出导管，再停止加热8.“防火胜于救火”，科学认识燃烧，增强安全防范意识是每个公民应具备的安全素养之一。

下列说法错误的是（）A. 身上着火不可乱跑，要就地打滚使火熄灭B. 水能灭火，是因为水能使可燃物的温度降低到着火点以下C. 对于不明原因引起的失火，我们宁可让其自生自灭，也不能贸然采取灭火措施D. 油库、面粉厂、纺织厂、轮穀厂、橡胶厂和煤矿的坑道内等场所要严禁烟火，以避免爆炸的发生9.下列说法中，正确的是（）①需要加热才能发生的反应一定是吸热反应；②化学能可转化为光能，光能不能转化为化学能；③镁与盐酸的反应中，参加反应的镁、盐酸的能量和大于氯化镁溶液、氢气的能量和；④化学反应一定伴随能量变化，有能量变化一定发生化学反应A. ①②③B. ③④C. ②③④D. 只有③10.下列有关燃烧、灭火的分析正确的是（）A. 火上浇油：增大可燃物与氧气的接触面积B. 钻木取火：提高可燃物的温度达到着火点C. 吹灭烛火：降低着火点D. 电器着火：用水浇灭11.运用如图所示装置探究可燃物的燃烧条件，下列说法错误的是（）A. ①②现象对比，说明温度达到可燃物的着火点是燃烧条件之一B. ①③现象对比，说明有氧气参与是燃烧条件之一C. 白磷的着火点低于80 ℃D. 热水只起到加热作用12.下列说法：①呼吸作用、食物腐烂、铁生锈都是缓慢氧化；②燃烧是可燃物与氧气发生的剧烈的化合反应；③急速的燃烧一定会爆炸；④自燃是缓慢氧化引起的；⑤白磷在空气中和氧气中的着火点不同；⑥燃烧、自燃、缓慢氧化的共同点都是氧化反应并都有热量产生。

第三章位置与坐标B卷压轴题考点训练(解析版)

第三章位置与坐标B 卷压轴题考点训练1．如图，在△ACB 中，∠ACB ＝90°，AC ＝BC ，点C 的坐标为（﹣2，0），点A 的坐标为（﹣8，3），点B 的坐标是_____．【答案】(1,6)【详解】解：如图所示，过A 和B 分别作AD OC^于D ，BE OC ^于E ，即12390Ð=Ð=Ð=°，∴∠DAC +∠ACD =∠ACD +∠ECB=90°，∴DAC ECB Ð=Ð，∴ACD CBE Ð=Ð，在Rt ACD △，Rt CEB △中，∵DAC ECB AC CB ACD CBE Ð=Ðìï=íïÐ=Ðî，∴(ASA)ADC CEB @V V ，∴DC BE =，AD CE =，∵点C 的坐标为(2,0)-，点A 的坐标为(8,3)-，∴2OC =，3AD CE ==，8OD =，∴6CD OD OC =-=，1OE CE OC =-=，∴6BE =，∴则B 点的坐标是(1,6)．故答案是：(1,6)．2．如图，P 为MON Ð内部的已知点，连接OP ，A 为OM 上的点，B 为ON 上的点，当PAB ∆周长的最小值与OP 的长度相等，MON Ð的度数为___°．【答案】30【详解】解：作点P 关于OM 的对称点C ，关于ON 的对称点D ，连接CD ，交OM 于A ，交ON 于B ．此时，△PAB 的周长最小．连接OC ，OD ，PA ，PB ．∵点P 与点C 关于OM 对称∴OM 垂直平分PC∴∠COM=∠MOP ，PA=CA ，OC=OP同理，可得∠DON=∠NOP ，PB=DB ，OD=OP∴∠COA+∠DOB=∠AOP+∠BOP=∠MON∴∠COD=2∠MON又∵△PAB 的周长=PA+AB+BP=CA+AB+BD=CD=OP∴OC=OD=CD∴△COD 是等边三角形∴∠MON 30=°故答案为：30．3．已知点A ，B 的坐标分别为(2，0)，(2，4)，以A ，B ，P 为顶点的三角形与ABO V 全等，点P 与点O 不重合，写出符合条件的点P 的坐标：___________．【答案】(4,4)或(0,4)或(4,0)4．如图，点A 的坐标为()4,0，点B 的坐标为()0,1-，分别以OB ，AB 为直角边在第三、第四象限作等腰Rt OBF △，等腰Rt ABE △，连接EF 交y 轴于P 点，点P 的坐标是______．【答案】()0,3-【详解】解：如图，作EN y ^轴于N ，5．如图，Rt△ABC≌Rt△FDE，∠ABC＝∠FDE＝90°，∠BAC＝30°，AC＝4，将Rt△FDE沿直线l向右平移，连接BD、BE，则BD+BE的最小值为___．别找一点E、F，使得BEFV周长的最小值为__________．V的周长最小，则BEF7．如图，在平面直角坐标系中，等腰直角三角形1OAA 的直角边OA 在x 轴上，点1A 在第一象限，且1OA =，以点1A 为直角顶点，1OA 为一直角边作等腰直角三角形12OA A ，再以点2A 为直角顶点，2OA 为直角边作等腰直角三角形23OA A ……依此规律，则点2022A 的坐标是________．8．如图，在平面直角坐标系中，点A （0，4）在y 轴正半轴上，点B （－3，0）在x 轴负半轴上，且AB =5，点M 坐标为（3，0），N 点为线段OA 上一动点，P 为线段AB 上的一动点，则MN +NP 的最小值为___________．9．如图，在平面直角坐标系中，点A 从()14,0A -依次跳动到()241A -，，()33,1A -，()430A -，，()520A -，，()623A -，，()713A -，，()810A -，，()913A --，，()1003A -，，()1100A ，，…，按此规律，则点2022A 的坐标是______________【答案】（804，1）【详解】解：观察图形可知，ｎ为正整数时，n A 的纵坐标为0，1，3，﹣3纵坐标为0的点：14581114,,,A A A A A A LL纵坐标为1的点：2312132223,,,A A A A A A LL纵坐标为3的点：6716172627,,,A A A A A A LL纵坐标为﹣3的点：91019202930,,,A A A A A A LL可以看出纵坐标为1，3，﹣3时，ｎ取连续的两个数为一组，则10个10个的增加，∵2021＝10×202＋1，纵坐标为1的规律()()()210121011n n A A +-+-+，∴2022A 的纵坐标为1，由()21012022n +-=，解得n ＝203，∵2022A 正好是2A 往右循环203次，∴2022A 横坐标为﹣4＋（203－1）×4＝804，∴点2022A 的坐标是（804，1），故答案为：（804，1）10．如图，四边形OABC 是正方形，点M ，N 都在OA 的延长线上，且OM ＝MN ＝2，则BM+BN 的最小值为______．则MN′=BM+BN 的值最小，由对称性可知，ON ON ¢=，11．如图，在平面直角坐标系上有点A （1，0），第一次点A 跳动至点A 1（﹣1，1），第二次点A 1跳动至点A 2（2，1），第三次点A 2跳动至点A 3（﹣2，2），第四次点A 3跳动至点A 4（3，2），依此规律跳动下去，则点A 2017与点A 2018之间的距离是__________．【答案】2019【详解】由跳动规律可归纳类推出以下3条规律：（其中n 为正整数）（1）点51213,,,,n A A A A -L 的横坐标依次为1,2,3,,n----L （2）点2462,,,,n A A A A L 的横坐标依次为2,3,4,,1n +L （3）点1A 与点2A ，点3A 与点4A ，点5A 与点6A ，L ，点21n A -与2n A 的纵坐标分别相等2017210091=´-Q ，201821009=´\点2017A 的横坐标为1009-，点2018A 的横坐标为100911010+=，且点2017A 与点2018A 的纵坐标相等则点2017A 与点2018A 之间的距离是10101009)0(219--=故答案为：2019．12．对于平面直角坐标系xOy 中的图形G 和点P ，给出如下定义：将图形G 沿上、下、左、右四个方向中的任意一个方向平移一次，平移距离小于或者等于1个单位长度，平移后的图形记为G ¢，若点P 在图形G ¢上，则称点P 为图形G 的稳定点，例如，当图形G 为点(2,3)-时，点(1,3),(2,3.5)M N --都是图形G 的稳定点．(1)已知点(1,0),(2,0)A B -．①在点1234133(2,0),(4,0),1,,,222P P P P æöæö--ç÷ç÷èøèø中，线段AB 的稳定点是___________．②若将线段AB 向上平移t 个单位长度，使得点(0,1)E 或者点(0,5)F 为线段AB 的稳定点，写出t 的取值范围___________．(2)边长为a 的正方形，一个顶点是原点O ，相邻两边分别在x 轴、y 轴的正半轴上，这个正方形及其内部记为图形G ．若以(0,2),(4,0)为端点的线段上的所有点都是这个图形G 的稳定点，直接写出a 的最小值___________．【答案】(1)①1P ，3P ；②0≤t ≤2或4≤t ≤6；(2)3【解析】（1）解：①如图1中，观察图象，根据图形G 的稳定点的定义可知：1P ，3P 是线段AB 的稳定点．故答案为：1P ，3P ；②如图2中，观察图象可知当0≤t ≤2或4≤t ≤6时，点E （0，1）或者点F （0，5）为线段AB 的稳定点．故答案为：0≤t ≤2或4≤t ≤6；（2）解：如图3中，正方形OABC 的边长为a ，P （0，2），Q （4，0），观察图象可知当3≤a 时，线段PQ 上的点都是图形G 的稳定点．∴a 的最小值为3，故答案为：3．13．在平面直角坐标系中，(6,),(,0),(0,)A a B b M c ，且2(2)|6|0b a -+-=，P 点为y 轴上一动点．(1)求点B 、M 的坐标；(2)当P 点在线段OM 上运动时，试问是否存在一个点P 使13PAB S =V ，若存在，请求出P 点的坐标；若不存在，请说明理由．(3)不论点P 点运动到直线OM 上的任何位置（不包括点O ，M ），PAM Ð、APB Ð、PBO Ð三者之间是否都存在某种固定的数量关系，如果有，请写出来并请选择其中一种结论进行证明；如果没有，请说明理由．于B．(1)求△ABC的面积；(2)如图2，过点B作BD CA∥交y轴于D，且AE，DE分别平分∠CAB与∠BDO，求∠AED的度数；(3)如图1，在y轴上是否存在点P，使得△ACP和△ABC的面积相等？若存在，求出点P坐标；若不存在，请说明理由．15．如图①，在平面直角坐标系中，A(a，0)，C(b，2)，且满足(a+2)2 +2b-=0，过C作CB⊥x轴于B．(1)直接写出三角形ABC的面积；(2)如图②，若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，求∠AED的度数；(3)在y轴上是否存在点P，使得三角形ACP和三角形ABC的面积相等？若存在，求出P点的坐标；若不存在，请说明理由．。

九年级数学(下)第三章知识点总结、测试题及答案

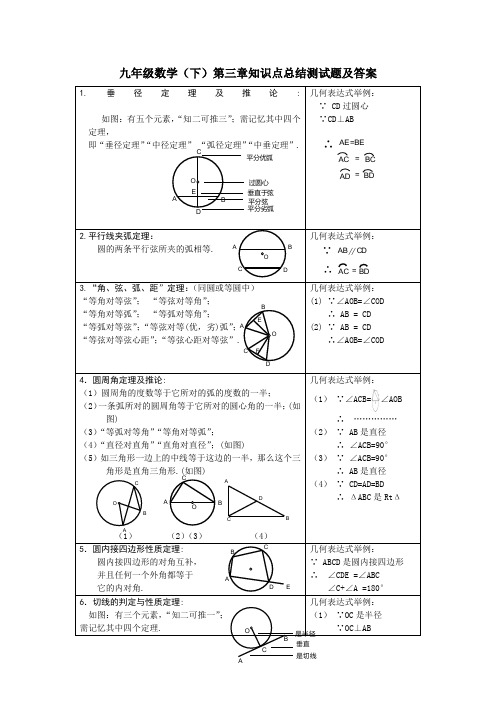
九年级数学（下）第三章知识点总结测试题及答案1.垂径定理及推论: 如图：有五个元素，“知二可推三”；需记忆其中四个定理，即“垂径定理”“中径定理” “弧径定理”“中垂定理”.几何表达式举例： ∵ CD 过圆心 ∵CD ⊥AB 2.平行线夹弧定理：圆的两条平行弦所夹的弧相等.几何表达式举例： 3.“角、弦、弧、距”定理：（同圆或等圆中）“等角对等弦”； “等弦对等角”；“等角对等弧”； “等弧对等角”；“等弧对等弦”；“等弦对等(优，劣)弧”；“等弦对等弦心距”；“等弦心距对等弦”.几何表达式举例： (1) ∵∠AOB=∠COD∴ AB = CD (2) ∵ AB = CD∴∠AOB=∠COD4．圆周角定理及推论:（1）圆周角的度数等于它所对的弧的度数的一半；（2）一条弧所对的圆周角等于它所对的圆心角的一半；(如图) （3）“等弧对等角”“等角对等弧”；（4）“直径对直角”“直角对直径”；(如图)（5）如三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.(如图)（1）（2）（3）（4）几何表达式举例：（1） ∵∠ACB=∠AOB∴ …………… （2） ∵ AB 是直径∴ ∠ACB=90° （3） ∵ ∠ACB=90°∴ AB 是直径（4） ∵ CD=AD=BD∴ ΔABC 是Rt Δ5．圆内接四边形性质定理:圆内接四边形的对角互补，并且任何一个外角都等于它的内对角.几何表达式举例：∵ ABCD 是圆内接四边形 ∴ ∠CDE =∠ABC∠C+∠A =180° 6．切线的判定与性质定理: 如图：有三个元素，“知二可推一”；需记忆其中四个定理.几何表达式举例：（1） ∵OC 是半径∵OC ⊥ABABCD OA B CDE O 平分优弧过圆心垂直于弦平分弦平分劣弧∴ AC BCAD BD ==AE=BEA BC DEFOA B COABCDEABC OA B CD∵ ∴ ∥=AB CD ACBDABCO是半径垂直是切线（1）经过半径的外端并且垂直于这条半径的直线是圆的切线；（2）圆的切线垂直于经过切点的半径；‴（3）经过圆心且垂直于切线的直线必经过切点； ‴（4）经过切点且垂直于切线的直线必经过圆心.∴AB 是切线（2） ∵OC 是半径∵AB 是切线 ∴OC ⊥AB （3） ……………7．切线长定理:从圆外一点引圆的两条切线，它们的切线长相等；圆心和这一点的连线平分两条切线的夹角.几何表达式举例：∵ PA 、PB 是切线 ∴ PA=PB ∵PO 过圆心 ∴∠APO =∠BPO 8．弦切角定理及其推论:（1）弦切角等于它所夹的弧对的圆周角；（2）如果两个弦切角所夹的弧相等，那么这两个弦切角也相等；（3）弦切角的度数等于它所夹的弧的度数的一半.（如图）几何表达式举例：（1）∵BD 是切线，BC 是弦∴∠CBD =∠CAB（2）∵ ED ，BC 是切线 ∴ ∠CBA =∠DEF9．相交弦定理及其推论: （1）圆内的两条相交弦，被交点分成的两条线段长的乘积相等；（2）如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段长的比例中项.几何表达式举例：（1） ∵PA ²PB=PC ²PD∴……… （2） ∵AB 是直径∵PC ⊥AB∴PC 2=PA ²PB10．切割线定理及其推论:（1）从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项；（2）从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等.几何表达式举例：（1） ∵PC 是切线，PB 是割线 ∴PC 2=PA ²PB （2） ∵PB 、PD 是割线∴PA²PB=PC ²PD11．关于两圆的性质定理:（1）相交两圆的连心线垂直平分两圆的公共弦；（2）如果两圆相切，那么切点一定在连心线上.几何表达式举例：（1） ∵O 1，O 2是圆心∴O 1O 2垂直平分AB （2） ∵⊙1 、⊙2相切∴O 1 、A 、O 2三点一线AB CD ABC DEF P ABO AB CPA BC D P AB O1O2A O1O2AB C D P A B CPO ∵ EF AB =A B O （1）（2）12．正多边形的有关计算:（1）中心角αn ，半径R N ，边心距r n ，边长a n ，内角βn ，边数n ；（2）有关计算在Rt ΔAOC 中进行.公式举例：(1) αn =； (2)几何B 级概念：（要求理解、会讲、会用，主要用于填空和选择题）一基本概念：圆的几何定义和集合定义、弦、弦心距、弧、等弧、弓形、弓形高三角形的外接圆、三角形的外心、三角形的内切圆、三角形的内心、圆心角、圆周角、弦切角、圆的切线、圆的割线、两圆的内公切线、两圆的外公切线、两圆的内（外）公切线长、正多边形、正多边形的中心、正多边形的半径、正多边形的边心距、正多边形的中心角. 二定理：1．不在一直线上的三个点确定一个圆.2．任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆.3．正n 边形的半径和边心距把正n 边形分为2n 个全等的直角三角形. 三公式：1.有关的计算：（1）圆的周长C=2πR ；（2）弧长L=；（3）圆的面积S=πR 2.（4）扇形面积S 扇形 =；（5）弓形面积S 弓形 =扇形面积S AOB ±ΔAOB 的面积.（如图）2.圆柱与圆锥的侧面展开图：（1）圆柱的侧面积：S 圆柱侧 =2πrh ； (r:底面半径；h:圆柱高)（2）圆锥的侧面积：S 圆锥侧 =. （L=2πr ，R 是圆锥母线长；r 是底面半径）四常识：1．圆是轴对称和中心对称图形.2．圆心角的度数等于它所对弧的度数.3．三角形的外心 ⇔ 两边中垂线的交点 ⇔ 三角形的外接圆的圆心；三角形的内心 ⇔ 两内角平分线的交点 ⇔ 三角形的内切圆的圆心. 4．直线与圆的位置关系：（其中d 表示圆心到直线的距离；其中r 表示圆的半径）直线与圆相交 ⇔ d ＜r ；直线与圆相切 ⇔ d=r ；直线与圆相离 ⇔ d ＞r. 5．圆与圆的位置关系：（其中d 表示圆心到圆心的距离，其中R 、r 表示两个圆的半径且R ≥r ）两圆外离 ⇔ d ＞R+r ；两圆外切 ⇔ d=R+r ；两圆相交 ⇔ R-r ＜d ＜R+r ；αnβnABCDEOa r n nnR两圆内切 ⇔ d=R-r ；两圆内含 ⇔ d ＜R-r. 6．证直线与圆相切，常利用：“已知交点连半径证垂直”和“不知交点作垂直证半径” 的方法加辅助线.7．关于圆的常见辅助线：O CAB已知弦构造弦心距.OA BC已知弦构造Rt Δ.OABC已知直径构造直角.OAB已知切线连半径，出垂直.O BC AD P圆外角转化为圆周角.OACD BP圆内角转化为圆周角.ODC PAB构造垂径定理.OACDPB构造相似形.M01ANO2两圆内切，构造外公切线与垂直.01CNO2DEABM两圆内切，构造外公切线与平行. NAM02O1两圆外切，构造内公切线与垂直.CBMNADEO 102两圆外切，构造内公切线与平行.CE A DB O两圆同心，作弦心距，可证得AC=DB.A CBO102两圆相交构造公共弦，连结圆心构造中垂线. BAC OPPA 、PB 是切线，构造双垂图形和全等.OABCDE相交弦出相似.OP ABC一切一割出相似, 并且构造弦切角.OBCEADP两割出相似,并且构造圆周角. OABCP双垂出相似,并且构造直角.BACD EF规则图形折叠出一对全等，一对相似.FED BAC O GH圆的外切四边形对边和相等.ABOCD若AD ∥BC 都是切线，连结OA 、OB 可证∠AOB=180°，即A 、O 、B 三点一线.EACBOD等腰三角形底边上的的高必过内切圆的圆心和切点,并构造相似形.EFCDBAORt ΔABC 的内切圆半径：r=.O补全半圆.ABCo1o2AB=.CABo1o2AB=.AC D PO BPC 过圆心，PA 是切线，构造双垂、Rt Δ. BCD OAPO 是圆心，等弧出平行和相似.DE MABCFN G作AN ⊥BC ，可证出:.九年级数学（下）第三章测试题（答题时间：120分钟总分：120分）一、选择题：（每题3分，共36分） 1. 下列五个命题：（1）两个端点能够重合的弧是等弧；（2）圆的任意一条弧必定把圆分成劣弧和优弧两部分；⑶经过平面上任意三点可作一个圆；⑷任意一个圆有且只有一个内接三角形；⑸三角形的外心到各顶点距离相等．其中真命题有（） A. 1个 B. 2个 C. 3个 D. 4个2. AB 是⊙O 的弦，∠AOB=88°，则弦AB 所对的圆周角等于（） A. 44° B. 22° C. 44°或136° D. 22°或68°3. O 是△ABC 的外心，且∠ABC+∠ACB=100°，则∠BOC=（） A. 100° B. 120° C. 130° D. 160°4. 一个点到圆的最大距离为9cm ，最小距离为4cm ，则圆的半径是（） A. 5cm 或13cm B. 2.5cm C. 6.5cm D. 2.5cm 或6.5cm5. 如图1，⊙O 外接于△ABC ，AD 为⊙O 的直径，∠ABC=30°，则∠CAD=（） A. 30° B. 40° C. 50° D. 60°6. 如图2，△ABC 的三边分别切⊙O 于D ，E ，F ，若∠A=50°，则∠DEF=（） A. 65° B. 50° C. 130° D. 80°BDCA OBEDCA FO图1 图2 图3 7.在Rt △ABC 中，∠C=90°，AB=5，内切圆半径为1，则三角形的周长为（） A. 15 B. 12 C. 13 D. 148. 在Rt △ABC 中，∠C=90°，AB=5cm ，BC=3cm ，以A 为圆心，以4cm 为半径作圆，•则直线BC 与⊙A 的位置关系是（）A. 相交B. 相切C. 相离D. 无法确定9. 已知两圆的圆心距为3，两圆的半径分别是方程x 2－4x+3=0的两根，•那么这两个圆的位置关系是（）A. 外离B. 外切C. 相交D. 内切10. ⊙O 的半径为3cm ，点M 是⊙O 外一点，OM=4cm ，则以M 为圆心且与⊙O •相切的圆的半径一定是（）A. 1cm 或7cmB. 1cmC. 7cmD. 不确定11. 一个扇形半径30cm ，圆心角120°，用它作一个圆锥的侧面，则圆锥底面半径为（） A. 5cm B. 10cm C. 20cm D. 30cm12. 如图3所示，在△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于点D ，交AC 于点E ，•连结OD 、AD ，则以下结论：①D 是BC 的中点；②AD ⊥BC ；③AD 是∠BAC 的平分线；④OD ∥AC ．其中正确结论的个数为（）A. 1个B. 2个C. 3个D. 4个二、填空题. （每题3分，共30分）13. ⊙O 中，弦MN 把⊙O 分成两条弧，它们的度数比为4：5，如果T 为MN 中点，则∠TMO=_________，则弦MN 所对的圆周角为_______．14. ⊙O 到直线L 的距离为d ，⊙O 的半径为R ，当d 、R 是方程x 2－4x+m=0的根，且L •与⊙O 相切时，m 的值为_________．15. ⊙O 中，若弦AB 、BC 所对的圆心角分别为120°、80°，则弦AC •所对的圆心角为_____；16. 如图4所示，AB 为⊙O 的直径，C 、D 是⊙O 上的两点，∠BAC=20°，⋂⋂=CD AD ，•则∠DAC 的度数是_______．17. 在△ABC 中，AB=5cm ，BC=3cm ，AC=4cm ，则△ABC 的内切圆的半径为_________．18. △ABC 三边与⊙O 分别切于D ，E ，F ，已知AB=7cm ，AC=5cm ，AD=2cm ，则BC=________．图419. 如图5所示，P 为⊙O 外一点，PA 、PB 、AB 都与⊙O 相切，∠P=40°，则∠AOB 的度数为_________．20. 两圆相切，圆心距等于2cm ，其中一个圆的半径等于3cm ，•则另一个圆的半径等于_________．21. 已知两圆外离，圆心距d=12，大圆半径R=7，则小圆半径r •的所有可能的正整数值为_________．22. 圆心角为120°的扇形的弧长是2πcm ，则此扇形的面积为___________．图5三、解答题. （第23、24、25题各6分、第26题各7分，第27题8分，共34分） 23. 如图6，从点P 向⊙O 引两条切线PA ，PB ，切点为A ，B ，AC 为弦，BC 为⊙O •的直径，若∠P=60°，PB=2cm ，求AC 的长．24. 如图，已知扇形AOB 的半径为12，OA ⊥OB ，C 为OB 上一点，以OA 为直径的半圆O 1与以BC 为直径的半圆O 2相切于点D ．求图中阴影部分面积．BCAPO图625. 如图所示，⊙I 是△ABC 的内切圆，AB=9，BC=8，CA=10，点D 、E 分别为AB 、AC 上的点，且DE 是⊙I 的切线，求△ADE 的周长．26. 如图，C 是⊙O 的直径AB 延长线上一点，过点C 作⊙O •的切线CD ，D 为切点，连结AD ，OD ，BD ．请根据图中给出的已知条件（不再标注字母，不再添加辅助线）写出两个你认为正确的结论．27. 如图，已知弦AB 与半径相等，连结OB ，并延长使BC=OB ．（1）问AC 与⊙O 有什么关系．（2）请你在⊙O 上找出一点D ，使AD=AC （自己完成作图，并证明你的结论）．mBDCAOB CAO【试题答案】一、选择题：1. A ．2. D ．3. C ．4. D5. D6. A ．7. B ．8. B ．9. C ． 10. A ． 11. B ． 12. D ．二、填空题：13. 10°，80°或100° 14. 4． 15. 40°或160°．16. 35°17. 1cm ． 18. 8cm ．19. 70°．20. 1cm 或5cm ．21. 1，2，3，4．22. 3πcm 2 三、解答题：23. 解：连结AB ．∵∠P=60°，AP=BP ， ∴△APB 为等边三角形．AB=PB=2cm ，PB 是⊙O 的切线，PB ⊥BC ， ∴∠ABC=30°， ∴AC=AB ²tan30°=2²33=233．24. 解：扇形的半径为12，则1O ⊙r =6，设⊙O 2的半径为R ．连结O 1O 2，O 1O 2=R+6，OO 2=12－R ．∴Rt △O 1OO 2中，36+（12－R ）2=（R+6）2， ∴R=4． S 扇形=14π·122=36π，S ′=12π·62=18π，S ″=12π²42=8π． ∴S 阴=S 扇形－S ′－S ″=36π－18π－8π=10π．25. 11．26. 答案：CD 2=CB ²CA 或∠CDB=∠A ． 27. 解：（1）证明：如图，∵AB 与半径相等，∴∠OAB=60°，∠OBA=60°．∵BC=OB=AB ，∴∠BAC=30°， ∴∠OAC=90°，∴AC 与⊙O 相切．（2）①延长BO 交⊙O 于D ，则必有AD=AC ．证明：∵∠BOA=60°，OA=OD ， ∴∠D=30°．又∵∠C=30°，∴∠C=∠D ，∴AD=AC ．②作∠OAB 的角平分线交⊙O 于D ，则AD=AC证明略。

浙教版七年级下册第三章事件的可能性练习及答案

浙教版七年级下册第三章事件的可能性练习及答案班级学号姓名一、细心选一选（每小题3分，共36分）1.数学老师抽一名同学回答问题，，抽到女同学是………………………………( )A.必定事件B.不确定事件C.不可能事件D.无法判定2.在一个装有黑色围棋的盒子中摸出一颗棋子，摸到一颗白棋是………………( )A.必定事件B.不确定事件C.不可能事件D.无法判定3.从一副扑克牌中任意抽出一张，可能性相同的的是……………………………( )A.大王与黑桃B.大王与10C.10与红桃D.红桃与梅花4.一个袋中装有8只红球，每个求出颜色外都相同，人一摸一个球，则…… ( )A.专门可能摸到红球B. 可能摸到红球C. 一定摸到红球D.不大可能摸到红球5.从一副扑克牌（除去大王）中任取一张，抽到的可能性较小的是………………( )A.红桃5B.5C.黑桃D.梅花5或86. 下列事件中，不确定事件是……………………………………………………( )A.在空气中，汽油遇上火就燃烧B.向上用力抛石头，石头落地C.下星期六是晴天D.任何数和零相乘，积仍为零7.甲袋中装着2只红球、8只白球，乙袋中装着8只红球、2只白球。

假如你想从两个口袋中取出一只白球，成功机会较大的是………………………………………( )A.甲袋B.乙袋C.甲、乙两个口袋一样D.无法确定8.如图是一个能够自由转动的转盘，转动那个转盘，当它停止转动时，指针最可能停留的区域是………………………………………( )A.1B. 2C. 3D. 49.掷一枚平均的骰子，骰子停止转动后朝上一面的点数显现以下情形的概率最小的是…………………………………………………………………………………( )A.偶数B.奇数C.比5小的数D.数610.从1到9这9个自然数中任取一个，是2的倍数的概率是………………( )A.39B.49C.59D.111. 从1到9这9个自然数中任取一个，是2的倍数或是3的倍数的概率是……( )A. 19B.29C.23D.5912.一个盒子里装有若干个红球和白球，每个球除颜色以外都相同.5位同学进行摸球游戏，每位同学摸10次（摸出1球后放回，摇匀后再连续摸），其中摸到红球数依次为8，5，9，7，6，则估量盒中红球和白球的个数是……………………………( )A.红球比白球多B.白球比红球多C.红球、白球一样多D.无法估量二、用心填一填：（每小题3分，共18分）13.围棋有黑、白两种棋子，混合在一起后，随意从中摸出3个棋子，正好颜色相同，这是事件（填“必定”、“不可能”或“不确定”）14.从装有8个红球、2个白球的袋子中随意摸出一个球，摸到可能性较小的是球.15.袋中装有10个小球，颜色为红、白、黑三种，除颜色外其他均相同。

2020春北师版九年级数学下册第3章点拨习题全章热门考点整合专训

(2)若 m＝6，通过计算判断⊙O 与 CD 的位置关系；解：当 m＝6 时， 23m＝3 3>5，故⊙O 与 CD 相离．
(3)若⊙O 与线段 CD 有两个公共点，求 m 的取值范围．解：若⊙O 与线段 CD 有两个公共点，则该圆和线段 CD 相交，当点 C 在圆上时，m＝12AB＝5；当线段 CD 与⊙O 相切时，m＝130 3. 所以 m 的取值范围是 5≤m<130 3.
【答案】A
14．(2019·泰安)如图，将⊙O 沿弦 AB 折叠，A︵B恰好经过圆心 O，若⊙O 的半径为 3，则A︵B的长为( C ) A．12π B．π C．2π D．3π
【点拨】如图，连接 OA，OB，作 OC⊥AB 于点 C.
由题意得 OC＝12OA，∴∠OAC＝30°.
∵OA＝OB，∴∠OBA＝∠OAC＝30°.
A．0 B．1 C．2 D．无数条
8．如图，在▱ABCD 中，∠D＝60°，以 AB 为直径作⊙O，已知 AB＝10，Aபைடு நூலகம்＝m.
(1)求点 O 到 CD 的距离(用含 m 的代数式表示)；解：根据平行线间的距离处处相等，得点 O 到 CD 的距离即为点 A 到 CD 的距离．根据∠D＝60°， AD＝m，利用“直角三角形中，30°角所对的直角边等于斜边的一半”及勾股定理，得点 O 到 CD 的距离是 23m.
20．(2019·包头)如图，BD 是⊙O 的直径，A 是⊙O 外一点，点 C 在⊙O 上，AC 与⊙O 相切于点 C，∠CAB＝90°.若 BD＝6， AB＝4，∠ABC＝∠CBD，则弦 BC 的长为__2__6____．
易知四边形 OFAE 为正方形．设 OE＝r，则 AE＝AF＝r. ∵△ABC 的内切圆⊙O 与 BC，CA，AB 分别相切于点 D，E，F， ∴BD＝BF＝5－r，CD＝CE＝12－r. ∴5－r＋12－r＝13. ∴r＝5＋122－13＝2. ∴阴影部分(即四边形 AEOF)的面积是 2×2＝4.

浙教版九年级下科学第三章3.1-3.3练习以及答案解析

浙教版九年级下科学第三章3.1-3.3练习以及答案解析一、单选题1.饮食安全与人体健康息息相关，下列事例不属于非细菌性食物中毒的是（）A.食用残留农药的蔬菜引起中毒B.食用含亚硝酸盐的腌制品引起中毒C.食用毒蘑菇引起中毒D.食用超过保质期的月饼引起中毒2.健康是人生最宝贵的财富之一。

下列关于现代生活与人类健康的叙述，正确的是（）A.感冒药是家庭常备药物，过期一两周仍可服用B.香烟中的尼古丁、焦油等会损坏人体的呼吸系统C.吸毒能使人在短时间内极度兴奋，可以少量使用毒品D.遇到好玩的网络游戏，可以废寝忘食地连续数日去攻关3.食品卫生与身体健康密切相关。

下列做法会导致食品对人体健康有害的是（）A.用石灰水保存鸡蛋B.蒸馒头加适量纯碱C.在食品中添加防腐D.在食盐中添加适量碘元素4.酒后驾车明显表现为反应慢、动作不协调，容易导致交通事故。

这主要是因为酒精影响驾驶员的（）A.脊髓、肝脏B.眼睛、心脏C.脑干、肺D.大脑、小脑5.体育课后口渴难耐，如果四位同学回到教室发现每个人只有半杯水，从各位的对话中，你认为需要加强心理健康教育的同学应该是( )A.“哈，还有半杯水，真不错!”B.“太渴了，有水喝真好!”C.“OK!半杯水也能解决问题．”D.“哎，真倒霉！怎么只有半杯水”6.在德州市春季中小学运动会上，多项记录被“尘封”，难以打破，学生身体素质总体下滑。

关于此现象的观点叙述，正确的是( )A.只要吃的好，身体素质就好B.科学文化素质比身体素质更重要C.实施健康计划，坚持阳光体育活动D.体育竞技是运动员的职责，与我们无关7.下列各项中，哪一个的健康状况最理想？( )A.对人生悲观失望，不存在任何幻想的小毕B.无病，精神萎靡不振的阿菊C.虽然没钱，但乐于助人的小红D.为了达到目的不择手段的小明8.人的身体、心理和社会适应性等方面都应该保持健康良好的状态。

下列做法中，不利于健康的是( )A.进行体育锻炼，增强身体体质B.遇到烦心事，就抽烟、喝酒解闷C.学习与他人相处、合作和交流D.发现食品过了保质期就不食用9.在日常生活中，下列行为习惯不利于健康的是( )①常换毛巾和牙刷②常到街边小摊吃零食③蒙着被子睡大觉④借酒解愁A.①②③B.①②④C.①③④D.②③④10.小青同学得了流感，他自己到药店里买了一些头孢类抗生素，可是吃了几天后并没有减轻鼻塞、头痛等症状，其原因可能是（）A.这种抗生素药力不够B.抗生素失效了C.流感病毒有很强的抗药性D.抗生素不能抑制病毒的生长和繁殖11.在公共场合咳嗽或打喷嚏时，口腔或鼻腔液滴喷出2米以外，对他人带来最大危害是（）A.在公共场合咳嗽或打喷嚏不礼貌，影响他人B.在公共场合咳嗽或打喷嚏，液滴容易溅到别人衣服上，不文明C.在公共场合咳嗽或打喷嚏，液滴中细菌等会四处散布，危害他人健康D.以上说法都正确12.青霉素为20世纪医学上的重大发现，小明列出了以下几项有关青霉素的知识，其中有错误的是（）A.青霉素是青霉分泌的一种抗生素B.青霉素能使细菌的细胞壁变薄C.青霉素是由多种成分组成的混合物，其中一些对细菌是致命的D.青霉素是治疗细菌性疾病的特效药，目前青霉素类抗生素还在使用13.幽门螺旋杆菌能损伤胃黏膜造成胃炎和胃溃疡，可通过饮食等途径传播给健康人，对此正确的认识是（）A.幽门螺旋杆菌与酵母菌都属于细菌B.幽门螺旋杆菌引起的胃炎不是传染病C.聚餐使用“公筷”可以防止传染幽门螺旋杆菌D.抗生素对抑制幽门螺旋杆菌没有效果14.手足口病是一种常见的儿童传染性疾病，CA16病毒感染是主要致病原因。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

国际米兰中文网 wwΒιβλιοθήκη
[单选]为了确定飞机的位置，FMGS用来自哪里的数据：（）A、DME、VOR或ILSB、时钟+地面速度计算C、三个ADIRSD、以上A和C [单选,A2型题,A1/A2型题]胰岛素与受体结合后细胞内的特征性变化是（）。A.热休克蛋白自激素结合区水解B.IP3、DAG浓度增高C.cAMP减少D.cAMP增加E.受体β亚单位上酪氨酸磷酸化 [单选]物业管理的风险类型包括（）。A.前期物业管理的风险、日常管理的风险B.早期介入的风险、前期物业管理的风险C.早期介入的风险、日常管理的风险D.早期介入的风险、前期物业管理的风险、日常管理的风险 [多选]航空运输市场供给的特点主要有()A.运输供给的整体不可分性B运输供求的平衡难以控制B.运输供给的部分可替代性C.运输供给的外部性D.运输供给总是与需求处于均衡状态 [单选]发生运输收入事故时，应保护好现场，并立即电告收入管理部门和（）部门，及时组织破案。A.有关B.公安C.财务D.主管 [单选]以下应用中，必须采用栈结构的是（）。A.使一个整数序列逆转B.递归函数的调用和返回C.申请和释放单链表中的节点D.装入和卸载可执行程序 [单选]根据言语的描述或图样的示意，在人脑中产生相应的新形象的过程称为（）A．想象B．表象C．再造想象D．创造想象 [单选]以下（）协议能够为语音、图像、数据等多种需要实时传输的数据提供端到端的传输功能。A.TCPB.RTPC.UDPD.RTCP [单选]发生液漏时，只要增加上升气量，适当（）氧气取出量，保持上升气流的正常流速，液漏即可消除。A、减少B、不变C、增加 [问答题,简答题]电力需求侧管理的内容是什么？ [问答题,案例分析题]阅读下列说明，回答问题1至问题3【说明】某公司要开发一个多媒体辅导系统，该系统准备利用B/S架构，用户通过网上注册、登录，登录成功后，可进行在线学习辅导。 [单选]一事一议筹资筹劳属于（）负担。A.间接B.直接C.国家D.集体 [单选,A1型题]下列哪项不是臀位剖宫产的指征（）A.骨盆入口轻度狭窄B.巨大儿C.软产道异常D.高龄初产妇E.第二产程、脐带脱垂、胎儿存活 [单选]骨盆外测量骶耻外径（EC）的后标志点是（）.A.第五腰椎棘突上B.米氏菱形窝的上角C.腰骶部菱形窝的中央D.髂后上棘连线中点下2～2.5cmE.髂嵴后连线中点上1.5cm [单选,A1型题]颈部副神经损伤的临床表现为（）A.肩下垂B.上睑下垂C.呼吸困难D.声音嘶哑E.上臂下垂 [单选]下列哪项不属于CT扫描成像基本步骤()A．产生X线B．采集数据C．重建图像D．显示图像E．图像后处理 [单选]感染邪毒型产后发热的发热特点为（）A.高热寒战，热势不退B.发热恶寒，鼻流清涕C.身热微寒，头晕眼花D.潮热盗汗，颧红唇赤E.寒热交替，恶露臭秽 [单选]女，29岁，头痛、头昏10年，伴记忆力下降，根据所提供图像，最可能的诊断是()A．胶样囊肿B．蛛网膜囊肿C．胶质瘤D．室管膜瘤E．表皮样囊肿 [单选]有限责任公司若需要修改公司章程、增加或者减少注册资本等事项，必须经过()以上股东表决通过。A.1/2B.2/3C.1/3D.3/4 [单选]货物应（）、整理地堆码在指定货位上。A、稳定B、稳固C、均衡D、分层 [问答题,简答题]国家计划生育政策还强调一“安”二“扎”吗？ [单选]收货人于5月9日到某站领取整车危险货物一车，交付时货票丁联注明发出催领通知的时间为5月5日，应向收货人核收（）。A.货车停放费B.货物暂存费C.货车使用费D.过秤费 [填空题]收入在（）元以上的县（市）邮政局，可配备专职检查员。 [单选,A1型题]111In-DOCT（铟［111In］奥曲肽注射液），主要聚集在哪些受体阳性的肿瘤（）A.整合素受体阳性B.生长抑素受体阳性C.多巴胺受体阳性D.雌激素受体阳性E.血管活性肠肽受体阳性显像 [单选]在世界合作实运动中，得到公认的合作社原则起源于（）罗虚戴尔公平先锋社。A.美国B.法国C.英国D.德国 [单选]下面哪一项乳腺病变或结构不伴有后方回声增强（）。A.囊肿B.脂肪小叶C.扩张的导管D.纤维腺瘤E.脓肿 [单选,A1型题]患者男，28岁。右腰部被汽车撞伤4小时时，自觉右腰部疼痛，肉眼血尿，应首先考虑（）A.膀胱损伤B.肾损伤C.输尿管损伤D.尿道损伤E.肝破裂 [问答题,论述题]企业应如何控制和管理营销人员的道德规范？ [名词解释]半终粉磨系统 [单选]建筑面积在（）m2以上的公共娱乐场所应当确定为消防安全重点单位。（易）A、100B、200C、300D、400 [多选]涂尔干认为社会事实具有的特点有（）A.外在性B.客观性C.普遍性D.强制性 [单选,A2型题,A1/A2型题]有关"窗口技术"的论述，错误的是（）A.利用窗技术可将任一范围的CT值调到人眼可识别的16个灰阶显示B.窗位是指窗宽上限与下限CT值的平均值（中点）C.窗位与窗中心指的是同一个概念D.调窗目的是为了适应胶片的感光度E.视不同组织影像，应适当地调整窗宽／窗 [名词解释]家庭的涵义与特点 [单选]对于意识不清的患者，如果专业救援人员在10s内不能确定是否有脉搏，接下来救援者应该（）A.仔细检查各处大动脉，确定是否有脉搏B.使用听诊器检查有无心音C.检查心电图，确认心电活动情况D.立即胸外按压E.寻找或等待除颤器 [单选,A2型题,A1/A2型题]脑性瘫痪肌张力测定不包括（）A.头背屈角B.臂弹回试验C.围巾征D.内收肌角E.WeeFIMSM [单选]出境邮寄物经检疫或经检疫处理合格的，检验检疫机构签发（）放行。检疫不合格又无有效方法处理的，不准出境。A.《出境货物通关单》B.《出境货物检疫证书》C.《出境邮寄货物通关单》D.《出境邮寄货物检疫证书》 [单选]关于恶性骨肿瘤的临床表现，下列描述错误的是（）A.无痛性肿块B.局部可有压痛C.血沉增快D.碱性磷酸酶增高E.一般有骨膜反应 [单选,A1型题]幼儿期的保健要点不包括（）A.合理安排饮食B.培养良好的生活习惯C.尽量送幼儿园尝试集体生活D.促进动作和语言的发展E.预防意外事故 [单选]钢中炭的含量超过1.00%时，钢材的性能表现为（）。A．塑性大B．强度下降C．硬度大D．易于加工 [单选]乳糖不耐症患者不宜吃()A．鸡蛋B．牛奶C．牛肉D．鱼E．兔肉