三年级奥数第31讲 假设问题
小学数学应用题解题思路——假设法,方法比努力更重要

⼩学数学应⽤题解题思路——假设法,⽅法⽐努⼒更重要
假设法,通常是根据题⽬先假设某个条件成⽴,由此得到某个结论或者引出⽭盾,从⽽得到⼀
个正确的答案。
在⼩学数学中,假设法常见的是:假设某量为“1”;假设某量为特殊的数;假设
某个量完全变成题⽬中的其他量。
⼀、假设某量为“1”
就是把题⽬中的某个量假设为“1”。
有时候还要通过列⽅程来把复杂的问题简单化。
例:
⼆、假设某量为特殊数值。
假设题⽬中的某个量为特殊的数值,化抽象为具体,使其量化,有时也需要列⽅程。
例:
三、假设某个量完全变为其他量。
解答鸡兔同笼问题通常要假设全是鸡或者全是兔,所求得的脚的总数⼀定与题⽬不⼀致,根据
数量上出现的⽭盾,找到正确答案。
例:。
三年级奥数举一反三第293031周年龄问题还原法解题假设法解题

三年级奥数举一反三第293031周年龄问题还原法解题假设法解题第二十九周年龄问题专题简析:年龄问题可以说是前面所讲的和差问题及差倍问题的综合,要正确解答这类题,首先要弄清:两个不同年龄的人,年龄之差始终不变,但两个人年龄的倍数关系却在不断地变化。
年龄问题的主要特征是:大小年龄差是一个不变的量。
我们可以抓住差不变这个特点,利用和差、差倍等知识来分析解答这类应用题。
例题1 三年前爸爸年龄是女儿的4倍,爸爸今年43岁,女儿今年多少岁?思路导航:由题意可知爸爸今年43岁,则三年前爸爸的年龄是43-3=40岁,40岁正好是女儿年龄的4倍,女儿三年前的年龄是40÷4=10岁,今年女儿的年龄是10+3=13岁。
练习一1,四年前小林年龄是小丽的2倍,小林今年12岁,小丽今年多少岁?2,五年前爷爷年龄是孙子的7倍,孙子今年14岁,爷爷今年多少岁?3,儿子今年10岁,爸爸今年34岁。
几年前,爸爸的年龄是儿子的4倍?例题2 明明4岁时,妈妈年龄是明明的8倍。
今年明明12岁,妈妈今年多少岁?思路导航:妈妈的年龄是明明的8倍,那么妈妈与明明的年龄相差4×8-4=28岁。
妈妈与明明的年龄差是不变的,今年明明12岁,那么妈妈的年龄是12+28=40岁。
练习二1,玲玲7岁时,爸爸年龄是玲玲的5倍。
今年爸爸40岁,玲玲今年多少岁?2,爷爷63岁时,他的年龄是小青的9倍。
今年小青12岁,爷爷今年多少岁?3,两年前妈妈年龄是儿子的5倍,儿子今年9岁,妈妈今年多少岁?例题3 女儿今年3岁,妈妈今年33岁。
几年后,妈妈的年龄是女儿的7倍?思路导航:女儿今年3岁,妈妈今年33岁,她们的年龄差是33-3=30岁。
她们年龄差不变,几年后,妈妈的年龄是女儿的3倍,把女儿的年龄看作1份,妈妈的年龄就有7份,相差7-1=6份,6份是30岁,所以几年后女儿的年龄是30÷6=5岁。
也就是说,5-3=2年后,妈妈的年龄是女儿的7倍。
小学三年级奥数用假设法解题例题及练习题

【导语】⽤假设法解答类似“鸡兔同笼”的问题时,可以根据题意假设⼏个量相同,然后进⾏推算,所得结果与题中对应的数量不符合时,要能够正确地运⽤别的量加以调整,从⽽找到正确的答案。
以下是整理的《⼩学三年级奥数⽤假设法解题例题及练习题》,希望帮助到您。
【篇⼀】 例题1、鸡、兔共笼,鸡⽐兔多30只,⼀共有脚168只,鸡、兔各多少只? 思路导航:因为鸡⽐兔多30只,则可以把30只鸡的脚从总数中去掉,剩下的鸡兔就同样多了。
每⼀对鸡和兔共4+2=6只脚,⽤6去除剩下的鸡兔总脚数,就可求出兔的只数。
兔的只数:(168-2×30)÷(4+2)=18只; 鸡的只数:18+30=48只。
练习题: 1、鸡兔共笼,鸡⽐兔多25只,⼀共有脚170只。
鸡、兔各⼏只? 2、买甲、⼄两种戏票,甲种票每张4元,⼄种票每张3元,⼄种票⽐甲种票多买了9张,⼀共⽤去97元。
两种票各买了⼏张? 3、鸡兔共有脚48只,如果将鸡的只数与兔的只数互换则共有脚42只。
鸡、兔各⼏只?【篇⼆】 例题2、⽔果糖的块数是巧克⼒糖的3倍,如果⼩红每天吃2块⽔果糖,1块巧克⼒糖,若⼲天后,⽔果糖还剩下7块,巧克⼒糖正好吃完。
原来⽔果糖有⼏块? 思路导航:⽔果糖的块数是巧克⼒糖的3倍,如果⼩红每天吃1块巧克⼒糖,3块⽔果糖,那若⼲天后,两种糖正好同时吃完。
现在⼩红每天吃2块⽔果糖,少吃3-2=1块,结果若⼲天后⽔果糖还剩下7块。
所以共吃了7÷1=7天,⽔果糖有2×7+7=21块。
练习题: 1、⼩英家有些梨和苹果,苹果的个数是梨的3倍,爸爸和⼩英每天各吃1个苹果,妈妈每天吃1个梨。
若⼲天后,苹果还剩9个,⽽梨恰巧吃完。
原来苹果有多少个? 2、某商店有些红⽓球和黄⽓球,红⽓球的只数是黄⽓球的4倍。
每天卖出2只红⽓球和1只黄⽓球,若⼲天后,红⽓球剩下12只,黄⽓球刚好卖完。
红⽓球原来有多少只? 3、四(3)班有彩⾊粉笔和⽩粉笔若⼲盒,⽩粉笔是彩⾊粉笔的7倍。
小学三年级奥数第31讲 用假设法解题(含答案分析)

第31讲用假设法解题一、专题简析:假设是数学中思考问题的一常见的方法,有些应用题乍看很难求出答案,但是如果我们合理地进行假设,往往会使问题得到解决。
所谓假设法就是依照已知条件进行推算,根据数量上出现的矛盾,作适当的调整,从而找到正确答案。
我国古代趣题“鸡兔同笼”就是运用假设法解决问题的一个范例。
解答“鸡兔同笼”问题的基本关系式是:兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)用假设法解答类似“鸡兔同笼”的问题时,可以根据题意假设几个量相同,然后进行推算,所得结果与题中对应的数量不符合时,要能够正确地运用别的量加以调整,从而找到正确的答案。
二、精讲精练例1:鸡、兔共30只,共有脚84只。
鸡、兔各有多少只?练习一1、鸡、兔共100只,共有脚280只。
鸡、兔各多少只?2、鸡、兔共50只,共有脚160只。
鸡、兔各几只?例2:鸡、兔共笼,鸡比兔多30只,一共有脚168只,鸡、兔各多少只?练习二1、鸡兔共笼,鸡比兔多25只,一共有脚170只。
鸡、兔各几只?2、买甲、乙两种戏票,甲种票每张4元,乙种票每张3元,乙种票比甲种票多买了9张,一共用去97元。
两种票各买了几张?例3:某学校举行数学竞赛,每做对一题得9分,做错一题倒扣3分。
共有12道题,王刚得了84分。
王刚做错了几题?练习三1、某小学进行英语竞赛,每答对一题得10分,答错一题倒扣2分,共15题,小华得了102分。
小华答对几题?2、运输衬衫400箱,规定每箱运费30元,若损失一箱,不但不给运费,并要赔偿100元。
运后运费为8880元,损失了几箱?例4 :水果糖的块数是巧克力糖的3倍,如果小红每天吃2块水果糖,1块巧克力糖,若干天后,水果糖还剩下7块,巧克力糖正好吃完。
原来水果糖有几块?1、小英家有些梨和苹果,苹果的个数是梨的3倍,爸爸和小英每天各吃1个苹果,妈妈每天吃1个梨。
若干天后,苹果还剩9个,而梨恰巧吃完。
小学数学奥数解题技巧 第30讲 四方阵法

把462分解质因数: 462=2×3×7×11
4
小升初数学解题技巧 第31讲 分解质因数法
【例题】把84名学生分成人数相等的小组(每组最少2人),一 共有几种分法?
【点拔】
把84分解质因数: 84=2×2×3×7 除了1和84外,84的约数有: 2,3,7,2×2=4,2×3=6,2×7=14,3×7=21,2×2×3=12, 2×2×7=28,2×3×7=42。下面可根据不同的约数进行分组。 84÷2=42(组),84÷3=28(组),84÷4=21(组),84÷6=14 (组),84÷7=12(组),84÷12=7(组),84÷14=6(组), 84÷21=4(组),84÷28=3(组),84÷42=2(组)。 因此每组2人分42组;每组3人分28组;每组4人分21组;每组6人分 14组;每组7人分12组;每组12人分7组;每组14人分6组;每组21人分 4组;每组28人分3组;每组42人分2组。一共有10种分法。
5
小升初数学解题技巧 第31讲 分解质因数法
【例题】 一个星期天的早晨,母亲对孩子们说:“你们是否发 现在你们中间,大哥的年龄等于两个弟弟年龄之和?”儿子们齐 声回答说:“是的,我们的年龄和您年龄的乘积,等于您儿子人 数的立方乘以1000加上您儿子人数的平方乘以10。”从这次谈话 中,你能否确定母亲在多大时,才生下第二个儿子?
2
小升初数学解题技巧 第31讲 分解质因数法
【例题】一块正方体木块,体积是1331立方厘米。这块正方体 木块的棱长是多少厘米?
【点拔】
把1331分解质因数: 1331=11×11×11
同步教材视频
3
小升初数学解题技巧 第31讲 分解质因数法
【例题】相邻两个自然数的最小公倍数是462,求这两个数。
例题讲解)三年级奥数“年龄”“还原”“假设”

年龄问题专题简析:年龄问题可以说是前面所讲的和差问题及差倍问题的综合,要正确解答这类题,首先要弄清:两个不同年龄的人,年龄之差始终不变,但两个人年龄的倍数关系却在不断地变化。
年龄问题的主要特征是:大小年龄差是一个不变的量。
我们可以抓住差不变这个特点,利用和差、差倍等知识来分析解答这类应用题。
例题1 三年前爸爸年龄是女儿的4倍,爸爸今年43岁,女儿今年多少岁?思路导航:由题意可知爸爸今年43岁,则三年前爸爸的年龄是43-3=40岁,40岁正好是女儿年龄的4倍,女儿三年前的年龄是40÷4=10岁,今年女儿的年龄是10+3=13岁。
例题3 女儿今年3岁,妈妈今年33岁。
几年后,妈妈的年龄是女儿的7倍?思路导航:女儿今年3岁,妈妈今年33岁,她们的年龄差是33-3=30岁。
她们年龄差不变,几年后,妈妈的年龄是女儿的3倍,把女儿的年龄看作1份,妈妈的年龄就有7份,相差7-1=6份,6份是30岁,所以几年后女儿的年龄是30÷6=5岁。
也就是说,5-3=2年后,妈妈的年龄是女儿的7倍。
例题4 4年前,妈妈的年龄是女儿的3倍,4年后,母女年龄和是56岁。
妈妈今年多少岁?思路导航:4年后,母子的年龄和是56岁,可求出今年母子年龄和是56-4×2=48岁。
4年前母子年龄和是48-4×2=40岁。
又根据4年前,妈妈年龄是女儿的3倍,把女儿年龄看作1份,妈妈的年龄就有这样的3份,共有3+1=4份。
所以4年前女儿的年龄是40÷4=10岁,妈妈今年的年龄是10×3+4=34岁。
例题5 明明今年12岁,强强今年7岁,当两人的年龄和是45岁时,两人各多少岁?思路导航:明明和强强的年龄差为12-7=5岁,这是一个不变量。
当两人的年龄和是45岁时,明明比强强还是大5岁,如果从两人的年龄和45岁里减去两人的年龄差5岁,得到的就是两个强强的年龄。
所以,强强的年龄是(45-5)÷2=20岁,明明的年龄是20+5=25岁。
精品奥数-高年级-第31讲-逻辑推理-3计算推理-答案
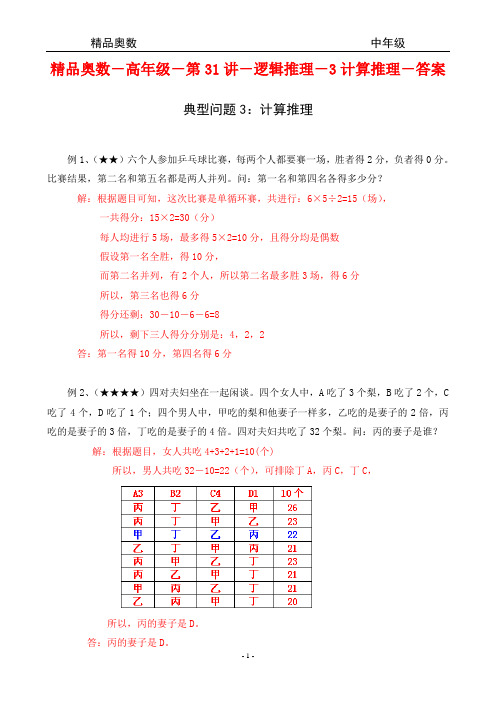
精品奥数-高年级-第31讲-逻辑推理-3计算推理-答案典型问题3:计算推理例1、(★★)六个人参加乒乓球比赛,每两个人都要赛一场,胜者得2分,负者得0分。
比赛结果,第二名和第五名都是两人并列。
问:第一名和第四名各得多少分?解:根据题目可知,这次比赛是单循环赛,共进行:6×5÷2=15(场),一共得分:15×2=30(分)每人均进行5场,最多得5×2=10分,且得分均是偶数假设第一名全胜,得10分,而第二名并列,有2个人,所以第二名最多胜3场,得6分所以,第三名也得6分得分还剩:30-10-6-6=8所以,剩下三人得分分别是:4,2,2答:第一名得10分,第四名得6分例2、(★★★★)四对夫妇坐在一起闲谈。
四个女人中,A吃了3个梨,B吃了2个,C 吃了4个,D吃了1个;四个男人中,甲吃的梨和他妻子一样多,乙吃的是妻子的2倍,丙吃的是妻子的3倍,丁吃的是妻子的4倍。
四对夫妇共吃了32个梨。
问:丙的妻子是谁?解:根据题目,女人共吃4+3+2+1=10(个)所以,男人共吃32-10=22(个),可排除丁A,丙C,丁C,所以,丙的妻子是D。
答:丙的妻子是D。
练习1、(★★★)A,B,C,D四个足球队进行循环比赛,赛了若干场后,A,B,C三队的比赛情况如下:问:D赛了几场?D赛的几场的比分各是多少?解:四个队进行循环赛,则每个队都要其他队赛一场,则每个队均要赛3场。
根据上表可知,A赛了3场,则A与B、C、D均赛过B、C各赛了2场,所以,B、C都未和D赛。
根据比分信息,A胜2场,平1场,B平1场,可知:A与B的那一场,与C、D的两场均胜。
所以:D赛了1场,比分是0:1。
答:D赛了1场。
比分是0:1。
2、六个人参加乒乓球比赛,每两个人都要赛一场,胜者得2分,负者得0分。
比赛结果,第二名和第五名都是两人并列。
问:第一名和第四名各得多少分?解:根据题目可知,这次比赛是单循环赛,共进行:6×5÷2=15(场),一共得分:15×2=30(分)每人均进行5场,最多得5×2=10分,且得分均是偶数假设第一名全胜,得10分,而第二名并列,有2个人,所以第二名最多胜3场,得6分所以,第三名也得6分得分还剩:30-10-6-6=8所以,剩下三人得分分别是:4,2,2答:第一名得10分,第四名得6分3、(★★)A,B,C,D四个队举行足球循环赛(即每两个队都要赛一场),胜一场得3分,平一场得1分,负一场得0分。
小学奥数各年级经典题解题技巧大全——假设法

小学奥数各年级经典题解题技巧大全——假设法假设法当应用题用一般方法很难解答时,可假设题中的情节发生了变化,假设题中两个或几个数量相等,假设题中某个数量增加了或减少了,然后在假设的基础上推理,调整由于假设而引起变化的数量的大小,题中隐蔽的数量关系就可能变得明显,从而找到解题方法。
这种解题方法就叫做假设法。
用假设法解应用题,要通过丰富的想象,假设出既合乎题意又新奇巧妙,既简单又便于计算的条件。
有些用一般方法能解答的应用题,用假设法解答可能更简捷。
(一)假设情节变化解:假设篮球没有借出,足球借出一个,那么,可以把现有篮球的个数看作是3份数,把现有足球的个数看作2份数,两种球的总份数是:3+2=5(份)原来篮球的个数是:原来足球的个数是:21-12=9(个)答略。
例2 :甲乙两个煤场共存煤92吨,从甲场运出28吨后,乙场的存煤比甲场的4倍少6吨。
两场原来各存煤多少吨?(适于六年级程度)解:假设从甲场运出的不是28吨,而是比28吨少6吨的22吨,那么,乙场的存煤数就正好是甲场的4倍,甲场的存煤是1份数,乙场的存煤是4甲场原来存煤:92-50=42(吨)答略。
(二)假设两个(或几个)数量相等例1:有两块地,平均亩产粮食185千克。
其中第一块地5亩,平均亩产粮食203千克。
如果第二块地平均亩产粮食170千克,第二块地有多少亩?(适于五年级程度)解:假设两块地平均亩产粮食都是170千克,则第一块地的平均亩产量比两块地的平均亩产多:203-170=33(千克)5亩地要多产:33×5=165(千克)两块地实际的平均亩产量比假设的平均亩产量多:185-170=15(千克)因为165千克中含有多少个15千克,两块地就一共有多少亩,所以两块地的亩数一共是:165÷15=11(亩)第二块地的亩数是:11-5=6(亩)答略。
解:此题可以有三种答案。
答:剩下的两根绳子一样长。
答:甲绳剩下的部分比乙绳剩下的部分长。
小学三年级奥数:假设法解应用题

用假设法解题教案教学目标:1、知识与技能:初步学会运用“假设”的策略分析数量关系,并能根据问题的特点确定合理的解题步骤。
2、过程与方法:在解决实际问题过程的不断反思中,感受假设的策略对于解决特定问题的价值,进一步发展分析、综合和简单推理能力。
3、情感态度与价值观:养成独立思考、主动与他人合作交流、自觉检验等习惯,积累解决问题的经验,增强解决问题的策略意识,获取解决问题的成功体验,提高学好数学的信心。
教学重点:理解并运用假设的策略解决问题。
教学难点:了解当假设与实际结果发生矛盾时该如何进行调整。
教学过程:一、新课导入(谈话法引入)1、谈话法引入:(1)想要知道这捆2元的钱有多少,必须知道什么?(2)想要知道这捆5元的钱有多少,必须知道什么?(直接数出张数)2、我有10张2元和5元的钱,一共32元,问2元的和5元的各几张?师:请同学们把题目读一读,在题目中你能找到哪些数学信息,要我们解决什么问题?现在你还能解决这个问题吗?有什么困难吗?接着引出解决此问题需要满足两个条件,张数和元数都得对。
生:通过读题,可知,(1)一共有32元(2)一共有10张(3)有5元面额,有2元面额。
要我们解决的问题是2元的和5元的有几张?师:先自己想一想,你准备怎样来解决这个问题?然后和小组里的同学交流一下,并动笔试一试你的策略是否有效。
二、探究新知(例题精析)1、师:下面我们一起交流一下自己的想法。
假如都是2元的,摆一下,你发现了什么,共多少钱?比32元是多了还是少了?(1)拿一张5元的换一张2元的后,你发现了什么?(2)又换一张呢?……(3)回顾演变你发现了什么变了?什么没变?有什么启发?(4)记录一下换到32元的过程。
完成算式。
2、还能假设5元吗?试一试,用自己的方法记录过程。
3、回顾小结:假设时完成了第一个条件,替换后完成了第二个条件。
例题1、鸡、兔共30只,共有脚84只。
鸡、兔各有多少只?解:假设全是鸡,那就有30×2=60只脚与实际相比差:84-60=24只脚所以兔子只数:24÷(4-2)=12(只)鸡只数:30-12=18(只)答:鸡有18只,兔有12只。
三年级奥数第31讲假设问题

三年级奥数第31讲假设问题第31讲:“假设”解题专题简析:假设是数学中思考问题的一种常见方法,有些应用题乍看很难求出答案,但是如果我们合理地进行假设,往往会使问题得到解决。
所谓假设法就是依照已知条件进行推算,根据数量上出现的矛盾作合适调整,从而找到正确答案。
我国古代趣题“鸡兔同笼”就是运用假设法解决问题的一个范例。
解答“鸡兔同笼”问题的基本关系式是:兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只兔脚数-每只鸡脚数)鸡数=鸡兔总数-兔数用假设法解答类似“鸡兔同笼”的问题时,可以根据题意假设多少个量相同,然后进行推算,所得结果与题中对应得数量不符时,要能够正确地运用别的量加以调整,从而得到正确的答案。
【例题1】鸡、兔共30只,共有脚84只,鸡、兔各有多少只?【习题一】1、鸡、兔共100只,共有脚280只。
鸡、兔各有多少只?2、鸡、兔共50只,共有脚160只。
鸡、兔各有多少只?3、阿奇的储蓄罐里有5角和1元的硬币共25枚,这些硬币总钱数为19元。
这两种硬币各有多少枚【例题2】鸡、兔同笼,鸡比兔多30只,一共有脚168只。
鸡、兔各多少只?【习题二】1、鸡、兔同笼,鸡比兔多25只,一共有脚170只。
鸡、兔各多少只?2、买甲、乙两种戏票,甲种戏票每张40元,乙种戏票每张30元,乙种戏票比甲种戏票多买了9张,一共用去970元。
两种戏票各买了多少张?3、鸡、兔共有脚48只,如果将鸡的只数与兔的只数互换则共有脚42只。
鸡、兔各多少只?【例题3】某学校举行数学竞赛,规定每做对一题得9分、做错一题倒扣3分,共有12道题。
王刚得了84分,王刚做错了几道题?(不能不做)【习题3】1、某小学进行英语竞赛,每答对一道题得10分,答错一道题倒扣2分,共15道题。
小华得了102分,小华答对了多少道题?(不能不做)2、某运输公司要运输衬衫400箱,规定每箱运费30元。
若损失一箱不但不给运费还要赔偿100元,该运输公司运完这批衬衣后获运费8880元。
【小学三年级奥数讲义】用假设法解题

【小学三年级奥数讲义】用假设法解题一、专题简析:假设是数学中思考问题的一常见的方法,有些应用题乍看很难求出答案,但是如果我们合理地进行假设,往往会使问题得到解决。
所谓假设法就是依照已知条件进行推算,根据数量上出现的矛盾,作适当的调整,从而找到正确答案。
我国古代趣题“鸡兔同笼”就是运用假设法解决问题的一个范例。
解答“鸡兔同笼”问题的基本关系式是:兔数二(总脚数-每只鸡脚数X鸡兔总数) + (每只兔子脚数-每只鸡脚数)用假设法解答类似“鸡兔同笼”的问题时,可以根据题意假设几个量相同,然后进行推算,所得结果与题中对应的数量不符合时,要能够正确地运用别的量加以调整,从而找到正确的答案。
二、精讲精练例1:鸡、兔共30 只,共有脚84 只。
鸡、兔各有多少只?练习一1、鸡、兔共100 只,共有脚280 只。
鸡、兔各多少只?2、鸡、兔共50 只,共有脚160只。
鸡、兔各几只?例2:鸡、兔共笼,鸡比兔多30只,一共有脚168 只,鸡、兔各多少只?练习二1、鸡兔共笼,鸡比兔多25 只,一共有脚170只。
鸡、兔各几只?2、买甲、乙两种戏票,甲种票每张4 元,乙种票每张3 元,乙种票比甲种票多买了9 张,一共用去97元。
两种票各买了几张?例3:某学校举行数学竞赛,每做对一题得9 分,做错一题倒扣3 分。
共有12 道题,王刚得了84 分。
王刚做错了几题?练习三1、某小学进行英语竞赛,每答对一题得10分,答错一题倒扣2分,共15题,小华得了102 分。
小华答对几题?2、运输衬衫400箱,规定每箱运费30 元,若损失一箱,不但不给运费,并要赔偿100 元。
运后运费为8880元,损失了几箱?例4 :水果糖的块数是巧克力糖的3倍,如果小红每天吃2块水果糖,1块巧克力糖,若干天后,水果糖还剩下7 块,巧克力糖正好吃完。
原来水果糖有几块?练习四1、小英家有些梨和苹果,苹果的个数是梨的3 倍,爸爸和小英每天各吃1个苹果,妈妈每天吃1 个梨。
三年级奥数 用假设法解题

第31讲用假设法解题一、专题简析:假设是数学中思考问题的一常见的方法, 有些应用题乍看很难求出答案, 但是如果我们合理地进行假设, 往往会使问题得到解决. 所谓假设法就是依照已知条件进行推算, 根据数量上出现的矛盾, 作适当的调整, 从而找到正确答案. 我国古代趣题“鸡兔同笼”就是运用假设法解决问题的一个范例.解答“鸡兔同笼”问题的基本关系式是:兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)用假设法解答类似“鸡兔同笼”的问题时, 可以根据题意假设几个量相同, 然后进行推算, 所得结果与题中对应的数量不符合时, 要能够正确地运用别的量加以调整, 从而找到正确的答案.二、精讲精练例1:鸡、兔共30只, 共有脚84只. 鸡、兔各有多少只?练习一1、鸡、兔共100只, 共有脚280只. 鸡、兔各多少只?2、鸡、兔共50只, 共有脚160只. 鸡、兔各几只?例2:鸡、兔共笼, 鸡比兔多30只, 一共有脚168只, 鸡、兔各多少只?练习二1、鸡兔共笼, 鸡比兔多25只, 一共有脚170只. 鸡、兔各几只?2、买甲、乙两种戏票, 甲种票每张4元, 乙种票每张3元, 乙种票比甲种票多买了9张, 一共用去97元. 两种票各买了几张?例3:某学校举行数学竞赛, 每做对一题得9分, 做错一题倒扣3分. 共有12道题, 王刚得了84分. 王刚做错了几题?练习三1、某小学进行英语竞赛, 每答对一题得10分, 答错一题倒扣2分, 共15题, 小华得了102分. 小华答对几题?2、运输衬衫400箱, 规定每箱运费30元, 若损失一箱, 不但不给运费, 并要赔偿100元. 运后运费为8880元, 损失了几箱?例4 :水果糖的块数是巧克力糖的3倍, 如果小红每天吃2块水果糖, 1块巧克力糖, 若干天后, 水果糖还剩下7块, 巧克力糖正好吃完. 原来水果糖有几块?1、小英家有些梨和苹果, 苹果的个数是梨的3倍, 爸爸和小英每天各吃1个苹果, 妈妈每天吃1个梨. 若干天后, 苹果还剩9个, 而梨恰巧吃完. 原来苹果有多少个?2、某商店有些红气球和黄气球, 红气球的只数是黄气球的4倍. 每天卖出2只红气球和1只黄气球, 若干天后, 红气球剩下12只, 黄气球刚好卖完. 红气球原来有多少只?例5 :学校买来8张办公桌和6把椅子, 共花去1650元. 每张办公桌的价钱是每把椅子的2倍, 每张办公桌和每把椅子各多少元?1、买4张办公桌9把椅子共用252元, 1张桌子和3把椅子的价钱正好相等. 桌、椅单价各多少元?2、学校买来4个篮球和5个排球, 共用了185元. 已知1个篮球比1个排球贵8元, 那么篮球每个多少元?排球每个多少元?三、课后作业1、鸡、兔共45只, 鸡的脚比兔的脚多60只. 鸡、兔各多少只?2、鸡兔共有脚48只, 如果将鸡的只数与兔的只数互换则共有脚42只. 鸡、兔各几只?3、某车间生产一批服装共250件, 生产1件可得25元, 如果有1件不符合要求, 则倒扣20元. 生产后得到费用5350元, 有几件不符合要求?4、四(3)班有彩色粉笔和白粉笔若干盒, 白粉笔是彩色粉笔的7倍. 每天用去2盒白粉笔和1盒彩色粉笔, 当彩色粉笔全部用完时, 白色粉笔还剩10盒. 原来白色粉笔有多少盒?5、小明买2个乒乓球和4个皮球共用去52元, 6个乒乓球的价钱相当于1个皮球的价钱. 乒乓球、皮球的单位各多少元?加减巧算一、知识要点在进行加减运算时, 为了又快又好, 除了要熟练地掌握计算法则外, 还需要掌握一些巧算的方法. 加减法的巧算主要是运用“凑整”的方法, 把接近整十、整百、整千的数看做所接近的数进行简算.进行加减巧算时, 凑整之后, 对于原数与整十、整百、整千……相差的数, 要根据“多加要减去, 少加要再加, 多减要加上, 少减要再减”的原则进行处理. 另外, 可以结合加法交换律、结合律以及减法的性质进行凑整, 从而达到简算的目的.二、精讲精练【例题1】你有好办法迅速算出结果吗?(1) 502+799-298-98 (2) 9999+999+99+9练习1:计算.(1) 308+203-399-97 (2) 99999+9999+999+99+9(3) 1999+199+19 (4) 375+483+525+617【例题2】计算.(1) 487+321+113+279 (2) 736-567+264(3) 877+345-677 (4) 528-248-152练习2:计算.(1) 321+127+73+279 (2) 235-125+365 (3) 987-733-167 (4) 487+(413-89)【例题3】计算下面各题.(1) 962-(284+262) (2) 432-(154-168)练习3:计算.(1) 421+(279-125) (2) 812+(168-112)(3) 823-(175+323) (4) 538-(283-162) 【例题4】2000-111-89-112-88-113-87-114-86-115-85-116-84练习4:计算.(1)800-99-1-98-2-97-3-96-4-95-5(2) 1000-10-20-30-40-50-60-70-80-90【例题5】计算: 98+97-96-95+94+93-92-91+90+89-88-87……-4-3+2+1练习5:计算.(1) 2009+1+2-3-4+5+6-7-8+9+10-11-12+13+14……+2006(2) 1+2-3+4+5-6+7+8-9……+97+98-99三、课后作业1、计算下列各题.(1)256+503+44 (2)953—267—133(3)465—198+335 (4)362—202+238文档仅供参考2、用简便方法计算下列各题.(1)43+40+39+41+37+42 (2)503+301-298-91+52(3)199999+19999+1999+199+19 (4)83+81+78+80+84+78+79+77+843、巧算1000-99-98-97-96-95-5-4-3-2-14、29999+2999+299+295、(1)2356-(356+187)(2)5723-(723-189)6、(534+786+896)+(104+214+466)文档仅供参考。
小学三年级奥数第31讲 用假设法解题附答案解析

第31讲用假设法解题一、专题简析:假设是数学中思考问题的一常见的方法,有些应用题乍看很难求出答案,但是如果我们合理地进行假设,往往会使问题得到解决。
所谓假设法就是依照已知条件进行推算,根据数量上出现的矛盾,作适当的调整,从而找到正确答案。
我国古代趣题“鸡兔同笼”就是运用假设法解决问题的一个范例。
解答“鸡兔同笼”问题的基本关系式是:兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)用假设法解答类似“鸡兔同笼”的问题时,可以根据题意假设几个量相同,然后进行推算,所得结果与题中对应的数量不符合时,要能够正确地运用别的量加以调整,从而找到正确的答案。
二、精讲精练例1:鸡、兔共30只,共有脚84只。
鸡、兔各有多少只?练习一1、鸡、兔共100只,共有脚280只。
鸡、兔各多少只?2、鸡、兔共50只,共有脚160只。
鸡、兔各几只?例2:鸡、兔共笼,鸡比兔多30只,一共有脚168只,鸡、兔各多少只?练习二1、鸡兔共笼,鸡比兔多25只,一共有脚170只。
鸡、兔各几只?2、买甲、乙两种戏票,甲种票每张4元,乙种票每张3元,乙种票比甲种票多买了9张,一共用去97元。
两种票各买了几张?例3:某学校举行数学竞赛,每做对一题得9分,做错一题倒扣3分。
共有12道题,王刚得了84分。
王刚做错了几题?练习三1、某小学进行英语竞赛,每答对一题得10分,答错一题倒扣2分,共15题,小华得了102分。
小华答对几题?2、运输衬衫400箱,规定每箱运费30元,若损失一箱,不但不给运费,并要赔偿100元。
运后运费为8880元,损失了几箱?例4 :水果糖的块数是巧克力糖的3倍,如果小红每天吃2块水果糖,1块巧克力糖,若干天后,水果糖还剩下7块,巧克力糖正好吃完。
原来水果糖有几块?练习四1、小英家有些梨和苹果,苹果的个数是梨的3倍,爸爸和小英每天各吃1个苹果,妈妈每天吃1个梨。
若干天后,苹果还剩9个,而梨恰巧吃完。
三年级思维训练 第31讲 假设问题

第31讲:假设问题专题简析:假设是数学中思考问题的一种常见方法,有些应用题乍看很难求出答案,但是如果我们合理地进行假设,往往会使问题得到解决。
所谓假设法就是依照已知条件进行推算,根据数量上出现的矛盾作合适调整,从而找到正确答案。
我国古代趣题“鸡兔同笼”就是运用假设法解决问题的一个范例。
解答“鸡兔同笼”问题的基本关系式是:兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只兔脚数-每只鸡脚数)鸡数=鸡兔总数-兔数用假设法解答类似“鸡兔同笼”的问题时,可以根据题意假设多少个量相同,然后进行推算,所得结果与题中对应得数量不符时,要能够正确地运用别的量加以调整,从而得到正确的答案。
【例题1】鸡、兔共30只,共有脚84只,鸡、兔各有多少只?【习题一】1、鸡、兔共100只,共有脚280只。
鸡、兔各有多少只?2、鸡、兔共50只,共有脚160只。
鸡、兔各有多少只?3、阿奇的储蓄罐里有5角和1元的硬币共25枚,这些硬币总钱数为19元。
这两种硬币各有多少枚【例题2】鸡、兔同笼,鸡比兔多30只,一共有脚168只。
鸡、兔各多少只?【习题二】1、鸡、兔同笼,鸡比兔多25只,一共有脚170只。
鸡、兔各多少只?2、买甲、乙两种戏票,甲种戏票每张40元,乙种戏票每张30元,乙种戏票比甲种戏票多买了9张,一共用去970元。
两种戏票各买了多少张?3、鸡、兔共有脚48只,如果将鸡的只数与兔的只数互换则共有脚42只。
鸡、兔各多少只?【例题3】某学校举行数学竞赛,规定每做对一题得9分、做错一题倒扣3分,共有12道题。
王刚得了84分,王刚做错了几道题?(不能不做)【习题3】1、某小学进行英语竞赛,每答对一道题得10分,答错一道题倒扣2分,共15道题。
小华得了102分,小华答对了多少道题?(不能不做)2、某运输公司要运输衬衫400箱,规定每箱运费30元。
若损失一箱不但不给运费还要赔偿100元,该运输公司运完这批衬衣后获运费8880元。
解竞赛题的金钥匙之四(假设问题)

四假设问题——以“假”求“真”,化难为易用假设的方法来解答问题是一种极其重要的思维方法。
恩格斯曾经指出:“只要自然科学在思维着,它的发展形式就是假设。
”科学史上的许多有重大影响的科学理论,如门捷列夫的元素周期表、哥白尼的太阳中心说等等,最初就是以假设的形式出现的。
在解答数学问题中,假设未知数为 x,列出方程进行解题,就是建立在假设的思想基础上的。
由于假设,可以把未知看作已知,可以把复杂的数量关系简单化。
我国古代算术中的“鸡兔同笼”问题,就是用假设法来解的,它往往先假设某种现象的存在,得到和已知条件不同的“差异”,再分析“差异”的原因,进行适当的调换,使问题得到解决。
例1 笼中共有鸡兔100 个头,350 只脚,问鸡兔各有多少头?(1990 年济南市历下区小学数学五年级竞赛题)分析:假设100 头全为兔,则应有4×100=400 只脚,比实际多了400- 350=50 只脚,如果把一只兔换成一只鸡,那么可减少4-2=2 只脚,要减少50 只脚,就要换50÷2=25 头鸡,这样就求出了鸡的头数。
解法一:(4×100-350)÷(4-2)=25(头)⋯⋯鸡,100-25=75 (头)⋯⋯兔。
或者(350-2×100)÷(4-2)=75(头)⋯⋯兔,100-75=25 (头)⋯⋯鸡。
解法二:设:鸡有x 头,则兔有(100-x)头。
2x+4×(100-x)=350,解之得x=25。
100-25=75(头)⋯⋯兔。
答:鸡有25 头,兔有75 头。
例2 光明书店卖出甲、乙两种书共120 本,甲种书每本5 元,乙种书每本3.75 元,卖出的甲种书比乙种书多收入162.5 元。
甲、乙两种书各卖出几本?(《小学生数学报》第五届初赛题)分析 1:假设全部卖出的为甲种本,则甲种本比乙种本多收入 5×120- 3.75×0=600 元,比实际的相差数多600-162.5=437.50 元。
举一反三、三年级假设问题

练 习 二 1,鸡兔共笼,鸡比兔多25只,一共有脚170只。鸡、 兔各几只? 2,买甲、乙两种戏票,甲种票每张4元,乙种票每张3 元,乙种票比甲种票多买了9张,一共用去97元。两种 票各买了几张? 3,鸡兔共有脚48只,如果将鸡的只数与兔的只数互换 则共有脚42只。鸡、兔各几只?
例题3 某学校举行数学竞赛,每做对一题 得9分,做错一题倒扣3分。共有12道题, 王刚得了84分。王刚做错了几题?
假设是数学中思考问题的一常见的方法,有些 应用题乍看很难求出答案,但是如果我们合理地进 行假设,往往会使问题得到解决。所谓假设法就是 依照已知条件进行推算,根据数量上出现的矛盾, 作适当的调整,从而找到正确答案。我国古代趣题 “鸡兔同笼”就是运用假设法解决问题的一个范例。 解答“鸡兔同笼”问题的基本关系式是:
兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只 兔子脚数-每只鸡脚数)
例题1 鸡、兔共30只,共有脚84只。鸡、兔 各有多少只? 思路导航: 假设全是鸡,共有脚:30×2=60只; 比实际少:84-60=24只; 这是因为把4只脚的兔子都按2只脚的鸡计算 了。 每把一只兔子算作一只鸡,少算:4-2=2只 脚,现在共少算了24只脚,说明把: 24÷2=12只兔子按鸡算了。 所以,共有兔子12只,有鸡30-12=18只。
练 习 一 1,鸡、兔共100只,共有脚280只。 鸡、兔各多少只? 2,鸡、兔共50只,共有脚16的 脚多60只。鸡、兔各多少只?
例题2 鸡、兔共笼,鸡比兔多30只,一共有脚 168只,鸡、兔各多少只?
兔的只数:(168-2×30)÷(4+2)=18只; 鸡的只数:18+30=48只。
作业:186页练习三
三年级奥数第31讲用假设法解题

第三十一周用假设法解题例题1 鸡、兔共30只,共有脚84只。
鸡、兔各有多少只?练习一1,鸡、兔共100只,共有脚280只。
鸡、兔各多少只?2,鸡、兔共50只,共有脚160只。
鸡、兔各几只?3,鸡、兔共45只,鸡的脚比兔的脚多60只。
鸡、兔各多少只?例题2鸡、兔共笼,鸡比兔多30只,一共有脚168只,鸡、兔各多少只?练习二1,鸡兔共笼,鸡比兔多25只,一共有脚170只。
鸡、兔各几只?2,买甲、乙两种戏票,甲种票每张4元,乙种票每张3元,乙种票比甲种票多买了9张,一共用去97元。
两种票各买了几张?3,鸡兔共有脚48只,如果将鸡的只数与兔的只数互换那么共有脚只。
鸡、兔各几只?例题3某学校举行数学竞赛,每做对一题得9分,做错一题倒扣3分。
共有12道题,王刚得了84分。
王刚做错了几题?练习三1,某小学进行英语竞赛,每答对一题得 10分,答错一题倒扣 4分,共15题,小华得了102分。
小华答对几题?2,运输衬衫400箱,规定每箱运费30元,假设损失一箱,不但不给运费,并要赔偿100元。
运后运费为8880元,损失了几箱?3,某车间生产一批服装共 250件,生产1件可得25元,如果有1件不符合要求,那么倒扣20元。
生产后得到费用5350元,有几件不符合要求?例题4水果糖的块数是巧克力糖的3倍,如果小红每天吃2块水果糖,1块巧克力糖,假设干天后,水果糖还剩下7块,巧克力糖正好吃完。
原来水果糖有几块?练习四1,小英家有些梨和苹果,苹果的个数是梨的3倍,爸爸和小英每天各吃1个苹果,妈妈每天吃1个梨。
假设干天后,苹果还剩9个,而梨恰巧吃完。
原来苹果有多少个?2,某商店有些红气球和黄气球,红气球的只数是黄气球的4倍。
每天卖出2只红气球和1只黄气球,假设干天后,红气球剩下12只,黄气球刚好卖完。
红气球原来有多少只?3,四〔3〕班有彩色粉笔和白粉笔假设干盒,白粉笔是彩色粉笔的7倍。
每天用去2盒白粉笔和1盒彩色粉笔,当彩色粉笔全部用完时,白色粉笔还剩10盒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第31讲:“假设”解题
专题简析:假设是数学中思考问题的一种常见方法,有些应用题乍看很难求出答案,但是如果我们合理地进行假设,往往会使问题得到解决。
所谓假设法就是依照已知条件进行推算,根据数量上出现的矛盾作合适调整,从而找到正确答案。
我国古代趣题“鸡兔同笼”就是运用假设法解决问题的一个范例。
解答“鸡兔同笼”问题的基本关系式是:
兔数=(总脚数-每只鸡脚数×鸡兔总数)÷(每只兔脚数-每只鸡脚数)
鸡数=鸡兔总数-兔数
用假设法解答类似“鸡兔同笼”的问题时,可以根据题意假设多少个量相同,然后进行推算,所得结果与题中对应得数量不符时,要能够正确地运用别的量加以调整,从而得到正确的答案。
【例题1】鸡、兔共30只,共有脚84只,鸡、兔各有多少只?
【习题一】1、鸡、兔共100只,共有脚280只。
鸡、兔各有多少只?
2、鸡、兔共50只,共有脚160只。
鸡、兔各有多少只?
3、阿奇的储蓄罐里有5角和1元的硬币共25枚,这些硬币总钱数为19元。
这两种硬币各有多少枚
【例题2】鸡、兔同笼,鸡比兔多30只,一共有脚168只。
鸡、兔各多少只?
【习题二】1、鸡、兔同笼,鸡比兔多25只,一共有脚170只。
鸡、兔各多少只?
2、买甲、乙两种戏票,甲种戏票每张40元,乙种戏票每张30元,乙种戏票比甲种戏票多买了9张,一共用去970元。
两种戏票各买了多少张?
3、鸡、兔共有脚48只,如果将鸡的只数与兔的只数互换则共有脚42只。
鸡、兔各多少只?
【例题3】某学校举行数学竞赛,规定每做对一题得9分、做错一题倒扣3分,共有12道题。
王刚得了84分,王刚做错了几道题?(不能不做)
【习题3】1、某小学进行英语竞赛,每答对一道题得10分,答错一道题倒扣2分,共15道题。
小华得了102分,小华答对了多少道题?(不能不做)
2、某运输公司要运输衬衫400箱,规定每箱运费30元。
若损失一箱不但不给运费还要赔偿100元,该运输公司运完这批衬衣后获运费8880元。
损失了多少箱衬衣?
3、某车间要加工250件服装,规定加工一件服装可得25元,如果有一件服装不符合要求则倒扣20元,该车间加工完这批服装后得到5350元加工费。
有多少件服装不符合要求?
【例题4】小红家有一些水果糖和巧克力糖,已知水果糖的块数是巧克力糖块数的3倍。
如果小红每天吃2块水果糖、1块巧克力糖,若干天后水果糖还剩下7块,巧克力糖正好吃完。
原来水果糖有多少块?
【习题4】1、小英家有一些梨和苹果,苹果的个数是梨的个数的3倍。
爸爸和小英每天各吃1个苹果,妈妈每天吃1个梨,若干天后苹果还剩9个,而梨恰好吃完。
原来苹果有多少个?
2、某商店有若干个红气球和黄气球,红气球的个数是黄气球个数的4倍。
每天卖出2个红气球和1个黄气球,若干天后红气球剩下12个,黄气球刚好卖完。
红气球原来有多少个?
3、四(3)班有彩色粉笔和白粉笔若干盒,白粉笔的盒数是彩色粉笔盒数的7倍。
每天用去2盒白粉笔和1盒彩色粉笔,当彩色粉笔全部用完时,白粉笔还剩10盒。
原来白粉笔有多少盒?
【例题5】晨新小学的教师和学生共100人去植树,教师每人植3棵树,学生平均每3人植一棵树,一共植了100棵树。
教师和学生各有多少人?
【习题5】1、中秋晚会上四(2)班43人一起吃月饼,男生每人吃2个月饼,女生每2人合吃1个月饼,一共吃了56个月饼。
四(2)班男生、女生各有多少人?
2、幼儿园分橘子,大班每人分2个橘子,小班每2人分1个橘子,大、小班180人共分了240个橘子。
大班、小班各有多少人?
3、超市里水果糖每千克卖20元,奶糖每千克卖25元,巧克力糖每千克卖30元。
某天这三种糖一共卖了20千克,总收入480元。
已知奶糖和巧克力糖总共卖了300元,其中奶糖卖了多少千克?
1、5元和10元的人民币共12张,合计95元。
5元、10元的人民币各有多少张?
2、鸡、兔同笼,鸡比兔多19只,一共有脚230只。
鸡、兔各有多少只?
3、搬运1000只瓷碗,规定安全运到一只瓷碗可得搬运费3角,但打碎一只瓷碗不仅不给搬运费还要赔5角钱。
如果共得运费260元,那么途中共打碎了几只瓷碗?
4、数学竞赛题共20道,评分标准是:每做对一道题得5分,每做错或不做一道题扣1分。
小明参加了这次数学竞赛,共得了64分。
小明做对了多少道题?
5、小红家有一些橘子和梨,橘子的个数是梨的个数的3倍。
小红家每天吃4个橘子和2个梨,若干天后,橘子还剩18个,梨正好吃完。
小红家原来有橘子多少个?
6、50个同学去划船,乘坐11条船,其中每条大船坐6人,每条小船坐4人。
大船和小船各有几条?
1、影院某天售出甲、乙两种电影票500张,共收人6500元。
甲种电影票每张15元,乙种电影票每张10元。
甲、乙两种电影票各售出多少张?
2、小雨把小猪储蓄罐里的钱倒出来数了数,1角的和5角的硬币共219校,5角的硬币比1角的硬币多93角。
两种硬币各有多少枚?
3、办公室买杯子和热水瓶共花去170元。
已知每个热水瓶15元,每个杯子2元,买的杯子比热水瓶多34个。
买热水瓶和杯子各多少个?
4、一批钢材,用小车装要用30辆车,用大车装只要25辆车,每辆小车比每辆大车少装4吨材。
这批钢材有多少吨?
5、某厂每天生产冰箱400台,在质量评比中,每生产一台合格冰箱记5分,每生产一台不合格冰箱扣20分。
已知该厂4天评比得了7950分,该厂这4天中生产了多少台合格冰箱?
6、有甲、乙、丙三种铅笔,它们的价钱分别是8角、6角3角,三种铅笔一共买了42支,付
了24元6角,已知乙种铅笔的支数是丙种铅笔支数的2倍。
三种铅笔各买了多少支?。
