第7章 角动量
角动量定理与万有引力

两个质点的孤立体系和角动量
而掠面速度对时间的微商为:
dS i 1 dri dv i 1 v i ri dt 2 dt 2 dt dv dv 1 1 1 v i v i ri i ri i 2 2 dt 2 dt
体系的角动量与质心的角动量
设在惯性系 K 中,体系相对原点的角动量为 L。在 质心系 KC 中,质心的角动量为 LC,则有: 令: L r m v 称为质心角动量 C C C C
LCM ( rC i mi v C i ) 称为体系相对于质心的角动量
i
则有:
L LC LCM
单质点孤立体系和掠面速度
单质点的孤立体系就是不 受外力作用的自由质点,它作 匀速直线运动(我们取惯性参 考系,且静止看成是匀速直线 运动的特例)。 如图,设该质点位于P点, 沿直线 AB 从 A 向 B 方向运动, 在相等的时间间隔 ⊿t的位移 是 ⊿s = v⊿t。 由于 OP 的方向(即 r 的方向)在不断改变,故 P 点相对于 O 点有转动。
单质点孤立体系和掠面速度
由图可见,各时间间隔 ⊿t 内矢径 r 扫过的那些小三角形具 有公共的高线 OH,因而有相等 的面积,于是我们找到的守恒量 是:矢径 r 在单位时间内扫过的 面积 S,我们称 该面积 S 为质点 P 的掠面速度。设矢径 r 与 AB 线的夹角为θ,故对单质点的孤 立体系有: 1 s 1 S r sin rv sin 常量 2 t 2
说明:
1. 角动量是矢量,单个质点的角动量是 r 和 p 的矢积, 因而既垂直于 r,又垂直于 p,即垂直于 r 和 p 所确 定的平面,其指向由右手定则决定。
自主学习01 教材内容 第七章 自旋与角动量
自主学习01 教材内容第七章自旋与角动量知识框架重点难点第一节第二节第三节第四节第五节第六节第七节第八节本章习题本章自测知识框架重点难点1.自旋算符与泡利矩阵2.轨道自旋耦合及自旋自旋耦合3.两电子体系的自旋波函数4.两个角动量的耦合(CG系数)7.1电子的自旋[教学目标]:理解电子的自旋[重点难点]:自旋[教学内容]:在较强的磁场下(∽T 10),我们发现一些类氢离子或碱金属原子有正常塞曼效应的现象,而轨道磁矩的存在,能很好的解释它但是,当这些原子或离子置入弱磁场(∽T 110-)的环境中,或光谱分辨率提高后,发现问题并不是那么简单,这就要求人们进一步探索。
大量实验事实证明,认为电子仅用三个自由度z ,y ,x 来描述并不是完全的。
我们将引入一个新的自由度—自旋,它是粒子固有的。
当然,自旋是Dirac 电子的相对论性理论的自然结果。
现在我们从实验事实来引入。
(1)电子自旋存在的实验事实(1)Stern-Gerlach 实验(1922年)当一狭窄的原子束通过非均匀磁场时,如果原子无磁矩,它将不偏转;而当原子具有磁矩μ,那在磁场中的附加能量为αμμcos B B U -=⋅-=如果经过的路径上,磁场在z 方向上有梯度,即不均匀,则受力dz dB U F αμcos =-∇=从经典观点看αcos 取值(从11--),因此,不同原子(磁矩取向不同)受力不同,而取值dz dB μ-—dz dB μ所以原子分裂成一个带。
但Stern-Gerlach 发现,当一束处于基态的银原子通 过这样的场时,仅发现分裂成二束,即仅二条轨道(两个态)。
而人们知道,银原子(47z =)基 态0l =,所以没有轨道磁矩,而分成二个状态(二 个轨道),表明存在磁矩,而这磁矩在任何方向上的 投影仅取二个值。
这磁矩既然不是由于轨道运动产生的,因此,只能是电子本身的(核磁矩可忽),这磁矩称为内禀磁矩sμ,与之相联系的角动量称为电子自旋,它是电子的一个新物理量,也是一个新的动力学变量。
第七章角动量

(1)在无耦合表象中,J
2 1
,
J
2 2
,
J 1z
,
J
2z
均为对角矩阵;
(2)对于给定的 j1, j2 ,m1 可取(2 j1 1)个值 ,m2 可取 (2 j2 1)
个值,所以无耦合表象基矢有 (2 j1 1)(2 j2 1)个,各自
以量子数 m1, m2 的不同取值而体现,所以无耦合表象基
的共同本征矢写为
j1m1 j2m2 j1m1 j2m2
(3)
(在坐标表象,r j1m1 j2m2 Yj1m1 (1,1)Yj2m2 (2 ,2 ))
它们构成正交归一完备系
j1m1 j2m2 j1m1 j2m2 j1 j1 j2 j2 m1m1 m2 m2
称为无耦合基矢 以此为基矢的表象称为无耦合表象
(13)
2.2 矢量耦合系数 矢量耦合系数的明显表达式的推导十分复杂,有专门表
可查,有兴趣的话可以参考有关高等量子力学书籍,在此仅
给出 j1(任意), j2 1/ 2 时的几个矢量耦合系数 ,并代入
(10)式得
• 3 光谱的精细结构 光谱的精细结构来自于能级的精细结构(以Na的D线为
例,精细结构是双线)。现在我们可以用考虑电子自旋后的 量子力学简并微扰理论加以解释。
j1 j2 jm
j1m1 j2m2 j1m1 j2m2 j1 j2 jm
m1 ,m2
(9)
展开系数 j1m1 j2m2 j1 j2 jm 是耦合表象基矢在无耦合表象基
矢上的分量,称为矢量耦合系数或称克来布希-高登系数
(Clebsch-Gorden),简称C-G系数。
由J z J 1z J 2z可知 m m1 m2 故 m1 m m2 所以将(9)改
量子力学第七章习题解答

即
h h 2 2 2 λ − cos γ − (cos α + cos β ) = 0 4 4
2
h λ − = 0 (利用 cos 2 α + cos 2 β + cos 2 γ = 1) 4
2
2
⇒
a h 设对应于 S n = 的本征函数的矩阵表示为 χ 1 ( S n ) = , b 2 2
由归一化条件,得
a 2 2 1 = χ 1 χ 1 = (a , b ) = a + b b 2 2 2 cos α + i cos β 2 2 a + a =1 1 + cos γ
+ * *
2 2 a =1 1 + cos γ
取
1 + cos γ a= 2
,得
b=
cos α + i cos β 2(1 + cos γ )
ˆ 在这些本征态中, 测量 S z 有哪些可能值?这些可 ˆ 能值各以多大的几率出现? S z 的平均值是多少?
ˆ ˆ 解:在 S z 表象, S n 的矩阵元为
ˆ = h 0 1 cos α + h 0 − i cos β + h 1 0 cos γ Sn 1 0 i 0 0 − 1 2 2 2
⇒
b1 a1 = ⇒ a b 1 1
b1 = a1
χ 1+/ 2 χ 1 / 2 = 1 ,得 由归一化条件 a * * 1 (a1 , a1 ) = 1 a 1
即
2 a1 = 1
2
∴
a1 =
1 2
b1 =
2-(8)角动量
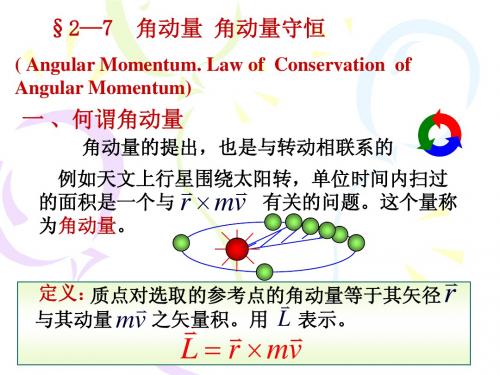
L r
2
mv
方向如图
L mvr sin rmv mr
Z Y O
ˆ L mvr sin mvd 或: L mvd k
L
r
X
mv
d
15 – 8 多普勒效应 质点系的角动量
1
此值为狄拉克h: h / 2
15 – 8
多普勒效应
4
第十五章 机械波
例3 一质量 m 1 . 20 10 kg 的登月飞船, 在离 月球表面高度 h 100 km 处绕月球作圆周运动.飞船 采用如下登月方式 : 当飞船位于点 A 时,它向外侧短 时间喷气 , 使飞船与月球相切地到达点 B , 且OA 与 OB 垂直 . 飞船所喷气体相对飞船的速度为 4 1 u 1 . 00 10 m s . 已知 v0 B vA 月球半径 R 1700 km ; vB 在飞船登月过程中,月球的 R 重力加速度视为常量 u v 2 g 1 . 62 m s . O A 试问登月飞船在登月过程 中所需消耗燃料的质量 h m 是多少?
i
第十五章 机械波 L Li r i p i
i
二 、力矩
中学时学过的力矩概念
二、力矩
M Fd Fr sin r F
o
d
r
M
F
定义:力对某点O的力矩等于力的 作用点的矢径r与力F的矢量积.
M
M r F
t2
Lz 2 z
M
t1
dt
dL
Lz 1
17第7章概念2-两个角动量的耦合

1 2
−1,1 + 2 2
1 2
1 2
, − 1 c 1 , − 1 + d − 1 , 1 2 2 2 2 2
=
1 2
(c + d ) = 0
0, 0 0, 0 = c*
2
1 2
, − 1 + d * − 1 , 1 c 1 , − 1 + d − 1 , 1 2 2 2 2 2 2 2
j1 + j2 , j1 + j2 − 1,L , jmin
因此,耦合表象基矢总数即空间维数为 因此, 1 首项+末项) ∑(2 j +1) = 2(首项+末项) 项数 j
×ቤተ መጻሕፍቲ ባይዱ
=
= ( jmax + jmin + 1)( jmax − jmin + 1)
(2 jmin + 1) + (2 jmax + 1) ( jmax − jmin + 1) 2
因此, ˆ 2 ˆ 2 ˆ 2 ˆ 也构成力学量完全集。 因此, J1 , J 2 , J , J z 也构成力学量完全集。 设它们的共同本征矢为 j1 j2 jm ,则
{
v v ˆ ˆ ˆ 2 = J 2 + J 2 + 2J ⋅ J ˆ ˆ J 1 2 1 2 ˆ ˆ ˆ ˆ ˆ ˆ2 [J 2 , J z ] = 0 [ J 2 , J12 ] = [ J 2 , J 2 ] = 0 且
j1 =1/ 2
,1 2
,1 2
m1 =1/ 2
j2 =1/ 2 m2 =1/ 2
=
( 1 − 1 + 1)( 1 + 1 ) 2 2 2 2
圆周运动:角动量和角动量守恒

角动量守恒在量子力学和粒子物理学中也有着重要的应用,对于理解微观世界的运动规律具有重要意义。
角动量守恒在未来的发展前景和影响将更加广泛,对于推动科学技术的发展和进步具有重要意义。
如何理解和掌握角动量守恒定律
6
学习角动量守恒定律的方法和技巧ຫໍສະໝຸດ 理解角动量守恒定律的难点和重点
角动量的定义:理解角动量的物理意义和数学表达式
角动量守恒可以帮助我们理解各种旋转运动现象,例如地球自转、陀螺旋转等。
角动量守恒还可以帮助我们解决一些实际问题,例如设计旋转机械、分析旋转物体的稳定性等。
角动量守恒在科技领域的应用价值
光学器件:利用角动量守恒原理,制造出高性能的光学器件,如光纤陀螺仪等
粒子加速器:利用角动量守恒原理,提高粒子加速器的性能和效率
角动量守恒定律
3
角动量守恒的条件
系统不受外力矩作用
系统的角动量守恒定律适用于旋转参考系和惯性参考系
系统的角动量变化率为零
系统内力矩之和为零
角动量守恒的证明方法
添加标题
添加标题
添加标题
添加标题
角动量守恒定律:L=mvr
牛顿第二定律:F=ma
角动量守恒的条件:系统不受外力矩作用
角动量守恒的证明:通过牛顿第二定律和角动量守恒定律,推导出角动量守恒的条件,从而证明角动量守恒定律。
角动量守恒定律:在圆周运动中,角动量保持恒定
角动量的大小:与物体的质量和速度成正比
角动量的变化:在圆周运动中,角动量不会发生变化,除非有外力作用
圆周运动中角动量守恒的证明
角动量守恒定律:在封闭系统中,系统内各物体的角动量之和保持不变
证明过程:假设物体在圆周运动中受到外力作用,根据牛顿第二定律,外力作用在物体上会产生加速度
第七章 第二讲

ˆ J ˆ 2J ˆ 2J ˆ 2, J x x y z
ˆ J ˆ 0 J y y,
ˆ 2, J ˆ Jx x
ˆ J ˆ 2, J x y
ˆ J ˆ 2, J x z
ˆ J ˆ J x z
ˆ J x
ˆ J ˆ , J x y
ˆ J ˆ ˆ ˆ J x y Jz Jz ,
1 1
上式与关系式
m1
j1 , j2 , j, m | j1 , m1 , j2 , m m1 j1 , m1 , j2 , m m1 | j1 , j2 , j , m jj
一起反映了C-G系数的么正性和实数性。
(3)j的取值范围(j与j1,j2的关系) 1.对给定j1 j2 ,求 jmax 因为m m1 m2 取值范围分别是:
Jmax = j1 + j2
等式两边基矢数应该相等
| j1 , j2 , j , m | j1 , m1 , j2 , m m1 j1 , m1 , j2 , m m1 | j1 , j2 , j , m
Jˆ ,
z
同理
Jˆ ,
z
ˆ 2 0 J 2
Jˆ
1z ,
ˆ 2 J ˆ , J 1 2z
ˆ 2 J 1
0
亦成立。 [证毕]
(二)耦合表象和无耦合表象
(1)本征函数
综合上述对易关系可 知:四个角动量算符
ˆ 2, J ˆ ,J ˆ 2, J ˆ 2 J z 1 2
两两 对易
jm
, j2 , m j1 , m1 2 |
动量定理和动量守恒定律

第 7 章动量定理和动量守恒定律§7-1 动量定理和动量守恒定律物体之间或物体内部各部分之间因运动发生相对地点变化的过程称为机械运动。
它是物质的各种各种运动形式中最简单、也是最广泛的一种,比如:行星绕太阳的转动、宇宙飞船的航行、机器的运行、弹簧的伸长或压缩、水和空气等流体的流动等等,都是机械运动。
而各种复杂的运动形式如生命现象、化学反响等,固然也有地点的变化,但其实不归纳为机械运动。
机械运动有两种量度:假如存在的机械运动仍以保持机械运动的形式进行传达,那么应以动量 mv 来量度;假如机械运动转变成其余形式的运动,应以动能12mv2来量度。
即动量是以机械运动来量度机械运动,动能是以机械运动转变成必定量的其余形式的运动的能力来量度机械运动的,动量和动能是研究机械运动不行缺乏的物理量。
动量、动量定理1、动量p物体的质量 m 与其速度 v 的乘积,称为该物体的动量p ,即p mv 。
在直角坐标系中动量 p 可表示为p mv mv x i mv y j mv z k p x i p y j p z k ( 7-1-1 )由( 7-1-1 )式知,动量是一个矢量,拥有刹时性。
2、动量定理若在时辰 t ,物体的动量为 p(t ) ,经过t 时间段,其动量为p(t t ) ,在t tt 时间微元段上,其动量的增量dp 为d p p(t t ) p(t)若在该时间元段t 内,物体受力 f 作用,由牛顿第二定律知有dp fdt ( 7-1-2 )关系建立。
若在t1 t 2的时间段上,物体受力 f 作用,将每一个时间元段上动量的增量dp 加起来,即在 t1 t2 的时间段上对其乞降,则该时间段上的动量增量p 为p p 2 p1 t 2 f dt ( 7-1-3 )t 1t 2f dt 称为力( 7-1-2 )式与( 7-1-3 )式就是动量定理的表述。
人们又常把(7-1-3 )式的右项t 1f的冲量。
关于由多个物体所构成的系统,其总动量等于各物体动量p i的矢量和,即系统总动量p为np p ii 1系统所受的力可分为:外力、内力,外力即来自系统外的作用,内力即指系统内各物体间的互相作使劲。
角动量 角动量定理

d M (r P) dt
定义: L r P ——角动量
——角动量定理
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量定理
3
作用在质点上的力矩等于质点角动量对时间的变化率。 此即质点对固定点的角动量定理。
t
t0
Mdt L L0
t
t0
Mdt
叫冲量矩
2–5 角动量 角动量定理
2
2 质点的角动量定理
M r F
dP F dt
dP d dr M r (r P) P dt dt dt
P mv
dr v dt
dL M dt
dr P v mv 0 dt
角动量
1. L r P
L 的方向符合右手法则.
L m vrsin
第2章 运动定律与力学中的守恒定律
z L mv
r
2–5 角动量 角动量定理
4
2.质点在垂直于 z 轴平面
上以角速度
作半径为 r
的圆运动,相对圆心
z
o r
90
A
L r p r mv
mv0 (m M )v1
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量定理
9
在由A→B的过程中,子弹、木块系统机械能守恒
1 1 1 2 2 (m M) v 1 (m M) v 2 k (l l0 ) 2 2 2 2
在由A→B的过程中木块在水平面内只受指向O点的 弹性有心力,故木块对O点的角动量守恒,设 v2 与OB方向成θ角,则有
第7章-刚体力学

d
3g
cos
d
0
0 2l
=
3g sin
l
运用质心运动定理,对质心C:
nˆ F1
F
F2
l
O C
ˆt
mg
x
nˆ : F1 mg sin man ˆt : F2 mg cos mat
F
an
r2
l 2 2
3g sin 2l
l 3g cos
at
r
2
4
F12 F22
arctan F1 F2
(7.5.2)
即刚体相对于质心的轴的转动同样服从定轴转 动定律. 式(7.5.1)和(7.5.2)称刚体平面运动的基本动 力学方程.
§7.5.2 作用于刚体上的力
1.作用于刚体上力的两种效果 ·滑移矢量
(1) 施于刚体的力的特点 施于刚体的某个点的力,决不可以随便移到另一点去.
A
F
作用力通过质心,对质心轴上的 力矩为零,使刚体产生平动.
FT
11 10
mg
比较上面结果,可见提升弧形闸门
所用的拉力较小.
W
图(b)
[例题3]如图表示一种用实验方法测量转动惯量的装置。
待测刚体装在转动架上,线的一端绕在转动架的轮轴上,
线与线轴垂直,轮轴的轴体半径为r,线的另一端通过定
滑轮悬挂质量为m的重物,已知转动架惯量为I0 ,并测得 m自静止开始下落 h 高度的时间为 t ,求待测物体的转动
L
r1
r1
L2
L1
r2
O r2
m2
k
2mr 2
v1 v2 r
2如.转图轴, 为非对称k 轴对O点同样有
动量与角动量

p.47例 人车之间的作用为
内力,不影响系统 建立坐标系:
质点系:人,车
系统受 外力:
重
力 支持力 側向力
忽略道轨摩擦
跳车后车速 轨车侧向力 应用质点系 的动量定理
= 200 kg = 50 kg = 6 m/s
= 3 m/s
= 30º
X:
跳车后 车的速度 跳车过程 轨道受 側向冲量
Y: y
y
代入 算得
冲量
恒力
作用时间
变力
作用时间
恒力的冲量
变力的冲量
方向:
同
全部 方向: 牛顿 • 秒 ( N • s)
矢量和
冲量的SI制单位是
动量定理
一质点 m 在合外力 F 作用下,由牛顿运动定律,可得
质点动量定理的微分形式 将 改写成 质点动量定理的积分形式
或 合外力的冲量
分量式
摩托
可移动缓冲物
简例一
一起运动
本身 为负 ( 气 对 箭 )
则
燃料用完时,火箭获得的最大速度 若合外力只考虑重力,即 火箭的最后质量为 选 竖向上为正 的直线运动坐标系,则
合外力
气对地为
称为火箭的 质量比 。 获得更大的 火箭的 则 加速度 的途径是 :提高 和提高 质量比。
火箭算例 根据火箭运
(忽略阻力)
火箭、燃气系统水平合外力为零
定律证明
瞬间 位矢扫过的微面积
即
(称为掠面速率)
守恒。
因行星受的合外力总指向是太阳,角动量
则
常量
故,位矢在相同时间内扫过的面积相等
质量的流动概念
物体 速度 惯性 质量
(但构成物体的原子、分子的数量并没有改变)
普通物理学第二版第七章课后习题答案

第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s 估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).[解 答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转[解 答](1)22(30001200)1/601.57(rad /s )t 12ωπβ⨯-⨯===V V(2)222220()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为球t 时刻的角速度和角加速度.[解 答]7.1.4 半径为0.1m 的圆盘在铅直平面内转动,在圆盘平面内建立O-xy 坐标系,原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A 当t=0时恰好在x 轴上,该点的角坐标满足21.2t t (:rad,t :s).θθ=+求(1)t=0时,(2)自t=0开始转45o 时,(3)转过90o时,A 点的速度和加速度在x 和y 轴上的投影.[解 答](1) A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==v(2)45θ=o时,由2A 1.2t t ,t 0.47(s)42.14(rad /s)v R πθωω=+==∴==⨯v v v得(3)当90θ=o时,由7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承,以角速度10rad/s ω=逆时针转动,求臂与铅直45o 时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动,门中心G 的速度、加速度与B 或D点相同。
所以:7.1.6 收割机拔禾轮上面通常装4到6个压板.拔禾轮一边旋转,一边随收割机前进.压板转到下方才发挥作用,一方面把农作物压向切割器,另一方面把切割下来的作物铺放在收割台上,因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反. 已知收割机前进速率为1.2m/s ,拔禾轮直径1.5m ,转速22rev/min,求压板运动到最低点挤压作物的速度.[解 答]取地面为基本参考系,收割机为运动参考系。
量子力学第七章7.4

2
ˆ ˆ ˆ ˆ ˆ ˆ2 ˆ ˆ ˆ ˆ2 = J12 + J 2 + J1 • J 2 + J 2 • J1 = J12 + J 2 + 2 J1 • J 2
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ J 2 = J • J = J xi + J y j + J z k • J xi + J y j + J z k
1 1 2 2
′ ′ ′ ′ = (m1 + m2 ) < j1 , m1 , j2 , m2 | j1 , j2 , j , m >
′ ′ m = m1 + m2
m = m1 + m2
| j1 , j2 , j, m >=
m1 , m2
∑
| j1 , m1 , j2 , m2 > < j1 , m1 , j2 , m2 | j1 , j2 , j, m >
ˆ ˆ [ J12 , J1z ] = 0
这四个角动量算符有共同 的正交归一完备的本征函 数系。记为:
ˆ ˆ2 [ J12 , J 2 ] = 0
ˆ ˆ [ J12 , J 2 z ] = 0
ˆ ˆ2 [ J1z , J 2 ] = 0
ˆ ˆ [ J1z , J 2 z ] = 0 ˆ2 ˆ [J2 , J 2z ] = 0
由 m = m1 + m2 知:
mmax = m1 max + m2 max
j max = j1 + j 2
②
j min :
对于给定的 j1 , m1 有 2 j1 + 1 个取值,即 | j1 , m1 > 共有 2 j1 + 1 个; 同理给定 j2 ,m2 有 2 j2 + 1 个取值, | j2 , m2 > 共有 2 j2 + 1 个。 即 所以,给定 j1 和 j2 ,无耦合表象基矢共有 ( 2 j1 + 1 )( 2 j2 + 1 ) 个, 也即无耦合表象空间的维数。
自旋和角动量

e e L (SI); M L = − L (CGS) (6.1.7) 2m 2mc e e 因而轨道运动的回转磁比率是 − (SI),或 − (CGS )。自旋回转磁比率是轨道运动回转磁比率 2m 2mc
ML = −
的两倍。 自旋是电子的一种固有的属性。千万不要认为,电子自旋是因为电子在作机械的自转引起。可 以证明,如果将电子想象成为一个电荷均匀分布的小球,由于电子的半径约为 2.8 × 10-13cm,要想使 它的磁矩由于自转而达到一个玻尔磁子,则它的表面旋转速度将超过光速。这当然是不可能的。(请 读者自己证明)电子自旋是一个新的自由度,与电子的空间运动完全无关。电子自旋是电子的内禀属 性。电子的自旋磁矩是内禀磁矩。事实上,随着人们认识的深入,越来越发现对于某些粒子,除了 时空自由度还有其他的自由度。 例如质子和中子, 除时空、 自旋外, 还有同位旋。 夸克则还具有 “味” 和“色”等自由度。不过,自旋自由度是除时空自由度外的第一个新发现。值得指出的是,电子自 旋角动量与轨道角动量不同, 电子自旋的取值是± h / 2 ,而不是 h 的整数倍。 电子自旋的 g 因子 | g s | 是 2,轨道的 | g l | 为 1。当然,自然界中也存在着自旋取 h 整数值的粒子,我们在全同粒子一章中再 作讨论。
第六章
自旋和角动量
非相对论量子力学在解释许多实验现象上获得了成功。用薛定谔方程算出的谱线频率,谱线强度 也和实验结果相符。但是,更进一步的实验事实发现,还有许多现象,如光谱线在磁场中的分裂, 光谱线的精细结构等,用前面几章的理论无法解择,根本原因在于以前的理论只涉及轨道角动量。 新的实验事实表明,电子还具有自旋角动量。 在非相对论量子力学中,自旋是作为一个新的附加的量子数引入的。本章只是根据电子具有自 旋的实验事实,在薛定谔方程中硬加入自旋。本章的理论也只是局限在这样的框架内。以后在相对 论量子力学中将证明,电子的自旋将自然地包含在相对论的波动方程——狄拉克方程中。电子轨道 角动量在狄拉克方程中不再守恒,只有轨道角动量与自旋角动量之和,总角动量才是守恒量。 本章将先从实验上引入自旋,分析自旋角动量的性质,建立包含自旋在内的非相对论量子力学 方程——泡利方程,然后讨论角动量的藕合,并进一步讨论光谱线在磁场中的分裂和精细结构,此 外还会对电子在磁场中的一些其他的有趣的重要现象做些探讨。
角动量守恒讲解

上一章讲了刚体的转动定律和转动惯量,和做水平物体的动量一样,刚体转动一样 有动量,在图1所示的刚体中,如果质点m的速度为v,则动量p为mv,而它相对于 原点的位置矢量为r,于是定义L=r×p = mr×v为质点相对于原点的角动量;
同样,角动量也是一个矢量,其方向的判断与力矩的判断方法一致;从定义可以看 出,角动量是由两个矢量的叉乘得来的,于是其大小就可以表示为rmvs)/dt = d(r×mv)/dt,
于是r×F = r×d(mv)/dt可化为r×F = d(r×mv)/dt,
其中r×F称为合力F对质点的合力矩,上式就可以表示为M=dL/dt,它表示作用于质 点的合力矩等于该点角动量随时间的变化率,式子变形后就是Mdt = dL,而Mdt叫做 冲量矩,在t1到t2时间内积分就是∫Mdt = L2-L1,这就是质点的角动量定理,即质 点所受冲量矩等于质点角动量的增量。
说完了质点的角动量,自然该说说刚体的角动量;如图2所示,因为单个质点的角动 量为ΔL=Δmi(ri^2)ω,将所有的质点的角动量加起来就是L=∑Δm(ri^2)ω = Jω, 这就是刚体绕定轴转动的角动量。
因为Mdt = dL =d(Jω),在t1到t2时间内积分得∫Mdt = Jω2 - Jω1,等式左边表示 力矩对定轴的冲量矩,右边表示刚体角动量的变化;显然,如果作用在刚体上的外 力等于零,那么刚体的角动量就保持不变,这就是角动量守恒定律,比如地球在宇 宙中的转动就可以近似为角动量守恒。
大家都知道芭蕾舞演员在原地旋转时,假设地面是光滑的,一般是手臂先水平打开, 当获得一定的旋转角速度时,再把手臂向身体靠拢,根据角动量守恒就知道,演员 的旋转角速度就会慢慢增大;这就是在角动量守恒的情况下,通过调整转动惯量来 改变旋转速度。
量子力学_陈洪_电子教案第7章自旋与角动量

σx, σy, σz 称为泡利矩阵
0 1 0 i 1 0 x 1 0 ; y i 0 ; z 0 1
7.3 电子自旋波函数
电子波函数写 成矩阵形式
1 ( x , y , z , t ) ( x, y, z, t ) 2
讨论: 1. 对波函数归一化时必须同时对自旋求 和和对空间坐标积分
2 1 2 2 d x r , S , t ( *, *) ( z 1 2 2 )d 1 1 Sz 2 2 2 1 表示在t时刻在(x , y , z)点周围单位体积找到 自旋S z 的几率 2 2 2 表示在t时刻在(x , y , z)点周围单位体积找到 自旋S z 的几率 2 3
2. 两个粒子的自旋-自旋耦合或轨道-轨道耦合
二. 两个角动量的耦合后的对易关系
J 1 , J 2 表示体系的两个角动量 算符, 且J 1与J 2 相互独立 则 [ J 1 x , J 1 y ] iJ 1 z [ J 2 x , J 2 y ] iJ 2 z [ J 1 y , J 1 z ] iJ 1 x [ J 2 y , J 2 z ] iJ 2 x [ J 1 z , J 1 x ] iJ 1 y [ J 2 z , J 2 x ] iJ 2 y 因为两角动量独立则 [ J 1 , J 2 ] 0 令 J J1 J 2
(1) 则 [ J x , J y ] iJ z [ J y , J z ] iJ x [ J z , J x ] iJ y
证 : [J x , J y ] [J1 x J 2 x , J1 y J 2 y ] ( J 1 x J 2 x )( J 1 y J 2 y ) ( J 1 y J 2 y )( J 1 x J 2 x ) J1 x J1 y J1 x J 2 y J 2 x J1 y J 2 x J 2 y J1 y J1 x J1 y J 2 x J 2 y J1 x J 2 y J 2 x (J1 x J1 y J1 y J1 x ) (J 2 x J 2 y J 2 y J 2 x ) i( J 1z J 2z ) iJ z
16第7章概念1-自旋角动量的本征_[1]...
![16第7章概念1-自旋角动量的本征_[1]...](https://img.taocdn.com/s3/m/29c5272f7375a417866f8ff3.png)
ℏ 同理, 同理,λ = − (自旋朝下 )对应的归一化本征矢为 2 sin(θ / 2) ↓n = iϕ −e cos(θ / 2)
讨论: 讨论:
ˆ S S 1. S x、ˆ y、ˆ z的本征矢 ˆ 可取任意值, (1) S z :θ = 0 ,ϕ 可取任意值,取 ϕ = 0 ,则本征矢为
e− iϕ sin θ − cos θ ˆ 的本征值 λ = λ ′ ℏ 满足久期方程 Sn 2 ℏ cos θ = iϕ 2 e sin θ
解得
a ℏ 自旋朝上) 设 λ = (自旋朝上)对应的归一化本征矢为 ↑ n = ,则 2 b
ℏ cos θ − λ ′ e− iϕ sin θ =0 iϕ 2 e sin θ − cos θ − λ ′ ℏ λ=± λ ′ = ±1 2
ˆ χ 1 ( S ) = ℏ 0 −i 1 = ℏ 0 = i ℏ χ ( S ) Sy z z −1 2 2 i 0 0 2 i 2 2 ℏ 0 −i 0 ℏ −i = −i ℏ χ ( S ) ˆ 1 S y χ− 1 (S z ) = z = 2 0 2 2 2 2 i 0 1
θ
2
和 sin
2
θ
2
。
的概率: 也可以采取下面的办法求 S z = ±ℏ / 2 的概率:
S z = ±ℏ / 2 的概率分别为
Pz (↑) = ↑ z ↑n
2
cos(θ / 2) 2θ = (1 0 ) iϕ = cos 2 e sin(θ / 2)
2
Pz (↓) = ↓ z ↑n
第七章
一、自旋角动量 1.电子自旋角动量算符 实验测得: 实验测得: S n = ±ℏ / 2
量子力学周世勋第二版课后习题解答第7章

7.1.证明:i z y x =σσσˆˆˆ 证:由对易关系z x y y x i σσσσσˆ2ˆˆˆˆ=- 及 反对易关系0ˆˆˆˆ=+x y y x σσσσ, 得 z y x i σσσˆˆˆ= 上式两边乘z σˆ,得 2ˆˆˆˆz z y x i σσσσ= ∵ 1ˆ2=z σ ∴ i z y x =σσσˆˆˆ 7.2 求在自旋态)(21z S χ中,xS ˆ和y S ˆ的测不准关系: ?)()(22=y x S S ∆∆解:在z S ˆ表象中)(21z S χ、xS ˆ、y S ˆ的矩阵表示分别为 ⎪⎪⎭⎫ ⎝⎛=01)(21z S χ ⎪⎪⎭⎫ ⎝⎛=01102ˆ x S ⎪⎪⎭⎫ ⎝⎛-=002ˆi i S y ∴ 在)(21z S χ态中00101102)0 1(2121=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛==+ χχx x S S 4010110201102)0 1(ˆ2222121 =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==+χχx x S S4)(2222=-=∆xxx S S S 001002)0 1(ˆ2121=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-==+i i S S y y χχ 401002002)0 1(ˆ2222121 =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-==+i i i i S S y y χχ4)(2222=-=∆yyy S S S 16)()(422=∆∆y x S S讨论:由xS ˆ、y S ˆ的对易关系[x S ˆ,y S ˆ]z S i ˆ = 要求4)()(2222zy x S S S ≥∆∆ 在)(21z S χ态中,2=z S ∴ 16)()(422≥y x S S ∆∆可见①式符合上式的要求。
16)()(422=∆∆y x S S7.3.求⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛=002ˆ01102ˆi i S S y x 及的本征值和所属的本征函数。
力学答案第七章

第七章刚体力学习题及解答7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).解:7.1.2 汽车发动机的转速在12s内由1200rev/min增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转?解:( 1)( 2)所以转数 =7.1.3 某发动机飞轮在时间间隔t内的角位移为球 t时刻的角速度和角加速度.解:7.1.4 半径为0.1m的圆盘在铅直平面内转动,在圆盘平面内建立坐标系,原点在轴上.x和y轴沿水平和铅直向上的方向.边缘上一点A当t=0时恰好在x轴上,该点的角坐标满足求(1)t=0时,(2)自t=0开始转时,(3)转过时,A点的速度和加速度在x和y轴上的投影. 解:( 1)( 2)时,由( 3)当时,由7.1.5 钢制炉门由两个各长1.5m的平行臂AB和CD支承,以角速度逆时针转动,求臂与铅直时门中心G的速度和加速度.解:因炉门在铅直面内作平动,门中心 G的速度、加速度与B或D点相同。
所以:7.1.6 收割机拔禾轮上面通常装4到6个压板.拔禾轮一边旋转,一边随收割机前进.压板转到下方才发挥作用,一方面把农作物压向切割器,另一方面把切割下来的作物铺放在收割台上,因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反.已知收割机前进速率为 1.2m/s,拔禾轮直径1.5m,转速22rev/min,求压板运动到最低点挤压作物的速度.解:取地面为基本参考系,收割机为运动参考系。
取收割机前进的方向为坐标系正方向7.1.7 飞机沿水平方向飞行,螺旋桨尖端所在半径为150cm,发动机转速2000rev/min.(1)桨尖相对于飞机的线速率等于多少?(2)若飞机以250km/h的速率飞行,计算桨尖相对于地面速度的大小,并定性说明桨尖的轨迹.解:取地球为基本参考系,飞机为运动参考系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对原子的同一组态而言,L和S都相同的状态,若不计及轨
道-自旋相互作用,且在没有外界磁场作用下,都具有完 全相同的能量。 将同一组态中,由相同L和S所构成的诸状态合称为一个 光谱项,每一个光谱项相当于一个能级。
24
对于一定的S,mS 可有S、S-1、…、-S共计2S+1个取值,
分别对应总自旋角动量在外磁场方向的分量MSz的2S+1种状态,
0
7
同样,我们还可以求得:
ˆ ˆ L2 , L y 0 ˆ ˆ L2 , Lz 0
根据各个算符间的对易关系,可以得出如下结
论:角动量大小的平方L2与任意一个分量可以同时
具有确定值,但是角动量的三个分量最多只有一个
有确定值,通常我们选取Lz 做为与L2 同时具有确定
5
ˆ f i y f z f Lx 同样: y z 2 2 2 2 f f f f 2 f ˆ L f 2 zy ˆ Ly x z xy 2 x xz xy z y zy xz
31
Hund规则
Hund第一规则
S最大时能量最低;S相同,则L最大时能量最低。
Hund第二规则
如L与S均相同,当电子壳层未达半充满时,J愈小能量愈低; 半充满后,则J愈大能量愈低。
32
S大,2S+1大,即具有最大多重度的状态是最稳定的。
值的角动量分量。
8
注意:我们说角动量大小的平方L2具有确定值并
不是意味着角动量矢量 完全确定,因为 是个矢量,
要完全确定之,必须要知道其在各个方向上的分量, L L
这一点我们是做不到的,因为角动量各个分量的量
子力学算符间是不可对易的,最多只能有一个具有
确定的值。
9
7.2 电子自旋
1.自旋角动量算符的对易关系 单电子情况
2
所以:
2 f 2 f 其中用了下列关系式: zx xz
ˆ ˆ ˆ [ Lx , Ly ] i Lz
(这对于品优波 函数总是成立的)
6
同样,我们可以求得:
ˆ ˆ ˆ [ Ly , Lz ] i Lx
ˆ2 , L L ˆx
ˆ ˆ ˆ [ Lz , Lx ] i Ly
1D三个光谱项,而np1(n+1)p1 型组态具有这六个光
谱项。
29
光谱项1S
L=0,S=0;J=0。光谱支项为:1S0。
光谱项1D
L=2,S=0;L+S=2,L-S=2,J=2。光谱支项
为:1D2。
三重态3P
L=1,S=1;L+S=2,L-S=0,J=2、1、0。三
个光谱支项分别为:3P2、3P1、3P0。
即自旋多重度为2S+1。因此,在光谱学符号中通常将自旋多重
度写在L值符号的左上角,即:2S+1L。 又由于轨道和自旋的相互作用,不同的J所对应的能级会有微 小的差别。将J的数值记在L的右下角,即:2S+1LJ。称为光谱支 项。
25
几点结论
凡是充满壳层s2、p6、d10、f14等的总轨道角动量和总 自旋角动量均为0。
z z S
1 2
3 2
1 2
3 2
S
14
7.3 多电子原子的量子数和光谱项
R多电子原子的量子数 R光谱项及其应用
15
一、多电子原子的量子数
1.总轨道角量子数L
单电子轨道角动量
M l (l 1)
原子的总轨道角动量
总轨道角量子数
M L M L L( L 1)
L l1 l2 lN , l1 l2 lN 1, l1 l2 lN 2,
最小值为0或
l 的最小正值
i i
16
N
单电子轨道角动量在外磁场方向上的分量
Mz m
原子总轨道角动量在外磁场方向上的分量
M Lz mL
总轨道磁量子数
2 2 x 2 y 2 z
S S S S
2
(1) (2)
[S , Si ] 0 i x, y, z
[ S x , S y ] i S z
[ S y , S z ] i S x [ S z , S x ] i S y
(3)
12
2.单电子自旋算符的本征函数和本征值
对于单电子, 和 S z 的本征态只有两个,以和表示。 S
1 1 1 2 S s( s 1) ( 1) , s 2 2 2 1 1 1 2 2 2 S s( s 1) ( 1) , s 2 2 2
分量。
2
1 经典力学中的角动量
根据角动量定义(1),可得:
L ypz zp y i zpx xpz j xp y ypx k Lx i Ly j Lz k
所以角动量的三个分量Lx,Ly,Lz等于
Lx ypz zp y ,
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ 这样: [ Lx , Ly ] f [ Lx Ly Ly Lx ] f Lx Ly f Ly Lx f f f 2 y x y x f y y x x
Ly zpx xpz ,
L L L L
2 2 x 2 y 2 z
Lz xp y ypx
3
2.量子力学中的角动量
在量子力学中有两种角动量:轨道角动量和自旋角动量。轨道 角动量对应于经典力学中的角动量动量,在经典力学中没有对应的物理量。
根据量子力学的基本假设,轨道角动量的分量的算符为:
对电子而言
1 s 2
N N N 1 S , 1, 2, , , 0 2 2 2 2
18
总自旋角动量在外磁场方向的分量
M Sz mS
总自旋磁量子数
mS msi
i 1
N
共有2S+1个取值:S、S-1、S-2、…、-S
19
3. 总角量子数J
原子中各电子的轨道角动量和自旋角动量相互作用,得到一个 总的角动量。两种耦合方式:
mL mi
i 1
N
共有2L+1个取值:L,L-1,L-2,…,-L
17
2. 总自旋量子数S
原子的总自旋角动量 原子的总自旋量子数
M S M S S ( S 1)
S s1 s2 sN , s1 s2 sN 1, s1 s2 sN 2,
ˆ2 Lx
ˆ2 Ly
ˆ2 , L Lz ˆ x
ˆ2 , L L2 , L L2 , L Lx ˆ x ˆ y ˆ x ˆ z ˆ x ˆ2 , L L2 , L Ly ˆ x ˆ z ˆ x ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ L y L y , Lx L y , Lx L y Lz Lz , Lx Lz , Lx Lz ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ i L y Lz i Lz L y i Lz L y i L y Lz
自旋角动量本征方程
2 t 2
2 t
(6) (7)
1 3 S Y S (S 1) Y , (S 0, , 1, , 2, ) 2 2
(8)
Szt Y M s Y , (M s S , S 1, , S 1, S )
(9)
上式中S为多电子体系的总自旋量子数,Ms为S沿z轴的分量。
M Jz mJ
共有2J+1个取值
mJ=mL+mS=J,J-1,J-2,…,-J
22
二、光谱项及其应用
1. 光谱项与光谱支项 单电子轨道 l=0 s 多电子原子 L=0 S 1 p 1 P 2 d 2 D f 3 F … 3 … … …
23
根据原子光谱的实验数据及量子力学理论可以得出结论:
ˆ Lx i y z y z
ˆ ˆ i z x Lz i x y Ly x z x y
4
3.轨道角动量分量的算符间的对易关系
ˆ ˆ ˆ ˆ ˆ ˆ [ Lx , Ly ] Lx Ly Ly Lx
轨道和自旋的相互作用比各电子间的相互作用都要大,
故采用j-j耦合将会得到较好的结果。
对于Z≤40的轻原子,各电子间的相互作用要远大于每
个电子自身的轨道和自旋相互作用,于是L-S耦合将是 更好、更方便的近似方法。
21
多电子原子的总角动量 总角量子数
M J J ( J 1)
J=L+S,L+S-1,L+S-2,…,│L-S│ 总角动量在外磁场方向上的分量 总磁量子数
第七章 角动量
1
7.1 单粒子体系的角动量
经典力学中的角动量
p 的矢量积,即: 到原点的矢量 r 和质点的线动量 i j k Lr p x y z 1 px p y pz
在经典力学中角动量可以用一个矢量 L 来表示。它定义为质点
和 p 在x,y和z轴方向的 式中的x,y,z和px,py,pz分别是矢量 r
10
多电子体系
S S S S
S xt Sxj
j
2 t
2 xt
2 yt
2 zt
(4)
S yt S yj
j
(5)
S zt S zj
j
