R语言求解线性规划和非线性规划
非线性规划

1. 非线性规划我们讨论过线性规划,其目标函数和约束条件都是自变量的线性函数。
如果目标函数是非线性函数或至少有一个约束条件是非线性等式(不等式),则这一类数学规划就称为非线性规划。
在科学管理和其他领域中,很多实际问题可以归结为线性规划,但还有另一些问题属于非线性规划。
由于非线性规划含有深刻的背景和丰富的内容,已发展为运筹学的重要分支,并且在最优设计,管理科学,风险管理,系统控制,求解均衡模型,以及数据拟合等领域得到越来越广泛的应用。
非线性规划的研究始于三十年代末,是由W.卡鲁什首次进行的,40年代后期进入系统研究,1951年.库恩和.塔克提出带约束条件非线性规划最优化的判别条件,从而奠定了非线性规划的理论基础,后来在理论研究和实用算法方面都有很大的发展。
非线性规划求解方法可分为无约束问题和带约束问题来讨论,前者实际上就是多元函数的极值问题,是后一问题的基础。
无约束问题的求解方法有最陡下降法、共轭梯度法、变尺度法和鲍威尔直接法等。
关于带约束非线性规划的情况比较复杂,因为在迭代过程中除了要使目标函数下降外,还要考虑近似解的可行性。
总的原则是设法将约束问题化为无约束问题;把非线性问题化为线性问题从而使复杂问题简单化。
求解方法有可行方向法、约束集法、制约函数法、简约梯度法、约束变尺度法、二次规划法等。
虽然这些方法都有较好的效果,但是尚未找到可以用于解决所有非线性规划的统一算法。
非线性规划举例[库存管理问题] 考虑首都名酒专卖商店关于啤酒库存的年管理策略。
假设该商店啤酒的年销售量为A 箱,每箱啤酒的平均库存成本为H 元,每次订货成本都为F 元。
如果补货方式是可以在瞬间完成的,那么为了降低年库存管理费用,商店必须决定每年需要定多少次货,以及每次订货量。
我们以Q 表示每次定货数量,那么年定货次数可以为QA,年订货成本为Q A F ⨯。
由于平均库存量为2Q,所以,年持有成本为2Q H ⨯,年库存成本可以表示为:Q HQ A F Q C ⨯+⨯=2)( 将它表示为数学规划问题:min Q H Q A F Q C ⋅+⋅=2)( ..t s 0≥Q其中Q 为决策变量,因为目标函数是非线性的,约束条件是非负约束,所以这是带约束条件的非线性规划问题。
线性和非线性最优化理论、方法、软件及应用

线性和非线性最优化理论、方法、软件及应用最优化在航空航天、生命科学、水利科学、地球科学、工程技术等自然科学领域和经济金融等社会科学领域有着广泛和重要的应用, 它的研究和发展一直得到广泛的关注. 最优化的研究包含理论、方法和应用.最优化理论主要研究问题解的最优性条件、灵敏度分析、解的存在性和一般复杂性等.而最优化方法研究包括构造新算法、证明解的收敛性、算法的比较和复杂性等.最优化的应用研究则包括算法的实现、算法的程序、软件包及商业化、在实际问题的应用. 这里简介一下线性和非线性最优化理论、方法及应用研究的发展状况.1. 线性最优化线性最优化, 又称线性规划, 是运筹学中应用最广泛的一个分支.这是因为自然科学和社会科学中许多问题都可以近似地化成线性规划问题. 线性规划理论和算法的研究及发展共经历了三个高潮, 每个高潮都引起了社会的极大关注. 线性规划研究的第一高潮是著名的单纯形法的研究. 这一方法是Dantzig在1947年提出的,它以成熟的算法理论和完善的算法及软件统治线性规划达三十多年. 随着60年代发展起来的计算复杂性理论的研究, 单纯形法在七十年代末受到了挑战. 1979年前苏联数学家Khachiyan提出了第一个理论上优于单纯形法的所谓多项式时间算法--椭球法, 曾成为轰动一时的新闻, 并掀起了研究线性规划的第二个高潮. 但遗憾的是广泛的数值试验表明, 椭球算法的计算比单纯形方法差.1984年Karmarkar提出了求解线性规划的另一个多项式时间算法. 这个算法从理论和数值上都优于椭球法,因而引起学术界的极大关注, 并由此掀起了研究线性规划的第三个高潮. 从那以后, 许多学者致力于改进和完善这一算法,得到了许多改进算法.这些算法运用不同的思想方法均获得通过可行区域内部的迭代点列,因此统称为解线性规划问题的内点算法. 目前内点算法正以不可抗拒的趋势将超越和替代单纯形法.线性规划的软件, 特别是由单纯形法所形成的软件比较成熟和完善.这些软件不仅可以解一般线性规划问题, 而且可以解整数线性规划问题、进行灵敏度分析, 同时可以解具有稀疏结构的大规模问题.CPLEX是Bi xby基于单纯形法研制的解线性和整数规划的软件, CPLEX的网址是/. 此外,这个软件也可以用来解凸二次规划问题, 且特别适合解大规模问题. PROC LP是SAS软件公司研制的SAS商业软件中OR模块的一个程序.这个程序是根据两阶段单纯形法研制的,可以用来解线性和整数规划问题并可进行灵敏度分析, 是一个比较完善的程序.用户可以根据需要选择不同的参数来满足不同的要求。
r语言 对指定范围的数据拟合曲线

文章标题:深入探讨R语言对指定范围的数据拟合曲线在数据分析和统计学中,拟合曲线是一种对观测数据进行数学建模的方法。
通过拟合曲线,我们可以揭示数据中的规律和趋势,并进一步进行预测和分析。
R语言作为一种强大的统计分析工具,提供了丰富的函数和包,可以帮助我们对指定范围的数据进行拟合曲线分析。
在本文中,我们将深入探讨R语言对指定范围的数据拟合曲线的方法和应用,以及个人对这一主题的理解和观点。
一、拟合曲线的基本概念拟合曲线是一种通过数学函数来拟合数据的方法,旨在找到最符合数据趋势的函数模型。
在R语言中,拟合曲线通常使用lm()函数进行线性拟合,或者使用非线性拟合的函数,如nls()或者自定义的函数。
通过拟合曲线,我们可以得到数据的趋势线,了解数据的分布规律和变化情况。
二、在R语言中进行数据拟合曲线在R语言中进行数据拟合曲线分析通常需要以下步骤:导入数据并进行数据预处理;选择适当的拟合函数进行数据拟合;对拟合结果进行评估和分析。
在导入数据方面,我们可以使用read.csv()或者read.table()等函数导入数据。
在进行数据拟合前,通常需要对数据进行清洗和处理,去除异常值或缺失值,确保数据的完整性和准确性。
接下来,根据数据的特点和需求,选择适当的拟合函数进行数据拟合。
对于线性拟合,我们可以使用lm()函数进行简单的线性回归分析;对于非线性拟合,我们可以使用nls()函数或者自定义的函数进行拟合。
对拟合结果进行评估和分析,可以通过summary()函数查看拟合参数的具体数值,或者绘制拟合曲线和原始数据的散点图进行可视化比较。
三、在指定范围的数据拟合曲线在实际应用中,我们经常需要对指定范围的数据进行拟合曲线分析。
我们可能只关注数据集中的某一部分数据,或者对数据的某一时间段或空间区域进行拟合。
在R语言中,可以通过子集操作或者筛选条件的方式,对指定范围的数据进行拟合曲线分析。
可以使用subset()函数或者逻辑条件来选择感兴趣的数据,并进行相应的拟合分析。
R语言实验三

实验三数组的运算、求解方程(组)和函数极值、数值积分【实验类型】验证性【实验学时】2 学时【实验目的】1、掌握向量的四则运算和内积运算、矩阵的行列式和逆等相关运算;2、掌握线性和非线性方程(组)的求解方法,函数极值的求解方法;3、了解 R 中数值积分的求解方法。
【实验内容】1、向量与矩阵的常见运算;2、求解线性和非线性方程(组);3、求函数的极值,计算函数的积分。
【实验方法或步骤】第一部分、课件例题:1.向量的运算x<-c(-1,0,2)y<-c(3,8,2)v<-2*x+y+1vx*yx/yy^xexp(x)sqrt(y)x1<-c(100,200); x2<-1:6; x1+x22.x<-1:5y<-2*1:5x%*%ycrossprod(x,y)x%o%ytcrossprod(x,y)outer(x,y)3.矩阵的运算A<-matrix(1:9,nrow=3,byrow=T);AA+1 #A的每个元素都加上1B<-matrix(1:9,nrow=3); BC<-matrix(c(1,2,2,3,3,4,4,6,8),nrow=3); C D<-2*C+A/B; D #对应元素进行四则运算x<-1:9A+x #矩阵按列与向量相加E<-A%*%B; E #矩阵的乘法y<-1:3A%*%y #矩阵与向量相乘crossprod(A,B) #A的转置乘以Btcrossprod(A,B) #A乘以B的转置4.矩阵的运算A<-matrix(c(1:8,0),nrow=3);At(A) #转置det(A) #求矩阵行列式的值diag(A) #提取对角线上的元素A[lower.tri(A)==T]<-0;A #构造A对应的上三角矩阵qr.A<-qr(A);qr.A #将矩阵A分解成正交阵Q与上三角阵R的乘积,该结果为一列表Q<-qr.Q(qr.A);Q;R<-qr.R(qr.A);R #显示分解后对应的正交阵Q与上三角阵Rdet(Q);det(R);Q%*%R #A=Q*Rqr.X(qr.A) #显示分解前的矩阵5.解线性方程组A<-matrix(c(1:8,0),nrow=3,byrow=TRUE)b<-c(1,1,1)x<-solve(A,b); x #解线性方程组Ax=bB<-solve(A); B #求矩阵A的逆矩阵BA%*%B #结果为单位阵6.非线性方程求根f<-function(x) x^3-x-1 #建立函数uniroot(f,c(1,2)) #输出列表中f.root为近似解处的函数值,iter为迭代次数,estim.prec为精度的估计值uniroot(f,lower=1,upper=2) #与上述结果相同polyroot(c(-1,-1,0,1)) #专门用来求多项式的根,其中c(-1,-1,0,1)表示对应多项式从零次幂项到高次幂项的系数7.求解非线性方程组(1)自编函数: (Newtons.R)Newtons<-function (funs, x, ep=1e-5, it_max=100){index<-0; k<-1while (k<=it_max){ #it_max 表示最大迭代次数x1 <- x; obj <- funs(x);x <- x - solve(obj$J, obj$f); #Newton 法的迭代公式norm <- sqrt((x-x1) %*% (x-x1))if (norm<ep){ index<-1; break #index=1 表示求解成功}; k<-k+1 }obj <- funs(x);list(root=x, it=k, index=index, FunVal= obj$f)} # 输出列表(2)调用求解非线性方程组的自编函数funs<-function(x){ f<-c(x[1]^2+x[2]^2-5, (x[1]+1)*x[2]-(3*x[1]+1)) # 定义函数组J<-matrix(c(2*x[1], 2*x[2], x[2]-3, x[1]+1), nrow=2,byrow=T) # 函数组的 Jacobi 矩阵list(f=f, J=J)} # 返回值为列表 : 函数值 f 和 Jacobi 矩阵 Jsource("F:/wenjian_daima/Newtons.R") # 调用求解非线性方程组的自编函数Newtons(funs, x=c(0,1))8.一元函数极值f<-function(x) x^3-2*x-5 # 定义函数optimize(f,lower=0,upper=2) # 返回值 : 极小值点和目标函数f<-function(x,a) (x-a)^2 # 定义含有参数的函数optimize(f,interval=c(0,1),a=1/3) # 在函数中输入附加参数9.多元函数极值(1)obj <-function (x){ # 定义函数F<-c(10*(x[2]-x[1]^2),1-x[1]) # 视为向量sum (F^2) } # 向量对应分量平方后求和nlm(obj,c(-1.2,1))(2)fn<-function(x){ # 定义目标函数F<-c(10*(x[2]-x[1]^2), 1-x[1])t(F)%*%F } # 向量的内积gr <- function(x){ # 定义梯度函数F<-c(10*(x[2]-x[1]^2), 1-x[1])J<-matrix(c(-20*x[1],10,-1,0),2,2,byrow=T) #Jacobi 矩阵2*t(J)%*%F } # 梯度optim(c(-1.2,1), fn, gr, method="BFGS")最优点 (par) 、最优函数值 (value)10.梯形求积分公式(1)求积分程序: (trape.R)trape<-function(fun, a, b, tol=1e-6){ # 精度为 10 -6N <- 1; h <- b-a ; T <- h/2 * (fun(a) + fun(b)) # 梯形面积 repeat{h <- h/2; x<-a+(2*1:N-1)*h; I <-T/2 + h*sum(fun(x)) if(abs(I-T) < tol) break; N <- 2 * N; T = I }; I}(2)source("F:/wenjian_daima/trape.R") # 调用函数f<-function(x) exp(-x^2)trape(f,-1,1)(3)常用求积分函数f<-function(x)exp(-x^2) # 定义函数integrate(f,0,1)integrate(f,0,10)integrate(f,0,100)integrate(f,0,10000) # 当积分上限很大时,结果出现问题integrate(f,0,Inf) # 积分上限为无穷大ft<-function(t) exp(-(t/(1-t))^2)/(1-t)^2 # 对上述积分的被积函数 e 2 作变量代换 t=x/(1+x) 后的函数integrate(ft,0,1) # 与上述计算结果相同,且精度较高第二部分、教材例题:1.随机抽样(1)等可能的不放回的随机抽样:> sample(x, n) 其中x为要抽取的向量, n为样本容量(2)等可能的有放回的随机抽样:> sample(x, n, replace=TRUE)其中选项replace=TRUE表示有放回的, 此选项省略或replace=FALSE表示抽样是不放回的sample(c("H", "T"), 10, replace=T)sample(1:6, 10, replace=T)(3)不等可能的随机抽样:> sample(x, n, replace=TRUE, prob=y)其中选项prob=y用于指定x中元素出现的概率, 向量y与x等长度sample(c("成功", "失败"), 10, replace=T, prob=c(0.9,0.1))sample(c(1,0), 10, replace=T, prob=c(0.9,0.1))2.排列组合与概率的计算1/prod(52:49)1/choose(52,4)3.概率分布qnorm(0.025) #显著性水平为5%的正态分布的双侧临界值qnorm(0.975)1 - pchisq(3.84, 1) #计算假设检验的p值2*pt(-2.43, df = 13) #容量为14的双边t检验的p值4.limite.central( )的定义limite.central <- function (r=runif, distpar=c(0,1), m=.5,s=1/sqrt(12),n=c(1,3,10,30), N=1000) {for (i in n) {if (length(distpar)==2){x <- matrix(r(i*N, distpar[1],distpar[2]),nc=i)}else {x <- matrix(r(i*N, distpar), nc=i)}x <- (apply(x, 1, sum) - i*m )/(sqrt(i)*s)hist(x,col="light blue",probability=T,main=paste("n=",i), ylim=c(0,max(.4, density(x)$y)))lines(density(x), col="red", lwd=3)curve(dnorm(x), col="blue", lwd=3, lty=3, add=T)if( N>100 ) {rug(sample(x,100))}else {rug(x)}}}5.直方图x=runif(100,min=0,max=1)hist(x)6.二项分布B(10,0.1)op <- par(mfrow=c(2,2))limite.central(rbinom,distpar=c(10,0.1),m=1,s=0.9)par(op)7.泊松分布: pios(1)op <- par(mfrow=c(2,2))limite.central(rpois, distpar=1, m=1, s=1, n=c(3, 10, 30 ,50)) par(op)8.均匀分布:unif(0,1)op <- par(mfrow=c(2,2))limite.central( )par(op)9.指数分布:exp(1)op <- par(mfrow=c(2,2))limite.central(rexp, distpar=1, m=1, s=1)par(op)10.混合正态分布的渐近正态性mixn <- function (n, a=-1, b=1){rnorm(n, sample(c(a,b),n,replace=T))}limite.central(r=mixn, distpar=c(-3,3),m=0, s=sqrt(10), n=c(1,2,3,10)) par(op)11.混合正态分布的渐近正态性op <- par(mfrow=c(2,2))mixn <- function (n, a=-1, b=1){rnorm(n, sample(c(a,b),n,replace=T))}limite.central(r=mixn, distpar=c(-3,3),m=0,s=sqrt(10),n=c(1,2,3,10)) par(op)第三部分、课后习题:3.1a=sample(1:100,5)asum(a)3.2(1)抽到10、J、Q、K、A的事件记为A,概率为P(A)=1(5220)其中在R中计算得:> 1/choose(52,20)[1] 7.936846e-15(2)抽到的是同花顺P(B)=(41)(91) (525)在R中计算得:> (choose(4,1)*choose(9,1))/choose(52,5) [1] 1.385e-053.3#(1)x<-rnorm(1000,mean=100,sd=100)hist(x)#(2)y<-sample(x,500)hist(y)#(3)mean(x)mean(y)var(x)var(y)3.4x<-rnorm(1000,mean=0,sd=1) y=cumsum(x)plot(y,type = "l")plot(y,type = "p")3.5x<-rnorm(100,mean=0,sd=1) qnorm(.025)qnorm(.975)t.test(x)由R结果知:理论值为[-1.96,1.96],实际值为:[-0.07929,0.33001]3.6op <- par(mfrow=c(2,2))limite.central(rbeta, distpar=c(0.5 ,0.5),n=c(30,200,500,1000))par(op)3.7N=seq(-4,4,length=1000)f<-function(x){dnorm(x)/sum(dnorm(x))}n=f(N)result=sample(n,replace=T,size = 1000)standdata=rnorm(1000)op<-par(mfrow=c(1,2)) #1行2列数组按列(mfcol)或行(mfrow)各自绘图hist(result,probability = T)lines(density(result),col="red",lwd=3)hist(standdata,probability = T)lines(density(standdata),col="red",lwd=3) par(op)。
实验二利用Lingo求解整数规划及非线性规划问题

例 3 用Lingo软件求解非线性规划问题
min z x1 12 x2 22
x2 x1 1,
x1
x2
2,
x1
0,
x2
0.
Lingo 程序: min= x1-1 ^2+ x2-2 ^2;
x2-x1=1;
x1+x2<=2;
注意: Lingo 默认变量的取值从0到正无穷大, 变量定界函数可以改变默认状态. @free x : 取消对变量x的限制 即x可取任意实数值
例 4 求函数 zx22y22 的最小值.
例 4 求函数 zx22y22 的最小值.
解: 编写Lingo 程序如下:
min= x+2 ^2+ y-2 ^2; @free x ; 求得结果: x=-2, y=2
二、Lingo 循环编程语句
1 集合的定义 包括如下参数: 1 集合的名称.
sets: endsets
44
minZ
aijxij
i1 j1
4
xij
1
j 1,2,3,4
s.t.
i 1 4
xij
1
i 1,2,3,4
j1
xij 0或1 i, j 1,2,3,4
LINGO程序如下:
MODEL: SETS: person/A,B,C,D/; task/1..4/; assign person,task :a,x; ENDSETS DATA: a=1100,800,1000,700,
77
63
67
丁
55
76
62
62
甲, 乙, 丙, 丁 四名队员各自游什么姿势 , 才最有可能取得好成绩
线性规划与非线性规划

一、线性规划
模型 设在甲车床上加工工件1、2、3的数量分别为 在乙车床上加工工件1、2、3的数量分别为
问题二:某厂每日8小时的产量不低于1800件.为了进行质量控制,计划聘请两种不同水平的检验员.一级检验员的标准为:速度25件/小时,正确率98%,计时工资4元/小时;二级检验员的标准为:速度15件/小时,正确率95%,计时工资3元/小时.检验员每错检一次,工厂要损失2元.为使总检验费用最省,该工厂应聘一级、二级检验员各几名?
01
模型 设需要一级、二级检验员的人数分别为 人, 应付检验员工资为 因检验员错检而造成的损失为
02
注;当前MATLAB只支持第一种形式。
或矩阵形式 其中 是决策变量, 是约束矩阵, ,
二、非线性规划
1、二次规划 标准形式: MATLAB调用格式: (1) x=quadprog(H,C,A1,b1); (2)x=quadprog(H,C,A1,b1,A2,b2,v1,v2); (3)[x,fval,exitflag,output]= quadprog(H,C,A1,b1, A2,b2 ,v1,v2,x0,options);
见MATLAB程序(xianxingguihua4)
例4:问题二的解答 改写为
结果: 即只需聘用9个一级检验员。 注:本问题应还有一个约束条件:x1、x2取整数,故它属于一个整数线性规划问题,这里当成一个线性规划求解,求得最优解刚好是整数x1=9,x2=0,故它就是该整数规划的最优解.若用线性规划解法求得的最优解不是整数,将其取整后不一定是相应整数规划的最优解,这样的整数规划应用专门的方法求解.
2、状态窗口(LINDO Solver Status)
当前状态:已达最优解 迭代次数:18次 约束不满足的“量”(不是“约束个数”):0 当前的目标值:94 最好的整数解:94 整数规划的界:93.5 分枝数:1 所用时间:0.00秒(太快了,还不到0.005秒) 刷新本界面的间隔:1(秒)
第5章 非线性规划

(水力约束) (水力摩阻系数约束)
KD GC
L (热力约束)
(粘温关系约束)
(工艺要求约束) (管道强度约束)
在目标函数中,f1(TR)、f2(Pd)一般为非线性函数,约束条 件中亦存在不少非线性函数,显然是一个NLP问题。
非线性规划的基本概念和定理
例3:最小二乘问题:该问题大量存在于工业生产和科学 实验的数据处理中。例如原油的粘度可以表示为:
凹函数的几何意义:
对 于 一 元 函 数 f(x) , 若
函数曲线上任意两点之 间的连线永远不在曲线
的 上 方 , 则 f(x) 为 凹 函
数(参见右图) 。
非线性规划的基本概念和定理 f(X)
f [X 1 (1 ) X 2 ]
对于二元函数 f(x1,x2), 若函数曲面上任意两点 之间的连线永远不在曲 面的上方,则f(x1,x2)为 凹函数(参见右图)。
1、一元函数:
①必要条件:f(x)在x*处取得极值的必要条件是f'(x*)=0;
②充分条件:若f"(x*)<0,则x*为极大点; 若f"(x*)>0,则x*为极小点。 2、多元函数: ①必要条件: f(X)在D域内存在极值点X*的必要条件为 * f ( X ) 0 (即f(X)在X*处的所有一阶偏导数等于0)。
非线性规划的基本概念和定理
根据定义,线性函数既是凸函数,又是凹函数。 凸函数的几何意义: 对 于 一 元 函 在曲线的下方, 则 f(x) 为 凸 函 数 ( 参 见 右
图) 。
非线性规划的基本概念和定理 f(X)
f ( X 1 ) (1 ) f ( X 2 )
§5.1 非线性规划的基本概念和定理
一、什么是非线性规划?
非线性规划

非线性规划(nonlinear programming)1.非线性规划概念非线性规划是具有非线性约束条件或目标函数的数学规划,是运筹学的一个重要分支。
非线性规划研究一个n元实函数在一组等式或不等式的约束条件下的极值问题,且目标函数和约束条件至少有一个是未知量的非线性函数。
目标函数和约束条件都是线性函数的情形则属于线性规划。
2.非线性规划发展史公元前500年古希腊在讨论建筑美学中就已发现了长方形长与宽的最佳比例为0.618,称为黄金分割比。
其倒数至今在优选法中仍得到广泛应用。
在微积分出现以前,已有许多学者开始研究用数学方法解决最优化问题。
例如阿基米德证明:给定周长,圆所包围的面积为最大。
这就是欧洲古代城堡几乎都建成圆形的原因。
但是最优化方法真正形成为科学方法则在17世纪以后。
17世纪,I.牛顿和G.W.莱布尼茨在他们所创建的微积分中,提出求解具有多个自变量的实值函数的最大值和最小值的方法。
以后又进一步讨论具有未知函数的函数极值,从而形成变分法。
这一时期的最优化方法可以称为古典最优化方法。
最优化方法不同类型的最优化问题可以有不同的最优化方法,即使同一类型的问题也可有多种最优化方法。
反之,某些最优化方法可适用于不同类型的模型。
最优化问题的求解方法一般可以分成解析法、直接法、数值计算法和其他方法。
(1)解析法:这种方法只适用于目标函数和约束条件有明显的解析表达式的情况。
求解方法是:先求出最优的必要条件,得到一组方程或不等式,再求解这组方程或不等式,一般是用求导数的方法或变分法求出必要条件,通过必要条件将问题简化,因此也称间接法。
(2)直接法:当目标函数较为复杂或者不能用变量显函数描述时,无法用解析法求必要条件。
此时可采用直接搜索的方法经过若干次迭代搜索到最优点。
这种方法常常根据经验或通过试验得到所需结果。
对于一维搜索(单变量极值问题),主要用消去法或多项式插值法;对于多维搜索问题(多变量极值问题)主要应用爬山法。
第四讲 线性规划与非线性规划

运筹学——线性规划与非线性规划线性规划与非线性规划是运筹学的一个分支.运筹学研究什么呢?运筹学是研究“如何做出正确决策或选择,以达到最好结果”的一门数学学科.有一句成语形象地说明了运筹学的特点:运筹帷幄,决胜千里.数学因实际的需要而产生,数学的很多重大发现也因实际的需要而出现.数学建模竞赛既因实际的重要需要而在世界范围内(在我国近十几年)各大学蓬勃开展.没有受到条条框框制约、富有聪明才智的大学生们,在每次竞赛中都能对实际中的一些重要问题与难题给出富有新鲜创意的解决办法,往往因此产生重大的社会效益和经济效益.建模竞赛就是知识的“强行军”.竞赛会极大地激发学生们的创造性思维,是对学生们思考能力和动手能力的考验.竞赛能让学生们切身感受到学习各科知识的必要性、重要性,成为学生们认真学习的推动力.数学建模会涉及数学的众多学科:微分方程,运筹学,概率统计,图论,层次分析,变分法……,要求建模者有较高的数学素养,有综合应用已学到的数学方法和思维对问题进行分析、抽象及简化的能力.数学建模既是建立实际问题的数学模型.一、最优化模型数学建模的目的是使决策人的“利益”最大化,因此而建立的数学模型即所谓的最优化模型.决策人在作决策时要有“科学观”,为实现目标(“利益”最大化)应进行“科学决策”.最优化模型正是为实现科学决策而建立的数学模型,是科学决策的科学体现.科学决策的目的是要对为实现目标而提出的设计和操作最佳化,最终实现决策人的“利益”最大化.一个最优化模型包括决策变量、目标函数和约束条件,它将“说明”决策变量在满足约束条件的前提下应使目标函数值最优化(最大或最小).决策变量是指影响并决定目标实现的变量,其变化范围一般是可控制的.目标函数是指根据决策变量建立的目标的函数表达式.约束条件是指决策变量所受的限制(用等式、不等式的函数方程表示).人们建立最优化模型的目的是,希望通过科学的计算方法(称为最优化方法)找出使目标函数值最优(最大或最小)的决策变量的值(称为最优决策).实际问题的7步建模过程:第1步:表述问题.说明目标及各种因素.第2步:分析数据或采集(或收集)并分析数据.第3步:建立数学模型.第4步:对模型求解.即寻找最优决策.第5步:检验、评价模型.如果与实际情况(或实际数据)吻合,则转到第7步,否则转到第6步.第6步:修改或矫正模型,并返回到第1步、第2步或第3步.第7步:模型应用,提出合理化建议.最优化数学模型的一般形式为.,,1,0),,,(,,,1,0),,,(..);,,,(max 212121min)(m p i x x x g p i x x x g t s x x x f z n i n i n +=≥===或 (1.1)其中,),,1(n j x j =是决策变量;),,,(21n x x x f z =是目标函数;),,1(0),,,(21p i x x x g n i ==和),,1(0),,,(21m p i x x x g n i +=≥是约束条件,前者称为等式约束,后者称为不等式约束.不带约束条件的(1)式是无约束问题的模型.由满足所有约束条件的决策向量Tn x x x x ),,,(21=组成的集合称为可行域,通常记为D .求解(1)是指,寻找D x x x x Tn ∈=),,,(**2*1* 使),,,(**2*1n x x x f z =为目标函数f 在可行域D 上的最小值(或最大值).*x称为最优解,),,,(**2*1n x x x f 称为最优值.最优解有严格与非严格和全局与局部之分.优化模型的最优解是指全局最优解. 严格极小点 严格极小点 局部 全局 非严格极小点图1 一维函数的最优解图示这里指出:最优化方法解出的多是优化模型的局部最优解.由于最优化方法多为迭代法,所以取不同的初始点一般会得到一个或多个局部最优解,然后再从这些局部最优解中找出“全局”最优解. 二、线性规划(LP)线性规划在银行、教育、林业、石油、运输……等各种行业以及科学的各个领域中有着广泛的应用. 1. 线性规划模型目标函数、约束函数均为线性函数的最优化模型既是所谓的线性规划模型.(1)标准形式.,,1,0,,,1,..;min 22112211max)(n j x m i b x a x a x a t s x c x c x c z j i n in i i n n =≥==++++++=或 (2.1)这里,约束i n in i i b x a x a x a =+++ 2211),,1(m i =是对决策变量的主要约束,称为主约束,而约束),,1(0n j x j =≥(),,1(n j x j =称为非负变量)是对决策变量的符号约束;(1,,)j b i m = 是主约束的右端常数项(通常不妨设为非负数);),,1(n j c j =称为价值系数.(2.1)式可以写成如下矩阵形式.0,..;min max)(≥==x b x A t s x c z T 或 (2.2)其中,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=m n n mn m m n n b b b b x x x x c c c c a a a a a a a a a A212121212222111211,,,. T n x x x x ),,,(21=——决策向量,T m b b b ),,(1 =——主约束右端常数向量,1(,,)T n c c c =——价值向量.(2)一般形式.,,1,,,,1,0,,,1,,,,1,,,,1,..;min 2211221122112211max)(n q j x q j x m u i b x a x a x a u p i b x a x a x a p i b x a x a x a t s x c x c x c z j j i n in i i i n in i i i n in i i n n +==≥+=≤++++=≥+++==++++++=任意或 (2.3)这里,约束),,1(2211p i b x a x a x a i n in i i ==+++、in in i i b x a x a x a ≥+++ 2211),,1(u p i +=和),,1(2211m u i b x a x a x a i n in i i +=≤+++是主约束,而约束),,1(0q j x j =≥和j x 任意),,1(n q j +=是符号约束,其中j x ),,1(n q j +=称为自由变量.一般形式可以(通过如下办法)转化为标准形式. (i)将不等式约束转化为等式约束引入剩余变量0≥i s ,将不等式约束i n in i i b x a x a x a ≥+++ 2211改写为i i n in i i b s x a x a x a =-+++ 2211,u p i ,,1 +=. (2.4)引入松弛变量0≥i e ,将不等式约束i n in i i b x a x a x a ≤+++ 2211改写为i i n in i i b e x a x a x a =++++ 2211,m u i ,,1 +=. (2.5)(ii)去除自由变量去掉自由变量),,1(n q j x j +=有两种办法: ①用非负变量的差表示自由变量 设j j j x x x +-=-, (2.6)其中0≥+j x ,0≥-j x ,代入到目标函数和其它约束中便可去掉j x .②取一个包含j x 的等式约束(如果有的话),比如:11i ij j in n i a x a x a x b ++++= ,由此解出11i i in j n ijijijb a a x x x a a a =---, (2.7)代入到目标函数和其它约束函数中便可去掉j x .第一种方法将增加变量的数目,导致问题的维数增大.第二种方法正好相反.用(2.4)、(2.5)两式替换(2.3)式中相应的不等式约束,将(2.6)式或(2.7)式代入目标函数和其它约束函数中,去掉目标函数与主约束中的所有自由变量,最后将),,1(0u p i s i +=≥、),,1(0m u i e i +=≥和),,1(0,0n q j x x j j +=≥≥-+加入(2.3)式的符号约束中,(2.3)式就此转化为标准形式的线性规划.,,1,0;,,1,0;,,1,0,0;,,1,0,,,1,,,,1,,,,1,..;min 11111111111111111111max)(m u i e u p i s n q j x x q j x m u i b e x x a x x a x a x a u p i b s x x a x x a x a x a p i b x x a x x a x a x a t s x x c x x c x c x c z i i j j j i i nn in q q iq q iq i i i n n in q q iq q iq i i n n inq q iq q iq i n n nq q q q q +=≥+=≥+=≥≥=≥+=≤+-++-++++=≥--++-+++==-++-+++-++-+++=-+++++++++++++++++++++++++++++)()()()()()()()(或,一般形式与其标准形式问题的求解等价,因为这两个问题的可行解一一对应,目标函数值对应相等.所以如果这两个问题之一有最优解,那么另一个也必有最优解,且最优值相等.2. 线性规划的特点(1)线性规划的可行域是凸集:凸多边形、凸多面体或空集.凸集非凸集凸多边形凸多面体(2)目标函数的等值面(或等值线)是平行的(超)平面(或直线).(3)如果线性规划有最优解,那么可行域的某个顶点必是最优解.(4)求解线性规划将出现下列4种情况之一.情况1:有唯一(最优)解.情况2:有无穷多(最优)解.情况3:解无界.情况4:无解.有唯一解有无穷多解有无界解无解3. 一般线性规划的解法线性规划的解法有Dantzig单纯形法,大M法,对偶单纯形法,Karmarkar法,列生成法,目标规划,分解算法等.软件中多为Dantzig单纯形法.参考书目:薛嘉庆.线性规划.北京:高等教育出版社,1989刁在筠郑汉鼑等. 运筹学.北京:高等教育出版社,20014. 特殊的线性规划当所有决策变量都取整数时,称为整数规划(IP).当所有决策变量只取0或1时,称为0-1规划.当只有部分决策变量取整数时,称为混合整数规划(混合IP).解整数规划的方法主要有穷举法(对决策变量过多的问题不适用)、分枝定界法和割平面法.分枝定界法比较常用.解小规模0-1规划的常用方法——隐枚举法.分枝定界法也适用于求解混合整数规划.参考书目:刁在筠郑汉鼑等. 运筹学.北京:高等教育出版社,2001胡运权.运筹学基础及应用.北京:高等教育出版社,20045. 特殊的线性规划问题及其解法(1)运输问题运输问题用“运输”单纯形法求解.(2)转运问题转运问题可以化为运输问题,所以也用“运输”单纯形法求解.(3)指派问题指派问题是特殊的0-1规划,常用匈牙利法求解.线性规划的算法可在Matlab “优化”工具箱中寻找. 6. 线性规划建模实例在一个线性规划模型中,(1)决策变量应当完全描述要做出的决策.(2)决策者都希望由决策变量表示的目标函数最大化(通常为收入或利润)或最小化(通常为成本).目标函数中的系数反映的是决策变量对目标函数的单位贡献.(3)主约束条件中决策变量的系数称为“技术”系数,这是因为技术系数经常影响用于“生产”不同“产品”的技术.右端项常表示可用资源的数量.示例1 一家汽车公司生产轿车和卡车.每辆车都必须经过车身装配车间和喷漆车间处理. 车身装配车间如果只装配轿车,每天可装配50辆;如果只装配卡车,每天可装配50辆.喷漆车间如果只喷轿车,每天可喷60辆;如果只喷卡车,每天可喷40辆. 每辆轿车的利润是1600元,每辆卡车的利润是2400元.公司的生产计划部门须制定一天的产量计划以使公司的利润最大化.建模过程:公司追求的目标是其利润的最大化,生产计划部门为此要决定每一种车型的产量,所以定义两个决策变量:=1x 每天生产的轿车数量,=2x 每天生产的卡车数量. 公司每天的利润为2124001600x x +,因此该公司追求利润最大化即为2124001600max x x z +=.按题意,决策变量须满足以下3个条件(如果把每天的时间设为1,那么每天的工作时间应该小于等于1.)(1)1x 辆轿车和2x 辆卡车的时间应满足11121≤+x x . (2)所以处理1x 辆轿车和2x 辆卡车的时间应满足140160121≤+x x . (3)非负限制j x 为负整数,2,1=j .该汽车公司追求利润最大化的数学模型为如下线性规划.2,1,,1401601,1501501..24001600max 212121=≤+≤++=j x x x x x t s x x z j 为非负整数;示例2(饮食问题) 有一个美国人的饮食方案要求他吃的所有食物都来自四个“基本食物组”之一(巧克力蛋糕、冰淇淋、苏打水和干酪蛋糕).目前他可以消费的食物有下列4种:胡桃巧克力糖、巧克力冰淇淋、可口可乐和菠萝干酪蛋糕.一块胡桃巧克力糖的价格为50美分,一勺巧克力冰淇淋的价格为20美分,一瓶可口可乐的价格为30美分,一块菠萝干酪蛋糕的价格为80美分.他每天至少必须摄取500卡路里、6盎司巧克力、10盎司糖和8盎司脂肪.表1列出了每种食物每单位的营养含量.这个美国人想以最小成本满足自己每天的营养要求,那他应该怎样做.建模过程:这个美国人追求的目标是使饮食的费用最少.因此这个美国人必须做出决策:对于每种食物,每天应当吃多少.因此,需要定义下列决策变量:=1x 每天吃的胡桃巧克力糖的数量(单位:块),=2x 每天吃的巧克力冰淇淋的数量(单位:勺), =3x 每天喝的可口可乐的数量(单位:瓶),=4x 每天吃的菠萝干酪蛋糕的数量(单位:块).他追求的目标是使饮食的费用最少,因此目标函数为432180302050x x x x z +++=.决策变量必须满足以下4个条件:(1) 每天摄取的卡路里至少必须达到500卡路里.即5005001502004004321≥+++x x x x .(2)每天摄取的巧克力至少必须达到6盎司.即62321≥+x x .(3)每天摄取的糖至少必须达到10盎司.即1044224321≥+++x x x x .(4)每天摄取的脂肪至少必须达到8盎司.即85424321≥+++x x x x .以及非负限制4,3,2,1,0=≥j x j .该美国人饮食费用最少的数学模型为.4,3,2,1,0,8542,104422,623,500500150200400..80302050max 432143212143214321=≥≥+++≥+++≥+≥++++++=i x x x x x x x x x x x x x x x t s x x x x z i ;这个问题的最优解是90,1,3,03241=====z x x x x ,表示每天最少花90美分便可得到符合饮食要求的750卡路里、6盎司巧克力、10盎司糖和13盎司脂肪.列出更现实的食物和营养需求的饮食问题是计算机解决的最早的LP 之一.整数规划已用于计划每周或每月的公共饮食业菜单.菜单计划模型包含反映可口性和多样性要求的约束条件.示例3 某服务部门一周中每天需要不同数目的雇员:周一到周四每天至少需要50人,周五至少需要80人,周六和周日至少需要90人.规定应聘者需连续工作5天.试确定聘用方案:使在满足需要的条件下聘用的总人数最少.建模过程:该服务部门追求的目标是一周中聘用的总人数最少.该服务部门因此必须做出决策:每天聘用多少人.为此,定义以下决策决量:721,,,x x x 分别表示周一至周日聘用的人数. 因此目标函数为7654321x x x x x x x z ++++++=.决策变量必须满足以下7个条件:周一工作的雇员应是周四到周一聘用的,按照需要至少有50人,即5076541≥++++x x x x x . 类似地,有.90,90,80,50,50,50765436543254321743217632176521≥++++≥++++≥++++≥++++≥++++≥++++x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x人数应该是整数,所以决策变量须是非负的整数变量,即i x 为非负整数,7,,2,1 =i .该服务部门聘用总人数最少的数学模型是如下的整数规划模型:.7,,2,1,,90,90,80,50,50,50,50..min 765436543254321743217632176521765417654321 =≥++++≥++++≥++++≥++++≥++++≥++++≥++++++++++=i x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x t s x x x x x x x z i 为非负整数;示例4(工作调度问题) 在每周的不同工作日,一个邮局需要不同数量的专职员工.表1给出了每天需要的专职员工的数量.工会章程规定:每个专职员工每周必须连续工作五天,然后休息两天.这个邮局希望通过只使用专职员工来满足每天的需要,那么这个邮局至少要聘用多少专职员工.首先来看一个不正确的模型.有许多学生定义决策变量i 为第天上班员工的数量(第1天=星期一,第2天=星期二,依次类推),然后推出邮局专职员工的数量=(星期一上班员工的数量+星期二上班员工的数量+…+星期日上班员工的数量)/5,于是得到如下目标函数7654321x x x x x x x z ++++++=.添加约束条件≥i x (第i 天需要的员工数量)和符号限制条件)7,,2,1(0 =≥i x i 后,得到如下不正确的线性规划模型:,11,16,14,19,15,13,17..;min 76543217654321≥≥≥≥≥≥≥++++++=x x x x x x x t s x x x x x x x zi x 为非负整数,7,,2,1 =i .这里目标函数是专职员工的数量的5倍,问题是约束条件不能反映员工连续工作五天然后休息两天的事实.建模过程:这个邮局追求的目标是聘用尽可能少的专职员工.正确表述这个问题的关键是,定义的决策变量不应该是每天有多少人上班,而是一周中每天有多少人开始上班.定义决策变量:i x =第i 天开始上班员工的数量. 例如,1x 是星期一开始上班员工的数量(这些人从星期一工作到星期五).那么邮局(专职员工的数量)=(星期一开始上班员工的数量)+(星期二开始上班员工的数量)+…+(星期日开始上班员工的数量).由于每个员工都只在一周的某一天开始上班,所以这个表达式不会重复计算员工.因此,追求聘用尽可能少的专职员工的目标函数为;7654321x x x x x x x z ++++++= 决策变量满足以下约束条件:在星期一上班员工的数量不少于17人:1776541≥++++x x x x x ;在星期二上班员工的数量不少于13人:1376521≥++++x x x x x ; 在星期三上班员工的数量不少于15人:1576321≥++++x x x x x ; 在星期四上班员工的数量不少于19人:1974321≥++++x x x x x ; 在星期五上班员工的数量不少于14人:1454321≥++++x x x x x ; 在星期六上班员工的数量不少于16人:1665432≥++++x x x x x ; 在星期日上班员工的数量不少于11人:1176543≥++++x x x x x . 及符号限制条件:i x 为非负整数,7,,2,1 =i .邮局追求聘用尽可能少的专职员工的调度方案数学模型为;min 7654321x x x x x x x z ++++++=,17 ..76541≥++++x x x x x t s,13 76521≥++++x x x x x 15 76321≥++++x x x x x , 19 74321≥++++x x x x x , 14 54321≥++++x x x x x , 16 65432≥++++x x x x x , 11 76543≥++++x x x x x ,i x 为非负整数,7,,2,1 =i .这个模型的一个最优解为3,4,0,6,2,4,47654321=======x x x x x x x ,最优值23=z . □该模型存在另外一个问题:只有在周一、周二开始上班的员工才能在周末休息,而在其它时间开始上班的员工永远不会有在公休日与家人团聚的机会.显然这不公平合理.从该模型的解出发,我们可以设计出如下公平合理的以23周为一个轮转周期的员工调度方案:·第1-4周:在星期一开始上班 ·第5-8周:在星期二开始上班 ·第9-10周:在星期三开始上班 ·第11-16周:在星期四开始上班 ·第17-20周:在星期六开始上班 ·第21-23周:在星期日开始上班员工1将遵守这个调度方案23周,员工2从第2周开始遵守这个调度方案23周(在星期一开始上班的时间为3周,在星期二开始上班的时间为4周,…,在星期日开始上班的时间为3周,在星期一开始上班的时间为1周).以这样的方式继续下去,就可以为每个员工制定一个23周调度方案.例如,员工13的调度方案如下:·第1-4周:在星期四开始上班 ·第5-8周:在星期六开始上班 ·第9-11周:在星期日开始上班 ·第12-15周:在星期一开始上班 ·第16-19周:在星期二开始上班 ·第20-21周:在星期三开始上班 ·第22-23周:在星期四开始上班 本示例提醒我们,所建立的模型一定要考虑合理性,符合实际.而本示例更符合实际的考虑是员工还有年休假.在邮局这个示例中,如果邮局可以同时使用专职员工和兼职员工来满足每天的需要,且在每一周,专职员工必须连续工作5天,每天工作8小时;兼职员工必须连续工作5天,每天工作4小时. 专职员工的工资是每小时15美元,而兼职员工的工资只有每小时10美元(没有附加福利).工会把每周的兼职劳动限制在25%,表述一个LP ,使这个邮局每周的劳动力成本最少.比示例5的单阶段工作调度模型更复杂的是多阶段工作调度模型. 类似的还有多阶段库存模型、多阶段财务管理(投资)模型等.示例5(指派问题) 某班准备从5名游泳队员中选4人,组队参加学校的1004⨯m 混合泳接力比赛.5名队员4种泳姿的百米平均成绩如表1所示,问应该怎样选拔接力队成员?建模过程:该班追求的目标是接力队的成绩最好.该班因此要做出决策:从5名队员中选出4人,每人一种泳姿,且4人的泳姿各不相同(容易想到的一个办法是穷举法,组成接力队的方案共有5!=120种.).设5,4,3,2,1=i 分别代表甲、乙、丙、丁和戊队员,4,3,2,1=j 分别代表蝶泳、仰泳、蛙泳和自由泳泳姿,ij c 表示队员i 的第j 种泳姿的百米平均成绩.定义决策决量ij x :若选择队员i 参加泳姿j 的比赛(4,3,2,1,5,4,3,2,1==j i ),则1=ij x ,否则0=ij x .该班追求的目标是接力队的成绩最好(只要对每一方案的成绩作比较,即可找出最优方案,但显然这不是解决问题的好办法.随着问题规模的变大,穷举法的计算量将是无法接受的).当队员i 入选泳姿j 时,ij ij x c 表示他的成绩,否则0=ij ij x c ,因此目标函数为∑∑===4151j i ij ij x c z .决策变量必须满足以下3个条件:(1) 每人最多只能入选4种泳姿之一,即141≤∑=j ijx,5,4,3,2,1=i .(2)每种泳姿必须有1人而且只能有1人入选,即151=∑=i ijx,4,3,2,1=j .(3)取值受限0=ij x 或1,4,3,2,1,5,4,3,2,1==j i .该班追求接力队成绩最好的数学模型为0-1规划:.4,3,2,1,5,4,3,2,1,10,4,3,2,1,1,5,4,3,2,1,1..;min 51414151======≤=∑∑∑∑====j i or x j xi xt s x c z ij i ijj ijj i ij ij三、非线性规划(NLP)非线性规划广泛存在于科学与工程领域. 1.非线性规划模型目标函数、约束函数中至少有一个非线性函数的最优化模型既是所谓的非线性规划模型..,,1,0)(,,,1,0)(..);(min max)(m p i x g p i x g t s x f z i i+=≥===或其中函数),,1(),,,1(,m p i g p i g f i i +==中至少有一个为非线性函数.非线性规划有无约束问题与有约束问题之分. 2.非线性规划的特点非线性规划的可行域及最优解的情况远比线性规划的可行域及最优解复杂的多:可能有最优解,也可能没有最优解;约束问题的最优解可能在可行域的内部,也可能在可行域的边界上.一些常用概念:等值面(线)——函数值相等的决策变量曲面(曲线)C x f =)(.上升/下降方向——至少在局部范围内,函数值升的方向/函数值降的方向),0(),()(/),0(),()(δδ∈>+∈>+t x f p t x f t x f p t x f.梯度——多元函数的“一阶导数”,由函数的偏导数组成的向量()()()()12,,,∂∂∂⎛⎫∇= ⎪∂∂∂⎝⎭Tn f x f x f x f x x x x .当梯度()f x ∇ 连续时,若()0f x ∇≠ ,则()f x ∇ 必垂直于()f x 过点x的等值面;梯度()f x ∇ 的方向是函数()f x 在点x具有最大变化率的方向.方向导数——函数在某方向上的变化率(下式中e 是p方向上的单位向量)tx f e t x f p x f t )()(lim )(0 -+=∂∂+→. e x f px f T)()(∇=∂∂. 若0)(>∂∂p x f,即()00T f x p ∇> ,则p方向是()f x 在点0x 处的上升方向;若0)(<∂∂px f,即()00T f x p ∇< ,则p 方向是()f x 在点0x 处的下降方向. 海赛矩阵——多元函数的“二阶导数”,由函数的二阶偏导数组成的矩阵()22⎛⎫∂∇=⎪ ⎪∂∂⎝⎭ i j nf f x x x . 空间中由点0x 和方向p所确定的直线方程为10,x x tp t R =+∈.图2 直线的几何图示3.非线性规划的解法(1)非线性规划基本解法 基本解法的迭代格式一般为1k k k k x x t p +=+, k = 0,1,….称0x 为初始点,k p 为k x处的搜索方向,k t 为步长因子,满足()()k k k k f x t p f x +<,且+k k k x t p 仍在可行域内.判断1k x + 是否为最优解.若是,则输出1k x + 和1()k f x +;否则,继续迭代.由基本解法解出的一般是局部最优解.k t 的确定方法——直线搜索(一维优化问题的数值迭代方法)()()k k t f x tp ϕ=+,min ()t ϕ.直线搜索方法有“精确的”对分法、黄金分割法、抛物线插值法……和不精确的直线搜索技术.k p的确定方法——各种优化方法求解无约束问题的基本方法按确定k p方法的不同,有使用导数的最速下降法、Newton 法、阻尼-Newton 法、共轭梯度法、逆Newton 法(DFP 法、BFGS 法)等,有不使用导数的单纯形替换法、步长加速法、Power 法等,以及最小二乘法.最速下降法——1()k k k k x x t f x +=-∇, k = 0,1,…. 特点:简单,存储量小,锯齿现象.线性收敛.Newton 法:211()()k k k k x x f x f x -+=-∇∇, k = 0,1,…. 特点:对目标函数的要求高,计算量、存储量大.二阶收敛.阻尼-Newton 法:211()()k k k k k x x t f x f x -+=-∇∇, k = 0,1,…. 特点:比Newton 法相对有效的方法,计算量、存储量大.F-R 共轭梯度法:1k k k k x x t p +=+, k = 0,1,…,其中211121()(),()k k k k k k k f x p f x p f x αα----∇=-∇+=∇. 特点:存储量小.是二次收敛算法.超线性收敛.DFP 法:1k k k k x x t p +=+, k = 0,1,…, 其中()k k k p H f x =-∇.特点:是二次收敛算法.是拟Newton 法.超线性收敛.∶ ∶ ∶单纯形替换法、步长加速法、Power 法等适用于目标函数的导数不存在或导数过于复杂的情形.最小二乘法是求解最小二乘问题的特定解法. 求解约束问题的基本方法有Z-容许方向法、梯度投影法、外点法(外部罚函数法)、内点法(内部罚函数法)、乘子法、线性化法、简约梯度法等.Z-容许方向法:利用线性规划得到搜索方向k p,然后再通过受限的直线搜索确定步长因子k t .梯度投影法:利用对梯度投影的方式得到搜索方向k p,然后再通过受限的直线搜索确定步长因子k t .外点法、内点法、乘子法:通过求解一系列的无约束问题解约束问题.而这一系列无约束问题的目标函数则是根据目标函数及约束函数,通过“惩罚”方式产生.∶ ∶ ∶ (2)非线性规划智能算法遗传算法、蚁群算法、粒子群算法、禁忌搜索算法……. 非线性规划的算法可在Matlab “优化”工具箱中寻找.参考书目:薛嘉庆.最优化方法.北京:冶金工业出版社邢文训,谢金星.现代优化计算方法.北京:清华大学出版社,1999《现代应用数学手册》编委会.现代应用数学手册—运筹学与最优化理论卷.北京:清华大学出版社,1998 4. 特殊的非线性规划问题及其解法 (1)二次规划(QPP)1min ()2..T T f x x Qx b x cs t Ax p Cx d =++≥=Wolfe 法.参考书目:赵凤治.约束最优化方法.北京:科学出版社,1991 (2)数据拟合问题(最小二乘问题) 最小二乘法 5. 非线性规划建模实例示例1 某公司有6个建筑工地要开工,每个工地的位置(用平面坐标),(b a 表示,距离单位:km)及水泥日用量d (单位:t (吨))由表1给出.目前有两个临时料场位于)1,5(A 和)7,2(B ,日储量各有20t .请回答以下两个问题:(1)假设从料场到工地之间均有直线道路相连,试制定每天从A 、B 两料场分别向各工地运送水泥的供应计划,使总的吨公里数最小.(2)为进一步减少吨公里数,打算舍弃目前的两个临时料场,修建两个新料场,日储量仍各为20t ,问建在何处最佳,可以节省多少吨公里数.表1 工地的位置),(b a 及水泥日用量d 的数据建模过程:公司追求的目标是每天从A 、B 两料场分别向各工地运送水泥总的吨公里数最小.为表述该问题,设工地的位置与水泥日用量分别为),(i i b a 和i d (6,,2,1 =i ),料场位置及其日储量分别为),(j j y x 和j e (2,1=j ).定义决策变量ij w (6,,2,1 =i ,2,1=j ):料场j 向工地i 的运送量(6,,2,1 =i ,2,1=j ),在问题(2)中,新建料场位置),(j j y x 也是决策变量.公司追求总的吨公里数最小的目标函数为∑∑==-+-=216122)()(j i i j i j ij b y a x w f .决策变量ij w (6,,2,1 =i ,2,1=j )必须满足以下约束条件:(i)满足各工地的水泥日用量6,,2,1,21==∑=i d wi j ij.(ii)各料场的运送量不能超过日储量2,1,61=≤∑=j e wj i ij.(iii)符号限制条件0≥ij w , 6,,2,1 =i ,2,1=j .(1)公司追求总的吨公里数最小的数学模型是如下线性规划模型∑∑==-+-+-+-=6122261221)7()2()1()5(min i i i i i i i i b a w b a w f ;6,,2,1,..21 ==∑=i d wt s i j ij,2,1,61=≤∑=j e wj i ij,0≥ij w , 6,,2,1 =i ,2,1=j .总的吨公里数为136.2275.(2)这时公司追求总的吨公里数最小的数学模型是如下有约束的非线性规划模型∑∑==-+-=216122)()(min j i i j i j ij b y a x c f ;6,,2,1,..21 ==∑=i d wt s i j ij,2,1,61=≤∑=j e wj i ij,0≥ij w , 6,,2,1 =i ,2,1=j .以(1)的解及临时料场的坐标为初始迭代值,利用Matlab 优化工具箱求得这个模型的一个数值解,两个新料场的位置为)3943.4,3875.6(A 和)1867.7,7511.5(B 和它们向6个工地运送总的吨公里数为105.4626,比用临时料场节省约31吨公里.若初始迭代值取为上面的计算结果,那么得到的数值解为)9194.4,5369.5(A 和)2852.7,8291.5(B 和它们向6个工地运送水泥的计划为总的吨公里数为103.4760,又节省约2吨公里.若初始迭代值取为上面的计算结果,却计算不出解.若初始迭代值取为ij w (6,,2,1 =i ,2,1=j )=[3,5,4,7,1,0,0,0,0,0,],),(j j y x (2,1=j )=[5.6348,4.8687;7.2479,7.7499],那么得到的数值解为)9285.4,6959.5(A 和)7500.7,2500.7(B 和它们向6个工地运送水泥的计划为总的吨公里数为89.8835,又节省约13.5吨公里.通过此例可以看出初始迭代值的选取对非线性规划方法的重要性.总结:以建线性规划模型为第一选择,单纯形法能求到全局最优解.非线性规划模型往往求不到全局最优解,而且数值解受初始迭代值的影响很大.6. 建模说明对于大规模实际问题,清晰地表述问题,以正确的方式和方法采集(或收集)数据,准确地分析数据是非常重要的.应该多角度建立既合理又尽可能简单的数学模型.这需要建模者有较高的数学素养,要有灵性、有想象力、判断力、洞察力.选择最适合模型的最优化解法,这要求建模者有较多的数学知识储备.掌握检验、评价模型的基本原理与方法.灵敏度分析常被用在检验与评价模型中. 如果模型的解明显不正确或与实际情况吻合的不好,建模者应该具有发现问题所在的能力:是第1步的问题、第2步的问题,还是第3步的问题.。
R语言中的数学计算

R语言中的`integrate()`函数可以计算函数的积分,该函数接受一 个函数表达式和自变量范围作为输入,并返回积分的值。
积分变换和复变函数运算
01
傅里叶变换
R语言中的`fft()`函数可以执行快 速傅里叶变换,将时域信号转换 为频域信号。
02
03
拉普拉斯变换
复数运算
R语言中的`laplace()`函数可以执 行拉普拉斯变换,将时域函数转 换为复平面上的函数。
整数规划的应用领域包括生产计划、物流、 金融等,可以用于求解如排班问题、车辆路
径问题等最优化问题。
感谢您的观看
THANKS
众数
在一组数据中出现次数最多的数。
概率分布函数
正态分布
连续型概率分布,曲线呈钟形,多数自然现 象的概率分布近似服从正态分布。
二项分布
离散型概率分布,适用于伯努利试验,即只 有两种可能结果的试验。
泊松分布
离散型概率分布,适用于单位时间或空间内 随机事件的次数。
指数分布
连续型概率分布,适用于描述独立随机事件 的时间间隔。
R语言提供了丰富的复数运算功 能,包括复数的加法、减法、乘 法和除法等操作。
05
R语言中的数学优化运算
线性规划
线性规划是一种数学优化技术,用于解决具有线性约束和 线性目标函数的最大化或最小化问题。在R语言中,可以 使用`lpSolve`包进行线性规划的求解。
线性规划的应用领域非常广泛,包括生产计划、资源分配 、运输问题等。
矩阵操作:可以对矩阵进行各种操作,如加法、减法、乘法 等。例如,将两个矩阵相加
矩阵的创建和操作
m2 <- matrix(c(7, 8, 9, 10, 11, 12), nrow = 2)
非线性规划的概念和原理

第五章 非线性规划的概念和原理非线性规划的理论是在线性规划的基础上发展起来的。
1951年,库恩(H.W.Kuhn )和塔克(A.W.Tucker )等人提出了非线性规划的最优性条件,为它的发展奠定了基础。
以后随着电子计算机的普遍使用,非线性规划的理论和方法有了很大的发展,其应用的领域也越来越广泛,特别是在军事,经济,管理,生产过程自动化,工程设计和产品优化设计等方面都有着重要的应用。
一般来说,解非线性规划问题要比求解线性规划问题困难得多,而且也不像线性规划那样有统一的数学模型及如单纯形法这一通用解法。
非线性规划的各种算法大都有自己特定的适用范围。
都有一定的局限性,到目前为止还没有适合于各种非线性规划问题的一般算法。
这正是需要人们进一步研究的课题。
5.1 非线性规划的实例及数学模型[例题6.1] 投资问题:假定国家的下一个五年计划内用于发展某种工业的总投资为b 亿元,可供选择兴建的项目共有几个。
已知第j 个项目的投资为j a 亿元,可得收益为j c 亿元,问应如何进行投资,才能使盈利率(即单位投资可得到的收益)为最高?解:令决策变量为j x ,则j x 应满足条件()10j j x x -=同时j x 应满足约束条件1nj j j a x b =≤∑目标函数是要求盈利率()1121,,,njjj n njjj cx f x x x ax ===∑∑ 最大。
[例题6.2] 厂址选择问题:设有n 个市场,第j 个市场位置为(),j j p q ,它对某种货物的需要量为jb ()1,2,,j n = 。
现计划建立m 个仓库,第i 个仓库的存储容量为i a ()1,2,,i m = 。
试确定仓库的位置,使各仓库对各市场的运输量与路程乘积之和为最小。
解:设第i 个仓库的位置为(),i i x y ()1,2,,i m = ,第i 个仓库到第j 个市场的货物供应量为ijz ()1,2,,,1,2,,i m j n == ,则第i 个仓库到第j 个市场的距离为i j d =目标函数为1111mnmni j i j iji j i j z d z =====∑∑∑∑约束条件为:(1) 每个仓库向各市场提供的货物量之和不能超过它的存储容量; (2) 每个市场从各仓库得到的货物量之和应等于它的需要量; (3) 运输量不能为负数。
第三讲 线性规划与非线性规划

1
2 x 2
6 x 2
s.t.
1 1 0 0
1 x1 2 x 2 x1 x 2
2 2
2、 输入命令:
H=[1 -1; -1 2]; c=[-2 ;-6];A=[1 1; -1 2];b=[2;2]; Aeq=[];beq=[]; VLB=[0;0];VUB=[]; [x,z]=quadprog(H,c,A,b,Aeq,beq,VLB,VUB)
1.先建立M-文件fun.m定义目标函数: function f=fun(x); f=-2*x(1)-x(2);
2.再建立M文件mycon2.m定义非线性约束: function [g,ceq]=mycon2(x) g=[x(1)^2+x(2)^2-25;x(1)^2-x(2)^2-7];
3. 主程序fxx.m为: x0=[3;2.5]; VLB=[0 0];VUB=[5 10]; [x,fval,exitflag,output] =fmincon('fun',x0,[],[],[],[],VLB,VUB,'mycon2')
例 2
min z 6 x1 3 x 2 4 x 3 s .t . x 1 x 2 x 3 120 x1 30 0 x 2 50 x 3 20
min z ( 6
3
x1 4) x 2 x3
s .t .
(0
1
x1 0) x2 50 x 3 x1 1) x 2 120 x 3
1 2
2 x2
s.t.
【原创】R语言线性回归 :多项式回归案例分析报告附代码数据

线性回归模型尽管是最简单的模型,但它却有不少假设前提,其中最重要的一条就是响应变量和解释变量之间的确存在着线性关系,否则建立线性模型就是白搭。
然而现实中的数据往往线性关系比较弱,甚至本来就不存在着线性关系,机器学习中有不少非线性模型,这里主要讲由线性模型扩展至非线性模型的多项式回归。
多项式回归多项式回归就是把一次特征转换成高次特征的线性组合多项式,举例来说,对于一元线性回归模型:一元线性回归模型扩展成一元多项式回归模型就是:一元多项式回归模型这个最高次d应取合适的值,如果太大,模型会很复杂,容易过拟合。
这里以Wage数据集为例,只研究wage与单变量age的关系。
> library(ISLR)> attach(Wage)> plot(age,wage) # 首先散点图可视化,描述两个变量的关系age vs wage可见这两条变量之间根本不存在线性关系,最好是拟合一条曲线使散点均匀地分布在曲线两侧。
于是尝试构建多项式回归模型。
> fit = lm(wage~poly(age,4),data = Wage) # 构建age的4次多项式模型>> # 构造一组age值用来预测> agelims = range(age)4次多项式回归模型从图中可见,采用4次多项式回归效果还不错。
那么多项式回归的次数具体该如何确定?在足以解释自变量和因变量关系的前提下,次数应该是越低越好。
方差分析(ANOVA)也可用于模型间的检验,比较模型M1是否比一个更复杂的模型M2更好地解释了数据,但前提是M1和M2必须要有包含关系,即:M1的预测变量必须是M2的预测变量的子集。
> fit.1 = lm(wage~age,data = Wage)> fit.2 = lm(wage~poly(age,2),data = Wage)。
r语言曲线拟合函数

r语言曲线拟合函数R语言是一种用于统计分析和数据可视化的编程语言,它具有强大的数据处理和图形绘制功能。
拟合函数是在数据分析中常用的一种方法,它可以用来找到数据背后的趋势和关系。
R语言提供了多种拟合函数的实现方法,包括线性拟合、非线性拟合、多项式拟合等。
线性拟合是一种常用的拟合方法,简单直观且易于理解。
它的基本思想是通过一条直线来拟合数据点,使得直线与数据点之间的残差最小。
R语言中提供了lm()函数来进行线性拟合,其使用方法如下:```R#创建示例数据x <- 1:10y <- 2*x + rnorm(10)#进行线性拟合fit <- lm(y ~ x)#打印拟合结果print(fit)```lm()函数中的第一个参数是一个公式,用来指定拟合的模型。
在这个示例中,我们使用`y ~ x`来表示y关于x的线性关系。
拟合结果会包含回归系数的估计值、残差和拟合优度等信息。
非线性拟合是另一种常见的拟合方法,它适用于数据存在非线性关系的情况。
R语言中提供了nls()函数来进行非线性拟合,其使用方法如下:```R#创建示例数据x <- 1:10y <- 2*x^2 + rnorm(10)#定义拟合函数model <- function(x, a, b, c) {a*x^2 + b*x + c}#进行非线性拟合fit <- nls(y ~ model(x, a, b, c), start = list(a = 1, b = 1, c = 1))#打印拟合结果print(fit)```在nls()函数中,第一个参数也是一个公式,用来指定拟合的模型。
需要注意的是,拟合函数需要事先定义好,其中的参数可以在start参数中给出初始值。
拟合结果中会包含参数的估计值、残差和拟合优度等信息。
多项式拟合是一种常用的拟合方法,它适用于数据存在多项式关系的情况。
R语言中提供了polyfit()函数来进行多项式拟合,其使用方法如下:```R#创建示例数据x <- 1:10y <- 2*x^3 + rnorm(10)#进行多项式拟合,拟合3次多项式fit <- polyfit(x, y, degree = 3)#打印拟合结果print(fit)```polyfit()函数的第一个参数是自变量x的值,第二个参数是因变量y的值,degree参数指定了拟合的多项式次数。
例谈线性规划中目标函数非线性问题的解法
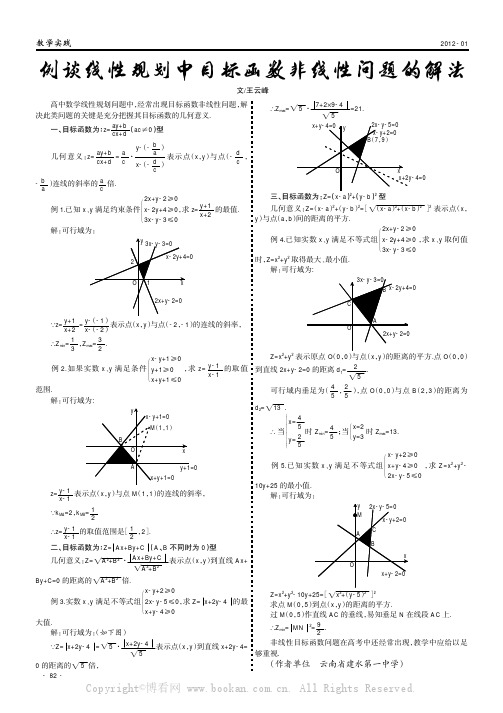
2012-01教学实践高中数学线性规划问题中,经常出现目标函数非线性问题,解决此类问题的关键是充分把握其目标函数的几何意义.一、目标函数为:z =ay+b cx+d (ac ≠0)型几何意义:z =ay+b cx+d =a c ·y-(-b a )x-(-d c )表示点(x ,y )与点(-d c ,-b a )连线的斜率的a c 倍.例1.已知x 、y 满足约束条件2x+y -2≥0x -2y +4≥0,3x-y -3≤0求z =y+1x+2的最值.解:可行域为:∵z =y+1x+2=y-(-1)x -(-2)表示点(x ,y )与点(-2,-1)的连线的斜率,∴Z min =13,Z max =32.例2.如果实数x 、y 满足条件x-y +1≥0y +1≥0x+y +1≤0{,求z =y -1x -1的取值范围.解:可行域为:z =y -1x -1表示点(x ,y )与点M (1,1)的连线的斜率,∵k MA =2,k MB =12∴z =y -1x -1的取值范围是[12,2].二、目标函数为:Z =Ax+By+C (A 、B 不同时为0)型几何意义:Z =A 2+B 2√·Ax+By+C A 2+B 2√表示点(x ,y )到直线Ax+By+C =0的距离的A 2+B 2√倍.例3.实数x 、y 满足不等式组x-y +2≥02x-y -5≤0,x+y -4≥0{求Z =x +2y -4的最大值.解:可行域为:(如下图)∵Z =x +2y -4=5√·x +2y -45√表示点(x ,y )到直线x +2y -4=0的距离的5√倍,∴Z max =5√·7+2×9-45√=21.y -4=0三、)几何意义:Z =(x-a )2+(y-b )2=[(x-a )2+(x-b )2√]2表示点(x ,y )与点(a ,b )间的距离的平方.例4.已知实数x 、y 满足不等式组2x+y -2≥0x -2y +4≥03x-y -3≤0{,求x 、y 取何值时,Z =x 2+y 2取得最大、最小值.解:可行域为:Z=x 2+y 2表示原点O (0,0)与点(x ,y )的距离的平方.点O (0,0)到直线2x+y -2=0的距离d 1=25√.可行域内垂足为(45,25),点O (0,0)与点B (2,3)的距离为d 2=13√.∴当x =45y =25⎧⎩⏐⏐⏐⏐⏐⎨⏐⏐⏐⏐⏐时Z min =45;当x =2y =3{时Z max =13.例5.已知实数x 、y 满足不等式组x-y +2≥0x+y -4≥02x-y -5≤0{,求Z=x 2+y 2-10y+25的最小值.解:可行域为:Z=x 2+y 2-10y x 2+(y -5)2√]2求点M (0,5)到点(x ,y )的距离的平方.过M (0,5)作直线AC 的垂线,易知垂足N 在线段AC 上.∴Z min =MN 2=92.非线性目标函数问题在高考中还经常出现,教学中应给以足够重视.(作者单位云南省建水第一中学)例谈线性规划中目标函数非线性问题的解法文/王云峰82--Copyright©博看网 . All Rights Reserved.。
r语言准确拟合曲线

r语言准确拟合曲线在数据分析和统计学中,准确地拟合曲线是非常重要的,它可以让我们更好地理解数据以及预测未来的走向。
而在 R 语言中,准确地拟合曲线也是可以实现的。
在 R 语言中,准确地拟合曲线的方法有多种,其中最常用的方法是线性回归和非线性回归。
下面我们将分别介绍这两种方法。
1. 线性回归线性回归是一种常用的参数检验方法,它可以用来确定两个变量之间的关系。
在 R 语言中,我们可以使用 lm() 函数进行线性回归分析。
具体地,我们可以按照以下步骤来进行线性回归分析:(1) 导入数据:data <- read.table("data.csv", header = TRUE)(2) 建立模型:model <- lm(dependent ~ independent, data = data)其中,dependent 和independent 分别为因变量和自变量的变量名。
(3) 分析结果:summary(model)在分析结果中,我们可以看到 R 平方值,它表示在模型中自变量所解释的方差所占总方差的比例。
而如果想要更好地理解模型的结果,我们还可以使用 ggplot2 包来进行数据可视化分析。
2. 非线性回归在一些实际应用中,我们往往需要使用非线性回归来进行拟合。
而在R 语言中,非线性回归的方法也有多种,其中最常用的方法是最小二乘法(LSE)、最小二乘法加正则项(LASSO)和最小二乘法加光滑度约束(Ridge)。
在下面的实例中,我们将使用 LSE 方法来进行非线性回归分析:(1) 导入数据:data <- read.table("data.csv", header = TRUE)(2) 建立模型:model <- nls(dependent ~ a * exp(-b * independent) + c, data = data, start = list(a = 2, b = 0.1, c = 1))其中,dependent 和independent 分别为因变量和自变量的变量名,exp(-b * independent) 的含义是e的-b倍方,a、b、c 是拟合参数的初始值。
R语言求解线性规划和非线性规划

第七章线性规划与非线性规划例1 max z=10x1+5x2s.t. 5x1+2x2<=83x1+4x2=9x1+x2>=1x1,x2>=0首先可化为标准形式:min - z = -10x1 -5x2s.t. 5x1+2x1<=8-x1-x2<=-13x1+4x2=9x1,x2>=0library(Rglpk)obj<-c(-10,-5)mat<-matrix(c(5,2,-1,-1,3,4),3,2,T)dir<-c("<=","<=","==")rhs<-c(8,-1,9)Rglpk_solve_LP(obj,mat,dir,rhs)#直接求解library(Rglpk)obj<-c(10,5)mat<-matrix(c(5,2,1,1,3,4),3,2,T)dir<-c("<=",">=","==")rhs<-c(8,1,9)Rglpk_solve_LP(obj,mat,dir,rhs,max=T) 非线性规划求解(Rdonlp2)例2 有如下的条件约束最优化问题:library(Rdonlp2)p = c(10,10) #迭代初始值#对求解问题进行描述fn = function(x){x[1]^2*sin(x[2])+x[2]^2*cos(x[1])}#对x,y值域描述## par.l和par.u分别为约束的左边和右边par.l = c(-100,-100); par.u = c(100,100) ## 目标值域#对线性约束进行描述A = matrix(c(1,1,3,-1),2,byrow=TRUE) ##线性约束系数lin.l = c(2,1); lin.u = c(+Inf,3) ## 分别为约束的左边和右边#对非线性约束进行描述nlcon1 = function(x){x[1]*x[2] ##公式x*y}nlcon2 = function(x){sin(x[1])*cos(x[2]) ##公式sin(x)*cos(y) }## 两个非线性约束的左右边## x*y=2 等价于 2<=x*y<=2nlin.l = c(2,-Inf) ; nlin.u = c(2,0.6)#将参数输入donlp2函数中进行求解## 输入参数第一行:x,y值域及目标函数## 输入参数第二行:线性约束条件## 输入参数第三,四行:非线性约束条件ret = donlp2(p, fn, par.u=par.u, par.l=par.l, A, lin.l=lin.l,lin.u=lin.u,nlin=list(nlcon1,nlcon2),nlin.u=nlin.u, nlin.l=nlin.l)## 输出结果ret$parret$par例3 解下列二次规划二次规划的优化问题,这是一种特殊形式的非线性约束优化问题。
用R语言求解非线性方程

⽤R语⾔求解⾮线性⽅程从本质上来说,Newtons就是⽤迭代⽅式,使近似解(泰勒公式)不断的逼近真实解,当满⾜精度要求时,即可认为近似解为真实解下⾯⽤R语⾔实现Newtons法Newtons<-function(fun,x,ep=1e-5,it_max=100) ##fun为需要求解的⽅程(组),x为初始解,ep为精度要求,it_max为最⼤迭代次数{index<-0 ##指⽰是否完成迭代成功,满⾜精度要求k<-1 ##迭代次数while(k<=it_max){x1<-x;obj<-fun(x);x<-x-solve(obj$J,obj$f) ##obj$J即为⽅程(组)的jacobj矩阵norm<-sqrt((x-x1)%*%(x-x1)) ##x(k+1)y与x(k)精度之差if(norm<ep){index<-1break}k<-k+1}obj<-fun(x);list(root=x,it=k,index=index,FunVal=obj$f,Jacobi=obj$J)}现在来构造需要求解的⽅程(组)和它的jacobj矩阵funs<-function(x){f<-c(x[1]^2+x[2]^2-5,(x[1]+1)*x[2]-(3*x[1]+1)) ##⽅程组J<-matrix(c(2*x[1],2*x[2],x[2]-3,x[1]+1),nrow=2,byrow=T) ##jacobj矩阵,分别对x1和x2求⼀阶导list(f=f,J=J)}计算结果:> Newtons(funs,c(0,1))$root[1] 1 2$it[1] 6$index[1] 1$FunVal[1] 1.598721e-14 6.217249e-15$Jacobi[,1] [,2][1,] 2 4[2,] -1 2有兴趣的同学,可以⽤debug(Newtons)来调试计算过程。
非线性规划的理论与算法

第五章 非线性规划:理论和算法5.5 约束优化我们现在继续讨论更一般的有约束的线性优化问题。
特别的,我们考虑一个具有非线性目标函数和(或者)非线性约束的优化问题。
我们可以将这种问题表示为下面的一般形式:I∈≥∈=i x g i x g x f i i x ,0)(,0)()(min ε (5.10) 在本节的末尾,我们假设f 和i g ,i ε∈⋃I 全部是连续可微的。
拉格朗日函数是研究有约束的优化问题的一个重要工具。
为了定义这个函数,我们结合每个约束的乘子i λ——称作拉格朗日乘子。
对于问题(5.10)拉格朗日函数如下定义:∑I⋃∈-=ελλi iix g x f x L )()(:),( (5.11) 本质上,我们考虑的是目标函数违反了可行约束时的惩罚函数。
选择合适的i λ,最小化无约束函数(),L x λ等价于求解约束问题(5.10)。
这就是我们对拉格朗日函数感兴趣的最根本的原因。
与这个问题相关的最重要问题之一是求解最优问题的充要条件。
总之,这些条件称为最优性条件,也是本节的目的。
在给出问题(5.10)最优性条件之前,我们先讨论一个叫做正则性的条件,由下面的定义给出:定义5.1:设向量x 满足ε∈=i x g i ,0)(和I ∈≥i x g i ,0)(。
设J ⊂I 是使得0)(≥x g i 等号成立的指标集。
x 是问题(5.10)约束条件的正则点,如果梯度向量)(x g i ∇(i J ∈⊂I )相互线性无关。
在上述定义中与J ε对应的约束,即满足0)(=x g i 的约束称为在x 点处的有效约束。
我们讨论第一章提到的两个优化的概念,局部和全局。
回顾(5.10)的全局最优解向量*x ,它是可行的而且满足)()(*x f x f ≤对于所有的x 都成立。
相比之下,局部最优解*x 是可行的而且满足)()(*x f x f ≤对于{}ε≤-*:x x x (0>ε)成立。
因此局部解一定是它邻域的可行点中最优的。
r语言中的计算公式

r语言中的计算公式R语言是一种专门用于数据分析和统计建模的编程语言。
在R语言中,我们可以使用各种计算公式进行数据处理和分析。
本文将介绍几个常用的计算公式及其在数据分析中的应用。
一、线性回归模型线性回归模型是一种用于建立因变量与一个或多个自变量之间关系的模型。
在R语言中,我们可以使用lm()函数来拟合线性回归模型。
下面是一个例子:```R# 构造数据x <- c(1, 2, 3, 4, 5)y <- c(2, 4, 6, 8, 10)# 拟合线性回归模型model <- lm(y ~ x)# 查看模型结果summary(model)```通过上述代码,我们可以得到线性回归模型的拟合结果,包括回归系数、残差、拟合优度等信息。
这些信息有助于我们了解自变量与因变量之间的关系,以及模型的拟合效果。
二、t检验t检验是一种用于比较两个样本均值是否有显著差异的统计方法。
在R语言中,我们可以使用t.test()函数进行t检验。
下面是一个例子:```R# 构造数据x <- c(1, 2, 3, 4, 5)y <- c(2, 4, 6, 8, 10)# 进行t检验result <- t.test(x, y)# 查看检验结果print(result)```通过上述代码,我们可以得到t检验的结果,包括检验统计量、自由度、p值等信息。
这些信息有助于我们判断两个样本均值是否存在显著差异。
三、卡方检验卡方检验是一种用于比较观察频数与理论频数是否存在显著差异的统计方法。
在R语言中,我们可以使用chisq.test()函数进行卡方检验。
下面是一个例子:```R# 构造数据observed <- c(10, 20, 30)expected <- c(15, 15, 20)# 进行卡方检验result <- chisq.test(observed, p = expected)# 查看检验结果print(result)```通过上述代码,我们可以得到卡方检验的结果,包括卡方统计量、自由度、p值等信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章线性规划与非线性规划
例1m a x z=10x
1+5x2
s.t.5x1+2x2<=8
3x1+4x2=9
x1+x2>=1
x1,x2>=0
首先可化为标准形式:min - z = -10x1 -5x2
s.t. 5x1+2x1<=8
-x1-x2<=-1
3x1+4x2=9
x1,x2>=0
library(Rglpk)
obj<-c(-10,-5)
mat<-matrix(c(5,2,-1,-1,3,4),3,2,T)
dir<-c("<=","<=","==")
rhs<-c(8,-1,9)
Rglpk_solve_LP(obj,mat,dir,rhs)
#直接求解
library(Rglpk)
obj<-c(10,5)
mat<-matrix(c(5,2,1,1,3,4),3,2,T)
dir<-c("<=",">=","==")
rhs<-c(8,1,9)
Rglpk_solve_LP(obj,mat,dir,rhs,max=T)
非线性规划求解(Rdonlp2)
例2 有如下的条件约束最优化问题:
22min(sin cos )
1001001001002133
2sin cos 3z x y y x x y x y x y xy x y =+-<<⎧⎪-<<⎪⎪≤+⎨≤-≤⎪⎪=⎪≤⎩
library (Rdonlp2) p = c(10,10) #迭代初始值
#对求解问题进行描述
22min(sin cos )z x y y x =+
fn = function (x){
x[1]^2*sin(x[2])+x[2]^2*cos(x[1])
}
#对x,y 值域描述
100100100100
x y -<<-<< ## par.l 和par.u 分别为约束的左边和右边
par.l = c(-100,-100); par.u = c(100,100) ## 目标值域
#对线性约束进行描述
2133
x y x y ≤+≤-≤ A = matrix(c(1,1,3,-1),2,byrow=TRUE ) ##线性约束系数
lin.l = c(2,1); lin.u = c(+Inf ,3) ## 分别为约束的左边和右边
#对非线性约束进行描述
2sin cos 3
xy x y =≤ nlcon1 = function (x){
x[1]*x[2] ##公式 x*y
}
nlcon2 = function (x){
sin(x[1])*cos(x[2]) ##公式 sin(x)*cos(y)
}
## 两个非线性约束的左右边
## x*y=2 等价于 2<=x*y<=2
nlin.l = c(2,-Inf ) ; nlin.u = c(2,0.6) #将参数输入donlp2函数中进行求解
## 输入参数第一行: x,y 值域及目标函数
## 输入参数第二行: 线性约束条件
## 输入参数第三,四行: 非线性约束条件
ret = donlp2(p, fn, par.u=par.u, par.l=par.l,
A, lin.l=lin.l,lin.u=lin.u,
nlin=list(nlcon1,nlcon2),
nlin.u=nlin.u, nlin.l=nlin.l)
## 输出结果
ret$par
ret$par
例3 解下列二次规划
[][]111222111()26122x x f x x x x x -⎡⎤⎡⎤⎡⎤=-⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦
二次规划的优化问题,这是一种特殊形式的非线性约束优化问题。
二次规划在许多领域都有运用,比如投资组合优化、求解支持向量机(SVM)分类问题等。
想要用quadprog 包求解二次规划,我们需要同时转化我们的目标函数和约束条件为矩阵形式。
quadprog 包默认是求解最小化问题,目标函数二次,约束一次。
所以,我们的约束条件默认的形式也就是AX>=bvec 。
通常我们需要把一些原来是求极大值的问题或者<=约束通过乘以负号来转化 library(quadprog)
Dmat <-matrix(c(1,-1,1,2),2,2,T)
Dmat
dvec <- c(2,6)
A<- matrix(-c(1,1,-1,2,2,1),3,2,T)
A
bvec <- c(-2,-2,-3)
Amat <- t(A)
sol <- solve.QP(Dmat, dvec, Amat, bvec)
sol
参数Dmat 表示海赛矩阵
参数dvet 表示一阶向量,和Dmat 的维数要相对应。
参数Amat 表示约束矩阵,默认的约束都是>=。
参数bvet 表示右边值,由向量,和Amat 的维数要相对应。
参数 meq 表示从哪一行开始Amat 矩阵中的约束是需要被当作等式约束的。
例4 假设以决策变量x1、x2、x3分别表示甲、乙、丙、丁4种肥料的用量,得线性规划模型
1234124134141234min 0.040.150.10.125..0.030.30.15320.050.20.1240.140.0742,,,0z x x x x s t x x x x x x x x x x x x =+++⎧⎪++≥⎪⎪++=⎨⎪+≤⎪⎪≥⎩
library(Rglpk)
obj<-c(0.04,0.15,0.1,0.125)
mat<-matrix(c(0.03,0.3,0,0.15,0.05,0,0.2,0.1,0.14,0,0,0.07),3,4,T)
mat
dir<-c(">=","==","<=")
rhs<-c(32,24,42)
Rglpk_solve_LP(obj,mat,dir,rhs)。
