质心质心运动定律
合集下载
物理-质心与质心运动定理
x
——动量中心系
在质质心心参位考矢系中r：C x 质心速度 υC
0drC
dt
0
质点系m的i总i 动m量C 0
质心系是零动量系
质心的运动轨迹？
——抛物线.
0 O x1
m xC x2 C
mx
二、 质心运动定理
锥体为什么会上滚？
锥体上滚是由其质（重）心下降所引起的。
令人称奇的“水往高处流”。
上坡省力，下坡费劲的“怪坡 ”
三、 质心参考系
【质心参考系】：以质心为坐标原点的参考系。
y
r2
O
y
mi
m2 ri
ri
C
rC m1 r1
m1
l
C
m2
x
O
xC
m2 m1 m2
l
m1
l
C
m2
m1l1 m2l2
l1
l2
（与坐标系无关）
质心坐标与所选坐标系有关，
但质心相对物体各部分位置是确定的.
一、 质心
例2 求半径为R的匀质半圆环的质心.
y
Rdθ
dθ
R
θ
O R cos θ
y R sin θ
x
一、 质心
例2 求半径为R的匀质半圆环的质心.
C 恒矢量
当质点系所受合外力为零时，其质心保持原来的 静止或匀速直线运动状态不变。 ——质心的“惯性运动”
质心的“惯性运动”与质点系动量守恒等价！
随堂练习
例：设有一枚炮弹发射的初速率为 0，发射角为 ，它飞 行在最高点处爆炸成质量相等的两个碎片，其中一个竖直 下落，另一个水平抛出，求这两部分的着地点（忽略空气 阻力）。
(1) 直角坐标系中的质心坐标
2 质心 质心运动定理
将质心的位置矢量 rC 对时间t求导，可得出
质心运动的速度为
dri m drC i dt vC dt m
mi v i m
由此可得
mvC mi vi
上式等号右边就是质点系的总动量
p mv C
即：质点系的总动量等于它的总质量与它的质心的运动 速度的乘积。
质心、质心运动定理
质心 质心运动定理
一．质心
当我们把一匀质薄三角板斜 向抛出时，它的空间运动很 复杂，但实际观测表明，在 薄板上有一点C仍然在作抛 物线运动。C点的运动规律 就象把薄板的质量都集中在 C点，全部的外力也象时作 用在C点一样。这个特殊点C 就是质点系统的质心。
2
质心运动定理 证明： 质点系的总动量等于它的总质量与它的质心的动速度的乘积。
根据牛顿第二定律的微分形式
dp dv C F m ma C dt dt
上式表明无论质点怎样运动，质点系的总质量与质心加速 度的乘积总等于质点系所受全部外力的矢量和，这就是质 心运动定理。它对刚体同样适用。
4
42 质心 质心运动定理 质心坐标系
m1 x1 + m2 x2 xc = m1 + m2
m1 x '1 + m2 x ' 2 x 'c = m1 + m2
得到：xc=x’c 得到
m2 ( x2 − x ' 2 ) = m1 ( x1 − x '1 )
x2-x2’为船移动的距离 ，人移动的距离为 为船移动的距离d，人移动的距离为(l-d) 为船移动的距离 得到： 得到：
Байду номын сангаас
∑ F dt = mdv
i i
c
mdvc ∑ Fi = dt = mac i
mdvc ∑ Fi = dt = mac i
质心的运动等同于一个质点的运动， 质心的运动等同于一个质点的运动，这个质 点具有质点系的总质量m， 点具有质点系的总质量 ，它受到的外力为 质点系所受的所有外力的矢量和。 质点系所受的所有外力的矢量和。这个结论 质心运动定理。 称为质心运动定理 称为质心运动定理。
y
dm=ρdl
yc =
π
∫ ydm
m
=
∫ yρdl
m
dl dθ θ x
由于y=Rsinθ,dl=ds=Rd θ,得到：
yc =
∫ R sin θ ⋅ ρ ⋅ Rdθ
0
m
2 ρR 2 = m
m = πRρ
⇒ yc =
2
π
R
二、质心运动定理 将质心位矢对时间求导： 将质心位矢对时间求导：
rc = ∑mi ri / m
例2、一质量为m1=50kg的人站在一条质量为 2=200kg，长度 、一质量为 的人站在一条质量为m ， 的人站在一条质量为 的船的船头上， 为l=4m的船的船头上，开始船静止，试求人走到船尾时船移 的船的船头上 开始船静止， 动的距离？ 动的距离？ 解一：以人和船为一个系统，在水平方向不受力， 解一：以人和船为一个系统，在水平方向不受力，质心速度 为0，质心的坐标值不变。 ，质心的坐标值不变。
质心与质心运动定律
质心与质心运动定律一、质心1. 定义我们先来回顾一下牛顿第二定律:是对单个质点而言的,由于质点系内各质点的运动情况各不相同,加速度也各不相同,并不能简单的等效于 (M是体系的总质量),但对质点系而言,确实存在一个特殊点C,而使成立,这个ac是该特殊点C的加速度.这个特殊点称为质心.2. 质心的位置如果将质点系各质点参量记为mi 、ri、vi、xi、yi、zi……，质点系质心记为C则对于由两个质点构成的简单质点系，质心在它们连线上，将这两个质点的质量分别记为m1和m2，间距记为l，那么质心与两者的间距依次为：二、质心运动定律1.质心动量定理：外力对体系的冲量等于质心动量的增量。
2.质心运动定律：体系总质量与质心加速度的乘积等于外力的矢量和，或者说，在诸外力作用下，体系质心的加速度等于质量为体系总质量的质点在这些外力共同作用下的加速度。
对一个质点系而言，同样可以应用牛顿第二定律。
三、习题1.试求匀质三角形板的质心位置。
答案：三条中线的焦点：即几何中的重心2. 试求匀质三角形框架的质心位置。
答案：三边中点构成的小三角形的内心。
3. 一轻弹簧两端各系有质量分别为m和2m的物块，用系于质量为m的物块上的细线悬挂在支点O上，如图。
今将细线突然剪断，求该瞬时体系质心的加速度。
答案：g。
4. 用质心运动定理解：长为l、总质量为m的柔软绳索盘放在水平台面上。
用手将绳索的一端以恒定速率vo向上提起，求当提起高度为x时手的提力F。
5. 如图所示，用劲度系数为k的轻弹簧连接质量分别为m1、m2的木块，放在光滑的水平面上。
让第一个木块紧靠竖直墙，在第二个木块的侧面上施加水平压力，将弹簧压缩l长度。
撤去这一压力后，试求系统质心可获得的最大加速度值和最大速度值。
多说两句：体系的总动量为：质心的动能为：质点系相对质心的动能为：质点系的总动能为：（克尼希定理）☆在使用质心参照系时要特别主要克尼希定理的使用！。
大学物理-质心质心运动定律
角动量守恒条件
当刚体绕定轴转动时，如果作用于刚体上的外力矩为零，则刚体的 角动量守恒。
角动量守恒应用
利用角动量守恒原理可以解决一些实际问题，如陀螺仪的工作原理、 天体运动中行星轨道的确定等。
角动量不守恒情况
当作用于刚体上的外力矩不为零时，刚体的角动量将发生变化。此时 需要根据外力矩的作用时间和大小来计算角动量的变化量。
适用范围和条件
01
适用范围：质心运动定律适用于任何由多个质点组成的系统，无论这 些质点之间是否存在相互作用力。
02
适用条件：质心运动定律的应用需要满足以下两个条件
03
质点系所受的外力可以视为作用于质心上的合力。
04
质点系内部的相互作用力对质心的运动没有影响，或者其影响可以忽 略不计。
质点系相对于质心参
角动量
描述刚体绕定轴转动时动量的大小 和方向，等于转动惯量与角速度的 乘积。
刚体绕定轴转动时质心位置变化规律
质心位置不变
刚体绕定轴转动时，其质 心位置保持不变，始终位 于转轴上。
质心速度为零
由于质心位于转轴上，因 此质心的速度为零。
质心加速度为零
由于质心速度为零，因此 质心的加速度也为零。
刚体绕定轴转动时角动量守恒原理
02
考系运动
质点系内各点相对于质心参考系位移
01
02
03
定义
质点系内各点相对于质心 的位置矢量称为相对位移。
性质
相对位移是描述质点系内 各点相对于质心位置变化 的物理量，具有矢量性。
计算方法
通过几何方法或解析方法 求出各点相对于质心的位 置矢量。
质点系内各点相对于质心参考系速度
定义
质点系内各点相对于质心的速度称为相对速度。
当刚体绕定轴转动时，如果作用于刚体上的外力矩为零，则刚体的 角动量守恒。
角动量守恒应用
利用角动量守恒原理可以解决一些实际问题，如陀螺仪的工作原理、 天体运动中行星轨道的确定等。
角动量不守恒情况
当作用于刚体上的外力矩不为零时，刚体的角动量将发生变化。此时 需要根据外力矩的作用时间和大小来计算角动量的变化量。
适用范围和条件
01
适用范围：质心运动定律适用于任何由多个质点组成的系统，无论这 些质点之间是否存在相互作用力。
02
适用条件：质心运动定律的应用需要满足以下两个条件
03
质点系所受的外力可以视为作用于质心上的合力。
04
质点系内部的相互作用力对质心的运动没有影响，或者其影响可以忽 略不计。
质点系相对于质心参
角动量
描述刚体绕定轴转动时动量的大小 和方向，等于转动惯量与角速度的 乘积。
刚体绕定轴转动时质心位置变化规律
质心位置不变
刚体绕定轴转动时，其质 心位置保持不变，始终位 于转轴上。
质心速度为零
由于质心位于转轴上，因 此质心的速度为零。
质心加速度为零
由于质心速度为零，因此 质心的加速度也为零。
刚体绕定轴转动时角动量守恒原理
02
考系运动
质点系内各点相对于质心参考系位移
01
02
03
定义
质点系内各点相对于质心 的位置矢量称为相对位移。
性质
相对位移是描述质点系内 各点相对于质心位置变化 的物理量，具有矢量性。
计算方法
通过几何方法或解析方法 求出各点相对于质心的位 置矢量。
质点系内各点相对于质心参考系速度
定义
质点系内各点相对于质心的速度称为相对速度。
2-1 质心 质心运动定理
Ch2 运动的守恒量和守恒定律§2-1质点系的内力外力质心质心运动定理§2-1 质心质心运动定理动量守恒定律1、质点系的内力和外力质心质心的位置例：任意三角形的每个顶点有一质量m 的小球，求/r m r M =∑G Gz yOΔm ir微元分割！例3-7 求腰长为a等腰直角三角形均匀薄板的质心位置。
3、质心运动定理质心运动定理G G G G G d v1 G m 1 a1 = m 1 = F1 外 + f 12 + f 13 + " + f 1 n , dt G G G G G d v2 G m 2a2 = m 2 = F2 外 + f 21 + f 23 + " + f 2 n , dt G G G G G d vn G = Fn外 + f n 1 + f n 2 + " + f n ( n − 1) , m nan = m n dt G G G G 由于内力 f12 + f 21 = 0," , f in + f ni = 0, ...由牛顿第二定律:""∴G ∑ m i ai =G ∑ F i外11/18中国矿业大学（北京）质心运动定理G ∑ m i ai =G ac =G ∑ F i外 G ∑ m i aiG ac =G ∑ Fi外∑m∑m=G ∑ Fi外 Mi∑G G Fi外 = M a ci质心运 动定理不管物体质量如何分布，也不管外力作用在物体 什么位置上，质心的运动就象是物体的质量全都集 中于此，而且所有外力也都集中作用其上的一个质 点的运动一样。
12/18 中国矿业大学（北京）补充例题1例1 质量为m1 和m2的两个小孩，在光滑水平冰面上用 绳彼此拉对方。
开始时静止，相距为l。
问他们将在何 处相遇？m2m1Ox20x10x13/18中国矿业大学（北京）补充例题1解：可直接由质心运动定律求出。
初始静止时，小孩系统的质 心位置： m 1 x 10 + m 2 x 20 1 xc = m1 + m 2m2C xcx10m1∑G G G Fi外 = M a c ⇒ a c = 0O x20x质心位置，在过程中应该始终保持静止。
4.4 质心 质心运动定理
解根据火箭速度公式,在第一级火箭燃料耗尽时 达到的速度为 v1 uln N1
大学物理 第三次修订本
17
第4章 冲量和动量
在第二级火箭燃料耗尽时, 火箭主体的 速度达到了v2 , 由公式得
v v0 uln
M0 M
v2 v1 uln N 2
在第三级火箭燃料耗尽时, 火箭主体最后 达到的速度为v, 应满足
M v [(M dM )(v dv) (dM )(v dv u )]
即
M dv udM 0
v
0
积分得 v
dv u
M
dM M
0
M0
v v 0 u(ln M ln M 0 ) 0 v v 0 u ln
M0 M
12
大学物理 第三次修订本
第4章 冲量和动量
16
第4章 冲量和动量
例3有一个三级火箭, 第一级火箭脱落前的质量 比为 N1 , 第二级火箭刚发动时火箭的质量与第 二级火箭燃料耗尽时火箭的质量之比为 N2 , 第 三级火箭刚点燃时火箭的质量与燃料耗尽时火 箭的质量之比为N3 。 若取N1 = N2 = N3 = 7.4；各级火箭的喷射速 度都为u =2.5kms-1。不计重力影响, 求该火箭最 后达到的速度。
第4章 冲量和动量
各级火箭中燃料烧完后, 火箭的速率为
v1 u ln N1
v2 v1 u ln N 2
v3 v2 u ln N 3
若火箭粒子流的喷射速率u=2.5kms-1，每 一级的质量比分别为N1=4, N2=3, N3=2, 可得: v3=7.93kms-1。
大学物理 第三次修订本
ri
rc
mi
大学物理 第三次修订本
17
第4章 冲量和动量
在第二级火箭燃料耗尽时, 火箭主体的 速度达到了v2 , 由公式得
v v0 uln
M0 M
v2 v1 uln N 2
在第三级火箭燃料耗尽时, 火箭主体最后 达到的速度为v, 应满足
M v [(M dM )(v dv) (dM )(v dv u )]
即
M dv udM 0
v
0
积分得 v
dv u
M
dM M
0
M0
v v 0 u(ln M ln M 0 ) 0 v v 0 u ln
M0 M
12
大学物理 第三次修订本
第4章 冲量和动量
16
第4章 冲量和动量
例3有一个三级火箭, 第一级火箭脱落前的质量 比为 N1 , 第二级火箭刚发动时火箭的质量与第 二级火箭燃料耗尽时火箭的质量之比为 N2 , 第 三级火箭刚点燃时火箭的质量与燃料耗尽时火 箭的质量之比为N3 。 若取N1 = N2 = N3 = 7.4；各级火箭的喷射速 度都为u =2.5kms-1。不计重力影响, 求该火箭最 后达到的速度。
第4章 冲量和动量
各级火箭中燃料烧完后, 火箭的速率为
v1 u ln N1
v2 v1 u ln N 2
v3 v2 u ln N 3
若火箭粒子流的喷射速率u=2.5kms-1，每 一级的质量比分别为N1=4, N2=3, N3=2, 可得: v3=7.93kms-1。
大学物理 第三次修订本
ri
rc
mi
质心与质心运动定理
xc
mi xi
i 1
N
m
同理对 y 和 z 分量
m1
l1
r1
rc
l2
m2
r2
m1 (rc r1 ) m2 (r2 rc )
m1l1= m2l2
m1 r1 m2 r2 rc m1 m 2
O
对连续分布的物质，可以将其分为N个小质元
质心运动定理
一 、质心(center of mass)
N个粒子系统，可定义质量中心
z
mi
rc
ri
y
rc
m i ri
N i 1 N
mi
i 1
m i ri
N i 1
x
m
1.质心位置与坐标系的选择有关，但质 心相对质点系是一个特定的位置。 2.外力作用在质心上，质点系内各质点 的运动状态相同
dt
dt
1.内力不改变质心的运动状态，但可以改变各质点的运动状态 如炮弹爆炸时，质心轨迹为抛物线
2.质点系所受合外力为零，则动量守恒，此时质心的速度不变
i
质心的运动只与系统所受的合外力相关
drc d ri 质点系的总动量 m m i v i dt dt dv c dP总 mv c mi v i m P总
m ac F
F外 mac
rc
xc
r dm m xdm
m
Z
Y
r
O
X
dm
例： 一均匀直杆，质量为M，长为L, 求其质量中心
解：1、建立坐标系 2、取微元dx dm=dx, 坐标为x
0
§2-4质心 质心的运动定律
m1v1x m2v2 x mn vnx =常量
m1v1 y m2v2 y mn vny =常量
m1v1z m2v2 z mn vnz
=常量
太原理工大学物理系
例1 质量为m1 和m2的两个小孩，在光滑水平冰面 上用绳彼此拉对方。开始时静止，相距为l。问他们 将在何处相遇？
y
o
解：
l
x
人和船组成系统，水平方向上不受外力。原来质 心静止，在人走动过程中质心始终静止，因而质 心的坐标值不变。 太原理工大学物理系
m1 x1 m2 x2 当人站在船的左端时 xc m1 m2 m1 x'1 m2 x'2 当人站在船的右端时 x'c m1 m2
m1x1 m2 x2 m2 x2 xc xc y x 1 x l d x x
m2 O m1
x
解 把两个小孩和绳看作一个系统，系统在水平 方向不受外力作用，水平方向质心速度不变。开 始时质心静止，两个孩子在运动过程中质心的位 置始终不变，所以在质心处相遇。
太原理工大学物理系
m2 O
C
m1
x20
xC
x10
x
m1 x1 m2 x2 xc m1 m2
在初始位置时，取 x20 0
F Mac 质心运动定理
质心的运动只由合外力决定，内力不能改变质 心的运动情况。
太原理工大学物理系
质心处的质点（质点系总质量）代替质点系 整体的平动.
4.合外力为零时质心的运动 如果系统所受的外力之和为零
由质心运动定理 F Ma c 得到 ac 0
Fi 0
太原理工大学物理系
质心和质心运动定律
2 M+m
根据质心位置不变，有 xC = xC0。
∴ M l = m(l + s) + M( l + s)
2
2
∴ s = − m l = − 50 × 4 = − 4 m
M + m 500 + 50
11
质心与质心运动定律
【例题 2】一质量为 M 的箱子内有一质量为 m 的物 体，通过一根轻弹簧与箱子顶连接，如图所示。现将挂 箱子的绳剪断，求剪断瞬间物块相对箱子的加速度。
)
+
+ m1 + m2
M ∆l
质心与质心运动定律
【解析】
=
(m1
−
m2
)
l 2
+
(M
+
m1
+
m2
)∆l
M + m1 + m2
由质心位置不变，得
(m2
−
m1 )
l 2
=
(m1
−
m2
)
l 2
+
(M
+
m1
+
m2 )∆l
∴(m2 − m1)l = (M + m1 + m2 )∆l
∴ m2
=
(M
+
m1 )∆l l − ∆l
【解析】
当小球全部发射到车厢右壁处后，
nm(l + s) + M ( l + s)
xC =
2 M + nm
Q xC = xC 0
∴ nm(l +
s) +
l M(
+
2_9质心与质心运动定理
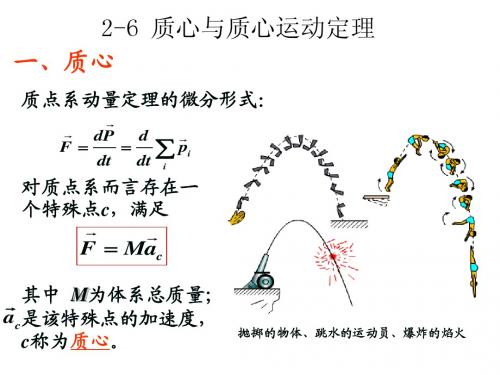
例3 有质量为2m的弹丸，从地面斜抛出去，它的落 地点为xC 。如果它在飞行到最高点处爆炸成质量相 等的两碎片。其中一碎片铅直自由下落，另一碎片水 平抛出，它们同时落地。问第二块碎片落在何处。
解： 在爆炸的前后，质心始终
只受重力的作用，因此， 质心的轨迹为一抛物线， 它的落地点为xc 。
m1 x1 m2 x2 xC m1 m2 mx2 xC 2m
dV r 2 dz
而
r a sin z a cos , 2 dV a sin d a cos
a 1 cos d cos
3 2
r a sin
z
z a cos x
a
0 设 u cos ，则 v z dV zdV a 4 1 1 u2 udu 2 a 3 zc 0 3 V dV
x1c R
y
O
x
1 2 小圆板质量为 m1 R， 4 质心坐标为
2
3 余下的质量为 m2 R 2，质心坐标用 x 2 c表示，则 4
1 3 2 R R R 2 x2 c 2 4 0 4 2 R
R x2c 6
例2
求半径为a的均质半圆球的质心
解：如图，以球心O为原点建立坐标系.将半球体划 分为若干半径为r厚为dz的平板状薄圆，体积元为dV
令
m1r1 m2 r2 rc m1 m2
（2）n个质点系统
分量形式
xc
i
rc
mi ri
m
i
i i
i
i
m x m
i i i
i
3.3 质心 质心运动定理
i
F iX 0
PX 0
画系统 受力图 M V X m x 0
x VX X
是m相对于小车的速度
VX m M m
X
8
第3章动量与角动量
VX
m M m
t 0
XX 来自t 0V X dt
m M m
t 0
dt X
M 例3 如图 已知： , m , l ，地面光滑。 m , l mg 起初：单摆水平，静止。 求：下摆至 时，车的位移。 V
o
N
X
以此例即将说明 动量守恒和质心速度不变是同义语。 动量守恒的问题也可以利用 质心速度不变来解。 解： 法一 用动量守恒定律 选 M + m 为系统
M
Mg
4
ac
i
m iai / m i
i
t2 t1
F外 d t
P P0
dP
第3章动量与角动量
讨论
F外
1）质点系动量定理微分和积分形式： t dP m a c （ F外 ） F d t P P0
dt
2
t1
外
2) 质心的运动，该质点集中整个系统质量，并集中系统 受的外力，代替质点系整体的平动。
i
说明: 1）不太大的物体的质心与重心重合； 2）均匀分布的物体，质心在几何中心； 3）质心是位置的加权平均值，质心处不一定有质量； 4）具有可加性，计算时可分解。
2 第3章动量与角动量
例1 已知一半圆环半径为 R，质量为M。
求 它的质心位置。
解 建坐标系如图
§2-4质心 质心的运动定律
系统所受外力与系统质心运动加速度的关系为 质心运动定理 质心的运动只由合外力决定， 质心的运动只由合外力决定，内力不能改变质 心的运动情况。 心的运动情况。 太原理工大学物理系
质心处的质点（质点系总质量） 质心处的质点（质点系总质量）代替质点系 整体的平动. 整体的平动
4.合外力为零时质心的运动 合外力为零时质心的运动 如果系统所受的外力之和为零 由质心运动定理 得到 太原理工大学物理系
直角坐标系下动量守恒定律的分量形式
=常量 常个小孩， 例1 质量为 1 和m2的两个小孩，在光滑水平冰面 上用绳彼此拉对方。开始时静止，相距为l。 上用绳彼此拉对方。开始时静止，相距为 。问他们 将在何处相遇？ 将在何处相遇？
m1
m2 O
当人站在船的左端时 当人站在船的右端时
y
′ d = x2 − x2
o
x
太原理工大学物理系
§2-4 质心 质心运动定律 一、质心 质心就是大量质点组成的质点系的质量中心， 质心就是大量质点组成的质点系的质量中心， 就是大量质点组成的质点系的质量中心 质心运动反映了质点系的整体运动趋势。 质心运动反映了质点系的整体运动趋势。 质心具有长度的量纲， 质心具有长度的量纲，描述与质点系有关的某 一空间点的位置。 一空间点的位置。 对于N个质点组成的质点系： 对于 个质点组成的质点系： 个质点组成的质点系 各质点的质量 各质点对同一坐标的位矢
=常矢量 常矢量 当质点系的合外力为零时， 当质点系的合外力为零时，质心静 止或作匀 速直线运动。 速直线运动。 =常矢量 常矢量 系统的总动量保持不变,叫做动量守恒定律. 系统的总动量保持不变 叫做动量守恒定律 叫做动量守恒定律 若质点系x向分动量守恒，质心在 向匀速直线 若质点系 向分动量守恒，质心在x向匀速直线 向分动量守恒 运动(或静止 或静止)。 运动 或静止 。 太原理工大学物理系
质心-质心运动定理
质心 质心运动定理
一、 质心(the center of mass)
质心位矢
rc
mir i m
坐标
xc
mi
x i
m
yc
mi
y i
m
z
ri
o x
mi
rc
m2
m1 r1
y
zc
mi zi m
对于质量连续分布的系统
rc
rdm
m
例: 已知一半圆环半径为 R，质量为m ，
y
d
求: 它的质心位置。 解: 建坐标系如图 取 dl
dm
dl
M
R
Rd
M
d
C dm
0.64R
o
x
x Rcos y Rsin
yc
ydm
Rsin M d
0
0.64R
M
M
xc
xdm
R cos M d
0
0
M
M
二、质心运动定理(theorem of the motion of center of mass)
1. 质心的速度
vc drc d (
解:炮弹炸裂前后所受外力始终是重力,所以炮弹炸裂
对质心运动没有影响, m1和m2落地时, 炮弹的质心坐标
为 xc= 2R0
y
由 xc
mi xi 得
mi
o
m1x1 m2 x2 m1 m2
2R0
m1 m2 炮弹质心轨迹
x1=R0 xc=2R0
x x2=?
将 x1 = R0
代入得 x2 = 5R0
miri )
mi
dri dt
一、 质心(the center of mass)
质心位矢
rc
mir i m
坐标
xc
mi
x i
m
yc
mi
y i
m
z
ri
o x
mi
rc
m2
m1 r1
y
zc
mi zi m
对于质量连续分布的系统
rc
rdm
m
例: 已知一半圆环半径为 R，质量为m ，
y
d
求: 它的质心位置。 解: 建坐标系如图 取 dl
dm
dl
M
R
Rd
M
d
C dm
0.64R
o
x
x Rcos y Rsin
yc
ydm
Rsin M d
0
0.64R
M
M
xc
xdm
R cos M d
0
0
M
M
二、质心运动定理(theorem of the motion of center of mass)
1. 质心的速度
vc drc d (
解:炮弹炸裂前后所受外力始终是重力,所以炮弹炸裂
对质心运动没有影响, m1和m2落地时, 炮弹的质心坐标
为 xc= 2R0
y
由 xc
mi xi 得
mi
o
m1x1 m2 x2 m1 m2
2R0
m1 m2 炮弹质心轨迹
x1=R0 xc=2R0
x x2=?
将 x1 = R0
代入得 x2 = 5R0
miri )
mi
dri dt
03-4质心和质心运动定理
3-2 质心和质心运动定理 ——基于整体运动的视角 基于整体运动的视角—— 基于整体运动的视角
牛顿定律只适用于质点
v v F = ma
由于质点系中各质点的运动情况各不相同， 由于质点系中各质点的运动情况各不相同，加速度也 不尽相同， 不尽相同，所以质点系的运动情况不能简单地等效成
v v F外 = mac
但对质点系而言， 但对质点系而言，确 实存在一个特殊的点， 实存在一个特殊的点， 能够使上式成立
当球棒从手中抛出后， 当球棒从手中抛出后，球棒在做上抛运动的同时还在 旋转，这时球棒上各点的运动比较复杂， 旋转，这时球棒上各点的运动比较复杂，但球棒上有 一点的运动却简单得象一个质点一样， 一点的运动却简单得象一个质点一样，沿抛物线的轨 迹运动
v d v v v (m1r1 + m2r2 + L + mn rn ) = ∑ Fi外 dt 2
质点化” 如何使质点系的运动规律 “质点化”呢？
2
v v v v d m1r1 + m2r2 + L + mn rn (m1 + m2 + L + mn ) 2 ( ) = ∑ Fi外 m1 + m2 + L + mn dt
跳水者不管在空 中作多复杂的动 作，其质心仍然 是沿抛物线运动
例1 一炮弹在轨道最高点炸成质量比m1:m2=3:1的两个 一炮弹在轨道最高点炸成质量比 的两个 碎片。其中m 自由下落， 碎片。其中 1自由下落，落地点与发射点的水平距离 继续向前飞行， 同时落地。 为R0，m2继续向前飞行，与m1同时落地。不计空气阻 的落地点。 力，求m2的落地点。
这个在质点系上的特殊点是什么，它又在哪里？ 这个在质点系上的特殊点是什么，它又在哪里？
牛顿定律只适用于质点
v v F = ma
由于质点系中各质点的运动情况各不相同， 由于质点系中各质点的运动情况各不相同，加速度也 不尽相同， 不尽相同，所以质点系的运动情况不能简单地等效成
v v F外 = mac
但对质点系而言， 但对质点系而言，确 实存在一个特殊的点， 实存在一个特殊的点， 能够使上式成立
当球棒从手中抛出后， 当球棒从手中抛出后，球棒在做上抛运动的同时还在 旋转，这时球棒上各点的运动比较复杂， 旋转，这时球棒上各点的运动比较复杂，但球棒上有 一点的运动却简单得象一个质点一样， 一点的运动却简单得象一个质点一样，沿抛物线的轨 迹运动
v d v v v (m1r1 + m2r2 + L + mn rn ) = ∑ Fi外 dt 2
质点化” 如何使质点系的运动规律 “质点化”呢？
2
v v v v d m1r1 + m2r2 + L + mn rn (m1 + m2 + L + mn ) 2 ( ) = ∑ Fi外 m1 + m2 + L + mn dt
跳水者不管在空 中作多复杂的动 作，其质心仍然 是沿抛物线运动
例1 一炮弹在轨道最高点炸成质量比m1:m2=3:1的两个 一炮弹在轨道最高点炸成质量比 的两个 碎片。其中m 自由下落， 碎片。其中 1自由下落，落地点与发射点的水平距离 继续向前飞行， 同时落地。 为R0，m2继续向前飞行，与m1同时落地。不计空气阻 的落地点。 力，求m2的落地点。
这个在质点系上的特殊点是什么，它又在哪里？ 这个在质点系上的特殊点是什么，它又在哪里？
3-3 质心 质心运动定律.
m r
iHale Waihona Puke 1i im2
rC
m r
i 1
n
i i
m
mi ri m
r
i 1
n
ri
y
m2
m
r2
m ri i
rc
c
o
z
r1 m1
rc
i
x
mi m : 总质量， 权重 m
即：质心位矢 rc 是各质点位矢 ri
的加权平均。
3
质心在直角系的计算公式 N m r ri xi i yi j zi k i 1 i i rc N N N M mi xi i mi yi j mi yi k i 1 i 1 rc xci yc j zc k i 1 m
12
y
H
d O o d
52.30
37.7 0
12 rC 6.8 10 mi
C
x
52.30
7
H
二 质心运动定律
y
m2
rC
m r
i 1
n
r2
m ri i
i i
rC
c
m
n
o
z
r1 m1
x
mrC mi ri
i 1
8
mrC mi ri
i 1
n
上式两边对时间 t 求导数，得
xc
m x
i 1 i
N
i
m
z
i
yc
m y
i 1 i
N
r1
m1
m2
3_9质心 质心运动定律
xc 0 yc0
m2 x20 1.5m m1 m2 m1 y10 1.9m m1 m2
3m
B 0 4m x
F2
3-9 质心 质心运动定律 由质心运动定律
dvx Fx F1 (m1 m2 ) dt dvy Fy F2 (m1 m2 ) dt
根据初始条件t=0时，v=0，对 上式积分得：
对质量连续分布的物体： 1 1 1 z y y d m xC x d m C C m' m' m'
zd m
说明 对密度均匀、形状对称的物体，质 心在其几何中心．
3-9 质心 质心运动定律
二 质心运动定律
rC
n
mi ri
i 1
n
y
m2
r2
m ri i
再对时间 t 求一阶导数，得 m 'aC
n
d( pi )
i 1
n
根据质点系动量定理
d( pi )
i 1
dt
ex F
dvC m' m' aC dt
dt
ex F
作用在系统上的合外力等于系统的总 质量乘以质心的加速度——质心运动定律
3-9 质心 质心运动定律
ex F
dvC m' m' aC dt
质心运动定律与牛顿第二定律在形式上完全相同， 相当于系统的质量全部集中于系统的质心，在合外力 的作用下，质心以加速度运动。 说明： 1）坐标系的选择不同，质心的坐标也不同； 2）对于密度均匀，形状对称的物体，其质心在物 体的几何中心处； 3）质心不一定在物体上，例如圆环的质心在圆环的 轴心上；
课件：质心 质心运动定律
Pi
i 1
dt
)
10
根据质点系动量定理
n
n dPi i1 dt
n Fiex
i 1
（因质点系内 Fiin 0 ）
F ex
i 1 m' dvC
dt
m'aC
作用在系统上的合外力等于系统的总
质量乘以质心的加速度——质心运动定律
11
例3 设有一
质量为2m的弹丸,
从地面斜抛出去,
它飞行在最高点
2m
处爆炸成质量相 等的两个碎片，
m O xC
m C xC x
其中一个竖直自由下落，另一个水平抛出，
它们同时落地．试问第二个碎片落地点在何
处?
12
解 选弹丸为
一系统，爆炸前、
后质心运动轨迹不
变. 建立图示坐标, 2m
m1=m2=m
x1=0
m1
m2
O xC C x2 x
xC为弹丸碎片落地时质心离原点的距离
i 1
m'
z
y
m2
r2
ri mi
rc
c r1
m1
o
x
n
m'rC miri
i 1
9
n
m'rC miri
i 1
上式两边对时间
m' drC dt
itn1求m一i d阶drti导数，得
n n
m'vC mi vi Pi
n
再对时间
t
i 1
i1
求一阶导数，得 m'aC
d(
yc
mi yi
λy
y 2
λ(l
y) 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
xC
1 m'
xdm
yC
1 m'
ydm
zC
1 m'
zdm
说明 对密度均匀、形状对称的物体，质
心在其几何中心．
第三章 动量守恒和能量守恒
4
物理学
第五版
3-9 质心 质心运动定律
例1 水分子H2O的结构如图．每个氢原 子和氧原子之间距离均为d=1.0×10-10 m，氢 原子和氧原子两条连线间的夹角为θ=104.6o.
18
物理学
第五版
3-9 质心 质心运动定律
例4 长为 L= 4m ，质量M=150kg的船 ，静 止在湖面上。一质量M=50kg的人，从船头走 到船尾，如图。求人和船相对湖岸各移动的 距离，忽略阻力。
第三章 动量守恒和能量守恒
19
物理学
第五版
3-9 质心 质心运动定律
解法一：动量守恒。选人和船为系统，水平
x2 2xC
第三章 动量守恒和能量守恒
15
物理学
第五版
3-9 质心 质心运动定律
例4 用质心运动定律 来讨论以下问题．
y F
一长为l、密度均匀的
柔软链条，其单位长度的质
量为 ．将其卷成一堆放在
地面． 若手提链条的一端，
y c
yC o
以匀速v 将其上提．当一端
被提离地面高度为 y 时，求手的提力．
物理学
第五版
3-9 质心 质心运动定律
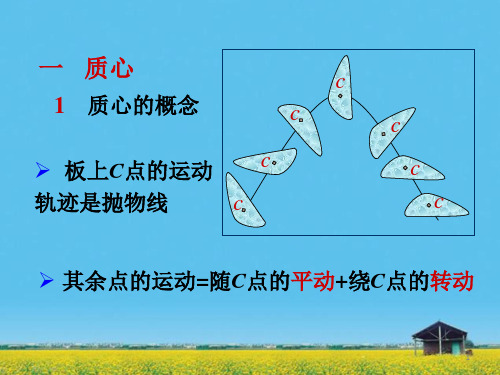
一 质心
1 质心的概念
c
c
c
➢ 板上C点的运动 c
c
轨迹是抛物线
c
c
➢ 其余点的运动=随C点的平动+绕C点的转动
第三章 动量守恒和能量守恒
1
物理学
第五版
3-9 质心 质心运动定律
2 质心的位置
y m2 ri mi
由n个质点组成 的质点系，其质心
r2
o
rc c r1 m1
求水分子的质心．
yH
d oC Od
H
52.3o
x
52.3o
第三章 动量守恒和能量守恒
5
物理学
第五版
3-9 质心 质心运动定律
解 yC=0
n
xC
mi xi
i 1
m i
mHd sin 37.7o mO 0 mHd sin 37.7o mH mO mH
xC 6.810 12 m
rvC
6.8
的位置：
x
z
rC
m1r1 m2r2 miri m1 m2 mi
n miri
i 1
m'
第三章 动量守恒和能量守恒
2
物理学
第五版
3-9 质心 质心运动定律
质心位置的确定 （由质点系动量定理）
v
F exdt d (
n
mi vvi )
v
F ex
d(
n
i1
mi vvi ) / dt
m'vC n mivi n pi
i 1
i 1
再对时间 t 求一阶导数，得 m'aC
n
d(
pi )
i 1
dt
第三章 动量守恒和能量守恒
12
物理学
第五版
3-9 质心 质心运动定律
根据质点系动量定理
n dpi i1 dt
n Fiex
i 1
（因质点系内 n Fiin 0 ）
i 1
F ex
方向动量守恒。设V 和 u分别表示任意时刻
船和人相对岸的速度。向右为正，由动量
1012
v i
m
yH
d oC Od
H
52.3o
x
52.3o
第三章 动量守恒和能量守恒
6
物理学
第五版
3-9 质心 质心运动定律
例2 求半径为 R 的匀质半薄球壳的质心.
y
Rsin θ
Rdθ
R θ dθ O
Rcos θ
x
解 选如图所示的坐标系． 在半球壳上取一如图圆环
第三章 动量守恒和能量守恒
7
物理学
第五版
3-9 质心 质心运动定律
➢ 圆环的面积 ds 2πRsin Rd
y
Rsinθ Rdθ
R θ dθ O
Rcosθ
x
➢ 圆环的质量 dm 2πR2 sin d
由于球壳关于y 轴对称，故xc= 0
第三章 动量守恒和能量守恒
8
物理学
第五版
Байду номын сангаас
3-9 质心 质心运动定律
y
Rsinθ Rdθ
R θ dθ O
它们同时落地．问第二个碎片落地点在何处?
第三章 动量守恒和能量守恒
14
物理学
第五版
3-9 质心 质心运动定律
解 选弹丸为
一系统，爆炸前、
后质心运动轨迹不
变．建立图示坐标 2m
系， m1 m2 m x1 0
m1
m2
O xC C x2 x
xC为弹丸碎片落地时质心离原点的距离
xC
m1x1 m2 x2 m1 m2
Rcosθ
x
yC
1 m'
ydm
y 2πR2 sind 2πR2
第三章 动量守恒和能量守恒
9
物理学
第五版
3-9 质心 质心运动定律
而 y R cosθ
y
Rsin θ Rdθ
R θ dθ O
Rcosθ
x
π
其所质以心yC位矢R：r0C2
cos
R
sin
2j
d
R
2
第三章 动量守恒和能量守恒
10
m'
dvC dt
m'aC
作用在系统上的合外力等于系统的总
质量乘以质心的加速度——质心运动定律
第三章 动量守恒和能量守恒
13
物理学
第五版
3-9 质心 质心运动定律
例3 设有一
质量为2m的弹丸,
从地面斜抛出去,
它飞行在最高点 处爆炸成质量相 等的两个碎片，
2m
m
m
O
C
x
其中一个竖直自由下落，另一个水平抛出，
第三章 动量守恒和能量守恒
16
物理学
第五版
3-9 质心 质心运动定律
解 建立图示坐标系 链条质心的坐标yc是变化的
y F
mi yi λy y λ(l y) 0
yc i
mi
2
λl
i
y2
2l
y c
yC o
竖直方向作用于链条的合外力为 F yg
第三章 动量守恒和能量守恒
17
物理学
第五版
i1
d 2 n r
= m dt 2 ( i1 miri / m)
=
m
d2 dt 2
r rC
r maC
n
m mi i1
第三章 动量守恒和能量守恒
3
物理学
第五版
3-9 质心 质心运动定律
➢对质量离散分布的物系：
n
mi xi
xC
i 1
m'
n
mi yi
yC
i 1
m'
n
mizi
zC
i 1
m'
➢对质量连续分布的物体：
3-9 质心 质心运动定律
由质心运动定律有
F
yg
l
d2 yC dt 2
而
d2 yc dt 2
1 l
(
dy dt
)2
y
d2 dt
y
2
考虑到
dy dt
v , d2 dt
y
2
dv dt
0
y F
y c
yC o
得到
F
yg
l
d2 yC dt 2
l v2
l
F yg v2
第三章 动量守恒和能量守恒
物理学
第五版
3-9 质心 质心运动定律
二 质心运动定律
rC
n miri
i 1
m'
z
y m2 ri mi
r2
rC
c r1
m1
o
x
mrC n miri i 1
第三章 动量守恒和能量守恒
11
物理学
第五版
3-9 质心 质心运动定律
m'rC n miri
i 1
上式两m边'对dr时C 间
dt
itn1求m一i d阶drti导数，得