初中数学相似三角形经典练习难题易错题附详解电子教案

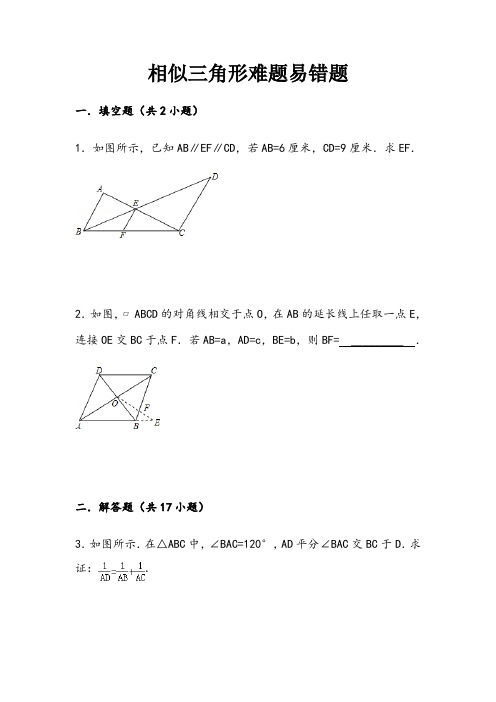
初中数学相似三角形经典练习难题易错题 )解详附(相似三角形难题易错题一．填空题（共2小题）1．如图所示，已知AB∥EF∥CD，若AB=6厘米，CD=9厘米．求EF．于BC，连接OE交OABCD的对角线相交于点，在AB的延长线上任取一点E2．如图，?．_________，AD=cBE=b，则BF=点F．若AB=a，小题）二．解答题（共17．求证：BC于DBACBAC=120°，AD平分∠交中，3．如图所示．在△ABC∠．，交FCD于OEADEOBDACABCD．如图所示，4?中，与交于点，为延长线上一点，．．求证：G于AB延长线交EO．．求证：F、E、、BC、CAAB（或它们的延长线）于点D5．一条直线截△ABC的边．和ABHI分别平行于，BCPP为△ABC内一点，过点作线段DE，FG，6．如图所示．．求d．AB=510，且DE=FG=HI=d，，BC=450，CA=425CA，ABOACBC∥，BD，交于O点，过的直线分别交ADABCD7．如图所示．梯形中，．EF厘米．求BC=20厘米，AD=12．BC∥EF，且F，E于CD．8．已知：P为?ABCD边BC上任意一点，DP交AB的延长线于Q点，求证：．．若OMN与对角线BD交于，ABCD中，AD∥BCMN∥BC，且9．如图所示，梯形．BC=BO=b，求MNAD=DO=a，（如图所示）．BCIH，分别平行于AB，，CAFGDEPABC为．10P△内一点，过点作，．求证：11．如图所示．在梯形ABCD中，AB∥CD，AB＜CD．一条直线交BA延长线于E，交DC延长线于J，交AD于F，交BD于G，交AC于H，交BC于I．已知EF=FG=GH=HI=IJ，求DC：AB．F，．并延长分别交对边于D，EBP．已知12P为△ABC内任意一点，连AP，，CP三者中，至少有一个不大于（2）求证：（1），也至少有一个不少于2．2的延长线AE，AE是BC边上的中线，平分∠BACBD⊥AMABC．如图所示．在13△中，ABEFFAMD于，且交延长线于．求证：∥．14．如图所示．P，Q分别是正方形ABCD的边AB，BC上的点，且BP=BQ，BH⊥PC于H．求证：QH⊥DH．．求QM⊥AC上，且PM的中点，P、Q分别在AB、是15．已知MRt△ABC中斜边BC222 +QC 证：PQ．=PB平分CF平分∠CAB，DACB=90°，CD⊥AB于，AE∠．如图所示．在16△ABC中，．EF∥BC ∠BCD．求证：，∠CB=CPA∠BPC=∠．若2∠∠A+APB=，满足内有一点△17．如图所示．在ABCP∠2 =PA?PC．求证：PB ．）PBC△∽PAB△（提示：设法证明18．已知：如图，△ABC为等腰直角三角形，D是直角边BC的中点，E在AB上，且AE：EB=2：1．求证：CE⊥AD．边上的中线，连接ACBE是N是边BC的三等分点，19．如图所示，△ABC中，M、GE的值．BF：FG：AN，分别交BE于F、G，求AM、111=+4．求证B20.在△ABC中，∠A∶∠∶∠C=1∶2∶BCABACb1a+b1a+b11===+，提示：要证明如几何题的常用方法：①比例法：将原等式变为或caababccc+所在三角形相似的三角形。

②通分法：将原等式变为b为边且与a、ca+b故构造成以、acnmcc==，利用相关定理将两个个比通分即：=1，则原式成立。

+，且，mnd= dbbba初中相似三角形难题易错题2013参考答案与解析2小题）一．填空题（共EF．CD，若AB=6厘米，CD=9厘米．求1．如图所示，已知AB∥EF∥考平行线分线段成比例．：点计算题．专题：，利用平行线分线段成比例AB∥EF∥CD由于BC是△ABC与△DBC分的公共边，且．的定理，可求EF析：，EF∥AB解：在解△ABC中，因为，CB①EF所以：AB=CF答：：②，CB同样，在△DBC中有EF：CD=BF：．CB=1AB+EF：CD=CF：CB+BF：③EF①+②得：得EF=x厘米，又已知AB=6厘米，CD=9厘米，代入③设6+xx：：9=1，x=．解得厘米．EF=故点考查了平行线分线段成比例定理，熟练运用等式的性质进行计算．评：于交的对角线相交于点ABCDO，在AB的延长线上任取一点E，连接OEBC2．如图，?．，则BF=AD=cF点．若AB=a，，BE=b相似三角形的判定与性质；平行四边形的性质．考：点计算题．专题：首先作辅助线：取AB分的中点M，连接OM，由平行四边形的性质与三角形中位线的性质，即可求得：析：△EFB∽△EOM与OM的值，利用相似三角形的对应边成比例的值．BF即可求得．解解：取AB的中点M，连接OM，∵四边形ABCD是平行四边形，答：∴AD∥BC，OB=OD，，，OM=AD=c∴OM∥AD∥BC ，EFB∽△EOM∴△∴，，BE=b，∵AB=a，AD=c，∴ME=MB+BE=AB+BE=a+b∴，∴BF=．故答案为：．此题考查了平行四边形的性质、相似三角形的判定与性质等知识．解此题的关键是点评：准确作出辅助线，合理应用数形结合思想解题．二．解答题（共17小题）．求证：于D中，ABC∠BAC=120°，AD平分∠BAC交BC3．如图所示．在△．考相似三角形的判定与性质；等边三角形的判定．点：专证明题．题：），所以（∠分BAC=120°AC过D引DE∥AB，交于E，因为AD平分为正三角形，从而△ADEE°∠BAD=∠EAD=60．若引DE∥AB，交AC于，则析：，可实现求证的目标．CEDAE=DE=AD，利用△∽△CAB D解证明：过引DE∥AB，交AC于．E °，BAC=120∠AD是BAC的平分线，∠∵答：．∠BAD=∠CAD=60°∴∠，EDA=60°又∠BAD= ADE是正三角形，所以∴△．∴EA=ED=AD①由于，CAB ∽△DE∥AB，所以CED△．=∴=②=1﹣得②，①由，﹣=1．+=．从而本题考查了相似三角形对应边比值相等的性质，考查了相似三角形的判定，考查了点是解题的∽△CAB评：等边三角形的判定，考查了角平分线的性质，本题中求证△CED 关键．，于F为AD延长线上一点，OE交CD交于4．如图所示，?ABCD中，AC与BDO点，E．EO延长线交AB于G．求证：考相似三角形的判定与性质；平行四边形的性质．：点证明题．专：题到一个三角形中来求“集中”应利用平行四边形的性质，通过添加辅助线使各线段分析：证．AIHB解．证明：延长CB与EG，其延长线交于H，如虚线所示，构造平行四边形答：，∥在△EIH中，由于DFIH ．∴=∴，∵IH=AB=，﹣===1+ 从而，．=①﹣中，在△OED与△OBH ，OHB，OD=OB∠BOH∠DOE=∠，∠OED= ）．（OED∴△≌△OBHAAS 从而DE=BH=AI，．②∴=1得②=2﹣．由①，此题考查学生对相似三角形的判定与性质和平行四边形的性质的理解和掌握，此题点，如虚线所示，构造平行四边形，其延长线交于HEGCB 评：的关键是延长与AIHB．这是此题的突破点，也是一个难点，因此属于一道难题．．F、E、D（或它们的延长线）于点AB、CA、BC的边ABC△．一条直线截5．．求证：考三角形的面积．点：专证明题．：题，并把线段之比转化为两三角形面积之比，然后约分即可求证．分连接BE、AD 析：BE证明：如图，连接、解AD，答：，=∵△BDE与△DCE等高，∴=∴，与∵△DCE△ADE等高，∴=，与∵△ADF△BDF等高，，=∴与∵△AEF△BEF等高，=，∴．??=1∴??=，并把此题考查学生对三角形面积的理解和掌握，解答此题的关键是连接点BEAD、线段之比转化为两三角形面积之比．评：和HIFGDEPABC为．如图所示．6P△内一点，过点作线段，，分别平行于BCAB，，BC=450AB=510，DE=FG=HI=dCA，且，．dCA=425．求考相似三角形的判定与性质；平行四边形的判定与性质．点：计算题．专题：由FG∥BC，HI∥CA，ED∥AB，易证四边形AIPE、四边形分BDPF、四边形CGPH均是平行四边形，利用平行线分线段成比例定理的推论可得析：，先计算式子右，再结合=AFG∽△ABC，于是=，=∽△IHB△，++，再把DE=FG=HI=d=2边的和，易求++=，从而有=2 CA=425代入此式，解即可．AB=510，BC=450，，解解：∵FG∥BC，HI∥CA，ED∥AB ∴四边形AIPE、四边形BDPF、四边形CGPH 均是平行四边形，答：∴△IHB∽△ABC，AFG∽△，∴=，=+，∴+= DE=PE+PD=AI+FB，又∵AF=AI+FI，，BI=IF+FB （∴DE+AF+BI=2×AI+IF+FB）=2AB，+∴+=，=2 ，CA=425∵DE=FG=HI=d，AB=510，BC=450，=+，+=2∴+++，+=2∴解得d=306．本题考查了相似三角形的判定和性质、平行线分线段成比例定理的推论、平行四边点形的判定和性质．评：，点，过，BDAC交于OO的直线分别交AB，∥．如图所示．梯形7ABCD中，ADBC 厘米．求厘米，∥，且，CD于EFEFBC．AD=12BC=20EF．考平行线分线段成比例．：点分的关系，进而即可=由平行线的性质可得=AD与OF，BC 与OE，得出= 析：的长．EF求解BC∥∵解：解AD，BC∥，EF答：，===∴．==，==，又AD=OF=，∴OE=BC=，∴．EF=OE+OF=15 点本题主要考查了平行线的性质问题，能够利用其性质求解一些简单的计算问题．评：点，求证：Q交DPAB的延长线于P8．已知：为?ABCD边BC上任意一点，．相似三角形的判定与性质．考：点专证明题．题：分，进而求解即，再由平行线的性质可得=由于AB=CD，所以将转化为析：可．CD，，解证明：在平行四边形ABCD中，则AD∥BCAB∥答：=∴==1．﹣∴﹣==本题主要考查了平行四边形的性质以及相似三角形的判定及性质问题，能够熟练掌点评：握．．若交于，且BCMN与对角线BDO∥，中，．如图所示，梯形9ABCDAD∥BCMN ，求MN．，AD=DO=aBC=BO=b相似三角形的判定与性质；梯形．考：点专计算题．题：的分由平行线分线段成比例可得对应线段的比，再由题中已知条件即可求解线段MN 析：长．解，=OM=，即=中，ABD△在∴，BC∥MN∵解：答：，同理ON==．∴MN=OM+ON= 点本题主要考查了平行线分线段成比例的性质问题，能够熟练掌握．评：，CA（如图所示）．FG，IH分别平行于AB，BC10．P为△ABC内一点，过P点作DE，．求证：考平行线分线段成比例．点：专证明题．题：分，同理得=△（1）由平行线可得△PIF∽CAB，得出对应线段成比例，即= 析：==，即可证明结论；出）证明方法与（1）相同．（2 FGAC，∥BC，DE解证明：（1）∵∥AB，IH∥∽△CAB，可得∴△PIF 答：∴==，=同理，=++=1=．++====，）可得）仿（（21，=++=1．=+∴+本题主要考查了平行线的性质问题，能够利用其性质通过线段之间的转化，证明一点些简单的结论．评：，交中，．如图所示．在梯形11ABCDAB．一条直线交CDBAE延长线于＜AB，∥CD．已知AC，交于BD，交于AD，交延长线于DCJFGBC，交H于I于．AB：DC，求EF=FG=GH=HI=IJ．相似三角形的判定与性质；梯形．考点：专计算题．题：、分ABEF=FG=CH=HI=IJ，可分别求出线段由平行线可得对应线段成比例，又由已知析：的关系，进而可求解结论．、CJCD与AE ，，解EF=FG=CH=HI=IJ∵AB∥CD解：答：∴=，=，=∴，===，又∴DJ=4AE=，AB=解得AE，CJ，又AE=，EB=4CJ，∴AB=CJ，== CD=5CJ，∴AB：CD=．5=1：2：本题主要考查了相似三角形对应边成比例或平行线分线段成比例的性质问题，应熟点练掌握．评：并延长分别交对边于，BPCPDF．，，E，内任意一点，连△P12．已知为ABCAP三者中，至少有一个不大于）求证：（1 （2）22，也至少有一个不少于．平行线分线段成比例．考：点专证明题．：题．分（1）第一问可由三角形的面积入手，即△PBC+△PAC+△PAB=△ABC，通过化简析：可得面积与线段之间的关系，进而即可求解．，即≤2）由（1）中得出，则其中至少有一个不大于，可设（，进而通过证明即可得出结论．3AD ≤PD，而AD=AP+PD ）由面积概念得：解解：（1 +S+S=S①答：S ABCPAB△PBC△PAC△△整理等式得：，②++=1 由面积概念得：，==，∴，==即③同理得：④==⑤得：②把式③、④、⑤、代入式；）由（2，知，中至少有一个不大于，，．3AD≤PD即不妨设≤而AD=AP+PD，≥2PD，AP∴∴不小于2，，即≥2 2同理可证三式中至少有一个不大于．本题主要考查了三角形的面积比与对应边的比值之间的关系，能够熟练掌握其内在点联系，并能求解一些比较复杂的问题．评：的延长线BD，⊥AEBAC∠平分边上的中线，BC是中，ABC△13．如图所示．在AMAE ．AB ∥EF．求证：F延长线于AM，且交D于相似三角形的判定与性质；角平分线的性质．考：点证明题．专：题利用角平分线分三角形中线段成比例的性质，构造三角形，设法证明分AB∥，从而EFMEF∽△MAB△析：H．解，交的延长线于GAM的延长线于证明：过B作BG∥AC 交AE BAC的平分线，∵AE是∠答：CAE．∴∠BAE=∠AC，∵BG∥G，∴∠CAE=∠G，∠BAE=∠∴AG，．又BD⊥∴BA=BG HBF，∠ABF=∠∴△ABG是等腰三角形，BH的距离相等，到AB 与∴FS∴，=AB：BH：S HBF△ABF△S∵，=AF：FH：S HBFABF△△．BH=AF：FH∴AB：，是平行四边形，从而BH=ACBH∥AC，易知ABHC又M是BC边的中点，且．：FH∴AB：AC=AF BAC 的平分线，∠是△ABC中∵AE EC，即AF：FH=BE：∴AB：AC=BE：EC，ME））：（BM﹣AM ﹣MF）=（BM+ME（AM+MF）：（）．AM=MH及BM=MC（这是因为ABHC是平行四边形，所以．MB=FM：ME由合分比定理，上式变为AM：，∠AMB△MAB中，∠EMF=在△MEF与MAB∽△△∴MEF AB．，所以EF∥∠∴∠ABM=FEM此题考查学生对相似三角形的判定与性质和角平分线的理解和掌握，证明此题的关点．和利用合分比定的延长线于AMH交AE的延长线于G，交∥键是过评：B引BGAC 理．于PC，BP=BQBH⊥上的点，且，的边分别是正方形，．如图所示．14PQABCDABBC ．DH⊥QH．求证：H．考相似三角形的判定与性质；直角三角形的性质；正方形的性质．点：专证明题．题：是直角三角形，且△PBC∠CHD．由于DH要证QH⊥分，只要证明∠BHQ= DHC相似．BHQ与△∠HBQ=∠HCD，因而△析：∠BH⊥PC，熟知∠PBH=PCB，从而，BH⊥PC解Rt证明：在△PBC 中，∵，∠PHB=90°∴∠PBC= 答：．PBH=∠PCB∴∠，Rt△BHC显然，Rt△PBC∽，∴= ，由已知，BP=BQ，BC=DC，∴=∴．= ，ABC=∠BCD=90°，∠PBH=∠PCB∵∠∴∠HBQ=∠HCD．HBQ=∠HCD，=在△HBQ与△HCD中，∵，∠△HCD，∴△HBQ∽DHC，∴∠BHQ=∠．BHQ+∠∠QHC=∠DHC+∠QHC 又∵∠BHQ+∠QHC=90°，，QHC+DHC=90°∴∠QHD=∠．⊥即DHHQ本题考查了相似三角形的判定与性质及正方形的性质，难度适中，关键是掌握相似点评：三角形的判定方法．．求⊥上，且、ABACPMQM分别在、的中点，中斜边△是．已知15MRtABCBCPQ222证：．=PBPQ+QC考直角三角形斜边上的中线；勾股定理．：点．专证明题．题：分以M点为中心，△MCQ顺时针旋转180°至△MBN，根据旋转的旋转可得△MCQ与△MBN 全等，根据全等三角形对应边相等可得BN=QC，MN=MQ，全等三角形对析：应角相等可得，∠MBN=∠C，再连接PN，可以证明PM垂直平分NQ，所以PN=PQ，然后证明△PBN为直角三角形，根据勾股定理即可证明．解证明：如图，以M点为中心，△MCQ顺时针旋转180°至△MBN，∴△MCQ≌△MBN，答：∴BN=QC，MN=MQ，∠MBN=∠C，连接PN，∵PM⊥QM，∴PM垂直平分NQ，∴PN=PQ，∵△ABC是直角三角形，BC是斜边，∴∠ABC+∠C=90°，∴∠ABC+∠MBN=90°，即△PBN是直角三角形，222，+BN=PB 根据勾股定理可得，PN222PQ∴．+QC=PB点本题考查了直角三角形的旋转，旋转变换的旋转，勾股定理的应用，利用旋转变换评：把构造出以PQ、PB、QC转化为同一个直角三角形的三边是证明的关键．16．如图所示．在△ABC中，∠ACB=90°，CD⊥AB于D，AE平分∠CAB，CF平分∠BCD．求证：EF∥BC．相似三角形的判定与性质；平行线的判定．考：点证明题．专：题，进而得出EC=EFACF是等腰三角形，所以由题中条件可得分AC=AF，即△EFC∠，结论得证．∠ECF= 析：证明：解AB，°，CD⊥∵∠ACB=90 答：BCD，CF平分∠BCD，又AE平分∠CAB，∠∴CAD=∠，B=∠ACD∠BCF=∠CAE，∠∴，∠AFC∠BCF，即∠ACF=ECF=∴∠B+∠∠B+ CE=EF，∴AC=AF，∴CAB又AE平分∠，EFC，∠ECF=∠即．EF∥BC∴∠EFC=∠BCF，即点本题主要考查了等腰三角形的性质以及平行线的判定问题，应熟练掌握．评：，CA+∠B=∠∠2CPABPC=APB=，满足内有一点△17．如图所示．在ABCP∠∠∠．若2．PC?=PAPB 求证：（提示：设法证明△PAB∽△PBC．）考相似三角形的判定与性质．点：专证明题．：题，根据PBCPAB∽△∠CBP=∠分BAP两个对应角相等证明△APC=120用∠APB=∠°，相似比可证到结论．析：解，∠APB=120°证明：∵，∠BAP=60°∴∠ABP+ 答：，ABC=60°∵又∠，CBP=60°∴∠ABP+∠，∠BAP∴∠CBP= ，APC=120°∵∠APB=∠又BCP，ABP∴△∽△∴=，2BP∴=PA?PC．本题考查相似三角形的判定和性质定理，先用判定定理证明相似，然后根据相似对点评：应边成比例证明结论．上，且在AB是直角边ABC为等腰直角三角形，DBC的中点，E18．已知：如图，△AD．：1．求证：CE⊥：AEEB=2考相似三角形的判定与性质；全等三角形的判定与性质；等腰直角三角形．点：专证明题．题：，根据平行线的性质∥BFCE作BC的垂线交的延长线于点F分，从而可推出ACB过，根据相似三角形的对应边对应成BFE可得到两组对应角相等从而可判定△析：ACE∽△，由全等△ACD ≌△CBF判定，进而得到比例可得到AC=2BFCD=BF，再利用HL 三角形的性质得其对应角相等，再根据等角的性质不难证得结论．解，（CE的延长线于点F1分）的垂线交作证明：过BBC答：．°ACB=90∠FBC=∠∴．∴AC∥BF．3分）∽△BFE．（∴△ACE．∴分）∴AC=2BF．（4∵AC=BC，．（5分）∴CD=BF △CBF中在△ACD和，6分）△ACD≌△CBF．（∴．∴∠1=∠2 ．3=∠1+∠3=90°∴∠2+∠．∴∠4=90°分）CE⊥AD．（7∴此题主要考查学生对全等三角形的判定及性质及相似三角形的判定及性质的综合运点评：用．边上的中的三等分点，BE是ACM19．（巧解妙解）如图所示，△ABC中，、N是边BC 的值．：GE于BEF、G，求BF：FG线，连接AM、AN，分别交考平行线分线段成比例．：点专应用题．题：，由平行线的性质，GE=c分BF=a，FG=b作已知图形的中心对称图形，如图所示，设之间的关系，即可得出其比值．b与c分别求出a，析：解解：如答图所示．GE=c．，作已知图形的中心对称图形，以E为对称中心．令BF=a，FG=b 答：AN∥∥M′CAM，N′C∵2：（2b+2c）=BM：MC=1：∴a1 ：2c=BNNC=2：，而（∴a=b+ca+b）：∴a+b=4c，所以a=c．b=c，：：：：∴BFFGGE=532．本题主要考查了平行线分线段成比例的性质问题，要求线段的比，通过作平行线构点造比例线段是一种重要的方法．评：111=+∶∠C=1∶2∶4．求证20.在△ABC中，∠A∶∠B BCABACAC1AB+AC11AB+AC1===+，为此若能设法利用长将原等式变为提示：要证明如或BCBCACBCAB?ACABAB条线段，构造一对相似三角形，问题可能解4＋AC这，BC，CA 及AB度分别为AB为ABC中，已含上述4条线段中的三条，因此，不妨以原三角形决．注意到，原△ABC 相似，期望能解决问题．基础添加辅助线，构造一个三角形，使它与△ABC，连结AE=ACE，使＋AC)，又延长BC至证延长AB至D，使BD=AC(此时，AD=AB ．∽△ABCED．下面证明，△ADE =180°．B+∠C=7αB=2α，∠C=4α，则:∠A+∠α，∠设∠A= 3α，-4α＝是等腰三角形ACE的外角，所以∠ACE=180°由作图知，∠ACB α．从而α=-3α=7α6-所以∠CAE=180°3α-．＝BEEAB=2α＝∠EBA，AE∠∵ AE=BD ，AE=AC，∴ BDE是等腰三角形， BE=BD，△∴，BED＝α＝∠CABD∠＝∠∴，△ABC∽△DAE ABABAB+ACAD==，即∴BCBCAEAC111=+∴BCABAC。