第八讲 矩阵对策概要
合集下载
矩阵对策
i j
max aij 对局中人 II，求 min j i
若 max min aij min max aij a i
i j j i
*
j*
策略 i ， j 为I，II 的最优策略
这一对策 的值为 V a i
j
几个术语
局势 对策的解
最优纯策略
对策的值 鞍点 e. g. 2 （续）求解取暖购煤问题
两人零和对策
对抗对策（antagonistic game）
矩阵对策（matrix game）
二．实际问题中的矩阵对策模型
e. g. 1 扩大销售模型
公司I，公司II 的同一产品竞争市场份额，各有三种办 法扩大销售额（由于市场需求一定，一家扩大，意味 另一家缩减），三种方法比如：①改进包装；②广告； ③降价．公司I 的三种策略表示为 1 , 2 , 3 ，公司II 的三种策略为 1 , 2 , 3 ，在不同策略下销售量增长百 分比不同．下表中表示公司I 的增长率，而公司II 的即 为相反数
e. g. 6 （续）求最优策略与值
作业
P206,
Ex 6. 3：1，2
1=急转 2 =不转
1
给急转弯者以1 分，不转弯者以5 分 局中人II 局中人I 局 =急转 1 中 人 2=不转 II
3 5
1 =急转 2=不转
1 0
0
II 的支付矩阵
此对策中，若两者都想得5 分，则发生惨祸， 全部玩完．实际上两人最好的做法是同时停车 或转弯，各得3 分． Remark 此例已不是 2 人有限零和对策问题（因为在 每个对局中，双方支付的代数和不为零）， 称为双矩阵对策．
e. g. 2 取暖购煤问题 某公司在秋末需决定冬季取暖用煤问题．根据气温 情况，用煤量和煤价均不同，可用下表表示： 正常气温 较冷气温 较暖气温 需求量15 吨 需求量20 吨 需求量10 吨 200元／吨 250元／吨 150元／吨
max aij 对局中人 II，求 min j i
若 max min aij min max aij a i
i j j i
*
j*
策略 i ， j 为I，II 的最优策略
这一对策 的值为 V a i
j
几个术语
局势 对策的解
最优纯策略
对策的值 鞍点 e. g. 2 （续）求解取暖购煤问题
两人零和对策
对抗对策（antagonistic game）
矩阵对策（matrix game）
二．实际问题中的矩阵对策模型
e. g. 1 扩大销售模型
公司I，公司II 的同一产品竞争市场份额，各有三种办 法扩大销售额（由于市场需求一定，一家扩大，意味 另一家缩减），三种方法比如：①改进包装；②广告； ③降价．公司I 的三种策略表示为 1 , 2 , 3 ，公司II 的三种策略为 1 , 2 , 3 ，在不同策略下销售量增长百 分比不同．下表中表示公司I 的增长率，而公司II 的即 为相反数
e. g. 6 （续）求最优策略与值
作业
P206,
Ex 6. 3：1，2
1=急转 2 =不转
1
给急转弯者以1 分，不转弯者以5 分 局中人II 局中人I 局 =急转 1 中 人 2=不转 II
3 5
1 =急转 2=不转
1 0
0
II 的支付矩阵
此对策中，若两者都想得5 分，则发生惨祸， 全部玩完．实际上两人最好的做法是同时停车 或转弯，各得3 分． Remark 此例已不是 2 人有限零和对策问题（因为在 每个对局中，双方支付的代数和不为零）， 称为双矩阵对策．
e. g. 2 取暖购煤问题 某公司在秋末需决定冬季取暖用煤问题．根据气温 情况，用煤量和煤价均不同，可用下表表示： 正常气温 较冷气温 较暖气温 需求量15 吨 需求量20 吨 需求量10 吨 200元／吨 250元／吨 150元／吨
矩阵对策的最优纯策略
,m α，
,
,n β；则分别为
},m α和},n β。
当局中人Ⅰ选定纯策略i α和局中人Ⅱ选定纯策略后，就形成了一个纯局)j ，这样的纯局势共有m n ⨯个。
对任一纯局势赢得值为ij a ，称
12122
212n n m m mn a a a a a ⎤⎥⎥⎥⎥⎦
为局中人Ⅰ的赢得矩阵。
局中人Ⅱ的赢得矩阵就是当局中人Ⅰ，Ⅱ的策略集12,S S 及局中人Ⅰ的赢得矩阵对策也就给定了，记为{}12,,G S S A =。
在齐王赛马的例子中，齐王的赢得矩阵
},
,m α，
},n β，max ）
成立，记其值为）成立的纯局势()
,i j αβ**
在纯策略意义下的解（或鞍点）
},m α，},n S β，
1,2,
,,m x ∑1,2,
,,n y ∑分别称为局中人Ⅰ和Ⅱ的混合策略集分别称为局中人Ⅰ和Ⅱ的混合策略（或策略），对
),m x 可设想成当两个局中人多次重复进行对策
12,,
,m ααα的频率。
若只进行一次时对策，混合
对策可设想成局中人Ⅰ对各纯策略的偏爱程度。
求解混合策略的问题有图解法，迭代法、线性方程组法和线性规划法，在。
对策问题的提出对策论模型矩阵对策的解法◎知识归纳
现代博弈论起源于19世纪末20世纪初，二战后发展成为一门完整而丰富的理论 学科。学术界一般将其发展历程分为以下几个阶段：
（1）萌芽阶段 从19世纪末到20世纪30年代可以说是博弈论的萌芽期，表现为学者们对社会经
济理论和现实的一些思考，研究者以数学家为主。 （2）产生阶段 20世纪四五十年代可说是博弈论的体系建立时期。1944年诺依曼和摩根斯坦的
（2）物流仓储优化策略 【例8.2】一仓储供应中心为其下游的一家生产企业供应某种原料。生产企业根 据产品订单情况对原料的需求进行分析，分别有淡季、旺季和正常三种情况，在正 常情况下需要原料15吨，在淡季和旺季情况下分别需要原料10吨和20吨；而原料的 价格与原料市场的需求有关，在淡季、正常、旺季三种情况下，每吨原料的价格分 别为100元、150元和200元，已知此时每吨原料的价格为100元。问在生产企业对原 料的需求没有确定预知的条件下，此时应采购多少吨原料才能使仓储供应中心的总 成本最少（不计存储费用）？ 这个问题可看成一个博弈问题。即仓储供应中心针对可能出现的三种不同的原
巨著《博弈论和经济行为》的出版，标志着博弈论作为一门学科的建立，也被视为 数理经济学学科建立的里程碑。巨著出版前后的若干年中，合作博弈理论的研究得 到了迅速的发展，提出了各种概念，并在20世纪50年代达到了研究的高峰。不久， 库克于1950年定义了“囚徒的困境”，纳什在1950年和1951年发表了两篇关于非合 作博弈的重要文章，这两位学者的研究工作，特别是纳什的研究工作奠定了非合作 博弈论的基础，所提出的纳什均衡概念，在非合作博弈论中起着核心作用。
8 对策论
8.1 对策问题的提出 8.2 对策论模型 8.3 矩阵对策的解法 ◎ 知识归纳 ◎ 习题与思考题
8.1 对策问题的提出
（1）萌芽阶段 从19世纪末到20世纪30年代可以说是博弈论的萌芽期，表现为学者们对社会经
济理论和现实的一些思考，研究者以数学家为主。 （2）产生阶段 20世纪四五十年代可说是博弈论的体系建立时期。1944年诺依曼和摩根斯坦的
（2）物流仓储优化策略 【例8.2】一仓储供应中心为其下游的一家生产企业供应某种原料。生产企业根 据产品订单情况对原料的需求进行分析，分别有淡季、旺季和正常三种情况，在正 常情况下需要原料15吨，在淡季和旺季情况下分别需要原料10吨和20吨；而原料的 价格与原料市场的需求有关，在淡季、正常、旺季三种情况下，每吨原料的价格分 别为100元、150元和200元，已知此时每吨原料的价格为100元。问在生产企业对原 料的需求没有确定预知的条件下，此时应采购多少吨原料才能使仓储供应中心的总 成本最少（不计存储费用）？ 这个问题可看成一个博弈问题。即仓储供应中心针对可能出现的三种不同的原
巨著《博弈论和经济行为》的出版，标志着博弈论作为一门学科的建立，也被视为 数理经济学学科建立的里程碑。巨著出版前后的若干年中，合作博弈理论的研究得 到了迅速的发展，提出了各种概念，并在20世纪50年代达到了研究的高峰。不久， 库克于1950年定义了“囚徒的困境”，纳什在1950年和1951年发表了两篇关于非合 作博弈的重要文章，这两位学者的研究工作，特别是纳什的研究工作奠定了非合作 博弈论的基础，所提出的纳什均衡概念，在非合作博弈论中起着核心作用。
8 对策论
8.1 对策问题的提出 8.2 对策论模型 8.3 矩阵对策的解法 ◎ 知识归纳 ◎ 习题与思考题
8.1 对策问题的提出
对策问题的提出对策论模型矩阵对策的解法◎知识归纳
8.2.1 对策模型的基本要素
（1）局中人 在一个对策行为中，有权决定自己行动方案的对策参加者被称为局中人。局中 人除了理解为个人外还可以理解为集体，如球队、交战国、企业公司等，也可以把大 自然理解为局中人（因为人类经常处于和大自然斗争的状态中）；另外，还假定局中 人都是聪明的，有理智的和利己的。同时，为使所研究的问题更加清晰，把那些利益 完全一致的参加者们看做一个局中人，因为他们利害一致，必使他们齐心合力，相互 配合行动如一个人。例如，桥牌游戏中，东西双方利益一致，南北两方得失相当，所 以虽有四人参加，只能算有两个局中人。 一个对策中一般要求至少有两个局中人。每个局中人用i表示，局中人的集合用 字母I表示，则I＝｛1，2，…，n｝。我们称只有两个局中人的对策现象为“两人对 策”，如象棋、桥牌等，显然上述齐王赛马中局中人也是两人，即I＝｛1，2｝。而 多于两个局中人的对策称为“多人对策”。另外根据局中人之间是否允许进行合作， 还可有“结盟对策”和“不结盟对策”，或称为“合作博弈”和“非合作博弈”。
（2）物流仓储优化策略 【例8.2】一仓储供应中心为其下游的一家生产企业供应某种原料。生产企业根 据产品订单情况对原料的需求进行分析，分别有淡季、旺季和正常三种情况，在正 常情况下需要原料15吨，在淡季和旺季情况下分别需要原料10吨和20吨；而原料的 价格与原料市场的需求有关，在淡季、正常、旺季三种情况下，每吨原料的价格分 别为100元、150元和200元，已知此时每吨原料的价格为100元。问在生产企业对原 料的需求没有确定预知的条件下，此时应采购多少吨原料才能使仓储供应中心的总 成本最少（不计存储费用）？ 这个问题可看成一个博弈问题。即仓储供应中心针对可能出现的三种不同的原
8.1.2 对策论在现代物流管理中的运用
在现代物流管理实践中，决策者们为了谋求自身的不断发展，保持自身的竞争 优势，必须不断地审时度势、不停地进行选择和作出决定，以保证最大限度地降低 物流成本、提高物流效率及服务水平。他们的选择和决定会影响到竞争对手的决策 结果，同样竞争对手的选择和决定也直接影响着他们的决策结果。也就是说，决策 者在决策时必须要考虑到对手的策略，因此，博弈论的思想已完全融入到现代物流 管理的每一个环节中。博弈论在现代物流管理中的运用主要有物流项目投资、物流 市场竞争对策、物流服务价格策略、物流中心选址、物流运输规划、物流仓储优化 等内容。以下仅就本书涉及到的有关博弈论中矩阵对策的例子作简要介绍。
（1）局中人 在一个对策行为中，有权决定自己行动方案的对策参加者被称为局中人。局中 人除了理解为个人外还可以理解为集体，如球队、交战国、企业公司等，也可以把大 自然理解为局中人（因为人类经常处于和大自然斗争的状态中）；另外，还假定局中 人都是聪明的，有理智的和利己的。同时，为使所研究的问题更加清晰，把那些利益 完全一致的参加者们看做一个局中人，因为他们利害一致，必使他们齐心合力，相互 配合行动如一个人。例如，桥牌游戏中，东西双方利益一致，南北两方得失相当，所 以虽有四人参加，只能算有两个局中人。 一个对策中一般要求至少有两个局中人。每个局中人用i表示，局中人的集合用 字母I表示，则I＝｛1，2，…，n｝。我们称只有两个局中人的对策现象为“两人对 策”，如象棋、桥牌等，显然上述齐王赛马中局中人也是两人，即I＝｛1，2｝。而 多于两个局中人的对策称为“多人对策”。另外根据局中人之间是否允许进行合作， 还可有“结盟对策”和“不结盟对策”，或称为“合作博弈”和“非合作博弈”。
（2）物流仓储优化策略 【例8.2】一仓储供应中心为其下游的一家生产企业供应某种原料。生产企业根 据产品订单情况对原料的需求进行分析，分别有淡季、旺季和正常三种情况，在正 常情况下需要原料15吨，在淡季和旺季情况下分别需要原料10吨和20吨；而原料的 价格与原料市场的需求有关，在淡季、正常、旺季三种情况下，每吨原料的价格分 别为100元、150元和200元，已知此时每吨原料的价格为100元。问在生产企业对原 料的需求没有确定预知的条件下，此时应采购多少吨原料才能使仓储供应中心的总 成本最少（不计存储费用）？ 这个问题可看成一个博弈问题。即仓储供应中心针对可能出现的三种不同的原
8.1.2 对策论在现代物流管理中的运用
在现代物流管理实践中，决策者们为了谋求自身的不断发展，保持自身的竞争 优势，必须不断地审时度势、不停地进行选择和作出决定，以保证最大限度地降低 物流成本、提高物流效率及服务水平。他们的选择和决定会影响到竞争对手的决策 结果，同样竞争对手的选择和决定也直接影响着他们的决策结果。也就是说，决策 者在决策时必须要考虑到对手的策略，因此，博弈论的思想已完全融入到现代物流 管理的每一个环节中。博弈论在现代物流管理中的运用主要有物流项目投资、物流 市场竞争对策、物流服务价格策略、物流中心选址、物流运输规划、物流仓储优化 等内容。以下仅就本书涉及到的有关博弈论中矩阵对策的例子作简要介绍。
矩阵对策问题及其解法
矩阵对策问题及其解法背景对策论研究具有竞争性质的现象。
有权决定⾃⾝⾏为的对策参加者称为局中⼈，所有局中⼈构成集合I，在⼀局对策中可供剧中⼈选择的⼀个实际可⾏的完整的⾏动⽅案成为策略，对于任意剧中⼈i∈I，都有⾃⼰的策略集S i。
⼀局对策中由各剧中⼈选定的策略构成的策略组称为局势s=(s1,...,s n)，⽽全体局势集合S=S1×...×S n。
局势决定了对策的结果，对局势s∈S，局中⼈i可以得到收益H i(s)，也称为局中⼈i的赢得函数。
矩阵对策即⼆⼈有限零和对策，是⼀类较为简单的对策模型。
矩阵对策基础我们假设，局中⼈ I 有纯策略α1,...,αm，局中⼈ II 有纯策略β1,...,βn，⼆者各选择⼀个纯策略则构成m×n个纯局势 (αi,βj)，将 (αi,βj)下 I 的赢得值记为a i,j，设矩阵A=[a i,j]，称为 I 的赢得矩阵或 II 的⽀付矩阵。
局中⼈ II 的赢得矩阵就是 −A T。
最优纯策略若纯局势 (a i∗,b j∗) 满⾜max i minj a i,j=minjmaxi a i,j=a i∗,j∗则称为矩阵对策 {S1,S2;A} 的最优纯策略。
显然，最有纯策略在赢得矩阵中对应的元素⼀定满⾜，其是所在⾏的最⼩元素，也是所在列的最⼤元素，即矩阵的鞍点。
混合策略当纯策略不存在时，我们希望给出⼀个选取不同策略的概率分布。
我们记 I,II 的概率分布向量分别为x,y，所有概率分布向量构成的集合为S1,S2，则局中⼈ I 的赢得函数为E(x,y)=x T Ay。
纯策略是混合策略的特例。
若混合局势 (x∗,y∗) 满⾜max x miny E(x,y)=minymaxx E(x,y)=E(x∗,y∗)则称为矩阵对策 {S1,S2;A} 的最优混合策略。
同样，混合策略 (x∗,y∗) 是最有混合策略的充要条件也是 (x∗,y∗) 是函数E(x,y) 的鞍点。
《运筹学》胡运权清华版-12-02矩阵对策基本定理
《运筹学》胡运权清华版 -12-02矩阵对策基本定理
运筹学中，矩阵对策是重要的决策分析工具。通过这个矩阵对策基本定理， 我们能够更好地理解并应用它在实际问题中。
Байду номын сангаас
矩阵对策的背景和定义
矩阵对策是一种决策分析方法，通过建立决策者与对手之间的策略矩阵，来 寻求最佳决策方案。它在解决有限决策问题中具有广泛的应用。
矩阵对策在实际问题中有广泛的应用，如在市场竞争、资源分配、风险管理 等领域。通过矩阵对策的应用，我们能够做出更明智和有效的决策。
矩阵对策在经济领域的案例分 析
矩阵对策在经济领域有着丰富的案例分析。通过深入研究这些案例，我们可 以更好地理解和应用矩阵对策的方法和技巧。
矩阵对策的优势和局限性
矩阵对策具有许多优势，如能够考虑多个因素和决策变量，以及能够量化和 比较各种策略。然而，它也存在一些局限性，如对信息和参数的需求较高。
矩阵对策的基本定理
矩阵对策的基本定理可以帮助我们确定最佳对策和策略组合。通过对矩阵对 策进行精确分析，我们能够得到优化的决策结果。
矩阵对策的解决方法
矩阵对策有多种解决方法，如通过优化算法和约束条件来求解最优解。同时， 可以利用计算机模拟和博弈理论等工具来辅助分析和决策。
矩阵对策在实际问题中的应用
结论和总结
矩阵对策是一种强大的决策分析工具，能够帮助我们做出更明智和优化的决 策。通过学习和应用矩阵对策，我们能够提高决策的准确性和效果，从而更 好地解决现实生活和工作中的问题。
运筹学中，矩阵对策是重要的决策分析工具。通过这个矩阵对策基本定理， 我们能够更好地理解并应用它在实际问题中。
Байду номын сангаас
矩阵对策的背景和定义
矩阵对策是一种决策分析方法，通过建立决策者与对手之间的策略矩阵，来 寻求最佳决策方案。它在解决有限决策问题中具有广泛的应用。
矩阵对策在实际问题中有广泛的应用，如在市场竞争、资源分配、风险管理 等领域。通过矩阵对策的应用，我们能够做出更明智和有效的决策。
矩阵对策在经济领域的案例分 析
矩阵对策在经济领域有着丰富的案例分析。通过深入研究这些案例，我们可 以更好地理解和应用矩阵对策的方法和技巧。
矩阵对策的优势和局限性
矩阵对策具有许多优势，如能够考虑多个因素和决策变量，以及能够量化和 比较各种策略。然而，它也存在一些局限性，如对信息和参数的需求较高。
矩阵对策的基本定理
矩阵对策的基本定理可以帮助我们确定最佳对策和策略组合。通过对矩阵对 策进行精确分析，我们能够得到优化的决策结果。
矩阵对策的解决方法
矩阵对策有多种解决方法，如通过优化算法和约束条件来求解最优解。同时， 可以利用计算机模拟和博弈理论等工具来辅助分析和决策。
矩阵对策在实际问题中的应用
结论和总结
矩阵对策是一种强大的决策分析工具，能够帮助我们做出更明智和优化的决 策。通过学习和应用矩阵对策，我们能够提高决策的准确性和效果，从而更 好地解决现实生活和工作中的问题。
矩阵对策
2 3 1 1 2 3 3 1 2
第三部分
二人有限非零和对策
一、非零和对策的一般表达 1、局中人集合：i = 1, 2 ,…，n 2、每个局中人的策略集：Si (i = 1,…,n) 3、每个局中人的赢得函数：ui (s1, …, s i , … sn)
对策的一般表达：G={S1, … Sn ; u1, … un }
1
1 3 1
1
1 1 3
4、优超原理
定义： 若A中第i, k 行有aij akj , j 1 n 称 i 优超于 k 。 记 i k 若A中第j, l列有aij ail , i 1 m 称 j 优超于l 记 j l 。
例： A
1 0 2 2 3 1
称为i的劣策略(Dominated strategy)。
' i
'' i
例： B1 Ⅰ A1 A2 1， 0 0， 3
Ⅱ
B2 1， 2 0， 1 B3 0， 1 2， 0
劣策略
可按如下思路寻找均衡解： 首先找出某个局中人的劣策略（如果存在），剔除该劣 策略，得到新的博弈；再剔除该新博弈中的某个中人的 劣策略。重复进行，直至只剩下唯一的策略组合为止， 这个剩下的策略称为重复剔除的占优均衡（Iterated dominance equilibrium）。
对策值V=1
(2) 多鞍点与无鞍点对策
例 设有一矩阵对策如下，求它的解。
6 1 A 8 0 5 4 5 2 6 2 7 6 5 - 1 5 2
局势 ( s1 , d 2 ) ( s1 , d 4 ) ( s3 , d 2 ) ( s3 , d 4 ) 均构成鞍点， 此对策有多个解。
矩阵对策纯策略意义下的解
此而来。通常把矩阵对策记为
G＝{Ⅰ,Ⅱ;S1,S2;A} 或
G＝{S1,S2;A}
例：G={S1,S2,A} S1={α1,α2,α3,α4} S2={β1,β2, β3}
-6 1 -8 A= 3 2 4
9 -1 -10 -3 0 6
对于G＝{S1,S2;A}， 若有等式
max min aij＝min max aij＝ai*j*
aij*≤ai*j*≤ai*j
例如
65 15 A= 8 5 02
65 2 -1 55 62
7.3 矩阵对策混合策略意义下的解
先看一个简单的例子: A= 3 6 54
一般地，设矩阵对策G＝{S1,S2;A}，其中 S1＝{α1,α2,…,αm}，S2＝{β1,β2,…,βn}， A＝（aij）m×n
为各局中人的最优混合策略。例
(2)线性规划法
当对策的值大于0时,可利用
线性规划法求解矩阵对策。构造
两个线性规划问题
min z＝∑xi i
∑i aijxi≥1 (j=1,2,…,n)
xi≥0
(i=1,2,…,m)
max w＝∑j yj
∑j aijyj≤1 (i=1,2,…,m)
பைடு நூலகம்
yj≥0
(j=1,2,…,n)
7.2 矩阵对策纯策略意义下的解
矩阵对策就是二人有限零和对策。设两个局中人为Ⅰ、
Ⅱ，它们各自的策略集为
S1＝{α1,α2,…,αm} S2＝{β1,β2,…,βn} 当局中人Ⅰ选定纯策略αi，局中人Ⅱ选定纯策略βj后，就 形成了一个纯局势(αi,βj)，这样的纯局势共有m·n个。
对任一纯局势(αi,βj)，记局中人Ⅰ的赢得值为aij，则得 矩阵 A=（aij），称为矩阵人Ⅰ的赢得矩阵。由于是零和对 策，则矩阵人Ⅱ的赢得矩阵为-A。矩阵对策的名称正是由
(优选)矩阵对策的解法详解.
矩阵对策的解法
3.1 公式法、图解法和方程组法
1. 2×2 对策的公式法
2×2 对策是指局中人Ⅰ的赢得矩阵为2×2 阶的, 即
A
a11 a21
a12
a22
如果 A 有鞍点, 则很快可求出各局中人的最优纯策略; 如果
A 没有鞍点,则可证明各局中人最优混合策略中的 xi* , yj* 均 大于零。于是, 由定理 6 可知, 为求最优混合策略可求下列
（5）确定经过点 P 的两相交直线，根据两相交直线列出对应方程 组，求出 y*.
（6）根据定理6的结论计算 x* 的值。
2020/7/19
10
例14
用图解法求解矩阵对策 G = { S1 , S2 ; A} , 其中
2 7
A
6
6
11 2
2020/7/19
11
2020/7/19
12
例 15
求解赢得矩阵A 的矩阵对策
A 4 1
8
3 5
4 5
2 7
2020/7/19
13
2020/7/19
14
3. 线性方程组方法
根据定理4 , 求解矩阵对策解( x*, y* ) 的问题等价于求解不 等式组，又根据定理5 和定理6 , 如果假设最优策略中的 xi* 和 yj* 均不为零, 即可将上述两个不等式组的求解问题转化 成求解下面两个方程组的问题:
(1) i
i
aij xi v, j 1,2,...,n
xi 1
(2)
j j
aij y j v,i 1,2,...,m yj 1
2020/7/19
15
3. 线性方程组方法
例16
求解矩阵对策——“齐王赛马”
3.1 公式法、图解法和方程组法
1. 2×2 对策的公式法
2×2 对策是指局中人Ⅰ的赢得矩阵为2×2 阶的, 即
A
a11 a21
a12
a22
如果 A 有鞍点, 则很快可求出各局中人的最优纯策略; 如果
A 没有鞍点,则可证明各局中人最优混合策略中的 xi* , yj* 均 大于零。于是, 由定理 6 可知, 为求最优混合策略可求下列
（5）确定经过点 P 的两相交直线，根据两相交直线列出对应方程 组，求出 y*.
（6）根据定理6的结论计算 x* 的值。
2020/7/19
10
例14
用图解法求解矩阵对策 G = { S1 , S2 ; A} , 其中
2 7
A
6
6
11 2
2020/7/19
11
2020/7/19
12
例 15
求解赢得矩阵A 的矩阵对策
A 4 1
8
3 5
4 5
2 7
2020/7/19
13
2020/7/19
14
3. 线性方程组方法
根据定理4 , 求解矩阵对策解( x*, y* ) 的问题等价于求解不 等式组，又根据定理5 和定理6 , 如果假设最优策略中的 xi* 和 yj* 均不为零, 即可将上述两个不等式组的求解问题转化 成求解下面两个方程组的问题:
(1) i
i
aij xi v, j 1,2,...,n
xi 1
(2)
j j
aij y j v,i 1,2,...,m yj 1
2020/7/19
15
3. 线性方程组方法
例16
求解矩阵对策——“齐王赛马”
矩阵对策的基本原理
对y为一个混合局势或局势局中人i的赢得函数记成这样得到的一个新的对策记成gs20局中人i可保证自己的赢得期望值不少于局中人ii可保证自己的所失期望值至多是minmaxmaxminmaxminminmax22定义4109式成立的混合局势xy为g在混合策略意义下的解或简称解x和y分别称为局中人i和ii的最优混合策略或简称最优策maxminminmax23定理2矩阵对策gs在混合策略意义下有解的充要条件是
xS1 yS2 yS2 xS1
(10 9)
记其值为VG。则称VG 为对策G*的值，称使 (10-9)式成立的混合局势(x*，y*)为G在混合 策略意义下的解(或简称解)，x*和y*分别称 为局中人I和II的最优混合策略(或简称最优策 略)。
21
定理 2 矩阵对策G={S1，S2；A} 在混合策 * x S 略意义下有解的充要条件是：存在 1， y S* 2 ，使(x*，y*)为函数E(x,y)的一个鞍 * 点，即对 x S1 ， ，有 y S* 2
6 1 A 8 0
5 4 5 2
6 2 7 6
5 - 1 5 2
11
性质 1 无差别性。即若( i1 , j1 ) 和 ( i , j ) 是对策G的两个解，则 ai1 j1 ai 2 j2 。
2 2
性质 2 可交换性。即若 ( i , j ) 和 ( i , j ) 是对策G的两个解，则 ( i , j ) 和 ( i , j ) 也是解。
0
0
31
n
x i 1 i 1
m
y j 1 j1
17
则S1*，S2*分别称为局中人I和II的混合策 * 略集(或策略集)； x S1 和 y S* 2 分别称为 * x S 局中人I和II的混合策略(或策略)；对 1 * y S2，称(x, y)为一个混合局势(或局势) ， ，局中人I的赢得函数记成
xS1 yS2 yS2 xS1
(10 9)
记其值为VG。则称VG 为对策G*的值，称使 (10-9)式成立的混合局势(x*，y*)为G在混合 策略意义下的解(或简称解)，x*和y*分别称 为局中人I和II的最优混合策略(或简称最优策 略)。
21
定理 2 矩阵对策G={S1，S2；A} 在混合策 * x S 略意义下有解的充要条件是：存在 1， y S* 2 ，使(x*，y*)为函数E(x,y)的一个鞍 * 点，即对 x S1 ， ，有 y S* 2
6 1 A 8 0
5 4 5 2
6 2 7 6
5 - 1 5 2
11
性质 1 无差别性。即若( i1 , j1 ) 和 ( i , j ) 是对策G的两个解，则 ai1 j1 ai 2 j2 。
2 2
性质 2 可交换性。即若 ( i , j ) 和 ( i , j ) 是对策G的两个解，则 ( i , j ) 和 ( i , j ) 也是解。
0
0
31
n
x i 1 i 1
m
y j 1 j1
17
则S1*，S2*分别称为局中人I和II的混合策 * 略集(或策略集)； x S1 和 y S* 2 分别称为 * x S 局中人I和II的混合策略(或策略)；对 1 * y S2，称(x, y)为一个混合局势(或局势) ， ，局中人I的赢得函数记成
15.3矩阵对策的混合策略
11
§3
矩阵对策的混合策略
Min x1+x2+x3+x4+x5+x6
建立对G′={S1，S2，A′}中求齐王最佳策略的线性规划如下：
约束条件： 5x1+3x2+3x3+x4+3x5+3x6 ≥1 3x1+5x2+x3+3x4+3x5+3x6 ≥1 3x1+3x2+5x3+3x4+3x5+x6 ≥1 3x1+3x2+3x3+5x4+x5+3x6 ≥1 x1+3x2+3x3+3x4+5x5+3x6 ≥1 3x1+x2+3x3+3x4+3x5+5x6 ≥1 xi ≥ 0,i=1,2,…,6 可解得解为：x1=x4=x5=0, x2=x3=x6=0.111, V ′=3, x1′=x4′=x5′= 0， x2′=x3′=x6′=1/3, 即X′* =(0,1/3,1/3,0,0,1/3)T，所以齐王的最优策略为作出策略2、3、
i j j i
一个自然的想法：对甲（乙）给出一个选取不 同策略的概率分布，以使甲（乙）在各种情况下的 平均赢得（损失）最多（最少）——即混合策略。
求解混合策略的问题有图解法、迭代法、线性 方程法和线性规划法等，我们这里只介绍线性规划 法，其他方法略。
4
§3
例1： A =
矩阵对策的混合策略
5 8 9 6
§3
矩阵对策的混合策略
例 .设对策问题局中人甲的赢得矩阵为
3 5 A = 7 4 6
2 0 3 6 0
矩阵对策的基本理论
解：采购员为局中人Ⅰ，他有三个策略：在秋季购煤 100 吨，150 吨和 200 吨，分别记 为α1、α2、α3；大自然为局中人Ⅱ，它也有三个策略，“选择”冬季气候较暖、正常、较冷， 分别记为 β1、β2 和 β3。以冬季取暖购煤的实际费用作为局中人Ⅰ的赢得，它等于秋季购煤 费用和冬季用煤不够时再补购的费用之和，赢得矩阵为
A
a21
a22
a2n
am1 am2 amn
（12-3）
为局中人Ⅰ的赢得 矩阵。由于对策为零和的，故局中人 Ⅱ的赢得矩阵为-A。
当局中人Ⅰ、Ⅱ的策略集 S1, S2 及局中人Ⅰ的赢得矩阵 A 确定后，一个矩阵对策就给定
了。因此将矩阵对策表示为 G S1，S2；A.
矩阵对策的最优纯策略
x E m
x
x , x ,, x
12
m
T
,
x i
0, i
1,,
m,
m
x i
i 1
1
S 2
y
E
n
y
y , y ,, y
12
n
T,
y j
0,
j
1,
n,
n
j 1
y j
1
S 和S 1
2
分别称为局中人Ⅰ和Ⅱ的混合策略集；
x
S
1
和y
S
2
分别称为局中人Ⅰ和Ⅱ
的混合策略；当
x
S 1
和y
S
2
其中， T G1
和T G 2
分别为局中人 I 和 II 的策略集。
运筹学
使自己的赢得尽可能的小，理性的选择就应该是从各自可能出现的最不利的情形中争取尽可
能好的结果。
A
a21
a22
a2n
am1 am2 amn
（12-3）
为局中人Ⅰ的赢得 矩阵。由于对策为零和的，故局中人 Ⅱ的赢得矩阵为-A。
当局中人Ⅰ、Ⅱ的策略集 S1, S2 及局中人Ⅰ的赢得矩阵 A 确定后，一个矩阵对策就给定
了。因此将矩阵对策表示为 G S1，S2；A.
矩阵对策的最优纯策略
x E m
x
x , x ,, x
12
m
T
,
x i
0, i
1,,
m,
m
x i
i 1
1
S 2
y
E
n
y
y , y ,, y
12
n
T,
y j
0,
j
1,
n,
n
j 1
y j
1
S 和S 1
2
分别称为局中人Ⅰ和Ⅱ的混合策略集；
x
S
1
和y
S
2
分别称为局中人Ⅰ和Ⅱ
的混合策略；当
x
S 1
和y
S
2
其中， T G1
和T G 2
分别为局中人 I 和 II 的策略集。
运筹学
使自己的赢得尽可能的小，理性的选择就应该是从各自可能出现的最不利的情形中争取尽可
能好的结果。
矩阵对策的基本原理
f ( x, y ) f ( x , y ) f ( x , y)
* * * *
(10 5)
则称(x*, y*)为函数f 的一个鞍点。
10
例8 求对策的解。设矩阵对策 G={S1，S2；A} 为矩阵对策，其中 S1 1 , 2 ,, m ， S2 1 , 2 ,, n ，赢 得矩阵为
* * ( , (10-1)式成立的纯局势 i j )为G在纯策略 * * 的解(或平衡局势)， i 与 j 分别称为局中 人 I、II的最优纯策略。
成立，记VG=ai*j*。则称VG为对策G的值，称使
7
例7 求解矩阵对策 G={S1，S2；A}，其中
7 1 8 3 2 4 A 16 1 3 5 3 0
a12 a22 am 2
a1n a2 n amn
1
为局中人I的赢得矩阵(或局中人II的支付矩阵)。由 于假定对策为零和的，故局中人II的赢得矩阵就是 -A。通常，将一个矩阵对策记成 G={I，II；S1，S2；A} 或 G={S1，S2；A}
例：齐王赛马
1 1
2
2
1
2
2
1
12
例9 某单位采购员在秋天要决定冬季取暖用 煤的储量问题。已知在正常的冬季气温条件下 要消耗15吨煤，在较暖与较冷的气温条件下要 消耗10吨和20吨。假定冬季时的煤价随天气寒 冷程度而有所变化，在较暖、正常、较冷的气 候条件下每吨煤价分别为100元，150元和200 元，又设秋季时煤价为每吨100元。在没有关 于当年秋季准确的气象预报的条件下，秋季储 煤多少吨能使单位的支出最少？
6 1 A 8 0
5 4 5 2
对策表矩阵图和pdpc图法
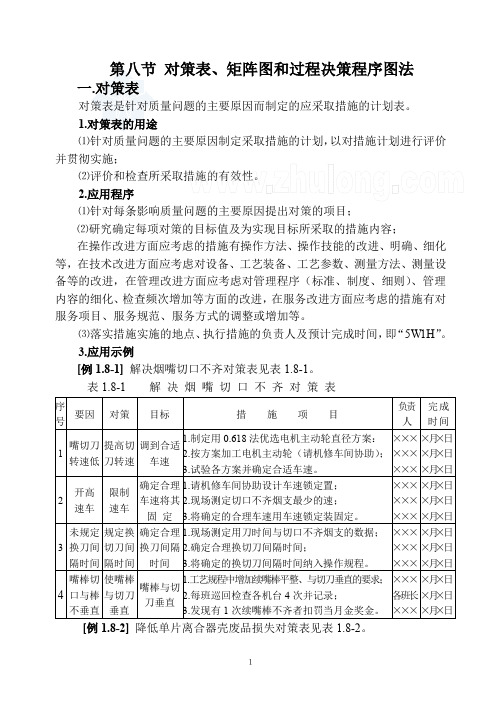
１第八节 对策表、矩阵图和过程决策程序图法一.对策表对策表是针对质量问题的主要原因而制定的应采取措施的计划表。
1.对策表的用途⑴针对质量问题的主要原因制定采取措施的计划，以对措施计划进行评价并贯彻实施；⑵评价和检查所采取措施的有效性。
2.应用程序⑴针对每条影响质量问题的主要原因提出对策的项目；⑵研究确定每项对策的目标值及为实现目标所采取的措施内容；在操作改进方面应考虑的措施有操作方法、操作技能的改进、明确、细化等，在技术改进方面应考虑对设备、工艺装备、工艺参数、测量方法、测量设备等的改进，在管理改进方面应考虑对管理程序（标准、制度、细则）、管理内容的细化、检查频次增加等方面的改进，在服务改进方面应考虑的措施有对服务项目、服务规范、服务方式的调整或增加等。
⑶落实措施实施的地点、执行措施的负责人及预计完成时间，即“5W1H ”。
3.应用示例[例1.8-1] 解决烟嘴切口不齐对策表见表1.8-1。
表1.8-1 解 决 烟 嘴 切 口 不 齐 对 策 表[例1.8-2] 降低单片离合器壳废品损失对策表见表1.8-2。
２表1.8-2 降低单片离合器壳废品损失对策表对策目标 4.易出现问题及注意事项 ⑴对策表项目不全（没有必须有的几项内容，即5W1H ）或项目顺序颠倒； ⑵要因不是经确认并和因果图中确定的项目内容相一致的内容； ⑶目标不定量，措施可操作性差,体现不出措施项目的主要内容； ⑷对策表的责任者不是小组全员而是少数几个人。
二.矩阵图矩阵图是以矩阵的形式分析问题与因素、因素与因素、现象与因素之间相互关系的图形。
1.矩阵图的用途⑴确定系列产品的研制或改进的着眼点；⑵产品质量及其它事项的展开，如广泛应用于质量功能展开（QFD ）； ⑶系统核实产品（工作）质量与影响因素（原材料、设备、工艺、操作、管理）之间的关系，便于全面系统地对质量进行管理；⑷了解市场与产品的关联分析，拟定与市场相关的产品战略方案； ⑸明确一系列项目与相关技术之间的关系； ⑹探讨现有产品（材料、技术）的应用领域。
矩阵对策定理
a
j
ij
y j * v*
a
i
ij i
x *
(4)
或 E(i,y*) v* E ( x*, j ) 又由 E ( x*, y*) E (i, y*)xi * v * xi * v * E ( x*, y*) E ( x*, j ) y j * v * y j * v *
E (i, y*) E ( x*, y*) E ( x*, j ) 其中，E (i, y) a y E( x, j ) aij xi ij j
j i
Hale Waihona Puke (3)证明：设(x*,y*)是G的解，则由引理2可知
E ( x, y*) E ( x*, y*) E ( x*, y)
E ( x, y*) E (i, y*)xi E ( x*, y*) xi E ( x*, y*)
定理2 对任一矩阵对策G={S1,S2; A}，一定存在混合策略意义下的解。 证明：由引理3，只要证明存在x*S1*，y*S2*，使得（3）式成立。为此， 考虑如下线性规划问题：
min v max w aij y j v i 1,2,...,m aij xi w j 1,2,...,n i j ( P) 和( D ) xi 1 y j 1 i j xi 0, i 1,2,...,m y j 0, j 1,2,...,n
j i j
ai* j* m ax aij* m in m ax aij
i j i
则由
i
m ax m in aij m in m ax aij ai* j*
i j j i j
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
矩阵G的一般解法
1）取每行的最小值：
min gij i 1, 2, , m
j
i
maxmin gij i 1, 2, , m 2）从上述值中选最大值： j
j
3）取每列的最大值： max gij j 1,
i
2, , n
max gij j 1, 2, , n 4）从3）项中选最大值：min j
E X ,Y E X ,Y
那么： X
x和y EX ,Y
都成立时
局中人P1的最优策略； 局中人P2的最优策略； 对策的值； 对策的解；
Y
E X ,Y
X
,Y
最优策略的解法
假设策略的值是V，最优策略及策略的解可 通过下式求得。
m
E X , j g ij xi V
Y , , 5） 13 13 13 25 V 13
E 1, Y 3 y1 y2 y3 V E 2, Y y1 y2 5 y3 V E 3, Y y1 4 y2 y3 V y1 y2 y3 1
i
min gij min max gij gi* j* 时， 5）若 max j j i i
ai* →P1的最优纯策略； b * →P2的最优纯策略； j
a , b 对策的解； V
i* j*
g i* j* 对策 a * , b * 的值。 i j
例3
某耕地根据种植划以及自然条件，规划 与收益存在如下表所示的关系。 试求出最佳规划方案。
E( x, y) 6 xy x(1 y) 2(1 x) y 4(1 x)(1 y)
2 3 22 7 x y 7 7 7
2 3 22 3）当 x 或 y 时， E ( x, y ) 7 7 7
4）对x, y在闭区间[0，1]上的任何值，
混合策略： X x1 , x2 , , xm xi 0 混合策略： Y y1 , y2 , , yn y j 0
mn
x
i 1
m
i
1
y
j 1
n
j
1
支付（赢得）： E X , Y
g
i 1 j 1
m
n
ij i
x yj
如果存在 X , Y ，对任意
例2 钱币游戏
两个参加者（称为局中人P1和P2）各出示 一枚钱币，在不让对方看见的情况下，将 钱币放在桌上。若两个钱币都呈正面或反 面，则P1得1分，P2得-1分；若一正一反， 则P1得-1分，P2得1分。
1. 支付矩阵的规则
局中人P1的策略用矩阵的行数表示； 局中人P2的策略用矩阵的列数表示； 矩阵中的数为局中人P2支付给局中人 P1的单位值；正值：P2 → P1 ，负值： P1 → P2； 局中人P1得到的值就是局中人P2失去 的值； 因此也称“二人零和对策”。
3 2 3 2 E X , E , E , Y 7 7 7 7
总 结
矩阵对策：
1 , 2 , , m 纯策略集： S1
纯策略集： S2 1 , 矩阵：
S1, S2 , G
G gij
2 , , n
xi 0
i 1, 2, 3
2）求取等号时的方程组解：
x1 6 13 3 x 2 13 4 x3 13 V 25 13
y1 6 13 4 y 2 13 4）求取等号时的方程组解： 3 y3 13 6 3 4 X , , P1方 V 25 13 13 13 13 6 4 3
公司B
1
2
1 0 -2
3
2 -3 0
1
公 司 A
2 3 -1
2
3
矩阵表示为
1 2 2 A 3 0 3 1 2 0
A 中行的编号为公司A的编号，称“行方”的策略编 号 A 中列的编号为公司B的编号，称“列方”的策略编号 矩阵 A 称为甲方或行方的支付矩阵
I
局 3 1 =急转 中 人 2 =不转 5 I I 的支付矩阵
1=急转 2 =不转
1
给急转弯者以1 分，不转弯者以5 分 局中人II 局中人I 局 1 =急转 中 人 2=不转 II
3 5
1 =急转 2 =不转
1 0
0
II 的支付矩阵
此对策中，若两者都想得5 分，则发生惨祸， 全部玩完．实际上两人最好的做法是同时停车 或转弯，各得3 分． Remark 此例已不是2 人有限零和对策问题（因为在 每个对局中，双方支付的代数和不为零）， 称为双矩阵对策．
3. 混合策略
举例
6 1 G 2 4
maxmin gij 2, min max gij 4
i
j
j
i
maxmin gij min max gij
i
j
j
i
解题步骤
1）假设 选a1概率为x，则选a2概率为1-x； 选b1概率为y，则选b2概率为1-y； 2）求P1的收入期望值：
i 1
j 1, 2,, n
xi 0
x
i 1
m
i
1
E i, Y gij y j V
j 1
n
i 1, 2,, m
yj 0
y
j 1
n
j
1
例4
S1 1 , 2 , 3
S1, S2 , G
S2 1, 2 , 3
每个局中人总希望取得尽可能大的胜利，即期望的 “最小利益” 为 “最大”，“最大损失” 为 “最
小”．
零和对策 有限对策
对策
非零和对策 无限对策
两人对策
多人对策
两人有限零和对策
局中人只有两人；
每人只有有限个对策；
局中人支付之和为零（赢为正；输为负 ）
例1 扩大销售型
公司A，公司B的同一产品竞争市场份额，各有 三种办法扩大销售额（由于市场需求一定，一 家扩大，意味另一家缩减），三种方法比如： ①改进包装；②广告；③降价．公司 A 的三种 策略表示为 α1, α2, α3 ，公司 B的三种策略为 β1, β2, β3，在不同策略下销售量增长百分比 不同．下表中表示公司A的增长率，而公司B的 即为相反数
解题思路
P1的选择：最坏的结果是G中每行的最小数， （-8，2，-10，-3）； 从中选出最好的结果：2。 P2的选择：最坏的结果是G中每列的最大数， （9，2，6）； 从中选出最好的结果：2。 （a2,b2）是P1 和P2双方最佳的选择。
2. 矩阵对策的数学模型
P1
P2
的策略：S1 a1 , a2 , , am 的策略： S2 b1 , b2 , , bn
三. 矩阵对策
(game theory)
对策现象 对策论
带有竞争或斗争性质的现象 用数学方法研究对策现象的 分支学科
对策现象的三要素
局中人: 策略： 一局对策中的决策者或不相容利益的参 与者或竞争者 局中人在整个决策过程中一系列行动的 一个方案 一局对策中最终结局获得的收益或损失
支付:
最大最小原则
例3
b1 b2 1 2 b3
S1 a1 , a2 , a3 , a4
S1, S2 , G
S2 b1 , b2 , b3 , b4
a1 6 a2 3 G a3 9 a4 3
8 4 1 10 0 6
求：该矩阵对策的最佳方案
3 1 1 G 1 1 5 1 4 1
求最优策略及对策Γ的值。
解题步骤：
1）列出求P1方的最优策略方程组
E X ,1 3 x1 x2 x3 V E X ,2 x1 x2 4 x3 V E X ,3 x1 5 x2 x3 V x1 x2 x3 1
b1 b2 bn g12 g 22 gm2 g1n g 2n g ij g mn
a1 g11 a2 g 21 G P1 的赢得矩阵： am g m1
上述对策可简化为： a, b, S1, S2 , G S1, S2 , G
3）列出求P2方的最优策略方程组
yj 0
j 1, 2, 3
P2方
对策的值
e.g.5 玩命 or 胆小鬼对策 两位驾车人驾车相向行驶，直到最后一秒才决定 是拐弯还是不拐弯 可能发生下列几种结果
◆ 谁也不急拐弯，最后两车相撞 ◆ 两局中人均拐弯
给以0 值
给以值3
◆ 一位局中人急转弯，另一位未让步而作为赢家