自动控制原理结构图及等效变换
合集下载
自动控制原理方框图

[注意]:
相临的信号相加点位置可以互换;见下例
X1(s)
X2(s)
X3(s)
Y (s)
X1(s)
X3(s)
X 2 (s)
Y (s)
同一信号的分支点位置可以互换:见下例
X1(s)
X (s) G(s) Y (s)
X 2 (s)
X (s) G(s) Y (s)
X 2 (s)
X1(s)
相加点和分支点在一般情况下,不能互换。
§2-3 控制系统的结构图与信号流图
一、结构图的组成和绘制
1、结构图的组成 由四种基本图形符号组成
(1)函数方块
R(s) r(t) G(s)
C(s) c(t)
(2)信号线
R(s) r(t)
(3)分支点(引出点)
R(s) r(t)
R(s) r(t) R(s) r(t)
(4)综合点(比较点或相加点)
R(s)
R
R1Cs
2I
2
(s)
UI (cs)(s)
R2
R1
Uc (s)
U c (s)
I1 (s)
Uc (s)
几点说明:
(1)在结构图中,每一个方框中的传递函数都应是考虑了负 载效应后的传递函数。
(2)描述一个系统的结构图不是唯一的,选择不同的中间变 量得到不同的结构图;
(3)结构图中的方框与实际系统的元部件并非一定是一一对 应的;
X1(s) G(s) X2(s) N(s)
Y (s)
N(s) ? Y (s) [X1(s) X 2 (s)]G(s), 又 : Y (s) X (s)1G(s) X 2 (s)N(s), N(s) G(s)
把相加点从环节的输出端移到输入端:
自动控制原理控制系统的结构图

比较点后移
R(s)
G(s)
比较点前移
+
Q(s)
C(s)
R(s)
+
C(s) G(s)
比较点后移
Q(s)
R(s)
+
C(s) G(s)
Q(s)
C(s) R(s)G(s) Q(s)
[R(s) Q(s) ]G(s) G(s)
R(s)
C(s) G(s)
+
Q(s)
G(s)
C(s) [R(s) Q(s)]G(s)
R(s)G(s) Q(s)G(1s6 )
(5)引出点旳移动(前移、后移)
引出点前移
R(s)
G(s)
分支点(引出点)前移
C(s) C(s)
引出点后移
R(s)
G(s)
R(s)
分支点(引出点)后移
R(s)
G(s)
C(s)
G(s)
C(s)
C(s) R(s)G(s)
G(s) R(s)
C(s) R(s)
将 C(s) E(s)G(s) 代入上式,消去G(s)即得:
E(s) R(s)
1
H
1 (s)G(s)
1
1 开环传递函数
31
N(s)
+ E(s)
++
C(s)
R(s)
G1(s)
G2 (s)
-
B(s)
H(s)
(1)
打开反馈
C(s) R(s)
1
G(s) H (s)G(s)
前向通路传递函数 1 开环传递函数
注意:进行相加减旳量,必须具有相同旳量纲。
X1 +
+
X1+X2 R1(s)
自动控制原理(2-2)

1 G(s)
B A
B
+
+
C
D
A
+
C
+
D
(a)
(b)
图2-17 相邻相加点的移动
A A
(a)
A A
A A
A A(b)AA源自图2-18 相邻分支点的移动
应当指出,在结构图简化过程中,两个相邻的相加
点和分支点不能轻易交换。 总之,根据实际系统中各环节(子系统)的结构图 和信息流向,可建立系统的结构图。在确定输入量
加,就可得到系统的总输出量。
系统对扰动N(s)的响应CN(s)为:
G2 ( s) CN ( s ) N ( s) 1 G1 ( s)G2 ( s) H ( s)
系统对参考输入量R(s)的响应CR(s)为:
G1 ( s )G2 ( s ) CR ( s ) R( s) 1 G1 ( s )G2 ( s ) H ( s )
X 3 ( s)
X 0 (s)
G1 ( s )G2 ( s )G3 ( s)
(b)
X 3 ( s)
图2-10 串联环节的简化
n个环节(每个环节的传递函数为Gi(s) ,i=1,2,3,…) 串联的等效传递函数等于各传递函数相乘。
G( s) G1 (s)G2 (s) Gn (s)
2.并联环节的简化
上式就是系统输出量C(s)和输入量R(s)之间的传递函 数,称为闭环传递函数。
闭环传递函数将闭环系统的动态特性与前向通道环 节和反馈通道环节的动态特性联系在一起。
G( s) C (s) R( s ) 1 G( s) H ( s)
可见,闭环系统的输出量取决于闭环传递函数和输 入量的性质。
自动控制原理第二章3
Uc(s)
第三节控制系统的结构图和信号流图
N(s) R(s) C(s) G1(s) G2(s)
+ _
H(s) 典型反馈控制系统方框图 1)信号线:带单向箭头,表示信号流向 信号线:带单向箭头, 2)引出点:信号从引出点分开,大小和性质相同 引出点:信号从引出点分开, 3)比较点:两个或两个以上的信号相加减 比较点: 4)方框:对信号进行数学变换,方框中写入环节的传递函数 方框:对信号进行数学变换,
R1 C2S 1 C(S) 1 1 R2 +R1C R2 +1)C2S C2S2S
R(s)
_
1 R1C1S+1 R1C2S
1 R2C2S+1
C(s)
第三节控制系统的结构图和信号流图
三、控制系统的信号流图: 控制系统的信号流图:
1、定义 、 一组线性代数方程式变量间传递关系的图形表示, 一组线性代数方程式变量间传递关系的图形表示,由节 支路和支路增益组成。 点、支路和支路增益组成。 y1 典型的信号流图 x1 1 x2 a e a y2=ay1 d x3 b f x4 c x5 g 1 x6 y2
第三节控制系统的结构图和信号流图
绘制动态结构图的一般步骤为: 绘制动态结构图的一般步骤为 (1)确定系统中各元件或环节的传递函数。 )确定系统中各元件或环节的传递函数。 (2)绘出各环节的方框,方框中标出其传 )绘出各环节的方框, 递函数、输入量和输出量。 递函数、输入量和输出量。 (3)根据信号在系统中的流向,依次将各 )根据信号在系统中的流向, 方框连接起来。 方框连接起来。
p1 = abc
L1与L3
p2 = d
L3 = g L2与L3
L1 = ae
L2 = bf
第三节控制系统的结构图和信号流图
N(s) R(s) C(s) G1(s) G2(s)
+ _
H(s) 典型反馈控制系统方框图 1)信号线:带单向箭头,表示信号流向 信号线:带单向箭头, 2)引出点:信号从引出点分开,大小和性质相同 引出点:信号从引出点分开, 3)比较点:两个或两个以上的信号相加减 比较点: 4)方框:对信号进行数学变换,方框中写入环节的传递函数 方框:对信号进行数学变换,
R1 C2S 1 C(S) 1 1 R2 +R1C R2 +1)C2S C2S2S
R(s)
_
1 R1C1S+1 R1C2S
1 R2C2S+1
C(s)
第三节控制系统的结构图和信号流图
三、控制系统的信号流图: 控制系统的信号流图:
1、定义 、 一组线性代数方程式变量间传递关系的图形表示, 一组线性代数方程式变量间传递关系的图形表示,由节 支路和支路增益组成。 点、支路和支路增益组成。 y1 典型的信号流图 x1 1 x2 a e a y2=ay1 d x3 b f x4 c x5 g 1 x6 y2
第三节控制系统的结构图和信号流图
绘制动态结构图的一般步骤为: 绘制动态结构图的一般步骤为 (1)确定系统中各元件或环节的传递函数。 )确定系统中各元件或环节的传递函数。 (2)绘出各环节的方框,方框中标出其传 )绘出各环节的方框, 递函数、输入量和输出量。 递函数、输入量和输出量。 (3)根据信号在系统中的流向,依次将各 )根据信号在系统中的流向, 方框连接起来。 方框连接起来。
p1 = abc
L1与L3
p2 = d
L3 = g L2与L3
L1 = ae
L2 = bf
自动控制原理 控制系统的结构图

其他变化(比较点的移动、引出点的移动)以此三种 基本形式的等效法则为基础。
12
(1)串联连接
R( s )
U (s) 1
G (s) 1
G (s) 2
C( s )
R(s)
C(s)
G(s)
(a)
(b)
特点:前一环节的输出量就是后一环节的输入量
U1(s) G1(s)R(s) C(s) G2 (s)U1(s) G2 (s)G1(s)R(s)
注意:进行相加减的量,必须具有相同的量纲。
X1 +
+
X1+X2 R1(s)
-
R1(s)R2(s)
X1
X2
R2(s)
X3
X1-X2 +X3 -
X2
4
(4) 引出点(分支点、测量点) 表示信号测量或引出的位置
R(s)
G (s) 1
X(s)
G (s) 2
C(s)
X(s) 引出点示意图
注意:同一位置引出的信号大小和性质完全一样
G(s)
分支点(引出点)前移
C(s) C(s)
引出点后移
R(s)
G(s)
R(s)
分支点(引出点)后移
R(s)
G(s)
C(s)
G(s)
C(s)
C(s) R(s)G(s)
G(s) R(s)
C(s) R(s)
C(s) R(s)
G1(s)G2
(s)
G(s)
结论:
n
G(s) Gi (s) n为相串联的环节数 i 1
串联环节的等效传递函数等于所有传递函数的乘积
13
(2)并联连接
G1 (s)
12
(1)串联连接
R( s )
U (s) 1
G (s) 1
G (s) 2
C( s )
R(s)
C(s)
G(s)
(a)
(b)
特点:前一环节的输出量就是后一环节的输入量
U1(s) G1(s)R(s) C(s) G2 (s)U1(s) G2 (s)G1(s)R(s)
注意:进行相加减的量,必须具有相同的量纲。
X1 +
+
X1+X2 R1(s)
-
R1(s)R2(s)
X1
X2
R2(s)
X3
X1-X2 +X3 -
X2
4
(4) 引出点(分支点、测量点) 表示信号测量或引出的位置
R(s)
G (s) 1
X(s)
G (s) 2
C(s)
X(s) 引出点示意图
注意:同一位置引出的信号大小和性质完全一样
G(s)
分支点(引出点)前移
C(s) C(s)
引出点后移
R(s)
G(s)
R(s)
分支点(引出点)后移
R(s)
G(s)
C(s)
G(s)
C(s)
C(s) R(s)G(s)
G(s) R(s)
C(s) R(s)
C(s) R(s)
G1(s)G2
(s)
G(s)
结论:
n
G(s) Gi (s) n为相串联的环节数 i 1
串联环节的等效传递函数等于所有传递函数的乘积
13
(2)并联连接
G1 (s)
自动控制原理--系统的结构图
R(s)
C(s)
G(s)
(-)
B(s)
R(s) G(s)
B(s) G(s)
C(s) (-)
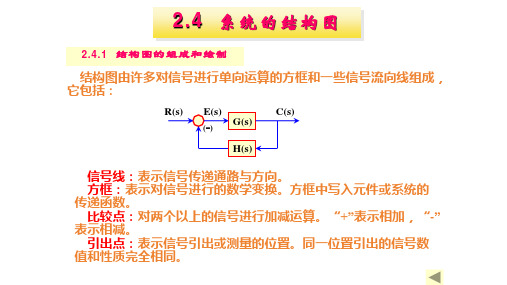
•相 加 点 的 移 动
3. 交换或合并相加点
C(s)=E1(s)+V2(s) = R(s)-V1(s)+V2(s) = R(s)+V2(s)-V1(s)
V2(s)
R(s)
E1(s)
C(s)
(-) V1(s)
系统动态结构图
定义:将系统中所有的环节用方框图表示, 图中标明其传递函数,并且按照在系统中各 环节之间的联系,将方框图连接起来。
系统动态结构图的绘制步骤:
● (1)首先按照系统的结构和工作原理,分解出各环 节并写出它的传递函数。
● (2)绘出各环节的动态方框图,方框图中标明它的 传递函数,并以箭头和字母符号表明其输入量和输 出量,按照信号的传递方向把各方框图依次连接起 来,就构成了系统结构图。
C(s)
G(s)
R(s)
1 G(s)H(s)
• 例2.9
R(s) G1(s)
G2(s)
(-)
G3(s)
(-)
C(s) G6(s)
G4(s) G5(s)
G 236 (G 2 G 3 )G 6
G 54 G 5 G 4
G
1
G 236 G 236G 54
G1
● 比较点和引出点的移动: 等效原则:前向通道和反馈通道传递函数都不变。
G4
(a)
(b)
•其 它 等 价 法 则
1. 等效为单位反馈系统
R(s)
C(s)
G(s)
(-)
H(s)
R(s) 1
2.3自动控制原理

自动控制原理
自动控制原理
自动控制原理
2.4 系统结构图的变换和简化
等效变换的原则:变换前后的变量之间关系保持不变 一、典型连接的等效传递函数
(1)串联等效 R(s) U (s) C (s) G1 ( s) G 2
G1 ( s)G 2 ( s)
C (s)
G1 ( s )
自动控制原理
三 信号流图
3.1信号流图的常用术语 : 节点:用以表示变量或信号的点称为节点,用 “o”表示。 传输:两节点间的增益或传递函数称为传输。 支路:连接两节点并标有信号流向的定向线段 支路的增益即为传输。 源点:只有输出支路而无输入支路的节点(与 系统的输入信号相对应)。
x1 a x2 c b x3 1 x4
X2 X3
相加点前移,在移动支路中串入所越过的传递函数的倒 数方框 (2) 相加点后移
x1 x3 x2 x1 x3 G(s) G(s) x2
G(s)
相加点后移,在移动支路中串入所越过的传递函数方框。
自动控制原理
3.方框图的简化原则
(1) 前向通道中各串联函数方框的传函乘积保持不变 ; (2) 各反馈回路所含函数方框的传函之积保持不变。
G(s)
C (s)
C(s) G(s)E(s) G(s)[R(s) B(s)] G(s)R(s) G(s)H (s)C(s)
R(s) G (s) C (s) R( s) ( s) R( s) 1 G ( s) H (s)
H (s)
G (s) 1 G (s) H (s)
不存在互不接触回路 1 ( L1 L2 L3 L4 L5 ) 1 G1G 2 H 1 G1G 2 G 3 G 2 G 3 H 2 G 4 H 2 G1G 4 五个回路均与 1 和P2 接触 P 1 1 2 1 C(S) 1 P P1 1 P2 2 R(S) G 1G 2 G 3 G 1G 4 1 G1G 2 H 1 G1G 2 G 3 G 2 G 3 H 2 G 4 H 2 G1G 4
自动控制原理控制系统的结构图

I1(s)
I2 (s)
CR1s
7
i2
C
i
i1 R1
ui
R2
uo
(3)
I(s) I1(s) I2 (s)
I2 (s)
I (s)
I1(s)
(4)U o (s) R2 I (s)
I (s)
Uo (s)
R2
8
(1)Ui (s)
(3)
- Uo(s)
I2 (s)
(2)
1
I1(s)
I1(s)
I2 (s)
- Uo (s)
(d)
将图(b)和(c)组合起来即得到图(d),图(d)为该 一阶RC网络的方框图。
11
2.3.3 系统结构图的等效变换和简化
为了由系统的方框图方便地写出它的闭环传递函 数,通常需要对方框图进行等效变换。
方框图的等效变换必须遵守一个原则,即: 变换前后各变量之间的传递函数保持不变
在控制系统中,任何复杂系统的方框图都主要由 串联、并联和反馈三种基本形式连接而成。
u
o
idt c
对其进行拉氏变换得:
I (s)
U
o
(s)
U
i (s)
I (s) sC
U R
o
(s)
(1) (2)
10
I (s)
U
o
(s)
U
i (s)
I (s) sC
U R
o
(s)
(1) (2)
Ui (s)
I(s)
(b)
Uo (s)
I(s)
(c)
Uo (s)
Ui (s)
I(s)
Uo (s)
自动控制原理第二章2-2
Uc(s)
超前校正装置
4
“由内而外”化简
R(s)
-
-
G1 H1
G2
H4
G3 H2 H3
G4
C(s)
思考:是否能用基本等效法则进行简化? H3 R(s) C(s) G1 G2 G3 G4 -
-
H1 H4
“支路交错”
H2
5
H2(s)
R(s) G1(s) G2(s) G3(s) G4(s) C(s)
H3(s)
E ( s) 1 Ger ( s ) = = R( s ) 1 + G1 ( s )G2 ( s ) H ( s)
- G2 ( s ) H ( s ) E( s) Gen ( s ) = = N ( s ) 1+ G1 ( s )G2 ( s ) H ( s )
24
第二章
d = s dt
小结
微分方程
干扰信号下的闭环传递函数 【令R(s)=0】
G2 ( s ) C ( s) GBN ( s ) = = N ( s ) 1 + G1 ( s )G2 ( s ) H ( s )
22
N(s) R(s) E(s)
G1(s) H(s)
C(s)
N
G2(s)
R
1
1 E
G1
1
G2
1
C
-H
二、系统误差传递函数
G2(s)
1
R 1
G1
G2
1
C
-H
E
一、系统开环传递函数
GK ( s) = G1( s)G2 ( s) H ( s)
21
N(s) R(s) E(s)
N C(s) 1 R 1
自动控制原理02结构图及其等效变换

e)
R( s )
G 1 G 2 G3G 4 C (s) 1 G 1 G 2 G3G 4 G 2 G3 H 1 G3G 4 H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统
N (s)
R( s )
E ( s)
G1 (s)
结构图。
2.3.2 结构图的建立
例2-7 RLC电路网络的结构图
解: U (s) U (s) U (s) U (s) i R L 0
U R ( s) RI ( s)
U L ( s) LsI ( s)
{
I ( s)
U i ( s) U 0 ( s ) U R ( s ) U L ( s )
C 传输到 ( s)
单位反馈: H ( s) 1 开环传递函数:
G( s) H ( s)
2.3.3 结构图的等效变换和简化
(4)比较点的移动
R1 (s)
G(s)
R2 ( s )
a)
C (s)
R2 ( s )
R1 (s)
G(s)
C (s)
1/ G(s)
b)
R1 (s)
R2 ( s )
a)
G(s)
C (s) G(s) ( s) R( s) 1 G ( s) H ( s )
2.3.3 结构图的等效变换和简化
反馈连接中的术语:
R( s)
E (s)
G (s)
H (s)
C (s)
B( s)
前向通道:信号从 R( 传输到 s) 反馈通道:信号从
的通道 C ( s) 的通道 R( s )
R(s)
R( s )
G 1 G 2 G3G 4 C (s) 1 G 1 G 2 G3G 4 G 2 G3 H 1 G3G 4 H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统
N (s)
R( s )
E ( s)
G1 (s)
结构图。
2.3.2 结构图的建立
例2-7 RLC电路网络的结构图
解: U (s) U (s) U (s) U (s) i R L 0
U R ( s) RI ( s)
U L ( s) LsI ( s)
{
I ( s)
U i ( s) U 0 ( s ) U R ( s ) U L ( s )
C 传输到 ( s)
单位反馈: H ( s) 1 开环传递函数:
G( s) H ( s)
2.3.3 结构图的等效变换和简化
(4)比较点的移动
R1 (s)
G(s)
R2 ( s )
a)
C (s)
R2 ( s )
R1 (s)
G(s)
C (s)
1/ G(s)
b)
R1 (s)
R2 ( s )
a)
G(s)
C (s) G(s) ( s) R( s) 1 G ( s) H ( s )
2.3.3 结构图的等效变换和简化
反馈连接中的术语:
R( s)
E (s)
G (s)
H (s)
C (s)
B( s)
前向通道:信号从 R( 传输到 s) 反馈通道:信号从
的通道 C ( s) 的通道 R( s )
R(s)
自动控制原理课件第4次课 传递函数、结构图

• 一阶微分环节: G ( s ) s 1 • 振荡环节 : • 延迟环节
2 n 1 G( s) 2 2 2 T s 2Ts 1 s 2n s n 2
G ( s ) e s
哈尔滨工程大学自动化学院
20
自动控制原理
第二章 控制系统的数学模型
注意: 环节是根据微分方程划分的,不是具体的物理 装置或元件。 一个环节往往由几个元件之间的运动特性共同 组成。
哈尔滨工程大学自动化学院
12
自动控制原理
第二章 控制系统的数学模型
Part 2-4-2 传递函数的零点和极点
b0 s m b1s m 1 bm 1s bm an 1s an M (s) N (s)
M (s) b0 s m b1s m1 ... bm1s bm
系统(或环节) 的输入量 系统(或环节) 的输出量
X r ( s)
X c ( s) X r ( s)G( s)
X c (s)
哈尔滨工程大学自动化学院
7
自动控制原理
第二章 控制系统的数学模型
系统传递函数的一般形式 设线性定常系统由n阶线性定常微分方程描述:
d d d a0 n c(t ) a1 n1 c(t ) an1 c(t ) an c(t ) dt dt dt m m 1 d d d b0 m r (t ) b1 m1 r (t ) bm1 r (t ) bm r (t ) dt dt dt
哈尔滨工程大学自动化学院
6
自动控制原理
第二章 控制系统的数学模型
Part 2-4-1 传递函数的定义和性质
定义:在零初始条件(输入量施加于系统之前,系统处于
自动控制原理 动态结构图及变换

U s (s)
Ka Ua (s)
系统各元部件的动态结构图(4)
e (s) r (s) c (s)
M m (s) CmIa (s)
U s (s) Kse (s)
U a (s) KaU s (s) Ua (s) Ra Ia (s) LasIa (s)
Eb (s)
Eb (s) Kbsm (s)
二、动态结构图的基本连接形式
1. 串联连接
X(s) G1(s)
Y(s) G2(s)
方框与方框通过信号线相连,前一个方框的输 出作为后一个方框的输入,这种形式的连接称 为串联连接。
2. 并联连接
G1(s)
X(s)
- Y(s)
+
G2(s)
两个或两个以上的方框,具有同一个输入信号,并 以各方框输出信号的代数和作为输出信号,这种形
式的连接称为并联连接。
3. 反馈连接
R(s)
-
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后,得 到的输出再返回到这个方框的输入端,构成输 入信号的一部分。这种连接形式称为反馈连接。
三、系统动态结构图的构成
• 构成原则:
按照动态结构图的基本连接形式,构 成系统的各个环节,连接成系统的动 态结构图。
Ua (s) Ra Ia (s) LasIa (s) Eb (s)
Js2 m (s) M m fsm (s)
c
(s)
1
i
m
(s)
r (s)
e (s)
c (s)
系统各元部件的动态结构图(2)
e (s) r (s) c (s) Us (s) Kse (s)
Ua (s) KaU s (s) Ua (s) Ra Ia (s) LasIa (s)
等效变换自动控制原理课件
G3 G4 / G2
C(s) +
R(s) -
(c) -
1/ G1 G1 G2
G3 G4 / G2
C(s) +
17
R(s) -
(c) -
1/ G1 G1 G2
G3 G4 / G2
C(s) +
R(s) -
1/ G1
G1G2 1 G1G2
G3 G4 / G2
C(s)
(d)
18
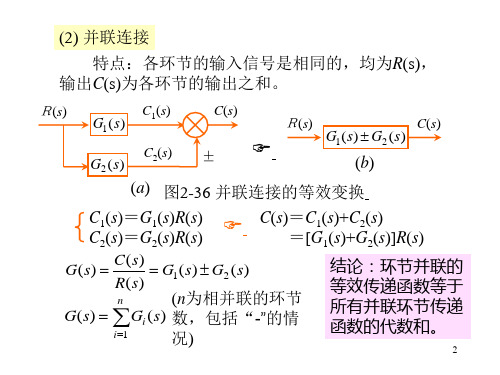
2、变换前后有关前向通道中各方框传递 函数的乘积应保持不变。
15
例2-11 试化简如图所示系统结构图,求出 传递函数Φ(s)=C(s)/R(s)。
R(s)
-
(a)
-
G1
C(s)
G2
G3
+
G4
R(s) -
(b) -
1/ G1 G1 G2
G3 G4 / G2
C(s) +
16
R(s) -
(b) -
1/ G1 G1 G2
G(s)
C(s) R(s)
G1(s)G2 (s)
结论:环节串联的等效 传递函数等于各串联连
n
G(s) Gi (s)
i1
(n为相串联 的环节数)
接传递函数的乘积。
1
(2) 并联连接
特点:各环节的输入信号是相同的,均为R(s), 输出C(s)为各环节的输出之和。
R(s)
G1(s) C1(s) G2 (s) C2(s)
R(s) -
(a)
G1
+
H1
C(s)
G2 H2
R(s) -
(b)
C(s)
G1
G2
H1
+
H1 H2
自动控制原理
1 C2s
C ( s)
(a)
39
(b)
方块图 消除局部反馈回路
2-3
R(s)
+ _
1 R1C1s + 1
1 R2C2s + 1
C (s)
R1C2 s
(b)
40
2-3 方块图
(C) 消除主反馈回路
R( s)
1 R1C1R2C2 s 2 + ( R1C1 + R2C2 + R1C2 ) s + 1
G(s) Q(s) 1/G(s)
23
综合点之间的移动
X(s) R(s)
±
X(s) C(s) R(s)
± ±
Y(s) ±
C(s)
Y(s)
24
4.综合点之间的移动 4.综合点之间的移动
结论: 结论:
X(s) R(s)
±
X(s) C(s) R(s)
± ±
Y(s) ±
C(s)
Y(s)
结论:多个相邻的综合点可以随意交换位置。 结论:多个相邻的综合点可以随意交换位置。
反馈结构图
R(s) B(s) ±
E(s)
C(s)
G(s) H(s)
C(s) = ?
9
3.
反馈结构的等效变换
等效变换证明推导
C (s) = G(s)E (s) B(s) = C ( s)H ( s) E ( s ) = R( s) ± B( s) 消去中间变量 E ( s ), B ( s )得 G(s) C (s) = R( s) 1 m G ( s)H ( s)
两个串联的方框可以 合并为一个方框, 合并为一个方框,合 并后方框的传递函数 等于两个方框传递函 数的乘积。 数的乘积。G1(Leabharlann )G2(s)R(s)
自动控制原理2.4 结构图的等效变换及简化计算

Pk—从R(s)到C(s)的第k条前向通道增益 △k —第k条前向通道的余子式
在△中,去掉与第k条前向通 道相接触的回路对应的项后
剩余的部分。
求法: 去掉第k条前向通路后所求的△ 用梅森公式求上例信号流图对应的传函。
南京工业职业技术学院机械工程学院——自动控制原理
梅森公式例1
GG44((ss))
R(s)
注:比较点和引出点之间不能换位。 3. 通过在被变换的支路上乘或除某个传函来保持等效。 4. 根据环节方框的连接方式(串联、并联和反馈)进行简化
计算。
南京工业职业技术学院机械工程学院——自动控制原理
结构图三种连接形式及其计算
串联
G1
G2
G1 G2
n
G(s) Gi (s) i 1
并联 G1 G2
反馈 G1
G5
R –
X1 G1
– G2 X2 –
G3 X3
G4
C
X3
G6
G7
南京工业职业技术学院机械工程学院——自动控制原理
G8 G5
R – G1 X1
X2 – G2
–
X3
G3
G4
C
X3 G6
G7
(2)求传函。用梅逊公式:
1 G1G2G3G4G7 G1G2G3G4G8 G2G3G6 G3G4G5
R(s)
-
G4
A
G1
-
B
G2
H1
G3 H2
C C(s)
P1 G1G2G3 1 1
P2 G1G4 2 1
C(S) P(S) P11 P22
P11 P22
R(S)
1 (L1 L2 L3 L4 L5 )
在△中,去掉与第k条前向通 道相接触的回路对应的项后
剩余的部分。
求法: 去掉第k条前向通路后所求的△ 用梅森公式求上例信号流图对应的传函。
南京工业职业技术学院机械工程学院——自动控制原理
梅森公式例1
GG44((ss))
R(s)
注:比较点和引出点之间不能换位。 3. 通过在被变换的支路上乘或除某个传函来保持等效。 4. 根据环节方框的连接方式(串联、并联和反馈)进行简化
计算。
南京工业职业技术学院机械工程学院——自动控制原理
结构图三种连接形式及其计算
串联
G1
G2
G1 G2
n
G(s) Gi (s) i 1
并联 G1 G2
反馈 G1
G5
R –
X1 G1
– G2 X2 –
G3 X3
G4
C
X3
G6
G7
南京工业职业技术学院机械工程学院——自动控制原理
G8 G5
R – G1 X1
X2 – G2
–
X3
G3
G4
C
X3 G6
G7
(2)求传函。用梅逊公式:
1 G1G2G3G4G7 G1G2G3G4G8 G2G3G6 G3G4G5
R(s)
-
G4
A
G1
-
B
G2
H1
G3 H2
C C(s)
P1 G1G2G3 1 1
P2 G1G4 2 1
C(S) P(S) P11 P22
P11 P22
R(S)
1 (L1 L2 L3 L4 L5 )
等效变换自动控制原理课件

等效变换自动控制原理课 件
本课件介绍了等效变换自动控制原理的基本概念和原理,探讨了等效变换在 自动控制中的广泛应用,并讨论了等效变换的优点和局限性。
通过数学方法和计算过程的详细说明,结合实例分析,帮助大家全面理解等 效变换在自动控制中的重要性。
最后,通过总结和结论,我们对等效变换自动控制原理进行了进一步的讨论 和思考。
等效变换在自动控制中的应用
等效变换在自动控制中有着广泛的应用,包括系统建模、系统分析和控制器设计等方面。 通过将系统转化为等效模型,可以更好地理解系统的动态特性、稳定性和性能。 等效变换还可以用于解决多变量系统的控制问题,提高系统的控制效果和鲁棒性。
等效变换的优点和局限性
优点
等效变换可以简化系统分析和设计过程,提高 工程效率。
等效变换的概念和原理
等效变换是一种在自动控制中广泛使用的数学方法,通过将复杂的系统转化 为等效的简化模型,简化了分析和设计过程。
等效变换的原理是通过变换系统的输入和输出,将系统转化为具有特定特性 的等效模型,从而更好地理解和控制系统的行为。
等效变换的概念和原理对于自动控制工程师和研究人员来说是非常重要的基 础知识。
等效变换实例分析
1
步骤 2
2
通过等效变换方法,将机械振动系统转
化为等效的电路模型。
3
步骤 1
选择一个复杂的系统,例如一个机械振 动系统。
步骤 3
分析和设计电路模型的控制器,以实现 对振动系统的良好控制。
总结和结论
通过本课件的学习,我们深入了解了等效变换自动控制原理的基本概念、原理和应用。 我们了解了等效变换的优点和局限性,并学会了使用数学方法和计算过程进行等效变换的分析和设计。 通过实例分析,我们进一步理解了等效变换在自动控制中的重要性和实际应用。 希望这些知识能够对大家在自动控制领域的学习和工作有所帮助。
本课件介绍了等效变换自动控制原理的基本概念和原理,探讨了等效变换在 自动控制中的广泛应用,并讨论了等效变换的优点和局限性。
通过数学方法和计算过程的详细说明,结合实例分析,帮助大家全面理解等 效变换在自动控制中的重要性。
最后,通过总结和结论,我们对等效变换自动控制原理进行了进一步的讨论 和思考。
等效变换在自动控制中的应用
等效变换在自动控制中有着广泛的应用,包括系统建模、系统分析和控制器设计等方面。 通过将系统转化为等效模型,可以更好地理解系统的动态特性、稳定性和性能。 等效变换还可以用于解决多变量系统的控制问题,提高系统的控制效果和鲁棒性。
等效变换的优点和局限性
优点
等效变换可以简化系统分析和设计过程,提高 工程效率。
等效变换的概念和原理
等效变换是一种在自动控制中广泛使用的数学方法,通过将复杂的系统转化 为等效的简化模型,简化了分析和设计过程。
等效变换的原理是通过变换系统的输入和输出,将系统转化为具有特定特性 的等效模型,从而更好地理解和控制系统的行为。
等效变换的概念和原理对于自动控制工程师和研究人员来说是非常重要的基 础知识。
等效变换实例分析
1
步骤 2
2
通过等效变换方法,将机械振动系统转
化为等效的电路模型。
3
步骤 1
选择一个复杂的系统,例如一个机械振 动系统。
步骤 3
分析和设计电路模型的控制器,以实现 对振动系统的良好控制。
总结和结论
通过本课件的学习,我们深入了解了等效变换自动控制原理的基本概念、原理和应用。 我们了解了等效变换的优点和局限性,并学会了使用数学方法和计算过程进行等效变换的分析和设计。 通过实例分析,我们进一步理解了等效变换在自动控制中的重要性和实际应用。 希望这些知识能够对大家在自动控制领域的学习和工作有所帮助。
自动控制原理第5讲(结构图化简)
1. 利用串联、并联和反馈的结论进行简化
2. 变成大闭环路套小闭环路
3. 解除交叉点(同类互移)
比较点移向比较点:比较点之间可以互移 引出点移向引出点:引出点之间可以互移 注:比较点和引出点之间不能互移
引出点移动
G1 G2
H2 G3 H3 H1 G4
H2
1 G4
G1
G2
H1
G3 a G4 H3
b
比较点移动
x2 x4 x5 x3 x2
x3 x4 x3
L1 a23 a32
x2 x5 x3 x2
x4 x4
……
L2 a24 a43 a32
L3 a34 a43
Mixed node input node (source) a12 x1
1
a53 a44
4
a32
(1) ( m) (1m)
k :
为不与第k条前向通路相接触的那一部分信号流图 的 值,称为第k条前向通路特征式的余因子。
G4(s)
R(s)
C(S)/R(S)=?
G G22(s) (s) G G33(s) (s)
H3(s)
C(s)
G11(s) (s) G H1(s)
△1=1
R(s)
C(s) G 1(s) =?
n
n为相并联的环节数,当然还有“-”的情况。
结论:并联环节的等效传递函数等于并联环节传递函数的代数和。
(3)反馈连接(闭环控制系统)
R(s)
E(s) + - B(s)
G(s) H(s)
C(s)
R(s)
C(s)
(a)
(b)
推导(负反馈): C (s) E (s)G(s) [ R(s) C (s) H (s)]G(s)
2. 变成大闭环路套小闭环路
3. 解除交叉点(同类互移)
比较点移向比较点:比较点之间可以互移 引出点移向引出点:引出点之间可以互移 注:比较点和引出点之间不能互移
引出点移动
G1 G2
H2 G3 H3 H1 G4
H2
1 G4
G1
G2
H1
G3 a G4 H3
b
比较点移动
x2 x4 x5 x3 x2
x3 x4 x3
L1 a23 a32
x2 x5 x3 x2
x4 x4
……
L2 a24 a43 a32
L3 a34 a43
Mixed node input node (source) a12 x1
1
a53 a44
4
a32
(1) ( m) (1m)
k :
为不与第k条前向通路相接触的那一部分信号流图 的 值,称为第k条前向通路特征式的余因子。
G4(s)
R(s)
C(S)/R(S)=?
G G22(s) (s) G G33(s) (s)
H3(s)
C(s)
G11(s) (s) G H1(s)
△1=1
R(s)
C(s) G 1(s) =?
n
n为相并联的环节数,当然还有“-”的情况。
结论:并联环节的等效传递函数等于并联环节传递函数的代数和。
(3)反馈连接(闭环控制系统)
R(s)
E(s) + - B(s)
G(s) H(s)
C(s)
R(s)
C(s)
(a)
(b)
推导(负反馈): C (s) E (s)G(s) [ R(s) C (s) H (s)]G(s)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K2 (s
1)
ua (s) u2 (s)
K3
u1(s) K2(s 1) u2 (s)
u2(s)K3 ua (s)
Wednesday, November 18, 2020
3
反馈环节:
u f (s) (s)
K
f
(s)
Kf
u f (s)
电动机环节: 返回例2-6
(Tms 1)(s) Kuua (s) KmMc (s)
相加点和分支点在一般情况下,不能互换。
X (s)
Xቤተ መጻሕፍቲ ባይዱ3 (s)
G(s)
X (s)
X 3 (s)
G(s)
X 2 (s)
X 2 (s)
所以,一般情况下,相加点向相加点移动,分支点向分支
点移动。
Wednesday, November 18, 2020
12
结构图的化简, 应注意以下两点:
1. 化简的关键是解除环路与环路的交叉,或形成大环套小环的 形式.
把相加点从环节的输入端移到输出端
X1(s) X2(s)
G(s) Y (s)
Wednesday, November 18, 2020
X1(s) G(s) X 2(s) N(s)
N(s) G(s)
Y (s)
8
信号相加点的移动和互换
把相加点从环节的输出端移到输入端:
X1(s) G(s) X 2 (s)
第三节 结构图及其等效变换
Wednesday, November 18, 2020
1
结构图的基本概念
一、结构图的基本概念:
我们可以用方块图表示系统的组成和信号流向。在引入传 递函数后,可以把环节的传递函数标在方块图的方块里,并把 输入量和输出量用拉氏变换表示。这时Y(s)=G(s)X(s)的关系可 以在结构图中体现出来。
X (s) G1(s) …
Y (s) Gn (s)
环节的并联:
G1 ( s )
X (s)
Y (s)
G(s)
Y (s) X (s)
n i 1
Gi (s)
反馈联接:
X (s) E(s) G(s) Y (s)
Gn (s)
Y (s) E(s)G(s)
H (s)
Y (s) n
G(s) X (s) i1 Gi (s)
2
结构图的基本概念
[例2-10]求例2-5所示的速度控制统的结 构图。各部分传递函数见例2-6.
比较环节:
ue (s) ug (s) u f (s)
ug (s) ue (s) u f (s)
运放Ⅰ:
u1 ( s) ue (s)
K1,
ue (s) K1 u1(s)
运放Ⅱ:
功放环节:
u2 (s) u1(s)
Wednesday, November 18, 2020
E(s) X (s) H (s)Y (s),
G(s)
Y (s) X (s)
1
G(s) G(s)H (s)
7
信号相加点的移动
(二)信号相加点和分支点的移动和互换:
如果上述三种连接交叉在一起而无法化简,则要考虑移动某 些信号的相加点和分支点。 ①信号相加点的移动:
Mc (s)
Km Tms 1
Ua (s)
Ku Tms 1
- (s)
将上面几部分按照逻辑连接起来,形成下页所示的完 整结构图。
Wednesday, November 18, 2020
4
结构图的基本概念
M c (s) Km (Tas 1)
TaTms Tms 1
ug (s)
ue (s)
K1
u1(s) K2(s 1) u2 (s)
K3
ua (s)
Ku TaTms Tms 1
u f (s)
Kf
- (s)
在结构图中,不仅能反映系统的组成和信号流向,还能表 示信号传递过程中的数学关系。系统结构图也是系统的数学模 型,是复域的数学模型。
Wednesday, November 18, 2020
5
结构图的等效变换
二、结构图的等效变换:
Y (s)
X1(s)
X2(s) N(s)
G(s) Y (s)
N(s) ? Y (s) X1(s)G(s) X 2(s), Y (s) X1(s)G(s) X 2(s)N(s)G(s), N(s) 1
G(s)
Wednesday, November 18, 2020
9
信号分支点的移动和互换
X3(s)
Y (s)
X1(s)
X3(s)
X 2 (s)
Y (s)
Wednesday, November 18, 2020
11
信号相加点和分支点的移动和互换
同一信号的分支点位置可以互换:见下例
X1(s)
X (s) G(s) Y (s)
X 2 (s)
X (s) G(s) Y (s)
X 2 (s)
X1(s)
2. 解除交叉连接的有效方法是移动相加点或分支点.
Wednesday, November 18, 2020
13
结构图等效变换例子||例2-11
[例2-11]利用结构图等效变换讨论两级RC串联电路的传递函数。
R1
R2
ui
i1
i, u
C1i2 C2
[解]:不能把左图简单地看成两个
i2
uo
[定义]:表示变量之间数学关系的方块图称为动态结构图或结 构图。
[例]:结构: X(t) 放大器 结Y(构t) 图:
X(s)
Y(s)
G(s)=K
微分方程:y(t)=kx(t)
若已知系统的组成和各部分的传递函数,则可以画出各个部 分的结构图并连成整个系统的结构图。
Wednesday, November 18, 2020
分支点从环节的输出端移到输入端:
X1(s) G(s) Y (s) Y (s)
X1(s) G(s) Y (s) N(s) Y (s)
N(s) ? X1(s)G(s) Y(s), X1(s)N(s) Y(s),N(s) G(s)
[注意]:
相临的信号相加点位置可以互换;见下例
X1(s)
X2(s)
②信号分支点的移动: 分支点从环节的输入端移到输出端
X1(s) G(s) Y (s)
X1(s)
X1(s) G(s)
Y (s)
N(s) X1(s)
N(s) ?
X1(s)G(s)N (s)
X1(s), N (s)
1 G(s)
Wednesday, November 18, 2020
10
信号相加点和分支点的移动和互换
[定义]:在结构图上进行数学方程的代数运算。 [原则]:变换前后环节的数学关系保持不变。
[类型]:①环节的合并; --串联 --并联 --反馈连接
②信号分支点或相加点的移动。
Wednesday, November 18, 2020
6
环节的合并
(一)环节的合并:有串联、并联和反馈三种形式。
环节的串联:
