选修11第一章常用逻辑用语1.4逻辑联结词“且”或“非”
2021年高中数学第一章常用逻辑用语1.4逻辑联结词“且”“或”“非”课件4北师大版选修2_1

所以 a 1, 解得a≤-1. 所以实a数<a0或的a取值4,范围是(-∞,-1]. 答案:(-∞,-1]
复合命题
p或q
p且q
非p
全真为真, 有假即假。
全假为假, 有真即真。
真假相反
1.命题“方程|x|=1的解是x=±1〞中,使用逻辑 词的情况是〔 B 〕 A.没有使用逻辑联结词 B.使用了逻辑联结词“或〞 C.使用了逻辑联结词“且〞 D.使用了逻辑联结词“或〞与“且〞
一般地,用逻辑联结词“ 或 〞把命题p和命题q联结起 来就得到一个新命题,记作p∨q, 读作“p或q〞
我们可以从并联电路理解联结词“或〞的 含义.假设开关p,q的闭合与断开分别对应 命题p,q的真与假,那么整个电路的接通与 断开分别对应命题p∨q的真与假.
p
q
s
例2 判断以下命题的真假: 〔1〕2 ≤ 2. 〔2〕集合A是A∩B的子集或是A∪B的子集.
一般地,对一个命题 p 加以否认,就能得到一个新命题,
记作 p,读作“非p”或“p的否定”.
p与﹁p的真假关系? 假设p是真命题,那么﹁p必是假命题; 假设p是假命题,那么﹁p必是真命题. 简记为:真假相反.
【提升总结】
一般地,对一个命题p全盘否认, 就得到一个新命题,记作:﹁p 读作“非p〞或“p的否认〞
q :平行四边形的对角线相等.
解: p ∧q : 平行四边形的对角线互相平分且相等. 假命题
〔2〕 p :35是15的倍数; q :35是7的倍数.
解: p∧q : 35是15的倍数且是7的倍数.
假命题
探究二 : 或 〔1〕27是7的倍数. 〔2〕27是9的倍数. 〔3〕27是7的倍数 或 是9的倍数.
等价于
高中数学第一章常用逻辑用语1.4逻辑联结词“且”“或”“非”1121数学

数或负数. 2、已知命题p :方程 x2+mx+1=0 有两个不相等的实负根,命题 q:方程
4x2+4(m-2)x+1=0无实根;若 p或q 为真,p 且 q为假,求实数 的取值范围.
(2)p: 2是无理数,q: 大2 于1 解:
(1) pq: 矩形的对角线互相垂直(chuízhí)且平 (2) pq: 分2 是大于1的无理数。
12/9/2021
第十页,共二十页。
pq 当p,q都是真命题(mìng tí)时,
是真命题(mìng ; tí)
当p ,q 两个命题中有一个命题是假命题时,
歌德是18世纪德国的一位著名文艺大师,一天,他与一位文
艺批评家“狭路相逢”。这位批评家生性古怪,遇到(yù dào)歌德 走来 ,不仅没有相让,反而卖弄聪明,一边高傲地往前走,一
边大声说道:“我从来不给傻子让路!”面对如此尴尬局面,但 见歌德笑容可掬,谦恭地闪在一旁,一边有礼貌地回答道:“呵 呵,我可恰恰相反。”结果故作聪明的批评家,反倒自讨个没趣。
12/9/2021
第五页,共二十页。
12/9/2021
第六页,共二十页。
思考(sīkǎo):命题的否定与 “若两个三角形全等,则它们(tā men)相似” 否命题的区别?
任何一个命题都有否定, 对于命题“若p,则 q”的否定可表示(biǎoshì)为 “若p,则非q”, 命题“若p,则 q”的否命题可表示为“若非p,则非q”
③ “ p或q ”形式的命题当p与q同时为假时为假, 否则为真.(全假为假,有真即真)
推荐高中数学第一章常用逻辑用语1.4.1_1.4.2逻辑联结词“且”逻辑联结词“或”课件北师大版选修1_1

Δ =m2-4>0,
[解] p 为真命题⇔-m<0,
⇒m>2.
1>0
q 为真命题⇔Δ =[4(m-2)]2-4×4×1<0⇒1<m<3.
因为“p 或 q”为真,“p 且 q”为假,
所以 p 与 q 一真一假.
若 p 真 q 假,则 m>2,且 m≤1 或 m≥3,
所以 m≥3.
若 p 假 q 真,则 m≤2,且 1<m<3,所以 1<m≤2.
2.如果命题“p 且 q”为真命题,则( B ) A.p,q 均为假命题 B.p,q 均为真命题 C.p,q 中至少有一个为真命题 D.p,q 中至多有一个为真命题 解析:当 p,q 均为真命题时,“p 且 q”为真命题.
3.“1≤1”是____p_或__q_______形式的命题(填“p 且 q”或“p 或 q”),此命题是__真______命题(填“真”或“假”).
[方法归纳] 判断 p 或 q 形式的命题的真假,首先判断命题 p 与命题 q 的 真假,只要有一个为真,即可判定 p 或 q 形式命题为真,而 p 与 q 均为假命题时,命题 p 或 q 为假命题,可简记为有真则 真,全假为假.
2.对下列各组命题,利用逻辑联结词“或”构造新命题,并 判断新命题的真假. (1)p:梯形有一组对边平行,q:梯形有一组对边相等; (2)p:-1 是方程 x2+4x+3=0 的解,q:-3 是方程 x2+4x +3=0 的解. 解:(1)p 或 q:梯形有一组对边平行或有一组对边相等.
用“且”联结两个命题 p 和 q,构成一个新命题 “____p_且__q______”.当两个命题 p 和 q 都是__真_____命题时,
新命题“p 且 q”是真命题;在两个命题 p 和 q 之中,只要有一 个命题是__假________命题,新命题“p 且 q”就是假命题.
高中数学第一章常用逻辑用语1.4逻辑联结词“且”“或”“非”5121数学

真假:
真
(1) p: 12是3的倍数, 真 p∧qq:: 1122是是34的的倍倍数数(b;èishù)且12是4的倍数. 真
真
(2) p: π > 3 , 假 p∧qq:: ππ大< 于2 ;3且小于2. 假
假
(3) p:
p∧qq::
666是是是奇奇素数数数,且. 是假素数.
假
第四页,共二十页。
小组讨论1:“p∧q”的真假与p、q的真假有何关系(guān xì)?
【思考】命题的否定的否定是原命题吗?
提示:是
第十页,共二十页。
探究4:命题的否定(fǒudìng)与否命题的区别? 原命题:正方形的四条边相等.
若一个四边形是正方形,则它的四条边相等.
命题的否定: 正方形的四条边不相等.
若一个四边形是正方形,则它的四条边不相等.
否命题: 若一个四边形不是正方形,则它的四条边不相等.
就得到一个新命题, 记作:“p∧q”,读作:“p且q”
从集合角度看:P∩Q={x|x∈P且x∈Q}
P
P∩Q
Q
第三页,共二十页。
P∩Q
小探究组(讨tànj论iū)11::逻“p辑∧联q”结的词真“假且与”p、q的真假有何关系?
例1 用“且”构造新命题(mìng tí),并判断命题(mìng tí)的
简记(jiǎn jì)“p且q,同真则真,有假则假”
【思考】
1.若“p∧q”是假命题,则命题p、q都是假命题吗?为何? 提示:不一定,因为命题p、q中只要有一个(yī ɡè)是假命题, “p∧q”就是假命题. 2.判断“p∧q”命题真假的关键是什么? 提示:关键是判断命题p、q的真假.
第五页,共二十页。
高中数学 第一章 常用逻辑用语 1.4 逻辑联结词“且”“或”“非”课件3 北师大版选修2-1

非p
真假相反
p且q
一假必假
p或q
K12课件 一真必真
21
假
K12课件
3
1.“且”与物理电路
pq
2.“且”与集合中交集的定义: A∩B={x|x∈A,且x∈B}中的“且”意义相同.
A∩B 与生活中的“且”
A
B
含义相同
K12课件
4
用逻辑联结词“且”改写下列命题,并判断它们的 真假:
(1) 1既 是奇数,又 是素数; 解:1 是奇数且 1 是素数
是假命题
(2)2 和 3 都是素数。
(4) 24既是8的倍数,也是6的倍数;真
(5) 2是偶数且2是素数; 真
K12课件
16
4.如果命题p是假命题,命题q是真命题,则
下列错误的是( D )
A.“p且q”是假命题 B.“p或q”是真命 题
C.“非p”是真命题 真命题
D.“非q”是
K12课件
17
5. 以下判断正确的是
(A)命题p是真命题时,命题“p且q”一定 是真命题
•
q: 12是4的倍数
• (2)p: ﹥3 ,
•
q: ﹤2
K12课件
6
探究2、将命题p和命题q用“或”联结 成新命题.
p: 27是3的倍数; q: 27是9的倍数;
一般地,用逻辑联结词“ 或 ”把命 题p和命题q联结起来就得到一个新命题,
记作p∨q, 读作“p或q”.
K12课件
7
1:命题p:函数 y x3 是奇函数;
真
命题q:函数 y x3 在定义域内是增函数;
真
命题p ∨ q:函数y x3 是奇函数或在定义
高中数学第一章常用逻辑用语1.4逻辑联结词“且”“或”“非”课件北师大版选修1_1

解得 m>0.
当 p 真 q 假时,有
> -2,
≤ 0,
解得 m≤-2.
当 p 假 q 真时,有
≤ -2,综上可知,实数 Nhomakorabeam 的取值范围是(-∞,-2]∪(0,+∞).
解得
−2
−1
-2
≤0⇔
-1
∵
(-2)(-1) ≤ 0,
⇔1<x≤2,
-1 ≠ 0
【规范展示】
解若 f(x)=2 + 的定义域为 R,必有 m>0,且 f(x)一定为奇函数,
故当命题 p 为真时,m>0.
若 g(x)=mx2 +2x-1 在
1
,
2
+ ∞ 上是减少的,必有
< 0,
-
1
1
2
≤ ,
m≤-2,故当命题 q 为真时,m≤-2.
因为命题 p∧q 为假,p∨q 为真,所以 p 与 q 一真一假.
学 习 目 标
1.了解逻辑联结词
“且”“或”“非”的含义.
2.掌握用逻辑联结词
改写命题的方法.
3.掌握判断含逻辑联
结词的命题真假的方
法.
4.掌握根据命题的真
假求参数取值范围的
方法.
思
维 脉 络
使用的逻辑联结词
命题形式
读法
且
p∧q
p且q
或
p∨q
p或q
非
p
非p
p
q
p∨q
p∧q
p
真
真
真
真
假
真
p 是 q 的充要条件⇔p 是q 的充要条件
高中数学 第一章 常用逻辑用语 1.4 逻辑联结词“且”“或”“非”1.4.2 逻辑联结词“非”课时

1.4.2 逻辑联结词“非”一、选择题1.已知p:2+2=5,q:3>2,则下列判断中,错误的是( )A.p∨q为真,¬q为真B.p∧q为假,¬p为真C.p∧q为假,¬q为假D.p∧q为假,p∨q为真解析:由于p是假命题,q是真命题,所以p∨q为真,p∧q为假,¬p真,¬q假,由此可知,A不正确,故选A.答案:A2.[2014·北京四中月考]若(¬p)∨q是假命题,则( )A. p∧q是假命题B. p∨q是假命题C. p是假命题D. ¬q是假命题解析:本题主要考查含有逻辑联结词的命题的真假性判断.由于(¬p)∨q是假命题,则¬p与q均是假命题,所以p是真命题,¬q是真命题,所以p∧q是假命题,p∨q是真命题,故选A.答案:A3.在一次射击比赛中,甲、乙两位运动员各射击一次,设命题p:“甲的成绩超过9环”,命题q:“乙的成绩超过8环”,则命题“p∨(¬q)”表示( )A. 甲的成绩超过9环或乙的成绩超过8环B. 甲的成绩超过9环或乙的成绩没有超过8环C. 甲的成绩超过9环且乙的成绩超过8环D. 甲的成绩超过9环且乙的成绩没有超过8环解析:本题主要考查含有逻辑联结词的命题的意义以及在生活中的应用.¬q表示乙的成绩没有超过8环,所以命题“p∨(¬q)”表示甲的成绩超过9环或乙的成绩没有超过8环,故选B.答案:B4.已知全集U=R,A⊆U,B⊆U,若命题p:a∈(A∩B),则命题“¬p”是( )A.a∈AB.a∈∁U BC.a∈(A∪B)D.a∈(∁U A)∪(∁U B)解析:∵p:a∈(A∩B),∴¬p:a∉(A∩B),即a∈∁U(A∩B).而∁U(A∩B)=(∁U A)∪(∁U B),故选D.答案:D二、填空题5.[2014·江西省临川一中月考]“末位数字是1或3的整数不能被8整除”的否定形式是________,否命题是________.解析:本题主要考查命题的否定与其否命题的区别.命题的否定仅否定结论,所以该命题的否定形式是:末位数字是1或3的整数能被8整除;而否命题要同时否定原命题的条件和结论,所以否命题是:末位数字不是1且不是3的整数能被8整除.答案:末位数字是1或3的整数能被8整除末位数字不是1且不是3的整数能被8整除6.命题p:{2}∈{1,2,3},q:{2}⊆{1,2,3},则对复合命题的下述判断:①p∨q为真;②p∨q为假;③p∧q为真;④p∧q为假;⑤¬p为真;⑥¬q为假.其中判断正确的序号是__________.(填上你认为正确的所有序号)解析:由已知得p为假命题,q为真命题,所以可判断①④⑤⑥为真命题.答案:①④⑤⑥7.若命题p:函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,若¬p是假命题,则a的取值范围是__________.解析:¬p是假命题,则p是真命题,因此问题就是求p真时a的取值范围.要使函数f(x)=x2+2(a-1)x+2在(-∞,4]上单调递减,只需对称轴1-a≥4,∴a≤-3.答案:(-∞,-3]三、解答题8.已知p:x2-x≥6,q:x∈Z,若p∧q和¬q都是假命题,求x的值.解:由x2-x≥6得x2-x-6≥0,解之得x≥3或x≤-2,即p:x≤-2或x≥3,q:x∈Z,若¬q假,则q真,又p∧q假,则p假.当p假,q真时,有-2<x<3,且x∈Z,∴x=-1,0,1,2.9.已知:p:方程x2+mx+1=0有两个不等的负实根;q:方程4x2+4(m-2)x+1=0无实根.若p且q为假,¬p为假,求m的取值范围.解:p :⎩⎪⎨⎪⎧ Δ=m 2-4>0,m >0,解得m >2.q :Δ=16(m -2)2-16=16(m 2-4m +3)<0. 解得1<m <3.∵p 且q 为假,¬p 为假.∴p 为真,q 为假,即⎩⎪⎨⎪⎧ m >2,m ≤1或m ≥3,解得m ≥3,∴m 的取值范围为[3,+∞).。
常用逻辑用语 逻辑联结词“且”“或”“非”

5.给出如下条件: (1)“p成立,q不成立”; (2)“p不成立,q成立”; (3)“p与q都成立”; (4)“p与q都不成立”. 其中能使“p或q”成立的是________(填序号). [答案] (1)(2)(3)
逻辑联结词非
新知导学
5.一般地,对命题p加以否定,就得到一个新的命题,记作 ____¬_p_,读作___非__p_或___p的__否__定___. 6.若p是真命题,则¬p是____假_命题,若p是假命题,则¬p是 ____真_命题.
[解析] (1)这个命题是“p且q”的形式,其中,p:小李是老 师;q:小赵是老师.
(2)这个命题是“p或q”的形式,其中,p:1是合数;q:1是 质数.
(3)这个命题是“p且q”的形式,其中,p:他是运动员;q: 他是教练员.
(4)这个命题是“p且q”的形式,其中,p:这些文学作品艺术 上有缺点;q:这些文学作品政治上有错误.
(2) 从 如 图 所 示 串 联 开 关 电 路 上 看 , 当 两 个 开 关 S1 、 S2 __________时,灯才能亮;当两个开关S1、S2中一个不闭合 或都两闭个合都不闭合时,灯都不会亮.
(3)从集合角度理解“且”即集合运算“_____交”.
设命题p:x∈A,命题q:x∈B,
则p且q⇔x∈A,且x∈B⇔x∈(A∩B).
(灯2)就从亮并联,开只关有电当路两上个看开,关当S两1 和个S开2_关_S__1、__S都_2_至断__少开时有,一灯个才闭不合时会, 亮.
(3)从集合角度理解“或”即集合运算“___”并. 设命题p:x∈A,命题q:x∈B, 则p或q⇔x∈A,或x∈B⇔x∈(A∪B).
(4)当p、q两个命题有一个命题是真命题时,p或q是____真命题; 当p、q两个命题都是假命题时,p或q是____假命题.
高中数学:1.4逻辑联结词“且,或,非” 教案 (北师大选修1-1)

第一章常用逻辑用语第4.1节逻辑联结词“且”第4.2节逻辑联结词“或”第4.3节逻辑联结词“非”一、创设情境前面我们学习了命题的概念、命题的构成和命题的形式等简单命题的基本框架。
本节内容,我们将学习一些简单命题的组合,并学会判断这些命题的真假。
问题1:下列语句是命题吗?如果不是,请你将它改为命题的形式①11>5 ②3是15的约数吗?③0.7是整数④x>8二、活动尝试①是命题,且为真;②不是陈述句,不是命题,改为3是15的约数,则为真;③是假命题④是陈述句的形式,但不能判断正确与否。
改为x2≥0,则为真;例如,x<2,x-5=3,(x+y)(x-y)=0.这些语句中含有变量x或y,在没有给定这些变量的值之前,是无法确定语句真假的.这种含有变量的语句叫做开语句(有的逻辑书也称之为条件命题)。
我们不要在判断一个语句是不是命题上下功夫,因为这个工作过于复杂,只要能从正面的例子了解命题的概念就可以了。
三、师生探究问题2:(1)6可以被2或3整除;(2)6是2的倍数且6是3的倍数;(3上述三个命题前面的命题在结构上有什么区别?比前面的命题复杂了,且(1)和(2)明显是由两个简单的命题组合成的新的比较复杂的命题。
命题(1)中的“或”与集合中并集的定义:A∪B={x|x∈A或x∈B}的“或”意义相同.命题(2)中的“且”与集合中交集的定义:A∩B={x|x∈A且x∈B}的“且”意义相同.命题(3否定而得出的新命题.四、数学理论1.逻辑连接词命题中的“或”、“且”、“非”这些词叫做逻辑联结词2. 复合命题的构成简单命题:不含有逻辑联结词的命题叫做简单命题复合命题:由简单命题再加上一些逻辑联结词构成的命题叫复合命题3.复合命题构成形式的表示常用小写拉丁字母p、q、r、s……表示简单命题.复合命题的构成形式是:p或q;p且q;非p.即:p或q 记作p∨q p且q 记作p∧q 非p (命题的否定) 记作⌝p释义:“p 或q ”是指p,q 中的任何一个或两者.例如,“x ∈A 或x ∈B ”,是指x 可能属于A 但不属于B (这里的“但”等价于“且”),x 也可能不属于A 但属于B ,x 还可能既属于A 又属于B (即x ∈A ∪B );又如在“p 真或q 真”中,可能只有p 真,也可能只有q 真,还可能p,q 都为真.“p 且q ”是指p,q 中的两者.例如,“x ∈A 且x ∈B ”,是指x 属于A ,同时x 也属于B (即x ∈A I B ). “非p ”是指p 的否定,即不是p. 例如,p 是“x ∈A ”,则“非p ”表示x 不是集合A 的元素(即x ∈U A ð).五、巩固运用例1:指出下列复合命题的形式及构成它的简单命题:(1)24既是8的倍数,也是6的倍数;(2)李强是篮球运动员或跳高运动员;(3)平行线不相交解:(1)中的命题是p 且q 的形式,其中p :24是8的倍数;q :24是6的倍数.(2)的命题是p 或q 的形式,其中p :李强是篮球运动员;q :李强是跳高运动员.(3)命题是非p 的形式,其中p :平行线相交。
高中数学第一章常用逻辑用语1.4逻辑联结词“且”“或”“非”课件北师大版选修11

使用的逻辑联结词
命题形式
读法
且
p∧q
p且q
或
p∨q
p或q
非
p
非p
名师点拨(diǎn bo)1.对于逻辑联结词“且”“或”“非”,可以
分别结合集合中的“交集”“并集”“补集”来进行理解.
2.简单命题与复合命题:不含逻辑联结词“且”“或”“非”的
命题是简单命题,由简单命题与逻辑联结词构成的命题是复合命题,
三
思维辨析
反思感悟1.用逻辑联结词构造新命题的两个步骤:
(1)确定两个简单命题p,q;
(2)分别用逻辑联结词“且”“或”“非”将p和q联结起来,即得新命题.
2.用逻辑联结词“且”“或”“非”联结两个命题,关键是正确理解这些词语
的意义及在日常生活中的同义词,选择合适的联结词,有时为了语法的要求
及语句的通顺也可进行适当的省略和变形.
探究(tànjiū)
一
探究
(tànjiū)二
探究
(tànjiū)三
思维辨析
变式训练2分别指出下列各组命题构成的“p∧q”“p∨q”“ p”形式的
命题的真假.
(1)p:梯形有一组对边平行;q:梯形有一组对边相等;
(2)p:1是方程x2-4x+3=0的根;q:3是方程x2-4x+3=0的根;
(3)p:不等式x2-2x+1>0的解集为R;q:不等式x2-2x+2≤1的解集为⌀.
1.4 逻辑(luó jí)联结词“且”“或”“非”
第一页,共30页。
学 习 目 标
思
维 脉 络
1.了解逻辑联结词
“且”“或”“非”的含义.
2.掌握用逻辑联结词
改写命题的方法.
高中数学 第一章 常用逻辑用语 1.4 逻辑联结词“且”“或”“非”跳出“非”的误区素材 北师大版选修21

跳出“非”的误区在高一新教材第一章集合与简易逻辑中介绍了“非”是三个逻辑联结词之一,课本上把p ⌝称为命题p 的否定(介绍的不透彻),不少高一学生对“非”的把握和运用上存在误区。
对于一个命题的否定,并不是简单的在判断词前添加否定词就可以完成的。
下面从两个方面举例加以说明。
1 “非”与集合求“补”意义一样例1 已知2:60,P x x +-> 4:02x q x +>-则p q ⌝⌝是的____________条件。
错解:2:60,32p x x x ⌝+-≤-≤≤因为即,4:0,422x q x x +⌝≤-≤<-即。
p q ⌝⌝所以是的即不充分也不必要条件。
分析:p ⌝是对原命题结论加以否定,它和原命题是“非此即彼”的矛盾关系,而不一定是一种对立关系。
从集合的角度考虑,逻辑中的求“非”相当于集合中的求“补”,所以402x x +>-的否定就是使它不成立,即40202x x x +≤-=-或(原式无意义)两种情况。
正解:2:6023P x x x x +->><-即或, 4:0242x q x x x +>><--即或, :32,p x ⌝-≤≤所以 :42q x ⌝-≤≤从而p q ⌝⌝是的充分不必要条件。
此题也可用原命题的等价命题——逆否命题来求解,即要求p q ⌝⌝是的什么条件,只要先求q p 是的什么条件,我们不难得到此题q p 是充分不必要条件,所以p q ⌝⌝是的充分不必要条件。
类似的例子还有:(1)若221p p x >⌝<则或,(2)若:lg 2:lg 20p x p x x >⌝≤≤则或。
上述例子都是以R 为全集来研究的,否则要说明清楚。
变式 已知关于x 的不等式250ax x a-<-的解集为M ,当3,5M M ∈∉时,求实数a 的取值范围。
解:因为3M ∈,所以3509a a -<-,解得593a a ><或, 又因为5M ∉,所以55025a a-≥-,解得125a ≤≤, 所以a 的取值范围5[1,](9,25)3U . 这是一个错误的解答,正确的答案为5[1,](9,25]3U ,请想想为什么? 2 “非p ” 必须包括p 的所有对立面 例2 已知p :方程210x mx ++=有两个不等的负实根;q :方程 244(2)10x m x +-+=无实根,若“p q 或”为真,“p q 且”为假,求实数m 的取值范围。
高中数学第一章常用逻辑用语1.4逻辑联结词“且”“或”“非”教案北师大版选修2-1(2021学年)

河南省确山县高中数学第一章常用逻辑用语1.4 逻辑联结词“且”“或”“非”教案北师大版选修2-1编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(河南省确山县高中数学第一章常用逻辑用语 1.4 逻辑联结词“且”“或”“非”教案北师大版选修2-1)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为河南省确山县高中数学第一章常用逻辑用语 1.4 逻辑联结词“且”“或”“非”教案北师大版选修2-1的全部内容。
逻辑连接词“且”“或”“非”【教学目标】1。
掌握逻辑联结词“或、且”的含义 2。
正确应用逻辑联结词“或、且”解决问题 3。
掌握真值表并会应用真值表解决问题 【知识梳理】1“复合命题”的概念” 2.复合命题的构成形式是什么?p 或q(记作“p ∨q ” ); p且q (记作“p ∧q ” );非p(记作“┑q ” )3。
一般地,用联结词“且”把命题p 和命题q 联结起来,就得到一个新命题,记作p ∧q 读作___________________。
4.一般地,用联结词“或"把命题p 和命题q 联结起来,就得到一个新命题,记作p ∨q,读作__________________。
5.一般地,对命题p加以否定,就得到一个新命题,记作“┑q ”,读作______。
6.命题的否定是否定命题的______,而命题的否命题是对原命题的_________同时进行否定二:真值表1。
p 且q 形式(同真为真,有假为假)2。
p 或q 形式(同假为假,有真为真)3.非p 形式:(真假相反)【典型例题】例1。
写出由下列各组命题构成的“p或q"、“p且q”、“┑q"形式的复合命题,并判断真假.(1)p:1是质数;q:1是方程x2+2x-3=0的根;(2)p:平行四边形的对角线相等;q:平行四边形的对角线互相垂直;(3)p:0∈∅;q:{x|x2-3x-5〈0}⊆R;(4)p:5≤5;q:27不是质数.例2.已知命题p:函数f(x)=x2+2mx+1在(-2,+∞)上单调递增;命题q:函数g(x)=2x2+2错误!(m-2)x+1的图像恒在x轴上方,若p或q为真,p且q为假,求m的取值范围.练习:1.设命题p:x〉2是x2〉4的充要条件;命题q:若错误!>错误!,则a>b,则( )A.p或q为真B.p且q为真 C.p真q假 D.p、q均为假2.由命题p:“函数y=错误!是减函数”与q:“数列a,a2,a3,…是等比数列”构成的命题,下列判断正确的是( )A.p或q为真,p且q为假B.p或q为假,p且q为假C.p或q为真,p且q为假D.p或q为假,p且q为真3.已知命题p:所有有理数都是实数;命题q:正数的对数都是负数,则下列命题中为真命题的是()A.(¬p)或q B.p且qC.(¬p)或(¬q) D.(¬p)且(¬q)4.已知命题p:a2+b2〈0(a,b∈R),命题q:a2+b2≥0(a,b∈R),下列结论正确的是( )A.“p或q”为真 B.“p且q”为真C.“¬p”为假D.“¬q"为真5.已知命题p:m〈0,命题q:x2+mx+1〉0对一切实数x恒成立,若p且q为真命题,则实数m的取值范围是( )A.m〈-2 B.m>2 C.m〈-2或m>2D.-2〈m〈06.下列命题错误的是( )A.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”B.若p且q为假命题,则p、q均为假命题C.命题p:存在x0∈R,使得x错误!+x0+1〈0,则¬p:任意x∈R,都有x2+x+1≥0D.“x>2”是“x2-3x+2>0”的充分不必要条件5.命题p:“若a、b、c成等比数列,则b2=ac",则¬p为________.6.已知命题p:m∈R,且m+1≤0,命题q:∀x∈R,x2+mx+1>0恒成立,若p且q为假命题且p或q为真命题,则m的取值范围是________.7.已知命题p:函数y=-x2+mx+1在(-1,+∞)上单调递减;命题q:函数y=mx2+x-1〈0恒成立.若p或q为真命题,p且q为假命题,求m的取值范围8。
高中数学第1章常用逻辑用语4逻辑联结词“且”“或”“非”课件北师大版选修11

逻辑联结词的综合应用
已知命题p:函数y=x2+2(a2-a)x+a4-2a3在[-2, +∞)上单调递增.q:关于x的不等式ax2-ax+1>0解集为R. 若p且q假,p或q真,求实数a的取值范围.
[思路导引] p真,求a的范围 ―→ q真,求a的范围 ―→
p,q一真一假,求a ―→ 结果
综合应用逻辑联结词求参数范围的一般步骤:
(3)此命题为“p 且 q”的形式,其中 p: 2∈Q,q: 2∈ R.因为 p 为假命题,q 为真命题,所以 p 且 q 为假命题,故原命 题为假命题.9 分
(4)此命题为“非 p”的形式,其中 p:A⊆(A∪B),因为 p 为真命题,所以“非 p”为假命题,故原命题为假命题.12 分
判断含逻辑联结词的命题真假的步骤
解析: 命题 p 为真⇔0<a<1.命题 q 为真⇔ax2-x+a>0 恒成立⇔aΔ>=01-4a2<0 ⇔a>12.
如果“p 或 q”为真命题,“p 且 q”为假命题,那么 p、q
中一个为真,另一个为假.
若 p 为真 q 为假,则 0<a<1 且 a≤21,所以 0<a≤21.
若 p 为假 q 为真,则 a≤0 或 a≥1,且 a>12,所以 a≥1.
“¬p”
“非p”
(1)不含逻辑联结词“且”“或”“非”的命题是简单命
题,由简单命题与逻辑联结词构成的命题是复合命题,因此就 有“p且q”“p或q”“非p”形式的复合命题,其中p、q是简单命题 ,由简单命题构成复合命题的关键是对逻辑联结词“且”“或”“ 非”的理解.
(2)用集合的观点理解“且”“或”“非”的含义 设集合A={x|x满足命题p},集合B={x|x满足命题q},U为 全集,则p且q对应于A∩B,p或q对应于A∪B,¬p对应于∁UA.
高中数学第一章常用逻辑用语4逻辑联结词“且”“或”“非”实用课件北师大版选修11
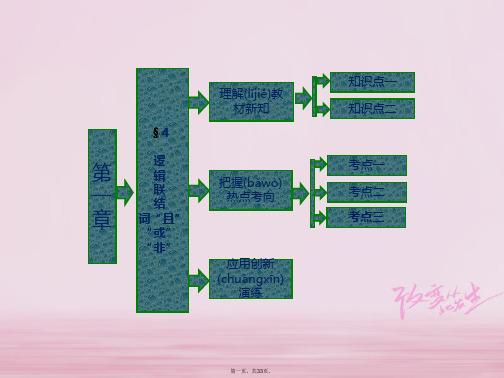
=1 的解是 x=±1.其中使用逻辑联结词的命题有 ( )
A.1 个
B.2 个
C.3 个
D.4 个
解析:①中使用逻辑联结词“且”;②中没有使用逻辑联
结词;③中使用逻辑联结词“非”;④中使用逻辑联结词
“或”,共有 3 个命题①③④使用逻辑联结词,故选 C. 答案:C
第十三页,共33页。
2.在一次射击比赛中,甲、乙两位运动员各射击一次,设命题 p: “甲的成绩超过 9 环”,命题 q:“乙的成绩超过 8 环”,则
q 为假,故选 D. 答案:D
第二十五页,共33页。
含逻辑联结词的命题真假的应用 [例 3] 已知 p:方程 x2+mx+1=0 有两个不等的负实根;q: 方程 4x2+4(m-2)x+1=0 无实根,若“p 或 q”为真,“p 且 q”为 假,求 m 的取值范围. [思路点拨] “p 或 q”为真,“p 且 q”为假,则 p,q 中必一 真一假;可分 p 真 q 假,p 假 q 真两种情况处理.
命题“p 或(綈 q)”表示
()
A.甲的成绩超过 9 环或乙的成绩超过 8 环 B.甲的成绩超过 9 环或乙的成绩没有超过 8 环 C.甲的成绩超过 9 环且乙的成绩超过 8 环 D.甲的成绩超过 9 环且乙的成绩没有超过 8 环
第十四页,共33页。
解析:綈 q 表示乙的成绩没有超过 8 环,所以命题“p 或(綈 q)” 表示甲的成绩超过 9 环或乙的成绩没有超过 8 环,故选 B. 答案:B
§4
第
逻 辑
一
联 结
章 词“且”
“或”
“非”
理解(lǐjiě)教 材新知
把握(bǎwò) 热点考向
应用创新 (chuàngxīn)
高中数学 第一章 常用逻辑用语 1.4.3 逻辑联结词“非”课件1高二选修11数学课件
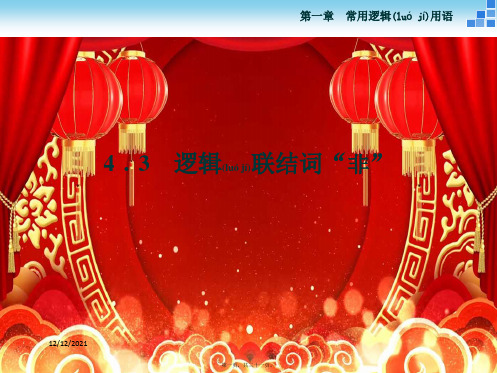
q”与“綈 q”同时为真命题,求实数 a 的取值范围.
解:命题 p:方程 x2+2ax+1=0 有两个大于-1 的实数根,
等价于
Δ=4a2-4≥0, x1+x2>-2,
a2-1≥0, ⇔-2a>-2,解得a≤-1.
(x1+1)(x2+1)>0 2-2a>0,
命题 q:关于 x 的不等式 ax2-ax+1>0 的解集为 R,等价于
4.已知全集 U=R,A⊆U,B⊆U,如果命题 p:a∈(A∪B), 则命题“綈 p”是( D )
A.綈 p:a∈A
B.綈 p:a∈∁UB
C.綈 p:a∉(A∩B)
D.綈 p:a∈[(∁UA)∩(∁UB)]
12/12/2021
第二十五页,共三十一页。
解析:借助 Venn 图,
因为 p:a∈(A∪B), 所以綈 p:a∈∁R(A∪B)=[(∁UA)∩(∁UB)].
12/12/2021
第三页,共三十一页。
2.真值表 一般地,“p 或 q”“p 且 q”与“非 p”形式的命题的真假性可 以用下面的表来分别表示:
p
q
真
真
p或q 真
p且q
非p
真
假
真
假
真
假
假
假
真
真
假
真
假
假
假
假
真
即“p且q”一假即假,全真(quán zhēn)方真;“p或q”一真即真,全假方 假;p与“非p”真假相对.
4.若 p:x2-1>0,q:(x+1)(x-2)>0,则綈 p 是綈 q 是
__充__分__(c_h_ōn_g_fè_n)_不__必__条件(填“充分不必要”“必要不充
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选修11第一章常用逻辑用语1.4逻辑联结词“且”或“非”
测试题 2019.9
1,当掷五枚硬币时,已知至少出现两个正面向上,则正好出现3个正面
向上的概率为
2,某射手每次射击击中目标的概率为0.8,此人每次射击相互没有影响,在此人10次射击中,击中目标的次数为X ,那么此人最有可能击中目标
的次数为
3,命题: 和是椭圆的两焦点,为椭圆上的点,过作∠的外角
平分线的垂线,垂足为, 则到椭圆中心的距离为该椭圆长轴长的一半.
经证明该命题正确.请你依照该命题研究双曲线中的情形,写出类似的正确命题: .
4,已知数列中,,且(n ≥2),
求这个数列的第m 项的值(m ≥2).现给出此算法流程图的一部分如
图
(1)请将空格部分(两个)填上适当的内容;
(2)用“For ”循环语句写出对应的算法;
1F 2F P 2F 12F PF T T {}n a 12a =1n n a n a -=+m a
m
(3)若输出S=16,则输入的的值是多少?
5,命题“线段垂直平分线上的点到线段两端的距离相等”与它的逆命题、否命题、逆否命题中,真命题有()
A. 4个
B. 3个
C. 2个
D. 1个
6,“p或q是假命题”是“非p为真命题”的()
A. 充分而不必要条件
B. 必要而不充分条件
C. 充要条件
D. 既不充分也不必要条件
7,下列命题
①“等边三角形的三内角均为60°”的逆命题
②若k>0,则方程x2+2x-k=0有实根“的逆命题
③“全等三角形的面积相等”的否命题
④“若ab≠0,则a≠0”的逆否命题,其中真命题的个数是()A.0个 B.1个 C.2个 D.3个
8,如图电路中,规定“开关A的闭合”为条件M,“灯泡B亮”为结论N,观察以下图1和图2,可得出的正确结论分别是
()
A.M是N的充分而不必要条件. B。
M是N的必要而不充分条件.
C.M是N的充要条件. D。
M是N的既不充分也必要不条件.
9,已知函数f(x)=347
2+++kx kx kx ,若R x ∈∀,则k 的取值范围是 ( )
A .0≤k<43
B .0<k<43
C .k<0或k>43
D .0<k ≤43
10,在ΔABC 中,条件甲:A<B ,条件乙:cos 2A> cos 2B,则甲是乙的( )
A 、充分非必要条件
B 、必要非充分条件
C 、既非充分又非必要条件
D 、充要条件
测试题答案
1, 5/13
2, 8
3, 和为双曲线的两焦点,P 为双曲线上的点,过作∠的平分线的垂线,垂足为 则到双曲线中心的距离为该双曲线的实轴长的一半. 4, 解:(1)2,m+1;
(2)
(3)m=5
5, A
6, A
7, C
8, A
9, A
10, D
1F 2F 2F 12F PF T
T。
