Park变换详解
park变换

park转换,也称派克变换,英文为Park transformation,为现在占主流地位的交流电机分析计算时的基本变换。
在电力系统分析和计算中,park转换具有重要的理论和实际意义。
关于park变换:
从数学意义上讲,park变换没有什么,只是一个坐标变换而已,从abc坐标变换到dq0坐标,ua,ub,uc,ia,ib,ic,磁链a,磁链b,磁链c这些量都变换到dq0坐标中,如果有需要可以逆变换回来。
从物理意义上讲,park变换就是将ia,ib,ic电流投影,等效到d,q轴上,将定子上的电流都等效到直轴和交轴上去。
对于稳态来说,这么一等效之后,iq,id正好就是一个常数了。
从观察者的角度来说,我们的观察点已经从定子转移到转子上去,我们不再关心定子三个绕组所产生的旋转磁场,而是关心这个等效之后的直轴和交轴所产生的旋转磁场了。
这样做使得在建立转子回路电磁关系的微分方程时,其系数矩阵成为常数矩阵,而不是随着时间和空间量变化的系数矩阵,这样大大化简了分析发电机、电动机的电磁关系的微分方程。
park反变换公式

park反变换公式摘要:1.公园反变换公式的概述2.公园反变换公式的计算方法3.公园反变换公式的应用实例4.公园反变换公式的优缺点分析正文:一、公园反变换公式的概述公园反变换公式,又称为Park 变换,是一种常用的离散余弦变换(Discrete Cosine Transform,简称DCT)的逆变换。
离散余弦变换是一种线性变换,广泛应用于信号处理、图像处理、数据压缩等领域。
公园反变换公式则是对离散余弦变换的结果进行逆向转换,从而恢复原始信号。
二、公园反变换公式的计算方法公园反变换公式的计算方法分为以下几个步骤:1.首先,对输入的离散余弦变换系数进行排序,按照升序或降序排列均可。
2.对排序后的离散余弦变换系数进行逆序置换。
3.将逆序置换后的离散余弦变换系数按照公园反变换公式进行计算,得到公园反变换后的系数。
4.最后,将公园反变换后的系数还原为原始信号。
三、公园反变换公式的应用实例公园反变换公式在图像处理、数据压缩、音频处理等领域有着广泛的应用。
例如,在图像压缩中,公园反变换公式可以对离散余弦变换后的图像系数进行逆向转换,从而恢复原始图像。
这使得公园反变换公式成为了离散余弦变换在图像压缩领域的重要工具。
四、公园反变换公式的优缺点分析公园反变换公式的优点在于其计算简便,且能够有效地将离散余弦变换后的系数恢复为原始信号。
然而,公园反变换公式也存在一定的缺点,例如在处理大量数据时,其计算复杂度较高,可能会导致计算速度较慢。
综上所述,公园反变换公式作为一种常用的离散余弦变换的逆变换方法,在信号处理、图像处理、数据压缩等领域具有广泛的应用价值。
park反变换公式

park反变换公式park反变换公式什么是park反变换公式Park反变换公式,也称为Park转换或Park变换,是一种电力系统中将三相坐标系下的变量转换为dq坐标系下的变量的数学方法。
它是由美国电机工程师在20世纪20年代初提出的。
Park变换的公式dq坐标系是一种于三相交流电机中描述电流和电压的坐标系,它可以将三相电量从传统的ABC坐标系转换为一个固定坐标系。
Park变换的公式如下:d轴变量q轴变量i d=i a⋅cos(θ)+i b⋅cos(θ+120∘)+i c⋅cos(θ−120∘)i q=−i a⋅sin(θ)−i b⋅sin(θ+120∘)−i c⋅sin(θ−120∘)v d=v a⋅cos(θ)+v b⋅cos(θ+120∘)+v c⋅cos(θ−120∘)v q=−v a⋅sin(θ)−v b⋅sin(θ+120∘)−v c⋅sin(θ−120∘)其中,i a,i b,i c分别为三相电流的幅值,θ为电流在ABC坐标系下的相位角。
v a,v b,v c为三相电压的幅值。
Park反变换的公式Park反变换的公式如下:a相变量b相变量c相变量a=i d⋅cos(θ)−i q⋅sin(θ)b=−i d⋅cos(θ+240∘)−i q⋅sin(θ+240∘)c=−i d⋅cos(θ−240∘)−i q⋅sin(θ−240∘)其中,i d,i q为dq坐标系下的电流变量,θ为电流在ABC坐标系下的相位角。
a,b,c为三相电流的幅值。
一个简单的示例假设有一台三相交流电机,其三相电流分别为i a=10A,i b=15A,i c=20A,相位角为θ=30∘。
我们想要将其转换到dq坐标系下。
首先,根据Park变换公式计算dq坐标系下的电流变量:i d=10⋅cos(30)+15⋅cos(30+120)+20⋅cos=25√3 2Ai q=−10⋅sin(30)−15⋅sin(30+120)−20⋅sin=−5√3 2A接下来,假设我们在dq坐标系下对电机进行控制,得到了i d=25√3 2A和i q=−5√32A。
FOCClarke变换和Park变换详解(动图+推导+仿真+附件代码)

FOCClarke变换和Park变换详解(动图+推导+仿真+附件代码)⽂章⽬录1 前⾔永磁同步电机是复杂的⾮线性系统,为了简化其数学模型,实现控制上的解耦,需要建⽴相应的坐标系变换,即Clark变换和Park变换。
2 ⾃然坐标系ABC三相永磁同步电机的驱动电路如下图所⽰;根据图⽰电路可以发现在三相永磁同步电机的驱动电路中,三相逆变输出的三相电压为UAU_{A}UA,UBU_{B}UB,UCU_{C}UC将作⽤于电机,那么在三相平⾯静⽌坐标系ABC中,电压⽅程满⾜以下公式:{UA=UmcosθeUB=Umcos(θe+2π3)UC=Umcos(θe−2π3)\begin{cases}U_{A} = U_{m}cos\theta_{e} \\ U_{B} = U_{m}cos(\theta_{e} + \cfrac{2\pi}{3}) \\ U_{C} =U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) \end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧U A=Um c osθe U B=Um c os(θe+32π)UC=Um c os(θe−32π)θe\theta_{e}θe为电⾓度UmU_{m}Um为相电压基波峰值所以根据上述公式可以发现,三相电压的⼤⼩是随时间变化的正弦波形,相位依次相差120°,具体如下图所⽰;3 αβ\alpha\betaαβ坐标系由静⽌三相坐标系ABCABCABC变换到静⽌坐标系αβ\alpha\betaαβ的过程称之为Clarke变换;在αβ\alpha\betaαβ静⽌坐标系中,α\alphaα轴和β\betaβ轴的相位差为90°,且αβ\alpha\betaαβ的⼤⼩是随时间变化的正弦波形,具体如下图所⽰;从⾃然坐标系ABCABCABC 变换到静⽌坐标系αβ\alpha\betaαβ,满⾜以下条件:[fαfβf0]=T3s/2s∗[fAfBfC]\begin{bmatrix} f_{\alpha} \\ f_{\beta} \\ f_{0} \end{bmatrix} = T_{3s/2s}*\begin{bmatrix} f_{A} \\ f_{B} \\ f_{C} \end{bmatrix} ⎣⎡fαfβf0⎦⎤=T3s/2s∗⎣⎡f A f B f C⎦⎤其中T3S/2ST_{3S/2S}T3S/2S为变换矩阵:T3S/2S=N∗[1−12−12032−32222222]T_{3S/2S} = N*\begin{bmatrix} 1 &-\cfrac{1}{2} &-\cfrac{1}{2} \\ \\ 0 &\cfrac{\sqrt{3}}{2} &-\cfrac{\sqrt{3}}{2} \\ \\ \cfrac{\sqrt{2}}{2}&\cfrac{\sqrt{2}}{2} &\cfrac{\sqrt{2}}{2} \end{bmatrix} T3S/2S=N∗⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1022−212322−21−2322⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤注意:NNN为系数,做等幅值变换和等功率变换NNN系数不同;等幅值变换 N=23N =\cfrac{2}{3}N=32等功率变换 N=23N =\sqrt\cfrac{2}{3}N=32下⾯均为等幅值变换3.1 Clarke变换三相电流ABCABCABC分别为iAi_{A}iA,iBi_{B}iB,iCi_{C}iC,根据基尔霍夫电流定律满⾜以下公式:iA+iB+iC=0i_{A}+i_{B}+i_{C} = 0iA+iB+iC=0静⽌坐标系αβ\alpha\betaαβ,α\alphaα轴的电流分量为iαi_{\alpha}iα,iβi_{\beta}iβ,则Clark变换满⾜以下公式:iα=iAiβ=13∗iA+23∗iBi_{\alpha} = i_{A} \\ \\ i_{\beta} = \cfrac{1}{\sqrt{3}}*i_{A}+\cfrac{2}{\sqrt{3}}*i_{B}iα=iA iβ=31∗iA+32∗iB在matlab的simulink仿真如下图所⽰;最终得到三相电流iAi_{A}iA,iBi_{B}iB,iCi_{C}iC的仿真结果如下;得到αβ\alpha\betaαβ坐标的 iαi_{\alpha}iα和 iβi_{\beta}iβ的仿真结果如下图所⽰;由上述两张图分析可以得到,等幅值Clark变换前后峰值不变,αβ\alpha\betaαβ坐标系中iαi_{\alpha}iα和iβi_{\beta}iβ相位相差90°。
导数的park变换

导数的park变换(原创实用版)目录1.导数与 Park 变换的概述2.Park 变换的定义与性质3.Park 变换在导数计算中的应用4.总结与展望正文1.导数与 Park 变换的概述导数是微积分学中的一个重要概念,它描述了函数在某一点的变化率。
在实际应用中,导数的计算往往涉及到复杂的运算,而 Park 变换作为一种常用的数学工具,可以在一定程度上简化导数的计算过程。
Park 变换,又称为帕克变换,是一种用于简化复杂函数的导数计算的技巧。
通过对函数进行 Park 变换,可以将原本难以求导的函数转化为易于求导的函数,从而简化导数的计算过程。
2.Park 变换的定义与性质Park 变换的定义如下:设函数 f(x) 的导数为 f"(x),如果存在一个函数 g(x),使得 g"(x) = f"(x),则称函数 g(x) 是函数 f(x) 的一个 Park 变换。
Park 变换具有以下性质:(1) 线性性:如果函数 f(x) 和 g(x) 分别是 Park 变换,那么它们的线性组合也是 Park 变换。
(2) 恒等性:对于任意函数 f(x),f(x) + 0 = f(x) 是 f(x) 的 Park 变换。
(3) 结合律:如果函数 f(x) 和 g(x) 分别是 Park 变换,那么[g(f(x))] 也是 Park 变换。
3.Park 变换在导数计算中的应用Park 变换在导数计算中的应用广泛,下面我们通过一个具体的例子来说明 Park 变换的应用。
假设我们要计算函数 f(x) = x^3 + 3x^2 - 2x + 1 的导数,我们可以通过 Park 变换来简化计算过程。
首先,我们构造一个新的函数 g(x) = x^3 + 3x^2 - 2x + 1 + (x - 1)^2,可以发现,函数 g(x) 的导数为 g"(x) = 3x^2 + 6x - 2 + 2(x - 1) = 3x^2 + 6x - 4。
park变换
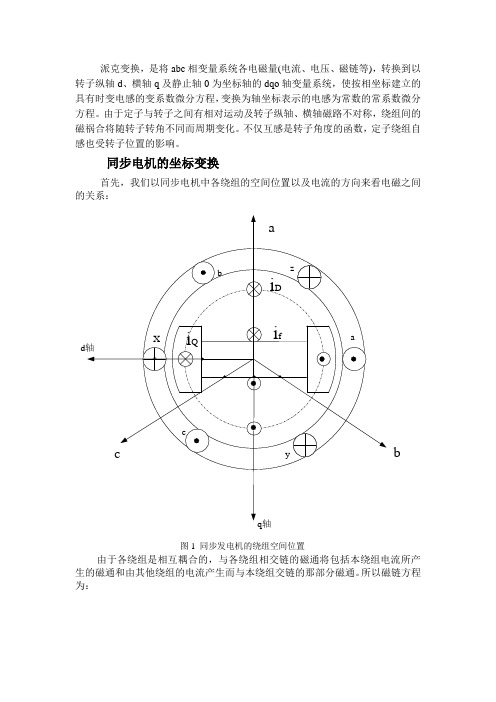
派克变换,是将abc相变量系统各电磁量(电流、电压、磁链等),转换到以转子纵轴d、横轴q及静止轴0为坐标轴的dqo轴变量系统,使按相坐标建立的具有时变电感的变系数微分方程,变换为轴坐标表示的电感为常数的常系数微分方程。
由于定子与转子之间有相对运动及转子纵轴、横轴磁路不对称,绕组间的磁祸合将随转子转角不同而周期变化。
不仅互感是转子角度的函数,定子绕组自感也受转子位置的影响。
同步电机的坐标变换首先,我们以同步电机中各绕组的空间位置以及电流的方向来看电磁之间的关系:db图1 同步发电机的绕组空间位置由于各绕组是相互耦合的,与各绕组相交链的磁通将包括本绕组电流所产生的磁通和由其他绕组的电流产生而与本绕组交链的那部分磁通。
所以磁链方程为:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛Q D f c b a QQ QDQfQcQbQaDQ DD Df Dc Db Da fQ fD ff fc fb fa cQ cD cf cc cb ca bQ bD bf bc bb ba aQ aD af ac ab aa Q D f c b a i i i i i i L M M M M M M L M M M M M M L M M M M M M L M M M M M M L M M M M M M L ψψψψψψ 下面我们分析一下各自的自感与互感的系数。
首先我们知道电机的旋转磁场与各定子绕组相交链的磁通的磁路发生周期性变换且周期为,由于电感与磁阻成反比,与绕组匝数的平方成正比。
所以定子绕组的自感也成周期性变化。
)120(2cos )120(2cos 2cos 202020︒++=︒-+=+=θθθl l L l l L l l L cc bb aa0l 为自感的平均值,2l 为自感的变化部分。
由于定子绕组间的空间位置相差120度,使得定子绕组间的互感恒为负值。
[][][])150(2cos )90(2cos )30(2cos 202020︒++-==︒-+-==︒++-==θθθm m M M m m M M m m M M ac ca cb bc ba ab 0m 为互感的平均值,2m 为互感变化部分。
park变换的原理

park变换的原理
Park变换是一种将三相交流电信号转换为两相直流电信号的数学变换方法。
它的原理基于三相交流电信号可以表示为三个正弦波的叠加,而两相直流电信号可以表示为两个相位差90度的正弦波的叠加。
因此,通过Park变换,我们可以将三相交流电信号转换为两个相位差90度的直流电信号,从而方便进行控制和计算。
具体来说,Park变换的原理如下:
1. 将三相交流电信号表示为矢量形式。
我们可以将三相电信号表示为三个矢量,分别代表三个正弦波的振幅和相位。
这些矢量可以在一个三维空间中表示,其中每个矢量的长度代表振幅,方向代表相位。
2. 旋转坐标系。
为了将三相电信号转换为两相直流电信号,我们需要旋转坐标系。
具体来说,我们需要将坐标系旋转一个角度,使得其中一个矢量与x轴重合。
这个角度可以通过计算得出,通常称为“电角度”。
3. 投影。
在旋转后的坐标系中,我们可以将每个矢量投影到x轴和y轴上,得到两个直流电信号。
这些信号可以表示为两个正弦波的叠加,相位差为90度。
4. 相位移动。
由于我们将坐标系旋转了一个角度,因此投影到x轴和y轴上的
信号会有一个相位偏移。
为了消除这个相位偏移,我们可以将y轴上的信号向前或向后移动90度,使得两个信号的相位差为90度。
通过以上步骤,我们就可以将三相交流电信号转换为两相直流电信号。
这些直流信号可以方便地进行控制和计算,例如用于电机控制、电力系统分析等领域。
park反变换公式

park反变换公式摘要:1.引言2.park 反变换公式的定义3.park 反变换公式在信号处理中的应用4.park 反变换公式的性质和特点5.总结正文:1.引言Park 反变换公式是数字信号处理中的一种重要变换方法,它可以将离散时间信号从时域转换到频域。
本文将介绍Park 反变换公式的定义、性质和特点以及在信号处理中的应用。
2.Park 反变换公式的定义Park 反变换公式是一种线性变换方法,它将离散时间信号x(n) 转换为离散频率信号X(k)。
Park 反变换公式可以表示为:X(k) = ∑_{n=0}^{N-1} x(n) * (e^(-j*2*pi*n*k/N))其中,x(n) 表示离散时间信号,N 表示离散时间信号的采样点数,k 表示离散频率信号的频率点,j 表示虚数单位,X(k) 表示离散频率信号。
3.Park 反变换公式在信号处理中的应用Park 反变换公式在信号处理中有着广泛的应用,主要包括以下几个方面:(1) 滤波:Park 反变换公式可以将信号从时域转换到频域,方便设计滤波器对信号进行滤波处理。
(2) 信号分析:Park 反变换公式可以用于信号的频谱分析,提取信号的频率成分。
(3) 数据压缩:Park 反变换公式可以用于信号的压缩和传输,将信号的频域表示有助于实现更高的数据压缩比。
4.Park 反变换公式的性质和特点Park 反变换公式具有以下性质和特点:(1) 线性性:Park 反变换公式是一种线性变换方法,满足叠加性和齐次性。
(2) 因果性:Park 反变换公式是因果变换,即输出信号只依赖于输入信号的过去值。
(3) 稳定性:Park 反变换公式具有稳定性,即输入信号的幅度和相位变化不会影响输出信号的幅度和相位。
(4) 频率响应:Park 反变换公式的频率响应为复指数函数,具有很好的频率分辨率。
5.总结Park 反变换公式是一种重要的时域到频域的变换方法,在信号处理中有着广泛的应用。
派克变换公式

派克变换公式一、派克变换公式的背景和意义派克变换公式(Park"s Transformation)起源于电磁学领域,是由著名物理学家派克(Parker)在20世纪30年代提出的。
该公式将复杂的电磁场问题简化为易于处理的数学表达式,对于电磁学理论的发展具有重要的意义。
二、派克变换公式的数学表达及其推导派克变换公式是一种坐标变换,它将柱坐标系(r,θ,z)中的电磁场量变换为球坐标系(r,θ,φ)中的电磁场量。
具体的数学表达如下:1.电场强度E:E" = E*sinθ2.磁场强度B:B" = B*cosθ3.电荷密度λ:λ" = λ*sec^2θ4.电流密度J:J" = J*tanθ三、派克变换公式在实际应用中的案例解析派克变换公式在许多实际应用中发挥着重要作用,如电磁场计算、无线通信、地球物理勘探等。
以地球物理勘探为例,科学家们利用派克变换公式将地表的电磁信号转换为地下的电磁场分布,从而为矿产资源勘探提供重要依据。
四、派克变换公式在我国的研究与应用现状我国对派克变换公式的研究始于20世纪50年代,经过几十年的发展,已经在多个领域取得了显著的成果。
在理论研究方面,我国的学者对派克变换公式的数学推导和物理内涵进行了深入探讨;在实际应用方面,派克变换公式已在我国的地磁观测、地震预测、矿产资源勘探等领域取得了广泛应用。
五、派克变换公式的发展趋势与前景随着科技的不断进步,派克变换公式在各个领域的应用将越来越广泛。
在未来,派克变换公式可能在以下几个方面取得新的突破:1.量子电动力学:派克变换公式有望在量子电动力学领域发挥更大作用,为基本粒子物理的研究提供新思路。
2.空间探测:随着我国航天事业的不断发展,派克变换公式将在空间探测领域发挥更大作用,如火星探测、黑洞探测等。
3.生物电磁学:派克变换公式有望在生物电磁学领域取得新突破,为疾病的早期诊断和治疗提供新方法。
总之,派克变换公式作为一种重要的数学工具,在电磁学、地球物理勘探等多个领域具有广泛的应用前景。
foc控制原理——clark变换和park变换

foc控制原理——clark变换和park变换一、导言在现代电力系统中,频繁使用交流电机作为主要动力源。
而在这些电机中,磁场定向控制(Field-Oriented Control,FOC)技术已经成为一种常见的控制策略。
其主要特点是将交流电机分解为两个独立的控制回路,即电流控制回路和转矩控制回路,以实现快速、准确的控制。
本文将重点介绍FOC控制原理中的两个重要变换——clark变换和park变换。
首先会介绍它们的基本概念和原理,然后会详细讨论它们在FOC控制中的应用。
二、clark变换1. 基本概念clark变换也被称为αβ变换,它是一种将三相交流电压或电流转换为两相直流信号的数学变换方法。
通过clark变换,我们可以将三相电流空间矢量转换为两相坐标系中的两个分量。
这两个分量通常被称为α轴和β轴电流。
2. 原理clark变换的原理可以通过公式表达为:α = aβ = (2/√3) * (b - a/2 - c/2)其中,a、b、c分别代表三相电流的幅值。
通过这些公式,我们可以将三相电流转换为两相αβ坐标系。
3. FOC控制中的应用在FOC控制中,clark变换通常用于将三相电流转换为两相电流。
这样一来,我们就可以将三相交流电机的控制问题转化为两相电机的控制问题,从而简化了整个系统的控制难度。
三、park变换1. 基本概念park变换也被称为dq变换,它是一种将αβ坐标系中的两相信号转换为dq坐标系中的信号的数学变换方法。
在FOC控制中,park变换用于将电机状态转换为以磁场和转矩为坐标轴的坐标系中,从而方便进行磁场定向控制。
2. 原理park变换的原理可以通过公式表达为:d = α * cos(θ) + β * sin(θ)q = -α * sin(θ) + β * cos(θ)其中,α、β代表αβ坐标系中的两相信号,θ代表旋转角度。
通过这些公式,我们可以将αβ坐标系中的信号转换为dq坐标系中的信号。
park反变换公式

park反变换公式
【原创实用版】
目录
1.介绍 Park 反变换公式的背景和意义
2.详细解释 Park 反变换公式的定义和原理
3.说明 Park 反变换公式的应用领域和实际案例
4.总结 Park 反变换公式的重要性和未来发展前景
正文
Park 反变换公式是一种在信号处理领域广泛应用的公式,它的出现解决了许多信号处理中的难题。
Park 反变换公式,又称为 Park 变换,是由韩国数学家 Park 于 1986 年提出的一种线性时不变系统模型。
该模型主要用于数字信号处理、图像处理以及通信系统等领域。
Park 反变换公式的定义和原理相对简单。
它是一种基于 Z 变换的反变换方法,可以将数字信号处理中的离散信号通过 Z 变换转换为连续信号,从而实现信号的反变换。
具体来说,Park 反变换公式是通过对 Z 变换的逆 Z 变换和初值条件的处理,得到离散信号的反变换结果。
Park 反变换公式在信号处理领域有着广泛的应用。
例如,在数字信号处理中,它可以用于求解线性时不变系统的输入输出关系,从而设计出符合特定要求的数字滤波器。
在图像处理中,Park 反变换公式可以用于图像的恢复和增强,提高图像的质量。
在通信系统中,Park 反变换公式可以用于信道均衡和信号解调,从而提高通信系统的性能。
总的来说,Park 反变换公式是一种重要的信号处理工具,它的应用领域正在不断扩大。
第1页共1页。
park反变换公式

park反变换公式摘要:1.介绍Park 反变换公式的背景和意义2.阐述Park 反变换公式的定义和原理3.详述Park 反变换公式的计算过程和方法4.分析Park 反变换公式的应用领域和实际案例5.总结Park 反变换公式的重要性和未来发展前景正文:一、Park 反变换公式的背景和意义Park 反变换公式,又称Park 变换,是一种在地球物理勘探中广泛应用的数学方法。
在地球物理勘探中,为了获取地下介质的信息,常常需要对地震波进行处理和分析。
Park 反变换公式就是在这种背景下应运而生的一种重要工具,可以帮助我们更好地理解和解释地震波的特性。
二、Park 反变换公式的定义和原理Park 反变换公式是一种将地震波的频域数据转换为其时域数据的数学方法。
其基本原理是利用傅里叶变换将地震波的时域数据转换为频域数据,然后通过Park 反变换公式将频域数据反变换回时域数据。
这样做的好处是,可以更好地分析地震波的频谱特性,从而更准确地判断地下介质的物理性质。
三、Park 反变换公式的计算过程和方法Park 反变换公式的计算过程主要包括以下几个步骤:1.对地震波的时域数据进行傅里叶变换,得到其频域数据;2.对频域数据进行Park 反变换,得到其时域数据;3.对得到的时域数据进行分析,以获取地下介质的信息。
四、Park 反变换公式的应用领域和实际案例Park 反变换公式在地球物理勘探中有广泛的应用,尤其在地震波数据处理和地下介质参数反演等方面。
例如,在油气资源勘探中,通过应用Park 反变换公式,可以有效地识别油气储层的位置和范围,从而指导钻井作业。
五、总结Park 反变换公式作为一种重要的数学方法,在地球物理勘探领域发挥着重要的作用。
park变换 零序电流

park变换零序电流在电力系统中,零序电流是指三相电流中相对于中性点或地的对称分量。
零序电流的存在可能会导致设备损坏、电压不平衡等问题,因此对零序电流进行监测和控制是电力系统运行中的重要任务之一。
为了更好地理解和分析零序电流,工程师们引入了一种数学工具——Park变换。
Park变换,也称为dq0变换,是一种用于将三相电量转换为两个坐标轴上的旋转矢量的数学方法。
通过Park变换,我们可以将三相电流分解为直轴(d轴)电流、交轴(q轴)电流和零轴(0轴)电流。
其中,零轴电流即为零序电流。
Park变换的基本原理是将三相电流变换到一个固定的坐标系中,该坐标系与电流的旋转速度相匹配。
在这个坐标系中,d轴与电流的幅值成正比,q轴与电流的相位差成正比,而0轴则表示电流的平衡分量。
通过对三相电流进行Park变换,我们可以将复杂的三相电流问题转化为简单的两相电流问题,从而更容易进行分析和计算。
零序电流的特点主要有以下几个方面。
首先,零序电流的幅值通常较小,一般情况下远小于正序电流的幅值。
其次,零序电流的相位通常与正序电流相差较大,一般为120度。
最后,零序电流一般呈现对称分布,即三相电流的幅值和相位差都相等。
在电力系统中,零序电流的产生主要有两个原因。
一是对称故障引起的零序电流,即三相电流中存在相同幅值和相位差的零序分量。
这种情况通常是由于电力系统中的设备短路或接地故障引起的。
二是非对称负载引起的零序电流,即三相电流中存在不同幅值和相位差的零序分量。
这种情况通常是由于电力系统中的非线性负载或不平衡负载引起的。
为了准确测量和控制零序电流,工程师们通常会使用专用的零序电流检测装置。
这些装置能够实时监测电力系统中的零序电流,并在电流超过设定阈值时发出警报或采取相应的控制措施。
常见的零序电流检测装置包括零序电流变压器、零序电流继电器等。
零序电流作为电力系统中的重要参数,对系统的安全稳定运行起着至关重要的作用。
通过Park变换,我们可以更好地理解和分析零序电流,从而采取相应的控制措施,确保电力系统的正常运行。
Clark变换与Park变换详解

Clark 变换与Park 变换详解很多同学对Clark 变换与Park 变换不求甚解,在运用的时候常常感到困惑,本文梳理了这两种变化的详细步骤,希望可以帮到大家。
设三相交流系统各相电压为:cos cos(120)cos(120)a mb mc m u V tu V t u V t ωωω=⎧⎪=-⎨⎪=+⎩ (0.1) a u b u c u 分别指ABC 三相电压的瞬时值,m V 指相电压基波幅值。
cos cos(120)cos120sin120122cos(120)cos120sin120122a m b m c m u V tV u V t V V V u V t V V V ααβαβαβαβωωω===-=+=-+=+=-=--(0.2)101/221/22a b c u V u V u αβ⎛⎫⎛⎫ ⎪⎛⎫ ⎪=- ⎪ ⎪ ⎪⎝⎭⎪ ⎪-⎝⎭⎝⎭ (0.3)0a b c u u u ++=(0.4)现在要求的是如何找到一个矩阵P 使a b c u V P u V u αβ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭(0.5) 书上有两种表达式11/21/211/21/22302/20/22P P ----⎛⎫⎫== ⎪⎪⎝⎭⎭与 (0.6) 于是有同学开始疑问了,为什么?为什么非得是这种表达形式?由Clark 变换推出Park 变换cos sin sin cos d q d q u u u u u u αβαααα+=⎧⎨-=⎩(0.7) cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.8) 由式(1.7)可以得:22cos sin cos cos sin sin cos sin d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩ (0.9) 两式相加有:cos sin d u u u αβαα=+ (0.10)22cos sin sin sin cos sin cos cos d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩(0.11)两式相减有:sin cos q u u u αβαα=- (0.12) 可得:cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.13) 将式(1.5)代入(1.13)中可得: cos cos(120)cos(120)23sin sin(120)sin(120)a d b q c u u u u u αααααα⎛⎫⎛⎫-+⎛⎫ ⎪= ⎪ ⎪ ⎪-+⎝⎭⎝⎭ ⎪⎝⎭ (0.14)。
park变换原理

park变换原理Park变换原理Park变换是一种将三相交流电信号转换为两相直流电信号的数学方法,它是控制交流电机的基础。
Park变换常用于电力系统中,特别是在交流电机控制中。
下面将详细介绍Park变换的原理。
一、三相交流电信号在介绍Park变换之前,首先需要了解三相交流电信号。
三相交流电信号是指由三个正弦波组成的信号,其中每个正弦波都有不同的振幅和相位。
这三个正弦波分别称为A、B和C相,它们之间的相位差为120度。
二、坐标系在Park变换中,需要用到两个坐标系:α-β坐标系和dq坐标系。
α-β坐标系是一个旋转坐标系,它随着时间旋转,并与三相交流电信号保持同步。
α轴与A相重合,β轴与A-B轴夹角为120度。
dq坐标系是一个固定坐标系,它与α-β坐标系之间存在一个旋转关系。
d轴与α轴重合,在AB平面上;q轴与dq平面垂直,并且指向最大磁通密度方向。
三、Park变换Park变换的目的是将三相交流电信号转换为两相直流电信号,以便进行控制。
具体步骤如下:1. 将三相交流电信号投影到α-β坐标系上。
2. 通过坐标变换,将α-β坐标系转换为dq坐标系。
3. 在dq坐标系中,d轴上的分量代表直流分量,q轴上的分量代表交流分量。
4. 最后,通过逆变换将dq坐标系转换回α-β坐标系,得到两相直流电信号。
四、应用Park变换在交流电机控制中应用广泛。
通过Park变换,可以将三相交流电信号转化为两相直流电信号,并且可以方便地进行控制。
例如,在感应电机中,可以通过控制d轴和q轴上的电压和电流来实现速度调节和扭矩控制。
五、总结Park变换是一种重要的数学方法,在交流电机控制中有着广泛的应用。
它通过将三相交流电信号转化为两相直流电信号,并且可以方便地进行控制。
同时,在实际应用中需要注意坐标系之间的旋转关系以及逆变换的过程。
park变换推导过程

park变换推导过程1. 什么是Park变换?Park变换是一种电气工程中常用的变换方法,用于将三相交流系统的三相电压或电流转换为两相电压或电流。
这种变换方法常用于电力系统的稳定性分析、控制器设计以及电机控制等领域。
2. Park变换的基本原理Park变换的基本原理是通过将三相旋转坐标系转换到一个固定坐标系,从而实现对三相信号的变换。
Park变换的核心思想是将三相信号投影到一个旋转坐标系上,通过旋转坐标系和正弦定理,将三相信号变换为两相信号。
3. Park变换的推导过程Park变换的推导过程可以分为以下几个步骤:第一步:建立旋转坐标系为了将三相信号投影到旋转坐标系上,我们需要先建立一个旋转坐标系。
旋转坐标系通常以一个基准信号为参考,这个基准信号可以是三相信号中的任意一相。
第二步:投影到旋转坐标系将三相信号投影到旋转坐标系上,可以通过将三相信号与旋转坐标系的基准信号进行内积运算得到。
这样就得到了在旋转坐标系上的两个分量,一个是直流分量,一个是交流分量。
第三步:旋转坐标系的变换为了得到两相信号,我们需要将旋转坐标系进行变换。
变换的方法通常是通过一个旋转矩阵来实现,这个旋转矩阵的元素可以通过正弦定理来计算得出。
第四步:得到Park变换通过以上步骤,我们最终可以得到Park变换的结果,即将三相信号转换为两相信号的变换矩阵。
4. Park变换的应用Park变换在电气工程中有着广泛的应用。
在电力系统的稳定性分析中,Park变换可以将三相电压或电流转换为两相信号,从而简化了系统的分析和计算。
在控制器设计和电机控制中,Park变换可以将三相电流转换为两相电流,实现对电机的控制。
总结:Park变换是一种将三相信号转换为两相信号的方法,通过建立旋转坐标系,将三相信号投影到旋转坐标系上,并通过旋转坐标系的变换得到Park变换的结果。
Park变换在电气工程中有着广泛的应用,特别是在电力系统的稳定性分析、控制器设计和电机控制等领域。
派克变换的基本原理

派克变换的基本原理1. 引言派克变换(Park Transform)是一种电力系统中常用的数学工具,用于将三相交流电量转换为两相旋转坐标系下的等效量。
它是电力系统分析与控制中的重要工具,广泛应用于电机控制、保护装置、无功补偿等领域。
本文将详细解释派克变换的基本原理,包括三相电压和电流的表示方式、旋转坐标系的建立、派克变换矩阵以及派克变换后得到的等效量。
2. 三相电压和电流表示方式在讲解派克变换之前,我们首先需要了解三相电压和电流的表示方式。
在三相交流系统中,通常使用相量(Phasor)来表示电压和电流。
2.1 相量表示法相量是一个复数,由实部和虚部组成。
在三相交流系统中,我们可以使用以下公式来表示一个时刻t的相量:V(t)=V m⋅cos(ωt+ϕ)+j⋅V m⋅sin(ωt+ϕ)其中,V m为幅值,ω为角频率,ϕ为初始相位角。
2.2 直角坐标表示法除了相量表示法,我们还可以使用直角坐标表示法来表示三相电压和电流。
直角坐标表示法使用实数形式的x和y来表示一个时刻t的电压或电流:V(t)=x(t)+j⋅y(t)其中,x(t)和y(t)分别为实部和虚部。
2.3 相量与直角坐标的转换相量与直角坐标之间可以进行互相转换。
对于一个给定的相量V(t)=V m⋅cos(ωt+ϕ)+j⋅V m⋅sin(ωt+ϕ),我们可以将其转换为直角坐标形式:x(t)=V m⋅cos(ωt+ϕ)y(t)=V m⋅sin(ωt+ϕ)反之,对于给定的x(t)和y(t),我们可以将其转换为相量形式:V(t)=x(t)+j⋅y(t)3. 旋转坐标系的建立派克变换需要建立一个旋转坐标系,使得三相电压和电流在该坐标系下能够方便地进行运算。
这个旋转坐标系通常称为“dq0”坐标系。
3.1 d轴和q轴在dq0坐标系中,我们定义了一个d轴和一个q轴。
d轴通常与三相电流的瞬时值相一致,q轴与d轴相垂直。
3.2 坐标变换为了将三相电压和电流转换到dq0坐标系下,我们需要进行坐标变换。
导数的park变换

导数的park变换摘要:一、导数的概念1.导数的定义2.导数与函数的关系二、Park变换的原理1.Park变换的提出2.Park变换的数学表达式三、Park变换在微分方程中的应用1.微分方程的Park变换2.Park变换对微分方程的简化作用四、Park变换在实际问题中的应用1.物理系统中的Park变换2.电路系统中的Park变换正文:一、导数的概念导数是微积分中的一个重要概念,它表示函数在某一点处的变化率。
导数的定义可以表示为:若函数f(x)在点x0的某一邻域内有定义,则称函数f(x)在点x0处可导,并把f(x)在点x0处导数定义为:f"(x0) = lim (f(x) - f(x0)) / (x - x0)其中,当x趋近于x0时,如果极限存在,则称f(x)在x0处可导,并把f"(x0)称为函数f(x)在x0处的导数。
二、Park变换的原理Park变换是一种线性变换方法,它可以将微分方程的输入输出关系进行变换,使得微分方程的求解更加容易。
Park变换的数学表达式如下:x(t) = G(s) * u(t)其中,x(t)是系统的输出,u(t)是系统的输入,G(s)是Park变换后的系统函数,s是变换后的变量。
三、Park变换在微分方程中的应用Park变换可以用于简化微分方程的求解过程。
例如,对于一个线性时不变系统,其输入输出关系可以表示为:y(t) = A * x(t) + B * u(t)其中,y(t)是系统的输出,x(t)是系统的状态,u(t)是系统的输入,A和B 是系统的参数。
通过Park变换,可以将上述关系变换为:y(t) = G(s) * u(t)其中,G(s)是Park变换后的系统函数,s是变换后的变量。
这样,就可以通过求解G(s)来得到系统的输出,从而简化微分方程的求解过程。
四、Park变换在实际问题中的应用Park变换不仅可以用于微分方程的求解,还可以用于实际问题的建模和分析。
派克变换与对称分量法的区别

派克变换与对称分量法的区别在电力系统和电机控制领域,派克变换(Park's Transformation)和对称分量法(Symmetrical Components Method)是两种常用的分析方法。
它们各自具有独特的应用场景和优势,但同时也存在明显的区别。
本文将从定义、原理、应用以及优缺点等方面对这两种方法进行深入探讨,以揭示它们之间的本质差异。
一、派克变换1. 定义派克变换,也称Park变换,是一种用于将三相交流量转换为两相直流量的数学变换。
它主要用于电机控制中,将定子电流的三相交流量转换为两相旋转坐标系下的直流量,从而简化控制算法和提高控制性能。
2. 原理派克变换的基本原理是通过坐标变换,将三相静止坐标系下的交流量转换为两相旋转坐标系下的直流量。
这种变换需要用到正弦和余弦函数,以及电机的转子位置信息。
通过派克变换,可以将电机的定子电流分解为与转子磁场同步的直流分量和与转子磁场垂直的交流分量,从而实现电机的解耦控制。
3. 应用派克变换广泛应用于电机控制领域,尤其是矢量控制(Vector Control)和直接转矩控制(Direct Torque Control)等先进控制策略中。
它可以帮助实现电机的精确控制,提高电机的运行效率和动态性能。
二、对称分量法1. 定义对称分量法是一种用于分析不平衡三相系统的方法。
当三相系统中的某一相或多相发生故障或不对称运行时,会产生不平衡的三相电压和电流。
对称分量法可以将这些不平衡的三相量分解为三组对称的正序、负序和零序分量,从而简化分析和计算过程。
2. 原理对称分量法的基本原理是根据线性叠加原理,将不平衡的三相量表示为三组对称分量的线性组合。
这三组对称分量分别是正序分量(与正常三相系统相同)、负序分量(与正常三相系统相反)和零序分量(三相相同)。
通过求解这三组对称分量的幅值和相位,可以得到不平衡三相系统的详细信息。
3. 应用对称分量法主要应用于电力系统故障分析和保护领域。
park反变换公式

park反变换公式【原创版】目录1.Park 反变换公式的概念2.Park 反变换公式的应用3.Park 反变换公式的优点和局限性正文Park 反变换公式是一种在通信系统中广泛应用的公式,主要用于解决信号处理中的反问题。
通信系统中,信号在传输过程中可能会受到各种干扰,导致接收端收到的信号与发送端发送的信号存在差异。
反变换公式就是用来估计发送端发送的信号,从而消除这种差异。
Park 反变换公式的应用主要包括以下几个方面:1.信道均衡:在无线通信系统中,信号经过传输后会受到多径效应、频率选择性衰落等因素的影响,导致信号在接收端出现失真。
通过使用Park 反变换公式,可以在接收端对信道进行均衡,从而恢复原始信号。
2.信号解调:在调制通信系统中,信号在传输过程中可能会受到各种干扰,导致接收端收到的信号与发送端发送的信号存在差异。
利用 Park 反变换公式,可以在接收端对信号进行解调,从而恢复原始信号。
3.信号去噪:在通信系统中,信号在传输过程中可能会受到各种噪声的影响,导致接收端收到的信号与发送端发送的信号存在差异。
通过使用Park 反变换公式,可以在接收端对信号进行去噪,从而恢复原始信号。
尽管 Park 反变换公式在通信系统中有着广泛的应用,但它仍然存在一些优点和局限性:1.优点:Park 反变换公式具有较好的解线性能力,可以有效地解决通信系统中的反问题。
此外,该公式还具有较低的计算复杂度,便于实时实现。
2.局限性:Park 反变换公式的性能受到输入数据的影响较大,当输入数据存在较大幅度的失真时,该公式的解线性能力会受到影响。
同时,Park 反变换公式在某些特殊情况下可能会出现不稳定的现象,需要采用其他方法进行改进。
