整体稳定计算
岸塔式进水口整体稳定的计算方法

岸塔式进水口整体稳定的计算方法卞全(中国水电顾问集团西北勘测设计研究院,西安710065 )摘要由于岸塔式进水口背靠岩体,靠基础和塔背的岩体来支撑并维持稳定,具有独特的优势,已被许多工程所采用;对于其整体稳定的方法,已有不少出版物进行了推导和论述,但在运用中,仍有不少问题还没有得到解决。
本文通过对其整体稳定计算方法的分析、总结、补充和验证,完善了岸塔式进水口整体稳定的计算方法,可供设计人员采用。
关键词岸塔式进水口稳定应力计算方法1 引言岸塔式进水口背靠岸坡岩体,是“镶嵌”在L型地基中的进水塔,塔体两侧平压,可将顺水流方向的荷载传递到基础和岸坡岩体,靠基础和塔背的岩体来支撑并维持稳定。
因此,岸塔式进水口沿水流方向的整体稳定,不同于一侧挡水、另一侧临空的重力坝和重力式挡土墙。
对于“镶嵌”在L型地基中的岸塔式进水口,其整体稳定问题不像重力坝和重力式挡土墙那样,有沿基础面滑动的可能和绕趾点倾覆的可能,只要基础应力和岸坡应力都在岩体允许应力或抗力范围之内,塔体就不致发生整体失稳。
借助于日趋流行的三维有限元技术,目前已经可以开展岸塔式进水口的有限元计算,得到比较接近实际的基础和岩体的应力结果。
但由于在三维有限元计算中,首先要模拟地基岩体、岸坡岩体、塔体结构,初始应力场、开挖应力释放过程等,然后才能进行进水塔完建后的各工况下的稳定及应力计算(采用弹塑性或非线性分析方法);前处理并不简单,不能很快地得到结果,费时费力,不利于体型初拟时的决策和分析。
而按常规结构力学的方法快速、方便,方法成熟可靠,符合目前的结构可靠度设计的国家标准,被广大设计人员普遍采用。
对于岸塔式进水口整体稳定的计算方法,已有不少出版物,包括《水电站进水口设计》(杨欣先、李彦硕主编,大连理工大学出版社),《水利水电工程技术设计阶段水电站岸塔式进水口设计大纲范本》(编号为FJD34030),以及《水工专业设计大纲范本汇编8》等,提出了岸塔式进水口的结构力学方法。
刚架梁柱平面内的整体稳定验算

国第家级8精讲品课程变—截钢结面构设刚计 架梁、柱的整体稳定、斜梁及隅 撑
隅撑设计: 隅撑构造:隅撑与刚架构件、檩条或墙梁的连接 应采用螺栓连接,每端通常采用单个螺栓。
0.75 ( N
N
' Ex0
)2
对两端弯应力基本相等的区段:
t 1.0
第2章 轻型门式刚架结构设计
国第家级8精讲品课程变—截钢结面构设刚计 架梁、柱的整体稳定、斜梁及隅 撑
整体稳定计算: (2) 平面外的整体稳定验算:
1)弹性设计
N0 tM1 f y Ae0 bWe1
第2章 轻型门式刚架结构设计
国第家级8精讲品课程变—截钢结面构设刚计 架梁、柱的整体稳定、斜梁及隅 撑
整体稳定计算:
(1) 刚架梁、柱平面内的整体稳定验算: 1)弹性设计
大头, M1 ,We1
小头,N0 ,A0,j
第2章 轻型门式刚架结构设计
国第家级8精讲品课程变—截钢结面构设刚计 架梁、柱的整体稳定、斜梁及隅 撑
整体稳定计算:
整体稳定计算:
(2)变截面柱在刚架平面外的整体稳定计算 1)弹性设计:应分段按下式计算:
N0 tM1 f y Ae0 bWe1
y -轴心受压构件弯矩作用平面外的稳定系数,以小头为
准,计算长度取侧向支撑点间的距离。
t -等效弯矩系数;
弯矩为零的区段:
t 1 N
N
' Ex0
y -轴心受压构件弯矩作用平面外的稳定系数,
以小头为准,计算长度取侧向支撑点间的距离。
t -等效弯矩系数;
弯矩为零的区段:
t 1 N
N
' Ex0
0.75 ( N
钢梁稳定性计算步骤
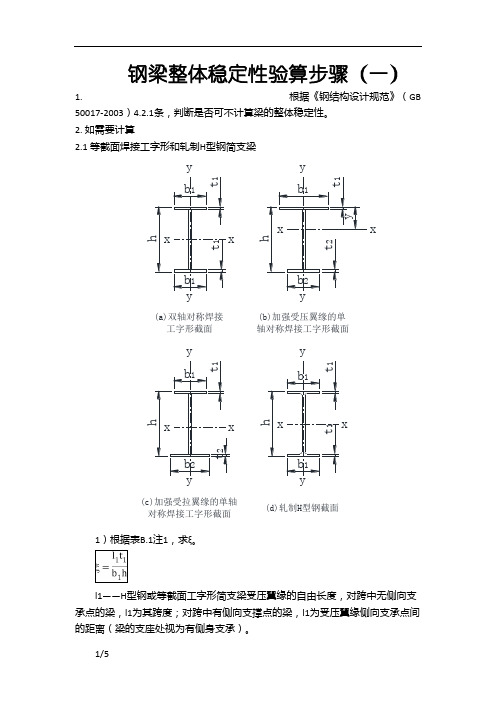
钢梁整体稳定性验算步骤(一)1.根据《钢结构设计规范》(GB50017-2003)4.2.1条,判断是否可不计算梁的整体稳定性。
2. 如需要计算2.1 等截面焊接工字形和轧制H 型钢简支梁b 1b 1t 1t 1hxx y yb 1b 2t 2xx y yht 1y(a)双轴对称焊接工字形截面(b)加强受压翼缘的单轴对称焊接工字形截面b 1b 2t 1xy y(c)加强受拉翼缘的单轴对称焊接工字形截面t 2x hb 1b 1t 1hxx y y(d)轧制H 型钢截面t 11)根据表B.1注1,求ξ。
l1——H 型钢或等截面工字形简支梁受压翼缘的自由长度,对跨中无侧向支承点的梁,l1为其跨度;对跨中有侧向支撑点的梁,l1为受压翼缘侧向支承点间的距离(梁的支座处视为有侧身支承)。
b1——截面宽度。
2)根据表B.1,求βb。
3)根据公式B.1-1注,求I1和I2,求αb。
如果αb>0.8,根据表B.1注6,调整βb。
4)根据公式B.1-1注,计算ηb。
5)根据公式B.1-1,计算φb。
6)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
7)根据公式4.2.2,验算稳定性。
2.2 轧制普通工字钢简支梁1)根据表B.2选取φb。
2)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
3)根据公式4.2.2,验算稳定性。
2.3 轧制槽钢简支梁1)根据公式B.3,计算φb。
2)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
3)根据公式4.2.2,验算稳定性。
2.4 双轴对称工字形等截面(含H型钢)悬臂梁1)根据表B.1注1,求ξ。
l1——悬臂梁的悬伸长度。
b1——截面宽度。
2)根据表B.4,求βb。
3)根据公式B.1-1,计算φb。
4)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
5)根据公式4.2.2,验算稳定性。
2.5 受弯构件整体稳定系数的近似计算(均匀弯曲,)2.5.1 工字形截面(含H型钢)双轴对称1)根据公式B.5-1,计算φb,当φb>0.6时,不必根据公式B.1-2,采用φ’b代替φb,当φb>1.0,取φb=1.0。
B94-实际轴心受压构件整体稳定计算公式

x
x
x
x
格构式
y
x
y
x
y
x
x
x
x 焊接,翼缘为 轧制或剪切边
b类
c类
y
y
y
y
焊接,翼缘为轧
y 焊接,板件
x
制或剪切边 x
宽厚比≤20
c类
c类
轴心受压构件截面分类(板厚t≥40mm)
截面形式
对x轴
b x
y
h
轧制工字形 或H形截面
t<80mm
b类
t≥80mm
c类
y
x
x
y
焊接工字 形形截面
翼缘为焰切边
b类
y
边
轧制等 边角钢
对x轴
y x
y
xx
x
y
x
x
y
y
y
y
y
b类
y 轧制、焊接
x
x
轧制或 焊接
x
板件宽厚比
大于20
y x
y
x 轧制截面和翼 缘为焰切边的 焊接截面
y
x
y
x 焊接,板件 边缘焰切
对y轴 b类
轴心受压构件截面分类(板厚t<40mm)
截面形式
对x轴 对y轴
y
y
y
y
y
x
x
x
x
x
焊接
y
y
y
y
b类 b类
计算 l0
i
据
截面类型
查表
得到
代入公 式验算
N f
A
如何提高轴心受压构件整体稳定性 ?
由公式 N f 及 l0
防波堤整体稳定计算说明

1、对土坡和条形基础的地基稳定计算,可按平面问题考虑,宜采用圆弧滑动面计算。
2、对不同情况的土坡和地基的稳定性验算,其危险滑弧均应满足以下极限状态设计表达式:式中M sd、M Rk——分别为作用于危险滑弧面上滑动力矩的设计值(kN·m/m)和抗滑力矩的标准值(kN·m/m);γR——抗力分项系数。
圆弧滑动稳定计算示意图对于持久状况土的抗剪强度宜采用固结快剪指标,M Rk、M sd宜按下列公式计算:M Sd =γs{[ΣR(q ki b i+W ki)sinαi]+M p式中R——滑弧半径(m);γs——综合分项系数,可取1.0;W——属永久作用,为第i土条的重力标准值(kN/m),可取均值,零压线以下ki用浮重度计算;当有渗流时:极端低水位以上零压线以下用饱和重度计算滑动力矩设计值M sd;u——第i土条滑动面上水头超过零压线以上的孔隙水压力标准值ki(kPa),可取均值;M——其它原因,如作用于直立式防波堤的波浪力标准值引起的滑动力矩p(kN·m/m);q——为第i土条顶面作用的可变作用的标准值(kN/m2),应按现行行ki业标准《港口工程荷载规范》(JTJ215)采用;b——第i土条宽度(m);i——第i土条的滑弧中点切线与水平线的夹角(o);αiφki、c ki——分别为第i土条滑动面上的固结快剪内摩擦角(o)和粘聚力(kPa)标准值,可取均值。
目前港口设计中滑弧稳定计算以采用简单条分法计算为主,此时,其抗滑力矩标准值可按下式计算:M=R[Σc ki L i+Σ(q ki b i+W ki)cosαi tgφki]Rk当采用总强度,如十字板强度或三轴不排水剪强度时,其抗滑力矩标准值可按以下公式计算:M=RΣS uki L iRkL=b i cosαii式中S uki——第i土条滑动面上十字板强度标准值或其它总强度标准值(kPa),标准值可取均值;L——第i土条对应弧长(m)。
整体稳定性验算方法

5.4.3 整体稳定性的验算方法1.计算公式由求得的临界弯矩可求得临界应力:(5.4.2)式中:为按受压纤维确定的梁毛截面抵抗矩。
保证梁整体稳定的条件是:(5.4.3)或:(5.4.4)式中:M x——绕强轴作用的最大弯矩;——梁的整体稳定系数。
双轴对称工字型截面简支梁受纯弯曲荷载作用时:(5.4.5)式中:——梁在侧向支承点间对截面弱轴(y轴)的长细比;——受压翼缘的自由长度;——梁的毛截面对y轴的截面回转半径;——梁的毛截面面积;——梁的截面高度和受压翼缘厚度(见图5-4-2)。
对于单轴对称工字型截面(图5-4-2b、c),应考虑截面不对称影响系数,对于其它种类的荷载和荷载的不同作用位置,还应乘以修正系数,从而可得通式为:(5.4.6)图5-4-2 焊接工字形截面式中:——等效弯矩系数,参见[表5-4-4];——截面不对称影响系数,双轴对称工字型截面,=0;加强受压翼缘的工字型截面,(图5-4-2b);加强受拉翼缘的工字型截面,(图5-4-2c);和分别为受压翼缘和受拉翼缘对y轴的惯性矩。
上述公式是按弹性工作阶段给出的,当时,已超出了弹性范围,应按下式修正或查[表5-4-1],用代替。
表(5-4-1)整体稳定系数值(5.4.7)对于轧制普通工字钢简支梁的整体稳定系数,同样应以代替。
在两个主平面内受弯曲作用的工字型截面构件,应按下式计算整体稳定性:(5.4.8) 2. 计算梁的整体稳定系数的简化方法Ⅰ热轧普通工字钢简支梁,可直接查[表5-4-2]。
Ⅱ轧制槽钢简支梁的整体稳定系数,均按下式计算:(5.4.9)式中:h﹑b﹑t——分别为槽钢截面的高度﹑翼缘宽度和平均厚度。
3. 不必计算整体稳定性的情况当梁的整体稳定性系数=1.0时,梁就不可能丧失整体稳定性,也不必计算梁的整体稳定性,具体条件如下:Ⅰ有铺板(各种钢筋混凝土板和钢板)密铺在梁的受压翼缘上并与其牢固相连接,能阻止梁受压翼缘的侧向位移时;Ⅱ工字型截面简支梁受压翼缘的自由长度与其宽度b1之比不超过[表5-4-3]所规定的数值时。
轴心受压构件的整体稳定性

2、缀条设计 内力: V1:分配到一个缀材面的剪力。当每根柱子都有两个缀材面时,此时V1为V/2; n 承受剪力V1的斜缀条数,单缀条体系,n =1;双缀条超静定体系,通常简单地认为每根缀条负担剪力V2之半,取n =2; 缀条夹角,在30~60之间采用。 斜缀条常采用单角钢。由于角钢只有一个边和构件的肢件连接,考虑到受力时的偏心作用,计算时可将材料强度设计值乘以折减系数r =0.85。
横缀条主要用于减小肢件的计算长度,其截面尺寸与斜缀条相同,也可按容许长细比确定,取较小的截面。
3、缀板设计
缀板用角焊缝与肢件相连接,搭接的长度一般为20~30 mm。角焊缝承受剪力T和弯矩M的共同作用。
剪力: 弯矩(与肢件连接处):
算例6 P136 例4-5 算例7 P138 例4-6
算例4 P124 例4-3 算例5 P124 例4-4
第五节 格构式轴心受压构件设计
格构式截面
肢件:槽钢、工字钢、角钢
缀件:缀条、缀板
一、 格构式轴心受压构件长细比计算
1、绕实轴长细比计算:同实腹式;
2、绕虚轴长细比计算:考虑剪切变形,采用换算长细比;
换算长细比
式中 y 整个构件对虚轴的长细比; A 整个构件的横截面的毛面积; A1y 构件截面中垂直于y轴各斜缀条的毛截面面积之和; 为防止单肢件失稳先于整体失稳,规范规定: 缀条构件:单肢长细比不大于两方向长细比较大值0.7倍;
轴心受压构件的截面分类(板厚t40mm)
1、轴心受压构件稳定系数表达式 1)当 2)当
1)钢材品种(即fy和E);2)长细比;3)截面分类;
稳定系数影响因素:
式中 N 轴心受压构件的压力设计值; A 构件的毛截面面积; 轴心受压构件的稳定系数,取两主轴稳定系数较小者; f 钢材的抗压强度设计值。
整体稳定计算

附件一 围堰堰顶高程计算1.上游围堰堰顶高程计算1.1 设计洪水位及堰顶超高计算公式根据Tender documents, BOOK 3 OF 4, VOLUME Ⅵ, PART 1, 1.3 (Hydrological Characteristics),Fig. 4.3 (Discharge rating curves of the Nile river at the Merowe HPP tailrace)可查知全年3%洪水频率,相应流量为12300m3/s ,厂房尾水处(靠近下游围堰)在左河道过流情况下,相应水位为259.3m ;根据水力学计算和水面线推求结果,推出上游围堰处相应水位为259.4m 。
为保证在发生设计洪水位时,不漫溢或溅过堰顶,堰顶高程要根据设计洪水位,考虑风浪高和安全超高确定。
堰顶超高可按下式计算:δ++=q h e d式中,d —围堰在静水位以上的超高,m ;e —堰前因风吹而使静水位超出库水位的壅水高度,m ; q h —波浪在堰坡上的爬高,m ;δ—波浪以上的安全超高,m 。
下面分别确定e 、q h 、δ。
1.2 风雍水面高度风雍水面高度可按下式计算:αcos 22m gHD KW e =式中W ———采用多年平均最大风速,m/s ;D ———风区长度(吹程),m ; m H ———堰前水深,m ;K ———综合摩阻系数,取3.6×10-6;α———风向与围堰轴线的法线方向所成的交角。
根据招标文件:MEROWE-03-B00K 3 OF 4-VOLUME Ⅵ-SUPPORTING DATA 水文气象和地质资料,风向: 北风45%, 东北风 21%。
20%频率暴风的年最大风速W 为20m/s 。
水位为259.4m 时,风区内水域平均深度m H m 4.152444.259=-=吹程D 取为从围堰算起沿库水面直到对岸的最大直线距离,约2000m 。
α取为20°将以上参数代入公式,得m gHD KW e m 009.04.158.92200020106.3cos 2262=⨯⨯⨯⨯⨯==-α1.3 波浪爬高1)波浪平均波高、平均波周期和平均波长计算 a.波浪平均波高h m 采用莆田试验站公式⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛=7.0245.027.0227.013.00018.07.013.0W gH th W gD th W gH th Wgh m mm 式中m h ———平均波高,m ;W ———计算风速,m/s ;D ———风区长度,m ;m H ———水域平均水深,m ;将s m W /20=,m D 2000=,m H m 4.15=代入以上公式,得gW W gH th W gD th W gH th h m mm27.0245.027.027.013.00018.07.013.0⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛= 8.920204.158.97.013.02020008.90018.0204.158.97.013.027.0245.027.02⨯⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⨯⨯⎪⎭⎫ ⎝⎛⨯⨯⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⨯⨯=th th th m 416.0=b.波浪平均波周期T msh T m m 86.2416.0438.4438.45.05.0=⨯==c.波浪平均波长L m⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=m mmmL th L Hth gT L 4.151416.321416.3286.28.92222ππ 通过试算得,mL m 77.12=2)波浪爬高值计算 a. 计算方法1正向来波在坡面上的波浪爬高按下式计算:mm W q L h mK K h 21+=∆式中q h ———波浪爬高,m ;m ———坡度系数;∆K ———斜坡的糙率渗透性系数,对于砌石护面,取0.75~0.80;wK ———经验系数,m ; 628.14.158.9/20/=⨯=gH W ,查相关表格,得03.1=w K将上述各参数代入公式,计算得波浪爬高为m h q 895.077.12416.08.1103.18.02=⨯⨯+⨯=b.计算方法2qh 亦可采用如下公式计算: θtg h K h q )2(3.3=式中h 2———波浪高,m ;θ———迎水堰面坡角(°); K ———堰坡护面粗糙系数(块石K=0.77)。
梁的整体稳定性计算

0.282
验算强度和稳定。 应重新计算荷截面面积; h, 1 — 梁截面的全高和受压翼缘厚度; t 缘厚度;
αb = I1 / (I1 + I2 ),I1 和I2分别是受拉翼缘和受压翼缘对y轴的惯性矩。 轴的惯性矩。
ηb — 截面不对称影响系数, 截面不对称影响系数, 对双轴对称截面, 对双轴对称截面,ηb =0 加强受压翼缘: 对单轴对称工字型截面:加强受压翼缘:ηb = 0.8(2αb −1) η 加强受拉翼缘: 加强受拉翼缘: b = 2α b −1
5.3.3 梁的整体稳定计算方法
当不满足前述不必计算整体稳定条件时, 当不满足前述不必计算整体稳定条件时,应对当梁的 整体稳定进行计算: 整体稳定进行计算:
M x σ cr σ cr f y σ= ≤ = =ϕ b f Wx γ R f yγ R
Mx ≤ f ϕ bW x
Mx—绕强轴作用的最大弯矩; 绕强轴作用的最大弯矩; Wx—毛截面模量; 毛截面模量; φb—梁的整体稳定系数。 梁的整体稳定系数。
图5.15 梁的侧向支撑
的计算( 梁的整体稳定系数 ϕ b 的计算(见P311,附录3)
1、焊接工字形等截面简支梁和扎制H型钢简支梁
λyt1 2 4320 Ah 235 [ 1 +( φ =β ) + η b] 2 b b λ y Wx 4.4h fy
β b — 梁整体稳定的等效临界 弯矩系数,查 P311,附表3.1; 弯矩系数, λ y = l 1 iy — 梁在侧向支承点间对截面弱轴y − y的长细比; 的长细比;
平台梁格布置如图5.15所示, 5.15所示 [例5.1] 平台梁格布置如图5.15所示, 主梁 主 梁 次梁支于主梁上面,平台板未与次梁翼 次梁支于主梁上面, 缘牢固连接。 缘牢固连接。次梁承受板和面层自重标 准值为3.1kN/mm 有包括次梁自重) 准值为3.1kN/mm2(有包括次梁自重), 次 活荷载标准值为12kN/mm 静力荷载). 次梁 活荷载标准值为12kN/mm2(静力荷载). 梁 次梁采用轧制工字钢I36a,钢材为Q235B. I36a,钢材为 次梁采用轧制工字钢I36a,钢材为Q235B. 要求:验算次梁整体稳定,如不满足, 要求:验算次梁整体稳定,如不满足, 另选次梁截面. 另选次梁截面.
受弯构件的强度、整体稳定和局部稳定计算

实用文档受弯构件的强度、整体稳定和局部稳定计算钢梁的设计应进行强度、整体稳定、局部稳定和刚度四个方面的计算。
一、强度和刚度计算1.强度计算强度包括抗弯强度、抗剪强度、局部承压强度和折算应力。
(1) 抗弯强度荷载不断增加时正应力的发展过程分为三个阶段,以双轴对称工字形截面为例说明如下:图1 梁正应力的分布1)弹性工作阶段 荷载较小时,截面上各点的弯曲应力均小于屈服点y f ,荷载继续增加,直至边缘纤维应力达到y f (图1b )。
2)弹塑性工作阶段 荷载继续增加,截面上、下各有一个高度为a 的区域,其应力σ为屈服应力y f 。
截面的中间部分区域仍保持弹性(图1c ),此时梁处于弹塑性工作阶段。
3)塑性工作阶段当荷载再继续增加,梁截面的塑性区便不断向内发展,弹性核实用文档心不断变小。
当弹性核心完全消失(图1d )时,荷载不再增加,而变形却继续发展,形成“塑性铰”,梁的承载能力达到极限。
计算抗弯强度时,需要计算疲劳的梁,常采用弹性设计。
若按截面形成塑性铰进行设计,可能使梁产生的挠度过大。
因此规范规定有限制地利用塑性。
梁的抗弯强度按下列公式计算: 单向弯曲时f W M nxx x≤=γσ(1)双向弯曲时f W M W M nyy y nx x x≤+=γγσ (2)式中 M x 、M y —绕x 轴和y 轴的弯矩(对工字形和H 形截面,x 轴为强轴,y 轴为弱轴);W nx 、W ny —梁对x 轴和y 轴的净截面模量;y x γγ,—截面塑性发展系数,对工字形截面,20.1,05.1==y x γγ;对箱形截面,05.1==y x γγ;f —钢材的抗弯强度设计值。
当梁受压翼缘的外伸宽度b 与其厚度t 之比大于y f /23513 ,但不超过y f /23515时,取0.1=x γ。
需要计算疲劳的梁,宜取0.1==y x γγ。
(2)抗剪强度实用文档主平面受弯的实腹梁,以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状态。
钢梁稳定性计算

钢梁整体稳定的计算要求和公式
单向受弯钢梁整体稳定计算公式:
/()x b x M W f ϕ≤
双向受弯工形截面钢梁整体稳定计算公式:
/()/()x b x y y y M W M W f ϕγ+≤
以上两式中:
M x 、M y ——绕强轴(x 轴)、弱轴(y 轴)作用的弯矩;
W x 、W y ——按受压纤维确定的对x 轴、y 轴的毛截面抵抗矩; φb ——绕强轴弯曲所确定的厂休稳定系数,计算见下节;
γy ——对弱轴的截面塑性发展系数,查下表1。
表1 截面塑性发展系数γx 、γy 值
规范规定符合下列情况之一的钢梁可不计算其整体稳定性:
(1) 有面板(各种钢筋混泥土板和钢板)密铺在梁的受压翼缘上与其牢固相连,能阻止梁受压翼缘的侧向位移时。
(2) 工形截面简支梁受压翼缘的自由长度l 1与其宽度b 1不超过下列数值时: 跨中无侧向支承点,荷载作用在上翼缘:
跨中无侧向支承点,荷载作用在下翼缘:
跨中有侧向支承点:
(3)箱形截面(图1)简支梁的截面高宽比h/b≤6且l1/b0≤95(235/f y)时。
当采用箱形截面时,这一点很容易满足。
最新-实际轴心受压构件的整体稳定的计算

度还因截面形状、尺寸和屈曲方向而不同。
实际需要考虑的缺陷, 包括残余应力、初弯曲、初偏心,后两者 常合并为一种,统一用初弯曲来代表。
考虑多种缺陷影响的压杆荷载—挠度曲线
l/2
N 初弯曲状 态
v0 v1 v
x y
N
N NE
初弯曲v0
b
弹性性曲线
Nu Np
0 v0
a c1
c
初弯曲v0 ,弹塑性
d
a1
cr
y
我国的柱子曲线
d1
初弯曲v0 ,弹塑性,有 残余应力
v
荷载—挠度曲线
l/2
实际压杆的失稳称为极值型失稳,是第二类稳定问题。
实际稳定承载力取极值点对应的荷载。
当实际构件处于 弹塑性阶段,其应 力 ~应变关系不但在 同 一截面各点有变化、 而且沿构件轴线方向 各截面都有变化。因 此极限承载力的计算 比较复杂。
l/2
规范根据不同截面形状和尺寸、不同加工条件和相应的残 余 应力分布及大小、不同的弯曲屈曲方向以及l/1000的初弯曲 ,按 极限承载力理论,采用数值积分法,对多种实腹式轴心受 压构件 弯曲屈曲算出了近200条柱子曲线。
柱子曲线---- / f 与构件长细比λ之间的关系曲线
cr
y
N
初弯曲v0
cr
l/2
N
初弯
N
曲状
态
v0 v1 v
Nu Np
x
0 y v0 N
初弯曲v0 弹性性曲线
b
c
初弯曲v0 ,
பைடு நூலகம்
a c1
d 弹塑性
a1
d1
初弯曲v0 ,弹塑 性,有残余应力
堤防整体稳定计算书-个人例子分享

堤防整体稳定计算书-个人例子分享1.1 堤防整体稳定计算(1)计算方法根据《堤防工程设计规范》GB50286-2013进行抗滑稳定计算。
计算软件采用河海大学开发的AUTOBANK7.0水工结构分析系统。
计算方法为简化毕肖普法,计算公式如下:[]{}∑∑+±'+'+'-±=]/sin )[()/tan tan 1/(sec tan sec sec )(R M a V W K a a b c a ub a V W K C式中:K ——土坡稳定安全系数W ——土条重。
V ——垂直地震惯性力(V 向上为负,向下为正) u ——作用于土条底面的孔隙压力(KN/m 2)α——条块重力线与通过此条块底面中点的半径之间的夹角(°)b ——土条的宽度''、c ——土条底面的有效凝聚力(KN/m 2)和有效内摩擦角(°)Mc ——水平地震惯性力对圆心的力矩(KN ?m )R ——圆弧半径(m )(2)计算工况水位组合根据《堤防工程设计规范》,并结合工程情况和水文条件,本工程按施工期、正常运行期、水位骤降期三种工况进行整体稳定分析计算。
施工期工况临水坡水位一般为常水位,堤后一般采用地下水位;正常运行期临水侧取设计洪水位,背水侧取地表高程;水位降落期工况临水侧取骤降36h 的水位,背水侧取地表水位。
(3)计算断面选取某河道堤岸结构型式主要分拓浚式斜坡式复合、回填河道直斜复合式断面两种。
本次堤防稳定计算选取各典型断面进行整体稳定分析。
根据本阶段地质提供的资料,选取8个典型断面和最不利断面进行计算。
(4)各土层物理力学指标a.地质指标取用分析根据《堤防工程设计规范》(GB50286-2013),在计算正常运行期、水位骤降期工况的安全系数时,采用建议值的固结快剪指标。
施工期采用总应力法,对应使用快剪指标。
在计算中,根据地质提供的快剪建议值计算,对于由Ⅲ3层淤泥和Ⅲ1层淤泥质粉质粘土控制的土层堤防设计断面安全系数很难达到1.0以上,由于本工程为拓浚河道,堤顶增加土体荷载较小,相对对地面以下土体扰动很小,原有土体大多仍保持原有饱和固结状态,施工期若采用快剪建议值指标,很多断面的安全系数都在0.7、0.8左右,需在设计断面基础上再退堤20m 甚至更远增加综合坡比,或采用地基处理措施,安全系数才能达到1.0以上,这会使工程的投资增大很多以及对征地等政策处理造成困难,计算采用快剪指标是不合适的。
整体稳定计算
整体稳定计算
1 计算参数
整体稳定计算方法: 瑞典条分法;
应力状态计算方法: 总应力法;
土钉法向力折减系数:ξ=0.5;
土钉切向力折减系数:ξ=1.0;
锚杆法向力折减系数:ξ=0.0;
锚杆切向力折减系数:ξ=0.0;
桩墙抗滑考虑方式:滑面绕桩;
浸润线不考虑止水帷幕;
滑弧搜索不考虑局部失稳;
考虑开挖工况;
搜索范围:坡顶:全范围;坡底:全范围;
搜索方法: 遗传算法。
2 计算结果
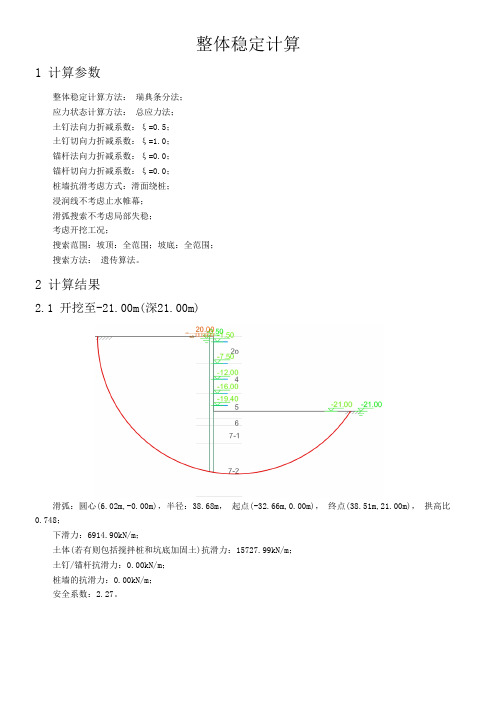
2.1 开挖至-21.00m(深21.00m)
滑弧:圆心(6.02m,-0.00m),半径:38.68m, 起点(-32.66m,0.00m), 终点(38.51m,21.00m), 拱高比0.748;
下滑力:6914.90kN/m;
土体(若有则包括搅拌桩和坑底加固土)抗滑力:15727.99kN/m;
土钉/锚杆抗滑力:0.00kN/m;
桩墙的抗滑力:0.00kN/m;
安全系数:2.27。
桥梁的整体稳定计算

桥梁的整体稳定计算摘要:城市桥梁尤其是高架桥或立交匝道桥,由于受桥下交通和桥梁美观的影响,设置单支点桥墩或横桥向小支座间距的设计形式被广泛采用,但由此造成桥梁的整体稳定问题日益突出,近年来由于车辆重型化和超载现象的发生,国内发生了多起桥梁整体失稳的事故,本文以工程案例为基础,介绍桥梁抗倾覆稳定性计算的方法,通过对相同参数曲线桥和直线桥的比较,得到相关结论。
关键词:整体稳定;脱空;倾覆轴线abstract:city bridge especially the viaduct and interchange ramp bridge, because of the influence of traffic condition under the bridge and bridge appearance, set the single supporting pier or transverse direction of bridge design in the form of small spacing is widely used, but the overall stability of bridges have become increasingly prominent, in recent years due to heavy vehicles and overloading phenomenon, the spate of whole bridge collapse accidents, this paper based on the engineering case, the bridge overturning stability calculation method, through the comparison of the same parameters of curved bridge and straight bridge, conclusion.keywords: overall stability; void; overturning axis中图分类号:u455.1文献标识码:a 文章编号:2095-2104(2013)现代桥梁设计已不仅仅是桥梁结构设计,桥梁的景观设计已经是城市桥梁设计中必须考虑的部分,因此受占地、桥下通透性空间及桥梁横断面的景观性等因素影响,单支点桥墩或小支座间距的桥梁被广泛应用于城市桥梁中,由于横桥向采用单支点或小间距支撑,在汽车偏载作用下,桥梁的横向抗倾覆稳定非常不利。
相关规范对土钉墙整体稳定性的计算公式

s k 0 ( wi q0 bi ) sin i 0
i 1
式中:
n --滑动体分条数; m --滑动体内土钉数;
k --整体滑动分项系数,可取 1.3;
0 --基坑侧壁重要性系数;
wi --第 i 条土重,滑裂面位于粘性土或
粉土中时,按上覆土层的饱和土重度计 算;滑裂面位于砂层或碎石类土中时, 按上覆土层的浮重度计算;
Tnj --第 j 根土钉在圆弧滑裂面外锚固体与土体的极限抗拉力。
2、中国工程建设标准化协会标准《基坑土钉支护技术规程》 (CEVS96-97)P12 5.3.1 土钉支护的内部整体稳定性分析是指边坡土体中可能出现的破坏面发生在支护内部并 穿过全部或部分土钉。 假定破坏面上的土钉只承受拉力且达到最大抗力, 按圆弧破坏面采用 普通条分法对支护作整体稳定分析, 取单位长度支护进行计算, 按下式算出内部整体稳定性 安全系数为:
bi --第 i 分条宽度; cik --第 i 分条滑裂面处土体固结不排水(快)剪粘聚力标准值;
ik --第 i 分条滑裂面处土体固结不排水(快)剪内摩擦角标准值; i --第 i 分条滑裂面处中点切线与水平面夹角;
j --土钉与水平面之间的夹角;
Li --第 i 分条滑裂面处弧长;
s --计算滑动体单元厚度;
--折减系数,根据经验取 0.5。
5、上海市标准《基坑工程技术规范》 (DG/TJ08-61-2010)P48 7.2.6 复合土钉墙支护应根据开挖和安设土钉工况分阶段验算稳定性,同时应按最终工况验 算整体稳定性。 复合土钉墙支护应采用瑞典条分法验算最危险滑动面的稳定性, 并按下式计 算水泥土搅拌桩、土钉等的抗滑作用:
c l S (w
整体稳定计算
轧制普通工字钢简支梁的整体稳定系数
当按表查得的 b 大于0.6时, 用下式中的 代替b' b
轧制槽钢简支梁
当按上式计算的
b
大于0.6时,用下式中的
' b
代替
b
双轴对称工字形等截面(含H型钢)悬臂梁
受弯构件整体稳定性系数近似计算
梁的整体稳定性系数(规范附录B)
轧制H型钢和等截面焊接工字形简支梁 轧制普通工字钢简支梁 轧制槽钢简支梁 双轴对称工字形等截面(含H型钢)悬臂梁 受弯构件整体稳定性系数近似计算
轧制H型钢和等截面焊接工字形简支梁整体稳定性系数
基本公式
当按上式计算的
b
b
代替
b
表B1. H型钢和等截面工字形简支梁系数 b
不进行整体稳定性计算的情况
有铺板密铺在梁的受压翼缘上并与其牢固 连接,能阻止梁受压翼缘的侧向位移
H型钢或等截面工字形简支梁受压翼缘的自由长度 与其宽度之比出超过表1规定的数值
箱形截面简支梁,其截面尺寸满足 h b0 6 且 l1 b0 95 235 f y
表1 H型钢或等截面工字形简支梁不需计算整体稳定的最大 l1 b1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表1 H型钢或等截面工字形简支梁不需计算整体稳定的最大
l1
b1
梁的整体稳定性系数(规范附录B)
轧制H型钢和等截面焊接工字形简支梁 轧制普通工字钢简支梁 轧制槽钢简支梁 双轴对称工字形等截面(含H型钢)悬臂梁 受弯构件整体稳定性系数近似计算
轧制H型钢和等截面焊接工字形简支梁整体稳定性系数
基本公式
' 当按上式计算的 b 大于0.6时,用下式中的 b 代替 b
表B1. H型钢和等截面工字形简支梁系数
b
轧制普通工字钢简支梁的整体稳定系数
当按表查得的 b 大于0.6时, ' b b 用下式中的 代替
轧制槽钢简支梁
' 当按上式计算的 b 大于0.6时,用下式中的 b 代替 b
受弯构件的整体稳定的计算
不进行整体稳定性计算的情况 受弯构件整体稳定性计算
不进行整体稳定性计算的情况
有铺板密铺在梁的受压翼缘上并与其牢固 连接,能阻止梁受压翼缘的侧向位移
H型钢或等截面工字形简支梁受压翼缘的自由长度 与其宽度之比出超过表1规定的数值
箱形截面简支梁,其截面尺寸满足 h b0 6 且 l1 b0 95 235 f y
双轴对称工字形稳定性系数近似计算
