和差积商的变化规律
商的变化规律的口诀三条

商的变化规律的口诀三条
(1)被除数扩大(缩小)n倍,除数不变,商也相应的扩大(缩小)n倍。
(2)除数扩大(缩小)n倍,被除数不变,商相应的缩小(扩大)n 倍。
(3)被除数与除数同乘以来自或同除以一个数(零除外360问答),商不变。
扩展资料:
积的变化规律是指因数的变化所引起的积的变化。
(1)如一个因数扩大n倍,另一个因数不变,则积也扩大n倍。
(2)一个因数扩大n倍,另一个因数缩小n倍,则积不变。
除法运算肥天裂性质
(1)若某数除以(或乘)一个数,又乘(或除以)同一个数,则这个数
不变。
例如:68÷17×17=68(或68×17÷1绿钱规云歌投建以玉7=68)。
(2)一个数除以几个数的积兴得乡讲从养属得都花你,可以用这个
数依次除以积里的各个因数。
例如:320÷(2×5×8)=320÷2÷5÷8=4。
(3)几个数的积除以一个数,可以让积里的任何一致段机个因数除
以这个数,再与光其他的因数相乘。
例如:8×管苦洲视联72X4÷9=72÷9×8×4=256。
运算定律 和差积商的变化 规律

名称定义字母表示加法交换律几个数相加,任意交换加数的位置,它们的和不变。
a+b=b+a加法结合律三个数相加,先把前两个数相加,再同第三个数相加;或者先把后两个数相加,再同第一个数相加,它们的和不变。
(a+b)+c=a+(b+c)乘法交换律几个数相乘,任意交换因数的位置,它们的积不变。
ab=ba乘法结合律三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个数相乘,再同第一个数相乘,它们的积不变。
(ab)c=a(bc)乘法分配律☆两个数的和同第三个数相乘,可以把和里的每个加数分别同第三个数相乘,再把两个积相加,结果不变。
☆两个数的差同第三个数相乘,可以把被减数和减数分别同第三个数相乘,再把两个积相减,结果不变。
(a+b)c=ac+bc(a-b)c=ac-bc乘法分配律逆运算☆一个数分别乘以两个数,然后把所得的积相加,等于这个数乘以这两个数的和,结果不变。
☆一个数分别乘以两个数,然后把所得的积相减,等于这个数乘以这两个数的差,结果不变。
ac+bc=(a+b)cac-bc=(a-b)cac+c=(a+1)cac-c=(a-1)c减法运算的性质☆一个数连续减去两个数,等于这个数减去这两个数的和,结果不变。
☆一个数减去两个数的和,等于这个数连续减去这两个数,结果不变。
a-b-c=a-(b+c)a-(b+c)=a-b-c除法运算的性质☆一个数连续除以两个数,等于这个数除以这两个数的积,结果不变。
☆一个数除以两个数的积,等于这个数连续除以这两个数,结果不变。
a÷b÷c=a÷(bc)a÷(bc)=a÷b÷c运算定律和差积商的变换规律名称文字叙述字母表示和的变化规律☆若一个加数增加(或减少)一个数,另一个加数不变,则它们的和也增加(或减少)同一个数。
☆若一个加数增加一个数,另一个加数减少同一个数,则它们的和不变若a+b=c则(a+d)+b=c+d(a-d)+b=c-d,(a+d)+(b-d)=c☆当减数不变,被减数增加(或减少),差也若a-b=c则(a+d)-b=c+d差的变化规律增加(或减少)相同的数☆当被减数不变,减数增加(或减少),差反而减少(或增加)相同的数☆若被减数和减数同时增加(或都减少)相同的数,差不变(a-d)-b=c-d a-(b+d)=c-da-(b-d)=c+d (a+d)-(b+d)=c (a-d)-(b-d)=c (a>b+d)积的变化规律☆当一个因数不变,另一个因数扩大(或缩小)若干倍,它们的积也扩大(或缩小)同样的倍数☆若一个因数扩大若干倍,另一个因数缩小同样的倍数,它们的积不变若ab=c则(an)b=cn (a÷n)b=c÷n,(an)(b÷n)=c(a÷n)(bn)=c商的变化规律(整除时)☆当除数不变,被除数扩大(或缩小),商也随着扩大(或缩小)同样的倍数☆当被除数不变,除数扩大(或缩小),商反而缩小(或扩大)同样的倍数。
四年级上册数学和差积商的变化

《和差积商的变化》教案。
教学目标1.使学生经历和、差、积、商变化规律的发现过程。
2.尝试用简洁的语言表达和、差、积、商的变化规律,培养学生初步的概括和表达能力。
3.初步获得探索规律的一般方法和经验,发展学生的推理能力。
教学重点理解和、差、积、商的变化规律。
教学难点运用规律解决问题。
教学准备多媒体课件。
教学过程一、兴趣导入昨天晚上,我灵光凸显,写下了一首诗。
你们想听吗?(想)听可以,但不准笑啊。
我写的诗如下:今天学习很有趣,和差积商在一起。
要问到底学什么?看看变化找规律。
没了,诗写得不好,请大家多多关照。
但是,它却告诉我们了今天的学习内容。
(多媒体展示课题:和差积商的变化)二、学习新课今天的学习当中,我们要通过例题和练习,来探讨和发现和、差、积、商的变化规律。
1 学习例一。
原有雪碧37箱,可乐26箱,所以原来两种饮料共有:37+2663箱;又运来可乐12箱,现在共有可乐38箱,那么,两种饮料共有:37+38=75箱。
本例题对于计算的方法学生都不陌生,关键在于如何引导学生得出结论:1一个加数加或减几,另一个加数不变,和也加或减相同的数;2一个加数加或减几,另一个加数反而减或加相同的数,和不变。
(交流讨论,举一反三,完成练一练1。
)2 学习例二。
去年的花费为:去年成语词典的价格+英语字典的价格:68+32=100元;今年的花费为:今年成语字典的价格+英语字典的价格:56+44=100元。
今年和去年相比花费不变。
本例题中,要结合学生情况让学生理解和不变的规律:一个加数增加多少,另一个加数减少多少,和不变。
(交流讨论,举一反三,完成练一练2。
)3 学习例三。
根据题意得:单价x数量=总价。
优优花了:12x2=24元;培培花了:36x2=72元。
在例题的讲解中,通过分析要让学生理解:1一个因数扩大,另一个因数不变,积也跟着扩大;2一个因数扩大,另一个因数缩小相同的倍数,积不变。
(交流讨论,老师从旁指导,完成练一练3。
小学数学四则运算的变化规则(和差积商变化规律)

四则运算的变化规则一、加法的变化规则(1)加法公式:加数+ 加数= 和加数= 和—另一个加数(2)加法的变化规则有:(一)如果一个加数增加几,另一个加数不变,那么和也增加几。
例如:13+5=18(13+2)+5=18+2题型1小丽在做一道加法题,一个加数十位上的4看作了7,个位上的5看作了2,算得的和是87。
正确的和是多少?一个加数十位4——7,个位5——2 增加 72-45=27另一个加数不变正确的和增加27即正确的和+27=87 => 正确的和=87-27=60(二)如果一个加数减少几,另一个加数不变,那么和也减少几。
例如:28+16=44(28-12)+16=44-12题型1小强在计算加法时,把一个加数十位上的7错写成1,把个位上的8错写成0,所得的和是285。
正确的和是多少?一个加数十位7——1,个位8——0 减少 78-10=68另一个加数不变正确的和减少68即正确的和-68=285 => 正确的和=285+68=353题型2两个数相加,一个加数减少29,另一个加数不变,和将有什么变化?一个加数减少29另一个加数不变和减少29题型3两个数相加,和是100,一个加数减少48,另一个加数不变,现在和是多少?一个加数减少48另一个加数不变和减少48即现在的和=100-48=52(三)如果一个加数增加几,另一个加数减少同样的几,那么和不变。
例如:112+23=135(112+3)+(23-3)=135题型1:两个加数的和是378,其中一个加数增加245,另一个加数减少245,现在这两个加数的和是(378 )。
题型2:一个加数增加6,要使和保持不变,另一个加数应(减少6 )。
(四)如果一个加数增加几,另一个加数增加另一个几,那么和增加了(几+另一个几)。
例如:35+48=83(35+12)+(48+5)=83+(12+5)题型1:小明在计算加法时,把一个加数十位上的0错写成8,把另一个加数个位上的6错写成9,所得的和是532。
四年级上册数学思维拓展题:和差积商变化规律

四年级上册数学思维拓展题:和差积商变化规律和的变化规律:如果一个加数增加(或减少)一个数(不为0),另一个加数不变,则它们的和也增加(或减少)同一个数。
如果一个加数增加一个数(不为0),另一个加数减少同一个数,和不变。
差的变化规律:如果一个被减数增加(或减少)一个数(不为0),减数不变,则差增加(或减少)同一个数。
如果一个被减数和减数同时增加(或减少)一个数(不为0),差不变。
如果被减数不变,一个减数增加(或减少)一个数(不为0),差也减少(或增加)同一个数。
积的变化规律:1.一个因数扩大(或缩小)若干倍,另一个因数不变,积也扩大(或缩小)相同的倍数。
2.一个因数扩大(或缩小)若干倍,而另一个因数缩小(或扩大)相同的倍数,它们的积不变。
3.一个因数乘以(或除以)a,另一个因数乘以(或除以)b,积就乘以(或除以)ab的积。
商的变化规律:1.被除数扩大(或缩小)若干倍,除数不变,商也扩大(或缩小)同样的倍数。
2.被除数不变,除数扩大(或缩小)若干倍,商反而缩小(或扩大)相同的倍数。
3.被除数乘以a,除数除以b,商就乘以ab的积。
4.被除数除以a,除数乘以b,商就除以ab的积。
参考答案:1、两个数相加,如果一个加数减少9,要使和增加9,另一个加数应该有什么变化?解题思路:一个加数减少9,假设另一个加数不变,和就减少了9;题目要求和增加9,所以另一个加数应该增加9+9=18。
2、两个数相减,如果被减数减少10,减数也减少10,差是否有变化?解题思路:被减数减少10,假设减数不变,差就减少10;假设被减数不变,减数减少10,和就增加10;差先减少10,再增加10,所以无变化。
3、被减数、减数、差相加得2076,差是减数的一半。
如果被减数不变,差增加42,减数应该变成多少?解题思路:减数与差的和即是被减数,2076里有2个被减数,被减数等于2076÷2=1038。
差是减数的一半,也就是说减数是差的2倍,差应该为1038÷(2+1)=346,减数为346×2=692。
小学数学四则运算的变化规则(和差积商变化规律)

四则运算的变化规则一、加法的变化规则(1)加法公式:加数+ 加数= 和加数= 和—另一个加数(2)加法的变化规则有:(一)如果一个加数增加几,另一个加数不变,那么和也增加几。
例如:13+5=18(13+2)+5=18+2题型1小丽在做一道加法题,一个加数十位上的4看作了7,个位上的5看作了2,算得的和是87。
正确的和是多少?一个加数十位4——7,个位5——2 增加 72-45=27另一个加数不变正确的和增加27即正确的和+27=87 => 正确的和=87-27=60(二)如果一个加数减少几,另一个加数不变,那么和也减少几。
例如:28+16=44(28-12)+16=44-12题型1小强在计算加法时,把一个加数十位上的7错写成1,把个位上的8错写成0,所得的和是285。
正确的和是多少?一个加数十位7——1,个位8——0 减少 78-10=68另一个加数不变正确的和减少68即正确的和-68=285 => 正确的和=285+68=353题型2两个数相加,一个加数减少29,另一个加数不变,和将有什么变化?一个加数减少29另一个加数不变和减少29题型3两个数相加,和是100,一个加数减少48,另一个加数不变,现在和是多少?一个加数减少48另一个加数不变和减少48即现在的和=100-48=52(三)如果一个加数增加几,另一个加数减少同样的几,那么和不变。
例如:112+23=135(112+3)+(23-3)=135题型1:两个加数的和是378,其中一个加数增加245,另一个加数减少245,现在这两个加数的和是(378 )。
题型2:一个加数增加6,要使和保持不变,另一个加数应(减少6 )。
(四)如果一个加数增加几,另一个加数增加另一个几,那么和增加了(几+另一个几)。
例如:35+48=83(35+12)+(48+5)=83+(12+5)题型1:小明在计算加法时,把一个加数十位上的0错写成8,把另一个加数个位上的6错写成9,所得的和是532。
四年级上册平时作业(积、商的变化规律)

四年级上册平时作业(积、商的变化规律)一、识记积的变化规律1、一个因数不变,另一个因数扩大(或缩小)几倍,积也扩大(或缩小)相同的倍数。
2、一个因数扩大(或缩小)几倍,另一个因数缩小(或扩大)相同的倍数,积不变。
3、如果两个因数同时扩大(或缩小)几倍,积也同时扩大(或缩小)它们扩大(或缩小)的乘积倍。
商的变化规律1、除数不变,被除数扩大(或缩小)几倍,商也扩大(或缩小)相同的倍数。
2、被除数不变,除数扩大(或缩小)几倍,商就缩小(或扩大)相同的倍数。
3、被除数和除数同时扩大(或缩小)相同的倍数,商不变,余数也同时扩大(或缩小)相同的倍数。
二、填一填。
1、两数相乘的积是300,一个因数不变,另一个因数乘2,这时积应()。
2、两数相乘的积是4500,如果一个因数除以100,另一个因数不变,积是()。
3、两个因数的积是322,其中一个因数是23,如果把它改成2300,另一个因数不变,这时积是()。
4、一个因数不变,另一个因数乘9,积就()。
如果一个因数乘8,另个因数除以8,积()。
5、在除法算式600÷30=20中如果被除数除以10,要使商仍然是20,除数应(),是()。
如果被除数乘2,除数不变,商是()。
如果被除数不变,除数乘2,商应()。
6、两数相除商是400,如果被除数和除数同时乘5,商应是()。
7、在除法算式56÷5=11……1中,如果被除数和除数同时扩大100,商是(),余数是()。
8、A数是B数的25倍,则A数除以B数的商是()。
如果B数缩小5倍,要使商不变,则A数应()。
9、一个乘法算式的积是182,如果两个因数都同时扩大了10倍,积应()。
是()。
10、一个数是25相乘的积是1500,如果这个数扩大10倍,积变成()。
如果这个数缩小100倍,积应()。
11、两个数相除的商是24,如果被除数和除数同时缩小2倍,现在的商是()。
12、480÷80=6中,480扩大10倍,80缩小10倍,商是()。
和、差积、商的变化规律

除数不变,被除数变化时商的变化规律
总结词
当除数保持不变,被除数增大或减小时,商 也相应地增大或减小。
详细描述
当除数保持不变,被除数增大时,商会增大 ;反之,被除数减小时,商会减小。这是因
为被除数的增减直接影响商的数值变化。
举例说明
例如:当被除数为100,除数从10增加到20时,商从10减小到5;当除数为10,被 除数从100增加到200时,商从10增大到20。
减数不变,被减数变化时差的变化规律
总结词
减数不变,被减数增大(或减小),差会增大(或减小)。
详细描述
当减数保持不变时,随着被减数的增大或减小,差值会相应地增大或减小。这是因为被减数的变化在起主导作用, 当被减数增加时,差值会增大;当被减数减小时,差值会减小。
举例说明
例子1
假设被减数是10,减数从5变为6,差 会从5减小到4;如果减数从5变为4, 差会从5增大到6。
详细描述
如果多个加数中有的扩大倍数大于其他加数缩小的倍数,则 它们的和会增大;反之,如果多个加数中有的扩大倍数小于 其他加数缩小的倍数,则它们的和会减小。
02 差的变化规律
被减数不变,减数变化时差的变化规律
总结词
被减数不变,减数增大(或减小)的增 大或减小,差值会相应地减小或增大。 这是因为减数在起主导作用,当减数 增加时,差值会减小;当减数减小时, 差值会增大。
举例说明
总结词
通过具体例子可以更好地理解积的变化规律。
详细描述
例如,假设有两个数a和b,它们的积是p。如果a增加1,b不变,则新的积是p+b;如 果a减少1,b不变,则新的积是p-b。如果a和b同时增加或减少相同的数值,则新的积 是原来的p+(增加或减少的数值)。如果a和b同时增加或减少不同的数值,则需要对
运算定律和性质

运算定律和性质1、加法运算定律交换律:连加法中,交换两个加法的位置,它们的和不变。
例如:96+4=4+96用字母表示:a + b=b + a同时也适用几个数相加的情况。
例如:28+75+25=25+75+28用字母表示:a + b + c=c + b+ a结合律:几个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加,它们的和不变。
例如:(25+8)+32=25+(8+32)用字母表示:(a + b)+c=(a + c)+b如果先交换,再结合,可得:a +b + c=( a +c )+ba +b +c + d=( a +d )+( b + c)2、乘法运算定律交换律:在乘法中,交换两个因数的位置,它们的积不变。
例如:12×23=23×12用字母表示:a×b=b×a同时也适用几个数相乘的情况。
例如:12×25×4=4×25×12用字母表示:a×b×c=c×a×b结合律:三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变。
例如:25×34×4=(25×4)×34用字母表示:a×b×c=a×(b×c)如先交换,后结合,可得a×b×c=(a×c) ×b同时也适用几个数相乘的情况。
例如:25×5×4×2=(25×4) ×(2×5)用字母表示:a×b×c×d=(a×d) ×(b×c)分配律:两个数的和或者两个数的差与一个数相乘可以用这个数分别去乘两个数,再把两个积相加或相减。
例如:(25+16)×4=25×4+16×4(25-16)×4=25×4-16×4用字母表示:(a + b)×c=a×c + b×c(a – b)×c=a×c - b×c3、加减混合运算性质(1)在加减混合运算中,改变运算顺序,结果不变。
积商的变化规律

五年级上积商的变化规律一、积的变化规律1、两个因数,一个因数不变,另一个因数扩大或缩小几倍,积就扩大或缩小相同的倍数;0除外;2、两个因数同时扩大或缩小几倍0除外积就扩大或缩小它们的乘积倍;3、两个因数,一个扩大几倍,另一个缩小相同的倍数,0除外积不变;4、两个因数,一个扩大,另一个缩小,倍数不相同,0除外,积扩大或缩小它们的商倍例1:给出乘法算式:×= 根据算式写出得数方法:1× =缩小10倍不变缩小10倍方法:2根据预算定律×=可知13×48=624;所以×的积里面应有3位小数,因此是二、商的变化规律1、被除数不变,除数扩大或缩小几倍,商就缩小或扩大几倍;注意商和除数的变化是相反的;0除外2、除数不变,被除数扩大或缩小几倍,商就扩大或缩小相同的倍数注意商和被除数的变化是相同的;0除外3、被除数和除数同时扩大扩缩小相同的倍数0除外商不变;4、被除数扩大,除数缩小,商就扩大乘积倍;5、被除数缩小,除数扩大,商就缩小乘积倍;6、被除数、除数同时扩大或缩小不相同的倍数0除外,商就变化它们的商倍注意:4---6的规律不用硬背,只是前两个规律的分步应用;例2:给出除法算式:÷= 根据算式写出得数方法:1624 ÷ = 1300扩大100倍缩小10倍商扩大100倍商扩大10倍×10倍方法2:可利用除法算式,130048 624 4862400变成将商的最高位写上,其余数字同上面的商相同,数位不足的用0占位;相应的练习1、根据35×49=1715,在下面的填上合适的数;= × = ×= × = ×2、两数相乘,如果一个因数缩小5倍,另一个因数扩大5倍,积是否起变化3、两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积会有什么变化4、两数相除,如果被除数扩大4倍,除数缩小2倍,商怎样变化5、两数相除,被除数缩小12倍,除数缩小2倍,商会怎样变化6、小科在计算除法时,把除数末尾的0漏写了,结果得到的商是70,正确的商应该是多少7、芳芳在计算乘法时,把一个因数末尾多写了1个0,结果得到800,正确的积是应该是多少8、两数相除,商是8,余数是10,如果被除数和除数同时扩大10倍,商是多少余数是多少9、10、两数相除,商是19,如果被除数扩大20倍,除数缩小4倍,那么商是多少1、160×40=64002、 160÷32=53、如果A ÷B=500 ×40=640 ÷8=5 A ×2÷B= 160× =64000 80÷ =5 A ÷B ×5= 80× =1600 ÷96=5 A ÷10÷B= ×80=6400 320÷ =5 A ÷B ÷2= ×200=64000 ÷3200=53、如果甲数乘以乙数是240,4、如果A ×B=800, 1甲数不变,乙数乘以4,积是 ; 那么A ×6×B ÷6= 2甲数除以2,乙数不变,积是 ; 那么A ÷ ×B × =800 3甲数乘以3,乙数乘以2,积是 ; 如果A ÷B=8004甲数乘以3,乙数除以3,积是 ; 那么A ÷6÷B ÷6= 5甲数除以4,乙数除以2,积是 ; 那么A × ÷B × =800 4、两数相除的商是80,1如果被除数不变,除数乘以2,商是 ; 2如果被除数不变,除数除以3,商是 ; 3如果除数不变,被除数乘以5,商是 ; 4如果除数不变,被除数除以10,商是 ; 三、判断1、被除数和除数同时乘或除以一个相同的数0除外,商不变;……2、除数除以3,商也要除以3;……………………………………………3、因为33÷2=16……1,所以3300÷200=16……1;……………………4、一个长方形的宽不变,长扩大3倍,它的面积和周长都扩大3倍;…5、一个正方形的边长扩大5倍,它的面积和周长都扩大5倍;…………四、选择1、两数相乘,一个因数扩大5倍,另一个因数缩小5倍,积 ;A 缩小25倍B 扩大25倍C 不变2、两数相加,一个加数不变,另一个加数增加7,和 ;A 也增加7B 减少7C 不变3、两数相除,如果被除数乘5,除数除以5,商 ;A 不变B 乘以10C 除以10D 乘以254、两数相减,如果被减数不变,减数增加5,那么差 ;A 增加5B 减少5C 不变5、被除数和除数同时乘以10,商 ;A 乘以10B 乘以100C 不变。
积商的变化规律

积商的变化规律 Prepared on 22 November 2020五年级上积商的变化规律一、积的变化规律1、两个因数,一个因数不变,另一个因数扩大(或缩小)几倍,积就扩大(或缩小)相同的倍数。
(0除外)。
2、两个因数同时扩大(或缩小)几倍(0除外)积就扩大(或缩小)它们的乘积倍。
3、两个因数,一个扩大几倍,另一个缩小相同的倍数,(0除外)积不变。
4、两个因数,一个扩大,另一个缩小,(倍数不相同,0除外),积扩大(或缩小它们的商倍)例1:给出乘法算式:×= 根据算式写出得数方法:1× =缩小10倍不变缩小10倍方法:2根据预算定律×=可知13×48=624;所以×的积里面应有3位小数,因此是二、商的变化规律1、被除数不变,除数扩大(或缩小几倍),商就缩小(或扩大)几倍。
(注意商和除数的变化是相反的。
)(0除外)2、除数不变,被除数扩大(或缩小)几倍,商就扩大(或缩小)相同的倍数)(注意商和被除数的变化是相同的。
)(0除外)3、被除数和除数同时扩大扩缩小相同的倍数(0除外)商不变。
4、被除数扩大,除数缩小,商就扩大乘积倍。
5、被除数缩小,除数扩大,商就缩小乘积倍。
6、被除数、除数同时扩大或缩小不相同的倍数(0除外),商就变化它们的商倍注意:4---6的规律不用硬背,只是前两个规律的分步应用。
例2:给出除法算式:÷= 根据算式写出得数方法:1624 ÷ = 1300扩大100倍缩小10倍商扩大100倍商扩大10倍扩大100×10倍方法2:可利用除法算式,13000 . 48 )624 48)62400移动小数点变成将商的最高位写上,其余数字同上面的商相同,数位不足的用0占位。
相应的练习1、根据35×49=1715,在下面的()填上合适的数。
=()×()=()×()=()×()=()×()2、两数相乘,如果一个因数缩小5倍,另一个因数扩大5倍,积是否起变化3、两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积会有什么变化4、两数相除,如果被除数扩大4倍,除数缩小2倍,商怎样变化5、两数相除,被除数缩小12倍,除数缩小2倍,商会怎样变化6、小科在计算除法时,把除数末尾的0漏写了,结果得到的商是70,正确的商应该是多少7、芳芳在计算乘法时,把一个因数末尾多写了1个0,结果得到800,正确的积是应该是多少8、两数相除,商是8,余数是10,如果被除数和除数同时扩大10倍,商是多少余数是多少9、两数相除,商是19,如果被除数扩大20倍,除数缩小4倍,那么商是多少一、 填表二、根据第一题的答案填空1、160×40=64002、 160÷32=53、如果A ÷B=500 ( )×40=640 ( )÷8=5 (A ×2)÷B=( ) 160×( )=64000 80÷( )=5 A ÷(B ×5)=( ) 80×( )=1600 ( )÷96=5 (A ÷10)÷B=( ) ( )×80=6400 320÷( )=5 A ÷(B ÷2)=( ) ( )×200=64000 ( )÷3200=53、如果甲数乘以乙数是240,4、如果A ×B=800,(1)甲数不变,乙数乘以4,积是 。
四年级寒假班教案第3次课------积、商的变化规律

积、商的变化规律知识要点1、积的变化规律(1)一个因数不变,另一个因数扩大(缩小)到原数的a倍,积就扩大(缩小)到原数的a 倍。
(2)一个因数扩大(缩小)到原数的a倍,另一个因数缩小(扩大)到原数的a倍,积不变。
(3)一个因数扩大(缩小)到原数的a倍,另一个因数扩大(缩小)到原数的b倍,积就扩大到原数的a×b倍。
扩展:一个因数扩大到原数的a倍,另一个因数缩小到原数的b倍,当a>b时,积就扩大a ÷b倍;当a<b时,积就缩小到原数的b÷a倍。
2、商的变化规律:(1)被除数和除数同时扩大(缩小)到原数的a倍,商不变。
(2)被除数和商同时扩大(缩小)到原数的a倍,除数不变。
(3)除数扩大(缩小)到原数的a倍,商缩小(扩大)到原数的a倍,被除数不变。
扩展:被除数扩大到原数的a倍,除数缩小到原数的b倍,商就扩大到原数的a×b倍。
被除数缩小到原数的a倍,除数扩大到原数的b倍,商就缩小到原数的a×b倍。
3、周长与面积公式(1)长方形:周长=(长+宽)×2 面积=长×宽(2)正方形:周长=边长×4 面积=边长×边长经典例题【例1】根据已知算式,直接写出下面各题的得数。
105×45=4725 18×24=432(105÷5)×(45×5)= (18×3)×(24×2)=(105×2)×(45÷6)= (18×6)×(24÷2)=【练习1】24×75=1800 36×104=3744(24○6)×(75×6)=1800 (36×4)×(104○4)=3744 (24○3)×(75○□)=1800 (36○□)×(104○□)=374415×24=36015×72=()60×12=()5×72=()30×6=()15×(24×)=3600 15×(24÷10)=()【例2】(1)18 ÷6=3 (2)4800÷10=480 (18×2)÷(6×2)= (4800 ÷2)÷(10 ÷2)= (18×3)÷(6÷3)= (4800÷10)÷(10×2)=(1)24÷8=(24×2)÷(8×)(2)360÷60=(360÷10)÷(10)(3)96÷6=()÷()【例3】1、两个因数的积是100,把其中一个因数扩大到原来的3倍,另一个因数不变,积是()2、两个因数的积是100,把其中一个因数扩大到原来的3倍,另一个因数也扩大到原来的3倍,积是()3、两数相除,被除数扩大3倍,除数缩小6倍,商( )4、小明在计算除法时,把除数末尾的0漏写了,结果得到的商是500,正确的商是()5、两个因数的积是100,把其中一个因数扩大到原来的3倍,另一个因数也缩小到原来的3倍,积是()6、一个因数不变,把其中另一个因数扩大到原来的3倍,积是90,原来两个因数的积是()【练习3】1、一个因数扩大到原来的3倍,另一个因数也扩大到原来的3倍,积是90,原来两个因数的积是()2、610×5=3050,把610缩小3倍,把5扩大倍15倍,那么积是()。
积商变与不变的规律

积和商不变规律和变化规律积的变化规律:一个因数不变,另一个因数乘或除以几,积就相应的乘或除以几。
积不变规律:一个因数乘或除以几,另一个因数相应的除以或乘几,积不变。
一个数乘一个比1大的数,积比原数大;一个数乘一个比1小的数,积比原数小。
商的变化规律:被除数不变,除数乘或除以几,商就相应的除以或乘几。
除数不变,被除数乘或除以几,商就相应的乘或除以几。
商不变规律:被除数和除数同时乘或除以几,商不变。
被除数大于除数,商就大于1;被除数小于除数,商就小于1.一个数除以一个比1大的数,商比被除数要小;一个数除以一个比1小的数,商比被除数要大。
1、根据78×12=936,填写下面各题的结果。
7.8×12=() 0.78×12=() 7.8×0.12=() 0.78×()=936 2、根据414÷18=23,填写下面各题的结果。
4.14÷1.8=() 4140÷1.8=() 0.414÷0.18=() 41.4÷18=()8、两个数相除,被除数不变,除数缩小到原数的1/10,商();若除数不变,被除数扩大到原数的1/100,商就()。
9、两数相乘,一个因数乘4,另一个因数不变,积就();若一个因数乘4,另一个因数除以4,积()。
10、两个因数的积是0.5,如果一个因数扩大10倍,另一个因数扩大100倍,积应该是()。
11、两数相除,商是7.6,被除数扩大10倍,除数缩小到原数的1/100,商应该是()。
12、26.87扩大到它的( )倍得到26870,再缩小到它的( )得268.7。
13、甲乙两数的和是418,甲数的小数点向右移到一位后就等于乙数,甲数是(),乙数是()。
14、1000张纸叠起来厚9.2厘米,平均每张纸厚( )厘米,一厘米约有( )张纸.15、一吨海水含盐0.03吨,10吨海水含盐( )吨,1000吨海水含盐( )吨.16、由45到0.045缩小到原数的( ). 17、由0.08到80,扩大到原数的( ).17、两个数相除,除数缩小到原数的1/4,商就()。
四年级思维拓展和差上积的变化规律

二、和差上积的变化A类题型1、两个数相加,一个加数增加25,另一个加数减少25,和是否有变化?2、两个数相加,一个加数增加13,另一个加数也增加13,和是否有变化?3、两个数相加,一个加数增加17,另一个加数减少2,和是否有变化?4、两个数相加,一个加数增加2,另一个加数减少19,和是否有变化?5、两个数相减,如果被减数增加9,减数也增加9,差是否有什么变化?6、两个数相减,如果被减数增加46,减数减少46,差是否有什么变化?7、两个数相减,如果被减数减少27,减数增加19,差是否有什么变化?8、两个乘数相乘,一个乘数扩大了5倍,另一个乘数不变,积有什么变化?9、两个乘数相乘,一个乘数扩大了3倍,另一个乘数缩小8倍,积有什么变化?10、两个乘数相乘,一个乘数扩大了4倍,另一个乘数8倍,积有什么变化?11、两个乘数相乘,一个乘数缩小2倍,另一个乘数缩小6倍,积有什么变化?B类题型1、两个数相加,如果一个加数增加45,要使和增加51,另一个加数应该有什么变化?2、两个数相加,如果一个加数增加23,要使和减少23,另一个加数应该有什么变化?3、两个数相加,如果一个加数减少18,要使和减少9,另一个加数应该有什么变化?4、两数相减,被减数减少21,要使差增加9,减数应该有什么变化?5、两数相减,被减数减少59,要使差减少74,减数应该有什么变化?6、两数相减,减数增加38,要使差减少49,减数应该有什么变化?7、两个乘数相乘积是420,如果一个乘数扩大8倍,另一个乘数也扩大8倍,积是多少?8、两个乘数相乘积是160,如果一个乘数缩小2倍,另一个乘数也缩小2倍,积是多少?9、在除法算式中,除数不变,被除数扩大8倍,商有什么变化?10、在除法算式中,被除数不变,除数扩大6倍,商有什么变化?11、如果除数缩小5倍,要使商不变,被除数应该有什么变化?C类题型1、在一个减法算式里,被减数、减数与差的和是160,而差是减数的3倍。
积商的变化规律巧记

积商的变化规律巧记
积商的变化规律可以巧记为三个关键词——递增、递减、波动。
1. 递增:当两个数相乘,且因子中有一个逐渐增大,那么积商就呈递增的趋势,即积商越来越大。
可以用“增”字来记忆。
2. 递减:当两个数相乘,且因子中有一个逐渐减小,那么积商就呈递减的趋势,即积商越来越小。
可以用“减”字来记忆。
3. 波动:当两个数相乘,且因子中有一个在增加和减小之间交替变化,那么积商就会波动,既可能增大也可能减小,没有明显的趋势。
可以用“波”字来记忆。
通过记忆这三个关键词,即递增、递减和波动,我们可以快速回忆积商的变化规律,使记忆更加巧妙。
变化规律
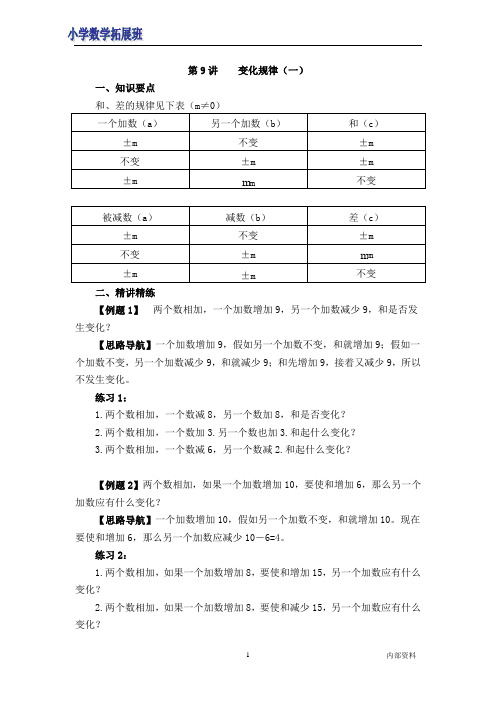
第9讲变化规律(一)一、知识要点和、差的规律见下表(m≠0)二、精讲精练【例题1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?【思路导航】一个加数增加9,假如另一个加数不变,和就增加9;假如一个加数不变,另一个加数减少9,和就减少9;和先增加9,接着又减少9,所以不发生变化。
练习1:1.两个数相加,一个数减8,另一个数加8,和是否变化?2.两个数相加,一个数加3.另一个数也加3.和起什么变化?3.两个数相加,一个数减6,另一个数减2.和起什么变化?【例题2】两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?【思路导航】一个加数增加10,假如另一个加数不变,和就增加10。
现在要使和增加6,那么另一个加数应减少10-6=4。
练习2:1.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?3.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?【例题3】两数相减,如果被减数增加8,减数也增加8,差是否起变化?【思路导航】被减数增加8,假如减数不变,差就增加8;假如被减数不变,减数增加8,差就减少8。
两个数的差先增加8,接着又减少8,所以不起什么变化。
练习3:1.两数相减,被减数减少6,减数也减少6,差是否起变化?2.两数相减,被减数增加12.减数减少12.差起什么变化?3.两数相减,被减数减少10,减数增加10,差起什么变化?【例题4】两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?【思路导航】如果一个因数扩大8倍,另一个因数不变,积将扩大8倍;如果一个因数不变,另一个因数缩小2倍,积将缩小2倍。
积先扩大8倍又缩小2倍,因此,积扩大了8÷2=4倍。
练习4:1.两数相乘,如果一个因数缩小4倍,另一个因数扩大4倍,和是否起变化?2.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?3.两数相乘,如果一个因数扩大3倍,另一个因数扩大6倍,积将有什么变化?【例题5】两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?【思路导航】如果被除数扩大4倍,除数不变,商就扩大4倍;如果被除数不变,除数缩小2倍,商就扩大2倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
老庄主摸摸胡子说:“那好吧,我先给你16个 西瓜,你要平均分成8天吃。”猪八戒连忙说:“好的, 好的。”然后,得意洋洋地走了。
在一个减法算式里,被减数、减数和差的和 是180,而差比减数少8,如果被减数不变,减数 减少16,差应变为多少?
分析: 差
8
减数
180
被减数
(1)原来的减数为: (180-8-8)÷(1+1+1+1)=41;
(2)现在的减数为:41+16=57。 答:差应变为57。
三星 训练
在一个减法算式里,被减数、减数、差相加 得90,而差是减数的2倍,减数是多少?
这时,老庄主和手下人都笑了起来。
为什么他们都笑了呢?
例1
两数相乘,如果一个因数扩大8倍,另一个因数 缩小2倍,积将会有扩大8倍,另一个因数不变,积将(扩大8倍);
如果一个因数不变,另一个因数缩小2倍,积将(缩小2倍);
积先扩大8倍,再缩小2倍,积就会( 扩大8÷2=4倍
不变 不变 ×a ÷a ×a ÷a
×a ÷a ÷a ×a 不变 不变
列式解答: 80-18=62 答:另一个加数要减少62。
从总体上把握和的增减,再确定加数的增减, 是一种逆向思维方式。
一星 训练
两个数相加,一个加数增加34,要使和增加15, 另一个加数应该如何变化?
34-15=19 答:另一个加数应该减少19。
例4
两个数相减,如果被减数减少10,减数减少8, 差将有什么变化?
分析:被减数减少10,减数不变的情况下,差怎么变? 减数减少8,被减数不变的情况下,差怎么变?
列式解答: 10-8=2
答:差减少2。
二星 训练
两个数相减,被减数减少10,减数增加10,差 将有什么变化?
10+10=20 答:差减少20。
例5 两个数相减,被减数增加5,如果
要使差增加8,减数应怎样变化?
)。
答:积会扩大4倍。
一星 训练
两数相乘,如果一个因数缩小5倍,另一个因数 扩大5倍,那么积将有什么变化?
5÷5=1 答:积不变。
例2
两个因数相乘,积是126。如果一个因数扩大2倍, 另一个因数缩小3倍,那么这时的两数之积是多少?
分析与解答: 如果一个因数扩大2倍,另一个因数不变,积扩大2倍; 如果一个因数不变,另一个因数缩小3倍,积缩小三倍; 所以:126×2÷3=84 答:两数的积是84。
列式解答:16-12=4 答:和减少4。
一星 训练
两个数相加,一个加数增加5,另一个加数也增加5, 和有什么变化?
5+5=10 答:和增加了10。
例2 两个数相加,如果一个加数增加80,要使和增加18, 那么另一个加数应有什么变化?
分析:一个加数增加80,和发生了什么变化?
要使总和增加18,说明什么?(另一个加数减少了。)
一星 训练
两个因数相乘,积是48。如果一个因数扩大2倍, 另一个因数缩小3倍,那么这时的两数之积是多少?
48×2÷3=32 答:两数之积是32。
例3 两个数相乘,一个因数缩小3倍,要使积不变,另一个
因数应有什么变化?
分析与解答: 一个因数缩小3倍,如果另一个因数不变,积会( 缩小3倍 ); 现在要使积不变,另一个因数就要( 扩大3倍 );
90÷(1+2+3)=15; 答:减数是15。
要点反馈:
加数 +a -a
不变 不变 +a
-a
加数 不变 不变 -a
+a -a
+a
和 +a -a
-a
+a 不变 不变
被减数 +a
-a 不变 不变 +a
-a
减数 不变 不变 -a
差
+a
-a
+a
+a
+a
-a
-a 不变 不变
猪八戒吃西瓜
有一天,猪八戒来到高老庄,为了表现一下自 己的本领,他在高老庄干起活来,但他那贪吃的本性没 有变,他对庄主说:“这么大热天的,你总得给些西瓜, 我吃吃吧。”
爷爷的题目是: 我今年65岁,你今年10岁,我比你大55岁。再过
五年,我比你大多少岁呢?
聪明的小朋友们,你知道答案吗?
例1
两个数相加,一个加数增加12,另一个加数减少16, 和会发生什么变化?
我增加12
她们两个的和发生 了什么变化?
我减少16
分析:一个加数增加12,和怎么变?(和增加12。) 另一个加数减少16,和怎么变?(和减少16。) 最终结果和会发生什么变化? (和减少。)
答:另一个因数要扩大3倍。
一星 训练
两个数相乘,如果一个因数缩小3倍,现在要使积 扩大4倍,另一个因数应有什么变化? 分析: 一个因数缩小3倍,另一个因数不变,积缩小3倍; 为使积不变,另一个因数要扩大3倍; 现在要使积扩大4倍,所以另一个因数要扩大:3×4=12倍。
答:另一个因数要扩大12倍。
因数 ×a ÷a 因数 不变 不变 积 ×a ÷a
课堂目标
1.加数和和的变化规律; 2.被减数、减数和差的变化规律;
3.因数和积的变化规律; 4.被除数、除数和商的变化规律。
晚上的夜空星光闪闪,小明和爷爷坐在阳台上, 爷爷给小明讲了个《嫦娥奔月》的故事,小明听得 入迷极了。爷爷讲完了,看着天穹上的月亮也在发呆。 “爷爷,你再讲个故事给我听啊!”小明撒娇着,爷爷 爽朗地说:“好啊,我出个数学题考考你,如果你答对 了,我就接着讲,如果你答错了,就不许再缠着爷爷了 啊!”
增加15,差会变成多少?
分析:被减数减少20,那么差( 减少20 ); 减数增加15,差( 减少15 )。
列式解答: 20+15=35
80-35=45
答:差会变成45。
二星 训练
两数相减,差是1999,如果被减数不变,减 数增加29,差就变成多少?
1999-29=1970 答:差就变成1970。
例7
被减数-减数=差
分析:被减数增加5,减数不变的情况下,差增加5;要 使差增加8,那必须要让减数有所变化,减数应该怎么变? 才能让差再增加3呢?
8-5=3
答:减数应该减少3。
二星 训练
两个数相减,被减数减少8,如果要使差减少12, 减数应该怎样变化?
12-8=4 答:减数应该增加4。
例6 两数相减,差是80,如果被减数减少20,减数
