药剂学:第10章 多剂量给药
第十讲 多剂量给药

第十章 多剂量给药临床用药过程中,象镇痛药、催眠药、止喘药等药物一次用药就可以获得满意的疗效,我们可以采用单剂量给药的方案。
但多数疾病是需要多次给药才能达到治疗目的,也就是要采用多剂量给药方案。
多剂量给药又称重复给药,是指按一定剂量、一定给药间隔、多次重复给药,才能达到并保持在一定有效治疗血药浓度范围内的给药方法。
多剂量给药血药浓度预测,可用单剂量给药函数导出的多剂量给药函数式求算,也可用叠加法求算。
第一节 多剂量给药血药浓度与时间的关系一、单室模型静脉注射给药 一)多剂量函数第一次给药 (X 1)max =X 0当给药时间间隔为τ时 (X 1)min =X 0e -kτ 第二次给药时(X 2)max =(X 1)min +X 0= X 0e -kτ+ X 0= X 0(1+e -kτ) (X 2)min = (X 2)max e -kτ= X 0(1+e -kτ)e -kτ第三次给药时(X 3)max = X 0(1+e -kτ)e -kτ+X 0 = X 0 (e -kτ+ e -2kτ+1) = X 0(1+e -kτ+ e -2kτ)(X 3)min = (X 3)max e -kτ= X 0(1+e -kτ+ e -2kτ)e -kτ 第n 次给药(X n )max = X 0(1+e -kτ+ e -2kτ+…+e -(n-1)kτ)(X n )min = X 0(1+e -kτ+ e -2kτ+…+e -(n-1)kτ)e -kτtC (u g /m l )单室模型n 次给药C-t 曲线(C 1)max(C 1)maxss C m axssC min我们看1、e -kτ、 e -2kτ、…、e -(n-1)kτ是一组公比为e -kτ的等比数列,其首项为1,第n 项为e -(n-1)kτ,根据等比数列前n 和的公式则有:∴式中 就是多剂量函数,用r 表示,n 为给药次数,τ为给药周期。
重复给药

= e0.2313
33.3mg/L
❖ 坪幅
坪幅即 max
Css min
X0 V(1 ek )
X V(1
0
ek
)
ekt
X0 V
❖ 达坪分数
达坪分数fss(n)指n 次给药后的血药浓度与坪浓 度相比,相当于坪浓度的分数
f (n) = C / C =C0
1 enk 1 ek
❖ 若继续给药则血药浓度在稳态水平上下波动, 随每次给药作周期性变化,药物在体内的消 除速率等于给药速率,此时的血药浓度称为 稳态血药浓度(stedy state plasma concentrtion),亦称坪浓度(plateau level),记为Css。
❖ 当n充分大时,此时达到稳态血药浓度
0.69312
1e 6
= 1.333
例题
❖ 卡那霉素的最小有效浓度为10μg/ml, 最大有效浓度为35ug/ml,消除半衰期为 3h,某患者以7.5mg/kg的剂量静脉注射 该药后测得C0=25μg/ml,请问应以多大 剂量及什么样的给药间隔时间重复给药, 才能使该患者的稳态血药浓度在治疗范 围内?
=X0(1+e-kτ) e-kτ+X0 = X0(1+e-kτ+e-2kτ) (X3)min =(X3)maxe-kτ =X0(1+e-kτ+e-2kτ) e-kτ
❖ 第n次给药
(Xn)max= X0(1+e-kτ+e-2kτ+…+e-(n-1)kτ) (Xn)min= X0(e-kτ+e-2kτ+e-3kτ+…+e-nkτ) ❖ 令 r = 1+e-kτ+e-2kτ+…+e-(n-1)kτ
第十章 多剂量给药

1 Cn = C0
1
e nk e k e
kt
多剂量给药稳态血药浓度
按一定剂量、一定给药间隔,多次重复给药,随着 给药次数n的增大,血药浓度不断增加,当n充分大时, 血药浓度不再升高,随每次给药作周期性变化,此时, 药物进入体内的速率等于从体内消除的速率,这时的 血药浓度称为稳态血药浓度,或称坪浓度(plateau level),记为Css。
所以 n = 3.32t1/ 2 lg(1 0.99) = 6.645t1/ 2
答:给药时间为4个半衰期,可达坪浓度的93.75%;达 到坪浓度的99%,需要6.645个半衰期。
(二)单室模型间歇静脉滴注给药
(二)单室模型间歇静脉滴注给药
(一)间歇静脉滴注给药的特点
• 每次固定滴注时间T,然后停止滴注τ-T 时间,给 药间隔时间为τ,如此反复进行。
当时间t=0时,体内最大药量为:
( X 3 ) max = X 0 (ek+ e 2 k ) + X 0 = X 0 (1 + e k+ e 2 k)
当时间t=τ时(即经过第三个给药周
期),体内最小药量为:
( X 3 ) min = X 0 (1 + e k + e 2 k ) e k = X 0 ( e k + e 2 k + e 3 k )
令 r =1+e k+e 2k+......+ e (n 1)k a
上式两边同时乘以e-kτ得:
r.e k=e
k +e2k
+.....+e(n +1)k e
nk
b
将上述两式相减后,再整理得单室模型多 剂量静脉注射给药,多剂量函数公式为:
第十讲多剂量给药
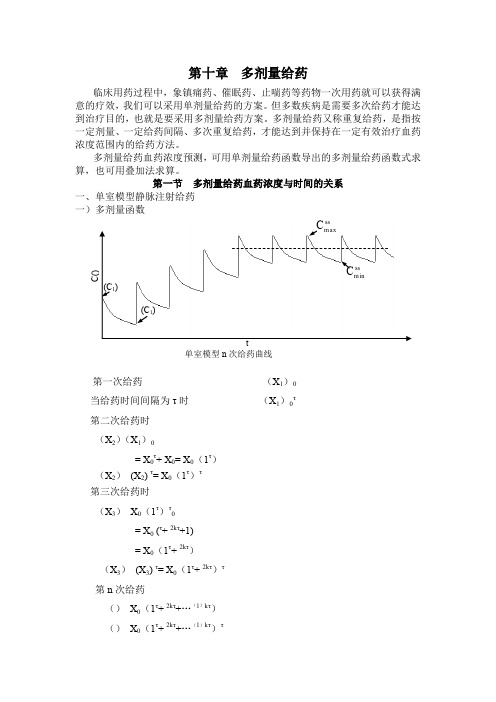
第十章多剂量给药临床用药过程中,象镇痛药、催眠药、止喘药等药物一次用药就可以获得满意的疗效,我们可以采用单剂量给药的方案。
但多数疾病是需要多次给药才能达到治疗目的,也就是要采用多剂量给药方案。
多剂量给药又称重复给药,是指按一定剂量、一定给药间隔、多次重复给药,才能达到并保持在一定有效治疗血药浓度范围内的给药方法。
多剂量给药血药浓度预测,可用单剂量给药函数导出的多剂量给药函数式求算,也可用叠加法求算。
第一节多剂量给药血药浓度与时间的关系一、单室模型静脉注射给药一)多剂量函数ss单室模型n次给药曲线第一次给药(X1)0当给药时间间隔为τ时(X1)0τ第二次给药时(X2)(X1)0= X0τ+ X0= X0(1τ)(X2)(X2) τ= X0(1τ)τ第三次给药时(X3)X0(1τ)τ0= X0 (τ+ 2kτ+1)= X0(1τ+ 2kτ)(X3)(X3) τ= X0(1τ+ 2kτ)τ第n次给药()X0(1τ+ 2kτ+…(1)kτ)()X0(1τ+ 2kτ+…(1)kτ)τ我们看1、τ、 2kτ、…、(1)kτ是一组公比为τ的等比数列,其首项为1,第n项为(1)kτ,根据等比数列前n 和的公式则有:∴式中 就是多剂量函数,用r 表示,n 为给药次数,τ为给药周期。
二)多剂量给药血药浓度与时间的关系前面讲到的多剂量函数,可以说就是一个转换因子,在等时间间隔,维持剂量相同的前提下,多剂量给药的体内动态规律可以用相应的单剂量公式经一定转换成多剂量公式。
对多剂量静脉注射给药,第n 次给药的血药浓度与时间t 的关系就等于单剂量给药的函数式与多剂量函数的乘积,即:三)稳态血药浓度多剂量给药时,随着n 的增大,血药浓度不断增加,当增加到一定程度时,血药浓度不再升高,随每次给药做周期性的变化,此时药物进入体内的速度等于体内消除的速度,这时的血药浓度叫稳态血药浓度或坪浓度,记为。
四)稳态最大血药浓度如图,在一个给药周期(τ)内,稳态血药浓度也有波动,会在一个恒定的水平范围内波动。
生物药剂与药物动力学(附习题及答案)
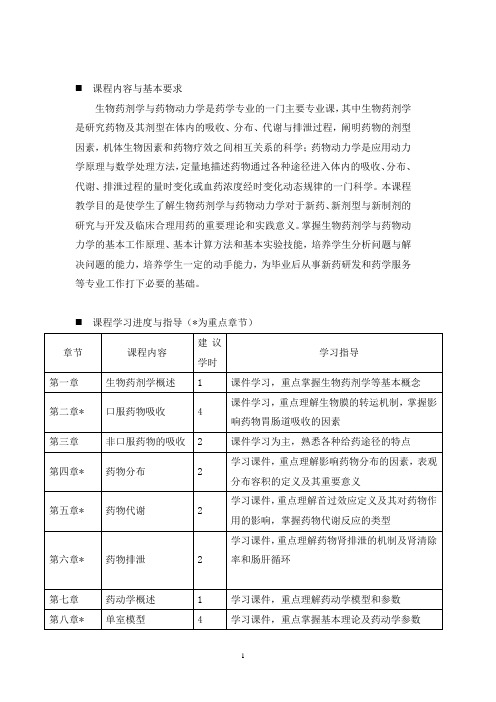
⏹课程内容与基本要求生物药剂学与药物动力学是药学专业的一门主要专业课,其中生物药剂学是研究药物及其剂型在体内的吸收、分布、代谢与排泄过程,阐明药物的剂型因素,机体生物因素和药物疗效之间相互关系的科学;药物动力学是应用动力学原理与数学处理方法,定量地描述药物通过各种途径进入体内的吸收、分布、代谢、排泄过程的量时变化或血药浓度经时变化动态规律的一门科学。
本课程教学目的是使学生了解生物药剂学与药物动力学对于新药、新剂型与新制剂的研究与开发及临床合理用药的重要理论和实践意义。
掌握生物药剂学与药物动力学的基本工作原理、基本计算方法和基本实验技能,培养学生分析问题与解决问题的能力,培养学生一定的动手能力,为毕业后从事新药研发和药学服务等专业工作打下必要的基础。
⏹课程学习进度与指导(*为重点章节)第九章多室模型 1 学习课件,理解多室模型特点和识别方法第十章* 多剂量给药 3 学习课件,重点掌握稳态血药浓度的计算第十一章非线性药物动力学 2 学习课件,重点理解特点,机制和识别方法第十二章统计矩分析 1 学习课件,掌握MRT含义及计算第十三章* 药物动力学在临床药学中的应用3 学习课件,重点掌握给药方法设计方法第十四章* 药物动力学在新药研究中的应用3 学习课件,重点掌握第一章生物药剂学概述一、学习目标掌握生物药剂学的定义,剂型因素与生物因素的含义。
熟悉生物药剂学的研究内容和进展,了解生物药剂学研究在新药开发中的作用。
二、学习内容生物药剂学的定义与研究内容;剂型因素与生物因素的含义。
三、本章重点、难点生物药剂学的概念;剂型因素与生物因素的含义。
四、建议学习策略通读教材后观看视频,并复习相关药剂药理知识帮助理解.五、习题一、名词解释1、生物药剂学(Biopharmacutics)2、吸收(absorption)3、分布(distribution)4、代谢 (metabolism) 5、排泄 (excretion) 6、转运 (transport) 7、处置 (disposition) 8、消除 (elimination) 二、简答题1.简述生物药剂学研究中的剂型因素。
药科大生物药剂学课件第十章 多剂量给药

(1) iv bolus injection, iv A. one-compt. drugs s.d. m.d.
B. two-compt. drugs
X 0 kel t C e Vd X 0 1 e nkel t kel t Cn e k el t Vd 1 e
C Ae t Be t
ss
ss C max k el t e ss C min
在一个 t内
ss t 0, C max
X0 1 Vd 1 e kel t X0 1 kel t e Vd 1 e kel t
t t, C
ss min
Bo Wang Associate Professor of Pharmaceutics Department of Pharmaceutics China Pharmaceutical University
1
LOGO
Chapter 11 多剂量给药药物动力学
• • • • •
3rd dose
( X e
0
kel t
X 0 )e kel t X 0 e k kel t X 0 )e kel t X 0 体内药量最 小值 ( X 0e kel t X 0 )e kel t X 0 e kel t
C
ka FX 0 (e kel t e ka t ) Vd ( ka kel )
m i 1
C Ne ka t Le t Me t
C Ai e l i t
li: 相关过程的表观一级速度常数
13
LOGO
single dosing
多剂量给药

二、重复给药血药浓度的波动程度
1、波动百分数(PF)
指稳态最大血药浓度与稳态最小血药浓度之
差与稳态最大血药浓度或稳态最小血药浓度比值
的百分数。
PF=Cmssax
C ss min
C ss max
100%
PF=Cmssax
C ss min
C ss min
100%
2、波动度(DF)
指稳态最大血药浓度与稳态最小血药浓度之 差与平均稳态血药浓度的百分数。
• 指稳态血药浓度波动的幅度。
C ss max
C ss min
X0 V (1 ek
)
V
X0 (1 ek
)
ek
X0 V
X ss max
X ss min
X0
可见,达稳态时体内药量波动范围等于给药剂量。
(五)达坪分数fss (Fraction of steady state concentration) 达到稳态平均血药浓度某一分数为达坪分数fss。
2、血管外给药负荷剂量的求算
给首剂量X0*,经过一给药周期τ后,血药浓度C1*为:
*
C
FX
* 0
ka
(ek eka )
1 V (ka k)
因为稳态最低血药浓度为:
Css min
FX V (ka
0 ka k)
( 1
ek ek
eka 1 eka )
假设
即
*
C 1
=Cmssin
FX
* 0
ka
DF=
C ss max
C ss min
100%
Css
波动度是评价缓控释制剂质量的重要指标 之一,新药申报需提供该参数。
《多剂量给药》课件

微注泵给药
微注泵能够精确控制药物的给予 速度,适用于特定需要药物浓度 范围的治疗。
ห้องสมุดไป่ตู้
多剂量给药的注意事项
• 给药间隔时间:药物的给予时间间隔需要根据药物的特性和患者的情况来确定。 • 不同途径组合使用:根据疾病需要和患者情况,可以选择不同途径的药物组合使用。 • 配合其他药物的使用:药物的相互作用需要谨慎考虑,避免药物间产生不良反应。 • 对不同人群的适用性:不同年龄段、不同代谢能力的患者对多剂量给药的适应性有所差异。
单剂量给药
定义及优缺点
单剂量给药是指一次给予药物所需的剂量,简 单方便,但不能满足长期治疗的需要。
口服给药
口服给药方便患者自行服药,但药物吸收受到 肠道吸收和首过效应的影响。
静脉注射
通过静脉注射药物,可以快速达到治疗浓度, 适用于紧急情况或需要迅速起效的治疗。
肌肉注射
通过肌肉注射药物,可以延长药物的作用时间, 但需注意注射部位和注射技巧。
多剂量给药
定义及优缺点
多剂量给药是在一定时间间隔内 多次给予药物,可以提高稳态浓 度,减少副作用。
分次给药
将总剂量分为多个次数给药,保 持药物浓度的稳定性,适用于长 期治疗。
滴注给药
通过滴注药物,可以较精确地调 整药物的给予速度和浓度,适用 于需要缓慢给药的情况。
持续给药
使用输液泵使药物持续缓慢地给 与,保持稳定药物浓度,适用于 需要连续给药的情况。
《多剂量给药》PPT课件
多剂量给药是指在治疗过程中按照一定时间间隔多次给予药物剂量的方法。 本课件将介绍多剂量给药的定义、优缺点以及不同的给药途径和注意事项。
前言
给药剂量和疗效之间存在关系,多剂量给药的目的在于优化药物治疗效果。 通过分次给药、滴注给药、持续给药和微注泵给药等手段,可以更好地控制 药物浓度和作用时间。
多剂量给药20191122精品文档

第n次给药
当时间t=0时,体内最大药量为:
( X n )max =X 0 (1+e k+ e 2k+ ....+e ( ) n1) k
当时间t=τ时(即经过第n个给药周期),
体内最小药量为:
(Xn )min=X 0 (ek+ e2k+e3k+....+e(n1)k+ enk)
(C 1)min =kk0V (1ek T )ek(T)
第2次滴注过程中
C 2=(C 1)minek
t+k0(1ek)t kV
=k0(ekT 1 )e k(+ t)+k0(1e k)t
kV
kV
C 2 =k k0V (1ek T )e(k+1)ekt
含义:单室模型,多剂量静脉注射给药,稳态血药浓度
与时间的关系。式中:X0为给药剂量;k为一级消除速度常 数;τ 为给药间隔时间;V为表观分布容积;Css为坪浓度。
稳态最大血药浓度
药物在体内达到稳态,任意给药间隔当 t=0时的血药浓度即稳态最大血药浓度。
用 Csms ax 表示。
C ss max
= V
范围,则根据此式,当T与k恒定时,对于治
疗浓度范围窄的药物,给药时间间隔τ 的取
值应小 。
坪幅
坪幅系指坪浓度的波动的幅度,即稳态最大浓
度稳态最小浓度的差值。
C mssaxC mssi=n V(1X0ek)V(X10ek)ek
C ss max
Cmssin
=
X V
0
XmssaxX mssin=X0
达坪分数
在临床用药实践中,人们常常在想,要经过多少 次静脉注射给药或经过多少个给药周期才能接近 坪浓度? 达到坪浓度的程度如何? 如果按半衰期给药,经过多少个半衰期,体内药 物浓度才能达到坪浓度的90%或99%以上?
第十讲多剂量给药
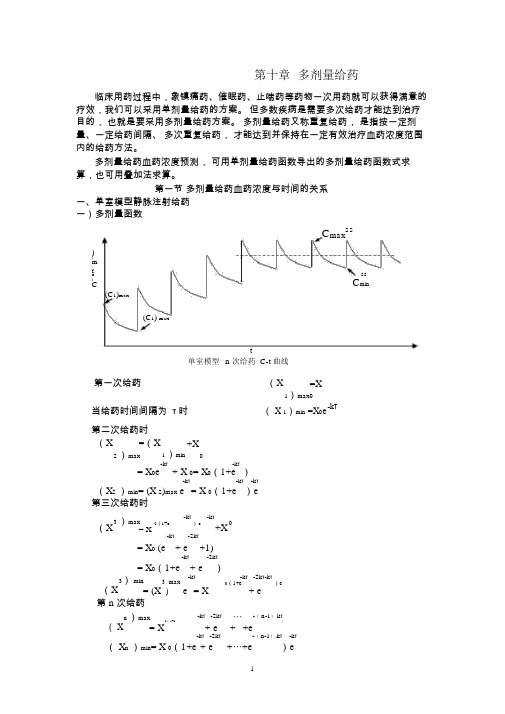
第十章 多剂量给药临床用药过程中,象镇痛药、催眠药、止喘药等药物一次用药就可以获得满意的疗效,我们可以采用单剂量给药的方案。
但多数疾病是需要多次给药才能达到治疗目的, 也就是要采用多剂量给药方案。
多剂量给药又称重复给药, 是指按一定剂量、一定给药间隔、 多次重复给药, 才能达到并保持在一定有效治疗血药浓度范围内的给药方法。
多剂量给药血药浓度预测, 可用单剂量给药函数导出的多剂量给药函数式求算,也可用叠加法求算。
第一节 多剂量给药血药浓度与时间的关系一、单室模型静脉注射给药 一)多剂量函数C max ss)lm/gssu(C minC(C 1)max(C 1) maxt单室模型 n 次给药 C-t 曲线第一次给药(X =X1)max0当给药时间间隔为 τ时( X 1)min =X 0e -k τ第二次给药时 (X =(X 1 )min +X2 )max-k τ-k τ= X 0e + X 0= X 0(1+e )-k τ-k τ -k τ(X 2 )min = (X 2)max e = X 0(1+e )e 第三次给药时3 )max -k τ -k τ 0(X 0(1+e ) e +X= X-k τ -2k τ= X 0 (e + e +1)-k τ-2k τ= X 0(1+e + e )3) min3max-k τ-k τ -2k τ-k τ(X) e = X 0(1+e+ e )e= (X第 n 次给药n )max -k τ -2k τ⋯ -( n-1) k τ( X0( 1+e+ e+e )= X+-k τ -2k τ-( n-1) k τ -k τ( X )= X (1+e + e +⋯ +e)e-k τ-2k τ -(n-1 )k τ-k τ我们看 1、e、 e、⋯、 e 是一组公比为 e 的等比数列,其首项-( n-1) k τ为 1,第 n 项为 e,根据等比数列前1 e-ke- 2-ke -(n-1)k∴(X n )maxX 0 1 e -nk1 e -k-nk(X n )maxX 0 1 e-ke - k1 e1 e -nk式中1 e-k 就是多剂量函数,用二)多剂量给药血药浓度与时间的关系n 和的公式则有:1 e -(n -1)k e -k1 e -nk 1 e-k1 e - kr 表示, n 为给药次数, τ为给药周期。
生物药剂学与药物动力学_第十章多剂量给药

达坪分数 f ss(n)= Cn / Css
f ss(n)=1- e-nkτ = 1 – e -0.693nτ/ t 1/2
nτ = -
2.303lg(1-
k
f
ss(n))
=
-3.32
t
1/2
lg(1-
f
ss(n))
蓄积系数(积累系数,蓄积因子) R= Css / C1 =1 /(1- e -kτ )
治疗浓度范围。
第一节 多剂量给药的血药浓度与时间关系
一、单室模型静脉注射 1. n次给药后血药浓度与时间的关系
(Xss)max
(X3)max (X2)max
(X4)max
(Xn)max
(X1)max
(X1)min
(X4)mix (X3)mix (X2)mix
(Xn)mix (Xss)mix
第一次给药: (X1)max=Xo (X1)mix =Xo e- Kτ
Css=
Xo
VKτ
口服给药时: Css=
FXo
VKτ
=
Xo V
×1.44
t 1/2
(τ
)
双室模型:
Xo
静脉给药时: Css= Vββτ
口服给药时: Css= FXo Vββτ
第三节 重复给药时体内药物量的蓄积
1. 稳态最低血药浓度
静脉给药:
Css min = C1
min
1 =R (蓄积因子)
1- e-Kτ
r• e- Kτ = e- Kτ+ e- 2Kτ+ …… + e- (n-1)2Kτ + e- nKτ
1- e-nKτ r=
1- e-Kτ
生物药剂学与药物动力学 第十章 重复给药

k?
e? kt
?
1?
1 e? ka?
e? kat )
3.稳态峰浓度及谷浓度、达峰时间
非血管给药达峰浓度不象静脉注射,在每次给 药开始,而是在 两次给药间隔时间的 某一点。 求函数的极大值 。
当t
?
t
max
时,dC ss dt
?
0,求 tmax 得
第n次给药后,给药间隔内任何时候体内药量:
Xn=Xo[(1- e
-nk ? )/(1- e-k ? )] e-kt
(Xn)max= Xo(1- e -nk ? )/(1- e-k ? )
(Xn)min=Xo[(1- e
-nk ? )/(1- e-k ? )] e-k ?
Cn=Xo/V [(1- e
-nk ? )/(1- e-k ? )] e-kt
(Cn)max=Xo/V(1- e -nk ? )/(1- e-k ? )
(Cn)min= Xo/V[(1- e
-nk ? )/(1- e-k ? )] e-k ?
2.多剂量函数:
r=(1- e -nki ? )/(1- e-k i? ) ki:ka 、k 、 a 、 ? 多剂量静脉注射血药浓度-时间关系:
5.蓄积系数
蓄积系数: (积累系数或蓄积因子)
指坪浓度与第一次给药后浓度的比值。用 R 表示。
R?
Css C1
?
C0
( 1?
1 e?
k?
)e? kt
C0e? kt
?
1 1? e?k?
意义:按 ?间隔给药时,坪浓度是 第一次给药浓度的 R倍。
二、单室模型血管外给药
1.n次给药血药浓度与时间关系 一级吸收,单室模型药物可以在各指数项
生物药剂学与药物动力学:第十章 多剂量给药

第三次给药: 第四次给药: 第 n次给药:
( X 3 )max X 0 (1 ek e2k ) ( X 3 )min X 0 (ek e2k e3k )
( X 4 )max X 0 (1 ek e2k e3k ) ( X 4 )min X 0 (ek e2k e3k e4k ) ( X n )max X 0 (1 ek e2k e(n1)k ) ( X n )min X 0 (ek e2k enk )
C ss m in
单室血管外: FX0
C ssVk
双室血管外: FX0
C ssV k
The end
1.44
X0 V
1.44C0
则:Xss 1.44X0
第二节 平均稳态血药浓度
一、单室模型平均稳态血药浓度
(二)血管外给药
0 Css (t)dt
0
ka FX0 V (ka k
)
( 1
ekt ek
1
e
kat
ek
a
)dt
FX0 kV
Css
0 Css (t)dt FX0
kV
第二节 平均稳态血药浓度
(X2)max
(X1)max
(X3)min (X4)min (X5)min (X6)min
(X2)min
MEC
(X1)min
τ
τ
τ
τ
τ
t
单室静注函数关系: X X 0 ekt
第一次给药:
(X1)max X0 ( X1)min X 0 ek
第二次给药:
( X 2 )max X 0 X 0 ek X 0 (1 ek ) ( X 2 )min X 0 (1 ek ) ek X 0 (ek e2k )
多剂量给药.

多剂量给药
前 言
在临床用药实践中,有些疾病如头痛、偶尔失 眠、胃肠痉挛等,一次用药即可获得满意的疗 效,常用药物如镇痛药、催眠药、止吐药等, 常采用单剂量给药方案。 但临床上多数疾病,需要采用多剂量给药的方 案,方可达到有效的治疗目的,如高血压、糖 尿病、肝、肾器官移植等。
多剂量给药的定义
k
e
2k
e
3k
...... e
( n1) k
e
nk
Байду номын сангаас
)
令
r 1 e e
k
k
2 k
...... e
( n1) k
( n 1) k
1
上式两边同时乘以e-kτ得:
r.e
e e
k
2 k
...... e
nk
即
含义:单室模型,多剂量静脉注射给药,稳态血药浓度与 时间的关系。式中:X0为给药剂量;k为一级消除速度常 数;τ为给药间隔时间;V为表观分布容积;Css为坪浓度。
4.稳态最大血药浓度
药物在体内达到稳态,任意给药间隔当t=0时的
ss 血药浓度即稳态最大血药浓度。用 Cmax 表示。
x0 kt 当t=0时 Css e k V (1 e ) kt
k
e
)e
e
2 k
e
3k
)
第n次给药
当时间t=0时,体内最大药量为:
( X n )max X 0 (1 e
k
e
2k
...... e
( n1) k
)
当时间t=τ 时(即经过第n个给药周期), 体内最小药量为:
生物药剂学与药物动力学:第十章 多剂量给药

二、单室模型血管外给药 (一)多剂量血管外给药血药浓度与时间关系
单次给药: C ka FX 0 ekt ekat V (ka k)
多剂量给药:
Cn
ka FX V (ka
0
k
)
1 enk 1 ek
ekt
1 enka 1 eka
ekat
二、单室模型血管外给药 (二)稳态最大血药浓度与达峰时
第十章 多剂量给药
第一节 多剂量给药血药浓度与时 间的关系
一、单室模型静脉注射给药 二、单室模型血管外给药 三、双室模型多剂量给药 四、利用叠加原理预测多剂量给药
一、单室模型静脉注射给药 (一)多剂量函数
1 enk r 1 ek
其中:n 为给药次数,τ 为给药间隔
c
MTC
(X4)max (X5)max (X6)max (X3)max
第三次给药: 第四次给药: 第 n次给药:
( X 3 )max X 0 (1 ek e2k ) ( X 3 )min X 0 (ek e2k e3k )
( X 4 )max X 0 (1 ek e2k e3k ) ( X 4 )min X 0 (ek e2k e3k e4k ) ( X n )max X 0 (1 ek e2k e(n1)k ) ( X n )min X 0 (ek e2k enk )
解:
C ss max
X0 V (1 ek
)
1000
0.6936
66.7(mg/L)
20(1 e 3 )
C ss m in
C ss max
e k
0.6936
66.7 e 3
16.7(mg/L)
C
1000
0.6936
药剂学:第10章 多剂量给药

问题
某病人病情危急,需立即达到稳 态浓度以控制,应如何给药
加大剂量 缩短给药间隔时间 其它方法
Plasma Drug Concentration
Time
Plasma Drug Concentra dose
Immediately effective treatment
(Css )min
Ka Ka K
FX 0 V
( 1
1 e
K
eK
1 1 eKa
eKa )
双室模型
❖ 静注
Cn
1 en A 1 e
et
B
1 en 1 e
et
t (0, )
(Cn )max
A
1 en 1 e
B
1 en 1 e
(Cn )min
A
1 en 1 e
e
B
1 en 1 e
e
稳态时,n → ∞:
Cn
Ka Ka K
FX 0 V
1 enK ( 1 eK
eKt
1 enKa 1 eKa
eKat )
t (0, )
稳态时, n → ∞ :
t (0, )
Css
Ka Ka K
FX 0 V
1
( 1
eK
e Kt
1
1 e
Ka
eKat )
(Css )max
Ka Ka K
FX 0 V
( 1
1 e
K
1 1 eKa )
Chapter 10 多剂量给药
LOGO
第一节 多剂量给药血药浓度 与时间的关系
单室模型
❖ n次静注
多剂量函数
1 enKi 1 eKi
多剂量给药方案

多剂量给药方案引言多剂量给药方案是指在治疗某些疾病或症状时使用多种不同剂量的药物来提供更好的疗效。
这种方案通常用于药物治疗中,通过调整药物剂量的大小和频率,以达到更好的治疗效果。
本文将探讨多剂量给药方案的优点、适用范围以及常见的多剂量给药方案。
优点多剂量给药方案相较于单一剂量给药方案具有以下优点:1. 个体化治疗多剂量给药方案可以根据患者的具体情况进行个体化治疗。
不同患者对同一药物的反应可能不同,因此根据患者的体质、病情以及其他因素,可以调整药物的剂量和给药频率,从而提高治疗效果。
2. 药物浓度调控多剂量给药方案可以通过调整药物的剂量和给药频率,控制药物在体内的浓度。
一些药物在体内的浓度过高或过低都可能导致治疗效果不佳,而多剂量给药方案可以有效地调节药物浓度,使其在合适的范围内,从而提高治疗效果。
3. 减少耐药性发生药物治疗中常常会出现耐药性的问题,即患者对某种药物的敏感性下降,导致药物治疗效果不佳。
多剂量给药方案可以通过调整药物剂量和给药频率,减少耐药性的发生。
通过轮换使用不同剂量的药物,可以降低患者对某种药物的过度依赖,从而减少耐药性发生的概率。
适用范围多剂量给药方案适用于许多不同类型的疾病和症状,包括但不限于:1.癌症治疗:癌症是一类严重的疾病,治疗难度较大。
多剂量给药方案可以根据肿瘤的类型、分期以及患者的具体情况,进行个体化治疗,提高治愈率和生存率。
2.慢性疾病治疗:慢性疾病如高血压、糖尿病等需要长期药物治疗。
多剂量给药方案可以根据疾病的严重程度和患者的反应,调整药物的剂量和给药频率,以维持疾病的稳定,减少并发症的发生。
3.感染性疾病治疗:感染性疾病如肺炎、感冒等常需要使用抗生素进行治疗。
多剂量给药方案可以根据感染的严重程度和患者的免疫状况,调整抗生素的剂量和给药频率,从而提高治疗效果,并减少耐药性的发生。
常见的多剂量给药方案以下是一些常见的多剂量给药方案:1. 递增剂量给药方案递增剂量给药方案是指从一个较低的剂量开始,逐步增加药物的剂量和给药频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Cn
Ka Ka K
FX 0 V
1 enK ( 1 eK
eKt
1 enKa 1 eKa
eKat )
t (0, )
稳态时, n → ∞ :
t (0, )
Css
Ka Ka K
FX 0 V
1
( 1
eK
e Kt
1
1 e
Ka
eKat )
(Css )max
Ka Ka K
FX 0 V
( 1
1 e
K
1 1 eKa )
t (0, )
Css
1 A1 e
et
1 B 1 e
et
(Css )max
A
1
1 e
B
1
1 e
(Css )min
1 A1 e
e
B
1
1 e
e
第二节 平均稳态血药浓度
C ss
反映血药浓度波动程度的参数
第四节 负荷剂量与最佳给药周期
Need for a loading dose
No effective treatment for (approx) first 4 hours
0
5
10
15
20
25
30
最佳给药周期
对稳态血药浓度(Css)的要求—— *有效而不产生毒性反应 MEC:最小有效血药浓度 MTC:最低中毒血药浓度
Css-max < MTC Css-min > MEC
Chapter 10 多剂量给药
LOGO
第一节 多剂量给药血药浓度 与时间的关系
单室模型
❖ n次静注
多剂量函数
1 enKi 1 eKi
τ为给药间隔
Xn
1 enK X 0 ( 1 eK
)e Kt
(Xn )max
1 enK X 0 ( 1 eK
)
(Xn )min (Xn )max eK
Cn
问题
某病人病情危急,需立即达到稳 态浓度以控制,应如何给药
加大剂量 缩短给药间隔时间 其它方法
Plasma Drug Concentration
Time
Plasma Drug Concentration
Time
Use of a loading dose
Immediately effective treatment
With loading dose No loading dose
负荷剂量 (Loading dose)
Log Concentration
Time
Time
plasma conc
7
toxic
6
5
4
effective
3
Cumulation and use of
2
loading doses
1
Time
0
X0 V
1 enK ( 1 eK
)e Kt
(Cn )max
X0 V
1 enK ( 1 eK
)
(Cn )min (Cn )max eK
t (0, )
稳态时,n → ∞:
Css
X0 V
1
( 1
e
K
)e Kt
(Css )max
X0 V
( 1
1 e
K
)
(Css )min (Css )max eK
口服
(Css )min
Ka Ka K
FX 0 V
( 1
1 e
K
eK
1 1 eKa
eKa )
双室模型
❖ 静注
Cn
1 en A 1 e
et
B
1 en 1 e
et
t (0, )
(Cn )max
A
1 en 1 e
B
1 en 1 e
(Cn )min
A
1 en 1 e
e
B
1 en 1 e
e
稳态时,n → ∞:
