讲义(打印)

合集下载

内经讲义打印重点

1.故重阴必阳，重阳必阴。

故曰：故曰:冬伤于寒，春必病温;春伤于风，夏生飧泄；夏伤于暑,秋必痎疟；秋伤于湿，冬生咳嗽。

2.阳气者，若天与日，失其所则折寿而不彰，故天运当以日光明。

是故阳因而上，卫外者也。

（因于寒，欲如运枢，起居如惊，神气乃浮。

因于暑，汗，烦则喘喝，静则多言,体若燔炭,汗出而散.因于湿，首如裹，湿热不攘，大筋緛短，小筋弛长,緛短为拘，弛长为屡。

因于气,为肿,四维相代，阳气乃竭.）3.阳气者，精则养神，柔则养筋。

4.凡阴阳之要，阳密乃固,两者不和，若春无秋，若冬无夏,因而和之，是谓圣度。

故阳强不能密，阴气乃绝；阴平阳秘，精神乃治；阴阳离决，精气乃绝。

5.肾藏精，精舍志，肾气虚则厥，实则胀，五藏不安。

6。

五脏：风掉眩，皆属于肝.诸寒收引，皆属于肾。

诸气膹郁，皆属于肺。

诸湿肿满，皆属于脾。

诸痛痒疮,皆属于心。

7.五火：诸热瞀瘛，皆属于火。

诸禁鼓栗,如丧神守，皆属于火.诸逆冲上，皆属于火。

诸躁狂越，皆属于火。

诸病胕肿，疼酸惊骇，皆属于火.8。

四热：诸胀腹大,皆属于热.诸病有声，鼓之如鼓，皆属于热。

诸转反戾,水液混浊，皆属于热。

诸呕吐酸，暴注下迫，皆属于热。

9.诸风掉眩，皆属于肝。

诸寒收引，皆属于肾。

诸气膹郁，皆属于肺.诸湿肿满，皆属于脾。

诸热瞀瘛,皆属于火。

诸痛痒疮，皆属于心.诸厥固泄，皆属于下.诸痿喘呕，皆属于上。

诸禁鼓栗，如丧神守，皆属于火。

诸痉项强,皆属于湿。

诸逆冲上，皆属于火。

诸胀腹大,皆属于热。

诸躁狂越，皆属于火。

诸暴强直，皆属于风。

诸病有声,鼓之如鼓，皆属于热。

诸病胕肿，疼酸惊骇，皆属于火。

诸转反戾，水液混浊,皆属于热。

诸病水液,澄澈清冷,皆属于寒.诸呕吐酸，暴注下迫，皆属于热。

10. 岐伯曰∶巨阳者,诸阳之属也,其脉连于风府，故为诸阳主气。

人之伤于寒也，则为病热,热虽甚不死；其两感于寒而病者，必不免于死。

11。

诊法常以平旦，阴气未动，阳气未散，饮食未进，经脉未盛，络脉调匀，气血未乱,故乃可诊有过之脉。

景观生态学讲义(打印版)

《景观生态学》讲义绪论景观生态学是地理学、生态学以及系统论、控制论等多学科交叉、渗透而形成的一门新的综合学科。

主要研究空间格局和生态过程的相互作用。

作为一门学科，景观生态学是20世纪60年代在欧洲形成的，土地利用规划和评价一直是其主要的研究内容。

直到20世纪80年代初，景观生态学在北美才受到重视，迅速发展成为一门很有朝气的学科，引起了越来越多的学者的重视与参与。

景观生态学给生态学和地理学带来了新的思想和新的方法，已成为生态学和地理学和前沿学科之一。

第一章景观生态学的概念及发展一景观生态学中的基本概念1 生态学2 景观3 景观生态系统4景观生态学1 景观景观的特征与表象是丰富的，人们对景观的感知和认识也是多样的。

因此，对于景观不同学科有着不同的理解，甚至在同一学科中（如地理学）也长期存在着不同解释。

由于景观概念的不确定性，经常导致它与“风景”、“土地”、“环境”等词意的混淆。

1．1景观定义理解：景观（landscape）的定义有多种表述，但大都是反映内陆地形、地貌或景色的（诸如草原、森林、山脉、湖泊等），或是反映某一地理区域的综合地形特征。

（图）在生态学中，景观的定义可概括为狭义和广义两种。

狭义景观是指在几十千米至几百千米范围内，由不同类型生态系统所组成的、具有重复性格局的异质性地理单元（如Forman 和Godron,1986;Forman,1995）。

而反映气候、地理、生物、经济、社会和文化综合特征的景观复合体相应地称为区域（region;见Forman,1995）。

狭义景观和区域即人们通常所指的宏观景观；广义景观则包括出现在从微观到宏观不同尺度上的，具有异质性或缀块性的空间单元。

广义景观概念强调空间异质性，景观的绝对空间尺度随研究对象、方法和目的而变化。

（图）它体现了生态学系统中多尺度和等级结构的特征。

(在欧洲,“景观”一词最早出现在希伯来文的《圣经》（旧约全书）中，用来描绘具有所罗门王国教堂、城堡和宫殿的耶路撒冷城美丽的景色。

曹显兵.概率论讲义（打印版）

曹显兵.概率论讲义（打印版）第⼀讲随机事件与概率考试要求1. 了解样本空间的概念, 理解随机事件的概念, 掌握事件的关系与运算.2. 理解概率、条件概率的概念, 掌握概率的基本性质, 会计算古典型概率和⼏何型概率, 掌握概率的加法公式、减法公式、乘法公式、全概率公式, 以及贝叶斯公式.3. 理解事件独⽴性的概念, 掌握⽤事件独⽴性进⾏概率计算；理解独⽴重复试验的概率, 掌握计算有关事件概率的⽅法. ⼀、古典概型与⼏何概型1．试验，样本空间与事件.2．古典概型：设样本空间Ω为⼀个有限集，且每个样本点的出现具有等可能性，则基本事件总数中有利事件数A A P =)(3．⼏何概型：设Ω为欧⽒空间中的⼀个有界区域, 样本点的出现具有等可能性，则、体积）Ω的度量（长度、⾯积、体积）A的度量（长度、⾯积=)(A P【例1】⼀个盒中有4个黄球, 5个⽩球, 现按下列三种⽅式从中任取3个球, 试求取出的球中有2个黄球, 1 个⽩球的概率. （1）⼀次取3个；（2）⼀次取1 个, 取后不放回；（3）⼀次取1个, 取后放回.【例2 】从（0，1）中随机地取两个数，试求下列概率：（1）两数之和⼩于1.2；（2）两数之和⼩于1且其积⼩于163. ⼀、事件的关系与概率的性质1. 事件之间的关系与运算律（与集合对应）, 其中特别重要的关系有：（1） A 与B 互斥（互不相容） ? Φ=AB （2） A 与B 互逆（对⽴事件） ? Φ=AB ,Ω=B A（3） A 与B 相互独⽴? P （AB ）=P （A ）P （B ）.P （B|A ）=P （B ）（P （A ）>0）. ?(|)(|)1P B A P B A += （0P （B|A ） =P （B|A ）（ 0 < P （A ） < 1 ）注: 若（00）1)|()|(=+B A P B A P （0（4） A, B, C 两两独⽴ ? P （AB ）=P （A ）P （B ）;P （BC ）=P （B ）P （C ）; P （AC ）=P （A ）P （C ）.（5） A, B, C 相互独⽴ ? P （AB ）=P （A ）P （B ）;P （BC ）=P （B ）P （C ）; P （AC ）=P （A ）P （C ）; P （ABC ）=P （A ）P （B ）P （C ）.2. 重要公式（1） )(1)(A P A P -=（2）)()()(AB P A P B A P -=-（3） )()()()(AB P B P A P B A P -+=)()()()()()()()(ABC P AC P BC P AB P C P B P A P C B A P +---++=（4）若A 1, A 2,…,A n 两两互斥, 则∑===ni i ni iA P AP 11)()(.（5）若A 21,A , …, A n 相互独⽴, 则 )(1)(11in i n i iA P A P ∏==-= )](1[11ini A P ∏=--=.∏===ni i n i i A P A P 11)()( .（6）条件概率公式: )()()|(A P AB P A B P =（P （A ）>0）【例3】已知（A ＋B ）（B A +）＋B A B A +++＝C, 且P （ C ）＝31, 试求P （B ）. 【例4】设两两相互独⽴的三事件A, B, C 满⾜条件: ABC ＝Φ, P （A ）＝P （B ）＝P （C ）< 21,且已知9()16P A B C =, 则P （A ）＝ .【例5】设三个事件A 、B 、C 满⾜P （AB ）＝P （ABC ）, 且0（A ）P （A B|C ）＝P （A|C ）+ P （B|C ）. （B ）P （A B|C ）＝P （AB ）.（C ）P （AB|C ）＝P （A|C ）+ P （B|C ）. （D ）P （AB|C ）＝P （AB ）.【例6】设事件A, B, C 满⾜条件: P （AB ）＝P （AC ）＝P （BC ）18=, P （ABC ）＝116, 则事件A, B, C 中⾄多⼀个发⽣的概率为 .【例7】设事件A, B 满⾜ P （B| A ）＝1则【】（A ） A 为必然事件. （B ） P （B|A ）=0.（C ） A B ?. （D ） A B ?.【例8】设A, B, C 为三个相互独⽴的事件, 且0B A +与C . （B ） AC 与C（C ）B A -与C （D ） AB 与C【例9】设A ，B 为任意两个事件，试证P （A ）P （B ）－P （AB ） ≤ P （A －B ） P （B －A ） ≤41. 三、乘法公式，全概率公式，Bayes 公式与⼆项概率公式 1．乘法公式：).|()|()|()()().|()()|()()(1212131212121212121-===n n n A A A A P A A A P A A P A P A A A P A A P A P A A P A P A A P 2．全概率公式：11()(|)(),,,.i i i j i i i P B P B A P A A A i j A ∞∞====Φ≠=Ω∑3．Bayes 公式：11(|)()(|),,,.(|)()j j j i j i i iii P B A P A P A B A i j A P B A P A ∞∞====Φ≠=Ω∑　A4．⼆项概率公式:()(1),0,1,2,,.k kn k n n P k C P P k n -=-=　,【例10】 10件产品中有4件次品, 6件正品, 现从中任取2件, 若已知其中有⼀件为次品,试求另⼀件也为次品的概率.【例11】设10件产品中有3件次品, 7件正品, 现每次从中任取⼀件, 取后不放回.试求下列事件的概率. （1）第三次取得次品; （2）第三次才取得次品;（3）已知前两次没有取得次品, 第三次取得次品; （4）不超过三次取到次品;【例12】甲, ⼄两⼈对同⼀⽬标进⾏射击,命中率分别为0.6和0.5, 试在下列两种情形下, 分别求事件“已知⽬标被命中,它是甲射中”的概率.（1）在甲, ⼄两⼈中随机地挑选⼀⼈, 由他射击⼀次; （ 2）甲, ⼄两⼈独⽴地各射击⼀次.【例13】设有来⾃三个地区的各10名、15名和25名考⽣的报名表,其中⼥⽣的报名表分别为3份,7份和5份. 随机地取⼀个地区的报名表,从中先后任意抽出两份. (1) 求先抽到的⼀份是⼥⽣表的概率p;(2)已知后抽到的⼀份是男⽣表,求先抽到的⼀份是⼥⽣表的概率q .第⼆讲随机变量及其分布考试要求1. 理解随机变量及其概率分布的概念.理解分布函数（()()F x P X x =≤）的概念及性质.会计算与随机变量有关的事件的概率.2. 理解离散型随机变量及其概率分布的概念，掌握0－1分布、⼆项分布、⼏何分布、超⼏何分布、泊松（Poisson ）分布及其应⽤.3. 了解泊松定理的结论和应⽤条件，会⽤泊松分布近似表⽰⼆项分布.4. 理解连续型随机变量及其概率密度的概念，掌握均匀分布、正态分布2(,)N µσ、指数分布及其应⽤，其中参数为(0)λλ>的指数分布的概率密度为,0,()0,0.x e x f x x λλ-?>=?≤?5. 会求随机变量函数的分布. ⼀、分布函数1．随机变量：定义在样本空间上，取值于实数的函数称为随机变量. 2．分布函数：∞+-∞=＜＜),≤ ()(x x X P x FF （x ）为分布函数 ?（1） 0≤F （x ） ≤1（2） F （x ）单调不减（3）右连续F （x+0）=F （x ）（4）1)(,0)(=+∞=-∞F F3．离散型随机变量与连续型随机变量（1）离散型随机变量∑∞=====1i 10,≥,,,2,1,)(i i i i p p n i p x X P分布函数为阶梯跳跃函数.（2）连续型随机变量∞-=xtt f x F d )( )(f （x ）为概率密度 ? （1） f （x ）≥0, （2） ?+∞∞- f （x ）1d =x=≤≤=<ax f b X a P b X a P )()()(4．⼏点注意【例1 】设随机变量X 的分布函数为0,1,57(),11,16161, 1.x F x x x x <-?=+-≤== .【例2 】设随机变量X 的密度函数为 f （x ）, 且 f （－x ） = f （x ）, 记()X F x 和()X F x -分别是X 和X -的分布函数, 则对任意实数x 有【】（A ）()()X X F x F x -=. （B ）()()X X F x F x -=-.（C ）()1()X X F x F x -=-.（D ）()2()1X X F x F x -=-.【例3 】设随机变量X 服从参数为0λ>的指数分布, 试求随机变量 Y= min { X, 2 } 的分布函数【例4 】设某个系统由 6 个相同的元件经两两串联再并联⽽成, 且各元件⼯作状态相互独⽴每个元件正常⼯作时间服从参数为0λ>的指数分布, 试求系统正常⼯作的时间 T 的概率分布.【例5】设随机变量X 的概率密度为<-=.,0,1|||,|1)(其他x x x f 试求（1）X 的分布函数)(x F ; （2）概率)412(<<-X P .⼆、常见的⼀维分布（1） 0-1分布：1,0,)1()(1 =-==-k p p k X P k k .（2）⼆项分布n k p p C k X P p n B k n k k n ,,1,0,)1()(:),( =-==- .（3） Poisson 分布)(λP ： ,2,1,0,0＞,e !)(===-k k k XP kλλλ.（4）均匀分布-=.,＜＜1)(:),(其他０，，　b x a a b x f b a U（5）正态分布N （µ，σ2）：22)(+∞<<∞->=--µσσσµ x x f（6）指数分布=-. ,0＞0,,e )(:)(其他x x f E x λλλ＞0λ.（7）⼏何分布.2110,)1()(:)(1 ,,k ,＜p＜p p k XP p G k =-==-（8）超⼏何分布H （N,M,n ）: },min{,,1,0,)(M n k C C C k X P nNkn M N k M ===--　. 【例6】某⼈向同⼀⽬标独⽴重复射击,每次射击命中⽬标的概率为p （0（B ） 2)1(6p p -.（C ） 22)1(3p p-. （D ） 22)1(6p p-.【例7】设X ～Ｎ（µ, σ2）, 则 P （ X ≤1＋µ）【】（A ）随µ的增⼤⽽增⼤ . （B ）随µ的增⼤⽽减⼩. （C ）随σ的增⼤⽽不变 . （D ）随σ的增⼤⽽减⼩. 【例8】设X ～Ｎ（µ, σ2）, ()F x 为其分布函数，0µ<，则对于任意实数a ，有【】（A ） ()() 1.F a F a -+> （B ） ()() 1.F a F a -+= （C ） ()() 1.F a F a -+< （D ） 1()().2F a F a µµ-++=【例9】甲袋中有1个⿊球，2个⽩球，⼄袋中有3个⽩球，每次从两袋中各任取⼀球交换放⼊另⼀袋中，试求交换n 次后，⿊球仍在甲袋中的概率.三、随机变量函数的分布： 1. 离散的情形2. 连续的情形3. ⼀般的情形【例10】设随机变量X 的概率密度为<≤<<-=.,0,20,41,01,21)(其他x x x f X令),(,2y x F X Y=为⼆维随机变量（X, Y ）的分布函数.（Ⅰ）求Y 的概率密度)(y f Y ;（Ⅱ）)4,21(-F . 第三讲多维随机变量及其分布考试要求1. 理解多维随机变量的概念，理解多维随机变量的分布的概念和性质，理解⼆维离散型随机变量的概率分布、边缘分布和条件分布，理解⼆维连续型随机变量的概率密度、边缘密度和条件密度.会求与⼆维随机变量相关事件的概率.2. 理解随机变量的独⽴性及不相关的概念，掌握随机变量相互独⽴的条件.3. 掌握⼆维均匀分布，了解⼆维正态分布的概率密度，理解其中参数的概率意义 .4. 会求两个随机变量简单函数的分布，会求多个相互独⽴随机变量简单函数的分布. ⼀、各种分布与随机变量的独⽴性 1. 各种分布（1）⼀般⼆维随机变量 F （x, y ）=P{ X ≤ x, Y ≤ y }, x ∈（?∞, +∞）, y ∈（?∞, +∞）的性质F （x, y ）为联合分布函数 ? 1） 0 ≤F （x, y ）≤1 , ?x ∈（?∞, +∞）,, y ∈（?∞, +∞）;2） F （?∞, y ）= F （x, ?∞）=0, F （+∞,+∞）=1;3） F （x, y ）关于x, y 均为单调不减函数； 4） F （x, y ）关于x, y 均分别右连续.（2）⼆维离散型随机变量的联合概率分布、边缘分布、条件分布联合概率分布律 P{X = x i , Y = y j } = p i j , i, j =1, 2 , , p i j 0,1=∑∑ijji p.边缘分布律 p i = P{X = x i }=∑j, i =1, 2 , ,pj= P{ Y = y j }=∑iji p, j =1, 2 , ,条件分布律 P{X = x i |Y = y j } =jj i p p ?, P{ Y = y j | X = x i } =i j i p p .⼆维连续型随机变量的联合概率密度、边缘密度和条件密度f （x, y ）为联合概率密度 ? 1? f （x, y ）≥0,2?1=??∞+∞-∞+∞- ),(dxdy y x f .设（ X, Y ）~ f （x, y ）则分布函数: ?∞-∞-=xydxdy y x f y x F ),(),(;边缘概率密度:∞+∞-= ),()(dy y x f x f X , ?-= ),()(dx y x f x f Y .条件概率密度:)(),()|(|y f y x f y x f Y Y X =, )(),()|(|x f y x f x y f X X Y =.=∈Ddxdy y x f D Y X P ),(}),{(.),(),(yx y x F y x f =22. 随机变量的独⽴性和相关性X 和Y 相互独⽴ ? F （x, y ）= F X （x ）F Y （y ）;p i j = p ipj（离散型）f （x, y ）= f X （x ）f Y （y ）（连续型）【注】1 X 与Y 独⽴, f （x ）, g （x ）为连续函数f （X ）与g （Y ）也独⽴.2若X 1, , X m , Y 1, , Y n 相互独⽴, f , g 分别为m 元与 n 元连续函数 f （X 1, , X m ）与g （Y 1, , Y n ）也独⽴.3 常数与任何随机变量独⽴.3. 常见的⼆维分布（1）⼆维均匀分布（X, Y ）~ U （D ）, D 为⼀平⾯区域. 联合概率密度为∈=.,.),(,)(),(其他01D y x D S y x f （2）⼆维正态分布（X, Y ）~ N （µ 1 , µ2, σ12,σ22, ）, ?∞ <µ1, µ2 < +∞, σ1>0, σ2 > 0, | | <1. 联合概率密度为221121ρσπσ?-=),(y x-+------22222121212122121σµσσµµρσµρ)())(()()(y y x x e性质:（ a ） X ~ N （µ1, σ12 ）, Y ~ N （µ2, σ22）（ b ） X 与Y 相互独⽴ρX Y =0 , 即 X 与Y 不相关.（ c ） C 1X+C 2Y ~ N （C 1 µ1+ C 2 µ2, C 12σ12+ C 22σ22+2C 1C 2 σ1σ2 ）. （ d ） X 关于Y=y 的条件分布为正态分布: )](),([22122111ρσµσσρµ--+y N 【例1 】设A ，B 为事件，且P （A ）＝41, P （B|A ）＝21, P （A|B ）＝12令 X ＝??否则发⽣若,0,1A , Y ＝?否则发⽣若,0B ,1（1）试求（X, Y ）的联合分布律；（2）计算Cov （ X, Y ）；（3）计算 2 2(2,43)Cov XY +.【例3 】设随机变量X 与Y 独⽴同分布, 且X 的概率分布为313221PX记{}{}Y X V Y X U,m in ,,m ax ==.（I ）求（U, V ）的概率分布;（II ）求（U, V ）的协⽅差Cov （U, V ）.【详解】（I ）易知U, V 的可能取值均为: 1, 2. 且{}{}})1,m in ,1,(m ax )1,1(=====Y X Y X P V U P)1,1(===Y X P 94)1()1(====Y P X P , {}{}0})2,m in ,1,(m ax )2,1(======Y X Y X P V U P , {}{}})1,m in ,2,(m ax )1,2(=====Y X Y X P V U P )2,1()1,2(==+===Y X P Y X P )2()1()1()2(==+===Y P X P Y P X P 94=, {}{}})2,m in ,2,(m ax )2,2(=====Y X Y X P V U P)2()2()2,2(======Y P X P Y X P 91=, 故（U, V ）的概率分布为:（II ） 9122941209411)(??+??++?=UV E 916=, ⽽ 914952941)(=+=U E , 910912981)(=?+?=V E . 故 814910914916)()()(),(=?-=（Ⅰ）随机变量X 和Y 的联合概率密度;（Ⅱ）Y 的概率密度; （Ⅲ）概率}1{>+Y XP .⼆、⼆维（或两个）随机变量函数的分布 1．分布的可加性（1）若X~B （m, p ）, Y~B （n, p ）, 且X 与Y 相互独⽴，则 X+Y ~ B （m+n, p ）. （2）若X~P （λ1）, Y~P （λ2）, 且X 与Y 相互独⽴，则 X+Y ~ P （λ1+λ2）.（3）若X~N （211,µσ）, Y~P （222,µσ）, 且X 与Y 相互独⽴，则 X+Y ~ N （221212,µµσσ++）.⼀般地，若X i ~N （2,i i µσ）, i =1, 2, …, n, 且X 1，X 2，…，X n 相互独⽴，则Y=C 1X 1+C 2X 2+…+C n X n +C 仍服从正态分布，且此正态分布为2211(,),n ni i i i i i N C C Cµσ==+∑∑ 其中C 1，…，C n 为不全为零的常数.2. 两个随机变量函数的分布. 【例5】设X 与Y 相互独⽴, 且~(1),~(2),X P Y P 则{max(,)0}______;P X Y ≠={min(,)0}__________.P X Y ≠=【例6】设X 与Y 相互独⽴, 其密度函数分别为:1,01,()X x f x <0,其他. ,0,()y Y e y f x -?>=??0,其他.求Z ＝2X ＋Y 的概率密度.【例7】设⼆维随机变量（X, Y ）的概率密度为2,01,01,(,)0,x y x y f x y --<<<其它. （I ）求{}Y X P 2>；（II ）求Z ＝Ｘ+Ｙ的概率密度)(z f Z .x dxdy y x f 2),(??--=12210)2(ydx y x dy 247=. （II ）⽅法⼀：先求Z 的分布函数: ??≤+=≤+=zy x Z dxdy y x f Z Y X P z F ),()()(当z<0时, 0)(=z F Z ; 当10<≤z 时, ??=1),()(D Z dxdy y x f z F ?---=yz zdx y x dy 00)2(3231z z -=；当21<≤z 时, ??-=2),(1)(D Z dxdy y x f z F ?-----=111)2(1yz z dx y x dy3)2(311z --=；当2≥z时, 1)(=z F Z .故Z ＝Ｘ+Ｙ的概率密度<≤-<<-=.,0,21,)2(,10,222其他z z z z z⽅法⼆：∞+∞--=dx x z x f z f Z ),()(，<-<<<---=-.,0,10,10),(2),(其他x z x x z x x z x f ??+<<<<-=.,0,1,10,2其他x z x x z 当z ≤0 或z ≥ 2时, 0)(=z f Z ;当01z <<时, ?-=z Z dx z z f 0)2()()2(z z -=；当21<≤z 时, ?--=11)2()(z Z dx z z f 2)2(z -=；故Z ＝Ｘ+Ｙ的概率密度)(z f Z ??<≤-<<-=.,0,21,)2(,10,222其他z z z z z【例8】设随机变量X 与Y 相互独⽴, X 有密度函数f （x ）, Y 的分布律为 ()i i P Y a p ==,　i =1,2. 试求Z ＝X ＋Y 的概率分布.第四讲数字特征与极限定理考试要求1．理解随机变量数字特征（数学期望、⽅差、标准差、矩、协⽅差、相关系数）的概念, 会运⽤数字特征的基本性质, 并掌握常⽤分布的数字特征.2．会根据随机变量X 的概率分布求其函数)(X g 的数学期望)(X Eg ；会根据随机变量X 和Y 的联合概率分布求其函数),(Y X g 的数学期望),(Y X Eg .3．了解切⽐雪夫不等式.4．了解切⽐雪夫⼤数定律、伯努利⼤数定律和⾟钦⼤数定律（独⽴同分布随机变量的⼤数定律）{}i i p x X P ==, ∑=iii px X E )(连续型)(~x f X , xx xf X E d )()(?+∞∞-=⽅差：[]222)()())(()(X E X E X E X E X D -=-=标准差：)(X D ,2. 期望的性质：1° )())((,)(X E X E E C C E == 2° )()()(2121Y E C X E C Y C X C E +=+ 3° )()()(Y E X E XY E ，Y X =则独⽴与若4° [])()(≤)(222Y E X E XY E3. ⽅差的性质：1° 0))((,0))((,0)(===X D D X E D C D 2°)()()(Y D X D Y X D Y X +=±相互独⽴，则与3° )()(2121X D C C X C D =+ 4° ⼀般有 ),Cov(2)()()(Y X Y D X D Y XD ±+=±)()(2)()(Y D X D Y D X D ρ±+=5°2()()C D X E X <-, )(X E C ≠【例1】设试验成功的概率为43, 失败的概率为4匙重新放回.【例3】设随机变量X 的概率密度为≤≤=.,0,0,2cos 21)(其他πx x x f 对X 独⽴地重复观察4次, ⽤Y 表⽰观察值⼤于3π的次数, 求2Y 的数学期望.【例4】设有20⼈在某11层楼的底层乘电梯上楼, 电梯在中途只下不上, 每个乘客在哪⼀层（2-11层）下是等可能的, 且乘客之间相互独⽴, 试求电梯须停次数的数学期望. ⼆、随机变量函数的期望（或⽅差） 1、⼀维的情形 )(X g Y =离散型：{}i i P Xx p == ， ∑=ii ipx g Y E )()(连续型：~()X f x x x f x g Y E d )()()(?+∞∞-=2、⼆维的情形 ),(Y X g Z =离散型{}iji i p y Y x X P Y X ===,~),(,∑∑=jij jiipy x g Z E ),()(连续型),(~-+∞∞-=【例5】设X 与Y 独⽴且均服从N （0，1），求Z ＝22Y X + 的数学期望与⽅差.【例6】设两个随机变量X 与Y 相互独⽴且均服从N （0，21）, 试求Z ＝｜X －Y ｜的数学期望与⽅差.三、协⽅差，相关系数与随机变量的矩 1、重要公式与概念：协⽅差 []))()((()Cov(Y E Y X E X E X,Y --=相关系数 )()()Cov(Y D X D X,Y XY =ρ)(k X E k 阶原点矩[]kX E X E k ))((- 阶中⼼矩2、性质：1°),(Cov ),(Cov X Y Y X =2° ),(Cov ),(Cov Y X ab bY aX = 3° ),(Cov ),(Cov ),(Cov 2121Y X Y X Y X X +=+4° |(,)|1X Y ρ≤5° 1)(1),(=+=?=b aX Y P Y X ρ )＞0(a 1)(1),(=+=?-=b aX Y P Y X ρ )＜0(a 3、下⾯5个条件互为充要条件：（1）0),(=Y X ρ（2）0)Cov(=X,Y （3）)()()(Y E X E XY E = （4）)()()(Y D X D Y X D +=+ （5）)()()(Y D X D Y X D +=- 【例7】设)2(,,,21>n X X X n 为独⽴同分布的随机变量, 且均服从)1,0(N , 记∑==n.,,2,1,n i X X Y i i =-= 求:（I ） i Y 的⽅差n iY D i ,,2,1),( =；（II ） 1Y 与n Y 的协⽅差),(1n Y Y Cov ; （III ） }.0{1≤+n Y Y P四、极限定理1. 切⽐雪夫不等式{}{}()()|()|,|()|<1-22D X D X P XE X P X E X εεεε-≥≤-≥或2. ⼤数定律3. Poisson 定理4. 中⼼极限定理列维—林德伯格定理: 设随机变量X 1，X 2，…，X n ，…相互独⽴同分布, 且2(),(),i i E X D X µσ== 1,2, ,,i n =，则对任意正数x ，有2-2lim dntixµ-∞→∞-≤=∑棣莫弗—拉普拉斯定理: 设~(,),nB n pη（即X1，X2，…，X n，…相互独⽴, 同服从0⼀1分布）则有22lim dtxnP x t--∞→∞≤=【例8】银⾏为⽀付某⽇即将到期的债券须准备⼀笔现⾦，已知这批债券共发放了500张，每张须付本息1000元，设持券⼈（1⼈1券）到期到银⾏领取本息的概率为0.4.问银⾏于该⽇应准备多少现⾦才能以99.9%的把握满⾜客户的兑换.【分析】若X为该⽇到银⾏领取本息的总⼈数，则所需现⾦为1000X，设银⾏该⽇应准备现⾦x元.为使银⾏能以99.9%的把握满⾜客户的兑换，则 P（1000X≤x）≥0.999.【详解】设X为该⽇到银⾏领取本息的总⼈数，则X~B（500，0.4）所需⽀付现⾦为1000X，为使银⾏能以99.9%的把握满⾜客户的兑换，设银⾏该⽇应准备现⾦x元，则 P（1000 X≤x）≥0.999.由棣莫弗—拉普拉斯中⼼极限定理知：(1000)()1000xP X x P X≤=≤5000.4xP-?=≤=≤0.999(3.1).ΦΦ≈≥=即3.1,≥得 x≥ 233958.798.因此银⾏于该⽇应准备234000元现⾦才能以99.9%的把握满⾜客户的兑换.第五讲数理统计考试要求1. 理解总体、简单随机样本、统计量、样本均值、样本⽅差及样本矩的概念.其中样本⽅差定义为212XXnSini--=∑=2. 了解2χ分布、t分布和F分布的概念及性质，了解分位数的概念并会查表计算.3. 了解正态总体的常⽤抽样分布.4. 理解经验分布函数的概念和性质, 会根据样本值求经验分布函数.5. 理解参数的点估计、估计量与估计值的概念.6. 掌握矩估计法（⼀阶、⼆阶矩）和最⼤似然的估计法.7. 了解估计量的⽆偏性、有效性（最⼩⽅差性）和⼀致性（相合性）的概念，并会验证估计量的⽆偏性.8. 理解区间估计的概念，会求单个正态总体的均值和⽅差的置信区间，会求两个正态总体的均值差和⽅差⽐的置信区间.9. 理解显著性检验的基本思想，掌握假设检验的基本步骤，了解假设检验可能产⽣的两类错误.10. 了解单个及两个正态总体的均值和⽅差的假设检验⼀、样本与抽样分布1. 总体、个体与简单随机样本:2. 常⽤统计量:1° 样本均值 i ni X nX ∑==112° 样本⽅差 21X X n S i ni --=∑=3° 样本标准差: S =4° 样本k 阶原点矩 11,1,2,n kk i i A X k n ===∑5° 样本k 阶中⼼矩 11(),1,2,n kk i i B X X k n ==-=∑3．分位数 4. 重要抽样分布（1）分布2χ（2） t 分布（3） F 分布5. 正态总体的常⽤抽样分布:22,,,(,),n X X X N µσ1设为来⾃正态总体的样本11nii X X n ==∑,2211()1ni i S X X n ==--∑, 则（1）2~,~(0,1).X X N N n σµ?? ??? （2）1(1)1()~(1).ni i n S X X n χσσ=-=--∑（3）22211()~().ni i X n µχσ=-∑（4） ~(1).X t n - （5）X 与2S 相互独⽴, 且 µ=)(X E , 22)(σ=S E , nX D 2)(σ=.【例1】设总体2~(,),XN µσ设12,,,n X X X 是来⾃总体X 的⼀个样本, 且22111,()nni nii i X X S X-∑∑，求21()n E X S .【例2】设总体2~(,),X N µσ设12,,,nX X X 是取⾃总体X 的⼀个样本, 且221111,()1nni i i i X X S X X nn ====--∑∑，则 2()_________D S =.【例3】设随机变量~()(1),X t n n >, 则 21~________Y X=【例4】设总体X 服从正态分布)2,0(2N , ⽽1521,,,X X X 是来⾃总体X 的简单随机样本, 求随机变量)(221521121021X X X X Y ++++= 的分布. 【例2~(,),X N µσ设121,,,,n n X X X X +是来⾃总体X 的⼀个样本, 且*221111,()()nni i i i X X S X X nn====-∑∑，试求统计量的分布. ⼆、参数估计1. 矩估计2. 最⼤似然估计3. 区间估计4. 估计量的评选标准【例6】设总体12~(,)XU θθ，n X X X ,,,21 为来⾃总体X 的样本，试求12,θθ的矩估计和最⼤似然估计.【例7】设总体X 的概率密度为<≤-<<=.,0,21,1,10,),(其他x x x f θθθ其中θ是未知参数)10(<<θ, n X X X ,,2,1 为来⾃总体X 的简单随机样本, 记N 为样本值n x x x ,,2,1 中⼩于1的个数, 求：（1）θ的矩估计；（2）θ的最⼤似然估计.【例8】设总体X 的概率密度为6(),0,()0,xx x f x θθθ?-<其他. n X X X ,,,21 为来⾃X 的简单随机样本，（1）求θ的矩估计量?θ；（2）判断θ的⽆偏性; （3）判断θ的⼀致性. 三、假设检验1. 假设检验的基本思想：对总体分布中的未知参数作出某种假设，根据样本在假设为真的前提下构造⼀个⼩概率事件，基于“⼩概率事件”在⼀次试验中⼏乎不可能发⽣⽽对假设作出拒绝或接受.2. 单个正态总体均值和⽅差的假设检验.3. 假设检验两类错误：第⼀类错误：原假设0H 为真，但拒绝了0H .第⼆类错误；原假设0H 为假，但接受到了0H .。

自考英语一讲义(打印版)

Unit 1Text A How to Be a Successful Language Learner？搭配：1. disagree with 不同意/动词词组2. guarantee sth. for sb. 保证某人某事/动词词组e.g. This will not guarantee success for every adult language learner. 这样不能确保每一位学习语言的成年人都成功。

3. be different from 与什么不同/形容词词组4. succeed in sth./ doing sth. 成功做某事/动词词组5. offer advice to sb. 给某人建议/动词词组6. play with sth. 轻松学习某事物/动词词组7. in many ways 再很多方面/介词词组8. depend on sb./sth. for sth. 依靠某人或某事而获得某事/动词词组9. discover one‘‘s own way to do sth. 发现并用自己的方法做某事/动词词组10. instead of sth./ doing sth. 想反/而没有做某事/介词词组11. wait for sb. to do sth. 等待某人做某事/动词词组12. look for sth./sb. 寻找某人或某物/动词词组13. make a mistake 犯错误/动词词组14. be afraid to do sth. 害怕做某事/形容词词组15. be willing to do sth. 愿意做某事/形容词词组16. do sth. with a purpose 有目的地做某事/故意做某事/动词词组17. be interested in sth./sb. 对某人或某物很感兴趣/形容词词组18. communicate with sb. 与某人交流/动词词组19. learn from sb. 想某人学习20. might do well to do sth. 最好做某事句型：1. S.+V.+it+adj.+to do sth. 形式宾语句型 n.e.g. Some people find it difficult to succeed in language learning.Some people find it difficult to succeed in other fields.They find it easy to practice using the language regularly.2. It is +adj.+for sb.+to do sth. 形式主语句型e.g. It is more important for them to learn to think in the language than to know the meaning of every word.It is necessary for them to learn the language in order to communicate with these people and to learn for them.语言点：1. success（n.）-successful（adj.）-succeed（v.）成功2. hundreds of people与 eight hundred people：请注意有数词存在后，表量名词的变化。

(完整word版)英语音标讲义-完美打印版

第二部分拼读基础知识一、英语国际音标学习英语，首先是掌握英语国际音标，掌握正确的英语发音。

英语共有48个音标，分元音和辅音两大类.元音有20个,分为双元音和单元音两种。

单元音按舌位可分为前元音、中元音和后元音。

辅音有28个，按声带振动与否可分为清辅音和浊辅音两种。

按不同发音方式可分为爆破音、摩擦音、破擦音、鼻音、舌边音、半元音.1。

元音和辅音第一节元音分类元音分双元音和单元音。

根据舌位的变化，元音又可分为前元音、中元音和后元音。

舌位在口腔前部的时候发出的元音叫做前元音,舌位在口腔中部的时候发出的元音叫做中元音，同理，舌位后缩到口腔后部发出的元音就叫做后元音。

请看以下的元音分类表:元音分类表第二节辅音分类英语辅音共有28个。

这28个辅音按发音时是否振动声带分为清辅音和浊辅音。

按发音时以不同方式调动的不同发音器官来分类，英语辅音又可分为爆破音、摩擦音、破擦音、鼻音、舌边音、半元音。

请看以下的辅音分类列表：辅音分类表2。

发音器官要想掌握好英语音标，我们要了解发音器官和发音部位，并学会运用舌、唇、软腭、硬腭等位置和形状的变化，正确地发出各种不同的音。

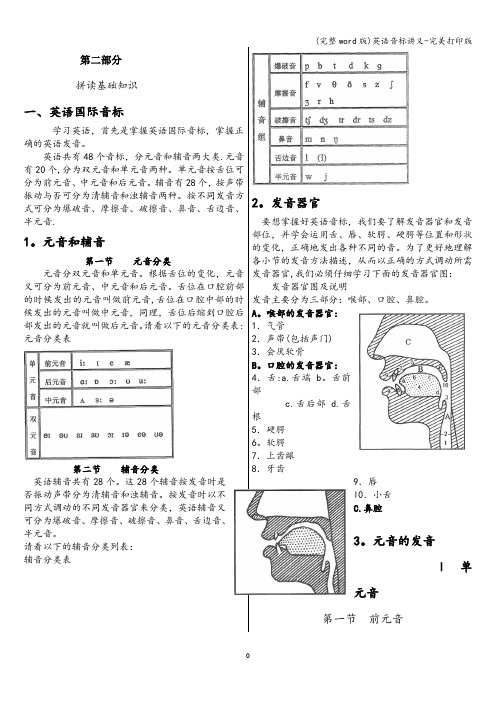
为了更好地理解各小节的发音方法描述，从而以正确的方式调动所需发音器官,我们必须仔细学习下面的发音器官图：发音器官图及说明发音主要分为三部分：喉部、口腔、鼻腔。

A。

喉部的发音器官：1．气管2．声带(包括声门)3．会厌软骨B。

口腔的发音器官：4．舌:a.舌端 b。

舌前部c.舌后部d.舌根5．硬腭6。

软腭7．上齿龈8．牙齿9．唇l0．小舌C.鼻腔3。

元音的发音Ⅰ单元音第一节前元音发音方法描述:发音时舌尖轻抵下齿,前舌部向上腭抬起,口形扁而平。

发音时间延续较长。

例词：l ea f树叶 ch ee se奶酪t ea茶 th ie f贼b ea ch海滩 w ee k星期t ea m队 m ea t肉sh ee p羊词组:Green Street格林街iced tea冰茶Chinese and Japanese food中国和日本菜发音方法描述：发音时舌尖抵下齿，舌前部向硬腭抬起,口形扁平，发音时间短促.例词：cl i p夹子 g y m体育馆 s i t坐 th i n薄的p i zza比萨饼 tax i出租车 un i t单元 v i s i t游览词组:play tennis打网球 pop music流行音乐 music festival音乐节发音方法描述：舌尖抵下齿，前舌部向硬腭抬起，口形扁平，气流从口腔泄出，声带振动。

有机化学实验内容讲义(打印版)

有机化学实验内容讲义注:鉴于有机实验的危险性,老师应写好各个实验板书，向学生讲清实验步骤和注意事项，并于实验全程指导监督，以防事故发生。

实验安排：第一、二周：(第1，2实验室)实验一、从果皮中提取果胶(第3实验室) 实验二、从茶叶中提取咖啡因第三、四周：(第1，2实验室)实验三、无水乙醇的蒸馏(第3实验室) 实验四、甲基橙的制备第五、六周：(第1，2实验室)实验五、乙酸异戊脂的合成(第3实验室) 实验六、性质实验（烃、醇、醛、醛、酮）第七、八周：(第1，2实验室)实验七、邻硝基苯酚和对硝基苯酚的合成(第3实验室) 实验八、性质实验（羧酸、胺、糖性质）实验一、从果皮中提取果胶一、实验目的了解用酸提法从植物中提取果胶的原理和操作方法二、实验原理果胶主要以不溶于水的原果胶形式存在于植物中，当用酸从植物中提取果胶时，原果被水解成果胶，果胶又叫果胶酯酸，其主要成分是牛乳糖尾酸甲酯，及半乳糖尾酸通过α-1,4-苷键连成的高分子化合物，结构片段示意如下：O COOCH 3H H H OH H HOH OO COOCH 3H H H OH H H OH O O COOCH 3H H H OH H H OH O O果胶不深于乙醇,在提取液中加入至约50%时,可使果胶沉淀下来而与杂质分离。

三、仪器药品及实验材料1．仪器：烧杯、量筒、酒精灯、台秤2．药品与实验材料：果皮（柑橘、苹果、梨）、浓盐酸、活性炭、95%乙醇、滤纸、纱布四、实验步骤取10g 果皮（柑橘、苹果、梨）放入烧杯中，加60 ml 水，再加入1.0~1.5 mL 浓盐酸加热至沸腾，在搅拌下维持沸腾30min ，减压过滤，滤液内加入少量活性炭，再加热20min ，用滤纸过滤得浅黄色滤液。

滤液放入一小烧杯中，在不断搅拌下慢慢加入等体积的95%乙醇，会看到出现絮状的果胶沉淀。

稍等片刻减压过滤，并用95%乙醇5mL 分2~3次洗涤沉淀，然后将沉淀烘干，即得到果胶固体。

公共基础知识讲义最新整理(打印版)—法律篇

公共基础知识讲义(法律篇）法律之宪法概述（什么是宪法）一、宪法的形式特点1．内容:规定国家最根本、最重要的问题：2．法律效力:法律效力最高。

3．制定和修改的程序:宪法比其他法律更加严格。

【真题-多选】宪法的特征主要有（）。

A. 宪法具有最高效力B. 宪法规定国家的根本性问题C. 宪法的制定要通过特定的程序D. 宪法的修改要通过特定的程序ABCD二、宪法的原则1. 人民主权原则2. 基本人权原则3. 权力制衡原则4. 法治原则核心价值：限制国家权力保障公民权利【真题-单选】我国现行宪法的结构体系是( )。

A 序言，总纲，国家机构，公民的基本权利和义务，国旗、国歌、国徽、首都B 序言，总纲，国家机构，公民的基本权利和义务，国徽、国歌、国旗、首都C 序言，总纲，公民的基本权利和义务，国家机构，国旗、国歌、国徽、首都D 序言，总纲，公民的基本权利和义务，国家机构，国徽、国歌、国旗、首都C权力机关一、全国人民代表大会1．性质：最高的国家权力机关，立法机关。

2．组成和任期：省级区域选出的代表组成。

每届任期为5 年。

3．职权（1）修改宪法和监督宪法实施提议：全国人民代表大会常务委员会或者1／5 以上的全国人大代表提议通过：全体代表的2／3 以上的多数通过。

（2）制定和修改国家基本法律(特别行政区基本法）【真题-多选】下列属于国家宪法修改程序组成部分的内容是：( )A. 1/5 以上的全国人大代表提议B. 全国人大常委会提议C. 全体到会代表的2/3 以上多数通过D. 全体代表2/3 以上多数通过ABD【真题-单选】香港特别行政区基本法修改权属于（）。

A. 特别行政区立法会B. 全国人民代表大会和全国人民代表大会常务委员会C. 全国人民代表大会D. 全国人民代表大会常务委员会C（3）监督权：对国家机构组成人员的选举、决定和罢免（注：总理由国家主席提名，全国人大决定）（4）决定国家的重大事项批准省、自治区和直辖市的建制；决定特别行政区的设立及其制度；决定战争与和平。

职业能力讲义(打印版)

第一节职业能力概述一、职业能力的含义职业能力是人们从事某种职业的多种能力的综合。

职业能力是人们从事某种职业活动必须具备的，影响职业活动效率的个人心理特征。

人的职业能力是由多种能力叠加并复合而成的，它是人们从事某项职业必须具备的多种能力的总和，是择业的基本参照和就业的基本条件，也是胜任职业岗位工作的基本要求。

（一）一般职业能力主要是指一般的学习能力、文字和语言运用能力、数学运用能力、空问判断能力、形体知觉能力、颜色分辨能力、手的灵巧度、手眼协调能力等。

此外，人际交往能力、团队协作能力、对环境的适应能力，以及遇到耐挫力都是我们在职业活动中不可缺少的能力。

（二）专业能力专业能力主要是指从事某一职业的专业能力。

（三）职业综合能力:主要包括四个方面：1）跨职业的专业能力一是运用数学和测量方法的能力；二是计算机应用能力；三是运用外语解决技术问题和进行交流的能力。

2）方法能力一是信息收集和筛选能力；二是掌握制定工作计划、独立决策和实施的能力；三是具备准确的自我评价能力和接受他人评价的承受力，并能够从成败经历中吸取经验教训。

3）社会能力社会能力主要是指一个人的团队协作能力、人际交往和善于沟通的能力能够协同他人共同完成工作，公正宽容，具有准确裁定事物的判断力和自律能力等。

4）个人能力社会责任心和诚信将越来越被重视，一个人的职业道德会越来越受到全社会的尊重和赞赏，爱岗敬业、工作负责、注重细节的职业人格会得到全社会的肯定和推崇。

二、能力的分类能力按照其获得的方式（先天具有与后天培养）1、能力倾向(apititude)与生俱来的、天赋的特殊才能，如音乐、运动能力等。

也可以理解为潜能。

2、技能(skill)经过后天学习和练习培养而形成的能力。

如阅读能力、人际交往能力、表达能力等。

三、讨论与案例讨论：一个聋哑人，到五金店买钉子。

他左手作持钉状，右手对着左手作锤打状，售货员拿来了一把锤子，聋哑人摇了摇头，随后用手指了指左手。

1现代心理学讲义(打印版)

第一讲绪论主要内容一、心理学是科学二、心理学是研究什么的三、研究心理学有什么意义四、为什么心理现象能够研究五、怎么研究心理现象六、西方心理学派别七、当代心理学的研究取向八、心理学发展的历史和现状一、心理学是科学1 特定的研究对象：心理现象2 独立的理论体系：3 科学的研究方法：实事求是、有目共睹二、心理学是研究什么的1 心理学是研究心理活动发生、发展规律的科学2 普通心理学是研究正常的成年人心理活动规律的科学3 心理现象的具体内容⏹心理学的学科性质⏹普通心理学的学科性质三、研究心理学有什么意义1 理论意义⏹克服唯心主义⏹不同的心理观⏹心理的实质⏹心理是脑的机能,是客观现实的反映。

2 实践意义⏹有利于教育：教育心理学等⏹有利于交往：社会心理学等⏹有利于生产：工程心理学等⏹有利于人才选拔和企业管理：管理心理学等⏹有利于商业：广告心理学等⏹有利于军事：军事心理学等⏹有利于司法：犯罪心理学等⏹有利于医疗：临床心理学等⏹……3 科学研究的四个层次⏹描述（description）⏹描述的目的是将研究问题时所获知的表面事实，客观地用口头或文字描述出来；只求事实的真实性，不涉及问题发生的原因。

⏹解释（explanation）⏹解释的目的是将问题发生的前因后果分析清楚。

解释以陈述的事实为根据，进一步分析形成问题的原因。

⏹预测（prediction）⏹预测的目的是只根据现有的资料，去推测将来发生问题的可能性。

适于因果关系明确的问题。

⏹控制（control）⏹控制的目的是指设法控制问题发生的原因，使可能发生的问题不致于发生；或将可能发生问题的严重性减少到最低限度。

四、为什么心理现象能够研究1 原因⏹从时间上看⏹过去⏹现在⏹过去 + 现在⏹内容上看⏹生理原因⏹心理原因⏹环境原因2 言行⏹从时间上看⏹即时⏹延时⏹从表现形式上看⏹内隐的⏹外显的五、怎么研究心理现象1 基本原则⏹客观性原则⏹发展性原则2 具体方法1）观察法⏹定义：在自然条件下，对表现心理现象的外部活动进行有系统、有计划的感知，从中发现心理现象产生和发展的规律性，这种方法叫观察法或自然观察法。

讲义(打印版)——成考英语情景对话

口语交际I．考试要求及考试范围 (2)II．对话的命题方式和题型 (2)(1)语境题 (2)(2)习语题 (3)(3)结构题 (3)III 口语交际的考察要点 (3)1. 完成对话 (4)2. 对话理解 (4)V命题特点及解题技巧 (5)VI复习要领 (6)1.理解对话的背景和场景 (6)2.理解对话的关键词和习惯用法 (6)3.采取排除法答题 (6)VII常用口语表达用语 (7)（28种不同语境情况下的口语表达用语） (7)1.见面时的对话 (7)2.分手时的对话 (7)3.相互介绍时的对话 (8)4.感谢与回答 (9)5.道歉与回答 (9)6.请求许可或帮助与回答 (10)7.邀请 (11)8.祝愿和祝贺 (11)9.打电话 (11)10.看病 (12)11.吃饭 (12)12.购物 (12)13.谈论天气 (12)14.劝告和建议 (13)15.请求 (13)16.表示惊讶 (13)18.同意与不同意 (13)19. 提建议与回答 (14)20. 与人相约 (15)21. 问路 (15)22. 表示态度 (16)23. 表示生气 (16)24. 表示失望 (17)25. 表示抱怨 (17)26. 表示同情 (17)27. 表示鼓励 (18)28．表示确定与不确定 (18)VIII真题链接 (18)Part 1 Complete the dialogue (18)1. 三大难点 (18)2. 必备场景及习惯用语 (20)3. 解题技巧 (24)4.例题解析 (24)5.[强化练习] (26)6.真题复习 (28)7.拓展练习Part 2 Dialogue comprehension (33)1.难点 (35)2. 解题技巧 (36)3.[真题演练] (37)4．[强化练习] (42)(附1 )常见的习语和固定短语 (45)(附2) 最常用口语表达： (45)口语交际I．考试要求及考试范围口语交际分为两部分：完成对话(Dialogue Completion)和对话理解(Dialogue Co mprehension)。

民间文学讲义打印版

民间文学讲义民间文学讲义提纲说明1. 提纲仅供大家参考，并非所谓“标准答案”。

2. 提纲中如有错误，请直接向郑老师反映。

3. 提纲只供选课生使用，请勿扩散。

绪论绪论部分初步清理关于民间文学的一些错误看法，就民间文学的地位和价值树立起基本的观念。

歌本与演唱歌本常宁塔山瑶族乡的“冈介”活动常宁塔山瑶族乡的“冈介”活动“冈介”录像片段“冈介”表演现场要点口传文化（oral culture）文化传统大传统（great tradition）小传统（little tradition）——罗伯特·雷德菲尔德钟敬文的文化分层生活文化文化展演狂欢化钟敬文先生的文化分层文化的范围很广泛，层次也不单一。

它是一个庞大的复杂的综合体。

我向来认为中国传统文化有三个主流。

首先是上层社会文化，从阶级上说，即封建地主阶级所创造和享有的文化；其次，是中层社会文化，即城市人民的文化，主要是商业市民所有的文化；最后，是底层社会的文化，即广大农民所创造和传承的文化。

（88年）——钟敬文《话说民间文化·自序》生活文化：一个关键词民俗学是一门社会科学，是一门人文科学。

它的研究对象，是一个国家或民族中广大人民（主要是劳动人民）所创造、享用和传承的生活文化。

（82年）——钟敬文《民俗学及其作用》生活文化是“民族的基层文化”、基本文化。

不过，它应被理解成生活世界意义上的基层文化，是经典文化或意识形态的基础。

（94年）——高丙中《民俗文化与民俗生活》P142生活文化概念的学术意义如果我们认真注意到民俗的生活形态，我们就有可能更加现实地认识民俗的广泛存在。

从生活的角度来看，不难发现，民俗构成了人的日常性活动、日历性活动和人生的基本框架和基本内容，民俗是人基本的生活世界的基本构成。

——高丙中《民俗文化与民俗生活》P170要点阈限（threshold）阈限意指所有间隙性的或模棱两可的状态，这个概念与维克多·特纳的作品，以及他所拓展的阿诺德·范·盖纳普的原创观点是分不开的。

新版标准日本语初级讲义(打印版)

新版标准日本语初级讲义（打印版）平假名 1.5 0音図行2 •浊音：在k 、s 、t 、h 行加点、圈之后，发生音变3 •拗音：在假名后加壬、㊇、/,两个假名构成一拍練習:1.2.3.4.拨音：人不能放在词头。

根据前面词，发出的音。

5.促音：^（小写，^的发音长度是一拍。

例子:n/m/ng2.力、3.冷力、4.力rm、力也、6 •长音：平假名在母音的后面加厉、―刁、元、：等音则变成原来的2倍。

片假名在后面加“一"符号表记长音。

例：1.力、厉2.4.七◎、七片假名1.5 0音図行2 •浊音：在k、s、t、h行加点、圈之后，发生音变3.n/m/ng 4 •拨音：A不能放在词头。

根据前面词，发出的音。

5•促音：、7（小写、7），少的发音长度是一拍。

例：力少卜6•长音：片假名后面加“-”符号表记长音。

例：一夕第一課李中国人内容：判断句.李曲国人注。

小李是中国人。

名词+^ +名词+^^O 〜是〜，肯定判断句.森肚学牛左处笳耳求它人。

小森不是学牛。

名词+^ +名词〜不是〜，否定判句。

.林肚日本人丁力、。

小森是日本人吗?名词+^ +名词+疋丁力、。

〜是〜吗？一般疑问句。

对籍、年龄、姓名等都可以进行提问肯定回答：怎^、、森日本人左^。

否定回答伉、森^^^0本人刘止厉◎求乜人元、占力"、求^。

4.李龙人0止jc企画①社員疋丁。

小李是JC策划公司的职员。

名词+0 +名词连接两个名词时，中间加◎，表示“的”。

第二課本左丁内容：使用指示代词作判断句乙料：离说话人最近的事物。

乞料：距听话人最近的事物。

厉料：离说话人和听话人都比较远的事物。

1.匚一扛本左丁。

这是书。

乙料、乞料、名词左^。

这是〜，以代词作主语的判断句。

疑问词:2.o 本左。

止厉◎求乜人。

这不是书。

乙札乞札名词这不是〜,否定句。

3.0池农本力、。

这是书吗？o料、乞料、名词力、。

这是〜吗？一般疑问句。

4.乞料处何力、。

那是什么。

0料、乞料、厉料处+何力、。

郑贵友语法讲义(已打印)重要

第一章语法概说一、语法和语法学二、语法单位三、句子成分四、句子分析——分析句子的两种方法第二章词类一、词类的含义与词类划分的目的二、词类划分的标准三、词的一级分类和再分类四、各类实词名词动词形容词区别词数词量词代词副词/象体词五、各类虚词介词连词助词语气词六、兼类问题第三章短语一、定义二、短语的种类三、短语的构成手段四、简单短语和复杂短语五、单义短语和多义短语六、自由短语和固定短语七、短语和词宏观上的同与异第四章句子成份一、句子成分的性质二、主语、谓语主语的语法构成主语的语义类型谓语的语法构成三、动语、宾语动语的语法构成有宾动词无宾动词宾语的语法构成宾语的语义类型四、定语五、状语六、补语补语的语法构成补语的语义类型宾语、补语的顺序数量宾语和数量补语七、中心语八、独立语第五章单句一、根本概念二、句型确定的原那么和方法三、主谓句主谓谓语句双宾语句连动句兼语句存现句“把〞字句“被〞字句“是〞字句“有〞字句“所〞字句四、非主谓句五、单句和短语第六章歧义分析一、歧义的含义与歧义研究的目的二、歧义的种类(1)同音造成的歧义同形造成的歧义一词多义造成的歧义词兼类造成的歧义语义关系不同造成的歧义三、歧义的种类(2)第七章复句一、复句的含义二、复句中的关系词语三、复句的分类四、广义的并列关系五、广义的因果句因果关系目的关系假设关系条件关系六、广义的转折句七、复句的扩大八、复句的紧缩第一章语法概说一、语法和语法学〔一〕语法1.语法的含义与其作用〔1〕语法的含义语法，是语言中的词、短语、句子的构造规律。

语言有三个要素，语音、词汇和语法。

其中，语音是由人的发音器官发出的、表达一定意义的声音，是语言的物质外壳。

词汇，是语言中的语素、词和固定短语以与现成话的集合，是语言的建筑材料。

而语法那么是语言“建筑体〞的建筑法那么。

西方传统语言学认为，语法包括两个大的方面：词法和句法。

词法，主要涉与词的构成、词的分类和词形变化等容。

句法，主要讨论短语和句子的构造规律。

郑贵友语法讲义(已打印)重要

第一章语法概说一、语法和语法学二、语法单位三、句子成分四、句子分析——分析句子的两种方法第二章词类一、词类的含义及词类划分的目的二、词类划分的标准三、词的一级分类和再分类四、各类实词名词动词形容词区别词数词量词代词副词/象体词五、各类虚词介词连词助词语气词六、兼类问题第三章短语一、定义二、短语的种类三、短语的构成手段四、简单短语和复杂短语五、单义短语和多义短语六、自由短语和固定短语七、短语和词宏观上的同与异第四章句子成份一、句子成分的性质二、主语、谓语主语的语法构成主语的语义类型谓语的语法构成三、动语、宾语动语的语法构成有宾动词无宾动词宾语的语法构成宾语的语义类型四、定语五、状语六、补语补语的语法构成补语的语义类型宾语、补语的顺序数量宾语和数量补语七、中心语八、独立语第五章单句一、基本概念二、句型确定的原则和方法三、主谓句主谓谓语句双宾语句连动句兼语句存现句“把”字句“被”字句“是”字句“有”字句“所”字句四、非主谓句五、单句和短语第六章歧义分析一、歧义的含义及歧义研究的目的二、歧义的种类(1)同音造成的歧义同形造成的歧义一词多义造成的歧义词兼类造成的歧义语义关系不同造成的歧义三、歧义的种类(2)第七章复句一、复句的含义二、复句中的关系词语三、复句的分类四、广义的并列关系五、广义的因果句因果关系目的关系假设关系条件关系六、广义的转折句七、复句的扩充八、复句的紧缩第一章语法概说一、语法和语法学（一）语法1.语法的含义及其作用（1）语法的含义语法，是语言中的词、短语、句子的构造规律。

语言有三个要素，语音、词汇和语法。

其中，语音是由人的发音器官发出的、表达一定意义的声音，是语言的物质外壳。

词汇，是语言中的语素、词和固定短语以及现成话的集合，是语言的建筑材料。

而语法则是语言“建筑体”的建筑法则。

西方传统语言学认为，语法包括两个大的方面：词法和句法。

词法，主要涉及词的构成、词的分类和词形变化等内容。

句法，主要讨论短语和句子的构造规律。

讲义(打印)

内经讲义 打印重点

景观生态学讲义(打印版)

曹显兵.概率论讲义（打印版）

自考英语一讲义(打印版)

(完整word版)英语音标讲义-完美打印版

有机化学实验内容讲义(打印版)

公共基础知识讲义最新整理(打印版)—法律篇

职业能力讲义(打印版)

1现代心理学讲义(打印版)

讲义(打印版)——成考英语情景对话

民间文学讲义打印版

新版标准日本语初级讲义(打印版)

郑贵友语法讲义(已打印)重要

郑贵友语法讲义(已打印)重要

内经讲义打印重点