信号系统课后习题答案
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示,试作出信号x(t)的波形图,并加以标注。
题图1-51- 6 试画出下列信号的波形图:1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图:⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角,并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下,试写出各自系统的输入输出方程。
《信号与系统》课后习题参考答案

《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、(1)解:∵系统的微分方程为:)(2)(3)(t e t r t r '=+',∴r(t)的阶数与e(t) 的阶数相等,则h(t)应包含一个)(t δ项。
又∵系统的特征方程为:03=+α,∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程(此时e(t)= )(t δ),得:)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解:①求)(t r zi : ∵系统的特征方程为:0)3)(2(652=++=++αααα,∴特征根:21-=α,32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs :t t e A eA t h 3221)(--+= (t ≥0),可求得:11=A ,12-=A (求解过程略) ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r :)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=,21=C 21=C ∴ 011=-C , ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi , ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解:(1)依题意,得:)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---,两边求导得:)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ (2)∵系统的起始状态保持不变,∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+,∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证:∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时:u(t-3k)为非零值 又∵0≤t ≤3,∴k 取负整数,则:3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(,且311--=e A 。
信号与系统课后习题答案(金波 华中科技大学出版社)

1-3 解 周期 T=7 ,一个周期的能量为 信号的功率为
P
E 56 8W T 7
1-5 解 (a) (3t 2 2) ( ) 4 (t ) ; (b) e
3t
t 2
(5 2t ) 0.5e 3t (t 2.5) 0.5e 7.5 (t 2.5)
2
1-10 已知一线性非时变系统,系统的初始状态为零,当输入信号为 f1 (t ) ,其输出信号为
y1 (t ) ,对应的波形如题图 1.10(a)(b)所示。试求: (a) 当输入信号为 f 2 (t ) 时,其波形如题图 1.15(c)所示,画出对应的输出 y 2 (t ) 的波形。 (b) 当输入信号为 f 3 (t ) 时,其波形如题图 1.10(d)所示,画出对应的输出 y 3 (t ) 的波形。
(b) 波形如图1.2(b)所示。显然是能量信号。
E 1 1 6 2 1 37 J
(c) 能量信号
E lim (e 5t ) 2 dt e 10t dt
T 0 0
T
1 10t e 0.1 J 10 0
(d) 功率信号,显然有
P 1W
习
基本练习题
题 一
1-1 判断下列信号是否是周期的,如果是周期的,求出它的基频和公共周期。 (a) f (t ) 4 3 sin(12 t ) sin(30 t ) ; (b) f (t ) cos(10 t ) cos(20 t ) ; (c) f (t ) cos(10 t ) cos(20t ) ; (d) f (t ) cos(2t ) 2 cos(2t
2
信号与系统课后习题与解答第三章
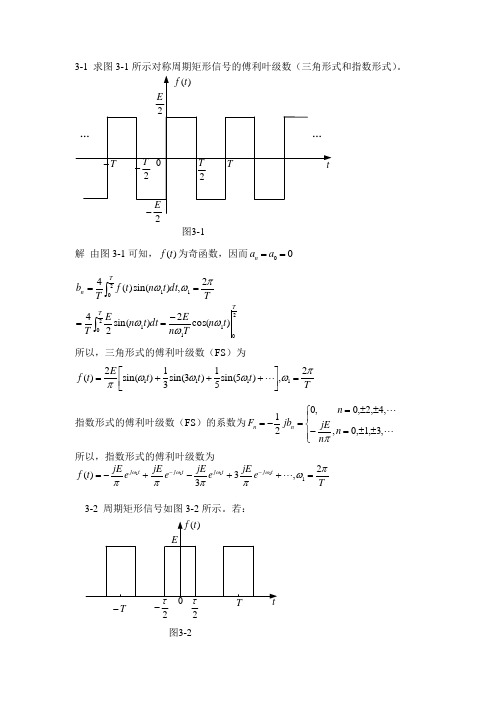
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统课后习题答案

《低频电子线路》一、单选题(每题2分,共28分:双号做双号题,单号做单号题)1.若给PN结两端加正向电压时,空间电荷区将()A变窄B基本不变C变宽D无法确定2.设二极管的端电压为 U,则二极管的电流与电压之间是()A正比例关系B对数关系C指数关系D无关系3.稳压管的稳压区是其工作()A正向导通B反向截止C反向击穿D反向导通4.当晶体管工作在饱和区时,发射结电压和集电结电压应为 ( ) A前者反偏,后者也反偏B前者反偏,后者正偏C前者正偏,后者反偏D前者正偏,后者也正偏5.在本征半导体中加入何种元素可形成N型半导体。
()A五价B四价C三价D六价6.加入何种元素可形成P 型半导体。
()A五价B四价C三价D六价7.当温度升高时,二极管的反向饱和电流将()。
A 增大B 不变C 减小D 不受温度影响8. 稳压二极管两端的电压必须( )它的稳压值Uz 才有导通电流,否则处于截止状态。
A 等于B 大于C 小于D 与Uz 无关9. 用直流电压表测得放大电路中某三极管各极电位分别是2V 、6V 、2.7V ,则三个电极分别是() A (B 、C 、E )B (C 、B 、E )C (E 、C 、B )D (B 、C 、E )10. 三极管的反向电流I CBO 是由( )形成的。
A 多数载流子的扩散运动B 少数载流子的漂移运动C 多数载流子的漂移运动D 少数载流子的扩散运动11. 晶体三极管工作在饱和状态时,集电极电流C i 将( )。
A 随B i 增加而增加B 随B i 增加而减少C 与B i 无关,只决定于e R 和CE uD 不变12. 理想二极管的正向电阻为( )A A.零 B.无穷大 C.约几千欧 D.约几十欧13. 放大器的输入电阻高,表明其放大微弱信号能力( )。
A 强B 弱C 一般D 不一定14. 某两级放大电路,第一级电压放大倍数为5,第二级电压放大倍数为20,该放大电路的放大倍数为( )。
A 100B25C 5D2015.如题47图所示电路中,静态时, T1、T2 晶体管发射极电位UEQ为( ) 。
信号与系统课后习题参考答案.pdf

-5
-4 -3 -2
-1
2 1
2
3
-1
x(-t+4)
t
45
6
2 1
4
6
-1
x(-t/2+4)
t 8 10 12
(e)[x(t)+x(-t)]u(t)
-2
-1
2
x(-t)
1
t
01
2
-1
(f)
x(t)[δ(t +
3) − δ(t - 3)]
2
2
3
[x(t)+x(-t)]u(t)
1 t
01
2
-1
-3/2 (-1/2)
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 (-1/2)
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
=
2π 4
=π 2
则:整个信号的周期为:T = LCM{T1,T2} = π
1.11
j 4πn
解: e 7
→
ω1
=
4πn 7
,则:
2π ω1
=
2π 4π
=7= 2
N1 k
,⇒
N1
=
7
7
j 2πn
e5
→ ω2
信号与系统版课后答案 郑君里 高等教育出版社
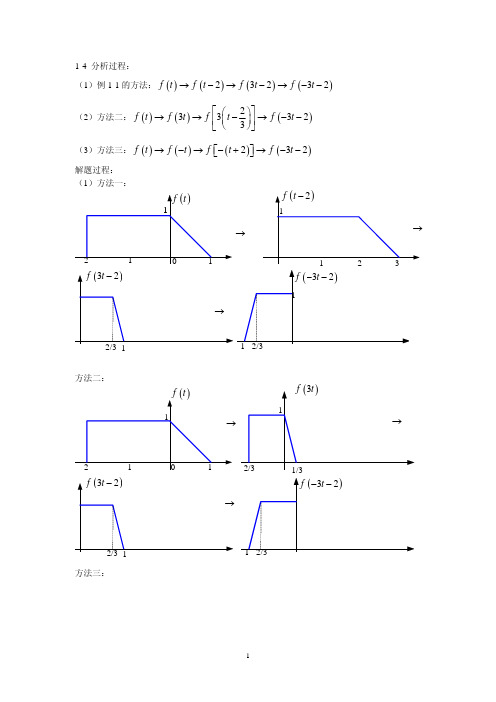
(1)例 1-1 的方法: f (t ) → f (t − 2) → f (3t − 2) → f (−3t − 2)
(2)方法二:
f
(t) →
f
(3t ) →
f
⎡⎢⎣3⎛⎜⎝ t −
2 ⎞⎤ 3 ⎟⎠⎥⎦
→
f
(−3t − 2)
(3)方法三: f (t ) → f (−t ) → f ⎡⎣− (t + 2)⎤⎦ → f (−3t − 2)
(R2
+
2L) C
d2 dt 2
v0 (t)
+
2R C
d dt
v0 (t)
+
1 C2
v0 (t)
=
MR
d3 dt 3
e(t)
∫ v0 (t)
图(c)微分方程:
=
L1i
' 1
=
1 C1
i2 dt
⇒
d
dt d2 dt 2
i1 i1
= =
1 L1 1 L1
v0 (t) v '0 (t)
∫
i1
=
1-18 分析过程:任何信号均可分解为奇分量与偶分量之和的形式,即
f (t) = fe (t) + fo (t)
(1)
其中, fe (t ) 为偶分量, fo (t ) 为奇分量,二者性质如下:
fe (t ) = fe (−t )
(2)
fo (t ) = − fo (−t )
(3)
(1) ∼ (3) 式联立得
5t −∞
e2
(τ
)
dτ
= c1r1 (t ) + c2r2 (t )
信号与系统课后习题与解答第二章
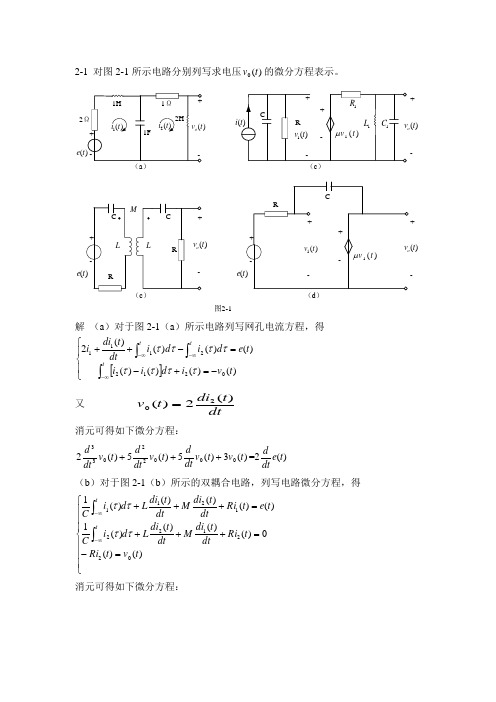
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。
2(t ei )(t +-(e )(e )(t +-图2-1解 (a )对于图2-1(a )所示电路列写网孔电流方程,得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程:)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d(b )对于图2-1(b )所示的双耦合电路,列写电路微分方程,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程:)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- (c )对于图2-1(c )所示电路列写电路方程,得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程:)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ (d )对图2-1(d )所示电路列写电路方程,电流)(t i 如图2-2所示,得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程:(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。
信号与系统课后习题答案

f 2 (−1) (t) =
δ (t − 2) − δ (t − 3)
*
t ε e(−t+1) (t + 1)dt
−∞
= [δ (t − 2) − δ (t − 3)]* (1 − e−(t+1) )ε (t + 1)
= (1 − e−(t−2+1) )ε (t − 2 + 1) − (1 − e−(t−3+1) )ε (t − 3 + 1)
) − iL (t) − uC (t) R1
R2
状态方程为:
⎪⎪⎧u&C (t) ⎨
=
f (t) R1C
−
uC (t) R1C
−
iL (t) C
⎪⎪⎩i&L
(t)
=
uC
(t)
− R2iL L
(t)
1.17 写出题图 1.8 系统的输入输出方程。
解: (b)系统框图等价为:
⎧x′′(t) = f (t) − 3x′(t) − 2 y(t)
x2(0-)=1 时,y2(t)=4e-t-2e-3t,t≥0 则 x1(0-)=5,x2(0-)=3 时,系统的零输入响应: yx(t)=y(t)=5y1(t)+3y2(t)=22e-t 十 9e-3t,t≥0
1.22 在题 1.21 的基础上,若还已知 f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,有 y(t)=2+e-t+2e-3t,t≥0 试求当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统响应 y(t)。 解: 记,f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,系统响应 yf(t)=y(t)=2+e-t+2e-3t,t≥0 则当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统全响应 y(t)为: y(t)=3yf(t)+2y1(t)+5y2(t)
信号与系统课后习题答案第4章

所示。
➢ 题解图 4.25
按直接形式Ⅰ画出模拟信号流图和 方框图分别如题解图4.25(e)、(f)
所示。
➢ 题解图 4.26
的系统函数H(s)如下,求系统的频
率响应,粗略地画出幅频响应和相 频响应曲线。
H(s)收敛域包含jω轴,故频率响应
(2) 依照系统方框图与信号流 图表示之间的对应关系,分别画出 两系统的信号流图表示,如题解图
2.23(c)、(d)所示。
图分别如题图 4.9(a)、(b)所示,求
系统函数H(s)。
➢ 题图 4.9
4.25 已知线性连续系统的系 统函数如下,用直接形式信号流图 模拟系统,画出系统的方框图。
所示。
点,列出节点电压方程:
h3(t)=ε(t)。
(1) 求系统的冲激响应;
(2) 若输入f(t)=ε(t),求零状
态响应。
➢ 题图 4.6
(1) 求系统的冲激响应;
(2) 若f(t)=tε(t),求零状态响
应。
➢ 题图 4.7
(1) 写出描述系统输入输出关 系的微分方程;
(2) 画出系统的信号流图。
4.4 求题图4.1所示信号的单 ➢ 题图 4.1 边拉氏变换。
(1) f(t)=ε(t)-ε(t-3)。因为
所以
4.7 题图4.2所示为从t=0起始
的周期信号, 求f(t)的单边拉氏变
➢ 题图 4.2
换。
于第一周期信号的象函数与周期因 子的乘积。
(a) 记f(t)中第一周期信号为 相应的象函数为F1(s)。由于
数为F(s),求下列F(s)的原函数f(t) 的初值f(0+)和终值f(∞)。
信号与系统课后答案
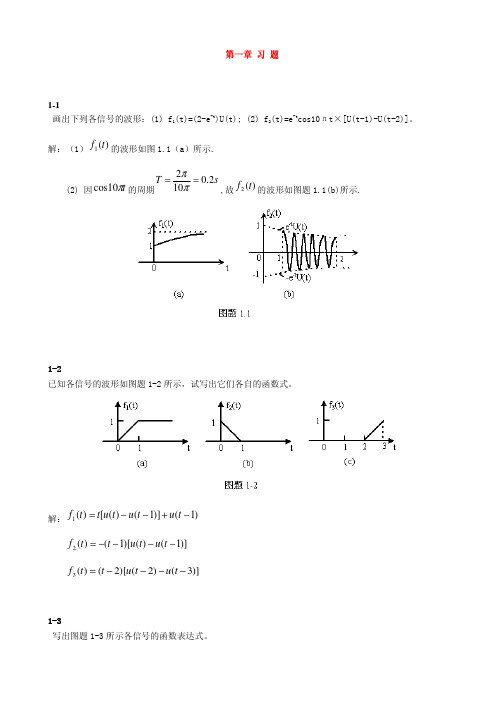
与奇分量的波形,相应如图题 1.12 中所示。
1-13 已知信号 f(t)的偶分量 fe(t)的波形如图题 1-13(a)所示, 信号 f(t+1)×U(-t-1)的波形如图题 1-13(b) 所示。求 f(t)的奇分量 fo(t),并画出 fo(t)的波形。
解 因
f (t ) = f e (t ) + f 0 (t )
∫
t
−∞
δ (τ )dτ ,故根据现行系统的积分性有
y (t ) = ∫ h(τ (dτ = ∫ [δ (τ ) − δ (τ − 1) − δ (τ − 2) + δ (τ − 3)]dτ = u (t ) − u (t − 1) − u (t − 2) + u (t − 3)
1-2 已知各信号的波形如图题 1-2 所示,试写出它们各自的函数式。
解: f 1 (t ) = t[u (t ) − u (t − 1)] + u (t − 1)
f 2 (t ) = −(t − 1)[u (t ) − u(t − 1)]
f 3 (t ) = (t − 2)[u(t − 2) − u(t − 3)]
y 2 (t ) 的波形如图题 1.17(c)所示.
1-18 图题 1-18(a)所示为线性时不变系统,已知 h1(t)=δ(t)-δ(t-1), h2(t)=δ(t-2)-δ(t-3)。(1)求响 应 h(t); (2) 求当 f(t)=U(t)时的响应 y(t)(见图题 1-18(b))。
解(1) h(t ) = h1 (t ) − h2 (t ) = δ (t ) − δ (t − 1) − δ (t − 2) + δ (t − 3) (2) 因 f (t ) = u (t ) =
信号与系统课后习题与解答第一章

1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
信号与系统课后习题参考答案

题图2-10
2-11已知系统得微分方程与起始条件,试求系统得零输入响应。
⑴
⑵
⑶
2-12已知系统得差分方程与起始条件,试求系统得零输入响应。
⑴
⑵
⑶
2-13已知系统得微分方程,试求系统得单位冲激响应。
⑴
⑵
⑶
2-14已知系统得差分方程,试求系统得单位样值响应。
1-1试分别指出以下波形就是属于哪种信号?
题图1-1
1-2试写出题1-1图中信号得函数表达式。
1-3已知信号与波形如题图1-3中所示,试作出下列各信号得波形图,并加以标注。
题图1-3
⑴⑵⑶
⑷⑸⑹
⑺⑻⑼
1-4已知信号与波形如题图1-4中所示,试作出下列各信号得波形图,并加以标注。
题图1-4
⑴⑵⑶
⑷⑸⑹
⑵
⑶
⑷
⑸
⑹
2-2试计算下列各对信号得卷积与:。
⑴(对与两种情况)
⑵
⑶
⑷
⑸
⑹
2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。
题图2-3
2-4试计算下图中各对信号得卷积与:,并作出结果得图形。
题图2-4
2-5已知,试求:
⑴⑵⑶
并作出她们得图形。
2-6系统如题图2-6所示,试求系统得单位冲激响应。已知其中各子系统得单位冲激响应分别为:
3-5设有一周期信号x(t),其复振幅为:
⑴x(t)就是实函数吗?⑵x(t)就是偶函数吗?⑶就是偶函数吗?
3-6设x(t)就是一基波频率为Ω得周期信号,其复振幅为,试用表示以下周期信号得复振幅。
⑴⑵
信号与系统课后习题答案

第1章 习题答案1-1 题1-1图所示信号中,哪些是连续信号哪些是离散信号哪些是周期信号哪些是非周期信号哪些是有始信号解: ① 连续信号:图a 、c 、d ; ② 离散信号:图b ; ③ 周期信号:图d ;④ 非周期信号:图a 、b 、c ; ⑤有始信号:图a 、b 、c;1-2 已知某系统的输入ft 与输出yt 的关系为yt=|ft|,试判定该系统是否为线性时不变系统; 解: 设T 为此系统的运算子,由已知条件可知: yt=Tft=|ft|,以下分别判定此系统的线性和时不变性; ① 线性 1可加性不失一般性,设ft=f 1t+f 2t,则y 1t=Tf 1t=|f 1t|,y 2t=Tf 2t=|f 2t|,yt=Tft=Tf 1t+f 2t=|f 1t+f 2t|,而|f 1t|+|f 2t|≠|f 1t+f 2t|即在f 1t →y 1t 、f 2t →y 2t 前提下,不存在f 1t +f 2t →y 1t +y 2t,因此系统不具备可加性; 由此,即足以判定此系统为一非线性系统,而不需在判定系统是否具备齐次性特性; 2齐次性由已知条件,yt=Tft=|ft|,则Taft=|aft|≠a|ft|=ayt 其中a 为任一常数即在ft →yt 前提下,不存在aft →ayt,此系统不具备齐次性,由此亦可判定此系统为一非线性系统;② 时不变特性由已知条件yt=Tft=|ft|,则yt-t 0=Tft-t 0=|ft-t 0|,即由ft →yt,可推出ft-t 0→yt-t 0,因此,此系统具备时不变特性; 依据上述①、②两点,可判定此系统为一非线性时不变系统; 1-3 判定下列方程所表示系统的性质: 解:a ① 线性 1可加性由 ⎰+=tdx x f dtt df t y 0)()()(可得⎪⎩⎪⎨⎧→+=→+=⎰⎰tt t y t f dxx f dt t df t y t y t f dxx f dt t df t y 01122011111)()()()()()()()()()(即即则即在)()()()()()()()(21212211t y t y t f t f t y t f t y t f ++前提下,有、→→→,因此系统具备可加性; 2齐次性由)()(t y t f →即⎰+=tdx x f dtt df t y 0)()()(,设a 为任一常数,可得 即)()(t ay t af →,因此,此系统亦具备齐次性; 由上述1、2两点,可判定此系统为一线性系统;② 时不变性)()(t y t f → 具体表现为:⎰+=tdx x f dtt df t y 0)()()( 将方程中得ft 换成ft-t 0、yt 换成yt-t 0t 0为大于0的常数,即 ⎰-+-=-tdx t x f dtt t df t t y 0000)()()( 设τ=-0t x ,则τd dx =,因此⎰--+-=-0)()()(00t t t d f dt t t df t t y ττ也可写成⎰--+-=-0)()()(00t t t dx x f dtt t df t t y , 只有ft 在t=0时接入系统,才存在)()(00t t y t t f -→-,当ft 在t ≠0时接入系统, 不存在)()(00t t y t t f -→-,因此,此系统为一时变系统;依据上述①、②,可判定此系统为一线性时变系统; b ① 线性 1可加性 在由)2()()(3)(2)(''''-+=++t f t f t y t y t y 规定的)()(t y t f →对应关系的前提下,可得 即由)()()()()()()()(21212211t y t y t f t f t y t f t y t f ++可推出→−−→−⎭⎬⎫→→,系统满足可加性;2齐次性 由)()(t y t f →,即)2()()(3)(2)(''''-+=++t f t f t y t y t y ,两边同时乘以常数a,有 即)()(t ay t af→,因此,系统具备齐次性;由1、2可判定此系统为一线性系统;② 时不变性分别将)()(00t t f t t y --和t 0为大于0的常数代入方程)2()()(3)(2)(''''-+=++t f t f t y t y t y 左右两边,则左边=)(3)(2)(00202t t y dt t t dy dtt t y d -+-+- 而 ,)()()(000t t y dt d t t y t t d d -=-- )()]()([)(022000t t y dtd t t y t t d d t t d d -=---所以,右边=)(3)(2)(00202t t y dt t t dy dtt t y d -+-+-=左边,故系统具备时不变特性; 依据上述①、②,可判定此系统为一线性时不变系统; c ① 线性 1可加性在由式)(3)(2)(2)('''t f t y t ty t y =++规定的)()(t y t f →对应关系的前提下,可得即在)()()()(2211t y t f t y t f →→、的前提下,有式)()()()(2121t y t y t f t f +→+存在,即系统满足可加性;2齐次性 由)()(t y t f →,即)(3)(2)(2)('''t f t y t ty t y =++,两边同时乘以常数a,有)]([3)]([2)]([2)]([)(3)(2)(2)(''''''t af t ay t ay t t ay t af t ay t aty t ay =++⇒=++,即有 )()(t ay t af→,因此,系统具备齐次性;依据上述1、2,此系统为一线性系统; ② 时不变性分别将)()(00t t f t t y --和 t 0为大于0的常数代入方程)(3)(2)(2)('''t f t y t ty t y =++ 左右两边,则因此,系统是时变的;依据上述①、②,可判定此系统为一线性时变系统; d ① 线性 1可加性在由式)()()]([2't f t y t y =+规定的)()(t y t f →对应关系的前提下,可得而不是:)]()([)]()([})]'()({[2121221t f t f t y t y t y t y +=+++ 即在)()()()(2211t y t f t y t f →→、的前提下,并不存在)()()()(2121t y t y t f t f +→+因此系统不满足可加性,进而系统不具备线性特性;下面的齐次性判定过程可省略 2齐次性 由)()(t y t f →,即)()()]([2't f t y t y =+,两边同时乘以常数a,有)()()]([2't af t ay t y a =+,即式)]([)]([})]({[2't af t ay t ay =+不成立,不存在)()(t ay t af →因此,系统也不具备齐次性;单独此结论,也可判定此系统为一非线性系统; ② 时不变性分别将)()(00t t f t t y --和 t 0为大于0的常数代入方程)()()]([2't f t y t y =+ 左右两边,则即以式)()()]([2't f t y t y =+规定的)()(t y t f →关系为前提,存在)()(00t t y t t f -→-因此,系统是非时变的;依据上述①、②,可判定此系统为一线性时不变系统; 1-4 试证明方程)()()('t f t ay t y =+所描述的系统为线性系统;提示:根据线性的定义,证明满足可加性和齐次性; 证明:1证明齐次性2证明可加性由以上1、2,可知系统是线性的;1-5 试证明题1-4的系统满足时不变性;提示:将方程中的t 换为t-t 0,导出ft-t 0与yt-t 0对应; 证明:分别将)()(00t t f t t y --和 t 0为大于0的常数代入方程)()()('t f t ay t y =+ 左右两边,则即以式)()()('t f t ay t y =+规定的)()(t y t f →关系为前提,存在)()(00t t y t t f -→-因此,系统满足时不变性;1-6 试一般性的证明线性时不变系统具有微分特性;提示:利用时不变性和微分的定义推导; 证明:设线性时不变系统的激励与响应的对应关系为)()(t y t f →,则由线性可加性可得)()()()(t t y t y t t f t f ∆--→∆--因此tt t y t y t t t f t f ∆∆--→∆∆--)()()()(所以t t t y t y t t t f t f t t ∆∆--→∆∆--→∆→∆)()()()(lim lim即)()(''t y t f → 线性时不变系统具有微分特性;1-7 若有线性时不变系统的方程为)()()('t f t ay t y =+,若在非零ft 作用下其响应te t y --=1)(,试求方程)()(2)()(''t f t f t ay t y +=+的响应;解:已知tet y t f --=→1)()(,由线性关系的齐次性特性,有又由线性系统的微分特性,有 再由线性关系的可加性特性,可得。
信号与系统课后答案(西南交大)

y x (t ) = 3e −2 t − 2 e−3 t t ≥ 0 y f ( t ) = te−2 t − e−2 t + e −3 t t ≥ 0
自由响应 2 e−2 t − e −3 t 强迫响应 te−2 t 稳态响应 0
暂态响应 te−2 t + 2e −2 t − e− 3t t ≥ 0
2.19 y f ( t ) =
2.22① t 3 u( t ) ④(
②∞
③( t−
1 2
1 1 −2 t + e )u( t ) 4 4
sin t + cost 1 −t − e )u( t ) ⑤ eu (t − 3) + e t − 2 u( 3 − t ) ⑥ cos(ωt + 45° ) 2 2 1 − cosπt cosπt − 1 1 1 2.23① u( t ) + u( t − 2) ② t 2 u( t ) − ( t − 1)2 u( t − 1) π π 2 2
3.6 f (t ) =
1 − j 3 ω0 t 3 − j 2 ω 0 t 3 1 e + e + e − jω 0 t + 1 + e jω 0 t + e j 2 ω0 t + e j 3 ω 0t 2 2 2 2
3.7 f (t ) = cos( 4ω0 t + 20°) + 2 cos( 2ω0 t + 30 °) + 3 cos(ω 0 t + 10° ) + 2
p2 + p +1 2.3 H ( p ) = 3 p + 2 p2 + 3p + 2 p2 + 3 p + 2 2.4 H ( p ) = 2p2 +3p +2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-7 试计算下列结果。
(1) t δ( t - 1 )(2) ⎰∞∞--t t t d )1(δ(3) ⎰∞--0d )()3πcos(t t t δω (4) ⎰+---003d )(e t t t δ解 (1) t δ( t - 1 ) = δ( t - 1 )(2) 1d )1(d )1(=-=-⎰⎰∞∞-∞∞-t t t t t δδ(3) 21d )()3πcos(d )()3πcos(00=-=-⎰⎰∞∞--t t t t t δδω (4) 1d )(d )(e d )(e 00003003===-⎰⎰⎰+-+-+---t t t t t t t t δδδ2-5 设有题2-6图示信号f ( t ),对(a)写出f ' ( t )的表达式,对(b)写出f " ( t )的表达式,并分别画出它们的波形。
题2-6图解 (a)20,21≤≤tf ' ( t ) = δ( t - 2 ), t = 2-2δ( t - 4 ), t = 4(b) f " ( t ) = 2δ( t ) - 2δ( t - 1 ) - 2δ( t - 3 ) + 2δ( t - 4 )图p2-63-11 试求下列卷积。
(a) δ( t ) * 2(b) ε( t + 3 ) * ε( t - 5 ) (c) t e -t ⋅ε( t ) * δ' ( t )解 (a) 由δ( t )的特点,故δ( t ) * 2 = 2(b) 按定义ε( t + 3 ) * ε( t - 5 ) = ⎰∞∞---+ττετεd )5()3(t考虑到τ < -3时,ε( τ + 3 ) = 0;τ > t -5时,ε( t -τ - 5 ) = 0,故ε( t + 3 ) * ε( t - 5 ) =2,2d 53>-=⎰--t t t τ也可以利用迟延性质计算该卷积。
因为ε( t ) * ε( t ) = t ε( t )f 1( t - t 1 ) * f 2( t - t 2 ) = f ( t -t 1 -t 2 )故对本题,有ε( t + 3 ) * ε( t - 5 ) = ( t + 3 - 5 )ε( t + 3 - 5 ) = ( t - 2 )ε( t - 2 )两种方法结果一致。
(c) t e -t ⋅ε( t ) * δ' ( t ) = [t e -t ε( t )]' = ( e -t - t e -t )ε( t )3-13 试求下列卷积。
(a) )()()()e 1(2t t t t εδε*'*--(b) )](e [d d )(e 3t tt t t δε--*解 (a)因为)()()()(t t t t δεεδ='=*',故)()e 1()()()e 1()()()()e 1(222t t t t t t t t t εδεεδε----=*-=*'*-(b)因为)()(e t t t δδ=-,故tt tt t t t t tt 333e 3)()()(e )](e [d d )(e -----='*=*δδεδε 4-3 试求下列信号的频谱函数。
(1) t t f 2e )(-=(2) )(sin e )(0t t t f at εω⋅=- 原题(a>0)解 (1)⎰⎰⎰∞--∞--∞∞--+==0j 20j 2j d e e d e e d e )()(t t t t f F t t t t t ωωωω244j 21j 21ωωω+=++-=(2)⎰⎰∞---∞∞---⋅==0j j j j d )e e (e 2j1e d e )()(00t t t f F t t t at tωωωωω ⎰∞-----⋅-⋅=0)j (j )j (j ]d e e e [e 2j 100t t a t t a t ωωωω ⎥⎦⎤⎢⎣⎡++--+=00j )j (1j )j (12j 1ωωαωωα 22022000)j ()j (j 22j 1ωωαωωωαω++=++⋅=4-10 试求信号f ( t ) = 1 + 2cos t + 3cos3t 的傅里叶变换。
解 因为1 ↔ 2πδ(ω)2cos t ↔ 2π[δ(ω - 1) + δ(ω + 1) ] 3cos3t ↔ 3π[δ(ω - 3) + δ(ω + 3) ]故有F (ω ) = 2π[δ(ω) + δ(ω - 1) + δ(ω + 1) ] + 3π[δ(ω - 3) + δ(ω + 3) ] 5-1 求下列函数的单边拉氏变换。
(1) t --e 2 (2) t t 3e )(-+δ (3) t t cos e 2-解 (1) )1(2112d e )e 2()(0++=+-=-=⎰∞--s s s s st s F st t(2) 311d e ]e )([)(03++=+=⎰∞---s t t s F st t δ (3)⎰⎰∞---∞--⋅+==02j j 02d e e )e (e 21d e )cos (e )(t t t s F st t t tst t 1)2(2j 21j 21212+++=⎪⎪⎭⎫ ⎝⎛+++-+=s s s s5-9 用部分分式法求下列象函数的拉氏反变换。
(1) 651)(2+++=s s s s F(2) )1(22)(22+++=s s s s s F (3) 231)(2++=s s s F (4)2)2(4)(+=s s s F解 (1)32)3)(2(1651)(212+++=+++=+++=s k s k s s s s s s s F1)()2(21-=+=-=s s F s k 2)()3(32=+=-=s s F s k故有3221)(+++-=s s s F 所以)()e 2e ()(32t t f t t ε--+-=(2) 1)1(22)(222+++=+++=s CBs s A s s s s s F 可得2)(0===s s F s A又Cs Bs A As s s +++=++22222可得B = 0,C = 1112)(2++=s ss F所以)()sin 2()(t t t f ε+=(3)21)2)(1(1231)(212+++=++=++=s k s k s s s s s F 1)()1(11=+=-=s s F s k 1)()2(22-=+=-=s s F s k故有2111)(+-++=s s s F故)()e e ()(2t t f t t ε---=(4) 2)2()2(4)(1221112++++=+=s k s k s k s s s F 故1)(01===s s F s k 24)()2(22211-==+=-=-=s s s s F s k 1)4(d d )]()2[(d d 22212-==+=-=-=s s s s s F s s k故有2)2(2211)(+-+-+=s s s s F所以)()e 2e 1()(22t t t f t t ε----=5-10 求下列象函数的拉氏反变换。
(类似) (1) s s F --=e 1)( (2) 2e 1)(+-=-s s F s(3))e 1(e 1)(2sss s F ----=解 (1) )1()()(--=t t t f δδ (2) )1(e )(e )()1(22--=---t t t f t t εε (3)+---+---+--=)5()2()3()1()2()()(t t t t t t t f εεεεεε5-13 设某LTI 系统的微分方程为)(3)(6)(5)(t f t y t y t y =+'+''试求其冲激响应和阶跃响应。
解 对方程取拉氏变换,得系统函数)3)(2(3653)(2++=++=s s s s s H当f ( t ) = δ( t )时,F ( s ) =1,得)3)(2(3)()(++==s s s H s Y从而0,e 3e 3)(32≥-=--t t h t t当f ( t ) = ε( t )时,ss F 1)(=,得)3)(2(3)(1)(++==s s s s H s s Y3125.15.0+++-+=s s s 故得0,e e 5.15.0)()(32≥+-==--t t s t y t t6-15 试判定下列系统的稳定性。
(1) 681)(2+++=s s s s H (2) 23413)(23+-++=s s s s s H(3))34)(1(42)(2++++=s s s s s H解 (1) 因H ( s )分母多项式各项系数均为正,故稳定。
(2) 因H ( s )分母多项式有负系数,故不稳定。
(3) 因)3)(1)(1(42)34)(1(42)(2++++=++++=s s s s s s s s s H 其极点均在左半平面,故系统稳定。
7-1 试画出下列离散信号的图形。
(a) )()21()(1n n f n ε=(b) )2()(2n n f -=ε(c) )2()(3n n f --=ε (d) )()5.01(2)(4n n f n ε-=解 各信号的图形分别如图p7-1所示。
图p7-17-2 试画出下列序列的图形。
(a) )6()2()(1---=n n n f εε(b) )()2()(2n n n f -++=εε(c) )]5()([)()(3--⋅=n n n n n f εεε(d) )4()3(2)2(2)1()()(4-+-+-+-+=n n n n n n f δδδδδ解 各序列的图形分别如图p7-2所示。
图p7-27-4 设有离散系统的差分方程为)1()(4)2(3)1(4)(-+=-+-+n f n f n y n y n y试画出其时域模拟图。
解 原方程可以写为)1()(4)2(3)1(4)(-++----=n f n f n y n y n y从而可得时域模拟图p7-4,图中D 为单位延时(位移)器。
图p7-47-6 设有序列f 1( n )和f 2( n ),如图7-6所示,试用二种方法求二者的卷积。
D DD题7-6图解 方法一:用“乘法”2 1.5 1 1 1.5 2⨯ 1 1 1 12 1.5 1 1 1.5 22 1.5 1 1 1.5 2 2 1.5 1 1 1.5 2 2 1.5 1 1 1.5 22 3.5 4.5 5.5 5 5.5 4.5 3.5 2即有}2,5.3,5.4,5.5,5,5.5,5.4,5.3,2{)()(021=↑=*n n f n f方法二:用单位序列表示各函数后卷积。
