中考二次函数压轴题解题通法(课堂PPT)
合集下载
中考二次函数压轴题PPT

∴ 点 F 到 AC 的距离为 9 × = , 4
又∵ AC=
=3 ,
∴ △ ACE 的最大面积=×3 × = ,此时 E 点坐标为( 5 ,﹣ 3 ).
24
9
7、(2013•曲靖压轴题)如图,在平面直角坐标系 xOy 中,直线 y=x+4 与坐标轴分别交 于 A、B 两点,过 A、B 两点的抛物线为 y=﹣x2+bx+c.点 D 为线段 AB 上一动点,过 点 D 作 CD⊥x 轴于点 C,交抛物线于点 E. (1)求抛物线的解析式. (2)当 DE=4 时,求四边形 CAEB 的面积. (3)连接 BE,是否存在点 D,使得△ DBE 和△ DAC 相似?若存在,求此点 D 坐标; 若不存在,说明理由.
解得
,
所以,直线 AC 的解析式为 y=x﹣1,
∵ y=x2﹣4x+3=(x﹣2)2﹣1,
∴ 抛物线的对称轴为直线 x=2,
当 x=2 时,y=2﹣1=1,
∴ 抛物线对称轴上存在点 D(2,1),使△ BCD 的周长最小;
8
(3)如图,设过点 E 与直线 AC 平行线的直线为 y=x+m,联立, 消掉 y 得,x2﹣5x+3﹣m=0, △ =(﹣5)2﹣4×1×(3﹣m)=0,
7
解:(1)∵ 抛物线 y=ax2+bx+3 经过点 A(1,0),点 C(4,3),
∴
,解得
,
所以,抛物线的解析式为 y=x2﹣4x+3;
(2)∵ 点 A、B 关于对称轴对称, ∴ 点 D 为 AC 与对称轴的交点时△ BCD 的周长最小, 设直线 AC 的解析式为 y=kx+b(k≠0),则,
S 四边形 CAEB=S△ ACE+S 梯形 OCEB﹣S△ BCO= ×2×6+ (6+4)×2﹣ ×2×4=12.
人教部初三九年级数学下册 二次函数的五大基本题型 名师教学PPT课件

可推出: x1+x2=x3+x4; y1+y2=y3+y4.并解方程.
3、检验点有没有重合或共线
4、写出坐标
如图,抛物线y=x2-2x-3与x轴交于点A(-1,0),B(3,0).点E在其对称轴
上直线x=1上,点F在抛物线上,且以B、A、F、E四点为顶点的四
边形为平行四边形,求点F的坐标。
解:设点F(x,x2-2x-3),E(1,h),已知A(-1,0) B(3,0)
C
2、理想状态以直角顶点讨论三次,并解方程
①A为直角顶点, 则AC2 +AP2=CP2;
②C为直角顶点,则AC2+CP2=AP2:
③P为直角顶点,则CP2+ AP2=AC2
3、检验点有没有重合或共线
4、写出坐标
如图,抛物线y=x2-2x-3与x轴交于点A(-1,0),B(3,0),与y轴交于点C, 对称轴直线x=1上是否存在点N,使得△ACN是直角三角形。若存在 ,请求出点M的坐标,若不存在,请说明理由。
解方程x2-2x-3=3(x-3)得m=3(含去),m=2,此时P点坐标为(2,0);
解方程x2-2x-3=-3(x-3)得m=3(含去),m=-4,此时P点坐标为(-4,0);
综上所述,P点坐标为(-2/3,0)(-4/3,0)或( 2,0)或(-4,0).
已知点Q是抛物线y=x2-2x-3上一个动点,作PQ⊥x轴于P,是否存
在一点P,使得△QBP与 △AOC相似?若存在,求出点P的坐标,若
不能,请说明理由。
解:设点P(x,0)Q(x,x2-2x-3)
则PQ=丨x2-2x-3丨,BP=丨x-3丨,
∵∠QPB=∠AOC
当PQ/OA=BP/OC时,△PQB∽△OAC, 即丨x2-2x-3丨/1=丨x-3丨/3
3、检验点有没有重合或共线
4、写出坐标
如图,抛物线y=x2-2x-3与x轴交于点A(-1,0),B(3,0).点E在其对称轴
上直线x=1上,点F在抛物线上,且以B、A、F、E四点为顶点的四
边形为平行四边形,求点F的坐标。
解:设点F(x,x2-2x-3),E(1,h),已知A(-1,0) B(3,0)
C
2、理想状态以直角顶点讨论三次,并解方程
①A为直角顶点, 则AC2 +AP2=CP2;
②C为直角顶点,则AC2+CP2=AP2:
③P为直角顶点,则CP2+ AP2=AC2
3、检验点有没有重合或共线
4、写出坐标
如图,抛物线y=x2-2x-3与x轴交于点A(-1,0),B(3,0),与y轴交于点C, 对称轴直线x=1上是否存在点N,使得△ACN是直角三角形。若存在 ,请求出点M的坐标,若不存在,请说明理由。
解方程x2-2x-3=3(x-3)得m=3(含去),m=2,此时P点坐标为(2,0);
解方程x2-2x-3=-3(x-3)得m=3(含去),m=-4,此时P点坐标为(-4,0);
综上所述,P点坐标为(-2/3,0)(-4/3,0)或( 2,0)或(-4,0).
已知点Q是抛物线y=x2-2x-3上一个动点,作PQ⊥x轴于P,是否存
在一点P,使得△QBP与 △AOC相似?若存在,求出点P的坐标,若
不能,请说明理由。
解:设点P(x,0)Q(x,x2-2x-3)
则PQ=丨x2-2x-3丨,BP=丨x-3丨,
∵∠QPB=∠AOC
当PQ/OA=BP/OC时,△PQB∽△OAC, 即丨x2-2x-3丨/1=丨x-3丨/3
中考二次函数压轴题解题通法PPT课件

6
方程总有固定根问题
• 可以通过解方程的方法求出该固定根
已知关于的方程(mx2 3(m 1)x 2m 3 0 为实数),
求证:无论为何值,方程总有一个固定的根。
解:当 m 0 时, x 1
x1
当 m 0 时,
2
3 m
、x2
1
m3
2
0
,x
3m
1
2m
,
综上所述无论:m 为何值,方程总有一个固
19
2、“平行于y轴的动线段长度的最大值”的问题
2020/3/23
20
3、求一个已知点关于一条已知直线的对称点的坐标 问题Leabharlann 2020/3/2321
4、“抛物线上是否存在一点,使之到定直线的距离 最大”的问题
2020/3/23
22
5.常数问题
2020/3/23
23
6.“在定直线(常为抛物线的对称轴,或x轴或y轴或其它的定 直线)上是否存在一点,使之到两定点的距离之和最小”的 问题
2020/3/23
2
两点间的距离公式
AB yA yB 2 xA xB 2
2020/3/23
3
中点坐标
• 线段的中点的坐标为:
xA xB ,yA yB 2 2
2020/3/23
4
一元二次方程有整数根问题
解题步骤如下:① 用和参数的其他要求确定
参数的取值范围 ② 解方程,求出方程的根
2020/3/23
28
10、“定四边形面积的求解”问题
• 有两种常见解决的方案: • 方案(一):连接一条对角线,分成两个三角形面积之和; • 方案(二):过不在x轴或y轴上的四边形的一个顶点,向
中考复习专题:二次函数与几何的综合题PPT课件

10
即y=∴∴13x–二23–次=a函83(0x数+–13的).(0解–析9),式解为4分得y=a=13(x3+1,)(x–9),
(2011资阳)已知抛物线C:y=ax2+bx+c(a<0)过原点,与x 轴的另一个交点为B(4,0),A为抛物线C的顶点.
(1) 如图14-1,若∠AOB=60°,求抛物线C的解析式;(3分)
2008年资阳24.(本小题满分12分)如图10,已知点A的坐标是(-1,0),
点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、 BC,过A、B、C三点作抛物线. (1)求抛物线的解析式;
解:(1) ∵以AB为直径作⊙O′,交y轴的负半轴于点C,
∴∠OCA+∠OCB=90°,
3.联立函数表达式.
互转化的基础是:点坐标与线段长。 一般解题思路是:
解析式方程组的解是图像交点坐标
(1)已知点坐标 线段长,线段长 点
坐标;
(2)用待定系数法求函数解析式;
(3)解析式 点坐标 线段长 面积
及其它。
(压轴题07) 点P为抛物线 y x2 2mx m2 (m为常数, )上任m一点0,将抛物线绕顶点G逆时针旋转90度后得到的 新图象与y轴交于A、B两点(点A在点B的上方),点Q 为点P旋转后的对应点.
(2) (3分) 求点D的坐标;
三垂直:横平竖直
F
O'D=O'A=2,DC=AC=4 ∆DO'F∽∆CDM,类似比1:2 设O'F=a,DF=b。 则DM=2a,CM=2b。 所以,2a+b=4.且2+a=2b。
DN=DF-FN=3/5
N
中考二次函数复习课件ppt(精选文档)

(2)、图象的顶点(2,3), 且经过点(3,1) ;
__________
1、已知抛物线经过三点(1,3)、 (-1,-1) 、 (2,-7),设抛物线解析式为____________+c (a≠0)
(2)对称轴位置由 a和b 决定 ∵抛物线经过点B(4,0)
答:横向活动范围是6米。 ∴抛物线的顶点纵坐标y=2
交点式 y=a(x-x1)(x-x2) (a≠0)
6–
3–
-2 -1
12
练习 根据下列条件,求二次函数的解析式。
(1)、图象经过(-1,3), (1,3) , (2,6) 三点;
(2)、图象的顶点(2,3), 且经过点(3,1) ; (3)、图象经过(0,0), (12,0) ,且最高点 的纵坐标是3 。
2
y
所示,则a、b、c 、 的符号为( C) 设抛物线解析式为y=a(x-h)+k
(3)、图象经过(0,0), (12,0) ,且最高点 二次函数的图象及性质
的△纵坐标是3 。
又∵抛物A线、的顶a点>在直0线,yb=x=+1上0,c>0,△>0 B、a<0,b>0,c<0,△=0
∴a (3-1)2+2=-6 ∴a=-2
顶点式 y=a(x-h) +k (a≠0)
(4)与x轴的交点位置由 △ 决定 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
__________
A、a<0,b>0,c>0 B、a<0,b>0,c<0
(3)、图象经过(0,0), (12,0) ,且最高点
的纵坐标是3 。
抛物线
__________
1、已知抛物线经过三点(1,3)、 (-1,-1) 、 (2,-7),设抛物线解析式为____________+c (a≠0)
(2)对称轴位置由 a和b 决定 ∵抛物线经过点B(4,0)
答:横向活动范围是6米。 ∴抛物线的顶点纵坐标y=2
交点式 y=a(x-x1)(x-x2) (a≠0)
6–
3–
-2 -1
12
练习 根据下列条件,求二次函数的解析式。
(1)、图象经过(-1,3), (1,3) , (2,6) 三点;
(2)、图象的顶点(2,3), 且经过点(3,1) ; (3)、图象经过(0,0), (12,0) ,且最高点 的纵坐标是3 。
2
y
所示,则a、b、c 、 的符号为( C) 设抛物线解析式为y=a(x-h)+k
(3)、图象经过(0,0), (12,0) ,且最高点 二次函数的图象及性质
的△纵坐标是3 。
又∵抛物A线、的顶a点>在直0线,yb=x=+1上0,c>0,△>0 B、a<0,b>0,c<0,△=0
∴a (3-1)2+2=-6 ∴a=-2
顶点式 y=a(x-h) +k (a≠0)
(4)与x轴的交点位置由 △ 决定 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
__________
A、a<0,b>0,c>0 B、a<0,b>0,c<0
(3)、图象经过(0,0), (12,0) ,且最高点
的纵坐标是3 。
抛物线
中考二次函数复习课件【优质PPT】

x=2,y最大值=3
练习 根据下列条件,求二次函数的解析式。
(1)、图象经过(-1,3), (1,3) , (2,6) 三点;
(2)、图象的顶点(2,3), 且经过点(3,1) ;
(3)、图象经过(0,0), (12,0) ,且最高点
的纵坐标是3 。
顶点(6,3)
解法一设解析式为y=a(x-0)(x-12)
令y=1.4,则-0.2x2+3.2=1.4
B x解得x=-3或x=3 ∴M(-3,1.4),N(3,1.4) ∴MN=6 20 答:横向活动范围是6米。
练习、已知二次函数y=ax2-5x+c的图象如图。
(1)、当x为何值时,y随x的增大而增大; (2)、当x为何值时,y<0。 (3)、求它的解析式和顶点坐标y ;
(3)、图象经过(0,0), (12,0) ,且最高点 的纵坐标是3 。
2021/10/10
14
5一.待般定式系数y法=a求x解2+b析x式+c (a≠0) 顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
6–
3–
-2 -1
12
练习 根据下列条件,求二次函数的解析式。
二次函数的图象是一条 对称轴平行于 y 轴.
抛物线
,它是 轴
对称图形,其
2021/10/10
2
y 3.二次函数的图象及性质y
0
x
0
x
抛物线 顶点坐标 对称轴 开口方向
y=ax2+bx+c(a>0)
b 2a
,
4acb2 4a
直线x b
2a
二次函数阶段专题复习课件ppt

详细描述
根据二次函数的单调 性,判断函数在某个 区间的单调性;
根据二次函数的奇偶 性,判断函数的奇偶 性并求出函数的对称 轴;
根据二次函数的周期 性,求函数的周期并 观察图像的变化规律 。
综合练习题及答案
详细描述
根据二次函数与实际问题的综合 应用,解决实际问题并求出最优 解;
总结词:二次函数与其他知识点 的综合应用
求二次函数的最大值或最小值的方法是:先确定函数的对称 轴,再根据a的符号确定最大值或最小值的坐标,最后代入函 数解析式计算最大值或最小值。
02
知识点详解
二次函数的表达式及求解
表达式
$y = ax^{2} + bx + c$
求法
通过已知的三个点或顶点及对称轴可求得 $a$、$b$、$c$的值,进而得到二次函数 的表达式
2023
二次函数阶段专题复习课 件ppt
目 录
• 知识点概述 • 知识点详解 • 经典例题解析 • 易错点及应对策略 • 练习题及答案
01
知识点概述
什么是二次函数
1
二次函数是指形如`y = ax^2 + bx + c`(其中a 、b、c为常数,且a≠0)的函数。
2
二次函数的图像是一个抛物线,其顶点坐标为(b/2a,c-b^2/4a),对称轴为x=-b/2a。
二次函数与实际问题的结合
要点一
总结词
要点二
详细描述
了解二次函数与实际问题的联系,能 够建立数学模型并解决实际问题。
二次函数与实际问题结合广泛,如最 优化问题、经济问题、物理问题等。 通过对实际问题的分析,可以更好地 理解二次函数的应用价值。
要点三
示例题目
中考数学复习---二次函数考点归纳与典型例题讲解PPT课件

【解析】解:(1)设 y 与 x 之间的函数关系式为 y kx b ( k 0 ),根据题意,得:
12k 14k
b b
90 80
,解得
k b
5 150
,∴
y
与
x
之间的函数关系式为
y
5x
150(10≤x≤15,
且 x 为整数);
(2)根据题意,得:w (x 10)(5x 150) 5x2 200x 1500 5(x 20)2 500 ,
舍去);
Байду номын сангаас
函数的应用
(2)∵ a 3 ,∴ C(0, 3) ,∵ SABP SABC .∴ P 点的纵坐标为±3,
把 y 3 代入 y x2 2x 3 得 x2 2x 3 3 ,解得 x 0 或 x 2 ,
把 y 3 代入 y x2 2x 3 得 x2 2x 3 3 ,解得 x 1 7 或 x 1 7 , ∴ P 点的坐标为 (2,3) 或 (1 7, 3) 或 (1 7, 3) .
得 810 40x=0 ,解得 x 20.25 .∴排队人数最多时是 490 人,全部考生都完成体温检测
需要 20.25 分钟.
(3)设从一开始就应该增加 m 个检测点,根据题意,得12 20(m 2) 810 ,解得 m 1 3 . 8
∵ m 是整数,∴ m 1 3 的最小整数是 2.∴一开始就应该至少增加 2 个检测点. 8
【点睛】此题主要考查二次函数的图像与性质,解题的关键是熟知待定系数法的应用.
本课结束
2、函数动点问题 (1)函数压轴题主要分为两大类:一是动点函数图像问题;二是与动点、存在点、相似等有关的二次函数 综合题. (2)解答动点函数图像问题,要把问题拆分,分清动点在不同位置运动或不同时间段运动时对应的函数表 达式,进而确定函数图像;解答二次函数综合题,要把大题拆分,做到大题小做,逐步分析求解,最后汇总 成最终答案. (3)解决二次函数动点问题,首先要明确动点在哪条直线或抛物线上运动,运动速度是多少,结合直线或 抛物线的表达式设出动点的坐标或表示出与动点有关的线段长度,最后结合题干中与动点有关的条件进行计 算.
【全文】中考数学专题《二次函数》复习课件(共54张PPT)

即: y=-2x2+4x
例2:某工厂大门是一抛物线水泥建筑物,如图所示,大门底部 宽AB=4m,顶点C离地面高度为4.4m,现有一辆满载货物的汽 车欲通过大门,货物顶部距地面2.8m,装货宽度为2.4米,请判 断这辆车能够顺利通过大门?(请用三种不同的方法解决)
y=ax²
y x
(-2,-4.4)
(2,-4.4)
y
o
x
6.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,
那么这个二次函数图象的顶点必在第 四象限
y 先根据题目的要求画出函数的草图,再根据 图象以及性质确定结果(数形结合的思想)
x
7.已知二次函数的图像如图所示,下列结论: ⑴a+b+c=0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a 其中正确的结论的个数是( ) A 1个 B 2个 C 3个 D 4个 D
写出满足此条件的抛物线的解析式.
解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
a=1或-1 又顶点在直线x=1上,且顶点到x轴的距离为5,
解:∵二次函数的最大值是2 ∴抛物线的顶点纵坐标为2 又∵抛物线的顶点在直线y=x+1上 ∴当y=2时,x=1 ∴顶点坐标为( 1 , 2) ∴设二次函数的解析式为y=a(x-1)2+2 又∵图象经过点(3,-6) ∴-6=a (3-1)2+2 ∴a=-2 ∴二次函数的解析式为y=-2(x-1)2+2
练习: 1、二次函数y=ax2+bx+c(a≠0)的图象如图
B 所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0 C、a<0,b<0,c>0 D、a<0,b<0,c<0
例2:某工厂大门是一抛物线水泥建筑物,如图所示,大门底部 宽AB=4m,顶点C离地面高度为4.4m,现有一辆满载货物的汽 车欲通过大门,货物顶部距地面2.8m,装货宽度为2.4米,请判 断这辆车能够顺利通过大门?(请用三种不同的方法解决)
y=ax²
y x
(-2,-4.4)
(2,-4.4)
y
o
x
6.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,
那么这个二次函数图象的顶点必在第 四象限
y 先根据题目的要求画出函数的草图,再根据 图象以及性质确定结果(数形结合的思想)
x
7.已知二次函数的图像如图所示,下列结论: ⑴a+b+c=0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a 其中正确的结论的个数是( ) A 1个 B 2个 C 3个 D 4个 D
写出满足此条件的抛物线的解析式.
解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
a=1或-1 又顶点在直线x=1上,且顶点到x轴的距离为5,
解:∵二次函数的最大值是2 ∴抛物线的顶点纵坐标为2 又∵抛物线的顶点在直线y=x+1上 ∴当y=2时,x=1 ∴顶点坐标为( 1 , 2) ∴设二次函数的解析式为y=a(x-1)2+2 又∵图象经过点(3,-6) ∴-6=a (3-1)2+2 ∴a=-2 ∴二次函数的解析式为y=-2(x-1)2+2
练习: 1、二次函数y=ax2+bx+c(a≠0)的图象如图
B 所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0 C、a<0,b<0,c>0 D、a<0,b<0,c<0
23中考二次函数压轴题解题通法省公开课获奖课件市赛课比赛一等奖课件

(2)1.已知在对称轴上存在一点P,使得 △PBC旳周长最 小.祈求出点P旳坐标. 2.若点D 是线段OC 上旳一种动点(不与点O、点C重 叠).过点D作 DE//PC交x 轴于点 E,连接PD 、PE .设
CD 旳长为m ,△PDE 旳面积为S .求S 与m 之间旳函数 关系式.试阐明S是否存在最大值,若存在,祈求出最大 值;若不存在,请阐明理由.
ቤተ መጻሕፍቲ ባይዱ1 2
MN
•
AD
割补法求面积
D(x3,y1)
F(x2,y1)
E(x2,y2)
S ABC S CDFE S ADC S AFB S BCE
X=-1 y
求△PBC旳 周长最小值
A (-3,0)
O
x
B(1,0)
•P
C(0,-2)
X=-1 y
y
2 x2
ac 3
x 1
A (-3,0)
O
• (3)存在,点M旳坐标为(1,),(1,-),(1,1),(1,0). • 理由如下: • ∵抛物线旳对称轴为: x=1,∴设M(1,m). • ∵A(-1,0)、C(0,3), • 根据勾股定理可得MA 2=m 2+4,MC 2=m 2-6m+10,AC 2=10. • ①若MA=MC,则MA 2=MC 2,得:m 2+4=m 2-6m+10,得:m=
图41-4
考向互动探究
第41课时┃ 二次函数与几何综合类存在性问题
解 (1)∵A(4,0),B(-1,0),
∴AB=5,半径是 PC=PB=PA=52,∴OP=52-1=32, 在△CPO 中,由勾股定理得:OC= CP2-OP2=2, ∴C(0,2). 设经过 A、B、C 三点的抛物线的解析式是 y=a(x-4)(x+1), 把 C(0,2)代入得:2=a(0-4)(0+1), ∴a=-12,∴y=-12(x-4)(x+1)=-12x2+32x+2, 故经过 A、B、C 三点的抛物线所对应的函数解析式是 y=-12x2+ 32x+2.
CD 旳长为m ,△PDE 旳面积为S .求S 与m 之间旳函数 关系式.试阐明S是否存在最大值,若存在,祈求出最大 值;若不存在,请阐明理由.
ቤተ መጻሕፍቲ ባይዱ1 2
MN
•
AD
割补法求面积
D(x3,y1)
F(x2,y1)
E(x2,y2)
S ABC S CDFE S ADC S AFB S BCE
X=-1 y
求△PBC旳 周长最小值
A (-3,0)
O
x
B(1,0)
•P
C(0,-2)
X=-1 y
y
2 x2
ac 3
x 1
A (-3,0)
O
• (3)存在,点M旳坐标为(1,),(1,-),(1,1),(1,0). • 理由如下: • ∵抛物线旳对称轴为: x=1,∴设M(1,m). • ∵A(-1,0)、C(0,3), • 根据勾股定理可得MA 2=m 2+4,MC 2=m 2-6m+10,AC 2=10. • ①若MA=MC,则MA 2=MC 2,得:m 2+4=m 2-6m+10,得:m=
图41-4
考向互动探究
第41课时┃ 二次函数与几何综合类存在性问题
解 (1)∵A(4,0),B(-1,0),
∴AB=5,半径是 PC=PB=PA=52,∴OP=52-1=32, 在△CPO 中,由勾股定理得:OC= CP2-OP2=2, ∴C(0,2). 设经过 A、B、C 三点的抛物线的解析式是 y=a(x-4)(x+1), 把 C(0,2)代入得:2=a(0-4)(0+1), ∴a=-12,∴y=-12(x-4)(x+1)=-12x2+32x+2, 故经过 A、B、C 三点的抛物线所对应的函数解析式是 y=-12x2+ 32x+2.
中考数学专题《二次函数》复习课件(共54张PPT)

当x b 时, y最小值为 4ac b2
2a
4a
y=ax2+bx+c(a<0)
b 2a
,
4ac 4a
b2
直线x b
2a
由a,b和c的符号确定
a<0,开口向下
在对称轴的左侧,y随着x的增大而增大. 在对 称轴的右侧, y随着x的增大而减小.
当x b 时, y最大值为 4ac b2
2a
例1: 已知二次函数 y 1 x2 x 3
2
2
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两
点,求C,A,B的坐标。
(3)x为何值时,y随的增大而减少,x为何值时,
y有最大(小)值,这个最大(小)值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
写出满足此条件的抛物线的解析式.
解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
a=1或-1 又顶点在直线x=1上,且顶点到x轴的距离为5,
二次函数复习
二次函数知识点:
• 1、二次函数的定义 • 2、二次函数的图像及性质 • 3、求解析式的三种方法 • 4、a,b,c及相关符号的确定 • 5、抛物线的平移 • 6、二次函数与一元二次方程的关系 • 7、二次函数的应用题 • 8、二次函数的综合运用
1、二次函数的定义
• 定义: y=ax² + bx + c ( a 、 b 、 c 是常数, a ≠ 0)
a= ___. -2
2、二次函数的图像及性质
y
y
0
x
0
x
抛物线 顶点坐标 对称轴
中考二次函数压轴题省名师优质课赛课获奖课件市赛课一等奖课件
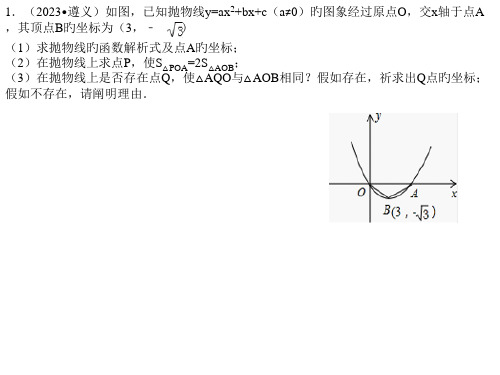
1.(2023•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)旳图象经过原点O,交x轴于点A ,其顶点B旳坐标为(3,﹣ )
(1)求抛物线旳函数解析式及点A旳坐标; (2)在抛物线上求点P,使S△POA=2S△AOB; (3)在抛物线上是否存在点Q,使△AQO与△AOB相同?假如存在,祈求出Q点旳坐标; 假如不存在,请阐明理由.
(1)请观察题中旳表格和图象,用所学过旳一次函数、反百分比函数或二次函数旳有关知识,分别
直接写出y1,y2与x之间旳函数关系式; (2)请你求出该企业去年哪个月用于污水处理旳费用W(元)最多,并求出这个最多费用;
(3)今年以来,因为自建污水处理设备旳全方面运营,该企业决定扩大产能并将全部污水全部本身
5.(2023•重庆)企业旳污水处理有两种方式,一种是输送到污水厂进行集中处理,另一 种是经过企业旳本身设备进行处理.某企业去年每月旳污水量均为12023吨,因为污水厂
处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同步进 行.1至6月,该企业向污水厂输送旳污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间 满足旳函数关系如下表:
4.(2023•株洲)如图,一次函数
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点. (1)求这个抛物线旳解析式; (2)作垂直x轴旳直线x=t,在第一象限交直线AB于M,交这个抛 物线于N.求当t取何值时,MN有最大值?最大值是多少? (3)在(2)旳情况下,以A、M、N、D为顶点作平行四边形,求 第四个顶点D旳坐标.
7.(2023•湛江)如图,在平面直角坐标系中,直角三角形AOB旳顶点A、B分别落在坐 标轴上.O为原点,点A旳坐标为(6,0),点B旳坐标为(0,8).动点M从点O出发. 沿OA向终点A以每秒1个单位旳速度运动,同步动点N从点A出发,沿AB向终点B以每秒 个 单位旳速度运动.当一种动点到达终点时,另一种动点也随之停止运动,设动点M、N 运动旳时间为t秒(t>0).(1)当t=3秒时.直接写出点N旳坐标,并求出经过O、A、 N三点旳抛物线旳解析式;
(1)求抛物线旳函数解析式及点A旳坐标; (2)在抛物线上求点P,使S△POA=2S△AOB; (3)在抛物线上是否存在点Q,使△AQO与△AOB相同?假如存在,祈求出Q点旳坐标; 假如不存在,请阐明理由.
(1)请观察题中旳表格和图象,用所学过旳一次函数、反百分比函数或二次函数旳有关知识,分别
直接写出y1,y2与x之间旳函数关系式; (2)请你求出该企业去年哪个月用于污水处理旳费用W(元)最多,并求出这个最多费用;
(3)今年以来,因为自建污水处理设备旳全方面运营,该企业决定扩大产能并将全部污水全部本身
5.(2023•重庆)企业旳污水处理有两种方式,一种是输送到污水厂进行集中处理,另一 种是经过企业旳本身设备进行处理.某企业去年每月旳污水量均为12023吨,因为污水厂
处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同步进 行.1至6月,该企业向污水厂输送旳污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间 满足旳函数关系如下表:
4.(2023•株洲)如图,一次函数
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点. (1)求这个抛物线旳解析式; (2)作垂直x轴旳直线x=t,在第一象限交直线AB于M,交这个抛 物线于N.求当t取何值时,MN有最大值?最大值是多少? (3)在(2)旳情况下,以A、M、N、D为顶点作平行四边形,求 第四个顶点D旳坐标.
7.(2023•湛江)如图,在平面直角坐标系中,直角三角形AOB旳顶点A、B分别落在坐 标轴上.O为原点,点A旳坐标为(6,0),点B旳坐标为(0,8).动点M从点O出发. 沿OA向终点A以每秒1个单位旳速度运动,同步动点N从点A出发,沿AB向终点B以每秒 个 单位旳速度运动.当一种动点到达终点时,另一种动点也随之停止运动,设动点M、N 运动旳时间为t秒(t>0).(1)当t=3秒时.直接写出点N旳坐标,并求出经过O、A、 N三点旳抛物线旳解析式;
2019【中考语文】初三九年级数学复习课件:解答题专题—二次函数压轴题(一)(共28张PPT)

时与抛物线的交点坐标即为所求.
解:存在. ∵抛物线的解析式y=-x2+2x+3=-(x-1)2+4, ∴P(1,4),如解图②,过点P且与BC平行的直线与抛物线的交
点Q1,即为所求Q点之一,
∴可得直线BC为y=-x+3, ∴过点P且与BC平行的直线l1为y=-x+b,将 点P(1,4)代入得l1的解析式为y=-x+5, y=-x+5 x2=1 x1=2 由 y=-x2+2x+3 ,解得 , , 例2题解图② y2=4 y1=3 ∴点Q1的坐标为(2,3).
PD,PF的长,进而求出即可;(3)根据题意当P,E,F三点
共线时,PE+PF最小,进而得出P点坐标以及利用△PDE的 面积可以等于4到13之间的所有整数,在面积为12时,a的 值有两个,进而得出答案. 【自主解答】
1 2 (1)抛物线的解析式为y=- 8 x +8.
(2)猜想正确.
1 2 理由:设P(x,- x +8), 8 1 则PF=8-(- x2+8)= 1 x2. 8 8
∴“好点”共有11个.
二、典例精讲
类型二 面积问题
例2:如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0), B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交
于点P、与直线BC相交于点M,连接PB.
(1)求该抛物线的解析式; (2)在(1)中位于第一象限内的抛物线上是否存在点D,使得 △BCD的面积最大?若存在,求出D点坐标及△BCD面积 的最大值;若不存在,请说明理由;
∵直线PM为直线x=1,直线BC的解析式为y=-x+3, ∴M(1,2). 设PM与x轴交于E点, ∵PM=EM=2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A (1)如图,直线 l1 l2 ,点 在l2 上,分别在 l2 、 l1上确定
N 两点M、 ,使得AM MN之和最小。
2020/8/4
9
路径最值问题
2020/8/4
10
路径最值问题
2020/8/4
11
在平面直角坐标系中求面积的方法
• 直接用公式、割补法
2020/8/4
12
函数的交点问题
2020/8/4
2020/8/4
29
11.“两个三角形相似”的问题
• 两个定三角形是否相似: • 已知有一个角相等的情形:运用两点间的距离公式求出已知角的两条
夹边,看看是否成比例?若成比例,则相似;否则不相似。 • 不知道是否有一个角相等的情形:运用两点间的距离公式求出两个三
角形各边的长,看看是否成比例?若成比例,则相似;否则不相似。 • 一个定三角形和动三角形相似: • 已知有一个角相等的情形: • 先借助于相应的函数关系式,把动点坐标表示出来(一母示),然后
2020/8/4
2
两点间的距离公式
AB yA yB 2 xA xB 2
2020/8/4
3
中点坐标
• 线段的中点的坐标为:
xA xB ,yA yB 2 2
2020/8/4
4
一元二次方程有整数根问题
解题步骤如下:① 用和参数的其他要求确定
参数的取值范围 ② 解方程,求出方程的根
③ 分析求解:若是分式,分母是分子的因数; 若是二次根式,被开方式是完全平方式。
2020/8/4
16
几何分析法
2020/8/4
17
几个自定义概念
2020/8/4
18
1.求证“两线段相等”的问题
2020/8/4
19
2、“平行于y轴的动线段长度的最大值”的问题
2020/8/4
20
3、求一个已知点关于一条已知直线的对称点的坐标 问题
2020/8/4
21
4、“抛物线上是否存在一点,使之到定直线的距离 最大”的问题
2020/8/4
28
10、“定四边形面积的求解”问题
• 有两种常见解决的方案: • 方案(一):连接一条对角线,分成两个三角形面积之和; • 方案(二):过不在x轴或y轴上的四边形的一个顶点,向
x轴(或y轴)作垂线,或者把该点与原点连结起来,分割 成一个梯形(常为直角梯形)和一些三角形的面积之和 (或差),或几个基本模型的三角形面积的和(差)
二次函数常见题型 及解题策略
2020/8/4
1
中考二次函数压轴题———解题通法研究
• 二次函数在全国中考数学中常常作为压轴题,同时在省级, 国家级数学竞赛中也有二次函数大题,在宜宾市的拔尖人 才考试中同样有二次函数大题,在成都,绵阳,泸县二中 等地的外地招生考试中也有二次函数大题,很多学生在有 限的时间内都不能很好完成。由于在高中和大学中很多数 学知识都与函数知识或函数的思想有关,学生在初中阶段 函数知识和函数思维方法学得好否,直接关系到未来数学 的学习。所以二次函数综合题自然就成了相关出题老师和 专家的必选内容。我通过近6年的研究,思考和演算了上 1000道二次函数大题,总结出了解决二次函数压轴题的通 法,供大家参考。
26
三角形面积的最大值问题
2020/8/4
27
9.“一抛物线上是否存在一点,使之和另外三个定 点构成的四边形面积最大的问题”
由于该四边形有三个定点,从而可把动四边形分割成一个 动三角形与一个定三角形(连结两个定点,即可得到一个 定三角形)的面积之和,所以只需动三角形的面积最大, 就会使动四边形的面积最大,而动三角形面积最大值的求 法及抛物线上动点坐标求法与7相同。
• 这种情形在相似性中属于高端问题,破解方法是,在定三 角形中,由各个顶点坐标求出定三角形三边的长度,用观 察法得出某一个角可能是特殊角,再为该角寻找一个直角 三角形,用三角函数的方法得出特殊角的度数,在动点坐 标“一母示”后,分析在动三角形中哪个角可以和定三角 形中的那个特殊角相等,借助于特殊角,为动点寻找一个 直角三角形,求出动点坐标,从而转化为已知有一个角相 等的两个定三角形是否相似的问题了,只需再验证已知角 的两边是否成比例?若成比例,则所求动点坐标符合题意, 否则这样的点不存在。简称“找特角,求(动)点标,再 验证”。或称为“一找角,二求标,三验证”。
2020/8/4
5
二次函数与轴的交点为整数点问题
• 解题步骤如下:① 用和参数的其他要
求确定参数的取值范围
•
② 解方程,求出方程的
根
③ 分析求解:若是分式,分母是分子的因
数;若是二次根式,被开方式是完全平方
式。
ห้องสมุดไป่ตู้
2020/8/4
6
方程总有固定根问题
• 可以通过解方程的方法求出该固定根
已知关于的方程(mx2 3(m 1)x 2m 3 0 为实数),
的点,并求出固定点的坐标。
解:把原解析式变形为关于m 的方程y x2 2 m1 x
∴
y x2 2
1
x
0
0
解得:
y x
1 1
∴ 抛物线总经过一个固定的点(1,-1)。
(题目要求:关于的方程不论为何值,方程恒成立)
ax b 小结:关于x的方程
2020/8/4
有无数解
a0
b
8
0
路径最值问题(待定的点所在的直线就是对称轴)
2020/8/4
22
5.常数问题
2020/8/4
23
6.“在定直线(常为抛物线的对称轴,或x轴或y轴或其它的定 直线)上是否存在一点,使之到两定点的距离之和最小”的 问题
2020/8/4
24
7.三角形周长的“最值(最大值或最小值)”问 题
2020/8/4
25
8.三角形面积的最大值问题
2020/8/4
把两个目标三角形(题中要相似的那两个三角形)中相等的那个已知 角作为夹角,分别计算或表示出夹角的两边,让形成相等的夹角的那 两边对应成比例(要注意是否有两种情况),列出方程,解此方程即 可求出动点的横坐标,进而求出纵坐标,注意去掉不合题意的点。
2020/8/4
30
“两个三角形相似”的问题
• 不知道是否有一个角相等的情形:
13
函数的交点问题
2020/8/4
14
方程法
• (1)设:设主动点的坐标或基本线段的长度 • (2)表示:用含同一未知数的式子表示其他相关的数量 • (3)列方程或关系式
2020/8/4
15
几何分析法
• 特别是构造“平行四边形”、“梯形”、“相似三角形”、 “直角三角形”、“等腰三角形”等图形时,利用几何分 析法能给解题带来方便。
求证:无论为何值,方程总有一个固定的根。
解:当 m 0 时, x 1
x1
当 m 0 时,
2
3 m
、x2
1
m3
2
0
,x
3m
1
2m
,
综上所述无论:m 为何值,方程总有一个固
定的根是1。
2020/8/4
7
函数过固定点问题
举例如下:已知抛物线 y x2 mx m 2(是常数),
求证:不论 m 为何值,该抛物线总经过一个固定
N 两点M、 ,使得AM MN之和最小。
2020/8/4
9
路径最值问题
2020/8/4
10
路径最值问题
2020/8/4
11
在平面直角坐标系中求面积的方法
• 直接用公式、割补法
2020/8/4
12
函数的交点问题
2020/8/4
2020/8/4
29
11.“两个三角形相似”的问题
• 两个定三角形是否相似: • 已知有一个角相等的情形:运用两点间的距离公式求出已知角的两条
夹边,看看是否成比例?若成比例,则相似;否则不相似。 • 不知道是否有一个角相等的情形:运用两点间的距离公式求出两个三
角形各边的长,看看是否成比例?若成比例,则相似;否则不相似。 • 一个定三角形和动三角形相似: • 已知有一个角相等的情形: • 先借助于相应的函数关系式,把动点坐标表示出来(一母示),然后
2020/8/4
2
两点间的距离公式
AB yA yB 2 xA xB 2
2020/8/4
3
中点坐标
• 线段的中点的坐标为:
xA xB ,yA yB 2 2
2020/8/4
4
一元二次方程有整数根问题
解题步骤如下:① 用和参数的其他要求确定
参数的取值范围 ② 解方程,求出方程的根
③ 分析求解:若是分式,分母是分子的因数; 若是二次根式,被开方式是完全平方式。
2020/8/4
16
几何分析法
2020/8/4
17
几个自定义概念
2020/8/4
18
1.求证“两线段相等”的问题
2020/8/4
19
2、“平行于y轴的动线段长度的最大值”的问题
2020/8/4
20
3、求一个已知点关于一条已知直线的对称点的坐标 问题
2020/8/4
21
4、“抛物线上是否存在一点,使之到定直线的距离 最大”的问题
2020/8/4
28
10、“定四边形面积的求解”问题
• 有两种常见解决的方案: • 方案(一):连接一条对角线,分成两个三角形面积之和; • 方案(二):过不在x轴或y轴上的四边形的一个顶点,向
x轴(或y轴)作垂线,或者把该点与原点连结起来,分割 成一个梯形(常为直角梯形)和一些三角形的面积之和 (或差),或几个基本模型的三角形面积的和(差)
二次函数常见题型 及解题策略
2020/8/4
1
中考二次函数压轴题———解题通法研究
• 二次函数在全国中考数学中常常作为压轴题,同时在省级, 国家级数学竞赛中也有二次函数大题,在宜宾市的拔尖人 才考试中同样有二次函数大题,在成都,绵阳,泸县二中 等地的外地招生考试中也有二次函数大题,很多学生在有 限的时间内都不能很好完成。由于在高中和大学中很多数 学知识都与函数知识或函数的思想有关,学生在初中阶段 函数知识和函数思维方法学得好否,直接关系到未来数学 的学习。所以二次函数综合题自然就成了相关出题老师和 专家的必选内容。我通过近6年的研究,思考和演算了上 1000道二次函数大题,总结出了解决二次函数压轴题的通 法,供大家参考。
26
三角形面积的最大值问题
2020/8/4
27
9.“一抛物线上是否存在一点,使之和另外三个定 点构成的四边形面积最大的问题”
由于该四边形有三个定点,从而可把动四边形分割成一个 动三角形与一个定三角形(连结两个定点,即可得到一个 定三角形)的面积之和,所以只需动三角形的面积最大, 就会使动四边形的面积最大,而动三角形面积最大值的求 法及抛物线上动点坐标求法与7相同。
• 这种情形在相似性中属于高端问题,破解方法是,在定三 角形中,由各个顶点坐标求出定三角形三边的长度,用观 察法得出某一个角可能是特殊角,再为该角寻找一个直角 三角形,用三角函数的方法得出特殊角的度数,在动点坐 标“一母示”后,分析在动三角形中哪个角可以和定三角 形中的那个特殊角相等,借助于特殊角,为动点寻找一个 直角三角形,求出动点坐标,从而转化为已知有一个角相 等的两个定三角形是否相似的问题了,只需再验证已知角 的两边是否成比例?若成比例,则所求动点坐标符合题意, 否则这样的点不存在。简称“找特角,求(动)点标,再 验证”。或称为“一找角,二求标,三验证”。
2020/8/4
5
二次函数与轴的交点为整数点问题
• 解题步骤如下:① 用和参数的其他要
求确定参数的取值范围
•
② 解方程,求出方程的
根
③ 分析求解:若是分式,分母是分子的因
数;若是二次根式,被开方式是完全平方
式。
ห้องสมุดไป่ตู้
2020/8/4
6
方程总有固定根问题
• 可以通过解方程的方法求出该固定根
已知关于的方程(mx2 3(m 1)x 2m 3 0 为实数),
的点,并求出固定点的坐标。
解:把原解析式变形为关于m 的方程y x2 2 m1 x
∴
y x2 2
1
x
0
0
解得:
y x
1 1
∴ 抛物线总经过一个固定的点(1,-1)。
(题目要求:关于的方程不论为何值,方程恒成立)
ax b 小结:关于x的方程
2020/8/4
有无数解
a0
b
8
0
路径最值问题(待定的点所在的直线就是对称轴)
2020/8/4
22
5.常数问题
2020/8/4
23
6.“在定直线(常为抛物线的对称轴,或x轴或y轴或其它的定 直线)上是否存在一点,使之到两定点的距离之和最小”的 问题
2020/8/4
24
7.三角形周长的“最值(最大值或最小值)”问 题
2020/8/4
25
8.三角形面积的最大值问题
2020/8/4
把两个目标三角形(题中要相似的那两个三角形)中相等的那个已知 角作为夹角,分别计算或表示出夹角的两边,让形成相等的夹角的那 两边对应成比例(要注意是否有两种情况),列出方程,解此方程即 可求出动点的横坐标,进而求出纵坐标,注意去掉不合题意的点。
2020/8/4
30
“两个三角形相似”的问题
• 不知道是否有一个角相等的情形:
13
函数的交点问题
2020/8/4
14
方程法
• (1)设:设主动点的坐标或基本线段的长度 • (2)表示:用含同一未知数的式子表示其他相关的数量 • (3)列方程或关系式
2020/8/4
15
几何分析法
• 特别是构造“平行四边形”、“梯形”、“相似三角形”、 “直角三角形”、“等腰三角形”等图形时,利用几何分 析法能给解题带来方便。
求证:无论为何值,方程总有一个固定的根。
解:当 m 0 时, x 1
x1
当 m 0 时,
2
3 m
、x2
1
m3
2
0
,x
3m
1
2m
,
综上所述无论:m 为何值,方程总有一个固
定的根是1。
2020/8/4
7
函数过固定点问题
举例如下:已知抛物线 y x2 mx m 2(是常数),
求证:不论 m 为何值,该抛物线总经过一个固定
