哈工大 数据库系统 第2章
哈尔滨理工大学数据库大作业2SQL查询数据库表

哈尔滨理工大学
数据库大作业2
班级:信息11-2 学号: 11060402
姓名:
指导教师:
2013.10
目录
第一章:运用SQL查询分析器查询数据库表 (1)
第二章、系统管理模块数据库表名称中文标注 (3)
第一章:运用SQL查询分析器查询数据库表
1.打开数据库查询分析器,连接到SQL Server2005,进入如图1所示界面。
图1
2.输入要查询的数据库表名称,如图2,3所示。
图2
图3
4.表名及属性中文标注
(1)WA_psn 人员表:(图4所示)
图4
(2)WA_PsnMsg 人员附加信息表:(图5所示)
图5
(3)Customer Class 客户分类体系:(图6所示)
图6
(4)Department 部门档案:(图7所示)
图7
第二章、系统管理模块数据库表名称中文标注
CA_Amo Ct 各项费用成本表
CA_CBS ys 系统设置表
CA_Class Def 产品类别定义
CA_Cost CD 费用明细定义表
CA_Dir MA 直接人工费用表
CA_Man Ct 制造费用表
Code 科目表
Customer 客户档案
Customer Class 客户分类体系
Department 部门档案
Dispatch Lists 发货单、委托代销结算单子表
District Class 地区分类体系
Dsign 凭证类别表
Dsigns 凭证类别子表。
哈工大文献检索课件

精炼检索结果
可利用 include或exclude来 找到更理想的结果 参考记录条数。可将这些统 计数字导出至表格
•Controlled Vocabulary
•Classification Code •Country •Document Type •Language •Year •Source Title •Publisher
“简单检索”可在检索对话框中输入检索词或检索表达 式
LOGO
检
索
结
果
界
面
LOGO
输入检索词
选择检索词之 间的概念关系
限定检索条件
点选之后,自动 取消词根检索
索引词典
快 速 检 索—Quick SearchLOGO
快速检索界面介绍
LOGO
LOGO
LOGO
LOGO
检索技巧
1. 逻辑算符、位置算符和截词符
逻辑算符及位置算符 : AND OR NOT NEAR ONNEAR
截词符: * ?
NEAR 词序可颠倒
ONNEAR 词序不可颠倒 * 代表无限字符,可以在任意位置 Transplant* 代表transplanting、 transplantation、transplanted等
? 代表一个字符
Wom?n 代表woman or women
类型 年 2000 2001 2002 2003 2004 2005 2006
EI收录 论文数量(篇) 379 502 694 846 1192 1186 2137
EI收录 较上一年增长℅ 40.89 32.45 38.25 21.90 40.90 58.22 13.31
EI收录
高校排名
4 3 4 4 4 5 4
数据库课件(哈工大)

第1章 数据库系统基本概念
第1页
数据库系统 第1章 数据库系统基本概念
1.1 数据库系统的基本概念 --数据库(信息库) --数据库系统(工作环境) --数据库管理系统(软件系统) 1.2 数据库工作者的分类及素质要求 1.3 数据库系统的标准结构 1.4 数据库系统的简要发展史及发展趋势
数据库系统 1.1数据库系统的基本概念
数据定义语言(DDL:DataDefinitionLanguage) --DBMS提供给用户,以便用户定义数据格式 例:用户定义表名,表标题、列名及其结构形式 数据操纵语言(DML:DataManipulationLanguage) --DBMS提供给用户,以便用户对数据进行操作 例:用户增加、删除、修改、查询和统计数据等 数据控制语言(DCL:DataControlLanguage) --DBMS提供给用户,以便用户对数据进行控制 例:用户定义对不同操作、对不同用户的约束 数据库各种操作的执行 --DBMS按用户要求进行定义、操纵、控制和维护
--数据库(信息库)(续) Table的构成/关于Table的常用术语
表名 表标题(格式) (关系)模式
表内容(值) 学生成绩单
班级 姓名 语文 2 李德 75 2 范燕美 76 2 张靖 81 2 许聪 82 2 黄佩婷 80
列(column)/ 字段(field)/ 属性(attribute)/ 数据项(data item)
第20页
数据库系统
用户/应用 数据库管理员 数据库管理员 DML命令 DCL命令 DDL命令 DBMS基本 功能程序 DML编译器 DCL编译器 DDL编译器 查询计划 执行数据库 系 系 施加控制 对索引、文件 基本命令 执行引擎 DCL维护引擎 统 统 和记录的请求 负 可 Data Format Data Data Control 责 越 索引/文件和 记录管理器 控制逻辑/ (Scheme) Table: Record:Field Information 过 物理映射 操 页面 作 内存 命令 操 系 缓冲区 控制内存分配,内 DataBase 统 作 存块/磁盘块交换 管理器 Buffer 系 直 内存页/快:偏置量 统 接 读页/ 负 负 写页 责 责 磁盘 存储 控制磁盘读写 DataBase 管理器 柱面:磁道:扇区簇/磁盘块
哈尔滨工程大学数据库原理(加试)考试大纲

考查要点: 要求学生掌握数据库系统的基本概念、基本原理和基本方法,了解典型数据库管
理系统的系统结构,学会使用数据库管理系统,进行数据库设计,进而能够开发数据 库应用系统。 1、数据库基本概念,数据模型,数据库系统结构等; 2、关系数据库的基本概念,关系模型及其描述,关系数据库语言,关系代数和关系演 算; 3、SQL 语言的数据定义,查询,更新,视图,数据控制; 4、查询优化的一般策略,基于关系代数表达式的优化算法,连接运算的优化; 5、关系模型的规范化,函数依赖的公理系统,模式的分解,多值依赖和 4NF,联接依赖; 6、数据库设计步骤,数据库的实施与维护; 7、数据库保护,包括:数据库恢复技术,并发控制技术,数据库安全性和数据库完 整性。
考试总分:100 分 考试时间:2 小时 考试题型: 选择题
填空题 简答题 简单应用题 综合应用题
考试方式:笔试
Hale Waihona Puke 参考书目(包括书名、作者、出版社、出版时间): 主要参考书:
萨师煊,王 珊. 数据库系统概论.北京:高等教育出版社(第四版),2006.
哈工大 数据库课件@姜守旭-第二讲ER模型

作为主码的属性上取值不能为null
属性的类型
派生(Derived)属性与基属性
可以从其他相关的属性或实体派生出来的属性值 如学生(学号,姓名,平均成绩),选课(学号, 课程号,成绩),则平均成绩可由学生所选课程 的总成绩除以课程总数来得到。称平均成绩为派 生属性,而成绩为基属性,或存储属性 数据库中,一般只存基属性值,而派生属性只存 其定义或依赖关系,用到时再从基属性中计算出 来 基本表 VS 视图
复合(Composite)属性
ห้องสมุดไป่ตู้
1NF vs 嵌套关系
属性的类型
属性的类型
单值属性
每一个特定的实体在该属性上的取值唯一 如学生的学号,年龄、性别、系别等 某个特定的实体在该属性上有多于一个的取值 如学生(学号,所选课程,联系电话) 学号与课程之间是一种多值依赖关系
多值属性
功能需求 规格说明 确定存储哪些数 据,建立哪些应 用,常用的操作 及对象有哪些等
ER模型 ODL
对需求分析所得 到数据的更高层 的抽象描述
将概念模型所描 述的数据映射为 某个特定的 DBMS模式数据
逻辑数据库设计 物理数据库设计
数据库的设计原则
避免冗余
帐户、客户名、地址、电话 贷款、客户名、地址、电话 问题:帐户和贷款中的客户信息重复
角色在E-R图中的表示
表示要点
当需要显式区分角色时,在连接菱形和矩形的线 上加上说明性标注以区别不同的角色
管理
职员
工作
雇佣
角色在E-R图中的表示
属性的类型
数据库系统(下):管理与技术_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年

数据库系统(下):管理与技术_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.DBMS管理数据库缓冲区有四种策略:No Steal, Steal, No Force, Force。
则效率较低但不会出现问题的策略组合是_________,而效率最高最常用但会出现问题的策略组合是_________。
参考答案:No Steal+ Force,Steal + No Force;2.下列说法正确的是___________。
参考答案:两阶段封锁法是可串行化的并行调度算法;3.T1,T2是两个事务,图(a)(b)给出这两个事务的两种调度S1,S2,关于S1,S2,说法正确的选项是_____________。
【图片】参考答案:S1是不可串行化调度,S2是可串行化调度;4.若事务T对数据M已加S锁,在不改变S锁的情况下,则其它事务对数据M__________。
参考答案:可以读,但不可以写;5.关于稀疏索引和稠密索引,下列说法正确的是_______。
参考答案:如果一个搜索码的值在稠密索引中不存在,则在主文件中对应该搜索码值的记录也不存在6.关于给出的九个关系代数操作:【图片】问任何时候都能够用一趟算法实现的操作的个数是_______。
参考答案:17.主索引通常确定“表”数据的__________。
参考答案:物理顺序8.有效性确认是一种并发控制方法。
如下图(a)(b)中T和U是两个事务,X和Y是数据对象。
T要进行有效性确认,下列说法正确的是__________。
【图片】参考答案:图(a)事务T的有效性可以确认;图(b)事务T的有效性不可以确认;9.关于基于散列的两趟算法,下列说法正确的是_______。
参考答案:第一趟散列的目的是使数据子集具有某一种特性(如具有相同的散列值),而第二趟散列的目的是提高数据处理的速度。
10.关于逻辑查询优化和物理查询优化,下列说法正确的是________。
参考答案:逻辑查询优化是关系代数操作次序的优化;物理查询优化是关系代数操作实现算法选择的优化11.关于B+树,下列说法不正确的是_________。
哈工程数据库课件

Jeffrey.D.Ullman, Jennifer Widom
Dept. Of Computer Science Stanford University
2015-4-4
杨 悦 yangyue@
3
教材及参考书(2)
数据定义功能
提供数据定义语言(DDL) 定义数据库中的数据对象
数据操纵功能
提供数据操纵语言(DML)
操纵数据实现对数据库的基本操作 (查询、插入、删除和修改)
2015-4-4
19
DBMS的主要功能
数据库的运行管理
保证数据的安全性、完整性、
多用户对数据的并发使用
发生故障后的系统恢复
数据库的建立和维护功能(实用程序)
数据库数据批量装载
数据库转储 介质故障恢复 数据库的重组织
性能监视等
2015-4-4
20
举例说明
仓库(DB)中存放商品(Data),保管员 (DBMS)负责商品(Data)的搬进、整理和搬出。
1.检查商品(Data)是否合法(定义问题)
数据库系统 操作系统…
9
数据库的地位
数据库技术产生于六十年代末,是数据管理的最新技术,
是计算机科学的重要分支
数据库技术是信息系统的核心和基础,它的出现极大建设规模、数据库信息量的大小和使用频度已
成为衡量一个国家信息化程度的重要标志
2015-4-4
文件系统阶段(50年代末--60年代中)
数据库系统阶段(60年代末--现在)
2015-4-4
25
哈工大数据库习题课

名词--数据独立性
数据库的数据独立性: 数据独立性表示应用程序与数据库中存储的数 据之间不存在依赖关系。包括逻辑数据独立性和物 理数据独立性。 逻辑数据独立性是指局部逻辑数据结构(外视 图)与全局逻辑数据结构(概念视图)之间的独立 性。当数据库的全局逻辑数据结构(概念视图)发 生变化(数据定义的修改、数据之间联系的变更或 增加新的数据类型等)时,它不影响某些局部的逻 辑结构的性质,应用程序不必修改。
- 7 -
关系代数与SQL语言(续-06)
查询全部学生都选修的课程的课程号 (C#)和课程名(CName); 关系代数表达式:
C #,CName
C
S #,C #
SC S # S
SQL语言表达式:(请参考教材P113的例43) select C#, CName from C where not exists ( select * from S where not exists (select * from SC where S.S# = S# and C# = C.C#));
- 24 -
简单的数据库设计实例(续-01)
(3)一个单位可有多个教师,一个教师只能属 于一个单位。 试完成如下工作: (1)分别设计学生选课和教师任课两个局部信 息的结构E-R图。 (2)将上述设计完成的E-R图合并成一个全局 E-R图。 (3)将该全局E-R图转换为等价的关系模型表 示的数据库逻辑结构。
- 8 -
关系代数与SQL语言(续-07)
查询选修课程包含“程军”老师所授
课程之一的学生学号(S#); 关系代数表达式: S # SC C# Teacher'程军' C SQL语言表达式: select S# from SC where C# in ( select C# from C where Teacher = ‘程军’);
数据库讲义 哈工大张建国 chapter1-5

第一章绪论1. 信息与数据信息Information信息是人类对于自然界的感知.物质世界:物质与信息物质存在⇒信息存在物质变化⇒信息变化数据Data数据是信息的符号化表示.在计算机中,数据是描述各种信息的符号记录.数据处理——对数据进入收集、存储、加工和传播等过程.2. 数据库DB(Data Base)长期存放在计算机存储介质中的有组织的、动态的、可共享的数据集合.3. 数据库管理系统DBMS(Data Base Management System)组织、存储、维护和获取数据库中数据的软件系统,是介于数据库用户和操作系统之间的数据管理软件.4. 数据库系统DBS(Data Base System)在计算机系统中引入数据库后的系统,包括:数据库DB, 数据库管理系统DBMS, 各种开发工具数据库应用系统, 计算机硬件及其他软件数据库管理员DBA (Data Base Administrator), 用户5. 数据处理与数据管理数据处理:对各种数据进行收集、存储、加工和传播的一系列活动的总和.数据管理:对数据进行分类、组织、编码、存储、检索和维护的过程.数据管理是数据处理的核心.6. 数据库系统的特点●数据面向整个组织●数据结构化从一个组织全部应用的角度,全面考虑并集成数据的结构;不仅能反映数据本身,而且还能反映数据之间的联系;数据之间的联系通过存取路径实现.●共享性高,冗余度低,可扩充性强●程序与数据具有较高的独立性数据独立性:数据与应用程序之间相互依赖的程度.三级逻辑结构全局逻辑结构:描述数据库的整体结构局部逻辑结构:描述某一用户观点的数据集合物理结构:描述数据的物理存储两种映象全局逻辑结构与局部逻辑结构映象:逻辑独立性✓在全局逻辑结构与局部逻辑结构之间有一种映象.✓当全局逻辑结构发生变化时,通过修改该映象,可以使局部逻辑结构不改变.✓用户程序是根据局部逻辑结构编写的,所以不必修改用户程序.全局逻辑结构与物理结构映象:物理独立性✓在全局逻辑结构与存储结构之间有一种映象.✓当存储结构发生变化时,通过修改该映象,可以使全局逻辑结构不改变.✓由此不必修改局部逻辑结构,所以不必修改用户程序.●数据管理灵活方便●易于被应用程序使用●安全性和保密性好●数据的算法相对较简单,但数据之间的关系复杂(1) 数据结构化(2) 数据共享性好、冗余度低、易扩充、避免不一致性(3) 数据独立性好(4) 数据由DBMS统一管理和控制DBMS提供了一种机制,保证数据的安全性、完整性、并发控制和数据库恢复等.(5) 数据存取最小单位是数据项第二章数据库系统结构模型对客观事务中感兴趣的内容进行模拟和抽象的工具.建立模型有助于加深对问题的理解数据模型对客观世界中的数据特征进行抽象的工具.数据库的数据模型概念层数据模型对数据应用部门的数据进行建模的工具.对数据库既要表示数据本身,又要表示数据之间的联系.组织层数据模型描述数据库系统内部数据组织结构的工具.数据库是某个组织所涉及的数据的集合.数据库不仅仅能表示数据本身,还能反映数据之间的联系.设计数据库的逻辑结构时,首先需要将现实世界中的信息及其相互联系用概念层数据模型(概念模型,信息模型)表示出来,然后将这种其转换成具体数据库的组织层数据模型(数据模型).1. 三个世界●现实世界(客观世界)客观世界研究的是对象; 对象是具体事务或抽象概念;组成客观世界的细胞称为事务;人们对事务的认识是通过事务的特征进行的.●信息世界对客观世界中的事务进行认识,经过选择、命名、分类后进入信息世界.实体Entity: 具有公共性质的客观存在的并可相互区分的事务.实体可以是具体的人、事、物,也可以是抽象的概念.属性Attribute: 实体所具有的某一特征.一个实体由若干个属性描述.键(码)Key:唯一标识实体的属性集.域Domain:属性的取值范围.属性是个变量,属性值是变量的取值,域是变量的取值范围.实体型Entity Type:用实体名和属性名来抽象和描述实体的框架.实体集Entity Set:同一类型实体的集合.联系Relationship:现实世界中的事务不是独立存在的,而是相互联系的.实体内部各属性之间的联系;实体之间的联系.概念层模型的联系: 指实体之间的联系.●机器世界将信息世界中的概念模型转换成计算机内部表示,就进入了机器世界(数据世界).2. 实体之间的联系●一对一联系(1:1)●一对多联系(1:n)●多对多联系(m:n)3. 概念模型的表示方法实体联系方法:ER 图(Entity Relationship Approach) P.P.S Chen于1976年提出来的一种表示客观世界信息模型的方法ER图的表示方法典型的组织层数据模型●层次模型:用树型结构组织数据只有一个结点无双亲结点,称根结点.除根结点外,其他结点有且只有一个双亲结点.●网状模型:用网状结构组织数据可以有一个以上结点无双亲结点.一个结点可以有多个双亲结点.●关系模型:用二维表结构组织数据用二维表(table)组织管理数据.表中数据及表之间的数据要满足一定的条件约束.●面向对象模型:用复杂表格及其他结构组织数据数据库的数据模型由三部分组成●数据结构:描述数据的组织结构(静态结构)描述数据的类型、性质、取值范围等✓在不同的数据模型中,数据结构的表示方法不同.描述数据之间的联系✓一个实体内部各数据项之间的联系.✓不同实体之间数据的联系.●数据操作:描述数据的操作(动态结构)检索(查询)数据更新数据:插入数据;修改数据;删除数据●数据完整性约束:描述对数据的约束条件——正确性、有效性和相容性.实体完整性;参照完整性;用户定义完整性实体完整性和参照完整性是任何数据库都必须满足的.用户定义完整性是根据用户的具体要求定义的.数据库系统应不仅能设置完整性,还能执行完整性约束.数据库的结构●内部结构(从数据库管理系统角度看数据结构)三级模式(外模式、模式和内模式)●外部结构(从最终用户角度看数据结构)集中式结构分布式结构客户/服务器结构(C/S结构-Client/Server)浏览器/服务器结构(B/S结构-Browser/Server)并行结构……●两层结构C/S:客户层/服务器层●三层结构B/A/S:浏览器/应用程序服务器/数据库服务器1. 数据库系统的三级模式结构●模式Schema用于描述数据库的结构;模式不涉及具体数据值.●要特别注意区分“型”和“值”的概念型是指对数据结构和属性的说明.值是型的具体取值,是数据库的一个实例.●三级模式结构是典型的数据库模式结构尽管实际数据库的软件产品是多种多样的,可以使用不同的语言,建立在不同的操作系统上,存储结构不同,但基本上都采用典型的三级模式结构和两种映象.(1) 模式Schema逻辑模式Logical Schema用于描述数据库的全局逻辑结构,是数据库的总体构架.一个数据库只有一个模式,其主要功能有:定义模式名,定义数据项及类型,定义记录,定义记录间的联系,定义安全性控制要求,定义数据完整性约束条件等.模式用模式数据定义语言Schema DDL(Data Definition Language)编写,称源模式.源模式经翻译后产生目标模式,存放在描述数据库中.(2) 外模式External Schema外模式也叫子模式Subschema或用户模式User Schema,用于描述某一用户观点的数据库的局部逻辑结构.●外模式通常是模式的子集,外模式与某一具体应用有关.同一外模式可以为某一用户的多个应用所使用,但一个用户通常只能使用一个外模式.不同用户的外模式可以互相覆盖.●外模式是由模式映象出来的.二者的功能一致,但有区别:数据项定义可以不同;记录的组成可以不同;可以有不同的密码和不同的使用权限.●外模式用外模式数据定义语言Subschema DDL定义.(3) 内模式Internal Schema●内模式也叫存储模式Storage Schema,是数据库数据的内部表示,用于定义数据的存储方式和物理结构.内模式由数据库管理员DBA使用.一个数据库只有一个内模式.●内模式的功能定义每一个数据项的物理表示方式;定义数据的寻址方法和检索技术;定义数据是否压缩存储,数据是否加密存储;定义数据的物理存储块的大小,溢出处理方法.●内模式用内模式数据定义语言Data Storage DDL描述.2. 数据库系统的组成●硬件——要求:大内存,大硬盘,较高的通道能力.●软件支持数据库的操作系统;数据库管理系统;具有与数据库接口的高级语言及其编译系统;以DBMS为核心的开发工具.●数据库: 具体的数据库应用系统.数据库的数据;数据库的描述.●人员: 数据库管理员、系统分析员、应用程序员和用户.第三章关系数据库1. 域Domain是一组具有相同数据类型的值的集合.2. 笛卡儿积Cartesian Product给定一组域D1,D2,…,Dn(这些域中可以有相同的)D1,D2,…,Dn 的笛卡尔积为:D1×D2×…×Dn={(d1,d2,…,dn)|di∈Di, i=1,2,…,n}其中:(d1,d2,…,dn)叫一个n元组(n-tuple),简称元组di叫一个分量3. 关系RelationD1×D2×…×Dn 的子集叫作在域D1,D2,…,Dn上的关系,表示为: R(D1, D2,…, Dn)其中:R为关系名,n为关系的度(或目),D1, D2,…, Dn为域名由于域名可以相同,为了加以区分,必须为每一列起一个名,称属性Attribute,故关系常表示为:R (A1,A2,…,An )4. 属性到域的映象●若属性名与域名相同,则用域名作属性名.●若属性名与域名不同,则需要指出属性到域的映象.Ai=Dom(Di) 表明:属性Ai来自于域Di5. 数据库关系与数学中关系的区别●关系模型对其数学定义作了适当的扩充:●笛卡尔积可以是一个无限集合,但关系必须是有限集合.在数学意义上, (d1,d2,…,dn)≠(d2,d1,…,dn)列之间不满足交换律,故通过为关系的每一个列加一个属性名,取消关系中列的有序性限制.6. 关系的性质●列是同质的:每一列中的数据类型相同●列名是唯一的:不同的列(属性)可以来自于同一个域,需要指●出属性到域的映象●行的顺序无关:任何两行可以互换●列的顺序无关:任何两列可以互换●任何两行不能完全相同:由主码区分●分量必须是原子量:每一列不可再分割7. 关系的优点与不足●关系模型的优点理论基础扎实:集合论,关系数据理论.概念单一: 实体用关系表示,联系也用关系表示.存取路径对用户是透明的: 用户不必知道存取路径规范化:最基本的要求是每一个属性不可再分割.表示单一: 数据用表表示,查询结果也用表表示.●关系模型的缺点效率不如非关系模型,因此需要进行查询优化, 增加了DBMS自身的开发难度.计算机处理速度的提高,数据库优化算法的改善,使关系数据库的效率仍远高于其他数据模型 关系模型是通过满足一定条件的二维表来表示实体集合及数据之间联系的一种数据模型.具有坚实的数学基础和较严密的理论,使用灵活方便,得到了迅速发展,80年代以后的数据库系统几乎都支持关系模型.●关系的逻辑数据结构实体和联系都用关系表示.从用户的观点看,关系是一张二维表.●关系的存储结构每个表可对应一个文件.也可以将多个表存储在一个文件中.8. 关系的术语●关系模式Relation Schema:关系的型,是对关系的描述,即关系的框架●关系Relation:关系模式的一组具体取值●关系数据库模式Relation Database Schema:关系模式的集合●关系数据库Relation Database:关系的集合●元组Tuple:关系中的一行●属性Attribute:由于域可以相同,为了区分,必须为每个列取一个名字,称为属性●域Domain:属性的取值范围●超码(键)Super Key:能唯一标识一个元组的属性组●候选码(键)Candidate Key:能唯一标识一个元组的最小属性组●主码(键)Primary Key:若候选码有多个,选择其中的一个作主码例:学号,身份证号●主属性Primary Attribute:候选码中的属性●非主属性Non-primary Attribute:不包含在任何候选码中的属性●全码All Key: 全部属性都是主属性9. 关系操作分类●关系代数:通过对关系的运算表示查询方式●关系演算:用谓词表示查询方式元组关系演算:谓词变元的基本对象是元组域关系演算:谓词变元的基本对象是域●结构化查询语言SQL10. 关系代数运算包括两大类●传统的集合运算:从行的角度进行运算.并∪, 交∩,差—,广义笛卡儿积×●专门的关系运算:从行和列两种角度进行运算.选择σ,投影π,连接⋈,除÷●在各种运算中,使用下列运算符比较运算符: <, ≤, =, >, ≥, ≠逻辑运算符:¬(非),∧(与),∨(或)11. 关系的完整性约束:关系中的所有数据必须满足的约束条件三类完整性——实体完整性、参照完整性、用户定义完整性●实体完整性规则——若属性A是基本关系R的主属性,则A不能取空值. 主健必须唯一. 关系模型的表分为基本表(基本关系),查询表和视图.基本表:实际存在的表查询表:查询结果表视图:定义的虚表空值与零值不同——空值:没有值,但不是0——零值:其值为0●参照完整性实体之间的联系是通过外健(外部码)进行的.定义: 外键Foreign Key设F是基本关系R的一个或一组属性,但F不是R的主健.若F与基本关系S的主健Ks相对应,则称F是基本关系R的外健(R可以与S是同一关系).称R 为参照关系,S为被参照关系或目标关系.例如:在学生(学号,姓名,性别,专业,班长学号)中班长学号是也是一个学号,必须与学号出自同一个域,故班长学号也是外健.●参照完整性规则——若属性或属性组F是基本关系R的外健,则: F在R中取空值;若F在R中非空则其在S中必须存在.●用户定义完整性:根据用户的具体要求定义的完整性.第四章SQL Server 数据库系统基础●SQL Server数据库的特点●SQL Server数据库的版本:企业版,标准版,个人版,开发版●SQL Server 的安装:软硬件环境、安装过程●SQL Server 数据库服务管理器的启动与登录:启动服务器管理器、登录企业管理器、登录查询分析器●SQL Server 的工具与实用程序●SQL Server 的系统数据库●SQL Server 的主要数据类型●数据库及基本表的创建第五章结构化查询语言SQL 0.1. SQL的特点(1) 一体化(2) 高度非过程化(3) 面向集合的操作方式(4) 两种使用方式、统一的语法结构自含式语言能独立地在联机方式下使用(命令方式),用户可以在终端键盘上直接输入SQL命令对DB进行操作.嵌入式语言嵌入到高级语言(VB、PB、Java等)程序中,利用主语言(高级语言)进行计算处理、利用DB语言进行数据管理.同一条命令在两种操作方式中的语法结构基本一致. (5) 语言简捷、易学易用0.2. SQL支持三级模式结构外模式●外模式对应于视图View和部分基本表Base Table ●用户可以用SQL语言对基本表和视图进行操作●从用户的观点看基本表和视图是一样的模式●模式对应于基本表●基本表是独立存在的表●每个基本表对应一个关系内模式●内模式对应于存储文件●存储文件是在计算机存储介质中存放的文件形式●一个或若干个基本表对应一个存储文件视图●视图是从一个或几个基本表或其他视图导出的表●视图并不存放实际的数据,仅保存视图的定义●使用视图时,根据视图定义,从基本表中取数据●因此,视图实际上是一个虚表1.3. 删除基本表2.1. 插入数据(3) 插入应注意的问题对于表Student和SC若在SC 中插入的记录的Sno 在Student 不存在,则系统不允许插入. 2.2. 修改数据对满足条件的元组中的指定列用相应的表达式的值修改.(4)修改应注意的问题对于表Student 和SC 若修改Student 中的Sno,而未修改SC 中对应记录的Sno.若修改SC 中的Sno,而未修改Student 中对应的Sno. 2.3. 删除数据一个学生的各种数据可能存放在多个表中,但一个删除语句只能对一个表进行删除,这样可能会引起数据不一致问题.3. 查询功能是数据库系统的核心.其中:● SELECT :表示查询● ALL :显示所有满足条件的元组 ● DISTINCT :消除重复元组 ● *:所有列● 目标列表达式:查询结果,可以有函数运算 ● FROM :从哪些表或视图中查询 ● WHERE :查询条件 ● GROUP BY:按指定的列分组,例如,计算每个学生平均成绩时,要按学号分组● HA VING :GROUP BY 分组的条件 ● ORDER BY :输出时按指定列排序 ● ASC :升序(缺省值) ● DESC :降序3.1. 单表查询 (1)查询指定列(2) 按用户要求的顺序查询指定列 (3) 查询全部列(6) 查询满足条件的元组(7) 对查询结果排序● 统计元组个数:COUNT([DISTINCT|ALL]|*)● 统计一列中值的个数:COUNT([DISTINCT|ALL]<列名>)● 对一列求和:SUM([DISTINCT|ALL]<列名>) ● 对一列求平均值:A VG([DISTINCT|ALL]<列名>) ● 求一列中最大值:MAX([DISTINCT|ALL]<列名>) ● 求一列中最小值:MIN([DISTINCT|ALL]<列名>) DISTINCT: 消除重复元组 ALL: 所有元组,缺省值 (9) 对查询结果分组分组方法——用GROUP BY 子句将查询结果按某一列或多列值分组,值相等的为一组.若分组后还要按一定条件进行筛选, 可以用HA VING 短注意WHERE 与HAVING 语句的区别● WHERE :作用于基本表或视图,选择满足条件的元组● HA VING :作用于GROUP 分成的子组,选择满足条件的组3.2. 连接查询——若一个查询同时涉及两上或两个以上的表,则称为连接查询. 连接查询的种类连接条件中各属性的值应是可比的. 字段名可以相同,也可以不同.3.3子查询一个SELECT-FROM-WHERE 结构是一个查询块.将一个查询块嵌套在一个WHERE 或HA VING 子句的条件中,称为嵌套查询.● 当内查询返回的值为多个值时,可以通过集合进行. ● 当内查询返回的值为一个值时,可以通过等号比较符进行.● 当内查询返回的值与外查询具有某种比较关系时,可●>ANY 大于某一个值●>ALL 大于所有值●<ANY 小于某一个值●<ALL 小于所有值●>=ANY 大于等于某一个值●>=ALL 大于等于所有值●<=ANY 小于等于某一个值●<=ALL 小于等于所有值●=ANY 等于某一个值●=ALL 等于所有值●!=ANY 不等于某一个值3.5.交运算3.6. 差运算4.1. 索引的概念●索引的意义改善系统性能,加快查询速度.更新基本表时自动修改索引●索引的数量一个基本表可以按需要建立多个索引例如:对Student表对主码要建立索引若经常按姓名查询,则可按姓名建立索引若经常按系名查询,则可按系名建立索引●索引的代价维护索引需要花费时间4.2. 索引的分类●聚簇索引Clustered对数据记录进行物理排序一个基本表只有一个聚簇索引一般对主码建立聚簇索引●非聚簇索引NonClustered对于需经常查询、计算、更新的属性可建立非聚会簇索引索引信息单独存放在另一个索引名中●惟一索引也是一种非聚簇索引索引的属性不包含重复值4.4. 删除索引索引建立后,由系统进行维护,不需用户干预.频繁增、删、改数据,将花费系统的时间维护索引,因此,●T-SQL的概念T-SQL是Microsoft对标准SQL的扩展.T-SQL语言是一种交互式查询语言.直接使用SQL语句将SQL语句嵌入到高级语言中T-SQL有自己的数据类型、表达式、关键字和语句结构.SQL语句在查询分析器中执行.●常量,变量,数据类型,运算符与表达式(2) 变量变量名变量的分类全局变量——系统提供的变量,作为函数引用——格式: @@变量名局部变量——用户定义的变量,存放单个值——格式:@变量名●流程控制语句——条件、case、循环、注释●函数聚合函数:聚合函数用于对一组值执行计算并返回一个值.数学函数:三角函数、幂函数、符号函数、其他数学函数●SQL语句简介。
数据库系统课程设计报告

目录1绪论 (1)1.1项目简介 (1)1.2设计目的 (1)1.3设计内容 (1)1.4应用范围 (1)2需求分析 (1)2.1数据需求 (1)2.2事务需求 (2)2.3详细功能分析 (2)2.4数据字典 (2)2.5开发运行环境 (3)2.6安全保障 (3)3概念设计 (3)3.1实体及联系抽象 (3)3.2E-R图 (4)3.3关系模式 (5)4逻辑设计 (5)4.1各表功能 (5)4.2各表结构 ...................................................................... 错误!未定义书签。
4.3表关系图 (11)5物理设计 (11)5.1物理存储 (11)5.2完整性约束 (11)5.3视图设计 ...................................................................... 错误!未定义书签。
5.4触发器设计 .................................................................. 错误!未定义书签。
6系统实现与维护 (13)6.1模块1 (13)6.2模块2 (17)6.3模块3 ........................................................................... 错误!未定义书签。
7总结 (1)7.1系统实现程度 (1)7.2问题及难点 (1)7.3收获与体会 (1)1绪论1.1项目简介近年来,中国医药行业迅速发展,药店企业多业态经营,仓储式大型超市、中等规模超市、便利连锁综合发展。
随着规模的扩大,传统的医药管理已经不能适应发展的需要,很难在激烈的竞争中生存。
通过对从事医药产品的零售、批发等工作企业的深入调查,发现其业务主要包括企业药品销售、出入库管理、企业的财务、人事管理等。
哈工大 数据库系统 第1章

数据库系统语言基础教研室:侯俊英第一章数据库引论1.1 数据库系统概述1.1.1 基本概念1. 数据:是描述事物的符号记录。
2. 数据库:是长期存在计算机内的,有组织的、可共享的数据集合。
3. 数据库管理系统(DataBase Management System DBMS)::数据库管理系统是位于用户和操作系统之间的一层数据管理软件。
科学组织、存储数据完成此任务的软件DBMS 高效获取和维护数据数据库管理系统的功能:•数据定义功能;•数据操纵功能;•数据库的运行管理;•数据库的建立和维护功能。
1.1.2 数据库管理技术的产生和发展(了解)1.人工阶段;2.文件管理阶段;3.数据库系统阶段。
1.1.3 数据库系统的特点:1.数据结构化;数据不再针对某一应用,而是面向全组织、具有整体的结构化。
2. 数据的共享性高、冗余度低、易扩充;3. 数据的独立性高;物理独立性数据的独立性逻辑独立性物理独立性:用户的应用程序与存储在磁盘上的数据库中的数据是相互独立的。
逻辑独立性:用户的应用程序与数据库的逻辑结构是相互独立的。
4. 数据由DBMS统一管理和控制。
数据库的共享是并发的共享,DBMS还必须提供以下几方面的数据控制功能:(1) 数据的安全性保护;(2) 数据的完整性检查;(3) 并发控制;( 4) 数据库恢复。
1.2数据模型数据模型就是现实世界的模拟。
概念模型:是按用户的观点对数据和信息建模;数据模型:是数据库系统的核心和基础。
现实世界机器世界信息世界1.2.1 数据模型的组成要素1. 数据结构——系统的静态特性的描述;2. 数据操作——系统的动态特性的描述;3. 完整性约束——一组完整性规则的集合。
1.2.2 概念模型一、信息世界中的基本概念:1. 实体:客观存在并可相互区别的事物。
2. 实体集:同型实体集合称为实体集。
3. 属性:实体所具有的某一方面的特性。
4. 码:唯一标识实体的属性集合。
5. 域:属性的取值范围。
第0章_《数据库导论》课程简介_V10

数据库导论Introduction of Data Base张建国哈工大计算机科学与技术学院本课程的基本信息课程中文名称:数据库导论课程英文名称:Introduction of Data Base 授课对象:DIT09总学时: 52理论学时:13实验学时: 26辅导学时:13先修课程:计算机基础, 高级语言程序设计课程要求:必修课课程信箱: zjghit@本课程的意义本课程主要培养学生掌握数据库系统的基本概念、基本理论和数据库应用的基本方法.通过本课的学习,可以使你了解数据库的基本知识理解数据库的基本概念建立数据库的基本思想熟悉数据库的基本操作体会数据库在计算机文化中的地位为以后学习和应用数据库技术打下较扎实的基础本课讲授的主要内容第1章数据库系统概述第2章数据库系统结构第3章关系数据库第4章SQL Server 简介第5章结构化查询语言SQL第6章索引与视图第7章数据库安全及SQL Server的安全管理本课程的考核要求考试以学生完成日常作业和实验环节为必要条件,期末考试采用笔试;本课程总成绩为100分,其中成绩评定由两部分组成:期末考试成绩: 70%实验成绩: 30%本课程的相关软件环境Windows XPWindows ServerSQL Server 2000Word 2003本课程的教材何玉洁编著, 数据库原理与应用教程, 机械工业出版社2003.1参考教材萨师煊、王珊编著, 数据库系统概论(第三版),高等教育出版社,2000.3参考教材(Cont.)周立柆等编著,SQL Server 数据库原理——设计与实现,清华大学出版社,2004.3Abraham Silberschatz,Database System Concepts(4th Edition), 高等教育出版社2003.2 影印版相关网站微软中文网站SQL Server网页:/china/sql/超越——数据库编程:/ 软件工程专家网:华章图书网站:。
数据库系统(下):管理与技术_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年

数据库系统(下):管理与技术_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.若事务T对数据R已加S锁,则其它事务对R__________。
答案:可以加S锁不能加X锁;2.T1,T2是两个事务。
图(a)(b)(c)给出这两个事务的三种调度,这三种调度会出现什么问题呢,正确的选项是_____________。
答案:图(a)的调度会出现“丢失修改”,图(b)的调度会出现“重复读错误”,图(c)的调度会出现“脏读”。
3.日志文件是用于记录__________。
答案:对数据的所有更新操作;4.下列说法正确的是__________。
答案:检查点是DBMS强制使内存DB Buffer中的内容与介质DB中的内容保持一致的时刻点。
5.介质故障的恢复需要_________。
答案:以上工作都需要,但需要注意操作的次序。
6.关于用Redo型日志进行数据库恢复,下列说法正确的是____________。
答案:用Redo型日志恢复是对已完成的事务,将日志记录的值写回磁盘;而对未完成的事务,跳过;7.一个磁盘的基本信息为32个圆盘,64个盘面,每个盘面有65536个磁道,每个磁道(平均)有256个扇区,每个扇区有512个字节,问该磁盘的存储容量为_________。
答案:8.关于索引的下列说法正确的是____________。
答案:主索引是DBMS自动建立和维护的,关于其他数据项上的索引需要DBA来建立,DBMS可自动维护DBA建立的索引9.关于索引的下列说法不正确的是__________。
答案:稠密索引,对于Table中的每一个记录,总是有一个索引项10.用B+树建立主索引,下列说法正确的是__________。
答案:非叶结点某索引项X的左侧指针指向键值<X记录所在的索引文件存储块11.已知一棵B+树,如下图所示。
若要在此B+树上增加一个键值为45的索引项,插入完成后的B+树是___________。
哈尔滨工程大学数据库课后习题

第二章1.设有数据库S(Sno,Sname,Sage,Ssex)C(Cno,Cname, Cpno) SC(Sno,Cno,Grade)试用关系代数表达式表示一下查询要求:1.查询选修了课程号为C2的学生号;πSno(σCno=‘2’(SC))2.查询选修数据库课程的女学生的学生号;πSno(σCname=‘DB’∧Ssex=‘女’(S C SC))3.查询至少选修C1和C3课程的学生号;πSno,Cno(SC)÷πCno(σCno=‘C1’∨Cno=‘C3’(C))4.查询至少选修一门先行课号为C5的学生姓名;πSname(σCpno=‘5’(C) SC πSno,Sname(S))第三章本章习题51.SELECT SNAME,CITYFROM S;2.SELECT PNAME,COLOR,WEIGHTFROM P;3.SELECT DISTINCT(JNO)FROM SPJWHERE SNO=‘S1’;4.SELECT P.PNAME,SPJ.QTYFROM P,SPJWHERE P.PNO=SPJ.PNO AND SPJ.JNO=‘J2’;5.SELECT DISTINCT PNOFROM SPJWHERE SNO IN (SELECT SNOFROM SWHERE CITY=‘上海’);6.SELECT JNAMEFROM J,SPJ,SWHERE J.JNO=SPJ.JNO ANDSPJ.PNO=P.PNO ANDSPJ.SNO=S.SNO7.SELECT JNOFROM SPJWHERE NOT EXISTS (SELECT * FROM SWHERE SPJ.SNO=S.SNOAND S.CITY=‘天津’);8.UPDATE PSET COLOR=‘蓝’WHERE COLOR=‘红’;9.UPDATE SPJSET SNO=‘S3’。
数据库系统与设计学习指导

《数据库系统与设计》学习指导徐汉川课程名称:数据库系统与设计英文名称:Database System and Design开课院系:计算机科学与技术学院语言基础教研室开课学时:48实验学时:12学分:3授课对象:远程教育学院专升本计算机科学与技术专业学生一、教学目的与课程性质、任务本课程是一门重要的计算机课程。
它主要介绍数据库的基础知识、数据库设计、数据库编程等。
《数据库系统与设计》是哈尔滨工业大学远程教育计算机专业(本科)教学计划中的一门专业课,它是一门开拓视野、增长知识、提高实际工作能力的计算机课程。
本课程既有理论基础,又有重要的实际应用价值。
二、教学要求通过本课程的学习,应使学生达到以下基本要求:了解和掌握数据库的发展及基础知识;了解和掌握数据库建模知识;能够熟练运用基本的SQL语句等;了解以java语言为主的客户端程序的开发。
数据库设计、SQL语言和编写java客户端程序作为实践的内容。
其中SQL语言和编写java客户端程序将在实验课中进行实践。
在教学环节上,对学生的学习提出“掌握”和“了解”两个层次上要求,所谓“掌握”,是指学生在课后,必须能将所学内容用自己理解后的计算机术语复述出来,这是将所学知识熟练应用到实践中的基础。
所谓“了解”,是要求学生对所学内容有初步的认知,不要求完全复述出来,但在遇到相关问题时要求能够辨识。
教学以课堂讲授为主,辅之以实验等方式。
三、教学进度表四、教学内容安排五、上机实验安排实验学时为12学时,要求完成6个实验。
为了保证能按时完成实验,学生应事先按照下面的具体要求编写好有关有程序,然后在安排的实验期间进行调试,只有程序调试通过后,实验方为合格。
其中实验六可根据学生程度选做。
实验一、数据库的建立及数据的录入(2课时)建立SQL的数据库表并装入数据。
具体内容按实验指导书要求。
实验二、数据库查询(2课时)数据库的一些简单查询。
具体内容按实验指导书要求。
实验三、数据库查询(2课时)表的连接及子查询。
2022年哈尔滨工业大学数据科学与大数据技术专业《数据库系统原理》科目期末试卷B(有答案)

2022年哈尔滨工业大学数据科学与大数据技术专业《数据库系统原理》科目期末试卷B(有答案)一、填空题1、在设计局部E-R图时,由于各个子系统分别有不同的应用,而且往往是由不同的设计人员设计,所以各个局部E-R图之间难免有不一致的地方,称为冲突。
这些冲突主要有______、______和______3类。
2、关系数据库中基于数学的两类运算是______________和______________。
3、从外部视图到子模式的数据结构的转换是由______________实现;模式与子模式之间的映象是由______________实现;存储模式与数据物理组织之间的映象是由______________实现。
4、设某数据库中有作者表(作者号,城市)和出版商表(出版商号,城市),请补全如下查询语句,使该查询语句能查询作者和出版商所在的全部不重复的城市。
SELECT城市FROM作者表_____SELECT城市FROM出版商表;5、在SELECT命令中,______子句用于选择满足给定条件的元组,使用______子句可按指定列的值分组,同时使用______子句可提取满足条件的组。
6、已知系(系编号,系名称,系主任,电话,地点)和学生(学号,姓名,性别,入学日期,专业,系编号)两个关系,系关系的主码是______________,系关系的外码是______________,学生关系的主码是______________,外码是______________。
7、安全性控制的一般方法有____________、____________、____________、和____________视图的保护五级安全措施。
8、数据库恢复是将数据库从______状态恢复到______的功能。
9、在SQL Server 2000中,某数据库用户User在此数据库中具有对T 表数据的查询和更改权限。
现要收回User对T表的数据更改权,下述是实现该功能的语句,请补全语句。
哈工大数据库系统练习题

数据库系统练习题一、选择题:1.()是按照一定的数据模型组织的、长期存储在计算机内,可为多个用户共享的数据的集合。
(A)数据库系统(B)数据库(C)关系数据库(D)数据库管理系统2.数据库系统的基础是()。
(A)数据结构(B)数据库管理系统(C)操作系统(D)数据模型3.()处于数据库系统的核心位置。
(A)数据字典(B)数据库(C)数据库管理系统(D)数据库管理员4.对数据库的操作要以()内容为依据。
(A)数据模型(B)数据字典(C)数据库管理系统(D)运行日志5.查询处理最复杂的最重要的部分是()。
(A)检查是否存在所查询的关系(B)检查该操作是否在合法的授权范围内(C)确定查询路径(D)查询优化6.有了模式/内模式的映象,可以保证数据和应用程序之间的()。
(A)逻辑独立性(B)物理独立性(C)数据一致性(D)数据安全性7.()是数据库中全部数据的逻辑结构和特征的描述。
(A)模式(B)外模式(C)内模式(D)存储模式8.()是数据库物理结构和存储方式的描述。
(A)模式(B)外模式(C)内模式(D)概念模式9.()是用户可以看见和使用的局部逻辑结构和特征的描述。
(A)模式(B)外模式(C)内模式(D)概念模式10.数据库管理系统允许用户把一个或多个数据库操作组成(),它是一组按顺序执行的操作单位。
(A)命令(B)事务(C)文件(D)程序11.关系中标题栏中各列的名称称为(A)对象(B)元组(C)属性(D)记录12.在下述关系的特点中,错误的是()。
(A)列可以交换(B)行可以交换(C)任意两元组不能相同(D)表中的数据项可分13.关系模式进行投影运算后()。
(A)元组个数等于投影前的元组个数(B)元组个数小于投影前的元组个数(C)元组个数小于或等于投影前的元组个数(D)元组个数大于或等于投影前的元组个数14.在关系中,能唯一标识元组的属性集称为关系模式的()。
(A)候选码(B)主码(C)外码(D)主键15.δF1(δF2(E))等价于(E)(B)δF1(E)(A)δF1∨F2(C)δF1(E)(D)δF2(E)∧F216.关系R与关系S只有一个公共属性,T1是R与S作θ连接的结果,T2是R 与S自然连接的结果,则()。
哈工大数据库作业_银行管理系统
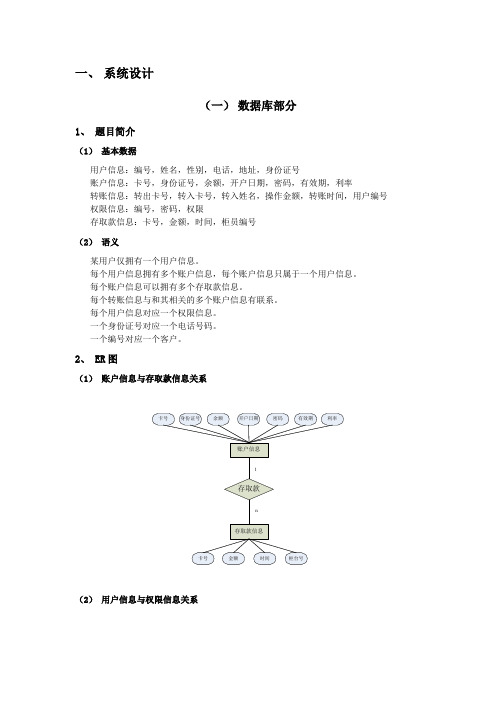
一、系统设计(一)数据库部分1、题目简介(1)基本数据用户信息:编号,姓名,性别,电话,地址,身份证号账户信息:卡号,身份证号,余额,开户日期,密码,有效期,利率转账信息:转出卡号,转入卡号,转入姓名,操作金额,转账时间,用户编号权限信息:编号,密码,权限存取款信息:卡号,金额,时间,柜员编号(2)语义某用户仅拥有一个用户信息。
每个用户信息拥有多个账户信息,每个账户信息只属于一个用户信息。
每个账户信息可以拥有多个存取款信息。
每个转账信息与和其相关的多个账户信息有联系。
每个用户信息对应一个权限信息。
一个身份证号对应一个电话号码。
一个编号对应一个客户。
2、 ER图(1)账户信息与存取款信息关系卡号身份证号余额开户日期密码有效期利率账户信息1存取款n存取款信息卡号金额时间柜台号(2)用户信息与权限信息关系用户信息权限信息姓名性别电话地址身份证号编号编号密码权限1授权11(3) 账户信息与转账信息关系账户信息转账信息转出卡号转入卡号转入姓名操作金额转账时间柜台号卡号身份证号余额开户日期密码有效期利率转账mn(4) 账户信息与用户信息关系用户信息姓名性别电话地址身份证号编号拥有1账户信息卡号身份证号余额开户日期密码有效期利率n(5) 所有实体之间的ER 图实体:(1)用户信息(编号,姓名,性别,电话,地址,身份证号)(2)账户信息(卡号,身份证号,余额,开户日期,密码,有效期,利率)(3)转账信息(转出卡号,转入卡号,转入姓名,操作金额,转账时间,柜台号)(4)权限信息(编号,密码,权限)(5)存取款信息(卡号,金额,时间,柜台号)3、关系模式图(1)用户信息Cinfo(第二范式)范式分析:关系中不包含重复着的关系,满足第一范式要求;在此基础上,此关系中只有一个主码‘ID’,满足第二范式要求;此关系中的非主属性为姓名、性别、地址,这三者之间不存在传递关系,但是ID→Cno,Cno→Addrs,所以Addrs传递依赖于ID,没有满足第三范式的要求,但是在此系统中,并没有造成很大的麻烦。
哈工大数据库作业(及答案)

第二章1. 在第59页的图2.3所示的三个关系Student,Course,SC 中,将下列关系代数表达式用汉语表示出来。
)))()(((12,12C SC S πππ÷∞答:查询选修了全部课程的学生姓名。
2.设有如图所示的两个关系E1和E2,其中E2是从E1中经过关系运算形成的结果,试给出该运算表达式。
答;从E1生成E2经过的关系运算是或3.已知一个关系数据库的模式如下:S(Sno,Sname,Scity)P(Pno,Pname,Color,Weight)J(Jno,Jname,Jcity)SPJ(Sno,Pno,Jno,Qty)其中,S表示供应商,它的各属性依次为供应商号、供应商名和供应商所在城市;P表示零件,它的各属性依次为零件号、零件名、零件颜色和零件重量;J表示工程,它的各属性依次为工程号、工程名和工程所在城市;SPJ表示供货关系,它的各属性依次为供应商号、零件号、工程号和供货数量。
用关系代数表达式表示下面的查询要求:找出向北京的供应商购买重量大于30的零件的工程名。
答:对应的关系代数表达式为:或4. 设有学生课程数据库中包含如下关系:S(Sno,Sname,Sex,SD,Age)C(Cno, Cname,Term,Credit)SC(Sno,Cno,Grade)其中,S为学生表,它的各属性依次为学号、姓名、性别、系别和年龄;C为课程表,它的各属性依次为课程号、课程名、上课学期和学分;SC为学生选课成绩表,它的各属性依次为学号、课程号和成绩。
请用关系代数表达式查询如下问题:(1)查询选修课程名为“数学”的学生学号和姓名。
(2)查询至少选修了课程号为“1”和“3”的学生学号。
(3)查询选修了课程号为“操作系统”或“数据库”课程的学生学号和姓名。
(4)查询年龄在18~20之间(含18和20)的女生的学号、姓名和年龄。
(5)查询选修了“数据库”课程的学生的学号、姓名和成绩。
(6)查询选修全部课程的学生姓名和所在的系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表示为: R(U,D,dom,F)
v R 关系名 v U 组成该关系的属性名集合 v D 属性组U中属性所来自的域 v dom 属性向域的映象集合 v F 属性间的数据依赖关系集合
ABC R-S a1 b1 c1
3. 交(Intersection) R∩S = { t|t ∈ R∧t ∈S } R∩S = R –(R-S)
仍为n目关系,由既属于R又属于S的元组组成 说明:同并、差。
ABC
R ∩ S a1 b2 c2
a2 b2 c1
4. 广义笛卡尔积(Extended Cartesian Product) 设关系R为n目关系,K1个元组;关系S为m目关系,K2个元 组, 则R×S 列:(n+m)列的元组的集合。元组的前n列是关系R的一个 元组,后m列是关系S的一个元组
v 用户定义后由系统支持。
2.2 关系数据结构及形式化定义
关系模型建立在集合代数的基础上的,从集合论角度给出关 系数据结构的形式化定义。 2.2.1 基本概念
1.域(Domain) 定义2.1 域是一组具有相同数据类型的值的集合。 举例:
v {男,女}; v 长度小于10字节的字符串; v 实数; v 介于某个取值范围的整数。
说明: (1) 实体完整性规则是针对基本关系而言的。一个基本表通 常对应现实世界的一个实体集或联系; (2) 现实世界中的实体和实体间的联系都是可区分的,即它 们具有某种唯一性标识; (3) 相应地,关系模型中以主码作为唯一性标识; (4) 主码中的属性即主属性不能取空值。空值就是“不知道”或 无意义”的值。 主属性取空值,就说明存在不可区分的实体,这 与第(2)点相矛盾,因此这个规则称为实体完整性。
(1) 关系语言是一种高度非过程化的语言; v 存取路径的选择由DBMS的优化机制来完成。 v 用户不必用循环结构就可以完成数据操作。
(2) 能够嵌入高级语言中使用; (3)关系代数、关系演算语言在表达能力上完全等价。
三、关系的三类完整性约束
实体完整性 参照完整性
必须满足
由关系系统自动支持
用户定义完整性 v 反映应用领域需要遵循的约束条件,体现了具体领域中的 语义约束;
列起一个名字,称为属性(Attribute)。 n目关系必有n个属性。
(5)码:
v 若关系中的某一属性组的值能唯一地标识一个元组,则称该 属性组为候选码; v 若一个关系有多个候选码,则选定其中一个为主码 (Primary key),主码的诸属性称为主属性。在最简单的情 况下,候选码只包含一个属性; v 在最极端的情况下,关系模式的所有属性组是这个关系模式 的候选码,称为全码(All-key)。
3. 关系
定义2.3 D1×D2×…×Dn的子集叫作在域D1,D2,…,Dn 上的关系,表示为 R(D1,D2,…,Dn)
R:关系名 n:关系的目或度(Degree)
注意:关系是笛卡尔积的有限子集。无限关系在数据库系统 中是无意义的。
例 在表2.1 的笛卡尔积中取出有实际意义的元组来构造关系 关系:SAP(SUPERVISOR,SPECIALITY,POSTGRADUATE)
例: 课程(课程号,课程名,学分) v “课程号”属性必须取唯一值 v 非主属性“课程名”也不能取空值 v “学分”属性只能取值{1,2,3,4}
2.4 关 系 代 数
关系代数介绍: 1. 关系代数:
一种抽象的查询语言,用对关系的运算来表达查询。
2. 关系代数运算的三个要素
运算对象 运算结果 运算符
例:学生(学号,姓名,性别,专业号,年龄,班长)
“班长”属性值可以取两类值:
(1)空值,表示该学生所在班级尚未选出班长,或该学生本人 即是班长; (2)非空值,这时该值必须是本关系中某个元组的学号值
三、用户定义完整性 用户定义完整性就是针对某一具体关系数据库的约束条件,
它反映某一具体应用所涉及的数据必须满足的语义要求。
例2 学生、课程、学生与课程之间的多对多联系 学生(学号,姓名,性别,专业号,年龄) 课程(课程号,课程名,学分) 选修(学号,课程号,成绩)
(3)同一关系内部属性间也可能存在引用关系。 例3 关系学生2(学号,姓名,性别,专业号,班长学号)
2. 外码与参照完整性规则: 若属性A不是基本关系R的主码,但却是另一基本关系S的主 码,则在关系R中A的取值或者取空值或者取在S中存在的A值。此 时A称为关系R的外码。
a1 b2 c2 a2 b2 c1
ABC
S a1 b2 c2 a1 b3 c2
a2 b2 c1
ABC a1 b1 c1 R∪S a1 b2 c2 a1 b3 c2 a2 b2 c1
2. 差(Difference) R -S = { t|t∈R∧t∉S } 仍为n目关系,由属于R而不属于S的所有元组组成 说明:同并
笛卡尔积元素(d1,d2,…,dn)中的每一个值di叫作一个分 量。
例 给出三个域:
D1=SUPERVISOR ={ 张清玫,刘逸 } D2=SPECIALITY={计算机专业,信息专业} D3=POSTGRADUATE={李勇,刘晨,王敏} 则D1,D2,D3的笛卡尔积为: D1×D2×D3 ={(张清玫,计算机专业,李勇),(张清玫, 计算机专业,刘晨), (张清玫,计算机专业,王敏), (张清玫,信息专业,李勇), (张清玫,信息专业,刘 晨),(张清玫,信息专业,王敏), (刘逸,计算机专业, 李勇),(刘逸,计算机专业,刘晨), (刘逸,计算机专 业,王敏),(刘逸,信息专业,李勇), (刘逸,信息专 业,刘晨),(刘逸,信息专业,王敏) }
关系名(属性名1, 属性名2 , 属性名3) 假设:导师与专业:1:1,导师与研究生:1:n 于是:SAP关系可以包含三个元组
{ (张清玫,信息专业,李勇), (张清玫,信息专业,刘晨), (刘逸,信息专业,王敏)
(1)元组 关系中的每个元素是关系中的元组,通常用t 表示。
(2)单元关系与二元关系
当n=1时,称该关系为单元关系(Unary relation)。 当n=2时,称该关系为二元关系(Binary relation)。
二、参照完整性
1. 关系间的引用
在关系模型中实体及实体间的联系都是用关系来描述的,因 此可能存在着关系与关系间的引用。
(1)两个关系之间存在着属性引用: 例1 学生实体、专业实体以及专业与学生间的一对多联系 学生(学号,姓名,性别,专业号,年龄) 专业(专业号,专业名)
(2)三个关系之间存在着属性引用:
传统的集合运算 并、差、交、广义笛卡尔积
专门的关系运算 选择、投影、连接、除
2.4.1 传统的集合运算 1. 并(Union)
R∪S = { t|t ∈ R∨t ∈S } 仍为n目关系,由属于R或属于S的元组组成
说明: Ø 具有相同的目n(即两个关系都有n个属性) Ø 相应的属性取自同一个域
ABC R a1 b1 c1
关系模式通常可以简记为 R (U) 或 R (A1,A2,…,An)
R 关系名 A1,A2,…,An 属性名
注:域名及属性向域的映象常常直接说明为 属性的类型、长度
定义2.5 在一个给定的应用领域中,所有实体及实体之间联 系的关系的集合构成一个关系数据库。
2.3 关系的完整性
一、实体完整性 规则2.1 实体完整性规则:若属性A 是基本关系R的主属
第二章 关 系 数 据 库
关系数据库简介:
系统而严格地提出关系模型的是美国IBM公司的E.F.Codd。 Ø 1970年提出关系数据模型; Ø之后,提出了关系代数和关系演算的概念; Ø 1972年提出了关系的第一、第二、第三范式; Ø 关系数据库应用数学方法来处理数据库中的数据; Ø 80年代后,关系数据库系统成为最重要、最流行的数据库 系统。
(3)关系的表示: 关系也是一个二维表,表的每行对应一个元组,表的每列对应 一个域。
举例:
SUPERVISOR 张清玫 张清玫 刘逸
表2.2 SAP关系
SPECIALITY 信息专业 信息专业 信息专业
POSTGRADUATE 李勇 刘晨 王敏
(4)属性: 关系中不同列可以对应相同的域,为了加以区分,必须对每
基本关系(基本表或基表)
(6)关系的种类 查询表
视图
Ø 基本表:实际存在的表,是实际存储数据的逻辑表示;
Ø 查询表:查询结果对应的表;
Ø 视图表:由基本表或其他视图表导出的表,是虚表,不对应实 际存储的数据
(8)关系的特性:
•列同性; •不同列可以选同一域值; •列可交换; •行可交
换;
•任意两元组不能完全相同; •表中数据项不可分。
性,则属性A不能取空值。 例:SAP(SUPERVISOR,SPECIALITY,POSTGRADUATE)
POSTGRADUATE属性为主码(假设研究生不会重名),则 其不能取空值
注意: 实体完整性规则规定基本关系的所有主属性都不能取空值,
而不仅是主码整体不能取空值。
例:学生选课关系“选修(学号,课程号,成绩)”中,“学 号、课程”为主码,则“学号”、“课程”两个属性都不能取空值。
1.常用的关系操作 (1)查询
选择、投影、连接、除、并、交、差。
(2)数据更新
插入、删除、修改。 注:查询的表达能力是其中最主要的部分。 2. 关系操作的特点:
集合操作方式,即操作的对象和结果都是集合。 3. 关系数据语言的种类:
关系代数语言 关系数据语言 关系演算语言
具有关系代数和关系演算双重特点的语 言——SQL语言 4. 关系数据语言的特点:
关系 关系 集合、专门、算术和逻辑运算符四类
