生产运作管理计算题1范文
生产运作管理课后计算机题及实践题部分答案

生产运作管理课后计算机题及实践题部分答案 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#生产运作管理课后计算机题及实践题(部分)答案一、计算题 第四章计算题1、一个制造厂计划在某车间旁增加一侧房,建一条新的生产线,……。
解:A 方案的月运输量是:(15+15)×2000+(15+10)×2000+(30+10)×3000+(15+10)×1000+(20+35)×3000 =420000(m ).B 方案的月运输量是:(25+35)×2000+(25+10)×2000+(10+10)×3000+(15+10)×1000+(10+25)×3000 =380000(m ).故B 方案的月运输量最小。
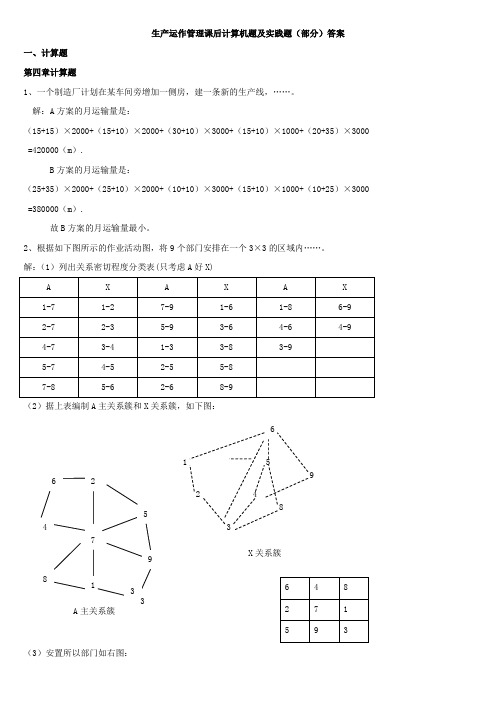
2、根据如下图所示的作业活动图,将9个部门安排在一个3×3的区域内……。
解:(1)列出关系密切程度分类表(只考虑A 好X)(2)据上表编制A 主关系簇和X 关系簇,如下图:(3)安置所以部门如右图:X 关系簇3、答案: 节拍为分/件,个工作日4、答案 :(2)节拍为分/件,(3)最小工作地数为5 (4)重新组合的工作地为:(A,B),(C,D,E),(F,G),(H,I),(J),(K,L),效率为%5、答案 :为A 第五章计算题:1、一个工作人员欲制定一个金属切削作业的时间定额…… 解:正常时间为:×125%=13(分)标准时间为:13×(1+16%)=(分)2、观测一项作业,共60次…… 解:(1)观测到的时间:分钟 (2)正常时间:×95%=分钟(3)标准时间:×95%×(1+10%)=分钟 3、答案:377分钟。
4、答案:分钟。
5、一新达成的工会合同允许……解:正常工作时间:1461+=6.35460⨯⨯()(分) 标准作业时间:24+106.351+=7.2240+14()(分)6、答案:57次观察。
生产运作管理习题集(计算)

有一批零件,需经四道工序加工,各工序单件加工时间分别为: T 1=15 分钟,T 2=10分钟,T 3=15分钟, T 4=10分钟,设批量为5件,试用求平行、顺序、平行顺序移动方式下的加工周期。
求总流程时间最小化的加工顺序,并计算加工周期.某公司现有两个工厂A 和B ,3个仓库U 、V 和W 。
这些工厂和仓库位于不同的城市,为满足日益增长的市场需求,公司决定再建一新工厂,现有X 和Y 两个备选厂址可供选择,各工厂生产能力、各仓库需求及工厂到仓库的单位运费如表所示,试比较选择运费较少的工厂选址方案。
用Johnson 算法求以下8/2/F/FmAx 问题的最优解。
某公司现有3个工厂A 、B 和C ,它们在3个不同的城市。
有2个仓库P 和Q ,它们位于不同的城市,仓库用来存放工厂生产的产品,随时供应用户,每个仓库每月需供应市场2100吨产品。
为了更好地为顾客服务,该公司决定再建一个新仓库。
经过调查分析,确定X与Y两个点可建仓库。
相关资料如下表所示。
东方制造公司组装安全监视器。
每年以65元的单价购买1800个单色阴极射线管。
订货成本是13元.年持有成本占购买价格的20%。
计算最佳订货批量,以及订购与持有成本的年总成本。
已知对某零件的净需求如下表所示,单位订货费用为100元,单位库存费用为0.25元/(件.周)。
试用MPG法确定订货安排。
某公司在一次事故中损坏了五台仪器,这些仪器都需要经过AB两道工序进行修复,每台仪器在各工序修理的时间如下表所示,且已知两工序分别由不同的人员担任。
任何一台仪器没有修复该公司都无法正常生产,试用Johnson方法对五台仪器修复顺序排序,使该公司能尽快恢复生产,并并计算流程时间。
某公司现有3个原料供应地MMM3和两个工厂FF2,准备在X城或Y城再建一个工厂。
现给出下表中的资料。
求最佳厂址。
据预测,市场每年对X公司生产的产品需求量为20000台,一年按250天计算,生产率为每天100台,生产提前期为4天。
生产运作管理课后计算机题及实践题答案
生产运作管理课后计算机题及实践题(部分)答案一、计算题 第四章计算题1、一个制造厂计划在某车间旁增加一侧房,建一条新的生产线,……。
解:A 方案的月运输量是:(15+15)×2000+(15+10)×2000+(30+10)×3000+(15+10)×1000+(20+35)×3000 =420000(m ).B 方案的月运输量是:(25+35)×2000+(25+10)×2000+(10+10)×3000+(15+10)×1000+(10+25)×3000 =380000(m ).故B 方案的月运输量最小。
2、根据如下图所示的作业活动图,将9个部门安排在一个3×3的区域内……。
解:(1)列出关系密切程度分类表(只考虑A 好X)(2)据上表编制A 主关系簇和X 关系簇,如下图:(3)安置所以部门如右图:X 关系簇3、答案: 节拍为分/件,个工作日4、答案 :(2)节拍为分/件,(3)最小工作地数为5 (4)重新组合的工作地为:(A,B),(C,D,E),(F,G),(H,I),(J),(K,L),效率为%5、答案 :为A 第五章计算题:1、一个工作人员欲制定一个金属切削作业的时间定额…… 解:正常时间为:×125%=13(分)标准时间为:13×(1+16%)=(分) 2、观测一项作业,共60次…… 解:(1)观测到的时间:分钟 (2)正常时间:×95%=分钟(3)标准时间:×95%×(1+10%)=分钟 3、答案:377分钟。
4、答案:分钟。
5、一新达成的工会合同允许……解:正常工作时间:1461+=6.35460⨯⨯()(分) 标准作业时间:24+106.351+=7.2240+14()(分)6、答案:57次观察。
7、答案:37个周期。
生产运作管理计算题及答案教学文案

⽣产运作管理计算题及答案教学⽂案【⽣产运作管理】重⼼法求⼯⼚设置地1、某企业决定在武汉设⽴⼀⽣产基地,数据如下表。
利⽤重⼼法确定该基地的最佳位置。
假设运输量与运输成本存在线性关系(⽆保险费)。
Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7.所以最佳位置为(3.05,3.7)。
1.某跨国连锁超市企业在上海市有3家超市,坐标分别为(37,61)、(12,49)、(29,20)。
现在该企业打算在上海建⽴分部,管理上海市的业务。
假设3家超市的销售额是相同的。
(6.3.24)(1)⽤重⼼法决定上海分部的最佳位置。
解:因为3家超市的销售额相同,可以将他们的销售额假设为1.上海分部的最佳位置,也就是3家超市的重⼼坐标,可以这样计算:x=(37+12+29)/3=27y=(61+49+20)/3=43.3(2)如果该企业计划在上海建⽴第四家超市,其坐标为(16,18),那么如果计划通过,上海分部的最佳位置应该作何改变?解:增加⼀家超市后,重⼼坐标将变为:x=(37+12+29+16)/4=24.3y=(61+49+20+18)/.4=37成本结构1、某商店销售服装,每⽉平均销售400件,单价180元/件,每次订购费⽤100元,单件年库存保管费⽤是单价的20%,为了减少订货次数,现在每次订货量是800件。
试分析:(1)该服装现在的年库存总成本是多少?(15000元)(2)经济订货批量(EOQ )是多少?(163件) (1)总成本=(800/2)*180*20%+(400*12/800)*100=15000元(2)EOQ =HDS 2=800/)12*400(100*12*400*2=163件(3)EOQ 总成本=(163/2)*180*20%+(400*12/163)*100=5879元(4)年节约额=15000-5879=9121元节约幅度=(9124/15000)*100%=60.81%2、某⾷品⼚每年需要采购3000吨⾯粉⽤于⽣产,每次采购订货⼿续费为300元,每吨产品的年库存成本为20元,请计算该⾷品⼚采购⾯粉的经济订货批量EOQ 。
(完整word版)生产与运作管理的计算题.docx

一、流水作业排序1.最长流程时间的计算例:有一个6/4/F/Fmax 问题,其加工时间如下表所示,当按顺序S=( 6, 1, 5, 2, 4, 3)加工时,求Fmax解:列出加工时间矩阵i615243Pi1348654Pi2137593Pi3875962Pi4352469根据公式:C kSi =max{C(k-1)Si, C kSi-1 }+ P Sik,计算各行加工时间,最后得出结果 Fmax=CmsnFmax=572.两台机器排序问题的最优算法( Johnson 算法)例:求下表所示的 6/2/F/Fmax 的最优解将工件 2 排在第 1 位2将工件 3 排在第 6 位23将工件 5 排在第 2 位253将工件 6 排在第 3 位2563将工件 4 排在第 5 位25643将工件 1 排在第 4 位256143最优加工顺序为S=(2,5,6,1,4,3)i256143ai134558bi274742由上表可算出,Fmax =283. 一般 n/m/F/Fmax 的最算法( 一 )Palmar 算法(λ i=∑ [k-(m+1)/2]P ik k=1,2,⋯,m按λ i不增的序排列工件)例:有一个 4/3/F/Fmax, 其加工如下表所示 , 用 Palmar 求解 .解:λ i=∑ [k-(3+1)/2]P ik,k=1,2,3λi=-Pi1+Pi3于是,λ 1=-P11+P13 =-1+4=3λ2=-P21+P23 ==2+5=3λ3=-P31+P33 =-6+8=2λ4=-P41+P43 =-3+2=-1按λ i不增的序排列工件,得到加工序(1, 2, 3, 4)和( 2,1,3,4),算,二者都是最序,Fmax=28( 二 ) 关工件法例 : 有一个 4/3/F/Fmax, 其加工如下表所示, 用关工件法求解.解:由上表可知,加工最的是 3 号工件, Pi1<=Pi3 的工件 1 和 2,按 Pi1 不减的序排成 Sa=(1,2),Pi1>Pi3 的工件 4 号工件,Sb=(4), 得到加工序( 1,2,3,4 )。
生产运作管理课后计算机题及实践题(部分)答案分析
生产运作管理课后计算机题及实践题(部分)答案一、计算题 第四章计算题1、一个制造厂计划在某车间旁增加一侧房,建一条新的生产线,……。
解:A 方案的月运输量是:(15+15)×2000+(15+10)×2000+(30+10)×3000+(15+10)×1000+(20+35)×3000 =420000(m ).B 方案的月运输量是:(25+35)×2000+(25+10)×2000+(10+10)×3000+(15+10)×1000+(10+25)×3000 =380000(m ).故B 方案的月运输量最小。
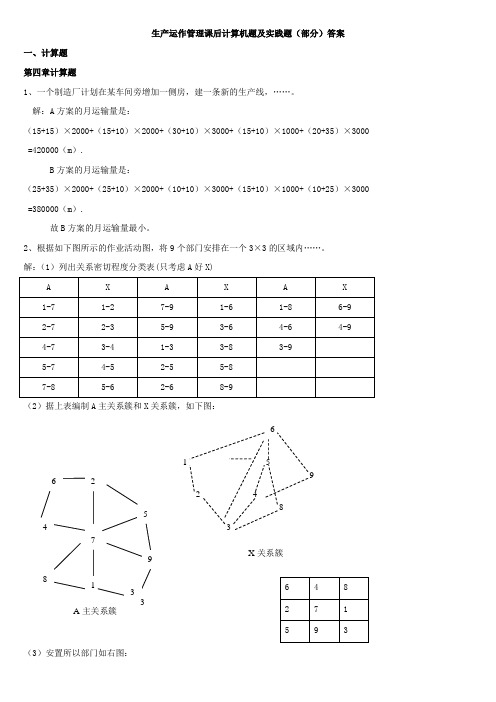
2、根据如下图所示的作业活动图,将9个部门安排在一个3×3的区域内……。
解:(1)列出关系密切程度分类表(只考虑A 好X)(2)据上表编制A 主关系簇和X 关系簇,如下图:(3)安置所以部门如右图:X 关系簇3、答案: 节拍为0.167分/件,31.86个工作日4、答案 :(2)节拍为0.25分/件,(3)最小工作地数为5 (4)重新组合的工作地为:(A,B),(C,D,E),(F,G),(H,I),(J),(K,L),效率为83.3%5、答案 :为A 第五章计算题:1、一个工作人员欲制定一个金属切削作业的时间定额…… 解:正常时间为:10.4×125%=13(分)标准时间为:13×(1+16%)=15.08(分) 2、观测一项作业,共60次…… 解:(1)观测到的时间:1.2分钟 (2)正常时间:1.2×95%=1.14分钟(3)标准时间:1.2×95%×(1+10%)=1.27分钟 3、答案:377分钟。
4、答案:5.85分钟。
5、一新达成的工会合同允许……解:正常工作时间:1461+=6.35460⨯⨯()(分) 标准作业时间:24+106.351+=7.2240+14()(分) 6、答案:57次观察。
生产与运作管理的计算题
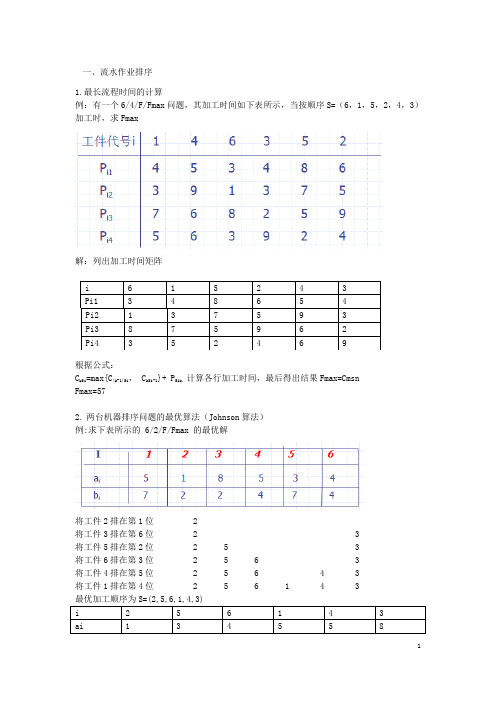
一、流水作业排序1.最长流程时间的计算例:有一个6/4/F/Fmax问题,其加工时间如下表所示,当按顺序S=(6,1,5,2,4,3)加工时,求Fmax解:列出加工时间矩阵i 6 1 5 2 4 3Pi1 3 4 8 6 5 4Pi2 1 3 7 5 9 3Pi3 8 7 5 9 6 2Pi4 3 5 2 4 6 9根据公式:C kSi=max{C(k-1)Si, C kSi-1}+ P Sik,计算各行加工时间,最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法(Johnson算法)例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3i 2 5 6 1 4 3ai 1 3 4 5 5 8bi 2 7 4 7 4 2由上表可计算出, Fmax =283. 一般n/m/F/Fmax 问题的最优算法(一)Palmar 算法(λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi 不增的顺序排列工件 ) 例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用Palmar 求解.解:λi= ∑ [k-(3+1)/2]P ik ,k=1,2,3λi=-Pi1+Pi3于是,λ1=-P11+P13 =-1+4=3 λ2=-P21+P23 ==2+5=3 λ3=-P31+P33 =-6+8=2 λ4=-P41+P43 =-3+2=-1按λi 不增的顺序排列工件 ,得到加工顺序(1,2,3,4)和(2,1,3,4),经计算,二者都是最优顺序,Fmax=28 (二)关键工件法例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用关键工件法求解.解:由上表可知,加工时间最长的是3号工件,Pi1<=Pi3的工件为1和2,按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件,Sb=(4),这样得到加工顺序为(1,2,3,4)。
生产运作管理习题集(计算)

有一批零件,需经四道工序加工,各工序单件加工时间分别为:T1=15 分钟,T2=10分钟,T3=15分钟,T4=10分钟,设批量为5件,试用求平行、顺序、平行顺序移动方式下的加工周期。
六种不同的零件,需经二台设备加工,各零件工艺顺序相同,资料如下:求总流程时间最小化的加工顺序,并计算加工周期.某公司现有两个工厂A和B,3个仓库U、V和W。
这些工厂和仓库位于不同的城市,为满足日益增长的市场需求,公司决定再建一新工厂,现有X和Y两个备选厂址可供选择,各工厂生产能力、各仓库需求及工厂到仓库的单位运费如表所示,试比较选择运费较少的工厂选址方案。
用Johnson算法求以下8/2/F/FmAx问题的最优解。
某公司现有3个工厂A、B和C,它们在3个不同的城市。
有2个仓库P和Q,它们位于不同的城市,仓库用来存放工厂生产的产品,随时供应用户,每个仓库每月需供应市场2100吨产品。
为了更好地为顾客服务,该公司决定再建一个新仓库。
经过调查分析,确定X与Y两个点可建仓库。
相关资料如下表所示。
试比较选公司应选择哪个点建新仓库使总运输成本最低。
东方制造公司组装安全监视器。
每年以65元的单价购买1800个单色阴极射线管。
订货成本是13元.年持有成本占购买价格的20%。
计算最佳订货批量,以及订购与持有成本的年总成本。
已知对某零件的净需求如下表所示,单位订货费用为100元,单位库存费用为0.25元/(件.周)。
试用MPG法确定订货安排。
某公司在一次事故中损坏了五台仪器,这些仪器都需要经过AB两道工序进行修复,每台仪器在各工序修理的时间如下表所示,且已知两工序分别由不同的人员担任。
任何一台仪器没有修复该公司都无法正常生产,试用Johnson方法对五台仪器修复顺序排序,使该公司能尽快恢复生产,并并计算流程时间。
某公司现有3个原料供应地MMM3和两个工厂FF2,准备在X城或Y城再建一个工厂。
现给出下表中的资料。
求最佳厂址。
据预测,市场每年对X公司生产的产品需求量为20000台,一年按250天计算,生产率为每天100台,生产提前期为4天。
生产运作管理试题(含答案).
综合练习题(一)一、名词解释(5×4=20分)JIT,并行工程,“浴盆”曲线,非独立性需求,生产系统二、分析计算题(40分)1、某企业决定在武汉设立一生产基地,数据如下表。
利用重心法确定该基地的最佳位置。
2、Piddling公司组装监视器,每年以65美元的价格购买3600个单色阴极管,订货成本为13美元,单个年持有成本为价格的20%。
计算最优订货批量及在最优订货条件下的定购及库存成本之和并说明经济订货批量的原理。
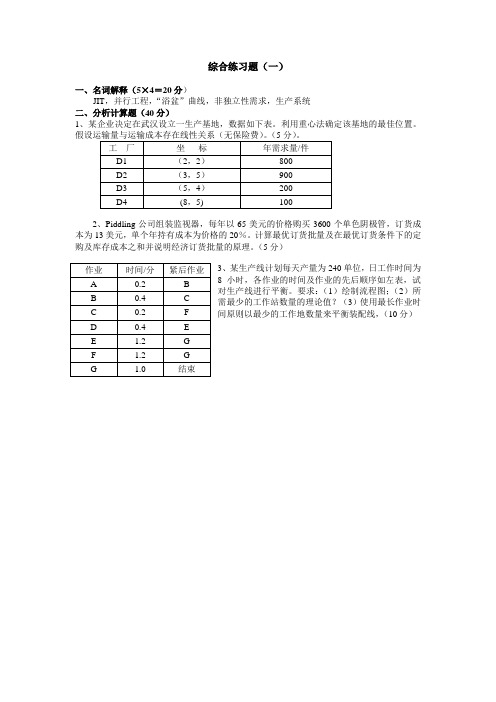
(5分)3、某生产线计划每天产量为240单位,日工作时间为8小时,各作业的时间及作业的先后顺序如左表,试对生产线进行平衡。
要求:(1)绘制流程图;(2)所需最少的工作站数量的理论值?(3)使用最长作业时间原则以最少的工作地数量来平衡装配线,(10分)4、某产品包括两个构件,A和B。
每制造一件产品需要2个A和4个B。
第6周开始时必须发送100单位该产品。
目前持有量为50个A和100个B。
另外还有两份应接收的B,每份为100单位,其中第一份在第4周初,第二份在第5周初收到。
该产品的生产提前期为2周,A、B各为1周。
用直接批量法为该产品作MRP。
(10分)5.某项工程的作业及有关数据如左表。
已知间接成本为每天1000元。
请确定工期缩短3周的方案。
(10)四、简答题(20分)1.服务系统有何特点?2.生产过程的组织有哪几种基本形式?3.有哪些针对需求变动变动的生产计划方法?4.质量管理经历了哪几个发展阶段?五、论述题(20分)请利用运作管理的相关知识谈谈如何提高企业的运作管理水平。
综合练习题(一)参考答案一、名词解释(5×4=20分)JIT:Just In Time的缩写,译为准时化生产。
JIT是由日本丰田公司首创的一种全新的管理体制,其目的是在原材料、在制品及产成品保持最小库存的情况下实现大批量生产,零件准时到达下道工序,并被下道工序迅速加工和转移。
基本思想是:只在需要的时候,按需要的量生产所需的产品;核心:追求库存或库存达到最小的生产系统,最终彻底消除无效劳动和浪费。
《生产与运作管理》计算题[可修改版ppt]
![《生产与运作管理》计算题[可修改版ppt]](https://img.taocdn.com/s3/m/a6bd807e6bd97f192379e91f.png)
项目 时间(小时) 1 2 3 4 5 6 7 7.5
A工序生产量 B工序生产量 两工序间流动
在制品
30 60 90 12 24 36 48 60 72 84 90 18 36 54 42 30 18 6 0
流动在制品占用量从0→最大值→0周而复始地循环变化。
生产提前期(提前期Lead Time—LT)
天数 55 50 45 40 35 30 25 20 15 10 5
毛坯生产周期
毛坯 保险期
机加工生产周期
加工 保险期
装配 生产周期
机加工投入提前期 毛坯出产提前期 毛坯投入提前期
装配 投入提前期 机加工出产提前期
工序或生产线正常工作而在它们之间设置的储备量标准。
Z3max=(T同×S上)/t上-(T同×S下)/t下
式中,T同:相邻两工序的同时工作时间 S上、S下:上、下道工序的工作地数目 t上、t下:上、下道工序的单件加工时间
例:某流水线中A、B为前后相邻两工序,前工序A,后工序 B,Ta=2分,Tb=5分,A、B都只一个工作地,流水线的计 划节拍为5分钟,工作班有效工作时间为7.5小时,两工序间 的流动在制品占用量在一个工作班内的变化如下表所示:
《生产与运作管理 》计算题
1
平行移动方式
m
T平= ti (n 1)t1 i 1
工序
t1:最长的单件工序时间
t1
t2
t3 t4
T平
时间
本例中,T平=(10+5+20+10)+(4-1)×20=105 (分钟) 平行移动方式的优点是时间最短,缺点是工(台)时利用率 较低,运输量较大。
平行顺序移动方式
本例中,T平顺=4×(10+5+20+10)-(4-1)×(5+5+10)=120 (分钟)
生产运作管理习题集(计算)

*********************************************************************有一批零件,需经四道工序加工,各工序单件加工时间分别为: T 1=15 分钟,T 2=10分钟,T 3=15分钟, T 4=10分钟,设批量为5件,试用求平行、顺序、平行顺序移动方式下的加工周期。
求总流程时间最小化的加工顺序,并计算加工周期.某公司现有两个工厂A 和B ,3个仓库U、V 和W 。
这些工厂和仓库位于不同的城市,为满足日益增长的市场需求,公司决定再建一新工厂,现有X 和Y 两个备选厂址可供选择,各工厂生产能力、各仓库需求及工厂到仓库的单位运费如表所示,试比较选择运费较少的工厂选址方案。
用Johnson 算法求以下8/2/F/FmAx 问题的最优解。
*********************************************************************某公司现有3个工厂A 、B 和C ,它们在3个不同的城市。
有2个仓库P 和Q ,它们位于不同的城市,仓库用来存放工厂生产的产品,随时供应用户,每个仓库每月需供应市场2100吨产品。
为了更好地为顾客服务,该公司决定再建一个新仓库。
经过调查分析,确定X 与Y 两个点可建仓库。
相关资料如下表所示。
东方制造公司组装安全监视器。
每年以65元的单价购买1800个单色阴极射线管。
订货成本是13元.年持有成本占购买价格的20%。
计算最佳订货批量,以及订购与持有成本的年总成本。
已知对某零件的净需求如下表所示,单位订货费用为100元,单位库存费用为0.25元/(件.周)。
试用MPG 法确定订货安排。
某公司在一次事故中损坏了五台仪器,这些仪器都需要经过AB 两道工序进行修复,每台仪器在各工序修理的时间如下表所示,且已知两工序分别由不同的人员担任。
任何一台仪器没有修复该公司都无法正常生产,试用Johnson 方法对五台仪器修复顺序排序,使该公司能尽快恢复生产,并并计算流程时间。
考试必备【生产运作管理】经典计算题(带解释和参考答案)
考试必备【生产运作管理】 经典计算题(带解释和答案)重心法求工厂设置地1、某企业决定在武汉设立一生产基地,数据如下表。
利用重心法确定该基地的最佳位置。
假设运输量与运输成本存在线性关系(无保险费)。
工 厂 坐 标 年需求量/件 D1 (2,2) 800 D2 (3,5) 900 D3 (5,4) 200 D4 (8,5) 100解:X=(800*2+900*3+200*5+100*8)/(800+900+200+100)=3.05 Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7. 所以最佳位置为(3.05,3.7)。
1. 某跨国连锁超市企业在上海市有3家超市,坐标分别为(37,61)、(12,49)、(29,20)。
现在该企业打算在上海建立分部,管理上海市的业务。
假设3家超市的销售额是相同的。
()(1) 用重心法决定上海分部的最佳位置。
解:因为3家超市的销售额相同,可以将他们的销售额假设为1. 上海分部的最佳位置,也就是3家超市的重心坐标,可以这样计算: x=(37+12+29)/3=27 y=(61+49+20)/3=43.3(2) 如果该企业计划在上海建立第四家超市,其坐标为(16,18),那么如果计划通过,上海分部的最佳位置应该作何改变?解:增加一家超市后,重心坐标将变为: x=(37+12+29+16)/4=24.3 y=(61+49+20+18)/.4=37成本结构1、某商店销售服装,每月平均销售400件,单价180元/件,每次订购费用100元,单件年库存保管费用是单价的20%,为了减少订货次数,现在每次订货量是800件。
试分析:(1)该服装现在的年库存总成本是多少?(15000元)(2)经济订货批量(EOQ )是多少?(163件) (1)总成本=(800/2)*180*20%+(400*12/800)*100=15000元 (2)EOQ =HDS 2=800/)12*400(100*12*400*2=163件(3)EOQ 总成本=(163/2)*180*20%+(400*12/163)*100=5879元(4)年节约额=15000-5879=9121元节约幅度=(9124/15000)*100%=60.81%2、某食品厂每年需要采购3000吨面粉用于生产,每次采购订货手续费为300元,每吨产品的年库存成本为20元,请计算该食品厂采购面粉的经济订货批量EOQ 。
生产与运作管理的计算题

⽣产与运作管理的计算题⼀、流⽔作业排序1.最长流程时间的计算例:有⼀个6/4/F/Fmax问题,其加⼯时间如下表所⽰,当按顺序S=(6,1,5,2,4,3)加⼯时,求Fmax解:列出加⼯时间矩阵根据公式:C kSi=max{C(k-1)Si, C kSi-1}+ P Sik,计算各⾏加⼯时间,最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法(Johnson算法)例:求下表所⽰的 6/2/F/Fmax 的最优解将⼯件2排在第1位 2将⼯件3排在第6位 2 3将⼯件5排在第2位 2 5 3将⼯件6排在第3位 2 5 6 3将⼯件4排在第5位 2 5 6 4 3将⼯件1排在第4位 2 5 6 1 4 3最优加⼯顺序为S=(2,5,6,1,4,3)由上表可计算出, Fmax =283.⼀般n/m/F/Fmax问题的最优算法(⼀)Palmar算法(λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi不增的顺序排列⼯件)例:有⼀个4/3/F/Fmax问题,其加⼯时间如下表所⽰,⽤Palmar求解.解:λi= ∑ [k-(3+1)/2]P ik,k=1,2,3λi=-Pi1+Pi3于是,λ1=-P11+P13 =-1+4=3λ2=-P21+P23 ==2+5=3λ3=-P31+P33 =-6+8=2λ4=-P41+P43 =-3+2=-1按λi不增的顺序排列⼯件,得到加⼯顺序(1,2,3,4)和(2,1,3,4),经计算,⼆者都是最优顺序,Fmax=28(⼆)关键⼯件法例:有⼀个4/3/F/Fmax问题,其加⼯时间如下表所⽰,⽤关键⼯件法求解.解:由上表可知,加⼯时间最长的是3号⼯件,Pi1<=Pi3的⼯件为1和2,按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的⼯件为4号⼯件,Sb=(4),这样得到加⼯顺序为(1,2,3,4)。
经计算,Fmax=28⼆、⽣产能⼒的计算(⼀)、对于加⼯装配式⽣产,⽣产能⼒是⼀个模糊的概念。
生产运作管理计算题及答案

(2)EOQ===163件
(3)EOQ总成本=(163/2)*180*20%+(400*12/163)*100=5879元
(4)年节约额=15000—5879=9121元
节约幅度=(9124/15000)*100%=60.81%
H
25
D,G
(1)画出装配网络图
(2)计算生产节拍.
解:节拍r = (450/360)min = 1。25min = 75s
(3)用后续作业最多规则平衡该装配线,用作业时间最长规则作为第二规则。
解:可能最小工作地数=作业时间和除以节拍=275/75 = 4 (取整数)
流水线平衡结果如表7—24所示
作业
年销售收入= 130x6000美元= 780000美元
年利润= 780000美元–600000美元= 180000美元
装配网络图生产产品的工作站数
作业
时间/分
紧后作业
A
0.2
B
B
0。4
C
C
0。2
F
D
0.4
E
E
1。2
G
F
1.2
G
G
1.0
结束
2、某生产线计划每天产量为240单位,日工作时间为8小时,各作业的时间及作业的先后顺序如上表,试对生产线进行平衡。要求:(1)绘制流程图;(2)所需最少的工作站数量的理论值?(3)使用最长作业时间原则以最少的工作地数量来平衡装配线。
解:效率= 275/(75 x 5) = 73。3%
跟踪策略与均匀策略混合策略算成本
3、假设相连季度产量变化的成本(指劳动力变动)为500元/单位;每一季度库存费为800元/单位;现有的季度生产能力为55单位。需求预测如下表。现有两种方案,一是调节库存(均匀策略,每季度的生产能力为年度需求的平均值),二是调节劳动力(跟踪策略)。哪种方案成本最低?(10分)
生产运作管理计算题

1运输问题表上作业法1某汽车制造公司决定在南方建一新厂.方案A总权重=0.2590+0.180+0.2590+0.290+0.290=89方案B总权重=0.2595+0.175+0.2580+0.285+0.280=84.25方案C总权重=0.2580+0.195+0.2580+0.280+0.280=81.5所以选址A2给出如下3个厂址的有关数据厂址A的总成本=18300000+1500000=6900000厂址A的利润=30300000—18300000—1500000=6900000厂址B的总成本=20250000+3000000=8000000厂址B的利润=30250000—20250000—3000000= -500000厂址C的总成本厂址C的利润=30325000—19.5325000—4000000= -587500 3某工厂下载3个工厂A,B,C和两个分配中心P,Q分配中心Y作为选定的费用=10013+8005+7006+6008=14300分配中心作为选定的费用=10013+8005+7006+6007=13700所以最佳分配中心地点为W2装配线平衡一装配线计划每小时装配200件产品,每小时用于生产的时间是50分钟,表1是装配工序、每道工序的作业时间及紧前工序等信息,请完成下列任务:3经济订货数的批量模型四达设备公司每年要按单价4元购入54000套轴承组合件.单位维持库存费为每年每套轴承9元,每次订货费用为20元.试求经济订货批量和年订货次数已知H=9元/套.年,S=200元/次,D=54000套则经济订购批量:订货次数4经济生产批量模型某自行车公司计划下年度生产特种轮胎40000只,生产率为每天200只,一年按250天计算.一次生产准备费用为200元,提前期为5天.单位生产费用为15元,单位维持库存费为11.5元.试求经济生产批量和订货点.H=11.5元/只年 S=200元/次,D=40000只,p=200只/天,LT=5天,d=40000/250=160只/天经济生产批量订货点:ROP=dLT=1605=800只5价格折扣模型①每年需用某零件3000单位,每次订购的固定成本为250.00元,单位维持库存费为货物价值的25%,现有三个货源可供选择,A:不论订购多少单价都为10.00元;B:订购量必须大于等于600单位,单价9.50元;C:订货起点为800单位,单价9.00元.试确定该公司的订货策略,并计算年最低库存费用EOQ9.00 .5=817因为EOQ=816.5落在>800区间内, 是9元/单位的优惠范围内, 所以是可行解把816换成817,最后结果CT=CH+CR=28837②某汽车配件供应商每三个月以批量为500盒购买一次垫圈.每盒价格为12.50元,每次订货费为15.00元,单位维持库存费为单价的20%.试以经济效益为标准评价其订货策略.年需求量D=5004=2000 P=12.5 S=15 H=2.5年最低库存费用=12.52000+2000/50015+500/22.5=25000+60+625=25685元EOQ=√2DS/H=√2200015/2.5=155年最低库存费用=200012.5+2000/15515+155/22.5=25387.25 25685>25387.25 所以不符合经济效益,不合算 6MPG 法单位订货费为100元,单位维持库存费为0.25,用MPG 法确定订货安排瓶计算库存总费用S=100 H=0.25 S/H=100/0.25=400 用MPG 法求订货批量的过程817113000816 2.25250300092891822816D TC Q C h S C D Q =⋅⋅+⋅+⋅=⨯⨯+⨯+⨯=元第五步停止时,最小周期=S/H时,此时CR总订货费=kS=5100=500元CH总维持库存费=0.50.253050=381.25C T =CH+CR=881.25元7Johnson算法所以,Fmax=478相同零件不同移动方式下加工周期的计算m=5,n=4,t 1=10,t 4=12,t 5=6,分别求在顺序移动,平行移动和平行顺序移动方式下,这批零件的加工周期.顺序移动: =410+44+48+412+46=160 平行移动: =10+4+8+12+6+4-112=76 平行顺序移动: =160-4-14+4+8+6=94。
生产运作管理习题集(计算)
有一批零件,需经四道工序加工,各工序单件加工时间分别为: T 1=15 分钟,T 2=10分钟,T 3=15分钟, T 4=10分钟,设批量为5件,试用求平行、顺序、平行顺序移动方式下的加工周期。
求总流程时间最小化的加工顺序,并计算加工周期.某公司现有两个工厂A 和B ,3个仓库U 、V 和W 。
这些工厂和仓库位于不同的城市,为满足日益增长的市场需求,公司决定再建一新工厂,现有X 和Y 两个备选厂址可供选择,各工厂生产能力、各仓库需求及工厂到仓库的单位运费如表所示,试比较选择运费较少的工厂选址方案。
用Johnson 算法求以下8/2/F/FmAx 问题的最优解。
某公司现有3个工厂A 、B 和C ,它们在3个不同的城市。
有2个仓库P 和Q ,它们位于不同的城市,仓库用来存放工厂生产的产品,随时供应用户,每个仓库每月需供应市场2100吨产品。
为了更好地为顾客服务,该公司决定再建一个新仓库。
经过调查分析,确定X与Y两个点可建仓库。
相关资料如下表所示。
东方制造公司组装安全监视器。
每年以65元的单价购买1800个单色阴极射线管。
订货成本是13元.年持有成本占购买价格的20%。
计算最佳订货批量,以及订购与持有成本的年总成本。
已知对某零件的净需求如下表所示,单位订货费用为100元,单位库存费用为0.25元/(件.周)。
试用MPG法确定订货安排。
某公司在一次事故中损坏了五台仪器,这些仪器都需要经过AB两道工序进行修复,每台仪器在各工序修理的时间如下表所示,且已知两工序分别由不同的人员担任。
任何一台仪器没有修复该公司都无法正常生产,试用Johnson方法对五台仪器修复顺序排序,使该公司能尽快恢复生产,并并计算流程时间。
某公司现有3个原料供应地MMM3和两个工厂FF2,准备在X城或Y城再建一个工厂。
现给出下表中的资料。
求最佳厂址。
据预测,市场每年对X公司生产的产品需求量为20000台,一年按250天计算,生产率为每天100台,生产提前期为4天。
生产运作管理习题集(计算)
有一批零件,需经四道工序加工,各工序单件加工时间分别为: T1=15 分钟,T 2=10分钟,T3=15分钟, T4=10分钟,设批量为5件,试用求平行、顺序、平行顺序移动方式下的加工周期。
求总流程时间最小化的加工顺序,并计算加工周期.某公司现有两个工厂A和B,3个仓库U、V和W。
这些工厂和仓库位于不同的城市,为满足日益增长的市场需求,公司决定再建一新工厂,现有X和Y两个备选厂址可供选择,各工厂生产能力、各仓库需求及工厂到仓库的单位运费如表所示,试比较选择运费较少的工厂选址方案。
用Johnson算法求以下8/2/F/FmAx问题的最优解。
们位于不同的城市,仓库用来存放工厂生产的产品,随时供应用户,每个仓库每月需供应市场2100吨产品。
为了更好地为顾客服务,该公司决定再建一个新仓库。
经过调查分析,确定X与Y两个点可建仓库。
相关资料如下表所示.东方制造公司组装安全监视器。
每年以65元的单价购买1800个单色阴极射线管。
订货成本是13元.年持有成本占购买价格的20%。
计算最佳订货批量,以及订购与持有成本的年总成本。
已知对某零件的净需求如下表所示,单位订货费用为100元,单位库存费用为0.25元/(件.周)。
试用MPG法确定订货安排。
复,每台仪器在各工序修理的时间如下表所示,且已知两工序分别由不同的人员担任.任何一台仪器没有修复该公司都无法正常生产,试用Johnson方法对五台仪器修复顺序排序,使该公司能尽快恢复生产,并并计算流程时间。
个工厂。
现给出下表中的资料。
求最佳厂址.生产率为每天100台,生产提前期为4天。
单位产品的生产成本为50元,单位产品年维持库存费为10元,每次生产的生产准备费为200元。
试求经济生产批量,年生产次数,订货点和最低年总费用.一家剪刀公司计划第四周生产300把剪刀,第五周运出400把剪刀,请制定一个完全的物料需求计划.物料库存信息表A、B和C,经专家调查和判断,对这3个厂址按5个因素进行了评分,评分如果如下,试计算比较哪个厂址较可取。
生产运作管理系统计算题及问题详解

【生产运作管理】重心法求工厂设置地1、某企业决定在武汉设立一生产基地,数据如下表。
利用重心法确定该基地的最佳位置。
假设运输量与运输成本存在线性关系(无保险费)。
工厂 坐标 年需求量/件 D1 (2,2) 800 D2 (3,5) 900 D3 (5,4) 200 D4 (8,5) 100解:X=(800*2+900*3+200*5+100*8)/(800+900+200+100)=3.05 Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7. 所以最佳位置为(3.05,3.7)。
1. 某跨国连锁超市企业在上海市有3家超市,坐标分别为(37,61)、(12,49)、(29,20)。
现在该企业打算在上海建立分部,管理上海市的业务。
假设3家超市的销售额是相同的。
(6.3.24)(1) 用重心法决定上海分部的最佳位置。
解:因为3家超市的销售额相同,可以将他们的销售额假设为1. 上海分部的最佳位置,也就是3家超市的重心坐标,可以这样计算: x=(37+12+29)/3=27 y=(61+49+20)/3=43.3(2) 如果该企业计划在上海建立第四家超市,其坐标为(16,18),那么如果计划通过,上海分部的最佳位置应该作何改变?解:增加一家超市后,重心坐标将变为: x=(37+12+29+16)/4=24.3 y=(61+49+20+18)/.4=37成本结构1、某商店销售服装,每月平均销售400件,单价180元/件,每次订购费用100元,单件年库存保管费用是单价的20%,为了减少订货次数,现在每次订货量是800件。
试分析:(1)该服装现在的年库存总成本是多少?(15000元)(2)经济订货批量(EOQ )是多少?(163件) (1)总成本=(800/2)*180*20%+(400*12/800)*100=15000元 (2)EOQ=HDS 2=800/)12*400(100*12*400*2=163件(3)EOQ 总成本=(163/2)*180*20%+(400*12/163)*100=5879元(4)年节约额=15000-5879=9121元节约幅度=(9124/15000)*100%=60.81%2、某食品厂每年需要采购3000吨面粉用于生产,每次采购订货手续费为300元,每吨产品的年库存成本为20元,请计算该食品厂采购面粉的经济订货批量EOQ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重心法求工厂设置地1、某企业决定在武汉设立一生产基地,数据如下表。
利用重心法确定该基地的。
Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7. 所以最佳位置为(3.05,3.7)。
1. 某跨国连锁超市企业在上海市有3家超市,坐标分别为(37,61)、(12,49)、(29,20)。
现在该企业打算在上海建立分部,管理上海市的业务。
假设3家超市的销售额是相同的。
(6.3.24)(1) 用重心法决定上海分部的最佳位置。
解:因为3家超市的销售额相同,可以将他们的销售额假设为1. 上海分部的最佳位置,也就是3家超市的重心坐标,可以这样计算: x=(37+12+29)/3=27 y=(61+49+20)/3=43.3(2) 如果该企业计划在上海建立第四家超市,其坐标为(16,18),那么如果计划通过,上海分部的最佳位置应该作何改变?解:增加一家超市后,重心坐标将变为: x=(37+12+29+16)/4=24.3 y=(61+49+20+18)/.4=37成本结构1、某商店销售服装,每月平均销售400件,单价180元/件,每次订购费用100元,单件年库存保管费用是单价的20%,为了减少订货次数,现在每次订货量是800件。
试分析:(1)该服装现在的年库存总成本是多少?(15000元)(2)经济订货批量(EOQ )是多少?(163件) (1)总成本=(800/2)*180*20%+(400*12/800)*100=15000元 (2)EOQ =HDS 2=800/)12*400(100*12*400*2=163件(3)EOQ 总成本=(163/2)*180*20%+(400*12/163)*100=5879元(4)年节约额=15000-5879=9121元节约幅度=(9124/15000)*100%=60.81%2、某食品厂每年需要采购3000吨面粉用于生产,每次采购订货手续费为300元,每吨产品的年库存成本为20元,请计算该食品厂采购面粉的经济订货批量EOQ 。
(300吨) EOQ=H DS 2=20300*3000*2=300吨 3、某服装店年销售服装2000件,每次订购费用约250元,单件年库存保管费用为4元,目前每次订货量为400件,试计算该服装店的年库存总成本。
(2050元) 总成本=Q/2(H)+D/Q*S=(400/2)*4+(2000/400)*250=2050元2. 某消费电子产品公司欲生产一款mp3产品,可能选择在中国香港、中国大陆、印尼生产。
该产品的售价预计为130美元/单位。
各地的成本结构如表6-17所示。
(6.3.27)表6-17 各地的成本结构解:年总成本(中国香港) = 美元+75x6000美元 = 美元年总成本(中国大陆) = 美元+50x6000美元 = 美元 年总成本(印尼) = 美元+25x6000美元 = 美元 因此,产地选择中国大陆的成本最低。
另外,仔细观察可以发现,产品售价在这个题目种对最终结果没有影响。
(2) 如果在中国香港制造该产品,那么预期的利润是多少?解:首先必须知道,利润等于销售收入减去总成本,而销售收入又等于售价乘以销售量。
如果在中国香港生产该产品,那么 年销售收入 = 130x6000美元= 美元 年利润 = 美元 – 美元 = 美元2、某生产线计划每天产量为240单位,日工作时间为8小时,各作业的时间及作业的先后顺序如上表,试对生产线进行平衡。
要求:(1)绘制流程图;(2)所需最少的工作站数量的理论值?(3)使用最长作业时间原则以最少的工作地数量来平衡装配线。
解:.(1)节拍=8*60/240=2分钟/个(2)所需工作地数=[作业时间和/节拍]=[(0.2+0.4+0.2+0.4+1.2+1.2+1.0)/2]=3 (3)各作业的关系图如下。
1.一条装配线的预定日产量为360单位,该装配线每天运行450min。
表7-10给出了生产(1)画出装配网络图(2)计算生产节拍。
解:节拍r = (450/360)min = 1.25min = 75s(3)用后续作业最多规则平衡该装配线,用作业时间最长规则作为第二规则。
解:可能最小工作地数=作业时间和除以节拍=275/75 = 4 (取整数)(4)流水线平衡后的效率是多少?解:效率= 275/(75 x 5)= 73.3%跟踪策略与均匀策略混合策略算成本3、假设相连季度产量变化的成本(指劳动力变动)为500元/单位;每一季度库存费为800元/单位;现有的季度生产能力为55单位。
需求预测如下表。
现有两种方案,一是调节库存(均匀策略,每季度的生产能力为年度需求的平均值),、(1跟踪策略成本低,选择跟踪策略学习曲线函数3. 某厂刚完成生产10件重要产品的任务,并发现每意见的作业时间如表8-12所示。
(8.3.33)(1) 估计学习率为多少?解:通过计算可估计出学习率为75%,则学习曲线函数为:415.01000-=x Y x(2) 根据(1)的结果,计算再生产90件需要多少时间?(假定学习能力不会丧失) 解:再生产90件需要花费的总时间⎰==-10011415.0183331000h dx x Y(3) 生产第1000件需要多少时间?解:生产第1000件需要花费时间h h Y 9.5610001000415.01000=⨯=- 需求预测4. 对某产品的需求预测如表9-12所示。
(9.4.2)表9-12 对某产品的需求预测设:Cw 为单位人工成本,每月分别为2520元/人、2400元/人、2760元/人、2520元/人、2640元/人、2640元/人;CH 为招聘一个工人的费用,CH=450元/人;CL 为解聘一个工人的费用,CL=600元/人;CI 为维持单件产品库存一个周期的费用,CI=5元/件/周期;Pi 为产品产量;产品单件工时为1h/件;Wi 为工人数;Hi 为招聘人数;Li 为解聘人数;Ii 为库存量;i 为月份。
试用线性规划模型求最优的总生产计划。
解:模型假设第1期的初期工人刷为35人,初始库存量为0.Min2520×W1 + 2400×W2+2760×W3+2520×W4+2640×W5+2640×W6+450×H1+450×H2+450×H3+450×H4+450×H5+450×H6+600×L1+600×L2+600×L3+600×L4+600×L5+600×L6+5×I1+5×I2+5×I3+5×I4+5×I5+5×I6 约束条件:1. 生产能力的约束P1≤84×W1 (84是1分月一个工人提供的工作小时数,下同) P2≤80×W2;P3≤92×W3;p4≤84×W4;P5≤88×W5;P6≤88×W4 2. 人工能力的约束W1=35+H1-L1;W2=W1+H2-L2 W3=W2+H3-L3;W4=W3+H4-L4W5=W4+H5-L5;W6=W5+H6-L63.库存能力的约束I1 = P1-2760;I2=I1+P2-3320I3=I2+P3-3970;I4=I3+P4-3540I5=I4+P5-3180;I6=I5+P6-29004.非负条件的约束(略)最后求得的最优解如表9-17所示。
月份产量/件库存量/件招聘人数/人解聘人数/人需要工人数/人1 2940.000 180.0000 35.000002 3232.857 92.85714 5. 40.410713 3877.143 1. 42.142864 3540.000 42.142865 3180.000 6. 36.136366 2900.000 3. 32.95455 总费用为.60元。
订购产品12.3.27 某大学的合作商店订购带有该大学校徽的运动衫进行销售,每件价格30元。
每月通常能销售100 件(包括从一个供应商进货各种尺寸和款式)订货成本每次为25 元,每年的仓储成本为25% 。
求:(1) 合作商店每次应该订购多少件运动衫?(2) 供应商希望每月送一次货,每次送货量要比最优订货量小,这样每年的总成本为多少?(3) 假设销售量增加到每周150 件,而合作商店仍然决定用(1)中的批量进行订货,这样合作商店为此要付的总成本为多少?12.3.28 上题中的合作商店认为应该为运动衫建立安全库存。
它使用具有3周准备时间的订货系统。
假设每周的平均需求为50 件,其标准差为25 件。
(1)如果确定的服务水平为95% ,合作商店的订货点应该是多少?(2) 为了保证一年里缺货情况不能多于一次,商店的订货点应该是多少?(3) 问题(2)中平均库存是多少?这里包括周期库存和安全库存。
12.3.29 某家电专卖店经营某种品牌的电视,经营情况如下:平均年销售量为200 台,每次订货成本是100 元,仓储成本为每年20%,每台电视成本是800 元,订货提前期为4天,每天需求的标准差为0.1台。
每年工作日按250天计算。
(1) 确定EOQ 的值。
(2) 计算95%的服务水平的订货点,假设需求服从正态分布。
(3) 订货提前期或标准差的改变对订货点有何影响?12.3.30 用上题中的数据,求解以下几个问题:(1) 确定一个95%服务水平的定期库存控制系统。
计算订货时间间隔。
(2) 确定目标库存水平。
(一)一批零件,批量为4,要完成加工需经过5道工序,工序的单件时间定额分别为:t1=10分钟,t2=5分钟,t3=20分钟,t4=15分钟,t5=5分钟。
用公式计算平行和平行顺序移动方式下的生产周周期。
答案:T平=(10+5+20+15+5)+(4-1)×20=115T平顺=4×(10+5+20+15+5)-(4-1)(5+5+15+5)=130(二)已知甲产品月计划产量250台,月工作日数25天,平均日产量10台,要求在六月份第5个工作日装配车间出产第一批发50台,各车间期量标准如表1所示。
试在表2相应空格中填写各车间投入和出产量及累计量。
表1 甲产品期量标准表表2 各车间投入和出产累计数计划表答案:(三)已知某工程项目各项活动之间的关系如表3所示:要求:⑴绘制网络图。
⑵用图上标号法计算各结点最早开工时间和最迟完工时间?⑶用列表法计算各项活动的最早开工时间和最迟开工时间?最早完工时间和最迟完工时间?⑷确定关键线路及总工期。
答案:解:根据给出的活动明细表,绘制工程项目网络图,结点时间参数已采用标号法在图中标出。
