用SuperDecision进行网络层次分析法(ANP)的应用实例
superdecisions 案例

superdecisions 案例在这个案例中,我们将探讨一个公司如何使用SuperDecisions软件来做出决策,以便在市场竞争中获得竞争优势。
该公司是一家运输和物流服务供应商,目前面临着选择购买新的货运车辆的决策。
公司的当前车辆已经老旧,需要更换以提高业务效率和客户满意度。
然而,该公司的资金有限,他们需要找到一种最优的购车方案,以最大限度地提高投资回报率。
为了做出这个决策,该公司的管理团队使用了SuperDecisions软件,并采用了层次分析法(AHP)的方法。
他们首先确定了该决策的整体目标,即提高运输效率和降低运营成本。
接下来,他们将这个目标细分为两个准则,分别是运输效率和运营成本。
每个准则又细分为几个子准则,如车辆噪音、燃油经济性、维护费用等。
最后,他们列出了不同车型的选择,如货车、厢式货车和小型货车。
接下来,管理团队使用SuperDecisions软件对每个准则和子准则进行了定量评估,以确定其重要性和满足度。
他们采用了1到9的标度,其中1表示不重要/不满足,9表示非常重要/非常满足。
然后,他们将这些评估结果输入软件中,进行计算和分析。
软件根据评估结果生成了一个权重矩阵,用于衡量每个准则和子准则的相对重要性。
在完成了准则和子准则的评估后,管理团队开始对不同车型进行评估。
他们使用相同的方法,对每个车型在每个准则和子准则上进行评估,以确定其优劣。
通过SuperDecisions软件的计算和分析,他们得出了每个车型在不同准则下的得分。
最后,管理团队将不同车型的得分加权求和,并使用SuperDecisions软件得出了最终的决策。
他们选择了一种符合公司目标、同时在运输效率和运营成本上表现较好的车型。
通过使用SuperDecisions软件,该公司能够清晰地了解每个准则和子准则的重要性,有效地评估了不同车型的优劣,并最终做出了明智的决策。
这帮助公司提高了运输效率和降低了运营成本,为其在市场竞争中获得了竞争优势。
层次分析法的应用实例

层次分析法的应用实例层次分析法(Analytic Hierarchy Process,简称AHP)是一种运用于多准则决策问题的定性和定量分析方法。
通过将决策问题分解为多个层次,从而使决策问题的结构更加清晰,更容易理解和处理。
下面将介绍几个AHP方法的应用实例。
1.项目选择在项目选择过程中,可能存在多个关键因素需要权衡。
通过应用AHP,可以将项目选择问题分解为几个层次,例如项目目标、资源投入、风险等等。
然后为每个层次的因素确定权重,从而帮助决策者更加客观地评估不同项目的优劣,并做出最佳选择。
2.供应商评估当公司需要选择供应商时,往往需要考虑多个方面的因素,例如价格、质量、交货时间等等。
通过使用AHP,可以将供应商评估问题分解为不同的准则和子准则,然后为每个准则和子准则赋予合适的权重,最终确定出最佳供应商。
3.市场调研在市场调研过程中,可能涉及到多个调研指标和因素。
通过应用AHP,可以将市场调研问题分解为几个层次,例如调研目标、调研方法、数据可靠性等等。
然后为每个层次的因素确定权重,从而辅助决策者选择最适合的市场调研方法和指标。
4.产品设计在产品设计过程中,需要考虑多个因素,例如功能、性能、成本等等。
通过使用AHP,可以将产品设计问题分解为不同的准则和子准则,然后为每个准则和子准则赋予合适的权重,从而帮助设计团队确定出最佳的产品设计方案。
5.企业战略规划在企业战略规划中,需要综合考虑多个战略选项的优劣。
通过应用AHP,可以将战略规划问题分解为不同的层次和因素,例如市场前景、竞争环境、技术能力等等。
然后为每个层次的因素确定权重,从而辅助决策者选择最佳的战略规划方案。
综上所述,层次分析法在多准则决策问题的应用非常广泛。
通过将决策问题分解为多个层次,然后根据不同层次的因素确定权重,能够帮助决策者更加客观地评估不同方案的优劣,并做出最佳选择。
这种方法在项目选择、供应商评估、市场调研、产品设计和企业战略规划等领域都有重要的应用。
层次分析法步骤及案例分析

层次分析法步骤及案例分析层次分析法(AHP)是一种通过对比判断不同因素的重要性来进行决策的方法。
它由匹兹堡大学的数学家托马斯·萨蒙在20世纪70年代初提出,并逐渐应用于各个领域。
本文将介绍层次分析法的步骤,并通过一个实际案例来进行分析。
一、层次分析法的步骤层次分析法主要包括以下几个步骤:1. 确定层次结构:首先,需要明确决策问题的层次结构。
将问题划分为若干个层次,从总目标到具体的子目标,形成一棵树状结构。
例如,在一个购车的决策问题中,总目标可以是“选择一辆适合自己的车”,下面的子目标可以包括“价格”、“外观”、“安全性”等因素。
2. 构造判断矩阵:在每个层次中,需要对不同因素之间的两两比较进行判断。
判断可以基于专家经验、问卷调查或实际数据。
对于两两比较,通常采用一个1到9的比较尺度,其中1表示相等,3表示略微重要,5表示中等重要,7表示强烈重要,9表示绝对重要。
如果因素A相对于因素B的重要性大于1,则B相对于A的重要性是1/A。
3. 计算权重向量:根据判断矩阵中的比较结果,可以计算出每个层次中各个因素的权重向量。
通过对判断矩阵的特征值和特征向量进行计算,可以得到各个因素的权重。
4. 一致性检验:在进行层次分析时,需要检验判断矩阵的一致性。
一致性是指在两两比较中的逻辑关系的一致性。
通常使用一致性指数和一致性比率来判断判断矩阵的一致性程度。
5. 综合评价:通过将各层次中因素的权重向量进行乘积运算,并将结果汇总得到最后的评价结果。
在这一步骤中,可以对不同的决策方案进行排序或进行多目标决策。
二、案例分析为了更好地了解层次分析法的应用,我们来看一个实际案例。
假设某公司需要选择新的供应商,供应商选择的主要考虑因素包括产品质量、交货周期和价格。
我们可以按照以下步骤进行决策:1. 确定层次结构:总目标是选择合适的供应商,下面的子目标是产品质量、交货周期和价格。
2. 构造判断矩阵:对于每个子目标,可以进行两两比较。
基于网络层次分析法的兰州市轨道交通建设对城市经济环境影响探究

摘要:于2014年正式启动的兰州地铁1号线一期工程在建设过程中对城市正常机制产生了影响。
本文通过实地调研、网络搜集、文献整合等方式收集相关数据,并运用SPSS、Super Decision、MATLAB等软件进行数据处理,挖掘信息以确定经济评价体系权重及算法,结合实际加以分析评价,从而探究地铁建设对城市生态、行居、文化等多方面的影响。
从对市民和专家调研结果可以看出,兰州市轨道交通建设对城市生态环境、行居环境、文化景观环境影响程度一般,相较对城市行居环境影响突出。
针对地铁建设中存在的一些问题,提出相关建议。
关键词:轨道交通;网络分析法;环境影响一、研究背景我国城市化进程的推进对于城市道路交通建设提出了巨大考验,城市居民对于出行的便捷、快速程度提出了更高的要求,如何解决道路拥堵,城市轨道交通尤为重要。
从北京、上海市的数据来看,地铁建设极为有效抑制了交通拥堵问题,占平均运载客流总量的三到五成,但是不可避免的是,在地铁建设中对于周边环境、交通乃至文化景观产生一定程度的负面影响。
从现有的国内外研究来看,降低人口稠密区的空气、噪声污染,减少施工建设引发的交通堵塞、施工噪音和地面振动、建筑垃圾、建筑物破坏等问题有待解决[1]。
王鑫[2]以西安地铁建设为例,从施工所导致的地层移位、变形对于地面古建筑的影响予以研究,提出如何最大限度避免或减小地铁施工队与古建筑的影响,运用APLD语言、三维有限元模型,分析了地面交通和地铁振动荷载叠加情况对钟楼的影响。
目前对于城市轨道施工建设中对于周边负面影响测评,仅限于某一个专业方面,欠缺综合的全面分析研究。
所以本文将构建地铁建设对城市环境影响的指标体系,通过向城市居民、领域专家学者、政府相关工作人员发放问卷,调查地铁施工建设对于自然、社会两方面的影响,通过网络层次分析法(ANP)确定指标权重,以探究地铁施工建设对于城市居民产生的直接影响。
二、地铁建设影响的体系构建地铁为满足城市居民出行需要及安全,往往具有投资规模大、建设时间长、施工范围聚集城市交通枢纽三大特点,这对于市政规划、交通疏导、垃圾运输及其他相关部门提出了更加严格要求。
基于依存和反馈的网络层次分析法(ANP)
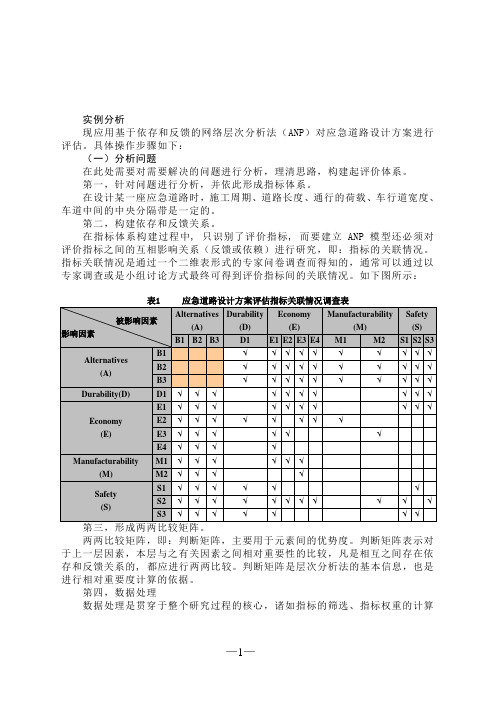
实例分析现应用基于依存和反馈的网络层次分析法(ANP)对应急道路设计方案进行评估。
具体操作步骤如下:(一)分析问题在此处需要对需要解决的问题进行分析,理清思路,构建起评价体系。
第一,针对问题进行分析,并依此形成指标体系。
在设计某一座应急道路时,施工周期、道路长度、通行的荷载、车行道宽度、车道中间的中央分隔带是一定的。
第二,构建依存和反馈关系。
在指标体系构建过程中, 只识别了评价指标, 而要建立ANP 模型还必须对评价指标之间的互相影响关系(反馈或依赖)进行研究,即:指标的关联情况。
指标关联情况是通过一个二维表形式的专家问卷调查而得知的,通常可以通过以专家调查或是小组讨论方式最终可得到评价指标间的关联情况。
如下图所示:两两比较矩阵,即:判断矩阵,主要用于元素间的优势度。
判断矩阵表示对于上一层因素,本层与之有关因素之间相对重要性的比较,凡是相互之间存在依存和反馈关系的, 都应进行两两比较。
判断矩阵是层次分析法的基本信息,也是进行相对重要度计算的依据。
第四,数据处理数据处理是贯穿于整个研究过程的核心,诸如指标的筛选、指标权重的计算要处理的原始数据大部分来自于问卷调查。
问卷处理主要采用Excel完成,而指标权重的计算则采用Super Decision完成。
此处我们主要利用Excel进行调查问卷的处理。
表2 1-9标度法赋值序号重要性等级Cij1 i,j两元素同等重要 12 i元素比j元素稍重要 33 i元素比j元素明显重要 54 i元素比j元素强烈重要75 i元素比j元素极端重要96 i元素比j元素稍不重要1/37 i元素比j元素明显不重要1/58 i元素比j元素强烈不重要1/79 i元素比j元素极端不重要1/9指标体系的构建主要指在Super Decision中完成整个模型的构建,包括:创建元素集、节点、链接等。
第一,创建元素集ClusterCluster,即元素集,对应的是网络层指标,也就是二级指标。
基于模糊网络分析法(F-ANP)的高速铁路运营安全评价

基于模糊网络分析法(F-ANP)的高速铁路运营安全评价王迎晗,陆键,彭一川(同济大学交通运输工程学院,上海201804)摘要:高速铁路故障致因复杂,安全评价难以定量化精确描述。
为保障高速铁路运营安全,从人员、设备、环境、管理4个方面构建高速铁路运营安全评价指标体系,并分析各安全因素间耦合关系;在评价指标体系基础上,运用网络层次分析法(ANP)和模糊综合评判相结合的模糊网络分析法(F-ANP)建立高速铁路运营安全评价模型。
首先通过调研考察和参考相关研究,建立安全评价因素集和评语集;然后运用网络层次分析法确定各安全因素权重,其中工作人员管理制度和列车信号与控制系统对高速铁路运营安全的贡献度最大;最后根据专家问卷调查统计结果建立评价矩阵,并通过模糊变换得出综合评价结果。
关键词:高速铁路;影响因素;安全评价;模糊网络分析法;网络层次分析法;模糊综合评判中图分类号:U298;X951文献标识码:A文章编号:1001-683X(2020)02-0057-09 DOI:10.19549/j.issn.1001-683x.2020.02.0571概述截至2018年底,我国已建成并投入运营的高速铁路里程达2.9万km以上,占全世界高速铁路运营里程的66%以上。
虽然我国高速铁路建设取得了举世瞩目的成就,但在运营管理和安全保障方面仍有待提高,高速铁路运营安全评估和风险管理更是受到越来越多的重视和关注。
安全评价作为系统工程的重要组成部分,其目的是对系统或工程在运行中可能遭受的损害或潜在的风险源做出定量的估计或定性的描述。
高速铁路系统构成复杂,其供电系统、信号与通信系统、轮轨系统和控制系统等的正常工作均关系着列车的安全运行。
此外,高速铁路在运营过程中,还容易受到天气情况、人为干扰等因素的影响。
目前,国内外有众多安全领域的专家学者运用不同方法和模型对高速铁路运营安全进行研究和分析:Guo等[1]研究高铁列车驾驶员的人格特征对行车安全的影响,采用NEO人格量表的方式,对原北京铁路局221名高铁列车驾驶员进行问卷调查,并建模分析调查结果。
层次分析法的经典例子

层次分析法的经典例子
层次分析法(AHP)是一种经典的决策分析方法,它可以帮助决策者在复杂的
环境中做出最佳决策。
它的基本思想是将复杂的决策问题分解成一系列的子问题,并对每个子问题进行分析,以便最终得出最佳决策。
层次分析法的经典例子是一个公司决定在哪里建立新的工厂。
首先,公司需要
确定建立新工厂的目标,例如,降低成本、提高效率、提高产品质量等。
然后,公司需要确定建立新工厂的基本要求,例如,地理位置、交通便利性、劳动力供应等。
接下来,公司需要确定建立新工厂的可行性,例如,财务可行性、技术可行性、环境可行性等。
最后,公司需要确定建立新工厂的最佳选择,例如,地理位置、交通便利性、劳动力供应等。
层次分析法可以帮助公司在复杂的环境中做出最佳决策。
它可以将复杂的决策
问题分解成一系列的子问题,并对每个子问题进行分析,以便最终得出最佳决策。
层次分析法的经典例子可以帮助公司在复杂的环境中做出最佳决策,从而提高公司的效率和竞争力。
层次分析法AHP、ANP与熵值法带例子和软件操作说明

对于判断矩阵B3,其计算结果为:
0.406 0.406 , max 4, CI 0, RI 0.90, CR 0 W 0.094 0.094
①计算判断矩阵每一行元素的乘积Mi
M i aij
j 1 n
②计算Mi的n次方根 Wi
Wi
③对向量 W W ,W ,
1 2
n
T
Mi
,Wn
正规化(归一化处理)
Wi
Wi
W
j 1
n
j
则 即为所求的特征向量。 ④计算判断矩阵的最大特征根
max
1-9标度方法
序号 1 2 3 4 5 6 7 8 9 重要性等级 i,j两元素同等重要 i元素比j元素稍重要 i元素比j元素明显重要 i元素比j元素强烈重要 i元素比j元素极端重要 i元素比j元素稍不重要 i元素比j元素明显不重要 i元素比j元素强烈不重要 i元素比j元素极端不重要 Cij赋值 1 3 5 7 9 1/3 1/5 1/7 1/9
B3 1/3 3 1
1 1/ 5 1/ 3 A 5 1 3 3 1/ 3 1
同样,可得:
1 2 3 4 1/ 3 1 3 2 B1 1/ 5 1/ 3 1 1/ 2 1/ 4 1/ 2 2 1 1/ 7 1/ 5 1/ 2 1/ 3
7 5 1 3 3 1 1 1 1 3 3 3 B 3 1/ 3 1/ 3 1 1 1
i 1
n
i
n
用SuperDecision进行网络层次分析法(ANP)的应用实例
用SuperDecision进行网络层次分析法(ANP)的应用实例一、网络层次分析法简介(一)ANP理论与方法20年代90年代,萨蒂教授(Saaty)在AHP的基础上于提出来的一种适应非独立递阶层次结构的决策方法——网络层次分析法(Analytic Network Process,ANP)[9]。
网络层次分析法将系统内各元素的关系用类似网络结构表示,而不再是简单的递阶层次结构,网络层中的元素可能相互影响、相互支配,这样ANP能更准确地描述客观事物之间的联系,是一种更加有效的决策方法。
网络层次分析法在进行决策分析时,需要决策者对每个因素(影响因子)进行两两相对重要程度的判定。
在实际生活中,决策者常常不是对所有的决策因素(影响因子)进行相对重要程度判断,而是根据自己的情况(知识、经验、喜好)对某几个因素(影响因子)进行相对重要程度判断,此时,两两判断矩阵就会出现一些空缺,我们称这种情况为信息不完备[1]。
为此,运用ANP进行分析,通过将问题化为一种二次规划问题来计算出权重,最后运用ANP的极限超矩阵得到总排序。
ANP经常被用来解决具有网络结构的系统评价与决策的实际问题[1]。
(二)ANP网络结构ANP考虑到递阶层次结构内部循环及其存在的依赖性和反馈性,将系统元素划分为两大部分,第一部分称为控制因素层,包括问题目标和决策准则,所有的决策准则均被认为是彼此独立的,且受目标元素支配。
控制元素中可以没有决策准则,但至少有一个目标,控制层中的每个准则的权重均可由传统的AHP获得。
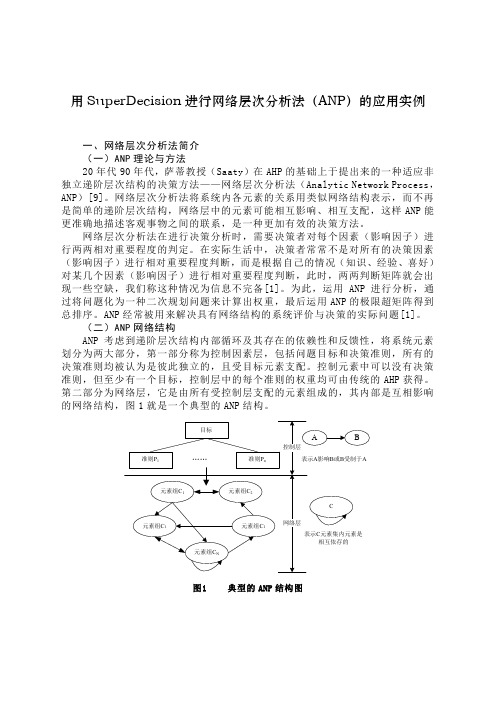
第二部分为网络层,它是由所有受控制层支配的元素组成的,其内部是互相影响的网络结构,图1就是一个典型的ANP结构。
图1 典型的ANP结构图二、ANP算法步骤(一)分析问题。
将决策问题进行系统的分析、组合形成元素和元素集。
主要分析判断元素层次是否内部独立, 是否存在依存和反馈。
可用会议讨论、专家填表等形式和方法进行。
(二)构造ANP的典型结构。
超级决策软件_SuperDecisions_在体育综合评价中的应用研究解析

创新教育2011NO.22科技创新导报超级决策软件(SuperDecisions)在体育综合评价中的应用研究①魏华(西安体育学院陕西西安710068)摘要:通过教练员能力综合评价案例,运用网络分析法(ANP法)构建指标框架,使用SuperDecision软件计算指标权重,为SuperDeci-sions和(ANP法)更好地应用于体育综合评价提供参考。
关键词:SuperDecision软件ANP法指标权重案例应用中图分类号:G80文献标识码:A文章编号:1674-098X(2011)08(a)-0187-01前言网络分析法(ANP法)是在AHP基础上发展而形成的一种新的实用决策方法。
由于采用了网络结构,因此使用ANP法计算指标权重能更好的反映指标之间的联系和反馈关系,能够给予评价对象较为科学和客观的评价。
但是ANP法的计算是极其繁琐,是该方法付诸于实践的瓶颈问题,不借助计算软件,很难将ANP模型应用于实际决策问题,因而许多研究者对ANP法望而生畏。
近年来RozannW.Satty和Wi11iamAdams在美国推出了超级决策(SuperDecision,下称SD软件),该软件基于ANP理论,己成功地将AHP法和ANP法的计算程序化,是计算权重的强大的计算工具,为两种方法的推广奠定了基础。
邻判断的中值。
2SuperDecision软件的应用在指标框架确定和所有的指标权重调查问卷收回之后,一级指标权重一般可通过专家直接指定,其他级别指标就可以使用SuperDecisions所软件来计算了。
2.1指标框架的创建创建指标框架,是指要将问卷筛选的指标框架通过菜单命令输入到的SuperDecisions系统中,二级指标表示为Cluster(元素集),三级指标表示为节点,同时根据指标间是否存在关联创建结点之间的关联。
具体方法如下。
(1)创建二级指标(元素集)。
打开SuperDecision软件后,在主界面中,选择【Design】|【Cluster】|【New】命令,弹出如图2所示的对1超级决策(SuperDecision,下称SD软件)话框,在【Name】Name框内输入“思想道简介德”,点【CreateAnother】按纽,反复执行直SuperDecisions的问世主要是为了解决到把所有的二级指标创建完毕。
基于ANP的超级决策软件介绍及其应用

2003年8月系统工程理论与实践第8期 文章编号:1000-6788(2003)08-0141-03基于AN P的超级决策软件介绍及其应用刘 睿1,余建星1,孙宏才2,田 平2(1.天津大学建筑工程学院,天津300072; 2.总装备部工程兵二所,北京100850)摘要: 从应用的角度介绍A N P(网络层次分析法)应用软件——超级决策软件系统,并利用该软件对水利水电项目导流施工方案进行评价.用同一组数据分别对A N P和A HP模型进行计算,出现了倒序现象,因此是否考虑系统内部元素间的反馈和依存关系将直接影响备选方案的排序.作者尝试性地应用该软件,说明A NP方法作为一种决策方法是可以用于工程实际的.关键词: AN P;超级决策;施工方案评价中图分类号: N94 文献标识码: A Introduction to the ANP Super Decisions Softw areand Its ApplicationLIU Rui1,YU Jian-x ing1,SU N Hong-cai2,T IAN Ping2(1.Scho ol o f Co nst ructio n Engineer ing,T ianjin U niver sity,T ianjin300072,China; 2.No.2inst itute,Eng ineering Cor ps, Equipment Depar tment of G ener al,Beijing100850,China)Abstract: In the v iew o f applica tio n,t he paper intr oduces the A N P super decisio n so ftwar e,mean-w hile use the so ftw are to ev aluate the constructio n plan in hydro electr ic po w er pro ject.F or r ank be-comes r ev er sed w hen calculating AHP model a nd A NP model w ith t he same data,it pro ves the pr io rityof the plan has the directly co nnection w ith t he model whether considering dependence and feedback ofelement s or not.As a decision met ho d,t he A NP theo ry can be used in pra ct ical eng ineer ing with t hehelp o f the so ftw are.Key words: A NP(A nalytic N etw o rk Pr ocess);super decisio n;constr uction plan evaluatio n1 引言AHP(Analytic Hierarchy Process)是美国Pittburg h大学T.L.Satty教授提出的一种多准则决策方法,已在系统决策中得到了广泛的应用.常规的AHP方法将系统划分为层次,只考虑上一层次元素对下一层次元素的支配和影响,同时假设同一层次的元素之间是相互独立的,不存在相互依存的关系.这种假设在简化了系统内部元素关系的同时,也限制了其在复杂系统中的应用.许多复杂系统必须考虑层次内部元素的依存和下层元素对上层元素的反馈影响,T.L.Satty教授为此在1996年系统地提出了ANP(Ana-lytic Netw o rk Process)理论[1],将系统内各元素的关系用类似网络结构表示,而不再是简单的递阶层次结构.ANP理论更准确地描述客观事物之间的联系,是一种更加有效实用的决策方法.传统的AH P方法只是A NP方法的一个特例.由于国内对ANP的理论研究还处于初级阶段,有关ANP理论的文章不多,如文献[2,3],加上ANP 模型的计算较为复杂,在不借助于计算软件的情况下,很难将ANP模型应用于解决实际决策问题.ANP 计算问题是解决ANP应用的瓶颈,其计算的复杂性严重阻碍ANP理论在实践中的应用.目前国内将收稿日期:2002-09-19作者简介:刘睿(1969-),女,安徽合肥人,博士研究生,研究方向为工程项目风险管理,Email:liuruibeijing@sohu. com;余建星,天津大学建工学院院长,博士生导师;孙宏才,总装备部工程兵二所所长,博士生导师;田平,总装备部工程兵二所总工程师.142系统工程理论与实践2003年8月ANP模型用于实际的例子尚不多见,文献[4]将一个简单的带反馈的AH P问题(ANP)转化为A HP之后,将问题得以求解.如果对较为复杂的ANP问题,文献[4]的方法将是无法推广的.最近Rozann W. Satty和W illiam Adams在美国推出了超级决策(Super decision,下称SD)软件,该软件基于ANP理论,已成功地将ANP的计算程序化,是ANP的强大的计算工具,为A NP的推广奠定了基础.本文从应用的角度介绍AN P的应用软件——超级决策SD软件,并成功地利用该软件对水利水电项目导流施工方案进行评估.2 ANP应用软件——超级决策SD软件介绍超级决策SD软件提供了强大的功能,可以计算任何ANP模型,并完整地表达计算结果.当然如果不输入相关元素之间的关系,则该软件也完全可以用来计算AHP模型.同时该软件也提供了良好的人机对话窗口,较方便于使用者,遗憾的是该软件没有汉化,在推广中会存在语言障碍.运用ANP超级决策SD 软件进行决策的基本步骤如下:1)对决策问题进行分析,将一个复杂问题分解成各个元素组(cluster)和元素(elem ent).同时在程序中选择相应按键,逐个输入元素组(C)和元素(E).输入方式有三种:三层结构模板、二层结构模板或是不用模板,自行设计.SD软件提供的标准模板是将任何一个决策问题归结为从利益(Benefits)、成本(Costs)、机会(Oppo rtunities)、风险(Risks)四个准则来考虑,即可以将决策问题转化为BOCR四个方面去评价.在每个准则之下,可分别构造子网络、子子网络,网络内部有元素组,元素组内有元素.自行设计的模型可将任何一个ANP模型在程序中表示出来.2)按支配关系将各个元素组(cluster)和元素(element)聚类形成网状结构,确定元素组(cluster)之间和元素(element)之间的关系,主要判断元素层次是否内部独立,是否有依存和反馈关系存在.按照比例标度经过人们的判断,针对某一目标,对元素组(cluster)之间和元素(element)之间进行逐一比较,构成两两对比矩阵.在输入方式上可采用矩阵式、百分比式、问卷式、口头方式,也可以直接以文件形式输入数据.凡是相互之间存在依存和反馈关系的,都应进行两两比较.当同一层元素之间相互独立,不作两两比较时,就转化为ANP模型的特例——A HP模型.以上两部分构成了SD软件的输入部分.3)计算分析部分:根据上述输入,SD软件就可以构造超矩阵、加权超矩阵、极限超矩阵,最终可得综合优势度,另外还可以进行灵敏度的计算,如不借助于SD软件,灵敏度计算的工作量是极其繁重的.改变两两对比矩阵、优势度的数值,可分别分析计算其灵敏度变化情况.超矩阵、加权超矩阵、极限超矩阵的数据可以在EXCEL表格中打开,最终优势度数据和灵敏度可用图表表示.3 案例研究水利水电工程中不过水围堰施工导流方案的选择是一个复杂的多目标决策问题,通常选择备选方案的准则有施工费用指标、工期指标、施工风险指标和施工难度指标[5].1)工程费用指标该项费用由确定性和不确定性两部分费用组成.一旦施工方案选定,确定性费用,包括导流泄水建筑物费用、围堰工程费用和基坑抽排水费用等,可视作恒定的值.当导流工程失效时,需采取补救措施,这时发生不确定性工程费用,如基坑再次抽排水费用、围堰修补费用和基坑清淤费用.2)施工工期指标当导流工程失效时,需采取补救措施,造成施工工期的延长,工期延长量由基坑再次抽排水时间、围堰修补时间和基坑清淤时间决定.3)施工风险指标施工风险度是由导流系统中的水文、水力等不确定因素引起的.通常,可用年导流风险率来表示风险度指标.4)施工难度指标施工难度主要集中在隧洞施工难度和围堰施工难度上.上述各项指标都可以通过模糊打分法确定.同时,通过上面的分析,各项指标之间存在一定的依存关系,如工程费用和工期都是由施工工程量确定,工程量包括确定和不确定两部分,其中不确定性工程量与施工风险指标和风险难度指标密切相关.可以说,施工风险指标和施工难度指标决定了施工方案的未来工程费用和工期.因此,在综合评价施工方案时,必须考虑到各项指标之间的依存关系,即施工风险指标和施工难度指标对工程费用和工期的影响.建立如图1所示的ANP 模型.图1 为比较ANP 与传统的AHP 模型的不同,笔者借助于超级决策(Super decisio n )软件,用同一组数据对这两种模型进行了计算ABC 方案的排序,用A HP 模型计算结果为A >C >B ;用AHP 模型计算结果为C >A >B .当然,ANP 模型中分别增加了施工风险指标和施工难度指标对工程费用和工期的影响判断.值得注意的是方案A 和方案C 的排序出现颠倒.这种排序的颠倒正说明了是否考虑因素内部依存关系会直接影响决策.另外,通过对敏感度的计算也得到了一些有意的启示.限于篇幅,这里无法将有关数据一一说明.4 结语基于ANP 理论的超级决策SD 软件成功地解决了超矩阵的复杂计算问题,解决了ANP 方法在决策中的实际应用困难.同时,由于对A NP 机理还存在许多的疑惑,如考虑因素之间的影响为多大时,会出现方案倒序等等问题,还需要进一步地进行研究和探索.参考文献:[1] Saaty T L.Desion M aking w ith D ependence and F eedback:T he Analyt ic N etw or k P ro cess [M ].Pittburg h,RW SPublicat ions.2001.84-136.[2] 王莲芬.网络分析法(A N P )理论和算法[J ].系统工程理论和实践,2001,21(3):44-50.[3] 孙宏才,田平.网络层次分析法(A N P)与科学决策[A ].孙宏才.决策科学理论与方法[C].北京:海洋出版社,2001,3-8.[4] 刘林.反馈系统排序方法及其在产业结构分析中的应用[D ].天津:天津大学系统所,1987.[5] 钟登华,毛寨汉,刘海东.施工导流方案的多目标总体综合评价方法[J ].水利水电技术,2002,33(5):17-20.(上接第140页)参考文献:[1] 李丛信,陈淼鑫,郭福田,周丽佩.注水系统的计算方法[J ].石油学报,1998,19(3):120-124.[2] 陈淼鑫,刘翠玲,陈晓昕,李天歇.大型注水系统的最优控制(一)、(二)[J ].黑龙江自动化技术与应用,1996,18(6):1-7.[3] 陈淼鑫,刘铁男,司光宇.大型注水系统的运行、计算和控制[J].大庆石油学院学报,1995,19(3):71-75.[4] 朱俊华,战长松.往复泵[M ].北京:机械工业出版社,1991.[5] 席少霖.非线性最优化方法[M ].北京:高等教育出版社,1992.143第8期基于AN P 的超级决策软件介绍及其应用。
用SuperDecision进行网络层次分析法的应用实例

用SuperDecision进行网络层次分析法(ANP)的应用实例一、网络层次分析法简介(一)ANP理论与方法20年代90年代,萨蒂教授(Saaty)在AHP的基础上于提出来的一种适应非独立递阶层次结构的决策方法——网络层次分析法(Analytic Network Process,ANP)[9]。
网络层次分析法将系统内各元素的关系用类似网络结构表示,而不再是简单的递阶层次结构,网络层中的元素可能相互影响、相互支配,这样ANP能更准确地描述客观事物之间的联系,是一种更加有效的决策方法。
网络层次分析法在进行决策分析时,需要决策者对每个因素(影响因子)进行两两相对重要程度的判定。
在实际生活中,决策者常常不是对所有的决策因素(影响因子)进行相对重要程度判断,而是根据自己的情况(知识、经验、喜好)对某几个因素(影响因子)进行相对重要程度判断,此时,两两判断矩阵就会出现一些空缺,我们称这种情况为信息不完备[1]。
为此,运用ANP进行分析,通过将问题化为一种二次规划问题来计算出权重,最后运用ANP的极限超矩阵得到总排序。
ANP经常被用来解决具有网络结构的系统评价与决策的实际问题[1]。
(二)ANP网络结构ANP考虑到递阶层次结构内部循环及其存在的依赖性和反馈性,将系统元素划分为两大部分,第一部分称为控制因素层,包括问题目标和决策准则,所有的决策准则均被认为是彼此独立的,且受目标元素支配。
控制元素中可以没有决策准则,但至少有一个目标,控制层中的每个准则的权重均可由传统的AHP获得。
第二部分为网络层,它是由所有受控制层支配的元素组成的,其内部是互相影响的网络结构,图1就是一个典型的ANP结构。
图1 典型的ANP结构图二、ANP算法步骤(一)分析问题。
将决策问题进行系统的分析、组合形成元素和元素集。
主要分析判断元素层次是否内部独立, 是否存在依存和反馈。
可用会议讨论、专家填表等形式和方法进行。
(二)构造ANP的典型结构。
用SuperDecision进行网络层次分析法(ANP)的应用实例
用SuperDecision进行网络层次分析法(ANP)的应用实例一、网络层次分析法简介(一)ANP理论与方法20年代90年代,萨蒂教授(Saaty)在AHP的基础上于提出来的一种适应非独立递阶层次结构的决策方法——网络层次分析法(Analytic Network Process,ANP)[9]。
网络层次分析法将系统内各元素的关系用类似网络结构表示,而不再就是简单的递阶层次结构,网络层中的元素可能相互影响、相互支配,这样ANP能更准确地描述客观事物之间的联系,就是一种更加有效的决策方法。
网络层次分析法在进行决策分析时,需要决策者对每个因素(影响因子)进行两两相对重要程度的判定。
在实际生活中,决策者常常不就是对所有的决策因素(影响因子)进行相对重要程度判断,而就是根据自己的情况(知识、经验、喜好)对某几个因素(影响因子)进行相对重要程度判断,此时,两两判断矩阵就会出现一些空缺,我们称这种情况为信息不完备[1]。
为此,运用ANP进行分析,通过将问题化为一种二次规划问题来计算出权重,最后运用ANP的极限超矩阵得到总排序。
ANP经常被用来解决具有网络结构的系统评价与决策的实际问题[1]。
(二)ANP网络结构ANP考虑到递阶层次结构内部循环及其存在的依赖性与反馈性,将系统元素划分为两大部分,第一部分称为控制因素层,包括问题目标与决策准则,所有的决策准则均被认为就是彼此独立的,且受目标元素支配。
控制元素中可以没有决策准则,但至少有一个目标,控制层中的每个准则的权重均可由传统的AHP获得。
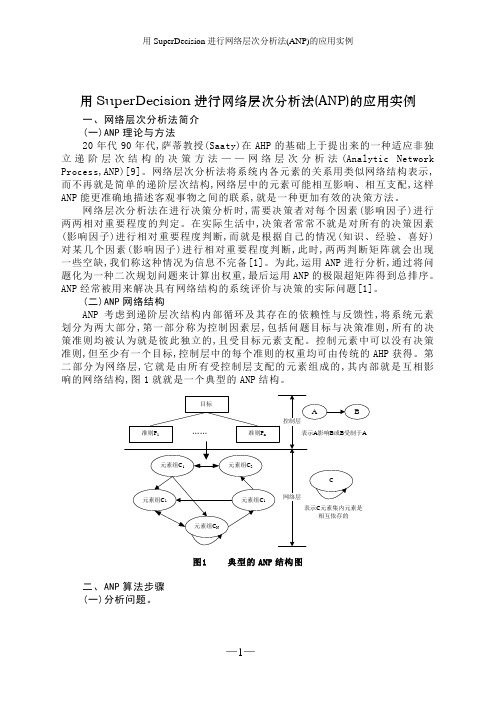
第二部分为网络层,它就是由所有受控制层支配的元素组成的,其内部就是互相影响的网络结构,图1就就是一个典型的ANP结构。
图1 典型的ANP结构图二、ANP算法步骤(一)分析问题。
将决策问题进行系统的分析、组合形成元素与元素集。
主要分析判断元素层次就是否内部独立, 就是否存在依存与反馈。
可用会议讨论、专家填表等形式与方法进行。
(二)构造ANP的典型结构。
基于ANP和模糊综合评价的京东到家众包风险评价研究

基于ANP和模糊综合评价的京东到家众包风险评价研究作者:宋苏杭来源:《中国市场·营销研究方向》 2017年第7期1 引言随着人们生活节奏的加快以及“互联网+”模式的发展,生鲜电商发展迅速。
生鲜电商的发展直接带动了生鲜物流的发展,到家服务越来越被消费者钟情。
由于订单量不断增长,商家自建物流团队已经很难胜任。
生鲜产品“最后一公里”的配送问题成为制约生鲜电商发展的瓶颈,众包物流模式应运而生。
但是众包物流模式作为一种在共享经济背景下新兴的物流模式,其在解决“最后一公里”配送问题的同时也存在着一定的风险。
如何通过一些可靠有效的管理方法,预防甚至消除“最后一公里”生鲜商品众包模式的风险,降低生鲜商品配送过程中的损耗,进而提高物流质量是促进生鲜电商行业发展,提高企业竞争力亟待解决的问题。
综上,为进一步了解众包物流模式为生鲜电商带来的风险,本文以京东到家为例,确立起众包风险评价指标体系,并利用网络层次分析法分析以及模糊综合评价法确定各级指标权重,进而确定其风险等级,为京东到家发展众包物流提供合理借鉴。
2生鲜电商众包物流风险等级评价指标体系的构建为了解生鲜电商众包物流风险等级评价指标,本文在对专家进行访谈和邮件问卷调查反馈征询意见的基础上,遵循科学性、相关性、系统性、全面性以及可操作性原则的基础上筛选出一级指标5个即人员风险、信息风险、管理风险、技术风险和操作风险,并进一步将各一级指标体系细化分解为12个二级指标体系,如表1所示。
其中,不难看出人员风险是制约众包服务水平的关键因素,主要从配送人员的素质风险、员工流失风险、客户拒收退货风险三个方面考虑。
虽然众包模式能充分利用社会上的闲散运力,但众包人员也充满了不确定因素。
到目前为止,想要成为众包快递员,并没有严格的准入门槛,只要成年并认路,都可以注册申请成为快递员。
但人恰恰是最不确定的因素。
信息风险主要包括线上线下信息不对称、信息共享风险、系统安全风险。
超市实体店的库存管理由于超市大、店面多,而且是分散式地存储,信息传递不是十分准确。
超级决策软件_SuperDecisions_在体育综合评价中的应用研究

ANP赋 权 的 核 心 工 作 :解 超 矩 阵 , 这 是 一 种 的 准 则 和 构 建 判 断 矩 阵 的 元 素 集 , 网 络 中 客 观 性 。本 课 题 采 用 网 络 分 析 法 确 定 指 标
非常复杂的计算过程,手工运算难度很大, 所有元素之间的联系影响和反馈,都将以 权重,在制定和具体实施过程中要广泛听
简介
德”,点【Create Another】按纽,反复执行直
Super Decisions的问世主要是为了解决 到 把 所 有 的 二 级 指 标 创 建 完 毕 。将 指 标 框 3 确定指标的权重
ANP模 型 的 计 算 问 题 ,因 此 它 的 计 算 原 理 架按单元输入SuperDecision软件中,只简化
新能力评价及评价系统研究,东南大学
另一个元素极端重要;2,4,6,8表示上述相 计 算 出 相 对 权 重 后 , 回 到 主 界 面 中, 单击
硕士学位论文,2006.
①作者简介:魏华(1977-),硕士,研究方向为计算机技术在体育领域中的应用。
科技创新导报 S c i e n c e a n d T e c h n o l o g y I n n o v a t i o n H e r a l d
第二步构造ANP 的典型结构。首先是构 间 的 关 联 了 。
项指标较为齐全,能全面反映优秀运动队
造控制层次 (Control Hierarchy),先界定
( 3 )建立判断矩阵。建立判断矩阵的目 教 练 员 在 训 练 过 程 中 的 各 项 因 素 。能 够 将
决策目标。再界定决策准则, 这是问题的基 的, 是为了确定各元素间的优势度, 并以此 一些比较模糊难以定量描述的评价因素加
网络层次分析法(anp)分析工具的设计与实现

(3. Naval Aviation University,Yantai
Abstract
JING Yuping3
264001)
200092)
According to the basic principle and method of ANP network analytic hierarchy process. Combined with operational
Class Number
1
TP311.5
引言
目前世界正在进入信息时代,深层次、大范围
的军事改革正加速进行,战争向信息化形式转变。
现代战争具有需求整体性和体系对抗的特点,战争
过于复杂[2]。为解决此问题,美国科学家 William
Adams 和 Rozann W.Satty 在 21 世纪初推出了超级
∗
无法根据领域特点对 ANP 模型进行验证、优化。
目前国内关于 ANP 的模型和案例应用有不少
的 研 究 ,但 ANP 基 础 工 具 的 研 究 还 未 见 相 关 报
道。基于以上问题,通过对相关的模型算法、计算
收稿日期:2019 年 7 月 18 日,修回日期:2019 年 8 月 17 日
基金项目:山东省重点研发计划(编号:2016YJS02A01)资助。
决策软件(Super decision,SD),支持对 ANP 可视化
建模与程序化计算[3]。但存在以下的问题:1)SD 软
件是十几年前的产品,界面风格与操作模式不够友
形态的各部分随着信息通讯的越来越快相互之间
好,例如不支持图元拖放,操作回溯,模型元素的快
影响更大,更多的不确定因素需要决策面对,这些
Network Process
网络层次分析法(ANP)在IT项目风险评估中的应用

2 1 A P和 A P的特 点 . H N
A P法是 由美国著名运筹学家 、 H 匹兹堡大学教授 T LSa 于 2 . .at y 0世纪 8 0年代创立的 , 它是一种强有
力的系统分析和运筹学方法 , 对多因素、 对准则 、 多方案的综合评价和趋势预测有效。19 96年,at Sa y首次 系统地论述了一种适用于非独立的阶梯层次结构的决策方法 A P J它是在 A P的基础上发展起来 的, N , H
是 复杂 化和具 体化 的 A P, H 能够应用 在更 加广 泛 的领 域 中。
A P和 A P的共同点是都能够处理不易定量化变量 的多准则问题 , H N 可以将定性的判断用数量的形式
收稿 日期 :1 7— 1 2 2 3 0 —1  ̄ 作者简介 : 莉 (9 8一) 女, 张 17 , 贵州贵阳人, 贵州大学经济学院助教 。
1 引言
I 行业 已经充分认识到对 I 目风险进行管理的能够提高项 目开发的成功率 , T T项 减少资源的浪费。根
据美 国斯坦迪 什 的研 究表 明 … , 至 到 20 截 04年 , 过对项 目进 行风 险管 理 , 通 全球 I 目的成功率 由 19 T项 94 年 的 1% 上 升到 2 % , 6 9 失败 率 由 3 %下 降到 1% , 是 ,0年 间依然 有 5 % 的 I 目只完 成 了预期 项 1 8 但 l 3 T项 目的部 分功 能 , 并且 费用 和时间大 大 的超 过 了预期 的计划 。影 响 I 目成 功 的风 险 因素 繁多 且 复杂 , T项 文
献[2 2 总结 了在 I 项 目整个生命周期中, 】 r I ’ 会导致 I 项 目陷入 困境的因素有 4 个 , r I ’ 0 并且前一阶段的风险因
层次分析法案例

层次分析法案例层次分析法(Analytic Hierarchy Process,简称AHP)是一种对决策问题进行排序和比较的数学模型和解决方法。
它广泛应用于各个领域,如管理学、经济学、工程学、环境科学等。
本文将以一个案例来介绍层次分析法的应用。
假设有一个公司要选择一种新的营销策略,以推广他们的产品。
他们面临的问题是如何确定最佳的营销策略以及相应的权重。
首先,公司需要确定评价标准。
在这个案例中,我们设定了三个评价标准:市场覆盖面、成本效益和品牌影响力。
市场覆盖面表示策略的推广范围,成本效益表示策略的投入与产出比例,品牌影响力表示策略对品牌形象的影响程度。
接下来,公司需要确定备选方案。
在这个案例中,我们选择了四种备选方案:A、B、C和D。
方案A是通过电视广告推广产品,方案B 是通过社交媒体推广产品,方案C是通过线下宣传推广产品,方案D 是通过搜索引擎优化推广产品。
然后,公司需要建立一个判断矩阵,用于比较不同评价标准之间的重要性。
在这个案例中,我们设定了市场覆盖面对成本效益、品牌影响力对市场覆盖面和成本效益的相对重要性。
通过对公司内部专家的意见进行调查,我们可以得到一个专家判断矩阵。
接下来,我们需要对备选方案进行两两比较,以确定它们在不同评价标准下的权重。
在这个案例中,我们需要比较每个备选方案在市场覆盖面、成本效益和品牌影响力上的相对重要性。
通过专家的意见调查,我们可以得到备选方案的比较矩阵。
通过逐步比较,我们可以得到每个备选方案在不同评价标准下的权重值。
最后,我们可以计算出每个备选方案的排名,以确定最佳的营销策略。
通过层次分析法,公司可以根据自己的需要和目标来确定最佳的营销策略。
这种方法能够系统地分析和比较各种因素,帮助决策者做出明智的决策。
除了在商业领域中的应用,层次分析法在其他领域也有广泛的应用。
例如,在环境科学中,可以使用层次分析法来评估不同的环境保护策略;在工程学中,可以使用层次分析法来选择最合适的工程方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用SuperDecision进行网络层次分析法(ANP)的应用实例一、网络层次分析法简介(一)ANP理论与方法20年代90年代,萨蒂教授(Saaty)在AHP的基础上于提出来的一种适应非独立递阶层次结构的决策方法——网络层次分析法(Analytic Network Process,ANP)[9]。
网络层次分析法将系统内各元素的关系用类似网络结构表示,而不再是简单的递阶层次结构,网络层中的元素可能相互影响、相互支配,这样ANP能更准确地描述客观事物之间的联系,是一种更加有效的决策方法。
网络层次分析法在进行决策分析时,需要决策者对每个因素(影响因子)进行两两相对重要程度的判定。
在实际生活中,决策者常常不是对所有的决策因素(影响因子)进行相对重要程度判断,而是根据自己的情况(知识、经验、喜好)对某几个因素(影响因子)进行相对重要程度判断,此时,两两判断矩阵就会出现一些空缺,我们称这种情况为信息不完备[1]。
为此,运用ANP进行分析,通过将问题化为一种二次规划问题来计算出权重,最后运用ANP的极限超矩阵得到总排序。
ANP经常被用来解决具有网络结构的系统评价与决策的实际问题[1]。
(二)ANP网络结构ANP考虑到递阶层次结构内部循环及其存在的依赖性和反馈性,将系统元素划分为两大部分,第一部分称为控制因素层,包括问题目标和决策准则,所有的决策准则均被认为是彼此独立的,且受目标元素支配。
控制元素中可以没有决策准则,但至少有一个目标,控制层中的每个准则的权重均可由传统的AHP获得。
第二部分为网络层,它是由所有受控制层支配的元素组成的,其内部是互相影响的网络结构,图1就是一个典型的ANP结构。
图1 典型的ANP结构图二、ANP算法步骤/(一)分析问题。
将决策问题进行系统的分析、组合形成元素和元素集。
主要分析判断元素层次是否内部独立, 是否存在依存和反馈。
可用会议讨论、专家填表等形式和方法进行。
(二)构造ANP的典型结构。
首先是构造控制层次(Control Hierarchy),先界定决策目标。
再界定决策准则,这是问题的基本。
各个准则相对决策目标的权重用AHP法得到。
(三)构造ANP超矩阵计算权重。
ANP赋权的核心工作:解超矩阵,这是一种非常复杂的计算过程,手工运算难度很大,应用Super Decision软件可以解决这个问题。
具体实施步骤如下:1、基于网络模型中各要素间的相互作用,进行两两比较;2、确定未加权超矩阵(基于两两判断矩阵,使用特征向量法获得归一化特征向量值,填入超矩阵列向量);3、确定超矩阵中各元素组的权重(保证各列归一);4、计算加权超矩阵;5、计算极限超矩阵;(使用幂法,即求超矩阵的n次方,直到矩阵各列向量保持不变)。
.三、ANP计算工具——SuperDecision由于ANP法的原理和过程比较复杂,考虑的元素较多时用手工计算几乎不可能完成,考虑的元素少则不符合实际情况,影响结果精确性。
,其人工运算极其繁琐,且难度很大,如果不借助计算软件,很难将ANP应用于解决实际决策问题。
和William Adams在美国推出了超级决策(Super Decision)软件,为ANP模型真正应用提供条件。
四、实例分析现应用基于依存和反馈的网络层次分析法(ANP)对应急桥梁设计方案进行评估。
具体操作步骤如下:(一)分析问题在此处需要对需要解决的问题进行分析,理清思路,构建起评价体系。
第一,针对问题进行分析,并依此形成指标体系。
在设计某一座应急桥梁时,施工周期、桥梁长度、通行的荷载、车行道宽度、车道中间的中央分隔带、桥下通航净空是一定的。
要比较的因素主要有:1、安全性S桥梁的安全性包括桥梁结构强度(S1)、刚度(S2)、稳定性(S3)。
结构强度、刚度和稳定性存在相互依赖性。
便桥高强度一定高刚度但未必高稳定性;高稳定性一定有高强度和高刚度;高刚度一定保证便桥的高强度和高稳定性。
}2、经济性E桥梁的经济性包括所采用的桥梁材料费用(E1)、制造费用(E2)、安装费用(E3)和使用维护费用(E4)。
经济性与安全性是一对矛盾。
经济性越高,安全性就会降低;安全性越高,经济性就越低。
桥梁材料费用和使用维护费用具有一定的依赖性。
若采用性能很好的桥梁材料(同时材料费用也高),则能降低桥梁使用维护费用。
3、耐久性D桥梁的耐久性就是桥梁的使用寿命(D1)。
一定要保证应急桥梁具有与施工周期相对应的耐久性。
耐久性与经济性、安全性存在相互依赖关系。
若桥梁耐久性大大超过施工周期,则桥梁的安全性是有保证的,而经济性就较差了;反之,若桥梁耐久性达不到施工周期的时间,则桥梁的经济性是好了,而安全性得不到保证了。
4、可制造性M所设计的应急桥梁一定要具有良好的可制造性,因为应急桥梁制造周期很短,如果制造周期长了,则势必影响主桥的施工进度。
可制造性包括良好的制造工艺(M1)、方便的现场安装(M2)。
良好的制造工艺、方便的现场安装可降低工厂制造费用和现场安装费用。
为了保证桥梁整体质量,现场连接应采用销接或螺栓连接,应尽量避免焊接,若要焊接,也应减少现场焊接的数量,因为现场焊接质量往往受外界因素的影响较大。
安全性和经济性是一对矛盾。
若要保证较高的安全性,如施工周期是3年,要保证6年的安全性,则材料费用就会高,制造性要求也高,但经济性差;若要保证较高的经济性,如施工周期是3年,仅保证3年的安全性,则材料费用就会低,制造性要求不高,但安全性差。
耐久性与安全性是依存的,与经济性是矛盾的。
耐久性好,则安全性好,但经济性差;安全性好,则耐久性好。
表1 ,表2 评估应急桥梁设计方案指标体系在指标体系构建过程中, 只识别了评价指标, 而要建立ANP 模型还必须对评价指标之间的互相影响关系(反馈或依赖)进行研究,即:指标的关联情况。
指标关联情况是通过一个二维表形式的专家问卷调查而得知的,通常可以通过以专家调查或是小组讨论方式最终可得到评价指标间的关联情况。
如下图所示:素。
请在左列因素影响顶部因素的相应空格中打“√”。
图2应急桥梁设计方案评估ANP 结构图第三,形成两两比较矩阵。
两两比较矩阵,即:判断矩阵,主要用于元素间的优势度。
判断矩阵表示对于上一层因素,本层与之有关因素之间相对重要性的比较,凡是相互之间存在依存和反馈关系的, 都应进行两两比较。
判断矩阵是层次分析法的基本信息,也是进行相对重要度计算的依据。
依据应急桥梁设计方案评估指标关联情况表(表2)对二级影响因素所影响的三级被影响因素进行计数,即:将作为影响因素的所有二级指标对应的三级影响因素中划了“√”的三级被影响因素进行计数,最终得到一个二维表,如表3所示。
表4 】表5应急桥梁设计方案评估二级指标关联情况即:只要相应计数大于0,就必须建立两两比较矩阵,按照“构造判断矩阵的方法”,构建本例的二级指标判断矩阵,如表4所示。
表6 ,表7根据应急桥梁设计方案评估二级指标两两比较矩阵(表4),设计用于获取二级指标重要度的调查表,以A 为例,如表5所示。
(依据表2(应急桥梁设计方案评估二级指标重要度调查表)对三级被影响因素进行计数运算,即:将作为影响因素的三级指标中划了“√”的三级被影响因素进行计数,最终得到一个二维表,如表6所示。
即:只要相应计数大于1,就必须建立两两比较矩阵,按照“构造判断矩阵的方法”,构建本例的二级指标判断矩阵,如表7所示。
表10 应急桥梁设计方案评估三级指标两两比较矩阵#;`三级指标重要度的调查表,方法类似二级指标重要度调查表,以Bridge1为例,如表8所示。
表11 应急桥梁设计方案评估Bridge1指标重要度调查表数据处理是贯穿于整个研究过程的核心,诸如指标的筛选、指标权重的计算要处理的原始数据大部分来自于问卷调查。
问卷处理主要采用Excel完成,而指标权重的计算则采用Super Decision完成。
此处我们主要利用Excel进行调查问卷的处理。
1.调查问卷的设计ANP法主要涉及到的调查问卷有两部分,包括:第一,指标间的关联情况,也就是指标间的反馈和依赖关系;第二,存在反馈或依赖关系指标间的重要程度。
调查问卷的设计在上一步已经进行,具体过程可以参看。
2.调查问卷的填写指标间关联情况的调查问卷在前面已经设计好了,填写方法也已注明。
在此要重点讲述的是存在反馈或依赖关系指标间的重要程度的调查问卷,即:判断矩阵权重的填写。
判断矩阵的填写方法大多采取的是:向填写人(专家)反复询问,针对判断矩阵的准则,其中两个元素两两比较哪个重要,重要多少,对重要性程度按1-9赋值。
若在实际操作中构造的判断矩阵不具有一致性,择需要进行一致性检验。
表12 1-9标度法ij ij 1/3,1/5,1/7,1/9}。
这些数字是根据人们进行定性分析的直觉和判断力而确定的。
3.调查问卷的处理调查问卷的处理,要尽量安排适当的人员进行,而且要尽量借助Excel 等工具来进行,在上面讲述的德尔菲法是我们进行问卷处理的主要步骤和方法,直接参考。
最终得到所有两两比较矩阵的权重,如表10所示。
%CR=CR= 》} 》…CR=0…," CR=CR=:CR=、CR=CR=—CR=(CR=CR=[CR=、CR=CR=(CR= ~CR=CR=%CR=…CR=CR=(CR= -CR=CR=;CR= .CR=CR=]CR= #CR=CR=、CR= >CR=>;:/!CR=!CR=@指标体系的构建主要指在Super Decision中完成整个模型的构建,包括:创建元素集、节点、链接等。
第一,创建元素集ClusterCluster,即元素集,对应的是网络层指标,也就是二级指标。
1.在桌面上单击“Super Decisions”图标或者选择“开始”→“程序”→“Super Decisions”→“Super ”,启动Super Decisions,Super Decisions 主界面,如图3所示。
图3 Super Decisions主界面注意:Super Decisions启动后,默认已经创建了一个“model”,即模式,也可以通过执行“【File】|【New】”菜单命令来创建,如图4所示。
然后会弹出“Template Selection”对话框,如图5所示,来选择模板。
在选择好模板后,单击“Continue”按钮完成模式创建。
&图4 创建模式菜单示意图图5 Template Selection对话框2.进入Super Decisions的主界面,执行“【Design】|【Cluster】|【New】”菜单命令,调用“New Cluster Dialog”对话框,如图6所示。
图6 创建Cluster菜单示意图3.在弹出的“New Cluster Dialog”对话中,“Name”框内输入二级指标“Alternatives(A)”,“Description”框内输入二级指标对应的描述,“Main Font”选项更改字体大小,“Icon”选项更改Cluster图标,“Color”选项更改Cluster颜色(利用颜色可以使层次结构更加清晰),点“Create Another”按纽,完成Cluster的创建,如图7所示。
