2015年湖南省高考数学试卷(理科)答案与解析
2015年湖南省高考数学试卷(理科)及答案

2015年湖南省高考数学试卷(理科)一、选择题,共10小题,每小题5分,共50分1.(5分)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i2.(5分)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.4.(5分)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7 B.﹣1 C.1 D.25.(5分)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数6.(5分)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6 D.﹣67.(5分)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386 B.2718 C.3413 D.47728.(5分)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则||的最大值为()A.6 B.7 C.8 D.99.(5分)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.10.(5分)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A. B. C.D.二、填空题,共5小题,每小题5分,共25分11.(5分)(x﹣1)dx=.12.(5分)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是.13.(5分)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.14.(5分)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=.15.(5分)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是.三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.选修4-4:坐标系与方程17.(6分)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.选修4-5:不等式选讲18.设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.19.设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.20.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望.21.如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ的体积.22.(13分)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(ⅰ)若|AC|=|BD|,求直线l的斜率;(ⅱ)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,△MFD总是钝角三角形.23.(13分)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.2015年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题,共10小题,每小题5分,共50分1.(5分)(2015•湖南)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i【分析】由条件利用两个复数代数形式的乘除法法则,求得z的值.【解答】解:∵已知=1+i(i为虚数单位),∴z===﹣1﹣i,故选:D.2.(5分)(2015•湖南)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】直接利用两个集合的交集,判断两个集合的关系,判断充要条件即可.【解答】解:A、B是两个集合,则“A∩B=A”可得“A⊆B”,“A⊆B”,可得“A∩B=A”.所以A、B是两个集合,则“A∩B=A”是“A⊆B”的充要条件.故选:C.3.(5分)(2015•湖南)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.【分析】列出循环过程中S与i的数值,满足判断框的条件即可结束循环.【解答】解:判断前i=1,n=3,s=0,第1次循环,S=,i=2,第2次循环,S=,i=3,第3次循环,S=,i=4,此时,i>n,满足判断框的条件,结束循环,输出结果:S===故选:B4.(5分)(2015•湖南)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7 B.﹣1 C.1 D.2【分析】由约束条件作出可行域,由图得到最优解,求出最优解的坐标,数形结合得答案.【解答】解:由约束条件作出可行域如图,由图可知,最优解为A,联立,解得C(0,﹣1).由解得A(﹣2,1),由,解得B(1,1)∴z=3x﹣y的最小值为3×(﹣2)﹣1=﹣7.故选:A.5.(5分)(2015•湖南)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数【分析】求出好的定义域,判断函数的奇偶性,以及函数的单调性推出结果即可.【解答】解:函数f(x)=ln(1+x)﹣ln(1﹣x),函数的定义域为(﹣1,1),函数f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣[ln(1+x)﹣ln(1﹣x)]=﹣f(x),所以函数是奇函数.排除C,D,正确结果在A,B,只需判断特殊值的大小,即可推出选项,x=0时,f(0)=0;x=时,f()=ln(1+)﹣ln(1﹣)=ln3>1,显然f(0)<f(),函数是增函数,所以B错误,A正确.故选:A.6.(5分)(2015•湖南)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6 D.﹣6【分析】根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为求得r,再代入系数求出结果.【解答】解:根据所给的二项式写出展开式的通项,T r+1==;展开式中含x的项的系数为30,∴,∴r=1,并且,解得a=﹣6.故选:D.7.(5分)(2015•湖南)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386 B.2718 C.3413 D.4772【分析】求出P(0<X≤1)=×0.6826=0.3413,即可得出结论.【解答】解:由题意P(0<X≤1)=×0.6826=0.3413,∴落入阴影部分点的个数的估计值为10000×0.3413=3413,故选:C.8.(5分)(2015•湖南)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P 的坐标为(2,0),则||的最大值为()A.6 B.7 C.8 D.9【分析】由题意,AC为直径,所以||=|2+|.B为(﹣1,0)时,|2+|≤7,即可得出结论.【解答】解:由题意,AC为直径,所以||=|2+|所以B为(﹣1,0)时,|2+|≤7.所以||的最大值为7.故选:B.9.(5分)(2015•湖南)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.【分析】利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.【解答】解:因为将函数f(x)=sin2x的周期为π,函数的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1﹣x2|min=,不妨x1=,x2=,即g(x)在x2=,取得最小值,sin(2×﹣2φ)=﹣1,此时φ=,不合题意,x1=,x2=,即g(x)在x2=,取得最大值,sin(2×﹣2φ)=1,此时φ=,满足题意.故选:D.10.(5分)(2015•湖南)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A. B. C.D.【分析】根据三视图可判断其为圆锥,底面半径为1,高为2,求解体积.利用几何体的性质得出此长方体底面边长为n的正方形,高为x,利用轴截面的图形可判断得出n=(1﹣),0<x<2,求解体积式子,利用导数求解即可,最后利用几何概率求解即.【解答】解:根据三视图可判断其为圆锥,∵底面半径为1,高为2,∴V=×2=∵加工成一个体积尽可能大的长方体新工件,∴此长方体底面边长为n的正方形,高为x,∴根据轴截面图得出:=,解得;n=(1﹣),0<x<2,∴长方体的体积Ω=2(1﹣)2x,Ω′=x2﹣4x+2,∵,Ω′=x2﹣4x+2=0,x=,x=2,∴可判断(0,)单调递增,(,2)单调递减,Ω最大值=2(1﹣)2×=,∴原工件材料的利用率为=×=,故选:A二、填空题,共5小题,每小题5分,共25分11.(5分)(2015•湖南)(x﹣1)dx=0.【分析】求出被积函数的原函数,代入上限和下限求值.【解答】解:(x﹣1)dx=(﹣x)|=0;故答案为:0.12.(5分)(2015•湖南)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是4.【分析】根据茎叶图中的数据,结合系统抽样方法的特征,即可求出正确的结论.【解答】解:根据茎叶图中的数据,得;成绩在区间[139,151]上的运动员人数是20,用系统抽样方法从35人中抽取7人,成绩在区间[139,151]上的运动员应抽取7×=4(人).故答案为:4.13.(5分)(2015•湖南)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.【分析】设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将中点M的坐标代入双曲线方程,结合离心率公式,计算即可得到.【解答】解:设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将点(﹣c,2b)代入双曲线方程可得,﹣=1,可得e2==5,解得e=.故答案为:.14.(5分)(2015•湖南)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=3n﹣1.【分析】利用已知条件列出方程求出公比,然后求解等比数列的通项公式.【解答】解:设等比数列的公比为q,S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,可得4S2=S3+3S1,a1=1,即4(1+q)=1+q+q2+3,q=3.∴a n=3n﹣1.故答案为:3n﹣1.15.(5分)(2015•湖南)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是{a|a<0或a>1} .【分析】由g(x)=f(x)﹣b有两个零点可得f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a的范围【解答】解:∵g(x)=f(x)﹣b有两个零点,∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,由x3=x2可得,x=0或x=1①当a>1时,函数f(x)的图象如图所示,此时存在b,满足题意,故a>1满足题意②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意③当0<a<1时,函数f(x)单调递增,故不符合题意④a=0时,f(x)单调递增,故不符合题意⑤当a<0时,函数y=f(x)的图象如图所示,此时存在b使得,y=f(x)与y=b 有两个交点综上可得,a<0或a>1故答案为:{a|a<0或a>1}三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)(2015•湖南)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.【分析】(1)证明O,M,E,N四点共圆,即可证明∠MEN+∠NOM=180°(2)证明△FEM∽△FON,即可证明FE•FN=FM•FO.【解答】证明:(1)∵N为CD的中点,∴ON⊥CD,∵M为AB的中点,∴OM⊥AB,在四边形OMEN中,∴∠OME+∠ONE=90°+90°=180°,∴O,M,E,N四点共圆,∴∠MEN+∠NOM=180°(2)在△FEM与△FON中,∠F=∠F,∠FME=∠FNO=90°,∴△FEM∽△FON,∴=∴FE•FN=FM•FO.选修4-4:坐标系与方程17.(6分)(2015•湖南)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.【分析】(1)曲线的极坐标方程即ρ2=2ρcosθ,根据极坐标和直角坐标的互化公式得x2+y2=2x,即得它的直角坐标方程;(2)直线l的方程化为普通方程,利用切割线定理可得结论.【解答】解:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x﹣1)2+y2=1;(2)直线l:(t为参数),普通方程为,(5,)在直线l上,过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,由切割线定理,可得|MT|2=|MA|•|MB|=18.选修4-5:不等式选讲18.(2015•湖南)设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.【分析】(ⅰ)由a>0,b>0,结合条件可得ab=1,再由基本不等式,即可得证;(ⅱ)运用反证法证明.假设a2+a<2与b2+b<2可能同时成立.结合条件a>0,b>0,以及二次不等式的解法,可得0<a<1,且0<b<1,这与ab=1矛盾,即可得证.【解答】证明:(ⅰ)由a>0,b>0,则a+b=+=,由于a+b>0,则ab=1,即有a+b≥2=2,当且仅当a=b取得等号.则a+b≥2;(ⅱ)假设a2+a<2与b2+b<2可能同时成立.由a2+a<2及a>0,可得0<a<1,由b2+b<2及b>0,可得0<b<1,这与ab=1矛盾.a2+a<2与b2+b<2不可能同时成立.19.(2015•湖南)设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.【分析】(Ⅰ)由题意和正弦定理可得sinB=cosA,由角的范围和诱导公式可得;(Ⅱ)由题意可得A∈(0,),可得0<sinA<,化简可得sinA+sinC=﹣2(sinA﹣)2+,由二次函数区间的最值可得.【解答】解:(Ⅰ)由a=btanA和正弦定理可得==,∴sinB=cosA,即sinB=sin(+A)又B为钝角,∴+A∈(,π),∴B=+A,∴B﹣A=;(Ⅱ)由(Ⅰ)知C=π﹣(A+B)=π﹣(A++A)=﹣2A>0,∴A∈(0,),∴sinA+sinC=sinA+sin(﹣2A)=sinA+cos2A=sinA+1﹣2sin2A=﹣2(sinA﹣)2+,∵A∈(0,),∴0<sinA<,∴由二次函数可知<﹣2(sinA﹣)2+≤∴sinA+sinC的取值范围为(,]20.(2015•湖南)某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望.【分析】(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件A2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},利用A1,A2相互独立,,互斥,B1,B2互斥,然后求出所求概率即可.(2)顾客抽奖1次可视为3次独立重复试验,判断X~B.求出概率,得到X的分布列,然后求解期望.【解答】解:(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件B2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},由题意A1,A2相互独立,,互斥,B1,B2互斥,且B1=A1A2,B2=+,C=B1+B2,因为P(A1)=,P(A2)=,所以,P(B1)=P(A1)P(A2)==,P(B2)=P()+P()=+==,故所求概率为:P(C)=P(B1+B2)=P(B1)+P(B2)=.(2)顾客抽奖1次可视为3次独立重复试验,由(1)可知,顾客抽奖1次获一等奖的概率为:所以.X~B.于是,P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==.故X的分布列为:X0123PE(X)=3×=.21.(2015•湖南)如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ的体积.【分析】(1)首先以A为原点,AB,AD,AA1所在直线分别为x,y,z轴,建立空间直角坐标系,求出一些点的坐标,Q在棱BC上,从而可设Q(6,y1,0),只需求即可;(2)设P(0,y2,z2),根据P在棱DD1上,从而由即可得到z2=12﹣2y2,从而表示点P坐标为P(0,y2,12﹣2y2).由PQ∥平面ABB1A1便知道与平面ABB1A1的法向量垂直,从而得出y1=y2,从而Q点坐标变成Q(6,y2,0),设平面PQD的法向量为,根据即可表示,平面AQD的一个法向量为,从而由即可求出y2,从而得出P点坐标,从而求出三棱锥P﹣AQD的高,而四面体ADPQ 的体积等于三棱锥P﹣AQD的体积,从而求出四面体的体积.【解答】解:根据已知条件知AB,AD,AA1三直线两两垂直,所以分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则:A(0,0,0),B(6,0,0),D(0,6,0),A1(0,0,6),B1(3,0,6),D1(0,3,6);Q在棱BC上,设Q(6,y1,0),0≤y1≤6;∴(1)证明:若P是DD1的中点,则P;∴,;∴;∴;∴AB1⊥PQ;(2)设P(0,y2,z2),y2,z2∈[0,6],P在棱DD1上;∴,0≤λ≤1;∴(0,y2﹣6,z2)=λ(0,﹣3,6);∴;∴z2=12﹣2y2;∴P(0,y2,12﹣2y2);∴;平面ABB1A1的一个法向量为;∵PQ∥平面ABB1A1;∴=6(y1﹣y2)=0;∴y1=y2;∴Q(6,y2,0);设平面PQD的法向量为,则:;∴,取z=1,则;又平面AQD的一个法向量为;又二面角P﹣QD﹣A的余弦值为;∴;解得y2=4,或y2=8(舍去);∴P(0,4,4);∴三棱锥P﹣ADQ的高为4,且;∴V四面体ADPQ =V三棱锥P﹣ADQ=.22.(13分)(2015•湖南)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(ⅰ)若|AC|=|BD|,求直线l的斜率;(ⅱ)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,△MFD总是钝角三角形.【分析】(Ⅰ)根据两个曲线的焦点相同,得到a2﹣b2=1,再根据C1与C2的公共弦长为2,得到=1,解得即可求出;(Ⅱ)设出点的坐标,(ⅰ)根据向量的关系,得到(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,设直线l的方程,分别与C1,C2构成方程组,利用韦达定理,分别代入得到关于k的方程,解得即可;(ⅱ)根据导数的几何意义得到C1在点A处的切线方程,求出点M的坐标,利用向量的乘积∠AFM是锐角,问题得以证明.【解答】解:(Ⅰ)抛物线C1:x2=4y的焦点F的坐标为(0,1),因为F也是椭圆C2的一个焦点,∴a2﹣b2=1,①,又C1与C2的公共弦长为2,C1与C2的都关于y轴对称,且C1的方程为x2=4y,由此易知C1与C2的公共点的坐标为(±,),所以=1,②,联立①②得a2=9,b2=8,故C2的方程为+=1.(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),(ⅰ)因为与同向,且|AC|=|BD|,所以=,从而x3﹣x1=x4﹣x2,即x1﹣x2=x3﹣x4,于是(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,③设直线的斜率为k,则l的方程为y=kx+1,由,得x2﹣4kx﹣4=0,而x1,x2是这个方程的两根,所以x1+x2=4k,x1x2=﹣4,④由,得(9+8k2)x2+16kx﹣64=0,而x3,x4是这个方程的两根,所以x3+x4=,x3x4=﹣,⑤将④⑤代入③,得16(k2+1)=+,即16(k2+1)=,所以(9+8k2)2=16×9,解得k=±.(ⅱ)由x2=4y得y′=x,所以C1在点A处的切线方程为y﹣y1=x1(x﹣x1),即y=x1x﹣x12,令y=0,得x=x1,M(x1,0),所以=(x1,﹣1),而=(x1,y1﹣1),于是•=x12﹣y1+1=x12+1>0,因此∠AFM是锐角,从而∠MFD=180°﹣∠AFM是钝角,故直线l绕点F旋转时,△MFD总是钝角三角形.23.(13分)(2015•湖南)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.【分析】(Ⅰ)求出导数,运用两角和的正弦公式化简,求出导数为0的根,讨论根附近的导数的符号相反,即可得到极值点,求得极值,运用等比数列的定义即可得证;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),求出导数,求得最小值,由恒成立思想即可得证.【解答】证明:(Ⅰ)f′(x)=e ax(asinx+cosx)=•e ax sin(x+φ),tanφ=,0<φ<,令f′(x)=0,由x≥0,x+φ=mπ,即x=mπ﹣φ,m∈N*,对k∈N,若(2k+1)π<x+φ<(2k+2)π,即(2k+1)π﹣φ<x<(2k+2)π﹣φ,则f′(x)<0,因此在((m﹣1)π﹣φ,mπ﹣φ)和(mπ﹣φ,(m+1)π﹣φ)上f′(x)符号总相反.于是当x=nπ﹣φ,n∈N*,f(x)取得极值,所以x n=nπ﹣φ,n∈N*,此时f(x n)=e a(nπ﹣φ)sin(nπ﹣φ)=(﹣1)n+1e a(nπ﹣φ)sinφ,易知f(x n)≠0,而==﹣e aπ是常数,故数列{f(x n)}是首项为f(x1)=e a(π﹣φ)sinφ,公比为﹣e aπ的等比数列;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),g′(t)=,当0<t<1时,g′(t)<0,g(t)递减,当t>1时,g′(t)>0,g(t)递增.t=1时,g(t)取得最小值,且为e.因此要使①恒成立,只需<g(1)=e,只需a>,当a=,tanφ==,且0<φ<,可得<φ<,于是π﹣φ<<,且当n≥2时,nπ﹣φ≥2π﹣φ>>,因此对n∈N*,ax n=≠1,即有g(ax n)>g(1)=e=,故①亦恒成立.综上可得,若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.。
2015湖南高考数学(理)试题及答案

2015湖南高考数学(理)试题及答案满分:班级:_________ 姓名:_________ 考号:_________一、单选题(共10小题)1.已知(为虚数单位),则复数=()A.B.C .D .2.设A,B是两个集合,则“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.执行如图所示的程序框图,如果输入,则输出的()A.B.C.D.4.若变量满足约束条件,则的最小值为()A.-7B.-1C.1D.25.设函数,则是()A.奇函数,且在上是增函数B.奇函数,且在上是减函数C.偶函数,且在上是增函数D.偶函数,且在上是减函数6.已知的展开式中含的项的系数为30,则()A.B.C.6D.-67.在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附:若,则,.A.2386B.2718C.3413D.47728.已知点A,B,C在圆上运动,且.若点P的坐标为(2,0),则的最大值为()A.6B.7C.8D.99.将函数的图像向右平移个单位后得到函数的图像,若对满足的,有,则()A.B.C.D.10.某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A.B.C.D.二、填空题(共5小题)11._________。
12.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示。
若将运动员按成绩由好到差编为号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是。
13.设F是双曲线C:的一个焦点,若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为。
14.设为等比数列的前项和,若,且成等差数列,则。
15.已知,若存在实数,使函数有两个零点,则的取值范围是。
2015年湖南省高考理科数学试卷及答案(全WORD版)

D.9
π 9. 将函数 f(x)=sin2x 的图象向右平移 φ 0<φ< 个单位后得到函数 g(x)的图象,若对满足| f(x1)-g(x2)| 2 π =2 的 x1,x2,有| x1-x2|min= ,则 φ=( 3 5π A. 12 π B. 3 ) π C. 4 π D. 6
18.(本小题满分 12 分) 某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.每次抽奖都是从装有 4 个红球、6 个白球的甲箱和装有 5 个红球、5 个白球的乙箱中,各随机摸出 1 个球.在摸出的 2 球中,若都是红 球,则获一等奖;若只有 1 个红球,则获二等奖;若没有红球,则不获奖. (Ⅰ)求顾客抽奖 1 次能获奖的概率; (Ⅱ)若某顾客有 3 次抽奖的机会,记该顾客在 3 次抽奖中获一等奖的次数为 X,求 X 的分布列和数学 期望.
5
5
考点:三角函数的图象和性质. 10. 【解析】问题等价于圆锥的内接长方体的体积,如下图所示,则有 x 2-h = ,∴h=2-2x, 1 2 ∴长方体的体积为 x2h=(2x)2(2-2x)=4x· x· (2-2x) ≤4 x+x+2-2x3 32 2 = ,当且仅当 x=2-2x 即x= 时,等号成立, 3 27 3 32 27
2015 年普通高等学校招生全国统一考试(湖南卷)
理科数学
本试题包括选择题,填空题和解答题三部分,共 6 页,时间 120 分钟,满分 150 分.
一、选择题:本大题共 10 小题,每小题 5 分,共 50 分,在每小题给出的四个选项中,只有一项是符合题 目要求的. (1-i)2 1.已知 =1+i( i 为虚数单位) ,则复数 z= ( z A. 1+i B.1-i ) D.-1-i )
2
2015年高考湖南理科数学试题及答案(详解纯word版)
2015年普通高等学校招生全国统一考试(湖南卷)数 学(理科)本试题卷包括选择题、填空题和解答题三部分,时量120分钟,满分150分一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知i zi +=-1)1(2(i 是虚数单位),则复数z=A. i +1B. i -1C. i +-1D. i --12. 设A 、B 是两个集合,则“A B A = ”是“B A ⊆”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 3. 执行如图所示的程序框图,如果输入的3=n ,则输出的S =A.76 B. 73C. 98D. 944. 若变量x, y 满足约束条件⎪⎩⎪⎨⎧≤≤--≥+1121y y x y x ,则yx z -=3的最小值为A. 7-B. 1-C. 1D. 2 5. 设函数)1ln()1ln()(x x x f --+=,则)(x f 是A. 奇函数,且在)1,0(是增函数B. 奇函数,且在)1,0(是减函数C. 偶函数,且在)1,0(是增函数D. 偶函数,且在)1,0(是减函数 6. 已知5)(xa x -的展开式中含23x 的项的系数为30,则=aA. 3B. 3-C. 6D. 6- 7. 在如图2所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C 为正态分布)1,0(N 的密度曲线)的点的个数的估计值为A. 2386B. 2718C. 3413D. 4772附:若),(~2σμN X ,则6826.0)(=+≤<-σμσμX P , 9544.0)22(=+≤<-σμσμX P.8. 已知点A, B, C 在圆122=+y x 上运动,且BC AB ⊥ . 若点P 的坐标为)0,2(, 则||PC PB PA ++的最大值为A. 6B. 7C. 8D. 9 9. 将函数x x f 2sin )(=的图象向右平移ϕ)20(πϕ<<个单位后得到函数)(x g 的图象,若对满足2|)()(|21=-x g x f 的1x ,2x ,有3||min 21π=-x x ,则=ϕA. 125πB. 3πC.4π D. 6π 10. 某工件的三视图如图所示,现将该工件通过切削,加工成体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料的利用率原工件的体积新工件的体积=) A. π98 B. π916C.π2124)-( D.π21212)-(二、填空题:本大题共5小题,每小题5分,共25分. 11.⎰=-20)1(dx x __________.12. 在一次马拉松比赛中,35名运动员的成绩(单位:分钟)茎叶图如图所示若将运动员按成绩由好到差编为1-35号,再用系统抽样的方法从中抽取7人,则其中成绩在区间]151,139[上的运动员的人数是_________.13. 设F 是双曲线C 1:2222=-by a x 的一个焦点,若C 上存在点P ,使线段PF 的中点恰为其虚轴的一个端点,则C 的离心率为________.14.设n S 为等比数列}{n a 的前n 项和,若11=a ,且321,2,3S S S 成等差数列,则=n a ___________.15. 已知函数⎪⎩⎪⎨⎧>≤=.,,,)(23a x x a x x x f 若存在实数b ,使函数b x f x g -=)()(有两个零点,则a 的取值范围是___________.俯视图侧视图正视图三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)本小题有Ⅰ、Ⅱ、Ⅲ三个选做题,请考生任选两题作答,并将解答过程写在答题纸中相应题号的答题区域内,如果全做,则按所做的前两题计分. Ⅰ.(本小题满分6分)选修4-1 几何证明选讲如图,在⊙O 中,相交于点E 的两弦AB ,CD 的中点分别是M ,N ,直线MO 与直线CD 相交于点F ,证明:(i ) 180=∠+∠NOM MEN ; (ii )FO FM FN FE ⋅=⋅. Ⅱ.(本小题满分6分)选修4-4 坐标系与参数方程已知直线l ⎪⎪⎩⎪⎪⎨⎧+=+=.213,235:t y t x (t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θρcos 2=.(i )将曲线C 的极坐标方程化为直角坐标方程;(ii )设点M 的直角坐标为)3,5(,直线l 与曲线C 的交点为A ,B ,求||||MB MA ⋅的值. Ⅲ.(本小题满分6分)选修4-5 不等式选讲 设0,0>>b a ,且ba b a 11+=+,证明: (i ) 2≥+b a ;(ii )22<+a a 与22<+b b 不可能同时成立.F17. (本小题满分12分)设ABC ∆的内角C B A ,,的对边分别为c b a ,,,A b a tan =,且B 为钝角. (Ⅰ) 证明:2π=-A B ;(Ⅱ) 求C A sin sin +的取值范围.18. (本小题满分12分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖. 每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球. 在摸出的2球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖. (Ⅰ) 求顾客抽奖1次能获奖的概率; (Ⅱ) 若某顾客有3次抽奖的机会,记该顾客在3次抽奖中获一等奖的次数为X ,求X 的分布列和数学期望.19. (本小题满分13分)如图,在四棱台1111D C B A ABCD -的上、下底面分别是边长为3和6的正方形,61=AA ,且⊥1AA 底面ABCD ,点P ,Q 分别在棱1DD ,BC 上. (Ⅰ) 若点P 是1DD 的中点,证明:PQ AB ⊥1; (Ⅱ) 若//PQ 平面11A ABB ,二面角A QD P --的余弦值为73,求四面体ADPQ 的体积.BDQ20. (本小题满分13分)已知抛物线1C y x 4:2=的焦点F 也是椭圆2C )0(1:2222>>=+b a bx a y 的一个焦点,1C 与2C 的公共弦长为62. (Ⅰ) 求2C 的方程;(Ⅱ) 过点F 的直线l 与1C 相交于A ,B 两点,与2C 相交于C ,D 两点,且与同向.(i ) 若||||BD AC =,求直线l 的斜率;(ii )设1C 在点A 处的切线与x 轴的交点为M ,证明:直线l 绕点F 旋转时,MFD ∆总是钝角三角形.21. (本小题满分13分)已知0>a ,函数)),0[(sin )(∞+∈=x x e x f ax ,记n x 为)(x f 的从小到大的第n *)(N n ∈个极值点. 证明: (Ⅰ) 数列)}({n x f 是等比数列; (Ⅱ) 若112-≥e a ,则对一切*N n ∈,|)(|n n x f x <恒成立.2015年高考湖南卷理科数学参考答案一、选择题D C B A A D C B D A 二、填空题 11. 0 12. 4 13.5 14. 13-n 15. ),1()0,(∞+-∞三、解答题 16. Ⅰ. 证明:(i )如图,因为M ,N 分别是两弦AB ,CD 的中点,所以AB OM ⊥, CD ON ⊥,即90=∠=∠ONE OME ,因此 180=∠+∠ONE OME ,又四边形的内角和等于 360,故 180=∠+∠NOM MEN .(ii ) 由(i )知, O ,M ,E ,N 四点共圆,故由割线定理即得FO FM FN FE ⋅=⋅.Ⅱ.解: (i )θρcos 2=等价于 θρρcos 22=,将222y x +=ρ,x =θρcos 代入上式即得曲线C 的直角坐标方程是0222=-+x y x .(ii ) 将⎪⎪⎩⎪⎪⎨⎧+=+=.213,235t y t x 代入0222=-+x y x 得018352=++t t .设这个方程的 两个实根分别为21,t t ,则由参数t 的几何意义知||||MB MA ⋅=.18||21=t tⅢ.证明: 由abb a b a b a +=+=+11,0,0>>b a 得 1=ab (i )由基本不等式及1=ab ,有22=≥+ab b a ,即2≥+b a .(ii ) 设22<+a a 与22<+b b 可同时成立,则由22<+a a 及0>a 可得10<<a ,同理 10<<b ,从而10<<ab 这与1=ab 相矛盾,故22<+a a 与22<+b b 不可能同时成立.17. 解:(Ⅰ)由A b a ta n =及正弦定理,得BAb a A A sin sin cos sin ==,所以A B cos sin =,即)2sin(sin A B +=π. 又B 为钝角,),2(2πππ∈+A ,故A B +=2π,即2π=-A B .(Ⅱ) 由(Ⅰ)知 022)(>-=+-=A B A C ππ, 所以)4,0(π∈A . 于是)22sin(sin sin sin A A C A -+=+πA A 2cos sin +=.89)41(s i n2s i n 21s i n 22+--=-+=A A AF因为40π<<A ,所以 22sin 0<<A ,因此8989)41(sin 2222≤+--<A .由此可得C A sin sin +的取值范围是]89,22(.18. 解:(Ⅰ)记事件1A ={从甲箱中摸出的一个球是红球},2A ={从乙箱中摸出的一个球是红球},1B ={顾客抽奖一次获一等奖},2B ={顾客抽奖一次获二等奖},C ={顾客抽奖一次能获奖}.由题意1A 与2A 相互独立,21A A 与21A A 互斥,1B 与2B 互斥,且 211A A B =,2B =21A A +21A A ,21B B C +=. 又因为52104)(1==A P ,21105)(2==A P ,所以 512152)()()()(21211=⨯===A P A P A A P B P , )()()()(212121212A A P A A P A A A A P B P +=+=2121)521()211(52)()()()(2121=⨯-+-⨯=+=A P A P A P A P , 故所求概率为1072151)()()()(2121=+=+=+=B P B P B B P C P .(Ⅱ) 顾客抽奖3次可视为3次独立重复实验,由(Ⅰ)知,顾客抽奖1次获一等奖的概率为51,所以)51,3(~B X ,于是 )3,2,1,0()54()51()(33===-K C K X P KK KX 的数学期望为553)(=⨯=X E . 19. 解法一: (Ⅰ)如图,取1AA 的中点R ,连结PR BR ,, 因为1AA ,1DD是梯形D D AA 11的两腰,点P 是1DD 的中点,所以AD PR //,于是由BC AD //知,BC PR //,所以C B R P ,,,四点共面. 由题设知 AB BC ⊥,1AA BC ⊥,A AA AB =1 ,所以⊥BC 平面11A ABB , ⊂1AB 平面11A ABB ,因此 1AB BC ⊥.因为11111tan 63tan AB A AA B A AB AR ABR ∠====∠,所以11AB A ABR ∠=∠,因此901111=∠+∠=∠+∠BAB AB A BABABR , 于是 1ABBR ⊥, 又已证得1AB BC ⊥,所以⊥1AB 平面BRPC ,显然有⊂PQ 平面BRPC , 故 PQ AB ⊥1.DB(Ⅱ) 如下图,过点P 作1//AA PM 交AD 于点M ,则//PM 平面11A ABB , 因为⊥1AA 底面ABCD ,所以⊥PM 底面ABCD ,过点M 作QD MN ⊥于点N ,连结PN ,则QD PN ⊥,PNM ∠是二面角A QD P --的平面角. 所以 73cos =∠PNM ,即 73=PN MN ,从而340=MN PM . 连结MQ ,由//PQ 平面11A ABB 及//PM 平面11A ABB 知,平面//PQM 平面11A ABB ,所以AB MQ //,又ABCD 是正方形,所以ABQM 是矩形,故MQ=AB=6. 设MD =t ,则.366222ttMD MQ MD MQ MN +=+⋅=过点1D 作A A E D 11//交AD 于点E ,则E D AA 11是矩形,所以 611==AA E D ,311==D A AE ,因此 3=-=AE AD DE . 于是21==DEED MD PM , 所以t MD PM 22==,从而t t t MN PM 63623402+⨯==,解得2=t ,所以4=PM . 故四面体ADPQ 的体积 24466213131=⨯⨯⨯⨯=⋅=∆PM S V ADQ .解法二:由题设知AB AD AA ,,1G 两两垂直,以A 为坐标原点,AB ,AD ,1AA 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,如图,则相关各点的坐标为)0,0,0(A ,)6,0,3(1B ,)0,6,0(D ,)6,3,0(1D , )0,,6(m Q ,其中m BQ =,60≤≤m .(Ⅰ) 若点P 是1DD 的中点,则)3,29,0(P ,)3,29,6(--=m PQ ,又)6,0,3(1=AB ,于是018181=-=⋅, 所以AB ⊥1,即PQ AB ⊥1.(Ⅱ) 由题设知,)0,6,6(-=m , )6,3,0(1-=DD 是平面PQD 内两个不共线的向量,设),,(1z y x n =是平面PQD 的一个法向量,则 ⎪⎩⎪⎨⎧=⋅=⋅0,0111DD n 即⎩⎨⎧=+-=-+063,0)6(6z y y m x 取6=y ,得)3,6,6(1m n -=. 又平面AQD 的一个法向量是BD)1,0,0(2=n ,所以45)6(336)6(3||||,cos 2222212121+-=++-=⋅>=<m m n n n n ,而二面角A QD P --的余弦值为73,所以7345)6(32=+-m ,解得m=4或m=8(舍去),此时)0,4,6(Q . 再设)10(1≤<=λλDD ,而)6,3,0(1-=DD ,由此得到)6,36,0(λλ-P ,)6,23,6(λλ--=. 因为//PQ 平面11A ABB ,且平面11A ABB 的一个法向量是)0,1,0(3=n ,所以 0233=-=⋅λn ,32=λ,从而)4,4,0(P .于是,将四面体ADPQ 视为ADQ ∆为底面的三棱锥ADQ P -,其高4=h ,故四面体ADPQ 的体积 24466213131=⨯⨯⨯⨯=⋅=∆PM S V ADQ .20. 解:(Ⅰ) 由1C y x 4:2=知其焦点F 的坐标为(0,1),因为F 也是椭圆2C 的一个焦点,所以 122=-b a (1)又1C 与2C 的公共弦长为62,1C 与2C 都关于y 轴对称,且1C 的方程为y x 42=,由此易知1C 与2C 的公共点坐标为)23,6(±,所以164922=+ba (2) 联立(1)(2)得8,922==b a ,故2C 的方程为18922=+x y . (Ⅱ) 如图,设),(11y x A ,),(22y x B ,),(33y x C ,),(44y x D .(i )因AC 与同向,且 ||||BD AC =,所以 =,从而 2413x x x x -=-,即4321x x x x -=-,于是43243212214)(4)(x x x x x x x x -+=-+. (3) 设直线l 的斜率为k ,则l 的方程为1+=kx y .由⎩⎨⎧=+=yx kx y 4,12 得0442=--kx x ,而21,x x 是这个方程的两根,所以 4,42121-==+x x k x x (4)由⎪⎩⎪⎨⎧=++=189,122x y kx y 得06416)89(22=-++kx x k ,而43,x x 是这个方程的两根,所以2212438964,8916kx x k k x x +-=+-=+ (5)将(4)(5)代入(3)得 22222289644)89(16)1(16k k k k +⨯++=+,即22222)89()1(916)1(16k k k ++⨯=+, 所以 916)89(22⨯=+k ,解得 46±=k ,即直线l 的斜率为46±. (ii )由 y x 42=得 2'xy =,所以1C 在点A 处的切线方程为)(2111x x x y y -=-,即42211x x x y -=,令0=y 得21x x =,即)0,2(1x M ,所以)1,2(1-=x ,而)14,(211-=x x ,于是014)14(2212121>+=--=⋅x x x ,因此AFM ∠总是锐角,从而AFM MFD ∠-=∠ 180是钝角. 故直线l 绕点F 旋转时,MFD ∆总是钝角三角形.21. 解:(Ⅰ) )cos sin (cos sin )('x x a e x e x ae x f ax ax ax +=+=)sin(12ϕ+⋅+=x e a ax ,其中a 1tan =ϕ,20πϕ<<. 令 0)('=x f ,由0≥x 得 πϕm x =+,即*,N m m x ∈-=ϕπ.对N k ∈,若πϕπ)12(2+<+<k x k ,即ϕπϕπ-+<<-)12(2k x k ,则0)('>x f ;若πϕπ)22()12(+<+<+k x k ,即ϕπϕπ-+<<-+)22()12(k x k ,则0)('<x f . 因此,在区间),)1((ϕππ--m m 与),(πϕπm m -上,)('x f 的符号总相反,于是,当*,N m m x ∈-=ϕπ时,)(x f 取得极值,所以*,N n n x n ∈-=ϕπ. 此时,)(1)()1()sin()(ϕπϕπϕπ-+--=-=n a n n a n e n e x f ,易知0)(≠n x f ,且πϕπϕπa n a n n a n n n e ee xf x f -=--=-+-+++)(1])1[(21)1()1()()(是常数,故数列)}({n x f 是首项为ϕϕπsin )()(1-=a e x f ,公比为πa e -的等比数列.(Ⅱ) 由(Ⅰ)知,11sin 2+=a ϕ,于是对一切*N n ∈,|)(|n n x f x <恒成立,即)(211ϕπϕπ-+<-n a e a n 恒成立,等价于)(1)(2ϕπϕπ-<+-n a e a a n a (*)恒成立(因为a>0). 设)0()(>=t t e t g t ,则0)1()('2=-=t t e t g t 得1=t ,当10<<t 时,0)('<t g ,所以)(t g 在)1,0(上单调递减;当1>t 时,0)('>t g ,所以)(t g 在),1(∞+上单调递增.从而当1=t 时,函数)(t g 取得最小值e g =)1(. 因此,要使(*)式恒成立,只需e g a a =<+)1(12,即只需112->e a . 而当112-=e a 时,由311t a n 2>-==e a ϕ且由20πϕ<<知,23πϕπ<<. 于是1322-<<-e πϕπ,第11页 共11页且当2≥n 时,12322->>-≥-e n πϕπϕπ,因此,对一切*N n ∈,112≠--=e n ax n ϕπ,所以a a e g ax g n 1)1()(2+==>,故(*)式也恒成立. 综上所述,若112-≥e a ,则对一切*N n ∈,|)(|n n x f x <恒成立.。
2015年湖南省高考数学试卷(理科)(含解析版)
2015年湖南省高考数学试卷(理科)一、选择题,共10小题,每小题5分,共50分1.(5分)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i2.(5分)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A .充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.4.(5分)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7B.﹣1C.1D.25.(5分)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数第 1 页共 32 页 1D.偶函数,且在(0,1)上是减函数6.(5分)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6D.﹣67.(5分)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386B.2718C.3413D.47728.(5分)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则||的最大值为()A.6B.7C.8D.99.(5分)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x 1、x 2,有|x 1﹣x 2|min=,则φ=()A.B.C.D.10.(5分)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()2第 2 页共 32 页A.B.C.D.二、填空题,共5小题,每小题5分,共25分11.(5分)(x﹣1)dx=.12.(5分)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是.13.(5分)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.14.(5分)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=.15.(5分)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是.第 3 页共 32 页 3三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO 与直线CD相交于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.选修4-4:坐标系与方程17.(6分)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.4第 4 页共 32 页选修4-5:不等式选讲18.设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.七、标题19.设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.第 5 页共 32 页 520.某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出一个球,在摸出的2个球中,若都是红球,则获得一等奖;若只有1个红球,则获得二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为ξ,求ξ的分布列和数学期望21.如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ 的体积.6第 6 页共 32 页22.(13分)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(1)若|AC|=|BD|,求直线l的斜率;(2)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,△MFD总是钝角三角形.23.(13分)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.第 7 页共 32 页72015年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题,共10小题,每小题5分,共50分1.(5分)已知=1+i(i为虚数单位),则复数z=()A.1+i B .1﹣i C.﹣1+i D .﹣1﹣i【考点】A5:复数的运算.【专题】5N:数系的扩充和复数.【分析】由条件利用两个复数代数形式的乘除法法则,求得z的值.【解答】解:∵已知=1+i(i为虚数单位),∴z===﹣1﹣i,故选:D.【点评】本题主要考查两个复数代数形式的乘除法法则的应用,属于基础题.2.(5分)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】29:充分条件、必要条件、充要条件.【专题】5J:集合;5L:简易逻辑.【分析】直接利用两个集合的交集,判断两个集合的关系,判断充要条件即可.【解答】解:A、B是两个集合,则“A∩B=A”可得“A⊆B”,“A⊆B”,可得“A∩B=A”.所以A、B是两个集合,则“A∩B=A”是“A⊆B”的充要条件.故选:C.【点评】本题考查充要条件的判断与应用,集合的交集的求法,基本知识的应用.8第 8 页共 32 页3.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.【考点】EF:程序框图.【分析】列出循环过程中S与i的数值,满足判断框的条件即可结束循环.【解答】解:判断前i=1,n=3,s=0,第1次循环,S=,i=2,第2次循环,S=,i=3,第3次循环,S=,i=4,此时,i>n,满足判断框的条件,结束循环,输出结果:S===故选:B.【点评】本题考查循环框图的应用,注意判断框的条件的应用,考查计算能力第 9 页共 32 页94.(5分)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7B.﹣1C.1D.2【考点】7C:简单线性规划.【专题】59:不等式的解法及应用.【分析】由约束条件作出可行域,由图得到最优解,求出最优解的坐标,数形结合得答案.【解答】解:由约束条件作出可行域如图,由图可知,最优解为A,联立,解得C(0,﹣1).由解得A(﹣2,1),由,解得B(1,1)∴z=3x﹣y的最小值为3×(﹣2)﹣1=﹣7.故选:A.【点评】本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.易错点是图形中的B点.5.(5分)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数10第 10 页共 32 页B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数【考点】3K:函数奇偶性的性质与判断;3N:奇偶性与单调性的综合.【专题】53:导数的综合应用.【分析】求出好的定义域,判断函数的奇偶性,以及函数的单调性推出结果即可.【解答】解:函数f(x)=ln(1+x)﹣ln(1﹣x),函数的定义域为(﹣1,1),函数f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣[ln(1+x)﹣ln(1﹣x)]=﹣f(x),所以函数是奇函数.排除C,D,正确结果在A,B,只需判断特殊值的大小,即可推出选项,x=0时,f(0)=0;x=时,f()=ln(1+)﹣ln(1﹣)=ln3>1,显然f(0)<f(),函数是增函数,所以B错误,A正确.故选:A.【点评】本题考查函数的奇偶性以及函数的单调性的判断与应用,考查计算能力.6.(5分)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6D.﹣6【考点】DA:二项式定理.【专题】5P:二项式定理.【分析】根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为求得r,再代入系数求出结果.【解答】解:根据所给的二项式写出展开式的通项,T r+1==;第 11 页共 32 页11展开式中含x的项的系数为30,∴,∴r=1,并且,解得a=﹣6.故选:D.【点评】本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.7.(5分)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386B.2718C.3413D.4772【考点】CP:正态分布曲线的特点及曲线所表示的意义.【专题】11:计算题;5I:概率与统计.【分析】求出P(0<X≤1)=×0.6826=0.3413,即可得出结论.【解答】解:由题意P(0<X≤1)=×0.6826=0.3413,∴落入阴影部分点的个数的估计值为10000×0.3413=3413,故选:C.【点评】本题考查正态分布曲线的特点及曲线所表示的意义,考查正态分布中两个量μ和σ的应用,考查曲线的对称性,属于基础题.12第 12 页共 32 页8.(5分)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则||的最大值为()A.6B.7C.8D.9【考点】9D:两向量的和或差的模的最值;9O:平面向量数量积的性质及其运算.【专题】11:计算题;5B:直线与圆.【分析】由题意,AC为直径,所以||=|2+|.B为(﹣1,0)时,|2+|≤7,即可得出结论.【解答】解:由题意,AC 为直径,所以||=|2+|所以B为(﹣1,0)时,|2+|≤7.所以||的最大值为7.另解:设B(cosα,sinα),|2+|=|2(﹣2,0)+(cosα﹣2,sinα)|=|(cosα﹣6,sinα)|==,当cosα=﹣1时,B为(﹣1,0),取得最大值7.故选:B.【点评】本题考查向量知识的运用,考查学生分析解决问题的能力,比较基础.9.(5分)将函数f(x)=sin2x 的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A.B.C.D.【考点】HJ:函数y=Asin(ωx+φ)的图象变换.第 13 页共 32 页13【专题】57:三角函数的图像与性质.【分析】利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.【解答】解:因为将函数f(x )=sin2x的周期为π,函数的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1﹣x2|min =,不妨x1=,x2=,即g(x)在x 2=,取得最小值,sin(2×﹣2φ)=﹣1,此时φ=,不合题意,x1=,x2=,即g(x )在x2=,取得最大值,sin(2×﹣2φ)=1,此时φ=,满足题意.另解:f(x)=sin2x ,g(x)=sin(2x﹣2φ),设2x1=2kπ+,k∈Z,2x2﹣2φ=﹣+2mπ,m∈Z,x1﹣x2=﹣φ+(k﹣m)π,由|x1﹣x2|min=,可得﹣φ=,解得φ=,故选:D.【点评】本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖.有一定难度,选择题,可以回代验证的方法快速解答.10.(5分)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()14第 14 页共 32 页A .B.C.D.【考点】L!:由三视图求面积、体积.【专题】2:创新题型;5F:空间位置关系与距离;5I:概率与统计.【分析】根据三视图可判断其为圆锥,底面半径为1,高为2,求解体积.利用几何体的性质得出此长方体底面边长为n的正方形,高为x,利用轴截面的图形可判断得出n=(1﹣),0<x<2,求解体积式子,利用导数求解即可,最后利用几何概率求解即.【解答】解:根据三视图可判断其为圆锥,∵底面半径为1,高为2,∴V=×2=第 15 页共 32 页15∵加工成一个体积尽可能大的长方体新工件,∴此长方体底面边长为n的正方形,高为x,∴根据轴截面图得出:=,解得;n=(1﹣),0<x<2,∴长方体的体积Ω=2(1﹣)2x,Ω′=x2﹣4x+2,∵,Ω′=x2﹣4x+2=0,x=,x=2,∴可判断(0,)单调递增,(,2)单调递减,Ω最大值=2(1﹣)2×=,∴原工件材料的利用率为=×=,故选:A.【点评】本题很是新颖,知识点融合的很好,把立体几何,导数,概率都相应的考查了,综合性强,属于难题.二、填空题,共5小题,每小题5分,共25分11.(5分)(x﹣1)dx=0.【考点】67:定积分、微积分基本定理.【专题】52:导数的概念及应用.【分析】求出被积函数的原函数,代入上限和下限求值.【解答】解:(x﹣1)dx=(﹣x)|=0;故答案为:0.【点评】本题考查了定积分的计算;关键是求出被积函数的原函数.12.(5分)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图16第 16 页共 32 页如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是4.【考点】BA:茎叶图.【专题】5I:概率与统计.【分析】根据茎叶图中的数据,结合系统抽样方法的特征,即可求出正确的结论.【解答】解:根据茎叶图中的数据,得;成绩在区间[139,151]上的运动员人数是20,用系统抽样方法从35人中抽取7人,成绩在区间[139,151]上的运动员应抽取7×=4(人).故答案为:4.【点评】本题考查了茎叶图的应用问题,也考查了系统抽样方法的应用问题,是基础题目.13.(5分)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.【考点】KC:双曲线的性质.【专题】5D:圆锥曲线的定义、性质与方程.【分析】设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将中点M的坐标代入双曲线方程,结合离心率公式,计算即可得到.【解答】解:设F(c,0),P(m,n),(m<0),第 17 页共 32 页17设PF的中点为M(0,b),即有m=﹣c,n=2b,将点(﹣c,2b)代入双曲线方程可得,﹣=1,可得e2==5,解得e=.故答案为:.【点评】本题考查双曲线的方程和性质,主要考查双曲线的离心率的求法,同时考查中点坐标公式的运用,属于中档题.14.(5分)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=3n﹣1.【考点】8M:等差数列与等比数列的综合.【专题】54:等差数列与等比数列.【分析】利用已知条件列出方程求出公比,然后求解等比数列的通项公式.【解答】解:设等比数列的公比为q,S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,可得4S2=S3+3S1,a1=1,即4(1+q)=1+q+q2+3,q=3.∴a n=3n﹣1.故答案为:3n﹣1.【点评】本题考查等差数列以及等比数列的应用,基本知识的考查.15.(5分)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是{a|a<0或a>1} .18第 18 页共 32 页【考点】51:函数的零点.【专题】11:计算题;2:创新题型;51:函数的性质及应用.【分析】由g(x)=f(x)﹣b有两个零点可得f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a的范围【解答】解:∵g(x)=f(x)﹣b有两个零点,∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,由x3=x2可得,x=0或x=1①当a>1时,函数f(x)的图象如图所示,此时存在b,满足题意,故a>1满足题意②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意③当0<a<1时,函数f(x)单调递增,故不符合题意第 19 页共 32 页19④a=0时,f(x)单调递增,故不符合题意⑤当a<0时,函数y=f(x)的图象如图所示,此时存在b使得,y=f(x)与y=b有两个交点综上可得,a<0或a>1故答案为:{a|a<0或a>1}【点评】本题考察了函数的零点问题,渗透了转化思想,数形结合、分类讨论的数学思想.三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.20第 20 页共 32 页【考点】N4:相似三角形的判定.【专题】17:选作题;5M:推理和证明.【分析】(1)证明O,M,E,N四点共圆,即可证明∠MEN+∠NOM=180°(2)证明△FEM∽△FON,即可证明FE•FN=FM•FO.【解答】证明:(1)∵N为CD的中点,∴ON⊥CD,∵M为AB的中点,∴OM⊥AB,在四边形OMEN中,∴∠OME+∠ONE=90°+90°=180°,∴O,M,E,N四点共圆,∴∠MEN+∠NOM=180°(2)在△FEM与△FON中,∠F=∠F,∠FME=∠FNO=90°,∴△FEM∽△FON,∴=∴FE•FN=FM•FO.【点评】本题考查垂径定理,考查三角形相似的判定与应用,考查学生分析解决问题的能力,比较基础.选修4-4:坐标系与方程17.(6分)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.【专题】17:选作题;5S:坐标系和参数方程.第 21 页共 32 页21【分析】(1)曲线的极坐标方程即ρ2=2ρcosθ,根据极坐标和直角坐标的互化公式得x2+y2=2x,即得它的直角坐标方程;(2)直线l的方程化为普通方程,利用切割线定理可得结论.【解答】解:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x﹣1)2+y2=1;(2)直线l:(t为参数),普通方程为,(5,)在直线l上,过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,由切割线定理,可得|MT|2=|MA|•|MB|=18.【点评】本题主要考查把极坐标方程化为直角坐标方程的方法,属于基础题.选修4-5:不等式选讲18.设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.【考点】R6:不等式的证明.【专题】59:不等式的解法及应用.【分析】(ⅰ)由a >0,b>0,结合条件可得ab=1,再由基本不等式,即可得证;(ⅱ)运用反证法证明.假设a2+a<2与b2+b<2可能同时成立.结合条件a>0,b>0,以及二次不等式的解法,可得0<a<1,且0<b<1,这与ab=1矛盾,即可得证.【解答】证明:(ⅰ)由a>0,b>0,则a+b=+=,由于a+b>0,则ab=1,即有a+b≥2=2,22第 22 页共 32 页当且仅当a=b取得等号.则a+b≥2;(ⅱ)假设a2+a <2与b2+b<2可能同时成立.由a2+a <2及a >0,可得0<a<1,由b 2+b<2及b>0,可得0<b<1,这与ab=1矛盾.a2+a<2与b2+b<2不可能同时成立.【点评】本题考查不等式的证明,主要考查基本不等式的运用和反证法证明不等式的方法,属于中档题.七、标题19.设△ABC的内角A 、B、C 的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.【考点】HP:正弦定理.【专题】58:解三角形.【分析】(Ⅰ)由题意和正弦定理可得sinB=cosA,由角的范围和诱导公式可得;(Ⅱ)由题意可得A∈(0,),可得0<sinA<,化简可得sinA+sinC=﹣2(sinA﹣)2+,由二次函数区间的最值可得.【解答】解:(Ⅰ)由a=btanA和正弦定理可得==,∴sinB=cosA,即sinB=sin(+A)又B为钝角,∴+A∈(,π),∴B=+A,∴B﹣A=;(Ⅱ)由(Ⅰ)知C=π﹣(A+B)=π﹣(A++A)=﹣2A>0,∴A∈(0,),∴sinA+sinC=sinA+sin(﹣2A)第 23 页共 32 页23=sinA+cos2A=sinA+1﹣2sin2A=﹣2(sinA ﹣)2+,∵A∈(0,),∴0<sinA<,∴由二次函数可知<﹣2(sinA﹣)2+≤∴sinA+sinC的取值范围为(,]【点评】本题考查正弦定理和三角函数公式的应用,涉及二次函数区间的最值,属基础题.20.某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出一个球,在摸出的2个球中,若都是红球,则获得一等奖;若只有1个红球,则获得二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为ξ,求ξ的分布列和数学期望【考点】CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.【专题】5I:概率与统计.【分析】(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件A2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},利用A1,A2相互独立,,互斥,B1,B2互斥,然后求出所求概率即可.(2)顾客抽奖1次可视为3次独立重复试验,判断X~B.求出概率,得到X的分布列,然后求解期望.【解答】解:(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱24第 24 页共 32 页中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件B2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},由题意A1,A2相互独立,,互斥,B1,B2互斥,且B 1=A1A2,B2=+,C=B1+B 2,因为P(A1)=,P(A2)=,所以,P(B1)=P(A1)P(A2)==,P(B2)=P()+P ()=+==,故所求概率为:P (C )=P(B1+B2)=P(B1)+P (B 2)=.(2)顾客抽奖1次可视为3次独立重复试验,由(1)可知,顾客抽奖1次获一等奖的概率为:所以.X~B.于是,P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==.故X的分布列为:X0123PE(X)=3×=.【点评】期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫,它在市场预测,经济统计,风险与决策等领域有着广泛的应用,为今后学习数学及相关学科产生深远的影响.21.如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ 的体积.第 25 页共 32 页25【考点】LW:直线与平面垂直;MJ:二面角的平面角及求法.【专题】5F:空间位置关系与距离;5G:空间角;5H:空间向量及应用.【分析】(1)首先以A为原点,AB,AD,AA1所在直线分别为x,y,z轴,建立空间直角坐标系,求出一些点的坐标,Q 在棱BC上,从而可设Q(6,y1,0),只需求即可;(2)设P(0,y2,z2),根据P在棱DD1上,从而由即可得到z2=12﹣2y2,从而表示点P坐标为P(0,y2,12﹣2y2).由PQ∥平面ABB1A1便知道与平面ABB1A1的法向量垂直,从而得出y1=y2,从而Q 点坐标变成Q (6,y2,0),设平面PQD的法向量为,根据即可表示,平面AQD的一个法向量为,从而由即可求出y2,从而得出P点坐标,从而求出三棱锥P﹣AQD 的高,而四面体ADPQ的体积等于三棱锥P﹣AQD的体积,从而求出四面体的体积.【解答】解:根据已知条件知AB,AD,AA1三直线两两垂直,所以分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则:A(0,0,0),B(6,0,0),D(0,6,0),A1(0,0,6),B1(3,0,6),D1(0,3,6);Q在棱BC上,设Q(6,y1,0),0≤y1≤6;26第 26 页共 32 页∴(1)证明:若P是DD1的中点,则P;∴,;∴;∴;∴AB1⊥PQ;(2)设P(0,y2,z2),y2,z2∈[0,6],P在棱DD1上;∴,0≤λ≤1;∴(0,y2﹣6,z2)=λ(0,﹣3,6);∴;∴z2=12﹣2y2;∴P(0,y2,12﹣2y2);∴;平面ABB1A1的一个法向量为;∵PQ∥平面ABB1A1;∴=6(y1﹣y2)=0;∴y 1=y2;∴Q(6,y2,0);设平面PQD的法向量为,则:;∴,取z=1,则;又平面AQD的一个法向量为;第 27 页共 32 页27又二面角P﹣QD﹣A的余弦值为;∴;解得y2=4,或y2=8(舍去);∴P(0,4,4);∴三棱锥P﹣ADQ的高为4,且;∴V四面体ADPQ =V三棱锥P﹣ADQ=.【点评】考查建立空间直角坐标系,利用空间向量解决异面直线垂直及线面角问题的方法,共线向量基本定理,直线和平面平行时,直线和平面法向量的关系,平面法向量的概念,以及两平面法向量的夹角和平面二面角大小的关系,三棱锥的体积公式.22.(13分)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F 的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(1)若|AC|=|BD|,求直线l的斜率;(2)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,第 28 页共 32 页28△MFD总是钝角三角形.【考点】K3:椭圆的标准方程;KH:直线与圆锥曲线的综合.【专题】2:创新题型;5E:圆锥曲线中的最值与范围问题.【分析】(Ⅰ)根据两个曲线的焦点相同,得到a2﹣b2=1,再根据C1与C2的公共弦长为2,得到=1,解得即可求出;(Ⅱ)设出点的坐标,(1)根据向量的关系,得到(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,设直线l的方程,分别与C1,C2构成方程组,利用韦达定理,分别代入得到关于k的方程,解得即可;(2)根据导数的几何意义得到C1在点A 处的切线方程,求出点M的坐标,利用向量的乘积∠AFM是锐角,问题得以证明.【解答】解:(Ⅰ)抛物线C1:x2=4y的焦点F的坐标为(0,1),因为F也是椭圆C 2的一个焦点,∴a 2﹣b2=1,①,又C1与C2的公共弦长为2,C 1与C2的都关于y轴对称,且C1的方程为x2=4y,由此易知C1与C2的公共点的坐标为(±,),所以=1,②,联立①②得a2=9,b2=8,故C 2的方程为+=1.(Ⅱ)设A(x1,y 1),B(x2,y2),C(x3,y3),D(x4,y4),(1)因为与同向,且|AC|=|BD|,所以=,从而x3﹣x1=x4﹣x2,即x1﹣x2=x3﹣x4,于是(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,③设直线的斜率为k,则l的方程为y=kx+1,第 29 页共 32 页29由,得x2﹣4kx﹣4=0,而x1,x2是这个方程的两根,所以x1+x2=4k,x1x2=﹣4,④由,得(9+8k2)x2+16kx﹣64=0,而x3,x4是这个方程的两根,所以x3+x4=,x3x4=﹣,⑤将④⑤代入③,得16(k2+1)=+,即16(k2+1)=,所以(9+8k2)2=16×9,解得k=±.(2)由x2=4y得y′=x,所以C1在点A处的切线方程为y﹣y 1=x1(x﹣x1),即y=x1x﹣x12,令y=0,得x=x1,M(x1,0),所以=(x1,﹣1),而=(x1,y1﹣1),于是•=x12﹣y1+1=x12+1>0,因此∠AFM是锐角,从而∠MFD=180°﹣∠AFM是钝角,故直线l绕点F旋转时,△MFD总是钝角三角形.【点评】本题考查了圆锥曲线的和直线的位置与关系,关键是联立方程,构造方程,利用韦达定理,以及向量的关系,得到关于k的方程,计算量大,属于难题.30第 30 页共 32 页23.(13分)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n <|f(x n)|恒成立.【考点】6D:利用导数研究函数的极值;6E:利用导数研究函数的最值.【专题】2:创新题型;53:导数的综合应用;54:等差数列与等比数列;59:不等式的解法及应用.【分析】(Ⅰ)求出导数,运用两角和的正弦公式化简,求出导数为0的根,讨论根附近的导数的符号相反,即可得到极值点,求得极值,运用等比数列的定义即可得证;(Ⅱ)由sinφ=,可得对一切n∈N *,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),求出导数,求得最小值,由恒成立思想即可得证.【解答】证明:(Ⅰ)f′(x)=e ax(asinx+cosx)=•e ax sin(x+φ),tanφ=,0<φ<,令f′(x)=0,由x≥0,x+φ=mπ,即x=mπ﹣φ,m∈N*,对k∈N,若(2k+1)π<x+φ<(2k+2)π,即(2k+1)π﹣φ<x<(2k+2)π﹣φ,则f′(x)<0,因此在((m﹣1)π﹣φ,mπ﹣φ)和(mπ﹣φ,(m+1)π﹣φ)上f′(x )符号总相反.于是当x=nπ﹣φ,n∈N*,f(x)取得极值,所以x n=nπ﹣φ,n∈N*,此时f(x n)=e a(nπ﹣φ)sin(nπ﹣φ)=(﹣1)n+1e a(nπ﹣φ)sinφ,易知f(x n)≠0,而==﹣e aπ是常数,第 31 页共 32 页31故数列{f(x n)}是首项为f(x1)=e a(π﹣φ)sinφ,公比为﹣e aπ的等比数列;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),g′(t)=,当0<t<1时,g′(t)<0,g (t)递减,当t >1时,g′(t)>0,g(t )递增.t=1时,g(t)取得最小值,且为e.因此要使①恒成立,只需<g(1)=e,只需a>,当a=,tanφ==,且0<φ<,可得<φ<,于是π﹣φ<<,且当n≥2时,nπ﹣φ≥2π﹣φ>>,因此对n∈N*,ax n=≠1,即有g(ax n)>g(1)=e=,故①亦恒成立.综上可得,若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.【点评】本题考查导数的运用:求极值和单调区间,主要考查三角函数的导数和求值,同时考查等比数列的定义和通项公式的运用,考查不等式恒成立问题的证明,属于难题.32第 32 页共 32 页。
2015高考试题——数学理(湖南卷)解析版

本试题包括选择题,填空题和解答题三部分,共6页,时间120分钟,满分150分. 一.选择题:本大题共10小题,每小题5分,共50分,贼每小题给出的四个选项中,只有一项是复合题目要求的.1.已知()211i i z-=+(i 为虚数单位),则复数z =( ) A.1i + B.1i - C.1i -+ D.1i -- 【答案】D. 【解析】试题分析:由题意得,i iii i z --=+-=+-=1121)1(2,故选D.考点:复数的计算.2.设A,B 是两个集合,则”AB A =”是“A B ⊆”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 【答案】C.考点:集合的关系.3.执行如图1所示的程序框图,如果输入3n =,则输出的S =( ) A.67 B.37 C.89 D.49【答案】B.考点:1程序框图;2.裂项相消法求数列的和.4.若变量,x y 满足约束条件1211x y x y y +≥-⎧⎪-≤⎨⎪≤⎩,则3z x y =-的最小值为( )A.-7B.-1C.1D.2 【答案】A. 【解析】试题分析:如下图所示,画出线性约束条件所表示的区域,即可行域,从而可知当2-=x ,1=y 时,y x z -=3的最小值是7-,故选A.考点:线性规划.5.设函数()ln(1)ln(1)f x x x =+--,则()f x 是( )A.奇函数,且在(0,1)上是增函数B. 奇函数,且在(0,1)上是减函数C. 偶函数,且在(0,1)上是增函数D. 偶函数,且在(0,1)上是减函数 【答案】A.考点:函数的性质.6.已知5的展开式中含32x 的项的系数为30,则a =( )B. C.6 D-6【答案】D. 【解析】试题分析:r rrrr x a C T -+-=2551)1(,令1=r ,可得6305-=⇒=-a a ,故选D.考点:二项式定理.7.在如图2所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C 为正态分布N(0,1)的密度曲线)的点的个数的估计值为( ) A.2386 B.2718 C.3413 D.4772【答案】C.考点:正态分布.8.已知点A,B,C 在圆221x y +=上运动,且AB BC ⊥.若点P 的坐标为(2,0),则PA PB PC ++的最大值为( )A.6B.7C.8D.9 【答案】B. 【解析】试题分析:由题意得,AC 为圆的直径,故可设),(n m A ,),(n m C --,),(y x B ,∴(6,)PA PB PC x y ++=-,而491237)6(22≤-=+-x y x ,∴PA PB PC ++的最大值为7,故选B. 考点:1.圆的性质;2.平面向量数量积.9.将函数()sin 2f x x =的图像向右平移(0)2πϕϕ<<个单位后得到函数()g x 的图像,若对满足12()()2f x g x -=的12,x x ,有12min3x x π-=,则ϕ=( )A.512π B.3π C.4π D.6π【答案】D. 【解析】试题分析:向右平移ϕ个单位后,得到)22sin()(ϕ-=x x g ,又∵2|)()(|21=-x g x f ,∴不妨ππk x 2221+=,ππϕm x 22222+-=-,∴πϕπ)(221m k x x -+-=-,又∵12min 3x x π-=,∴632πϕπϕπ=⇒=-,故选D.考点:三角函数的图象和性质.10.某工件的三视图如图3所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)( )A.89πB.169π【答案】A.考点:1.圆锥的内接长方体;2.基本不等式求最值. 二、填空题:本大题共5小题,每小题5分,共25分.11.20(1)x dx ⎰-= .【答案】0.考点:定积分的计算.12.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图4所示. 若将运动员按成绩由好到差编为135号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是 .【答案】4. 【解析】试题分析:由茎叶图可知,在区间]151,139[的人数为20,再由系统抽样的性质可知人数为435720=⨯人. 考点:1.系统抽样;2.茎叶图.13.设F 是双曲线C :22221x y a b-=的一个焦点,若C 上存在点P ,使线段PF 的中点恰为其虚轴的一个端点,则C 的离心率为 . 【答案】5.考点:双曲线的标准方程及其性质.14.设n S 为等比数列{}n a 的前n 项和,若11a =,且1233,2,S S S 成等差数列,则n a = . 【答案】13-n . 【解析】 试题分析:∵13S ,22S ,3S 成等差数列,∴333)(2223321121=⇒=⇒+++=+⨯q a a a a a a a a ,又∵等比数列}{n a ,∴1113--==n n n q a a . 考点:等差数列与等比数列的性质.15.已知32,(),x x af x x x a⎧≤=⎨>⎩,若存在实数b ,使函数()()g x f x b =-有两个零点,则a 的取值范围是 .【答案】),1()0,(+∞-∞ . 【解析】试题分析:分析题意可知,问题等价于方程)(3a xb x ≤=与方程)(2a xb x >=的根的个数和为2,若两个方程各有一个根:则可知关于b 的不等式组⎪⎪⎩⎪⎪⎨⎧≤->≤a b a b a b 31有解,从而1>a ;若方程)(3a xb x ≤=无解,方程)(2a xb x >=有2个根:则可知关于b 的不等式组⎪⎩⎪⎨⎧>->ab ab 31有解,从而 0<a ;,综上,实数a 的取值范围是),1()0,(+∞-∞ .考点:1.函数与方程;2.分类讨论的数学思想. 三、解答题16.(Ⅰ)如图,在圆O 中,相交于点E 的两弦AB 、CD 的中点分别是M 、N ,直线MO 与直线CD 相交于点F ,证明:(1)0180MEN NOM ∠+∠=; (2)FE FN FM FO ∙=∙【答案】(1)详见解析;(2)详见解析.考点:1.垂径定理;2.四点共圆;3.割线定理.(Ⅱ)已知直线5:12x l y t ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2cos ρθ=. (1) 将曲线C 的极坐标方程化为直角坐标方程;(2) 设点M的直角坐标为,直线l 与曲线C 的交点为A ,B ,求||||MA MB ∙的值.【答案】(1)0222=-+x y x ;(2)18.考点:1.极坐标与直角坐标的互相转化;2.直线与圆的位置关系. (Ⅲ)设0,0a b >>,且11a b a b+=+. (1)2a b +≥;(2)22a a +<与22b b +<不可能同时成立.【答案】(1)详见解析;(2)详见解析. 【解析】试题分析:(1)将已知条件中的式子可等价变形为1=ab ,再由基本不等式即可得证;(2)利用反证法,假设假设22<+a a 与22<+b b 同时成立,可求得10<<a ,10<<b ,从而与1=ab 矛盾,即可得证 试题解析:由abba b a b a +=+=+11,0>a ,0>b ,得1=ab ,(1)由基本不等式及1=ab ,有22=≥+ab b a ,即2≥+b a ;(2)假设22<+a a 与22<+b b 同时成立,则由22<+a a 及0>a 得10<<a ,同理10<<b ,从而1<ab ,这与1=ab 矛盾,故22<+a a 与22<+b b 不可能成立.考点:1.基本不等式;2.一元二次不等式;3.反证法.17.设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,tan a b A =,且B 为钝角》 (1)证明:2B A π-=(2)求sin sin A C +的取值范围【答案】(1)详见解析;(2),98]. 【解析】试题分析:(1)利用正弦定理,将条件中的式子等价变形为inB=sin (2π+A ),从而得证;(2)利用(1)中的结论,以及三角恒等变形,将C A sin sin +转化为只与A 有关的表达式,再利用三角函数的性质即可求解. 试题解析:(1)由a=btanA 及正弦定理,得sin sin cos cos A b BA a B==,所以sinB=cosA ,即sinB=sin (2π+A ).又B 为钝角,因此2π+A ∈(2π,A ),故B=2π+A ,即B-A=2π;(2)由(I )知,C=π-(A+B ) =π-(2A+2π)=2π-2A>0,所以A 0,4π⎛⎫∈ ⎪⎝⎭,于是sinA+sinC=sinA+sin (2π-2A )=sinA+cos2A=-22sin A+sinA+1 =-2(sinA-14)2+98,因为0<A<4π,所以,因此<-22199sin 488A ⎛⎫-+≤ ⎪⎝⎭由此可知sinA+sinC ,98]. 考点:1.正弦定理;2.三角恒等变形;3.三角函数的性质.18.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X ,求X 的分布列和数学期望. 【答案】(1)107;(2)详见解析. 【解析】试题分析:(1)记事件1A ={从甲箱中摸出的1个球是红球},2A ={从乙箱中摸出的1个球是红球}1B = {顾客抽奖1次获一等奖}2B ={顾客抽奖1次获二等奖},C={顾客抽奖1次能获奖},则可知1A 与2A 相互独立,12A A 与12A A 互斥,1B 与2B 互斥,且1B =12A A ,2B =12A A +12A A ,C=1B +2B ,再利用概率的加法公式即可求解;(2)分析题意可知X~B (3,15),分别求得P(X=0)=003314()()55C =64125,P(X=1)=112314()()55C =48125,P(X=2)=221314()()55C =12125,即可知X 的概率分布及其期望. 试题解析:(1)记事件1A ={从甲箱中摸出的1个球是红球},2A ={从乙箱中摸出的1个球是红球}1B = {顾客抽奖1次获一等奖}2B ={顾客抽奖1次获二等奖},C={顾客抽奖1次能获奖}.由题意,1A 与2A 相互独立,12A A 与12A A 互斥,1B 与2B 互斥,且1B =12A A ,2B =12A A +12A A ,C=1B +2B .因P (1A )=410=25,P(2A )=510=12,所以P (1B )=P(12A A )=P(1A )P(2A )=25⨯12=15, P (2B )=P (12A A +12A A )=P (12A A )+P (12A A )=P (1A )(1- P(2A ))+(1- P (1A ))P(2A )=25⨯(1-12)+(1-25)⨯12=12,故所求概率为P(C)= P(1B +2B )=P (1B )+ P (2B )=15+12=710. ;(2)顾客抽奖3次独立重复试验,由(I )知,顾客抽奖1次获一等奖的概率为15,所以X~B (3,15).于是P(X=0)=003314()()55C =64125,P(X=1)=112314()()55C =48125,P(X=2)=221314()()55C =12125, P(X=3)=330314()()55C =1125X 的数学期望为 E (X )=3⨯15=35. 考点:1.概率的加法公式;2.离散型随机变量的概率分布与期望.19.如图,已知四棱台1111ABCD A B C D -上、下底面分别是边长为3和6的正方形,16AA =,且1AA ⊥底面ABCD ,点P 、Q 分别在棱1DD 、BC 上.(1)若P 是1DD 的中点,证明:1AB PQ ⊥; (2)若PQ//平面11ABB A ,二面角P-QD-A 的余弦值为37,求四面体ADPQ 的体积.【答案】(1)详见解析;(2)24. 【解析】试题分析:(1)建立空间直角坐标系,求得相关点的坐标可知问题等价于证明1=0AB PQ ⋅;(2)根据条件 二面角P-QD-A 的余弦值为37,利用空间向量可将四面体ADPQ 视为以△ADQ 为底面的三棱锥P-ADQ , 其高h=4,从而求解试题解析:解法一 由题设知,1AA ,AB,AD 两两垂直,以A 为坐标原点,AB ,AD, 1AA 所在直线分别为x 轴,y 轴,z 轴,建立如图b 所示的空间直角坐标系,则相关各点的坐标为A(0,0,0),1B (3,0,6),D(0,6,0),1D (0,3,6) , Q(6,m,0),其中m=BQ ,06m ≤≤, (1)若P 是1DD 的中点,则P (0,92,3),1AB =(3,0 ,6),于是1AB PQ ⋅=18-18=0,所以1AB ⊥PQ ,即1AB PQ ⊥;(2)由题设知,DQ =(6,m-6,0),1DD =(0,-3,6)是平面PQD 内的两个不共线向量.设1n =(x ,y ,z )是平面PQD 的一个法向量,则11100n DQ n DD ⎧⋅=⎪⎨⋅=⎪⎩,即6(6)0360x m y y z +-=⎧⎨-+=⎩,取y=6,得1n =(6-m ,6,3).又平面AQD 的一个法向量是2n =(0,0,1),所以 cos<1n ,2n >=1212||||n n n n ⋅⋅=而二面角P-QD-A 的余弦值为37=37,解得m=4,或者m=8(舍去),此时Q (6,4,0)设DP =1DD λ(0<λ≤1),而1DD =(0,-3,6),由此得点P (0,6-3λ,6λ),PQ =(6,3λ-2,-6λ).因为PQ//平面11ABB A ,且平面11ABB A 的一个法向量是1n =(0,1,0),所以PQ 3n ⋅=0,即3λ-2=0,亦即λ=23,从而P (0,4,4),于是,将四面体ADPQ 视为以△ADQ 为底面的三棱锥P-ADQ ,则其高h=4,故四面体ADPQ 的体积,11166424332ADQV Sh =⋅=⨯⨯⨯⨯=. 解法二 (1)如图c ,取1A A 的中点R ,连结PR,BR,因为1A A ,1D D 是梯形11A AD D 的两腰,P 是1D D 的中点,所以PR//AD ,于是由AD//BC 知,PR//BC,所以P,R,B,C 四点共面.由题设知,BC ⊥AB,BC ⊥1A A ,所以BC ⊥平面11ABB A ,因此BC ⊥1AB ○1 因为tan ABR ∠=AR AB =36=11AB A A=tan 11A AB ∠,所以tan ABR ∠=tan 11A AB ∠,因此 1ABR BAB ∠+∠=111A AB BAB ∠+∠=90o ,于是1AB ⊥BR ,再由○1即知1AB ⊥平面PRBC ,又PQ ⊂平面PRBC ,故1AB ⊥PQ.(2)如图d ,过点P 作PM//1A A 交AD 于点M ,则PM//平面11ABB A .因为1A A ⊥平面ABCD ,所以OM ⊥平面ABCD,过点M 作MN ⊥QD 于点N ,连结PN ,则PN ⊥QD ,PNM ∠为二面角P-QD-A 的平面角,所以cos PNM ∠=37,即MN PN =37,从而PM MN =○3连结MQ ,由PQ//平面11ABB A ,所以MQ//AB ,又ABCD 是正方形,所以ABQM 为矩形,故MQ=AB=6. 设MD=t ,则.○4过点1D 作11//D E A A 交AD 于点E ,则11AA D E 为矩形,所以1D E =1A A =6,AE=11A D =3,因此ED=AD-AE=3,于是1623D E PM MD ED ===,所以PM=2MD=2t ,再由○3○4,解得t=2,因此PM=4.故四面体ADPQ 的体积11166424332ADQV Sh =⋅=⨯⨯⨯⨯=. 考点:1.空间向量的运用;2.线面垂直的性质;3.空间几何体体积计算.20.已知抛物线21:4C x y =的焦点F 也是椭圆22222:1(0)y x C a b a b+=>>的一个焦点,1C 与2C 的公共弦的长为(1)求2C 的方程;(2)过点F 的直线l 与1C 相交于A 、B 两点,与2C 相交于C 、D 两点,且AC 与BD 同向 (ⅰ)若||||AC BD =,求直线l 的斜率(ⅱ)设1C 在点A 处的切线与x 轴的交点为M ,证明:直线l 绕点F 旋转时,MFD ∆总是钝角三角形【答案】(1)22198y x +=;(2)(i ),(ii )详见解析. 【解析】试题分析:(1)根据已知条件可求得2C 的焦点坐标为)1,0(,再利用公共弦长为62即可求解;(2)(i )设直线l 的斜率为k ,则l 的方程为y=kx+1.由214y kx x y=+⎧⎨=⎩得2x +16kx-64=0,根据条件可知AC =BD ,从而可以建立关于k 的方程,即可求解;(ii )根据条件可说明FA ⋅FM =122x -11y +=124x +1>0,因此AFM ∠是锐角,从而180o MFD AFM ∠=-∠是钝角,即可得证试题解析:(1)由1C :24x y =知其焦点F 的坐标为(0,1),因为F 也是椭圆2C 的一焦点,所以 221a b -=○1又1C 与2C 的公共弦的长为,1C 与2C 都关于y 轴对称,且1C 的方程为24x y =,由此易知1C 与2C的公共点的坐标为(32),所以229614a b+= ○2,联立○1,○2得2a =9,2b =8,故2C 的方程为22198x y += ○3;(2)如图f ,设A (11,x y )B (22,x y )C (33,x y )D (44,x y ).(i )因AC 与BD 同向,且|AC|=|BD|,所以AC =BD ,从而31x x -=42x x -,即12x x -=34x x -,于是()212x x +-412x x = ()234x x +-434x x ○3 设直线l 的斜率为k ,则l 的方程为y=kx+1.由214y kx x y=+⎧⎨=⎩得2x +16kx-64=0.而1x ,2x 是这个方程的两根.所以12x x +=4k ,12x x =-4○4 ,由221189y kx x y =+⎧⎪⎨+=⎪⎩得(9+82k )2x +16kx-64=0.而3x ,4x 是这个方程的两根.所以34x x +=-21698k k +,34x x =-26498k +○5,将○4○5带入○3 ,得16(2k +1)=()221698k k ++246498k⨯+,即16(2k +1)=()2222169(1)98k k ⨯++,所以()2298k+=169⨯,解得k=,即直线l的斜率为(ii )由24x y =得'y =2x,所以1C 在点A 处的切线方程为y-1y =12x (x-1x ),即 y=1x x -124x .令y=0得x=12x ,即M (12x ,0),所以FM =(12x,-1).而FA =(11,1x y -).于是 FA ⋅FM =122x -11y +=124x +1>0,因此AFM ∠是锐角,从而180o MFD AFM ∠=-∠是钝角.故直线l 绕点F 旋转时,△MFD 总是钝角三角形.考点:1.椭圆的标准方程及其性质;2.直线与椭圆位置关系.21.已知0a >,函数()sin ([0,))axf x e x x =∈+∞. 记n x 为()f x 的从小到大的第n *()n N ∈个极值点,证明: (1)数列{()}n f x 是等比数列 (2)若a ≥*n N ∈,|()|n n x f x <恒成立.【答案】(1)详见解析;(2)详见解析. 【解析】 试题分析:(1)求导,可知'()sin cos ax ax f x ae x e x =+(sin cos )ax e a x x =+sin()ax x ρ=+,求得)(x f 的极值点诶*() n x n n N πρ∈=-,即可得证;(2)分析题意可知,问题等价于()() a n e a n πρπρ-<-恒成立,构造函数g (t )=te t,利用导数判断其单调性即可得证 试题解析:(1)'()sin cos ax ax f x ae x e x =+(sin cos )ax e a x x =+sin()ax x ρ=+其中tan ρ=1a ,0<ρ<2π.令'()f x =0,由x 0≥得x+ρ=mx, 即x=m π-ρ,m ∈*N . 对k ∈N ,若2k π<x+ρ<(2k+1) π,即2k π-ρ<x<(2k+1) π-ρ,则'()f x >0;若(2k+1)π<x+ρ<(2k+2)π,即(2k+1)π-ρ<x<(2k+2) π-ρ,则'()f x <0.因此,在区间((m-1)π,m π-ρ)与(m π-ρ,m π)上,'()f x 的符号总相反.于是 当x= m π-ρ(m *N ∈)时,()f x 取得极值,所以*() n x n n N πρ∈=-. 此时,()()1sin()()(1)sin .a n a n n n x e n f e πρπρπρρ--+=-=-易知()n f x ≠0,而()()1121()(1)()(1 s n in )i s a n ax n n n a n n f e f x e x e πρπρρρ+-⎡⎤⎣-+⎦++-==--是常数,故数列{}()n f x 是首项为1()f x =() sin a n e πρρ-,公比为ax e -的等比数列;(2)由(I )知,sin ρ,于是对一切*n N ∈,n x <|()n f x |恒成立,即()a n n πρπρ--<恒成立,()()a n e a n πρπρ-<-(∙)恒成立(因为a>0), 设g (t )=t e t (t )0),则2'(1)t g t e t t-()=.令'g t ()=0得t=1, 当0<t<1时,'g t ()<0,所以g (t )在区间(0,1)上单调递减; 当t>1时,'g t ()>0,所以g (t )在区间(0,1)上单调递增. 从而当t=1时,函数g (t )取得最小值g (1)=e因此,要是(∙()1g e <=,即只需a >.而当tan ρ=1a>02πρ<<.于是23ππρ-<<,且当n 2≥时,232n ππρπρ-≥-≥>.因此对一切*n N ∈,1n ax =≠,所以g (n ax )(1)g e >==.故(∙)式亦恒成立. 综上所述,若a ≥*n N ∈,()||n n x x f <恒成立.考点:1.三角函数的性质;2.导数的运用;3.恒成立问题.。
【高考试题】2015年普通高考数学试题----湖南卷(数学理)解析版

2015年普通高等学校招生全国统一考试·湖南卷(理科)检索号:231.(2015·湖南高考理科·T1)已知=1+i(i为虚数单位),则复数z=()A.1+iB.1-iC.-1+iD.-1-i【解析】选D.验证各选项,只有z=-1-i时,==1+i.检索号:22.(2015·湖南高考理科·T2)设A,B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解题指南】直接利用充分必要条件进行判断,可先判断充分性是否成立,再判断必要性是否成立.【解析】选C.由题意得,A∩B=A⇒A⊆B;反之,A⊆B⇒A∩B=A,故为充要条件.检索号:493.(2015·湖南高考理科·T3)执行如图所示的程序框图.如果输入n=3,则输出的S=()A. B. C. D.【解析】选B.由题意得,输出的S为数列的前三项和,而=(-),所以S n=(1-)=,所以S3=.检索号:314.(2015·湖南高考理科·T4)若变量x,y满足约束条件则z=3x-y的最小值为()A.-7B.-1C.1D.2【解题指南】画出满足约束条件的可行域,结合图象确定目标函数的最优解.【解析】选A.如图所示,画出线性约束条件所表示的区域,即可行域,从而可知,当x=-2,y=1时,z=3x-y的最小值是-7.检索号:105.(2015·湖南高考理科·T5)设函数f(x)=ln(1+x)-ln(1-x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数【解题指南】先判断函数的奇偶性,再判断函数的单调性.【解析】选A.显然, f(x)的定义域为(-1,1),关于原点对称,又因为f(-x)=ln(1-x)-ln(1+x)=-f(x),所以f(x)为奇函数.因为f'(x)=+=,在(0,1)上f'(x)>0,所以f(x)在(0,1)上是增函数.检索号:536.(2015·湖南高考理科·T6)已知(-)5的展开式中含的项的系数为30,则a=()A. B.-C.6D.-6=(-1)r a r,由题意列式可求a的值.【解题指南】先写出通项T【解析】选D.T r+1=(-1)r a r,令=,得r=1,可得-5a=30,得a=-6.检索号:567.(2015·湖南高考理科·T7)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()A.2 386B.2 718C.3 413D.4 772附:若Χ~N(μ,σ2),则P(μ-σ<Χ≤μ+σ)=0.6826P(μ-2σ<Χ≤μ+2σ)=0.9544【解题指南】根据正态分布的性质,P(0<x≤1)=P(-1<x≤1),计算即得.【解析】选C.根据正态分布的性质,P(0<x≤1)=P(-1<x≤1)=0.3413.10000×0.3413=3413.检索号:438.(2015·湖南高考理科·T8)已知点A,B,C在圆x2+y2=1上运动,且AB⊥BC.若点P的坐标为(2,0),则的最大值为()A.6B.7C.8D.9【解题指南】由题意可得AC为圆的直径,可设坐标A(m,n),C(-m,-n),B(x,y),转化为x的函数求其最大值即得.【解析】选B.由题意得,AC为圆的直径,故可设A(m,n),C(-m,-n),B(x,y),所以++=(x-6,y),而(x-6)2+y2=37-12x≤49,所以的最大值为7.检索号:169.(2015·湖南高考理科·T9)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象,若对满足=2的x1,x2有=,则φ=()A. B. C. D.【解题指南】本题主要考查三角函数的平移变换及三角函数的图象与性质,考虑特殊情况下才能成立,从而求解.【解析】选D.向右平移φ个单位后,得到g(x)=sin(2x-2φ),又因为|f(x1)-g(x2)|=2,所以不妨令2x1=+2kπ,2x2-2φ=-+2mπ,所以x1-x2=-φ+(k-m)π,又因为|x1-x2|min=,所以-φ=⇒φ=.检索号:3610.(2015·湖南高考理科·T10)某工件的三视图如图所示.现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为()(材料利用率=)A. B.C. D.【解题指南】第一步:设长方体的长、宽、高;第二步:转化为用截面圆半径x表示;第三步:确定x取何值时长方体的体积最大;第四步:求得材料的利用率.【解析】选A.分析题意可知,问题等价于圆锥的内接长方体的体积的最大值,设长方体的长,宽,高分别为a,b,h,长方体上底面截圆锥的截面半径为x,对角面截面图如图所示.。
2015年湖南省高考数学试题及答案(理科)【解析版】

2015年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题,共10小题,每小题5分,共50分1.(5分)(2015•湖南)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i考点: 复数代数形式的乘除运算.专题:数系的扩充和复数.分析:由条件利用两个复数代数形式的乘除法法则,求得z的值.解答:解:∵已知=1+i(i为虚数单位),∴z===﹣1﹣i,故选:D.点评:本题主要考查两个复数代数形式的乘除法法则的应用,属于基础题.2.(5分)(2015•湖南)设A、B是两个集合,则“A∩B=A”是“A⊆B”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:集合;简易逻辑.分析:直接利用两个集合的交集,判断两个集合的关系,判断充要条件即可.解答:解:A、B是两个集合,则“A∩B=A"可得“A⊆B",“A⊆B",可得“A∩B=A”.所以A、B是两个集合,则“A∩B=A"是“A⊆B”的充要条件.故选:C.点评:本题考查充要条件的判断与应用,集合的交集的求法,基本知识的应用.3.(5分)(2015•湖南)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.考点:程序框图.分析:列出循环过程中S与i的数值,满足判断框的条件即可结束循环.解答:解:判断前i=1,n=3,s=0,第1次循环,S=,i=2,第2次循环,S=,i=3,第3次循环,S=,i=4,此时,i>n,满足判断框的条件,结束循环,输出结果:S===故选:B点评:本题考查循环框图的应用,注意判断框的条件的应用,考查计算能力4.(5分)(2015•湖南)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7 B.﹣1 C.1D.2考点:简单线性规划.专题: 不等式的解法及应用.分析:由约束条件作出可行域,由图得到最优解,求出最优解的坐标,数形结合得答案.解答:解:由约束条件作出可行域如图,由图可知,最优解为A,联立,解得C(0,﹣1).由解得A(﹣2,1),由,解得B(1,1)∴z=3x﹣y的最小值为3×(﹣2)﹣1=﹣7.故选:A.点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.易错点是图形中的B点.5.(5分)(2015•湖南)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数考点:利用导数研究函数的单调性.专题:导数的综合应用.分析:求出好的定义域,判断函数的奇偶性,以及函数的单调性推出结果即可.解答:解:函数f(x)=ln(1+x)﹣ln(1﹣x),函数的定义域为(﹣1,1),函数f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣[ln(1+x)﹣ln(1﹣x)]=﹣f(x),所以函数是奇函数.排除C,D,正确结果在A,B,只需判断特殊值的大小,即可推出选项,x=0时,f(0)=0;x=时,f()=ln(1+)﹣ln(1﹣)=ln3>1,显然f(0)<f(),函数是增函数,所以B错误,A正确.故选:A.点评:本题考查函数的奇偶性以及函数的单调性的判断与应用,考查计算能力.6.(5分)(2015•湖南)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6D.﹣6考点:二项式定理的应用.专题:二项式定理.分析:根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x 的指数为求得r,再代入系数求出结果.解答:解:根据所给的二项式写出展开式的通项,T r+1==;展开式中含x的项的系数为30,∴,∴r=1,并且,解得a=﹣6.故选:D.点评:本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.7.(5分)(2015•湖南)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0。
2015年湖南省高考数学试卷(理科)

高考注意事项1.进入考场时携带的物品。
考生进入考场,只准携带准考证、二代居民身份证以及2B铅笔、0.5毫米黑色墨水签字笔、直尺、圆规、三角板、无封套橡皮、小刀、空白垫纸板、透明笔袋等文具。
严禁携带手机、无线发射和接收设备、电子存储记忆录放设备、手表、涂改液、修正带、助听器、文具盒和其他非考试用品。
考场内不得自行传递文具等物品。
由于标准化考点使用金属探测仪等辅助考务设备,所以提醒考生应考时尽量不要佩戴金属饰品,以免影响入场时间。
2.准确填写、填涂和核对个人信息。
考生在领到答题卡和试卷后,在规定时间内、规定位置处填写姓名、准考证号。
填写错误责任自负;漏填、错填或字迹不清的答题卡为无效卡;故意错填涉嫌违规的,查实后按照有关规定严肃处理。
监考员贴好条形码后,考生必须核对所贴条形码与自己的姓名、准考证号是否一致,如发现不一致,立即报告监考员要求更正。
3.考场面向考生正前方的墙壁上方悬挂时钟,为考生提供时间参考。
考场时钟的时间指示不作为考试时间信号,考试时间一律以考点统一发出的铃声信号为准。
2015年湖南省高考数学试卷(理科)一、选择题,共10小题,每小题5分,共50分1.(5分)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i2.(5分)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.4.(5分)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7 B.﹣1 C.1 D.25.(5分)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数6.(5分)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6 D.﹣67.(5分)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C 为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386 B.2718 C.3413 D.47728.(5分)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则||的最大值为()A.6 B.7 C.8 D.99.(5分)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.10.(5分)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A. B. C.D.二、填空题,共5小题,每小题5分,共25分11.(5分)(x﹣1)dx=.12.(5分)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是.13.(5分)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.14.(5分)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=.15.(5分)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b 有两个零点,则a的取值范围是.三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO 与直线CD相交于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.选修4-4:坐标系与方程17.(6分)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.选修4-5:不等式选讲18.设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.七、标题19.设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.20.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X 的分布列和数学期望.21.如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ的体积.22.(13分)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(1)若|AC|=|BD|,求直线l的斜率;(2)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,△MFD 总是钝角三角形.23.(13分)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.2015年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题,共10小题,每小题5分,共50分1.(5分)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i【分析】由条件利用两个复数代数形式的乘除法法则,求得z的值.【解答】解:∵已知=1+i(i为虚数单位),∴z===﹣1﹣i,故选:D.【点评】本题主要考查两个复数代数形式的乘除法法则的应用,属于基础题.2.(5分)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】直接利用两个集合的交集,判断两个集合的关系,判断充要条件即可.【解答】解:A、B是两个集合,则“A∩B=A”可得“A⊆B”,“A⊆B”,可得“A∩B=A”.所以A、B是两个集合,则“A∩B=A”是“A⊆B”的充要条件.故选:C.【点评】本题考查充要条件的判断与应用,集合的交集的求法,基本知识的应用.3.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.【分析】列出循环过程中S与i的数值,满足判断框的条件即可结束循环.【解答】解:判断前i=1,n=3,s=0,第1次循环,S=,i=2,第2次循环,S=,i=3,第3次循环,S=,i=4,此时,i>n,满足判断框的条件,结束循环,输出结果:S===故选:B.【点评】本题考查循环框图的应用,注意判断框的条件的应用,考查计算能力4.(5分)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7 B.﹣1 C.1 D.2【分析】由约束条件作出可行域,由图得到最优解,求出最优解的坐标,数形结合得答案.【解答】解:由约束条件作出可行域如图,由图可知,最优解为A,联立,解得C(0,﹣1).由解得A(﹣2,1),由,解得B(1,1)∴z=3x﹣y的最小值为3×(﹣2)﹣1=﹣7.故选:A.【点评】本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.易错点是图形中的B点.5.(5分)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数【分析】求出好的定义域,判断函数的奇偶性,以及函数的单调性推出结果即可.【解答】解:函数f(x)=ln(1+x)﹣ln(1﹣x),函数的定义域为(﹣1,1),函数f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣[ln(1+x)﹣ln(1﹣x)]=﹣f(x),所以函数是奇函数.排除C,D,正确结果在A,B,只需判断特殊值的大小,即可推出选项,x=0时,f(0)=0;x=时,f()=ln(1+)﹣ln(1﹣)=ln3>1,显然f(0)<f(),函数是增函数,所以B错误,A正确.故选:A.【点评】本题考查函数的奇偶性以及函数的单调性的判断与应用,考查计算能力.6.(5分)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6 D.﹣6【分析】根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为求得r,再代入系数求出结果.【解答】解:根据所给的二项式写出展开式的通项,T r+1==;展开式中含x的项的系数为30,∴,∴r=1,并且,解得a=﹣6.故选:D.【点评】本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.7.(5分)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C 为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386 B.2718 C.3413 D.4772【分析】求出P(0<X≤1)=×0.6826=0.3413,即可得出结论.【解答】解:由题意P(0<X≤1)=×0.6826=0.3413,∴落入阴影部分点的个数的估计值为10000×0.3413=3413,故选:C.【点评】本题考查正态分布曲线的特点及曲线所表示的意义,考查正态分布中两个量μ和σ的应用,考查曲线的对称性,属于基础题.8.(5分)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则||的最大值为()A.6 B.7 C.8 D.9【分析】由题意,AC为直径,所以||=|2+|.B为(﹣1,0)时,|2+|≤7,即可得出结论.【解答】解:由题意,AC为直径,所以||=|2+|所以B为(﹣1,0)时,|2+|≤7.所以||的最大值为7.另解:设B(cosα,sinα),|2+|=|2(﹣2,0)+(cosα﹣2,sinα)|=|(cosα﹣6,sinα)|==,当cosα=﹣1时,B为(﹣1,0),取得最大值7.故选:B.【点评】本题考查向量知识的运用,考查学生分析解决问题的能力,比较基础.9.(5分)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.【分析】利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.【解答】解:因为将函数f(x)=sin2x的周期为π,函数的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1﹣x2|min=,不妨x1=,x2=,即g(x)在x2=,取得最小值,sin(2×﹣2φ)=﹣1,此时φ=,不合题意,x1=,x2=,即g(x)在x2=,取得最大值,sin(2×﹣2φ)=1,此时φ=,满足题意.另解:f(x)=sin2x,g(x)=sin(2x﹣2φ),设2x1=2kπ+,k∈Z,2x2﹣2φ=﹣+2mπ,m ∈Z,x1﹣x2=﹣φ+(k﹣m)π,由|x1﹣x2|min=,可得﹣φ=,解得φ=,故选:D.【点评】本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖.有一定难度,选择题,可以回代验证的方法快速解答.10.(5分)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A. B. C.D.【分析】根据三视图可判断其为圆锥,底面半径为1,高为2,求解体积.利用几何体的性质得出此长方体底面边长为n的正方形,高为x,利用轴截面的图形可判断得出n=(1﹣),0<x<2,求解体积式子,利用导数求解即可,最后利用几何概率求解即.【解答】解:根据三视图可判断其为圆锥,∵底面半径为1,高为2,∴V=×2=∵加工成一个体积尽可能大的长方体新工件,∴此长方体底面边长为n的正方形,高为x,∴根据轴截面图得出:=,解得;n=(1﹣),0<x<2,∴长方体的体积Ω=2(1﹣)2x,Ω′=x2﹣4x+2,∵,Ω′=x2﹣4x+2=0,x=,x=2,∴可判断(0,)单调递增,(,2)单调递减,Ω最大值=2(1﹣)2×=,∴原工件材料的利用率为=×=,故选:A.【点评】本题很是新颖,知识点融合的很好,把立体几何,导数,概率都相应的考查了,综合性强,属于难题.二、填空题,共5小题,每小题5分,共25分11.(5分)(x﹣1)dx=0.【分析】求出被积函数的原函数,代入上限和下限求值.【解答】解:(x﹣1)dx=(﹣x)|=0;故答案为:0.【点评】本题考查了定积分的计算;关键是求出被积函数的原函数.12.(5分)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是4.【分析】根据茎叶图中的数据,结合系统抽样方法的特征,即可求出正确的结论.【解答】解:根据茎叶图中的数据,得;成绩在区间[139,151]上的运动员人数是20,用系统抽样方法从35人中抽取7人,成绩在区间[139,151]上的运动员应抽取7×=4(人).故答案为:4.【点评】本题考查了茎叶图的应用问题,也考查了系统抽样方法的应用问题,是基础题目.13.(5分)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.【分析】设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将中点M的坐标代入双曲线方程,结合离心率公式,计算即可得到.【解答】解:设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将点(﹣c,2b)代入双曲线方程可得,﹣=1,可得e2==5,解得e=.故答案为:.【点评】本题考查双曲线的方程和性质,主要考查双曲线的离心率的求法,同时考查中点坐标公式的运用,属于中档题.14.(5分)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=3n﹣1.【分析】利用已知条件列出方程求出公比,然后求解等比数列的通项公式.【解答】解:设等比数列的公比为q,S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,可得4S2=S3+3S1,a1=1,即4(1+q)=1+q+q2+3,q=3.∴a n=3n﹣1.故答案为:3n﹣1.【点评】本题考查等差数列以及等比数列的应用,基本知识的考查.15.(5分)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是{a|a<0或a>1} .【分析】由g(x)=f(x)﹣b有两个零点可得f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a的范围【解答】解:∵g(x)=f(x)﹣b有两个零点,∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,由x3=x2可得,x=0或x=1①当a>1时,函数f(x)的图象如图所示,此时存在b,满足题意,故a>1满足题意②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意③当0<a<1时,函数f(x)单调递增,故不符合题意④a=0时,f(x)单调递增,故不符合题意⑤当a<0时,函数y=f(x)的图象如图所示,此时存在b使得,y=f(x)与y=b有两个交点综上可得,a<0或a>1故答案为:{a|a<0或a>1}【点评】本题考察了函数的零点问题,渗透了转化思想,数形结合、分类讨论的数学思想.三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO 与直线CD相交于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.【分析】(1)证明O,M,E,N四点共圆,即可证明∠MEN+∠NOM=180°(2)证明△FEM∽△FON,即可证明FE•FN=FM•FO.【解答】证明:(1)∵N为CD的中点,∴ON⊥CD,∵M为AB的中点,∴OM⊥AB,在四边形OMEN中,∴∠OME+∠ONE=90°+90°=180°,∴O,M,E,N四点共圆,∴∠MEN+∠NOM=180°(2)在△FEM与△FON中,∠F=∠F,∠FME=∠FNO=90°,∴△FEM∽△FON,∴=∴FE•FN=FM•FO.【点评】本题考查垂径定理,考查三角形相似的判定与应用,考查学生分析解决问题的能力,比较基础.选修4-4:坐标系与方程17.(6分)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.【分析】(1)曲线的极坐标方程即ρ2=2ρcosθ,根据极坐标和直角坐标的互化公式得x2+y2=2x,即得它的直角坐标方程;(2)直线l的方程化为普通方程,利用切割线定理可得结论.【解答】解:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x ﹣1)2+y2=1;(2)直线l:(t为参数),普通方程为,(5,)在直线l上,过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,由切割线定理,可得|MT|2=|MA|•|MB|=18.【点评】本题主要考查把极坐标方程化为直角坐标方程的方法,属于基础题.选修4-5:不等式选讲18.设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.【分析】(ⅰ)由a>0,b>0,结合条件可得ab=1,再由基本不等式,即可得证;(ⅱ)运用反证法证明.假设a2+a<2与b2+b<2可能同时成立.结合条件a>0,b>0,以及二次不等式的解法,可得0<a<1,且0<b<1,这与ab=1矛盾,即可得证.【解答】证明:(ⅰ)由a>0,b>0,则a+b=+=,由于a+b>0,则ab=1,即有a+b≥2=2,当且仅当a=b取得等号.则a+b≥2;(ⅱ)假设a2+a<2与b2+b<2可能同时成立.由a2+a<2及a>0,可得0<a<1,由b2+b<2及b>0,可得0<b<1,这与ab=1矛盾.a2+a<2与b2+b<2不可能同时成立.【点评】本题考查不等式的证明,主要考查基本不等式的运用和反证法证明不等式的方法,属于中档题.七、标题19.设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.【分析】(Ⅰ)由题意和正弦定理可得sinB=cosA,由角的范围和诱导公式可得;(Ⅱ)由题意可得A∈(0,),可得0<sinA<,化简可得sinA+sinC=﹣2(sinA ﹣)2+,由二次函数区间的最值可得.【解答】解:(Ⅰ)由a=btanA和正弦定理可得==,∴sinB=cosA,即sinB=sin(+A)又B为钝角,∴+A∈(,π),∴B=+A,∴B﹣A=;(Ⅱ)由(Ⅰ)知C=π﹣(A+B)=π﹣(A++A)=﹣2A>0,∴A∈(0,),∴sinA+sinC=sinA+sin(﹣2A)=sinA+cos2A=sinA+1﹣2sin2A=﹣2(sinA﹣)2+,∵A∈(0,),∴0<sinA<,∴由二次函数可知<﹣2(sinA﹣)2+≤∴sinA+sinC的取值范围为(,]【点评】本题考查正弦定理和三角函数公式的应用,涉及二次函数区间的最值,属基础题.20.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X 的分布列和数学期望.【分析】(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件A2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},利用A1,A2相互独立,,互斥,B1,B2互斥,然后求出所求概率即可.(2)顾客抽奖1次可视为3次独立重复试验,判断X~B.求出概率,得到X的分布列,然后求解期望.【解答】解:(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件B2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},由题意A1,A2相互独立,,互斥,B1,B2互斥,且B1=A1A2,B2=+,C=B1+B2,因为P(A1)=,P(A2)=,所以,P(B1)=P(A1)P(A2)==,P(B2)=P()+P()=+==,故所求概率为:P(C)=P(B1+B2)=P(B1)+P(B2)=.(2)顾客抽奖1次可视为3次独立重复试验,由(1)可知,顾客抽奖1次获一等奖的概率为:所以.X~B.于是,P(X=0)==,P (X=1)==,P(X=2)==,P(X=3)==.故X的分布列为:X0123PE(X)=3×=.【点评】期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫,它在市场预测,经济统计,风险与决策等领域有着广泛的应用,为今后学习数学及相关学科产生深远的影响.21.如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ的体积.【分析】(1)首先以A为原点,AB,AD,AA1所在直线分别为x,y,z轴,建立空间直角坐标系,求出一些点的坐标,Q在棱BC上,从而可设Q(6,y1,0),只需求即可;(2)设P(0,y2,z2),根据P在棱DD1上,从而由即可得到z2=12﹣2y2,从而表示点P坐标为P(0,y2,12﹣2y2).由PQ∥平面ABB1A1便知道与平面ABB1A1的法向量垂直,从而得出y1=y2,从而Q点坐标变成Q(6,y2,0),设平面PQD的法向量为,根据即可表示,平面AQD的一个法向量为,从而由即可求出y2,从而得出P点坐标,从而求出三棱锥P﹣AQD的高,而四面体ADPQ的体积等于三棱锥P﹣AQD的体积,从而求出四面体的体积.【解答】解:根据已知条件知AB,AD,AA1三直线两两垂直,所以分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则:A(0,0,0),B(6,0,0),D(0,6,0),A1(0,0,6),B1(3,0,6),D1(0,3,6);Q在棱BC上,设Q(6,y1,0),0≤y1≤6;∴(1)证明:若P是DD1的中点,则P;∴,;∴;∴;∴AB1⊥PQ;(2)设P(0,y2,z2),y2,z2∈[0,6],P在棱DD1上;∴,0≤λ≤1;∴(0,y2﹣6,z2)=λ(0,﹣3,6);∴;∴z2=12﹣2y2;∴P(0,y2,12﹣2y2);∴;平面ABB1A1的一个法向量为;∵PQ∥平面ABB1A1;∴=6(y1﹣y2)=0;∴y1=y2;∴Q(6,y2,0);设平面PQD的法向量为,则:;∴,取z=1,则;又平面AQD的一个法向量为;又二面角P﹣QD﹣A的余弦值为;∴;解得y2=4,或y2=8(舍去);∴P(0,4,4);∴三棱锥P﹣ADQ的高为4,且;∴V四面体ADPQ =V三棱锥P﹣ADQ=.【点评】考查建立空间直角坐标系,利用空间向量解决异面直线垂直及线面角问题的方法,共线向量基本定理,直线和平面平行时,直线和平面法向量的关系,平面法向量的概念,以及两平面法向量的夹角和平面二面角大小的关系,三棱锥的体积公式.22.(13分)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(1)若|AC|=|BD|,求直线l的斜率;(2)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,△MFD 总是钝角三角形.【分析】(Ⅰ)根据两个曲线的焦点相同,得到a2﹣b2=1,再根据C1与C2的公共弦长为2,得到=1,解得即可求出;(Ⅱ)设出点的坐标,(1)根据向量的关系,得到(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,设直线l的方程,分别与C1,C2构成方程组,利用韦达定理,分别代入得到关于k 的方程,解得即可;(2)根据导数的几何意义得到C1在点A处的切线方程,求出点M的坐标,利用向量的乘积∠AFM是锐角,问题得以证明.【解答】解:(Ⅰ)抛物线C1:x2=4y的焦点F的坐标为(0,1),因为F也是椭圆C2的一个焦点,∴a2﹣b2=1,①,又C1与C2的公共弦长为2,C1与C2的都关于y轴对称,且C1的方程为x2=4y,由此易知C1与C2的公共点的坐标为(±,),所以=1,②,联立①②得a2=9,b2=8,故C2的方程为+=1.(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),(1)因为与同向,且|AC|=|BD|,所以=,从而x3﹣x1=x4﹣x2,即x1﹣x2=x3﹣x4,于是(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,③设直线的斜率为k,则l的方程为y=kx+1,由,得x2﹣4kx﹣4=0,而x1,x2是这个方程的两根,所以x1+x2=4k,x1x2=﹣4,④由,得(9+8k2)x2+16kx﹣64=0,而x3,x4是这个方程的两根,所以x3+x4=,x3x4=﹣,⑤将④⑤代入③,得16(k2+1)=+,即16(k2+1)=,所以(9+8k2)2=16×9,解得k=±.(2)由x2=4y得y′=x,所以C1在点A处的切线方程为y﹣y1=x1(x﹣x1),即y=x1x﹣x12,令y=0,得x=x1,M(x1,0),所以=(x1,﹣1),而=(x1,y1﹣1),于是•=x12﹣y1+1=x12+1>0,因此∠AFM是锐角,从而∠MFD=180°﹣∠AFM是钝角,故直线l绕点F旋转时,△MFD总是钝角三角形.【点评】本题考查了圆锥曲线的和直线的位置与关系,关键是联立方程,构造方程,利用韦达定理,以及向量的关系,得到关于k的方程,计算量大,属于难题.23.(13分)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.【分析】(Ⅰ)求出导数,运用两角和的正弦公式化简,求出导数为0的根,讨论根附近的导数的符号相反,即可得到极值点,求得极值,运用等比数列的定义即可得证;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),求出导数,求得最小值,由恒成立思想即可得证.【解答】证明:(Ⅰ)f′(x)=e ax(asinx+cosx)=•e ax sin(x+φ),tanφ=,0<φ<,令f′(x)=0,由x≥0,x+φ=mπ,即x=mπ﹣φ,m∈N*,对k∈N,若(2k+1)π<x+φ<(2k+2)π,即(2k+1)π﹣φ<x<(2k+2)π﹣φ,则f′(x)<0,因此在((m﹣1)π﹣φ,mπ﹣φ)和(mπ﹣φ,(m+1)π﹣φ)上f′(x)符号总相反.于是当x=nπ﹣φ,n∈N*,f(x)取得极值,所以x n=nπ﹣φ,n∈N*,此时f(x n)=e a(nπ﹣φ)sin(nπ﹣φ)=(﹣1)n+1e a(nπ﹣φ)sinφ,易知f(x n)≠0,而==﹣e aπ是常数,故数列{f(x n)}是首项为f(x1)=e a(π﹣φ)sinφ,公比为﹣e aπ的等比数列;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),g′(t)=,当0<t<1时,g′(t)<0,g(t)递减,当t>1时,g′(t)>0,g(t)递增.t=1时,g(t)取得最小值,且为e.因此要使①恒成立,只需<g(1)=e,只需a>,当a=,tanφ==,且0<φ<,可得<φ<,于是π﹣φ<<,且当n≥2时,nπ﹣φ≥2π﹣φ>>,因此对n∈N*,ax n=≠1,即有g(ax n)>g(1)=e=,故①亦恒成立.综上可得,若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.【点评】本题考查导数的运用:求极值和单调区间,主要考查三角函数的导数和求值,同时考查等比数列的定义和通项公式的运用,考查不等式恒成立问题的证明,属于难题.。
2015年湖南省高考数学试卷(理科)

2015年湖南省高考数学试卷(理科)一、选择题,共10小题,每小题5分,共50分1.(5分)已知(1−i)2z=1+i (i 为虚数单位),则复数z=( )A .1+iB .1﹣iC .﹣1+iD .﹣1﹣i2.(5分)设A 、B 是两个集合,则“A ∩B=A”是“A ⊆B”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件3.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=( )A .67B .37C .89D .494.(5分)若变量x 、y 满足约束条件{x +y ≥−12x −y ≤1y ≤1,则z=3x ﹣y 的最小值为( )A .﹣7B .﹣1C .1D .25.(5分)设函数f (x )=ln (1+x )﹣ln (1﹣x ),则f (x )是( ) A .奇函数,且在(0,1)上是增函数 B .奇函数,且在(0,1)上是减函数 C .偶函数,且在(0,1)上是增函数 D .偶函数,且在(0,1)上是减函数 6.(5分)已知(√x ﹣√x)5的展开式中含x 32的项的系数为30,则a=( )A .√3B .﹣√3C .6D .﹣67.(5分)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C 为正态分布N (0,1)的密度曲线)的点的个数的估计值为( ) 附“若X ﹣N=(μ,a 2),则 P (μ﹣σ<X ≤μ+σ)=0.6826. p (μ﹣2σ<X ≤μ+2σ)=0.9544.A .2386B .2718C .3413D .47728.(5分)已知A ,B ,C 在圆x 2+y 2=1上运动,且AB ⊥BC ,若点P 的坐标为(2,0),则|PA →+PB →+PC →|的最大值为( ) A .6B .7C .8D .99.(5分)将函数f (x )=sin2x 的图象向右平移φ(0<φ<π2)个单位后得到函数g (x )的图象.若对满足|f (x 1)﹣g (x 2)|=2的x 1、x 2,有|x 1﹣x 2|min =π3,则φ=( )A .5π12B .π3C .π4D .π610.(5分) 某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)( )A .89πB .169π C .4(√2−1)3πD .12(√2−1)3π二、填空题,共5小题,每小题5分,共25分 11.(5分)∫2(x ﹣1)dx= .12.(5分)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是 .13.(5分)设F 是双曲线C :x 2a 2﹣y 2b 2=1的一个焦点.若C 上存在点P ,使线段PF 的中点恰为其虚轴的一个端点,则C 的离心率为 .14.(5分)设S n 为等比数列{a n }的前n 项和,若a 1=1,且3S 1,2S 2,S 3成等差数列,则a n = .15.(5分)已知函数f (x )={x 3,x ≤ax 2,x >a 若存在实数b ,使函数g (x )=f (x )﹣b有两个零点,则a 的取值范围是 .三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)如图,在⊙O 中,相交于点E 的两弦AB ,CD 的中点分别是M ,N ,直线MO 与直线CD 相交于点F ,证明: (1)∠MEN +∠NOM=180° (2)FE•FN=FM•FO .选修4-4:坐标系与方程17.(6分)已知直线l :{x =5+√32ty =√3+12t(t 为参数).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的坐标方程为ρ=2cosθ. (1)将曲线C 的极坐标方程化为直坐标方程;(2)设点M 的直角坐标为(5,√3),直线l 与曲线C 的交点为A ,B ,求|MA |•|MB |的值.选修4-5:不等式选讲18.设a >0,b >0,且a +b=1a +1b.证明:(ⅰ)a +b ≥2;(ⅱ)a 2+a <2与b 2+b <2不可能同时成立.19.设△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,a=btanA ,且B 为钝角.(Ⅰ)证明:B ﹣A=π2;(Ⅱ)求sinA +sinC 的取值范围.20.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖. (1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X ,求X 的分布列和数学期望.21.如图,已知四棱台ABCD ﹣A 1B 1C 1D 1的上、下底面分别是边长为3和6的正方形,AA 1=6,且AA 1⊥底面ABCD ,点P 、Q 分别在棱DD 1、BC 上. (1)若P 是DD 1的中点,证明:AB 1⊥PQ ;(2)若PQ ∥平面ABB 1A 1,二面角P ﹣QD ﹣A 的余弦值为37,求四面体ADPQ 的体积.22.(13分)已知抛物线C 1:x 2=4y 的焦点F 也是椭圆C 2:y2a 2+x 2b2=1(a >b >0)的一个焦点.C 1与C 2的公共弦长为2√6.(Ⅰ)求C 2的方程;(Ⅱ)过点F 的直线l 与C 1相交于A 、B 两点,与C 2相交于C 、D 两点,且AC →与BD →同向.(1)若|AC |=|BD |,求直线l 的斜率;(2)设C 1在点A 处的切线与x 轴的交点为M ,证明:直线l 绕点F 旋转时,△MFD 总是钝角三角形.23.(13分)已知a >0,函数f (x )=e ax sinx (x ∈[0,+∞]).记x n 为f (x )的从小到大的第n (n ∈N *)个极值点.证明: (Ⅰ)数列{f (x n )}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.√e2−12015年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题,共10小题,每小题5分,共50分1.(5分)已知(1−i)2z=1+i (i 为虚数单位),则复数z=( )A .1+iB .1﹣iC .﹣1+iD .﹣1﹣i【解答】解:∵已知(1−i)2z =1+i (i 为虚数单位),∴z=(1−i)21+i =−2i(1−i)(1+i)(1−i)=﹣1﹣i , 故选:D .2.(5分)设A 、B 是两个集合,则“A ∩B=A”是“A ⊆B”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件【解答】解:A 、B 是两个集合,则“A ∩B=A”可得“A ⊆B”, “A ⊆B”,可得“A ∩B=A”.所以A 、B 是两个集合,则“A ∩B=A”是“A ⊆B”的充要条件. 故选:C .3.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=( )A .67B .37C .89D .49【解答】解:判断前i=1,n=3,s=0,第1次循环,S=11×3,i=2,第2次循环,S=11×3+13×5,i=3,第3次循环,S=11×3+13×5+15×7,i=4,此时,i >n ,满足判断框的条件,结束循环,输出结果:S=11×3+13×5+15×7=12(1−13+13−15+15−17)=37故选:B4.(5分)若变量x 、y 满足约束条件{x +y ≥−12x −y ≤1y ≤1,则z=3x ﹣y 的最小值为( )A .﹣7B .﹣1C .1D .2【解答】解:由约束条件{x +y ≥−12x −y ≤1y ≤1作出可行域如图,由图可知,最优解为A ,联立{x +y =−12x −y =1,解得C (0,﹣1).由{x +y =−1y =1解得A (﹣2,1),由{2x −y =1y =1,解得B(1,1)∴z=3x﹣y的最小值为3×(﹣2)﹣1=﹣7.故选:A.5.(5分)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数【解答】解:函数f(x)=ln(1+x)﹣ln(1﹣x),函数的定义域为(﹣1,1),函数f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣[ln(1+x)﹣ln(1﹣x)]=﹣f(x),所以函数是奇函数.排除C,D,正确结果在A,B,只需判断特殊值的大小,即可推出选项,x=0时,f(0)=0;x=12时,f(12)=ln(1+12)﹣ln(1﹣12)=ln3>1,显然f(0)<f(12),函数是增函数,所以B错误,A正确.故选:A.6.(5分)已知(√x﹣√x )5的展开式中含x32的项的系数为30,则a=()A.√3B.﹣√3C.6 D.﹣6【解答】解:根据所给的二项式写出展开式的通项,T r+1=C5r(√x)5−r a√x )r=(−a)r C5r x5−r2−r2;展开式中含x 32的项的系数为30,∴5−2r 2=32,∴r=1,并且(−a)1C 51=30,解得a=﹣6.故选:D .7.(5分)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C 为正态分布N (0,1)的密度曲线)的点的个数的估计值为( ) 附“若X ﹣N=(μ,a 2),则 P (μ﹣σ<X ≤μ+σ)=0.6826. p (μ﹣2σ<X ≤μ+2σ)=0.9544.A .2386B .2718C .3413D .4772【解答】解:由题意P (0<X ≤1)=12×0.6826=0.3413,∴落入阴影部分点的个数的估计值为10000×0.3413=3413, 故选:C .8.(5分)已知A ,B ,C 在圆x 2+y 2=1上运动,且AB ⊥BC ,若点P 的坐标为(2,0),则|PA →+PB →+PC →|的最大值为( ) A .6B .7C .8D .9【解答】解:由题意,AC 为直径,所以|PA →+PB →+PC →|=|2PO →+PB →| 所以B 为(﹣1,0)时,|2PO →+PB →|≤7. 所以|PA →+PB →+PC →|的最大值为7. 另解:设B (cosα,sinα),|2PO →+PB →|=|2(﹣2,0)+(cosα﹣2,sinα)|=|(cosα﹣6,sinα)|=√(cosα−6)2+sin 2α=√37−12cosα,当cosα=﹣1时,B 为(﹣1,0),取得最大值7. 故选:B .9.(5分)将函数f (x )=sin2x 的图象向右平移φ(0<φ<π2)个单位后得到函数g (x )的图象.若对满足|f (x 1)﹣g (x 2)|=2的x 1、x 2,有|x 1﹣x 2|min =π3,则φ=( )A .5π12B .π3C .π4D .π6【解答】解:因为将函数f (x )=sin2x 的周期为π,函数的图象向右平移φ(0<φ<π2)个单位后得到函数g (x )的图象.若对满足|f (x 1)﹣g (x 2)|=2的可知,两个函数的最大值与最小值的差为2,有|x 1﹣x 2|min =π3,不妨x 1=π4,x 2=7π12,即g (x )在x 2=7π12,取得最小值,sin (2×7π12﹣2φ)=﹣1,此时φ=−π6,不合题意, x 1=3π4,x 2=5π12,即g (x )在x 2=5π12,取得最大值,sin (2×5π12﹣2φ)=1,此时φ=π6,满足题意.另解:f (x )=sin2x ,g (x )=sin (2x ﹣2φ),设2x 1=2kπ+π2,k ∈Z ,2x 2﹣2φ=﹣π2+2mπ,m ∈Z ,x 1﹣x 2=π2﹣φ+(k ﹣m )π,由|x 1﹣x 2|min =π3,可得π2﹣φ=π3,解得φ=π6,故选:D .10.(5分) 某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)( )A.89πB.169πC.4(√2−1)3πD.12(√2−1)3π【解答】解:根据三视图可判断其为圆锥,∵底面半径为1,高为2,∴V=13×π×12×2=2π3∵加工成一个体积尽可能大的长方体新工件,∴此长方体底面边长为n的正方形,高为x,∴根据轴截面图得出:x2=1−√2n21,解得;n=√2(1﹣12x),0<x<2,∴长方体的体积Ω=2(1﹣12x)2x,Ω′=32x2﹣4x+2,∵,Ω′=32x2﹣4x+2=0,x=23,x=2,∴可判断(0,23)单调递增,(23,2)单调递减,Ω最大值=2(1﹣12×23)2×23=1627,∴原工件材料的利用率为16272π3=1627×32π=89π,故选:A二、填空题,共5小题,每小题5分,共25分 11.(5分)∫2(x ﹣1)dx= 0 . 【解答】解:∫2(x ﹣1)dx=(12x 2﹣x )|02=0;故答案为:0.12.(5分)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是4 .【解答】解:根据茎叶图中的数据,得; 成绩在区间[139,151]上的运动员人数是20, 用系统抽样方法从35人中抽取7人, 成绩在区间[139,151]上的运动员应抽取7×2035=4(人).故答案为:4.13.(5分)设F 是双曲线C :x 2a 2﹣y 2b 2=1的一个焦点.若C 上存在点P ,使线段PF 的中点恰为其虚轴的一个端点,则C 的离心率为 √5 . 【解答】解:设F (c ,0),P (m ,n ),(m <0), 设PF 的中点为M (0,b ), 即有m=﹣c ,n=2b ,将点(﹣c ,2b )代入双曲线方程可得,c 2a ﹣4b 2b =1,可得e 2=c 2a 2=5,解得e=√5. 故答案为:√5.14.(5分)设S n 为等比数列{a n }的前n 项和,若a 1=1,且3S 1,2S 2,S 3成等差数列,则a n = 3n ﹣1 .【解答】解:设等比数列的公比为q ,S n 为等比数列{a n }的前n 项和,若a 1=1,且3S 1,2S 2,S 3成等差数列, 可得4S 2=S 3+3S 1,a 1=1, 即4(1+q )=1+q +q 2+3,q=3. ∴a n =3n ﹣1. 故答案为:3n ﹣1.15.(5分)已知函数f (x )={x 3,x ≤ax 2,x >a 若存在实数b ,使函数g (x )=f (x )﹣b有两个零点,则a 的取值范围是 {a |a <0或a >1} . 【解答】解:∵g (x )=f (x )﹣b 有两个零点,∴f (x )=b 有两个零点,即y=f (x )与y=b 的图象有两个交点, 由x 3=x 2可得,x=0或x=1①当a >1时,函数f (x )的图象如图所示,此时存在b ,满足题意,故a >1满足题意②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意③当0<a<1时,函数f(x)单调递增,故不符合题意④a=0时,f(x)单调递增,故不符合题意⑤当a<0时,函数y=f(x)的图象如图所示,此时存在b使得,y=f(x)与y=b 有两个交点综上可得,a <0或a >1 故答案为:{a |a <0或a >1}三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)如图,在⊙O 中,相交于点E 的两弦AB ,CD 的中点分别是M ,N ,直线MO 与直线CD 相交于点F ,证明: (1)∠MEN +∠NOM=180° (2)FE•FN=FM•FO .【解答】证明:(1)∵N 为CD 的中点, ∴ON ⊥CD , ∵M 为AB 的中点, ∴OM ⊥AB ,在四边形OMEN 中,∴∠OME +∠ONE=90°+90°=180°, ∴O ,M ,E ,N 四点共圆, ∴∠MEN +∠NOM=180°(2)在△FEM 与△FON 中,∠F=∠F ,∠FME=∠FNO=90°, ∴△FEM ∽△FON ,∴FE FO =FM FN∴FE•FN=FM•FO .选修4-4:坐标系与方程17.(6分)已知直线l :{x =5+√32ty =√3+12t(t 为参数).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,√3),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.【解答】解:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x﹣1)2+y2=1;(2)直线l:{x=5+√32ty=√3+12t (t为参数),普通方程为y=√33x−2√33,(5,√3)在直线l上,过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,由切割线定理,可得|MT|2=|MA|•|MB|=18.选修4-5:不等式选讲18.设a>0,b>0,且a+b=1a +1b.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.【解答】证明:(ⅰ)由a>0,b>0,则a+b=1a +1b=a+bab,由于a+b>0,则ab=1,即有a+b≥2√ab=2,当且仅当a=b取得等号.则a+b≥2;(ⅱ)假设a2+a<2与b2+b<2可能同时成立.由a2+a<2及a>0,可得0<a<1,由b2+b<2及b>0,可得0<b<1,这与ab=1矛盾.a2+a<2与b2+b<2不可能同时成立.19.设△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,a=btanA ,且B 为钝角. (Ⅰ)证明:B ﹣A=π2;(Ⅱ)求sinA +sinC 的取值范围.【解答】解:(Ⅰ)由a=btanA 和正弦定理可得sinA cosA =a b =sinAsinB,∴sinB=cosA ,即sinB=sin (π2+A )又B 为钝角,∴π2+A ∈(π2,π),∴B=π2+A ,∴B ﹣A=π2;(Ⅱ)由(Ⅰ)知C=π﹣(A +B )=π﹣(A +π2+A )=π2﹣2A >0,∴A ∈(0,π4),∴sinA +sinC=sinA +sin (π2﹣2A )=sinA +cos2A=sinA +1﹣2sin 2A=﹣2(sinA ﹣14)2+98,∵A ∈(0,π4),∴0<sinA <√22,∴由二次函数可知√22<﹣2(sinA ﹣14)2+98≤98∴sinA +sinC 的取值范围为(√22,98]20.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖. (1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X ,求X 的分布列和数学期望.【解答】解:(1)记事件A 1={从甲箱中摸出一个球是红球},事件A 2={从乙箱中摸出一个球是红球},事件B 1={顾客抽奖1次获一等奖},事件B 2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},由题意A 1,A 2相互独立,A 1A 2,A 2A 1互斥,B 1,B 2互斥,且B 1=A 1A 2,B 2=A 1A 2+A 2A 1C=B 1+B 2,因为P (A 1)=410=25,P (A 2)=510=12,所以,P (B 1)=P (A 1)P (A 2)=25×12=15,P (B 2)=P (A 1A 2)+P (A 2A 1)=P(A 1)P(A 2)+P(A 1)P(A 2)=25×(1−12)+(1−25)×12=12,故所求概率为:P (C )=P (B 1+B 2)=P (B 1)+P (B 2)=15+12=710.(2)顾客抽奖1次可视为3次独立重复试验,由(1)可知,顾客抽奖1次获一等奖的概率为:15所以.X ~B (3,15).于是,P (X=0)=C 30(15)0(45)3=64125,P (X=1)=C 31(15)1(45)2=48125,P (X=2)=C 32(15)2(45)1=12125,P (X=3)=C 33(15)3(45)0=1125.故X 的分布列为:X 0 1 2 3 P6412548125121251125E (X )=3×15=35.21.如图,已知四棱台ABCD ﹣A 1B 1C 1D 1的上、下底面分别是边长为3和6的正方形,AA 1=6,且AA 1⊥底面ABCD ,点P 、Q 分别在棱DD 1、BC 上. (1)若P 是DD 1的中点,证明:AB 1⊥PQ ;(2)若PQ ∥平面ABB 1A 1,二面角P ﹣QD ﹣A 的余弦值为37,求四面体ADPQ 的体积.【解答】解:根据已知条件知AB ,AD ,AA 1三直线两两垂直,所以分别以这三直线为x ,y ,z 轴,建立如图所示空间直角坐标系,则:A (0,0,0),B (6,0,0),D (0,6,0),A 1(0,0,6),B 1(3,0,6),D 1(0,3,6);Q 在棱BC 上,设Q (6,y 1,0),0≤y 1≤6;∴(1)证明:若P 是DD 1的中点,则P (0,92,3);∴PQ →=(6,y 1−92,−3),AB 1→=(3,0,6);∴AB 1→⋅PQ →=0; ∴AB 1→⊥PQ →; ∴AB 1⊥PQ ;(2)设P (0,y 2,z 2),y 2,z 2∈[0,6],P 在棱DD 1上; ∴DP →=λDD 1→,0≤λ≤1;∴(0,y 2﹣6,z 2)=λ(0,﹣3,6); ∴{y 2−6=−3λz 2=6λ;∴z 2=12﹣2y 2;∴P (0,y 2,12﹣2y 2);∴PQ →=(6,y 1−y 2,2y 2−12);平面ABB 1A 1的一个法向量为AD →=(0,6,0); ∵PQ ∥平面ABB 1A 1; ∴PQ →⋅AD →=6(y 1﹣y 2)=0; ∴y 1=y 2;∴Q (6,y 2,0);设平面PQD 的法向量为n →=(x ,y ,z),则: {n →⋅PQ →=6x +(2y 2−12)z =0n →⋅DQ →=6x +(y 2−6)y =0; ∴{x =6−y 23z y =2z,取z=1,则n →=(6−y 23,2,1); 又平面AQD 的一个法向量为AA 1→=(0,0,6);又二面角P ﹣QD ﹣A 的余弦值为37; ∴cos <n →,AA 1→>=66√(23)2+5=37; 解得y 2=4,或y 2=8(舍去);∴P (0,4,4);∴三棱锥P ﹣ADQ 的高为4,且S ADQ =12×6×6=18;∴V 四面体ADPQ =V 三棱锥P ﹣ADQ =13⋅18⋅4=24.22.(13分)已知抛物线C 1:x 2=4y 的焦点F 也是椭圆C 2:y 2a 2+x 2b2=1(a >b >0)的一个焦点.C 1与C 2的公共弦长为2√6.(Ⅰ)求C 2的方程;(Ⅱ)过点F 的直线l 与C 1相交于A 、B 两点,与C 2相交于C 、D 两点,且AC →与BD →同向.(1)若|AC |=|BD |,求直线l 的斜率;(2)设C 1在点A 处的切线与x 轴的交点为M ,证明:直线l 绕点F 旋转时,△MFD 总是钝角三角形.【解答】解:(Ⅰ)抛物线C 1:x 2=4y 的焦点F 的坐标为(0,1),因为F 也是椭圆C 2的一个焦点,∴a 2﹣b 2=1,①,又C 1与C 2的公共弦长为2√6,C 1与C 2的都关于y 轴对称,且C 1的方程为x 2=4y ,由此易知C 1与C 2的公共点的坐标为(±√6,32), 所以94a 2+6b 2=1,②, 联立①②得a 2=9,b 2=8,故C 2的方程为y 29+x 28=1. (Ⅱ)设A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),D (x 4,y 4),(1)因为AC →与BD →同向,且|AC |=|BD |,所以AC →=BD →,从而x 3﹣x 1=x 4﹣x 2,即x 1﹣x 2=x 3﹣x 4,于是(x 1+x 2)2﹣4x 1x 2=(x 3+x 4)2﹣4x 3x 4,③设直线的斜率为k ,则l 的方程为y=kx +1,由{y =kx +1x 2=4y ,得x 2﹣4kx ﹣4=0,而x 1,x 2是这个方程的两根, 所以x 1+x 2=4k ,x 1x 2=﹣4,④由{y =kx +1x 28+y 29=1,得(9+8k 2)x 2+16kx ﹣64=0,而x 3,x 4是这个方程的两根, 所以x 3+x 4=−16k 9+8k 2,x 3x 4=﹣649+8k 2,⑤ 将④⑤代入③,得16(k 2+1)=162k 2(9+8k 2)2+4×649+8k 2, 即16(k 2+1)=162×9(k 2+1)(9+8k 2)2, 所以(9+8k 2)2=16×9,解得k=±√64. (2)由x 2=4y 得y′=12x , 所以C 1在点A 处的切线方程为y ﹣y 1=12x 1(x ﹣x 1), 即y=12x 1x ﹣14x 12, 令y=0,得x=12x 1,M (12x 1,0), 所以FM →=(12x 1,﹣1), 而FA →=(x 1,y 1﹣1),于是FM →•FA →=12x 12﹣y 1+1=14x 12+1>0, 因此∠AFM 是锐角,从而∠MFD=180°﹣∠AFM 是钝角,故直线l 绕点F 旋转时,△MFD 总是钝角三角形.23.(13分)已知a >0,函数f (x )=e ax sinx (x ∈[0,+∞]).记x n 为f (x )的从小到大的第n (n ∈N *)个极值点.证明:(Ⅰ)数列{f (x n )}是等比数列;(Ⅱ)若a ≥√e 2−1,则对一切n ∈N *,x n <|f (x n )|恒成立. 【解答】证明:(Ⅰ)f′(x )=e ax (asinx +cosx )=√a 2+1•e ax sin (x +φ),tanφ=1a ,0<φ<π2, 令f′(x )=0,由x ≥0,x +φ=mπ,即x=mπ﹣φ,m ∈N *,对k ∈N ,若(2k +1)π<x +φ<(2k +2)π,即(2k +1)π﹣φ<x <(2k +2)π﹣φ, 则f′(x )<0,因此在((m ﹣1)π﹣φ,mπ﹣φ)和(mπ﹣φ,(m +1)π﹣φ)上f′(x )符号总相反.于是当x=nπ﹣φ,n ∈N *,f (x )取得极值,所以x n =nπ﹣φ,n ∈N *,此时f (x n )=e a (nπ﹣φ)sin (nπ﹣φ)=(﹣1)n +1e a (nπ﹣φ)sinφ,易知f (x n )≠0,而f(x n+1)f(x n )=(−1)n+2e a((n+1)π−φ)sinφ(−1)n+1e a(nπ−φ)sinφ=﹣e aπ是常数, 故数列{f (x n )}是首项为f (x 1)=e a (π﹣φ)sinφ,公比为﹣e aπ的等比数列; (Ⅱ)由sinφ=√2,可得对一切n ∈N *,x n <|f (x n )|恒成立. 即为nπ﹣φ<√1+a 2e a (nπ﹣φ)恒成立⇔√a 2+1a <e a(nπ−φ)a(nπ−φ),① 设g (t )=e t t (t >0),g′(t )=e t (t−1)t 2,当0<t <1时,g′(t )<0,g (t )递减,当t >1时,g′(t )>0,g (t )递增. t=1时,g (t )取得最小值,且为e .因此要使①恒成立,只需√a 2+1a<g (1)=e , 只需a >√2,当a=√2,tanφ=1a =√e 2−1>√3,且0<φ<π2, 可得π3<φ<π2,于是π﹣φ<2π3<√e 2−1,且当n ≥2时,nπ﹣φ≥2π﹣φ>3π2>√e 2−1,因此对n ∈N *,ax n =√e 2−1≠1,即有g (ax n )>g (1)=e=√a 2+1a , 故①亦恒成立.综上可得,若a ≥√2,则对一切n ∈N *,x n <|f (x n )|恒成立.。
2015年湖南理科数学解析版
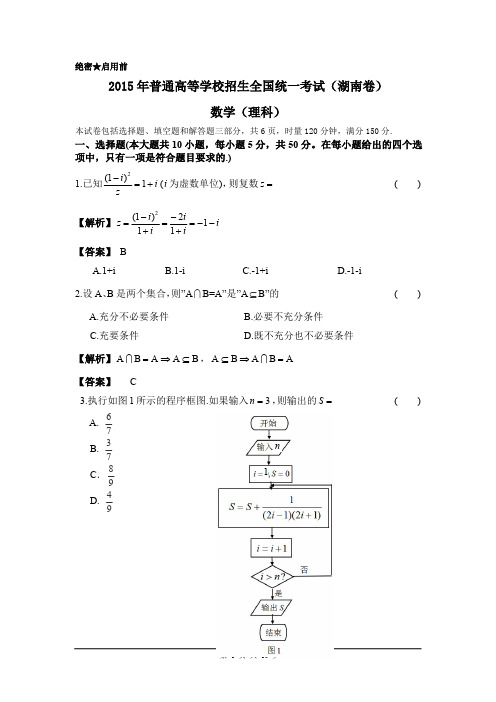
x y 1 4.若变量 x, y 满足约束条件 2 x y 1 则 z 3x y 的最小值为 y 1
A. 7 B. 1 C.1 D.2
x y 1 【解析】作出变量 x, y 满足约束条件 2 x y 1 的可行域为 y 1
2 2
1 p( 1 x 1) 0.3413 2
PC 的最大值为
A.6 B.7 C.8
第 3 页 共 15 页
( D.9
)
【解析】因为 AB BC ,不妨设 A( 1,0), C (1,0) , B 在圆 x 2 y 2 1 除去 A, C 两点
的圆周上,设 B (sin , cos ) . PA PB PC ( 3,0) ( 1,0) (sin 2, cos )
2 2 cos
将 2 x 2 y 2 , cos x 代入①即得曲线 C 的直角坐标方程为
①
x2 y2 2 x 0
②
(ii)将直线 l 的参数方程化为一般方程得: 3 y x 2 0
③
1 3 ), B ( 2,0) . 将③代入②,得 A( , 2 2
(i)证明 : B A
2
(ii)求 sin A sin C 的取值范围. 【答案】(i)由 a b tan A 及正弦定理,得 sin A sin B
sin B sin(
2
sin A ,所以 sin B cos A ,即 cos A
A)
又 B 为钝角,因此
若将运动员按成绩由好到差编为 1-35 号,再用系统抽样方法从中抽取 7 人 , 则其中成绩在区间[139,151]上的运动人数为________. 【答案】 4 13.设 Sn 为等比数列 an 前 n 项和, 若 a1 1, 且3S1 ,2 S2 , S3 成等差数列, 则 an 【解析】因为 3S1 ,2 S2 , S3 成等差数列 所以 4 S2 3S1 S3 即 4( a1 a2 ) 3a1 a1 a2 a3 即 3a2 a3 即q .
2015年湖南省高考数学试卷(理科)

2015年湖南省高考数学试卷(理科)一、选择题,共10小题,每小题5分,共50分1.(5分)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i2.(5分)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.4.(5分)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7 B.﹣1 C.1 D.25.(5分)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数6.(5分)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6 D.﹣67.(5分)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386 B.2718 C.3413 D.47728.(5分)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则||的最大值为()A.6 B.7 C.8 D.99.(5分)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.10.(5分)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A. B. C.D.二、填空题,共5小题,每小题5分,共25分11.(5分)(x﹣1)dx=.12.(5分)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是.13.(5分)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.14.(5分)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=.15.(5分)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是.三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.选修4-4:坐标系与方程17.(6分)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.选修4-5:不等式选讲18.设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.19.设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.20.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望.21.如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ的体积.22.(13分)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(ⅰ)若|AC|=|BD|,求直线l的斜率;(ⅱ)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,△MFD总是钝角三角形.23.(13分)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.2015年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题,共10小题,每小题5分,共50分1.(5分)(2015•湖南)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i【分析】由条件利用两个复数代数形式的乘除法法则,求得z的值.【解答】解:∵已知=1+i(i为虚数单位),∴z===﹣1﹣i,故选:D.【点评】本题主要考查两个复数代数形式的乘除法法则的应用,属于基础题.2.(5分)(2015•湖南)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】直接利用两个集合的交集,判断两个集合的关系,判断充要条件即可.【解答】解:A、B是两个集合,则“A∩B=A”可得“A⊆B”,“A⊆B”,可得“A∩B=A”.所以A、B是两个集合,则“A∩B=A”是“A⊆B”的充要条件.故选:C.【点评】本题考查充要条件的判断与应用,集合的交集的求法,基本知识的应用.3.(5分)(2015•湖南)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.【分析】列出循环过程中S与i的数值,满足判断框的条件即可结束循环.【解答】解:判断前i=1,n=3,s=0,第1次循环,S=,i=2,第2次循环,S=,i=3,第3次循环,S=,i=4,此时,i>n,满足判断框的条件,结束循环,输出结果:S===故选:B【点评】本题考查循环框图的应用,注意判断框的条件的应用,考查计算能力4.(5分)(2015•湖南)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7 B.﹣1 C.1 D.2【分析】由约束条件作出可行域,由图得到最优解,求出最优解的坐标,数形结合得答案.【解答】解:由约束条件作出可行域如图,由图可知,最优解为A,联立,解得C(0,﹣1).由解得A(﹣2,1),由,解得B(1,1)∴z=3x﹣y的最小值为3×(﹣2)﹣1=﹣7.故选:A.【点评】本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.易错点是图形中的B点.5.(5分)(2015•湖南)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数【分析】求出好的定义域,判断函数的奇偶性,以及函数的单调性推出结果即可.【解答】解:函数f(x)=ln(1+x)﹣ln(1﹣x),函数的定义域为(﹣1,1),函数f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣[ln(1+x)﹣ln(1﹣x)]=﹣f(x),所以函数是奇函数.排除C,D,正确结果在A,B,只需判断特殊值的大小,即可推出选项,x=0时,f(0)=0;x=时,f()=ln(1+)﹣ln(1﹣)=ln3>1,显然f(0)<f(),函数是增函数,所以B错误,A正确.故选:A.【点评】本题考查函数的奇偶性以及函数的单调性的判断与应用,考查计算能力.6.(5分)(2015•湖南)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6 D.﹣6【分析】根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为求得r,再代入系数求出结果.【解答】解:根据所给的二项式写出展开式的通项,T r+1==;展开式中含x的项的系数为30,∴,∴r=1,并且,解得a=﹣6.故选:D.【点评】本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.7.(5分)(2015•湖南)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386 B.2718 C.3413 D.4772【分析】求出P(0<X≤1)=×0.6826=0.3413,即可得出结论.【解答】解:由题意P(0<X≤1)=×0.6826=0.3413,∴落入阴影部分点的个数的估计值为10000×0.3413=3413,故选:C.【点评】本题考查正态分布曲线的特点及曲线所表示的意义,考查正态分布中两个量μ和σ的应用,考查曲线的对称性,属于基础题.8.(5分)(2015•湖南)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P 的坐标为(2,0),则||的最大值为()A.6 B.7 C.8 D.9【分析】由题意,AC为直径,所以||=|2+|.B为(﹣1,0)时,|2+|≤7,即可得出结论.【解答】解:由题意,AC为直径,所以||=|2+|所以B为(﹣1,0)时,|2+|≤7.所以||的最大值为7.故选:B.【点评】本题考查向量知识的运用,考查学生分析解决问题的能力,比较基础.9.(5分)(2015•湖南)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.【分析】利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.【解答】解:因为将函数f(x)=sin2x的周期为π,函数的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1﹣x2|min=,不妨x1=,x2=,即g(x)在x2=,取得最小值,sin(2×﹣2φ)=﹣1,此时φ=,不合题意,x1=,x2=,即g(x)在x2=,取得最大值,sin(2×﹣2φ)=1,此时φ=,满足题意.故选:D.【点评】本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖.有一定难度,选择题,可以回代验证的方法快速解答.10.(5分)(2015•湖南)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A. B. C.D.【分析】根据三视图可判断其为圆锥,底面半径为1,高为2,求解体积.利用几何体的性质得出此长方体底面边长为n的正方形,高为x,利用轴截面的图形可判断得出n=(1﹣),0<x<2,求解体积式子,利用导数求解即可,最后利用几何概率求解即.【解答】解:根据三视图可判断其为圆锥,∵底面半径为1,高为2,∴V=×2=∵加工成一个体积尽可能大的长方体新工件,∴此长方体底面边长为n的正方形,高为x,∴根据轴截面图得出:=,解得;n=(1﹣),0<x<2,∴长方体的体积Ω=2(1﹣)2x,Ω′=x2﹣4x+2,∵,Ω′=x2﹣4x+2=0,x=,x=2,∴可判断(0,)单调递增,(,2)单调递减,Ω最大值=2(1﹣)2×=,∴原工件材料的利用率为=×=,故选:A【点评】本题很是新颖,知识点融合的很好,把立体几何,导数,概率都相应的考查了,综合性强,属于难题.二、填空题,共5小题,每小题5分,共25分11.(5分)(2015•湖南)(x﹣1)dx=0.【分析】求出被积函数的原函数,代入上限和下限求值.【解答】解:(x﹣1)dx=(﹣x)|=0;故答案为:0.【点评】本题考查了定积分的计算;关键是求出被积函数的原函数.12.(5分)(2015•湖南)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是4.【分析】根据茎叶图中的数据,结合系统抽样方法的特征,即可求出正确的结论.【解答】解:根据茎叶图中的数据,得;成绩在区间[139,151]上的运动员人数是20,用系统抽样方法从35人中抽取7人,成绩在区间[139,151]上的运动员应抽取7×=4(人).故答案为:4.【点评】本题考查了茎叶图的应用问题,也考查了系统抽样方法的应用问题,是基础题目.13.(5分)(2015•湖南)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.【分析】设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将中点M的坐标代入双曲线方程,结合离心率公式,计算即可得到.【解答】解:设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将点(﹣c,2b)代入双曲线方程可得,﹣=1,可得e2==5,解得e=.故答案为:.【点评】本题考查双曲线的方程和性质,主要考查双曲线的离心率的求法,同时考查中点坐标公式的运用,属于中档题.14.(5分)(2015•湖南)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=3n﹣1.【分析】利用已知条件列出方程求出公比,然后求解等比数列的通项公式.【解答】解:设等比数列的公比为q,S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,可得4S2=S3+3S1,a1=1,即4(1+q)=1+q+q2+3,q=3.∴a n=3n﹣1.故答案为:3n﹣1.【点评】本题考查等差数列以及等比数列的应用,基本知识的考查.15.(5分)(2015•湖南)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是{a|a<0或a>1} .【分析】由g(x)=f(x)﹣b有两个零点可得f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a的范围【解答】解:∵g(x)=f(x)﹣b有两个零点,∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,由x3=x2可得,x=0或x=1①当a>1时,函数f(x)的图象如图所示,此时存在b,满足题意,故a>1满足题意②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意③当0<a<1时,函数f(x)单调递增,故不符合题意④a=0时,f(x)单调递增,故不符合题意⑤当a<0时,函数y=f(x)的图象如图所示,此时存在b使得,y=f(x)与y=b 有两个交点综上可得,a<0或a>1故答案为:{a|a<0或a>1}【点评】本题考察了函数的零点问题,渗透了转化思想,数形结合、分类讨论的数学思想.三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)(2015•湖南)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.【分析】(1)证明O,M,E,N四点共圆,即可证明∠MEN+∠NOM=180°(2)证明△FEM∽△FON,即可证明FE•FN=FM•FO.【解答】证明:(1)∵N为CD的中点,∴ON⊥CD,∵M为AB的中点,∴OM⊥AB,在四边形OMEN中,∴∠OME+∠ONE=90°+90°=180°,∴O,M,E,N四点共圆,∴∠MEN+∠NOM=180°(2)在△FEM与△FON中,∠F=∠F,∠FME=∠FNO=90°,∴△FEM∽△FON,∴=∴FE•FN=FM•FO.【点评】本题考查垂径定理,考查三角形相似的判定与应用,考查学生分析解决问题的能力,比较基础.选修4-4:坐标系与方程17.(6分)(2015•湖南)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.【分析】(1)曲线的极坐标方程即ρ2=2ρcosθ,根据极坐标和直角坐标的互化公式得x2+y2=2x,即得它的直角坐标方程;(2)直线l的方程化为普通方程,利用切割线定理可得结论.【解答】解:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x﹣1)2+y2=1;(2)直线l:(t为参数),普通方程为,(5,)在直线l上,过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,由切割线定理,可得|MT|2=|MA|•|MB|=18.【点评】本题主要考查把极坐标方程化为直角坐标方程的方法,属于基础题.选修4-5:不等式选讲18.(2015•湖南)设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.【分析】(ⅰ)由a>0,b>0,结合条件可得ab=1,再由基本不等式,即可得证;(ⅱ)运用反证法证明.假设a2+a<2与b2+b<2可能同时成立.结合条件a>0,b>0,以及二次不等式的解法,可得0<a<1,且0<b<1,这与ab=1矛盾,即可得证.【解答】证明:(ⅰ)由a>0,b>0,则a+b=+=,由于a+b>0,则ab=1,即有a+b≥2=2,当且仅当a=b取得等号.则a+b≥2;(ⅱ)假设a2+a<2与b2+b<2可能同时成立.由a2+a<2及a>0,可得0<a<1,由b2+b<2及b>0,可得0<b<1,这与ab=1矛盾.a2+a<2与b2+b<2不可能同时成立.【点评】本题考查不等式的证明,主要考查基本不等式的运用和反证法证明不等式的方法,属于中档题.19.(2015•湖南)设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.【分析】(Ⅰ)由题意和正弦定理可得sinB=cosA,由角的范围和诱导公式可得;(Ⅱ)由题意可得A∈(0,),可得0<sinA<,化简可得sinA+sinC=﹣2(sinA﹣)2+,由二次函数区间的最值可得.【解答】解:(Ⅰ)由a=btanA和正弦定理可得==,∴sinB=cosA,即sinB=sin(+A)又B为钝角,∴+A∈(,π),∴B=+A,∴B﹣A=;(Ⅱ)由(Ⅰ)知C=π﹣(A+B)=π﹣(A++A)=﹣2A>0,∴A∈(0,),∴sinA+sinC=sinA+sin(﹣2A)=sinA+cos2A=sinA+1﹣2sin2A=﹣2(sinA﹣)2+,∵A∈(0,),∴0<sinA<,∴由二次函数可知<﹣2(sinA﹣)2+≤∴sinA+sinC的取值范围为(,]【点评】本题考查正弦定理和三角函数公式的应用,涉及二次函数区间的最值,属基础题.20.(2015•湖南)某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望.【分析】(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件A2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},利用A 1,A2相互独立,,互斥,B1,B2互斥,然后求出所求概率即可.(2)顾客抽奖1次可视为3次独立重复试验,判断X~B.求出概率,得到X的分布列,然后求解期望.【解答】解:(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件B2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},由题意A 1,A2相互独立,,互斥,B 1,B2互斥,且B1=A1A2,B2=+,C=B1+B2,因为P(A1)=,P(A2)=,所以,P(B1)=P(A1)P(A2)==,P(B2)=P()+P()=+==,故所求概率为:P(C)=P(B1+B2)=P(B1)+P(B2)=.(2)顾客抽奖1次可视为3次独立重复试验,由(1)可知,顾客抽奖1次获一等奖的概率为:所以.X~B.于是,P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==.故X的分布列为:X0123PE(X)=3×=.【点评】期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫,它在市场预测,经济统计,风险与决策等领域有着广泛的应用,为今后学习数学及相关学科产生深远的影响.21.(2015•湖南)如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ的体积.【分析】(1)首先以A为原点,AB,AD,AA1所在直线分别为x,y,z轴,建立空间直角坐标系,求出一些点的坐标,Q在棱BC上,从而可设Q(6,y1,0),只需求即可;(2)设P(0,y2,z2),根据P在棱DD1上,从而由即可得到z2=12﹣2y2,从而表示点P坐标为P(0,y2,12﹣2y2).由PQ∥平面ABB1A1便知道与平面ABB1A1的法向量垂直,从而得出y1=y2,从而Q点坐标变成Q(6,y2,0),设平面PQD的法向量为,根据即可表示,平面AQD的一个法向量为,从而由即可求出y2,从而得出P点坐标,从而求出三棱锥P﹣AQD的高,而四面体ADPQ 的体积等于三棱锥P﹣AQD的体积,从而求出四面体的体积.【解答】解:根据已知条件知AB,AD,AA1三直线两两垂直,所以分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则:A(0,0,0),B(6,0,0),D(0,6,0),A1(0,0,6),B1(3,0,6),D1(0,3,6);Q在棱BC上,设Q(6,y1,0),0≤y1≤6;∴(1)证明:若P是DD1的中点,则P;∴,;∴;∴;∴AB1⊥PQ;(2)设P(0,y2,z2),y2,z2∈[0,6],P在棱DD1上;∴,0≤λ≤1;∴(0,y2﹣6,z2)=λ(0,﹣3,6);∴;∴z2=12﹣2y2;∴P(0,y2,12﹣2y2);∴;平面ABB1A1的一个法向量为;∵PQ∥平面ABB1A1;∴=6(y1﹣y2)=0;∴y1=y2;∴Q(6,y2,0);设平面PQD的法向量为,则:;∴,取z=1,则;又平面AQD的一个法向量为;又二面角P﹣QD﹣A的余弦值为;∴;解得y2=4,或y2=8(舍去);∴P(0,4,4);∴三棱锥P﹣ADQ的高为4,且;∴V四面体ADPQ =V三棱锥P﹣ADQ=.【点评】考查建立空间直角坐标系,利用空间向量解决异面直线垂直及线面角问题的方法,共线向量基本定理,直线和平面平行时,直线和平面法向量的关系,平面法向量的概念,以及两平面法向量的夹角和平面二面角大小的关系,三棱锥的体积公式.22.(13分)(2015•湖南)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(ⅰ)若|AC|=|BD|,求直线l的斜率;(ⅱ)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,△MFD总是钝角三角形.【分析】(Ⅰ)根据两个曲线的焦点相同,得到a2﹣b2=1,再根据C1与C2的公共弦长为2,得到=1,解得即可求出;(Ⅱ)设出点的坐标,(ⅰ)根据向量的关系,得到(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,设直线l的方程,分别与C1,C2构成方程组,利用韦达定理,分别代入得到关于k的方程,解得即可;(ⅱ)根据导数的几何意义得到C1在点A处的切线方程,求出点M的坐标,利用向量的乘积∠AFM是锐角,问题得以证明.【解答】解:(Ⅰ)抛物线C1:x2=4y的焦点F的坐标为(0,1),因为F也是椭圆C2的一个焦点,∴a2﹣b2=1,①,又C1与C2的公共弦长为2,C1与C2的都关于y轴对称,且C1的方程为x2=4y,由此易知C1与C2的公共点的坐标为(±,),所以=1,②,联立①②得a2=9,b2=8,故C2的方程为+=1.(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),(ⅰ)因为与同向,且|AC|=|BD|,所以=,从而x3﹣x1=x4﹣x2,即x1﹣x2=x3﹣x4,于是(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,③设直线的斜率为k,则l的方程为y=kx+1,由,得x2﹣4kx﹣4=0,而x1,x2是这个方程的两根,所以x1+x2=4k,x1x2=﹣4,④由,得(9+8k2)x2+16kx﹣64=0,而x3,x4是这个方程的两根,所以x3+x4=,x3x4=﹣,⑤将④⑤代入③,得16(k2+1)=+,即16(k2+1)=,所以(9+8k2)2=16×9,解得k=±.(ⅱ)由x2=4y得y′=x,所以C1在点A处的切线方程为y﹣y1=x1(x﹣x1),即y=x1x﹣x12,令y=0,得x=x1,M(x1,0),所以=(x1,﹣1),而=(x1,y1﹣1),于是•=x12﹣y1+1=x12+1>0,因此∠AFM是锐角,从而∠MFD=180°﹣∠AFM是钝角,故直线l绕点F旋转时,△MFD总是钝角三角形.【点评】本题考查了圆锥曲线的和直线的位置与关系,关键是联立方程,构造方程,利用韦达定理,以及向量的关系,得到关于k的方程,计算量大,属于难题.23.(13分)(2015•湖南)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.【分析】(Ⅰ)求出导数,运用两角和的正弦公式化简,求出导数为0的根,讨论根附近的导数的符号相反,即可得到极值点,求得极值,运用等比数列的定义即可得证;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),求出导数,求得最小值,由恒成立思想即可得证.【解答】证明:(Ⅰ)f′(x)=e ax(asinx+cosx)=•e ax sin(x+φ),tanφ=,0<φ<,令f′(x)=0,由x≥0,x+φ=mπ,即x=mπ﹣φ,m∈N*,对k∈N,若(2k+1)π<x+φ<(2k+2)π,即(2k+1)π﹣φ<x<(2k+2)π﹣φ,则f′(x)<0,因此在((m﹣1)π﹣φ,mπ﹣φ)和(mπ﹣φ,(m+1)π﹣φ)上f′(x)符号总相反.于是当x=nπ﹣φ,n∈N*,f(x)取得极值,所以x n=nπ﹣φ,n∈N*,此时f(x n)=e a(nπ﹣φ)sin(nπ﹣φ)=(﹣1)n+1e a(nπ﹣φ)sinφ,易知f(x n)≠0,而==﹣e aπ是常数,故数列{f(x n)}是首项为f(x1)=e a(π﹣φ)sinφ,公比为﹣e aπ的等比数列;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),g′(t)=,当0<t<1时,g′(t)<0,g(t)递减,当t>1时,g′(t)>0,g(t)递增.t=1时,g(t)取得最小值,且为e.因此要使①恒成立,只需<g(1)=e,只需a>,当a=,tanφ==,且0<φ<,可得<φ<,于是π﹣φ<<,且当n≥2时,nπ﹣φ≥2π﹣φ>>,因此对n∈N*,ax n=≠1,即有g(ax n)>g(1)=e=,故①亦恒成立.综上可得,若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.【点评】本题考查导数的运用:求极值和单调区间,主要考查三角函数的导数和求值,同时考查等比数列的定义和通项公式的运用,考查不等式恒成立问题的证明,属于难题.参与本试卷答题和审题的老师有:caoqz;qiss;吕静;刘长柏;sdpyqzh;changq;742048;双曲线;lincy;wkl197822;whgcn(排名不分先后)菁优网2017年3月17日。
15年高考真题——理科数学(湖南卷)

2015年普通高等学校招生全国统一考试(湖南)卷数学(理科)一.选择题(本大题共10小题,每小题5分,共50分。
在每小题给也的四个选项中,只有一项是符合题目要求的)1.已知()211i i z-=+(i 为虚数单位),则复数z =( ) (A )1i + (B )1i - (C )1i -+ (D )1i --2.设,A B 是两个集合,则“AB A =”是“A B ⊆”的( )(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件3.执行如图所示的程序框图,如果输入3n =,则输出的S =( ) (A )67 (B )37 (C )8 (D )494.若变量,x y 满足约束条件1211x y x y y +≥-⎧⎪-≤⎨⎪≤⎩,则3z x y =-的最小值为( ) (A )7- (B )1- (C )1 (D )25.设函数()()()ln 1ln 1f x x x =+--,则()f x 是( ) (A )奇函数,且在()0,1上是增函数 (B )奇函数,且在()0,1上是减函数 (C )偶函数,且在()0,1上是增函数 (D )偶函数,且在()0,1上是减函数6.已知5的展开式中含32x 的项的系数为30,则a =( )(A(B) (C )6 (D )6-7.在如图2所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C 为正态分布()0,1N 的密度曲线)的点的个数的估计值为( )(A )2386 (B )2718 (C )3413 (D )47728.已知点,,A B C 在圆221x y +=上运动,且AB BC ⊥。
若点P 的坐标为()2,0,则||PA PB PC ++的最大值为( ) (A )6(B )7 (C )8(D )99.将函数()sin 2f x x =的图像向右平移()02ϕϕπ<<个单位后得到函数()g x 的图像,若对满足()()12||2f x g x -=的12,x x ,有12min ||x x π-=,则ϕ=( )结束开始11y xOC(A )512π (B )3π (C )4π (D )6π 10.某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)( )(A)(-∞ (B)(-∞ (C)(- (D)(二.填空题(本大题共5小题,每小题5分,共25分)11.()201x dx ⎰-=____________。
2015年高考湖南理科数学试题及答案(详解纯word版)

2015年普通高等学校招生全国统一考试〔XX 卷〕数学〔理科〕本试题卷包括选择题、填空题和解答题三部分,时量120分钟,满分150分一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知i zi +=-1)1(2(i 是虚数单位),则复数z= A. i +1 B. i -1C. i +-1D. i --12.设A 、B 是两个集合,则“A B A = 〞是“B A ⊆〞的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3.执行如图所示的程序框图,如果输入的3=n ,则输出的S =A.76B. 73 C. 98D. 944.若变量x, y 满足约束条件⎪⎩⎪⎨⎧≤≤--≥+1121y y x y x ,则y x z -=3的最小值为A. 7-B. 1-C. 1D. 25. 设函数)1ln()1ln()(x x x f --+=,则)(x f 是A. 奇函数,且在)1,0(是增函数B. 奇函数,且在)1,0(是减函数C. 偶函数,且在)1,0(是增函数D. 偶函数,且在)1,0(是减函数 6.已知5)(xax -的展开式中含23x 的项的系数为30,则=aA.3B.3-C. 6D. 6-7. 在如图2所示的正方形中随机投掷10000个点,则落入阴影部分〔曲线C 为正态分布)1,0(N 的密度曲线〕的点的个数的估计值为 A. 2386B.2718C. 3413D. 4772附:若),(~2σμN X ,则6826.0)(=+≤<-σμσμX P , 9544.0)22(=+≤<-σμσμX P .8.已知点A, B, C 在圆122=+y x 上运动,且BC AB ⊥ . 若点P 的坐标为)0,2(, 则||PC PB PA ++的最大值为A. 6B. 7C. 8D. 9 9.将函数x x f 2sin )(=的图象向右平移ϕ)20(πϕ<<个单位后得到函数)(x g 的图象,若对满足2|)()(|21=-x g x f 的1x ,2x ,有3||min 21π=-x x ,则=ϕA. 125πB. 3πC. 4πD.6π 10. 某工件的三视图如图所示,现将该工件通过切削,加工成体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为〔材料的利用率原工件的体积新工件的体积=〕 A.π98 B. π916 C.π2124)-( D.π21212)-(二、填空题:本大题共5小题,每小题5分,共25分. 11.⎰=-2)1(dx x __________.12. 在一次马拉松比赛中,35名运动员的成绩〔单位:分钟〕茎叶图如图所示若将运动员按成绩由好到差编为1-35号,再用系统抽样的方法从中抽取7人,则其中成绩在区间]151,139[上的运动员的人数是_________.13. 设F 是双曲线C 1:2222=-by a x 的一个焦点,若C 上存在点P ,使线段PF 的中点恰为其虚轴的一个端点,则C 的离心率为________.14.设n S 为等比数列}{n a 的前n 项和,若11=a ,且321,2,3S S S 成等差数列,则=n a ___________.15. 已知函数⎪⎩⎪⎨⎧>≤=.,,,)(23a x x a x x x f 若存在实数b ,使函数b x f x g -=)()(有两个零点,则a 的取值X 围是___________.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)俯视图侧视图正视图222121本小题有Ⅰ、Ⅱ、Ⅲ三个选做题,请考生任选两题作答,并将解答过程写在答题纸中相应题号的答题区域内,如果全做,则按所做的前两题计分. Ⅰ.〔本小题满分6分〕选修4-1 几何证明选讲如图,在⊙O 中,相交于点E 的两弦AB ,CD 的中点分别是M ,N ,直线MO 与直线CD 相交于点F ,证明:〔i 〕180=∠+∠NOM MEN ; 〔ii 〕FO FM FN FE ⋅=⋅.Ⅱ.〔本小题满分6分〕选修4-4 坐标系与参数方程已知直线l ⎪⎪⎩⎪⎪⎨⎧+=+=.213,235:t y t x 〔t 为参数〕,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θρcos 2=. 〔i 〕将曲线C 的极坐标方程化为直角坐标方程;〔ii 〕设点M 的直角坐标为)3,5(,直线l 与曲线C 的交点为A ,B ,求||||MB MA ⋅的值.Ⅲ.〔本小题满分6分〕选修4-5 不等式选讲 设0,0>>b a ,且ba b a 11+=+,证明: 〔i 〕2≥+b a ;〔ii 〕22<+a a 与22<+b b 不可能同时成立.17. (本小题满分12分)设ABC ∆的内角C B A ,,的对边分别为c b a ,,,A b a tan =,且B 为钝角.F(Ⅰ) 证明:2π=-A B ;(Ⅱ) 求C A sin sin +的取值X 围.18. (本小题满分12分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖. 每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球. 在摸出的2球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.(Ⅰ) 求顾客抽奖1次能获奖的概率; (Ⅱ) 若某顾客有3次抽奖的机会,记该顾客在3次抽奖中获一等奖的次数为X ,求X 的分布列和数学期望.19. (本小题满分13分)如图,在四棱台1111D C B A ABCD -的上、下底面分别是边长为3和6的正方形,61=AA ,且⊥1AA 底面ABCD ,点P ,Q 分别在棱1DD ,BC 上. (Ⅰ) 若点P 是1DD 的中点,证明:PQ AB ⊥1; (Ⅱ) 若//PQ 平面11A ABB ,二面角A QD P --的余弦值为73,求四面体ADPQ 的体积.20. (本小题满分13分)BDQ已知抛物线1C y x 4:2=的焦点F 也是椭圆2C )0(1:2222>>=+b a bx a y 的一个焦点,1C 与2C 的公共弦长为62. (Ⅰ) 求2C 的方程;(Ⅱ) 过点F 的直线l 与1C 相交于A ,B 两点,与2C 相交于C ,D 两点,且AC 与BD 同向.〔i 〕 若||||BD AC =,求直线l 的斜率;〔ii 〕设1C 在点A 处的切线与x 轴的交点为M ,证明:直线l 绕点F 旋转时,MFD ∆总是钝角三角形.21. (本小题满分13分)已知0>a ,函数)),0[(sin )(∞+∈=x x e x f ax,记n x 为)(x f 的从小到大的第n *)(N n ∈个极值点. 证明: (Ⅰ) 数列)}({n x f 是等比数列; (Ⅱ) 若112-≥e a ,则对一切*N n ∈,|)(|n n x f x <恒成立.2015年高考XX 卷理科数学参考答案一、选择题D C B A A D C B D A 二、填空题11. 0 12. 4 13. 5 14. 13-n 15. ),1()0,(∞+-∞ 三、解答题16. Ⅰ.证明:(i )如图,因为M ,N 分别是两弦AB ,CD的中点,所以AB OM ⊥, CD ON ⊥,即90=∠=∠ONE OME ,因此 180=∠+∠ONE OME ,又四边形的内角和等于 360,故 180=∠+∠NOM MEN .(ii ) 由〔i 〕知, O ,M ,E ,N 四点共圆,故由割线定理即得FO FM FN FE ⋅=⋅.Ⅱ.解: (i )θρcos 2=等价于 θρρcos 22=,将222y x +=ρ,x =θρcos 代入上式即得曲线C 的直角坐标方程是0222=-+x y x .(ii ) 将⎪⎪⎩⎪⎪⎨⎧+=+=.213,235t y t x 代入0222=-+x y x 得018352=++t t .设这个方程的 两个实根分别为21,t t ,则由参数t 的几何意义知||||MB MA ⋅=.18||21=t tⅢ.证明: 由abba b a b a +=+=+11,0,0>>b a 得 1=ab 〔i 〕由基本不等式与1=ab ,有22=≥+ab b a ,即2≥+b a .(ii ) 设22<+a a 与22<+b b 可同时成立,则由22<+a a 与0>a 可得10<<a ,同理 10<<b ,从而10<<ab 这与1=ab 相矛盾,故22<+a a 与22<+b b 不可能同时成立.17. 解:〔Ⅰ〕由A b a tan =与正弦定理,得BAb a A A sin sin cos sin ==,所以A B cos sin =,即)2sin(sin A B +=π. 又B 为钝角,),2(2πππ∈+A ,故A B +=2π,即2π=-A B . (Ⅱ) 由〔Ⅰ〕知 022)(>-=+-=A B A C ππ, 所以)4,0(π∈A . 于是 )22sin(sin sin sin A A C A -+=+πA A 2cos sin +=.89)41(sin 2sin 21sin 22+--=-+=A A A因为40π<<A ,所以 22sin 0<<A ,因此8989)41(sin 2222≤+--<A . 由此可得C A sin sin +的取值X 围是]89,22(.F18. 解:〔Ⅰ〕记事件1A ={从甲箱中摸出的一个球是红球},2A ={从乙箱中摸出的一个球是红球},1B ={顾客抽奖一次获一等奖},2B ={顾客抽奖一次获二等奖},C ={顾客抽奖一次能获奖}.由题意1A 与2A 相互独立,21A A 与21A A 互斥,1B 与2B 互斥,且211A A B =,2B =21A A +21A A ,21B B C +=. 又因为52104)(1==A P ,21105)(2==A P ,所以 512152)()()()(21211=⨯===A P A P A A P B P , )()()()(212121212A A P A A P A A A A P B P +=+=2121)521()211(52)()()()(2121=⨯-+-⨯=+=A P A P A P A P ,故所求概率为1072151)()()()(2121=+=+=+=B P B P B B P C P .(Ⅱ)顾客抽奖3次可视为3次独立重复实验,由〔Ⅰ〕知,顾客抽奖1次获一等奖的概率为51,所以)51,3(~B X ,于是 )3,2,1,0()54()51()(33===-K C K X P K K KX 的数学期望为553)(=⨯=X E .19.解法一:〔Ⅰ〕如图,取1AA 的中点R ,连结PR BR ,, 因为1AA ,1DD 是梯形D D AA 11的两腰,点P 是1DD 的中点,所以AD PR //,于是由BC AD //知,BC PR //,所以C B R P ,,,四点共面. 由题设知 AB BC ⊥,1AA BC ⊥,A AA AB =1 ,所以 ⊥BC 平面11A ABB ,⊂1AB 平面11A ABB ,因此 1AB BC ⊥.因为11111tan 63tan AB A AA B A AB AR ABR ∠====∠,所以11AB A ABR ∠=∠,因此901111=∠+∠=∠+∠BAB AB A BAB ABR , 于是 1AB BR ⊥, 又已证得1AB BC ⊥,所以⊥1AB 平面BRPC ,显然有⊂PQ 平面BRPC , 故 PQ AB ⊥1.(Ⅱ) 如下图,过点P 作1//AA PM 交AD 于点M ,则//PM 平面11A ABB , 因为⊥1AA 底面ABCD,所以⊥PM 底面ABCD ,过点M 作QD MN ⊥于点N ,连结PN ,则QD PN ⊥,PNM ∠是二面角A QD P --的平面角. 所以DB73cos =∠PNM ,即 73=PN MN , 从而340=MN PM . 连结MQ ,由//PQ 平面11A ABB 与//PM 平面11A ABB 知,平面//PQM 平面11A ABB ,所以AB MQ //,又ABCD 是正方形,所以ABQM 是矩形,故MQ=AB=6. 设MD =t ,则.366222ttMD MQ MD MQ MN +=+⋅=过点1D 作A A E D 11//交AD 于点E ,则E D AA 11是矩形,所以 611==AA E D ,311==D A AE ,因此 3=-=AE AD DE . 于是 21==DEED MD PM , 所以t MD PM 22==,从而t t t MN PM 63623402+⨯==,解得2=t ,所以4=PM . 故四面体ADPQ 的体积 24466213131=⨯⨯⨯⨯=⋅=∆PM S V ADQ .解法二:由题设知AB AD AA ,,1G 两两垂直,以A为坐标原点,AB ,AD ,1AA 所在直线分别为x 轴,y轴,z 轴,建立空间直角坐标系,如图,则相关各点的坐标为)0,0,0(A ,)6,0,3(1B ,)0,6,0(D ,)6,3,0(1D , )0,,6(m Q ,其中m BQ =,60≤≤m .(Ⅰ) 若点P 是1DD 的中点,则)3,29,0(P ,)3,29,6(--=m PQ ,又)6,0,3(1=AB ,于是018181=-=⋅PQ AB , 所以PQ AB ⊥1,即PQ AB ⊥1.(Ⅱ) 由题设知,)0,6,6(-=m DQ , )6,3,0(1-=DD 是平面PQD 内两个不共线的向量,设),,(1z y x n =是平面PQD 的一个法向量,则 ⎪⎩⎪⎨⎧=⋅=⋅0,0111DD n DQ n 即⎩⎨⎧=+-=-+063,0)6(6z y y m x 取6=y ,得)3,6,6(1m n -=. 又平面AQD 的一个法向量是)1,0,0(2=n ,所以45)6(336)6(3||||,cos 2222212121+-=++-=⋅>=<m m n n n n ,而二面角A QD P --的余弦值为73,所以7345)6(32=+-m ,解得m=4或m=8(舍去),此时)0,4,6(Q . 再设)10(1≤<=λλDD DP ,而)6,3,0(1-=DD ,由此得到)6,36,0(λλ-P ,)6,23,6(λλ--=PQ . 因为//PQ 平面11A ABB ,且平面11A ABB 的一个法向量是)0,1,0(3=n ,所以 0233=-=⋅λn PQ ,32=λ,从而)4,4,0(P .于是,将四面体ADPQ 视为ADQ ∆为底面的三棱锥ADQ P -,其高4=h ,故四面体ADPQ 的体积 24466213131=⨯⨯⨯⨯=⋅=∆PM S V ADQ .20. 解:(Ⅰ) 由1C y x 4:2=知其焦点F 的坐标为〔0,1〕,因为F 也是椭圆2C 的一个焦点,所以 122=-b a 〔1〕又1C 与2C 的公共弦长为62,1C 与2C 都关于y 轴对称,且1C 的方程为y x 42=,由此易知1C 与2C 的公共点坐标为)23,6(±,所以164922=+ba 〔2〕 联立〔1〕〔2〕得8,922==b a ,故2C 的方程为18922=+x y . (Ⅱ)如图,设),(11y x A ,),(22y x B ,),(33y x C ,),(44y x D .(i )因AC 与BD 同向,且||||BD AC =,所以 BD AC =,从而 2413x x x x -=-,即4321x x x x -=-,于是43243212214)(4)(x x x x x x x x -+=-+. 〔3〕 设直线l 的斜率为k ,则l 的方程为1+=kx y .由⎩⎨⎧=+=y x kx y 4,12 得0442=--kx x ,而21,x x 是这个方程的两根,所以 4,42121-==+x x k x x 〔4〕 由⎪⎩⎪⎨⎧=++=189,122x y kx y 得06416)89(22=-++kx x k ,而43,x x 是这个方程的两根,所以2212438964,8916k x x k k x x +-=+-=+ 〔5〕 将(4)(5)代入(3)得 22222289644)89(16)1(16k k k k +⨯++=+,即22222)89()1(916)1(16k k k ++⨯=+, 所以 916)89(22⨯=+k ,解得 46±=k ,即直线l 的斜率为46±. (ii )由 y x 42=得 2'xy =,所以1C 在点A 处的切线方程为)(2111x x x y y -=-,即42211x x x y -=,令0=y 得21x x =,即)0,2(1x M ,所以)1,2(1-=xFM ,而)14,(211-=x x FA ,于是014)14(2212121>+=--=⋅x x x FA FM ,因此AFM ∠总是锐角,从而AFM MFD ∠-=∠180是钝角. 故直线l 绕点F 旋转时,MFD ∆总是钝角三角形.21. 解:(Ⅰ))cos sin (cos sin )('x x a e x ex ae x f ax axax +=+=)sin(12ϕ+⋅+=x e a ax ,其中a 1tan =ϕ,20πϕ<<.令 0)('=x f ,由0≥x 得 πϕm x =+,即*,N m m x ∈-=ϕπ. 对N k ∈,若πϕπ)12(2+<+<k x k ,即ϕπϕπ-+<<-)12(2k x k ,则0)('>x f ;若πϕπ)22()12(+<+<+k x k ,即ϕπϕπ-+<<-+)22()12(k x k ,则0)('<x f . 因此,在区间),)1((ϕππ--m m 与),(πϕπm m -上,)('x f 的符号总相反,于是,当*,N m m x ∈-=ϕπ时,)(x f 取得极值,所以*,N n n x n ∈-=ϕπ. 此时,)(1)()1()sin()(ϕπϕπϕπ-+--=-=n a n n a n e n e x f ,易知0)(≠n x f ,且πϕπϕπa n a n n a n n n e ee xf x f -=--=-+-+++)(1])1[(21)1()1()()(是常数,故数列)}({n x f 是首项为ϕϕπsin )()(1-=a e x f ,公比为πa e -的等比数列.(Ⅱ) 由(Ⅰ)知,11sin 2+=a ϕ,于是对一切*N n ∈,|)(|n n x f x <恒成立,即)(211ϕπϕπ-+<-n a e a n 恒成立,等价于)(1)(2ϕπϕπ-<+-n a e a a n a 〔*〕恒成立〔因为a>0〕. 设)0()(>=t t e t g t ,则0)1()('2=-=tt e t g t 得1=t ,当10<<t 时,0)('<t g ,所以)(t g 在)1,0(上单调递减;当1>t 时,0)('>t g ,所以)(t g 在),1(∞+上单调递增.从而当1=t 时,函数)(t g 取得最小值e g =)1(. 因此,要使〔*〕式恒成立,只需e g aa =<+)1(12,即只需112->e a . 而当112-=e a 时,由311tan 2>-==e a ϕ且由20πϕ<<知,23πϕπ<<. 于是1322-<<-e πϕπ,且当2≥n 时,12322->>-≥-e n πϕπϕπ,因此,对一切*N n ∈,112≠--=e n ax n ϕπ,所以aa e g ax g n 1)1()(2+==>,故〔*〕式也恒成立. 综上所述,若112-≥e a ,则对一切*N n ∈,|)(|n n xf x <恒成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题,共10小题,每小题5分,共50分1.(5分)(2015•湖南)已知=1+i(i为虚数单位),则复数z=()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:由条件利用两个复数代数形式的乘除法法则,求得z的值.解答:解:∵已知=1+i(i为虚数单位),∴z===﹣1﹣i,故选:D.点评:本题主要考查两个复数代数形式的乘除法法则的应用,属于基础题.2.(5分)(2015•湖南)设A、B是两个集合,则“A∩B=A”是“A⊆B”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:集合;简易逻辑.分析:直接利用两个集合的交集,判断两个集合的关系,判断充要条件即可.解答:解:A、B是两个集合,则“A∩B=A”可得“A⊆B”,“A⊆B”,可得“A∩B=A”.所以A、B是两个集合,则“A∩B=A”是“A⊆B”的充要条件.故选:C.点评:本题考查充要条件的判断与应用,集合的交集的求法,基本知识的应用.3.(5分)(2015•湖南)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.考点:程序框图.分析:列出循环过程中S与i的数值,满足判断框的条件即可结束循环.解答:解:判断前i=1,n=3,s=0,第1次循环,S=,i=2,第2次循环,S=,i=3,第3次循环,S=,i=4,此时,i>n,满足判断框的条件,结束循环,输出结果:S===故选:B点评:本题考查循环框图的应用,注意判断框的条件的应用,考查计算能力4.(5分)(2015•湖南)若变量x、y满足约束条件,则z=3x﹣y的最小值为()A.﹣7 B.﹣1 C.1D.2考点:简单线性规划.专题:不等式的解法及应用.分析:由约束条件作出可行域,由图得到最优解,求出最优解的坐标,数形结合得答案.解答:解:由约束条件作出可行域如图,由图可知,最优解为A,联立,解得C(0,﹣1).由解得A(﹣2,1),由,解得B(1,1)∴z=3x﹣y的最小值为3×(﹣2)﹣1=﹣7.故选:A.点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.易错点是图形中的B点.5.(5分)(2015•湖南)设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数考点:利用导数研究函数的单调性.专题:导数的综合应用.分析:求出好的定义域,判断函数的奇偶性,以及函数的单调性推出结果即可.解答:解:函数f(x)=ln(1+x)﹣ln(1﹣x),函数的定义域为(﹣1,1),函数f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣[ln(1+x)﹣ln(1﹣x)]=﹣f(x),所以函数是奇函数.排除C,D,正确结果在A,B,只需判断特殊值的大小,即可推出选项,x=0时,f (0)=0;x=时,f()=ln(1+)﹣ln(1﹣)=ln3>1,显然f(0)<f(),函数是增函数,所以B错误,A正确.故选:A.点评:本题考查函数的奇偶性以及函数的单调性的判断与应用,考查计算能力.6.(5分)(2015•湖南)已知(﹣)5的展开式中含x的项的系数为30,则a=()A.B.﹣C.6D.﹣6考点:二项式定理的应用.专题:二项式定理.分析:根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为求得r,再代入系数求出结果.解答:解:根据所给的二项式写出展开式的通项,T r+1==;展开式中含x的项的系数为30,∴,∴r=1,并且,解得a=﹣6.故选:D.点评:本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.7.(5分)(2015•湖南)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附“若X﹣N=(μ,a2),则P(μ﹣σ<X≤μ+σ)=0.6826.p(μ﹣2σ<X≤μ+2σ)=0.9544.A.2386 B.2718 C.3413 D.4772考点:正态分布曲线的特点及曲线所表示的意义.专题:计算题;概率与统计.分析:求出P(0<X≤1)=×0.6826=0.3413,即可得出结论.解答:解:由题意P(0<X≤1)=×0.6826=0.3413,∴落入阴影部分点的个数的估计值为10000×0.3413=3413,故选:C.点评:本题考查正态分布曲线的特点及曲线所表示的意义,考查正态分布中两个量μ和σ的应用,考查曲线的对称性,属于基础题.8.(5分)(2015•湖南)已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则||的最大值为()A.6B.7C.8D.9考点:圆的切线方程.专题:计算题;直线与圆.分析:由题意,AC为直径,所以||=|2+|=|4+|.B为(﹣1,0)时,|4+|≤7,即可得出结论.解答:解:由题意,AC为直径,所以||=|2+|=|4+|.所以B为(﹣1,0)时,|4+|≤7.所以||的最大值为7.故选:B.点评:本题考查向量知识的运用,考查学生分析解决问题的能力,比较基础.9.(5分)(2015•湖南)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A.B.C.D.考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.解答:解:因为将函数f(x)=sin2x的周期为π,函数的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1﹣x2|min=,不妨x1=,x2=,即g(x)在x2=,取得最小值,sin(2×﹣2φ)=﹣1,此时φ=,不合题意,x1=,x2=,即g(x)在x2=,取得最大值,sin(2×﹣2φ)=1,此时φ=,满足题意.故选:D.点评:本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖.有一定难度,选择题,可以回代验证的方法快速解答.10.(5分)(2015•湖南)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A.B.C.D.考点:简单空间图形的三视图.专题:创新题型;空间位置关系与距离;概率与统计.分析:根据三视图可判断其为圆锥,底面半径为1,高为2,求解体积.利用几何体的性质得出此长方体底面边长为n的正方形,高为x,利用轴截面的图形可判断得出n=(1﹣),0<x<2,求解体积式子,利用导数求解即可,最后利用几何概率求解即.解答:解:根据三视图可判断其为圆锥,∵底面半径为1,高为2,∴V=×2=∵加工成一个体积尽可能大的长方体新工件,∴此长方体底面边长为n的正方形,高为x,∴根据轴截面图得出:=,解得;n=(1﹣),0<x<2,∴长方体的体积Ω=2(1﹣)2x,Ω′=x2﹣4x+2,∵,Ω′=x2﹣4x+2=0,x=,x=2,∴可判断(0,)单调递增,(,2)单调递减,Ω最大值=2(1﹣)2×=,∴原工件材料的利用率为=×=,故选:A点评:本题很是新颖,知识点融合的很好,把立体几何,导数,概率都相应的考查了,综合性强,属于难题.二、填空题,共5小题,每小题5分,共25分11.(5分)(2015•湖南)(x﹣1)dx=0.考点:定积分.专题:导数的概念及应用.分析:求出被积函数的原函数,代入上限和下限求值.解答:解:(x﹣1)dx=(﹣x)|=0;故答案为:0.点评:本题考查了定积分的计算;关键是求出被积函数的原函数.12.(5分)(2015•湖南)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是4.考点:茎叶图.专题:概率与统计.分析:根据茎叶图中的数据,结合系统抽样方法的特征,即可求出正确的结论.解答:解:根据茎叶图中的数据,得;成绩在区间[139,151]上的运动员人数是20,用系统抽样方法从35人中抽取7人,成绩在区间[139,151]上的运动员应抽取7×=4(人).故答案为:4.点评:本题考查了茎叶图的应用问题,也考查了系统抽样方法的应用问题,是基础题目.13.(5分)(2015•湖南)设F是双曲线C:﹣=1的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为.考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将中点M的坐标代入双曲线方程,结合离心率公式,计算即可得到.解答:解:设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=﹣c,n=2b,将点(﹣c,2b)代入双曲线方程可得,﹣=1,可得e2==5,解得e=.故答案为:.点评:本题考查双曲线的方程和性质,主要考查双曲线的离心率的求法,同时考查中点坐标公式的运用,属于中档题.14.(5分)(2015•湖南)设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n=3n﹣1.考点:等差数列与等比数列的综合.专题:等差数列与等比数列.分析:利用已知条件列出方程求出公比,然后求解等比数列的通项公式.解答:解:设等比数列的公比为q,S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,可得4S2=S3+3S1,a1=1,即4(1+q)=1+q+q2+3,q=3.∴a n=3n﹣1.故答案为:3n﹣1.点评:本题考查等差数列以及等比数列的应用,基本知识的考查.15.(5分)(2015•湖南)已知函数f(x)=若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是{a|a<0或a>1}.考点:函数的零点.专题:计算题;创新题型;函数的性质及应用.分析:由g(x)=f(x)﹣b有两个零点可得f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a的范围解答:解:∵g(x)=f(x)﹣b有两个零点,∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,由x3=x2可得,x=0或x=1①当a>1时,函数f(x)的图象如图所示,此时存在b,满足题意,故a>1满足题意②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意③当0<a<1时,函数f(x)单调递增,故不符合题意④a=0时,f(x)单调递增,故不符合题意⑤当a<0时,函数y=f(x)的图象如图所示,此时存在b使得,y=f(x)与y=b有两个交点综上可得,a<0或a>1故答案为:{a|a<0或a>1}点评:本题考察了函数的零点问题,渗透了转化思想,数形结合、分类讨论的数学思想.三、简答题,共1小题,共75分,16、17、18为选修题,任选两小题作答,如果全做,则按前两题计分选修4-1:几何证明选讲16.(6分)(2015•湖南)如图,在⊙O中,相较于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相较于点F,证明:(1)∠MEN+∠NOM=180°(2)FE•FN=FM•FO.考点:相似三角形的判定.专题:选作题;推理和证明.分析:(1)证明O,M,E,N四点共圆,即可证明∠MEN+∠NOM=180°(2)证明△FEM∽△FON,即可证明FE•FN=FM•FO.解答:证明:(1)∵N为CD的中点,∴ON⊥CD,∵M为AB的中点,∴OM⊥AB,在四边形OMEN中,∴∠OME+∠ONE=90°+90°=180°,∴O,M,E,N四点共圆,∴∠MEN+∠NOM=180°(2)在△FEM与△FON中,∠F=∠F,∠FME=∠FNO=90°,∴△FEM∽△FON,∴=∴FE•FN=FM•FO.点评:本题考查垂径定理,考查三角形相似的判定与应用,考查学生分析解决问题的能力,比较基础.选修4-4:坐标系与方程17.(6分)(2015•湖南)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.考点:参数方程化成普通方程;简单曲线的极坐标方程.专题:选作题;坐标系和参数方程.分析:(1)曲线的极坐标方程即ρ2=2ρcosθ,根据极坐标和直角坐标的互化公式得x2+y2=2x,即得它的直角坐标方程;(2)直线l的方程化为普通方程,利用切割线定理可得结论.解答:解:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x﹣1)2+y2=1;(2)直线l:(t为参数),普通方程为,(5,)在直线l上,过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,由切割线定理,可得|MT|2=|MA|•|MB|=18.点评:本题主要考查把极坐标方程化为直角坐标方程的方法,属于基础题.选修4-5:不等式选讲18.(2015•湖南)设a>0,b>0,且a+b=+.证明:(ⅰ)a+b≥2;(ⅱ)a2+a<2与b2+b<2不可能同时成立.考点:不等式的证明.专题:不等式的解法及应用.分析:(ⅰ)由a>0,b>0,结合条件可得ab=1,再由基本不等式,即可得证;(ⅱ)运用反证法证明.假设a2+a<2与b2+b<2可能同时成立.结合条件a>0,b >0,以及二次不等式的解法,可得0<a<1,且0<b<1,这与ab=1矛盾,即可得证.解答:证明:(ⅰ)由a>0,b>0,则a+b=+=,由于a+b>0,则ab=1,即有a+b≥2=2,当且仅当a=b取得等号.则a+b≥2;(ⅱ)假设a2+a<2与b2+b<2可能同时成立.由a2+a<2及a>0,可得0<a<1,由b2+b<2及b>0,可得0<b<1,这与ab=1矛盾.a2+a<2与b2+b<2不可能同时成立.点评:本题考查不等式的证明,主要考查基本不等式的运用和反证法证明不等式的方法,属于中档题.19.(2015•湖南)设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.考点:正弦定理.专题:解三角形.分析:(Ⅰ)由题意和正弦定理可得sinB=cosA,由角的范围和诱导公式可得;(Ⅱ)由题意可得A∈(0,),可得0<sinA<,化简可得sinA+sinC=﹣2(sinA ﹣)2+,由二次函数区间的最值可得.解答:解:(Ⅰ)由a=btanA和正弦定理可得==,∴sinB=cosA,即sinB=sin(+A)又B为钝角,∴+A∈(,π),∴B=+A,∴B﹣A=;(Ⅱ)由(Ⅰ)知C=π﹣(A+B)=π﹣(A++A)=﹣2A>0,∴A∈(0,),∴sinA+sinC=sinA+sin(﹣2A)=sinA+cos2A=sinA+1﹣2sin2A=﹣2(sinA﹣)2+,∵A∈(0,),∴0<sinA<,∴由二次函数可知<﹣2(sinA﹣)2+≤∴sinA+sinC的取值范围为(,]点评:本题考查正弦定理和三角函数公式的应用,涉及二次函数区间的最值,属基础题.20.(2015•湖南)某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望.考点:离散型随机变量的期望与方差;离散型随机变量及其分布列.专题:概率与统计.分析:(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件A2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},利用A1,A2相互独立,,互斥,B1,B2互斥,然后求出所求概率即可.(2)顾客抽奖1次可视为3次独立重复试验,判断X~B.求出概率,得到X的分布列,然后求解期望.解答:解:(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件A2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},由题意A1,A2相互独立,,互斥,B1,B2互斥,且B1=A1A2,B2=+,C=B1+B2,因为P(A1)=,P(A2)=,所以,P(B1)=P(A1)P(A2)==,P(B2)=P()+P()=+==,故所求概率为:P(C)=P(B1+B2)=P(B1)+P(B2)=.(2)顾客抽奖1次可视为3次独立重复试验,由(1)可知,顾客抽奖1次获一等奖的概率为:所以.X~B.于是,P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==.故X的分布列为:X 0 1 2 3PE(X)=3×=.点评:期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫,它在市场预测,经济统计,风险与决策等领域有着广泛的应用,为今后学习数学及相关学科产生深远的影响.21.(2015•湖南)如图,已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上.(1)若P是DD1的中点,证明:AB1⊥PQ;(2)若PQ∥平面ABB1A1,二面角P﹣QD﹣A的余弦值为,求四面体ADPQ的体积.考点:二面角的平面角及求法;直线与平面垂直的性质.专题:空间位置关系与距离;空间角;空间向量及应用.分析:(1)首先以A为原点,AB,AD,AA1所在直线分别为x,y,z轴,建立空间直角坐标系,求出一些点的坐标,Q在棱BC上,从而可设Q(6,y1,0),只需求即可;(2)设P(0,y2,z2),根据P在棱DD1上,从而由即可得到z2=12﹣2y2,从而表示点P坐标为P(0,y2,12﹣2y2).由PQ∥平面ABB1A1便知道与平面ABB1A1的法向量垂直,从而得出y1=y2,从而Q点坐标变成Q(6,y2,0),设平面PQD的法向量为,根据即可表示,平面AQD的一个法向量为,从而由即可求出y2,从而得出P点坐标,从而求出三棱锥P﹣AQD的高,而四面体ADPQ的体积等于三棱锥P﹣AQD的体积,从而求出四面体的体积.解答:解:根据已知条件知AB,AD,AA1三直线两两垂直,所以分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则:A(0,0,0),B(6,0,0),D(0,6,0),A1(0,0,6),B1(3,0,6),D1(0,3,6);Q在棱BC上,设Q(6,y1,0),0≤y1≤6;∴(1)证明:若P是DD1的中点,则P;∴,;∴;∴;∴AB1⊥PQ;(2)设P(0,y2,z2),y2,z2∈[0,6],P在棱DD1上;∴,0≤λ≤1;∴(0,y2﹣6,z2)=λ(0,﹣3,6);∴;∴z2=12﹣2y2;∴P(0,y2,12﹣2y2);∴;平面ABB1A1的一个法向量为;∵PQ∥平面ABB1A1;∴=6(y1﹣y2)=0;∴y1=y2;∴Q(6,y2,0);设平面PQD的法向量为,则:;∴,取z=1,则;又平面AQD的一个法向量为;又二面角P﹣QD﹣A的余弦值为;∴;解得y2=4,或y2=8(舍去);∴P(0,4,4);∴三棱锥P﹣ADQ的高为4,且;∴V四面体ADPQ=V三棱锥P﹣ADQ=.点评:考查建立空间直角坐标系,利用空间向量解决异面直线垂直及线面角问题的方法,共线向量基本定理,直线和平面平行时,直线和平面法向量的关系,平面法向量的概念,以及两平面法向量的夹角和平面二面角大小的关系,三棱锥的体积公式.22.(13分)(2015•湖南)已知抛物线C1:x2=4y的焦点F也是椭圆C2:+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2.(Ⅰ)求C2的方程;(Ⅱ)过点F的直线l与C1相交于A、B两点,与C2相交于C、D两点,且与同向.(ⅰ)若|AC|=|BD|,求直线l的斜率;(ⅱ)设C1在点A处的切线与x轴的交点为M,证明:直线l绕点F旋转时,△MFD总是钝角三角形.考点:直线与圆锥曲线的关系;椭圆的标准方程.专题:创新题型;圆锥曲线中的最值与范围问题.分析:(Ⅰ)根据两个曲线的焦点相同,得到a2﹣b2=1,再根据C1与C2的公共弦长为2,得到=1,解得即可求出;(Ⅱ)设出点的坐标,(ⅰ)根据向量的关系,得到(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,设直线l的方程,分别与C1,C2构成方程组,利用韦达定理,分别代入得到关于k的方程,解得即可;(ⅱ)根据导数的几何意义得到C1在点A处的切线方程,求出点M的坐标,利用向量的乘积∠AFM是锐角,问题得以证明.解答:解:(Ⅰ)抛物线C1:x2=4y的焦点F的坐标为(0,1),因为F也是椭圆C2的一个焦点,∴a2﹣b2=1,①,又C1与C2的公共弦长为2,C1与C2的都关于y轴对称,且C1的方程为x2=4y,由此易知C1与C2的公共点的坐标为(±,),所以=1,②,联立①②得a2=9,b2=8,故C2的方程为+=1.(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),A(x4,y4),(ⅰ)因为与同向,且|AC|=|BD|,所以=,从而x3﹣x1=x4﹣x2,即x1﹣x2=x3﹣x4,于是(x1+x2)2﹣4x1x2=(x3+x4)2﹣4x3x4,③设直线的斜率为k,则l的方程为y=kx+1,由,得x2﹣4kx﹣4=0,而x1,x2是这个方程的两根,所以x1+x2=4k,x1x2=﹣4,④由,得(9+8k2)x2+16kx﹣64=0,而x3,x4是这个方程的两根,所以x3+x4=,x3x4=﹣,⑤将④⑤代入③,得16(k2+1)=+,即16(k2+1)=,所以(9+8k2)2=16×9,解得k=±.(ⅱ)由x2=4y得y′=x,所以C1在点A处的切线方程为y﹣y1=x1(x﹣x1),即y=x1x﹣x12,令y=0,得x=x1,M(x1,0),所以=(x1,﹣1),而=(x1,y1﹣1),于是•=x12﹣y1+1=x12+1>0,因此∠AFM是锐角,从而∠MFD=180°﹣∠AFM是钝角,故直线l绕点F旋转时,△MFD总是钝角三角形.点评:本题考查了圆锥曲线的和直线的位置与关系,关键是联立方程,构造方程,利用韦达定理,以及向量的关系,得到关于k的方程,计算量大,属于难题.23.(13分)(2015•湖南)已知a>0,函数f(x)=e ax sinx(x∈[0,+∞]).记x n为f(x)的从小到大的第n(n∈N*)个极值点.证明:(Ⅰ)数列{f(x n)}是等比数列;(Ⅱ)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.考点:利用导数研究函数的极值;导数在最大值、最小值问题中的应用.专题:创新题型;导数的综合应用;等差数列与等比数列;不等式的解法及应用.分析:(Ⅰ)求出导数,运用两角和的正弦公式化简,求出导数为0的根,讨论根附近的导数的符号相反,即可得到极值点,求得极值,运用等比数列的定义即可得证;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a (nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),求出导数,求得最小值,由恒成立思想即可得证.解答:证明:(Ⅰ)f′(x)=e ax(asinx+cosx)=•e ax sin(x+φ),tanφ=,0<φ<,令f′(x)=0,由x≥0,x+φ=mπ,即x=mπ﹣φ,m∈N*,对k∈N,若(2k+1)π<x+φ<(2k+2)π,即(2k+1)π﹣φ<x<(2k+2)π﹣φ,则f′(x)<0,因此在((m﹣1)π,mπ﹣φ)和(mπ﹣φ,mπ)上f′(x)符号总相反.于是当x=nπ﹣φ,n∈N*,f(x)取得极值,所以x n=nπ﹣φ,n∈N*,此时f(x n)=e a(nπ﹣φ)sin(nπ﹣φ)=(﹣1)n+1e a(nπ﹣φ)sinφ,易知f(x n)≠0,而==﹣e aπ是常数,故数列{f(x n)}是首项为f(x1)=e a(π﹣φ)sinφ,公比为﹣e aπ的等比数列;(Ⅱ)由sinφ=,可得对一切n∈N*,x n<|f(x n)|恒成立.即为nπ﹣φ<e a(nπ﹣φ)恒成立⇔<,①设g(t)=(t>0),g′(t)=,当0<t<1时,g′(t)<0,g(t)递减,当t>1时,g′(t)>0,g(t)递增.t=1时,g(t)取得最小值,且为e.因此要使①恒成立,只需<g(1)=e,只需a>,当a=,tanφ==,且0<φ<,可得<φ<,于是π﹣φ<<,且当n≥2时,nπ﹣φ≥2π﹣φ>>,因此对n∈N*,ax n=≠1,即有g(ax n)>g(1)=e=,故①亦恒成立.综上可得,若a≥,则对一切n∈N*,x n<|f(x n)|恒成立.点评:本题考查导数的运用:求极值和单调区间,主要考查三角函数的导数和求值,同时考查等比数列的定义和通项公式的运用,考查不等式恒成立问题的证明,属于难题.。
