关键路径法--计算方法
14.2 关键路径法

概念
1
A 20
3
B 1
H 10
I 0
2
4
C 2
5
D 45
9
E
J
30
6
F 10
7
G 3
8
0
1、路径:从开始节点到终止节点的一条路,叫做一条路 径。 2、路径的长度:一条路径上各工序工期的和叫做路径的 长度。 3、关键路径:长度最长的那条路径叫做关键路径。 4、关键节点:关键路径上的每一件工作都叫做关键工作, 表示关键工作的两个节点叫做关键节点。 5、总工期:关键路径的长度就是工程的总工期。
5H
E 3
0
4
F 4
7
I 0
6
P136 习题答案
14D
G 3C
0
1
1
A 5
2
B 3
4
F
6D
7
2
4
1
H0
5
1
A 3
8
2
B 3
L
0
3
F 2
5
M 0
4
G 4
D 3
N 0
6 H
2
C 1
9
I 6
E 2
7
10
试列出从开始节点1到终止节点10的所有路径,指出
哪条是关键路径,并确定完成该工程的最短总工期。
(20d)
P133 练习
某项工程的流程图如下:
6
J
1C
1
A 1
3
0H
B 3
5E 1
0
4
D
2
7
G 3
I0
9
施工项目进度控制方法关键路径法

施工项目进度控制方法关键路径法一、背景介绍随着现代社会的发展,施工项目的规模和复杂程度日益增加,项目管理变得愈发重要。
项目进度控制作为项目管理的重要组成部分,是保障项目按时完工的关键。
而关键路径法则是一种经典的项目进度控制方法,已被广泛应用于各类施工项目中。
本文将从关键路径法的原理、应用步骤、优缺点以及案例分析等方面来探讨施工项目进度控制方法关键路径法。
二、关键路径法原理1.定义关键路径关键路径是指在项目中无法延误的一系列活动所构成的路径,其总时间就是整个项目的最短完成时间。
在关键路径上的任何活动的延误都会导致整个项目的延误。
因此,关键路径的确定是项目进度控制的关键。
2.计算关键路径关键路径法通过绘制网络计划图,标记各活动的起始时间、持续时间和结束时间,然后进行路径分析,找出整个项目中最长的路径就是关键路径。
在网络计划图中,还需要确定各活动间的依赖关系,以确保项目按序进行。
3.确定关键活动关键路径上的活动被称为关键活动,其完成时间决定了整个项目的完成时间。
因此,在项目实施过程中,需要特别关注关键活动,确保其顺利进行,以保证项目能够按时完工。
三、关键路径法应用步骤1.制定项目计划在项目启动之初,需要制定详细的项目计划,包括确定项目的目标和范围、分解项目任务、制定活动清单、确定活动持续时间等。
这些信息将作为关键路径法的输入数据。
2.绘制网络计划图根据制定的项目计划,将各活动按照其依赖关系绘制成网络计划图。
在图中标记各活动的持续时间和依赖关系,以便后续的路径分析。
3.分析关键路径利用网络计划图,进行路径分析,找出整个项目中最长的路径,即为关键路径。
同时确定关键路径上的关键活动,以便后续的项目进度控制。
4.编制进度计划根据关键路径上的关键活动,制定详细的进度计划,包括具体的活动开始时间、结束时间和完成时间等。
同时设置项目的里程碑,以便监控项目的整体进度。
5.实施进度控制在项目实施过程中,不断监控关键活动的进度,及时发现问题并进行调整。
关键路径计算、总时差、自由时差

关键路径计算、总时差、自由时差网络图中的关键路径、自由时差、总时差等相关的知识作为进度管理中非常重要的一个内容,是历年软考中必考的一个知识点,要求大家一定要掌握,关键路径是怎么计算的,最早开始,最早结束,最迟开始,最迟结束是怎么得来的,总时差的计算、自由时差的计算。
在2013年上半年的考试中就曾经考到了计算自由时差。
1. 关键路径是什么2. 总时差与自由时差的区别总时差是指在不延误项目完成日期或违反进度因素的前提下,某活动可以推迟的时间。
总时差=LS-ES=LF-EF自由时差是指在不影响紧后活动最早开始的情况下,当前活动可以推迟的时间。
自由时差=(后一活动)ES-(前一活动的)EF所以总时差影响总工期,自由时差影响紧后活动。
3. 如何计算ES,EF,LS,LF前推法来计算最早时间某一活动的最早开始时间(ES)=指向它的所有紧前活动的最早结束时间的最大值。
某一活动的最早结束时间(EF)=ES+T(作业时间)逆推法来计算最迟时间某一活动的最迟结束时间(LF)=指向它的所有紧后活动的最迟开始时间的最小值。
某一活动的最迟开始时间(LS)=LF-T(作业时间)4.计算关键路径的步骤1. 用有方向的线段标出各结点的紧前活动和紧后活动的关系,使之成为一个有方向的网络图(PDM)2. 用正推和逆推法计算出各个活动的ES,LS, EF, LF,并计算出各个活动的自由时差。
找出所有总时差为零或为负的活动,就是关键活动3. 关键路径上的活动持续时间决定了项目的工期,总和就是项目工期。
自由时差例子1:打比方你有个朋友坐晚上9点的火车去合肥到火车站发现忘带身份证了,打电话让你帮他送过去,为了不耽误他赶火车你必须在9点前将身份证交给他。
那么当你交给他身份证时的时间与晚上9点之间的差距就是自由时差把身份证交给他是紧前工作赶火车是紧后工作把身份证交给他不能影响他赶火车也就是紧前工作最早完成不能影响紧后工作最早开始。
例子2:是活动可以推迟,但是不影响后面活动按时开始的等待时间。
工程施工进度怎么算

工程施工进度是指工程施工过程中各个阶段的工作量、工作时间和相互关系。
在施工过程中,合理地安排施工进度可以使工程按照预定的时间、质量和成本完成。
那么,工程施工进度是怎么算的呢?工程施工进度的主要算法有两种:关键路径法和网络图法。
一、关键路径法关键路径法(Critical Path Method,简称CPM)是一种基于网络图的算法,用于计算工程项目的最短完成时间和各个活动的最早开始时间、最晚开始时间、最早完成时间和最晚完成时间。
1. 绘制网络图:首先,将工程中的各个活动用节点表示,将活动之间的依赖关系用箭头表示,形成一个有向无环图(DAG)。
2. 计算最早开始时间和最早完成时间:从网络图的起始节点开始,逐步向前计算每个节点的最早开始时间和最早完成时间。
计算方法是:最早开始时间等于其前一个节点的最早完成时间,最早完成时间等于最早开始时间加上该节点的持续时间。
3. 计算最晚开始时间和最晚完成时间:从网络图的终点节点开始,逐步向后计算每个节点的最晚开始时间和最晚完成时间。
计算方法是:最晚开始时间等于其后一个节点的最晚完成时间减去该节点的持续时间,最晚完成时间等于最晚开始时间加上该节点的持续时间。
4. 计算关键路径:关键路径是指工程中从起始节点到终点节点,总持续时间最长的路径。
在关键路径上的活动称为关键活动。
5. 调整施工进度:根据关键路径法计算出的结果,对关键活动进行调整,以保证工程按时完成。
二、网络图法网络图法(Activity on Node Method,简称AON)是一种基于活动与节点关系的算法,用于计算工程项目的最短完成时间和各个活动的最早开始时间、最晚开始时间、最早完成时间和最晚完成时间。
1. 绘制网络图:首先,将工程中的各个活动用节点表示,将活动之间的依赖关系用箭头表示,形成一个有向无环图(DAG)。
2. 计算最早开始时间和最早完成时间:从网络图的起始节点开始,逐步向前计算每个节点的最早开始时间和最早完成时间。
关键路径法tf计算方式

关键路径法tf计算方式关键路径法(Critical Path Method,简称CPM)是一种项目管理中常用的工具,用于确定项目中的关键路径和关键活动。
在CPM中,关键路径是指完成整个项目所需的最长时间路径,关键活动则是指影响项目完成时间的活动。
在计算关键路径时,需要计算每个活动的最早开始时间(Early Start,ES)、最晚开始时间(Late Start,LS)、最早完成时间(Early Finish,EF)和最晚完成时间(Late Finish,LF),以及活动的总浮时(Total Float,TF)。
1. 最早开始时间(Early Start,ES)最早开始时间是指一个活动可以开始的最早时间。
对于第一个活动来说,其最早开始时间为0;对于后续的活动,其最早开始时间取决于前驱活动的最早完成时间。
最早开始时间可以通过以下公式计算:ES = Max{EF(前驱活动)}2. 最晚开始时间(Late Start,LS)最晚开始时间是指一个活动必须开始的最晚时间,以不影响整个项目的完成时间。
对于最后一个活动来说,其最晚开始时间等于其最晚完成时间;对于其他活动,其最晚开始时间取决于后继活动的最晚开始时间。
最晚开始时间可以通过以下公式计算:LS = Min{LS(后继活动)} - 活动持续时间3. 最早完成时间(Early Finish,EF)最早完成时间是指一个活动可以完成的最早时间。
最早完成时间等于最早开始时间加上活动持续时间:EF = ES + 活动持续时间4. 最晚完成时间(Late Finish,LF)最晚完成时间是指一个活动必须完成的最晚时间,以不影响整个项目的完成时间。
对于最后一个活动来说,其最晚完成时间等于其最早完成时间;对于其他活动,其最晚完成时间取决于后继活动的最晚完成时间。
最晚完成时间可以通过以下公式计算:LF = Min{LF(后继活动)}5. 总浮时(Total Float,TF)总浮时是指一个活动可以延迟多久而不影响整个项目的完成时间。
5.3关键路径法——单代号网络计划时间参数的计算ppt课件

2 1、 系 统 转 换
Be th
2
54 56 47 49 -7
2 2、 准 备 实 施 报 告
Ja c k
1
58 59 49 50 -9
Hale Waihona Puke 10项目的开 始时间为 0
0
3
收集数据
1 Beth 3 -8 -5
0
4
可行性研究
2 Jack 4 -9 -5
4
5
准备问题
界定报告
3 Rose 1 -5 -4
5
10
26 28 评估
10 Cathy 2 17 19
28 30 准备系统 设计报告
11 Sharon 2 19 21
30 45
开发软件
12 Hannah 15 21 36 30 40 开发硬件
13 Joe 10 26 36 30 36
开发网络
14 Gerri 6 30 36
45 47 准备系统 开发报告
4
• 计算活动的总时差 TFi=LFi-EFi=LSi-ESi
• 计算相邻两项活动之间的时间间隔LAG 当终点节点为虚拟节点时,其时间间隔 为:
LAGi,n=Tp-EFi 其他节点之间的时间间隔为:
LAGi,j=ESj-EFi 5
• 计算工作的自由时差 FFn=Tp-EFn FFi=min{LAGi,j}
45 准备问题 界定报告
3 Rose 1 -5 -4
5 10 会晤用户
4 Jim 5 -4 1
10 15 明确用户要求
6 Jeff 5 16
5 13 研究现行系统
5 Steve 8 -2 6
15 16 准备系统 分析报告
建筑施工组织流水建筑施工的组织方式及工期计算

建筑施工组织流水建筑施工的组织方式及工期计算建筑施工组织流水是指在施工过程中,根据工程的具体要求和施工方法,进行合理的组织、安排和协调工程人力、材料、机械和施工工艺等各项资源,以达到施工质量、进度、安全和经济的目标。
下面将介绍建筑施工的组织方式以及工期计算的方法。
1.建筑施工的组织方式(1)功能线组织方式:功能线是指建筑施工中各项专业施工工序的组织线路,按照功能线组织,能够实现施工工序之间的连续、高效进行。
常见的功能线包括地下工程施工线、地上主体结构施工线、装饰装修施工线等。
这种组织方式适用于较大规模的建筑工程,可以提高施工效率和质量。
(2)作业区域组织方式:按作业区域进行施工组织,将施工现场划分为不同的工区,每个工区进行独立的施工作业。
这种组织方式适用于施工面积较大,工序繁多且相互干扰较大的项目。
通过划分作业区域可以有效控制施工过程中的施工质量和安全。
(3)模块化组织方式:将建筑工程划分为多个相对独立的模块,在施工过程中分别进行施工,最后组装起来。
这种组织方式适用于施工期限紧、施工环境受限等情况。
通过使用模块化组织方式可以提高施工速度和质量。
2.工期计算的方法在建筑施工中,工期计算是对施工活动的时间进行合理安排和控制的过程。
下面介绍两种常用的工期计算方法。
(1)关键路径法(CPM):关键路径法是一种通过网络图来计算工期的方法。
首先,将工程的各个施工工序进行排序,并根据工序之间的先后顺序确定各工序之间的节点关系和时间关系。
然后,根据这些节点和时间关系,画出一个网络图。
最后,通过计算出每个工序的最早开始时间和最晚完成时间,以及整个工程的最早开始时间和最晚完成时间,可以确定出关键路径,即工期最长的路径。
关键路径上的工序不能延误,否则将影响整个工程的工期。
(2)平均负荷法:平均负荷法是一种通过对施工活动的时间进行合理安排和分配的方法。
首先,将施工活动按工序进行排序,并确定每个工序的工期。
然后,根据施工活动的时序关系,将工序进行逐步安排,使得工作处于平衡状态,即在施工过程中各个工序的开始时间和结束时间都能最大限度地重叠。
关键路径法

关键路径法(CPM)一、关键路径法参数计算1.最早可以开始的时间(Earliest Start Time,ES)该活动如果有前序活动,那么需要等前序活动完成,它才能开始。
ES就是该活动最早可以开始的时间,取决于前序活动结束的时间。
2.活动历时(Duration,DU)活动历时是用类比法、专家判断法、三点估算法等方法估算出来的完成活动需要的持续的时间。
3.最早可以结束的时间(Earliest Finish Time,EF)我们用最早可以开始的时间(ES)加上活动历时(DU),就可以得到活动最早可以结束的时间(EF)。
EF=ES+DU4.最晚必须结束的时间(Latest Finish Time,LF)如果该活动有后序活动,而且受总工期制约,必须给后序活动留出足够的时间,那么该活动就必须在某个时间点完成,这个时间点就是最晚必须结束的时间。
5.最晚必须开始的时间(Latest Start Time,LS)我们用最晚必须结束的时间(LF)减去活动历时(DU),就可以得到该活动最晚必须开始的时间(LS)6.总浮动时间(Total Float,TF)总浮动时间是LF与EF之差,或者LS与ES之差,这两个差值相等。
总浮动时间反映的是在不影响总工期的前提下,该活动可以拖延的总时间。
●关键路径决定了项目的总工期●关键路径所需要的时间最长●关键路径上的浮动时间最少●活动延误可能导致关键路径变化二、项目的三种浮动时间1.自由浮动时间:不影响后续工作最早可以开始时间的前提下,这项工作可以拖延的时间叫自由浮动时间。
不影响别人。
2.总浮动时间:不影响项目总工期的前提下,活动可以拖延的总时间。
3.项目浮动时间:总工期计划上甲方主动给出的时间。
三、资源优化:1.资源平衡:数量有限,或过度分配,如一个资源在同一时段内分配两个或多个活动,就需要进行资源平衡,资源平衡往往导致关键路径改变。
2.资源平滑:对进度模型中的活动进行调整,从而使项目资源需求不超过预定的资源限制的一种技术,资源平滑不会改变项目关键路径,完工日期也不会延迟。
关键路径分析法
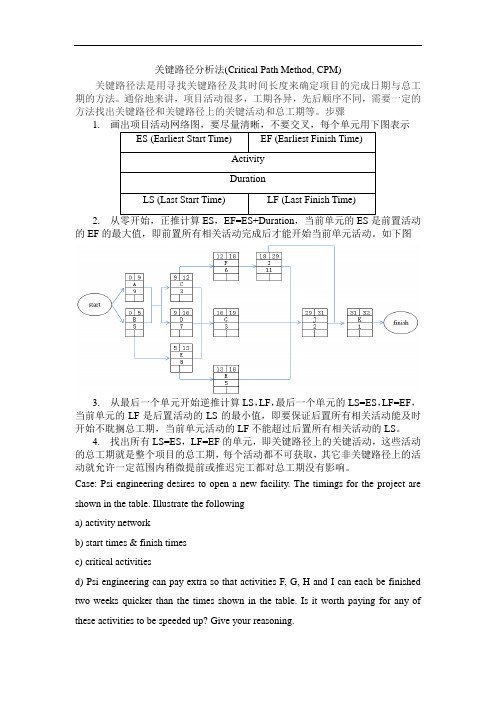
关键路径分析法(Critical Path Method, CPM)关键路径法是用寻找关键路径及其时间长度来确定项目的完成日期与总工期的方法。
通俗地来讲,项目活动很多,工期各异,先后顺序不同,需要一定的方法找出关键路径和关键路径上的关键活动和总工期等。
步骤1.2.的EF的最大值,即前置所有相关活动完成后才能开始当前单元活动。
如下图3.从最后一个单元开始逆推计算LS,LF,最后一个单元的LS=ES,LF=EF,当前单元的LF是后置活动的LS的最小值,即要保证后置所有相关活动能及时开始不耽搁总工期,当前单元活动的LF不能超过后置所有相关活动的LS。
4.找出所有LS=ES,LF=EF的单元,即关键路径上的关键活动,这些活动的总工期就是整个项目的总工期,每个活动都不可获取,其它非关键路径上的活动就允许一定范围内稍微提前或推迟完工都对总工期没有影响。
Case: Psi engineering desires to open a new facility. The timings for the project are shown in the table. Illustrate the followinga) activity networkb) start times & finish timesc) critical activitiesd) Psi engineering can pay extra so that activities F, G, H and I can each be finished two weeks quicker than the times shown in the table. Is it worth paying for any of these activities to be speeded up? Give your reasoning.Solution: a) activity network。
工期计算公式范文

工期计算公式范文工期是指完成一项工程项目所需的时间。
在工程管理中,工期的计算是非常重要的,它直接关系到项目的进度和时间成本。
下面是一些常用的工期计算公式。
1.网络计划法(PERT)工期计算公式PERT是一种常用的项目管理技术,它通过分析和评估项目的各项任务所需的时间,来计算整个项目的工期。
PERT工期计算公式如下:项目工期=最早开始时间+最后完成时间-1其中,最早开始时间是指每个活动的最早可以开始的时间,最后完成时间是指每个活动的最后要完成的时间。
2.关键路径法(CPM)工期计算公式CPM是一种常用的工程管理方法,它通过确定关键路径来计算项目的工期。
关键路径是指项目中最长的路径,它决定了整个项目的最短工期。
CPM工期计算公式如下:项目工期=关键路径上的活动时间之和关键路径上的活动时间之和是指关键路径上所有活动的持续时间之和。
3.时间网格法工期计算公式时间网格法是一种常用的工期计算方法,它通过将项目分为若干个时间段,来计算整个项目的工期。
时间网格法工期计算公式如下:项目工期=各阶段的活动时间之和其中,各阶段的活动时间之和是指每个时间段内所有活动的持续时间之和。
4.里程碑法工期计算公式里程碑法是一种常用的工期计算方法,它通过设置里程碑来计算项目的工期。
里程碑是项目中的重要节点,它代表了项目的关键事件。
里程碑法工期计算公式如下:项目工期=最后一个里程碑时间-第一个里程碑时间其中,最后一个里程碑时间是指最后一个里程碑的完成时间,第一个里程碑时间是指第一个里程碑的开始时间。
5.里程碑链法工期计算公式里程碑链法是一种常用的工期计算方法,它通过确定每个里程碑之间的依赖关系,来计算项目的工期。
里程碑链法工期计算公式如下:项目工期=各个里程碑之间的活动时间之和其中,各个里程碑之间的活动时间之和是指每个里程碑之间所有活动的持续时间之和。
这些工期计算公式可以根据具体的项目需求进行灵活运用。
在工程管理中,选择正确的计算方法以及合理的工期计算公式将对项目的进度和成本控制起到重要的作用。
PMP常考计算题之关键路径法

1.关键路径法关键路径法(Critical Path Methodology ,CPM):一种进度网络分析技术,用来确定项目进度网络中各条逻辑路径的灵活性大小(浮动时间大小),进而确定整个项目的最短工期。
从规定的开始日期开始,利用顺推计算法计算最早开始和完成日期。
从规定的完成日期(可能是顺推计算所得到的项目最早完成日期)开始,利用逆推计算法计算最晚开始和完成日期。
关键路径上可以有虚活动可能会有多条关键路径关键路径的总浮动时间为零或负数进度压缩只能在关键路径上压缩关键路径法不考虑任何资源限制活动的时间属性Activity Name ESEFDULFLSTF ES :最早开始时间LS :最晚开始时间TF :总浮动时间EF :最早结束时间LF :最晚结束时间DU :活动历时➢总浮动时间(Total Float ):是指一个活动在不影响整个项目结束时间或中间某个里程碑的情况下,可以延迟的时间总和。
公式:总浮动时间TF = 最晚开始时间LS -最早开始时间ES ;总浮动时间TF = 最晚结束时间LF -最早结束时间EF ➢自由浮动时间(Free Float ):是指一个活动在不影响其紧后活动最早开始时间的情况下,可以延迟的时间总和。
公式:自由浮动时间FF = 紧后最早开始时间ES -最早结束时间EF➢松弛量(Slack ):也称“浮动时间”。
Activity Name ES EF DU LFLSTF➢任意活动的最早开始时间,等于其所有前置活动的最早结束时间的最大值➢任意活动的最早结束时间,等于该活动的最早开始时间+ 该活动工期➢没有前置活动的,最早开始时间等于项目的开始时间✓从项目开始向后推✓取“大”原则✓多个前置活动存在时,取最长活动时间,可以计算项目的总工期取紧前活动的最大值EF=ES+DUActivity Name ESEFDULFLSTF ➢任意活动的最晚结束时间,等于其所有后续活动的最晚开始时间的最小值➢任意活动的最晚开始时间,等于该活动的最晚完成时间-该活动工期➢没有后续活动的,最晚结束时间等于项目的结束时间✓从项目结束向前推✓取“小”原则✓根据各活动的最晚完成时间和最晚开始时间,计算出自由浮动时间FF 和总浮动时间TF ,进而确定关键路径CP取紧后活动的最小值LS=LF-DU关键链法✓关键链法= 关键路径法+ 有限资源✓资源约束型进度计划经常改变项目的关键路径关键链法是一种根据有限的资源来调整项目进度计划的进度网络分析技术。
关键路线法(CPM)

规则:某项活动的最迟结束时间=该活动直接指向的所有活 动最迟开始时间的最早时间
3 工程项目管理规划
PERT图正向计算
正向计算 (自左向右,加法,取大值) 目的:计算最早时间 方法:根据逻辑关系 • 方向:从PERT图始端向终端计算 • 第一个任务的开始为项目开始时间 • 任务完成时间为开始时间加持续时间 • 后续任务开始时间根据前置任务的时间和搭接时 间而定
A/4
C/6
F/9
B/6
D/7
G/7
I/8
H/4
E/5
路径1:A-C-F-H:4+6+9+4=23天 路径2:A-C-G-I:4+6+7+8=25天 路径3:B-D-G-I:6+7+7+8=28天 路径4:B-D-F-H:6+7+9+4=26天 路径5:B-E-H:6+5+4=15天 关键路径 B3-工D程-项G目-管I理:规划6+7+7+8=28天
A/1
D/4
H/6
B/2
E/5
F/4
J/3
路 路径 径12::ABC/--3ED--HH--JJ G长/长6 度度==21++5I4/2++66++33==1164天天 路径3:C-G-I-J 长度=3+6+2+3=14天 由于关键路径是整个PERT图中最长的路径,故路
径2,即 B-E-H-J 是项目的关键路径
工程项目管理计算公式

1. 关键路径法(CPM)计算公式:(1)最早开始时间(ES):ES = 前导活动最早完成时间 + 本活动持续时间(2)最早结束时间(EF):EF = 前导活动最早完成时间 + 本活动持续时间(3)最迟开始时间(LS):LS = 后续活动最迟开始时间 - 本活动持续时间(4)最迟结束时间(LF):LF = 后续活动最迟结束时间 - 本活动持续时间(5)总时差(TF):TF = LS - ES 或 LF - EF(6)自由时差(FF):FF = 后续活动最早开始时间 - 本活动最早结束时间2. 投资回收期(Payback Period)计算公式:投资回收期 = 初始投资 / 年净现金流量3. 投资收益率(ROI)计算公式:投资收益率 = 年净收益 / 项目总投资4. 成本估算(Cost Estimate)计算公式:(1)类比估算:成本估算 = 类似项目成本× 指数(2)参数估算:成本估算 = 参数× 参数值5. 沟通渠道计算公式:沟通渠道数量= n × (n - 1) / 2其中,n 为项目干系人数量。
6. 三点估算法计算公式:(1)预期活动持续时间(Te):Te = (To + 4Tm +Tp) / 6(2)标准差(σ):σ = (Tp - To) / 6(3)方差(Var):Var = σ^27. 挣值分析(Earned Value Management, EVM)计算公式:(1)计划价值(PV):PV = 计划工作进度× 计划成本(2)实际成本(AC):AC = 实际完成工作进度× 实际成本(3)挣值(EV):EV = 实际完成工作进度× 计划成本(4)成本偏差(CV):CV = EV - AC(5)进度偏差(SV):SV = EV - PV8. 系统可用性(Availability)计算公式:系统可用性 = 可用时间 / 总时间× 100%其中,可用时间 = 平均无故障时间× (平均无故障时间 + 平均维修时间)9. 盈亏平衡分析计算公式:盈亏平衡点(BEP)= 固定成本 / (单价 - 可变成本)通过掌握这些工程项目管理计算公式,项目管理者可以更加科学、合理地制定项目计划,控制项目成本,确保项目按时、按质、按预算完成。
关键路径的计算方法及例题

关键路径的计算方法及例题摘要:一、关键路径的定义与作用二、关键路径的计算方法1.列出所有路径2.计算各路径的持续时间3.找出最长路径4.确定关键路径三、关键路径的应用场景四、例题解析五、总结与建议正文:一、关键路径的定义与作用关键路径是指在项目管理中,影响项目完成时间的关键任务序列。
它决定了项目整体的进度,一旦关键路径上的任务出现延误,整个项目的完成时间都会受到影响。
因此,识别和掌握关键路径对于项目管理者来说至关重要。
二、关键路径的计算方法1.列出所有路径:首先,我们需要将项目的所有任务进行排序,并确定它们之间的依赖关系,从而得出所有可能的路径。
2.计算各路径的持续时间:根据项目任务的顺序,计算每条路径的总持续时间。
这里需要注意的是,要考虑到任务之间的等待时间和缓冲时间。
3.找出最长路径:通过计算得到的各路径持续时间,找出最长的一条路径,这条路径就是关键路径。
4.确定关键路径:分析其他路径与最长路径的差异,找出对项目进度有最大影响的关键任务。
三、关键路径的应用场景关键路径法(Critical Path Method,CPM)主要用于以下场景:1.项目管理:通过分析项目进度,找出影响项目完成时间的关键任务,以便采取相应的措施进行优化。
2.生产调度:在制造业领域,关键路径法可以帮助企业优化生产计划,提高生产效率。
3.工程管理:在建筑、土木等领域,关键路径法有助于合理安排工程进度,降低项目风险。
四、例题解析以下是一个简单的关键路径例题:某项目包含四个任务,分别是A、B、C、D。
任务间的依赖关系如下:1.A -> B2.B -> C3.C -> D任务A的持续时间为10天,任务B的持续时间为8天,任务C的持续时间为6天,任务D的持续时间为4天。
根据上述信息,我们可以计算出各路径的持续时间:1.A->B->C->D:10+8+6+4=28天2.A->D:10+4=14天由此可知,关键路径为A->B->C->D,总持续时间为28天。
关键路径法(CriticalPathMethod,CPM)

关键路径法(CriticalPathMethod,CPM)1、活动节点描述及计算公式通过分析项⽬过程中哪个活动序列进度安排的总时差最少来预测项⽬⼯期的⽹络分析。
产⽣⽬的:为了解决,在庞⼤⽽复杂的项⽬中,如何合理⽽有效地组织⼈⼒、物⼒和财⼒,使之在有限资源下以最短的时间和最低的成本费⽤下完成整个项⽬。
关键路径是相对的,也可以是变化的。
关键路径可以有多条,关键路径上的活动时差为0。
活动节点图如下:ES:最早开始时间(Earliest Start),是指某项活动能够开始的最早时间,只决定于项⽬计划,只要计划的条件满⾜了就可以开始的时间。
EF:最早结束时间(Earliest Finish),是指某项活动能够完成的最早时间。
其中EF = ES+DU, DU为活动持续时间,顺推法先知道开始时间。
LF:最迟结束时间(Latest Finish),是指为了使项⽬在要求完⼯时间内完成,某项活动必须完成的最迟时间。
往往决定于相关⽅(客户或管理层)的限制。
LS:最迟开始时间(Latest Start),是指为了使项⽬在要求完⼯时间内完成,某项活动必须开始的最迟时间。
其中LS = LF -DU,DU为持续时间,逆推法先知道结束时间。
顺推法:1、任⼀活动的最早开始时间,等于所有前置活动的最早结束时间的最⼤者;2、任⼀活动的最早结束时间,等于该活动的最早开始时间 + 该活动⼯期 ;3、没有前置活动的,ES等于项⽬的开始时间。
EF = ES + DU逆推法:从⽹络图右侧开始,为每项活动制定最迟开始和最迟结束时间,进⾏到⽹络图开始(最左边)。
1、任⼀活动的最迟结束时间,等于所有后续活动的最迟开始时间的最⼩者;2、任⼀活动的最迟开始时间,等于该活动的最迟结束时间 - 该活动⼯期 ;3、没有后续活动的,LF等于项⽬的结束时间或者规定的时间。
LS = LF - DU总浮动时间:TF = LF – EF 或者 LS- ES,活动在TF之间推迟不影响总⼯期(注意如果超出该TF,则关键路径将发⽣变化),TF为0的路径为CP(关键路径)⾃由时差FF = 紧后ES - EF,活动在FF内推迟不影响紧后活动。
关键线路法网络图具有以下三个基本要素工作时间和线路

关键线路法网络图具有以下三个基本要素工作时间和线路1、最长线路法(也叫关键路径法)在关键线路法(CPM)中,线路上所有工作的持续时间总和称为总持续时间。
在所有线路中总持续时间最长的线路即为关键线路。
此法确定关键线路的步骤如下:1.计算各个线路的总持续时间寻找从始节点①至终节点⑥的所有线路并求其总历时①②④⑥t=1+2+5=8①②④⑤⑥t=1+2+3=6①②③④⑥t=1+3+6+5=15①②③④⑤⑥t=1+3+6+3=13①②③⑤⑥t=1+3+5+3=12①③④⑥t=5+6+5=16①③④⑤⑥t=5+6+3=14①③⑤⑥t=5+5+3=13注意:从上到下,从外向内逐条计算,防止漏掉个别路线进行时间对比,用时最长的线路为关键线路从以上八条线路中总持续时间,可以看出关键线路是①③④⑥总工期T=16。
2、利用关键工作确定关键线路在网络计划中,总时差值最小[]的工作为关键工作,关键工作从开始节点到终止节点的连线就是关键线路。
(当网络的计划工期等于计算工期时,总时差等于零的工作是关键工作,关键工作连线为关键线路。
)这种方法需要将各时间参数(最早开始时间ES:从起始节点开始自左向右逐项“求和取大”;最迟开始时间LS:从起始节点开始自右向左逐项“求差取小”;工作持续时间D:最早可能完工时间EF与最早可能开工时间ES之差或最迟必须完工LF时间与最迟必须开工LE时间之差。
)都算出来,所以较麻烦、费时多,只有当题目要求需要计算最早开始时间、最迟开始时间以及工作持续时间的情况下,在已有计算参数值的基础上,用此方法判断才方便。
这种方法的优点是可靠、不易出错、省心。
3、关键节点法在双代号网络计划中,关键线路上的节点称为关键节点。
关键节点的最迟时间LT与最早时间ET的差值最小。
关键工作两端的节点必为关键节点,但两端为关键节点的工作不一定是关键工作。
节点①②④⑤⑥都是关键节点但它们组成的线路并不是关键线路,而①②③④⑤⑥才是关键线路。
关键路线法(CPM)

起源:1957年美国杜邦公司和蓝德公司提出, 1958年3月首先用于建造化工厂,使计划提前 两个月完成。
适用于已有实际经验的项目,各活动所需作业 时间属于确定的。
确定关键路径的目的在于找出项目的总工期, 根据项目具体情况确定每个活动的ES、EF、 LS、LF
1
CHENLI
关键路径(critical path)
48 113 邮寄问卷并 获得反馈
9 Steve 65 40 105
50 55 测试软件 10 Andy 5 100 105
113 120
输入反馈 数据
11 Jim 7
105 112
120 128 128 138
分析结果
准备报告
12 Jim 8 13 Jim 10 112 120 120 130
要求完工时间: 130个工作日
8 Susan 2 14 98 100
38 40 准备邮寄 标签
5 Steve 2 38 40 38 48
打印问卷 调查表
6 Steve 10 30 40 38 50
开发数据 分析软件
7 Andy 12 88 100 38 40 设计软件 测试数据 8 Susan 2
98 100
市场调研项目网络图
1 写报告
2 6/16 6/17 6/16 6/17
2 审批
1 6/20 6/20 6/20 6/20
3 借款
3 6/21 6/23 6/21 6/23
4 借运输工具 1 6/21 6/21 6/23 6/23
5 采购
3 6/24 6/26 6/24 6/26
总时差
0 0 0 2 0
6
注:18、1C9H是EN休LI 息日
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关键路径法--计算方法关键路径法定义关键路径法(Critical Path Method, CPM)是一种基于数学计算的项目计划管理方法,是网络图计划方法的一种,属于肯定型的网络图。
关键路径法将项目分解成为多个独立的活动并确定每个活动的工期,然后用逻辑关系(结束-开始、结束-结束、开始-开始和开始结束)将活动连接,从而能够计算项目的工期、各个活动时间特点(最早最晚时间、时差)等。
在关键路径法的活动上加载资源后,还能够对项目的资源需求和分配进行分析。
关键路径法是现代项目管理中最重要的一种分析工具。
关键路径法的分类根据绘制方法的不同,关键路径法可以分为两种,即箭线图(ADM)和前导图(PDM)。
箭线图(ADM)法又称为双代号网络图法,它是以横线表示活动而以带编号的节点连接活动,活动间可以有一种逻辑关系,结束-开始型逻辑关系。
在箭线图中,有一些实际的逻辑关系无法表示,所以在箭线图中需要引入虚工作的概念。
绘制箭线图时主要有以下一些规则:1、在箭线图(ADM)中不能出现回路。
如上文所述,回路是逻辑上的错误,不符合实际的情况,而且会导致计算的死循环,所以这条规则是必须的要求。
2、箭线图(ADM)一般要求从左向右绘制。
这虽然不是必须的要求,但是符合人们阅读习惯,可以增加箭线图(ADM)的可读性。
3、每一个节点都要编号,号码不一定要连续,但是不能重复,且按照前后顺序不断增大。
这条规则有多方面的考虑,在手工绘图时,它能够增加图形的可读性和清晰性,另外,在使用计算机运行箭线图(ADM)这一条就非常重要,因为在计算机中一般通过计算节点的时间来确定各个活动的时间,所以节点编号不重复是必须的。
4、一般编号不能连续,并且要预留一定的间隔。
主要是为了在完成的箭线图(ADM)中可能需要增加活动,如果编号连续,新增加活动就不能满足编号由小到大的要求。
5、表示活动的线条不一定要带箭头,但是为了表示的方便,一般推荐使用箭头。
这一条主要是绘制箭线图(ADM)时可以增加箭线图(ADM)的可读性。
6、一般要求双代号网络图要开始于一个节点,并且结束于一个节点。
此要求可以在手工绘图增加可读性,而在计算机计算时,可以增加效率和结果的清晰性。
7、在绘制网络图时,一般要求连线不能相交,在相交无法避免时,可以采用过桥法或者指向法等方法避免混淆。
此要求主要是为了增加图形的可读性。
箭线图(ADM)要表示的是一个项目的计划,所以其清晰的逻辑关系和良好的可读性是非常重要的,除了箭线图(ADM)本身具有正确的逻辑性,良好的绘图习惯也是必要的。
因此在绘图时遵守上面的这些规则就是非常重要的,另外,在绘图时,一般尽量使用直线和折线,在不可避免的情况下可以使用斜线,但是要注意逻辑方向的清晰性。
前导图(PDM)法又称为单代号网络图法,它是以节点表示活动而以节点间的连线表示活动间的逻辑关系,活动间可以有四种逻辑关系,结束-开始、结束-结束、开始-开始和开始-结束。
关键路径法的起源关键路径法(CPM)最早出现于1956年,当时杜邦当时美国杜邦(Du Pont)公司拥有一台UNIVAC 1 计算机,他们使用这台计算机进行他们公司几乎所有的数据处理工作,但是仍然还有大量的剩余时间,杜邦(Du Pont)公司的管理层开始研究计算机在其它方面使用的可能性,因为当时电脑的费用是非常高昂的,他们考虑工程计划可能是应用电脑的一个方向。
他们联系了雷明顿兰德(Remington Rand)公司的Macuchy 博士,帮他们解决计算机使用的问题,后者派出了年轻的数学家James E. Kelly去协助杜邦(Du Pont)公司解决问题,杜邦公司方面的负责人是Morgan Walker。
他们要解决的问题是在工程项目中工期和费用之间的关系,他们研究的是如何能够采取正确的措施,在减少工期的情况下能尽可能少的增加费用。
1957年5月7日,在特拉华州内瓦克召开的一个会议正式确定开始新计划技术的开发。
Kelly借用了线性规划的概念来解决项目计划自动计算的问题,简单的说就是确定了每个活动的工期和活动间的逻辑关系,输入电脑后就能自动计算项目的工期,为了电脑的计算,Kelly在活动间使用了i,j这样的节点来表示活动间的前后逻辑关系。
当时遇到的一个问题是,杜邦公司的管理层并不理解Kelly所使用的方法,为了让其他人能够理解所使用方法的原理,Kelly就绘制了图形来解释电脑所作的工作,图形以箭线表示活动,以节点表示活动间的逻辑关系,这就是最早的箭线图(ADM)。
前面提到过,Kelly和Walker最初研究的目的是为了解决项目中工期和费用之间关系的问题,所以在Kelly和Walker最初提出的方法中,也包括费用的计划方法,其做法是,在每个活动上加载其相应的费用,从而得到整个项目的费用,就能分析与进度相关的费用问题,这种做法与现在所用的方法没有太大差别。
不过,在当时的情况下,项目收集费用并分解到各个活动上存在较大困难。
所以,在之后的很长时期内,关键路径法主要还是用于进度的计划和控制方面。
Kelly和Walker还提出了资源加载和分配的方法,当然也存在和费用分析一样的问题。
尽管存在这些问题,在1957年7月24日,他们已经做了一个简化的例子,称为”George Fischer Works”,这个计划包括了61条活动,其中有8个时间限制和16条虚工作。
在刚开发出这种方法时,他们将这种方法称为Kelly-Walker法,而计划中的关键线路,他们称之为主链路(Main chain)。
根据Kelly和Walker的论文和其它相关书籍的记载,当时他们一共进行了三个试验对Kelly-Walker法进行检验。
第一个试验是在1957年12月份,杜邦公司成立了一个测试小组对这种新的计划方法测试,有一个传统的计划组与他们同时独立对一个价值1000万美元的化学设备项目进行计划。
这个测试小组的成员没有参与Kelly-Walker法的开发,但是在开始测试之前,他们接受40个小时的培训。
此项目的计划从初步设计的完成开始,在编制计划时,他们首先将整个项目分解成一些较小的工作包,然后再将这些工作包最终分解成为活动,项目共有800条活动,其中包括400条施工活动,150条采购和设计活动。
根据记载,在此项目中显示出的Kelly-Walker法的最大优势在于,此项目在实施中出现了较大的变更,相对于传统计划方法,使用Kelly-Walker法更容易更新计划,其工作量仅有最初建立计划的10%,另外,在设计信息只有30%的情况下,能够比较准确的预测劳动力,还有就是能够比较准确的识别关键的采购工作。
1958年,他们进行了第二次试验,此试验所针对的是一个价值2000万美元的化学设备项目,根据Kelly 和Walker在1959年发表的论文,此次试验显示的最主要的优点是能够比较容易的包含设计部分的计划。
不过现在人们最常提及的一个试验是他们随后进行的维护设备的试验,在此项目中,他们使用Kelly-Walker法进行分析和计划,使得设备维护时间减少了25%。
1959年,Kelly和Walker共同发表了”Critical Path Planning and Scheduling” 论文,在这篇长达25页的论文中,Kelly和Walker不仅阐述了关键路径法的基本原理,还提出了资源分配与平衡,费用计划的方法。
我们今天所使用的方法的原理,与Kelly和Walker在论文中提出的方法,并没有原则上的不同。
不过随后关键路径法的发展并不是很顺利,杜邦公司开发此项技术的领导层更换之后,不再使用这项技术,而雷明顿兰德公司也认为这项技术没有太大前途。
对于关键路径法的发展起到重要作用的是Mauchly博士和Kelly随后成立的Mauchly合伙公司。
在60年代初期,在Kelly的带领下,此公司进行了大量的关键路径法的培训和推广工作。
与此同时,另外一个对关键路径法(CPM)的发展起到重要作用的是美国海军北极星计划开发的计划评审技术(PERT)。
在1955年11月17日,美国海军北极星计划成立了一个特别项目管理办公室(SPO),管理其Fleet Ballistic Missile计划,负责人是Admiral Raborn。
在1956年和1957年期间,他们研究了各种已经存在的项目管理技术,在大约1957年秋季的时候,他们接触到了杜邦公司开发的计划管理技术,这对他们开发PERT起到了重要的作用。
1958年1月份,SPO研究了在计算机上实现计划和控制的可行性,1958年1月27日,SPO正式成立了一个小组开发PERT技术,在大约一年以后,PERT技术成为一种可操作性的技术,计划评审技术(PERT)和关键路径法(CPM)基本上一样,唯一的区别是计划评审技术的每个活动的工期不是确定的,而是包括了悲观值,乐观值和最有可能值三个值。
比较有趣的是,1959年,北极星计划的这个特别项目管理办公室(SPO)开了一个招待会,介绍他们的这种新技术,并希望参会者能给出更多的意见,Kelly和Walker在被邀请之列,在会上,他们发现SPO开发的PERT和他们的Kelly-Walker法原理上完全一样,而SPO所说的关键线路(Critical Path),就是他们的Kelly-Walker法中的主链路(Main Chain)。
回去之后,他们决定将它们的方法的名称改为关键路径法(Critical Path Method)。
在60年代初期,PERT的发展比较迅速,据统计,到1964年,关于PERT的参考书目和论文达到了1000多种。
到1961年,各种基于PERT的类似的方法出现,如PERT/Cost, PERT-RAMPS(Resource Allocation & Multi-Project Schedule),MAPS,SCANS,TOPS,PEP,TRACE,LESS和PAR等。
其中PEP法是将甘特图的活动赋以逻辑关系,这是现在的计划软件一般采用的一种图形输出方法。
在1962年的时候,时任美国国防部长MacNamara在起草一项法令时,指出计划评审法和关键路径法同时并存的局面容易引起混淆,以后国防部的所有部门一律使用计划评审法(PERT),这在当时对于关键路径法的提倡者是一个重大打击,不过在随后的发展中,关键路径法(CPM)逐渐占了优势,现在真正使用计划评审法的其实已经很少。
而且即使是在当时,很多所谓的计划评审法(PERT),其实质其实是关键路径法(CPM)。
如美国航空局(NASA)当时使用的NASA-PERT,实际就是关键路径法(CPM)。
无论是关键路径法(CPM)还是计划评审法(PERT),最初使用的表示方法都是箭线法(ADM),在之后很长的一段时间箭线法(ADM)都是人们主要使用的方法,直到70年代以后,前导图(PDM)才开始逐渐流行起来,但是箭线法(ADM)仍然使用极为广泛。
