5.2.2 平行线的判定最新课件PPT
合集下载
5-2-2平行线的判定-七年级下册人教版数学课件

课堂练习
1.如图5.2-35,己知∠1=145°,∠2=145°,则AB∥CD,依据是 _同___位__角__相__等___,__两__直__线___平__行___.
图5.2-35
课堂练习
2.如图5.2-36 是一条街道的两个拐角,∠ABC与∠BCD均为140°,则 街道AB与CD的关系是_________,这是因___________________.
中考在线 考点:平行线的判定
【例1】如图5.2-27,下列说法错误的是( C ).
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
知识梳理
图5.2-27
【解析】根据平行线的判定进行判断:A.若a∥b,b∥c,则a∥c,利用了 平行公理,正确;B.若∠1=∠2,则a∥c,利用了内错角相等,两直线平行, 正确;C.∠3=∠2,不能判断b∥c,错误;D.若∠3+∠5=180°,则a∥c,利 用同旁内角互补,两直线平行,正确;故选C.
【答案】证明:∵AB⊥BC,BC⊥CD, ∴∠ABC=∠DCB=90°,∵∠1=∠2, ∴∠ABC-∠1=∠DCB-∠2, ∴∠CBE=∠BCF,∴BE∥CF.
图5.2-51
课后习题
9.如图5.2-52所示,已知∠1=50°,∠2=65°,CD平分∠ECF,则 CD∥FG.请说明理由.
图5.2-52
第5章 相交线与平行线
5.2.2 平行线的判定
教学新知
方法1:平行线的定义. 方法2:两条直线都与第三条直线平行,那么这两条直线也平行. 方法3:同位角相等,两直线平行. 方法4:内错角角相等,两直线平行. 方法5:同旁内角互补,两直线平行.
七年级数学5.2.2平行线的判定PPT课件
如图:B= D=45°, C=135°,
问图中有哪些直线平行?
A
D
答:AB//CD,AD//BC B
C
∵ B=45°(已知)
C=135°(已知) B+ C=180° AB//CD(同旁内角互补,两直线平行) 同理:AD//BC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
纸条,
(点阵中相邻的四个点构成正方形).
E
G
A
B
C
D
F
H
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
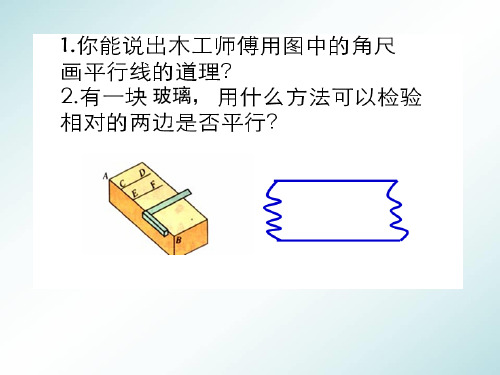
画平行线的事 实
同位角相等, 两直线平行。
同旁内角互补, 两直线平行。
内错角相等, 两直线平行。
判定方法3 两条直线被第三条直线所截,如果 同旁内角互补,那么这两条直线平行
简单说成:同旁内角互补,两直线平行
1a
几何语言: ∵∠1+∠4=1800(已知)
3
4
2b
∴a∥b(同旁内角互补,两直线平行)
想一想 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
简记为“垂直于同一直线的两直线平行”。
∵ a⊥b,a⊥c(已知) ∴ b//c(垂直于同一直线的两条直线平行)
a
1
c
2
b
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
七年级数学下册《5.2.2平行线的判定》课件

书 香
知道了...... 学会了......
1、课本P125 练习1、2 2、同步练习10.2(一)
如图:
(1) 和 是直线AB,BC被直线AC所截而得 到的 ____同__旁__内__角______
(2) 和 是直线AB,AC被直线BD 所截而得
到的_____同__位___角___________
是内错角。
与________
A
E1
D
3
2
B
4
F
C
(3) 与 是直线AB和直线AF被直线ED所截而
得到的___内__错___角。
A
E
2
B
(4)
1
D
3
4
F
C
识别同位角、内错角、同旁 内角步骤: 先抽取;看三线;找截线; 再判断。
和______是直线AB和直线AF被直线BC所截而得
的__同__位____角。
点?
A
E
21
34
B
65
D
图中还有其它同旁内角吗?C
7
8
F
讨论:
你能用什么符号来表示这三类角? 同位角: 内错角: 同旁内角:
两手的拇指和食指如何组合得 到同位角、内错角、同旁内角?
练一练
1、如图,找出图中的同位角、内错角、同旁内角
14
23
同位角: 65 7 8 内错角:
同旁内角:
2、如图:(1)________________是同位角。
E
2
1
34
B
6
5
7 F8
D
1.同位角
如图,∠4和∠8与截线及两条被截直线在位置上有什么特
七年级数学下册教学课件《5.2.2平行线的判定》

第3题图
第 4 题图
第 5 题图
5.如图,能判定 AB∥CD 的条件有___①①③③④④ ___.(填序号)
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
当堂检测
6.如图所示,∠B=∠C,∠DEF=∠A.试问CD与EF平行吗?为什么? 解:CD∥EF.理由:∵∠B=∠C,∴AB∥CD(内错角相等,两直线平行). ∵∠DEF=∠A,∴EF∥AB(同位角相等,两直线平行). ∴CD∥EF(平行于同一条直线的两条直线平行).
方法二:∵∠1+∠4=180°(平角定义), ∵∠1+∠2=180°(已知),∴∠2=∠4(同角的 补角相等),∴a∥b(内错角相等,两直线平行).
预习成果
1.如图1,∠C=60°,当∠ABE= 60° 时,就能使 BE∥CD.根据 同位角相等,两直线平行 . 2.如图2,∠1=120°,∠2=60°,问a与b的位置关系? 3.如图3,直线CD、EF被直线AB所截. (1)量得∠3=120°,∠4=120°,就可以判定 CD ∥ EF , 根据 内错角相等,两直线平行 . (2)量得∠1=60°,∠3=120°,就可以判定 CD ∥ EF , 根据 同旁内角互补,两直线平行 .
巩固例题
【例 2】如图,BE平分∠ABD,DE平分∠BDC,且 ∠1+∠2=90°. 求证:AB∥CD. 解:∵BE平分∠ABD,DE平分∠BDC(已知), ∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义). ∵∠1+∠2=90°, ∴∠ABD+∠BDC=2(∠1+∠2)=180°. ∴AB∥CD(同旁内角互补,两直线平行).
②当∠2+∠3=180°时,a∥b.证明: ∵∠2+∠4=180°,∠3+∠6=180°(平角定义), ∴∠2+∠4+∠3+∠6=360°,∵∠2+∠3=180° ∴∠4+∠6=180°∴a∥b(同旁内角互补,两直线平行).
5.2.2平行线的判定课件.ppt

德惠市第二十一中学 杜永旺
复习回顾:
一、判断:
1.在同一平面内不相交的两条直线叫做平行线.
2. 过直线外一点有且只有一条直线与已知直线平行.
3.平行的传递性:如果a∥b,b∥c,那么a∥c.
引入新课
在同一平面内不相交的两条直线是平行线, 你有办法测定两条直线是平行线吗?
平行线的画法:
“推平行线法”: 回忆所学
C
2.已知∠3=45 °,∠1与∠2互余,试说明 AB//CD ? 解:∵∠1=∠2(对顶角相等) ∠1+∠2=90°(已知)
3 2 A 1 C
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
B
D
∴ AB∥CD(内错角相等,两直线平行)
3. 如图:已知 ∠1=75 , ∠2 =105
o
一、放 二、靠 三、推 四、画
探索新知
1 (1)画图过程中, 什么角始终保持相等? 同位角相等 ∠1=∠2
(2)直线a,b位置关系
a
2
c a 2 c b
b
如何? 两直线平行 a∥b
1
要判断直线a //b,你有办法了吗? 平行线的判定方法一 c
两条直线被第三条直线所截,如果同 位角相等,那么两直线平行。 简单说成: 同位角相等,两直线平行。 如图: 【符号语言】
C 3 1 A 2
(第2题)
D
M
A
B
D
E
(第3题)
C
B
N
2.如图,AD平分∠BAC, ∠1=∠3,
能推出AB∥CD吗?说明理由。 3.如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B, 那么DE∥MN吗?为什么?
复习回顾:
一、判断:
1.在同一平面内不相交的两条直线叫做平行线.
2. 过直线外一点有且只有一条直线与已知直线平行.
3.平行的传递性:如果a∥b,b∥c,那么a∥c.
引入新课
在同一平面内不相交的两条直线是平行线, 你有办法测定两条直线是平行线吗?
平行线的画法:
“推平行线法”: 回忆所学
C
2.已知∠3=45 °,∠1与∠2互余,试说明 AB//CD ? 解:∵∠1=∠2(对顶角相等) ∠1+∠2=90°(已知)
3 2 A 1 C
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
B
D
∴ AB∥CD(内错角相等,两直线平行)
3. 如图:已知 ∠1=75 , ∠2 =105
o
一、放 二、靠 三、推 四、画
探索新知
1 (1)画图过程中, 什么角始终保持相等? 同位角相等 ∠1=∠2
(2)直线a,b位置关系
a
2
c a 2 c b
b
如何? 两直线平行 a∥b
1
要判断直线a //b,你有办法了吗? 平行线的判定方法一 c
两条直线被第三条直线所截,如果同 位角相等,那么两直线平行。 简单说成: 同位角相等,两直线平行。 如图: 【符号语言】
C 3 1 A 2
(第2题)
D
M
A
B
D
E
(第3题)
C
B
N
2.如图,AD平分∠BAC, ∠1=∠3,
能推出AB∥CD吗?说明理由。 3.如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B, 那么DE∥MN吗?为什么?
人教版数学七年级下册 5.2.2 平行线的判定 课件

为什么?
解:直线与平行. 理由如下:
∵∠1 + ∠ = 180°, ∠1 + ∠ = 180°,
∴∠ = ∠.
∵∠ = ∠,
∴∠ = ∠.
∴∥(同位角相等,两直线平行).
【例题2】如图,∠ + ∠ = 180°,∠ = ∠,试说明∥.
∥
∥
∥
∠ + ∠ = ∠
∠ = ∠ − ∠
∠ = ∠
∠ = ∠ − ∠ = ∠
【例题3】如图,∠ + ∠ = ∠,试说明∥.
解: 如图,作∠ = ∠.
∵∠ = ∠
∴∥.
又∵∠ + ∠ = ∠,
解: ∵∠1=∠2, ∴AB∥CD.
∵∠3+∠4=180°,∴CD∥EF,
∴AB∥EF.
3.如图,B、A、E三点在同一直线上,请你添加一个条件,使AD∥BC.你
∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180°
所添加的条件是___________________________________________(不允许添加
任何辅助线).
4.如图,下列条件不能判断直线a∥b的是( D
).
A. ∠1=∠4 B. ∠3=∠5 C. ∠2+∠5=180° D. ∠2+∠4=180°
平行线的判定方法
1. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
2. 同位角相等,两直线平行.
3. 内错角相等,两直线平行.
4. 同旁内角互补,两直线平行.
∠1 = ∠2
∥
判定方法2
线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直
《平行线的判定》_精品课件

还记得如何用三角板和直尺画平行线吗?
一放、二靠、三推、四画。
C
·P
1
D
A
B
2
从画图过程,三角板起到什么作用?
E3
A
B
C
7
D
F
两条直线被第三条直线所截, 如果同位角相等,那么这两条直线平行.
简单地说: 同位角相等 ,两直线平行.
两直线平行的判定(1):
两条直线被第三条直线所截,如果同位角
相等,那么两直线平行。 简单地说:
由此你能发现判定两直线平行的方法吗? B
判定两条直线平行的方法有两种:
定义:在同一平面内,不相交的两条直线叫平行线。 平行公理的推论(平行线的传递性):
如果两条直线同平行于一条直线,那么两条 直线平行。
同学们想一想:
除应用以上两种方法以外,是否还有其它方法呢?
过直线AB外一点P作直线AB的平行线 CD,看看你能作出吗?能作出几条?
平行线的判定
例2
① ∵ ∠1 =__∠__2_(已知)
CF
E
∴ AB∥CE( 内错角相等,两直线平行 ) 1 3
② ∵ ∠1 +__∠__3_=180o(已知)
∠1 =∠3(同角的补角相等). A
B
AB∥CD(内错角相等,两直线平行).
F
【获奖课件ppt】《平行线的判定》_ 精品课 件1-课 件分析 下载
如图,已知∠1+∠2=180°,AB与 CD平行吗?为什么?
E
∠1 +∠2=180°(已知), C
D
∠2 +∠3=180°(邻补角互补),
∠1 =∠3(同角的补角相等). A
同位角相等,两直线平行。
一放、二靠、三推、四画。
C
·P
1
D
A
B
2
从画图过程,三角板起到什么作用?
E3
A
B
C
7
D
F
两条直线被第三条直线所截, 如果同位角相等,那么这两条直线平行.
简单地说: 同位角相等 ,两直线平行.
两直线平行的判定(1):
两条直线被第三条直线所截,如果同位角
相等,那么两直线平行。 简单地说:
由此你能发现判定两直线平行的方法吗? B
判定两条直线平行的方法有两种:
定义:在同一平面内,不相交的两条直线叫平行线。 平行公理的推论(平行线的传递性):
如果两条直线同平行于一条直线,那么两条 直线平行。
同学们想一想:
除应用以上两种方法以外,是否还有其它方法呢?
过直线AB外一点P作直线AB的平行线 CD,看看你能作出吗?能作出几条?
平行线的判定
例2
① ∵ ∠1 =__∠__2_(已知)
CF
E
∴ AB∥CE( 内错角相等,两直线平行 ) 1 3
② ∵ ∠1 +__∠__3_=180o(已知)
∠1 =∠3(同角的补角相等). A
B
AB∥CD(内错角相等,两直线平行).
F
【获奖课件ppt】《平行线的判定》_ 精品课 件1-课 件分析 下载
如图,已知∠1+∠2=180°,AB与 CD平行吗?为什么?
E
∠1 +∠2=180°(已知), C
D
∠2 +∠3=180°(邻补角互补),
∠1 =∠3(同角的补角相等). A
同位角相等,两直线平行。
(新人教版)七年级数学下册:5.2.2《平行线的判定》教学课件PPT

【答案】平行
5.2.2直线平行的条件
1.如图5-41,点E在CD上,点F在BA上,G是AD延长线上一点. (1)若∠A=∠1,则可判断__C__D___∥__A__B___,因为 ___同__位__角__相__等__,_两__直__线__平__行___. (2)若∠1=∠____C_____,则可判断 AG∥BC,因为_内__错__角__相__等__,__两__直__线__平__行. (3)若∠2+ ∠__E__F_B__=180°,则可判 断CD∥AB,因为_同__旁__内__角__互__补__,_两__直__线_ 平行
5.2.2直线平行的条件
【例3】如图3,E是AB上的一点.
(1)知道了∠DEC=∠ADE,可以判定哪两条直线平行?为 什么?
(2)知道了∠AEC+∠DCE=180°,
可以判定哪两条直线平行?为什么? D
C
(3)知道了∠AED=∠B,可以判定 哪两条直线平行?为什么?
A
E
B
【解答】(1)AD∥CE,内错角相等,两直线平行;
方法2:两条直线被第三条直线所截,如果内错角相等,那么 这两条直线平行.(简称:内错角相等,两直线平行.)
5.2.2直线平行的条件
问题:在图4中,如果同旁内角∠2+∠4=180°,那么a,b 平行吗? 解∵∠2+∠4=180°(已知) 又∵∠1+∠4=180°(邻补角的定义)
∴∠1=∠2(同角的补角相等) ∴a∥b (同位角相等,两直线平行) 方法3: 两条直线被第三条直线所截,如果同旁内角互补,那 么这两条直线平行.(简称:同旁内角互补,两直线平行.)
4.如图5-44,直线AB、CD被直线EF所截,使
∠1=∠2≠90°,则( D )
5第五章5.2.2平行线的判定精品PPT课件

定a//b 吗?
c
解:能, 因为1+2=180°
3 a
1
1+3=180° 所以 2=3
2
b
所以 a//b
平行线的判定三:
两条直线被第三条直线所截,如果同旁内角互补, 那么这两条直线平行. 简单说成:同旁内角互补,两直线平行.
同旁内角互补,两直线平行
如图,BE平分∠ABD,DE平分∠BDC, ∠1+∠2=90°,试问AB∥CD吗?为什么? 解析:因为BE平分∠ABD,DE平分∠BDC, 所以∠ABD=2∠1,∠CDB=2∠2, 所以∠ABD+∠CDB=2(∠1+∠2), 又∠1+∠2=90°, 所以∠ABD+∠CDB=180°, 所以AB∥CD.
5.2.2 平行线的判定
复习回顾:
一、判断:
1.两条直线不相交,就叫平行线.
2.与一条直线平行的直线只有一条.
c a 3.如果直线 、b 都和 平行,
那么 a 、b 就平行.
二、如何用直尺和三角 板过直线AB外一点P作 AB 的平行线CD。
平行线的画法:
(1)放 (2)靠 (3)推 (4)画
引入新课
平行线的判定二 两条直线被第三条直线所截,如果内错角相等, 那么这两条直线平行. 简单说成:内错角相等,两直线平行.
内错角相等,两直线平行
如图,∠1=∠3,∠1=∠2,那么DE与BC 有怎样的位置关系?为什么?
解析:DE∥BC. ∵∠1=∠2,∠1=∠3, ∴∠2=∠3, ∴DE∥BC(内错角相等,两直线平行)
1.如图,直线AB、CD被直线EF所截.若∠1=50°,当 ∠2= 50°时,AB∥CD.
2.如图,∠2=3∠1,且∠1+∠3=90°,试说明 AB∥CD. 解:因为∠2=3∠1, 又∠2+∠1=180°, 所以∠1=45°, 因为∠1+∠3=90°, 所以∠3=45°, 所以∠1=∠3, 所以AB∥CD
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①同位角相等,两直线平行 ②内错角相等,两直线平行 ③同旁内角互补,两直线平行
作业:同步练习册5.2 (二)(三)
④同一平面内,垂直于同一直线的两直线平行
⑤平行于同一直线的两直线平行
• 努力,未来老婆的婚纱都是租的。只有你的笑才能让你在无尽黑暗中找到光明。我受过的伤都是我的勋章。知世故而不 世故,是最善良的成熟。愿你早日领教过这世界深深的恶意,然后开启爱他吗谁谁的快意人生。第二名就意味着你是头 号输家——科比·布莱恩特。当你感觉累的时候,你正在走上坡路。如果每个人都理解你,那你得普通成什么样。赚钱的 速度一定要超过父母变老的速度。不断地发现以前的自己是个傻逼的过程,就是成长。脾气永远不要大于本事。你那能 叫活着么?你那“你如今的气质里,藏着你走过的路,读过的书,和爱过的人。”素质是家教的问题,和未成年没关系。 总会有人是第一,那为什么不能是我?你可以没钱没颜,但你不可以不努力。如果今天我取得了成功,一定是昨天我拼 上了全部努力。阳光里做个孩子风雨里做个大人。枯木逢春犹再发,人无两度再少年世界那么大,我要赚钱带父母去看 看人情世故要看透,赤子之心不能丢。所有的人都在努力,不是只有你受尽委屈爱情可以没有物质,但生活不行你才二 十岁,你可以成为任何想成为的人。人生就像一杯茶,不会苦一辈子,但总会苦一阵子。中学时候本子上写的一句话: 想看日出的人,必须守到拂晓。对人只说三分话,不可全抛一片心。看到的不要全信,知道的不要都说。我20岁,没有 什么输不起,也没有什么不敢赢,致所有20岁和即将20岁的我们。小时候觉得这个世界不公平,后来发现这个世界就是 不公平,但不公平是好事情,它会让你更努力……成熟不是心变老而且泪在打转还在笑。越努力,越幸运。牛羊才会成 群,狮虎只会独行。智者寡言”越来越懂这句话了我只负责精彩,上天自有安排。你凭什么不努力有什么都想要。不要 到处宣扬自己的内心,这世上不止你一个人有故事。既然选择了远方,便只顾风雨兼程。你有多自律,就有多自由。我 喜欢海,可我不能跳海;我喜欢你,可我不能一直不要脸。提高一分,干掉千人。一生不喜与人抢,但得到的也不会让。 一百张嘴里一百个我,我是天使但也是恶魔。你要记得,只有你的笑才能让你在无尽黑暗中找到光明。一时的忍耐是为 了更广阔的自由,一时的纪律约束是为了更大的成功。越是复杂的人,对简单越有特殊的需求;越是自己内心肮脏的人, 越喜欢纯净的东西。过于欣赏自己,就发现不了别人的优点;过于赞赏别人的优点,就会看不见自己的长处。失去金钱 的人损失甚少,失去健康的人损失极多,失去勇气的人损失一切。谎言容易越说越爽,因为谎言比现实要美好,但是谎 言像多米诺骨牌一样,说一个慌要十个谎来圆,最后难以自拔。有些烦恼,只有你丢掉了,才有云淡风轻的机会每个人 心中所希望的,与最终所抵达的,都会有一段距离,这才是生活。成功不是将来才有的,而是从决定去做的那一刻起, 持续累积而成。财富是猫的尾巴,只要勇往直前,财富就会悄悄跟在后面。不要说没体力,不要说对手肘子硬,不要说 球太滑,你只需做好基本功。就算对手难缠,就算他小动作多,就算他嘴里不干净,你只需做好基本功。创业前的准备, 创业过程中的坚持都至关重要。当别人开始说你是疯子的时候,你离成功就不远了……当你感到悲哀痛苦时,最好是去 学些什么东西。学习会使你永远立于不败之地。等待的方法有两种:一种是什么事也不做空等,一种是一边等一边把事 业向前推动。互联网上失败一定是自己造成的,要不就是脑子发热,要不就是脑子不热,太冷了。含泪播种的人一定能 含笑收获。关于人的因素:这点相当重要。不管是蒙是骗还是软硬兼施,都一定要保证公司员工的相对稳定性。人员流 失就像放血,开始没什么感觉,却会要你的命。地球是运动的,一个人不会永远处在倒霉的位置。工作上的执着实际上 是人的一种意志。登高莫问顶,途中耳目新。最困难的时候,也就是我们离成功不远的时候。不屈不挠的奋斗是取得胜 利的唯一道路。我们都有兽性的一面,作为人类,我们的责任是成为驯兽师那样的人。勇敢,世界就会让步。如果有时 候你被它打败了,不断地勇敢再勇敢,它就会屈服。最高的圣德便是为旁人着想。我应当生活得仿佛自己的生命是为别 人的利益而存在。世界上能为别人减轻负担的都不是庸庸碌碌之徒。从错误中比从混乱中易于发现真理。我们有时从错 误中学到的东西,可能比从美德中学到的还要多。在生活中示曾做过任何傻事的人,决不象他自己想象得那么聪明。人 的思想是了不起的,只要专注于某一项事业,就一定会做出使自己感到吃惊的成绩来。没有播种,何来收获;没有辛劳, 何来成功;没有磨难,何来荣耀;没有挫折,何来辉煌。天行健,君子以自强不息;地势坤,君子以厚德载物。过去属 于死神,现在属于自己。伟大的事业是根源于坚韧不断地工作,以全副精神去从事,不避艰苦。书山有路勤为径,学海 无崖苦作舟。有志者,事竟成。我们比较容易承认行为上的错误、过失和缺点,而对于思想上的错误、过失和缺点则不 然。每个人都有错,但只有愚者才会执迷不悟。不经一翻彻骨寒,怎得梅花扑鼻香。所有的科学都是错误先真理而生, 错误在先比错误在后好。意志坚强的乐观主义者用“世上无难事”人生观来思考问题,越是遭受悲剧打击,越是表现得 坚强。一时的失误不会毁掉一个性格坚强的人。如果我们把每个人的不幸堆一堆由大家均分,大多数人都甘愿接受一份, 欣然离去。在世界的前进中起作用的不是我们的才能,而是我们如何运用才能。困难只能吓倒懦夫、懒汉,而胜利永远 属于攀登高峰的人。除了我们自己以外,没有人能贬低我们。如果我们坚强,就没有什么不良影响能够打败我们。包含
∴a∥b
2
随堂练习1:已知直线a,b被l所截,如图,∠1=50°,∠2=
50°,试判断直线a与b是否平行.并说明理由.
l
1
2
a
∵ ∠1=50°,∠2=50° (已知)
b
∴ a∥b(同位角相等,两直线平行)
2
随堂练习2:已知直线a,b被l所截,如图,∠1=45°,∠2=
135°,试判断直线a与b是否平行.并说明理由.AD与B来自平行吗?D AB
C
12
如图,在同一平面内,直线CD、EF均与直线AB垂直, D、F为垂足。试判断CD与EF是否平行。
平行线判定方法四:
在同一平面内,垂
直于同一直线的两 直线平行
A
CE
DF
B
3
1.在下列解答中,填上适当的理由:
(1)∵∠B=∠1(已知) ∴AD∥BC( (2)∵∠D=∠1(已知)
)
1 A
D
∴AB∥CD(
)
B
C
3
2.在下列解答中,填空: (1)∵∠BAD+∠ABC=180°(已知) ∴( )∥( )(同旁内角互补,两直线 平行 ) (2)∵∠BCD+∠ABC=180°(已知) ∴( )∥( )(同旁内角互补,两直线 平行 )
A
D
B
C
34
谈谈本节课你有哪些收获。
一、平行线判定的五种方法 二、推理格式的规范书写
5.2.2 平行线的判定
学习目标: • 能灵活运用平行线的三个判定方法解决简单
问题 • 初步应用推理格式解答问题
1
(1)平面内两条直线的位置关系有几种? (2)怎样过已知直线外一点画已知直线的平行线?
一放,二靠,三推,四画
12
平行线判定方 法一:同位角 相等,两直线 平行
1·
b
a 2
l
符号表示:∵∠1=∠2
错
2
已知直线a,b被l所截,如图,∠2=∠3,试判断直线a与b是否平
行.并说明理由.
l
∵ ∠2=∠3, ∠1与∠3是对顶角(已知)
∴∠1=∠3(对顶角相等)
∴ ∠1=∠2 (等量代换) ∴ a∥b (同位角相等,两直线平行)
3
1
2
a
b
2
平行线判定方法二:内错角相 等,两直线平行
符号表示:∵∠2=∠3 ∴a∥b
l
3
1
2
a
b
12
已知直线a,b被l所截,如图,∠1=110°,∠2=70°。试判断a与 b是否平行.并说明理由.
平行线判定方法三:同旁内角 互补,两直线平行
符号表示:∵∠1+∠2=180° ∴a∥b
a
1 2
3
b
l
2
教材P172读一读
演绎 推理
推理
归纳 推理
一般 特殊 特殊 一般
12
例2:在四边形ABCD中,∠B=50°,∠C=130°,AB与CD平行吗?
l
2
∵ ∠2+∠3=180°
3
∠2=135°(已知)
∴∠3=180°-∠2=45°(等式的性质)
1 a
b
∵∠1=45°(已知) ∴∠1=∠3 (等量代换)
∴a∥b(同位角相等,两直线平行)
2
判断下列说法是否正确: (1)∠1=45°,∠2=45°,所以∠1=∠2,理由是等式的性质 错 (2)∠1=45°,∠2=50°,所以∠1+∠2=95°,理由是等式的性质 (3)对∠a=∠c,∠b=∠c,所以∠a=∠b,理由是等量代换 (4)∠AOB=60°,所以2∠AOB=2x60°=120°,理由是等量代对换
