微积分基本公式
高等数学微积分公式

高等数学微积分公式高等数学微积分公式微积分是数学中的一个重要分支,它研究的是函数的变化规律。
在微积分的学习中,我们需要掌握许多公式,在处理函数的变化过程中起到了非常重要的作用。
下面是高等数学中常见的微积分公式。
一、导数公式1.常数函数的导数公式:\[\frac{d}{dx} C=0\]其中C为常数。
2.幂函数的导数公式:\[\frac{d}{dx} x^{n}=nx^{n-1}\]其中n为常数。
3.自然指数函数的导数公式:\[\frac{d}{dx} e^{x}=e^{x}\]4.对数函数的导数公式:\[\frac{d}{dx} ln(x)=\frac{1}{x}\]5.三角函数的导数公式:\[\frac{d}{dx} sin(x)=cos(x)\]\[\frac{d}{dx} cos(x)=-sin(x)\]6.反三角函数的导数公式:\[\frac{d}{dx} sin^{-1}(x)=\frac{1}{\sqrt{1-x^{2}}}\] \[\frac{d}{dx} cos^{-1}(x)=-\frac{1}{\sqrt{1-x^{2}}}\]7.复合函数的导数公式(链式法则):设y=f(u)和u=g(x),则有\[\frac{dy}{dx}=\frac{dy}{du}\times \frac{du}{dx}\]二、微分公式1.常数函数的微分公式:\[d(C)=0\]其中C为常数。
2.幂函数的微分公式:\[d(x^{n})=nx^{n-1}dx\]其中n为常数。
3.指数函数的微分公式:\[d(e^{x})=e^{x}dx\]4.三角函数的微分公式:\[d(sin(x))=cos(x)dx\]\[d(cos(x))=-sin(x)dx\]5.反三角函数的微分公式:\[d(sin^{-1}(x))=\frac{dx}{\sqrt{1-x^{2}}}\]\[d(cos^{-1}(x))=-\frac{dx}{\sqrt{1-x^{2}}}\]6.复合函数的微分公式(链式法则):设y=f(u)和u=g(x),则有\[dy=\frac{dy}{du}\times du\]三、泰勒公式泰勒公式是微积分中的一个重要定理,它可以将一个函数在某点的值表示为一系列关于该点的导数的和。
微积分基本公式与计算

微积分基本公式与计算微积分是数学的一个分支,主要研究函数的极限、导数、积分等基本概念和基本运算法则。
本文将介绍微积分的基本公式和计算方法。
1.极限:极限是微积分的基本概念之一,用来描述函数在特定点处的趋势。
极限的计算有以下几个基本公式:-基本极限公式:- $\lim_{x\to c} x = c$:常数函数的极限是其本身。
- $\lim_{x\to c} k f(x) = k \lim_{x\to c} f(x)$:常数倍法则。
- $\lim_{x\to c} (f(x) + g(x)) = \lim_{x\to c} f(x) +\lim_{x\to c} g(x)$:和法则。
- $\lim_{x\to c} (f(x) \cdot g(x)) = \lim_{x\to c} f(x)\cdot \lim_{x\to c} g(x)$:积法则。
- $\lim_{x\to c} \frac{f(x)}{g(x)} = \frac{\lim_{x\to c}f(x)}{\lim_{x\to c} g(x)}$(假设$\lim_{x\to c} g(x) \neq 0$):商法则。
-重要极限:- $\lim_{x\to \infty} \frac{1}{x} = 0$:无穷小的定义。
- $\lim_{x\to 0} \frac{\sin x}{x} = 1$:著名的夹逼定理的应用。
- $\lim_{n\to \infty} (1+\frac{1}{n})^n = e$:自然对数的底数。
2.导数与微分:导数是函数在其中一点处的变化率,表示函数的斜率。
导数的计算有以下几个基本公式:-基本导数公式:- $\frac{d}{dx} (k f(x)) = k \frac{d}{dx} f(x)$:常数倍法则。
- $\frac{d}{dx} (f(x) + g(x)) = \frac{d}{dx} f(x) +\frac{d}{dx} g(x)$:和法则。
微积分计算公式

微积分计算公式微积分是研究可以量化连续变化的数学分支,主要包括积分、微分及函数的求导、求积等内容。
与其他的数学学科不同的是,微积分把求解过程和求解结果联系在一起,其结果可以表示为一个方程,即公式。
微积分公式是这一学科的核心内容,也是最重要的知识点,正确的掌握和应用公式是这一学科取得成功的关键所在。
首先,最基本的微积分公式,也就是微分的基本公式,是:f′(x)=limh→0f(x+h)f(x)h 。
这个公式表明,函数 f(x)点 x的导数,等于函数在点 x+h的取值与函数在点 x的取值的差值,除以此时的h。
在这个基本的微分公式之上,还有一些常用的微分公式,例如:微分 y= ax n公式为:Dy=nax n1 。
积分也是微分的一个重要方面,其最基本的公式是:∫f(x)dx=F(x)+C这里 F(x)示函数 f(x)积分,C示积分常数。
积分是用来求取函数的积分面积,而积分公式是进行函数求积的基本公式。
此外,还有许多其它的常用的微积分公式,例如积分微分公式,椭圆积分公式,余弦积分公式等。
积分微分公式是将微分操作和积分操作结合起来的公式,椭圆积分公式是根据椭圆来求解函数积分的公式,余弦积分公式是使用余弦函数求解函数积分的公式。
此外,微积分还有一种特殊情况,也是其重要分支,即积分变换。
积分变换是把分析问题变换成数学模型,并使用积分来求解这些模型的解决方案的一种方法。
积分变换的基本思想是,根据原始问题,利用积分的运算建立合适的模型,并解决这些模型,从而得到最终的结果。
总之,以上就是微积分中常用的公式。
对于学习微积分,要牢记这些公式,并熟练应用在实际的问题中,才能取得更好的学习成果。
微积分基本公式16个

微积分基本公式16个1. 微分:微分是数学中最重要的概念之一,它指的是在一定时间内几何形状的变化率。
可以理解为小步长地移动拟合函数,接近曲线本身。
可以表示为\frac{dy}{dx} 或f'(x) 。
2. 泰勒公式:泰勒公式是一个重要的微积分工具,它可以在某一特定点附近对任意连续函数进行展开,也就是说任意设定一个位置x0,可以根据它附近的数值向量求出函数在该位置的平均值。
可以用公式表示为:f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)(x-x_0)^2}{2!} + \frac{f^{n}(x_0)(x-x_0)^n}{n!} + ...3. 高斯积分公式:高斯积分是指将函数抽象为一次多项式曲线,采用指数型或线性型积分方法求解积分。
它可以用公式f(x)=\sum_{i=0}^n a_i x^i 表示,其中a_i为积分下限、上限和积分点x_i处函数值相乘所得到的系数。
4. 黎曼积分:黎曼积分是一种常用的积分方法,它通过对连续函数求和,来确定函数在给定区间上的定积分。
可以用公式表示为:\int_{a}^{b}f(x)dx=\sum_{i=1}^{n}f(x_i)\Delta x_i ,其中n为梯形的节点数。
5. Stokes公式:Stokes公式是一种将多变量函数投影到多方向进行积分的方法,可以用公式表示为:\int_{\Omega}\nabla\times{\bf F} dA =\int_{\partial\Omega}{\bf F}\cdot{\bf n}dS,其中\nabla\times{\bf F} 为梯度矢量场,\partial\Omega 为边界,{\bfn}dS 为单位向量与边界面积的乘积。
6. Γ函数:Γ函数是一种重要的数学函数,通常用来表示非负整数的排列组合,也可以表示实数的阶乘,可以用公式表示为:\Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}dt7. 方阵的行列式:方阵的行列式是指一个n阶矩阵的行列式,可以用公式表示为:D= |a_{i,j}| = \begin{vmatrix} a_{1,1} & a_{1,2} & ... & a_{1,n} \\ a_{2,1} & a_{2,2} & ... & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & ... & a_{n,n} \end{vmatrix} ,其中a_{i,j} 为矩阵中的元素。
微积分的公式大全

微积分的公式大全1.极限的基本公式:(1)常数规则:lim(c) = c (c 为常数)(2)零规则:lim(0) = 0(3)单位规则:lim(x) = x (x 为自变量)(4)和差规则:lim(f(x) ± g(x)) = lim(f(x)) ± lim(g(x))(5)乘法规则:lim(f(x) * g(x)) = lim(f(x)) * lim(g(x))(6)除法规则:lim(f(x) / g(x)) = lim(f(x)) / lim(g(x)) (若lim(g(x)) ≠ 0)2.导数的基本公式:(1)常数函数的导数:(c)'=0(c为常数)(2)幂函数的导数:(x^n)' = nx^(n-1) (n 为实数)(3)指数函数的导数:(e^x)'=e^x(4)对数函数的导数:(ln(x))' = 1/x(5)三角函数的导数:(sin(x))' = cos(x)、(cos(x))' = -sin(x)、(tan(x))' = sec^2(x)(6)反三角函数的导数:(arcsin(x))' = 1/√(1-x^2)、(arccos(x))' = -1/√(1-x^2)、(arctan(x))' = 1/(1+x^2)3.基本积分公式:(1)幂函数的积分:∫(x^n)dx = (x^(n+1))/(n+1) + C (n ≠ -1)(2)指数函数的积分:∫(e^x)dx = e^x + C(3)对数函数的积分:∫(1/x)dx = ln,x, + C(4)三角函数的积分:∫sin(x)dx = -cos(x) + C、∫cos(x)dx = sin(x) + C、∫tan(x)dx = -ln,cos(x), + C(5)反三角函数的积分:∫(1/√(1-x^2))dx = arcsin(x) + C、∫(-1/√(1-x^2))dx = arccos(x) + C、∫(1/(1+x^2))dx = arctan(x)+ C4.微分中值定理:(1)罗尔定理:若函数f(x)在[a,b]上连续,在(a,b)内可导,并且f(a)=f(b),则存在一个c(a<c<b),使得f'(c)=0。
微积分基本公式
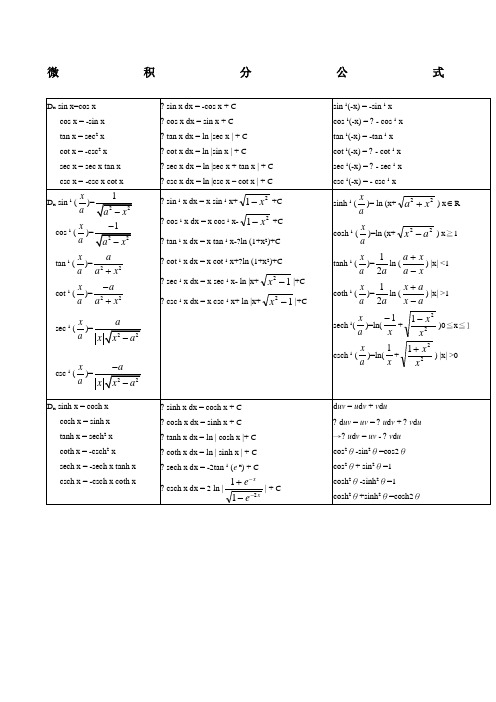
微积分公式D x sinh -1(ax)=221x a +cosh -1(ax )=221ax -tanh -1(a x)= 22a a x - coth -1(a x)=22a a x --sech -1(a x)= 22xa x a --csch -1(a x )=22x a x a +- ? sinh -1 x dx = x sinh -1 x-21x ++ C ? cosh -1 x dx = x cosh -1 x-12-x + C? tanh -1 x dx = x tanh -1 x+ ? ln | 1-x 2|+ C ? coth -1 x dx = x coth -1 x- ? ln | 1-x 2|+ C ? sech -1 x dx = x sech -1 x- sin -1 x + C ? csch -1 x dx = x csch -1 x+ sinh -1 x + Csin 3θ=3sin θ-4sin 3θ cos3θ=4cos 3θ-3cos θ →sin 3θ= ? (3sin θ-sin3θ) →cos 3θ=?(3cos θ+cos3θ)sin x = j e e jx jx 2-- cos x = 2jxjx e e -+sinh x = 2x x e e -- cosh x = 2xx e e -+正弦定理:αsin a= βsin b =γsin c =2R余弦定理: a 2=b 2+c 2-2bc cos αb 2=a 2+c 2-2ac cos β c 2=a 2+b 2-2ab cos γsin (α±β)=sin α cos β ± cos α sin β cos (α±β)=cos α cos βμsin α sin β2 sin α cos β = sin (α+β) + sin (α-β) 2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β) 2 sin α sin β = cos (α-β) - cos (α+β)sin α + sin β = 2 sin ?(α+β) cos ?(α-β) sin α - sin β = 2 cos ?(α+β) sin ?(α-β) cos α + cos β = 2 cos ?(α+β) cos ?(α-β) cos α - cos β = -2 sin ?(α+β) sin ?(α-β) tan (α±β)=βαβαtan tan tan tan μ±, cot (α±β)=βαβαcot cot cot cot ±μe x =1+x+!22x +!33x +…+!n xn + …sin x = x-!33x +!55x -!77x +…+)!12()1(12+-+n x n n + …cos x = 1-!22x +!44x -!66x +…+)!2()1(2n x n n -+ …ln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1x = x-33x +55x -77x +…+)12()1(12+-+n x n n + …(1+x)r =1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni 11= n∑=ni i 1= ?n (n +1)∑=ni i12=61n (n +1)(2n +1) ∑=ni i13= [?n (n +1)]2Γ(x) =⎰∞0t x-1e -td t = 2⎰∞t2x-12t e-d t =⎰∞)1(ln tx-1 d tβ(m , n ) =⎰10xm -1(1-x)n -1d x =2⎰2sin π2m -1x cos 2n -1x d x =⎰∞+-+01)1(nm m x x d x希腊字母 (Greek Alphabets)大写 小写读音 大写 小写读音 大写 小写 读音 Α α alpha Ι ι iota Ρ ρ rho Β β beta Κ κ kappa Σ σ, ? sigma Γ γ gamma Λ λ lambda Τ τ tau Δδ deltaΜμ muΥυupsilona bcα βγ R倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ? 顺位高d 顺位低 ;1 000 000 000 000 000 000 000 000 10 yotta Y 1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分,十分之一0.01 10-2 centi c 厘(或写作「厘」),百分之一0.001 10-3 milli m 毫,千分之一0.000 001 10-6 micro ? 微,百万分之一0.000 000 001 10-9 nano n 奈,十亿分之一0.000 000 000 001 10-12 pico p 皮,兆分之一0.000 000 000 000 001 10-15 femto f 飞(或作「费」),千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y。
大学数学微积分基本公式

大学数学微积分基本公式微积分是数学的一门基础学科,是研究变化率和积分的学科。
微积分理论的基础是一些基本公式,这些公式在微积分的各个领域中都有重要的应用。
本文将介绍一些大学数学微积分中常用的基本公式。
1. 导数公式导数是函数变化率的度量,表示函数在某一点上的斜率。
以下是几个常用的导数公式:1.1 常数函数的导数:对于常数c,其导数为0,即d(cx)/dx = 0。
1.2 幂函数的导数:对于函数f(x) = x^n,其中n是实数,其导数为d(x^n)/dx = nx^(n-1)。
1.3 指数函数的导数:对于函数f(x) = e^x,其中e是自然对数的底数,其导数为d(e^x)/dx = e^x。
1.4 对数函数的导数:对于函数f(x) = ln(x),其中ln表示自然对数,其导数为d(ln(x))/dx = 1/x。
1.5 三角函数的导数:对于函数f(x) = sin(x),其导数为d(sin(x))/dx= cos(x)。
类似地,d(cos(x))/dx = -sin(x),d(tan(x))/dx = sec^2(x)等。
2. 积分公式积分是导数的逆运算,表示函数的累积变化量。
以下是几个常用的积分公式:2.1 幂函数的积分:对于函数f(x) = x^n,其中n不等于-1,其积分为∫(x^n)dx = (1/(n+1))x^(n+1) + C,其中C是常数。
2.2 指数函数的积分:对于函数f(x) = e^x,其积分为∫(e^x)dx = e^x+ C。
2.3 对数函数的积分:对于函数f(x) = 1/x,其积分为∫(1/x)dx = ln|x|+ C。
2.4 三角函数的积分:对于函数f(x) = sin(x),其积分为∫sin(x)dx = -cos(x) + C。
类似地,∫cos(x)dx = sin(x) + C,∫sec^2(x)dx = tan(x) + C等。
3. 极限公式极限是微积分中一个重要概念,用于描述函数在某点趋近于某个值的行为。
微积分基本公式

微积分公式D x sin x=cos x cos x = -sin x tan x = sec 2 x cot x = -csc 2 x sec x = sec x tan x csc x = -csc x cot x⎰ sin x dx = -cos x + C⎰ cos x dx = sin x + C ⎰ tan x dx = ln |sec x | + C ⎰ cot x dx = ln |sin x | + C⎰ sec x dx = ln |sec x + tan x | + C ⎰ csc x dx = ln |csc x – cot x | + C sin -1(-x) = -sin -1 x cos -1(-x) = π - cos -1 x tan -1(-x) = -tan -1 x cot -1(-x) = π - cot -1 x sec -1(-x) = π - sec -1 x csc -1(-x) = - csc -1 xD x sin -1 (a x)=221a x-cos -1 (a x)=221a x--tan -1 (a x)=22a a x +cot -1 (a x)=22a a x -+ sec -1 (a x )=22a xx a -csc -1 (a x)=22a xx a--⎰ sin -1 x dx = x sin -1 x+21x -+C ⎰ cos -1 x dx = x cos -1 x-21x -+C ⎰ tan -1 x dx = x tan -1 x-½ln (1+x 2)+C ⎰ cot -1 x dx = x cot -1 x+½ln (1+x 2)+C ⎰ sec -1 x dx = x sec -1 x- ln |x+12-x |+C⎰ csc -1 x dx = x csc -1x+ ln |x+12-x |+Csinh -1 (a x)= ln (x+22x a +) x ∈Rcosh -1 (a x)=ln (x+22a x -) x ≧1tanh -1 (a x )=a 21ln (xa xa -+) |x| <1coth -1 (a x )=a 21ln (a x a x -+) |x| >1 sech -1(a x )=ln(x 1-+221xx -)0≦x ≦1 csch -1(a x )=ln(x 1+221xx +) |x| >0 D x sinh x = cosh xcosh x = sinh x tanh x = sech 2 x coth x = -csch 2 xsech x = -sech x tanh x csch x = -csch x coth x⎰ sinh x dx = cosh x + C⎰ cosh x dx = sinh x + C ⎰ tanh x dx = ln | cosh x |+ C ⎰ coth x dx = ln | sinh x | + C ⎰ sech x dx = -2tan -1 (e -x ) + C⎰ csch x dx = 2 ln |xxee 211---+| + Cd uv = u d v + v d u⎰ d uv = uv = ⎰ u d v + ⎰ v d u →⎰ u d v = uv - ⎰ v d u cos 2θ-sin 2θ=cos2θ cos 2θ+ sin 2θ=1 cosh 2θ-sinh 2θ=1cosh 2θ+sinh 2θ=cosh2θD x sinh -1(ax)=221x a + cosh -1(ax)=221ax - tanh -1(a x)= 22a a x -coth -1(a x)=22a a x -- sech -1(a x )= 22x a x a -- csch -1(a x )=22xa x a+-⎰ sinh -1 x dx = x sinh -1 x-21x ++ C ⎰ cosh -1 x dx = x cosh -1 x-12-x + C ⎰ tanh -1 x dx = x tanh -1 x+ ½ ln | 1-x 2|+ C⎰ coth -1 x dx = x coth -1 x- ½ ln | 1-x 2|+ C⎰ sech -1 x dx = x sech -1 x- sin -1 x + C ⎰ csch -1 x dx = x csch -1 x+ sinh -1 x + Csin 3θ=3sin θ-4sin 3θ cos3θ=4cos 3θ-3cos θ →sin 3θ= ¼ (3sin θ-sin3θ) →cos 3θ=¼(3cos θ+cos3θ)sin x = j e e jx jx 2-- cos x = 2jxjx e e -+sinh x = 2x x e e -- cosh x = 2xx e e -+正弦定理:αsin a= βsin b =γsin c =2R余弦定理: a 2=b 2+c 2-2bc cos α b 2=a 2+c 2-2ac cos β c 2=a 2+b 2-2ab cos γsin (α±β)=sin α cos β ± cos α sin β cos (α±β)=cos α cos β μsin α sin β 2 sin α cos β = sin (α+β) + sin (α-β) 2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β) 2 sin α sin β = cos (α-β) - cos (α+β)sin α + sin β = 2 sin ½(α+β) cos ½(α-β) sin α - sin β = 2 cos ½(α+β) sin ½(α-β)cos α + cos β = 2 cos ½(α+β) cos ½(α-β) cos α - cos β = -2 sin ½(α+β) sin ½(α-β) tan (α±β)=βαβαtan tan tan tan μ±, cot (α±β)=βαβαcot cot cot cot ±μe x=1+x+!22x +!33x +…+!n x n+ …sin x = x-!33x +!55x -!77x +…+)!12()1(12+-+n x n n + …cos x = 1-!22x +!44x -!66x +…+)!2()1(2n x n n -+ …ln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1 x = x-33x +55x -77x+…+)12()1(12+-+n x n n + …(1+x)r=1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni 11= n∑=ni i 1= ½n (n +1)∑=ni i 12=61n (n +1)(2n +1) ∑=ni i13= [½n (n +1)]2Γ(x) =⎰∞t x-1e -t d t = 2⎰∞t 2x-12t e -d t =⎰∞)1(ln tx-1 d t β(m , n ) =⎰10x m -1(1-x)n -1 d x =2⎰20sin π2m -1x cos 2n -1x d x=⎰∞+-+01)1(nm m x x d x 希腊字母 (Greek Alphabets)大写小写读音 大写 小写读音 大写 小写读音 Α α alpha Ι ι iota Ρ ρrhoΒ β beta Κ κ kappa Σ σ, ς sigmaΓ γ gamma Λ λ lambda Τ τtau Δ δ delta Μ μ mu Υ υ upsilonΕεepsilonΝνnuΦφphi a b cαβγ RΖ ζ zeta Ξ ξ xi Χ χ khi Η η eta Ο ο omicron Ψ ψ psi ΘθthetaΠπpiΩωomega倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ⎰ 顺位高d 顺位低 ;0*∞ =∞1 *∞ = ∞∞= 0*01 = 0000 = )(0-∞e ; 0∞ = ∞⋅0e ; ∞1 = ∞⋅0e顺位一: 对数; 反三角(反双曲) 顺位二: 多项函数; 幂函数 顺位三: 指数; 三角(双曲)算术平均数(Arithmetic mean)nX X X X n+++= (21)中位数(Median) 取排序后中间的那位数字 众数(Mode)次数出现最多的数值几何平均数(Geometric mean)n n X X X G ⋅⋅⋅= (21)调和平均数(Harmonic mean))1...11(1121nx x x n H +++=平均差(Average Deviatoin)nX Xni||1-∑变异数(Variance)nX Xni21)(-∑ or1)(21--∑n X Xni标准差(Standard Deviation)nX Xni21)(-∑ or1)(21--∑n X Xni分配 机率函数f (x )期望值E(x )变异数V(x )动差母函数m (t )Discrete Uniform n1 21(n +1) 121(n 2+1) tnt t e e e n --1)1(1 Continuous Uniforma b -1 21(a +b ) 121(b -a )2 ta b e e atbt )(--Bernoulli p x q 1-x (x =0, 1)p pq q +pe t Binomial ⎪⎪⎭⎫ ⎝⎛x n p x q n -x npnpq(q+ pe t )nNegative Binomial ⎪⎪⎭⎫ ⎝⎛-+x x k 1p k q x pkq 2p kq kt kqe p )1(-Multinomialf (x 1, x 2, …, x m -1)= m xm x x m p p p x x x n ...!!...!!212121np inp i (1-p i )三项 (p 1e t 1+ p 2e t 2+ p 3)nGeometricpq x-1p 1 2p q ttqepe -1 Hypergeometric ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛n N x n k N x k n ⎪⎭⎫ ⎝⎛N k ⎪⎭⎫ ⎝⎛--1N n N n ⎪⎭⎫ ⎝⎛N kPoisson !x e xλλ- λλ)1(--t e eλ Normal 2)(21 21σμπσ--x eμσ222 21 t t eσμ+Beta11)1(),(1---βαβαx x Bβαα+2))(1(βαβααβ+++Gammax e x λαλαλ--Γ1)()( λα 2λα αλλ-⎪⎭⎫ ⎝⎛-t Exponentxeλλ-λ1 21λt-λλ Chi-Squared χ2=f (χ2)=212222)(221χχ--⎪⎭⎫ ⎝⎛Γen n n E(χ2)=nV(χ2)=2n2)21(n t --Weibullαβα--x e1⎪⎭⎫⎝⎛+Γ+111λαβλ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+Γ-⎪⎭⎫ ⎝⎛+Γ111222λλαλ1 000 000 000 000 000 000 000 000 10 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z 1 000 000 000 000 000 000 1018 exa E 1 000 000 000 000 000 1015 peta P 1 000 000 000 000 1012 tera T 兆 1 000 000 000 109 giga G 十亿 1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分,十分之一0.01 10-2 centi c 厘(或写作「厘」),百分之一0.001 10-3 milli m 毫,千分之一0.000 001 10-6 micro ? 微,百万分之一0.000 000 001 10-9 nano n 奈,十亿分之一0.000 000 000 001 10-12 pico p 皮,兆分之一0.000 000 000 000 001 10-15 femto f 飞(或作「费」),千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y。
大学数学微积分基本公式

大学数学微积分基本公式微积分是数学中的重要分支,是研究变化和累积的数学方法。
它包括微分学和积分学两个部分,通过研究函数的导数和不定积分来揭示数学问题的本质。
微积分中有一些基本公式,对于学习和应用微积分来说是至关重要的。
本文将介绍大学数学微积分的基本公式。
一. 导数的基本公式1. 常数函数导数公式对于常数c,其函数f(x) = c的导数为f'(x) = 0。
这是因为常数函数在任意点处的斜率都为0。
2. 幂函数导数公式对于幂函数f(x) = x^n,其中n是常数,它的导数为f'(x) = nx^(n-1)。
这是通过应用幂函数的导数定义得到的。
3. 指数函数导数公式对于指数函数f(x) = a^x,其中a是常数且a>0,它的导数为f'(x) =a^x·ln(a)。
这个公式是指数函数的特性之一。
4. 对数函数导数公式对于对数函数f(x) = log_a(x),其中a是常数且a>0且a≠1,它的导数为f'(x) = 1/(x·ln(a))。
这是对数函数的基本导数公式。
5. 三角函数导数公式常见的三角函数sin(x),cos(x),tan(x)等它们的导数公式分别为:sin'(x) = cos(x)cos'(x) = -sin(x)tan'(x) = sec^2(x)这些导数公式可以通过极限定义和三角函数的基本性质推导得到。
6. 反三角函数导数公式反三角函数的导数公式与三角函数导数公式相对应,具体如下:arcsin'(x) = 1/√(1-x^2)arccos'(x) = -1/√(1-x^2)arctan'(x) = 1/(1+x^2)这些导数公式可以通过反函数的导数性质得到。
二. 积分的基本公式1. 不定积分基本公式不定积分是积分学中的重要概念,它表示函数的反导数。
不同函数的不定积分有不同的基本公式,常见的如下:∫x^n dx = (1/(n+1))·x^(n+1) + C,其中n≠-1∫e^x dx = e^x + C∫1/x dx = ln|x| + C∫sin(x) dx = -cos(x) + C∫cos(x) dx = sin(x) + C∫sec^2(x) dx = tan(x) + C∫1/√(1-x^2) dx = arcsin(x) + C∫1/(1+x^2) dx = arctan(x) + C这些不定积分的基本公式可以通过求导的逆过程得到。
微积分基本公式

微积分公式D x sinh -1(a x )= 221x a + cosh -1(a x )= 221ax - tanh -1(a x)= 22a a x -coth -1(a x )=22a a x -- sech -1(a x )= 22x a x a -- csch -1(a x )=22x a x a +- ? sinh -1 x dx = x sinh -1 x-21x ++ C? cosh -1 x dx = x cosh -1 x-12-x + C? tanh -1 x dx = x tanh -1 x+ ? ln | 1-x 2|+ C? coth -1 x dx = x coth -1 x- ? ln | 1-x 2|+ C ? sech -1 x dx = x sech -1 x- sin -1 x + C ? csch -1 x dx = x csch -1 x+ sinh -1 x + C sin 3θ=3sin θ-4sin 3θcos3θ=4cos 3θ-3cos θ →sin 3θ= ? (3sin θ-sin3θ)→cos 3θ=?(3cos θ+cos3θ) sin x = j e e jxjx 2-- cos x =2jx jx e e -+ sinh x = 2x x e e -- cosh x =2x x e e -+ 正弦定理:αsin a = βsin b =γsin c =2R 余弦定理: a 2=b 2+c 2-2bc cos αb 2=a 2+c 2-2ac cos β c 2=a 2+b 2-2ab cos γsin (α±β)=sin α cos β ± cos α sin βcos (α±β)=cos α cos β μsin α sin β 2 sin α cos β = sin (α+β) + sin (α-β) 2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β)2 sin α sin β = cos (α-β) - cos (α+β)sin α + sin β = 2 sin ?(α+β) cos ?(α-β) sin α - sin β = 2 cos ?(α+β) sin ?(α-β) cos α + cos β = 2 cos ?(α+β) cos ?(α-β) cos α - cos β = -2 sin ?(α+β) sin ?(α-β)tan (α±β)=βαβαtan tan tan tan μ±, cot (α±β)=βαβαcot cot cot cot ±μe x=1+x+!22x +!33x +…+!n x n+ …sin x = x-!33x +!55x -!77x +…+)!12()1(12+-+n x n n + …cos x = 1-!22x +!44x -!66x +…+)!2()1(2n x n n -+ …ln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1x = x-33x +55x -77x +…+)12()1(12+-+n x n n + …(1+x)r =1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni 11= n∑=ni i 1= ?n (n +1)∑=ni i 12= 61 n (n +1)(2n +1) ∑=ni i13= [?n (n +1)]2Γ(x) = ⎰∞0t x-1e -td t = 2⎰∞0t2x-12t e-d t = ⎰∞0)1(ln tx-1 d tβ(m , n ) =⎰10x m -1(1-x)n -1d x =2⎰20sin π2m -1x cos 2n -1x d x= ⎰∞+-+01)1(nm m x x d x希腊字母 (Greek Alphabets)大写小写读音 大写 小写读音 大写 小写读音 Ααalpha Ιιiota Ρρrhoa b c α β γR倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ? 顺位高d 顺位低 ;1 000 000 000 000 000 000 000 000 10 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分,十分之一0.01 10-2 centi c 厘(或写作「厘」),百分之一0.001 10-3 milli m 毫,千分之一0.000 001 10-6 micro 微,百万分之一0.000 000 001 10-9 nano n 奈,十亿分之一0.000 000 000 001 10-12 pico p 皮,兆分之一0.000 000 000 000 001 10-15 femto f 飞(或作「费」),千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y。
微积分基本公式16个

微积分基本公式16个微积分是数学的一门重要分支,它主要研究函数的极限、导数、积分等概念和性质。
微积分的基本公式是我们学习和应用微积分的基础,下面将介绍微积分的16个基本公式。
1.1+1=2这是微积分的最基本的公式,表示两个数相加得到另一个数。
2.a*b=b*a这是乘法交换律,表示两个数相乘的结果与顺序无关。
3.a+(b+c)=(a+b)+c这是加法结合律,表示三个数相加的结果与加法的顺序无关。
4.a*(b+c)=a*b+a*c这是乘法分配律,表示一个数与两个数相加的结果等于这个数与每个数相加的结果之和。
5.a-b=-(b-a)这是减法的性质,表示两个数相减的结果与减法的顺序无关。
6.a/b=b/a这是除法的性质,表示两个数相除的结果与除法的顺序无关。
7. (a+b)^2=a^2+2ab+b^2这是二次方的展开公式,表示两个数的和的平方等于它们的平方和加上两倍的乘积。
8. (a-b)^2=a^2-2ab+b^2这是二次方差的公式,表示两个数的差的平方等于它们的平方差减去两倍的乘积。
9.(a+b)*(a-b)=a^2-b^2这是差的平方公式,表示两个数的和与差的乘积等于它们的平方差。
10. (a+b)^3=a^3+3a^2b+3ab^2+b^3这是立方和的展开公式,表示两个数的和的立方等于它们的立方和加上三倍的乘积加上三倍的乘积再加上立方。
11. (a-b)^3=a^3-3a^2b+3ab^2-b^3这是立方差的公式,表示两个数的差的立方等于它们的立方差减去三倍的乘积加上三倍的乘积再减去立方。
12. (a+b)*(a^2-ab+b^2)=a^3+b^3这是立方和的因式分解公式,表示两个数的和与和的平方差的乘积等于它们的立方和。
13. (a-b)*(a^2+ab+b^2)=a^3-b^3这是立方差的因式分解公式,表示两个数的差与差的平方和的乘积等于它们的立方差。
14. (a+b)^n=a^n+na^(n-1)b+(n(n-1)/2)a^(n-2)b^2+...+nb^(n-1)+b^n这是二项式定理,表示两个数的和的n次方等于它们的各种组合的乘积之和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
x
f (t)dt,
由积分中值定理得,
y
f ( )x, [ x, x x],
f ( ), lim lim f ( )
( x)
x
x0 x x0
o a xx x b x
x 0, x (x) f (x).
即
(x) d
x
f (t)dt f (x)
dx a
5
例1 已知F ( x) x cos 2 tdt,求 F( x). 0
原式= 1 2xdx 2 5dx 6.
0
1
o 12x
说明: f (x)在 [a, b] 上分段连续,即有有
限个第一类间断点时,牛顿莱布尼兹公式仍成立,
但需可加性. 若是第二类间断点,Leabharlann 公式不成立.如:1 1
1 x2 dx
[
1 x
]11
1
1
2.
显然错误.
20
2x (0 x 1)
例7
设
f (x)
x
1)dt
x
cos
(
2t
1)dt
cos(2x 1).
6
例4 已知F ( x) 2x sintdt, 求 F( x) 3
解 令 2x u,则F (u)
u
s in tdt ,
3
u
F( x) F (u) ux ( 3 sintdt )u (2x)x
sinu(2x) sin2x (2x) 2sin2x.
1
2
(1
x
, 2)
求F ( x)
x
0
f (t)dt.
解 当0 x 1时,F ( x)
x
f (t)dt
x
2t dt
t2
x
x 2,
0
0
0
x
当1<x 2时,F ( x) f (t )dt 0
1
2t dt
x 1 dt 1 ( x 1).
0
12 2
x2
0 x1
F
(
x)
1 2
(
(3) 可加性: b f ( x)dx
c
f ( x)dx
b
f ( x)dx
a
a
c
(5)若 f (x) g(x), 则
b
f (x)dx
bg(x)dx.(a b)
a
a
(6) (估值定理) 设M及m分别是函数f(x)在区间[a,b]上
的最大值及最小值,则
b
m(b a) f (x)dx M(b a). (a b) a
f (t)dt F(a)
a
当 x b时,F(b)
b
f (t)dt F(a)
a
故有: b f (x)dx F(b) F(a). a
牛顿—莱布尼茨公式
14
b a
f
( x)dx
F(b)
F (a)
F ( x)ba
F(x)
b a
微积分基本公式表明:
一个连续函数在区间[a,b]上的定积分,等于它的
dx x2
95年考研题
解 Q 0 x cos t 2dt x x2 cos t 2dt,
x2
0
d 0 x cos t 2dt d ( x x2 cos t 2dt )
dx x2
dx
0
x2 cos t 2dt 2x2 cos x4 .
0
10
例10 设 f (x) 在 0,1 上连续,且 f (x) 1.
例5 设 f (x) x t sin(t2 )dt, 求 f ( x). 2
解 令 u
x,
f ( x) [
u 2
t
sin(
t
2
)dt
]u
(
x )
u sin(u2 ) ( x ) x sin( x )2 ( x )
x sin x 1 1 sin x. 2x 2
7
sin x
例6 已知F ( x) x2 arctan tdt,求 F(x).
(3) 当 f (x) 在[a,b]上有正有负时, b f ( x)dx表示各部分 a 面积的代数和,x轴上方的取正号,x轴下方的取负号.
4.定积分的性质
(1)
a f ( x)dx 0;b f ( x)dx
a
f (x)dx.
a
a
b
1
b
b
b
(2) a f ( x)dx a f (t)dt a f (u)du.
2
sin
x 2
dx
x2 2 cos )
2
20
2
2
2(1
2)2 2
2(
2 2
1)
4
2 4.
注意:所给函数与积分区间的关系.
19
例6
设
f (x)
2 x 5
0 x 1,求
2
f ( x)dx.
1 x2 0
y
解
2 f ( x)dx 1 f ( x)dx
2
f ( x)dx
0
0
1
在 [1,2]上规定当x=1时,f (x) 5,
x
1)
1<x 2
21
例8 设 f ( x)
x 0
t
2
t
1 2t
dt 5
,
求
f ( x)在[0,1]上的最大
值和最小值.
解
f ( x)
x 0
t2
t 1
dt
2t 5
x2
x1 2x 5
x1 ( x 1)2 4
当
x [0,1]时,f
(
x)
(x
x1 1)2
4
0,
则 f ( x) 在[0,1]上是单调递增,则最小值为 f (0) 0,
即得一个新函数
y
x
( x) f (t)dt (a x b) a
则称之为积分变上限函数.
o
( x)
ax
bx
3
二、积分上限函数的性质:
定理1:如果f(x)在区间[a,b]上连续,则积分上限函数
( x) x f (t)dt 在[a,b] 上具有导数,并且它的导数 a
是 ( x) d x f (t)dt f (x) (a x b)
解 F(x) [
sin x
arctan tdt]
x2
0
sin x
[ arctan tdt arctan tdt]
x2
0
x2
sin x
[ 0 arctantdt] [0 arctan tdt]
arctan x2 ( x2 ) arctan(sinx) (sin x)
2x arctan( x2 ) arctan(sinx)cos x.
最大值为 f (1)
1
0t
2
t
1 2t
dt 5
1 2
1d( t 2 2t 5) 0 t 2 2t 5
1 2
ln
x2
2x
5
1 0
1 2
[ln8
ln 5]
1 2
ln
8 5
.
22
例9 一汽车以每小时36公里的速度行驶,到某处需要
减速停车,设汽车以等加速度a = -5m/ s2 刹车. 问从
任意一个原函数在区间[a,b]上的增量.
注意:当a>b时,b f ( x)dx F(b) F(a)仍成立. a
b
a
a f ( x) dx b f ( x)dx
[F(a) F(b)] F(b) F(a)
求定积分的问题转化为求原函数的问题.
15
例1 求下列定积分
(1) 1 e xdx; 0
变速直线运动中路程为 vT2 (t)dt; T1
另一方面这段路程可表示为 s(T2 ) s(T1);
vT2 (t )dt
T1
s(T2 )
s(T1 ).
其中:s(t) v(t).
13
三、牛顿—莱布尼茨公式
定理 3(微积分基本公式)
如果F(x) 是连续函数 f (x)在区间[a,b] 上的任意
一个原函数,则
5
2
v(t)dt
0
2
(10
0
5t )dt
[10t
5
t2 2
]
2 0
10(m).
即汽车刹车后,需驶过10米才能停住.
23
四、小结
1.积分上限函数 ( x)
x
f (t)dt
a
x
2.积分上限函数的导数 ( x) [ f (t)dt ] f ( x) a
3.微积分基本公式
b
f ( x)dx F(b) F(a)
dx
0 1 x2
0 1 x2
1
2
0
1 2
(1
x2
1
)2
d(1
x2
)
1
[arcsinx]0 2
[
1
1 x2 ]0 2 arcsin
1 1
2
2 .
24
17
例3 求 1 1 dx . 2 x
解 当x<0时,1 的一个原函数是ln x ,
x
1 2
1 x
dx ln |
x
|
1 2
ln1
ln
2
ln
证明:2 x
x
0
f
(t )dt
1在
0,1 上只有一个解.
证 令F ( x) 2x
x
