数字积分圆弧第一二三四象限顺逆插补计算
第三四象限数字积分法插补计算报告

第三四象限直线插补计算1. 引言随着微电子技术,计算机技术的发展,数控机床的性能不断完善,其应用范围也不断增大。
而数控技术作为数控机床的关键技术,越来越得到更多高校的重视。
2.数字积分法直线插补原理设将要加工的直线XOY 平面内第一象限直线OE ,如图.一所示,直线起点在坐标原点,终点为E (Xe ,Ye )。
同样,假设坐标值均为以脉冲当量为单位的整数。
图.一若此时刀具在两坐标轴上的进给速度分量分别是Vx ,Vy ,则刀具在X 轴,Y 轴方向上位移增量分别是△X = Vx △t 式一a△ Y = Vy △t 式一b由图.一 所示的几何关系可得V/OE=Vx/Xe=Vy/Ye=K (常数) 式二将式二中的Vx ,Vy 分别代入式一 可得:△X = KXe △t 式三a△ Y = KYe △t 式三b可见刀具由原点O 走向E 的过程,可以看作式每经过一个单位时间间隔△t ,就分别以增量[KXe],[ KYe]同时在两个坐标轴累加的结果。
也可以这样认为,数字积分法插补实际上就是利用速度分量,进行数字积分来确定刀具在各坐标轴上位置的过程,即XO当取△ti=“1”(一个单位时间间隔)则X = nKXe 式五aY = nKYe 式五b设经过n 次累加后,刀具正好到达终点E(Xe,Ye),则要求式五中常量满足 下式nK=1 式六n 是累加次数必须取整数,所有K 取小数。
为了保证每次分配给坐标轴的进给脉冲不超过一个单位,则△ X=KXe<1 式七a△ Y=KYe<1 式七b上式中Xe ,Ye 的最大允许值受系统中相应寄存器容量的限制。
现假设寄存器 为N 位则容量为2N ,对应存储的最大允许数字量为(2N - 1)将其带入式七得 K<=1/(2N - 1) 式八现不妨取 K =1/2N 式九显然它满足式七,式八的约束条件,再将K 值代入式六可得累加次数为 n =2N 式十如果将n ,K,值代入式五则动点坐标为X = nKXe =Xe 式十一aY = nKYe =Ye 式十一b根据以上分析,在进行直线插补时,先开辟两个被积函数寄存器Jvx ,Jvy 分别存放终点坐标值Xe ,Ye ,还有两个余数寄存器Jrx ,Jry 。
数控机床插补原理

对圆弧,提供起点、终点、顺圆或逆圆、以及圆心相对于起点的位置。为满
足零件几何尺寸精度要求,必须在刀具(或工件)运动过程中实时计算出满足 线形和进给速度要求的若干中间点(在起点和终点之间),这就是数控技术中
插补(Interpolation)的概念。据此可知,插补就是根据给定进给速度和给定
轮廓线形的要求,在轮廓已知点之间,确定一些中间点的方法,这种方法称 为插补方法或插补原理。
Xm+1=Xm+1, Ym+1=Ym
新的偏差为
Fm+1=Ym+1Xe-Xm+1Ye=Fm-Ye
若Fm<0时,为了逼近给定轨迹,应向+Y方向进给一步,走一步后新的坐标值为
Xm+1=Xm, Ym+1=Ym +1
新的偏差为
Fm+1=Fm+Xe
4. 终点判别法
逐点比较法的终点判断有多种方法,下面主要介绍两种:
直到∑为零时,就到了终点。
2.2
不同象限的直线插补计算
上面讨论的为第一象限的直线插补计算方法,其它三个象
限的直线插补计算法,可以用相同的原理获得,表5-1列出了
四个象限的直线插补时的偏差计算公式和进给脉冲方向,计 算时,公式中Xe,Ye均用绝对值。
表1-1 四个象限的直线插补计算
二、数字积分法插补

例:插补第一象限直线OA,起点为O( 0 , 0 ) ,终点为 A ( 5 , 3 )。取被积函数寄存器分别为JVx, JVy,余数寄存 器分别为JRx 、JRy ,终点计数器为 JE,且都是三位 二进制寄存器。试写出插补计算过程并绘制轨迹。 Y 3 2 1 O 1 2 3 4 5 X A( 5 , 3 )
∆X,∆Y同时溢出 JE=0,插补结束
110 000
加工轨迹如下:
Y 6 5 4 3 2 1 O 1 2
A( 2 , 6 )
X
(三)数字积分圆弧插补 如图所示,设加工半径为R的第一象限逆时针圆弧AB, 坐标原点定在圆心上,A(Xo,Yo)为圆弧起点,B(Xe,Ye) 为圆弧终点,Pi(Xi,Yi)为加工动点。 Y B(Xe,Ye) Pi(Xi,Yi) A(Xo,Yo) O X
插补计算过程如下:
累加 次数 (∆t) X积分器 Y积分器 终点 JVx JRx 溢出 JVy JRy 溢出 计数器 JE ∆X ∆Y
备注
0 1 2 3 4 5 6 7 8
010 000 010 010 010 100 010 110 010 000 1 010 010 010 100 010 110 010 000 1
插补计算过程如下
累加 次数 (∆t) X积分器 Y积分器 终点 JVx JRx 溢出 JVy JRy 溢出 计数器 JE ∆X ∆Y
备注
0 1 2 3 4 5 6 7 8
101 000 101 101 101 010 101 111 101 100 101 001 101 110 101 011
1 1 1 1
O ∆t
t T
若∆t取最小基本单位“1”,则上式可简化为: n-1 S=∑ Yi
数控机床DDA数字积分法插补第一象限直线,逐点比较法插补二三象限顺圆弧

3.2 执行计算
在右侧面板中有参数输入区,方式选择区以及执行按钮等操作。
若输入参数和符合要求则出现错误对话框;“参数有误”
若不选择插补对象为‘直线’或‘圆弧’直接按下‘复位’按钮会出现警示对话框提示“请选择插补对象”
注:在直线插补中,对起始点坐标和终点坐标不作要求,但步长必须不能为0;在圆弧插补中,起始点坐标必须为二三象限的点,且终止点必须在起始点下侧,这事保证圆弧为劣弧的条件之一。步长在任何情况下不能为0 。
4.2 主要算法的实现
4.2.1参数声明
起点坐标(sx,sy);终点坐标(ex,ey);
圆心坐标(cx,cy);步长bc;
4.2.2复位操作程序:
functionfw_Callback(hObject, eventdata, handles)
globalsx sy ex ey cx cy bc m vx1 vy1 rx1 ry1
3.2 执行计算……………………………………………………………5
3.3DDA法直线插补实例………………………………………………6
3.4逐点比较法插补第二三象限逆时针圆弧…………………………7
四、主要算法及源程序
4.1 程序设计概述………………………………………………………8
set(gca,'YTick',[-10:1:10]);
axis([-10 10 -10 10]);
axismanual;
ifs_1==0&&s_2==0
warndlg('请选择插补对象');
else
ifget(handles.zx,'value')
m=str2double(get(handles.m,'String'));
数字积分法插补

数字积分法插补前面提到过数字积分法插补是脉冲增量插补的一种,它是用数字积分的方法计算刀具沿各坐标轴的移动量,从而使刀具沿着设定的曲线运动。
实现数字积分插补计算的装置称为数字积分器,或数字微分器(Digital Differential Analyzer, DDA),数字积分器可以用软件来实现。
数字积分器具有运算速度快,脉冲分配均匀,可以实现一次、二次曲线的插补和各种函数运算,而且易于实现多坐标联动,但传统的DDA 插补法也有速度调节不方便,插补精度需要采取一定措施才能满足要求的缺点,不过目前CNC 数控系统中多采用软件实现DDA 插补时,可以很容易克服以上缺点,所以DDA 插补是目前使用范围很广的一种插补方法。
它的基本原理可以用图4.1所示的函数积分表示,从微分几何概念来看,从时刻0到时刻t 求函数y=f(t)曲线所包围的面积时,可用积分公式: (4.1)如果将0~t 的时间划分成时间间隔为Δt 的有限区间,当Δt 足够小时,可得近似公式:(4.2)式中y i-1为t=t i-1时f(t)的值,此公式说明:积分可以用数的累加来近似代替,其几何意义就是用一系列小矩形面积之和来近似表示函数f(t)下面的面积,t y d t f S ni i t t ∆==∑⎰=-110)(⎰=t t d t f S 0)(如果在数字运算时,用取Δt 为基本单位“1”,则4.2式可以简化为:∑=-=n i i y S 11(4.3)如果系统的基本单位Δt 设置得足够小,那么就可以满足我们所需要的精度。
一般地,每个坐标方向需要一个被积函数寄存器和一个累加器,它的工作过程可用图4.2表示:图 4.2 一个坐标方向上的积分器示意图Fig 4.2 Sketch of DDA in one coordinate direction图4.1 数字积分原理Fig 4.1 Principle of DDA被积函数寄存器用以存放坐标值f(t),累加器也称余数寄存器用于存放坐标的累加值。
第四章 插补原理
y L2 F0 F<0 F<0 F0 L3
四象限直线偏差符号和进给方向
L1 F0 F<0 x F<0 F0 L4
由图可见,靠近Y轴区域偏差大等于零,靠近X轴区域偏差小于零。F≥0时,进 给都是沿X轴,不管是+X向还是-X向,X的绝对值增大;F<0时,进给都是沿Y轴, 不论+Y向还是-Y向,Y的绝对值增大。
v y 60f y
式中 δ—脉冲当量(mm/脉冲)。合成进给速度为
v v x 2 v y 2 60 f x2 f y2
若fx=0或fy=0时,也就是刀具沿平行于坐标轴的方向切削,这时对 应轴切削速度最大
第四章 插补原理
3.1 数字积分法的基本原理
第 三 节 数 字 积 分 法
F5 F4 2Y4 1 3 F6 F5 2 X 5 1 4
F7 F6 2Y6 1 1
F8 F7 2Y7 1 0
5. 四个象限中圆弧插补 第一象限逆圆弧CD:即Fi≥0时,走—X轴, 动点的偏差函数为
Fi 1=Fi 2 X i 1
第四章 插补原理
2.3 逐点比较法圆弧插补
第 二 节 逐 点 比 较 法
第一象限圆弧插补 流程图
例3 现欲加工第一象限顺圆弧AB,如图所示,起点A(0,4),终点B(4,0), 试用逐点比较法进行插补。
Y 4 3 2 1 B(4,0) O 1 2 3 4 X A(0,4)
表3 圆弧插补过程
步数 起点 偏差判别 坐标进给 偏差计算 坐标计算 终点判别
如图4-14所示,从t=0时
刻到t时刻,函数y=f(t) 曲线所包围的面积可表示
Y
Y=f(t)
YO
数控技术第3章(2)

动点从原点出发走向终点的过程,可以看作是各坐 标轴每经过一个单位时间间隔t,分别以增量kXe及kYe 同时累加的结果。
X Y
X kX t
i e i 1 m i=1 m i e i i 1 i 1
m
m
i
Y kY t
取 ti 1(一个单位时间间隔),则 m
0.100 1 0.100 1 0.100 1 0.100 1 0.100 1 0.100 1 0.100 1 0.100
100 0.100 100+100=1 000 0.100+0.100=1.000 100+000=100 0.100+0.000=0.100 100+ 100=1 000 0.100+0.100=1.000 100+ 000=100 0.100+0.000=0.100 100+ 100=1 000 0.100+0.100=1.000 100+ 000= 100 0.100+0.000=0.100 100+ 100=1 000 0.100+0.100=1.000
(二) 数字积分法
数 字 积 分 法 又 称 数 字 微 分 分 析 法 DDA(Digital differential Analyzer),是在数字积分器的基础上建立起 来的一种插补算法。数字积分法的优点是,易于实现 多坐标联动,较容易地实现二次曲线、高次曲线的插 补,并具有运算速度快,应用广泛等特点。 如图3-15所示,设有一函数Y=f(t),求此函数在 t0~tn区间的积分,就是求出此函数曲线与横坐标t在区 间(t0,tn)所围成的面积。如果将横坐标区间段划分 为间隔为t的很多小区间,当t取足够小时,此面积 可近似地视为曲线下许多小矩形面积之和。
第4章插补原理刀补原理与速度控制
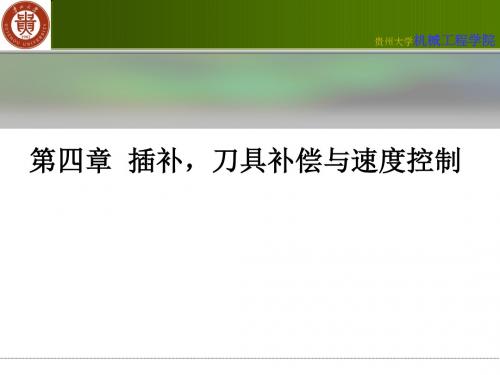
Fi ,i 1 F X e
X e 1
Fi 1,i F Ye F (Ye )
Ye 1
插补前将坐标数据符号与数据本体分离,用数据本体进行插补计算,由 数据符号确定坐标进给方向。
插补工作寄存器:
FR:偏差函数寄存器 LR:X坐标偏差函数递推项寄存器,存放(-Ye) MR:Y坐标偏差函数递推项寄存器,存放Xe LC: X坐标终点判别寄存器,存放X坐标应输出的脉冲总数 MC:Y坐标终点判别寄存器,存放Y坐标应输出的脉冲总数 RL: X坐标进给方向寄存器,存放X坐标数据的符号 RM:Y坐标进给方向寄存器,存放Y坐标数据的符号
贵州大学机械工程学院
第四章 插补,刀具补偿与速度控制
贵州大学机械工程学院
第一节 插补原理与程序设计 一. 插补及其算法 插补的任务就是在一段零件轮廓的起点和终点之间,计算 出若干个中间点的坐标值。 直线和圆弧是构成工件轮廓的基本线条,大多数CNC系统 都具有直线和圆弧的插补功能。高档CNC系统还具有抛物 线、螺旋线等插补功能。
若F<0, 下一步应该向+Y方向走,则: Fi,i1 X eYi 1 X iYe X eYi X iYe X e F X e Yi 1 Yi 1
插补开始
逐点比较法直线插补,每进一步需要四个节拍: 偏差判别 1,偏差判别; 2,坐标进给; 3, 偏差计算;4, 终点判别
动点沿OA匀速移动, V,Vx,Vy, 均为常数。
V V V X Y K OA X e Ye
X Vx t KX e t, Y Vy t KYe t,
直线积分插补近似表达式
X ( KX e )t , Y ( KYe )t
i 1 i 1 m m
机械制造与自动化专业《数控系统插补原理》

数控系统插补原理机床数控系统的核心问题,就是如何控制刀具或工件的运动。
一般情况是运动轨迹的起点坐标、终点坐标和轨迹的曲线方程,由数控系统实时地计算出各个中间点的坐标。
即需要“插入、补上〞运动轨迹各个中间点的坐标,通常这个过程被称为“插补〞。
每种插补方法又可能用不同的方法来实现,这种具体的计算方法称之为插补算法。
插补算法的好坏将直接影响CNC系统的性能指标。
插补的结果是输出运动轨迹的中间点坐标值,机床伺服系统根据此坐标值控制各坐标轴之间的相互协调运动,走出预定轨迹。
在早期的数控机床中,插补器是一种硬件数字逻辑电路装置,故称为硬件插补器。
而在CNC系统中,插补器的局部或全部功能可由计算机中的插补程序实现。
能实现插补的程序软件称软件插补器。
软件插补算法可分为两大类:脉冲增量插补和数字采样插补。
脉冲增量插补算法主要为各坐标轴进行脉分配计算,插补结果产生单位行程增量,即工作台移动一个脉冲当量。
常用的脉冲增量插补算法有逐点比拟法和数字积分法,本节通过介绍直线、圆弧逐点比拟插补法,让读者了解插补软件运行的过程。
1.逐点比拟插补法工件的轮廓无论是什么曲线,都可以用简单的直线、圆弧等逼进。
例如图2-13〔a〕中,为了加工圆弧曲线AB,可以让刀具先从A点沿-X方向走一步,刀具处在圆内1点,然后沿+Y方向走一步,使刀具靠近圆弧,刀具到达2点,但仍在圆内,故沿+Y再前进一步,刀具到达圆外3点,为靠近圆弧应沿-X方向走一步,如此继续移动,走完9步后到达终点B,其过程如图2-7a 所示。
图2-7 逐点比拟插补示意图加工如图2-7〔b〕所示中的直线AB也一样,先从A点沿+X方向走一步,刀具到达1点,为了逼近直线,第二步沿+Y方向移动一步到达2点,如此继续,直到终点B结束。
这种插补方法是走一步计算一次,并比拟刀具与工件轮廓的相对位置,使刀具向减小误差的方向进给,故称为逐点比拟法。
用逐点比拟法控制机床加工,需要四个节拍:1偏差判别根据刀具的实际位置,确定进给方向。
数字积分插补法顺圆插补

数控原理与系统课程设计课题名称:数字积分插补法顺圆插补专业:班级:姓名:指导老师:数控原理与系统课程设计任务书班级姓名学号一、课程设计的目的1)了解连续轨迹控制数控系统的组成原理。
2) 掌握数字积分插补的基本原理。
3)掌握数字积分插补的软件实现方法。
二、课程设计的任务数字积分法又称数字微分分析法DDA(Digital Differential Analyzer)。
数字积分法具有运算速度快、脉冲分配均匀、易于实现多坐标联动及描绘平面各种函数曲线的特点,应用比较广泛。
其缺点是速度调节不便,插补精度需要采取一定措施才能满足要求。
由于计算机有较强的计算功能和灵活性,采用软件插补时,上述缺点易于克服。
本次课程设计具体要求如下:1)数字积分插补法基本原理2)数字积分插补法插补软件流程图3)算法描述(逐点比较法算法在VB中的具体实现)4)编写算法程序清单5)软件运行仿真效果二、课程设计报告要求1)按课程设计任务5点要求为标题,编写课程设计报告,最后加一点:此次课程设计小结(包括设计过程中所碰到的问题、解决办法以及有关设计体会等)。
2)字数在3000字左右。
3)仿真软件一份。
三、学生分组数控原理与系统课程设计说明书一、数字积分法顺圆弧插补的基本原理数字积分法是利用数学积分的方法,计算刀具沿各坐标轴的位移,使得刀具沿着所加工的轮廓曲线运动。
利用数字积分原理构成的插补装置称为数字积分器,又称数字微分分析器,简称DDA。
数字积分器插补的最大优点在于容易实现多坐标轴的联动插补,能够描述空间直线及平面各种函数曲线等。
因此,数字积分法插补在轮廓数控系统中得到广泛的应用。
从几何角度来看,积分运算就是求出函数Y=f(t)曲线与横轴所围成的面积。
如右图所示,从t=t0到tn时刻,函数Y=f(t)积分值可以表述为如果进一步将t∈[t0, tn]的时间区间划分为若干个等间隔Δt的小区间,则当Δt足够小时,函数Y的积分可用下式近似表示在几何上就是用一系列的小矩形面积之和来近似表示函数f(t)以下的积分面积。
第三节 数字积分法插补

第三节 数字积分法插补一、数字积分法的基本原理数字积分法又称数字微分分析法(Digital Differential Analyzer )。
这种插补方法可以实现一次、二次、甚至高次曲线的插补,也可以实现多坐标联动控制。
只要输入不多的几个数据,就能加工出圆弧等形状较为复杂的轮廓曲线。
作直线插补时,脉冲分配也较均匀。
从几何概念上来说,函数)(t f y =的积分运算就是求函数曲线所包围的面积S (图3-10所示)。
图3-10 函数)(t f y =的积分S=⎰tydt 0(3-9)此面积可以看作是许多长方形小面积之和,长方形的宽为自变量t ∆,高为纵坐标i y 。
则 S=⎰tydt 0=t y ni i ∆∑=0(3-10)这种近似积分法称为矩形积分法,该公式又称为矩形公式。
数学运算时,如果取t ∆=1,即一个脉冲当量,可以简化为:S=∑=ni iy(3-11)由此,函数的积分运算变成了变量求和运算。
如果所选取的脉冲当量足够小,则用求和运算来代替积分运算所引起的误差一般不会超过容许的数值。
二、DDA 直线插补 1.DDA 直线插补原理图3-11 直线插补设xy 平面内直线OA ,起点(0,0),终点为(e x ,e y ),如图3-11所示。
若以匀速V 沿OA 位移,则V 可分为动点在x 轴和y 轴方向的两个速度x V 、y V ,根据前述积分原理计算公式,在x 轴和y 轴方向上微小位移增量x ∆、y ∆应为⎩⎨⎧∆=∆∆=∆t V y tV x y x (3-12) 对于直线函数来说,x V 、y V ,V 和L 满足下式⎪⎪⎩⎪⎪⎨⎧==L y VV Lx V V e y e x 从而有⎩⎨⎧==e yex ky V kx V (3-13) 其中:LVk =因此坐标轴的位移增量为⎩⎨⎧∆=∆∆=∆tky y tkx x e e (3-14) 各坐标轴的位移量为⎪⎪⎩⎪⎪⎨⎧∆==∆==⎰∑⎰∑==tn i e e t n i e e ty k dt ky y t x k dt kx x 0101(3-15) 所以,动点从原点走向终点的过程,可以看作是各坐标轴每经过一个单位时间间隔t ∆,分别以增量e kx 、e ky 同时累加的过程。
5.3 数字积分法插补原理

主讲人:罗福源原理利用数字积分的原理,计算各坐标轴的位移,形成插补轨迹。
在计算机里,积分即是求和,也就是累加。
那么加数是什么?是微位移(Δx、Δy、......),因此数字积分法又称为DDA法,(Digital Differential Analyzer),即数字微分分析器法。
特点允许多个坐标轴同时输出脉冲。
优点运算速度快、脉冲分配均匀,易于实现多坐标联动。
X Δx01234取微位移Δx(<1个脉冲当量)进行累加运算。
随着累加次数逐渐增加,对应动点的x坐标也不断增大。
当完成若干次累加后,位移之和已经超出1个脉冲当量。
此时,利用这个溢出信号让数控系统向x坐标轴发出一个控制脉冲,使之产生一个脉冲当量的位移。
如此不断累加,每当位移之和超出1个脉冲当量,就向x 坐标轴发出一个控制脉冲,直至到达终点,插补结束。
保证Δx 与Δy 符合斜率关系即可:DDA法直线插补e ex y x y =∆∆⎪⎪⎩⎪⎪⎨⎧<=∆<=∆11m y y m x x e e设经累加m 次到达终点,则若取m =2n ,(n 为累加器位数),则易于计算机实现。
因为Δx=x e •2-n 与x e 相比,只是小数点位置不同,不影响累加运算后的有效数位与溢出的判别。
这样,把对Δx 、Δy的累加转变为对x e 与y e 的累加。
Y XA(x e ,y e )Δx2ΔxΔy 2Δy OX -Y平面第一象限直线DDA插补器的示意图:Δt Y轴溢出脉冲X轴溢出脉冲+Y 积分累加器J RYX积分累加器J RX被积函数寄存器J VX (x e )+控制脉冲被积函数寄存器J VY (y e )其它象限的直线DDA插补,参照前述逐点比较法,对终点坐标进行取绝对值并按实际方向进给即可。
累加次数m JVX(存xe)JRX(∑xe)△x JVY(存ye)JRY(∑ye)△y0100000011000 11000001100 20000111000 31000000101 40000110000 51000011100 60000101001 71000010100 80000100001 91000001100 100000111000 111000000101 120000110000 131000011100 140000101001 151000010000 160000100001A (8,6)插补轨迹理想轨迹8756123456O1234YX以第一象限逆圆弧为例V yV x VARYOXP (x i ,y j )B (x e ,y e )DDA法圆弧插补222x y R+=等式两边同时对时间参数t 求导,可得220dx dy x dy dxx y dt dt dt dty+=⇒=-由此可导出第一象限逆圆弧加工时动点沿坐标轴方向的速度分量为=x j y i dx V ky ky dt dy V kx kx dt ⎧==--⎪⎪⎨⎪===⎪⎩在一个单位时间Δt 内,X 和Y 方向上的移动距离微小增量Δ x 、Δ y 为:⎪⎩⎪⎨⎧∆=∆=∆∆=∆=∆tkx t V y t ky t V x i y j x -⎪⎩⎪⎨⎧=∆=∆=∆=∆n --n22--i i j j x t kx y y t ky x 令Δt =1,取k=2-n ,得:插补时寄存的是动点坐标x i 或y j ,是变量。
圆弧插补指令格式

圆弧插补指令格式
圆弧插补指令的格式如下:
1.G02为顺时针插补,G03为逆时针插补,在XY平面中,格式如下:G02/G03 X_ Y_ I_ K_ F_或G02/G03 X_ Y_ R_ F_,其中X、Y为圆弧终点坐标,I、J为圆弧起点到圆心在X、Y轴上的增量值,R为圆弧半径,F为进给量。
2.在圆弧切削时注意,q≤180°,R为正值;q>180°,R为负值;I、K的指定也可用R指定,当两者同时被指定时,R指令优先,I、K无效;R不能做整圆切削,整圆切削只能用I、J、K编程,因为经过同一点,半径相同的圆有无数个。
当有I、K为零时,就可以省略;无论G90还是G91方式,I、J、K都按相对坐标编程;圆弧插补时,不能用刀补指令G41/G42。
3.G54~G59是在加工前设定好的坐标系,而G92是在程序中设定的坐标系,用了G54~G59就没有必要再使用G92,否则G54~G59会被替换,应当避免。
第三章插补原理及控制方法

及
控
终点判别
N
终点?
制
方
法
结束
25
二、逐点比较法圆弧插补---其它象限
y
F>0
y
F>0
第
F<0
F<0
三 章
o
x
o
x
插
补
原
理
逆圆
顺圆
及 控
各象限插补进给方向, 各象限插补进给方向,远
制
远离原点坐标值加一接 离原点坐标值加一,接近
方
近原点坐标值减一。
原点坐标值减一。
法
26
作业
试推导逐点比较法第一象限顺圆弧 第 插补的递推公式,并画出程序流程图。
逐点比较插补计算法(简称逐点比较法)
第
三 章
数字积分插补计算法(简称数字积分法)
插 时间分割插补计算法(简称时间分割法)
补
原
理 及
样条插补计算方法等。
控
制
方
法
2
3-1 逐点比较法插补
逐点比较插补计算法(简称逐点比
第 较法)又称区域判别法。
三
章
其原理是:计算机在控制加工轨迹过
插 程中逐点计算和判断加工偏差以控制坐
章
当M点在直线上时, + Δ X
y
插 补
(αi= α)
原
M (x i y j )
A
理
及 控
tg αi= tg α
制
方 法
αi
oα
x
6
其中 tg αi= y j / xi
tgα= y e / x e
tg αi -tgα= y j / xi - y e / x e
逐点比较法数字积分法等插补原理

A3(xe , ye )
x F 0
F 0
A4 (xe , ye ) -y
由上图可以推导得出,四个象限直线插补的坐标进给方向和偏差计算公式。
所在象限
Fm≥0
进给方向
偏差计算
所在象限
Fm<0
进给方向
偏差计算
一、四 二、三
+x
一、二-xBiblioteka Fm+1=Fm-ye
三、四
+y
-y
Fm+1=Fm+xe
3.直线插补运算的程序实现
(3) 圆弧插补计算过程比直线插补计算过程多一个环节,即要计
算加工点瞬时坐标(动点坐标)值。
因此圆弧插补计算过程分为五个步骤即偏差判别、坐标进给、
2.四个象限的圆弧插补
(1)第一象限顺圆弧的插补计算
第一象限顺圆弧CD,圆弧的圆心在坐标原点,并已知起点C(x0,y0),终 点D(xe,ye),如图所示。设加工点现处于m(xm,ym)点, 若Fm≥0,则沿-y方向进给一步,到(m+1)点,新加工点坐标将是(xm,ym-1),
Nxy=9
+y
F2=F1+xe=2
Nxy=8
+x
F3=F2-ye=-2
Nxy=7
+y
F4=F3+xe=4
Nxy=6
+x
F5=F4-ye=0
Nxy=5
+x
F6=F5-ye=-4
Nxy=4
+y
F7=F6+xe=2
Nxy=3
+x
F8=F7-ye=-2
Nxy=2
+y
2--插补象限、圆弧走向处理以及逐点比较法合成进给速度

① F=F-2*|X|+1 ② |X|=|X|-1 SR2、NR3 N -X
① F=F+2*|Y|+1 ② |Y|=|Y|+ 1 Y SR2、NR1 N +Y -Y
① F=F+2*|X|+1 ② |X|=|X|+1 Y SR1、NR4 N +X -X
∑= ∑-1 ∑= 0 Y 结束 N
(三)圆弧过象限 直线只可能处于一个象限中,因此不存在过象限问题。但是圆弧有可能 跨越几个象限,这时需要在两象限的交接处做相应的处理,此即圆弧过象限 问题。 当圆弧过象限时,具有如下特点: ① 在过象限前后,动点坐标的符号会发生改变; ② 在过象限后,圆弧的走向不变。 逆圆弧过象限的顺序为:NR1 → NR2 → NR3 → NR4 → NR1 →• • • 顺圆弧过象限的顺序为:SR1 → SR4 → SR3 → SR2 → SR1 →• • • ③ 过象限圆弧与坐标轴必有交点,当动点处在坐标轴上时必有一个坐 标值为零。此点可以作为过象限的标志。 ④ 终点判别不能简单地直接使用前述的三种方法,否则将丢失一部分 圆弧轮廓。
Y (0,4) (1,3) Y
X
X
为减少误差,对于 F = 0 的情况,应该根据直线的具体情况,分别进行 处理。 ① 对于 |Ye|>|Xe| 的直线,约定在Y轴方向走一步; ② 对于 |Xe|>|Ye| 的直线,则约定在X轴方向走一步。 根据改进后的算法设计的直线插补流程图如下。
开始 ① F=0 ② ∑=|Xe|+ |Ye| F=0? N N F < 0 ? Y Y +X Xe > 0? N -X Y +Y Ye > 0? N -Y Y |Ye|≥|Xe|? Y Ye > 0? N -Y N
5.3 数字积分法插补原理

主讲人:罗福源原理利用数字积分的原理,计算各坐标轴的位移,形成插补轨迹。
在计算机里,积分即是求和,也就是累加。
那么加数是什么?是微位移(Δx、Δy、......),因此数字积分法又称为DDA法,(Digital Differential Analyzer),即数字微分分析器法。
特点允许多个坐标轴同时输出脉冲。
优点运算速度快、脉冲分配均匀,易于实现多坐标联动。
X Δx01234取微位移Δx(<1个脉冲当量)进行累加运算。
随着累加次数逐渐增加,对应动点的x坐标也不断增大。
当完成若干次累加后,位移之和已经超出1个脉冲当量。
此时,利用这个溢出信号让数控系统向x坐标轴发出一个控制脉冲,使之产生一个脉冲当量的位移。
如此不断累加,每当位移之和超出1个脉冲当量,就向x 坐标轴发出一个控制脉冲,直至到达终点,插补结束。
保证Δx 与Δy 符合斜率关系即可:DDA法直线插补e ex y x y =∆∆⎪⎪⎩⎪⎪⎨⎧<=∆<=∆11m y y m x x e e设经累加m 次到达终点,则若取m =2n ,(n 为累加器位数),则易于计算机实现。
因为Δx=x e •2-n 与x e 相比,只是小数点位置不同,不影响累加运算后的有效数位与溢出的判别。
这样,把对Δx 、Δy的累加转变为对x e 与y e 的累加。
Y XA(x e ,y e )Δx2ΔxΔy 2Δy OX -Y平面第一象限直线DDA插补器的示意图:Δt Y轴溢出脉冲X轴溢出脉冲+Y 积分累加器J RYX积分累加器J RX被积函数寄存器J VX (x e )+控制脉冲被积函数寄存器J VY (y e )其它象限的直线DDA插补,参照前述逐点比较法,对终点坐标进行取绝对值并按实际方向进给即可。
累加次数m JVX(存xe)JRX(∑xe)△x JVY(存ye)JRY(∑ye)△y0100000011000 11000001100 20000111000 31000000101 40000110000 51000011100 60000101001 71000010100 80000100001 91000001100 100000111000 111000000101 120000110000 131000011100 140000101001 151000010000 160000100001A (8,6)插补轨迹理想轨迹8756123456O1234YX以第一象限逆圆弧为例V yV x VARYOXP (x i ,y j )B (x e ,y e )DDA法圆弧插补222x y R+=等式两边同时对时间参数t 求导,可得220dx dy x dy dxx y dt dt dt dty+=⇒=-由此可导出第一象限逆圆弧加工时动点沿坐标轴方向的速度分量为=x j y i dx V ky ky dt dy V kx kx dt ⎧==--⎪⎪⎨⎪===⎪⎩在一个单位时间Δt 内,X 和Y 方向上的移动距离微小增量Δ x 、Δ y 为:⎪⎩⎪⎨⎧∆=∆=∆∆=∆=∆tkx t V y t ky t V x i y j x -⎪⎩⎪⎨⎧=∆=∆=∆=∆n --n22--i i j j x t kx y y t ky x 令Δt =1,取k=2-n ,得:插补时寄存的是动点坐标x i 或y j ,是变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数控技术课程设计说明书设计题目:数字积分法圆弧插补计软件设计指导老师:专业:机械设计制造及其自动化班级:机姓名:学号:目录一、课程设计题目 (1)二、课程设计的目的 (1)三、课程设计使用的主要仪器设备 (1)四、课程设计的任务题目描述和要求 (1)五、数字积分法插补原理 (2)5.1从几何角度来看积分运算 (2)5.2数字积分圆弧插补 (3)5.3数字积分法圆弧插补程序流程图 (5)5.4插补实例 (6)六、程序清单 (7)七、软件运行效果仿真 (18)八、课程小节 (21)九、参考文献 (22)一、课程设计题目数字积分法第一、二、三、四象限顺、逆圆插补计算二、课程设计的目的《数控原理与系统》是自动化(数控)专业的一门主要专业课程,安排课程设计的目的是通过课程设计方式使学生进一步掌握和消化数控原理基本内容,了解数控系统的组成,掌握系统控制原理和方法,通过设计与调试,掌握各种功能实的现方法,为今后从事数控领域的工作打下扎实的基础。
1)了解连续轨迹控制数控系统的组成原理。
2) 掌握数字积分法(DDA)插补的基本原理。
3)掌握数字积分法(DDA)插补的软件实现方法。
三、课程设计使用的主要仪器设备1、PC计算机一台2、数控机床实验装置一台3、支持软件若干(选用VB环境)四、课程设计的任务题目描述和要求数字积分法又称数字微分分析法DDA(Digital Differential Analyzer)。
数字积分法具有运算速度快、脉冲分配均匀、易于实现多坐标联动及描绘平面各种函数曲线的特点,应用比较广泛。
其缺点是速度调节不便,插补精度需要采取一定措施才能满足要求。
由于计算机有较强的计算功能和灵活性,采用软件插补时,上述缺点易于克服。
本次课程设计具体要求如下:(1)掌握数字积分插补法基本原理(2)设计出数字积分(DDA)插补法插补软件流程图(3)编写出算法程序清单算法描述(数字积分法算法在VB中的具体实现)(4)要求软件能够实现第一、二、三、四象限顺、逆圆插补计算(5)软件运行仿真效果插补结果要求能够以图形模式进行输出五、数字积分法插补原理数字积分法又称数字积分分析法DDA(Digital differential Analyzer),简称积分器,是在数字积分器的基础上建立起来的一种插补算法。
具有逻辑能力强的特点,可实现一次、两次甚至高次曲线插补,易于实现多坐标联动。
只需输入不多的几个数据,就能加工圆弧等形状较为复杂的轮廓曲线。
直线插补时脉冲较均匀。
并具有运算速度快,应用广泛等特点。
5.1从几何角度来看积分运算如下图所示,从时刻到t 求函数曲线所包围的面积时,可用积分公式表示,如果将0~t 的时间划分成时间间隔为的有限区间,当足够小时,可得近似公式 :若△t 取“1”,上式简化为:这种累加求和运算,即积分运算可用数字积分器来实现,∑⎰⎰=∆===n i i t t ty dt t y dt t f S 100)()(∑==ni iy S 1∑∑⎰===∆−−→−∆==n i in i t i ty t y dt t y S 111)(若求曲线与坐标轴所包围的面积,求解过程如下:被积函数寄存器用以存放Y值,每当Δt 出现一次,被积函数寄存器中的Y 值就与累加器中的数值相加一次,并将累加结果存于累加器中,如果累加器的容量为一个单位面积,则在累加过程中,每超过一个单位面积,累加器就有溢出。
当累加次数达到累加器的容量时,所产生的溢出总数就是要求的总面积,即积分值。
被积函数寄存器与累加器相加的计算方法:例:被积函数寄存器与累加器均为3位寄存器,被积函数为5,求累加过程。
101 101 101 101 +)000 +)101 +)010 +)111101 010 111 100101 101 101 101 +) 100 +)001 +)110 +) 011001 110 011 000经过2 = 8次累加完成积分运算,因为有5次溢出,所以积分值等于5。
5.2对t如图所示,设加工半径为R的第一象限逆时针圆弧AB,坐标原点定在圆心上,A(Xo,Yo)为圆弧起点,B(Xe,Ye)为圆弧终点,Pi(Xi,Yi)为加工动点。
如下图所示,可以得到:V/R = Vx/Yi = Vy/Xi = K即Vx=K Yi,Vy=K Xi因而可以得到坐标微小位移增量为:ΔX=VxΔt = KYiΔt ΔY=VyΔt = KXiΔt设Δt=1,K=1/2 则有:可看出,用DDA法进行圆弧插补时,是对加工动点的坐标Xi和Yi的值分别进行累加,若积分累加器有溢出,则相应坐标轴进给一步,则圆弧积分插补器如图所示:5.3数字积分法圆弧插补程序流程图DDA法插补不同象限圆弧时,算法也有所不同。
当采用软件插补时,如果参与积分运算的寄存器均采用绝对值数据,则DDA法插补的积分累加过程完全相同,即JR+JV→JR,只是进给脉冲分配方向和圆弧插补动点坐标的修正有所不同。
5.5插补实例设有第Ⅰ象限逆圆弧SE,起点为S(4,0),终点为E(0,4),且寄存器位数N=3。
试用DDA法对该圆弧进行插补,并画出插补轨迹。
解:插补开始时,被积函数寄存器初值分别为JVX=YS=0,JVY=XS=4,终点判别寄存器JSX=|Xe-XS|=4,JSY=|Ye-YS|=4。
该圆弧插补运算过程见下表,插补轨迹如下图所示的折线。
六、程序清单Private Sub 建立坐标系_Click()Picture1.ForeColor = vbBlackPicture1.DrawWidth = 2Picture1.Line (500, 4500)-(8500, 4500) '画直线坐标轴Picture1.Line (4500, 500)-(4500, 8500)Picture1.CurrentX = 230 '当前位置Picture1.CurrentY = 4400Picture1.Print "-X" '坐标轴标注Picture1.CurrentX = 4300Picture1.CurrentY = 4300Picture1.Print "(0,0)"Picture1.CurrentX = 8650Picture1.CurrentY = 4400Picture1.Print "X"Picture1.CurrentX = 4400Picture1.CurrentY = 8600Picture1.Print "-Y"Picture1.CurrentX = 4500Picture1.CurrentY = 400Picture1.Print "Y"End SubPrivate Sub 画圆弧_Click()Dim a, b, c, d, n, m As IntegerDim r As Singlea = Val(Text1.Text)b = Val(Text2.Text)c = Val(Text3.Text)d = Val(Text4.Text)n = a * a + b * bm = c * c + d * dr = Sqr(n)If Option1.Value = True ThenIf a < 0 Or b < 0 Or c < 0 Or d < 0 Thenans = MsgBox("出错了,起点、终点坐标不在同一象限内,请重新输入", 48, "提示信息")End IfEnd IfIf Option2.Value = True ThenIf a > 0 Or b < 0 Or c > 0 Or d < 0 Thenans = MsgBox("出错了,起点、终点坐标不在同一象限内,请重新输入", 48, "提示信息")End IfEnd IfIf Option3.Value = True ThenIf a > 0 Or b > 0 Or c > 0 Or d > 0 Thenans = MsgBox("出错了,起点、终点坐标不在同一象限内,请重新输入", 48, "提示信息")End IfEnd IfIf Option4.Value = True ThenIf a < 0 Or b > 0 Or c < 0 Or d > 0 Thenans = MsgBox("出错了,起点、终点坐标不在同一象限内,请重新输入", 48, "提示信息")End IfEnd IfPicture1.ForeColor = vbRedPicture1.DrawWidth = 4Const PI = 3.1415926535If Option1.Value = True ThenIf a > c And b < d ThenIf Option1.Value = True ThenIf b = 0 ThenIf c = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 0 * 3.14159, 3.14159 / 2ElsePicture1.Circle (4500, 4500), r * 300, , 0 * 3.14159, 3.14159 / 2 - Atn(d / c) End IfElseIf c = 0 ThenPicture1.Circle (4500, 4500), r * 300, , Atn(b / a), 3.14159 / 2ElsePicture1.Circle (4500, 4500), r * 300, , Atn(b / a), 3.14159 / 2 - Atn(d / c) End IfEnd IfElseIf a < c And b > d ThenIf Option1.Value = True ThenIf a = 0 ThenIf d = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 0 * 3.14159, 3.14159 / 2ElsePicture1.Circle (4500, 4500), r * 300, , Atn(d / c), 3.14159 / 2End IfElseIf d = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 0 * 3.14159, Atn(b / a)ElsePicture1.Circle (4500, 4500), r * 300, , Atn(d / c), Atn(b / a)End IfEnd IfElseans = MsgBox("出错了,起点或终点坐标位置错误,请重新输入", 48, "提示信息")End IfEnd IfIf Option2.Value = True ThenIf a > c And b > d ThenIf Option2.Value = True ThenIf a = 0 ThenIf d = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3.14159 / 2, 3.14159ElsePicture1.Circle (4500, 4500), r * 300, , 3.14159 / 2, 3.14159 - Atn(-d / c)End IfElseIf d = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3.14159 / 2 + Atn(-a / b), 3.14159 ElsePicture1.Circle (4500, 4500), r * 300, , 3.14159 / 2 + Atn(-a / b), -Atn(-d / c) + 3.14159End IfEnd IfElseIf a < c And b < d ThenIf Option2.Value = True ThenIf b = 0 ThenIf c = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3.14159 / 2, 3.14159ElsePicture1.Circle (4500, 4500), r * 300, , Atn(-c / d), 3.14159End IfElseIf c = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3.14159 / 2, 3.14159 - Atn(-b / a) ElsePicture1.Circle (4500, 4500), r * 300, , Atn(-c / d), 3.14159 - Atn(-b / a) End IfEnd IfElseans = MsgBox("出错了,起点或终点坐标位置错误,请重新输入", 48, "提示信息")End IfEnd IfIf Option3.Value = True ThenIf a < c And b > d ThenIf Option3.Value = True ThenIf b = 0 ThenIf c = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3.14159, 3 * 3.14159 / 2ElsePicture1.Circle (4500, 4500), r * 300, , 3.14159, Atn(d / c) + 3.14159End IfElseIf c = 0 ThenPicture1.Circle (4500, 4500), r * 300, , Atn(b / a) + 3.14159, 3 * 3.14159 / 2ElsePicture1.Circle (4500, 4500), r * 300, , Atn(b / a) + 3.14159, Atn(d / c) + 3.14159End IfEnd IfElseIf a > c And b < d ThenIf Option3.Value = True ThenIf a = 0 ThenIf d = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3.14159, 3 * 3.14159 / 2ElsePicture1.Circle (4500, 4500), r * 300, , 3.14159 + Atn(d / c), 2 * 3.14159 / 2End IfElseIf d = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3.14159, 3 * 3.14159 / 2 - Atn(a / b)ElsePicture1.Circle (4500, 4500), r * 300, , Atn(d / c) + 3.14159, 3 * 3.14159 / 2 - Atn(a / b)End IfEnd IfElseans = MsgBox("出错了,起点或终点坐标位置错误,请重新输入", 48, "提示信息")End IfEnd IfIf Option4.Value = True ThenIf a < c And b < d ThenIf Option4.Value = True ThenIf a = 0 ThenIf d = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3 * 3.14159 / 2, 2 * 3.14159ElsePicture1.Circle (4500, 4500), r * 300, , 3 * 3.14159 / 2, Atn(d / c) + 3.14159 * 2End IfElseIf d = 0 ThenPicture1.Circle (4500, 4500), r * 300, , Atn(b / a) + 3.14159 * 2, 2 * 3.14159 ElsePicture1.Circle (4500, 4500), r * 300, , Atn(b / a) + 3.14159 * 2, Atn(d / c) + 3.14159 * 2End IfEnd IfElseIf a > c And b > d ThenIf Option4.Value = True ThenIf b = 0 ThenIf c = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3 * 3.14159 / 2, 2 * 3.14159ElsePicture1.Circle (4500, 4500), r * 300, , 3 * 3.14159 / 2 + Atn(-c / d), 2 * 3.14159 End IfElseIf c = 0 ThenPicture1.Circle (4500, 4500), r * 300, , 3 * 3.14159 / 2, -Atn(-b / a)ElsePicture1.Circle (4500, 4500), r * 300, , 3 * 3.14159 / 2 + Atn(-c / d), -Atn(-b / a)End IfEnd IfElseans = MsgBox("出错了,起点或终点坐标位置错误,请重新输入", 48, "提示信息")End IfEnd IfEnd SubPrivate Sub 插补计算_Click()Dim a, b, c, d, ni, mi, ai, bi, ci, k, f, g, m, n, l, i, xs, yx, xe, ye, jvx, jvy, xi, yi As IntegerDim r As Singlea = Val(Text1.Text)b = Val(Text2.Text)c = Val(Text3.Text)d = Val(Text4.Text)ni = a * a + b * bmi = c * c + d * dr = Sqr(ni)form2.ClsIf Option1.Value = True ThenIf a < 0 Or b < 0 Or c < 0 Or d < 0 Thenans = MsgBox("出错了,起点、终点坐标不在同一象限内,请重新输入", 48, "提示信息")End IfEnd IfIf Option2.Value = True ThenIf a > 0 Or b < 0 Or c > 0 Or d < 0 Thenans = MsgBox("出错了,起点、终点坐标不在同一象限内,请重新输入", 48, "提示信息")End IfEnd IfIf Option3.Value = True ThenIf a > 0 Or b > 0 Or c > 0 Or d > 0 Thenans = MsgBox("出错了,起点、终点坐标不在同一象限内,请重新输入", 48, "提示信息")End IfEnd IfIf Option4.Value = True ThenIf a < 0 Or b > 0 Or c < 0 Or d > 0 Thenans = MsgBox("出错了,起点、终点坐标不在同一象限内,请重新输入", 48, "提示信息")End IfEnd Ifci = 2f = 1g = 1k = 0 '正X进给标志 1 正向 -1负向m = 0 '负Y进给标志 1 正向 -1负向n = 0 '累加次数i = CInt(Text5) '寄存器位数赋给il = 2 ^ ixs = CInt(Text1)ys = CInt(Text2)xe = CInt(Text3)ye = CInt(Text4)jvx = Abs(CInt(Text2))jvy = Abs(CInt(Text1))jrx = 0jry = 0xi = Abs(CInt(Text3) - CInt(Text1)) 'X方向总步yi = Abs(CInt(Text4) - CInt(Text2)) 'Y方向总步长ai = xsbi = ysPicture1.ForeColor = vbGreenPicture1.DrawWidth = 3form1.CurrentX = 200form1.CurrentY = 200Print " " & " X积分器 " & " Y 积分器 "form1.CurrentX = 100form1.CurrentY = 400Print "累加次数 n" & " jvx " & "Jrx=Jrx+Jvx" & " △X " & "J∑x" & " Jvy" & " Jry=Jry+Jvy" & " △Y " & " J∑y "form1.CurrentX = 100form1.CurrentY = 600Print " 开始 " & " " & jvx & " " & jrx & " " & k & " " & xi & " " & jvy & " " & jry & " " & m & " " & yiwz: k = 0 'X方向进给标志 1 X正向进给 -1负向进给m = 0 'Y方向进给标志 1 Y正向进给 -1负向进给If xi > 0 Then 'X方向判断jrx = jrx + jvxIf jrx >= l Then '判断寄存器是否溢出jrx = jrx - l '溢出修正If jrx >= l Then '寄存器位数判断GoTo ww5End IfIf Option1.Value = True ThenIf a > c And b < d Thenk = -1Elsek = 1End IfEnd IfIf Option2.Value = True ThenIf a > c And b > d Thenk = -1ElseEnd IfEnd IfIf Option3.Value = True ThenIf a > c And b < d Thenk = -1Elsek = 1End IfEnd IfIf Option4.Value = True ThenIf a > c And b > d Thenk = -1Elsek = 1End IfEnd Ifxi = xi - 1End IfEnd IfIf yi > 0 Then 'Y方向判断jry = jry + jvyIf jry >= l Then '判断寄存器是否溢出 jry = jry - l '溢出修正If jry >= l Then '寄存器位数判断GoTo ww5End IfIf Option1.Value = True ThenIf a > c And b < d Thenm = 1Elsem = -1End IfEnd IfIf Option2.Value = True ThenIf a < c And b < d Thenm = 1Elsem = -1End IfEnd IfIf Option3.Value = True ThenIf a > c And b < d ThenElsem = -1End IfEnd IfIf Option4.Value = True ThenIf a < c And b < d Thenm = 1Elsem = -1End IfEnd Ifyi = yi - 1 'Y方向总步长减1End IfEnd Ifn = n + 1 '累加次数加1form1.CurrentX = 100form1.CurrentY = 600 + n * 200If xi = 0 Or yi = 0 ThenIf xi = 0 And yi <> 0 And f = 0 ThenPrint " " & n & " " & jvx & " " & "停止" & " " & "" & " " & "" & " " & jvy & " " & jry & " " & m & " " & yiGoTo wz2End IfIf xi = 0 And yi <> 0 And f < 0 ThenPrint " " & n & " " & jvx & " " & " " & " " & "" & " " & "" & " " & jvy & " " & jry & " " & m & " " & yiGoTo wz2End IfIf xi <> 0 And yi = 0 And g = 0 ThenPrint " " & n & " " & jvx & " " & jrx & " " & k & " " & xi & " " & jvy & " " & "停止"GoTo wz2End IfIf xi <> 0 And yi = 0 And g < 0 ThenPrint " " & n & " " & jvx & " " & jrx & " " & k & " " & xi & " " & jvyGoTo wz2End IfIf xi = 0 And yi = 0 And f = 1 And g < 0 ThenPrint " " & n & " " & jvx & " " & jry & " " & k & " " & xi & " " & jvyGoTo wz2End IfIf xi = 0 And yi = 0 And f < 0 And g = 1 ThenPrint " " & n & " " & jvx & " " & " " & " " & "" & " " & "" & " " & jvy & " " & jry & " " & m & " " & yiGoTo wz2End IfIf xi = 0 And yi = 0 And f = 0 And g = 0 ThenPrint " " & n & " " & jvx & " " & "停止" & " " & "" & " " & "" & " " & jvy & " " & "停止"GoTo wz2End IfIf xi = 0 And yi = 0 And f = 0 And g < 0 ThenPrint " " & n & " " & jvx & " " & "停止" & " " & k & " " & xi & " " & jvy & " "GoTo wz2End IfIf xi = 0 And yi = 0 And f < 0 And g = 0 ThenPrint " " & n & " " & jvx & " " & " " & " " & "" & " " & "" & " " & jvy & " " & "停止"GoTo wz2End IfEnd IfPrint " " & n & " " & jvx & " " & jrx & " " & k & " " & xi & " " & jvy & " " & jry & " " & m & " " & yiwz2: If xi = 0 Thenf = f - 1End IfIf yi = 0 Theng = g - 1End IfIf xi = 0 And yi = 0 Thenci = ci - 1If ci = 0 ThenGoTo wz3End IfEnd IfIf Option1.Value = True ThenIf a > c And b < d And k = -1 Thenjvy = jvy - 1ElseIf a > c And b < d And m = 1 Thenjvx = jvx + 1ElseIf a < c And b > d And k = 1 Thenjvy = jvy + 1ElseIf a < c And b > d And m = -1 Thenjvx = jvx - 1End IfEnd IfIf Option2.Value = True ThenIf a > c And b > d And k = -1 Thenjvy = jvy + 1ElseIf a > c And b > d And m = -1 Thenjvx = jvx - 1ElseIf a < c And b < d And k = 1 Thenjvy = jvy - 1ElseIf a < c And b < d And m = 1 Thenjvx = jvx + 1End IfEnd IfIf Option3.Value = True ThenIf a > c And b < d And k = -1 Thenjvy = jvy + 1ElseIf a > c And b < d And m = 1 Thenjvx = jvx - 1ElseIf a < c And b > d And k = 1 Thenjvy = jvy - 1ElseIf a < c And b > d And m = -1 Thenjvx = jvx + 1End IfEnd IfIf Option4.Value = True ThenIf a > c And b > d And k = -1 Thenjvy = jvy - 1ElseIf a > c And b > d And m = -1 Thenjvx = jvx + 1ElseIf a < c And b < d And k = 1 Thenjvy = jvy + 1ElseIf a < c And b < d And m = 1 Thenjvx = jvx - 1End IfEnd IfPicture1.Line (4500 + 300 * ai, 4500 - bi * 300)-(4500 + 300 * (ai + k), 4500 - (bi + m) * 300) ai = ai + kbi = bi + mGoTo wzww3: Text1.Text = ""Text2.Text = ""Text3.Text = ""Text4.Text = ""Text5.Text = ""Text1.SetFocusww5: form1.Clsans = MsgBox("出错了,寄存器位数偏小,请输入", 48, "提示信息") Text5.Text = ""Text5.SetFocusww4:wz3:End SubPrivate Sub 清除_Click()Text1.Text = ""Text2.Text = ""Text3.Text = ""Text4.Text = ""Text5.Text = ""Option1.Value = FalseOption2.Value = FalseOption3.Value = FalseOption4.Value = FalsePicture1.Clsform2.ClsEnd SubPrivate Sub 退出_Click()EndEnd Sub七、软件运行效果仿真1 进入2 第三象限3第二象限4 第四象限5 第一象限及错误提示八、课程小节通过此次课程设计,使我更好的掌握了有关数字积分法一二三四象限顺、逆圆插补计算方面的知识,在设计过程中虽然遇到了一些问题,但经过一次又一次的思考和询问,终于找出了原因所在,也暴露出了前期我在这方面的知识欠缺和经验不足。
