初中数学《全等三角形》主题单元教学设计以及思维导图
初中数学思维导图完整版

初中数学思维导图完整版、全等三角形思维导图全等三角形的刊奋角平分线的性烦全等三角形考蔡题型全等三角形的性质直角三角形具备昔通三角形的判疋方法斜边和一糸直角边(HU ) 边边边(SSS )边角边(SAS ) 角边角(ASA )角角边(AAS )角平分拔上任倉一点到角两边的距剧相等尺规柞圉拢吏角(SAS)已知T_甬找直角(HL)找策三边{S 5S) 覘已如角的月一边(SAS)边为却的邻边找己知边的对角(AAS )抉夹已知边的角(ASA ) 边为角的对边」拢任逹角(AAS )找两角肿夹边(A£A) 找任意T ( AAS }对应边相等对应角相等对应中扯髙和角平分建相等面积相等、相似三角形思维导图相似三角形的对应吊相等 稲妊角形的对应边成比例周长比等于对应边之比 租(以三角形的定义相(疟角形的定义表示方法、相似比 表示方法相似比两边对应成比例夹角招等包对应就匕例 两角对应相等具备普通三角形的判定方法F 直角边三斜边对应成比例相似三角形的性辰定义 比例相似相彳以三角形性质以三角形的对应嵩址的比等于相似比 相彳趾三角形的对应中找的比等于相似比 相似三角形的对应站平分钱的比等于相似比 相似三甬形的周长比等于相似比 相彳直角形的面积比等于相似比的平方 相似三角形具育f 饌性形状相同、对应角相等、对应边成tt;樹的图形两个比值相等的式子 形状相同 对应角相等 对应边成比例面积比是对应边比值的平方普逼三角形相彳以三角形的判定言甬三角形三、几何初步和三角形思维导图几何初步角前包角的分类甬的计算和比狡直线、射猊馥段定义对顶角两克娃垂直F耳件质相交找几何初步和三角形平行线两条直蜒被第三蕖直线所戯平n歧的性底和判库平行公理及推论内错角同位珀同欝内角三角形羽拓文和强三角形锐角二角形钝角-角惑等边三角形等腥三角形普通三角形三却形的性质三角形三边关累三角形的内外角关累■嵌四、投影与视图思维导图定义用光线照射物理「在某个平面上得到的影子平行投影分类中心投影正睡从一点发出的光线照射所形成的投影与投影面垂直的般照射所形成的投影投影与视图视点、视线和盲区走义从某f角度观察物理所看到的图像视图三视图主视團俯视图左视图立体图形的表面展开图在〜平面内,线段0检固定端点O 旋转一周.另七点A 所形成的图形 对称性直线与圆的计算 圜与圆的计算圆周角定理 圆心角 垂径定理五、圆思维导图定义罔的认识旋转不变性几何表亦 o 淘區心的圆记看(£©o"三角形外接圆和内切圆外接圆 内切圍 点在圆上与点的位置关系園的位置与直线的位置关萦 与圆的位置关系点在圆外 点在圆内 相切相交 相离相交 相离外切 内切 外离 内含5醴盅与圆相关的计算正多边形与圆的相关计算 与圆相关的定理六、实数思维导图 liftII刮蹶护战尢SV瞄琲敖肺删也:■1:I 棘出廿鹼正領D 0iWr 般辭横■互械關谢施舅£ffiHfi¥SL 辭托制'•I團制剧蛭翻珈雕宙曲底叫) 啊絢聯価〕止聲iFHfl抄if 负舲.0瞅理妍8姉啣■Ovtt«L R 颤 .MiKt&L哪删帥・nr七、代数式思维导图1收瞅 僅眦65K一爼/ 镰K 屢一蹲粗网 mfct 用恥替阳谧si 達勤盼柯锄t 豪魁般亂.™™醃歸引肌«熱就砺开方丨髓蛀旷挪J7雅師IW 单啣姑馳耐盘.狀皺切扎別密式,且时堆茁網.盹郦7 ■ D 憎讽 财瞇」側1瀚辅昕強刊;©磁榊F v '代脱|脚盼和购那壬苗和] 同一U 椰I?狀骨咖U| Ottat 林朋利公的踽汕法- 遷恥因脚?w 方张 目期舫讹脯紡云畝IS 鵡讯f 儼第赃鯉觀胴定乩飆..阳«M離塾』晅-合测障师同硼鮒 痢啣1舫 洲联逸式蓟城 亢全平育爼X 迥畫鮒鱼銃xf Jn -■ 5■酣湍*iei 」r 鏈剤闻if 掴黔齡瞅分册珈翹邂 輔.;捌游.約朝媲j 盍\片蹦祐=歸酚觀炳戟删"…那;子 R 啾有輕㈱U+川t 叮 翩我臥同券M 駄帕册眦爾能不轴 研方脚不龊卅 瀬洒威酣號攻根圖敕営悄网T 次斟RW 川礙』理咖确法HWML删。
八年级数学思维导图

八年级数学思维导图第十一章三角形本章介绍了三角形的概念及其相关性质。
三角形由三条边和三个顶点组成,可以用边、顶点或内角表示。
三角形的三边满足两边之和大于第三边的条件,同时有高、中线、角平分线等与三角形相关的线段。
三角形的内角和定理表明,三角形三个内角的和等于180°。
外角是指三角形内角的补角,三角形外角的性质也在本章中介绍。
此外,本章还涉及到多边形的相关概念及其内角和外角和的计算公式。
第十二章全等三角形本章介绍了全等三角形的概念及其相关性质。
全等三角形的对应边和对应角分别相等,有SSS、SAS、ASA、AAS等多种全等三角形的判定方法。
此外,本章还介绍了利用全等三角形解决实际问题的方法。
第十三章轴对称本章介绍了轴对称的概念及其性质。
轴对称是指平面上的一条直线,将图形沿着这条直线对称后,两边完全重合。
轴对称具有对称性和可逆性,轴对称的图形可以分为对称图形和非对称图形。
第十四章整式的乘法与因式分解本章介绍了整式的乘法与因式分解的方法。
整式是指只包含有理数、变量和加减乘幂运算的代数式,整式的乘法可以利用分配律和结合律进行展开。
因式分解是将一个整式分解为多个整式的乘积的过程,可以使用提公因式法、配方法、分组分解法等多种方法。
第十五章分式本章介绍了分式的概念及其相关性质。
分式是指形如a/b的表达式,其中a和b都是整式,b不为0.分式的化简、约分、通分、加减乘除等运算方法都在本章中介绍。
第十六章二次根式本章介绍了二次根式的概念及其相关性质。
二次根式是指形如√a的表达式,其中a是非负实数。
最简二次根式是指被开方数不含分母,分母中不含二次根式,并且被开方数中不含开得尽方的因数或因式的二次根式。
本章介绍了二次根式的乘法、除法、加减和混合运算的方法,以及二次根式的性质。
第13章全等三角形思维导图
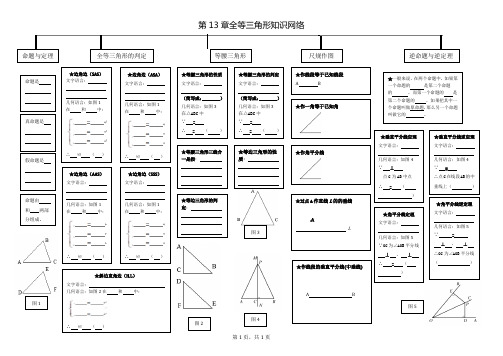
第1页,共1页第13章全等三角形知识网络命题与定理命题是★边角边(SAS )文字语言: 几何语言:如图1在 和 中:∴ ≌ ( )全等三角形的判定等腰三角形尺规作图逆命题与逆定理真命题是假命题是命题由 和 两部分组成。
★边角边(ASA ) 文字语言: 几何语言:如图1 在 和 中:∴ ≌ ( )★边角边(AAS ) 文字语言: 几何语言:如图1 在 和 中:∴ ≌ ( ) ★边角边(SSS ) 文字语言:几何语言:如图1 在 和 中:∴ ≌ ( )图1★作线段等于已知线段A B★斜边直角边(H.L )文字语言: 几何语言:如图2在 和 中:∴ ≌ ( )★等腰三角形的性质 文字语言: (简写成: ) 几何语言:如图3在△ABC 中 ∵ =∴ = ( )★等腰三角形的判定 文字语言: (简写成: ) 几何语言:如图3在△ABC 中 ∵ =∴ = ( )★等腰三角形三线合一是指:★等边三角形的性质:★等边三角形的判定: 图3图2★作一角等于已知角★作角平分线★过点A 作直线L 的的垂线.AL ★作线段的垂直平分线(中垂线)A B★一般来说,在两个命题中,如果第一个命题的 是第二个命题的 ,而第一个命题的 是第二个命题的 ,如果把其中一个命题叫做原命题,那么另一个命题叫做它的 。
★垂直平分线定理 文字语言: 几何语言:如图4∵ ⊥点C 为AB 中点∴ = ( )图4★垂直平分线逆定理 文字语言: 几何语言:如图4∵ =∴点C 在线段AB 的中垂线上( )★角平分线定理 文字语言:几何语言:如图5∵OC 为∠AOB 平分线⊥ , ⊥ ∴ = ( )图5★角平分线逆定理文字语言: 几何语言:如图5∵ =⊥ , ⊥ ∴OC 为∠AOB 平分线( )。
教学设计与思维导图:全等三角形初中数学单元

教学设计与思维导图:全等三角形初中数学单元1. 单元概述本单元主要围绕全等三角形进行讲解,帮助学生理解全等三角形的概念、性质以及判定方法。
通过本单元的研究,学生能够掌握全等三角形的判定定理,并能运用其解决实际问题。
2. 教学目标知识与技能1. 理解全等三角形的概念及其性质。
2. 掌握全等三角形的判定方法(SSS、SAS、ASA、AAS)。
3. 能够运用全等三角形的知识解决实际问题。
过程与方法1. 培养学生的观察能力、分析能力及逻辑思维能力。
2. 学会使用思维导图进行知识梳理和总结。
情感态度与价值观1. 培养学生对数学的兴趣和热情。
2. 培养学生的团队协作能力和自主研究能力。
3. 教学内容3.1 全等三角形的概念与性质1. 全等三角形的定义。
2. 全等三角形的性质。
3.2 全等三角形的判定方法1. SSS(三边相等)。
2. SAS(两边及夹角相等)。
3. ASA(两角及夹边相等)。
4. AAS(两角及非夹边相等)。
3.3 实际问题解决1. 运用全等三角形的知识解决实际问题。
2. 培养学生的应用能力。
4. 教学过程4.1 导入通过生活中的实例引入全等三角形的概念,激发学生的兴趣。
4.2 新课讲解1. 讲解全等三角形的概念与性质。
2. 讲解全等三角形的判定方法。
4.3 案例分析分析实际问题,引导学生运用全等三角形的知识解决问题。
4.4 课堂练设计相关练题,巩固所学知识。
4.5 思维导图制作引导学生制作思维导图,总结本节课的主要知识点。
4.6 课堂小结对本节课的内容进行总结,强调重点和难点。
4.7 作业布置布置相关作业,巩固所学知识。
5. 教学评价通过课堂表现、作业完成情况以及思维导图的制作,评价学生在全等三角形单元的研究效果。
同时,关注学生在解决问题过程中的创新能力和团队协作能力。
6. 教学资源1. 教学PPT。
2. 思维导图模板。
3. 练题及答案。
4. 实际问题案例。
7. 教学建议1. 注重学生基础知识的培养,加强对全等三角形概念和性质的理解。
初中数学思维导图完整详细版

初中数学思维导图完整详细版
思维导图在数学研究中是一个非常有用的工具,可以帮助学生更好地理解和记忆知识点。
以下是初中数学思维导图的完整版,包括中考考点。
一、全等三角形思维导图:全等三角形的定义、全等三角形的性质、全等三角形的判定方法、全等三角形的应用等。
二、相似三角形思维导图:相似三角形的定义、相似三角形的性质、相似三角形的判定方法、相似三角形的应用等。
三、几何初步和三角形思维导图:几何基本概念、角的概念与性质、三角形的概念与性质、三角形的内角和定理、三角形的外角和定理等。
四、投影与视图思维导图:投影的概念、投影的性质、视图的概念、视图的性质、视图的应用等。
五、圆思维导图:圆的概念、圆的性质、圆的判定方法、圆的应用等。
六、实数思维导图:实数的概念、实数的性质、实数的运算、实数的应用等。
七、代数式思维导图:代数式的概念、代数式的基本运算、代数式的因式分解、代数式的应用等。
以上是初中数学思维导图的完整版,其中包括了中考考点,希望能够帮助学生更好地研究和掌握数学知识。
初中数学《全等三角形》主题单元教学设计以及思维导图教学提纲

全等三角形适用年级八年级所需时间课内8课时,课外2课时。
主题单元学习概述从知识的特点上来讲,关于全等三角形的相关知识注重学生通过动手实践发现规律,注重培养学生的思维能力,注重数学与现实的联系;从心理学上讲,八年级学生的认知正从具体运算阶段向形式运算阶段转化,适当的动手操作活动以及问题丰富的现实背景可以帮助他们能更好地掌握相关知识。
《全等三角形》的内容,主要包括全等三角形的概念、全等三角形的性质、全等三角形的判定、角平分线的性质。
全等三角形是研究图形的重要工具,只有灵活运用它们,才能学好相关知识。
本章开始,使学生理解证明的过程,学会用综合法证明的格式。
这是本章的重点,也是难点。
对角平线的性质与判定中也不提出互逆定理。
这样不致于一下给同学们过多的概念,而加大学生负担。
本章中注重让学生经历三角形全等条件的探索过程,更注重对学生能力的培养与联系实际的能力。
我将采用以下的教法与学法:1、引导学生通过动手操作,探究规律;2、注重推理能力的培养,提高理性思维水平;3、联系生产生活实际,增加学习动力;发展学生的思维能力,沟通知识与现实的联系。
主题单元规划思维导图主题单元学习目标(知识与技能:1.掌握全等三角形的概念和性质,能够准确的辨认全等三角形中的对应元素。
2. 探索三角形全等的判定方法,并能灵活、综合运用。
3. 会作角的平分线,掌握角的平分线的性质并会利用它进行证明。
过程与方法:1.经历三角形全等的探索过程,将两个三角形的六个要素随意组合针对每种情况做出分析与验证,得出三个定理,然后将其迁移到直角三角形的判定中来。
2.经历应用全等三角形及解角平分线的有关知识去解决简单的实际问题的全过程。
3.通过开放的设计题来发展思维,培养学生的创造力。
情感态度与价值观:1.培养学习数学的兴趣,初步建立数学化归和建模的思想,积极参与探索,体验成功的喜悦。
2.通过体验抽象的数学来源于生活,同时又服务于生活。
增强了学习数学的兴趣及对生活的热爱对应课标1.通过实例认识图形的各种变换;理解全等形的概念,并能理解掌握全等三角形的性质与判定,并能应用到实际中。
全等三角形教学设计:初中数学单元与思维导图

全等三角形教学设计:初中数学单元与思维导图目标本教学设计的目标是帮助初中生理解和掌握全等三角形的概念、性质以及判定方法,并能够运用所学知识解决与全等三角形相关的问题。
教学内容1. 全等三角形的定义和性质2. 全等三角形的判定方法3. 全等三角形的运用:解决与全等三角形相关的问题教学步骤步骤一:引入在引入部分,可以通过提问或引用实际生活中与全等三角形相关的例子,引起学生的兴趣,并激发他们对于全等三角形的思考。
步骤二:概念讲解在概念讲解部分,向学生介绍全等三角形的定义和性质。
可以结合图示和实例,让学生直观地理解全等三角形的概念,并引导他们发现全等三角形的性质,如边长相等、角度相等等。
步骤三:判定方法在判定方法部分,向学生介绍几种常用的全等三角形判定方法,如SSS(边边边)、SAS(边角边)、ASA(角边角)等。
通过讲解和练,让学生掌握各种判定方法的使用条件和步骤。
步骤四:运用与解决问题在运用与解决问题部分,通过给学生提供一些与全等三角形相关的问题,让他们应用所学知识解决问题。
可以设计一些实际生活中的问题,如建筑设计、地图测量等,让学生将所学知识应用于实际情境中,提高他们的问题解决能力。
步骤五:总结与复在总结与复部分,对全等三角形的概念、性质和判定方法进行总结,并进行相关的练和复。
可以设计一些练题,让学生巩固所学知识,并评价他们的研究效果。
思维导图思维导图可以帮助学生整理和归纳所学知识,提高他们的思维能力和记忆效果。
以下是一个简单的思维导图示例:全等三角形- 定义和性质- 边长相等- 角度相等- ...- 判定方法- SSS- SAS- ASA- ...- 运用与解决问题- 实际应用- 建筑设计- 地图测量- ...- 总结与复- 概念总结- 练题复以上是一份关于全等三角形教学设计的初步构想,具体教学内容和步骤可根据实际情况进行调整和完善。
希望能对您有所帮助!。
初中数学《全等三角形》单元教学设计以及思维导图

初中数学《全等三角形》单元教学设计以及思维导图全等三角形”是八年级数学教材第十一章的重要内容。
学生需要理解全等三角形的概念和性质,掌握五种判定全等的方法,并能熟练应用这些方法解决实际问题。
此外,学生还需要结合角的平分线的性质综合运用这些知识,为后续研究打下基础。
本主题单元共分为三个专题:全等三角形、三角形全等的判定、全等三角形的应用。
教学方式主要是通过小组讨论和交流,引导学生自主探究和归纳得出全等三角形的性质和判定定理,并能熟练应用。
研究重点是全等三角形的性质和判定的综合运用,难点是让学生理解证明的基本过程和运用综合法证明的格式。
研究目标包括知识与技能、过程与方法、情感态度与价值观三个方面。
学生需要了解全等三角形的概念和性质,掌握五种判定全等的方法,并能初步应用这些方法判定三角形全等。
同时,学生还需要在图形变换和实际操作中发展空间观念和几何直觉,体验用操作归纳得出数学结论的过程,并能在生活、生产中应用角平分线的性质和判定进行推理计算。
通过本单元研究,学生可以观察、发现生活中的全等三角形,并在实际操作中获得全等三角形的体验。
同时,通过探究判定三角形全等方法的活动,培养学生合作交流的意识和大胆猜想、乐于探索的品质及发现问题、解决问题的能力。
通过折纸、画图、文字与符号的互译活动,培养学生的联想、探索、概括归纳的能力,激发学生研究数学的兴趣。
对应课标要求学生理解全等三角形的概念和性质,掌握全等三角形的判定方法,并能运用综合法进行证明。
同时,学生还需要掌握角平分线的性质和判定方法。
1、教师用课件展示全等三角形的性质,引导学生观察、分析、总结。
2、学生自主探究、验证全等三角形的性质。
1)学生在纸板上画出两个全等三角形,并标出对应元素。
2)学生通过测量、计算、推理等方法验证全等三角形的性质,如对应角相等、对应边相等、对应顶点连线相等等。
3)学生归纳总结全等三角形的性质。
活动三:应用全等三角形的性质活动步骤】1、教师用课件展示一些实际问题,引导学生运用全等三角形的性质解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形适用年级八年级所需时间课内8课时,课外2课时。
主题单元学习概述从知识的特点上来讲,关于全等三角形的相关知识注重学生通过动手实践发现规律,注重培养学生的思维能力,注重数学与现实的联系;从心理学上讲,八年级学生的认知正从具体运算阶段向形式运算阶段转化,适当的动手操作活动以及问题丰富的现实背景可以帮助他们能更好地掌握相关知识。
《全等三角形》的内容,主要包括全等三角形的概念、全等三角形的性质、全等三角形的判定、角平分线的性质。
全等三角形是研究图形的重要工具,只有灵活运用它们,才能学好相关知识。
本章开始,使学生理解证明的过程,学会用综合法证明的格式。
这是本章的重点,也是难点。
对角平线的性质与判定中也不提出互逆定理。
这样不致于一下给同学们过多的概念,而加大学生负担。
本章中注重让学生经历三角形全等条件的探索过程,更注重对学生能力的培养与联系实际的能力。
我将采用以下的教法与学法:1、引导学生通过动手操作,探究规律;2、注重推理能力的培养,提高理性思维水平;3、联系生产生活实际,增加学习动力;发展学生的思维能力,沟通知识与现实的联系。
主题单元规划思维导图主题单元学习目标(知识与技能:1.掌握全等三角形的概念和性质,能够准确的辨认全等三角形中的对应元素。
2. 探索三角形全等的判定方法,并能灵活、综合运用。
3. 会作角的平分线,掌握角的平分线的性质并会利用它进行证明。
过程与方法:1.经历三角形全等的探索过程,将两个三角形的六个要素随意组合针对每种情况做出分析与验证,得出三个定理,然后将其迁移到直角三角形的判定中来。
2.经历应用全等三角形及解角平分线的有关知识去解决简单的实际问题的全过程。
3.通过开放的设计题来发展思维,培养学生的创造力。
情感态度与价值观:1.培养学习数学的兴趣,初步建立数学化归和建模的思想,积极参与探索,体验成功的喜悦。
2.通过体验抽象的数学来源于生活,同时又服务于生活。
增强了学习数学的兴趣及对生活的热爱对应课标1.通过实例认识图形的各种变换;理解全等形的概念,并能理解掌握全等三角形的性质与判定,并能应用到实际中。
2.掌握角平线的性质与判定并能灵活运用。
3.经历三角形全等的性质的研究,进一步体验迁移思想、主动提出全等三角形中对应高线、中线,角平分线是否也相等。
掌握判定两个三角形全等的基本方法;掌握角平线的性质与判定,会用它们解决简单的几何问题和实际问题主题单元问题设计1.全等三角形有哪些性质?2.怎样判定两个三角形全等?直角三角形有没有特殊的判断方法?3.角平分线上的点有什么规律?4. 平面内的点满足什么条件时在角平线上?专题划分专题1:全等三角形的概念与性质。
1课时专题2:三角形全等的判定。
6课时专题3:角平线的性质与判定。
2课时专题4:各种活动及小结。
2课时专题一专题1:全等三角形的概念与性质。
所需课时课内1课时课外1课时专题学习目标了解全等三角形的概念和性质,能准确的辩认全等三角形中的对应元素。
同时培养学生探索与知识的迁移原理。
专题问题设计 1 同一底片复印的几张照片,它们是完全一样的2 把一块三角板按在纸上,画下图形裁下图形与三角板的形状大小一样吗?3 将一个图形进行平移、翻折、旋转变换,得到的图形全等吗。
4 当△ABC≌△DEF时,你能快速找出对应边与对应角吗所需教学环境和教学资源作图工具(直尺,一副三角尺,量角器等)几何画板课件纸笔等学习活动设计一、创设情境活动1出示教材中的图形,寻找形状大小相同的图形,归纳全等形的概念,进而得出全等三角形的概念.全等形:能够完全重合的两个图形叫做全等形.全等三角形:能够完全重合的两个三角形叫做全等三角形.二、合作探究活动2△ABC与△DEF重合(多媒体课件演示)这时,点A与点D 重合.点B与点E重合.我们把这样互相重合的一对点叫做对应顶点;AB边与DE边重合,这样互相重合的边就叫做对应边;∠A与∠D重合,它们就是对应角.△ABC与△DEF全等,我们把它记作:“△ABC≌△DEF”.读作“△ABC全等于△DEF”.注意:记两个三角形全等时,通常把对应顶点的字母写在对应的位置上.问题:你能找出其他的对应点、对应边和对应角吗?点C点F是对应点,BC边与EF边是对应边,CA与FD也是对应边.∠B与∠E对应角,∠C∠F也是对应角.活动3问题:用两块全等的三角板重合放在桌面上,让其中一块绕一个顶点旋转,你能画出几种不同的位置关系,画出图形并说出对应元素.学生活动设计:学生小组合作,动手操作,一块三角板绕一个顶点旋转,画出以下四种位置关系:不论哪种图形,点A与点A是对应顶点,点B与点E是对应顶点,点C与点D是对应顶点;AB边与AE边是对应边,ac边与ad边、DE边与CB边也是对应边;∠BAC与∠EAD是对应角,∠B与∠E,∠C与∠D是对应角.教师活动设计:本活动主要加深学生对全等三角形概念的理解,以及动手操作能力的培养.活动4 拿一张纸对折后,剪成两个全等的三角形,△ABC和△ECD,把这两个三角形一起放在下列图中△abc的位置上,试一试,如果其中一个三角形不动,怎样移动另一个三角形,能够得到下列图中的各图形,从中你能得到什么启发?学生活动设计:经过观察、操作可以发现,可以经过平移、翻折、旋转得到,变化前后对应角、对应边不变.教师活动设计:组织学生观察、归纳,引导学生归纳全等三角形的性质:全等三角形的对应边相等.全等三角形的对应角相等.三、拓展创新问题:如图,△ABC≌△AEC,∠B=30°,∠ACB=85°.求出△AEC 各内角的度数.解:在△ABC中,已知∠ACB=85°,∠B=30°,根据三角形的内角和等于180°,可得:∠BAC=65°.因为△ABC≌△AEC,所以∠EAC=∠BAC=65°,∠E=∠B=30°,∠ACB=85°.答:△AEC的内角的度数分别为65°、30°、85°.四、归纳小结1.全等形、全等三角形及相关概念.2.全等三角形的性质.五、布置作业教科书p4 第1题第2题第3题教科书p5 第4题评价要点对学生分类中出现的问题,予以纠正,对学生提出的解决问题的不同策略,要给予肯定和鼓励,以满足多样化的学生需要,发展学生个性思维。
专题二三角形全等的判定所需课时课内4课时课外2课时专题学习目标1、学生在教师引导下,积极主动地经历探索三角形全等的条件的过程,体会利用操作、归纳获得数学结论的过程。
2、掌握三角形全等的“边边边”、“边角边”、“角边角”、“角角边”的判定方法,了解三角形的稳定性,能用三角形的全等解决一些实际问题。
3、培养学生的空间观念,推理能力,发展有条理地表达能力,积累数学活动经验。
专题问题设计1. 怎样判定两个三角形全等?2.直角三角形有没有特殊的判断方法?3.角平分线上的点有什么规律?4. 平面内的点满足什么条件时在角平线上?所需教学环境和教学资多媒体教室,三角尺,圆规等学习活动设计1 先任意画一个△ABC,再画一个△A1B1C1,使A1B1=AB,∠A1=∠A,∠B1=∠B(即使两角和它们的夹边对应相等)。
把画好的△A1B1C1剪下,放到△ABC上,它们全等吗?(让学生通过画图了解,画第一边后,已经定好两个顶点,再画两个角,两个角已确定,那么三角形的第三个顶点也确定,所以这两个三角形全等)2、探究的结果反映了什么规律?你能得出什么结论?(板书:两角和它们的夹边对应相等的两个三角形全等,可以简写成“角边角”或“ASA”)3、动手做一做在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC 和△DEF全等吗?能利用角边角条件证明你的结论吗?4、证明的结果得出什么结论?(板书:两个角和其中一个角的对边对应相等的两个三角形全等,可以简写成“角角边”或“AAS”)5、你能利用上面的结论解决上课开始提出的问题吗?评价能探索得到并会使用判定要点专角平分线的性质和判定题三所课内2课时课外1课时需课时专题学习目标1、掌握“角平分线线上的点到角的两边距离相等”这一的性质;2、能运用“角平分线线上的点到角的两边距离相等”这一性质解决简单的几何问题;3、初步学会将文字语言转化为图形和符号语言并按步骤进而证明,提高分析问题及逻辑推理能力。
专题问题设此节内容是在学生学习了角平分线的概念和证明直角三角形全等的基础上进行教学。
角平分线的性质是为证明线段或角相等,是全等三角形知识的计延续。
此节内容为下一节课学习角平分线的判定作铺垫,同时让学生通过运用本节知识,得出三角形的三条角平分线交于一点这个结论,为学生今后在“圆”一章学习内心作好准备。
因此,本节内容在数学知识体系中起到了承上启下的作用。
同时教材的安排由浅入深、由易到难、知识结构合理,符合学生的心理特点和认知规律。
学情分析刚进入初二的学生观察、操作、猜想能力较强,但归纳、运用数学意识的思想比较薄弱,思维的广阔性、敏捷性、灵活性比较欠缺,需要在课堂教学中进一步加强引导。
根据学生的认知特点和接受水平,我把第一课时的教学重点定为:掌师(多媒体展示)问题情境:如图1,在公路和铁路交叉所成的角平分线上有一空旷场地,市政府决定利用此空旷地投资修建一个批发市场,那么这个批发市场到公路和铁路的距离哪个更近?生:有的回答“一样近”。
师:为什么会“一样近”?本节课我们就带着这个问题走进今天的学习内容。
板书:角平分线的性质。
所需教学环境和教学资源多媒体三角尺学习活动设计活动一:折纸实验。
师:不利用工具,请你将一张用纸片做的角分成两个相等的角。
你有什么办法?生:对拆。
师:再打开纸片,看看折痕与这个角有何关系?(让五个学生上讲台演示自己的活动成果)。
众生:角平分线。
评析:活动一的教学目的是让学生通过折纸实验初步感知“角平线上的点到角的两边距离相等”这一事实。
但是,此活动只让学生折出角平分线是一个不完整的活动,学生在折纸过程中没有达到实验探究的效果。
教科书中通过折纸活动得到“角平分线上的点到角的两边距离相等”的结论是由如图2所示通过两次折纸得到的。
这里只完成了第一次。
而第二次是再折出一个直角三角形并展开后会出现两条折痕,这两条折痕的数量关系如何,此时没有体现出来。
至于在第二种折法中再折一次,又会出现两条折痕,而且这两条折痕是等长的,这种方法可以做无数次,所以这种等长的折痕可以折出无数确被教师忽略了(即角平分线上的点的任意性),从而导致教学过程变成了信马由缰的活动,学生在“蒙”和“碰”中前行,漫无目的。
问题产生的主要原因是教师没有领悟探究角平分线的性质折纸实验的本质是首先寻找到角的两边距离等长的两条折痕,教学抓不住“本质”就会变得无的放矢。
(注:在课堂上确有学生折出直角三角形来了,可惜教师没有发现或被忽视。
