利用对角线法则计算下列三阶行列式

合集下载

线性代数课后习题答案全)习题详解

线性代数课后习题答案全)习题详解第一章行列式1.利用对角线法则计算下列三阶行列式：（1）381141102---；（2）b a c a c b c b a ; （3）222111c b a c b a ；（4）y x y x x y x yyx y x +++. 解（1）=---381141102811)1()1(03)4(2⨯⨯+-⨯-⨯+⨯-⨯)1()4(18)1(2310-⨯-⨯-⨯-⨯-⨯⨯-=416824-++-=4-（2）=ba c a cb cb a ccc aaa bbb cba bac acb ---++3333c b a abc ---=（3）=222111c b a c b a 222222cb ba ac ab ca bc ---++))()((a c c b b a ---=（4）yx y x x y x y yx y x +++yx y x y x yx y y x x )()()(+++++=333)(x y x y -+-- 33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序，求下列各排列的逆序数：（1）1 2 3 4；（2）4 1 3 2；（3）3 4 2 1；（4）2 4 1 3；（5）1 3 … )12(-n 2 4 … )2(n ；（6）1 3 … )12(-n )2(n )22(-n … 2. 解（1）逆序数为0（2）逆序数为4：4 1，4 3，4 2，3 2 （3）逆序数为5：3 2，3 1，4 2，4 1,2 1 （4）逆序数为3：2 1，4 1，4 3 （5）逆序数为2)1(-n n ： 3 2 1个 5 2，5 4 2个 7 2，7 4，7 6 3个 ……………… …)12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n )1(-n 个（6）逆序数为)1(-n n3 2 1个 5 2，54 2个 ……………… …)12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n )1(-n 个4 2 1个 6 2，6 4 2个 ……………… …)2(n 2，)2(n 4，)2(n 6，…，)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项.解由定义知，四阶行列式的一般项为43214321)1(p p p p t a a a a -，其中t 为4321p p p p 的逆序数．由于3,121==p p 已固定，4321p p p p 只能形如13□□，即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式：（1）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢7110025*********4；（2）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-265232112131412；（3）⎥⎥⎦⎥⎢⎢⎣⎢---ef cf bf de cd bd ae ac ab ；（4）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a100110011001解(1)7110025102021421434327c c c c --1002310021214---34)1(142101+-⨯--=143102211014-- 321132c c c c ++141717001099-(2)2605232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=e c b e c b e c b adf ---=111111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 10111--+23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -; (2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=y x z x z y z y x b a )(33+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--= 右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bz ay y x by ax x z bx az z y b +++zy x y x z xz y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c c b b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+ddd c c c bb b a a a (4)4444442222220001ad a c a b a ad a c a b a ad a c a b a ---------=左边)()()222222222222a d d a c c a a d a c ad a c ------ =)()()(111))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =⨯---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立，即,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x xa xD D n n n n 右边=+=-n n a xD 1 所以，对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转，依次得n nn n a a a a D 11111 =， 11112n nn n a a a a D = ，11113a a a a D n nnn =，证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnnn nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-= 同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n Tn n 2)1(2)1()1()1(---=-= D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式（阶行列式为k D k ）：(1)aaD n 11=,其中对角线上元素都是a ，未写出的元素都是0；(2)xa a ax aa a x D n =; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n nn n n ------=---+; 提示：利用范德蒙德行列式的结果． (4) nnn nn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 00010000000000001000 =按最后一行展开)1()1(1000000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n na a a (再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行，得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上，得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始，第1+n 行经过n 次相邻对换，换到第1行，第n 行经)1(-n 次对换换到第2行…，经2)1(1)1(+=++-+n n n n 次行交换，得 nnn n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-•-•-=---=111)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nn nnn d c d c b a b a D 011112=n n n nd c d c b a b a a 0000111111--展开按第一行0000)11111111112c d c d c b a b a b nn n n n nn ----+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式：222)(--=n n n n n n D c b d a D即 ∏=-=ni i i iin D c b da D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=0432********0122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0432111111111111111111111 --------------n n n n,,141312c c c c c c +++152423210222102210002100001---------------n n n n n =212)1()1(----n n n(6)nn a a D a +++=11111111121n n n n a a a a a a a a +------10001001000100100010000114332展开（由下往上）按最后一列1(+n a nn n a a a a a a a ------00000000000000000000000224332 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组：⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x 解 (1)11213513241211111----=D 8120735032101111------=145008130032101111---=1421420005410032101111-=---= 112105132412211151------=D 11210513290501115----=1121023313090509151------=2331309050112109151------=1202300461000112109151-----=000100210151---= 112035122412111512-----=D 11503120270151------=313911230231115-2842840001910023101151-=----=426110135232422115113-=----=D ; 14202132132212151114=-----=D1,3,2,144332211-========∴DDx D D x D D x D D x (2) 510006510006510065100065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',) 5100165100065100650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507= 5101065100065000601000152=D 展开按第二列5100651006500061-6510065000610005-365510651065⨯-= 1145108065-=--= 51100650000601000051001653=D 展开按第三列0000105165610050066100510656510650061+= 703114619=⨯+= 51000601000051000651010654=D 展开按第四列61000510065100655000610005100651--51065106565--=395-= 11051000651000651100655=D 展开按最后一列D '+10005100651006512122111=+= 665212;665395;665703;6651145;665150744321=-==-==∴x x x x x ． 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解？解 μλμμμλ-==12111113D ，齐次线性方程组有非零解，则03=D即 0=-μλμ 得 10==λμ或不难验证，当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ 有非零解？解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-=3)1(2)1(23-+-+-=λλλ齐次线性方程组有非零解，则0=D 得 32,0===λλλ或不难验证，当32,0===λλλ或时，该齐次线性方程组确有非零解.第二章矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换.解由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T .4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635.(2)⎪⎪⎭⎫ ⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫⎝⎛---=632142. (4)⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B)2=A 2+2AB +B 2吗? 解 (A +B)2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A ,⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610,所以(A +B)2≠A 2+2AB +B 2.(3)(A +B)(A -B)=A 2-B 2吗? 解 (A +B)(A -B)≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B)(A -B)≠A 2-B 2.6. 举反列说明下列命题是错误的:(1)若A 2=0, 则A =0;解取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k.解⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k .8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k.解首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立，则k +1时，⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵，且A 为对称矩阵，证明B T AB 也是对称矩阵. 证明因为A T =A , 所以(B T AB)T =B T (B T A)T =B T A T B =B T AB ,从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵，证明AB 是对称矩阵的充分必要条件是AB =BA . 证明充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB)T =(BA)T =A T B T =AB ,即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB)T =AB , 所以 AB =(AB)T =B T A T =BA . 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解⎪⎭⎫ ⎝⎛=5221A . |A|=1, 故A -1存在. 因为⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225.(2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A|=1≠0, 故A -1存在. 因为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos .(3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫ ⎝⎛---=145243121A . |A|=2≠0, 故A -1存在. 因为 ⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012. (4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ; 解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232.(2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ; 解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫ ⎝⎛---=32538122.(3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; 解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X . 解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫⎝⎛---=201431012. 13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明因为A k =O , 所以E -A k =E . 又因为E -A k =(E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E ,由定理2推论知(E -A)可逆, 且(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明一方面, 有E =(E -A)-1(E -A).另一方面, 由A k =O , 有E =(E -A)+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A),故 (E -A)-1(E -A)=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A),两端同时右乘(E -A)-1, 就有(E -A)-1(E -A)=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E)-1. 证明由A 2-A -2E =O 得A 2-A =2E , 即A(A -E)=2E ,或 E E A A =-⋅)(21, 由定理2推论知A 可逆, 且)(211E A A -=-. 由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E)(A -3E)=-4E ,或 E A E E A =-⋅+)3(41)2( 由定理2推论知(A +2E)可逆, 且)3(41)2(1A E E A -=+-.证明由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得|A 2-A|=2,即 |A||A -E|=2,故 |A|≠0,所以A 可逆, 而A +2E =A 2, |A +2E|=|A 2|=|A|2≠0, 故A +2E 也可逆.由 A 2-A -2E =O ⇒A(A -E)=2E⇒A -1A(A -E)=2A -1E ⇒)(211E A A -=-, 又由 A 2-A -2E =O ⇒(A +2E)A -3(A +2E)=-4E⇒ (A +2E)(A -3E)=-4 E ,所以 (A +2E)-1(A +2E)(A -3E)=-4(A +2 E)-1,)3(41)2(1A E E A -=+-. 16. 设A 为3阶矩阵,21||=A , 求|(2A)-1-5A*|. 解因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |1-A =|-2A -1|=(-2)3|A -1|=-8|A|-1=-8⨯2=-16.17. 设矩阵A 可逆, 证明其伴随阵A*也可逆, 且(A*)-1=(A -1)*.证明由*||11A A A =-, 得A*=|A|A -1, 所以当A 可逆时, 有 |A*|=|A|n |A -1|=|A|n -1≠0,从而A*也可逆.因为A*=|A|A -1, 所以(A*)-1=|A|-1A . 又*)(||)*(||1111---==A A A A A , 所以 (A*)-1=|A|-1A =|A|-1|A|(A -1)*=(A -1)*.18. 设n 阶矩阵A 的伴随矩阵为A*, 证明:(1)若|A|=0, 则|A*|=0;(2)|A*|=|A|n -1.证明(1)用反证法证明. 假设|A*|≠0, 则有A*(A*)-1=E , 由此得A =A A*(A*)-1=|A|E(A*)-1=O ,所以A*=O , 这与|A*|≠0矛盾，故当|A|=0时, 有|A*|=0.(2)由于*||11A A A =-, 则AA*=|A|E , 取行列式得到 |A||A*|=|A|n .若|A|≠0, 则|A*|=|A|n -1;若|A|=0, 由(1)知|A*|=0, 此时命题也成立.因此|A*|=|A|n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B . 解由AB =A +2E 可得(A -2E)B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫ ⎝⎛-=011321330. 20. 设⎪⎪⎭⎫ ⎝⎛=101020101A , 且AB +E =A 2+B , 求B . 解由AB +E =A 2+B 得(A -E)B =A 2-E ,即 (A -E)B =(A -E)(A +E).因为01001010100||≠-==-E A , 所以(A -E)可逆, 从而⎪⎪⎭⎫ ⎝⎛=+=201030102E A B . 21. 设A =diag(1, -2, 1), A*BA =2BA -8E , 求B .解由A*BA =2BA -8E 得(A*-2E)BA =-8E ,B =-8(A*-2E)-1A -1=-8[A(A*-2E)]-1=-8(AA*-2A)-1=-8(|A|E -2A)-1=-8(-2E -2A)-1=4(E +A)-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-= =2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫ ⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解由|A*|=|A|3=8, 得|A|=2.由ABA -1=BA -1+3E 得AB =B +3A ,B =3(A -E)-1A =3[A(E -A -1)]-1A 11*)2(6*)21(3---=-=A E A E ⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--=-1030060600600006603001010010000161.23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A=P Λ11P -1.|P|=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P , 而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001, 故 ⎪⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 24. 设AP =P Λ, 其中⎪⎪⎭⎫ ⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A)=A 8(5E -6A +A 2).解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)]=diag(1,1,58)diag(12,0,0)=12diag(1,0,0).ϕ(A)=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112 ⎪⎪⎭⎫⎝⎛=1111111114. 25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明因为A -1(A +B)B -1=B -1+A -1=A -1+B -1,而A -1(A +B)B -1是三个可逆矩阵的乘积, 所以A -1(A +B)B -1可逆, 即A -1+B -1可逆. (A -1+B -1)-1=[A -1(A +B)B -1]-1=B(A +B)-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121. 解设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B , 则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A , 而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠. 解 41001200210100101002000021010010110100101==--=--=D C B A , 而 01111|||||||| ==D C B A ,故 |||||||| D C B A D C B A ≠. 28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫ ⎝⎛=21A O O A A , 故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,1682818281810||||||||||===A A A A A . ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ;解设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则 ⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A .解设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得 ⎪⎩⎪⎨⎧=+=+==s nE BD CD O BD CD OAD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001.解设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A BC O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001.第三章矩阵的初等变换与线性方程组1．把下列矩阵化为行最简形矩阵：(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2)⎪⎪⎪⎭⎫⎝⎛----174034301320; (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; (4)⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--340313*********2)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020*********)2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫ ⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫ ⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----1740343013201312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫ ⎝⎛---31003100132021233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫⎝⎛000031005010 (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311141312323~r r r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311)5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311 2423213~r r r r r r ---⎪⎪⎪⎪⎭⎫⎝⎛---000000000022********(4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110141312782~rr r r r r --+⎪⎪⎪⎪⎭⎫⎝⎛--410004100020201111134221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎭⎫⎝⎛----0000041000111102020132~rr +⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.设⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ，求A 。

线性代数第6版第1章课后习题解答

1 −15 −7
1 2 2
−720| −4
r3 +15r2 r4 + 7r2
|00 0
1 0 0
1 17 9
875| = 0 45
2141
（2）D r2 + r1 |51
0 2
6 3
22| = 0
5062
（3）D r1 a
−�� | ��
�� −��
�� + ��
�� + ��
�� + ��
r2 (a + b + c) (�� + �� + ��) |
1 1
1 1
1 1 |=0
�� + �� + �� + ��
(�� − ��)�� − ��
��2
�� + ��
2��| = (�� − ��)2 | 2
�� 1
��2 2��|
c2 − c3
0
0
1
0 01
c1
−
2c2
(��
−
��)2
�� + 1 2 −1 （1） | 2 �� + 1 1 | = 0
−1 1 �� + 1
解：
1111
（2）|��2

线性代数课后习题答案全解.pdf

第一章行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102−−−;解 381141102−−−=2×(−4)×3+0×(−1)×(−1)+1×1×8 −0×1×3−2×(−1)×8−1×(−4)×(−1) =−24+8+16−4=−4. (2)b a c a c b cb a ;解 ba c a cb cb a=acb +bac +cba −bbb −aaa −ccc =3abc −a 3−b 3−c 3. (3)222111c b a c b a ;解 222111c b a c b a=bc 2+ca 2+ab 2−ac 2−ba 2−cb =(a −b )(b −c )(c −a ). 2(4)y x y x x y x y yx y x +++.解 yx y x x y x y yx y x +++=x (x +y )y +yx (x +y )+(x +y )yx −y 3−(x +y )3−x =3xy (x +y )−y 3 3−3x 2 y −x 3−y 3−x =−2(x 3 3+y 3 2. 按自然数从小到大为标准次序, 求下列各排列的逆序数:).(1)1 2 3 4; 解逆序数为0 (2)4 1 3 2;解逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n −1) 2 4 ⋅ ⋅ ⋅ (2n );解逆序数为2)1(−n n : 3 2 (1个) 5 2, 5 4(2个) 7 2, 7 4, 7 6(3个)⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n −1)2, (2n −1)4, (2n −1)6, ⋅ ⋅ ⋅, (2n −1)(2n −2) (n −1个)(6)1 3 ⋅ ⋅ ⋅ (2n −1) (2n ) (2n −2) ⋅ ⋅ ⋅ 2. 解逆序数为n (n −1) : 3 2(1个) 5 2, 5 4 (2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n −1)2, (2n −1)4, (2n −1)6, ⋅ ⋅ ⋅, (2n −1)(2n −2) (n −1个) 4 2(1个) 6 2, 6 4(2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n )2, (2n )4, (2n )6, ⋅ ⋅ ⋅, (2n )(2n −2) (n −1个) 3. 写出四阶行列式中含有因子a 11a 23 解含因子a 的项. 11a 23(−1)的项的一般形式为t a 11a 23a 3r a 4s 其中rs 是2和4构成的排列, 这种排列共有两个, 即24和42. ,所以含因子a 11a 23 (−1)的项分别是t a 11a 23a 32a 44=(−1)1a 11a 23a 32a 44=−a 11a 23a 32a 44 (−1), t a 11a 23a 34a 42=(−1)2a 11a 23a 34a 42=a 11a 23a 34a 42 4. 计算下列各行列式:.(1)71100251020214214; 解 71100251020214214010014231020211021473234−−−−−======c c c c 34)1(143102211014+−×−−−= 143102211014−−=01417172001099323211=−++======c c c c .(2)2605232112131412−; 解 2605232112131412−26053212213041224−−=====c c 041203212213041224−−=====r r 0000003212213041214=−−=====r r . (3)efcf bf de cd bd aeac ab −−−;解 ef cf bf de cd bd ae ac ab −−−ec b e c b ec b adf −−−=abcdef adfbce 4111111111=−−−=.(4)dc b a 100110011001−−−. 解d c b a 100110011001−−−dc b aab ar r 10011001101021−−−++===== d c a ab 101101)1)(1(12−−+−−=+01011123−+−++=====cd c ada ab dc ccdad ab +−+−−=+111)1)(1(23=abcd +ab +cd +ad +1. 5. 证明:(1)1112222b b a a b ab a +=(a −b )3 证明;1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c −−−−−−=====ab a b a b a ab 22)1(22213−−−−−=+21))((a b a a b a b +−−==(a −b )3 (2) . y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=y x z x z y zy x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ; 证明 2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4−c 3, c 3−c 2, c 2−c 1 得) 5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4−c 3, c 3−c 2得)022122212221222122222=++++=d d c c b b a a . (4)444422221111d c b a d c b a d c b a =(a −b )(a −c )(a −d )(b −c )(b −d )(c −d )(a +b +c +d ); 证明 444422221111d c b a d c b a d c b a )()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b −−−−−−−−−=)()()(111))()((222a d d a c c a b b dc b ad a c a b +++−−−= ))(())((00111))()((a b d b d d a b c b c c bd b c a d a c a b ++−++−−−−−−= )()(11))()()()((a b d d a b c c b d b c a d a c a b ++++−−−−−= =(a −b )(a −c )(a −d )(b −c )(b −d )(c −d )(a +b +c +d ). (5)12211 000 00 1000 01a x a a a a x x xn n n+⋅⋅⋅−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−−− =x n +a 1x n −1+ ⋅ ⋅ ⋅ +a n −1x +a n .证明用数学归纳法证明.当n =2时, 2121221a x a x a x a x D ++=+−=, 命题成立. 假设对于(n −1)阶行列式命题成立, 即 D n −1=x n −1+a 1 x n −2+ ⋅ ⋅ ⋅ +a n −2x +a n −1则D , n 按第一列展开, 有 11100 100 01)1(11−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−−+=+−x x a xD D n n n n =xD n −1+a n =x n +a 1x n −1+ ⋅ ⋅ ⋅ +a n −1x +a n 因此, 对于n 阶行列式命题成立. .6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90°、或依副对角线翻转, 依次得n nn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nnn a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n n nn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(−−==, D 3 证明因为D =det(a =D .ij ), 所以 nnn n n n nnnn a a a a a a a a a a D 2211111111111 )1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=−⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−−=−− )1()1(331122111121nnn n nn n n a a a a a a a a D D n n n n 2)1()1()2( 21)1()1(−−+−+⋅⋅⋅++−=−=.同理可证 nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−=− )1(11112)1(2D D n n T n n 2)1(2)1()1()1(−−−=−=. D D D D D n n n n n n n n =−=−−=−=−−−−)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k (1)为k 阶行列式): aa D n 1 1⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解 aa a a a D n 010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 000 00 000 0010 000)1(−×−+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−=n n n aa a )1()1(2 )1(−×−⋅⋅⋅⋅−+n n n a a an n n n n a a a+⋅⋅⋅−⋅−=−−+)2)(2(1)1()1(=a n −a n −2=a n −2(a 2−1).(2)xa aa x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解将第一行乘(−1)分别加到其余各行, 得 ax x a ax x a a x x a aa a x D n −−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−−⋅⋅⋅−−⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n −⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−+=0000 0 000 00 )1(=[x +(n −1)a ](x −a )n −1 (3). 111 1 )( )1()( )1(1111⋅⋅⋅−⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅⋅⋅⋅−⋅⋅⋅−−⋅⋅⋅−=−−−+n a a a n a a a n a a a D n n n n nn n ; 解根据第6题结果, 有 nnn n n n n n n n a a a n a a a n a a aD )( )1()( )1( 11 11)1(1112)1(1−⋅⋅⋅−−⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−=−−−++此行列式为范德蒙德行列式.∏≥>≥++++−−+−−=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++−−−=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+−++−⋅−⋅−=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+−=11)(j i n j i .(4)nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112; 解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开) nn n n n nd d c d c b a b a a 00011111111−−−−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn −−−−+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−+. 再按最后一行展开得递推公式D 2n =a n d n D 2n −2−b n c n D 2n −2, 即D 2n =(a n d n −b n c n )D 2n −2于是 . ∏=−=ni i i i i n D c b d a D 222)(.而 111111112c b d a d c b a D −==,所以 ∏=−=ni i i i i n c b d a D 12)(.(5) D =det(a ij ), 其中a ij 解 a =|i −j |; ij =|i −j |, 043214 01233 10122 21011 3210)det(⋅⋅⋅−−−−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−⋅⋅⋅==n n n n n n n n a D ij n 04321 1 11111 11111 11111 1111 2132⋅⋅⋅−−−−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−−−−⋅⋅⋅−−−⋅⋅⋅−−⋅⋅⋅−−⋅⋅⋅−=====n n n n r r r r15242321 0 22210 02210 00210 0001 1213−⋅⋅⋅−−−−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−−−−⋅⋅⋅−−−⋅⋅⋅−−⋅⋅⋅−+⋅⋅⋅+=====n n n n n c c c c =(−1)n −1(n −1)2n −2 (6).nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121 nn n n a a a a a a a a a c c c c +−⋅⋅⋅−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−=====−−100001 000 100 0100 0100 0011332212132 1111312112111000011 000 00 11000 01100 001 −−−−−−+−⋅⋅⋅−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅⋅⋅⋅=nn n a a a a a a a a∑=−−−−−−+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 00010 000 00 10000 01000 001)11)((121∑=+=ni i n a a a a .8. 用克莱姆法则解下列方程组: (1) =+++−=−−−−=+−+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解因为 14211213513241211111−=−−−−=D , 142112105132412211151−=−−−−−−=D , 284112035122412111512−=−−−−−=D , 426110135232422115113−=−−−−=D , 14202132132212151114=−−−−−=D , 所以 111==D D x , 222==D Dx , 333==DD x , 144−==D D x .(2)=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解因为 665510006510006510065100065==D , 15075100165100065100065000611==D , 114551010651000650000601000152−==D , 703511650000601000051001653==D , 39551601000051000651010654−==D , 2121100005100065100651100655==D , 所以66515071=x , 66511452−=x , 6657033=x , 6653954−=x , 6652124=x .9. 问λ, µ取何值时, 齐次线性方程组 =++=++=++0200321321321x x x x x x x x x µµλ有非零解？解系数行列式为µλµµµλ−==1211111D .令D =0, 得 µ=0或λ=1.于是, 当µ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组 =−++=+−+=+−−0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解？解系数行列式为λλλλλλλ−−+−−=−−−−=101112431111132421D=(1−λ)3 =(1−λ)+(λ−3)−4(1−λ)−2(1−λ)(−3−λ) 3+2(1−λ)2 令D =0, 得+λ−3. λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解.第二章矩阵及其运算1. 已知线性变换:++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3 解由已知:的线性变换.= 221321323513122y y y x x x ,故= −3211221323513122x x x y y y−−−−=321423736947y y y ,−+=−+=+−−=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换++=++−=+=32133212311542322y y y x y y y x y y x ,+−=+=+−=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3 解由已知的线性变换.−= 221321514232102y y y x x x−− −=321310102013514232102z z z−−−−=321161109412316z z z ,所以有 +−−=+−=++−=3213321232111610941236z z z x z z z x z z z x .3. 设 −−=111111111A ,−−=150421321B , 求3AB −2A 及A T 解 B .−−− −− −−=−1111111112150421321111111111323A AB−−−−= −−− −=2294201722213211111111120926508503,−= −− −−=092650850150421321111111111B A T.4. 计算下列乘积: (1)−127075321134;解 −127075321134 ×+×+××+×−+××+×+×=102775132)2(71112374=49635.(2)123)321(;解123)321(=(1×3+2×2+3×1)=(10).(3))21(312−;解 )21(312−×−××−××−×=23)1(321)1(122)1(2−−−=632142. (4)−−−−20413121013143110412 ; 解−−− −20413121013143110412 −−−=6520876. (5)321332313232212131211321)(x x x a a a a a a a a a x x x ;解321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3a 13x 1+a 23x 2+a 33x 3321x x x )322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设 =3121A ,=2101B , 问: (1)AB =BA 吗? 解 AB ≠BA . 因为=6443AB ,=8321BA , 所以AB ≠BA .(2)(A +B )2=A 2+2AB +B 2 解 (A +B )吗? 2≠A 2+2AB +B 2 因为.=+5222B A ,=+52225222)(2B A=2914148,但 + +=++43011288611483222B AB A=27151610,所以(A +B )2≠A 2+2AB +B 2 (3)(A +B )(A −B )=A . 2−B 2 解 (A +B )(A −B )≠A 吗? 2−B 2 因为.=+5222B A ,=−1020B A ,==−+906010205222))((B A B A ,而= −=−718243011148322B A ,故(A +B )(A −B )≠A 2−B 2 6. 举反列说明下列命题是错误的:.(1)若A 2 解取=0, 则A =0;=0010A , 则A 2 (2)若A =0, 但A ≠0. 2 解取=A , 则A =0或A =E ;=0011A , 则A 2 (3)若AX =AY , 且A ≠0, 则X =Y .=A , 但A ≠0且A ≠E . 解取=0001A , −=1111X ,=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k 解 . ==12011011012λλλA , ===1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,=101λk A k . 8. 设=λλλ001001A , 求A k 解首先观察. =λλλλλλ0010010010012A=222002012λλλλλ,=⋅=3232323003033λλλλλλA A A ,=⋅=43423434004064λλλλλλA A A ,=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,=k A k k k k k k k k k k λλλλλλ0002)1(121−−−−. 用数学归纳法证明:当k =2时, 显然成立.假设k 时成立，则k +1时，−=⋅=−−−+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A+++=+−+−−+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:−=−−−k k k k k k k k k k k A λλλλλλ0002)1(121. 9. 设A , B 为n 阶矩阵，且A 为对称矩阵，证明B T 证明因为A AB 也是对称矩阵.T (B =A , 所以T AB )T =B T (B T A )T =B T A T B =B T 从而B AB ,T 10. 设A , B 都是n 阶对称矩阵，证明AB 是对称矩阵的充分必要条件是AB =BA .AB 是对称矩阵.证明充分性: 因为A T =A , B T (AB )=B , 且AB =BA , 所以 T =(BA )T =A T B T 即AB 是对称矩阵.=AB ,必要性: 因为A T =A , B T =B , 且(AB )T AB =(AB )=AB , 所以T =B T A T 11. 求下列矩阵的逆矩阵:=BA .(1)5221; 解=5221A . |A |=1, 故A −1 存在. 因为−−= =1225*22122111A A A A A ,故 *||11A A A =−−−=1225. (2)−θθθθcos sin sin cos ; 解−=θθθθcos sin sin cos A . |A |=1≠0, 故A −1 存在. 因为−= =θθθθcos sin sin cos *22122111A A A A A , 所以 *||11A A A =−−=θθθθcos sin sin cos . (3)−−−145243121; 解−−−=145243121A . |A |=2≠0, 故A −1 存在. 因为−−−−−= =214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =−−−−−−=1716213213012. (4)n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解=n a a a A 0021, 由对角矩阵的性质知=−n a a a A 10011211 . 12. 解下列矩阵方程:(1) −=12643152X ; 解 −=−126431521X − −−=12642153 −=80232. (2) −=−−234311*********X ; 解 1111012112234311−−− −=X−−− −=03323210123431131 −−−=32538122. (3) −= − −101311022141X ;解 11110210132141−− − − −=X− −=210110131142121 =21010366121=04111. (4)−−−= 021102341010100001100001010X . 解 11010100001021102341100001010−−−−− =X −−− =010100001021102341100001010 −−−=201431012. 13. 利用逆矩阵解下列线性方程组:(1) =++=++=++3532522132321321321x x x x x x x x x ; 解方程组可表示为= 321153522321321x x x , 故 = = −0013211535223211321x x x ,从而有 ===001321x x x . (2) =−+=−−=−−05231322321321321x x x x x x x x x . 解方程组可表示为=−−−−−012523312111321x x x , 故 =−−−−−= −3050125233121111321x x x , 故有 ===305321x x x . 14. 设A k =O (k 为正整数), 证明(E −A )−1=E +A +A 2+⋅ ⋅ ⋅+A k −1 证明因为A . k =O , 所以E −A k E −A =E . 又因为k =(E −A )(E +A +A 2+⋅ ⋅ ⋅+A k −1所以 (E −A )(E +A +A ),2+⋅ ⋅ ⋅+A k −1由定理2推论知(E −A )可逆, 且)=E ,(E −A )−1=E +A +A 2+⋅ ⋅ ⋅+A k −1.证明一方面, 有E =(E −A )−1 另一方面, 由A (E −A ).k E =(E −A )+(A −A =O , 有2)+A 2−⋅ ⋅ ⋅−A k −1+(A k −1−A k )=(E +A +A 2+⋅ ⋅ ⋅+A k −1故 (E −A ))(E −A ),−1(E −A )=(E +A +A 2+⋅ ⋅ ⋅+A k −1两端同时右乘(E −A ))(E −A ),−1 (E −A ), 就有−1(E −A )=E +A +A 2+⋅ ⋅ ⋅+A k −1.15. 设方阵A 满足A 2−A −2E =O , 证明A 及A +2E 都可逆, 并求A −1及(A +2E )−1 证明由A .2 A −A −2E =O 得2或 −A =2E , 即A (A −E )=2E ,E E A A =−⋅)(21, 由定理2推论知A 可逆, 且)(211E A A −=−. 由A 2 A −A −2E =O 得2或 −A −6E =−4E , 即(A +2E )(A −3E )=−4E ,E A E E A =−⋅+)3(41)2( 由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A −=+−.证明由A 2−A −2E =O 得A 2 |A −A =2E , 两端同时取行列式得 2即 |A ||A −E |=2,−A |=2,故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2由 A ≠0, 故A +2E 也可逆. 2 ⇒A −A −2E =O ⇒A (A −E )=2E−1A (A −E )=2A −1)(211E A A −=−E ⇒,又由 A 2 ⇒ (A +2E )(A −3E )=−4 E ,−A −2E =O ⇒(A +2E )A −3(A +2E )=−4E所以 (A +2E )−1(A +2E )(A −3E )=−4(A +2 E )−1 ,)3(41)2(1A E E A −=+−.16. 设A 为3阶矩阵, 21||=A , 求|(2A )−1 解因为−5A *|.*||11A A A =−, 所以 |||521||*5)2(|111−−−−=−A A A A A |2521|11−−−=A A=|−2A −1|=(−2)3|A −1|=−8|A |−1 17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)=−8×2=−16.−1=(A −1 证明由)*.*||11A A A =−, 得A *=|A |A −1 |A *|=|A |, 所以当A 可逆时, 有n |A −1|=|A |n −1从而A *也可逆.≠0,因为A *=|A |A −1 (A *), 所以−1=|A |−1又A .*)(||)*(||1111−−−==A A A A A , 所以(A *)−1=|A |−1A =|A |−1|A |(A −1)*=(A −1 18. 设n 阶矩阵A 的伴随矩阵为A *, 证明:)*.(1)若|A |=0, 则|A *|=0;(2)|A *|=|A |n −1 证明.(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)−1 A =A A *(A *)=E , 由此得 −1=|A |E (A *)−1所以A *=O , 这与|A *|≠0矛盾，故当|A |=0时, 有|A *|=0.=O ,(2)由于*||11A A A =−, 则AA *=|A |E , 取行列式得到 |A ||A *|=|A |n 若|A |≠0, 则|A *|=|A |.n −1 若|A |=0, 由(1)知|A *|=0, 此时命题也成立.;因此|A *|=|A |n −1.19. 设−=321011330A , AB =A +2B , 求B . 解由AB =A +2E 可得(A −2E )B =A , 故− −−−=−=−−321011330121011332)2(11A E A B −=011321330. 20. 设 =101020101A , 且AB +E =A 2+B , 求B .解由AB +E =A 2 (A −E )B =A +B 得 2即 (A −E )B =(A −E )(A +E ).−E , 因为01001010100||≠−==−E A , 所以(A −E )可逆, 从而=+=201030102E A B .21. 设A =diag(1, −2, 1), A *BA =2BA −8E , 求B . 解由A *BA =2BA −8E 得 (A *−2E )BA =−8E , B =−8(A *−2E )−1A =−8[A (A *−2E )]−1 =−8(AA *−2A )−1 =−8(|A |E −2A )−1 =−8(−2E −2A )−1 =4(E +A )−1 =4[diag(2, −1, 2)]−1−1)21 ,1 ,21(diag 4−==2diag(1, −2, 1).22. 已知矩阵A 的伴随阵−=8030010100100001*A , 且ABA −1=BA −1+3E , 求B .解由|A *|=|A |3 由ABA =8, 得|A |=2. −1=BA −1 AB =B +3A ,+3E 得 B =3(A −E )−1A =3[A (E −A −1)]−1 A 11*)2(6*)21(3−−−=−=A E A E−=−−=−1030060600600006603001010010000161. 23. 设P −1 −−=1141P AP =Λ, 其中,−=Λ2001, 求A 11 解由P . −1AP =Λ, 得A =P ΛP −1, 所以A 11= A =P Λ11P −1 |P |=3, .−=1141*P ,−−=−1141311P ,而−= −=Λ11111120 012001,故−− −−−=31313431200111411111A −−=68468327322731. 24. 设AP =P Λ, 其中−−=111201111P ,−=Λ511,求ϕ(A )=A 8(5E −6A +A 2 解 ϕ(Λ)=Λ). 8(5E −6Λ+Λ2 =diag(1,1,5)8)[diag(5,5,5)−diag(−6,6,30)+diag(1,1,25)]=diag(1,1,58 ϕ(A )=P ϕ(Λ)P )diag(12,0,0)=12diag(1,0,0).−1 *)(||1P P P Λ=ϕ−−−−−− −−−=1213032220000000011112011112=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A −1+B −1 证明因为也可逆, 并求其逆阵.A −1(A +B )B −1=B −1+A −1=A −1+B −1而A ,−1(A +B )B −1是三个可逆矩阵的乘积, 所以A −1(A +B )B −1可逆, 即A −1+B −1 (A 可逆.−1+B −1)−1=[A −1(A +B )B −1]−1=B (A +B )−1 26. 计算A .−−−30003200121013013000120010100121. 解设 =10211A , =30122A , −=12131B ,−−=30322B ,则 2121B O B E A O E A+=222111B A O B B A A ,而 −= −−+−=+4225303212131021211B B A ,−−= −− =90343032301222B A , 所以 2121B O B E A O E A +=222111B A O B B A A−−−=9000340042102521, 即−−−30003200121013013000120010100121−−−=9000340042102521. 27. 取==−==1001D C B A , 验证|||||||| D C B A D C B A ≠.解 4100120021010*********0021010010110100101==−−=−−=D C B A , 而 01111|||||||| ==D C B A ,故 ||||||||D C B A D C B A ≠. 28. 设 −=22023443O O A , 求|A 8|及A 4解令. −=34431A ,=22022A , 则=21A O O A A ,故 8218=A O O A A=8281A O O A ,1682818281810||||||||||===A A A A A .= =464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求 (1)1−O B A O ; 解设 =−43211C C C C O B A O , 则O B A O 4321C C C C = =s n E O O E BC BC AC AC 2143. 由此得====s n EBC OBC O AC E AC 2143⇒ ====−−121413B C O C O C A C ,所以= −−−O A B O O B A O 111. (2)1−B C O A . 解设 =−43211D D D D B C O A , 则 = ++= s nE O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得=+=+==s nEBD CD O BD CD O AD E AD 423121⇒ =−===−−−−14113211B D CA B D O D A D ,所以−= −−−−−11111B CA B O A BC O A . 30. 求下列矩阵的逆阵: (1)2500380000120025; 解设 =1225A , =2538B , 则−−= =−−5221122511A ,−−==−−8532253811B .于是 −−−−= = =−−−−850032000052002125003800001200251111B A B A .(2)4121031200210001. 解设 =2101A ,=4103B ,=2112C , 则−= =−−−−−−1111114121031200210001B CA B O A BC O A−−−−−=411212458103161210021210001.第三章矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵: (1)−−340313021201;解−−340313021201(下一步: r 2+(−2)r 1, r 3+(−3)r 1 ~. )−−−020*********(下一步: r 2÷(−1), r 3 ~÷(−2). )−−010*********(下一步: r 3−r 2 ~. )−−300031001201(下一步: r 3 ~÷3. )−−100031001201(下一步: r 2+3r 3 ~. )−100001001201(下一步: r 1+(−2)r 2, r 1+r 3 ~. )100001000001.(2)−−−−174034301320;解−−−−174034301320(下一步: r 2×2+(−3)r 1, r 3+(−2)r 1 ~. )−−−310031001320(下一步: r 3+r 2, r 1+3r 2 ~. )0000310010020(下一步: r 1 ~÷2. )000031005010.(3)−−−−−−−−−12433023221453334311;解−−−−−−−−−12433023221453334311(下一步: r 2−3r 1, r 3−2r 1, r 4−3r 1~. )−−−−−−−−1010500663008840034311(下一步: r 2÷(−4), r 3÷(−3) , r 4~÷(−5). )−−−−−22100221002210034311(下一步: r 1−3r 2, r 3−r 2, r 4−r 2~. )−−−00000000002210032011.(4)−−−−−−34732038234202173132. 解−−−−−−34732038234202173132(下一步: r 1−2r 2, r 3−3r 2, r 4−2r 2~. )−−−−−1187701298804202111110(下一步: r 2+2r 1, r 3−8r 1, r 4−7r 1 ~. )−−41000410002020111110(下一步: r 1↔r 2, r 2×(−1), r 4−r 3~. )−−−−00000410001111020201(下一步: r 2+r 3~. )−−00000410003011020201. 2. 设= 987654321100010101100001010A , 求A .解100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身.100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(−1))−=100010101.− =100010101987654321100001010A= − =287221254100010101987321654.3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵: (1)323513123;解 100010001323513123~−−−101011001200410123~ −−−−1012002110102/102/3023~−−−−2/102/11002110102/922/7003~−−−−2/102/11002110102/33/26/7001故逆矩阵为−−−−21021211233267.(2)−−−−−1210232112201023.解−−−−−10000100001000011210232112201023~−−−−00100301100001001220594012102321~−−−−−−−−20104301100001001200110012102321~ −−−−−−−106124301100001001000110012102321 ~−−−−−−−−−−10612631110`1022111000010000100021 ~−−−−−−−106126311101042111000010000100001故逆矩阵为−−−−−−−10612631110104211. 4. (1)设 −−=113122214A ,−−=132231B , 求X 使AX =B ;解因为−−−−=132231 113122214) ,(B A−−412315210 100010001 ~r ,所以−−==−4123152101B A X .(2)设−−−=433312120A , −=132321B , 求X 使XA =B . 解考虑A T X T =B T . 因为−−−−=134313*********) ,(T T B A−−−411007101042001 ~r ,所以−−−==−417142)(1T T T B A X ,从而−−−==−4741121BA X . 5. 设−−−=101110011A , AX =2X +A , 求X .解原方程化为(A −2E )X =A . 因为−−−−−−−−−=−101101110110011011) ,2(A E A−−−011100101010110001~,所以−−−=−=−011101110)2(1A E A X .6. 在秩是r 的矩阵中,有没有等于0的r −1阶子式? 有没有等于0的r 阶子式?解在秩是r 的矩阵中, 可能存在等于0的r −1阶子式, 也可能存在等于0的r 阶子式. 例如,=010*********A , R (A )=3.0000是等于0的2阶子式, 010001000是等于0的3阶子式. 7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样?解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, −1, 0, 0, 0).解用已知向量容易构成一个有4个非零行的5阶下三角矩阵:−0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式: (1)−−−443112112013;解−−−443112112013(下一步: r 1↔r 2 ~. )−−−443120131211(下一步: r 2−3r 1, r 3−r 1 ~. )−−−−564056401211(下一步: r 3−r 2 ~. )−−−000056401211, 矩阵的2秩为, 41113−=−是一个最高阶非零子式.(2)−−−−−−−815073*********;解−−−−−−−815073*********(下一步: r 1−r 2, r 2−2r 1, r 3−7r 1 ~. )−−−−−−15273321059117014431(下一步: r 3−3r 2~. )−−−−0000059117014431, 矩阵的秩是2, 71223−=−是一个最高阶非零子式.(3)−−−02301085235703273812. 解−−−02301085235703273812(下一步: r 1−2r 4, r 2−2r 4, r 3−3r 4~. )−−−−−−023*********63071210(下一步: r 2+3r 1, r 3+2r 1~. )−0230114000016000071210(下一步: r 2÷16r 4, r 3−16r 2. )~−02301000001000071210 ~−00000100007121002301, 矩阵的秩为3, 070023085570≠=−是一个最高阶非零子式.10. 设A 、B 都是m ×n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ).证明根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设−−−−=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 −−−−=32321321k k k A+−−−−−)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =−2且k ≠1时, R (A )=2;(3)当k ≠1且k ≠−2时, R (A )=3.12. 求解下列齐次线性方程组: (1) =+++=−++=−++02220202432143214321x x x x x x x x x x x x ;解对系数矩阵A 进行初等行变换, 有 A = −−212211121211~ −−−3/410013100101,于是 ==−==4443424134334x x x x x x x x ,故方程组的解为−= 1343344321k x x x x (k 为任意常数).(2) =−++=−−+=−++05105036302432143214321x x x x x x x x x x x x ;解对系数矩阵A 进行初等行变换, 有 A = −−−−5110531631121~−000001001021,于是 ===+−=4432242102x x x xx x x x ,故方程组的解为+−= 10010*********k k x x x x (k 1, k 2 (3)为任意常数).=−+−=+−+=−++=+−+07420634072305324321432143214321x x x x x x x x x x x x x x x x ;解对系数矩阵A 进行初等行变换, 有 A =−−−−−7421631472135132~1000010000100001,于是 ====0004321x x x x ,故方程组的解为 ====00004321x x x x .(4) =++−=+−+=−+−=+−+03270161311402332075434321432143214321x x x x x x x x x x x x x x x x .解对系数矩阵A 进行初等行变换, 有 A =−−−−−3127161311423327543~−−000000001720171910171317301,于是 ==−=−=4433432431172017191713173x x x x x x x xx x ,故方程组的解为−−+= 1017201713011719173214321k k x x x x (k 1, k 2为任意常数).13. 求解下列非齐次线性方程组: (1) =+=+−=−+83111021322421321321x x x x x x x x ;解对增广矩阵B 进行初等行变换, 有。

线性代数课后习题1-4作业答案(高等教育出版社)

第一章行列式1. 利用对角线法则计算下列三阶行列式:(1)381141102---;解381141102--- =2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4.(3)222111c b a cb a ;解222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).4. 计算下列各行列式:(1)7110025*******214; 解 7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---=143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-;解 2605232112131412-260503212213041224--=====cc 041203212213041224--=====rr000003212213041214=--=====r r .(3)efcf bf decd bd ae ac ab ---;解 ef cf bf de cd bd ae ac ab ---e c b ec b e c b ad f ---=a b c d e fa d fbc e 4111111111=---=.(4)dc b a 100110011001---.解dc b a100110011001---dc b a ab ar r 10011001101021---++=====d c a ab 101101)1)(1(12--+--=+01011123-+-++=====cdc ad a ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 6. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213ab a b a a b a ab ac c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)yx z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=yx z x z y zy x b a )(33+=.8. 计算下列各行列式(D k 为k 阶行列式):(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解a a a a a D n 0 0010 000 00 0000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n行展开))1()1(10 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a a n n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1 )1()1(=an-a n -2=a n -2(a 2-1).(2)xa a a x aa a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0 ,再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 000 00 )1(=[x +(n -1)a ](x -a )n 第二章矩阵及其运算 1. 计算下列乘积: (5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.2. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B ,求3AB -2A 及A T B .解⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.3.已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4.设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A , ⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.5. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0.(2)若A 2=A , 则A =0或A =E ;解取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y . 7.设⎪⎪⎭⎫⎝⎛=λλλ001001A ,求A k .解首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫.用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立，则k +1时，⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.8. 设A , B 为n 阶矩阵，且A 为对称矩阵，证明B T AB 也是对称矩阵.证明因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵. 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫⎝⎛5221;解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为⎪⎭⎫⎝⎛--=⎪⎭⎫⎝⎛=1225*22122111A A A A A , 故 *||11A A A =-⎪⎭⎫⎝⎛--=1225.(3)⎪⎪⎭⎫ ⎝⎛---145243121;解⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以*||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解⎪⎪⎪⎭⎫ ⎝⎛=n a a a A0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=-n a a a A 10011211 .12. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有⎪⎩⎪⎨⎧===001321x x x . 19.设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫⎝⎛-=Λ2001, 求A 11. 解由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 20. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511,求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)]=diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫ ⎝⎛=1111111114.21. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.22. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.第三章矩阵的初等变换与线性方程组 1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫ ⎝⎛--340313021201;解⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. ) ~⎪⎪⎭⎫ ⎝⎛100001000001.(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311;解⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011.3. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z , 所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛323513123;解⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫ ⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001 故逆矩阵为⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解⎪⎪⎪⎭⎫⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321~⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021~⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010********* 故逆矩阵为⎪⎪⎪⎭⎫ ⎝⎛-------10612631110104211.5. (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫⎝⎛-=132321B , 求X 使XA =B .解考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫ ⎝⎛---411007101042001 ~r ,所以⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫⎝⎛---==-4741121BA X . 9. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量. 12.设⎪⎪⎭⎫⎝⎛----=32321321k k k A ,问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3. 解⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r .(1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3. P106/ 1.已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示. 证明由⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r⎪⎪⎪⎭⎫ ⎝⎛------531400251552000751610421301~r ⎪⎪⎪⎭⎫ ⎝⎛-----000000531400751610421301~r知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示. 由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示. 4. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.5. 问a 取什么值时下列向量组线性相关？ a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关.9.设b 1=a 1+a 2, b 2=a 2+a 3, b 3=a 3+a 4, b 4=a 4+a 1, 证明向量组b 1, b 2, b 3, b 4线性相关.证明由已知条件得a 1=b 1-a 2, a 2=b 2-a 3, a 3=b 3-a 4, a 4=b 4-a 1,于是 a 1 =b 1-b 2+a 3 =b 1-b 2+b 3-a 4 =b 1-b 2+b 3-b 4+a 1, 从而 b 1-b 2+b 3-b 4=0,这说明向量组b 1, b 2, b 3, b 4线性相关.11.(1) 求下列向量组的秩, 并求一个最大无关组:(1)a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 解由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000000010291032001900820291844210141002291) , ,(~~321r r a a a ,知R (a 1, a 2, a 3)=2. 因为向量a 1与a 2的分量不成比例, 故a 1, a 2线性无关, 所以a 1, a 2是一个最大无关组.12.利用初等行变换求下列矩阵的列向量组的一个最大无关组: (1)⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125;解因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513121433~r r r r r r ---⎪⎪⎪⎭⎫ ⎝⎛531053103210431731253423~r r r r --⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125, 所以第1、2、3列构成一个最大无关组.(2)⎪⎪⎪⎭⎫⎝⎛---14011313021512012211. 解因为⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221113142~r r r r --⎪⎪⎪⎭⎫ ⎝⎛------222001512015120122112343~r r r r +↔⎪⎪⎪⎭⎫ ⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组. 13. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=52001110311161101110311131********) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5. 20.求下列齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;解对系数矩阵进行初等行变换, 有 ⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ,于是得⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x .取(x 3, x 4)T =(4, 0)T , 得(x 1, x 2)T =(-16, 3)T ; 取(x 3, x 4)T =(0, 4)T , 得(x 1, x 2)T =(0, 1)T . 因此方程组的基础解系为ξ1=(-16, 3, 4, 0)T , ξ2=(0, 1, 0, 4)T .(2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x . 解对系数矩阵进行初等行变换, 有 ⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛----=000019/719/141019/119/201 367824531232~r A ,于是得⎩⎨⎧+-=+-=432431)19/7()19/14()19/1()19/2(x x x x x x . 取(x 3, x 4)T =(19, 0)T , 得(x 1, x 2)T =(-2, 14)T ; 取(x 3, x 4)T =(0, 19)T , 得(x 1, x 2)T =(1, 7)T . 因此方程组的基础解系为ξ1=(-2, 14, 19, 0)T , ξ2=(1, 7, 0, 19)T .26. 求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=+++=+++=+3223512254321432121x x x x x x x x x x ;解对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛=2100013011080101 322351211250011~r B . 与所给方程组同解的方程为⎪⎩⎪⎨⎧=+=--=213 843231x x x x x . 当x 3=0时, 得所给方程组的一个解η=(-8, 13, 0, 2)T . 与对应的齐次方程组同解的方程为⎪⎩⎪⎨⎧==-=043231x x x x x . 当x 3=1时, 得对应的齐次方程组的基础解系ξ=(-1, 1, 1, 0)T .(2)⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x . 解对增广矩阵进行初等行变换, 有 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛-----=0000022/17/11012/17/901 6124211635113251~r B . 与所给方程组同解的方程为⎩⎨⎧--=++-=2)2/1((1/7)1)2/1()7/9(432431x x x x x x . 当x 3=x 4=0时, 得所给方程组的一个解η=(1, -2, 0, 0)T .与对应的齐次方程组同解的方程为⎩⎨⎧-=+-=432431)2/1((1/7))2/1()7/9(x x x x x x . 分别取(x 3, x 4)T =(1, 0)T , (0, 1)T , 得对应的齐次方程组的基础解系ξ1=(-9, 1, 7, 0)T . ξ2=(1, -1, 0, 2)T .。

线性代数课后习题1-4作业答案(高等教育出版社)

第一章行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102---;解 381141102---=2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4. (3)222111c b a c b a ; 解 222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).4. 计算下列各行列式:(1)71100251020214214; 解 7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-;解 2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r 000003212213041214=--=====r r . (3)efcf bf de cd bd aeac ab ---;解 ef cf bf de cd bd ae ac ab ---e c b e c b ec b adf ---=abcdef adfbce 4111111111=---=.(4)dc b a 100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ada ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 6. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=yx z x z y zy x b a )(33+=.8. 计算下列各行列式(D k 为k 阶行列式): (1)aa D n 1 1⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 000 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解将第一行乘(-1)分别加到其余各行, 得 ax x a ax x a a x x a a a a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n 第二章矩阵及其运算 1. 计算下列乘积:(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.2. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T . 3.已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4.设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问: (1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.5. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k .解首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立，则k +1时，⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.8. 设A , B 为n 阶矩阵，且A 为对称矩阵，证明B T AB 也是对称矩阵.证明因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵. 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 利用逆矩阵解下列线性方程组: (1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解方程组可表示为 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有 ⎪⎩⎪⎨⎧===001321x x x .19.设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 20. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.21. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.22. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.第三章矩阵的初等变换与线性方程组 1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫⎝⎛100001000001.(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; 解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011. 3. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫⎝⎛-------106126311101042111000010000100001 故逆矩阵为⎪⎪⎪⎭⎫⎝⎛-------10612631110104211. 5. (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 9. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.12. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3. P106/ 1.已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示.证明由 ⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r ⎪⎪⎪⎭⎫⎝⎛------531400251552000751610421301 ~r ⎪⎪⎪⎭⎫ ⎝⎛-----000000531400751610421301~r 知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示.由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示. 4. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.5. 问a 取什么值时下列向量组线性相关？ a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关.9.设b 1=a 1+a 2, b 2=a 2+a 3, b 3=a 3+a 4, b 4=a 4+a 1, 证明向量组b 1, b 2, b 3, b 4线性相关.证明由已知条件得a 1=b 1-a 2, a 2=b 2-a 3, a 3=b 3-a 4, a 4=b 4-a 1,于是 a 1 =b 1-b 2+a 3 =b 1-b 2+b 3-a 4 =b 1-b 2+b 3-b 4+a 1, 从而 b 1-b 2+b 3-b 4=0,这说明向量组b 1, b 2, b 3, b 4线性相关.11.(1) 求下列向量组的秩, 并求一个最大无关组:(1)a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 解由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000000010291032001900820291844210141002291) , ,(~~321r r a a a , 知R (a 1, a 2, a 3)=2. 因为向量a 1与a 2的分量不成比例, 故a 1, a 2线性无关, 所以a 1, a 2是一个最大无关组.12.利用初等行变换求下列矩阵的列向量组的一个最大无关组:(1)⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125;解因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513121433~r r r r r r ---⎪⎪⎪⎭⎫ ⎝⎛531053103210431731253423~rr r r --⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125, 所以第1、2、3列构成一个最大无关组.(2)⎪⎪⎪⎭⎫⎝⎛---140113*********12211. 解因为⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221113142~rr r r --⎪⎪⎪⎭⎫ ⎝⎛------222001512015120122112343~rr r r +↔⎪⎪⎪⎭⎫ ⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组. 13. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=52001110311161101110311131********) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5. 20.求下列齐次线性方程组的基础解系: (1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;解对系数矩阵进行初等行变换, 有⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ,于是得⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x .取(x 3, x 4)T =(4, 0)T , 得(x 1, x 2)T =(-16, 3)T ; 取(x 3, x 4)T =(0, 4)T , 得(x 1, x 2)T =(0, 1)T . 因此方程组的基础解系为ξ1=(-16, 3, 4, 0)T , ξ2=(0, 1, 0, 4)T .(2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x .解对系数矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛----=000019/719/141019/119/201 367824531232~r A ,于是得⎩⎨⎧+-=+-=432431)19/7()19/14()19/1()19/2(x x x x x x .取(x 3, x 4)T =(19, 0)T , 得(x 1, x 2)T =(-2, 14)T ; 取(x 3, x 4)T =(0, 19)T , 得(x 1, x 2)T =(1, 7)T . 因此方程组的基础解系为ξ1=(-2, 14, 19, 0)T , ξ2=(1, 7, 0, 19)T .26. 求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=+++=+++=+3223512254321432121x x x x x x x x x x ;解对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛=2100013011080101 322351211250011~r B . 与所给方程组同解的方程为⎪⎩⎪⎨⎧=+=--=213 843231x x x x x . 当x 3=0时, 得所给方程组的一个解η=(-8, 13, 0, 2)T . 与对应的齐次方程组同解的方程为⎪⎩⎪⎨⎧==-=043231x x x x x . 当x 3=1时, 得对应的齐次方程组的基础解系ξ=(-1, 1, 1, 0)T .(2)⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x . 解对增广矩阵进行初等行变换, 有⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-----=0000022/17/11012/17/901 6124211635113251~r B . 与所给方程组同解的方程为⎩⎨⎧--=++-=2)2/1((1/7)1)2/1()7/9(432431x x x x x x . 当x 3=x 4=0时, 得所给方程组的一个解η=(1, -2, 0, 0)T .与对应的齐次方程组同解的方程为⎩⎨⎧-=+-=432431)2/1((1/7))2/1()7/9(x x x x x x . 分别取(x 3, x 4)T =(1, 0)T , (0, 1)T , 得对应的齐次方程组的基础解系ξ1=(-9, 1, 7, 0)T . ξ2=(1, -1, 0, 2)T .。

线性代数课后习题1-4作业答案(高等教育出版社)

= 1 2 −2 ====== 0 0 − 2 =0.
10
3
14
c1
+
1 2
c3
17
17
14
2 1 41
(2)
3 1
−1 2
2 3
1 2
;
5 0 62
解
2 3 1
1 −1 2
4 2 3
1 1 2
c4 − c2 =====
2 3 1
1 −1 2
4 2 3
0 2 0
r4 − r2 =====
2 3 1
2 2
52⎟⎠⎞⎜⎝⎛00
12 ⎟⎠⎞ = ⎜⎝⎛ 00
96⎟⎠⎞ ,
而
A2
−
B2
=
⎜⎝⎛
3 4
181⎟⎠⎞ − ⎜⎝⎛13
40⎟⎠⎞ = ⎜⎝⎛ 12
78⎟⎠⎞ ,
故(A+B)(A−B)≠A2−B2.
5. 举反列说明下列命题是错误的:
(1)若 A2=0, 则 A=0;
解取 A=⎜⎝⎛00 01⎟⎠⎞ , 则 A2=0, 但 A≠0. (2)若 A2=A, 则 A=0 或 A=E;
4. 计算下列各行列式:
4 124
(1)1 10Fra bibliotek2 5
0 2
2 0
;
0 117
解
4 1 10 0
1 2 5 1
2 0 2 1
4 2 0 7
=cc=42=−−=7c=c33=10140
−1 2 3 0
2 0 2 1
−10 2
−14 0
4 =1
10
−1 2 3
−10 2 ×(−1)4+3

线性代数第五版(同济大学)课后习题答案

−b b b 0 2
c −c c 2 0
e e −e = adf bce
−1 1 1
1 −1 1
1 1 −1
−1 1
r +r r3 +r1
0 0 a −1 0 0
0 2 1 b −1 0
= −adf bce
= 4abcdef.
(4)
0
1 2 = = = = = =
1 + ab b −1 0
a 1 c
= = = =a
裂开
再次
2
y z x
2 (3) 逆序数为 5: 3 2, 3 1, 4 2, 4 1, 2 1. (4) 逆序数为 3: 2 1, 4 1, 4 3. (5) 逆序数为
n(n−1) : 2
第一章行列式
3 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1 个 5 2, 5 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 个 7 2, 7 4, 7 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 个 .................................................................................. (2n − 1) 2, (2n − 1) 4, (2n − 1) 6, . . . , (2n − 1) (2n − 2). . . . . . . . . . . . . .(n − 1) 个 (6) 逆序数为 n(n − 1): 3 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1 个 5 2, 5 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 个 7 2, 7 4, 7 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 个 .................................................................................. (2n − 1) 2, (2n − 1) 4, (2n − 1) 6, . . . , (2n − 1) (2n − 2). . . . . . . . . . . . . .(n − 1) 个 4 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1 个 6 2, 6 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 个 .................................................................................. (2n) 2, (2n) 4, (2n) 6, . . . , (2n) (2n − 2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (n − 1) 个 3 . 写出四阶行列式中含有因子 a11 a23 的项.

同济大学线性代数第六版标准答案(全)

第一章行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102---;解 381141102---=2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4. (2)b a c a c b cb a ;解 ba c a cb cb a=acb +bac +cba -bbb -aaa -ccc=3abc -a 3-b 3-c 3.(3)222111c b a c b a ;解 222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2=(a -b )(b -c )(c -a ).(4)y x y x x y x y yx y x +++.解 yx y x x y x y yx y x +++=x (x +y )y +yx (x +y )+(x +y )yx -y 3-(x +y )3-x 3 =3xy (x +y )-y 3-3x 2 y -x 3-y 3-x 3 =-2(x 3+y 3).2. 按自然数从小到大为标准次序, 求下列各排列的逆序数:(1)1 2 3 4; 解逆序数为0 (2)4 1 3 2;解逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解逆序数为3: 2 1, 4 1, 4 3.(5)1 3 ⋅⋅⋅ (2n-1) 2 4 ⋅⋅⋅ (2n);解逆序数为2)1(-nn:3 2 (1个)5 2, 5 4(2个)7 2, 7 4, 7 6(3个)⋅⋅⋅⋅⋅⋅(2n-1)2, (2n-1)4, (2n-1)6, ⋅⋅⋅, (2n-1)(2n-2) (n-1个) (6)1 3 ⋅⋅⋅(2n-1) (2n) (2n-2) ⋅⋅⋅ 2.解逆序数为n(n-1) :3 2(1个)5 2, 5 4 (2个)⋅⋅⋅⋅⋅⋅(2n-1)2, (2n-1)4, (2n-1)6, ⋅⋅⋅, (2n-1)(2n-2) (n-1个)4 2(1个)6 2, 6 4(2个)⋅⋅⋅⋅⋅⋅(2n)2, (2n)4, (2n)6, ⋅⋅⋅, (2n)(2n-2) (n-1个)3. 写出四阶行列式中含有因子a11a23的项.解含因子a11a23的项的一般形式为(-1)t a 11a 23a 3r a 4s ,其中rs 是2和4构成的排列, 这种排列共有两个, 即24和42. 所以含因子a 11a 23的项分别是(-1)t a 11a 23a 32a 44=(-1)1a 11a 23a 32a 44=-a 11a 23a 32a 44, (-1)t a 11a 23a 34a 42=(-1)2a 11a 23a 34a 42=a 11a 23a 34a 42. 4. 计算下列各行列式:(1)71100251020214214; 解 7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-; 解 2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r 000003212213041214=--=====r r .(3)efcf bf de cd bd aeac ab ---;解 ef cf bf de cd bd ae ac ab ---e c b e c b ec b adf ---=abcdef adfbce 4111111111=---=.(4)dc b a 100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ada ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 5. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=y x z x z y zy x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;证明 2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2, c 2-c 1得) 5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2得) 022122212221222122222=++++=d d c c b b a a . (4)444422221111d c b a d c b a d c b a =(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ); 证明 444422221111d c b a d c b a d c b a )()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b ---------=)()()(111))()((222a d d a c c a b b d c b a d a c a b +++---=))(())((00111))()((a b d b d d a b c b c c bd b c a d a c a b ++-++------= )()(11))()()()((a b d d a b c c b d b c a d a c a b ++++-----==(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ).(5)1221 1 000 00 1000 01a x a a a a x x xn n n +⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--- =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n . 证明用数学归纳法证明.当n =2时, 2121221a x a x a x a x D ++=+-=, 命题成立. 假设对于(n -1)阶行列式命题成立, 即 D n -1=x n -1+a 1 x n -2+ ⋅ ⋅ ⋅ +a n -2x +a n -1, 则D n 按第一列展开, 有11100 100 01)1(11-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--+=+-x x a xD D n n n n =xD n -1+a n =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n . 因此, 对于n 阶行列式命题成立.6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90︒、或依副对角线翻转, 依次得n nn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nn n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n nnn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(--==, D 3=D .证明因为D =det(a ij ), 所以 nnn n n n nnnn a a a a a a a a a a D 2211111111111 )1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=- ⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--=-- )1()1(331122111121nnn n nn n n a a a a a a a a D D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=.同理可证nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n T n n 2)1(2)1()1()1(---=-=. D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k 为k 阶行列式): (1)aa D n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0;解 aa a a a D n 010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 000 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解将第一行乘(-1)分别加到其余各行, 得 ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n -1.(3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n nn n n ; 解根据第6题结果, 有nn n n n n n n n n a a a n a a a n a a aD )( )1()( )1( 11 11)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++此行列式为范德蒙德行列式. ∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112; 解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开) nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+. 再按最后一行展开得递推公式D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2. 于是 ∏=-=ni i i i i n D c b d a D 222)(.而 111111112c b d a d c b a D -==, 所以 ∏=-=n i i i i i n c b d a D 12)(. (5) D =det(a ij ), 其中a ij =|i -j |;解 a ij =|i -j |, 043214 01233 10122 21011 3210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n 0 4321 1 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r 152423210 22210 02210 00210 0001 1213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c =(-1)n -1(n -1)2n -2. (6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--10 0001 000 100 0100 0100 0011332212132 1111312112111011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=nn n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 00010 000 00 10000 01000 001)11)((121∑=+=ni i n a a a a .8. 用克莱姆法则解下列方程组:(1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解因为14211213513241211111-=----=D ,142112105132412211151-=------=D , 284112035122412111512-=-----=D , 426110135232422115113-=----=D , 14202132132212151114=-----=D , 所以 111==D D x , 222==D D x , 333==D D x , 144-==DD x . (2)⎪⎪⎩⎪⎪⎨⎧=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解因为 665510006510006510065100065==D , 150751001651000651000650000611==D , 114551010651000650000601000152-==D , 703511650000601000051001653==D , 39551601000051000651010654-==D ,2121100005100065100651100655==D , 所以66515071=x , 66511452-=x , 6657033=x , 6653954-=x , 6652124=x .9. 问l , m 取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解？解系数行列式为μλμμμλ-==1211111D .令D =0, 得 m =0或l =1.于是, 当m =0或l =1时该齐次线性方程组有非零解.10. 问l 取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解？解系数行列式为λλλλλλλ--+--=----=101112431111132421D=(1-l )3+(l -3)-4(1-l )-2(1-l )(-3-l ) =(1-l )3+2(1-l )2+l -3. 令D =0, 得l =0, l =2或l =3.于是, 当l =0, l =2或l =3时, 该齐次线性方程组有非零解.第二章矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换. 解由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y ,⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A T B .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫⎝⎛=49635.(2)⎪⎪⎭⎫⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫⎝⎛---=632142. (4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA . (2)(A +B )2=A 2+2AB +B 2吗? 解 (A +B )2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610, 所以(A +B )2≠A 2+2AB +B 2. (3)(A +B )(A -B )=A 2-B 2吗?解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A , 故(A +B )(A -B )≠A 2-B 2. 6. 举反列说明下列命题是错误的:(1)若A 2=0, 则A =0;解取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k .解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k . 8. 设⎪⎪⎭⎫ ⎝⎛=λλλ001001A , 求A k . 解首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ, ⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A , ⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A , ⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=k A k k k k k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫ . 用数学归纳法证明:当k =2时, 显然成立.假设k 时成立，则k +1时，⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121. 9. 设A , B 为n 阶矩阵，且A 为对称矩阵，证明B T AB 也是对称矩阵.证明因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB ,从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵，证明AB 是对称矩阵的充分必要条件是AB =BA .证明充分性: 因为A T =A , B T =B , 且AB =BA , 所以(AB )T =(BA )T =A T B T =AB ,即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB )T =AB , 所以AB =(AB )T =B T A T =BA .11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A , 故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解 ⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A |=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A , 所以 *||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos .(3)⎪⎪⎭⎫ ⎝⎛---145243121; 解 ⎪⎪⎭⎫ ⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为 ⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012. (4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) . 解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ;解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ; 解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫ ⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; 解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X . 解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012. 13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ; 解方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x . (2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x . 解方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x ,故有 ⎪⎩⎪⎨⎧===305321x x x . 14. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明因为A k =O , 所以E -A k =E . 又因为E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E ,由定理2推论知(E -A )可逆, 且(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ),故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ),两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明由A 2-A -2E =O 得A 2-A =2E , 即A (A -E )=2E ,或 E E A A =-⋅)(21, 由定理2推论知A 可逆, 且)(211E A A -=-. 由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E ,或 E A E E A =-⋅+)3(41)2( 由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-. 证明由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2,即 |A ||A -E |=2,故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆.由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-, 又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1,)3(41)2(1A E E A -=+-. 16. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|. 解因为*||11A A A =-, 所以 |||521||*5)2(|111----=-A A A A A |2521|11---=A A =|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16.17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)-1=(A -1)*.证明由*||11A A A =-, 得A *=|A |A -1, 所以当A 可逆时, 有 |A *|=|A |n |A -1|=|A |n -1≠0,从而A *也可逆.因为A *=|A |A -1, 所以(A *)-1=|A |-1A . 又*)(||)*(||1111---==A A A A A , 所以 (A *)-1=|A |-1A =|A |-1|A |(A -1)*=(A -1)*.18. 设n 阶矩阵A 的伴随矩阵为A *, 证明: (1)若|A |=0, 则|A *|=0; (2)|A *|=|A |n -1. 证明(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)-1=E , 由此得 A =A A *(A *)-1=|A |E (A *)-1=O ,所以A *=O , 这与|A *|≠0矛盾，故当|A |=0时, 有|A *|=0. (2)由于*||11A A A =-, 则AA *=|A |E , 取行列式得到|A ||A *|=|A |n . 若|A |≠0, 则|A *|=|A |n -1;若|A |=0, 由(1)知|A *|=0, 此时命题也成立. 因此|A *|=|A |n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B . 解由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1 =-8(AA *-2A )-1 =-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B . 解由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E )-1A =3[A (E -A -1)]-1A 11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11.解由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511,求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0).ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明因为A -1(A +B )B -1=B -1+A -1=A -1+B -1,而A -1(A +B )B -1是三个可逆矩阵的乘积, 所以A -1(A +B )B -1可逆, 即A -1+B -1可逆.(A -1+B -1)-1=[A -1(A +B )B -1]-1=B (A +B )-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B ,则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫⎝⎛+=222111B A O B B A A ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠.解 4100120021010*********0021010010110100101==--=--=D C B A , 而 01111|||||||| ==D C B A ,故 |||||||| D C B A D C B A ≠.28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫⎝⎛=21A O O A A ,故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A , 1682818281810||||||||||===A A A A A . ⎪⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求 (1)1-⎪⎭⎫ ⎝⎛O B A O ;解设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则 ⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n EBC OBC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A . 解设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得 ⎪⎩⎪⎨⎧=+=+==s nEBD CD O BD CD O AD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025;解设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001. 解设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A B C O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001. 第三章矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫⎝⎛100001000001.(2)⎪⎪⎭⎫⎝⎛----174034301320;解 ⎪⎪⎭⎫⎝⎛----174034301320(下一步: r 2⨯2+(-3)r 1, r 3+(-2)r 1. )~⎪⎪⎭⎫⎝⎛---310031001320(下一步: r 3+r 2, r 1+3r 2. )~⎪⎪⎭⎫⎝⎛0000310010020(下一步: r 1÷2. )~⎪⎪⎭⎫⎝⎛000031005010.(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; 解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011. (4)⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 ⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132(下一步: r 1-2r 2, r 3-3r 2, r 4-2r 2. ) ~⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110(下一步: r 2+2r 1, r 3-8r 1, r 4-7r 1. ) ~⎪⎪⎪⎭⎫ ⎝⎛--41000410002020111110(下一步: r 1↔r 2, r 2⨯(-1), r 4-r 3. ) ~⎪⎪⎪⎭⎫ ⎝⎛----00000410001111020201(下一步: r 2+r 3. ) ~⎪⎪⎪⎭⎫ ⎝⎛--00000410003011020201. 2. 设⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A . 解 ⎪⎪⎭⎫ ⎝⎛100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身. ⎪⎪⎭⎫ ⎝⎛100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(-1)) ⎪⎪⎭⎫ ⎝⎛-=100010101. ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=100010101987654321100001010A ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=287221254100010101987321654. 3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛323513123; 解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫ ⎝⎛---101011001200410123 ~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫ ⎝⎛----2/102/11002110102/922/7003 ~⎪⎪⎭⎫ ⎝⎛----2/102/11002110102/33/26/7001 故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023. 解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023 ~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321 ~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321 ~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010000100001故逆矩阵为⎪⎪⎪⎭⎫ ⎝⎛-------10612631110104211. 4. (1)设⎪⎪⎭⎫ ⎝⎛--=113122214A , ⎪⎪⎭⎫ ⎝⎛--=132231B , 求X 使AX =B ; 解因为⎪⎪⎭⎫ ⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫ ⎝⎛--412315210 100010001 ~r , 所以 ⎪⎪⎭⎫ ⎝⎛--==-4123152101B A X . (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(TT B A ⎪⎪⎭⎫ ⎝⎛---411007101042001 ~r , 所以 ⎪⎪⎭⎫ ⎝⎛---==-417142)(1T T T B A X , 从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 5. 设⎪⎪⎭⎫ ⎝⎛---=101110011A , AX =2X +A , 求X .解原方程化为(A -2E )X =A . 因为⎪⎪⎭⎫ ⎝⎛---------=-101101110110011011) ,2(A E A ⎪⎪⎭⎫ ⎝⎛---011100101010110001~, 所以 ⎪⎪⎭⎫ ⎝⎛---=-=-011101110)2(1A E A X . 6. 在秩是r 的矩阵中,有没有等于0的r -1阶子式? 有没有等于0的r 阶子式?解在秩是r 的矩阵中, 可能存在等于0的r -1阶子式, 也可能存在等于0的r 阶子式.例如, ⎪⎪⎭⎫ ⎝⎛=010*********A , R (A )=3. 0000是等于0的2阶子式, 010001000是等于0的3阶子式. 7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样?解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式:(1)⎪⎪⎭⎫ ⎝⎛---443112112013; 解 ⎪⎪⎭⎫ ⎝⎛---443112112013(下一步: r 1↔r 2. ) ~⎪⎪⎭⎫ ⎝⎛---443120131211(下一步: r 2-3r 1, r 3-r 1. ) ~⎪⎪⎭⎫ ⎝⎛----564056401211(下一步: r 3-r 2. )~⎪⎭⎫ ⎝⎛---000056401211, 矩阵的2秩为, 41113-=-是一个最高阶非零子式. (2)⎪⎪⎭⎫ ⎝⎛-------815073*********; 解 ⎪⎪⎭⎫ ⎝⎛-------815073*********(下一步: r 1-r 2, r 2-2r 1, r 3-7r 1. ) ~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步: r 3-3r 2. ) ~⎪⎭⎫ ⎝⎛----0000059117014431, 矩阵的秩是2, 71223-=-是一个最高阶非零子式. (3)⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812. 解 ⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812(下一步: r 1-2r 4, r 2-2r 4, r 3-3r 4. )~⎪⎪⎪⎭⎫ ⎝⎛------02301024205363071210(下一步: r 2+3r 1, r 3+2r 1. ) ~⎪⎪⎪⎭⎫ ⎝⎛-0230114000016000071210(下一步: r 2÷16r 4, r 3-16r 2. ) ~⎪⎪⎪⎭⎫ ⎝⎛-02301000001000071210 ~⎪⎪⎪⎭⎫ ⎝⎛-00000100007121002301, 矩阵的秩为3, 070023085570≠=-是一个最高阶非零子式. 10. 设A 、B 都是m ⨯n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ).证明根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设⎪⎪⎭⎫ ⎝⎛----=32321321k k k A , 问k 为何值, 可使 (1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1;(2)当k =-2且k ≠1时, R (A )=2;(3)当k ≠1且k ≠-2时, R (A )=3.12. 求解下列齐次线性方程组:(1)⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ; 解对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎭⎫ ⎝⎛---3/410013100101, 于是 ⎪⎪⎩⎪⎪⎨⎧==-==4443424134334x x x x x x x x , 故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数). (2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ; 解对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫ ⎝⎛-000001001021,于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x x x x x x , 故方程组的解为 ⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10010012214321k k x x x x (k 1, k 2为任意常数). (3)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x ; 解对系数矩阵A 进行初等行变换, 有。

《应用型本科线性代数及其应用》习题参考解答

一1、利用对角线法则计算下列三阶行列式：（1）413201512-；（2）a c b b a c cb a ；（3）222111c c b b a a ；（4）yx y x x y x yy x yx+++ 解（1）：1413201512=-解（2）：])()())[((3222333a c c b b a c b a abc c b a acbb a cc ba -+-+-++=-++= 解（3）：))()((111222a c cb b ac c b ba a ---= 解（4）：)(233y x yxyx x yx yy x y x+-=+++2、求下列各排列的逆序数，并确定排列的奇偶性：（1）3617254；（2）891476235；（3）（2n+1）(2n-1) …531 解（1）：逆序数为10，偶排列。

解（2）：逆序数为23，奇排列。

解（3）：逆序数为2)1(12)1(+=+++-+n n n n 。

当k n 4=或14+=k n 时为偶排列，当24+=k n 或34+=k n 时为奇排列．3、写出四阶行列式)det(ij a D =中所有包含23a 并带正号的项。

解：项的一般形式为43143143231)3()1(i i i i i i a a a a τ-，其中，431i i i 是1，2，4的全排列。

所有可能的列标序列的逆序数为1)1324(=τ，3)2341(=τ，5)4312(=τ 2)1342(=τ，2)2314(=τ，6)4321(=τ故包含23a 且带正号的项有42342311a a a a ，44312312a a a a ，41322314a a a a 。

4、若n 阶行列式)det(ij a D =的元素满足ji ij a a -=（n j i ,,2,1, =），则称这样的行列式为反对称行列式，试证：当n 为奇数时，0=D 。

解：一方面，D D ='另一方面，D D D n -=-=')1( 于是，D D -=，02=D ，0=D 。

同济大学-线性代数-习题册+答案

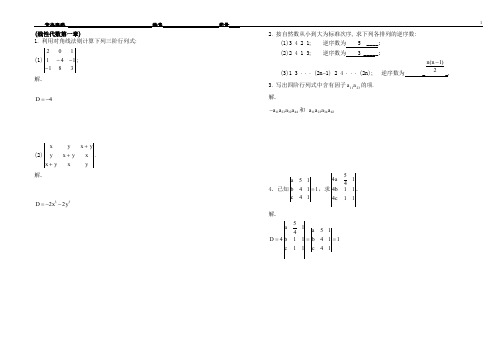
所以 B A E
1
0 0 1 1 0 2 2 0 1 A E 0 1 0 0 3 0 0 3 0 1 0 0 2 0 1 1 0 2
2
13 设方阵 A 满足 A A 2E O 证明 A 及 A 2E 都可逆并求 A 及 ( A 2 E )
解.
0 0 ; 1 d
a
1 4 D 10 0 2 1 5 1 0 2 2 1 2 1 2 4 0 7 0 0 15 7 0 1 0 2 1 2 2 4 0 1 2 20 0 15 1 7 0 7 0 2 1 2 0 2 1 7 0 1 1 7 0 2 20 0 0 17 85 2 4 0 0 9 45
D 2 x3 2 y3
解.
a D4b c
5 1 a 5 1 4 1 1 b 4 1 1 1 1 c 4 1
专业班级
姓名
学号
2
5 计算下列各行列式
4 1 (1) 10 0
解.
1 2 5 1
2 0 2 1
4 2 ; 0 7
a 1 0 1 b 1 (3) 0 1 c 0 0 1
所以 B AB 也是对称矩阵。
T
10.设 A 为 n 阶方阵，且 A
专业班级
姓名
学号
6
1 4 2 0 3 1 12 解矩阵方程 X . 1 2 1 1 0 1
解.
1 4 2 0
1 0 1 14 设 A 0 2 0 且 AB E A2 B 求 B 1 0 1
1 | B | _______ 9 ______.
* 1 ，则 2A* 2 A 2 11．设矩阵 A 、 B 、C 满足 AB AC ，则 B C 成立的一个充分条件是____C_____. (A) A 为方阵（B） A 为非零矩阵 (C) A 为可逆方阵 (D) A 为对角阵

同济大学工程数学线性代数第六版答案(全)

第一章行列式1.利用对角线法则计算下列三阶行列式： (1)381141102---;解381141102--- =2⨯（-4）⨯3+0⨯(-1)⨯（ 1）+1⨯1⨯8 -0⨯1⨯3 2⨯（ 1）⨯8-1⨯(-4)⨯( 1) =-24+8+16-4=-4。

（2)b a c a c b cb a ;解ba c a cbc b a =acb +bac +cba -bbb -aaa ccc =3abc a 3-b 3 c 3.(3）222111c b a c b a ；解222111c b a c b a =bc 2+ca 2+ab 2-ac 2-ba 2 cb 2 =（a -b ）(b c ）(c a ）。

（4）y x y x x y x y yx y x +++.解 yx y x x y x y yx y x +++=x (x +y ）y +yx （x +y )+(x +y )yx -y 3-(x +y ）3 x 3 =3xy (x +y ）-y 3-3x 2y x 3 y 3-x 3 =-2(x 3+y 3)。

2。

按自然数从小到大为标准次序，求下列各排列的逆序数: （1)1 2 3 4；解逆序数为0 (2）4 1 3 2；解逆序数为4: 41, 43， 42， 32。

(3)3 4 2 1；解逆序数为5： 3 2, 3 1， 4 2， 4 1, 2 1。

(4）2 4 1 3；解逆序数为3： 2 1, 4 1， 4 3. （5）1 3 ⋅⋅⋅ (2n -1） 2 4 ⋅⋅⋅ (2n ）；解逆序数为2)1(-n n ：3 2 (1个) 5 2， 5 4（2个)7 2，7 4，7 6(3个)⋅⋅⋅⋅⋅⋅（2n 1）2,（2n 1）4, (2n 1）6，⋅⋅⋅，(2n-1）（2n-2)(n 1个)(6）1 3 ⋅⋅⋅(2n 1）（2n）(2n-2) ⋅⋅⋅ 2.解逆序数为n(n 1）:3 2(1个）5 2，5 4 （2个)⋅⋅⋅⋅⋅⋅（2n 1)2，(2n-1)4，(2n 1）6，⋅⋅⋅,（2n 1)(2n 2)(n-1个) 4 2(1个)6 2，6 4（2个)⋅⋅⋅⋅⋅⋅（2n）2,（2n)4, (2n)6,⋅⋅⋅，(2n)(2n 2）(n-1个)3.写出四阶行列式中含有因子a11a23的项.解含因子a11a23的项的一般形式为（-1)t a11a23a3r a4s,其中rs是2和4构成的排列,这种排列共有两个,即24和42.所以含因子a11a23的项分别是（-1）t a11a23a32a44=（-1）1a11a23a32a44=-a11a23a32a44,(-1)t a11a23a34a42=(-1）2a11a23a34a42=a11a23a34a42.4.计算下列各行列式：（1)71100251020214214; 解7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c 。

线性代数第五版答案(全)

第一章行列式1. 利用对角线法则计算下列三阶行列式:(1)381141102---;解381141102--- =2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4.(2)ba c a cbc b a ;解ba c a cbc b a =acb +bac +cba -bbb -aaa -ccc=3abc -a 3-b 3-c 3.(3)222111c b a c b a ;解222111c b a c b a =bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).(4)yx y x x y x y y x y x +++. 解yx y x x y x y y x y x +++ =x (x +y )y +yx (x +y )+(x +y )yx -y 3-(x +y )3-x 3 =3xy (x +y )-y 3-3x 2 y -x 3-y 3-x 3 =-2(x 3+y 3).2. 按自然数从小到大为标准次序, 求下列各排列的逆序数: (1)1 2 3 4; 解逆序数为0 (2)4 1 3 2;解逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n -1) 2 4 ⋅ ⋅ ⋅ (2n ); 解逆序数为2)1(-n n : 3 2 (1个) 5 2, 5 4(2个) 7 2, 7 4, 7 6(3个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n -1)2, (2n -1)4, (2n -1)6, ⋅ ⋅ ⋅, (2n -1)(2n -2) (n -1个)(6)1 3 ⋅ ⋅ ⋅ (2n -1) (2n ) (2n -2) ⋅ ⋅ ⋅ 2. 解逆序数为n (n -1) : 3 2(1个) 5 2, 5 4 (2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n -1)2, (2n -1)4, (2n -1)6, ⋅ ⋅ ⋅, (2n -1)(2n -2) (n -1个)4 2(1个) 6 2, 6 4(2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n )2, (2n )4, (2n )6, ⋅ ⋅ ⋅, (2n )(2n -2) (n -1个) 3. 写出四阶行列式中含有因子a 11a 23的项. 解含因子a 11a 23的项的一般形式为 (-1)t a 11a 23a 3r a 4s ,其中rs 是2和4构成的排列, 这种排列共有两个, 即24和42.所以含因子a 11a 23的项分别是(-1)t a 11a 23a 32a 44=(-1)1a 11a 23a 32a 44=-a 11a 23a 32a 44,(-1)t a 11a 23a 34a 42=(-1)2a 11a 23a 34a 42=a 11a 23a 34a 42. 4. 计算下列各行列式:(1)7110025*******214; 解71100251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---=143102211014--=01417172001099323211=-++======c c c c . (2)2605232112131412-; 解2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r000003212213041214=--=====r r . (3)efcf bf decd bd ae ac ab ---;解efcf bf de cd bd aeac ab ---e c b e c b e c b adf ---=abcdefadfbce 4111111111=---=.(4)dc b a 100110011001---. 解d c b a 100110011001---dc b a ab ar r 10011001101021---++=====dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ad a ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1.5. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 .(2)yx z x z y z y x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++; 证明bzay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++bzay by ax x by ax bx az z bx az bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bx az z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y z y x b y x z x z y z y x a 33+=yx z x z y z y x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;证明2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4-c 3,c 3-c 2, c 2-c 1得)5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2得)022122212221222122222=++++=d d c c b b a a .(4)444422221111d c b a d c b a d c b a=(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d );证明444422221111d c b a d c b a d c b a)()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b a d a c a b ---------=)()()(111))()((222a d d a c c a b b dc b ad a c a b +++---=)(())((00111))()((db d d a bc b c cd b c a d a c a b -++------=()(11))()()()((d d a b c c b d b c a d a c a b +++-----==(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ).(5)1221 1 000 00 1000 01a x a a a a x x x n n n+⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--- =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .证明用数学归纳法证明. 当n =2时, 2121221a x a x a x a x D ++=+-=,命题成立.假设对于(n -1)阶行列式命题成立, 即 D n -1=x n -1+a 1 x n -2+ ⋅ ⋅ ⋅ +a n -2x +a n -1, 则D n 按第一列展开, 有11100 100 01)1(11-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--+=+-xx a xD D n n n n=xD n -1+a n=x n +a1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .因此, 对于n 阶行列式命题成立.6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90︒、或依副对角线翻转, 依次得n nn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nnn a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ,11113 a a a a D n nnn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(--==, D 3=D .证明因为D =det(a ij ), 所以nnn n n n nnnn a a a a a a a a a a D 2211111111111 )1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=- ⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--=-- )1()1(331122111121nnn n nn n n a a a a a a a aD D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=.同理可证nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n T n n 2)1(2)1()1()1(---=-=.D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k 为k 阶行列式):(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解aa a a a D n 0 0010 000 00 0000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开))1()1(10 000 00 0000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a)1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a aan n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1 )1()1(=a n -a n -2=a n -2(a 2-1).(2)xa aa x a a a x D n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a a a a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n -1.(3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n nn n n ; 解根据第6题结果, 有nnn n n n n n n n a a a n a a a n a a aD )( )1()( )1( 11 11)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++此行列式为范德蒙德行列式.∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)n nnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112;解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开)nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+.再按最后一行展开得递推公式 D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2.于是∏=-=ni i i i i n D c b d a D 222)(.而111111112c b d a d c b a D -==,所以∏=-=n i i i i i n c b d a D 12)(.(5) D =det(a ij ), 其中a ij =|i -j |; 解 a ij =|i -j |,43214 0123310122 210113210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n0 43211 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r152423210 22210 02210 00210 00011213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c=(-1)n -1(n -1)2n -2. (6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n ≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--100001 000 100 0100 0100 00113322121321111312112111000011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=nn n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 00010 000 00 10000 01000 001)11)((121∑=+=ni in a a a a .8. 用克莱姆法则解下列方程组:(1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解因为14211213513241211111-=----=D , 142112105132412211151-=------=D , 28411235122412111512-=-----=D , 42611135232422115113-=----=D , 14202132132212151114=-----=D , 所以 111==DD x , 222==D D x , 333==D D x , 144-==DDx .(2)⎪⎪⎩⎪⎪⎨⎧=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解因为665510006510006510065100065==D , 15075100165100065100650000611==D , 11455101065100065000601000152-==D , 7035110065000060100051001653==D , 3955100060100005100651010654-==D , 2121100005100065100651100655==D , 所以66515071=x , 66511452-=x , 6657033=x ,6653954-=x , 6652124=x .9. 问λ, μ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解？解系数行列式为μλμμμλ-==1211111D .令D =0, 得 μ=0或λ=1.于是, 当μ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解？解系数行列式为λλλλλλλ--+--=----=101112431111132421D=(1-λ)3+(λ-3)-4(1-λ)-2(1-λ)(-3-λ)=(1-λ)3+2(1-λ)2+λ-3. 令D =0, 得λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解. 第二章矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换. 解由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解由已知⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B ,求3AB -2A 及A T B . 解⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T .4. 计算下列乘积:(1)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635. (2)⎪⎪⎭⎫ ⎝⎛123)321(; 解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10). (3))21(312-⎪⎪⎭⎫⎝⎛;解)21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫⎝⎛---=632142. (4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ;解⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫⎝⎛---=6520876.(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA . 因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B )2=A 2+2AB +B 2吗? 解 (A +B )2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610, 所以(A +B )2≠A 2+2AB +B 2. (3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.6. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0; 解取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X ,⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k . 解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k. 8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k .解首先观察 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A , ⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A , ⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA k k kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明:当k =2时, 显然成立. 假设k 时成立，则k +1时，⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵，且A 为对称矩阵，证明B T AB也是对称矩阵.证明因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵，证明AB 是对称矩阵的充分必要条件是AB =BA .证明充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB )T =(BA )T =A T B T =AB , 即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB )T =AB , 所以 AB =(AB )T =B T A T =BA . 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解 ⎪⎭⎫ ⎝⎛-=θθθθco s sin sin co s A . |A |=1≠0, 故A -1存在. 因为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos .(3)⎪⎪⎭⎫⎝⎛---145243121;解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为 ⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以 *||11A A A =-⎪⎪⎪⎭⎫⎝⎛-----=1716213213012. (4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程: (1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ;解⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311111012112X ;解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131⎪⎪⎭⎫⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; 解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .解11010100001021102341100001010--⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012. 13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明一方面, 有E =(E -A )-1(E -A ). 另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ),故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1. 证明由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得|A 2-A |=2,即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆.由 A 2-A -2E =O ⇒A (A -E )=2E ⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1,)3(41)2(1A E E A -=+-.16. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|. 解因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16.17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)-1=(A -1)*. 证明由*||11A A A =-, 得A *=|A |A -1, 所以当A可逆时, 有|A *|=|A |n |A -1|=|A |n -1≠0, 从而A *也可逆.因为A *=|A |A -1, 所以 (A *)-1=|A |-1A . 又*)(||)*(||1111---==A A A A A , 所以(A *)-1=|A |-1A =|A |-1|A |(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A *, 证明: (1)若|A |=0, 则|A *|=0; (2)|A *|=|A |n -1. 证明(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)-1=E , 由此得A =A A *(A *)-1=|A |E (A *)-1=O ,所以A *=O , 这与|A *|≠0矛盾，故当|A |=0时, 有|A *|=0. (2)由于*||11A A A =-, 则AA *=|A |E , 取行列式得到|A ||A *|=|A |n . 若|A |≠0, 则|A *|=|A |n -1;若|A |=0, 由(1)知|A *|=0, 此时命题也成立. 因此|A *|=|A |n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫ ⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B . 解由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1=-8(AA *-2A )-1=-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E得AB =B +3A , B =3(A -E )-1A =3[A (E -A -1)]-1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P ,⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11.解由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3,⎪⎭⎫ ⎝⎛-=1141*P ,⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛-=Λ11111120 012001,故⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P ,⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0).ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明因为A -1(A +B )B -1=B -1+A -1=A -1+B -1,而A -1(A +B )B -1是三个可逆矩阵的乘积, 所以A -1(A +B )B -1可逆, 即A -1+B -1可逆.(A -1+B -1)-1=[A -1(A +B )B -1]-1=B (A +B )-1A .26. 计算⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121.解设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B ,则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A ,所以⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B EA O E A ⎪⎭⎫⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠. 解4100120021010*********0021010010110100101==--=--=D C B A , 而01111|||||||| ==D C B A , 故|||||||| D C B A D C B A ≠. 28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫ ⎝⎛=21A O O A A , 故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ; 解设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A .解设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321. 由此得⎪⎩⎪⎨⎧=+=+==s n E BD CD O BD CD OAD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D , 所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A B C O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是⎝⎛---=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛----50020005202125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001. 解设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛------1111114121031200210001B CA B O A B C O A ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----=411212458103161210021210001. 第三章矩阵的初等变换与线性方程组 1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201; 解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. ) ~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫ ⎝⎛100001000001.(2)⎪⎪⎭⎫⎝⎛----174034301320; 解 ⎪⎪⎭⎫⎝⎛----174034301320(下一步: r 2⨯2+(-3)r 1, r 3+(-2)r 1. )~⎪⎪⎭⎫⎝⎛---310031001320(下一步: r 3+r 2, r 1+3r 2. ) ~⎪⎪⎭⎫⎝⎛0000310010020(下一步: r 1÷2. )~⎪⎪⎭⎫⎝⎛000031005010.(3)⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311;解 ⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311(下一步: r 2-3r 1,r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4),r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2,r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011.(4)⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 ⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132(下一步: r 1-2r 2,r 3-3r 2, r 4-2r 2. )~⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110(下一步: r 2+2r 1,r 3-8r 1, r 4-7r 1. )~⎪⎪⎪⎭⎫⎝⎛--41000410002020111110(下一步: r 1↔r 2, r 2⨯(-1),r 4-r 3. )~⎪⎪⎪⎭⎫⎝⎛----00000410001111020201(下一步: r 2+r 3. )~⎪⎪⎪⎭⎫⎝⎛--00000410003011020201. 2. 设⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A .解 ⎪⎪⎭⎫⎝⎛100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身.⎪⎪⎭⎫⎝⎛100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(-1)) ⎪⎪⎭⎫⎝⎛-=100010101.⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=100010101987654321100001010A⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=287221254100010101987321654. 3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123~⎪⎪⎭⎫⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫ ⎝⎛----2/102/11002110102/922/7003 ~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001 故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267. (2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021~⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010000100001故逆矩阵为⎪⎪⎪⎭⎫ ⎝⎛-------10612631110104211.4. (1)设⎪⎪⎭⎫ ⎝⎛--=113122214A , ⎪⎪⎭⎫⎝⎛--=132231B , 求X 使AX =B ; 解因为⎪⎪⎭⎫⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫ ⎝⎛--412315210 100010001 ~r , 所以 ⎪⎪⎭⎫ ⎝⎛--==-4123152101B A X .(2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B ,求X 使XA =B . 解考虑A T X T =B T . 因为⎪⎪⎭⎫⎝⎛----=134313231221320) ,(T T B A ⎪⎪⎭⎫ ⎝⎛---411007101042001 ~r , 所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X , 从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X .5. 设⎪⎪⎭⎫⎝⎛---=101110011A , AX =2X +A , 求X . 解原方程化为(A -2E )X =A . 因为⎪⎪⎭⎫⎝⎛---------=-101101110110011011) ,2(A E A⎪⎪⎭⎫⎝⎛---011100101010110001~, 所以 ⎪⎪⎭⎫ ⎝⎛---=-=-011101110)2(1A E A X . 6. 在秩是r 的矩阵中,有没有等于0的r -1阶子式? 有没有等于0的r 阶子式?解在秩是r 的矩阵中, 可能存在等于0的r -1阶子式, 也可能存在等于0的r 阶子式.例如, ⎪⎪⎭⎫⎝⎛=010*********A , R (A )=3.0000是等于0的2阶子式, 010001000是等于0的3阶子式.7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样?解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是 (1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式:(1)⎪⎪⎭⎫⎝⎛---443112112013; 解 ⎪⎪⎭⎫⎝⎛---443112112013(下一步: r 1↔r 2. ) ~⎪⎪⎭⎫⎝⎛---443120131211(下一步: r 2-3r 1, r 3-r 1. ) ~⎪⎪⎭⎫⎝⎛----564056401211(下一步: r 3-r 2. ) ~⎪⎭⎫ ⎝⎛---000056401211, 矩阵的2秩为, 41113-=-是一个最高阶非零子式.(2)⎪⎪⎭⎫⎝⎛-------815073131213123; 解 ⎪⎪⎭⎫⎝⎛-------815073131223123(下一步: r 1-r 2, r 2-2r 1, r 3-7r 1. )~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步: r 3-3r 2. )~⎪⎭⎫ ⎝⎛----0000059117014431, 矩阵的秩是2, 71223-=-是一个最高阶非零子式.(3)⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812.解 ⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812(下一步: r 1-2r 4, r 2-2r 4,r 3-3r 4. )~⎪⎪⎪⎭⎫⎝⎛------02301024205363071210(下一步: r 2+3r 1,r 3+2r 1. )~⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210(下一步: r 2÷16r 4,r 3-16r 2. )~⎪⎪⎪⎭⎫⎝⎛-02301000001000071210~⎪⎪⎪⎭⎫ ⎝⎛-00000100007121002301,矩阵的秩为3,070023085570≠=-是一个最高阶非零子式.10. 设A 、B 都是m ⨯n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ).证明根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3. 解⎪⎪⎭⎫⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3.12. 求解下列齐次线性方程组:(1)⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ;解对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎭⎫ ⎝⎛---3/410013100101, 于是 ⎪⎪⎩⎪⎪⎨⎧==-==4443424134334x x x x x x x x ,故方程组的解为⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数). (2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ;解对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫⎝⎛-000001001021,于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x x x x x x ,故方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10010012214321k k x x x x (k 1, k 2为任意常数).(3)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x ;解对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫⎝⎛-----7421631472135132~⎪⎪⎪⎭⎫ ⎝⎛1000010000100001,。

线性代数课后习题答案全习题详解

线性代数课后习题答案全习题详解(总92页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章行列式1.利用对角线法则计算下列三阶行列式：（1）381141102---；（2）b a c a c b c b a ; （3）222111c b a c b a ；（4）y x y x x y x yyx y x +++. 解（1）=---381141102811)1()1(03)4(2⨯⨯+-⨯-⨯+⨯-⨯)1()4(18)1(2310-⨯-⨯-⨯-⨯-⨯⨯- =416824-++-=4-（2）=ba c a cb cb a ccc aaa bbb cba bac acb ---++3333c b a abc ---=（3）=222111c b a c b a 222222cb ba ac ab ca bc ---++))()((a c c b b a ---=（4）yx y x x y x y yx y x +++yx y x y x yx y y x x )()()(+++++=333)(x y x y -+-- 33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序，求下列各排列的逆序数：（1）1 2 3 4；（2）4 1 3 2；（3）3 4 2 1；（4）2 4 1 3；（5）1 3 … )12(-n 2 4 … )2(n ；（6）1 3 … )12(-n )2(n )22(-n … 2. 解（1）逆序数为0（2）逆序数为4：4 1，4 3，4 2，3 2（3）逆序数为5：3 2，3 1，4 2，4 1,2 1 （4）逆序数为3：2 1，4 1，4 3（5）逆序数为2)1(-n n ：3 2 1个 5 2，54 2个 7 2，7 4，7 6 3个 ……………… … )12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n )1(-n 个（6）逆序数为)1(-n n3 2 1个 5 2，54 2个 ……………… … )12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n )1(-n 个4 2 1个 6 2，6 4 2个 ……………… … )2(n 2，)2(n 4，)2(n 6，…，)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项.解由定义知，四阶行列式的一般项为43214321)1(p p p p t a a a a -，其中t 为4321p p p p 的逆序数．由于3,121==p p 已固定，4321p p p p 只能形如13□□，即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式：（1）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢71100251020214214；（2）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-265232112131412；（3）⎥⎥⎦⎥⎢⎢⎣⎢---ef cf bf de cd bd ae acab ；（4）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a 100110011001 解(1)7110025*******21434327c c c c --0100142310202110214---=34)1(143102211014+-⨯---=143102211014-- 321132c c c c ++1417172001099-=0(2)265232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=e c b e c b e c b adf ---=111111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 10111--+ 23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -;(2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=yx z x z y zy x b a )(33+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 .证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--= 右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bz ay y x by ax x z bx az z y b +++zy x y x z xz y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c c b b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a 949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+ddd c c c bb b a a a (4) 444444422222220001ad a c a b a ad a c a b a a d a c a b a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)()()(111))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =⨯---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立，即 ,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x xa xD D n n n n 右边=+=-n n a xD 1 所以，对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转，依次得n nn n a a a a D 11111 =， 11112n nn n a a a a D = ，11113a a a a D n nnn =，证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnnn nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-= 同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n Tn n 2)1(2)1()1()1(---=-= D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式（阶行列式为k D k ）：(1)aaD n 11 =,其中对角线上元素都是a ，未写出的元素都是0；(2)xaaax aa a x D n=; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n nn n n ------=---+; 提示：利用范德蒙德行列式的结果． (4) nnn nn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 010000000000001000=按最后一行展开)1()1(1000000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n n a a a (再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行，得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上，得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始，第1+n 行经过n 次相邻对换，换到第1行，第n 行经)1(-n 次对换换到第2行…，经2)1(1)1(+=++-+n n n n 次行交换，得nn n n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-•-•-=---=111)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) n nnnn d c d c b a b a D 011112=nn n n n nd d c d c b a b a a 0000000011111111----展开按第一行0000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式：222)(--=n n n n n n D c b d a D 即 ∏=-=ni i i i i n D c b d a D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=0432********0122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0432111111111111111111111 --------------n n n n,,141312c c c c c c +++152423210222102210002100001---------------n n n n n =212)1()1(----n n n(6)nn a a D a +++=11111111121 ,,433221c c c c c c ---n n n n a a a a a a a a a a +-------10000100010000100010001000011433221展开（由下往上）按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------00000000000000000000000000022433221 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组：⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x解 (1)11213513241211111----=D 8120735032101111------=145008130032101111---=1421420005410032101111-=---= 112105132412211151------=D 11210513290501115----=1121023313090509151------=2331309050112109151------=1202300461000112109151-----=14200038100112109151----=142-= 112035122412111512-----=D 811507312032701151-------=3139011230023101151-=2842840001910023101151-=----=426110135232422115113-=----=D ; 14202132132212151114=-----=D1,3,2,144332211-========∴DDx D D x D D x D D x (2) 510006510006510065100065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',) 5100165100065100650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507= 51165100065000601000152=D 展开按第二列5100651006500061-6510065000610005-365510651065⨯-=1145108065-=--= 51100650000601000051001653=D 展开按第三列5100650006100051650061000510065+6100510656510650061+= 703114619=⨯+= 51000601000051000651010654=D 展开按第四列61000510065100655000610005100651--51065106565--=395-= 110051000651000651100655=D 展开按最后一列D '+10005100651006512122111=+= 665212;665395;665703;6651145;665150744321=-==-==∴x x x x x ． 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解解 μλμμμλ-==12111113D ，齐次线性方程组有非零解，则03=D即 0=-μλμ 得 10==λμ或不难验证，当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ 有非零解解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-=3)1(2)1(23-+-+-=λλλ齐次线性方程组有非零解，则0=D 得 32,0===λλλ或不难验证，当32,0===λλλ或时，该齐次线性方程组确有非零解.第二章矩阵及其运算1 已知线性变换⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x求从变量x 1 x 2 x 3到变量y 1 y 2 y 3的线性变换解由已知⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y2 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y求从z 1 z 2 z 3到x 1 x 2 x 3的线性变换解由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x3 设⎪⎪⎭⎫ ⎝⎛--=111111111A ⎪⎪⎭⎫⎝⎛--=150421321B 求3AB 2A 及A TB解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T4 计算下列乘积(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635(2)⎪⎪⎭⎫⎝⎛123)321(解 ⎪⎪⎭⎫⎝⎛123)321((132231)(10)(3))21(312-⎪⎪⎭⎫⎝⎛解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫ ⎝⎛---=632142(4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫⎝⎛---=6520876(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x(a 11x 1a 12x 2a 13x 3 a 12x 1a 22x 2a 23x 3 a 13x 1a 23x 2a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=5 设⎪⎭⎫ ⎝⎛=3121A ⎪⎭⎫⎝⎛=2101B 问(1)AB BA 吗解 AB BA 因为⎪⎭⎫ ⎝⎛=6443AB ⎪⎭⎫⎝⎛=8321BA 所以AB BA(2)(A B)2A 22AB B 2吗解 (A B)2A 22AB B 2 因为⎪⎭⎫ ⎝⎛=+5222B A⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148但⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫⎝⎛=27151610所以(A B)2A 22AB B 2 (3)(A B)(A B)A 2B 2吗解 (A B)(A B)A 2B 2因为⎪⎭⎫ ⎝⎛=+5222B A⎪⎭⎫ ⎝⎛=-1020B A⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A故(A B)(A B)A 2B 26 举反列说明下列命题是错误的 (1)若A 20 则A 0 解取⎪⎭⎫ ⎝⎛=0010A 则A 20 但A 0(2)若A 2A 则A 0或A E 解取⎪⎭⎫ ⎝⎛=0011A 则A 2A 但A 0且A E(3)若AX AY 且A 0 则X Y 解取⎪⎭⎫ ⎝⎛=0001A⎪⎭⎫ ⎝⎛-=1111X ⎪⎭⎫ ⎝⎛=1011Y则AX AY 且A 0 但X Y7 设⎪⎭⎫ ⎝⎛=101λA 求A 2A 3Ak解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A⎪⎭⎫ ⎝⎛=101λk A k8设⎪⎪⎭⎫ ⎝⎛=λλλ001001A 求A k解首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A ⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A⎝⎛=kA k k kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫用数学归纳法证明当k 2时显然成立假设k 时成立，则k 1时，⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ 由数学归纳法原理知⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(1219 设A B 为n 阶矩阵，且A 为对称矩阵，证明B T AB 也是对称矩阵证明因为A T A 所以(B T AB)T B T (B T A)T B T A T B B T AB 从而B T AB 是对称矩阵10 设A B 都是n 阶对称矩阵，证明AB 是对称矩阵的充分必要条件是AB BA 证明充分性因为A T A B T B 且AB BA 所以(AB)T (BA)T A T B T AB 即AB 是对称矩阵必要性因为A T A B T B 且(AB)T AB 所以 AB (AB)T B T A T BA 11 求下列矩阵的逆矩阵 (1)⎪⎭⎫⎝⎛5221解⎪⎭⎫ ⎝⎛=5221A |A|1 故A 1存在因为 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225 (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos 解 ⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A |A|10 故A 1存在因为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos(3)⎪⎪⎭⎫⎝⎛---145243121解 ⎪⎪⎭⎫⎝⎛---=145243121A |A|20 故A 1存在因为⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A所以 *||11A A A =-⎪⎪⎪⎭⎫⎝⎛-----=1716213213012(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2a n0)解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 12 解下列矩阵方程 (1)⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛12643152X解⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232(2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311111012112X 解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫⎝⎛---=32538122 (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111 (4)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=20143101213 利用逆矩阵解下列线性方程组(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x解方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x从而有 ⎪⎩⎪⎨⎧===001321x x x(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x解方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x故有 ⎪⎩⎪⎨⎧===35321x x x14 设A k O (k 为正整数) 证明(E A)1E A A 2 A k1证明因为A k O 所以E A k E 又因为E A k (E A)(E A A 2A k 1)所以 (E A)(E A A 2 A k 1)E 由定理2推论知(E A)可逆且(E A)1E A A 2A k1证明一方面有E (E A)1(E A) 另一方面由A k O 有 E (E A)(A A 2)A 2A k1(A k1A k )(E A A 2 A k 1)(E A)故 (E A)1(E A)(E A A 2 A k 1)(E A) 两端同时右乘(E A)1就有(E A)1(E A)E A A 2A k115 设方阵A 满足A 2A 2E O 证明A 及A 2E 都可逆并求A 1及(A 2E)1证明由A 2A 2E O 得A 2A 2E 即A(A E)2E 或E E A A =-⋅)(21由定理2推论知A 可逆且)(211E A A -=-由A 2A 2E O 得 A 2A 6E 4E 即(A 2E)(A 3E)4E或 E A E E A =-⋅+)3(41)2( 由定理2推论知(A 2E)可逆且)3(41)2(1A E E A -=+-证明由A 2A 2E O 得A 2A 2E 两端同时取行列式得 |A 2A|2 即 |A||A E|2 故 |A|0所以A 可逆而A 2E A 2 |A 2E||A 2||A|20 故A 2E 也可逆由 A 2A 2E O A(A E)2E A 1A(A E)2A 1E)(211E A A -=-又由 A 2A 2E O (A 2E)A 3(A 2E)4E(A 2E)(A 3E)4 E所以 (A 2E)1(A 2E)(A 3E)4(A 2 E)1)3(41)2(1A E E A -=+- 16 设A 为3阶矩阵 21||=A 求|(2A)15A*|解因为*||11A A A =- 所以 |||521||*5)2(|111----=-A A A A A |2521|11---=A A|2A 1|(2)3|A 1|8|A|1821617 设矩阵A 可逆证明其伴随阵A*也可逆且(A*)1(A 1)*证明由*||11A A A =- 得A*|A|A 1所以当A 可逆时有|A*||A|n |A 1||A|n 1从而A*也可逆因为A*|A|A 1所以(A*)1|A|1A又*)(||)*(||1111---==A A A A A 所以(A*)1|A|1A |A|1|A|(A 1)*(A 1)*18 设n 阶矩阵A 的伴随矩阵为A* 证明 (1)若|A|0 则|A*|0 (2)|A*||A|n 1证明(1)用反证法证明假设|A*|0 则有A*(A*)1E 由此得A A A*(A*)1|A|E(A*)1O所以A*O 这与|A*|0矛盾，故当|A|0时有|A*|0 (2)由于*||11A A A =- 则AA*|A|E 取行列式得到|A||A*||A|n 若|A|0 则|A*||A|n 1若|A|0 由(1)知|A*|0 此时命题也成立因此|A*||A|n119设⎪⎪⎭⎫ ⎝⎛-=321011330A AB A 2B 求B解由AB A 2E 可得(A 2E)B A 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E AB ⎪⎪⎭⎫⎝⎛-=01132133020 设⎪⎪⎭⎫⎝⎛=101020101A 且AB E A 2B 求B解由AB E A 2B 得 (A E)B A 2E 即 (A E)B (A E)(A E)因为01001010100||≠-==-E A 所以(A E)可逆从而⎪⎪⎭⎫⎝⎛=+=201030102E A B21 设A diag(1 2 1) A*BA 2BA 8E 求B解由A*BA 2BA 8E 得(A*2E)BA 8EB 8(A*2E)1A 1 8[A(A*2E)]1 8(AA*2A)1 8(|A|E 2A)18(2E 2A)14(E A)14[diag(2 1 2)]1)21 ,1 ,21(diag 4-=2diag(1 2 1)22已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A且ABA 1BA13E 求B 解由|A*||A|38 得|A|2 由ABA1BA13E 得AB B 3AB 3(A E)1A 3[A(E A 1)]1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-103006060060000660300101001000016123 设P 1AP 其中⎪⎭⎫ ⎝⎛--=1141P ⎪⎭⎫⎝⎛-=Λ2001求A 11解由P 1AP得A P P 1所以A 11 A=P 11P 1.|P|3 ⎪⎭⎫⎝⎛-=1141*P ⎪⎭⎫ ⎝⎛--=-1141311P而 ⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛-=Λ11111120 012001故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=6846832732273124 设AP P 其中⎪⎪⎭⎫⎝⎛--=111201111P ⎪⎪⎭⎫ ⎝⎛-=Λ511 求(A)A 8(5E 6A A 2) 解 ()8(5E 62)diag(1158)[diag(555)diag(6630)diag(1125)]diag(1158)diag(1200)12diag(100) (A)P ()P 1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=111111111425 设矩阵A 、B 及A B 都可逆证明A 1B 1也可逆并求其逆阵证明因为 A 1(A B)B 1B1A1A1B1而A 1(A B)B 1是三个可逆矩阵的乘积所以A 1(A B)B 1可逆即A1B 1可逆(A1B 1)1[A 1(A B)B 1]1B(A B)1A26 计算⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121解设⎪⎭⎫ ⎝⎛=10211A ⎪⎭⎫ ⎝⎛=30122A ⎪⎭⎫ ⎝⎛-=12131B ⎪⎭⎫ ⎝⎛--=30322B则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A 所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫⎝⎛---=9000340042102521 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521 27 取⎪⎭⎫ ⎝⎛==-==1001D C B A 验证|||||||| D C B A D C B A ≠解41001200210100101002000021010010110100101==--=--=D C B A而01111|||||||| ==D C B A故 |||||||| D C B A D C B A ≠28 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A 求|A 8|及A 4解令⎪⎭⎫ ⎝⎛-=34431A ⎪⎭⎫ ⎝⎛=22022A 则 ⎪⎭⎫ ⎝⎛=21A O O A A故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A 1682818281810||||||||||===A A A A A⎪⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A29 设n 阶矩阵A 及s 阶矩阵B 都可逆求 (1)1-⎪⎭⎫⎝⎛O B A O解设⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛-43211C C C C O B A O 则 ⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⎪⎩⎪⎨⎧====--121413B C O C O C A C所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111(2)1-⎪⎭⎫ ⎝⎛B C O A解设⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛-43211D D D D B C O A 则 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321由此得 ⎪⎩⎪⎨⎧=+=+==s nE BD CD O BD CD OAD E AD 423121⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A30 求下列矩阵的逆阵(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025 解设⎪⎭⎫ ⎝⎛=1225A ⎪⎭⎫ ⎝⎛=2538B 则⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A ⎪⎭⎫⎝⎛--=⎪⎭⎫⎝⎛=--8532253811B于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛----850032000052002125003800001200251111B A B A(2)⎪⎪⎪⎭⎫ ⎝⎛4121031200210001解设⎪⎭⎫ ⎝⎛=2101A ⎪⎭⎫ ⎝⎛=4103B ⎪⎭⎫ ⎝⎛=2112C 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A BC O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001第三章矩阵的初等变换与线性方程组1．把下列矩阵化为行最简形矩阵：(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2)⎪⎪⎪⎭⎫⎝⎛----174034301320; (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; (4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--340313*********2)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020********* )2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫ ⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----1740343013201312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫ ⎝⎛---31003100132021233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫⎝⎛000031005010 (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311141312323~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311)5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311 2423213~r r r r r r ---⎪⎪⎪⎪⎭⎫⎝⎛---000000000022********(4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110141312782~rr r r r r --+⎪⎪⎪⎪⎭⎫⎝⎛--410004100020201111134221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎭⎫⎝⎛----0000041000111102020132~rr +⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.设⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ，求A 。

利用对角线法则计算下列三阶行列式

(1)
解因为
所以 , , , .
(2)
解因为
所以
, , , , .
9.问l,m取何值时,齐次线性方程组有非零解？
解系数行列式为
令D=0,得
m=0或l=1
于是当m=0或l=1时该齐次线性方程组有非零解.
10.问l取何值时,齐次线性方程组有非零解？
解系数行列式为
=(1-l)3+(l-3)-4(1-l)-2(1-l)(-3-l)
解逆序数为4: 41, 43, 42, 32.
(3)3 4 2 1;
解逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1.
(4)2 4 1 3;
解逆序数为3: 2 1, 4 1, 4 3.
(5)1 3 × × × (2n-1) 2 4 × × × (2n);
解逆序数为 :
3 2 (1个)
再按最后一行展开得递推公式
D2n=andnD2n-2-bncnD2n-2,即D2n=(andn-bncn)D2n-2
于是 .
而
所以
(5)D=det(aij),其中aij=|i-j|;
解aij=|i-j|,
(-1)n-1(n-1)2n-2.
(6) ,其中a1a2× × ×an¹0.
解
8.用克莱姆法则解下列方程组:
=(1-l)3+2(1-l)2+l-3.
令D=0,得
l=0,l=2或l=3.
于是当l=0,l=2或l=3时,该齐次线性方程组有非零解.
5 2, 5 4 (2个)
× × × × × ×
(2n-1)2, (2n-1)4, (2n-1)6, × × ×, (2n-1)(2n-2)(n-1个)

线性代数第一章习题及答案

第一章行列式1.利用对角线法则计算下列三阶行列式：（1）381141102---；（2）b a c a c b cb a （3）222111c b a c b a；（4）yxy x x y x yy x y x+++.解（1）=---381141102811)1()1(03)4(2⨯⨯+-⨯-⨯+⨯-⨯)1()4(18)1(2310-⨯-⨯-⨯-⨯-⨯⨯-=416824-++- =4-（2）=ba ca cbc b a ccc aaa bbb cba bac acb ---++ 3333c b a abc ---= （3）=222111c b a c b a222222cb ba ac ab ca bc ---++ ))()((a c c b b a ---= （4）yxyx x y x y yx y x+++yx y x y x yx y y x x )()()(+++++=333)(x y x y -+--33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序，求下列各排列的逆序数：（1）1 2 3 4；（2）4 1 3 2；（3）3 4 2 1；（4）2 4 1 3；（5）1 3 … )12(-n 2 4 … )2(n ；（6）1 3 … )12(-n )2(n )22(-n … 2. 解（1）逆序数为0（2）逆序数为4：4 1，4 3，4 2，3 2（3）逆序数为5：3 2，3 1，4 2，4 1,2 1 （4）逆序数为3：2 1，4 1，4 3（5）逆序数为2)1(-n n ：3 2 1个 5 2，54 2个 7 2，7 4，7 6 3个 ……………… … )12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n)1(-n 个（6）逆序数为)1(-n n3 2 1个 5 2，54 2个 ……………… … )12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n)1(-n 个4 2 1个 6 2，6 4 2个 ……………… … )2(n 2，)2(n 4，)2(n 6，…，)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项. 解由定义知，四阶行列式的一般项为43214321)1(p p p p t a a a a -，其中t 为4321p p p p 的逆序数．由于3,121==p p 已固定，4321p p p p 只能形如13□□，即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式：（1）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢71100251020214214；（2）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-2605232112131412；（3）⎥⎥⎥⎦⎥⎢⎢⎢⎣⎢---ef cf bf de cd bd ae ac ab ；（4）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a100110011001 解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-⨯--- =143102211014--321132c c c c ++141717201099-=0(2)2605232112131412-24c c -260532122130412-24r r -0412032122130412-14r r -0000032122130412-=0(3)ef cfbfde cd bdaeac ab ---=ecb ec b ec badf ---=111111111---adfbce =abcdef 4(4)d cb a 10110011001---21ar r +d cb a ab 10011011010---+=12)1)(1(+--d c a ab 101101--+ 23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明:(1)1112222b b a a b ab a +=3)(b a -;(2)bz ay by ax bxaz by ax bxaz bzay bxaz bz ay by ax +++++++++=yxzx z yz y xb a )(33+; (3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a dcbad c b a))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅;(5)1221100000100001a x a a a a x x x n n n +----- n n n n a x a x a x ++++=--111 .证明(1)0122222221312a b a b aa b a ab a c c c c ------=左边 ab a b ab a ab 22)1(22213-----=+ 21))((ab a a b a b +--=右边=-=3)(b a (2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax zx bxaz y z bz ay x a 分别再分bzay y xby ax x zbxaz z y b +++ zyx y x zx z y b y x zx z y z y x a 33+分别再分右边=-+=233)1(yxz x z y zy x b yxzx z yz y x a (3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c964496449644964422222++++++++d d dd c c c cb b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a949494949464222224232423dd c cb b a ac c c c c c c c ----第二项第一项06416416416412222=+d dd c c c b b b a a a(4) 444444422222220001a d a c ab a ad ac ab aa d a c ab a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)()()(111))()((222a d d a c c a b b ad ac ab a d ac a b ++++++---=⨯---))()((a d a c a b)()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b)()()()(112222b d a b bd d b c a b bc c ++++++++ =))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立，即 ,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x x a xD D n n n n 右边=+=-n n a xD 1 所以，对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转，依次得n nnn a a a a D 11111=， 11112n nn n a a a a D = ，11113a a a a D n nnn =，证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnn n n n nnnn a a a a a a a a a a D 2211111111111)1(--==∴=--=--nnn n nn n n a a a a a a a a 331122111121)1()1( nnn nn n a a a a111121)1()1()1(---=-- D D n n n n 2)1()1()2(21)1()1(--+-+++-=-=同理可证nnnn n n a a a a D 11112)1(2)1(--=D D n n T n n 2)1(2)1()1()1(---=-=D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式（阶行列式为k D k ）：(1)aaD n 11=,其中对角线上元素都是a ，未写出的元素都是0；(2)xa a ax a aa x D n =;(3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n n n n n ------=---+; 提示：利用范德蒙德行列式的结果．(4) nnnnn d c d c b a b a D000011112=;(5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121,021≠n a a a 其中.解(1) aa aa a D n 00010000000000001000=按最后一行展开)1()1(100000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n n a aa(再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行，得ax x a a x xa a x x a a a a x D n ------=0000000 再将各列都加到第一列上，得ax a x a x a a a an x D n ----+=0000000000)1( )(])1([1a x a n x n --+=-(3)从第1+n 行开始，第1+n 行经过n 次相邻对换，换到第1行，第n行经)1(-n 次对换换到第2行…，经2)1(1)1(+=++-+n n n n 次行交换，得nn nn n n n n n n a a a n a a a n a a a D )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-∙-∙-=---=1121)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nnnnn d c d c b a b a D 0011112=n n n n n nd d c d c b a b a a 00000011111111----展开按第一行0000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222---n n n n n n D c b D d a 都按最后一行展开由此得递推公式：222)(--=n n n n n n D c b d a D 即 ∏=-=ni i i i i n D c b d a D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=432140123310122210113210)det(--------==n n n n n n n n a D ij n,3221r r r r --0432111111111111111111111--------------n n n n ,,141312c c c c c c +++1524232102221002210002100001---------------n n n n n=212)1()1(----n n n(6)n n a a a D +++=11111111121,,433221c c c c c c ---nn n n a a a a a a a a a a +-------10000100010000100010001000011433221展开（由下往上）按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------0000000000000000000000022433221n n n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------0000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑+==n i in a a a a8.用克莱姆法则解下列方程组：⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x 解 (1)11213513241211111----=D 8120735032101111------=14508130032101111---=14214205410032101111-=---=112105132412211151------=D 11210513290501115----=112123313090509151------=233130905112109151------=1202300461000112109151-----=14238100112109151----=142-=112035122412111512-----=D 811507312032701151-------=31390011230023101151-=28428401910023101151-=----=42611135232422115113-=----=D14202132132********4=-----=D1,3,2,144332211-========∴DD x D D x D D x DD x(2)510006510006510065100065=D 展开按最后一行61000510065100655-'D D D ''-'=65D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',) 5100165100065100650000611=D 展开按第一列6510065100650006+'D46+'=D 460319+''''-'''=D 1507=5101065100065000601000152=D 展开按第二列5100651006500061-6510065*********-365510651065⨯-=1145108065-=--=5110065000060100051001653=D 展开按第三列51006500061000516500061*********+6100510656510650061+=703114619=⨯+= 5100060100005100651010654=D 展开按第四列61000510065100655000610005100651--51065106565--=395-=110005100065100651100655=D 展开按最后一列D '+1000510********12122111=+=665212;665395;665703;6651145;665150744321=-==-==∴x x x x x ． 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解？解 μλμμμλ-==12111113D ，齐次线性方程组有非零解，则03=D 即 0=-μλμ 得 10==λμ或不难验证，当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解？解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-= 3)1(2)1(23-+-+-=λλλ 齐次线性方程组有非零解，则0=D 得 32,0===λλλ或不难验证，当32,0===λλλ或时，该齐次线性方程组确有非零解.。

线代作业答案

a2 b2 (3) 2 c d2 1
(4)
(a + 1) 2 (b + 1) 2 (c + 1) 2
( a + 2) 2 ( b + 2) 2 ( c + 2) 2
( a + 3) 2 ( b + 3) 2 = 0; ( c + 3) 2 ( d + 3) 2
(d + 1) 2 ( d + 2) 2 1 1 1
x +b y z
x ( −1) 2 = 右边 y
( a + 3) 2 ( b + 3) 2 ( c + 3) 2 ( d + 3) 2
z
a2 b2 (3) 左边 = 2 c d2
a 2 + ( 2a + 1) (a + 2) 2 b 2 + ( 2b + 1) (b + 2) 2 c 2 + ( 2c + 1) (c + 2) 2 d 2 + ( 2d + 1) (d + 2) 2
第一章
行列式
1.利用对角线法则计算下列三阶行列式： 2 0 1 a b （1） 1
− 4 −1 ； 3 −1 8 1 1 b b2 2 1 c ； c2 0 1
c （2） b c a c a b x y x+ y y x+ y x x+ y x . y
（3） a
（4）
a2
解（1） 1
− 4 − 1 = 2 × ( −4) × 3 + 0 × ( −1) × ( −1) + 1 × 1 × 8 −1 8 3 − 0 × 1 × 3 − 2 × ( −1) × 8 − 1 × ( −4) × ( −1) = − 24 + 8 + 16 − 4 =− 4

1利用对角线法则计算下列三阶行列式

第一章行列式1.利用对角线法则计算下列三阶行列式：（1）381141102---；（2）ba c a cb cb a ; （3）222111c b a c b a ；（4）y x y x x y x yy x y x +++. 解（1）=---381141102811)1()1(03)4(2⨯⨯+-⨯-⨯+⨯-⨯)1()4(18)1(2310-⨯-⨯-⨯-⨯-⨯⨯-=416824-++-=4-（2）=ba c a cb cb a ccc aaa bbb cba bac acb ---++3333c b a abc ---=（3）=222111c b a c b a 222222cb ba ac ab ca bc ---++))()((a c c b b a ---=（4）yx y x x y x y yx y x +++yx y x y x yx y y x x )()()(+++++=333)(x y x y -+-- 33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序，求下列各排列的逆序数：（1）1 2 3 4；（2）4 1 3 2；（3）3 4 2 1；（4）2 4 1 3；（5）1 3 … )12(-n 2 4 … )2(n ；（6）1 3 … )12(-n )2(n )22(-n … 2. 解（1）逆序数为0（2）逆序数为4：4 1，4 3，4 2，3 2 （3）逆序数为5：3 2，3 1，4 2，4 1,2 1 （4）逆序数为3：2 1，4 1，4 3 （5）逆序数为2)1(-n n ： 3 2 1个 5 2，5 4 2个 7 2，7 4，7 6 3个 ……………… …)12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n )1(-n 个（6）逆序数为)1(-n n3 2 1个 5 2，54 2个 ……………… …)12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n )1(-n 个4 2 1个 6 2，6 4 2个 ……………… … )2(n 2，)2(n 4，)2(n 6，…，)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项.解由定义知，四阶行列式的一般项为43214321)1(p p p p t a a a a -，其中t 为4321p p p p 的逆序数．由于3,121==p p 已固定，4321p p p p 只能形如13□□，即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式：（1）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢7110025*********4；（2）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-2605232112131412；（3）⎥⎥⎦⎥⎢⎢⎣⎢---ef cf bf de cd bd ae ac ab ；（4）⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a100110011001解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-⨯---=143102211014-- 321132c c c c ++1417172001099-=0(2)2605232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=e c b e c b e c b adf ---=111111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 101101--+ 23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -; (2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=y x z x z y z y x b a )(33+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--= 右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bz ay y x by ax x z bx az z y b +++zy x y x z xz y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c964496449644964422222++++++++d d d d c c c cb b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+ddd c c c bb b a a a(4) 444444422222220001ad a c a b a ad a c a b a ad a c a b a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)()()(111))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =⨯---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立，即,122111-----++++=n n n n n a x a xa x D :1列展开按第则n D1110010001)1(11----+=+-x x a xD D n n n n右边=+=-n n a xD 1 所以，对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转90、或依副对角线翻转，依次得n nn n a a a a D 11111 =， 11112n nn n a a a a D = ，11113a a a a D n nnn =，证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnn n nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-= 同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n T n n 2)1(2)1()1()1(---=-=D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式（阶行列式为k D k ）：(1)aaD n 11=,其中对角线上元素都是a ，未写出的元素都是0；(2)xa a ax aa a xD n =; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n nn n n ------=---+; 提示：利用范德蒙德行列式的结果． (4) nnn nn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 00010000000000001000 =按最后一行展开)1()1(1000000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n n a a a (再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行，得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上，得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始，第1+n 行经过n 次相邻对换，换到第1行，第n 行经)1(-n 次对换换到第2行…，经2)1(1)1(+=++-+n n n n 次行交换，得 nnn n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-•-•-=---=1121)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nn nnn d c d c b a b a D 011112=nn n n n nd d c d c b a b a a 0000000011111111----展开按第一行0000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式：222)(--=n n n n n n D c b d a D 即 ∏=-=ni i i iin D c b da D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=0432********0122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0432111111111111111111111 --------------n n n n,,141312c c c c c c +++1524232102221002210002100001---------------n n n n n =212)1()1(----n n n(6)nn a a D a +++=11111111121 ,,433221c c c c c c ---nn n n a a a a a a a a a a +-------10000100010000100010001000011433221展开（由下往上）按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------00000000000000000000000000022433221 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组：⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x 解 (1)11213513241211111----=D 8120735032101111------=145008130032101111---=1421420005410032101111-=---= 112105132412211151------=D 11210513290501115----=1121023313090509151------=2331309050112109151------=1202300461000112109151-----=14200038100112109151----=142-= 112035122412111512-----=D 811507312032701151-------=3139011230023101151-=2842840001910023101151-=----=426110135232422115113-=----=D ; 14202132132212151114=-----=D1,3,2,144332211-========∴DDx D D x D D x D D x (2) 510006510006510065100065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',) 5100165100065100650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507= 51165100065000601000152=D 展开按第二列510651006500061-6510065000610005-365510651065⨯-= 1145108065-=--= 51100650000601000051001653=D 展开按第三列5100650006100051650061000510065+6100510656510650061+= 703114619=⨯+= 51000601000051000651010654=D 展开按第四列61000510065100655000610005100651--51065106565--=395-= 11051000651000651100655=D 展开按最后一列D '+15100651006512122111=+=665212;665395;665703;6651145;665150744321=-==-==∴x x x x x ． 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解？解 μλμμμλ-==12111113D ，齐次线性方程组有非零解，则03=D即 0=-μλμ 得 10==λμ或不难验证，当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ 有非零解？解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-=3)1(2)1(23-+-+-=λλλ齐次线性方程组有非零解，则0=D 得 32,0===λλλ或不难验证，当32,0===λλλ或时，该齐次线性方程组确有非零解.。

(完整word版)利用对角线法则计算下列三阶行列式

第一章行列式1. 利用对角线法则计算下列三阶行列式:（1）381141102---;解 381141102---=2´(—4)´3+0´（—1)´(-1）+1´1´8 -0´1´3—2´（-1)´8—1´(—4)´(—1） =—24+8+16—4=-4.（2）b a c ac b cb a解 ba c a cb cb a=acb +bac +cba —bbb —aaa -ccc=3abc -a 3—b 3-c 3.(3）222111c b a c b a ;解 222111cb ac b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2（a -b ）（b -c ）（c -a )。

(4)y x y x x y x y yx y x +++.解 yx y x x y x y yx y x +++=x （x +y )y +yx （x +y )+(x +y )yx —y 3-(x +y )3-x 3=3xy（x+y）-y3-3x2y-x3-y3—x3=-2（x3+y3）。

2。

按自然数从小到大为标准次序，求下列各排列的逆序数: （1)1 2 3 4;解逆序数为0（2）4 1 3 2；解逆序数为4： 41， 43， 42, 32。

(3)3 4 2 1；解逆序数为5： 3 2, 3 1, 4 2, 4 1, 2 1。

（4）2 4 1 3;解逆序数为3: 2 1， 4 1， 4 3。

（5）1 3 × × × (2n-1) 2 4 × × × （2n）；解逆序数为2)1(nn:3 2 (1个）5 2， 5 4（2个）7 2， 7 4, 7 6（3个)× × × × × ×(2n—1)2， (2n—1）4，（2n—1)6，× × ×， (2n-1）(2n-2) （n-1个）（6)1 3 × × × (2n—1） (2n） (2n-2）× × × 2.解逆序数为n(n-1） :3 2(1个)5 2， 5 4 (2个)× × × × × ×(2n-1）2， (2n—1)4, (2n—1)6, × × ×， (2n—1)（2n—2) (n-1个)4 2(1个)6 2, 6 4(2个) × × × × × ×（2n )2, (2n ）4，（2n ）6， × × ×，（2n )（2n -2) （n -1个） 3. 写出四阶行列式中含有因子a 11a 23的项. 解含因子a 11a 23的项的一般形式为（1)ta 11a 23a 3r a 4s ，其中rs 是2和4构成的排列这种排列共有两个即24和42所以含因子a 11a 23的项分别是（1）t a 11a 23a 32a 44（1)1a 11a 23a 32a 44a 11a 23a 32a 44 （1）ta 11a 23a 34a 42(1)2a 11a 23a 34a 42a 11a 23a 34a 424. 计算下列各行列式:（1）71100251020214214；解 7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c 。

利用对角线法则计算下列三阶行列式

第一章行列式1. 利用对角线法则计算下列三阶行列式: 2 0 1(1) 1 一4 —1 ;-18 3 2 0 1 解 1 一4 -1 -18 3二2' (—4)'3+0' (―1)' (-1)+1'1'8-0'「3-2' (-1)'8-1' (一4)‘(-1)二-24+8+16-4二-4.-acb^bac^cbarbbkraaarccc =3abc-才 -c 3. 1 1 1 a bc 7 f ? 2 6T tr CT1 1 17 f 9 76Tb- (T二方 c'+ ca 2+alJ-a^- b 才- elf(a~方)(Z?-c) (C ~<3).\17y x+y ⑷y x+y X ・x+y X y解X y x+y y x+y X x+y X y-x{x^y）T+M（屮y） + （对7）yx~^~（对力3~x-3xy{x^y） -y-3Y y-x~y~x二-2（y+y）.2.按自然数从小到大为标准次序，求下列各排列的逆序数：（1） 1 2 3 4;解逆序数为0（2） 4 1 3 2;解逆序数为4: 41, 43, 42, 32.（3） 3 4 2 1;解逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1.（4） 2 4 1 3;解逆序数为3: 2 1, 4 1, 4 3.（5） 1 3 X X X （2/2-1） 2 4 X X X （2刀）；解逆序数为小字2：3 2 （1 个）5 2, 5 4（2 个）7 2, 7 4, 7 6（3 个）X X X X X X(2n-l)2, (2/7-D4, (2/?-l)6, XXX, (2旷1) (2丁2)(77-1 个)(6) 1 3 XXX (2/7-1) (2z?) (2/7-2) X X X 2.解逆序数为刀(丁1):32(1 个)52, 5 4 (2 个)X X X X X X(2旷1)2, (277-1)4, (2/?-1)6, XXX, (2旷1) (2丁2) (n~l个)42(1 个)62, 6 4(2 个)X X X X X X(2/2)2, (2/7)4, (2/?)6, XXX, (2/7)(2/T~2) (n~l 个)3.写出四阶行列式中含有因子②辺3的项.解含因子加亦的项的一般形式为(1) &1103 &其中右是2和4构成的排列这种排列共有两个即24和42所以含因子刘亦的项分别是(1) &32&I4 ( 1)白11&23 白32 刘\ 丄丿 <311523531 <912\ 1/ 511^23 <931512目11<323&3 1&124. 计算下列各行列式： (1)解-ab ac ae(3) bd -cd de bf cf -efo - 02490 902411 - 11 -123 411101122 423 61-12O 231502423 41-12 1 231 2 -0202 4236 1-12023 15C7_Yq112242 361-12023 15o-0200 4230 1-120 2314207 2021 1251 411001251 411100-ab ac ae-bee bd -cd de =adf b -c ebf cf -efb c -e-1 1 =adfbce 1 -1 11 =4abcdef-23 41110 - 0 4 -12-1O2021 -1230 4111004207 20215. 证明：证明a 2 ab b 2 C2~C \a 2 ab-crb 2-a 2 2a a+b 2b2a b —a 2b-2a 1 1 1c 厂q 1 0 0=^Ma b-a 茫纭&罗二 d ax+by ay+bz az+bx兀y z⑵ ay+bz az+bx ax+by=(/+//)y z xaz+bx ax+by ay+bzz x y证明cix+by ay+bz, az+bx ay+bz az+bx ax+by az+bx ax+byay+bz.ool Jo 1 c-1lb 」oQ 」oo⑷o 一oo 6- d+rq- ooldo 1 c」lb-lo a」l+ab a = (—1)(—1严-1 C 0 -1 心+d 唧+ " a ad： -1 c l+cd| | 0 -1 0=(-1)(-1严1 坪ad j l+cd|abcd^ab^ cchad^ 1. a 2 ab (1) 2a a+b 1 1b 22b 二(旷方)';ooldb 竽-1O(&厂6, 得）ay+bz Z az+bx x ax+by y Z az+bx x ax+by yay+bz.X y Zy z x =a 3 y z x +夕 z X yz x yx y zx y zx y zy z x +夕 y z xz x yz X yx y z=(R+Z/)y z 兀z 兀ya 2 (a+ 1尸(a+ 2尸(a+3)，b 20+1)2 (b+2)2 0+3)2 c 2 (c+l)2(c+2)2 (c+3)2 d 2(d + l)2 (d + 2)2 (d+3)2证明a 2 2a+ 1 2a+3 加+5b 2 2b+\ 2Z?+3 2b+5=a x ay+bz az+bx y az+bx ax+by+bz az+bx ax+by Z ax+by ay+bz y ay+bz, az+bxx ax+by ay+bz x =a 2 y z y +b 2 z X =0; b 2 -2 S+ 1尸 (b + l)2 (C+l)2 0+ 1)2 (a+ 2)2 (b+2)2 (c+2)2 (d + 2)2(a+3)2 0+3)2 (c+3)2 0+3)2 (c厂 C3,C3~~ C2, Q-C1得)c2 2c+l 2c+3 2c+5cl2 2d+l 2J+3 2cl+5(&厂6, 得）(5)二才+②尹^ XXX +如］-{a~b) (a~c) (a~d) (b~d) lb~d) (c~d) (&+決c+6 ; 证明1 1 c-a d -a c(c-ci) d(d-a) c 2(c 2-^2) d 2(d 2-a 2)1 1 1=(b-a)(c-a)(d-a) bed b 2(b+a) C 2(C +<7)d 2(d+a) 1 1 1=(b-a)(c-a)(〃-a)O c-b d-b0 c(c-b)(c+b+a) d(〃-b)(d+b+a) =(b-G )(C -Q )(d-Q )(c-b)(d-b )c (c+,+°)d(d+b+a)二(旷方)(旷q) (a~d) (b~c) (b~d) (c^d) (a^b^c^d).x -1 0 0 x -1 • • • ••• ••• 0 0 0 ⑷l d 6/2^4l b fe2?4o222 22 2 2 2 11111111 +oox -1 c 妇 x+a {lb/22Ml 〃6/26/41 b-a b(b-a) b 2(b 2~a 2)x^a n•证明用数学归纳法证明当77=2 时，X；； =/+0/ + °2，命题成立.假设对于(旷1)阶行列式命题成立，即几*产+X X X +乔屮则2按第一列展开有-1 0・ (00)殆心+6(-1严• ••-1 •• • •• 0• • • • •• ••1 1・•- X-1二JV0 丁i+&F#+ <31#^+ X X X +乔屮②.因此，对于刀阶行列式命题成立.6.设刀阶行列式Z^det(^),把〃上下翻转、或逆时针旋转90°、或依副对角线翻转，依次得n(n-l)证明D}=D2=(-l)^D, D^D . 证明因为Z^det (aj,所以Gm D\= ..................................Q\\ …a\na\\ •…a\n =(_l)〃-ia川…%+ (—1严 V=(一 ])1+2+…+e-2)+gl) £) = (_ ]^~2~ D 同理可证n(n-l) n(n-V)=(—i )h D =(—in - D .n(n-l) n(/i-l)2=(—l)h 0=(—1)=(—l)h D=(-l)n(,t ~l}D=D.7. 计•算下列各行列式（2为R 阶行列式）:1・,其屮对角线上元素都是2未写出的元素都是0;解("一 1)x(〃一 1)a 0 0 …0 1 0 a 0 …0 0 0 0 a …0 00 0 ・・・ a 010 0a （按第刀行展开）D… = /i(n-l)0=(—ILn(n-l)00000 d o do n /Iloo 000。

利用对角线法则计算下列三阶行列式

线性代数课后习题答案全)习题详解

线性代数第6版第1章课后习题解答

线性代数课后习题答案全解.pdf

线性代数课后习题1-4作业答案(高等教育出版社)

线性代数课后习题1-4作业答案(高等教育出版社)

线性代数课后习题1-4作业答案(高等教育出版社)

线性代数 第五版(同济大学)课后习题答案

同济大学线性代数第六版标准答案(全)

《应用型本科线性代数及其应用》习题参考解答

同济大学-线性代数-习题册+答案

同济大学工程数学线性代数第六版答案(全)

线性代数第五版答案(全)

线性代数课后习题答案全习题详解

利用对角线法则计算下列三阶行列式

线性代数第一章习题及答案

线代作业答案

1利用对角线法则计算下列三阶行列式

(完整word版)利用对角线法则计算下列三阶行列式

利用对角线法则计算下列三阶行列式

线性代数第五版(同济大学)课后习题答案