古德投影
世界地图常用地图投影知识大全

世界地图常用地图投影知识大全2009-09-30 13:20在不同的场合和用途下使用不同的地图投影,地图投影方法及分类名目众多,象:墨卡托投影,空间斜轴墨卡托投影,桑逊投影,摩尔维特投影,古德投影,等差分纬线多圆锥投影,横轴等积方位投影,横轴等角方位投影,正轴等距方位投影,斜轴等积方位投影,正轴等角圆锥投影,彭纳投影,高斯-克吕格投影,等角圆锥投影等等。
一、世界地图常用投影1、等差分纬线多圆锥投影(Polyconic Projection With Meridional Interval o nSame Parallel Decrease AwayFrom Central Meridian by E qual Difference)普通多圆锥投影的经纬线网具有很强的球形感,但由于同一纬线上的经线间隔相等,在编制世界地图时,会导致图形边缘具有较大面积变形。
1963年中国地图出版社在普通多圆锥投影的基础上,设计出了等差分纬线多圆锥投影。
等差分纬线多圆锥投影的赤道和中央经线是相互垂直的直线,中央经线长度比等于1;其它纬线为凸向对称于赤道的同轴圆弧,其圆心位于中央经线的延长线上,中央经线上的纬线间隔从赤道向高纬略有放大;其它经线为凹向对称于中央经线的曲线,其经线间隔随离中央经线距离的增加而按等差级数递减;极点投影成圆弧(一般被图廓截掉),其长度等于赤道的一半(图2-30)。
通过对大陆的合理配置,该投影能完整地表现太平洋及其沿岸国家,突出显示我国与邻近国家的水陆关系。
从变形性质上看,等差分纬线多圆锥投影属于面积变形不大的任意投影。
我国绝大部分地区的面积变形在10%以内。
中央经线和±44º纬线的交点处没有角度变形,随远离该点变形愈大。
全国大部分地区的最大角度变形在10º以内。
等差分纬线多圆锥投影是我国编制各种世界政区图和其它类型世界地图的最主要的投影之一。
类似投影还有正切差分纬线多圆锥投影(Polyconic Projectionwith Me ridional Intervals on Decrease Away From Central Meridian by T angent),该投影是1976年中国地图出版社拟定的另外一种不等分纬线的多圆锥投影。
常用地图投影

常用的几种地图投影世界地图常用投影一、墨卡托投影(等角正切圆柱投影)投影方法:圆柱投影。
经线彼此平行且间距相等。
纬线也彼此平行,但离极点越近,其间距越大。
不能显示极点。
应用:标准海上航线图(方向)。
其他定向使用:航空旅行、风向、洋流。
等角世界地图。
此投影的等角属性最适合用于赤道附近地区,例如,印尼和太平洋部分地区。
特点:形状等角。
由于该投影维持局部角度关系不变,所以能很好地描绘微小形状。
面积明显变形方向保持了方向和相互位置关系的正确距离沿赤道或沿割纬线的比例是真实的。
局限:在墨卡托投影上无法表示极点。
可以对所有经线进行投影,但纬度的上下限约为80° N 和80° S。
大面积变形使得墨卡托投影不适用于常规地理世界地图。
墨卡托投影坐标系:取零子午线或自定义原点经线(L0)与赤道交点的投影为原点,零子午线或自定义原点经线的投影为纵坐标X轴,赤道的投影为横坐标Y轴,构成墨卡托平面直角坐标系。
二、桑逊投影(正轴等积伪圆柱投影)应用:除用于编制世界地图外,更适合编制赤道附近南北延伸地区的地图,如非洲、南美洲地图等特点:该投影的纬线为间隔相等的平行直线,经线为对称于中央经线的正弦曲线,是等面积投影,赤道和中央经线是两条没有变形的线,离开这两条线越远,长度、角度变形越大。
因此,该投影中心部分变形较小。
三、摩尔维特投影(伪圆柱等积投影)投影方法:伪圆柱等积投影。
所有纬线都是直线,所有经线都是等间距的椭圆弧。
唯一例外的是中央子午线,中央子午线是直线。
极点是点。
应用:适用于绘制世界专题或分布地图,经常采用不连续的形式。
将其与正弦曲线投影组合使用可创造出古蒂等面积和博格斯投影。
属性:形状在中央子午线和40°44' N 与40°44' S 纬线的交点处,形状未发生变形。
向外离这些点越远,变形越严重,在投影边处变形严重。
面积等积。
方向仅在中央子午线和40°44' N 与40°44' S 纬线的交点处,局部角度才是真实的。
《地图学原理》复习资料

地图学原理复习资料第一章引论1、地图的定义:地图是按照一定的数学法则,将地球(或星体)表面上的空间信息,经概括综合,以可视化、数字或触摸的符号形式,缩小表达在一定载体上的图形模型,用以传输、模拟和认识客观世界的时空信息。
2、地图的基本特征:(1)严密的数学法则;(2)特定的符号系统;(3)科学的地图概括;(4)独特的传输信息的通道。
地图投影方法、比例尺和控制方向构成了地图的数学法则,它是地图制图的基础。
3、地图的构成要素:(1)数学要素(地图投影、坐标网、比例尺、控制点等);(2)地理要素①普通地图包括(水系、地貌、土质植被、居民地、交通线境界线等自然和社会经济内容)②专题地图包括(专题要素和底图要素);(3)图边要素(图名、图号、图例、接图表、图廓、分度带、比例尺、附图、坡度角、成图时间及单位、有关资料说明等)。
4、地图的功能:(1)获取认知信息功能;(2)模拟客观世界的功能;(3)传输信息功能;(4)载负信息功能;(6)感受信息功能。
5、现代地图学定义:以地学信息传输与地学可视化为手段,以区域综合制图与地图概括为核心,以地图的科学认知和分析应用为目的,研究地图的理论实质、制图技术与使用方法的综合性学科。
第二章地图的数学基础1、地球形状的三级逼近:(1)地球形状的一级逼近——大地水准面:人们设想当海洋静止时,平均海水面穿过大陆和岛屿,形成一个闭合的曲面,该面上的各点与重力方向(铅垂线)成正交,这就是大地水准面。
大地水准面所包围的球体,叫大地球体。
意义: (1. 地球形体的一级逼近:对地球形状的很好近似,其面上高出与面下缺少的相当。
(2. 起伏波动在制图学中可忽略:对大地测量和地球物理学有研究价值,但在制图业务中,均把地球当作正球体。
(3. 重力等位面:可使用仪器测得海拔高程(某点到大地水准面的高度)。
(2)地球形状的二级逼近——地球椭球体:假想一个扁率极小的椭圆,绕大地球体短轴旋转所形成的规则椭球体称之为地球椭球体意义:地球椭球体表面是一个规则的数学表面,可以用数学公式表达,所以在测量和制图中就用它替代地球的自然表面,用于测量计算的基准面。
地图学试题4套集合(含答案)

地图学习题一一、名词解释(每小题3分,共15分)1。
地图 :地图是根据一定的数学法则,将地球(或其它星体)上的自然和人文现象、使用地图语言,通过制图综合,缩小反映在平面上,反映各种现象的空间分布、组合、联系、数量和质量特征及其在时间中的发展变化。
2。
地图投影 :将地球椭球面上的点转换为平面上的点的方法称为地图投影。
3。
变形椭圆:地球面上一个微分圆在地图平面上的投影,是一种显示投影变形的几何图形。
4.视觉阈值:刚刚能引起视觉的持续一定时间的刺激量。
5。
SOM :空间斜轴墨卡托。
6.接图表:是表示各图幅间相互位置的图表。
根据其用途和范围可分为图幅接图表和区域接图表。
7。
图形开窗:在整个图形中选取需要处理的部分,称为图形的开窗。
8.编图任务书:是由上级主管部门或委托单位提供的,其内容包括:地图名称、主题、区域范围、地图用途、地图比例尺、有时还指出所采用的地图投影、对地图的基本要求、制图资料的保障情况以及成图周期和投入的资金等项目。
9。
制图综合:就是采取简单扼要的手法,把空间信息中主要的、本质的数据提取后联系在一起,形成新的概念。
10.GUASS-KRUAGER:等角横切椭圆柱投影.二、选择题(每小题2分,共20分)1。
下面那一项可能是1:10万地形图的编号(B)A。
I-48-A (1:50万)B。
I—52-12 C。
I-50—[8] (1:25万)D.J—50—148(没有这个编号)3.按投影的变形性质,地图投影分为三种,以下那项不属于这三种之一(B)A。
等积投影B。
等距投影 C。
任意投影 D。
等角投影4。
我国1:100万地形图使用的地图投影是(D)A. Gauss-Kruger B。
UTM C. 斜轴等角方位投影D。
等角割圆锥投影5.从几何意义上说,属于圆锥投影的是(C )A。
UTM (圆柱投影) B. Gauss-Kruger (圆柱投影)C. Lambert D。
UPS(方位投影)//C。
世界地图常用地图投影知识大全

世界地图常用地图投影知识大全2009-09-30 13:20在不同的场合和用途下使用不同的地图投影,地图投影方法及分类名目众多,象:墨卡托投影,空间斜轴墨卡托投影,桑逊投影,摩尔维特投影,古德投影,等差分纬线多圆锥投影,横轴等积方位投影,横轴等角方位投影,正轴等距方位投影,斜轴等积方位投影,正轴等角圆锥投影,彭纳投影,高斯-克吕格投影,等角圆锥投影等等。
一、世界地图常用投影1、等差分纬线多圆锥投影(Polyconic Projection With Meridional Interval on Same Parallel Decrease Away From Central Meridian by Equal Difference)普通多圆锥投影的经纬线网具有很强的球形感,但由于同一纬线上的经线间隔相等,在编制世界地图时,会导致图形边缘具有较大面积变形。
1963年中国地图出版社在普通多圆锥投影的基础上,设计出了等差分纬线多圆锥投影。
等差分纬线多圆锥投影的赤道和中央经线是相互垂直的直线,中央经线长度比等于1;其它纬线为凸向对称于赤道的同轴圆弧,其圆心位于中央经线的延长线上,中央经线上的纬线间隔从赤道向高纬略有放大;其它经线为凹向对称于中央经线的曲线,其经线间隔随离中央经线距离的增加而按等差级数递减;极点投影成圆弧(一般被图廓截掉),其长度等于赤道的一半(图2-30)。
通过对大陆的合理配置,该投影能完整地表现太平洋及其沿岸国家,突出显示我国与邻近国家的水陆关系。
从变形性质上看,等差分纬线多圆锥投影属于面积变形不大的任意投影。
我国绝大部分地区的面积变形在10%以内。
中央经线和±44º纬线的交点处没有角度变形,随远离该点变形愈大。
全国大部分地区的最大角度变形在10º以内。
等差分纬线多圆锥投影是我国编制各种世界政区图和其它类型世界地图的最主要的投影之一。
类似投影还有正切差分纬线多圆锥投影(Polyconic Projection with Meridional Intervals on Decrease Away From Central Meridian by Tangent),该投影是1976年中国地图出版社拟定的另外一种不等分纬线的多圆锥投影。
地图的数学基础

研究全球区域投影时,可将地球视为圆球体。 主要有圆柱投影、伪圆柱投影、多圆锥投影等。 世界各国编制世界航海图、时区图时,经常 采用正轴圆柱投影; 编制世界行政区划图时,欧美一些国家常采 用摩尔维特投影、桑逊投影等, 中国主要采用等差分纬线多圆锥投影和正切差 分纬线多圆锥投影。
伪方位投影
多圆锥投影
1.纬线为同轴圆弧 其圆心均位于中 央经线上; 2.中央经线为直线, 3.其余经线均为对 称于中央经线的 曲线。
多圆锥投影示意图
等差分纬线多圆锥投影
1.经线对称于中央直经线,离中央 经线愈远,经线间隔成等差比例递减; 2.纬线投影为对称于赤道的同轴圆 弧,其圆心位于中经上; 3.极点表示为圆。圆长度为赤道投 影长度的二分之一。 它是任意投影。我国的世界地图 多采用该投影。 我国位于地图中接近中央的位置, 形状比较正确。
等积
投影特性: 1.等积(P=1); 2.所有纬线无长度变形(n=1); 3.中央经线保持等长(m=1)。 4.该投影离中经愈远、纬度愈高变形愈大。 适于:沿赤道或中央经线伸展的地区。
伪圆柱投影(桑逊投影)
经线为对称于中经(直线)的正弦曲线; 纬线为等距平行线,
⑵ 摩尔威特(Mollweide)投影
40°44 ′11.8 ″
S90 = Searth / 2
常用于编制世界地图
及东、西半球地图
伪圆柱投影
等积
基于正弦与摩尔维特投影的分瓣投影
40° 正弦 投影 40°
⑶ 古德(Goode)投影
美地理学家古德(J.Paul Goode)于1923年提出在整 个制图区域主要部分中央都设置一条中央经线,分别进 行投影,则全图就分成几瓣,各瓣沿赤道连接在一起。
历史:别急着嘲笑“地图开疆”,你以前是否知道有这么多种世界地图?

别急着嘲笑“地图开疆”中俄边境谈判,清政府只能使用俄方提供的地图,以至被骗,丢失30多万平方公里土地。
三沙市辖西沙群岛、中沙群岛、南沙群岛的岛礁及其海域,政府驻地位于西沙永兴岛近日,越南政府搞了一次“地图开疆”之举,向国际民航组织提出,要求修改有关三亚飞行情报区的航行地图。
这是因为越南声称对“长沙群岛”(即南沙群岛)、永暑礁拥有主权,而在国际民航组织的地图上,“长沙群岛”上写有中文“中国三沙市”;永暑礁上标注了“三沙永暑机场”。
越南的要求固属无理取闹,但也不应无视,因为从历史教训而言,“地图开疆”确实是件大事。
“地图开疆”很重要。
中国曾因无精确地图,丢失数十万平方公里雍正时代,与沙俄签署《恰克图条约》,没有精确地图可用,只能被俄方地图所骗在近代国际政治,尤其是领土谈判中,地图常常发挥着举足轻重的作用。
中国古代同周边国家并无明确国界,也没有完整、准确的疆域地图。
1689年,尼布楚谈判期间,中方代表手上只有现存《吉林九合图》的原图,精度有限。
康熙帝为了解黑龙江流域的地理情况,要求进呈相关地图。
参与尼布楚谈判的法国传教士张诚,献出一张亚洲地图,但因资料缺乏,中国东北地区竟存在一片空白。
①清政府同沙俄在1727年签订《布连斯奇界约》、1728年签订《恰克图条约》时,中方代表依旧没有精确地图,对边界情况几乎一无所知,只能使用俄方提供的地图,以至被骗,损失惨重,丢失贝加尔湖以南、恰克图以北的安加拉河流域30多万平方公里土地。
②光绪年间,因使用地图有误,中俄伊犁谈判,中方代表错算了所失领土的多少甚至到了晚清,这种情况都没有改变。
1878年,崇厚同沙俄谈判伊犁问题失败,一个重要原因也是无图可用。
胡林翼在康熙《皇舆全览图》等基础上修订的《大清一统舆图》虽有经纬网,但1:200万的比例过小,边地译名混乱。
崇厚参照俄方《分界图说》,绘制《伊犁分界图》时,出现地名定位错误、天山位置偏移等问题,让地图上划归俄方的面积,比实际划归俄方的面积,要小很多。
3.3常用地图投影

摩尔维特投影常用来编制世界,大洋图,由于离中央 经线经差±900的经线是一个圆,且圆面积恰好等于半 球面积,因此,该投影也用来编制东、西半球地图。
4、分瓣伪圆柱投影
——古德投(Goode
•
Projection)
1923年美国地理学家古德(J.Paul Goode)提出了一种对伪圆柱投影进行分 瓣的投影方法,即古德投影。 • 全图被分成几瓣,各瓣通过赤道连接在 一起,地图上仍无面积变形,核心区域的 长度、角度变形和相应的伪圆柱投影相比 明显减小,但投影的图形却出现了明显的 裂缝,这种尽量减少投影变形,而不惜图 面的连续性是古德投影的重要特征
17
3、伪圆柱投影
(1)桑逊投影(Sanson Projection)
•
桑逊投影是一种经线为正炫曲线的正轴等 积伪圆柱投影,又称桑逊-弗兰斯蒂德 (Sanson- Flamsteed)投影。该投影的纬线 为间隔相等的平行直线,经线为对称于中央经 线的正弦曲线(图2-27)。中央经线长度比为 1,即m0=1,且n=1, p=1。桑逊投影为等面 积投影,赤道和中央经线是两条没有变形的线, 离开这两条线越远,长度、角度变形越大。因 此,该投影中心部分变形较小,除用于编制世 界地图外,更适合编制赤道附近南北延伸地区 的地图,如非洲、南美洲地图等。
• 彭纳投影 4、伪圆柱投影
3.3.3 中国地图常用投影
斜轴方位投影
正轴割圆锥投影
1、斜轴方位投影
(1)斜轴等积方位投影 全中国地图,亚洲地图,半球地图 (2)斜轴等角割方位投影 中国全图 (3)斜轴等距方位投影 行政区图,交通地图
2、正轴割圆锥投影
1)正轴等角割圆锥投影 全中国及各省或大区域的地势图、气象 图与气候图,专题图。 2)正轴等积割圆锥投影 行政区划图、土地利用图、土壤图。森 林分布图。 3)正轴等距割圆锥投影 交通图及要求距离不变形的图
第二章投影及判断和选择

常用方位投影
5.2
正轴方位投影
5.2.3
正轴等距方位投影(波斯托投影)
特点: 由投影中心至任意一点 的距离均与实地相等。即该 投影后长度比 m=1。由于该 投影具有由投影中心至任意 点的距离和方位均保持与实 地的距离和方位不变,因此 在国际上应用的也比较广泛, 多用于两极地区图。
采用正轴等距方位投 影绘制的南极地图
常用方位投影
5.2
正轴方位投影
特点:投影中心为极点, 纬线为同心圆,经线为同 心圆的半径,两经线间的 夹角与实地相等。等变形 线都是以投影中心为圆心 的同心圆,包括等角、等 积、等距三种变形性质。 正轴方位投影主要用于制 作两极地区图。
三种方位投影纬线间隔变化示意图
常用方位投影
5.2
正轴方位投影
°等分,分别交线A于abc…,分别 以abc为圆心,以到C的长度为半径画 圆弧,即得各经线。 B C
①
②
常用方位投影
5.4
斜轴方位投影
5.4.2 斜轴等距方位投影
经纬线形式:
中央经线为直线,其
它经纬线均是曲线。在中 央经线上纬线间隔相等。
常用方位投影
5.4
斜轴方位投影
5.4.2 斜轴等距方位投影
非透视方位投影是借助于透视投影的方式,而附加上一定的 条件,如加上等积、等距等条件所构成的投影。在这类投影 中有等距方位投影和等积方位投影。
5.1.3
特点
在投影平面上,由投影中心(平面与球面相切的切点, 或平面与球面相割的割线的同心圆)向各个方向的方位角与 实地相等,其等变形线是以投影中心为圆心的同心圆,该投 影适合作区域轮廓大致为圆形的地图。
§4
地图投影的应用
高斯-克吕格投影(等角横切椭圆柱投影) 通用横轴墨卡托投影——UTM 投影 百万分一地形图投影 方位投影(正轴方位投影、正轴等角方位投影、正轴
地图学几种投影的主要参数

几种投影的主要参数Gauss Kruger(高斯-克吕格投影):除中央经线和赤道为直线外,其他经线均为对称于中央经线的曲线。
该投影没有角度变形,在长度和面积上变形也很小,中央经线无变形,自中央经线向投影带边缘,变形逐渐增加,变形最大处在投影带内赤道的两端。
限制长度变形最有效的方法是将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。
经差6度为六度带,经差3度为三度带。
六度带自0度子午线起自西向东分带,带号为1—60带。
三度带基于六度带,自 1.5度子午线起每隔经差3度自西向东分带,带号为1—120带。
我国经度范围73W—135E,十一个六度带。
各带中央经线:75,75+6n。
三度带为二十二个。
主要参数:投影代号(Type),基准面(Datum),单位(Unit),中央经度(OriginLongitude),原点纬度(OriginLatitude),比例系数(ScaleFactor),东伪偏移(FalseEasting),北纬偏移(FalseNorthing)Transverse Mercator(横轴墨卡托投影):墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
主要参数有:投影代号(Type),基准面(Datum),单位(Unit),原点经度(Origin Longitude),原点纬度(Origin Latitude),标准纬度(Standard ParallelOne)。
UTM(通用横轴墨卡托投影):是一种“等角横轴割圆柱投影”,椭圆柱割地球于南纬80度、北纬84度两条等高圈,投影后两条相割的经线上没有变形,而中央经线上长度比0.9996,是为了保证离中央经线左右约330km处有两条不失真的标准经线。
地图投影的判别与选择

地图投影的判别与选择第五节地图投影的判别与选择⼀、地图投影的判别地图投影是地图的数学基础,它直接影响地图的使⽤。
地图是地理⼯作者不可缺少的⼯具,有很多地理知识是从图上获得的。
如果在使⽤地图时,不了解投影的特性,往往会得出错误的结论。
例如在⼩⽐例尺等⾓或等积投影图上量算距离,在等⾓投影图上对⽐不同地区的⾯积,以及在等积投影图上观察各地区的形状特征等。
⽬前,国内外出版的地图上⼤多数都注明地图投影名称,这对于使⽤地图,当然是很⽅便的。
但是,也有⼀些地图不注明投影名称和有关说明,因此,我们必须运⽤地图投影的知识,根据不同投影的特征——经纬线形状,结合制图区域所在的地理位置、轮廓形状及地图的内容和⽤途等,综合进⾏分析、判断和进⾏必要的量算来判别它们。
地图投影的判别,主要是对⼩⽐例尺地图⽽⾔。
⼤⽐例尺地图往往是属于国家地形图系列,投影资料⼀般易于查知。
另外由于⼤⽐例尺地图包括的地区范围⼩,不管采⽤什么投影,变形都是很⼩的,在使⽤时可以忽略不计。
判别地图投影⼀般是先根据经纬线⽹形状确定投影种类,如⽅位、圆柱、圆锥等,其次是判定投影的变形性质,如等⾓、等积或任意投影。
(⼀)确定投影种类对于常见的地图投影,⼀般还是⽐较容易确定它的种类的,表2-16列出⼀些常见投影,供判别时参考。
判别经纬线形状的⽅法如下:直线只要⽤直尺量度,便可确定。
判断曲线是否为圆弧,可以将透明纸覆盖在曲线之上,在透明纸上沿曲线按⼀定间隔定出三个以上的点,然后沿曲线移动透明纸,使这些点位于曲线的不同位置,如这些点处处都与曲线吻合,则证明曲线是圆弧,否则就是其他曲线。
判别同⼼圆弧与同轴圆弧,则可以量测相邻圆弧间的垂线距离,若处处相等则为同⼼圆弧,否则是同轴圆弧。
(⼆)确定投影的变形性质当已确定投影的种类后,对有些投影的变形性质是⽐较容易判定的。
例如已确定为圆锥投影,那么只须量任⼀条经线上纬线间隔从投影中⼼向南、北⽅向的变化就可以判别变形性质:如果相等,则为等距投影;逐渐扩⼤,为等⾓投影;逐渐缩⼩,为等积投影。
不同投影经纬网特性总结
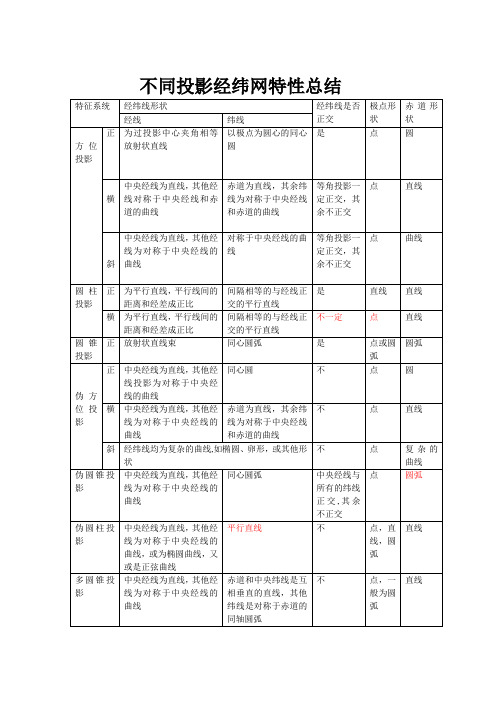
不同投影经纬网特性总结特征系统经纬线形状经纬线是否正交极点形状赤道形状经线纬线方位投影正为过投影中心夹角相等放射状直线以极点为圆心的同心圆是点圆横中央经线为直线,其他经线对称于中央经线和赤道的曲线赤道为直线,其余纬线为对称于中央经线和赤道的曲线等角投影一定正交,其余不正交点直线斜中央经线为直线,其他经线为对称于中央经线的曲线对称于中央经线的曲线等角投影一定正交,其余不正交点曲线圆柱投影正为平行直线,平行线间的距离和经差成正比间隔相等的与经线正交的平行直线是直线直线横为平行直线,平行线间的距离和经差成正比间隔相等的与经线正交的平行直线不一定点直线圆锥投影正放射状直线束同心圆弧是点或圆弧圆弧伪方位投影正中央经线为直线,其他经线投影为对称于中央经线的曲线同心圆不点圆横中央经线为直线,其他经线为对称于中央经线的曲线赤道为直线,其余纬线为对称于中央经线和赤道的曲线不点直线斜经纬线均为复杂的曲线,如椭圆、卵形,或其他形状不点复杂的曲线伪圆锥投影中央经线为直线,其他经线为对称于中央经线的曲线同心圆弧中央经线与所有的纬线正交,其余不正交点圆弧伪圆柱投影中央经线为直线,其他经线为对称于中央经线的曲线,或为椭圆曲线,又或是正弦曲线平行直线不点,直线,圆弧直线多圆锥投影中央经线为直线,其他经线为对称于中央经线的曲线赤道和中央纬线是互相垂直的直线,其他纬线是对称于赤道的同轴圆弧不点,一般为圆弧直线思考题根据所学的地图投影知识,为下述地图选择合适的投影:1、世界、非洲、亚洲、中国政区图(每个区域选两种);世界:等差分纬线多圆锥投影、伪圆柱投影(摩尔维特投影)、伪圆柱投影(古德投影)、圆柱、派生非洲:普通多圆锥投影、伪圆柱投影(桑逊投影)、正轴割圆柱亚洲:斜轴等面积方位投影、彭纳投影中国政区图:正轴等角割圆锥投影、正轴等面积割圆锥投影、斜轴方位投影2、中国、北极地形图;中国:正轴等角割圆锥投影、高斯投影北极:等角方位投影(正轴)3、航海图、某一机场空中航线图;航海图:等角正轴圆柱投影(墨卡托投影)空中航线图:斜轴等距方位4、中国地势图中国地势图:斜轴等面积方位投影、斜轴等角方位投影、正轴割圆锥(等角、等积)地图学投影总结资源与环境学院资源环境与城乡规划管理水院阿乐 200900609 QQ:471049705正轴横轴斜轴等积等角等距等积等角等距等积等角等距方位投影经纬网形状投影中心为极点,纬线为同心圆,经线为同心圆的半径,两条经线间的夹角与实地相等通过投影中心的中央经线和赤道投影为直线,其他经纬线投影后都是对称于中央经线和赤道的曲线中央经线投影为直线,其他经线投影为对称于中央经线的曲线,纬线投影为曲线变形规律离投影中心越远,变形越大离投影中心越远,变形越大投影中心是没有变形的点,离投影中心越远,变形越大中央经线上从中心向南向北,纬线间隔是逐渐缩小的;在赤道上,自投影中心向西,向东,经线间隔也是逐渐缩小变形分布特征与横轴等积方位投影相似在中央经线上从中心向南向北,纬线间隔相等;在赤道上,自投影中心向西,向东,经线间隔是逐渐扩大的中央经线上自投影中心向上、向下的纬线间隔逐渐减小中央经线上自投影中心向上、向下的纬线间隔逐渐增大中央经线上自投影中心向上、向下纬线间隔是相等的应用主要用于制作两极地区图、南北半球图赤道附近圆形区域图中纬度圆形区域图正轴等角圆柱投影经纬网形状1、经线投影为平行直线,平行线间的距离和经差成正比。
投影的定义

古德投影的定义:一种用分瓣法表示的等积伪圆柱投影。
是将伪圆柱投影的非制图区加以断裂,使制图区变形减少,编制成断裂地图的方法。
它的作法是在地图上把几个主要制图区的中央都定为中央经线,使地图分为几个部分,沿赤道连接在一起。
古德投影的优缺:1、减少变形2、缺点是在40°纬线附近有一折角,离中央经线越远,折角越显著(两个投影不同,结合处不太平滑)古德投影的特点:尽可能减小投影变形,不惜图面连续性。
高斯投影的定义:,又名"等角横切椭圆柱投影”,是地球椭球面和平面间正形投影的一种。
假想有一个椭圆柱与地球椭球体上某一经线相切,其椭圆柱的中心轴与赤道平面重合,将地球椭球体面有条件地投影到椭球圆柱面上。
高斯克吕格投影条件:a) 中央经线和赤道投影为互相垂直的直线,且为投影的对称轴;b) 具有等角投影的性质;c) 中央经线投影后保持长度不变;高斯投影的优缺:高斯一克吕格投影后,除中央经线和赤道为直线外,其他经线均为对称于中央经线的曲线。
高斯-克吕格投影没有角度变形,在长度和面积上变形也很小,中央经线无变形,自中央经线向投影带边缘,变形逐渐增加,变形最大处在投影带内赤道的两端。
由于其投影精度高,变形小,而且计算简便(各投影带坐标一致,只要算出一个带的数据,其他各带都能应用),因此在大比例尺地形图中应用,可以满足军事上各种需要,并能在图上进行精确的量测计算。
缺点:等角投影的缺点是面积变形比其他投影大,只有在小面积内可保持形状和实际相似。
高斯投影的特点:1.经投影后,中央子午线为一直线,且长度不变,其它经线为凹向中央子午线的曲线,且长度改变,中央子午线两侧经差相同的子午线互相对称;2.经投影后,赤道为一直线,且长度改变,其它纬线呈凸向赤道的曲线,赤道两侧纬差相同的纬线互相对称;3.中央子午线与赤道经投影后仍保持正交。
墨卡托投影的定义:是正轴等角圆柱投影。
假想一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网投影到圆柱面上,将圆柱面展为平面后,即得本投影。
第四章圆柱投影

2)非几何投影 不借助几何面, 不借助几何面,根据某些条件用数学解析法确定球面与平 面之间点与点的函数关系。在这类投影中, 面之间点与点的函数关系。在这类投影中,一般按经纬线 形状又分为下述几类: 形状又分为下述几类: (2.1)伪方位投影: 伪方位投影: (2.2)伪圆柱投影: 伪圆柱投影: (2.3)伪圆锥投影: 伪圆锥投影: (2.4)多圆锥投影: 多圆锥投影:
第二节、 第二节、墨卡托投影
二 等角航线
等角航线是地球表面上与经线相交的相同角度的曲线,或 等角航线是地球表面上与经线相交的相同角度的曲线, 者说地球上两点间的一条等方位线,船只要按等角航线航 者说地球上两点间的一条等方位线, 行,不用改变方位角就能从起点到达终点。 不用改变方位角就能从起点到达终点。
等角航线在墨卡托投影图上表 现为直线, 现为直线,这一点对于航海航 空具有重要意义。因为有这个 空具有重要意义。 特征,航行时,在墨卡托投影 特征,航行时, 图上只要将出发地和目的地连 一直线,用量角器测出直线与 一直线, 经线的夹角,船上的航海罗盘 经线的夹角, 按照这个角度指示船只航行, 按照这个角度指示船只航行, 就能达到目的地。 就能达到目的地。
投影特性和用途
特性:在该投影图上,等角航线表现为直线, 特性:在该投影图上,等角航线表现为直线, 投影图上 表现为直线 用途:主要用于编制航海图 航海图, 用途:主要用于编制航海图,还可绘赤道附近 的分国图等。 的分国图等。 等角航线——在地球表面上 等角航线——在地球表面上,与经线相交成同 在地球表面上, 一角度的曲线。 一角度的曲线。 大圆航线 航线——表现地球表面两点间最短距离的 大圆航线——表现地球表面两点间最短距离的 大圆弧。 大圆弧。
Behrmann 等面积圆柱投影(标准纬线 ±30°) 等面积圆柱投影(标准纬线:± °
地图学几种投影的主要参数

几种投影的主要参数Gauss Kruger(高斯-克吕格投影):除中央经线和赤道为直线外,其他经线均为对称于中央经线的曲线。
该投影没有角度变形,在长度和面积上变形也很小,中央经线无变形,自中央经线向投影带边缘,变形逐渐增加,变形最大处在投影带赤道的两端。
限制长度变形最有效的方法是将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。
经差6度为六度带,经差3度为三度带。
六度带自0度子午线起自西向东分带,带号为1—60带。
三度带基于六度带,自 1.5度子午线起每隔经差3度自西向东分带,带号为1—120带。
我国经度围73W—135E,十一个六度带。
各带中央经线:75,75+6n。
三度带为二十二个。
主要参数:投影代号(Type),基准面(Datum),单位(Unit),中央经度(OriginLongitude),原点纬度(OriginLatitude),比例系数(ScaleFactor),东伪偏移(FalseEasting),北纬偏移(FalseNorthing)Transverse Mercator(横轴墨卡托投影):墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
主要参数有:投影代号(Type),基准面(Datum),单位(Unit),原点经度(Origin Longitude),原点纬度(Origin Latitude),标准纬度(Standard ParallelOne)。
UTM(通用横轴墨卡托投影):是一种“等角横轴割圆柱投影”,椭圆柱割地球于南纬80度、北纬84度两条等高圈,投影后两条相割的经线上没有变形,而中央经线上长度比0.9996,是为了保证离中央经线左右约330km处有两条不失真的标准经线。
Ch2-3 常用地球投影及其判别和选择

距 离 最 短
1)何谓墨卡托投影?
∗2
2
墨卡托投影-正轴等角圆柱投影
• 即设想与地轴方向一致的圆柱与地球 相切或相割,将球面上的经纬网按等 角的条件投影到圆柱面上,然后把圆柱 面沿着一条母线剪开并展成平面。
2)经纬网形状及经纬距变化规律
2 3
• 经线和纬线是两组相互垂直的平行直线 • 经线间隔相等 • 纬线间隔由赤道向两极逐渐扩大
• 广义的多圆锥投影
•即指纬线为同轴圆弧的投影。
(1)普通多圆锥投影
4
8 • 投影条件:m0=1,n=1 • 经纬网特征: • 变形情况: • 属于任意投影,中央经线是一条没有变 形的线,离开中央经线愈远变形愈大。
• 用途:地球仪
(2)等差分纬线多圆锥投影
4
9 • 这是中国地图出版社于1963年设计的一种任意 性质的,不等分纬线的多圆锥投影。
– 中央经线为直线,其余的经线为椭圆曲线。 – 纬线是间隔不等的平行直线,其间隔从赤道向两极逐
渐减小。同一纬线上的经线间隔相等。 – 等积投影。
(3) 伪圆柱投影——摩尔威特投影
4
4 • 用途:世界地图、东西半球图、大洋图
(4) 伪圆柱投影——古德投影
4 5
• 设计思想:对摩尔维特等积伪圆柱投影进行“分瓣投
4 6
• 特点:海/陆完整(尽量
减少投影变形,而不惜
图面的连续性)
• 用途:世界地图
2. 多圆锥投影
4 7
• 狭义的多圆锥投影
•是指用多个不同锥顶角的圆锥与地 球相切,并获得若干以各标准纬线 为中心的投影带,然后将这些投影 带沿着某一经线连接起来。由于圆 锥顶点不是一个,所以纬线投影为 同轴圆弧。
地图投影的基本方法

地图投影的基本方法:数学解析法是在球面与投影面之间建立点与点的函数关系,通过数学的方法确定经纬线交点位置的一种投影方法。
几何透视法是利用透视的关系,将地球体面上的点投影到投影面(借助的几何面)上的一种投影方法。
地球仪上的经纬线的长度的特点:第一,纬线长度不等;第二,在同一条纬线上,经差相同的纬线弧长相等; 第三,所有经线长度相等。
地球仪上的经纬线网格面积的特点:第一,在同一纬度带内,经差相同的球面网格面积相等; 第二,在同一经度带内,纬度愈高,网格面积愈小。
地球仪上的经纬线角度的特点:a bc在图(b、c)上,只有中央经线和各纬线相交成直角,其余的经线和纬线均不呈直角相交,而在地球仪上经线和纬线处处都呈直角相交,这表明地图上有角度变形。
变形椭圆指地球椭球体面上的一个微小圆,投影到地图平面上后变成的椭圆,特殊情况下为圆。
可证明球面上的一个微小圆,投影到平面上之后是个椭圆。
在分析地图投影时,可借助对变形椭圆和微小圆的比较,说明变形的性质和大小。
椭圆半径与小圆半径之比,可说明长度变形。
很显然,长度变形随方向的变化而变化,其中有一个极大值,即椭圆长轴方向,一个极小值,即椭圆短轴方向。
这两个方向是相互垂直的,称为主方向。
椭圆面积与小圆面积之比,可说明面积变形。
椭圆上两方向线的夹角和小圆上相应两方向线的夹角的比较,可说明角度变形。
baxy几何投影方位投影圆柱投影圆锥投影条件投影伪圆柱投影 伪方位投影 多圆锥投影 伪圆锥投影常用地图投影一、世界地图常用投影(1)墨卡托投影(Mercator Projection)墨卡托投影属于正轴等角圆柱投影。
该投影设想与地轴方向一致的圆柱与地球相切或相割,将球面上的经纬线网按等角的条件投影到圆柱面上,然后把圆柱面沿一条母线剪开并展成平面。
经线和纬线是两组相互垂直的平行直线,经线间隔相等,纬线间隔由赤道向两极逐渐扩大(如图)。
图上无角度变形,但面积变形较大。
等角航线:是地球表面上与经线相交成相同角度的曲线。
地图学题库及答案

地图学习题集参考答案一、名词解释1.大地经纬度:大地经纬度是建立在地球参考椭球面上的地理坐标系,大地经度是指参考椭球面上某点的大地子午面与本初子午面间的两面角(1分)。
自本初面向东为东经0-180度,向西为西经0-180度(1分)。
大地纬度是指过该点与椭球面垂直的直线与赤道面的夹角。
(1分)自赤道向北为北纬0-90度,向南为南纬0-90度。
(1分)2. 墨卡多投影:墨卡托投影是正轴等角圆柱投影,由墨卡托于1569年专门为航海的目的设计的,故名。
其设计思想是令一个与地轴方向一致的圆柱切于或割于地球,将球面上的经纬网按等角条件投影于圆柱表面上,然后将圆柱面沿一条母线剪开展展成平面,即得墨卡托投影。
在墨卡托投影中,面积变形最大。
在纬度60度地区,经线和纬线比都扩大了2倍,面积比P=m*n=2*2=4,扩大了4倍,愈接近两极,经纬线扩大的越多,在φ=80度时,经纬线都扩大了近6倍,面积比扩大了33倍,所以墨卡托投影在80度以上高纬地区通常就不绘出来了。
在墨卡托投影上等角航线表现为直线。
3.变形椭圆:取地面上一个微分圆,将它投影到平面上将为一个椭圆(少数情况下为正圆),(1分)通过研究其在投影平面上的变化,作为地图投影变形的几何解释,这样的椭圆称为变形椭圆。
(2分)利用变形椭圆能更为科学和准确地阐述地图投影变形的概念、变形性质及变形大小。
(1分)。
4.视觉变量:视觉变量是构成图形的基本要素,它包括:形状、尺寸、方向、颜色、网纹5个方面(2分)。
在细分时,颜色的色相、亮度、彩度也可以理解为独立的视觉变量;网纹的排列、纹理、方向也具备视觉变量特性(2分)。
5.地图:是遵循一定的数学法则,将地理信息通过科学的概括综合,运用符号系统表示在一定的载体上的图形,以传递它们的数量、质量在时间和空间上的分布规律和发展变化。
6地球参考椭球体:地球椭球体是对地球形状的理想模拟,参考椭球体是对地球形状的第三级逼近,即与局部地区大地水准面切合的最好的椭球体。
古德投影

谢谢!
古德分瓣方
南美洲:中央经线为60°W
澳大利亚:中央经线为150°E
幻灯片 6
也就是在地图上把几个主要制图区的中央都 定为中央经线,使地图分为几个部分,沿赤 道连接在一起。
古德投影:
优点:减少变形
(每瓣中央经线投影区域不大,从伪圆柱 投影的变形情况可知,中央经线是一条没 有变形的线,离中央经线越远,变形就越 大) 如果以表现大陆为主的世界地图,则要求各大 陆部分保持完整,不同大陆部分可采用不同中 央经线。 如果以表现大洋为主的世界地图,则要求 各大洋部分保持完整,而将大陆割裂开来。
尽可能减小投影变形,不惜图面连续性是古德投 影的重要特征。 我们有时见到的切瓣式世界全图即采用 此投影。美国出版的世界地图主要用这 种投影。 国际上著名的地图集,如德国的《施蒂勒地图 集》、英国的《泰晤士世界地图集》、意大利的 《旅行俱乐部国际大地图集》、前苏联的《世界 大地图集》 、美国的《古德世界地图集》 也在其 中,它们都有数十年的历史
地图投影
库德投影 Goode’s projection
古德投影为美国科学家古德拟 定,故名。
美国J.P.Goode于1923年提 出了一种分瓣伪圆柱投影方 法来绘制世界地图。
具体做法:(设计思想)
将全制图区域根据需要,确定若干个中央经 线位置,然后进行分瓣投影,要求分裂的各 部分必须在赤道处连接在一起。
目前较为系统和详细的全球土地利用和土地 覆盖空间数据主要有古德世界地图集(Goode's World Atlas)的分洲环境地图、联合国粮农组织 (FAO)的分国土地利用统计数据(FAOSTAT)和美 国马里兰大学全球土地覆盖研究室(GLCF, University of Mary1and)利用美国海洋大气局 (NOAA)和美国宇航局(NASA)的高级甚高分辨 率辐射计(AVHRR)1992—1993年的遥感数据生 成的全球土地覆盖分类数据。古德世界地图集 分洲环境地图的基本比例尺为3600万分之一
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
谢谢!
古德分瓣方法:非:中央经线为20°E
北美洲:中央经线为100°W
南美洲:中央经线为60°W
澳大利亚:中央经线为150°E
幻灯片 6
尽可能减小投影变形,不惜图面连续性是古德投 影的重要特征。 我们有时见到的切瓣式世界全图即采用 此投影。美国出版的世界地图主要用这 种投影。 国际上著名的地图集,如德国的《施蒂勒地图 集》、英国的《泰晤士世界地图集》、意大利的 《旅行俱乐部国际大地图集》、前苏联的《世界 大地图集》 、美国的《古德世界地图集》 也在其 中,它们都有数十年的历史
目前较为系统和详细的全球土地利用和土地 覆盖空间数据主要有古德世界地图集(Goode's World Atlas)的分洲环境地图、联合国粮农组织 (FAO)的分国土地利用统计数据(FAOSTAT)和美 国马里兰大学全球土地覆盖研究室(GLCF, University of Mary1and)利用美国海洋大气局 (NOAA)和美国宇航局(NASA)的高级甚高分辨 率辐射计(AVHRR)1992—1993年的遥感数据生 成的全球土地覆盖分类数据。古德世界地图集 分洲环境地图的基本比例尺为3600万分之一
地图投影
库德投影 Goode’s projection
古德投影为美国科学家古德拟 定,故名。
美国J.P.Goode于1923年提 出了一种分瓣伪圆柱投影方 法来绘制世界地图。
具体做法:(设计思想)
将全制图区域根据需要,确定若干个中央经 线位置,然后进行分瓣投影,要求分裂的各 部分必须在赤道处连接在一起。
也就是在地图上把几个主要制图区的中央都 定为中央经线,使地图分为几个部分,沿赤 道连接在一起。
古德投影:
优点:减少变形
(每瓣中央经线投影区域不大,从伪圆柱 投影的变形情况可知,中央经线是一条没 有变形的线,离中央经线越远,变形就越 大) 如果以表现大陆为主的世界地图,则要求各大 陆部分保持完整,不同大陆部分可采用不同中 央经线。 如果以表现大洋为主的世界地图,则要求 各大洋部分保持完整,而将大陆割裂开来。
不论是桑森投影,摩尔威特投影及其他伪 圆柱投影都可断裂,因为凡是纬线平行的 投影,断裂后都有可能相互对照。 还可采用桑生投影和摩尔威特投影结合在 一起的断裂方法,在南北纬40°44′11.8° 以内,采用桑生投影。以外采用摩尔威特 投影。
优点:减少变形
缺点:在40°纬度附近有一折角,离中央经线越 远,折角越明显(2个投影不同,结合处不太平滑)
