平面体与回转体相交
平面与回转体相交
平面与回转体相交
平面与球相交
1.平面与球面的截交情况 球体被平面截切后的截交线是个圆。
平面与回转体相交
平面与球相交
2.作图举例
例 完成半球上部开 槽后的俯视图和左视图。
平面与回转体相交
平面与球相交
2.作图举例
例 完成半球上部开 槽后的俯视图和左视图。
分析：半球上部的 缺口是由一个水平面和 两个侧平面切割半球体 形成的。
平面与回转体相交
平面与回转体相交
回转体的截交线 平面与圆柱相交 平面与圆锥相交 平面与球相交
平面与回转体相交
回转体的截交线
1.截交线的特点 平面与回转体相交产生的截交线通常是一条封闭的平面曲线，
或曲线和直线围成的平面图形或多边形。
平面与回转体相交
回转体的截交线
1.截交线的特点
平面与回转体相交产生的截交线通常是一条封闭的平面曲线， 或曲线和直线围成的平面图形或多边形。
平面与回转体相交
平面与球相交
2.作图举例
例 完成半球上部开 槽后的俯视图和左视图。
作图：判断截交线 的可见性及球面轮廓线 投影范围，完成全图。
平面与回转体相交
小结
回转体的截交线 平面与圆柱相交 平面与圆锥相交 平面与球相交
2.求截交线的步骤 ★ 空间及投影分析
确定截交 线的形状
☆ 截平面与轴线的相对位置 ☆ 截平面与投影面的相对位置
确定截交线 的投影特性
平面与回转体相交
回转体的截交线
2.求截交线的步骤
★ 空间及投影分析 ★ 画截交线的步骤
转向轮廓线上的点
☆求截交线的特殊点： 极限位置点 截交线的形状特殊点
☆求一般点
平面与回转体相交
工程制图2-6章答案
7. 求线段EF与由两相交线段AB、AC确定的平面的交点，并判断可见性。
注： .线与面相交转化为两个面相交 .点 A 为△ABC与△AEF的共有点 .利用辅助面PV求两△的另一共有点L .取 PV∥a′f′ 即 1 2∥AF .点 K 为所求
8. 求线段 EF 与三角形ABC的交点，并判断可见性。
3. 正平线AB，距V面20，与H面成60°，实长25，点B位于点A的右上方，画出AB的三面投影。
4. 侧平线AB，距W面30，与H面成30°，实长25，点B位于点A的前上方，画出AB的三面投影。
5. 根据线段AB的两个投影，求作第三投影。
6. 已知线段AB、BC、CD的两个投影，求作侧面投影，并判断其各为何种位置直线。
AB是 水平 线 BC是 一般位置 线 CD是 侧垂 线
7. 在线段AB上取一点C，使A、C两点之间的距离为20。
* 8. 在线段AB上取一点C ，使它与H面和V面的距离相等。
9. 过点C作 AB 的平行线CD，实长为20（先作出AB的水平投影，后作CD的三面投影）。
10. 作一线段MN与已知线段CD、EF相交，同时与AB平行（点M在CD上，点N在EF上）。
2. 求作主视图，并标出圆锥面上各点的其余两个投影。
3. 求作球的左视图，并标出球面上各点的其余两个投影。
3. 求作球的左视图，并标出球面上各点的其余两个投影。
4. 求作左视图，并标出圆环面上各点的其余两个投影。
4. 求作左视图，并标出圆环面上各点的其余两个投影。
5 平面与立体相交
5.1 平面与平面体相交
2. 已知线段MN和三角形ABC平行，求作此三角形的水平投影。 注：c′1′∥n′m′ , c1∥nm ; b 在 a1 的延长线上
相贯线1-两平面立体,平面与曲面立体相交.
2、求相贯线上的贯穿点。
3、先判断可见性，依次
连接贯穿点。
4、补全棱线。
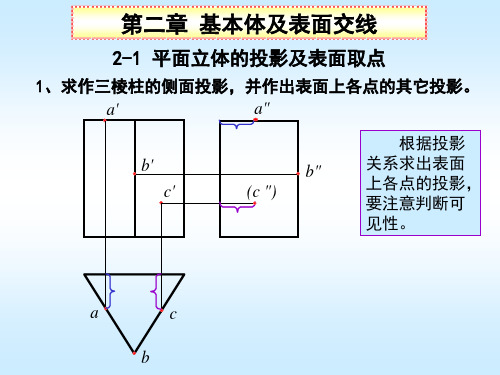
例5：补全带孔三棱柱的水平投影，求作侧面投影。
空间分析
d' a' b'
c'
1、三个截平面相交，在三棱 d" 柱体内形成三条交线。
2、三个截平面与三棱柱形成
a"
b" 前、后 两部分截交线，且截交
(c")
线均在棱柱表面，其水平投影
7
(3) 立体相对位置不同，相贯线形状不一样：
两圆柱轴 线斜交
两圆柱轴线 偏交
8
图例：
全贯
互贯
平×曲
柱柱正交
柱柱正交(等径) 孔孔正交
柱柱偏交
柱穿锥
锥穿柱
球柱偏交
球柱正交 9
二、 平面体与平面体 相交
10
相贯及相贯线的概念
相贯：两立体相交。
相贯线：两立体相交，
其表面的交线。
相贯线
11
平面立体相贯种类及 相贯线的特点
(11’) 1’ 2’ 3’
(31’)
(41’) 4’
11
41 31
1
3
11” 1” (31”) (3”)
41”
2” 4”
解题步骤： 1、分析两立体的 空间关系，确定相 贯线的已知投影。
2、从已知投影出发，确定相贯 线上的贯穿点。
3、先判断可见性，再连接贯穿点。
2 4
例2：已知三棱锥上穿有三棱柱孔洞，求作相贯线。
(41’) 4’
11
(41) 31
1
3
2 (4)
11” 1” (31”) (3”)
第四章 2.平面与回转面的交线
第四章 组合体第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图P 22P 23P 24P 25首 页下一页平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-2A（1）4-2A（2）4-2B（1）4-2B（2）下页题答 案P22平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-2A（1）4-2A（2）4-2B（1）4-2B（2）题 目下页题返 回P22平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页 下页题4-2A（2）4-2B（1）4-2B（2）题 目答 案P22平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-2A（1）4-2B（1）4-2B（2）下页题题 目答 案P22平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-2A（1）4-2A（2）4-2B（2）下页题题 目答 案P22平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-2A（1）4-2A（2）4-2B（1）下页题题 目答 案P22平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-34-44-54-6上页题下页题答 案P23平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-34-44-54-6题 目下页题返 回P23平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页 上页题4-44-54-6下页题题 目答 案P23平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-34-54-6上页题下页题题 目答 案P23平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-34-44-6上页题下页题题 目答 案P23平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-34-44-5上页题下页题题 目答 案P23平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-74-84-94-10上页题下页题答 案P24平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-74-84-94-10题 目下页题返 回P24平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页 上页题4-84-94-10下页题题 目答 案P24平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-74-94-10上页题下页题题 目答 案P24平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-74-84-10上页题下页题题 目答 案P24平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-74-84-9上页题下页题题 目答 案P24平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-114-12上页题答 案P25平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-114-12题 目返 回P25平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页 上页题4-12题 目答 案P25平面与回转体表面的交线第一章 制图基本知识 第二章 正投影法基础 第三章 换面法 第四章 组合体 1. 组合体视图的画法 2. 平面与回转面的交线3. 两回转面的交线4. 组合体视图及其尺寸注法 5. 读组合体视图 第五章 轴测图 第六章 机件形状的基本表示 方法 1. 视图、剖视 2. 断面、简化画法 第七章 零件图 第八章 常用标准件和齿轮、 弹簧表示法 第九章 装配图模 型 首 页4-11上页题题 目答 案P25。
回转体截交线
投影
7'
Ⅱ Ⅳ Ⅰ Ⅴ
Ⅵ
1
Ⅲ VII
图5-33 连杆头的截交线 -
【例5-14】试完成连杆头的截交线的投影。 - 】试完成连杆头的截交线的投影。
作图步骤： 作图步骤： ③判别可见性，连线 判别可见性，
6' 4' 1' 5' 3' 7' 2' 6" 2" 4" 1" 5" 3" 7"
Ⅵ Ⅱ Ⅳ Ⅰ Ⅴ Ⅲ VII
● ●
e′
●
E C
●
D B
c′
●
d′ b′ A
a′
a
●
c
●
●
e
●
d
●
b
图5-30 平面截切圆锥 -
(3) 平面与圆球相交
平面与球面的交线总是圆
图5-31 平面与球面交线的基本作图 -
【例5-13】已知半球上通槽的正面投影，试完成其另两面 - 】已知半球上通槽的正面投影， 投影。 投影。
空间分析与投影分析; 空间分析与投影分析 作图:①完成平面P 作图 ①完成平面 的投影 完成平面Q的投影 ②完成平面 的投影
图5-33 连杆头的截交线 -
1
Ⅱ Ⅳ Ⅲ
2 1 5 3 4
图5-29 平面截切圆锥 -
Ⅰ
Ⅴ
【例5-12】已知一直立圆锥被正垂面截切，求作截交线， - 】已知一直立圆锥被正垂面截切，求作截交线， 完成其水平投影和侧面投影。 完成其水平投影和侧面投影。
⑥检查、完成。 检查、完成。
图5-29 平面截切圆锥 -
【例5-13】 圆锥被一与其轴线平行的截平面切割，试完 - 】 圆锥被一与其轴线平行的截平面切割， 成截交线的正面投影。 成截交线的正面投影。
平面体与回转体表面的交线
截交线的每条边是截平面与棱面的交线。
截交线的性质：
第3页/共62页
二、平面截切体的画图
⒈ 求截交线的两种方法：
★ 求各棱线与截平面的交点→棱线法。
★ 求各棱面与截平面的交线→棱面法。
关键是正确地画出截交线的投影。
先找特殊点。
⒊ 作图过程
补充中间点。
第43页/共62页
当圆柱直径变化时，相贯线的变化趋势。
交线向大圆柱一侧弯
交线为两条平面曲线（椭圆）
第44页/共62页
当圆柱直径变化时，相贯线的变化趋势。
第45页/共62页
第46页/共62页
例 1 ：圆柱与圆柱相贯，求其相贯线。
●
空间及投影分析： 小圆柱轴线垂直于H面，水平投影积聚为圆，根据相贯线的共有性，相贯线的水平投影即为该圆。大圆柱轴线垂直于W面，侧面投影积聚为圆，相贯线的侧面投影在该圆上。
第四章 平面体与回转体表面的交线
§4-1 平面体及回转体的截切 §4-1-1 概述 §4-1-2 平面体的截切 §4-1-3 回转体的截切§4-2 平面体与回转体的相贯 §4-2-1 概述 §4-2-2 平面体与回转体相贯 §4-2-3 回转体与回转体相贯
第1页/共62页
截切： 用一个平面与立体相交，截去立体的一部分。
★ 共有性
★ 表面性
相贯线位于两立体的表面上。
相贯线是两立体表面的共有线。
★ 封闭性
相贯线一般是封闭的空间折线（通常由直线和曲线组成）或空间曲线。
第36页/共62页
1.相贯线的性质
相贯线是由若干段平面曲线（或直线）所组成的空间折线，每一段是平面体的棱面与回转体表面的交线。
3[1] 4 平面与回转体相交
![3[1] 4 平面与回转体相交](https://img.taocdn.com/s3/m/7232c830b42acfc789eb172ded630b1c58ee9b77.png)
3[1] 4 平面与回转体相交平面和回转体是几何学中的两个基本概念。
一个平面是一个无限大的二维区域，它由无数个点组成。
一个回转体是一个三维空间中的体积，它围绕一个轴旋转而形成。
在几何学中，平面和回转体是常常被使用来描述和分析物体在空间中的形状和位置。
而当平面和回转体相交时，我们可以得到一些有趣的几何图形和问题。
平面和回转体相交的形状可以分为三种：圆形、椭圆形和长方形。
因此，在讨论平面和回转体相交时，我们将分别讨论这三种形状的情况。
圆形的情况当一个平面与一个回转体相交时，如果相交部分的形状是圆形，那么我们可以得到一个非常有用的结论：相交部分的圆心在回转体的轴上。
这个结论可以用于计算一个回转体的体积。
我们可以采用以下的步骤来计算一个回转体的体积。
步骤1：通过相交部分的圆心和轴的交点确定回转体的高度（高度等于交点到圆心的距离）。
步骤2：计算相交部分圆形面积（面积等于半径的平方乘以π）。
步骤1：通过相交部分的两个焦点和轴的交点构成一个锥形体。
步骤2：计算锥形体的体积（体积等于锥形体的高度乘以底面积的1/3）。
平行截面定理是指，若一个回转体被一组平面所截，这些平面与轴平行且相邻平面之间的距离为Δx，那么回转体的体积为：V=∫a^bA(x)dx其中，a和b是相邻平面的横坐标，A(x)是第x个平面所截的面积。
步骤1：将椭圆形或圆形的相交部分分成若干个长方形。
步骤2：通过平行截面定理计算回转体的体积。
总结通过以上的分析，我们可以得到平面与回转体相交的计算方法。
不仅可以计算回转体的体积，还可以用于解决其他一些几何问题。
因此，了解平面与回转体相交的特点和计算方法对于学习和应用几何知识非常重要。
《机械制图习题集》习题答案——第2章
由于棱
锥体的棱面 无积聚性， 表面取点要 利用辅助线 法。
2-2 回转体的投影及表面取点
完成回转体的投影，并作出表面上各点的三面投影。
（1
）
a'
a"
b'
(b")
(b) a
回转体表面取点， 根据已知点的可见性 判断点所处的位置， 按投影关系，找出各 点的投影。
（2 ）
(c') 1'
a'
b'
1" c" a"
4、完成相贯体的三视图。
1'
5'(6') 3'(4') 2' 7'(8')
1"
5" 6"
4"
3"
8"
7" 2"
4 86 21
75 3
圆锥体与圆
柱形孔正交。因 圆锥面的投影无 积聚性，利用辅 助平面求一般位 置的点。
5、完成相贯体的三视图。
1'
5'(6') 3'(4') 7'(8') 2'
1"
6"
b"
c
a
b
圆锥面的投
影无积聚性，表 面取点利用辅助 素线或辅助纬圆 法求解。底面上 的点可利用投影 关系直接求出。
（3 ）
a'
b'
a" (b")
1a
圆锥台的表面
2 b
投影无积聚性，表 面上取点利用辅助
纬圆法。
（4 ）
平面与回转体相交
g'(h' ) •
c'(d') • e' (f ') •
a'
•f d•
h •
作图：1、求特殊点 截交线的最低点A和最高点 B是水平投影的最右点和最左点，也是截交线水平 投影椭圆短轴的交点，水平投影a、b在其正面投 影轮廓线的水平投影上。 a' b'的中点c' d'是截交 线水平投影椭圆长轴端点的正面投影，其水平投影 cd投影在辅助纬圆上。 e' f'是截交线与球的水平
动画
根据立体图绘制三视图 【形体分析】槽的侧面P为侧平面，并和圆锥的轴线平行， 所以，P平面和锥面的交线为双曲线段，并且侧面投影反映 实形。槽的上面R为水平面，并和圆锥的轴线垂直，所以， R平面和锥面的交线为圆弧，并且水平投影反映实形，圆弧 的半径可从主视图上求得。
动画
三、平面与球体相交
球被平面截切，截交线均为圆。由于截平面位置不同，截交 线的投影可能是圆、直线或椭圆。 1、截平面为平行面
完成后的投影图
例3、求如图所示的开槽圆柱的左视图。
5'（6'） •
• 6"
• 5"
1'（2'）
• • 2" •
••
3'（4'•） 4"
31""
2• •64
分析：槽是由三个截平面形 成的，左右对称的两个截平 面是平行于圆柱轴线的侧平 面，它们与圆柱面的截交线 均为两条直素线，与上底面 的截交线为正垂线。另一个 截平面是垂直于圆柱轴线的 水平面，它与圆柱面的截交 线为两段圆弧。三个截平面 间产生了两条交线，均为正 垂线。
两回转体表面相交
●
1
●
35
三面共点
●
●
●
作图时要抓住 一个关键点，相贯 线汇交于这一点。
36
例2 分析并想象出物体相贯线投影的形状
37
小结
一、本节的基本内容
⒈ 立体表面相贯线的概念
相贯线的性质：表面性 共有性 封闭性 ⒉ 求相贯线的基本方法
面上找点法 辅助平面法
二、解题过程
⒈ 交线分析
⑴ 空间 分析相交两立体的表面形状， 形体大小及 分析： 相对位置，预见交线的形状。
39
三、平面体与圆柱体相贯
⒈ 相贯线的产生：
外表面与外表面相交， 外表面与内表面相交， 内表面与内表面相交。
⒉ 求相贯线的方法：
求平面体的棱面与圆柱面的截交线，依次连接起来。
⒊ 相贯线的形状及投影：
相贯线为封闭的空间折线。相贯线在非积聚性投影上总 是向被穿的圆柱体里面弯折，而且在两体相交区域内不应有 圆柱体轮廓线的投影。
2．两圆柱相贯线的变化趋势（二）： 两圆柱的相对位置发生变化
29
圆柱相贯线的变化趋势（一）
30
两圆柱相贯线的变化趋势（二）
31
例1：补全主视图
●
●
●
●
●
●
●
●
●
● ●
● ●
●
●
● ●
● ●
★ 外形交线
◆ 两外表面相贯 ◆ 一内表面和一外表面相贯
★ 内形交线
◆ 两内表面相贯
32
小 结：
无论是两外表面相贯， 还是一内表面和一外表面 相贯，或者两内表面相贯， 求相贯线的方法和思路是 一样的。
1.相贯线的性质
相贯线是由若干段平面曲线 (或 直线)所组成的空间折线，每一段是平 面体的棱面与回转体表面的交线。
4.3平面立体与回转体相交平面立体与圆柱体相交
平面与立体表面的交线称为截交线。
立体与立体表面的交线称Байду номын сангаас相贯线。
4.1 平面立体的截切
一、截交线的性质
1、截交线是由直线组成的平面图形（封闭多边形）。 2、多边形的各边是立体表面与截平面的交线。
3、多边形的各顶点是立体各棱线与截平面的交点。
截断面
截平面
截交线
分析圆筒内外交线投影
[例10]补画视图中所缺的图线。
[例10]补画视图中所缺的图线。
[例11] 已知主、俯视图，补画左视图。
[例12] 已知主、俯视图，补画左视图。
[例13] 已知主、俯视图，补画左视图。
●
●
1、空间及投影分析。
截平面与体的相对位置。 截平面与投影面的相对位置。
●
2、求截交线。
[例18] 画出球体开槽的三视图。
[例18] 画出球体开槽的三视图。
4.3 平面立体与回转体相交
平面立体与圆柱体相交，内外交线画法分析
4.4 两回转体相交
两回转体相交产生的交线称为相贯线。
相贯线的性质
1、一般情况下，相贯线是封闭的空间曲线，在特 殊情况下，可以是平面曲线或直线。
2、相贯线是两回转体表面的共有线,也是相贯体 两表面的分界线，相贯线上所有点都是两曲面 体的共有点。
分析切割式平面立体的形成
[例2] 根据物体的立体图,画出三视图。
b´ a´
a b
b" a"
B
[例3] 已知物体的主、左视图，补画出俯视图。
[例3] 已知物体的主、左视图，补画出俯视图。
a'
b'
P´
c' d'
3.4相贯体
作图方法：
假想用辅助平面截切两回转体，分别得出 两回转体表面的截交线。由于截交线的交点 既在辅助平面内，又在两回转体表面上，因 而是相贯线上的点。
辅助平面的选择原则：
使辅助平面与两回转体表面的截交线的投 影简单易画，例如直线或圆。 一般选择投影面平行面
例1、求圆柱与半球相贯线的投影 相贯线的侧面投影积聚在圆柱的表面上。水平圆柱与半球 的公共对称面平行于V面，故相贯线是一条前后对称的空间曲 线。
求圆柱与半球的相贯线
作图步骤： 1）求特殊点：
2）求一般点：
3）判断可见性，依次光滑连接各点： 4）补画水平转向轮廓线。
Pv
Qv
3’
2’ (5’)
1’Байду номын сангаас
(6’) 6” 5”
1”
2” 3”
Pw
Qw
4”
4’
Ⅰ
5 6
1 4
3 2
求圆柱与半球的相贯线
Ⅳ
例2、求半圆柱与圆台相贯线的投影，如图所示。
分析：
由投影图可知，半圆 柱与圆台的轴线垂直交叉， 相贯线是一条左右对称封 闭的空间曲线。由于半圆 柱轴线垂直于侧面，所以 相贯线的侧面投影已知， 可以用表面取点的方法求 相贯线的投影。
相贯线的求法
例1.如图所示已知两圆柱的三面投影，求作它们的相贯线。 分析： 由投影图可知， 直径不同的两圆柱轴 线垂直相交，由于大 圆柱轴线垂直于W面， 小圆柱轴线垂直于H面， 所以，相贯线的侧面 投影和水平投影为圆， 只有正面投影需要求 作。 相贯线为前后左 右对称的空间曲线。
求正交两圆柱的相贯线
求圆柱与圆锥的相贯线
作图步骤：
1）求特殊点：
5’ 2’
3’ 6’ 1’