多面体的表面展开图
多面体的表面展开图 29页PPT文档

体若图干形平,面(但3图) 不形是可任以意围的成若一干个平立面 图形都可以围成一个立体图形。
下面4个图是一些多面体的表面展 开图,你能说出这些多面体的名字吗?
正方体
长方体
四棱锥
三棱柱
考考你的空间想象力:
下列图形是哪些多面体的展开图?
(1)
长方体
(2) (3)
三棱柱 五棱锥
将一个正方体的表面沿某些棱剪开,
了! 太棒 你们
答案 棒
1、下面的图形那些是立方体的展开图?
(1)
(2)
(3)
(4)
2、下列的三幅平面图是三棱柱的表面展 开 图的有( )
甲
乙
丙
3、如图是一个立方体纸盒的展开图,使 展开图沿虚线折叠成正方体后相对面上的两 个数互为相反数,求:
a_ -_ 2_,b_-_ 7_,c___ 1_
下列立体图形的平面展开图 是什么?Fra bibliotek圆 柱
展开
圆锥
展开
长方体
展开
长
方
长方体的展开图
体
底面
侧侧 侧 面面 面
底面
底 侧面 面
侧 侧 侧侧 面 面 面面
底面
立体图形按不同的方式展开可得到不同的表面展开图
下面图形都是由4个三边都相等的三角形组成 的,哪一个可以折叠成多面体呢?动手做做看。
(1)
(2)
上左
下右
隔隔
蓝
一一
行列
黄
?
巧记正方体的展开图口诀 : “一四一”“一三二”, “一”在同层可任意, “三个二”成阶梯, “二个三”“日”相连, 异层必有“日”,
“凹”“田”不能有,
掌握此规律,运用定自如。
【2024秋】最新鲁教版五四制六年级上册数学第一章《丰富的图形世界》测试卷(含答案)
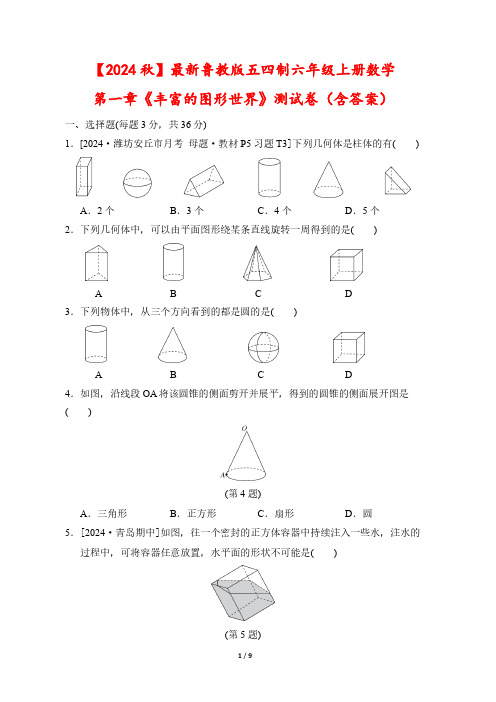
【2024秋】最新鲁教版五四制六年级上册数学第一章《丰富的图形世界》测试卷(含答案)一、选择题(每题3分,共36分)1.[2024·潍坊安丘市月考母题·教材P5习题T3]下列几何体是柱体的有()A.2个B.3个C.4个D.5个2.下列几何体中,可以由平面图形绕某条直线旋转一周得到的是()A B C D3.下列物体中,从三个方向看到的都是圆的是()A B C D4.如图,沿线段OA将该圆锥的侧面剪开并展平,得到的圆锥的侧面展开图是()(第4题)A.三角形B.正方形C.扇形D.圆5.[2024·青岛期中]如图,往一个密封的正方体容器中持续注入一些水,注水的过程中,可将容器任意放置,水平面的形状不可能是()(第5题)A.三角形B.正方形C.六边形D.七边形6.[2023·枣庄滕州市西岗中学期末]一个棱柱有10个顶点,所有侧棱长的和是40cm,则每条侧棱长是()A.7cm B.8cm C.9cm D.10cm7.下列说法错误的是()A.长方体、正方体都是棱柱B.六棱柱有18条棱、6个侧面、12个顶点C.三棱柱的侧面是三角形D.圆柱由2个平面和1个曲面围成8.[立德树人爱国教育]如图是一个多面体的表面展开图,每个面都标注了字.若该多面体的底面的字是5,则该多面体的上面的字是()(第8题)A.建B.国C.周D.年9.[2024·济南市中区期末母题·教材P14习题T3]如图,图①和图②中所有的正方形都完全相同,将图①的正方形放在图②中的某一位置,其中所组成的图形不能围成正方体的是()(第9题)A.①B.②C.③D.④10.[2023·烟台]如图,对正方体进行两次切割,得到如图⑤所示的几何体,则图⑤几何体从上面看到的平面图形为()A B C D 11.[2024·烟台牟平区期中]用大小相同的小立方体搭成如图所示的几何体,现拿掉其中的一个小立方体后,从左面看这个几何体得到的平面图形的面积与拿掉前相同,则这个拿掉的小立方体可以是()(第11题)A.②或④B.②或③C.①或②或③D.②或③或④12.[新视角规律探究题]如图①,将正方体骰子放置于水平桌面上(相对面上的点数分别为1和6,2和5,3和4),在图②中,将骰子向右旋转90°,然后在桌面上按顺时针方向旋转90°,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成2023次变换后,骰子朝上一面的点数是()(第12题)A.6 B.5 C.3 D.1二、填空题(每题3分,共18分)13.将一枚硬币在桌面上快速旋转,可看到一个球,这种现象说明.14.[2024·淄博一模]用相同的小正方体摆成某种模型,从三个不同方向看到的模型的形状图如图所示,则这个模型是由个小正方体摆放而成的.(第14题)15.从三个不同方向看同一个几何体的形状图如图所示,则这个几何体的侧面积是cm2.(第15题)16.[2024·青岛城阳区期末]如图,将此长方形绕虚线旋转一周,得到的几何体的侧面积是cm2.(结果保留π)(第16题)17.如图,用经过A,B,C三点的平面截去正方体的一角,变成一个新的多面体,若这个多面体的面数为m,棱数为n,则m+n=.(第17题)18.[2024·烟台芝罘区期末]如图是由相同大小的小正方体搭成的几何体从不同方向看到的形状图,搭这个几何体最多需要用个小正方体.(第18题)三、解答题(共66分)19.(10分)写出如图所示的平面展开图折叠后所得几何体的名称.20.(10分)[2024·济南济阳区期中]从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.21.(10分)如图是一个几何体从正面、左面、上面看到的形状图,求这个几何体的表面积.(结果保留π)22.(12分)[2024·泰安新泰市期中]如图,加工一个长5cm,宽3cm,高4cm 的长方体铁块,选择面积最小的一个面,从该面的正中间打一个直径为2cm 的圆孔,一直贯穿到对面就可以做成一个零件.(1)这个零件的体积大约是多少立方厘米(π取3)?(2)为了防止零件生锈,工人师傅给该零件与空气接触的面都喷上油漆,则所喷油漆的面积大约是多少平方厘米(π取3)?23.(12分)[新考向知识情境化]某同学的茶杯是圆柱形,如图①所示,有一只蚂蚁从A处沿侧面爬行到母线CD的中点B处,如果蚂蚁爬行的路线最短,请利用展开图画出这条最短路线.解:将圆柱的侧面展开成一个长方形,如图②所示,则A,B分别位于图②中所示的位置,连接AB,AB即是这条最短路线.问题:一个正方体放在桌面上,如图③所示,有一只蚂蚁从A处沿正方体表面爬行到侧棱GF的中点M处,如果蚂蚁爬行的路线最短,最短路线有几条?请利用展开图画出最短路线.24.(12分)[新视角归纳猜想题]如图①②③是将正方体截去一部分后得到的几何体.(1)根据要求填写表格:(2)猜想(3)根据(2)中的猜想计算,若一个几何体有2024个顶点,3036条棱,试求出它的面数.答案一、1.C【点拨】如图,各个几何体的名称如下:因此这些几何体中,是柱体的有四棱柱、三棱柱、圆柱、三棱柱,共有4个.2.B3.C【点拨】A.从正面、上面、左面看到的形状图分别是长方形、圆、长方形;B.从正面、上面、左面看到的形状图分别是三角形、圆(有圆心)、三角形;D.从正面、上面、左面看到的形状图都是正方形.4.C5.D【点拨】正方体有六个面,注水的过程中,可将容器任意放置,水平面最多与六个面相交得六边形,最少与三个面相交得三角形,所得水平面的形状可能是三角形、四边形、五边形和六边形,不可能出现七边形.6.B【点拨】因为一个棱柱有10个顶点,所以该棱柱是五棱柱,所以它的每条侧棱长是40÷5=8(cm).7.C【点拨】三棱柱的侧面是长方形.8.A9.A【点拨】根据正方体的展开图的特征,11种情况中,“1-4-1型”6种,“2-3-1型”3种,“2-2-2型”1种,“3-3型”1种,逐一对四个位置进行判断,发现只有放在①处时,不能围成正方体.10.A【点拨】注意所有看到的棱都应表现在看到的平面图形中.11.D【点拨】拿掉小立方体②或③或④后,从左面看这个几何体所得到的平面图形都与原几何体从左面看所得到的平面图形相同,因此可以拿掉小立方体②或③或④.12.B【点拨】根据题意可知,连续3次变换是一个循环,因为2023÷3=674……1,所以第2023次变换与第1次变换相同.所以连续完成2023次变换后,骰子朝上一面的点数是5.二、13.面动成体14.515.36【点拨】这个几何体是三棱柱,4×3×3=36(cm2).故这个几何体的侧面积是36cm2.16.12π【点拨】由题意可知该长方形绕虚线旋转得到圆柱体,其侧面积=2π×2×3=12π(cm2).17.19【点拨】根据题意得m=6+1=7,n=12,所以m+n=7+12=19.18.7【点拨】由从正面看到的形状图可以看出,几何体从左到右共三列,第一列最多2层,第二列最多1层,第三列最多1层;由从左面看到的形状图可以看出,几何体从左到右共两列,第一列最多1层,第二列最多2层,所以第一层最多有6个,第二层最多有1个,最多需要小正方体6+1=7(个).三、19.【解】①圆锥.②五棱柱.③圆柱.20.【解】几何体的形状图如图所示.21.【解】由题图可得这个几何体的表面展开后是3个长方形与2个扇形,其侧面积为3×3×2π×2+3×2+3×2=9π+12,上、下底面的面积和为4π×22=6π,2×34故这个几何体的表面积为9π+12+6π=15π+12.=1(cm).22.【解】(1)圆孔的半径r=22根据题意,得5×3×4-πr2×5≈45(cm3),所以这个零件的体积大约是45cm3.(2)由题意,得(3×4+3×5+4×5)×2-2×πr2+2πr×5≈118(cm2).所以所喷油漆的面积大约是118cm2.23.【解】将正方体的部分侧面展开,作出线段AM,最短路线有2条,如图①②所示.24.【解】(1)7;9;14;6;8;12;7;10;15(2)f+v-e=2.(3)因为v=2024,e=3036,f+v-e=2,所以f+2024-3036=2,解得f=1014,即它的面数是1014.。
北师大版数学七年级上册 第一章 丰富的图形世界 填空题训练很实用
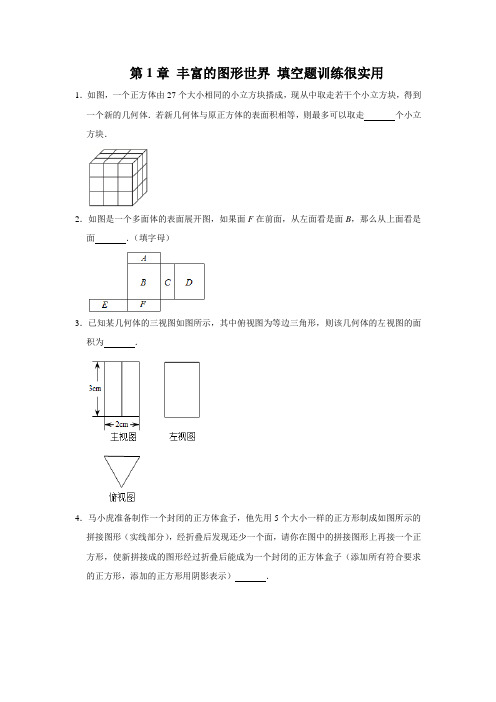
第1章丰富的图形世界填空题训练很实用1.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走个小立方块.2.如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面.(填字母)3.已知某几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的左视图的面积为.4.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示).5.在如图所示的几何体中,其三视图中有矩形的是.(写出所有正确答案的序号)6.一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.7.三棱柱的三视图如图所示,已知△EFG中,EF=8cm,EG=12cm,∠EFG=45°.则AB的长为cm.8.一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”对面的字是.9.如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是.10.在一个高与底面直径相等的圆柱内放置一个体积最大的球.已知球的表面积公式为S n =4πr2,其中r为球的半径.那么该球与它的外切圆柱的表面积的比为.11.如图,圆柱的侧面是由一张长16πcm、宽3cm的长方形纸条围成(接缝处重叠部分忽略不计),那么该圆柱的体积是cm3.12.一个几何体的三视图如图,根据图示的数据计算该几何体的体积为.(结果保留π)13.用一张边长是10cm的正方形铁皮围成一个圆柱体,这个圆柱的侧面积是cm2.14.如图,一个5×5×5的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则所得几何体的体积为.15.若某几何体从某个方向观察得到的视图是正方形,则这个几何体可以是.16.如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是cm2.17.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为cm2.18.如图为某几何体的展开图,该几何体的名称是.19.如图是由几个相同的小正方体搭建而成的几何体的主视图和俯视图,则搭建这个几何体所需要的小正方体至少为个.20.如图是一个立体图形的三种视图,则这个立体图形的体积(结果保留π)为.21.如图,该正方体的主视图是形.22.已知一个几何体的三视图如图所示,这个几何体是.23.如图是由一些大小相同的小正方体组成的简单几何体的左视图和俯视图,符合条件的几何体有种.24.如图,在边长为12cm的正方形纸片ABCD中,EF∥AD,M、N是线段EF的六等分点,若把该正方形纸片折成一个正六棱柱,使AB与点DC重合,则M、N两点间的距离是cm.25.如图,是用8个大小相同的小正方体搭成的几何体,仅在该几何体中取走一块小正方体,使得到的新几何体同时满足两个要求:(1)从正面看到的形状和原几何体从正面看到的形状相同;(2)从左面看到的形状和原几何体从左面看到的形状也相同.在不改变其它小正方体位置的前提下,可取走的小正方体的标号是.26.一个几何体的三视图如图所示,这个几何体的侧面积为.27.如图是一个包装盒的三视图,则这个包装盒的体积是.28.用硬纸壳做一个如图所示的几何体,其底面是圆心角为300°的扇形,则该几何体的表面积为cm2.29.如图所示是一种棱长分别为3cm,4cm,5cm的长方体积木,现要用若干块这样的积木来搭建大长方体,如果用3块来搭,那么搭成的大长方体表面积最小是cm,如果用4块来搭,那么搭成的大长方体表面积最小是cm,如果用12块来搭,那么搭成的大长方体表面积最小是cm.30.如图,是一个长方体的主视图,左视图与俯视图,根据图中数据计算这个长方体的表面积是.31.如图是一个几何体的三视图,根据图中标注的数据可求得该几何体的侧面积为.32.如图是正方体的一个表面展开图,在这个正方体中,与“晋”字所在面相对的面上的汉字是.33.如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数最少是.34.如图,在四个小正方体搭成的几何体中,每个小正方体的棱长都是1,则该几何体的三视图的面积之和是.35.如图所示,是一个简单几何体的三视图,则这个几何体的侧面积等于.36.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的体积为.37.一个油桶靠在墙边(其俯视图如图所示),量得AC=0.65米,并且AC⊥BC,这个油桶的底面半径是米.38.一个长方体的主视图和左视图如图所示,则这个长方体的俯视图的面积是.第1章丰富的图形世界填空题训练参考答案与试题解析1.【分析】根据表面积不变,只需留11个,分别是正中心的3个和四角上各2个.【解答】解:若新几何体与原正方体的表面积相等,最多可以取走16个小正方体,只需留11个,分别是正中心的3个和四角上各2个,如图所示:故答案为:16【点评】本题主要考查了几何体的表面积.2.【分析】由面F在前面,从左面看是面B知上面是E,左侧面是B,前面是F,后面是A,右侧面是D,下面是C.【解答】解:由题意知,上面是E,左侧面是B,前面是F,后面是A,右侧面是D,下面是C,故答案为:E.【点评】考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.3.【分析】由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.【解答】解:该几何体是一个三棱柱,底面等边三角形边长为2cm,高为cm,三棱柱的高为3,所以,其左视图的面积为3×=3(cm2),故答案为3cm2.【点评】本题考查了三视图,三视图是中考经常考查的知识内容,难度不大,但要求对三视图画法规则要熟练掌握,对常见几何体的三视图要熟悉.4.【分析】由平面图形的折叠及正方体的展开图解题.【解答】解:,故答案为:.【点评】本题通过考查正方体的侧面展开图,展示了这样一个教学导向,教学中要让学生确实经历活动过程,而不要将活动层次停留于记忆水平.我们有些老师在教学“展开与折叠”时,不是去引导学生动手操作,而是给出几种结论,这样教出的学生肯定遇到动手操作题型时就束手无策了.5.【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,据此作答.【解答】解:长方体主视图,左视图,俯视图都是矩形,圆柱体的主视图是矩形,左视图是矩形,俯视图是圆,圆锥的主视图、左视图是等腰三角形,俯视图是带有圆心的圆,故答案为:①②.【点评】本题主要考查三视图的知识,熟练掌握常见几何体的三视图是解题的关键.6.【分析】先根据主视图确定每一列最大分别为4,2,3,再根据左视确定每一行最大分别为4,3,2,总和要保证为16,还要保证俯视图有9个位置.【解答】解:由题意和主视图、左视图可知俯视图必定由9个正方形组成,并设这9个位置分别如图所示:由主视图和左视图知:①第1个位置一定是4,第6个位置一定是3;②一定有2个2,其余有5个1;③最后一行至少有一个2,当中一列至少有一个2;根据2的排列不同,这个几何体的搭法共有10种:如下图所示:故答案为:10.【点评】本题考查几何体的三视图.由几何体的主视图、左视图及小立方块的个数,可知俯视图的列数和行数中的最大数字.7.【分析】根据三视图的对应情况可得出,△EFG中FG上的高即为AB的长,进而求出即可.【解答】解:过点E作EQ⊥FG于点Q,由题意可得出:EQ=AB,∵EF=8cm,∠EFG=45°,∴EQ=AB=×8=4(cm).故答案为:4.【点评】此题主要考查了由三视图解决实际问题,根据已知得出EQ=AB是解题关键.8.【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“你”对面的字是顺.故答案为:顺.【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.9.【分析】首先判断出该几何体,然后计算其面积即可.【解答】解:观察三视图知:该几何体为圆柱,高为2,底面直径为1,侧面积为:πdh=2×π=2π,∵是按1:10的比例画出的一个几何体的三视图,∴原几何体的侧面积=100×2π=200π,故答案为:200πcm2【点评】本题考查了由三视图判断几何体及圆柱的计算,解题的关键是首先判断出该几何体.10.【分析】设球的半径为r,根据球的表面积=4πr2,圆柱的表面积=2×πr2+2πr×2r=6πr2,即可得到该球与它的外切圆柱的表面积的比.【解答】解:设球的半径为r,依题意得球的表面积=4πr2,圆柱的表面积=2×πr2+2πr×2r=6πr2,∴该球与它的外切圆柱的表面积的比为2:3,故答案为:2:3.【点评】本题主要考查了几何体的表面积,几何体的表面积=侧面积+底面积(上、下底的面积和).11.【分析】由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高,长方形的长已知,从而可以求出底面积半径,进一步求得该圆柱的体积.【解答】解:16π÷(2×π)=8(cm)π×82×3=192π(cm3)故该圆柱的体积是192πcm3.故答案为:192π.【点评】本题主要考查了立体图形,解答此题的关键是明白:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高.12.【分析】根据圆锥侧面积公式首先求出圆锥的侧面积,再求出底面圆的面积,即可得出表面积.【解答】解:∵如图所示可知,圆锥的高为4,底面圆的直径为6,∴圆锥的体积为π×32×4=12π,故答案为:12π.【点评】此题主要考查了圆锥侧面积公式,根据已知得母线长,再利用圆锥侧面积公式求出是解决问题的关键.13.【分析】易得此几何体为圆柱,那么侧面积=底面周长×高,依此即可求解.【解答】解:10×10=100(cm2).答:这个圆柱的侧面积是100cm2.故答案:100.【点评】考查了展开图折叠成几何体,本题难点是确定几何体的形状,关键是找到等量关系里相应的量.14.【分析】从5×5×5的正方体的8个顶点进行分割,可得8个2×2×2的正方体,再加上12条棱中间的12个小正方体,依此求得小正方体的个数,再乘以1个小正方体的体积即可求解.【解答】解:如图所示:该正方体可按如图方式分割,则体积为(1×1×1)×(8×8+12)=1×76=76故所得几何体的体积为76.故答案为:76.【点评】考查了截一个几何体,正方体的体积,关键是得到小正方体的个数.15.【分析】根据主视图是从正面看到的图形直接回答即可.【解答】解:主视图是正方形的几何体可以是正方体,故答案为:正方体(答案不唯一).【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认识.16.【分析】根据三视图确定该几何体是圆柱体,再计算圆柱体的侧面积.【解答】解:先由三视图确定该几何体是圆柱体,底面半径是2÷2=1cm,高是3cm.所以该几何体的侧面积为2π×1×3=6π(cm2).故答案为:6π.【点评】此题主要考查了由三视图确定几何体和求圆柱体的侧面积,关键是根据三视图确定该几何体是圆柱体.17.【分析】根据三视图易得此几何体为圆锥,再根据圆锥侧面积公式=(底面周长×母线长)÷2 可计算出结果.【解答】解:由题意得底面直径为10cm,母线长为=13cm,∴几何体的侧面积为×10π×13=65πcm2.故答案为65π.【点评】此题主要考查了由三视图判断几何体,以及圆锥的侧面积公式的应用,关键是找到等量关系里相应的量.18.【分析】展开图为两个圆,一个长方形,易得是圆柱的展开图.【解答】解:∵圆柱的展开图为两个圆和一个长方形,∴展开图可得此几何体为圆柱.故答案为:圆柱.【点评】此题主要考查了由展开图得几何体,关键是考查同学们的空间想象能力.19.【分析】主视图、俯视图是分别从物体正面、上面看,所得到的图形.【解答】解:综合主视图和俯视图,底层最少有5个小立方体,第二层最少有2个小立方体,第三层至少有1个,因此搭成这个几何体的小正方体的个数最少是8个.故答案为:8.【点评】考查了由三视图判断几何体的知识,根据题目中要求的以最少的小正方体搭建这个几何体,可以想象出左视图的样子,然后根据“俯视图打地基,正视图疯狂盖,左视图拆违章”很容易就知道小正方体的个数.20.【分析】从三视图可以看正视图以及左视图为矩形,而俯视图为圆形,故可以得出该立体图形为圆柱.由三视图可以圆柱的半径,长和高,易求体积.【解答】解:该立体图形为圆柱,∵圆柱的底面半径r=5,高h=10,∴圆柱的体积V=πr2h=π×52×10=250π(立方单位).答:所以立体图形的体积为250π立方单位,故答案为:250π.【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查;圆柱体积公式=底面积×高.21.【分析】根据主视图为正面所看到的图形进而得出答案.【解答】解:正方形的主视图为正方形,故答案为:正方.【点评】本题考查了三视图的知识,主视图即为从正面所看到的图形.22.【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.【解答】解:由该几何体的三视图知,这个几何体是正三棱柱,故答案为:正三棱柱.【点评】考查了由三视图判断几何体.主视图和左视图的大致轮廓为长方形的几何体为柱体,俯视图为几边形就是几棱柱.23.【分析】从俯视图中可以看出最底层小正方体的个数及形状,从左视图可以看出每一层小正方体的层数和个数,从而得出答案.【解答】解:该几何体中小正方体的分布情况有如下7种可能结果,故答案为:7.【点评】本题主要考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.24.【分析】根据正六边形的性质解答即可.【解答】解:如图所示:∵正六边形的周长为12cm,∴MQ=QN=2cm,∠MQN=120°,连接MN,过Q作QP⊥MN,在Rt△MQP中,MP=,同理可得PN=,∴MN=2,故答案为:2【点评】此题考查几何体的展开图,关键是根据正六边形的性质解答.25.【分析】若要使从正面看到的形状和原几何体从正面看到的形状相同,则可取走的小正方体是3号或5号或7号;若要使从左面看到的形状和原几何体从左面看到的形状也相同,则可取走的小正方体是1号或3号或5号;据此可得.【解答】解:若要使从正面看到的形状和原几何体从正面看到的形状相同,则可取走的小正方体是3号或5号或7号,若要使从左面看到的形状和原几何体从左面看到的形状也相同,则可取走的小正方体是1号或3号或5号,故答案为:3号或5号.【点评】本题主要考查由三视图判断几何体,根据题意正确掌握三视图的观察角度是解题关键.26.【分析】俯视图为圆的只有圆锥,圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,那么侧面积=底面周长×母线长÷2.【解答】解:此几何体为圆锥;∵直径为2cm,母线长为4cm,∴侧面积=2π×4÷2=4π(cm2).故答案为4πcm2.【点评】本题考查了由三视图判断几何体,圆锥的有关计算,由该三视图中的数据确定圆锥的底面直径和母线长是解本题的关键;本题体现了数形结合的数学思想,熟记圆锥的侧面积公式是解题的关键.27.【分析】根据三视图,易判断出该几何体是圆柱.已知底面半径和高,根据圆柱的体积公式可求.【解答】解:综合三视图,可以得出这个几何体应该是个圆柱体,且底面半径为10,高为20.因此它的体积应该是:π×10×10×20=2000π.故答案为2000π.【点评】本题主要考查了由三视图确定几何体的形状以及圆柱的体积的求法.28.【分析】求得该几何体的侧面积以及底面积,相加即可得到表面积.【解答】解:侧面积为10×(6+)=60+50π,底面积之和为:2×=15π,∴该几何体的表面积为60+50π+15π=60+65π,故答案为:60+65π.【点评】本题主要考查了几何体的表面积,由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.29.【分析】如果用3块来搭,那么搭成的大长方体表面积最小是长3×3=9cm,宽4cm,高5cm的长方体的表面积,根据长方体的表面积公式即可求解;如果用4块来搭,那么搭成的大长方体表面积最小是长4×2=8cm,宽3×2=6cm,高5cm的长方体的表面积,根据长方体的表面积公式即可求解;如果用12块来搭,那么搭成的大长方体表面积最小是长3×3=9cm,宽4×2=8cm,高5×2=10cm的长方体的表面积,根据长方体的表面积公式即可求解.【解答】解:长3×3=9cm,宽4cm,高5cm,(9×4+9×5+4×5)×2=(36+45+20)×2=101×2=202(cm2).答:如果用3块来搭,那么搭成的大长方体表面积最小是202cm2.长4×2=8cm,宽3×2=6cm,高5cm,(8×6+8×5+6×5)×2=(48+40+30)×2=118×2=236(cm2).答:如果用4块来搭,那么搭成的大长方体表面积最小是236cm2.长3×3=9cm,宽4×2=8cm,高5×2=10cm,(9×8+9×10+8×10)×2=(72+90+80)×2=242×2=484(cm2).答:如果用12块来搭,那么搭成的大长方体表面积最小是484cm2.故答案为:202;258;484.【点评】考查了几何体的表面积,关键是熟练掌握长方体的表面积公式,难点是得到搭成的大长方体的长宽高.30.【分析】根据三视图我们可以得出这个几何体应该是个长方体,进而得出其表面积.【解答】解:该几何体的主视图以及左视图都是相同的矩形,俯视图也为一个矩形,可确定这个几何体是一个长方体,依题意可求出该几何体的表面积为:2×(2×3+3×4+2×4)=52.故答案为:52.【点评】此题考查了由三视图判断几何体,本题要先判断出几何体的形状,然后根据其表面积公式进行计算即可.31.【分析】易得此几何体为圆柱,圆柱的侧面积=底面周长×高.【解答】解:由主视图和左视图为长方形可得此几何体为柱体,由俯视图为圆形可得此几何体为圆柱;易得圆柱的底面直径为2,高为1,∴侧面积=2π×1=2π,故答案为:2π.【点评】本题考查圆柱的侧面积计算公式,关键是得到该几何体的形状.32.【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“晋”与“祠”是相对面,“汾”与“酒”是相对面,“恒”与“山”是相对面.故答案为:祠.【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.33.【分析】首先根据几何体的左视图,可得这个几何体共有3层;然后从俯视图中可以看出最底层小正方体的个数及形状;最后从左视图判断出第二层、第三层的个数,进而求出组成这个几何体的小正方体的个数是多少即可.【解答】解:根据几何体的左视图,可得这个几何体共有3层,从俯视图可以可以看出最底层的个数是4个,(1)当第一层有1个小正方体,第二层有1个小正方体时,组成这个几何体的小正方体的个数是:1+1+4=6(个);(2)当第一层有1个小正方体,第二层有2个小正方体时,或当第一层有2个小正方体,第二层有1个小正方体时,组成这个几何体的小正方体的个数是:1+2+4=7(个);(3)当第一层有2个小正方体,第二层有2个小正方体时,组成这个几何体的小正方体的个数是:2+2+4=8(个).综上,可得组成这个几何体的小正方体的个数是6或7或8.所以组成这个几何体的小正方体的个数最少是6故答案为:6【点评】此题主要考查了由三视图判断几何体,考查了空间想象能力,解答此题的关键是要明确:由三视图想象几何体的形状,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状.34.【分析】根据三视图的定义求解即可.【解答】解:主视图是第一层是三个小正方形,第二层右边一个小正方形,主视图的面积是4,俯视图是三个小正方形,俯视图的面积是3,左视图是下边一个小正方形,第二层一个小正方形,左视图的面积是2,几何体的三视图的面积之和是4+3+2=9,故答案为:9.【点评】本题考查了简单组合体的三视图,利用三视图的定义是解题关键.35.【分析】由几何体的三视图可知,该几何体是底面边长为2的等边三角形、高为3的三棱柱,再根据侧面积公式可得.【解答】解:由几何体的三视图可知,该几何体是底面边长为2的等边三角形、高为3的三棱柱,∴这个几何体的侧面积等于3×2×3=18,故答案为:18.【点评】本题考查了由三视图求几何体的侧面积,根据三视图判断几何体的形状是关键.36.【分析】由主视图所给的图形可得到俯视图的对角线长为2,利用勾股定理可得俯视图的面积,乘以高即为这个长方体的体积.【解答】解:设俯视图的正方形的边长为a.∵其俯视图为正方形,正方形的对角线长为2,∴a2+a2=(2)2,解得a2=4,∴这个长方体的体积为4×3=12.【点评】解决本题的关键是理解长方体的体积公式为底面积乘高,难点是利用勾股定理得到长方体的底面积.37.【分析】圆的圆心为O,连接OA、OB,可得四边形OBCA为正方形,从而求得这个油桶的底面半径.【解答】解:连接OA、OB,如图,∵BC⊥AC,OA⊥AC,OB⊥BC,OB=OA,∴四边形OBCA为正方形,∴OB=AC,∵AC=0.65m,∴这个油桶的底面半径是0.65m.故答案为:0.65【点评】本题考查了切线的性质,是基础知识比较简单.38.【分析】通过观察长方体的主视图和左视图可以得到,这个长方体的高4厘米,长3厘米,宽2厘米,因此俯视图是长3厘米,宽2厘米的长方形,因此得解.【解答】解:3×2=6(平方厘米);答:则其俯视图的面积是6平方厘米.故答案为:6.【点评】此题考查了从不同方向观察问题和几何体,锻炼了学生的空间想象力和抽象思维能力.北师版七年级上册第一章丰富的图形世界1.2.2棱柱、圆柱、圆锥的展开与折叠同步测试一.选择题(共10小题,3*10=30)1.如图由7个小正方体组合而成的几何体,从物体正面看所得到的是( )2.将五个相同的小正方体堆成如图所示的物体,从上面看到的是( )3.如图所示的几何体是由五个小正方体组成的,从左面看到的是( )4.如图,几何体上半部分为正三棱柱,下半部为圆柱,其从上面看的形状图是( )5.下列四个几何体从上面看到的图形中与众不同的是( )6.下列四个几何体:其中从左面看与从上面看得到的形状图相同的几何体共有( )A.1个B.2个C.3个D.4个7.图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的从三个方向看的形状图说法正确的是( )A.从正面看的形状图相同。
展开与折叠(2)课件 2022—2023学年苏科版数学七年级上册

5.3 展开与折叠(2) 第2课时 折叠
学习目标
学习目标
1.进一步感受立体图形与平面图形之间的关系,能根 据表面展开图判断、制作简单几何体;
2.感受正方体表面展开图中各个面之间的关系,会确 定正方体的对应面;
3.理解表面展开图中各个面之间的关系,会利用表 面展开图进行计算;
④
新知归纳
如果表面展开图由6个正方形组成,那么立体图形是正方体; 如果由3个或3个以上的三角形与1个多边形组成,那么立体图形是棱锥; 如果由3个或3个以上的长方形与2个形状、大小都相同的多边形组成, 那么立体图形是棱柱.
复习巩固
数学实验
3.如图,纸板上有10个无阴影的小正方形,从中选出1个,使 它与图中5个有阴影的正方形一起制作成一个正方体包装盒. 先想一想,再折一折,验证你的想法.
蚊子
●
你有何 高招?
壁虎 ● ●
壁 虎
拓展延伸
小壁虎的难题: 如图:如果圆桶改为正方体了呢?有多少条路径?哪条路径最短?
B
壁虎 ● A
B
●
蚊子
展开
B
A
B A 这样的路径有几条?
解:(1)这个包装盒是一个长方体. (2)此包装盒的表面积为2·b2+4·ab=2b2+4ab,体积为b2·a=ab2.
还原几何体是解答此类题的关键,动手操作是还原几何体的一个有效方法.
拓展延伸
小壁虎的难题:
如图:一只圆桶的下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃
到蚊子,应该走哪条路径?
● 蚊子
A
BCD
BCD
F
A
E
F
E
课堂小结
本节课你有什么新的收获!
立体图形的表面展开图例题与讲解

立体图形的表面展开图例题与讲解(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--立体图形的表面展开图1.圆柱、圆锥、棱柱的表面展开图将一个几何体的外表面展开,就像打开一件礼物的包装纸.礼物外形不同,包装纸的形状也各不相同.那么我们熟悉的一些几何体,如圆柱、圆锥、棱柱的表面展开图是什么形状呢(1)圆柱的表面展开图是两个圆(作底面)和一个长方形(作侧面).(2)圆锥的表面展开图是一个圆(作底面)和一个扇形(作侧面).(3)棱柱的表面展开图是两个完全相同的多边形(作底面)和几个长方形(作侧面).【例1】如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB,DC重合,则所围成的几何体图形是().解析:此题可用排除法.因为阴影部分是个扇环,而圆柱的侧面展开图是长方形,所以排除A;圆锥的侧面展开图是扇形,所以排除B;长方体的侧面展开图是长方形,所以C 也要排除;故选D.答案:D2.正方体的表面展开图(1)正方体的表面展开图按展开图中正方形所在的行数及正方形的个数,归纳起来有四种情形,各种类型的共同特点是行与行之间有且只有一个“日”型结构,由此可知正方体的展开图不会出现如下面图形所示的“凹”字型和“田”字型结构,因为这里的行与行之间出现了两组“日”型结构.(2)正方体展开图中相对面的寻找技巧:相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,如图1中的A面和B面;‘Z’字两端处的小正方形是正方体的对面,如图2、图3的A面和B面.此种方法简称为“相间、‘Z’端是对面”.解技巧正方体的表面展开图的判断思路(1)是否满足四种阵型中的一种;(2)行与行之间有且只有一个“日”型结构.【例2】一个正方形的每一个面上都写有一个汉字,其平面展开图如图所示,那么在该正方形中,与“爱”相对的字是().A.家B.乡C.孝D.感解析:本题以热爱家乡为素材,考查正方体的表面展开图.解题时可亲自动手剪一剪、折一折,即可得到与“爱”相对的字是“乡”;另外也可对展开图加以分析,根据展开图对面之间不能有公共边或公共的顶点,“爱”的对面不可能是“我”或“家”,折叠起来后“孝”、“感”与“爱”相邻,所以“爱”的对面不可能是“孝”、“感”,所以与“爱”相对的字是“乡”;但如果本题应用正方体展开图的对面寻找技巧——“相间、‘Z’端是对面”来解决,会非常简单,由相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面易知“爱”与“乡”相对.答案:B【例3】如图是正方体的展开图,则原正方体相对两个面上的数字和最小是().A.4 B.6 C.7D.8解析:将展开图还原成正方体,2和6相对,3和4相对,1和5相对,则原正方体相对两个面上的数字和最小为6.答案:B谈重点解决正方体展开图问题的关键熟练掌握正方体展开图的对面寻找技巧可以有效降低解题的难度,起到事半功倍的效果.3.正方体表面展开图的应用如果不考虑由于旋转等造成的相对位置的不同,正方体表面展开图一共有11个.正方体表面展开图的特点是每一个顶点周围的棱不超过三条.(1)“1–4–1”型有6个,其中通过“1”的移动可以由一个得到另外的5个,如图.(2)“1–3–2”型有3个,其中通过“1”的移动可以由1个得到另外的2个,如图.(3)“3–3”型有一个,“2–2–2”型有一个,如图.【例3-1】一个正方体的每一个面上都写着一个汉字,其表面展开图如图所示,那么,在该正方体中和“超”所对的汉字是__________.解析:这是“1–3–2”型的正方体表面展开图.根据展开图可知对面之间不能有公共边或公共顶点,所以“超”字的对面不能是“沉”、“着”、“越”,根据上下相对和左右相对,由于“信”和“着”相对,“着”和“超”相邻,所以“信”和“超”相邻.这样和“超”相对的字只能是“自”.答案:自【例3-2】六一儿童节时,阿兰准备用硬纸片通过裁剪、折叠制作一个封闭的正方体礼盒.她先在硬纸片上设计了一个如图1所示的裁剪方案(实线部分),经裁剪、折叠后成为一个封闭的正方体礼盒.请你参照如图,帮她设计另外两种不同的裁剪方案,使之经裁剪、折叠后也能成为一个封闭的正方体礼盒.图1 图2分析:阿兰设计的是正方体的11种展开图中的一种,可以从剩下的10种展开图中任选两种在如图的小方格中画出.解:如图2所示.4.其他立体图形展开图的应用由平面图形围成的立体图形叫多面体,其表面展开图可以有不同的形状.应多实践,观察,并大胆想象立体图形与表面展开图的关系.立体图形的表面展开图包括侧面展开图和底面展开图,画立体图形的展开图时,一定先观察立体图形的每一个面的形状.圆柱的侧面展开图是长方形,底面是圆;圆锥的侧面展开图是扇形,底面是圆;n棱柱的侧面展开图是n个高相等的长方形,底面是n边形;n棱锥的侧面展开图是n个三角形,底面是n边形.【例4】小新的茶杯是圆柱形,如图所示.左边下方有一只蜘蛛,从A处爬行到对面的中点B处,如果蜘蛛爬行路线最短,请画出这条最短路线图.分析:先画出圆柱的侧面展开图,再连接得到最短路线.解:如图所示.5.立体图形展开图的应用立体图形展开图的考查一般以选择题为主要方式,答案的获得需要学生经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生的空间观念.解决此类问题,要充分考虑带有各种符号和各种图案的面的特点及位置,解题时,先正确画出立体图形的表面展开图,再仔细观察图案以及符号的不同特点,从而选出正确的答案.有时,根据图案的位置和方向可以先把一些很明显的不符合题目要求的选择项先排除掉,再一步步的寻找正确的选项.要想灵活解决此类问题,一要熟练掌握立体图形展开图的基本知识和解题技巧;二要充分发挥自己的空间想象力;三要不断积累生活经验和解题经验.【例5-1】如图所示的正方体的展开图是().解析:利用正方体及其表面展开图的特点解题.选项A和选项D折叠后,箭头不指向白三角形,C项折叠后与原正方体不符.B折叠后与原正方体相同.故选B.答案:B【例5-2】图1是由白色纸板拼成,将其中两面涂上颜色,如图2所示.下列四个中哪一个是图2的表面展开图().解析:由图中阴影部分的位置,首先可以排除B,D,又阴影部分正方形在左,三角形在右.故选A.答案:A。
多面体的表面展开图

点拨 根据这个多面体的表面展开图的特点解答即可; 解 共有3个长方形组成侧面,2个三角形组成底面,故是三棱柱.
点拨 解 答案
(2)根据图中所标的尺寸,计算这个多面体的全面积.
点拨 这个多面体的全面积是侧面积与上下底面积之和.
解 由图可得,AB= 32+42=5,AD=3,BE=4,DF=6,
则侧面积=3×6+5×6+4×6=18+30+24=72, 上下底面积之和=3×4=12, 故全面积=72+12=84.
(2)“二三一型”:
(3)“二二二型”:
(4)“三三型”:
基础诊断
1.一个几何体的展开图如图,这个几何体是( C )
A.三棱柱
B.三棱锥
C.四棱柱
D.四棱锥
2.下列图形中,是正方体表面展开图的是( A )
A.3.下列图形中可以作为一个三棱柱的展开图的是( A )
A.
B.
C.
D.
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长.
解
解
蚂蚁沿着木柜表面经线段 A1B1 到 C′1,爬过的路径长是:AC′1
= 42+5+42= 97; 蚂 蚁 沿 着 木 柜 表 面 经 线 段 BB1 到 C1 , 爬 过 的 路 径 长 是 : AC1 = 52+4+42= 89. ∵ 89< 97, ∴最短路径的长是 AC1= 89.
剖析
正确解答
分析与反思
正确解答 B
分析与反思 当遇到立方体展开图的问题时,最好先确定两个面,这样
其他的面也就跟着确定了,不会因为旋转的原因而导致错误.
剖析
正确解答
分析与反思
返回
本课结束
更多精彩内容请登录:
柏拉图的多面体

并不是由柏拉图所发明,但是却是由柏拉图及其追随者对它们所作的研究而得名,由于它们具有高度的对称性及次序感,因而通常被称为正多面体,但是,在这里,我们仍以柏拉图多面体称之,以免与其它有规则的多面体产生混淆。
柏拉图多面体所有的面都是不自交、以直线段为边长的正凸多边形平面,每一种多面体都只有一种正多边形的表面,而且在每一个顶点处都有相同数目的面交会。
不仅在每一个顶点处都有相同数目的面交会,而且在每一个顶点处所有交会的面的内角之总和会相等。
简介熟悉柏拉图多面体的最佳方法莫过于经由构造模型并透过模型研究它们。
下图表示一种称之为”展开图”的个别柏拉图多面体平面排列图示。
为了构造柏拉图多面体的模型,一组类似的展开图必须被描绘在适当的材料上。
同学可以将本资料所附之多面体的展开图直接剪下或经放大、缩小影印在合适的漂亮纸张上。
如果材料不方便影印,您也可以依样绘制或把影印展开图并贴在所用材料上。
Albrecht Durei早在1525年,于他所著的《Unterweisung der Messung Mit dem Zirkel und Richtsheit》一书中,给出了几个多面体的展开图。
编辑本段为什么只有五个柏拉图多面体很容易看出柏拉图多面体每一个都是凸的,并且在每一个顶点处交会着相同数目、相似、正的凸多边形。
要理解为什么只有五个柏拉图多面体是相当简单的,这是因为在每一个顶点处交会着至少三个面才能构造出一个立体图形,而且围绕每一个顶点的面的角度和不能等于或超过360°,否则所得的面将是平的或是凹的。
具有最少边数的正多边形是正三角形,三个如此的多边形可以使它们交会在一个顶点上,接下来,加入第四个面,如此,每三个面就会交会在图形的四个顶点处之一。
由于这个图形有四个全等的面,故称之为正四面体(TETRAHEDRON)。
四个正三角形可以使它们交会在一个顶点上,而且加入四个面之后,在图形的六个顶点处都会有四个面交会在这里。
5.3展开与折叠(课件)-七年级数学上册(苏科版)【01】

02 知识精讲 注意:下列平面图形不是正方体的展开图哦~
正方体的展开图
L型
田字型
凹字型
02 知识精讲
探究2:为什么要剪7条棱, 才能得到正方体的展开图呢?
∵正方体共12条棱, 每种展开图内都有5条棱相连, ∴要剪7条棱。
03 典例精析
例1、下列七个图形中是正方体的平面展开图的有( B )
“二二二”型,√
02 知识精讲
同一个正方体展开所得到的平面图形有11种, 在展成平面图形的过程中,一共剪了7条棱。
02 知识精讲 探究1:11种展开图,如何快速记忆呢?
做好分类就行 啦~
“一四一”型
02 知识精讲 “三三”型
“二三一”型 “二二二”型
02 知识精讲
正方体的展开图
“一四一”型:6个 “二三一”型:3个 “三三”型:1个 “二二二”型:1个
× “一四一”型,√
×
×
A. 1个
×
B. 2个
×
C. 3个
D. 4个
03 典例精析
例2、如图是一个正方体,如图哪个选项是它的展开图( B )
A.
B.
C.
D.
03 典例精析 例3、一个正方体的表面展开图如图所示,把它折成正方体后
,与“山”字相对的字是(D )
A.水 B.绿 C.建 D.共
正方体找某一面的对面的口诀: 隔面有面是对面,隔面无面就拐弯。
例3、如图是一个不完整的正方体平面展开图,需再添上一个面, 折叠后才能围成一个正方体.下列添加方式(图中阴影部分)正
确的是( D )
A.
×
B.
×
C.
×
D.
√常见几何体的侧面展开图:来自(1)圆柱:矩形(长方形) (2)圆锥:扇形 (3)正方体:矩形(长方形)
2023年吉林省长春市中考数学试卷含答案解析

绝密★启用前2023年吉林省长春市中考数学试卷学校:___________姓名:___________班级:___________考号:___________注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)一、选择题(本大题共8小题,共24.0分。
在每小题列出的选项中,选出符合题目的一项)1. 实数a、b、c、d在数轴上对应点的位置如图所示,这四个数中绝对值最小的是( )A. aB. bC. cD. d2.长春龙嘉国际机场T3A航站楼设计创意为“鹤舞长春”.如图所示.航站楼的造型如仙鹤飞翔,蕴含了对吉春大地未来发展的美好愿景.本期工程是按照满足2030年旅客吞吐量38000000人次目标设计的,其中38000000这个数用科学记数法表示为( )A. 0.38×108B. 38×106C. 3.8×108D. 3.8×1073. 下列运算正确的是( )A. a3−a2=aB. a2⋅a=a3C. (a2)3=a5D. a6÷a2=a34.如图是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是( )A. 面①B. 面②C. 面⑤D. 面⑥5.如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA′、BB′的中点,只要量出A′B′的长度,就可以知道该零件内径AB的长度.依据的数学基本事实是( )A. 两边及其夹角分别相等的两个三角形全等B. 两角及其夹边分别相等的两个三角形全等C. 两条直线被一组平行线所截,所得的对应线段成比例D. 两点之间线段最短6.学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳AB到地面,如图所示.已知彩旗绳与地面形成25°角(即∠BAC=25°),彩旗绳固定在地面的位置与图书馆相距32米(即AC=32米),则彩旗绳AB的长度为( )A. 32sin25°米B. 32cos25°米C. 32sin25∘米 D. 32cos25∘米7.如图,用直尺和圆规作∠MAN的角平分线,根据作图痕迹,下列结论不一定正确的是( )A. AD=AEB. AD=DFC. DF=EFD. AF⊥DE8. 如图,在平面直角坐标系中,点A、B在函数y=kx(k>0,x>0)的图象上,分别以A、B为圆心,1为半径作圆,当⊙A与y轴相切、⊙B与x轴相切时,连接AB,AB=3√ 2,则k的值为( )A. 3B. 3√ 2C. 4D. 6第II卷(非选择题)二、填空题(本大题共6小题,共18.0分)9. 分解因式:m2−1=______.10. 若关于x的方程x2−2x+c=0有两个不相等的实数根,则实数c的取值范围是______ .11. 2023长春马拉松于5月21日在南岭体育场鸣枪开跑,某同学参加了7.5公里健康跑项目,他从起点开始以平均每分钟x公里的速度跑了10分钟,此时他离健康跑终点的路程为______ 公里.(用含x的代数式表示)12.如图,△ABC和△A′B′C′是以点O为位似中心的位似图形,点A在线段OA′上.若OA:AA′=1:2,则△ABC与△A′B′C′的周长之比为______ .13. 如图,将正五边形纸片ABCDE折叠,使点B与点E重合,折痕为AM,展开后,再将纸片折叠,使边AB落在线段AM上,点B的对应点为点B′,折痕为AF,则∠AFB′的大小为______ 度.14. 2023年5月28日,C919商业首航完成——中国民就商业运营国产大飞机正式起步.12时31分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”,是国际民航中高级别的礼仪).如图①,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图②,当两辆消防车喷水口A、B的水平距离为80米时,两条水柱在抛物线的顶点H处相遇.此时相遇点H距地面20米,喷水口A、B距地面均为4米.若两辆消防车同时后退10米,两条水柱的形状及喷水口A′、B′到地面的距离均保持不变,则此时两条水柱相遇点H′距地面______ 米.三、解答题(本大题共10小题,共78.0分。
展开图的画法非常有用

§8-2 可展曲面的展开
例8-5 已知由四节圆柱面管节组成的直角弯管
的投影图,管径为d,试作其展开图。
•各管节的 展开图拼 合成一个 矩形,这 样可以充 分利用板 料。
§8-2 可展曲面的展开
例8-6 已知圆柱面叉管的投影图,主管直径
为D1,支管直径为d1,试作其展开图。
•首先,作叉管的相贯线,通过 作支管圆柱面端部的辅助半圆, 得出相贯线上的点。然后,作支 管展开图。为了便于作图,将支 管正截面(圆)展开成长度为 d1的直线,使此直线位于支管 端部底圆正面投影的延长线上, 这样,就可按例8-4截头圆柱面 展开的方法作出支管柱面展开图 。
§8-2 可展曲面的展开
例8-4 已知直径为d的截头圆柱的投影图,试
作圆柱面的展开图。
• 柱底为水平面,且为柱的正截面。将柱底圆展开
成一条水平线(长度为d),将其与正面投影对齐。
将柱底圆及其展开线作相同的等分,过各等分点作 柱面素线的正面投影。用光滑曲线连接各点,得到 截交线的展开曲线。即得截头圆柱面的展开图。
开图。
• 从展开作图可以看出, 这样展开所得到的上、下两 部分棱柱表面的展开图可以 拼画在一起,从而可节省板 料,而且上、下两部分连接 处的展开折线在安装时能准 确地拼合。
§8-1 多面体表面展开
棱锥
棱椎的侧表面都是三角形,只要求出各棱 线和底边的实长,依次画出各棱面(三角 形)的实形,即为展开图。
§8-1 多面体表面展开
例8-1 已知料斗下部出料管的投影图,试作其展
开图。
• 然后,过 出料管边线AB 作棱柱的正截 面,在展开图 中作水平线 RBAKR,将其 上各点正面投 影中的长度量 取到相应的竖 直线上,连点 ,即得展开图 。
柏拉图的多面体

并不是由柏拉图所发明,但是却是由柏拉图及其追随者对它们所作的研究而得名,由于它们具有高度的对称性及次序感,因而通常被称为正多面体,但是,在这里,我们仍以柏拉图多面体称之,以免与其它有规则的多面体产生混淆。
柏拉图多面体所有的面都是不自交、以直线段为边长的正凸多边形平面,每一种多面体都只有一种正多边形的表面,而且在每一个顶点处都有相同数目的面交会。
不仅在每一个顶点处都有相同数目的面交会,而且在每一个顶点处所有交会的面的内角之总和会相等。
简介熟悉柏拉图多面体的最佳方法莫过于经由构造模型并透过模型研究它们。
下图表示一种称之为”展开图”的个别柏拉图多面体平面排列图示。
为了构造柏拉图多面体的模型,一组类似的展开图必须被描绘在适当的材料上。
同学可以将本资料所附之多面体的展开图直接剪下或经放大、缩小影印在合适的漂亮纸张上。
如果材料不方便影印,您也可以依样绘制或把影印展开图并贴在所用材料上。
Albrecht Durei早在1525年,于他所著的《Unterweisung der Messung Mit dem Zirkel und Richtsheit》一书中,给出了几个多面体的展开图。
编辑本段为什么只有五个柏拉图多面体很容易看出柏拉图多面体每一个都是凸的,并且在每一个顶点处交会着相同数目、相似、正的凸多边形。
要理解为什么只有五个柏拉图多面体是相当简单的,这是因为在每一个顶点处交会着至少三个面才能构造出一个立体图形,而且围绕每一个顶点的面的角度和不能等于或超过360°,否则所得的面将是平的或是凹的。
具有最少边数的正多边形是正三角形,三个如此的多边形可以使它们交会在一个顶点上,接下来,加入第四个面,如此,每三个面就会交会在图形的四个顶点处之一。
由于这个图形有四个全等的面,故称之为正四面体(TETRAHEDRON)。
四个正三角形可以使它们交会在一个顶点上,而且加入四个面之后,在图形的六个顶点处都会有四个面交会在这里。
2021年北师大版小升初数学衔接专题02《展开与折叠》达标检测

2021年北师大版暑假小升初数学衔接达标检测专题02《展开与折叠》试卷满分:100分考试时间:100分钟班级:姓名:学号:一.选择题(共9小题,满分18分,每小题2分)1.(2分)某个长方体的展开图如图所示,各个面上分别标有1~6的不同数字,若将其围成长方体,则这个长方体有公共顶点的三个面上的数字之和最大是()A.15 B.14 C.9 D.72.(2分)2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动.文德中学初一年级学习小组送给医务工作者的正方体6面上都有一个汉字,如图所示是它的一种展开图,那么在原正方体中,与“最”字所在面相对的面上的汉字是()A.美B.的C.逆D.人3.(2分)下列图形中,是正方体平面展开图的图形的个数是()A.4个B.3个C.2个D.1个4.(2分)下面四个图形中,经过折叠能围成如图所示的几何图形的是()A.B.C.D.5.(2分)图1是一个小正方体的展开图,小正方体从图2的所示位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是()A.常B.州C.越D.来6.(2分)正方体的六个面分别标有1,2,3,4,5,6六个数字,如图是其三种不同的放置方式,与数字“2”相对的面上的数字是()A.1 B.3 C.4 D.57.(2分)如图,是一个正方体的展开图,这个正方体可能是()A.B.C.D.8.(2分)如图,一个正方体的六个面上分别标有数字1,2,3,4,5,6.根据图中三种状态所显示的数字,正方体的正面“?”表示的数字是()A.1 B.2 C.4 D.69.(2分)如图所示的正方体,如果把它展开,可以是下列图形中的()A.B.C.D.二.填空题(共9小题,满分18分,每小题2分)10.(2分)如图所示的三个图中,不是三棱柱的展开图的是.(只填序号)11.(2分)将如图所示的平面图形折成一个正方体形的盒子,折好以后,与1相对的数是.12.(2分)如图,下列图形中,①能折叠成,②能折叠成,③能折叠成.13.(2分)将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是(填编号).14.(2分)一个小立方体的六个面分别标有数字1、2、3、4、5、6.从三个不同的方向看到的情形如图所示,则数字6的对面是.15.(2分)已知图1是图2所示的小正方体的表面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上一面的字是.16.(2分)如图,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为0,则x﹣2y=.17.(2分)如图是一个正方体的表面展开图,则图中“加”字所在面的对面所标的字是.18.(2分)将一个正方体的表面沿某些棱剪开,展开成一个平面图形(如图),则下列可能的图形有:.三.解答题(共11小题,满分64分)19.(4分)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.20.(4分)如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).21.(5分)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中只添加一个正方形并用阴影表示,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.22.(5分)如图是一个多面体的表面展开图,每个面上都标注了字母(字母在多面体的外表面),请根据要求回答问题.(1)如果C面在多面体的上边,那么A面在哪里?(2)E面和哪一面是相对面?(3)如果E面在前面,从上面看到的是C面,那么从左面能看到哪一面?23.(5分)如图①所示,从大正方体中截去一个小正方体之后,可以得到图②的几何体.(1)设原大正方体的表面积为a,图②中几何体的表面积为b,那么a与b的大小关系是;A.a>b;B.a<b;C.a=b;D.无法判断.(2)小明说“设图①中大正方体的棱长之和为m,图②中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图③是图②几何体的表面展开图吗?如有错误,请予修正.24.(6分)小明将一个底面为正方形,高为n的无盖纸盒展开,如图(a)所示.(1)请你计算图(a)所示的无盖纸盒的表面展开图的面积S1;(2)将阴影部分剪拼成一个长方形,如图(b)所示,请你计算该长方形的面积S2.(3)比较(1)(2)的结果,你得出什么结论?25.(7分)在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:(1)阿中总共剪开了几条棱?(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.26.(8分)顾琪在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是她在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:(1)顾琪总共剪开了条棱.(2)现在顾琪想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为她应该将剪断的纸条粘贴到①中的什么位置?请你帮助她在①上补全.(3)已知顾琪剪下的长方体的长、宽、高分别是6cm、6cm、2cm,求这个长方体纸盒的体积.27.(8分)张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.(1)共有种弥补方法;(2)任意画出一种成功的设计图(在图中补充);(3)在你帮忙设计成功的图中,要把﹣8,10,﹣12,8,﹣10,12这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加得0.(直接在图中填上)28.(6分)如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.(1)求该纸盒的体积;(2)求该纸盒的全面积(外表面积);(3)为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时x与y之间的倍数关系.(直接写出答案即可)29.(6分)如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z 的值.。
展开图

2、(1)判断下面一些平面图形是哪个立体图形的展开图?
(2)观察下图经过折叠能否围成一个正方体。
立体图形的表面展开 图
正方体
长方体
三棱柱
四棱锥
三棱柱
五棱锥
找朋友
考考你
1、如果“你”在前面,那么谁在后面? 了 太 你 们 棒 !
KEY: 棒
2、“坚”在下,“就”在后,胜利在哪里?
坚
持
就
胜 利
6
展开图
1、观察实物、欣赏图片,你认为设计制作一个包装盒需要了解什么? 2、自己动手把一个包装盒剪开铺平,看看它的展开图由哪些平面图形组 成?再把展开的纸板复原为包装盒,体会包装盒与它的展开图的关系。
小壁虎的难题: 如图:一只圆桶的下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃到蚊 子,应该走哪条路径?
●
蚊子
你有何高招?
壁虎 ●
●
蚊子
壁虎
蚊子
●
●
●
壁虎
比一比
猜一猜
把下列立体图形展开后,猜猜 看它的平面展开图是什么。
圆柱
长方体
五棱柱
圆锥
圆 柱
展开
长方体
展开
棱柱
展开
圆锥
展开
三棱柱
下列图形是哪些多面体的展开图?
正方体
长方体
四棱锥
三棱柱
练习 : 2 65
4 2 3
用剪刀把正方体纸盒按任意方式沿棱 展开,你能得到哪些不同的展开图?
第一类,中间四连方,两侧各一 个,共六种。
1 2 3
4
5
6
第二类,中间三连方,两侧各有一、二个,共三种。
第三类,中间二连方,两侧各有二个,只有一种。
多面体的概念由若干个多边形围成的空间图形叫多面体

A'
∴ BO AC ,∴ BOB 是二面角 B AC B 的平面角,
D
在 RtBOB 中, OB 1 AC 2 ,又 BB 2 , 2
A
B'
H
C
O
B
∴ BOB 45 ,∴二面角 B AC B 为 45 .
(2)作 BH BO 于 H ,∵ AC 平面 BOB ,∴ BH AC , ∴ BH 平面 ABC ,即 BH 为点 B 到平面 ABC 的距离,
B
AB
AD
a,
AA
b ,求对角面
BBDD
的面积 新疆 王新敞 奎屯
3.已知:正四棱柱 ABCD ABCD 的底面边长为 2 ,侧棱长为 2 ,
(1)求二面角
B
AC
B
的大小;(2)求点
B
到平面
ABC
的距离 新疆 王新敞
奎屯
D'
C'
A' D
A
B'
H
C
O
B
4.棱长为 a 的正方体 OABC OABC 中,E, F 分别为棱 AB, BC 上的动点, O'
新疆 王新敞
奎屯
如图棱锥可表示为 S ABCDE ,或 S AC .
11.棱锥的分类:(按底面多边形的边数) 分别称底面是三角形,四边形,五边形……的棱锥为三棱锥,四棱锥,五棱锥……(如图) 12.棱锥的性质:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似, 截面面积与底面面积比等于顶点到截面的距离与棱锥高的平方比. 中截面:经过棱锥高的中点且平行于底面的截面,叫棱锥的中截面
DEB 是二面角 P AC B 的平面角, DEB 120 ,
立体图形的表面展开图例题与讲解

立体图形的表面展开图1.圆柱、圆锥、棱柱的表面展开图将一个几何体的外表面展开,就像打开一件礼物的包装纸.礼物外形不同,包装纸的形状也各不相同.那么我们熟悉的一些几何体,如圆柱、圆锥、棱柱的表面展开图是什么形状呢(1)圆柱的表面展开图是两个圆(作底面)和一个长方形(作侧面).(2)圆锥的表面展开图是一个圆(作底面)和一个扇形(作侧面).(3)棱柱的表面展开图是两个完全相同的多边形(作底面)和几个长方形(作侧面).【例1】如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB,DC重合,则所围成的几何体图形是( ).解析:此题可用排除法.因为阴影部分是个扇环,而圆柱的侧面展开图是长方形,所以排除A;圆锥的侧面展开图是扇形,所以排除B;长方体的侧面展开图是长方形,所以C也要排除;故选D.答案:D2.正方体的表面展开图(1)正方体的表面展开图按展开图中正方形所在的行数及正方形的个数,归纳起来有四种情形,各种类型的共同特点是行与行之间有且只有一个“日”型结构,由此可知正方体的展开图不会出现如下面图形所示的“凹”字型和“田”字型结构,因为这里的行与行之间出现了两组“日”型结构.(2)正方体展开图中相对面的寻找技巧:相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,如图1中的A面和B面;‘Z’字两端处的小正方形是正方体的对面,如图2、图3的A面和B面.此种方法简称为“相间、‘Z’端是对面”.解技巧正方体的表面展开图的判断思路(1)是否满足四种阵型中的一种;(2)行与行之间有且只有一个“日”型结构.【例2】一个正方形的每一个面上都写有一个汉字,其平面展开图如图所示,那么在该正方形中,与“爱”相对的字是( ).A.家B.乡C.孝D.感解析:本题以热爱家乡为素材,考查正方体的表面展开图.解题时可亲自动手剪一剪、折一折,即可得到与“爱”相对的字是“乡”;另外也可对展开图加以分析,根据展开图对面之间不能有公共边或公共的顶点,“爱”的对面不可能是“我”或“家”,折叠起来后“孝”、“感”与“爱”相邻,所以“爱”的对面不可能是“孝”、“感”,所以与“爱”相对的字是“乡”;但如果本题应用正方体展开图的对面寻找技巧——“相间、‘Z’端是对面”来解决,会非常简单,由相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面易知“爱”与“乡”相对.答案:B【例3】如图是正方体的展开图,则原正方体相对两个面上的数字和最小是( ).A.4 B.6 C.7 D.8解析:将展开图还原成正方体,2和6相对,3和4相对,1和5相对,则原正方体相对两个面上的数字和最小为6.答案:B谈重点解决正方体展开图问题的关键熟练掌握正方体展开图的对面寻找技巧可以有效降低解题的难度,起到事半功倍的效果.3.正方体表面展开图的应用如果不考虑由于旋转等造成的相对位置的不同,正方体表面展开图一共有11个.正方体表面展开图的特点是每一个顶点周围的棱不超过三条.(1)“1–4–1”型有6个,其中通过“1”的移动可以由一个得到另外的5个,如图.(2)“1–3–2”型有3个,其中通过“1”的移动可以由1个得到另外的2个,如图.(3)“3–3”型有一个,“2–2–2”型有一个,如图.【例3-1】一个正方体的每一个面上都写着一个汉字,其表面展开图如图所示,那么,在该正方体中和“超”所对的汉字是__________.解析:这是“1–3–2”型的正方体表面展开图.根据展开图可知对面之间不能有公共边或公共顶点,所以“超”字的对面不能是“沉”、“着”、“越”,根据上下相对和左右相对,由于“信”和“着”相对,“着”和“超”相邻,所以“信”和“超”相邻.这样和“超”相对的字只能是“自”.答案:自【例3-2】六一儿童节时,阿兰准备用硬纸片通过裁剪、折叠制作一个封闭的正方体礼盒.她先在硬纸片上设计了一个如图1所示的裁剪方案(实线部分),经裁剪、折叠后成为一个封闭的正方体礼盒.请你参照如图,帮她设计另外两种不同的裁剪方案,使之经裁剪、折叠后也能成为一个封闭的正方体礼盒.图1 图2分析:阿兰设计的是正方体的11种展开图中的一种,可以从剩下的10种展开图中任选两种在如图的小方格中画出.解:如图2所示.4.其他立体图形展开图的应用由平面图形围成的立体图形叫多面体,其表面展开图可以有不同的形状.应多实践,观察,并大胆想象立体图形与表面展开图的关系.立体图形的表面展开图包括侧面展开图和底面展开图,画立体图形的展开图时,一定先观察立体图形的每一个面的形状.圆柱的侧面展开图是长方形,底面是圆;圆锥的侧面展开图是扇形,底面是圆;n棱柱的侧面展开图是n个高相等的长方形,底面是n边形;n棱锥的侧面展开图是n个三角形,底面是n边形.【例4】小新的茶杯是圆柱形,如图所示.左边下方有一只蜘蛛,从A处爬行到对面的中点B处,如果蜘蛛爬行路线最短,请画出这条最短路线图.分析:先画出圆柱的侧面展开图,再连接得到最短路线.解:如图所示.5.立体图形展开图的应用立体图形展开图的考查一般以选择题为主要方式,答案的获得需要学生经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生的空间观念.解决此类问题,要充分考虑带有各种符号和各种图案的面的特点及位置,解题时,先正确画出立体图形的表面展开图,再仔细观察图案以及符号的不同特点,从而选出正确的答案.有时,根据图案的位置和方向可以先把一些很明显的不符合题目要求的选择项先排除掉,再一步步的寻找正确的选项.要想灵活解决此类问题,一要熟练掌握立体图形展开图的基本知识和解题技巧;二要充分发挥自己的空间想象力;三要不断积累生活经验和解题经验.【例5-1】如图所示的正方体的展开图是( ).解析:利用正方体及其表面展开图的特点解题.选项A和选项D折叠后,箭头不指向白三角形,C项折叠后与原正方体不符.B折叠后与原正方体相同.故选B.答案:B【例5-2】图1是由白色纸板拼成,将其中两面涂上颜色,如图2所示.下列四个中哪一个是图2的表面展开图( ).解析:由图中阴影部分的位置,首先可以排除B,D,又阴影部分正方形在左,三角形在右.故选A.答案:A。
判断推理题库

刷题课判断推理讲义判断推理(九)1. 【单选题】下图为给定的多面体及其外表面展开图,问字母A、B、C、D 和数字1、2、3、4 代表的棱的对应关系为:A. 1-D ,2-A,3-C,4-BB. 1-C ,2-A,3-D,4-BC. 1-D,2-B,3-C,4-AD. 1-C,2-B,3-D,4-A2.3. 【单选题】从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:5. 【单选题】培养基是指供给微生物、植物或动物(或组织)生长繁殖的,由不同营养物质组合配制而成的营养基质,一般都含有碳水化合物、含氮物质、无机盐、维生素、水等物质。
天然培养基是利用动物、植物或微生物包括其提取物制成的培养基;合成培养基是根据天然培养基的成分,用化学物质模拟合成、人工设计而配制的培养基;半组合培养基是以化学试剂配制为主,同时还加有少量天然成分的培养基。
根据上述定义,下列属于半组合培养基的是:A. 为研究鸡胚细胞的生长,在一定比例的盐水氨基酸溶液中加入少量玉米汁制成的培养基B. 为促进乳酸菌生长,使用小麦的麦芽汁制成的培养基C. 为加速诱发绿萝生长,将有机成分、矿物元素、琼脂等按3:1:2 的比例制成的培养基D. 为观察产气荚膜梭菌的生成,在1000 毫升新鲜牛奶中加入10毫升硫酸亚铁制成的培养基6. 【单选题】按照我国继承法的规定,第一顺序的法定继承为:配偶、子女、父母,第二顺序的法定继承人为:兄弟姐妹、继父母、外祖父母。
法定继承开始后,由第一顺序继承人继承,第二顺序继承人不继承。
没有第一顺序继承人继承的,由第二顺序继承人继承,相互有继承关系的几个人在同一事件中死亡,如不能确定死亡先后时间的,推定没有继承人的先死亡,死亡人各自都有继承人的,如几个死亡人身份不同,推定长辈先死亡;几个死亡人辈份相同,推定同时死亡,彼此不发生继承,由他们各自的继承人分别继承。
根据上述定义,按照法定继承的上述规定,下列各项正确的是:A. 王一夫妇与王一的父母在一次水灾中丧生,无法确定死亡先后时间,王一只有弟弟王二,王一的妻子只有父亲,则王二既可以继承父母的那份遗产,又可以继承王一的全部遗产B. 离异的刘大与儿子(未成年)、弟弟刘二在一次事故中死亡,无法确定死亡先后时间,刘大和刘二有父母和弟弟刘三在世,则刘三也可分得那份遗产C. 李某和李妻与独生女(已婚)乘车外出,途中发生车祸,三人全部死亡,但无法确定死亡先后时间,则李女丈夫对李某夫妇遗产的继承顺序先于李某父母D. 马某与大儿子马大、孙子(马大所生独子)丧生,无法确定死亡先后时间,只有马某留下100 万遗产,其亲属中只有马大之妻和二儿子马二,则马大之妻与马二继承的财产份额不同7. 【单选题】小麦:麦穗:麦粒A. 车子:车轮:轮胎B. 棋类:围棋:棋子C. 学校:教室:学生D. 房子:房间:卧室8. 【单选题】书籍:人类进步的阶梯:《进化论》A. 跑步:使人健康的方式:强壮B. 语言:心灵的桥梁:汉语C. 月亮:天空中的小船:天体D. 舞蹈:流动的符号:表演9. 【单选题】随着气温上升,热带雨林遭受闪电雷击并引发大火的几率也会上升。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
甲
B
C
乙
D 丙
4、如果“你”在前面,那么谁在后面?
了 !
太 棒
你 们
答案
棒
1、下面的图形那些是立方体的展开图?
(1)
(2)
(3)
(4)
2、下列的三幅平面图是三棱柱的表面展 开 图的有( )
甲
乙
丙
3、如图是一个立方体纸盒的展开图,使 展开图沿虚线折叠成正方体后相对面上的两 个数互为相反数,求: -7 1 a ___, b ___, c ____ -2
可以动手剪,也 可以想着画.
1 7
2 8
3 9
4
5 10
6 11
分一分:
要求:1、观察上面的11种正方体的展开图有没有什
么规律? 2、小组讨论这些正方体展开图可以分为几类 ?哪几号展开图可以分为一类,为什么?
-
-
相 对 黄
?
巧记正方体的展开图口诀 : “一四一”“一三二”, “一”在同层可任意, “三个二”成阶梯, “二个三”“日”相连, 异层必有“日”, “凹”“田”不能有, 掌握此规律,运用定自如。
2 c
7 -1 a b
4、“坚”在下,“就”在后,“胜”、 “利”在哪里?
坚
持 就 是 胜 利
课后反思:
通过本节的学习活动,你了解了 立体图形与平面图形的关系吗?
大多数的立体图形可以展开为平面图形, 平面图形可以折叠成立体图形. 1.是不是所有的立体图形都 能展开图成平面图形呢?
2.球能展开成平面图形吗? 大家试试看
设计并制作一个包装礼盒。
1.是不是所有的立体图形都 能展开图成平面图形呢?
2.圆能展开成平面图形吗? 大家试试看
聪明的小壁虎:
一面长方形的墙壁,壁虎在下方,蚊 子在上方,饥饿的壁虎想尽快的吃掉上 方的蚊子,该走哪条路最近呢?
蚊子
●
●
壁虎
小壁虎遇难题:
有一天壁虎在圆桶的下方,发现上方 有一只蚊子,饥饿的它要想尽快吃到蚊 子,应该走哪条路最近呢?
●
蚊子
你有何高招?
壁虎
●
●
蚊子
壁虎
●
蚊子
●
●
壁虎
你还记得他们的展开图是什么吗?
(1)
(2)
若干平面图形可以围成一个立 (3) 体图形,但不是任意的若干平面 图形都可以围成一个立体图形。
下面4个图是一些多面体的表面展 开图,你能说出这些多面体的名字吗?
正方体
长方体
四棱锥
三棱柱
考考你的空间想象力:
下列图形是哪些多面体的展开图?
(1)
长方体
(2) (3)
三棱柱
五棱锥
将一个正方体的表面沿某些棱剪开, 能展成哪些平面图形?与同伴进行交流. 友情提示: 1、沿着棱剪 2、展开后是 一个图形
下列立体图形的平面展开图 是什么?
圆 柱
展开
圆锥
展开
长方体
展开
长 方 体
长方体的展开图 底面 侧 面 底面 侧 面 侧 面 底 面 侧 面 侧 面 侧面
侧 面
侧 面 底面
立体图形按不同的方式展开可得到不同的表面展开图
下面图形都是由4个三边都相等的三角形组成 的,哪一个可以折叠成多面体呢?动手做做看。
红 蓝
黄
全体总动员:
1、下面几个图形是一些常见几何体的展开 图,你能正确说出这些几何体的名字么?
圆锥
四棱锥
长方体
三棱柱
三棱锥
三棱柱
正方体
圆柱
2、如图,上面的图形分别是下面哪个立 3、有一种牛奶包装盒如图所 体图形展开的形状?把它们用线连起来。
示。为了生产这种包装盒,需要 先画出展开图纸样。如图给出的 2 4 3 三种纸样,它们都正确吗? 1
