概率统计A 期末样卷(2)答案
【概率论与数理统计经典计算题题2】期末复习题含答案

【概率论与数理统计经典计算题题2】期末复习题含答案work Information Technology Company.2020YEAR概率论与数理统计计算题(含答案)计算题1.一个盒子中装有6只晶体管,其中2只是不合格品。
现作不放回抽样,接连取2次,每次随机地取1只,试求下列事件的概率:(1)2只都是合格品;(2)1只是合格品,1只是不合格品;(3)至少有1只是合格品。
1-2,9-2.设甲,乙,丙三个工厂生产同一种产品,三个厂的产量分别占总产量的20%,30%,50%,而每个工厂的成品中的次品率分别为5%,4%,2%,如果从全部成品中抽取一件,(1)求抽取的产品是次品的概率;(2)已知得到的是次品,求它依次是甲,乙,丙工厂生产的概率。
3.设随机变量X 的分布函数为1(1), 0() 0, 0x x e x F x x -⎧-+>=⎨≤⎩,试求:(1)密度函数()f x ;(2)(1)P X ≥,(2)P X < 。
4.二维随机变量(,)X Y 只能取下列数组中的值:1(0,0),(1,1),(1,),(2,0)3--,且取这些组值的概率分别为1115,,,312612。
求这二维随机变量分布律,并写出关于X和关于Y 的边缘分布律。
5. 总经理的五位秘书中有两位精通英语,今偶遇其中的三位秘书,试求下列事件的概率:(1)其中恰好有一位精通英语;(2)其中恰好有两位精通英语;(3)其中有人精通英语。
6.某大型体育运动会有1000名运动员参加,其中有100人服用了违禁药品。
在使用者中,假定有90人的药检呈阳性,而在未使用者中也有5人检查为阳性。
如果一个运动员的药检是阳性,则这名运动员确实使用违禁药品的概率是多少?7.设随机变量X 的密度函数为||(),x f x Ae x R -=∈,试求:(1)常数A ;(2)(01)P X << 。
8. 设二维随机变量(X ,Y)的分布律为求:(1)(X ,Y)关于X 的边缘分布律;(2)X+Y 的分布律.9. 已知A B ⊂,()0.36P A =,()0.79P B =,求()P A ,()P A B -,()P B A -。
学应用概率统计大学数学2试卷(A卷)附答案

2011-2012学年第 2 学期 考试科目: 大学数学Ⅱ一、填空题(本大题共6小题,每小题3分,共18分)1. 设A 、B 为两个随机事件,已知()0.3,()0.4,()0.5P A P B P A B ===U ,则()P A B =U ______________.2. 设随机变量X 服从参数为3的泊松分布,则(1)P X ≥= ______________.3. 设二维离散型随机变量),(Y X 的联合分布律为:),(Y X 的联合分布函数为),(y x F ,则(1,3)F =______________.4. 设随机变量X 表示100次独立重复射击命中目标的次数,每次命中目标的概率为0.2, 则2X 的数学期望是______________.5. 设X 、Y相互独立,且都服从标准正态分布,则~Z =______________. (要求写出分布及其参数).6. 设由来自总体~(,0.81)X N μ,容量为9的样本得到样本均值5=X ,则未知参数μ的置信度为95%的置信区间为___________________.( 0.025 1.96u =) 二、单项选择题(本大题共6小题,每小题3分,共18分)1. 某人花钱买了C B A 、、三种不同的奖券各一张.已知各种奖券中奖是相互独立的, 中奖的概率分别为,02.0)(,01.0)(,03.0)(===C p B P A p 如果只要有一种奖券中奖此人就一定赚钱, 则此人赚钱的概率约为( ). A. 0.05B. 0.06C. 0.07D. 0.082. 设A 、B 为两个随机事件,且B A ⊂,()0>B P ,则下列选项必然正确的是( ). A. ()()B A P A P < B. ()()B A P A P >C. ()()B A P A P ≤D. ()()B A P A P ≥3. 下列各函数中可以作为某个随机变量X 的分布函数的是( ).A. 21,0()11,0x F x x x ⎧≤⎪=+⎨⎪>⎩ B. 0,0() 1.1,011,1x F x x x <⎧⎪=≤≤⎨⎪>⎩14. 设随机变量()2~2,3X N ,随机变量25Y X =-+, 则~Y ( ). A. (1,41)N B. (1,36)N C. (1,18)N - D. (1,13)N -5. 设某地区成年男子的身高()100,173~N X ,现从该地区随机选出20名男子,则这20名男子身高平均值的方差为( ).A. 100B. 10C. 5D. 0.56. 设12,,,n X X X ⋅⋅⋅是取自总体X 的一个样本, X 为样本均值,则不是总体期望μ的无偏估计量的是( ).A. XB. 123X X X +-C. 1230.20.30.5X X X ++D. 1nii X=∑三、计算题(本大题共4小题,共40分)1.(本题8分)已知一批产品中90%是合格品,检查时,一个合格品被误认为是次品的概率为0.05,一个次品被误认为是合格品的概率为0.02,求: (1)一个产品经检查后被认为是合格品的概率;(2)一个经检查后被认为是合格品的产品确是合格品的概率.2.(本题8分)设离散型随机变量X 只取1,2,3三个可能值,取各相应值的概率分别是21,,4a a -,求:(1) 常数a ; (2) 随机变量X 的分布律; (3) 随机变量X 的分布函数()F x .3.(本题10分)设随机变量X 的密度函数为:()1()2x f x e x -=-∞<<+∞.(1) 求{1}P X <; (2) 求2Y X =的密度函数.4.(本题14分)设随机变量X 与Y 相互独立,它们的密度函数分别为1,03()30,X x f x ⎧≤≤⎪=⎨⎪⎩其他, 33,0()0,0y Y e y f y y -⎧>=⎨≤⎩ 试求:(1) (,)X Y 的联合密度函数; (2) ()P Y X <; (3)()D X Y -.四、解答题(本大题共3小题,每小题8分,共24分)1. 从一台车床加工的一批轴料中抽取15件测量其椭圆度,计算得样本方差220.025s =,已知椭圆度服从正态分布,问该批轴料椭圆度的总体方差与规定的方差200.0004σ=有无显著差异(取检验水平0.05α=)?(20.025(14)26.1χ=, 20.975(14) 5.63χ=, 20.025(15)27.5χ=,20.975(15) 6.26χ=)2. 某粮食加工厂用4种不同的方法贮藏粮食,一段时间后,分别抽样化验其含水率,每种方法重复试验次数均为5次,所得粮食含水率的方差分析表的部分数据如下. (0.05(4,19) 5.01F=,0.01(4,16) 4.77F=,0.01(3,16) 5.29F=) (1) 完成下面的方差分析表.(2) 给出分析结果.3. 有人认为企业的利润水平和它的研究费用间存在着近似的线性关系. 下面是某10个企业的利润水平(x )与研究费用(y )的调查资料:102101=∑=i ix,2390101=∑=i i y ,10661012=∑=i ix ,6243001012=∑=i iy ,25040101=∑=i i i y x建立研究费用y 与企业利润水平x 的回归直线方程.2011-2012学年第 2 学期 大学数学Ⅱ 华南农业大学期末考试试卷(A 卷)-参考答案 一、1. 0.8; 2. 31e --; 3.518; 4. 416 ; 5. )1(t ; 6. (4.412,5.588) 二、1. B 2. C 3. A 4. B 5. C 6. D 三、1. 解 设A =“任取一产品,经检验认为是合格品” B =“任取一产品确是合格品” 依题意()0.9,()0.1,()0.95,()0.02P B P B P A B P A B ==== (2分)则(1)()()(|)()(|)P A P B P A B P B P A B =+0.90.950.10.020.857.=⨯+⨯=(5分) (2) ()(|)0.90.95(|)0.9977()0.857P B P A B P B A P A ⨯===. (8分)2. 解 (1) 由2114a a -+=得1231().22舍去或a a ==- (3分) (2) X 的分布律为(5分)(3) X 的分布函数为 0,10,111,12,1244()113,23,234241111,3,3424x x x x F x x x x x <⎧<⎧⎪⎪⎪≤<⎪≤<⎪⎪⎪==⎨⎨+≤<⎪⎪≤<⎪⎪⎪⎪≥++≥⎩⎪⎩ (8分) 3. 解(1)111011{1}{11}12x x P X P X e dx e dx e---<=-<<===-⎰⎰. (3分)(2)当0y ≤时,()()()20F y P Y y P X y =<=<=; (5分) 当0y >时,()()(20xx F y P X y P X dx dx --=<=<<== (8分) 所以2Y X =的密度函数为0,0()()0y f y F y y ≤⎧⎪'==>. (10分) 4. 解 (1)因为随机变量X 与Y 相互独立, ( 1分)所以它们的联合密度函数为:3,03,0(,)()()0,y X Y e x y f x y f x f y -⎧≤≤>==⎨⎩其他 (3分)(2){}(,)y xP Y X f x y dxdy <<=⎰⎰330[]xy e dy dx -=⎰⎰ (6分)330(1)x e dx -=-⎰3390181()333x x e e --=+=+()9183e -=+ (8分) (3)解:由密度函数可知~(0,3),~(3)X U Y E (10分)所以,22(30)311(),(),12439D X D Y -==== (12分) 由X 与Y 相互独立,得3131()()()4936D X Y D X D Y -=+=+=(14分) 四、1. 解 检验假设 20:0.0004H σ=,21:0.0004H σ≠. (1分)依题意,取统计量:2222(1)~(1)n S n χχσ-=-,15n =. (3分)查表得临界值:220.0252(1)(14)26.1n αχχ-==,220.97512(1)(14) 5.63n αχχ--==, (5分)计算统计量的观测值得: 22140.02521.8750.0004χ⨯==. (6分)因2220.9750.025(14)(14)χχχ<<,故接受原假设0H ,即认为总体方差与规定的方差无显著差异.(8分) 2. 解 (1)(2) 解 因为F =5.6681>0.01(3,16) 5.29F =,所以拒绝0H ,即认为不同的贮藏方法对粮食含水率的影响在检验水平0.01α=下有统计意义. (8分)3. 解 2.10=x ,239=y (2分)6.252.10101066221012=⨯-=-=∑=x n x l i i xx (3分)6622392.101025040101=⨯⨯-=-=∑=y x n y x l i i i xy (4分)故1662ˆ25.8625.6xy xx l l β==≈;01ˆˆ23925.8610.224.77y x ββ=-=-⨯=- (6分) 因此所求回归直线方程为 ˆ24.7725.86yx =-+ (8分)。
2020-2021大学《概率论与数理统计》期末课程考试试卷A(含答案)

2020-2021大学《概率论与数理统计》期末课程考试试卷A适用专业: 考试日期:试卷类型:闭卷 考试时间:120分钟 试卷总分:100分一.填空题(每题2分,共10分)1设事件A,B 互不相容,若P (A )=0.3,P (B )=0.7,则P (AB )为_________。
设事件A,B 相互独立,若P (A )=0.3,P (B )=0.7,则P (AB )为______.3.设母体X 服从正态分布N (μ,σ2),X 1,X 2⋯,X n 为取自母体的子样,X̄为子样均值,则X ̄服从的分布为__________.4.设X 1,X 2⋯,X n 相互独立,且都服从正态分布N (0,1),则∑X i 2n i=1服从的分布为_____________.5. 将一枚硬币重复掷N 次,以X 和Y 分别表示正面向上和反面向上的次数,则X 和Y 的相关系数等于__________.二、选择题(每小题2分共10分)1.设A,B 为互不相容事件,且P (A )>0,P (B )>0,则结论正确的有( )(A )P (A |B )>0 (B )P (A |B )>P(A) (C) P (A |B )=0 (D) P (A |B )=P (A )P (B ) 2、设随机变量ξ,η相互独立,且有Dξ=6,Dη=3.则D (2ξ+η)为( ) (A )9 (B )15 (C)21 (D)27 3、设随机变量X 服从正态分布N (μ,σ2),则随着σ的增大,P (|X −μ|<σ)( )(A )单调增大 (B )单调减少 (C )保持不变 (D )增减不定4、任一连续型随机变量的概率密度函数ϕ(x )一定满足( )(A )0≤ϕ(x )≤1;(B )定义域内单调不减;(C )∫ϕ(x )+∞−∞dx =1;(D )lim x→+∞ϕ(x )=1。
5、设随机变量ξ,η满足条件D (ξ+η)=D (ξ−η),则有( )事实上 (A ) Dη=0 (B )ξ,η不相关 (C )ξ,η相互独立 (D )Dξ⋅Dη=0三、综合题(每小题5分共30分)1.某射击小组共有20名射手,其中一级射手4名,二级射手8名,三级射手7名,四级射手1名,一、二、三、四级射手能通过选拔进入决赛的概率分别是0.9,0.7,0.5,0.2,求在小组内任选一名射手,该射手能通过选拔进入决赛的概率。
(理)概率统计试卷和答案2
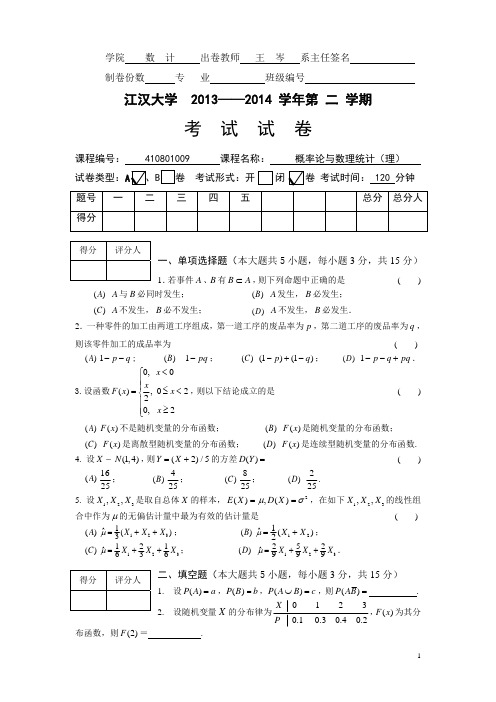
3
x 1 2 xe , x 0 6. 设总体 X 具有概率密度 f ( x) , 其中 0 为未知参数,X 1 , X 2 , , X n 0, x0
是来自 X 的样本, x1 , x2 , , xn 是相应的样本观察值. (1)求 的最大似然估计量. (2)试判断求得的估计量是否是无偏估计量.
x
n
ˆ X . 为 2
(2)因为 E (
6分
X 1 n 2n ) E( X i ) ,所以最大似然估计量是无偏估计量. 2 2n i 1 2n
10 分
7.解:本题要求在显著性水平 0.05 下检验假设 H 0 : 0 0.005,
H1 : 0 .
3. 一批机器零件共有 100 件,其中有 5 件次品,从中抽取 20 件,每次抽 1 件,设 X 表示其 中包含的次品数, 如果抽取后放回, 则 X 的分布律为 可估计 P{| X | 10 } 5. Z 检验和 t 检验都是关于 当 未知时,用 t 检验. .
4. 设随机变量 X 的数学期望 E ( X ) 及方差 D ( X ) 2 ,由切比雪夫(Chebyshev)不等式 . 的假设检验. 当 已知时,用 Z 检验;
p ,故由全概率公式 2
p p2 p (1 p) ; 2 2 p2 p 3 p p2 p2 P ( AB ) P ( B | A) P ( A) p 2 ,故 P (C ) p . 2 2 p2 p P ( AB ) p2 2p 2 (2) P ( AB ) p 2 , P( B) ,故 P ( A | B) . P( B) ( p p) / 2 p 1 2 p 注:(1)中也可用 P ( A B ) P ( A) P ( AB ) p (1 p ) 直接求解. 2
概率统计a期末样卷(2)答案

当前位置:概率论与数理统计样卷库→概率论与数理统计试卷参考答案概率论与数理统计(I)期末考试样卷2参考答案一、填空题( 每小题3分,共24分)1. 设A,B,C为三件事,且P(A)=P(B)=P(C)=1/4,P(AB)=P(BC)=0,P(AC)=1/8,则A,B,C至少有一个发生的概率= 5/82. 某油漆公司发出17桶油漆,其中白漆10桶,黑漆4桶,红漆3桶,在搬运过程中所有的标签脱落,交货人随意将这些油漆发给顾客。
问一个订货4桶白漆、3桶黑漆和2桶红漆的顾客能按所定颜色如数得到货的概率= 。
3. 已知若和独立,则=1/2 ;4.设随机变量X在区间[2,5]上服从均匀分布,求对X进行的三次独立观测中,至少有两次的观测值大于3的概率为20/27 。
.5.设随机变量X的概率分布为P(X=1)=,P(X=2)=,P(X=3)=,则其分布函数F(x)=。
6.设,且=, 则= 。
7.设,则之值为 6 。
8.设随机变量X和Y的数学期望分别为-2和2,方差分别为1和4,而相关系数为,则根据切比雪夫不等式有1/12 。
二、单项选择题( 每小题2分,共8分)1. 设A,B为两事件且P(AB)=0,则( C )。
A. A与B互斥B.AB是不可能事件C.AB未必是不可能事件D.P(A)=0或P(B)=02.设A,B为两事件,且0<P(A)<1,P(B)>0,P(B|A)=P(B|),则(C )成立。
A. P(A|B)=P(|B)B. P(A|B)≠P(|B)(AB)=P(A)P(B) D. P(AB) ≠P(A)P(B)3.若为连续型随机变量的密度函数,则一定满足(C )(A) (B) 单调递减(C) (D)4.若随机变量满足,且,则必有( B ).(A)独立;(B)不相关;(C);(D)..三、计算题(共48分)1(6分). 据以往资料表明,某一3口之家,患某种传染病的概率有以下规律:P{孩子得病}=,P{母亲得病│孩子得病}=,P{父亲得病│母亲及孩子得病}=.求母亲及孩子得病但父亲未得病的概率。
概率论与数理统计试题-a_(含答案)

深圳大学期末考试试卷参考解答及评分标准一、选择题3. 已知随机变量X ,Y 相互独立,且都服从标准正态分布,则X 2+Y 2服从 ( ) (A) 自由度为1的χ2分布 (B) 自由度为2的χ2分布 (C) 自由度为1的F 分布 (D) 自由度为2的F 分布答:选B ,因为n 个相互独立的服从标准正态分布的随机变量的平方和服从自由度为n 的χ2分布。
4. 已知随机变量X ,Y 相互独立,X ~N (2,4),Y ~N (-2,1), 则( ) (A) X +Y ~P (4) (B) X +Y ~U (2,4) (C) X +Y ~N (0,5) (D) X +Y ~N (0,3) 答:选C ,因为相互独立的正态变量相加仍然服从正态分布,而E (X +Y )=E (X )+E (Y )=2-2=0, D (X +Y )=D (X )+D (Y )=4+1=5, 所以有X +Y ~N (0,5)。
5. 样本(X 1,X 2,X 3)取自总体X ,E (X )=μ, D (X )=σ2, 则有( ) (A) X 1+X 2+X 3是μ的无偏估计(B)1233X X X ++是μ的无偏估计(C) 22X 是σ2的无偏估计(D) 21233X X X ++⎛⎫ ⎪⎝⎭是σ2的无偏估计答:选B ,因为样本均值是总体期望的无偏估计,其它三项都不成立。
6. 随机变量X 服从在区间(2,5)上的均匀分布,则X 的数学期望E (X )的值为( ) (A) 2 (B) 3 (C) 3.5 (D) 4 答:选C ,因为在(a ,b )区间上的均匀分布的数学期望为(a +b )/2。
二、填空题(共6小题,每小题5分,满分30分。
把答案填在题中横线上) 1. 已知P (A )=0.6, P (B |A )=0.3, 则P (A B )= __________ 答:填0.18, 由乘法公式P (A B )=P (A )P (B |A )=0.6⨯0.3=0.18。
《线性代数、概率统计》期末考试试卷及详细答案 二

《线性代数、概率论》期末考试试卷答案一、选择题(每小题后均有代号分别为A, B, C, D的被选项, 其中只有一项是正确的, 将正确一项的代号填在横线上,每小题2分,共40分):1.行列式G的某一行中所有元素都乘以同一个数k得行列式H,则------------C-------------;(A) G=H ;(B) G= 0 ;(C) H=kG ;(D) G=kH 。
2.在行列式G中,A ij是元素a ij的代数余子式,则a1j A1k+ a2j A2k+…+a nj A nk--------D------;(A) ≠G (j=k=1,2,…,n时) ;(B) =G(j, k=1,2,…,n; j≠k时) ;(C) =0 (j=k=1,2,…,n时) ;(D) =0(j, k=1,2,…,n ;j≠k时) 。
3.若G,H都是n⨯ n可逆矩阵,则----------B------------;(A) (G+H)-1=H-1+G-1;(B) (GH)-1=H-1G-1;(C) (G+H)-1=G-1+H-1;(D) (GH)-1=G-1H-1。
4.若A是n⨯ n可逆矩阵,A*是A的伴随矩阵, 则--------A----------;(A) |A*|=|A|n-1;(B) |A*|=|A|n ;(C) |A*|=|A|n+1;(D) |A*|=|A|。
5.设向量组α1, α2,…,αr (r>2)线性相关, 向量β与α1维数相同,则------------C----------- (A) α1, α2,…,αr-1 线性相关;(B) α1, α2,…,αr-1 线性无关;(C) α1, α2,…,αr ,β线性相关;(D) α1, α2,…,αr ,β线性无关。
6.设η1, η2, η3是5元齐次线性方程组AX=0的一组基础解系, 则在下列中错误的是D-------------------(A) η1, η2, η3线性无关;(B) X=η1+η2+ η3是AX=0的解向量;(C) A的秩R(A)=2;(D) η1, η2, η3是正交向量组。
2018~2019(二)概率统计试卷(理工类)A卷答案

������ − ������
U=
~������(0,1)
������/√������
������ − ������ W = {u|U > ������ } = u ������ > 1.64
√������
代入样本值
33.85 − 32 1.85
u=
=
= 1.83
√102/√100 √1.02
标准答案
(2)L(x, θ) = ∏
=( )
������ = min(������ , ������ , … , ������ )
(六)(10)设随机变量 X~B(100,0.2)(二项分布),用中心极限定理求 P(X>10)。
解 : P(X > 10) = P 0. .99989
>
= 1−Φ
()
()
= 1 − Φ(−2.5) = Φ(2.5) =
3������ − 6������ + 3, 0 < ������ < 1
������ (������) =
0,
其它
同理:
������ (������) = ������(������, ������)������������ = 6(1 − ������)������������ = 6(1 − ������)������
(2)D(X) = E(X − ������) = ������(������ − + − ������) = ������(������ − ) + 2������ ������ −
− ������ +
������( − ������) = ������(������ − ) + − ������ ������ ������ − + ( − ������)
概率统计A期末模拟试卷(二)参考答案

诚信应考 考出水平 考出风格浙江大学城市学院2011 — 2012 学年第 一 学期期末考试试卷《 概率统计A 》参考答案开课单位: 计算分院 ;考试形式:闭卷;考试时间:2012年1月6日;所需时间: 120分钟参考数据:(),2622.2999.0)325.2(,8399.0)99.0(,5.0)0(025.0==Φ=Φ=Φt ,()()()645.1,96.18125.110,2281.210,8331.1905.0025.005.0025.005.0=====u u t t t ,.一.选择题 (本大题10题,每题2分,共20分)1.某人射击,每次射击相互独立,但每次中靶的概率均为3/4。
如果射击直到中靶为止,则射击次数为3的概率为( C )。
343)(⎪⎭⎫⎝⎛A ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛4143)(2B ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛4341)(2C 341)(⎪⎭⎫ ⎝⎛D 2.设随机变量X 与Y 均服从正态分布,),4,(~2μN X ),5,(~2μN Y 而()41-≤=μX P p ,()52+≥=μY P p ,则( A )。
)(A 对任何实数μ,都有21p p = )(B 对任何实数μ,都有21p p < )(C 对任何实数μ,都有21p p > )(D 只对μ的个别值,才有21p p =3.设随机变量X 与Y 满足),()(Y X D Y X D +=-,则必有( B )。
)(A X 与Y 相互独立 )(B X 与Y 不相关 )(C 0)(=X D )(D 0)()(=Y D X D4.设总体)1,0(~N X ,样本n X X X ,,,21 )1(>n 为来自该总体的简单随机样本,X 与S 分别为样本均值和样本标准差,则有( C ))(A )1,0(~N X )(B )1,0(~N X n )(C)(~212n X ni i χ∑= )(D)1(~-n t SX第1页共4页5.一种零件需两道工序加工完成,两道工序相互独立。
09-10学年第二学期概率统计期末考试试卷A及答案

Þ (E 2X 2 - 1)= 2E(X )2 - 1 = 9
评注:本题考查了正态分布密度函数与其期望和方差的对应问题.
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
南京工业大学《概率统计》课程试题A及参考答案

南京工业大学概率统计课程考试试题(A 、闭)(江浦)(第二学期)1.假设P (A )=0.4, P (A ∪B )=0.7,那么(1)若A 与B 互不相容,则P (B )= ______ ;(2)若A 与B 相互独立,则P (B )= ____ 。
2.将英文字母C,C,E,E,I,N,S 随机地排成一行,那么恰好排成英文单词SCIENCE 的概率为____________。
3.设随机变量X 的概率密度为442e 1)(-+-=x xx f π,则=2EX 。
4.设随机变量X 与Y 相互独立,且均服从参数为0.6的0-1分布,则{}Y X p ==______。
5.某人有外观几乎相同的n 把钥匙,只有一把能打开门,随机地取出一把开门,记X 为直到把门打开时的开门次数,则平均开门次数为__________。
6.设随机变量X 服从)21,8(B (二项分布), Y 服从参数为3的泊松分布,且X 与Y 相互独立,则)32(--Y X E =__________;)32(--Y X D =__________。
7.设总体X ~),(2σμN , (X 1,X 2,…X n )是来自总体X 的样本,已知2111)(∑-=+-⋅n i i i X Xc 是2σ的无偏估计量,则=c 。
二、选择题(每题3分,计9分)1.当事件A 和B 同时发生时,必然导致事件C 发生,则下列结论正确的是( )。
(A )P (C )≥ P (A )+ P (B )1- (B )P (C )≤P (A )+ P (B )1- (C )P (C )=P (A ⋃B ) (D )P (C )= P (AB )2.设X 是一随机变量,C 为任意实数,E X 是X 的数学期望,则( )。
(A )E (X -C )2=E (X -E X )2 (B ) E (X -C )2≥E (X -E X )2 (C ) E (X -C )2 <E (X -E X )2 (D ) E (X -C ) 2 = 03.设总体X ~),(2σμN , (X 1,X 2, X 3)是来自总体X 的样本,则下列估计总体X 的均值μ的估计量中最好的是( )。
概率统计期末考试试卷及参考答案1

3.1概率统计期末考试试卷及参考答案1一、单项选择题1、在一个班级同学中选出一个班长,一个团支书;则事件“选出的班长是男生,选出的团支书是女生”的对立事件是(B )A.“选出的班长是女生,选出的团支书是男生”;B.“选出的班长是女生或选出的团支书是男生”;C.“选出的班长是女生,选出的团支书是女生”;D.“选出的班长是男生,选出的团支书是男生”.2、随机变量2~(3,)XN σ,且有{36}0.4P X <<=,则{0}P X <=(A).A.0.1B.0.2C.0.3D.0.43、随机变量,X Y 独立同分布,且{1}{1}0.5P XP X ===-=,则有(B ).A.{}1P X Y ==.B.{}0.5P X Y ==.C.{0}0.25P X Y +== D.{0}0.25P XY ⋅==.4、设~()X P λ(泊松分布)且{2}2{1}P X P X ===,则()E X =(D ).A.1B.2C.3D.45、设连续型随机变量的分布函数和密度函数分别为(), ()F x f x ,则下列选项中正确的是(A )A.0()1F x ≤≤ B.0()1f x ≤≤C.{}()P X x F x ==D.{}()P Xx f x ==.6、设2~(,)XN μσ,其中μ已知,2σ未知,1234,,,X X X X 为其样本.下列各项不是统计量的是(C)A.4114ii X X ==∑B.142X X μ+-C.42211()ii K XX σ==-∑D.42211()3i i S X X ==-∑二、填空题1、某生做四题作业,设i A 表示该生第i 题做对,则事件“他前两题都没有做对而后两题没有都做错”可表示为4123()A A A A .2、设A,B 为随机事件,A 与B 互不相容,{}0.2P B =,则()P AB =0.2.3、袋中有50个球,其中20个黄球、30个白球,今有2人依次随机地从袋中各取一球,取后不放回,则第2个人取得黄球的概率为0.44、设随机变量~(12,0.5),~(18,0.4),XB Y B 且X 与Y 相互独立,则:()D X Y -=0.95、设随机变量X 的分布函数为20, 0(), 011 1x F x Ax x x <⎧⎪=⎨⎪<⎩≤≤,,则A =1;6、设22~()n χχ,则有2()E χ=n7、设12,,,n X X X 是来自[2,]θθ-上的均匀分布总体的一个样本,则θ的矩估计量是1X +三、计算题(一)1、甲乙丙三人同时对飞机进行射击,三人击中的概率分别为0.4,0.5,0.7,飞机被一人击中而被击落的概率为0.2,被两人击中而被击落的概率为0.6,若三人都击中,飞机必定被击落,求飞机被击落的概率.解:设i A 表示i 人击中飞机,i=1,2,3.B 表示飞机被击落。
概率论与数理统计考试a(含答案)

深圳大学期末考试试卷参考解答及评分标准开/闭卷 闭卷A/B 卷A 课程编号 2219002801-2219002811课程名称概率论与数理统计学分3命题人(签字) 审题人(签字) 年 月 日 基本题6小题,每小题5分,满分30分。
在每小题给出的四个选项中,只有一(每道选择题选对满分,选0分)事件表达式A B 的意思是 ( ) 事件A 与事件B 同时发生 (B) 事件A 发生但事件B 不发生 事件B 发生但事件A 不发生 (D) 事件A 与事件B 至少有一件发生 D ,根据A B 的定义可知。
假设事件A 与事件B 互为对立,则事件A B ( ) 是不可能事件 (B) 是可能事件 发生的概率为1 (D) 是必然事件 A ,这是因为对立事件的积事件是不可能事件。
已知随机变量X ,Y 相互独立,且都服从标准正态分布,则X 2+Y 2服从 ( ) 自由度为1的χ2分布 (B) 自由度为2的χ2分布 自由度为1的F 分布 (D) 自由度为2的F 分布选B ,因为n 个相互独立的服从标准正态分布的随机变量的平方和服从自由度为n 的2分布。
已知随机变量X ,Y 相互独立,X ~N (2,4),Y ~N (-2,1), 则( ) X +Y ~P (4) (B) X +Y ~U (2,4) (C) X +Y ~N (0,5) (D) X +Y ~N (0,3) 选C ,因为相互独立的正态变量相加仍然服从正态分布,而E (X +Y )=E (X )+E (Y )=2-2=0, (X +Y )=D (X )+D (Y )=4+1=5, 所以有X +Y ~N (0,5)。
样本(X 1,X 2,X 3)取自总体X ,E (X )=μ, D (X )=σ2, 则有( ) X 1+X 2+X 3是μ的无偏估计(B)1233X X X ++是μ的无偏估计22X 是σ2的无偏估计(D) 21233X X X ++⎛⎫ ⎪⎝⎭是σ2的无偏估计B ,因为样本均值是总体期望的无偏估计,其它三项都不成立。
(完整版),概率论与数理统计期末试卷及答案,推荐文档

X
1 1
2 1
P 2 2
令 Z maxX ,Y,则 PZ 1 (
).
1
1
1
A.
B.
C.
D.1
4
2
3
3、如果 X 和Y 满足 DX Y DX Y ,则必有( B )
A. X 与Y 独立
C. DY 0
B. X 与Y 不相关
D. DX DY 0
4、设 1,2,2,3,4 为来自均匀分布总体U (0, ) 的样本值,则未知参数 的最大似然估计为(
1 3 2
2
时, cY 服从
1
二、选择题(共 10 分,每小题 2 分)
1、设随机变量 X 在 2,4上服从均匀分布,则 P3 X 4 ( B )
A. P1.5 X 2.5
B. P2.25 X 3.25
C. P3.5 X 4.5
D. P4.5 X 5.5
2、设相互独立的随机变量 X ,Y 具有同一分布,且 X 的分布律为( A )
_-0.4
, D( X ) 1.44
.
5. 若 X ~ N (3,9) ,则 P{| X | 6}= 1 31
(用标准正态分布函数表示).
6.设随机变量
X
的密度函数为
f(x)ke1 2xx 0 , 则 k 0.5
,
0 x 0
P( X 2) 0
.
7.设随机变量 X 的数学期望 EX ,方差 DX 2 ,则由切比雪夫不等式有 P( X 5 ) ____ 24 _______ .
解: A 表示该学生被录取, B1 表示该生报考普通高中, B2 表示该生报考中专,
B3 表示该生报考职业高中.
PA
《概率论与数理统计》习题二答案解析

《概率论与数理统计》习题及答案习题二1•一袋中有5只乒乓球,编号为1 , 2, 3, 4, 5,在其中同时取3只,以X 表示取出的3只 球中的最大号码,写出随机变量 X 的分布律•【解】X =3,4,5 3P(X =4) 3 =0.3 C 5C 2P(X =5)3=0.6C52•设在15只同类型零件中有 2只为次品,在其中取 3次,每次任取1只,作不放回抽样, 以X 表示取出的次品个数,求: (1)X 的分布律; (2)X 的分布函数并作图;(3)1 3 3P{X }, P{1 :: X }, P{1 乞 X }, P{1 :: X :: 2}.2 2 2【解】X =0,1,2. C 13 P(X =2)13C15P(X =3) C ;= 0.1P(X =0) C 13C152235P(X =1)C ;C 23C 512 35丄 3534 34 门 0 2' 2' ' '35 3533 12P(1 _ X ) = P(X =1)P(1 :: X 厂2 2 3534 1P(1 ::: X ::2) = F(2) _ F(1)_ P(X =2) =1 0.35 35 3•射手向目标独立地进行了 3次射击,每次击中率为 0.8,求3次射击中击中目标的次数的 分布律及分布函数,并求 3次射击中至少击中 2次的概率. 【解】设X 表示击中目标的次数.则X=0,1,2,3.P(X = 0) = (0.2)3 = 0.0081 2P(X =1)70.8(0.2) =0.096 P(X 二 2) =C 3(O.8)2O.2 = 0.384P(X =3) =(0.8)3 =0.512故X 的分布律为 X 0 1 2 3 P0.0080.0960.3840.512分布函数” 0,X <00.008, 0 兰 xc1F(X )» 0.104, 1^x<20.488, 2 兰x<31,x^3P(X — 2) = P(X =2) P(X =3^ 0.8964.( 1)设随机变量X 的分布律为P{X=k}= a -,k!其中k=0, 1, 2,…,入〉0为常数,试确定常数 a.(2)设随机变量X 的分布律为P{ X=k}= a/N ,k=1, 2,…,N ,试确定常数a.0,x ::: 0 22 0 _ x :: 13534 1 _x :: 2351, x_2F(x)= (2)当 x<0 时,F (x ) =P (X w x ) =0当 0 w x<1 时, F (x ) 当 1 w x<2 时, F (x ) 22 =P (X w x ) =P(X=0)=- 35 34 =P (X w x ) =P(X=0)+P(X=1)=-35当x >2时,F 故X 的分布函数(x ) =P (X w x ) =1 1 1 22P(X =)★(;) ,2 2 353 3P(1 ::: X ) = F(:)-【解】(1)由分布律的性质知二:• k1 P(X 二k) =a aLe'k z0 k^o k!故 a = e_,(2)由分布律的性质知N Na1 =為P(X =k) akw k a N即 a = 1.5•甲、乙两人投篮,投中的概率分别为0.6,0.7,今各投3次,求:(1)两人投中次数相等的概率;(2)甲比乙投中次数多的概率.【解】分别令X、Y表示甲、乙投中次数,贝U X~b (3, 0.6) Y~b(3,0.7)(1) P(X 二Y)二P(X =0,Y =0) P(X =1,Y =1) P(X =2,Y =2)P(X =3,Y =3)3 3 1 2 1 2-(0.4) (0.3) C30.6(0.4) C30.7(0.3) +2 2 2 23 3C3(0.6) 0.4C3(0.7) 0.3 (0.6) (0.7)=0.32076(2) P(X Y) = P(X =1,Y =0) P(X =2,Y =0) P(X =3,Y =0)P(X =2,Y =1) P(X =3,Y =1) P(X =3,Y =2)1 2 3 2 2 3-C30.6(0.4) (0.3) C3(0.6) 0.4(0.3)3 3 2 2 1 2(0.6) (0.3) C3(0.6) 0.4C30.7(0.3)(0.6)3C;0.7(0.3)2(0.6)3C:(0.7)20.3=0.2436•设某机场每天有 200架飞机在此降落,任一飞机在某一时刻降落的概率设为 0.02,且设各飞机降落是相互独立的•试问该机场需配备多少条跑道,才能保证某一时刻飞机需立即降 落而没有空闲跑道的概率小于0.01(每条跑道只能允许一架飞机降落)?【解】设X 为某一时刻需立即降落的飞机数,则X~b(200,0.02),设机场需配备 N 条跑道,则有P(X ■ N) <0.01200即送 C k 00(O.O2)k (O.98)200上 £0.01k =N 1利用泊松近似-np = 200 0.02 = 4.血 e 44kP(X_N)0.01宀k!查表得N > 9.故机场至少应配备 9条跑道.7. 有一繁忙的汽车站,每天有大量汽车通过,设每辆车在一天的某时段出事故的概率为0.0001,在某天的该时段内有 1000辆汽车通过,问出事故的次数不小于 2的概率是多少(利 用泊松定理)?【解】设X 表示出事故的次数,则 X~b (1000, 0.0001)P(X _2) =1 -P(X =0) -P(X =1)0.1 0.1=1 —e - 0.1 e8.已知在五重贝努里试验中成功的次数 X 满足P{X=1}= P{X=2},求概率P{X=4}.【解】设在每次试验中成功的概率为p ,则14 2 2 3C 5p(1 - p) 9p (1 - p)9.设事件A 在每一次试验中发生的概率为 0.3,当A 发生不少于3次时,指示灯发出信号 (1)进行了 5次独立试验,试求指示灯发出信号的概率;(2)进行了 7次独立试验,试求指示灯发出信号的概率.【解】(1)设X 表示5次独立试验中 A 发生的次数,则 X~6 ( 5, 0.3)5P(X 工3)=送 c 5(0.3)k (0.7)5^ =0.16308k=3⑵ 令Y 表示7次独立试验中 A 发生的次数,则 Y 〜b ( 7,0.3)故 所以P(X =4)=C :(1)4拿10 2437 ■—k k 7 —kP(Y^3)=送C k(0.3)k(0.7)7=0.35293 k=310•某公安局在长度为t 的时间间隔内收到的紧急呼救的次数X 服从参数为(1/2) t 的泊松分63 1 13.进行某种试验,成功的概率为一,失败的概率为一.以X 表示试验首次成功所需试验的次44数,试写出X 的分布律,并计算 X 取偶数的概率. 【解】X =1,2,,k,|||1 k —1 p (x =k )y4P(X =2) P(X =4)P(X =2k)谱64 W …布,而与时间间隔起点无关(时间以小时计)(1) (2) 【解】(1) 求某一天中午12时至下午 求某一天中午12时至下午3P(X =0)3时没收到呼救的概率; 5时至少收到1次呼救的概率.5(2) P(X _1) =1 — P(X =0) =1 -k k2 _k11.设 P{X=k}= C 2P (1 - p) ,k=0,1,2mm4_mP{ Y=m}= C 4 p (1 - p)m=0,1,2,3,45分别为随机变量 X , Y 的概率分布,如果已知 P{X > 1}=,试求P{ Y > 1}.954I 解】因为P(X 牛,故P(X (9)P(X ::: 1) = P(X =0) =(1 - P)2故得24(仆)飞1 「3从而P(Y _1) =1 _P(Y =0) =1_(1_ p)465 0.80247810.001,试求在这 2000册书中 12•某教科书出版了 2000册,因装订等原因造成错误的概率为 恰有5册错误的概率. 【解】令X 为2000册书中错误的册数,则X~b(2000,0.001).利用泊松近似计算,■ - np 二 2000 0.001 二 2P(X =5)「255!-0.001811 514•有2500名同一年龄和同社会阶层的人参加了保险公司的人寿保险•在一年中每个人死亡的概率为0.002,每个参加保险的人在 1月1日须交12元保险费,而在死亡时家属可从 保险公司领取2000元赔偿金•求: (1) 保险公司亏本的概率; (2)保险公司获利分别不少于 10000元、20000元的概率.【解】以“年”为单位来考虑.(1) 在1月1日,保险公司总收入为 2500 X 12=30000元. 设1年中死亡人数为 X ,则X~b(2500,0.002),则所求概率为P(2000X • 30000) =P(X 15) P(X <14)由于n 很大,p 很小,入=np=5,故用泊松近似,有:4 e'5kP(X 15) = 10.000069k 竺k !⑵P(保险公司获利不少于 10000)= P(30000 -2000X _ 10000) =P(X < 10)20000) = P(30000 -2000X 一20000) = P(X 乞5)5 _5 k_ e 5 0.615961 k =0 k!即保险公司获利不少于 20000元的概率约为62% 15.已知随机变量 X 的密度函数为f(x)=Ae ,「8 <x<+ ,求:(1) A 值;(2) P{0<X<1}; (3) F(x).【解】(1)由 f (x)dx =1得1=Ae ^dx =2 Ae "dx =2A--:: 01 故 A . 2⑵ p(0 :X ::1)匚 0「dxs (1-e')⑶当x<0时,x1 1F (x )=[石 e x dx 匚 e x10k =0k!0.986305即保险公司获利不少于 10000元的概率在 98%以卜.P (保险公司获利不少于中任意小区间内的概率与这小区间长度成正比例,试求 X 的分布函数 【解】 由题意知X~ U [0,a ],密度函数为故当x<0时F (x ) =0 当 0< x w a 时 F(x)=当 x >0 时,F(x)= f^e X dx + 2 -::22 [-e~dx o 2F(x) =1 x 0 -e , x :::0 1」e 」x_0 2 16•设某种仪器内装有三只同样的电子管,电子管使用寿命 100, X —100,x x ::100. 在开始150小时内没有电子管损坏的概率; 在这段时间内有一只电子管损坏的概率; F ( x ). X 的密度函数为f(x)= 0,求: (1)(2) (3) 【解】 (1) 150 100 1 P(X < 150) r dx . ' )応 x 2 3 3 2 3 8 P 1 <P(X 150)]3 珂2)3 二石 3 2/⑵卩2 二 c ;3(2)2 ⑶当 x<100 时 F (x ) =0 x 当 x > 100 时 F(x) f (t)dtJ JO O 100 x 」(t )d t100f (t )dtx豁1t 2100x i 0,x _100x ::17•在区间]0, a ]上任意投掷一个质点,以 X 表示这质点的坐标,设这质点落在]1f (X )二 a' 0,0乞x 乞a其他xx;f (t )dt 「0x1 xf(眄0了蔦当 x>a 时,F (x ) =1即分布函数x F(x)二l a 1,18.设随机变量X 在[2 , 5]上服从均匀分布•现对 值大于3的概率. 【解】X~U [2,5],即Pf(x) = 3’【0,故所求概率为119•设顾客在某银行的窗口等待服务的时间X(以分钟计)服从指数分布E(-).某顾客在窗口55次,以Y 表示一个月内他未等 P{Y > 1}.> _xf(x)二孑5【0,该顾客未等到服务而离开的概率为Y~b(5,e 冷,即其分布律为P(Y =k) =c 5(e')k (1—e')5=k =0,1,2,3,4,5P(Y 一1)=1 -P(Y = 0) =1 -(1-e‘)5 =0.516720.某人乘汽车去火车站乘火车,有两条路可走.第一条路程较短但交通拥挤,所需时间X 服从N (40, 102);第二条路程较长,但阻塞少,所需时间 X 服从N (50, 42).(1)若动身时离火车开车只有 1小时,问应走哪条路能乘上火车的把握大些?(2) 又若离火车开车时间只有 45分钟,问应走哪条路赶上火车把握大些? 【解】(1)若走第一条路,X~N (40, 102),则「0, x :: 0P(X 3)=Qdx =3 3X 进行三次独立观测,求至少有两次的观测其他p=c 3(2)21 c 3(2)3 3 3 3 20 27等待服务,若超过10分钟他就离开•他一个月要到银行 到服务而离开窗口的次数,试写出 Y 的分布律,并求1【解】依题意知X ~ E(”),即其密度函数为x'5dx = -2ef x —4060—40 )斗 P(X :::60) = P(2) =0.97727V 1010 丿若走第二条路,X~N ( 50, 42),则X 「50 60「50 P(X ::: 60) = P(2.5) = 0.9938++V 441故走第二条路乘上火车的把握大些•(2)若 X~N (40, 102),则P(X :::45)=P X -4° :: 45一4° =::,(0.5)=0.6915I 10 10 丿若 X~N (50 , 42),则:::45 -5° = : :」(_1.25)4=1 -门(1.25) =0.1056故走第一条路乘上火车的把握大些.21•设 X~N (3,22),(1) 求 P{2<X<5}, P{4<X <10} , P{ | X |> 2}, P{X >3}; (2)确定 c 使 P{X > c}= P{X < c}.【解】(1) P(2:::X E5)=P 口」3 空口V 2 2 2 丿()2 () 2= 0.8413 -1 0.6915 =0.5328 P(—4 ::X —10) =P i.X 色一!^3V 222 丿 =O.9996P(| X | 2) = P(X 2) P(X :: -2)f X -3 2_3]丄 f X -3 _2_3; =P --------- > ------ (+P ---------- < ---------I 2 2丿 12 2丿 “—①i —丄①i —5匚①I 丄r —①i-l 2丿I 2丿12丿 12丿-0.6915 1 -0.9938 =0.6977P(X ::45) = P X -50—4X —3 3-3P(X 3) = P() J —::」(0) =0.5⑵c=322. 由某机器生产的螺栓长度(cm ) X~N (10.05,0.062),规定长度在10.05土 0.12内为合格品 求一螺栓为不合格品的概率.=1一门(2)亠处(一2)=2[1-::」(2)]二 0.045623. 一工厂生产的电子管寿命 X (小时)服从正态分布 N (160, (I),若要求P{120 v X < 200 =>0.8,允许i 最大不超过多少?(1) 求常数A , B ;(2) 求 P{X W 2} , P{X > 3}; (3)求分布密度f (x ).匹 F(x)=1 「A = 1【解】(1)由 … 得伽+F (x)巳监F(x)旧一1(2) P(X _2) = F(2) =1 -e ,'P(X 3) =1 _F(3) =1 _(1_eA )25.设随机变量X 的概率密度为・x,f (x )=」2 - x,0,求X 的分布函数F (x ),并画出f (x )及F (x )f (x^ F (x)0,x 一0 x :: 0 【解】P(|X -10.05| 0.12) =PX —10.05 0.060.12>0.06』【解】P(120::"200)=P 1^1坐3 乞叱型 故24.设随机变量X 分布函数为40-31.251.29F (x )A Be*,0,x 一0,x 0.0 空 x :: 1,仁 x :: 2,【解】当x<0时F (x ) =0xtdt当 1W x<2 时 F(x)二 f (t)dt1-0tdt (2-t)dt1 2x22 2 2x2x -1x 当 x >2 时 F (x) f (t)dt = 126•设随机变量X 的密度函数为(1) f(x)=ae_ |x|,入 >0;f(x)二 2c 'X2e当 x W 0 时 F (x) = J 』(x)dx =访e% = 2,当 0W x<1 时 F(x)=xJ (t)仁x.f(t)dtF(x)二x 22x 2x -1,21,x :: 0x _2⑵f(x)= 试确定常数 【解】(1)由bx, 12,x 0,0 ■ x :: 1, 1 < x < 2,其他•a,b ,并求其分布函数 F ( x )."f (x)dx =1知 1J JO O2ax 2 3即密度函数为当 x>0 时 F (x) =(x)dx =J :eMdx 壮专e —x dx故其分布函数x _01 f (x)2, |x 0,当 x < 0 时 F (x ) =0当 0<x<1 时 F(x) f (x)dx f(x)dx 亠 I f (x)dx当 1 w x<2 时 F(x)二 J-f (x)d ^j-Qdx当 x > 2 时 F (x ) =1 故其分布函数为广0, 2xJF(x)二 23_12 x1,27•求标准正态分布的上:-分位点,(1) : =0.01,求 z ; (2) : =0.003,求 z-., z-./2. 【解】(1) P(X Z.H0.01即 :G( z :.)=0.09故z —2.33x=0xdxx 21 八-3 - 2F(x)1丄」 2(2)由 1 = f°°f(x)dx = f1bxdx — dxx得即X 的密度函数为b=1x, 0 : x :: 1其他xdx1严x-0 0 ■ x ■■■ 1 1 < x ::即心(zj =0.012a(2)由 P(X .乙)=0.003得 1 (zj =0.003即 :•:」(乙)=0.997 查表得乙.=2.75由 P(X z ./2) =0.0015 得1-:」(Z-./2)=0.0015即 ■->( Z") =0.9985查表得z :./2 =2.96求Y=X 的分布律.【解】Y 可取的值为0, 1, 4, 9P(Y =0) =P(X =0)」5P(Y =1) = P(X =「1) P(X =1)=1 -~6 15301 p (Y =4) =P(X - -2): 5 11 P(Y =9) = P(X =3)=3029•设 P{X=k}=( 1): k=1,2,…,令Y 「1,当X 取偶数时 1-1,当X 取奇数时.求随机变量X 的函数Y 的分布律.【解】P(Y =1) =P(X =2) P(X =4) "I P(X =2k)川=G )2 G )4 川(1)2k 川2 2 2 1 1 1 =()/(1 厂4 4 3P(Y =—1) = 1 — P(Y =1) = 2 30•设 X~N (0, 1).(1) 求Y=e X 的概率密度; (2) 求Y=2X 2+1的概率密度; (3)求Y= | X |的概率密度•【解】(1)当 y w 0 时,F Y (y)二 P(Y 曲)=0x当 y>0 时,F Y (y) =P(Y 空 y) =P(e < y^P(X < ln y)In y二:i- fX (x)dx(2) P(Y =2X 2 1 _1) = 1当 y w 1 时 F Y (y) =P (丫 乞 y) =02当 y>1 时 F Y (y) =P (丫 乞 y) =P(2X 1 乞 y)(y J)/2「一 R f X (x)dx故 f 丫(y)=f F 丫(y)三民:f x (厅]+f x 「F]]⑶ P(Y-0)=1当 y w 0 时 F Y (y)二 P (Y — y) =0dF y (y)11 1 j n 2y /2 JEW ,y 0= PX 2 哼二P< X <4y 4)/4e , y 1当 y>0 时 F Y (y) = P(| X 国 y)二 P( —y 乞 X 乞 y)y二 y f x (x)dx故 f Y (y):F Y (y )二 f x (y) f x (-y)dy31. 设随机变量X~U (0,1),试求:(1) Y=e x 的分布函数及密度函数; (2)Z= -21 nX 的分布函数及密度函数【解】(1) P(0 ::X :::1) =1故 p( 1 ::: Y 二 e ::: e) 1 当 y _1 时 F Y (y) =P(Y 乞 y) =0当 1<y<e 时 FY (y) =P(e X 乞 y) =P(X On y)In y「0 dx=lnyX当 y 》e 时 F Y (y)二 P(e < y) = 1 即分布函数J, y^e故Y 的密度函数为口 f Y (y)二 y,0,(2) 由 P ( 0<X<1) =1 知P(Z 0) =1当 z w 0 时,F z (z) =P(Z Ez) =0当 z>0 时,F Z (z)二 P(Z 乞 z)二 P(—2ln X ^z)=P(ln X _ -自二 P(X _e 亠2)y 0,F /(y)=七n y,y 乞1 1 ::1 ::y e故Z的密度函数为32. 设随机变量X的密度函数为2xf(x)= n io,0 ::xn其他.试求Y=sinX的密度函数.【解】P(0 Y:::1) =1当y w o 时,F Y(y)二P(Y ^y) =0当0<y<1 时,F Y(y)二P(Y 空y)二P(sin x 乞y)二P(0 :: X M arcsin y) P( n- arcsin y 玄X ::narcsiny 2x n2x2dx 2dx0 n -arcsin y 彳=4( arcsiny)2 1- arcsin®2n n2 .arcs in yn当y》1 时,F Y(y)=1故Y的密度函数为33. 设随机变量X的分布函数如下:z/2即分布函数I z/2 dx = 1 - eu a -----z<0-z/21-ez 0zMX』2,X 』2,18试填上(1),(2),(3)项.F(x) = 1 x‘(2)X-(3) •19【解】由lim F(x) =1知②填1。
概率论期末考试题及答案pdf

概率论期末考试题及答案pdf一、单项选择题(每题3分,共30分)1. 随机变量X服从标准正态分布,则P(X<0)的值为()。
A. 0.5B. 0.3C. 0.7D. 0.9答案:A2. 已知随机变量X服从二项分布B(n, p),则E(X)的值为()。
A. npB. n(1-p)C. pD. 1答案:A3. 两个随机变量X和Y相互独立,则P(X>1, Y>1)等于()。
A. P(X>1)P(Y>1)B. P(X>1) + P(Y>1)C. P(X>1) - P(Y>1)D. P(X>1) / P(Y>1)答案:A4. 随机变量X服从泊松分布,其参数为λ,则P(X=k)的值为()。
A. λ^k * e^(-λ) / k!B. λ^k * e^(-λ) * k!C. λ^k * e^(-λ) / (k-1)!D. λ^k * e^(-λ) * (k-1)!答案:A5. 随机变量X服从均匀分布U(a, b),则其期望E(X)的值为()。
A. (a+b)/2B. a+bC. 2a-bD. 2b-a答案:A6. 已知随机变量X服从正态分布N(μ, σ^2),则其方差Var(X)的值为()。
A. μB. σ^2C. 1/σ^2D. 1/μ答案:B7. 随机变量X服从指数分布,其参数为λ,则其期望E(X)的值为()。
A. 1/λB. λC. 1D. 0答案:A8. 随机变量X和Y相互独立,且都服从标准正态分布,则P(X+Y<0)的值为()。
A. 0.5B. 0.25C. 0.75D. 0.9答案:A9. 随机变量X服从二项分布B(n, p),则其方差Var(X)的值为()。
A. npB. np(1-p)C. pD. 1-p答案:B10. 随机变量X服从正态分布N(μ, σ^2),若P(X<μ)=0.5,则μ的值为()。
A. 0B. 1C. μD. σ^2答案:C二、填空题(每题4分,共20分)11. 随机变量X服从标准正态分布,若P(X<1.96)=0.975,则P(X>1.96)=________。
2020年大二必修概率论与数理统计期末考试题及答案(新版)

2020年大二必修概率论与数理统计期末考试题及答案(新版)一、单选题1、设是未知参数的一个估计量,若,则是的___ _____(A)极大似然估计 (B)矩法估计 (C)相合估计 (D)有偏估计 【答案】D 2、设为来自正态总体的一个样本,若进行假设检验,当___ __时,一般采用统计量(A) (B)(C)(D)【答案】D3、1621,,,X X X 是来自总体),10(N ~X 的一部分样本,设:216292821X X Y X X Z ++=++= ,则YZ~( ) )(A )1,0(N )(B )16(t )(C )16(2χ )(D )8,8(F【答案】D4、设n X X X ,,21为来自正态总体),(2σμN 简单随机样本,X 是样本均值,记2121)(11X X n S ni i --=∑=,2122)(1X X n S n i i -=∑=,2123)(11μ--=∑=n i i X n S , 22411()ni i S X n μ==-∑,则服从自由度为1-n 的t 分布的随机变量是A) 1/1--=n S X t μ B) 1/2--=n S X t μ C) nS X t /3μ-=D) nS X t /4μ-=【答案】B5、以A 表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件A 为 (A )“甲种产品滞销,乙种产品畅销”; (B )“甲、乙两种产品均畅销” (C )“甲种产品滞销”; (D )“甲种产品滞销或乙种产品畅销”。
【答案】DˆθθˆE θθ≠ˆθθnX X X ,,,21 2(,)N μσX U =220μσσ未知,检验=220μσσ已知,检验=20σμμ未知,检验=20σμμ已知,检验=6、若()1P B A =,那么下列命题中正确的是(A )A B ⊂ (B )B A ⊂ (C )A B -=∅ (D )()0P A B -= 【答案】D7、设X 1,X 2,…X n ,X n+1, …,X n+m 是来自正态总体2(0,)N σ的容量为n+m 的样本,则统计量2121ni i n mi i n m V n =+=+X =X ∑∑服从的分布是(A) (,)F m n (B) (1,1)F n m -- (C) (,)F n m (D)(1,1)F m n -- 【答案】C8、若X ~()t n 那么2χ~A )(1,)F nB )(,1)F nC )2()n χD )()t n 【答案】A9、设12,,,n X X X ⋅⋅⋅为总体X 的一个随机样本,2(),()E X D X μσ==,12211()n i i i C XX θ-+==-∑为 2σ的无偏估计,C =(A )1/n (B )1/1n - (C ) 1/2(1)n - (D ) 1/2n - 【答案】C10、设X 1,X 2,…X n ,X n+1, …,X n+m 是来自正态总体2(0,)N σ的容量为n+m 的样本,则统计量2121ni i n mi i n m V n =+=+X =X ∑∑服从的分布是(A) (,)F m n (B) (1,1)F n m -- (C) (,)F n m (D)(1,1)F m n -- 【答案】C 二、填空题1、设容量n = 10 的样本的观察值为(8,7,6,9,8,7,5,9,6),则样本均值= ,样本方差= 【答案】X =7,S 2=22、已知随机变量X 的密度为()f x =⎩⎨⎧<<+其它,010,x b ax ,且{1/2}5/8P x >=,则a =________ b =________【答案】1=a ,=b 1/23、将C,C,E,E,I,N,S 等7个字母随机的排成一行,那末恰好排成英文单词SCIENCE 的概率为 【答案】4/7! = 1/12604、甲、乙两人独立的对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为 【答案】0.755、测得自动车床加工的10个零件的尺寸与规定尺寸的偏差(微米)如下: +2,+1,-2,+3,+2,+4,-2,+5,+3,+4 则零件尺寸偏差的数学期望的无偏估计量是 【答案】2三、解答题(难度:中等)1、(10分)某出租车公司欲了解:从金沙车站到火车北站乘租车的时间。
2021年大二必修课概率论与数理统计期末考试卷及答案(新版)

2021年大二必修课概率论与数理统计期末考试卷及答案(新版)一、单选题1、设X 1,X 2,…X n ,X n+1, …,X n+m 是来自正态总体2(0,)N σ的容量为n+m 的样本,则统计量2121ni i n mi i n m V n =+=+X =X ∑∑服从的分布是A) (,)F m n B) (1,1)F n m -- C) (,)F n m D) (1,1)F m n -- 【答案】C2、设n X X X ,,21为来自正态总体),(2σμN 简单随机样本,X 是样本均值,记2121)(11X X n S ni i --=∑=,2122)(1X X n S n i i -=∑=,2123)(11μ--=∑=n i i X n S , 22411()ni i S X n μ==-∑,则服从自由度为1-n 的t 分布的随机变量是(A) 1/1--=n S X t μ(B) 1/2--=n S X t μ(C) n S X t /3μ-=(D) nS X t /4μ-=【答案】B3、设n X X X ,,21为来自正态总体),(2σμN 简单随机样本,X 是样本均值,记2121)(11X X n S ni i --=∑=,2122)(1X X n S n i i -=∑=,2123)(11μ--=∑=n i i X n S , 22411()ni i S X n μ==-∑,则服从自由度为1-n 的t 分布的随机变量是(A) 1/1--=n S X t μ(B) 1/2--=n S X t μ(C) n S X t /3μ-=(D) nS X t /4μ-=【答案】B4、设 ()2~,X N μσ,其中μ已知,2σ未知,1234,,,X X X X 为其样本, 下列各项不是统计量的是____(A)4114i i X X ==∑ (B)142X X μ+-(C)42211()i i K X X σ==-∑ (D)4211()3i i S X X ==-∑【答案】C5、设某个假设检验问题的拒绝域为W ,且当原假设H 0成立时,样本值(x 1,x 2, …,x n )落入W 的概率为0.15,则犯第一类错误的概率为__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当前位置:概率论与数理统计样卷库→概率论与数理统计试卷参考答案
概率论与数理统计(I)期末考试样卷2参考答案
一、填空题( 每小题3分,共24分)
1. 设A,B,C为三件事,且P(A)=P(B)=P(C)=1/4,P(AB)=P(BC)=0,P(AC)=1/8,则A,B,C 至少有一个发生的概率= 5/8
2. 某油漆公司发出17桶油漆,其中白漆10桶,黑漆4桶,红漆3桶,在搬运过程中所有的标签脱落,交货人随意将这些油漆发给顾客。
问一个订货4桶白漆、3桶黑漆和2桶红
漆的顾客能按所定颜色如数得到货的概率= 。
3. 已知若和独立,则= 1/2 ;
4.设随机变量X在区间[2,5]上服从均匀分布,求对X进行的三次独立观测中,至少有
两次的观测值大于3的概率为 20/27 。
.
5.设随机变量X的概率分布为P(X=1)=,P(X=2)=,P(X=3)=,则其分布函数F(x)=。
6.设,且=, 则= 。
7.设,则之值为 6 。
8.设随机变量X和Y的数学期望分别为-2和2,方差分别为1和4,而相关系数为,则根
据切比雪夫不等式有 1/12 。
二、单项选择题( 每小题2分,共8分)
1. 设A,B为两事件且P(AB)=0,则( C )。
A. A与B互斥B.AB是不可能事件
C.AB未必是不可能事件D.P(A)=0或P(B)=0
2.设A,B为两事件,且0<P(A)<1,P(B)>0,P(B|A)=P(B|),则( C )成立。
A. P(A|B)=P(|B)
B. P(A|B)≠P(|B)
(AB)=P(A)P(B) D. P(AB) ≠P(A)P(B)
3.若为连续型随机变量的密度函数,则一定满足( C )
(A) (B) 单调递减(C) (D)
4.若随机变量满足,且,则必有( B ).
(A)独立;(B)不相关;(C);(D)..
三、计算题(共48分)
1(6分). 据以往资料表明,某一3口之家,患某种传染病的概率有以下规律:P{孩子得病}=,P{母亲得病│孩子得病}=,P{父亲得病│母亲及孩子得病}=.求母亲及孩子得病但父亲未得病的概率。
解:设A=“孩子得病”,B=“母亲得病”,C=“父亲得病”,则所求概率为。
已知P(A)=,P(B│A)=,P(C│AB)=,则由乘法定理有
由,,有
2(10分).设考生的报名表来自三个地区,分别有10份,15份,25份,其中女生的分别为3份,7份,5份。
随机地从一地区,先后任取两份报名表,求:
(1)先取的那份报名表是女生的概率;
(2)已知后取到的报名表是男生的,而先取的那份报名表是女生的概率。
解:(1) 设={考生的报名表是第个地区的},=1,2,3,B={先取到的报名表是女生的},由全概率公式知:P(B)= P()P(B|)+
P()P(B|)+P()P(B|)=
(2)设C={先取的那份报名表是女生的},D={后取到的报名表是男生的},则P(CD)= P()P(CD|)+ P()P(CD|)+P()P(CD|)
=
P(D)= P()P( D |)+ P()P( D |)+P()P( D |)=
所以可计算得:===
3(8分)设随机变量X的分布函数为试求
(1)系数A;(2)X落在区间(,)内的概率;(3)X的密度函数。
解:(1)由的连续性,有,由此得(2)
(3)X的密度函数为
4(8分)设随机变量X和Y同分布,X的密度函数为
已知事件和独立,且,求常数。
解:由设且与同分布,与独立,可知当时,
,即
与相矛盾,因而,即
,即
即,即,(不合题意,舍去)。
5(8分)设二维随机变(X,Y)量具有概率密度,
(1)确定常数C; (2) 求概率。
解:(1),由此得。
(2)积分区域为,所以
6(8分)设随机变量(X,Y)具有概率密度
求。
解:
,。
四、应用题(14分)
1. (6分)设顾客在某银行的窗口等待服务的时间X(以分计)服从指数分布,其概
率密度为,某顾客在窗口等待服务,若超过10分钟,他就离开,他一个月要到银行5次,以Y表示一个月内他未等到服务而离开窗口的次数,写出Y的分布律,并求P{Y}。
解:因为Y表示一个月内他未等到服务而离开窗口的次数,所以Y,其中p =P{X}=
Y的分布律为P{Y=k}=,k=0,1,2,3,4,5
P{Y}=1-P{Y}=1-P{Y=0}=1-=
2(8分). 某单位设置一电话总机,共有200架电话分机。
设每个电话分机是否使用外线通话是相互独立的。
设每时刻每个分机有5%的概率要使用外线通话。
问总机需要多少外线才能以不低于90%的概率保证每个分机要使用外线时可供使用()
解设总机需要安装N条外线X=“200架电话分机中使用外线的数目”,则X服从二项
分布。
利用棣莫
佛-拉普拉斯中心极限定理,得
由,查表得,解出,故总机需要安装14条外线才能以不低于90%的概率保证每个分机要使用外线时可供使用。
五、证明题(6分 ) 设{X n}为独立同分布的随机变量序列,其共同的密度函数为
,令,试证:。
证明:因为的分布函数为所以当时,有
对任意的,当时有即。
嘉兴学院教务处。
