音高和频率转换表
钢琴的音高与频率对照表

钢琴的音高与频率对照表十二音律(twelve pitches of the temperament octave)用绿色标注。
此表通过连续的乘法每次乘1.0594631得出的结果(2的十二次方)。
调音参考频率(A-440)为紫色标注。
最低频率用红色标注,最高频率用蓝色标注。
一、人声及各乐器频率范围表实际人声频率男:低音82~392Hz,基准音区64~523Hz男中音123~493Hz,男高音164~698Hz女:低音82~392Hz,基准音区160~1200Hz女低音123~493Hz,女高音220~1.1KHz录音时各频率效果男歌声150Hz~600Hz影响歌声力度,提升此频段可以使歌声共鸣感强,增强力度。
女歌声1.6~3.6KHz影响音色的明亮度,提升此段频率可以使音色鲜明通透。
语音800Hz是“危险”频率,过于提升会使音色发“硬”、发“楞”沙哑声提升64Hz~261Hz会使音色得到改善。
喉音重衰减600Hz~800Hz会使音色得到改善鼻音重衰减60Hz~260Hz,提升1~2.4KHz可以改善音色。
齿音重6KHz过高会产生严重齿音。
咳音重4KHz过高会产生咳音严重现象(电台频率偏离时的音色)乐器重要频率范围表:贝司:低音吉它:频响在700~1KHz之间,提高拨弦音为60~80Hz电贝司:低音在80~250Hz,拨弦力度在700~1KHz吉它:电吉它:65~1.7KHz,响度在2.5KHz,饱满度在240Hz 木吉它:低音弦:80~120Hz,琴箱声:250Hz,清晰度:2.5KHz、3.75KHz、5KHz鼓:低音鼓:27~146Hz,低音:60~80Hz,敲击声:2.5KHz 小鼓:饱满度:240Hz,响度:2KHz通通鼓:丰满度:240Hz,硬度:8KHz地筒鼓:丰满度:80~120Hz吊钗:130~2.6KHz,金属声:200Hz,尖锐声:7.5~10KHz,镲边声:12KHz手风琴:饱满度:240Hz钢琴:低音在80~120Hz,临场感2.5~8KHz,声音随频率的升高而变单薄二、人声各频率段音色效果2K~3KHz频率:这段频率是影响声音明亮度最敏感的频段,如果这段频率成分丰富,则音色的明亮度会增强,如果这段频率幅度不足,则音色将会变得朦朦胧胧;而如果这段频率成分过强,音色就会显得呆板、发硬、不自然.1K~2KHz频率:这段频率范围通透感明显,顺畅感强。
声子能量频率对照表

声子能量频率对照表声子能量频率对照表如下:1. 男歌声:低音82~392Hz,基准音区64~523Hz;男中音123~493Hz,男高音164~698Hz。
录音时,150Hz~600Hz影响歌声力度,提升此频段可以使歌声共鸣感强,增强力度。
2. 女歌声:低音82~392Hz,基准音区160~1200Hz;女低音123~493Hz,女高音220~。
录音时,~影响音色的明亮度,提升此段频率可以使音色鲜明通透。
3. 语音:800Hz是“危险”频率,过于提升会使音色发“硬”、发“楞”。
4. 沙哑声:提升64Hz~261Hz会使音色得到改善。
5. 喉音重:衰减600Hz~800Hz会使音色得到改善。
6. 鼻音重:衰减60Hz~260Hz,提升1~可以改善音色。
7. 齿音重:6KHz过高会产生严重齿音。
8. 咳音重:4KHz过高会产生咳音严重现象(电台频率偏离时的音色)。
9. 小提琴:200Hz-400Hz影响音色的丰满度;1-2KHz是拨弦声频带;6-10KHz是音色明亮度。
10. 中提琴:150Hz-300Hz影响音色的力度;3-6KHz影响音色表现力。
11. 大提琴:100Hz-250Hz影响音色的丰满度;3KHz是影响音色音色明亮度。
12. 贝斯提琴:50Hz-150Hz影响音色的丰满度;1-2KHz影响音色的明亮度。
13. 长笛:250Hz-1KHz影响音色的丰满度;5-6KHz影响的音色明亮度。
14. 黑管:150Hz-600Hz影响音色的丰满度;3KHz影响音色的明亮度。
15. 双簧管:300Hz-1KHz影响音色的丰满度;5-6KHz影响音色的明亮度;1-5KHz提升使音色明亮华丽。
16. 大管:100Hz-200Hz音色丰满、深沉感强;2-5KHz影响音色的明亮度。
17. 小号:150Hz-250Hz影响音色的丰满度;是明亮清脆感频带。
18. 圆号:60Hz-600Hz提升会使音色和谐自然;强吹音色光辉,1-2KHz明显增强。
钢琴的音高与频率对照表

钢琴的音高与频率对照表十二音律(twelve pitches of the temperament octave)用绿色标注。
此表通过连续的乘法每次乘1.0594631得出的结果(2的十二次方)。
调音参考频率(A-440)为紫色标注。
最低频率用红色标注,最高频率用蓝色标注。
一、人声及各乐器频率范围表实际人声频率男:低音82~392Hz,基准音区64~523Hz男中音123~493Hz,男高音164~698Hz女:低音82~392Hz,基准音区160~1200Hz女低音123~493Hz,女高音220~1.1KHz录音时各频率效果男歌声150Hz~600Hz影响歌声力度,提升此频段可以使歌声共鸣感强,增强力度。
女歌声1.6~3.6KHz影响音色的明亮度,提升此段频率可以使音色鲜明通透。
语音800Hz是“危险”频率,过于提升会使音色发“硬”、发“楞”沙哑声提升64Hz~261Hz会使音色得到改善。
喉音重衰减600Hz~800Hz会使音色得到改善鼻音重衰减60Hz~260Hz,提升1~2.4KHz可以改善音色。
齿音重6KHz过高会产生严重齿音。
咳音重4KHz过高会产生咳音严重现象(电台频率偏离时的音色)乐器重要频率范围表:贝司:低音吉它:频响在700~1KHz之间,提高拨弦音为60~80Hz电贝司:低音在80~250Hz,拨弦力度在700~1KHz吉它:电吉它:65~1.7KHz,响度在2.5KHz,饱满度在240Hz 木吉它:低音弦:80~120Hz,琴箱声:250Hz,清晰度:2.5KHz、3.75KHz、5KHz鼓:低音鼓:27~146Hz,低音:60~80Hz,敲击声:2.5KHz 小鼓:饱满度:240Hz,响度:2KHz通通鼓:丰满度:240Hz,硬度:8KHz地筒鼓:丰满度:80~120Hz吊钗:130~2.6KHz,金属声:200Hz,尖锐声:7.5~10KHz,镲边声:12KHz手风琴:饱满度:240Hz钢琴:低音在80~120Hz,临场感2.5~8KHz,声音随频率的升高而变单薄二、人声各频率段音色效果2K~3KHz频率:这段频率是影响声音明亮度最敏感的频段,如果这段频率成分丰富,则音色的明亮度会增强,如果这段频率幅度不足,则音色将会变得朦朦胧胧;而如果这段频率成分过强,音色就会显得呆板、发硬、不自然.1K~2KHz频率:这段频率范围通透感明显,顺畅感强。
钢琴的音高与频率对照表

十二音律(twelve pitches of the temperament octave) 用绿色标注。
此表通过连续的乘法每次乘1.0594631得出的结果(2的十二次方)。
调音参考频率(A-440)为紫色标注。
最低频率用红色标注,最高频率用蓝色标注。
、人声及各乐器频率范围表实际人声频率男:低音82〜392Hz,基准音区64〜523Hz男中音123〜493Hz,男高音164〜698Hz女:低音82〜392Hz ,基准音区160〜1200Hz女低音123〜493Hz ,女高音220〜1.1KHz录音时各频率效果男歌声150Hz~600Hz 影响歌声力度,提升此频段可以使歌声共鸣感强,增强力度。
女歌声1.6~3.6KHz 影响音色的明亮度,提升此段频率可以使音色鲜明通透。
语音800Hz 是“危险”频率,过于提升会使音色发“硬”、发“楞” 沙哑声提升64Hz~261Hz 会使音色得到改善。
喉音重衰减600Hz~800Hz 会使音色得到改善鼻音重衰减60Hz~260Hz ,提升1~2.4KHz 可以改善音色。
齿音重6KHz 过高会产生严重齿音。
咳音重4KHz 过高会产生咳音严重现象(电台频率偏离时的音色)乐器重要频率范围表:贝司:低音吉它:频响在700〜1KHz之间,提高拨弦音为60〜80Hz电贝司:低音在80〜250Hz,拨弦力度在700〜1KHz吉它:电吉它:65〜1.7KHz,响度在2.5KHz,饱满度在240Hz木吉它:低音弦:80〜120Hz,琴箱声:250Hz,清晰度:2.5KHz、3.75KHz、5KHz鼓:低音鼓:27〜146Hz,低音:60〜80Hz,敲击声:2.5KHz 小鼓:饱满度:240Hz,响度:2KHz通通鼓:丰满度:240Hz,硬度:8KHz地筒鼓:丰满度:80〜120Hz吊钗:130〜2.6KHZ,金属声:200Hz,尖锐声:7.5〜10KHz , 镲边声:12KHz手风琴:饱满度:240Hz钢琴:低音在80〜120Hz,临场感2.5〜8KHz,声音随频率的升高而变单薄二、人声各频率段音色效果2K〜3KHz频率:这段频率是影响声音明亮度最敏感的频段,如果这段频率成分丰富,则音色的明亮度会增强,如果这段频率幅度不足,则音色将会变得朦朦胧胧;而如果这段频率成分过强,音色就会显得呆板、发硬、不自然.1K〜2KHz 频率:这段频率范围通透感明显,顺畅感强。
钢琴的音高与频率对照表
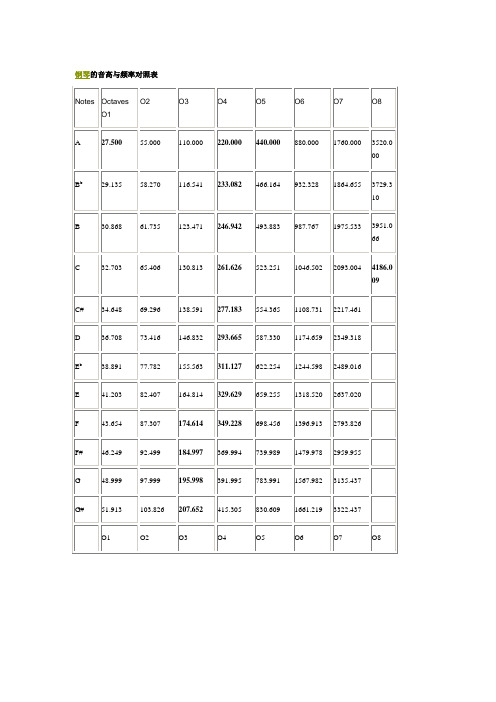
十二音律(twelve pitches of the temperament octave)用绿色标注。
此表通过连续的乘法每次乘1.0594 631得出的结果(2的十二次方)。
调音参考频率(A-440)为紫色标注。
最低频率用红色标注,最高频率用蓝色标注。
(上面的频率表是google上找来的,转帖,致谢!)
各音频率的计算
小字1组的A音(简谱的6=啦)是440Hz,国际标准。
把A4=440 乘以1.0594631 就是A#4=466.164,
再把A#4 X 1.0594631=493.883=B4.
往下440 除以1.0594631就得到G#4
这样就可以计算出88个音的各自频率.
任意相临两音的比值永远是1.0594631, 为什么?
它是2的开12次方, 这就是十二平均律!
Tunelab 软件中把88键钢琴最左边的音叫A0, 最低的C叫C1, 以后顺序为C#1, D1, D#1,.......中央C 叫C4.
调律的标准音是小字1组的A音,叫A4=440赫兹。
音高和频率转换表

音高和频率转换表如下一些解释:•O ctave 0-9 表示八度区。
C-D-E-F-G-A-B 为C 大调七个主音:do re mi fa so la si(简谱记为1 到7)。
科学音调记号法(scientific pitch notation)就是将上面这两者合在一起表示一个音,比如A4 就是中音la,频率为440 Hz。
C5 则是高音do(简谱是1 上面加一个点)。
•升一个八度也就是把频率翻番。
A5 频率880 Hz,正好是A4 的两倍。
一个八度区有12 个半音,就是把这两倍的频率间隔等比分为12,所以两个相邻半音的频率比是2 开12 次方,也即大约1.05946。
这种定音高的办法叫做twelve-tone equal temperament,简称12-TET。
•两个半音之间再等比分可以分100 份,每份叫做一音分(cent)。
科学音调记号加上音分一般足够表示准确的音高了。
比如A4 +30 表示比440 Hz 高30 音分,可以算出来具体频率是447.69 Hz。
•A4 又称A440,是国际标准音高。
钢琴调音师或者大型乐队乐器之间调音都用这个频率。
•C4 又称Middle C,是中音八度的开始。
有一种音高标定方法是和C4 比较相隔的半音数,比方B4 就是+11,表示比C4 高11 个半音。
•M IDI note number p 和频率f 转换关系:p = 69 + 12 x log2(f/440)。
这实际上就是把C4 定为MIDI note number 60,然后每升降一个半音就加减一个号码。
•可以看到E-F 和B-C 的间隔是一个半音,而七个主音别的间隔都是两个半音,也叫一个全音。
•标准钢琴琴键有大有小,大的白色琴键是主音,小的黑色琴键是主音升降一个半音后的辅音(图)。
一般钢琴是88 个琴键,从A0 到C8。
知道了上面这些,看到钢琴键盘应该就马上能找到Middle C 了,如下•音高间隔(音程)有各类说法,某些间隔的两个音同时发出来会比较令人身心愉快,比如频率比3:2 的perfect fifth 在各类乐曲都会广泛用作和弦。
钢琴的音高与频率对照表

钢琴的⾳⾼与频率对照表钢琴的⾳⾼与频率对照表⼗⼆⾳律(twelve pitches of the temperament octave)⽤绿⾊标注。
此表通过连续的乘法每次乘1.0594631得出的结果(2的⼗⼆次⽅)。
调⾳参考频率(A-440)为紫⾊标注。
最低频率⽤红⾊标注,最⾼频率⽤蓝⾊标注。
⼀、⼈声及各乐器频率范围表实际⼈声频率男:低⾳82~392Hz,基准⾳区64~523Hz男中⾳123~493Hz,男⾼⾳164~698Hz⼥:低⾳82~392Hz,基准⾳区160~1200Hz⼥低⾳123~493Hz,⼥⾼⾳220~1.1KHz录⾳时各频率效果男歌声150Hz~600Hz影响歌声⼒度,提升此频段可以使歌声共鸣感强,增强⼒度。
⼥歌声1.6~3.6KHz影响⾳⾊的明亮度,提升此段频率可以使⾳⾊鲜明通透。
语⾳800Hz是“危险”频率,过于提升会使⾳⾊发“硬”、发“楞”沙哑声提升64Hz~261Hz会使⾳⾊得到改善。
喉⾳重衰减600Hz~800Hz会使⾳⾊得到改善⿐⾳重衰减60Hz~260Hz,提升1~2.4KHz可以改善⾳⾊。
齿⾳重6KHz过⾼会产⽣严重齿⾳。
咳⾳重4KHz过⾼会产⽣咳⾳严重现象(电台频率偏离时的⾳⾊)乐器重要频率范围表:贝司:低⾳吉它:频响在700~1KHz之间,提⾼拨弦⾳为60~80Hz电贝司:低⾳在80~250Hz,拨弦⼒度在700~1KHz吉它:电吉它:65~1.7KHz,响度在2.5KHz,饱满度在240Hz ⽊吉它:低⾳弦:80~120Hz,琴箱声:250Hz,清晰度:2.5KHz、3.75KHz、5KHz⿎:低⾳⿎:27~146Hz,低⾳:60~80Hz,敲击声:2.5KHz ⼩⿎:饱满度:240Hz,响度:2KHz通通⿎:丰满度:240Hz,硬度:8KHz地筒⿎:丰满度:80~120Hz吊钗:130~2.6KHz,⾦属声:200Hz,尖锐声:7.5~10KHz,镲边声:12KHz⼿风琴:饱满度:240Hz钢琴:低⾳在80~120Hz,临场感2.5~8KHz,声⾳随频率的升⾼⽽变单薄⼆、⼈声各频率段⾳⾊效果2K~3KHz频率:这段频率是影响声⾳明亮度最敏感的频段,如果这段频率成分丰富,则⾳⾊的明亮度会增强,如果这段频率幅度不⾜,则⾳⾊将会变得朦朦胧胧;⽽如果这段频率成分过强,⾳⾊就会显得呆板、发硬、不⾃然.1K~2KHz频率:这段频率范围通透感明显,顺畅感强。
纯律与十二平均律音高频率表(对比)

纯律与十二平均律音高频率表(对比)一、纯律音高频率表纯律是一种基于自然泛音列的音律系统,其音高频率关系如下:1. 基音(C)频率:f2. 纯一度(C)频率:f 1.06783. 纯二度(D)频率:f 1.12254. 纯小三度(D)频率:f 1.18925. 纯大三度(E)频率:f 1.25996. 纯四度(F)频率:f 1.33487. 纯增四度(F)频率:f 1.41428. 纯五度(G)频率:f 1.49839. 小六度(G)频率:f 1.587410. 大六度(A)频率:f 1.681811. 小七度(A)频率:f 1.781812. 大七度(B)频率:f 1.887713. 纯八度(C)频率:f 2二、十二平均律音高频率表十二平均律是一种将一个八度等分为十二个半音的音律系统,其音高频率关系如下:1. 基音(C)频率:f2. 半音(C)频率:f 1.05953. 全音(D)频率:f 1.12254. 半音(D)频率:f 1.18925. 全音(E)频率:f 1.25996. 半音(F)频率:f 1.33487. 全音(F)频率:f 1.41428. 半音(G)频率:f 1.49839. 全音(G)频率:f 1.587410. 半音(A)频率:f 1.681811. 全音(A)频率:f 1.781812. 半音(B)频率:f 1.887713. 八度(C)频率:f 2通过对比纯律与十二平均律音高频率表,我们可以发现两者在音高频率上的差异。
纯律更接近自然泛音列,而十二平均律则在演奏和调音方面具有更高的便利性。
三、纯律与十二平均律的差异分析1. 音色和谐度纯律由于其音高频率比是根据自然泛音列得出的,因此在和弦的和谐度上更为优越。
尤其是在和声进行中,纯律能够展现出更加丰满、自然的音色效果。
相比之下,十二平均律的和声效果虽然稳定,但在某些和弦的连接上可能会显得略微生硬。
2. 调音难度由于纯律的音高频率比不是等比关系,因此在乐器调音时,纯律的要求更为严格,难度也相对较大。
音阶与频率对应关系表

音阶与频率对应关系表一首音乐是许多不同的音阶组成的,而每个音阶对应着不同的频率,这样我们就可以利用不同的频率的组合,即可构成我们所想要的音乐了,当然对于单片机来产生不同的频率非常方便,我们可以利用单片机的定时/计数器T0来产生这样方波频率信号,因此,我们只要把一首歌曲的音阶对应频率关系弄正确即可。
现在以单片机12MHZ晶振为例,例出高中低音符与单片机计数T0相关的计数值如下表所示音符频率(HZ)简谱码(T值)音符频率(HZ)简谱码(T值)低1 DO 262 63628 # 4 FA# 740 64860#1 DO# 277 63731 中 5 SO 784 64898低2 RE 294 63835 # 5 SO# 831 64934 #2 RE# 311 63928 中 6 LA 880 64968 低 3 M 330 64021 # 6 932 64994低 4 FA 349 64103 中 7 SI 988 65030# 4 FA# 370 64185 高 1 DO 1046 65058低 5 SO 392 64260 # 1 DO# 1109 65085# 5 SO# 415 64331 高 2 RE 1175 65110低 6 LA 440 64400 # 2 RE# 1245 65134 # 6 466 64463 高 3 M 1318 65157低 7 SI 494 64524 高 4 FA 1397 65178中 1 DO 523 64580 # 4 FA# 1480 65198# 1 DO# 554 64633 高 5 SO 1568 65217中 2 RE 587 64684 # 5 SO# 1661 65235# 2 RE# 622 64732 高 6 LA 1760 65252 中 3 M 659 64777 # 6 1865 65268中 4 FA 698 64820 高 7 SI 1967 65283下面我们要为这个音符建立一个表格,有助于单片机通过查表的方式来获得相应的数据低音0-19之间,中音在20-39之间,高音在40-59之间TABLE: DW 0,63628,63835,64021,64103,64260,64400,64524,0,0DW 0,63731,63928,0,64185,64331,64463,0,0,0DW 0,64580,64684,64777,64820,64898,64968,65030,0,0DW 0,64633,64732,0,64860,64934,64994,0,0,0DW 0,65058,65110,65157,65178,65217,65252,65283,0,0DW 0,65085,65134,0,65198,65235,65268,0,0,0DW 02、音乐的音拍,一个节拍为单位(C调)曲调值DELAY 曲调值DELAY 调4/4 125ms 调4/4 62ms 调3/4 187ms 调3/4 94ms 调2/4 250ms 调2/4 125ms对于不同的曲调我们也可以用单片机的另外一个定时/计数器来完成。
钢琴的音高与频率对照表

z HK1 .1�022 音高女 �zH394�32 1 音低女 zH0021�061 区 音准基�z H293�28 音低�女 zH8 96�461 音高男 �zH394�32 1 音中男 z H325� 46 区 音准基�z H293� 28 音低�男 率频声人际实
果效色 音段率频各声人、二
。听难锐尖且而次层有没来起听 乐音 的你使会只这 �升提面全地味一是不而� 整调性应适互 相间之源声各是应作 工的做里 这在以所�音 声的出突为更 到听耳人让可升提的 段频 一这。锐尖变 会多过�度亮 加增可�升提的右左 Bd3 作 可�z HK4�2 。声属金生 产免以�升提 多过作不率频的点一 上以 z HK1 在但�音声 的器乐些某出 突可�升提内 Bd 6 在可�zHK2�008 。度 程薄厚的它吉 整调可时同� 暖温更鼓通�来出示 显司 贝使可�度力 曲乐加增可�升提的右左 B d5�3 作可�zH zh008�005 。 感暖温的声人加增可 Bd5�3 升 提 z H004 在。晰清得显 等镲、声人使可段频个 这减衰。感暖温 的它吉�感质木的鼓军加增也升提段频个这�zh00 4�002 。内 围范的 切低在应也声 人的段频一这。架打会不才 者两样这�鼓底 整调 z H052 和 z H00 1 在�司贝升 提间之 z H 007~053 在欢喜人各我。觉 感的胸击的鼓底 和度满丰加增 可�升提做里这在�点频要主的 ssaB�z H001 。段 手测检的错不种一是也放播中机音 录带磁、机 DC 的同不在�带磁、 DC 成做果 结的好整调终最把而 。准标为此以 并�析分行进率 频之对�里盘硬在放 EVA W 的片唱的错不为 认己自把以可 你�果结的好更 到得了为�的须必是对决说来作工 音混和 音录对�箱音听监业专的滑 平线曲应响率频对一 �系 关的大很有也箱音听监的你 和果结的好到 得能否是作工 的做里这�意注 。内围范的 切低在应段频 一这理处的声人对意 注时同。沌混会多过�多过 要不但�力撼振加增可升提略�段频的力有劲强的 鼓底的到听所 外吧的在们我 是正段频一这�z H08�03 �式 方理处的段频各、三 .度懂可 和度晰清的音 语了响影地重严�音声的振 共频低的嗡嗡种一生 产会� 强过率频段这 果如而�虚空 得变会色音�乏缺率 频段 这果如�受感 的中之厅大于 身置种一生产人使会�分充 的现表率频段这果如 。率频 振谐的堂厅或 间房是率频段 这。上以率频段这在 多大音基的 音乐为因是这� 感间空的色音 响影率频段这�率频 z H06�zH02 。觉感的声 鸣轰 有�声振共频 低现出会色音 �强过率频段这果如而�力 无得变会色音�足不 率频段这 果如。强感厚 混、实厚得显 会色音�满丰很率频 段这果如 。区音基的音低是�感厚混 的音声响影率频 段这�z H001�zH06 。差变 度晰清的音语�浊浑 得显 会将色音�强过分成率频段 这果如�白苍 、薄单得变会 色音�少缺分成率频 段这果 如�感厚混、感间空的鸣共 间房种一生产会就� 强增分成率频段 这果如。度满 丰的色音响影率 频段这�率频 z H051�z H001 。 色特有没且�然自不 而硬生 得变会音声� 强过分成率频 段这果如�绵绵软得 变会 则音语�飘发 、软发得显会 色音�乏缺分成率频段这果 如。率频音根的弦和 中音乐 是也时同�率频音基频低的 音声声男是率频段这 。度力的音声声 男是其尤�度 力的音声响影率 频段这�率频 z H003�z H051 。调单很得显�样一 色音的 音声中话 电像 成变会音语� 了少也分成频高�了 少分 成频低说来对 相�调单得变 会色音�强过度幅率频段这 果如�实坚不、洞空 得显会 音声�足不度幅率频段这果 如。度力有音语�满 丰度幅的率频段 这。率频区音 要主的音语是率 频段这�率频 z H005�z H003 。受感觉听的耳 人人进 前提种一生产 音语使�觉感 的出凸前向种一生产 会就 音语�强过率 频段这果如� 感缩收种一生产会音语�足 不度幅率频段这果如 � 好感 体 整 �朗 明廓轮的声人�满丰率频段这果 如。围范 率频的要 重个一是�域区率 频音基的声人 是率频段这�率频 zHK1�z H005 。用 使慎谨要�"率频 险危"为称 率频个这把师响音�此因。感 美色音掉 失、性个的音 语掉失会则�了多过分成 音喉的中色音 果如�音喉的定一 有 都人人�腔 喉个一有都人 人。感音喉 生产会则�了多过 率频个这果如而�显明就分成频低�了 出突现表性特分成的下以 z H008 是就也 �弛松得 显会将色音� 足不率频个这 果如�力有劲强得显 会 色音�满丰率 频个这果如。度 力的色音响影 度幅率频个这�率频 z H008 。感跃跳有 则色音 �强过率频段 这果如�节脱 色音且散松则色音� 乏缺率频段 这果如。强感畅 顺�显明感透 通围范率频段这�率频 z HK2�K1 .然自不、硬发、 板呆 得显会就色音 �强过分成率 频段这果如而 �胧胧朦朦得变会将色音则�足不 度幅率 频段这果如� 强增会度亮明 的色音则�富丰分成 率频段这果 如�段频的感敏 最度亮明音声 响影是率频段这�率频 z HK3�K2
各个音阶的对应频率

各个音阶的对应频率各个音阶的对应频率我刚刚知道了6对应的是440赫兹,那么1,2,3,4.5,7,高音1,23,4,什么的,总之希望得到钢琴全部键位对应的频率音名 A2 #A2 B2频率 27.5 29.1 30.9音名 C1 #C1 D1 #D1 E1 F1 #F1 G1 #G1 A1 #A1 B1频率 32.7 34.6 36.7 38.9 41.2 43.7 46.2 49.0 51.9 55.0 58.3 61.7 音名 C #C D #D E F #F G #G A #A B频率 65.4 69.3 73.4 77.8 82.4 87.3 92.5 98.0 103.8 110.0 116.5 123.5音名 c #c d #d e f #f g #G a #a b频率 130.8 138.6 146.8 155.6 164.8 174.6 185.0 196.0 207.7 220.0 233.1 246.9音名 c1 #c1 d1 #d1 e1 f1 #f1 g1 #g1 a1 #a1 b1频率 261.6 277.2 293.7 311.1 329.6 349.2 370.0 392.0 415.3 440.0 466.2 493.9音名 c2 #c2 d2 #d2 e2 f2 #f2 g2 #g2 a2 #a2 b2频率 523.3 554.4 587.3 622.3 659.3 698.5 740.0 784.0 830.6 880.0 932.3 987.8音名 c3 #c3 d3 #d3 e3 f3 #f3 g3 #g3 a3 #a3 b3频率 1047 1109 1175 1245 1319 1397 1480 1568 1661 1760 1865 1976音名 c4 #c4 d4 #d4 e4 f4 #f4 g4 #g4 a4 #a4 b4频率 2093 2217 2349 2489 2637 2794 2960 3136 3322 3520 3729 3951音名 c5频率4186以上为钢琴88个音对应的频率,需要注意的是十二平均律定律的乐器包括钢琴,吉他等所有半音的频率之比均为十二次根号2,是一个无理数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
音高和频率转换表中央C之上的A作为440 Hz时,中央C的频率约赫兹。
详见音高(pitch)。
另外,如果以纯律计算,中央C的频率是2 61HZ。
一些解释:Octave 0-9 表示八度区。
C-D-E-F-G-A-B 为 C 大调七个主音:do re mi fa so la si(简谱记为 1 到 7)。
科学音调记号法(scientific pitch notation)就是将上面这两者合在一起表示一个音,比如 A4 就是中音 la,频率为 440 Hz。
C5 则是高音 do(简谱是 1上面加一个点)。
升一个八度也就是把频率翻番。
A5 频率 880 Hz,正好是 A4 的两倍。
一个八度区有 12个半音,就是把这两倍的频率间隔等比分为 12,所以两个相邻半音的频率比是 2 开 12次方,也即大约。
这种定音高的办法叫做 twelve-tone equal temperament,简称 12-TET。
两个半音之间再等比分可以分 100 份,每份叫做一音分(cent)。
科学音调记号加上音分一般足够表示准确的音高了。
比如 A4 +30 表示比 440 Hz 高 30 音分,可以算出来具体频率是 Hz。
A4 又称 A440,是国际标准音高。
钢琴调音师或者大型乐队乐器之间调音都用这个频率。
C4 又称 Middle C,是中音八度的开始。
有一种音高标定方法是和 C4 比较相隔的半音数,比方 B4 就是 +11,表示比 C4 高 11 个半音。
MIDI note number p 和频率 f 转换关系:p = 69 + 12 x log2(f/440)。
这实际上就是把C4 定为 MIDI note number 60,然后每升降一个半音就加减一个号码。
可以看到 E-F 和 B-C 的间隔是一个半音,而七个主音别的间隔都是两个半音,也叫一个全音。
标准钢琴琴键有大有小,大的白色琴键是主音,小的黑色琴键是主音升降一个半音后的辅音(图)。
一般钢琴是 88 个琴键,从 A0 到 C8。
知道了上面这些,看到钢琴键盘应该就马上能找到 Middle C 了,如下音高间隔(音程)有各类说法,某些间隔的两个音同时发出来会比较令人身心愉快,比如频率比 3:2 的 perfect fifth 在各类乐曲都会广泛用作和弦。
具体音高间隔名称:间隔半音数间隔名大致频率比0perfect unison 完全一度1:11minor second 小二度16:152major second 大二度9:83minor third 小三度6:54major third 大三度5:45perfect fourth 完全四度4:36augmented fourth 增四度 45:32diminished fifth 减五度64:457perfect fifth 完全五度3:28minor sixth 小六度8:59major sixth 大六度5:310minor seventh 小七度16:911major seventh 大七度15:812perfect octave 完全八度2:1人的听觉和很多音乐设备的频率范围是 20 Hz – 20000 Hz,但是成年人一般只能听到 30– 15000 Hz,所以上面表格的频率范围已经足够用了。
音高和频率(二)乐理2009-11-01 16:29 阅读51 评论0字号:大中小上次说到现在最通用的音阶是把一个八度的倍频等比分为 12 份,那么为什么要这么做呢?在开始讲这个之前,先看两条人民群众总结的规律:人耳对音高的感觉主要取决于频率比,而不是频率差。
比如 220 Hz 到 440 Hz 的音差,和 440 Hz 到 880 Hz 的音差,一般人认为是一样大的音差。
如果两个音的频率比值很接近小整数比,那么这两个音同时发出来人会感觉很和谐。
比如440 Hz 和 660 Hz 的两个音,频率比值是 2:3,一般叫做完全五度,同时发出来很和谐。
至于为什么有以上的规律,这个问题太深刻了,折磨了一代又一代的音乐家、数学家、物理学家、心理学家、生理学家、哲学家……这里不深入说了,就把它们当作公理好了。
下面是某个测试人对各种频率比评价的结果,峰越高表示人觉得越和谐。
可以看见,1:1 1:2 是很和谐的,接下来是 2:3 3:5 3:4 等小整数比。
(这张图的出处不祥,应该是某个论文或者教科书。
)有了上述公理,怎么样来定音阶?早在公元前,伟大的毕达哥拉斯就发现了小整数频率比很和谐的规律。
首先最简单的整数比是 1:2,接下来分别是 2:3 和 3:4,于是他先定出四个音(按照现在的写法):F: C=4:3,G:C=3:2,高八度C’:C=2:1。
然后他把 F 和 G 之间的间隔 9:8 叫做一个全音,按照 9:8 全音间隔填补空档他定下来这样的音阶:C:C = 1:1 =D:C = 9:8 =E:C = 81:64 =F:C = 4:3 =G:C = 3:2 =A:C = 27:16 =B:C = 243:128 =C’:C = 2:1 =可以看到 E:F 和B:C’ 之间的间隔是 256:243 = ,差不多是 9:8 的一半,毕达哥拉斯把这种间隔叫做半音。
这样定出来的音阶其实已经蛮好用的了,现在把这种用整数比定音的方法叫做纯律(just in tonation)。
纯律的主要问题是有些音之间的比例很古怪,比如上面的 F:D 是 32:27,非常不和谐。
另外,巴赫同学后来出了各种奇怪变调的钢琴曲,而纯律变调之后音阶就变了,于是巴赫就开始鼓吹当时已经建立起来的平均律(equal temperament)了。
平均律沿用了这种七个基本音的全音阶(diatonic scale)系统,但是让全音刚好等于两个半音,这样无论如何变调,整个音阶只要偏移一下即可,而各个音之间音程不变。
我们知道,一个八度之间是 5 个全音间隔 + 2 个半音间隔,也就是 12 个半音间隔,于是就一刀切,直接把 2 等比分 12 份就是半音间隔了。
下面是十二平均律(12-TET)和毕达哥拉斯的纯律的对比:音程纯律十二平均律C:CD:CE:CF:CG:CA:CB:CC’:C可以看到,十二平均律和纯律很接近,特别是 F:C 完全四度和 G:C 完全五度非常接近应有的整数比4:3 和 3:2,只相差 2 个音分(cents)。
一般没有受过音乐训练的人对 20 音分以下的音差已经不敏感;即使专业调音师,不靠仪器的话 5 个音分也基本是分辨极限了。
所以在实际使用中,十二平均律对完全五度这么小的误差是完全可以忽略的。
理论上说,如果把 2 等比分为别的份数,也可以制造出可用的音阶。
一个例子是等比分为 29 份,这样出来的音阶比 12-TET 更接近 3:2,但是大三度 5:4 却惨不忍睹,相差很大。
一个小细节是有些音程是互补的,比如某个平均律如果很接近 G:C 3:2 完全五度,那么C’:G 4:3 完全四度也同时被搞定。
一般人们评价一个平均律,主要看它和大三度、完全五度、大六度的偏差总和(同时搞定的互补音程为小六度、完全四度、小三度),计算表明,比十二平均律更好的下一个音律是十九平均律,接下去更好的分别是 31、34 和 53。
可以想象,即使是十九平均律,钢琴键盘也会复杂很多,而且由于多了很多音,不和谐的音高组合也会更多,所以非十二等分的平均律使用很有限,现在一般只局限在理论研究上。
中国古代各类弦乐器五声音阶宫商角徵羽按照五度相生律定音,演奏起来非常优美。
五度相生律可以算是纯律的一种,中国人发现这个小整数比的规律应该比毕达哥拉斯早好多年。
不过到了现代,特别是键盘乐器的普及以及大型乐队的配合需要,最后还是十二平均律胜出了。
音高和频率(三)乐理2009-11-01 16:35 阅读37 评论0字号:大中小为什么小整数频率比的两个音比较和谐?这个问题,要从乐音的谐波说起。
一般乐器发出的音都不是纯频率的音,而是由好多谐波(harmonic)组成的;其中频率最低的那个通常最强,叫做基音。
比如小提琴发出音高 A4 的音,指的就是其基音是 440 Hz,而声波频谱里面同时有二次谐波 880 Hz、三次谐波 1320 Hz、四次谐波……等等。
不同乐器发出的声音,其谐波强度分布往往完全不同,因此音色(timbre)也就不同(比如高谐波强的话听起来就亮一些)。
乐音含有谐波这个特性和小整数比的和音规则有什么关系?以完全五度举例,A4 和 E5 的两个乐音,频率比为 2:3,而A4 的三次谐波和 E5 的二次谐波刚好重合,都是 1320 Hz。
相隔完全五度的两个乐音同时听起来比较好听,是不是因为它们大部分的谐波都重合了?于是就有科学家做实验了。
人们发现,把纯频率的音(不含谐波)A4 和 E5 同时发出来听并不怎么好听。
还有人用电脑制作了扭曲的乐音,把 N 次谐波搞成 N log/log(2)倍(谐波从 2 倍拉宽到倍,自然界是没有这种声音的),然后发现谐波重合的扭曲乐音同时听起来还比较和谐,而它们的基音却不是小整数比了。
还有一些别的实验,但是结论都是差不多的,就是两个乐音和谐主要是因为他们的谐波重合,转换为数学语言,就是基音必须是小整数比。
为啥谐波重合就好听呢?这是因为,如果谐波不重合但是距离很近,它们就会干涉形成低频率的拍(b eat),这种低频拍音嗡嗡作响,非常难听。
两个频率距离多近才会形成不好听的拍?人们一般把这个临界距离叫做临界频宽(critical bandwidth),处于临界频宽之内的两个频率就会互相干涉。
这个临界频宽本身是频率的函数,频率越高,临界频宽带也就越宽,如下图所示:可以看到,临界频宽在低频区是 100 Hz 左右;高频区大约是本身频率的 1/6。
比如,900 Hz 的临界频宽是 150 Hz,这就是说,750 – 1050 Hz 频率范围内的音都会和 900 Hz 的音干涉。
用音乐术语,1/6 频宽介于大二度和小三度之间(上图所示 2&3 semitones 之间),所以在高频区域里,间隔一个或者两个半音的音就会相互干涉形成不愉悦的拍。
