音高和频率转换表讲解学习

合集下载

音高和频率转换表

音高和频率转换表中央C之上的A作为440 Hz时，中央C的频率约赫兹。

详见音高（pitch）。

另外，如果以纯律计算，中央C的频率是2 61HZ。

一些解释：Octave 0-9 表示八度区。

C-D-E-F-G-A-B 为 C 大调七个主音：do re mi fa so la si（简谱记为 1 到 7）。

科学音调记号法（scientific pitch notation）就是将上面这两者合在一起表示一个音，比如 A4 就是中音 la，频率为 440 Hz。

C5 则是高音 do（简谱是 1上面加一个点）。

升一个八度也就是把频率翻番。

A5 频率 880 Hz，正好是 A4 的两倍。

一个八度区有 12个半音，就是把这两倍的频率间隔等比分为 12，所以两个相邻半音的频率比是 2 开 12次方，也即大约。

这种定音高的办法叫做 twelve-tone equal temperament，简称 12-TET。

两个半音之间再等比分可以分 100 份，每份叫做一音分（cent）。

科学音调记号加上音分一般足够表示准确的音高了。

比如 A4 +30 表示比 440 Hz 高 30 音分，可以算出来具体频率是 Hz。

A4 又称 A440，是国际标准音高。

钢琴调音师或者大型乐队乐器之间调音都用这个频率。

C4 又称 Middle C，是中音八度的开始。

有一种音高标定方法是和 C4 比较相隔的半音数，比方 B4 就是 +11，表示比 C4 高 11 个半音。

MIDI note number p 和频率 f 转换关系：p = 69 + 12 x log2(f/440)。

这实际上就是把C4 定为 MIDI note number 60，然后每升降一个半音就加减一个号码。

可以看到 E-F 和 B-C 的间隔是一个半音，而七个主音别的间隔都是两个半音，也叫一个全音。

标准钢琴琴键有大有小，大的白色琴键是主音，小的黑色琴键是主音升降一个半音后的辅音（图）。

音调与频率知识点

音调与频率知识点音调与频率是音乐和声音学中的重要概念，它们之间存在着密切的关系。

音调是对音高的主观感受，而频率则是对声波振动快慢的客观描述。

本文将从基本概念、计算公式、影响因素等方面，逐步解析音调与频率之间的关系。

一、基本概念音调是人们对于音高的感知和理解。

一般来说，音调越高，人们感觉到的音高就越高，反之亦然。

音调通常用相对音高的概念来描述，即高音、中音和低音。

在乐谱上，高音一般用大字谱号表示，中音用大、小字谱号表示，低音则用小字谱号表示。

频率是指单位时间内振动的次数，通常用赫兹（Hz）来表示。

一个物体振动的频率越高，产生的声音就越高。

频率与音调之间存在着直接的关系，即频率越高，则对应的音调感知越高。

二、计算公式音调和频率之间存在着具体的数学关系。

一般来说，音调与频率之间的转换可以使用以下的计算公式：频率（Hz）= 440 × 2^((n-49)/12) 其中，n代表音符在音阶上的位置，以A4音为标准音，其频率为440Hz。

通过这个公式，我们可以通过给定的音调，计算出对应的频率。

三、影响因素影响音调和频率的因素有很多，下面列举几个主要的因素：1.音源本身的物理属性：不同的乐器和声音源具有不同的频率特征，这是由其结构和振动方式所决定的。

例如，钢琴和吉他的频率分布是不同的，因此它们在演奏同一音符时所产生的音调也会有所不同。

2.音调的调性：不同的调性对应着不同的音阶，因此在不同的调性下，相同的音符对应的频率也会有所差异。

3.环境的影响：环境中的声音反射和吸收会对声音的频率产生影响。

例如，声音在密闭空间中会产生共鸣效应，使得声音的频率特征更加明显。

4.个人听觉差异：每个人的听觉灵敏度和感知能力都存在差异，因此对于相同频率的声音，不同的人可能会有不同的音调感受。

综上所述，音调与频率之间存在着紧密的关系。

音调是人们对于声音高低的主观感受，而频率则是对声波振动快慢的客观描述。

通过计算公式和影响因素的分析，我们可以更好地理解音调与频率之间的相互关系。

声音的频率与音高了解声音的频率与音高的关系

声音的频率与音高了解声音的频率与音高的关系声音的频率与音高：了解声音的频率与音高的关系声音在我们的日常生活中扮演着至关重要的角色。

从我们说话、听音乐到听到远处传来的汽车喇叭声，声音无处不在。

然而，你是否曾思考过声音的频率与音高之间的关系？本文将探讨声音的频率与音高之间的关系，并带您对声音的奥秘有更深入的了解。

首先，我们来了解声音频率的概念。

声音的频率是指声波振动的频率，即单位时间内声波通过某一点的次数。

频率的单位通常用赫兹（Hz）来表示，即每秒内的振动次数。

一般来说，当频率较低时，声音听起来较低沉，而当频率较高时，声音听起来较尖锐。

那么，声音的频率与音高之间是否存在关联呢？答案是肯定的。

频率越高，我们所感知到的音高就越高。

这是因为当声波振动频率增加时，它们以更快的速度进入我们的耳朵，耳膜也会更快地振动，从而产生了高音。

相反，频率较低的声音听起来较低，因为它们以较慢的速度进入我们的耳朵。

此外，我们可以借助一些具体的例子来解释声音的频率与音高之间的关系。

想象一下，当您拉紧吉他的琴弦时，琴弦振动的频率会增加，进而发出更高的音高。

同样的道理，当您放松琴弦时，频率减小，音高也随之降低。

这就是为什么在音乐演奏中，不同的琴弦被调整到不同的频率，以便产生所需的音高。

了解声音频率与音高之间的关系对于语言和交流也具有重要意义。

一般来说，男性声音通常低沉，频率较低；而女性声音则更高亢，频率较高。

因此，在辨认性别时，声音频率起到了关键作用。

除了频率外，声音的音量也是一个重要的因素。

音量是指声音的强度或振幅，通常以分贝（dB）来衡量。

较高的音量表示声音更强烈，而较低的音量则表示声音较弱。

虽然音量与音高没有直接关系，但与音高一起影响了我们对声音的感知。

最后，虽然我们能够感知并区分不同的音高，但是世界上的声音其实是由无数不同频率的声波叠加而成的。

这些声波在我们的耳朵中被解释为不同的音调和音高，使我们能够分辨不同的乐器、声音和语音。

钢琴的音高与频率对照表

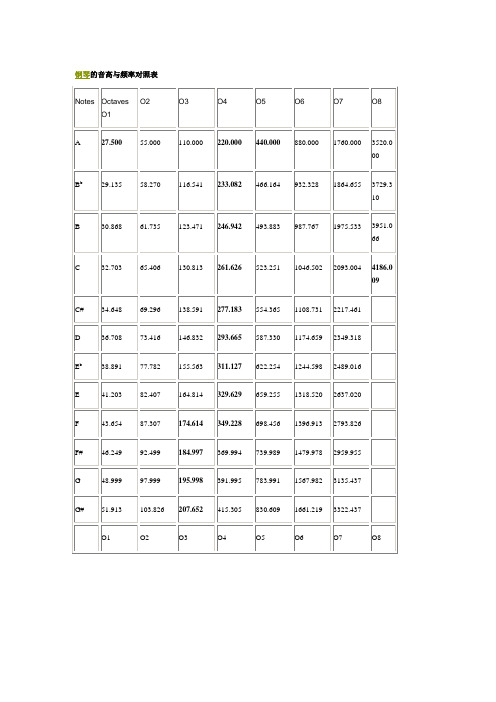
十二音律(twelve pitches of the temperament octave)用绿色标注。

此表通过连续的乘法每次乘1.0594 631得出的结果(2的十二次方)。

调音参考频率(A-440)为紫色标注。

最低频率用红色标注，最高频率用蓝色标注。

（上面的频率表是google上找来的，转帖，致谢！）
各音频率的计算
小字1组的A音（简谱的6=啦）是440Hz，国际标准。

把A4=440 乘以1.0594631 就是A#4=466.164,
再把A#4 X 1.0594631=493.883=B4.
往下440 除以1.0594631就得到G#4
这样就可以计算出88个音的各自频率.
任意相临两音的比值永远是1.0594631, 为什么?
它是2的开12次方, 这就是十二平均律!
Tunelab 软件中把88键钢琴最左边的音叫A0, 最低的C叫C1, 以后顺序为C#1, D1, D#1,.......中央C 叫C4.
调律的标准音是小字1组的A音,叫A4=440赫兹。

钢琴的音高与频率对照表

钢琴的音高与频率对照表十二音律(twelve pitches of the temperament octave)用绿色标注。

此表通过连续的乘法每次乘1.0594631得出的结果(2的十二次方)。

调音参考频率(A-440)为紫色标注。

最低频率用红色标注，最高频率用蓝色标注。

一、人声及各乐器频率范围表实际人声频率男：低音82～392Hz，基准音区64～523Hz男中音123～493Hz，男高音164～698Hz女：低音82～392Hz，基准音区160～1200Hz女低音123～493Hz，女高音220～1.1KHz录音时各频率效果男歌声150Hz~600Hz影响歌声力度，提升此频段可以使歌声共鸣感强，增强力度。

女歌声1.6~3.6KHz影响音色的明亮度，提升此段频率可以使音色鲜明通透。

语音800Hz是“危险”频率，过于提升会使音色发“硬”、发“楞”沙哑声提升64Hz~261Hz会使音色得到改善。

喉音重衰减600Hz~800Hz会使音色得到改善鼻音重衰减60Hz~260Hz，提升1~2.4KHz可以改善音色。

齿音重6KHz过高会产生严重齿音。

咳音重4KHz过高会产生咳音严重现象（电台频率偏离时的音色）乐器重要频率范围表：贝司：低音吉它：频响在700～1KHz之间，提高拨弦音为60～80Hz电贝司：低音在80～250Hz，拨弦力度在700～1KHz吉它：电吉它：65～1.7KHz，响度在2.5KHz，饱满度在240Hz 木吉它：低音弦：80～120Hz，琴箱声：250Hz，清晰度：2.5KHz、3.75KHz、5KHz鼓：低音鼓：27～146Hz，低音：60～80Hz，敲击声：2.5KHz 小鼓：饱满度：240Hz，响度：2KHz通通鼓：丰满度：240Hz，硬度：8KHz地筒鼓：丰满度：80～120Hz吊钗：130～2.6KHz，金属声：200Hz，尖锐声：7.5～10KHz，镲边声：12KHz手风琴：饱满度：240Hz钢琴：低音在80～120Hz，临场感2.5～8KHz，声音随频率的升高而变单薄二、人声各频率段音色效果2K～3KHz频率：这段频率是影响声音明亮度最敏感的频段，如果这段频率成分丰富，则音色的明亮度会增强，如果这段频率幅度不足，则音色将会变得朦朦胧胧；而如果这段频率成分过强，音色就会显得呆板、发硬、不自然.1K～2KHz频率：这段频率范围通透感明显，顺畅感强。

纯律与十二平均律音高频率表(对比)

纯律与十二平均律音高频率表（对比）一、纯律音高频率表纯律是一种基于自然泛音列的音律系统，其音高频率关系如下：1. 基音（C）频率：f2. 纯一度（C）频率：f 1.06783. 纯二度（D）频率：f 1.12254. 纯小三度（D）频率：f 1.18925. 纯大三度（E）频率：f 1.25996. 纯四度（F）频率：f 1.33487. 纯增四度（F）频率：f 1.41428. 纯五度（G）频率：f 1.49839. 小六度（G）频率：f 1.587410. 大六度（A）频率：f 1.681811. 小七度（A）频率：f 1.781812. 大七度（B）频率：f 1.887713. 纯八度（C）频率：f 2二、十二平均律音高频率表十二平均律是一种将一个八度等分为十二个半音的音律系统，其音高频率关系如下：1. 基音（C）频率：f2. 半音（C）频率：f 1.05953. 全音（D）频率：f 1.12254. 半音（D）频率：f 1.18925. 全音（E）频率：f 1.25996. 半音（F）频率：f 1.33487. 全音（F）频率：f 1.41428. 半音（G）频率：f 1.49839. 全音（G）频率：f 1.587410. 半音（A）频率：f 1.681811. 全音（A）频率：f 1.781812. 半音（B）频率：f 1.887713. 八度（C）频率：f 2通过对比纯律与十二平均律音高频率表，我们可以发现两者在音高频率上的差异。

纯律更接近自然泛音列，而十二平均律则在演奏和调音方面具有更高的便利性。

三、纯律与十二平均律的差异分析1. 音色和谐度纯律由于其音高频率比是根据自然泛音列得出的，因此在和弦的和谐度上更为优越。

尤其是在和声进行中，纯律能够展现出更加丰满、自然的音色效果。

相比之下，十二平均律的和声效果虽然稳定，但在某些和弦的连接上可能会显得略微生硬。

2. 调音难度由于纯律的音高频率比不是等比关系，因此在乐器调音时，纯律的要求更为严格，难度也相对较大。

音阶与频率的转换

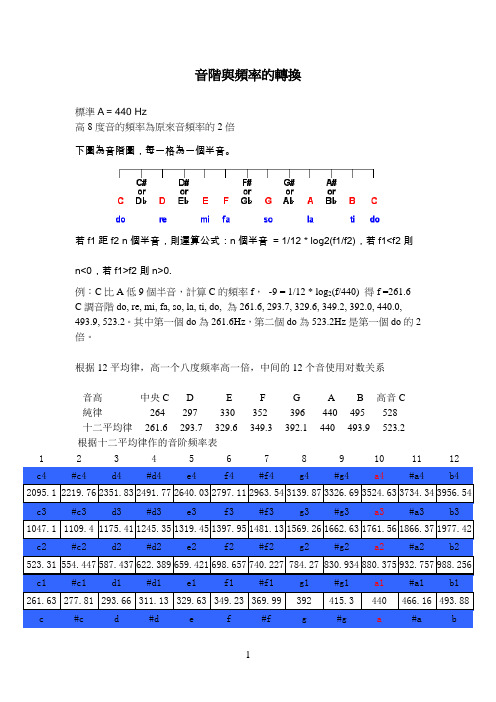
音階與頻率的轉換標準A = 440 Hz高8度音的頻率為原來音頻率的2倍下圖為音階圖，每一格為一個半音。

若f1距f2 n個半音，則運算公式：n個半音= 1/12 * log2(f1/f2)，若f1<f2則n<0，若f1>f2則n>0.例：C比A低9個半音，計算C的頻率f，-9 = 1/12 * log2(f/440) 得f =261.6C調音階do, re, mi, fa, so, la, ti, do, 為261.6, 293.7, 329.6, 349.2, 392.0, 440.0,493.9, 523.2。

其中第一個do為261.6Hz，第二個do為523.2Hz是第一個do的2倍。

根据12平均律，高一个八度频率高一倍，中间的12个音使用对数关系音高中央C D E F G A B 高音C純律264 297 330 352 396 440 495 528十二平均律261.6 293.7 329.6 349.3 392.1 440 493.9 523.2根据十二平均律作的音阶频率表1 2 3 4 5 6 7 8 9 10 11 12ViewX 音階頻率表音階Octave0 Octave1 Octave2 Octave3Do C 262 523 1047 2093Db 277 554 1109 2217Re D 294 587 1175 2349Eb 311 622 1245 2489Mi E 330 659 1329 2637Fa F 349 698 1397 2794Gb 370 740 1480 2960Sol G 392 784 1568 3136Ab 415 831 1661 3322La A 440 880 1760 3520Bb 466 923 1865 3729Si B 494 988 1976 39512007-08-03 20:43一拍= 四分音符，若建議速度=120(BPM)，則表示一秒= 兩拍= 兩個四分音符，若建議速度=60(BPM)，則表示一秒= 一拍= 一個四分音符。

音乐中的各音阶与频率的关系

音乐中的各音阶与频率的关系标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]音乐中的各音阶与频率的关系--十二平均律zz2009-09-18 14:46“律”，即“音律”（intonation），指为了使音乐规范化，人们有意选择的一组高低不同的音符所组成的体系，以及这些音符之间的相互关系。

比如大家都知道的do、re、mi、fa、so、la、si，这7个音符就组成了一组音律。

研究音律的学问叫做“律学”。

也就是研究为什么要选择do、re、mi……这7个音（当然也可以选择其它音）作为规范、这些被当成“标尺”的音是怎么产生的、以及它们之间到底是什么关系的学问。

对于任何民族来说，只要他们有着丰富的音乐体验，只要他们想积累起关于音乐的知识，迟早都会遇到关于律学的问题。

令人惊讶的是，古今不同民族，虽然各自钟爱的音乐形式可谓万紫千红、百花争艳，彼此也没有互相借鉴，但大家的律学的基础概念却出奇地相似。

这也许是音乐本身超文化、超地域的魅力所致吧。

（BTW：现代人学习的do、re、mi、fa、so、la、si，这些好像没有意义的单词，其实都是中世纪时西方教会中很流行的一些拉丁文圣咏（chant）的首音节。

这些圣咏是西方现代音乐的源头。

）学过高中物理的都知道，声音的本质是空气的振动。

而空气的振动是以波的形式传播的，也就是所谓的声波。

所有的波（包括声波、电磁波等等）都有三个最本质的特性：频率／波长、振幅、相位。

对于声音来说，声波的频率（声学中一般不考虑波长）决定了这个声音有多“高”，声波的振幅决定了这个声音有多“响”，而人耳对于声波的相位不敏感，所以研究音乐时一般不考虑声波的相位问题。

律学当然不考虑声音有多“响”，所以律学研究的重点就是声波的频率。

一般来说，人耳能听到的声波频率范围是20HZ（每秒振动20次）到20000HZ（每秒振动20000次）之间。

声波的频率越大（每秒振动的次数越多），听起来就越“高”。

音乐中的各音阶与频率的关系

精心整理音中的各音与率的关系-- 十二均匀律 zz2009-09-1814:46“律”，即“乐律”（ intonation），指了使音范化，人存心的一高低不同的音符所成的系统，以及些音符之的相互关系。

比方大家都知道的do、re 、mi、fa 、so、la 、si ， 7 个音符就成了一乐律。

研究乐律的学叫做“律学”。

也就是研究什么要 do、re 、mi⋯⋯ 7 个音（自然也能够其余音）作范、些被当作“ 尺”的音是怎么生的、以及它之究竟是什么关系的学。

于任何民族来，只需他有着丰富的音体，只需他想累起对于音的知，早都会碰到对于律学的。

令人惊的是，古今不同民族，然各自的音形式可万紫千、百花争，相互也没有相互借，但大家的律学的基观点却出奇地相像。

也是音自己超文化、超地区的魅力所致吧。

（BTW：代人学的 do、re 、mi、fa 、so、la 、si ，些仿佛没存心的，其都是中世西方教会中很流行的一些拉丁文圣咏（ chant ）的首音。

些圣咏是西方代音的源。

）学高中物理的都知道，声音的本是空气的振。

而空气的振是以波的形式播的，也就是所的声波。

所有的波（包含声波、磁波等等）都有三个最本的特征：率／波、振幅、相位。

于声音来，声波的率（声学中一般不考波）决定了个声音有多“高”，声波的振幅决定了个声音有多“响”，而人耳于声波的相位不敏感，因此研究音一般不考声波的相位。

律学自然不考声音有多“响”，因此律学研究的要点就是声波的率。

一般来，人耳能听到的声波率范是 20HZ（每秒振 20 次）到 20000HZ（每秒振 20000 次）之。

声波的率越大（每秒振的次数越多），听起来就越“高”。

率低于 20HZ的叫“次声波”，高于20000HZ的叫“超声波”。

（BTW：人耳能分辨的最小率差是 2HZ。

例而言就是，人能听出 100HZ和 102HZ 的声音是不同的，但听不出 100HZ和 101HZ的声音有什么不同。

此外，人耳在高音区的分辨能力快速降落，原由后。

音阶与频率对应关系表

音阶与频率对应关系表一首音乐是许多不同的音阶组成的，而每个音阶对应着不同的频率，这样我们就可以利用不同的频率的组合，即可构成我们所想要的音乐了，当然对于单片机来产生不同的频率非常方便，我们可以利用单片机的定时/计数器T0来产生这样方波频率信号，因此，我们只要把一首歌曲的音阶对应频率关系弄正确即可。

现在以单片机12MHZ晶振为例，例出高中低音符与单片机计数T0相关的计数值如下表所示音符频率（HZ）简谱码（T值）音符频率（HZ）简谱码（T值）低1 DO 262 63628 # 4 FA# 740 64860#1 DO# 277 63731 中 5 SO 784 64898低2 RE 294 63835 # 5 SO# 831 64934 #2 RE# 311 63928 中 6 LA 880 64968 低 3 M 330 64021 # 6 932 64994低 4 FA 349 64103 中 7 SI 988 65030# 4 FA# 370 64185 高 1 DO 1046 65058低 5 SO 392 64260 # 1 DO# 1109 65085# 5 SO# 415 64331 高 2 RE 1175 65110低 6 LA 440 64400 # 2 RE# 1245 65134 # 6 466 64463 高 3 M 1318 65157低 7 SI 494 64524 高 4 FA 1397 65178中 1 DO 523 64580 # 4 FA# 1480 65198# 1 DO# 554 64633 高 5 SO 1568 65217中 2 RE 587 64684 # 5 SO# 1661 65235# 2 RE# 622 64732 高 6 LA 1760 65252 中 3 M 659 64777 # 6 1865 65268中 4 FA 698 64820 高 7 SI 1967 65283下面我们要为这个音符建立一个表格，有助于单片机通过查表的方式来获得相应的数据低音0－19之间，中音在20－39之间，高音在40－59之间TABLE: DW 0,63628,63835,64021,64103,64260,64400,64524,0,0DW 0,63731,63928,0,64185,64331,64463,0,0,0DW 0,64580,64684,64777,64820,64898,64968,65030,0,0DW 0,64633,64732,0,64860,64934,64994,0,0,0DW 0,65058,65110,65157,65178,65217,65252,65283,0,0DW 0,65085,65134,0,65198,65235,65268,0,0,0DW 02、音乐的音拍，一个节拍为单位（C调）曲调值DELAY 曲调值DELAY 调4/4 125ms 调4/4 62ms 调3/4 187ms 调3/4 94ms 调2/4 250ms 调2/4 125ms对于不同的曲调我们也可以用单片机的另外一个定时/计数器来完成。

钢琴b调频率对照表

钢琴b调频率对照表钢琴是一种非常受欢迎的乐器，它的音色优美，演奏起来既能表达情感，又能展示技巧。

钢琴的音调是由琴弦的振动频率决定的，而不同的音调对应着不同的频率。

本文将为大家介绍钢琴b调的频率对照表，帮助大家更好地理解和掌握钢琴b调的音高。

在音乐理论中，b调是指从C音开始的自然音阶中的第七个音。

在钢琴上，钢琴b调的起始音是中央C下方的黑键B。

在国际音名中，b调被记为Bb，是指升半音。

钢琴b调频率对照表可以帮助我们了解每个音符对应的频率，从而更好地理解和演奏钢琴b调的乐曲。

下面是钢琴b调的频率对照表：1. Bb2：频率约为116.54 Hz2. C3：频率约为130.81 Hz3. Db3：频率约为138.59 Hz4. Eb3：频率约为155.56 Hz5. F3：频率约为174.61 Hz6. Gb3：频率约为185.00 Hz7. Ab3：频率约为207.65 Hz8. Bb3：频率约为233.08 Hz9. C4：频率约为261.63 Hz10. Db4：频率约为277.18 Hz11. Eb4：频率约为311.13 Hz12. F4：频率约为349.23 Hz13. Gb4：频率约为369.99 Hz14. Ab4：频率约为415.30 Hz15. Bb4：频率约为466.16 Hz以上是钢琴b调的频率对照表，每个音符都有其特定的频率。

通过掌握这些频率，我们可以更准确地演奏钢琴b调的音乐作品。

在演奏钢琴时，我们可以根据乐谱上的音符来确定正确的按键，并根据频率对照表来调整音高，使演奏的音乐更加准确和谐。

钢琴b调的音域较宽，可以演奏出不同音色和情感。

通过钢琴b调频率对照表，我们可以更好地理解和感受钢琴b调的音乐特点。

在演奏钢琴b调的乐曲时，我们可以根据频率对照表来调整手指的位置和力度，以达到更好的演奏效果。

钢琴b调的频率对照表是学习钢琴的重要参考资料之一。

通过熟练掌握频率对照表，我们可以更好地理解和演奏钢琴b调的音乐作品。

音乐中的各音阶与频率的关系

音乐中的各音阶与频率的关系--十二平均律zz2009-09-18 14:46“律”,即“音律”intonation,指为了使音乐规范化,人们有意选择的一组高低不同的音符所组成的体系,以及这些音符之间的相互关系;比如大家都知道的do、re、mi、fa、so、la、si,这7个音符就组成了一组音律;研究音律的学问叫做“律学”;也就是研究为什么要选择do、re、mi……这7个音当然也可以选择其它音作为规范、这些被当成“标尺”的音是怎么产生的、以及它们之间到底是什么关系的学问;对于任何民族来说,只要他们有着丰富的音乐体验,只要他们想积累起关于音乐的知识,迟早都会遇到关于律学的问题;令人惊讶的是,古今不同民族,虽然各自钟爱的音乐形式可谓万紫千红、百花争艳,彼此也没有互相借鉴,但大家的律学的基础概念却出奇地相似;这也许是音乐本身超文化、超地域的魅力所致吧;BTW：现代人学习的do、re、mi、fa、so、la、si,这些好像没有意义的单词,其实都是中世纪时西方教会中很流行的一些拉丁文圣咏chant的首音节;这些圣咏是西方现代音乐的源头;学过高中物理的都知道,声音的本质是空气的振动;而空气的振动是以波的形式传播的,也就是所谓的声波;所有的波包括声波、电磁波等等都有三个最本质的特性：频率／波长、振幅、相位;对于声音来说,声波的频率声学中一般不考虑波长决定了这个声音有多“高”,声波的振幅决定了这个声音有多“响”,而人耳对于声波的相位不敏感,所以研究音乐时一般不考虑声波的相位问题;律学当然不考虑声音有多“响”,所以律学研究的重点就是声波的频率;一般来说,人耳能听到的声波频率范围是20HZ每秒振动20次到20000HZ每秒振动20000次之间;声波的频率越大每秒振动的次数越多,听起来就越“高”;频率低于20HZ的叫“次声波”,高于20000HZ的叫“超声波”;BTW：人耳能分辨的最小频率差是2HZ;举例而言就是,人能听出100HZ和102HZ的声音是不同的,但听不出100HZ和101HZ 的声音有什么不同;另外,人耳在高音区的分辨能力迅速下降,原因见后;需要特别指出的是,人耳对于声波的频率是指数敏感的;打比方说,100HZ、200HZ、300HZ、400HZ……这些声音,人听起来并不觉得它们是“等距离”的,而是觉得越到后面,各个音之间的“距离”越近;100HZ、200HZ、400HZ、800HZ……这些声音,人听起来才觉得是“等距离”的为什么会这样我也不清楚;换句话说,某一组声音,如果它们的频率是严格地按照×1、×2、×4、×8……,即按2n的规律排列的话,它们听起来才是一个“等差音高序列”;比如这里有16个音,它们的频率分别是110HZ的1倍、2倍、3倍……16倍;大家可以听一下,感觉它们是不是音越高就“距离”越近;用音乐术语来说,这些音都是110HZ的“谐波”harmonics,即这些声波的频率都是某一个频率的整数倍;这个ogg文件可以用“暴风影音”／StormCodec软件来试听;由于人耳对于频率的指数敏感,上面提到的“×2就意味着等距离”的关系是音乐中最基本的关系;用音乐术语来说,×2就是一个“八度音程”octave;前面提到的do、re、mi中的do,以及so、la、si后面的那个高音do,这两个do之间就是八度音程的关系;也就是说,高音do的频率是do的两倍;同样的,re和高音re之间也是八度音程的关系,高音re的频率是re的两倍;而高音do上面的那个更高音的do,其频率就是do的4倍;也可以说,它们之间隔了两个“八度音程”;显然,一个音的所有“八度音程”都是它的“谐波”,但不是它的所有“谐波”都是自己的“八度音程”;很自然,用do、re、mi写的歌,如果换用高音do、高音re、高音mi来写,听众只会觉得音变高了,旋律本身不会有变化;这种等效性,其实就是“等差音高序列”的直接结果;“八度音程”的重要性,世界各地的人们都发现了;比如我国浙江的河姆渡遗址,曾经出土了一管距今9000年的笛子是用鹤的腿骨做的,它能演奏8个音符,其中就包含了一个八度音程;当然这个八度音程不会是do到高音do,因为只要是一个音的频率是另一个的两倍,它们就是八度音程的关系,和具体某一个音有多高没有关系;明白了八度音程的重要性,下面来介绍在一个八度音程之内,还有那些音是重要的;这其实是律学的中心问题;也就是说,如果某一个音的频率是F,那么我们要寻找F和2F之间还有那些重要的频率;如果大家有学习弦乐器比如吉它、古琴、小提琴的经验的话,都明白它们能发声是因为琴弦的振动;而琴弦的振动是和琴弦的长度有关系的;如果在一根弦振动的时候,用手指按住弦的中点,即让原来全部振动的弦,变成两根以1/2长度振动的弦,我们会听到一个比较高的音;这个音和原来的音之间就是八度音程的关系;因为在物理上,弦的振动频率和其长度是成反比的;由于弦乐器是世界各地发展得最早的乐器种类之一,所以这种现象古人早已熟悉;他们自然会想：如果八度音程的2:1的关系在弦乐器上用这么简单一按中点的方式就能实现,那么试试按其它的位置会怎么样呢数学上2:1是最简单的比例关系了,简单性仅次于它的就是3:1;那么,我们如果按住弦的1/3点,会怎么样呢其结果是弦发出了两个高一些的音;一个音的频率是原来的3倍因为弦长变成了原来的1/3,另一个音是原来的3/2倍因为弦长变成了原来的2/3;这两个音彼此也是八度音程的关系因为它们彼此的弦长比是2:1;这样,在我们要寻找的F～2F的范围内,出现了第一个重要的频率,即3/2F;那个3F的频率正好处于下一个八度,即2F～4F中的同样位置;接着再试,数学上简单性仅次于3:1的是4:1,我们试试按弦的1/4点会怎样又出现了两个音;一个音的频率是原来的4倍因为弦长变成了原来的1/4,这和原来的音术语叫“主音”是两个八度音程的关系,可以不去管它;另一个音的频率是主音的4/3倍因为弦长是原来的3/4;现在我们又得到了一个重要的频率,4/3F;同一根弦,在不同的情况下振动,可以发出很多频率的声音;在听觉上,与主音F最和谐的就是3/2F和4/3F除了主音的各个八度之外;这个现象也被很多民族分别发现了;比如最早从数学上研究弦的振动问题的古希腊哲学家毕达哥拉斯Pythagoras,约公元前6世纪;我国先秦时期的管子·地员篇、吕氏春秋·音律篇也记载了所谓“三分损益律”;具体说来是取一段弦,“三分损一”,即均分弦为三段,舍一留二,便得到3/2F;如果“三分益一”,即弦均分三段后再加一段,便得到4/3F;得到这两个频率之后,是否继续找1/5点、1/6点等等继续试下去呢不行,因为听觉上这些音与主音的和谐程度远不及3/2F、4/3F;实际上4/3F已经比3/2F的和谐程度要低不少了;古人于是换了一种方法;与主音F最和谐的3/2F已经找到了,他们转而找3/2F的3/2F,即与最和谐的那个音最和谐的音,这样就得到了3/22F即9/4F;可是这已经超出了2F的范围,进入了下一个八度;没关系,不是有“等差音高序列”吗在下一个八度中的音,在这一个八度中当然有与它等价的一个音,于是把9/4F的频率减半,便得到了9/8F;接着把这个过程循环一遍,找3/2的3次方,于是就有了27/8F,这也在下一个八度中,再次频率减半,得到了27/16F;就这样一直循环找下去吗不行,因为这样循环下去会没完没了的;我们最理想的情况是某一次循环之后,会得到主音的某一个八度,这样就算是“回到”了主音上,不用继续找下去了;可是3/2n,只要n是自然数,其结果都不会是整数,更不用说是2的某次方;律学所有的麻烦就此开始;数学上不可能的事,只能从数学上想办法;古人的对策就是“取近似值”;他们注意到3/25≈,和23＝8很接近,于是决定这个音就是他们要找的最后一个音,比这个音再高一点就是主音的第三个八度了;这样,从主音F开始,我们只需把“按3/2比例寻找最和谐音”这个过程循环5次,得到了5个音,加上主音和4/3F,一共是7个音;这就是为什么音律上要取do、re、mi等等7个音符而不是6个音符或者8个音符的原因;这7个音符的频率,从小到大分别是F、9/8F、81/64F、4/3F、3/2F、27/16F、243/128F; 如果这里的F是do,那么9/8F就是re、81/64F就是mi……,这7个频率组成了7声音阶;这7个音都有各自正式的名字,在西方音乐术语中,它们分别被叫做主音tonic、上主音supertonic、中音mediant、下属音subdominant、属音dominant、下中音submediant、导音leading tone;其中和主音关系最密切的是第5个“属音”so和第4个“下属音”fa,原因前面已经说过了,因为它们和主音的和谐程度分别是第一高和第二高的;由于这个音律主要是从“属音”so即3/2F推导出来的,而3/2这个比例在西方音乐术语中叫“纯五度”,所以这种音律叫做“五度相生律”;西方最早提出“五度相生律”的是古希腊的毕达哥拉斯所以西方把按3/2比例定音律的做法叫做Pythagorean tuning,东方是管子一书的作者不一定是管仲本人;我国历代的各种音律,大部分也都是从“三分损益律”发展出来的,也可以认为它们都是“五度相生律”;仔细看上面“五度相生律”7声音阶的频率,可以发现它们彼此的关系很简单：do～re、re～mi、fa～so、so～la、la～si 之间的频率比都是9:8,这个比例被称为全音tone；mi～fa、si～do 之间的频率比都是256:243,这个比例被称为半音semitone;“五度相生律”产生的7声音阶,自诞生之日起就不断被批评;原因之一就是它太复杂了;前面说过,如果按住弦的1/5点或者1/6点,得到的音已经和主音不怎么和谐了,现在居然出现了81/64和243/128这样的比例,这不会太好听吧于是有人开始对这7个音的频率做点调整,于是就出现了“纯律”just intonation;“纯律”的重点是让各个音尽量与主音和谐起来,也就是说让各个音和主音的频率比尽量简单;“纯律”的发明人是古希腊学者塔壬同今意大利南部的塔兰托城的亚理斯托森努斯Aristoxenus of Tarentum;东方似乎没有人独立提出“纯律”的概念;此人是亚理士多德的学生,约生活在公元前3世纪;他的学说的重点就是要靠耳朵,而不是靠数学来主导音乐;他的书籍现在留下来的只有残篇,不过可以证实的是他最先提出了所谓“自然音阶”;自然音阶也有7个音,但和“五度相生律”的7声音阶有不小差别;7个自然音阶的频率分别是：F、9/8F、5/4F、4/3F、3/2F、5/3F、15/8F;确实简单多了吧也确实好听多了;这么简单的比例,就是“纯律”;可以看出“纯律”不光用到了3/2的比例,还用到了5/4的比例;新的7个频率中和原来不同的就是5/4F、5/3＝5/4×4/3F、15/8＝5/4×3/2F;虽然“纯律”的7声音阶比“五度相生律”的7声音阶要好听,数学上也简单,但它本身也有很大的问题;虽然各个音和主音的比例变简单了,但各音之间的关系变复杂了;原来“五度相生律”7声音阶之间只有“全音”和“半音”2种比例关系,现在则出现了3种：9:8被叫做“大全音”,major tone,就是原来的“全音”、10:9被叫做“小全音”,minor tone、16:15新的“半音”;各位把自然音阶的频率互相除一下就能得到这个结果;更进一步说,如果比较自然音阶中的re和fa,其频率比是27/32,这也不怎么简单,也不怎么好听呢所以说“纯律”对“五度相生律”的修正是不彻底的;事实上,“纯律”远没有“五度相生律”流行;对于“五度相生律”的另一种修正是从另一个方向展开的;还记得为什么要取7个音符吗是因为3/25≈,和23＝8很接近;可这毕竟是近似值,而不是完全相等;在一个八度之内,这么小的差距也许没什么,但是如果乐器的音域跨越了好几个八度,那么这种近似就显得不怎么好了;于是人们开始寻找更好的近似值;通过计算,古人发现3/212≈,和27＝128很接近,于是他们把“五度相生律”中“按3/2比例寻找最和谐音”的循环过程重复12次,便认为已经到达了主音的第7个八度;再加上原来的主音和4/3F,现在就有了12个音符;注意,现在的“规范”音阶不是do、re、mi……等7个音符了,而是12个音符;这种经过修改的“五度相生律”推出的12声音阶,其频率分别是：F、2187/2046F、9/8F、19683/16384F、81/64F、4/3F、729/512F、3/2F、6561/4096F、27/16F、59049/32768F、243/128F;和前面的“五度相生律”的7声音阶对比一下,可以发现原来的7个音都还在,只是多了5个,分别插在它们之间;用正式的音乐术语称呼原来的7个音符,分别是C、D、E、F、G、A、B;新多出来的5个音符于是被叫做C读做“升C”、D、F、G、A;12音阶现在不能用do、re、mi的叫法了,应该被叫做：C、C、D、D、E、F、F、G、G、A、A、B;把相邻两个音符的频率互相除一下,就会发现它们之间的比例只有两种：256:243就是原来的“半音”,也叫做“自然半音”,2187:2048这被叫做“变化半音”;也就是说,这12个音符几乎可以说又构成了一个“等差音高序列”;它们之间的“距离”几乎是相等的;当然,如果相邻两个音符之间的比例只有一种的话,就是严格的“距离”相等了;原来的7声音阶中,C～D、D～E、F～G、G～A、A～B之间都相隔一个“全音”,现在则认为它们之间相隔了两个“半音”;这也就是“全”、“半”这种叫法的根据;既然C被认为是从C“升”了半音得到的,那么C也可以被认为是从D“降”了半音得到的,所以C和Db读做“降D”就被认为是等价的;事实上,5个新加入的音符也可以被写做：Db、Eb、Gb、Ab、Bb;这种12声音阶在音乐界的地位,我只用举一个例子就能说明了;钢琴上的所有白键对应的就是原来7声音阶中的C、D……B,所有的黑键对应的就是12声音阶中新加入的C、Eb……Bb;从7声音阶发展到12声音阶的做法,在西方和东方都出现得很早;管子中实际上已经提出了12声音阶,后来的中国音律也大多是以“五度相生律”的12声音阶为主;毕达哥拉斯学派也有提出这12声音阶的;不过西方要到中世纪晚期才重新发现它们;能不能把“五度相生律”的12声音阶再往前发展一下呢可以的;12声音阶的依据就是3/2^12≈,和2^7＝128很接近,按照这个思路,继续找接近的值就可以了嘛;还有人真地找到了,此人就是我国西汉的着名学者京房77 BC－47 BC;他发现3/2^53≈×109,和2^31≈×109也很接近,于是提出了一个53音阶的新音律;要知道古人并没有我们现在的计算器,计算这样的高次幂问题对他们来说是相当麻烦的;当然,京房的新律并没有流行开,原因就是53个音阶也太麻烦了吧开始学音乐的时候要记住这么多音符,谁还会有兴趣哦但是这种努力是值得肯定的,也说明12声音阶也不完美,也确实需要改进;“五度相生律”的12声音阶中的主要问题是,相邻音符的频率比例有两种自然半音和变化半音,而不是一种;而且两种半音彼此差距还不小;2187:2048/256:243≈;好像差不多哦但其实自然半音本身就是256:243≈了;如果12声音阶是真正的“等差音高序列”的话,每个半音就应该是相等的,各个音阶就应该是“等距离”的;也就是说,真正的12声音阶可以把一个八度“等分”成12份;为什么这么强调“等分”、“等距离”呢因为在音乐的发展过程中,人们越来越觉得有“转调”的必要了;所谓转调,其实就是用不同的音高来唱同一个旋律;比方说,如果某一个人的音域是C～高音C也就是以前的do～高音do,乐器为了给他伴奏,得在C～高音C之内弹奏旋律；如果另一个人的音域是D～高音D也就是以前的re～高音re,乐器得在D～高音D之内弹奏旋律;可是“五度相生律”的12声音阶根本不是“等差音高序列”,人们会觉得C～高音C之内的旋律和D～高音D之内的旋律不一样;特别是如果旋律涉及到比较多的半音,这种不和谐就会很明显;可以说,如果现在的钢琴是按“五度相生律”来决定各键的音高,那么只要旋律中涉及到许多黑键,弹出来的效果就会一塌糊涂;这种问题在弦乐器上比较好解决,因为弦乐器的音高是靠手指的按压来决定的;演奏者可以根据不同的音域、旋律的要求,有意地不在规定的指位上按弦,而是偏移一点按弦,就能解决问题;可是键盘乐器比如钢琴、管风琴、羽管键琴等的音高是固定的,无法临时调整;所以在西方中世纪的音乐理论里,就规定了有些调、有些音是不能用的,有些旋律是不能写的;而有些教堂的管风琴,为了应付可能出现的各种情况,就预先准备下许多额外的发音管;以至于有的管风琴的发音管有几百甚至上万根之多;这种音律规则上的缺陷,导致一方面作曲家觉得受到了限制,一方面演奏家也觉得演奏起来太麻烦;问题的根源还是出在近似值上;“五度相生律”所依据的3/2^12毕竟和2^7并不完全相等;之所以会出现两种半音,就是这个近似值造成的;对“五度相生律”12声音阶的进一步修改,东、西方也大致遵循了相似的路线;比如东晋的何承天370 AD－447 AD,他的做法是把3/2^12和2^7之间的差距分成12份,累加地分散到12个音阶上,造成一个等差数列;可惜这只是一种修补工作,并没有从根本上解决问题;西方的做法也是把3/2^12和2^7之间的差距分散到其它音符上;但是为了保证主音C和属音G 的3/2的比例关系这个“纯五度”是一个音阶中最重要的和谐,即使是在12声音阶中也是如此,这种分散注定不是平均的,最好的结果也是12音中至少有一个“不在调上”;如果把差距全部分散到12个音阶上的话,就必须破坏C和G之间的“纯五度”,以及C和F之间的4/3比例术语是“纯四度”;这样一来,虽然方便了转调,但代价就是音阶再也没有以前好听了;因为一个八度之内最和谐的两个关系――纯五度和纯四度――都被破坏了;一直到文艺复兴之前,西方音乐界通行的律法叫“平均音调律”Meantone temperament,就是在保证纯五度和纯四度尽量不受影响的前提下,把3/2^12和2^7之间的差距尽量分配到12个音上去;这种折衷只是一种无可奈何的妥协,大家其实都在等待新的音律出现;终于还是有人想到了彻底的解决办法;不就是在一个八度内均分12份吗直接就把2:1这个比例关系开12次方不就行了也就是说,真正的半音比例应该是2^1/12;如果12音阶中第一个音的频率是F,那么第二个音的频率就是2^1/12F,第三个音就是2^2/12F,第四个音是2^3/12F,……,第十二个是2^11/12F,第十三个就是2^12/12F,就是2F,正好是F的八度;这是“转调”问题的完全解决;有了这个新的音律,从任何一个音弹出的旋律可以复制到任何一个其它的音高上,而对旋律不产生影响;西方巴洛克音乐中,复调音乐对于多重声部的偏爱,有了这个新音律之后,可以说不再有任何障碍了;后来的古典主义音乐,也间接地受益匪浅;可以说没有这个新的音律的话,后来古典主义者、浪漫主义者对于各种音乐调性的探索都是不可能的;这种新的音律就叫“十二平均律”;首先发明它的是一位中国人,叫朱载堉yù;他是明朝的一位皇室后代,生于1536年,逝世于1611年;他用珠算开方的办法珠算开12次方,难度可想而知,首次计算出了十二平均律的正确半音比例,其成就见于所着的律学新书一书;很可惜,他的发明,和中国古代其它一些伟大的发明一样,被淹没在历史的尘埃之中了,很少被后人所知;西方人提出“十二平均律”,大约比朱载堉晚50年左右;不过很快就传播、流行开来了;主要原因是当时西方音乐界对于解决转调问题的迫切要求;当然,反对“十二平均律”的声音也不少;主要的反对依据就是“十二平均律”破坏了纯五度和纯四度;不过这种破坏程度并不十分明显;“十二平均律”的12声音阶的频率近似值分别是：FC、C／Db、D、D／Eb、E、F、F／Gb、G、G／Ab、A、A／Bb、B;注意,现在所有的半音都一样了,都是2^1/12,即;以前的自然半音和变化半音的区别没有了;另外,原来“五度相生律”的12音阶中,C和G的比例是3/2即纯五度,现在“十二平均律”的12音阶中,C和G的比例是,和纯五度所要求的3/2非常接近;原来“五度相生律”的12音阶中,C和F的比例是4/3即纯四度,现在“十二平均律”的12音阶中,C和F的比例是,和纯四度所要求的4/3也非常接近;所以“十二平均律”基本上保留了“五度相生律”最重要的特性;又加上它完美地解决了转调问题,所以后来“十二平均律”基本上取代了“五度相生律”的统治地位;现在的钢琴就是按“十二平均律”来确定各键音高的;现在学生们学习的do、re、mi也是按“十二平均律”修改过的7声音阶;现在如果想听“五度相生律”或者“纯律”的do、re、mi,已经很不容易了;BTW：现在钢琴的音高标准是按“中央C”即通常的do右边的第五个白键按术语说是A4的频率来定的;这个A键的频率被确定为440HZ;确定了它,钢琴上其它键的频率都可以按“十二平均律”类推得到;不过在某些国家比如东欧,也有把这个键的频率定为444HZ的;历史上,这个A键的标准曾经有过很多次变化;比如在1759年,英国剑桥的“三一学院”Trinity College Cambridge的管风琴的这个A键,就曾经被定在309HZ;可以想像在这里听到的旋律和我们现在听到的旋律该有怎样大的差别;研究古代音乐家的作品的时候,对于当时音高标准的研究也是很重要的一部分;关于“十二平均律”,最后要提的是所谓“大调”、“小调”的问题;自从“五度相生律”提出12音阶以来,12音阶和原来的7音阶之间的关系一直就被人们所研究;也就是说,在原来的7音阶之外,现在人们可以在12音阶中选取其它的7个音来作为音乐的“标尺”了;这可以给作曲家们以更大的创作自由;以C～高音C的八度为例,如果我们选择原来的7音阶,即C、D、E、F、G、A、B,这就被称为“大调”major scale,又因为这个大调的主音是C,所以被称为“C大调”;而如果我们选择C、D、DEb、F、G、GAb、ABb,这就被称为“c小调”C minor scale;用小写c的原因是表示这是小调;大调和小调的区别就在于,大调和小调里各音之间的“距离感”不同,以它们为基础来作曲,给听众的感觉也不相同;这就让作曲家有了用音乐表现不同情绪的机会;西方中世纪的音乐理论里,曾经提出了8种不同的方法在12音中选7个音作为基准,其中就包含了我们现在谈的大调和小调;当时的音乐理论给予这8种调性mode以不同的感情色彩,比如有的被认为是“悲伤的”,有的被认为是“快乐的”,有的被认为是“朝气蓬勃的”等等;这8种调性中有一些现在已经很少用了,现在最流行的是大调和小调这两种;由于“十二平均律”允许随意转调,这就让作曲家可以更为地自由创作;以前由于各音之间的半音“不等距”的问题,有些调被认为不能写作的,现在也可以毫无阻碍的进行创作了;调式是按照一定关系高低关系、稳定与不稳定关系等组织起来的一组音一般在七个音之内,并以某一个音为中心音即主音联结成一个体系,这个体系就叫调式;大调音阶由七个基本音级组成;根据大调构成法则,第三、四级mi和fa之间、第七八级si 和do之音的距离都是半音即小二度;而其他相邻两级之间的距离都是全音即大二度的音阶称为大调音阶; 如C大调自然大调的七个基本音级为C、D、E、F、G、A、B；G大调的七个基本音级为G、A、B、C、D、E、F,等等;小调也是由一种七个音构成的调式,根据各音级相邻音的音高关系不同又可分为自然小调、和声小调和旋律小调,小调的特征表现在主音上方的小三度,它最能说明小调的色彩和性格;如a自然小调的七个音级为a、b、c、d、e、f、g；a和声小调为 a、b、c、d、e、f、g等等,如非指明,我们一般称自然小调为“小调”;。

音高频率——精选推荐

⾳⾼频率⼀、钢琴的⾳⾼与频率对照表在上表中，⼗⼆⾳律(twelve pitches of the temperament octave)⽤绿⾊标注。

此表通过连续的乘法每次乘1.0594631得出的结果(2的n次⽅)。

调⾳参考频率(A-440)为⿊⾊加粗标注。

最低频率⽤红⾊标注，最⾼频率⽤蓝⾊标注。

从表上可以看到，中央C对应的是261.626 Hz，⽽A440对应的就是440.000 Hz。

A440 是440赫兹的声⾳⾳调，西⽅⾳乐上，此⾳为标准⾳⾼。

西⽅乐理中，A440乃是中央C上⽅的A⾳符（参照A4）。

⼆、⼈声及各乐器频率范围表实际⼈声频率男：低⾳82～392Hz，基准⾳区64～523Hz 男中⾳123～493Hz，男⾼⾳164～698Hz⼥：低⾳82～392Hz，基准⾳区160～1200Hz ⼥低⾳123～493Hz，⼥⾼⾳220～1.1KHz三、录⾳时各频率效果男歌声 150Hz~600Hz影响歌声⼒度，提升此频段可以使歌声共鸣感强，增强⼒度。

⼥歌声 1.6~3.6KHz影响⾳⾊的明亮度，提升此段频率可以使⾳⾊鲜明通透。

语　⾳ 800Hz是“危险”频率，过于提升会使⾳⾊发“硬”、发“楞”沙哑声提升64Hz~261Hz会使⾳⾊得到改善。

喉⾳重衰减600Hz~800Hz会使⾳⾊得到改善⿐⾳重衰减60Hz~260Hz，提升1~2.4KHz可以改善⾳⾊。

齿⾳重 6KHz过⾼会产⽣严重齿⾳。

咳⾳重 4KHz过⾼会产⽣咳⾳严重现象（电台频率偏离时的⾳⾊）四、乐器重要频率范围表贝司：低⾳吉它：频响在700～1KHz之间，提⾼拨弦⾳为60～80Hz电贝司：低⾳在80～250Hz，拨弦⼒度在700～1KHz吉它：电吉它：65～1.7KHz，响度在2.5KHz，饱满度在240Hz⽊吉它：低⾳弦：80～120Hz，琴箱声：250Hz，清晰度：2.5KHz、3.75KHz、5KHz⿎：低⾳⿎：27～146Hz，低⾳：60～80Hz，敲击声：2.5KHz⼩⿎：饱满度：240Hz，响度：2KHz通通⿎：丰满度：240Hz，硬度：8KHz地筒⿎：丰满度：80～120Hz吊钗：130～2.6KHz，⾦属声：200Hz，尖锐声：7.5～10KHz，镲边声：12KHz⼿风琴：饱满度：240Hz钢琴：低⾳在80～120Hz，临场感2.5～8KHz，声⾳随频率的升⾼⽽变单薄Trumpet（⼩号）：146～2.6KHz，丰满度：120～240Hz，临场感：5～7.5KHz⼩提琴：174～3.1KHz，丰满度：240～400Hz，拨弦声：1～2KHz，明亮度：7.5～10KHz⼤提琴：61～2.6KHz，丰满度：300～500Hz中提琴：123～2.6KHz琵琶：110～1.2KHz，丰满度：600～800Hz⼆胡：293～1318HzFlute（笛⼦）：220～2.3KPiccolo（短笛）：494～4.1KHzClarinet（单簧管）：146～2.6KHzBassoon（巴松管、低⾳管）：55～2.6KHzFrench Horn（法国号）：73～2.8KHzTrombone（长号）：65～2.6KHzTuba（低⾳号）：43～2.6KHz五、⼈声各频率段⾳⾊效果1）2K～3KHz频率：这段频率是影响声⾳明亮度最敏感的频段，如果这段频率成分丰富，则⾳⾊的明亮度会增强，如果这段频率幅度不⾜，则⾳⾊将会变得朦朦胧胧；⽽如果这段频率成分过强，⾳⾊就会显得呆板、发硬、不⾃然.2）1K～2KHz频率：这段频率范围通透感明显，顺畅感强。

声音的频率与音高的计算

声音的频率与音高的计算声音是我们日常生活中不可或缺的一部分，我们常常用音高来描述声音的高低。

但是，你是否想过声音的频率与音高之间的关系是如何计算的呢？本文将解析声音的频率与音高的计算方法。

1. 频率与音高的定义首先，我们需要了解频率和音高的概念。

频率是指声波振动的次数，单位是赫兹（Hz），表示每秒钟发生的振动次数。

而音高则是人耳对声音高低的主观感觉，高音对应高频率，低音对应低频率。

2. 频率与音高的关系频率与音高之间存在着一定的关系，即频率越高，音高越高；频率越低，音高越低。

这是因为人耳对于不同频率的声波振动有不同的感知。

3. 计算音高的方法那么，如何计算音高呢？在音乐理论中，常用的计算音高的公式是达能公式（Dane's Law）。

该公式可以计算人耳感知到的音高（f）与声波的频率（f₀）之间的关系：音高（f）= k × log₂（f/f₀）其中，k是一个常数，用来调整计算结果，具体数值根据音高的标准选择不同。

对于常用的A音（440Hz）作为参考音的情况下，k的取值为39.86。

使用达能公式可以将频率转换为人耳感知的音高。

例如，当声波频率为880Hz时，计算公式为：音高（f）= 39.86 × log₂（880/440）= 12.04. 进一步理解音高的计算除了达能公式，音高的计算还可以使用其他方法。

在音乐理论中，常用的一种方法是将各个音符与参考音A进行比较，确定它们之间的音高关系。

以A音（440Hz）为基准，其他音符相对于A音的音高关系如下：- 升高一个八度，频率翻倍；降低一个八度，频率减半。

- 升高一个半音，频率乘以2^(1/12)；降低一个半音，频率除以2^(1/12)。

通过以上公式，可以计算出任意音符相对于A音的音高关系。

5. 结论通过以上的介绍，我们了解到声音的频率与音高之间的关系。

频率越高，音高越高；频率越低，音高越低。

我们可以使用达能公式或其他方法计算声音的音高，以便更好地理解和描述声音。

各个音阶的对应频率

各个音阶的对应频率各个音阶的对应频率我刚刚知道了6对应的是440赫兹，那么1,2,3，4.5,7，高音1,23,4，什么的，总之希望得到钢琴全部键位对应的频率音名 A2 #A2 B2频率 27.5 29.1 30.9音名 C1 #C1 D1 #D1 E1 F1 #F1 G1 #G1 A1 #A1 B1频率 32.7 34.6 36.7 38.9 41.2 43.7 46.2 49.0 51.9 55.0 58.3 61.7 音名 C #C D #D E F #F G #G A #A B频率 65.4 69.3 73.4 77.8 82.4 87.3 92.5 98.0 103.8 110.0 116.5 123.5音名 c #c d #d e f #f g #G a #a b频率 130.8 138.6 146.8 155.6 164.8 174.6 185.0 196.0 207.7 220.0 233.1 246.9音名 c1 #c1 d1 #d1 e1 f1 #f1 g1 #g1 a1 #a1 b1频率 261.6 277.2 293.7 311.1 329.6 349.2 370.0 392.0 415.3 440.0 466.2 493.9音名 c2 #c2 d2 #d2 e2 f2 #f2 g2 #g2 a2 #a2 b2频率 523.3 554.4 587.3 622.3 659.3 698.5 740.0 784.0 830.6 880.0 932.3 987.8音名 c3 #c3 d3 #d3 e3 f3 #f3 g3 #g3 a3 #a3 b3频率 1047 1109 1175 1245 1319 1397 1480 1568 1661 1760 1865 1976音名 c4 #c4 d4 #d4 e4 f4 #f4 g4 #g4 a4 #a4 b4频率 2093 2217 2349 2489 2637 2794 2960 3136 3322 3520 3729 3951音名 c5频率4186以上为钢琴88个音对应的频率，需要注意的是十二平均律定律的乐器包括钢琴，吉他等所有半音的频率之比均为十二次根号2，是一个无理数。

b调音符与频率对照表

b调音符与频率对照表在音乐中，不同的音符代表着不同的音高。

b调是西方音乐中常用的调式之一，它包含了七个音符，分别是B、C、D、E、F、G、A。

每个音符都有一个对应的频率，可以通过科学的测量方法得到。

下面我们将列出b调的音符与频率对照表，以便更好地理解它们之间的关系：1. B音符对应的频率为246.94赫兹。

B音符通常被认为是b调的基音，其他音符都是相对于它来定位的。

2. C音符对应的频率为261.63赫兹。

C音符是b调中的第二个音符，它的频率稍高于基音B。

3. D音符对应的频率为293.66赫兹。

D音符是b调中的第三个音符，它的频率相对于C音符又有所增加。

4. E音符对应的频率为329.63赫兹。

E音符是b调中的第四个音符，它的频率比D音符再次增加。

5. F音符对应的频率为349.23赫兹。

F音符是b调中的第五个音符，它的频率略高于E音符。

6. G音符对应的频率为392.00赫兹。

G音符是b调中的第六个音符，它的频率比F音符再次增加。

7. A音符对应的频率为440.00赫兹。

A音符是b调中的最后一个音符，它的频率相对于G音符有所增加。

通过以上的对照表，我们可以清晰地看到每个音符与其对应的频率之间的关系。

音符的频率越高，音高也就越高。

在演奏乐器或唱歌时，我们可以根据音符对应的频率来调整声音的高低，从而准确地演奏出所需的音调。

除了b调，音符和频率的对应关系在其他调式中也是适用的。

不同的调式有不同的音符和频率对照表，但基本原理是相同的。

通过学习和了解这些对照关系，我们可以更好地理解音乐的内涵，更好地掌握音乐表达的技巧。

音符和频率之间的对照关系是音乐理论中的基础知识，对于学习音乐和演奏乐器的人来说是必不可少的。

它帮助我们更好地理解和掌握音乐的构成和表达方式，为我们的音乐之旅增添了更多的乐趣和挑战。

总结一下，音符和频率之间存在着明确的对应关系，通过对照表我们可以清晰地看到不同音符对应的频率。

这些对照关系对于理解音乐和演奏乐器都具有重要意义。

音高和频率转换表讲解学习