离散数学平面图及图的着色共31页文档
离散数学 平面图与着色

这样的构造是可能的,因为G是联通的。在 添加m条边之后就获得G。设rk,mk,nk和 分别为Gk的面数、边数和顶点数。 现在用归纳法来进行证明。对G1来说关系 r1=m1-n1 +2为真,因为m1=1,n1=2 而r1=1。 现在假定 rk=mk-nk +2,我们来考虑Gk+1。 设Gk+1= Gk +(ak+1,bk+1),此时分两 种情况来讨论。
【定理12.3】若G的每个面的边界至少含k kr k 条边,则 m (n 2)
2 k 2
【例12.4】 证明K5是不可平面图 。 【例12.5】 证明K3, 3是不可平面图。
略
【定义12.3】在图G的边(u, v)上添加k个 顶点v1,v2,…,vk,从而使得边(u, v)变为 (k+1)条边(u,v),(v1, v2), …,( vk, v), 则称为对边(u, v)的加细。两个图称为同 胚的,其中一个图是另一个图的加细图。 【定理12.4】一个图G是可平面图的充要条 件是G没有同胚于K5或K3, 3的子图。
Theorem If every vertex of G has degree d(v) < k, then G is k-colorable. Proof: Use induction on n (number of vertices). 1.If n = 1 or n = 2, the assertion is easily seen to be true. Suppose n > 2, and assume that the proposition is valid for all graphs with fewer than n vertices. 2.Choose any vertex v of G and delete it and all the edges incident to v. This leaves a subgraph H of G with n - 1 vertices satisfying the given hypothesis (i.e. that every vertex has degree less than k). By the inductive hypothesis, (H) k. Now, consider any particular k-coloring of H. Since d(v) < k, the vertices of H that were adjacent to v in G are colored with at most k 1 different colors. Thus, there’s at least one color left with which we may color v, so that it is of a different color to each of its neighbors. This gives a coloring of G using the same colors as H. Therefore, G is k-colorable.
离散数学着色基础知识

离散数学着色基础知识离散数学是数学的一个重要分支,它关注离散的数学结构和对象。
在离散数学中,图论作为一个重要的研究领域,着色问题受到广泛的关注。
着色问题是指给定一个图的顶点或边,用不同的颜色给它们进行标记的问题。
本文将介绍离散数学中的着色基础知识,包括图的着色、四色定理以及一些常见的着色应用。
1. 图的着色在图的着色问题中,我们通常要求相邻的顶点或边不能使用相同的颜色。
对于给定的图,我们可以用一个函数来为每个顶点或边赋予一个颜色。
这个函数被称为着色函数。
如果对于每个相邻的顶点或边,它们被赋予了不同的颜色,那么这个着色函数就满足着色条件。
图的着色问题可以分为顶点着色和边着色两种情况。
在顶点着色中,我们使用不同的颜色为图中的每个顶点上色;而在边着色中,我们使用不同的颜色为图中的每条边上色。
通常情况下,我们更关注的是顶点着色问题。
2. 四色定理四色定理是图论中的一个著名的定理,它指出任意一个平面图都可以用四种颜色给其顶点进行着色,使得任意相邻的顶点使用不同的颜色。
具体地说,对于任意一个平面图,我们可以用四种颜色对其顶点进行着色,并且一定能够满足着色条件。
这个定理的证明非常复杂,涉及到大量的数学推理和计算。
它的证明分为两个步骤:首先,通过对所有可能的情况进行穷举和排除,证明了五种颜色是充分的;然后,通过反证法证明了四种颜色就足够了。
四色定理在实际应用中具有重要的意义。
它可以用来解决地图着色问题,即给定一幅地图,用尽可能少的颜色对每个行政区域进行着色,使得相邻的行政区域颜色不同。
四色定理的证明为解决这个问题提供了理论支持。
3. 着色的应用着色问题在现实生活中有许多应用。
除了地图着色问题外,还有课程表着色问题、时间表着色问题等等。
在课程表着色问题中,我们需要为学校的每个班级安排一个课程表,并且要求相邻时间段的课程使用不同的颜色。
这个问题可以转化为图的着色问题,其中图的每个顶点代表一个时间段,边代表时间段的相邻关系。
离散数学中的图的平面图与平面图的着色

图是离散数学中的重要概念,而平面图和平面图的着色是图论中的两个关键概念。
平面图是指在平面上绘制的图形,使得图中的边不会相交。
平面图的着色是指对平面图中的顶点进行染色,且相邻的顶点不会被染成相同的颜色。
平面图的概念最早由欧拉在1736年提出。
他发现,如果一个图是可以在平面上绘制而不会边相交的,那么这个图是一个平面图。
欧拉还引入了一个重要的公式,即欧拉定理,它描述了平面图中的顶点、边和面的关系:V - E + F = 2,其中V代表顶点数,E代表边数,F代表面数。
对于平面图的着色问题,四色定理是一个非常重要的结果。
四色定理指出,任何一个平面图,在不考虑多重边和自环的情况下,最多只需要使用四种颜色就能够对图的顶点进行染色,使得相邻的顶点不会有相同的颜色。
这个定理在1976年被由英国数学家Tomás Oliveira e Silva使用计算机辅助证明,被认为是图论史上的一大突破。
对于平面图的着色,有一种特殊的染色方法叫做四色标号。
四色标号是指对于任意一个平面图,都可以给图中的每个顶点赋予一个自然数,使得相邻的顶点之间的差值不超过3。
这种染色方法保证了相邻的顶点不会被染成相同的颜色,同时最多只需要使用四种颜色。
平面图的着色不仅在图论中有着重要的应用,同时在现实生活中也有很多实际的应用。
比如,考虑地图上的城市,如果我们希望将城市标记成不同的颜色,以表示它们的关系,那么可以利用平面图的着色来实现。
另外,平面图的着色还有很多其他的实际应用,比如在工程规划中用于规划电路的布线、在计算机科学中用于处理图像等等。
总之,离散数学中的图的平面图与平面图的着色是图论中的两个重要概念。
平面图是指在平面上绘制的图形,使得边不会相交;平面图的着色是指对平面图中的顶点进行染色,且相邻的顶点不会被染成相同的颜色。
四色定理是平面图着色的重要结果,它指出任意一个平面图可以使用最多四种颜色进行着色。
平面图的着色在现实生活中有着广泛的应用,是离散数学中的一个重要研究领域。
离散数学 第四章平面图与图【完全免费,强烈推荐】.ppt

f (Tn , t ) t (t 1)n1.
这由 (Tn ) 2即可得证。当 t 2时,f (Tn ,t) 2.
色数与色数多项式
定理 4.6.7
设i,j是G的不相邻结点,则
_
0
—0
f (G, t) f (Gij , t) f (Gij , t). 其中Gij ,Gij 由定义4.6.3给出
d0
,因此
(G' ) d0
1.即
d0
1 种颜
色可以对G '的结点着色,放回结点 vi 恢复成G,由
于d (vi ) d0 ,所以比有一种与 vi邻点都不同的颜色可
对vi 着色.
色数与色数Байду номын сангаас项式
定理 4.6.3 对于任意一个图G. γ(G) <= 1 + maxδ(G’) 其中δ(G’)是G的导出子图G’中结点的最小度, 极大是对所有的G’而言.
定理 4.5.4 若任何一个3-正则平面图的域可四着色,则任何 一个平面的域也可以四着色.
4.6 色数与色数多项式
定义 4.6.1 给定图G,满足相邻点结点着以不同颜色的最少 颜色数为G的色数,记为γ(G).
定义 4.6.2 给定图G,满足相邻边着以不同颜色的最少颜色 数目称为G的边色数,记为β(G).
色数与色数多项式
定理 4.6.1 一个非空图,γ(G) = 2,当且仅当它没有奇回路.
证明:充分性:在G中确定一个林 T ',其每个连通子
图都是树T, (T ) 2.由于每个回路都是偶回路.所
以加入每一条余树边都不会使结点着色发生变化,因
此 (G) 2.
必要性:如果G中有奇回路,则 (G) 3 .矛盾.
离散数学PPT课件 9平面图(ppt文档)

v1 v2 v7 v6 v10 v5
v8 v9
v3
v4
v1 v2 v7 v6 v10 v5
v8 v9
v3
v4
v1 v3 v8 v2v7 v6
v9 v10 v4
v5
本节要求掌握: 平面图的概念, 平面图的边界, 欧拉公式及其应用 平面图的判定.
面的边界中出现, 所以所有面的边界总数=2e, 所以有:
2e=(r个面边界总数)≥ 3r, 即2e≥3r 所以r≤
2 3
e
由欧拉公式: v-e+r=2
得
v-e+
2 3
e≥2
整理得 e≤3v-6
用此定理可以判定一个图不是平面图, 例如证明K5不是
平面图: K5中有v=5 e=10 3v-6=3×5-6=9 不满足e≤3v-6,
K5
e条边的连通简单平面图, 若v≥3, 则e≤3v-6.
证明:⑴ 当e=2 时, 因为G是简单连通图, 所以v=3, 显然有
2≤3×3-6 即e≤3v-6
⑵当e>2时, (通过计算每个面的边界来证明)
设G有r个面, 因为G是简单图, 所以每个面至少由三条边
围成, 所以r个面的总边界数≥3r, 另外由于每条边在两个
例如右图.就是
v1
可平面化的图. v2
v3
下面是两个
重要的非平面图: v4
v5
K5和K3,3
v1
v2
v3
v4
v5
1 3 5 2 4 6
a b
c
f e
d
v1
v2
v3
v4
离散数学--6.5 平面图

13
同Hale Waihona Puke 与收缩消去2度顶点v 如图从(1)到(2) 插入2度顶点v 如图从(2)到(1) G1与G2同胚: G1与G2同构, 或 经过反复插入、或消去2度顶 点后同构 收缩边e 如图从(3)到(4)
10
欧拉公式(续)
推论 设平面图G有 p (p2) 个连通分支, 则 nm+r=p+1 其中n, m, r 分别是G的阶数, 边数和面数. 证 设第 i 个连通分支有 ni个顶点, mi 条边和 ri 个面. 对各 连通分支用欧拉公式, ni mi + ri = 2, i = 1, 2, … , p 求和并注意 r = r1+…+rp p+1, 即得 nm+r=p+1
R3 R2 R1
(2)
说明: (1) 一个平面图可以有多个不同形式的平面嵌入, 它们都同构. (2) 可以通过变换(测地投影法)把平面图的任何一面作为 外部面
5
平面图的面与次数(续)
定理6.13 平面图各面的次数之和等于边数的2倍 证 一条边或者是2个面的公共边界, 或者在一个面的边界 中出现2次. 在计算各面的次数之和时, 每条边恰好被计算 2次.
与K5同胚 也可收缩到K5
16
对偶图
定义6.28 设平面图G有n个顶点, m条边和r个面, G的对偶 图G*=<V*,E*>构造如下: 在G的每一个面Ri中任取一个点vi*作为G*的顶点, V*= { vi*| i=1,2,…,r }. 对G每一条边ek, 若ek在G的面Ri与Rj的公共边界上, 则作边
离散数学7-5平面图7-6对偶图与着色

第十六页,编辑于星期二:九点 四十六分。
K5和K3,3常称作库拉托夫斯基图。
K3,3
K5
第十七页,编辑于星期二:九点 四十六分。
作业
P317: (1)(2)
一、对偶图
1、对偶图 定义7-6.1 对具有面F1 ,F2,..., Fn的连通平面图 G=<V,E>实施下列步骤所得到的图G*称为图G的对偶 图(dual of graph):
第二十二页,编辑于星期二:九点 四十六分。
如果存在一个图G*=<V*,E*>满足下述条件: (a)在G的每一个面Fi的内部作一个G*的顶点vi* 。 即对图G的任一个面Fi内部有且仅有一个结点vi*∈V*。
第十八页,编辑于星期二:九点 四十六分。
7-6 对偶图与着色
掌握对偶图的定义,会画图G的对偶图 G* 掌握自对偶图的定义及必要条件。
第十九页,编辑于星期二:九点 四十六分。
与平面图有密切关系的一个图论的应用是图形的着色问 题,这个问题最早起源于地图的着色,一个地图中相邻国 家着以不同颜色,那么最少需用多少种颜色? 一百多年前,英国格色里(Guthrie)提出了用四种颜色即 可对地图着色的猜想,1879年肯普(Kempe)给出了这个 猜想的第一个证明,但到1890年希伍德(Hewood)发现肯 普证明是错误的,但他指出肯普的方法 虽不能证明地图 着色用四种颜色就够了,但可证明用五种颜色就够了,即 五色定理成立。
(c)当且仅当ek只是一个面Fi的边界时(割边),vi*存在 一个环e*k与ek相交。
即当ek为单一面Fi的边界而不是与其它面的公共边 界时,作vi*的一条环与ek相交(且仅交于一处)。所作的 环不与 G*的边相交。
离散第23讲 平面图的着色与树

n = 1时显然T无回路,因这时m=n–1=0。
设顶点数为n–1 的满足题设的图无回路,顶点数为n的图T至少有 两个悬挂点。去掉一悬挂点构成T’。显然T’仍连通,且m’=m– 1=n–2 = n’–1 ,因此由归纳假设T’无回路。在T’上加回所删去的 悬挂点得T,故T亦无回路。
第23讲 平面图的着色与树
-5-
对偶图例
第23讲 平面图的着色与树
-6-
对偶图例
同构图的对偶图可能不同构 左边的对偶图有5度顶点, 右边的对偶图却没有 平面图的对偶图仍为平面图
第23讲 平面图的着色与树
-7-
可k着色
定义: 无环图G称为可k-着色的,如果可用k种颜色 给G的所有顶点着色,使每个顶点着一种颜色,而同 一边的两个端点着不同颜色。
v5 v4
v1 v2
v0
v3
第23讲 平面图的着色与树
-10-
5色定理
为叙述简明,令RY表示G-v0中所有着红、黄顶点的集合,BW表 示G - v0中所有着黑、白顶点的集合。考虑RY生成的G的子图 G(RY)。
若v1,v3分属于G(RY)的两个不同的连通分支,那么只要将v 1所在分支的红、黄顶点的着色作一对换(从而v1着黄色), 便可给v0着红色以完成对G的5-着色。
若任意平面图可k-着色,则任意平面图的面可用k种 颜色之一着色,使得相邻的面着不同颜色
第23讲 平面图的着色与树
-8-
5色定理
定理: 任何平面图都是可5-着色的。 证:
连通分支、环和平行边与着色问题无关,因此 可只讨论平 面连通简单图。 设G为任一平面连通简单图,顶点个数为n 。对n归纳。 当n≤5时命题显然成立。 设n-1个顶点的平面图都是可5-着色的。考虑n个顶点的图G。
离散数学平面图及图的着色解析

二、平面图与对偶图的阶数、边数与面数之间的关系。 结论 设G*是连通平面图G的对偶图,n*、m*、r*和n、 m
、r分别为G*和G的顶点数、边数和面数,则 (1)n*= r (2)m*=m (3)r*=n (4)设G*的顶点v*i位于G的面Ri中,则dG*(vi *)=deg(Ri)
定理17.7 设G为n(n3) )阶简单连通的平面图,G为极大平面图 当且仅当G的每个面的次数均为3。
四、极小非平面图 定义17.4 若在非平面图G中任意删除一条边,所得图G为平面
图,则称G为极小非平面图。 由定义不难看出: K5, K3,3都是极小非平面图。 极小非平面图必为简单图。 例如:以下各图均为极小非平面图。
r ri k 1
i 1
于是,对(17.1)的两边同时求和得
k
k
k
k
2k (ni mi ri ) ni mi ri n m r k 1
i 1
i 1
i 1
i 1
经整理得 n-m+r = k+1。
2、 与欧拉公式有关的定理
定理17.10 设G为连通的平面图,且每个面的次数至少为 l(l<=3),则 G的边数与顶点数有如下关系:
第17章平面图及图的着第17章平面图及图的着江苏科技大学本科生必修课程计算机系本章的主要内容平面图的基本概念欧拉公式平面图的判断平面图的对偶图顶点着色及点色数地图的着色与平面图的点着色特别说明
江苏科技大学本科生必修课程
离散数学
第17章 平面图及图的着 色
计算机系 周塔
本章说明
离散数学(Ch15平面图及色数)
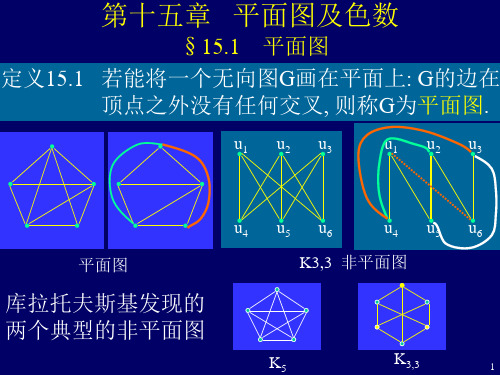
定理15.4 设G为任一平面图, 则(G)≤5. (五色定理)
用第一数学归纳法对G的顶点数n进行归纳: 显然, 当n≤5时, 有(G)≤5. 假设 n–1 (n≥6)时, (G)≤5成立.
显然, 平面图G中必有度数小于6的顶点u0. (因m≤3n-2) 将顶点u0从G中去掉(含u0邻接的边), 得G0=G – u0, 则G0仍是平面图且顶点数为n-1, 根据假设, 有(G0)≤5. 再从G0加入顶点u0及邻接的边, 还原为G. ⑴如果d(u0)≤4, 则与u0邻接顶点最多涂4色, 有(G)≤5成立. ⑵如果d(u0)=5, 令与u0邻接的顶点按顺时钟排为u1,u2,u3,u4,u5. 并设这5个顶点涂色为C1,C2,C3,C4,C5.
3
定义15.2 设G是一个平面图, 如果连接G的任意两个 不邻接顶点u和v, 都会使G+(u,v)变成非平 面图, 则称G为极大平面图. (边数极大)
极大平面图
K5非平面图
K3
定理15.2 设G是至少具有三个顶点的极大平面图, 则G的任何一个面都是K3.
假设G是极大平面图, 但有一个面不是K3面, 不妨设为{u1,u2,u3,u4,…,u1}, 考察: ⑴ (u1,u3)邻接, (u2,u4)邻接 两边会在圈外相交 ⑵ (u1,u3)不邻接 可加边(u1,u3), 仍是平面图 ⑶ (u2,u4)不邻接 可加边(u2,u4), 仍是平面图
6
§15.2 色数
1. 对偶图 定义15.3 设G是一个平面图, 具有k个面F1,F2,…,Fk, 其中包括无限面, 构造对偶图G*: ⑴ 在G的每个面Fi的内部取一点fi, 作为G*的顶点; ⑵ 对应于G的任意一条边e,
如果e是Fi和Fj的公共边, 则与e交叉连接fi和fj, 使(fi, fj)G* 如果e仅是Fj的悬挂边或桥, 则连一个自环, 使(fj, fj)G*
离散数学 7-5 平面图7-6对偶图与着色

证明一个图的色数为n,首先 必须证明用n种颜色可以着色该 图,其次证明用少于n种颜色不 能着色该图。
4、对点着色的鲍威尔方法: 第一步:对每个结点按度数递减次序进行排列(相 同度数的结点次序可随意) 第二步:用第一种颜色对第一个结点着色,并按次
颜色即可对地图着色的猜想,1879年肯普(Kempe) 给出了这个猜想的第一个证明,但到1890年希伍德
(Hewood)发现肯普证明是错误的,但他指出肯普
的方法 虽不能证明地图着色用四种颜色就够了,但 可证明用五种颜色就够了,即五色定理成立。
此后四色猜想一直成为数学家感兴趣而未能解 直到1976年美国数学家阿佩尔和黑肯宣布:他
(2)归纳假设:设G有k个结点时结论成立。即G是最多可5-着色 的。 (3)归纳推理:需要证明G有k+1个结点时结论仍成立。 先在G中删去度数小于5的结点u,根据归纳假设,所得的图G-{u} 有k个结点,结论成立。然后考虑在G-{u}中加上一个结点的情况。 若加入的结点满足deg (u)<5,则可以对u正常着色。若加入的结 点满足deg (u)=5,则与它邻接的5个结点可以用4种颜色着色。 分两中情况证明: . 对调v1,v3两个结点的颜色后,给着v1的颜色。 .对调v2,v4两个结点的颜色后,给着v2的颜色。
r=8,则e=2r=16。
5.定理7-5.3 设G为一简单连通平面图,其顶点数 v≥3,其边数为e,那么 e≤3v – 6 证明思路:设G的面数为r,当v=3,e=2时上式成立, 若e≥3,则每一面的次数不小于3。由欧拉定理,各面 次数之和不小于2e。因此 2e≥3r, r≤2e/3 代入欧拉公式: 2=v-e+r≤v-e+ 2e/3 整理后得: e≤3v – 6
离散数学中的图的颜色数与四色定理

离散数学是研究离散结构和离散运算的数学分支,它在计算机科学、信息技术、密码学等领域中具有重要的应用价值。
而图论作为离散数学的一个重要分支,在实际应用中扮演着重要的角色。
图是由节点和连接节点的边组成的抽象表示,可以用来描述许多现实生活中的问题,如交通网络、社交网络等。
而图的着色问题,即如何给图的节点上色,是图论中一个重要的课题。
在离散数学中,图的颜色数是指给图的每个节点赋予的不同颜色的数量。
解决图的着色问题,即求解最小的颜色数,是离散数学中的一个经典问题。
根据图的邻接关系,我们可以将图分为不相邻的节点集合,或称为独立点集。
而在每个独立点集中,节点之间不存在连接,即没有边相连。
因此,在同一个独立点集中的节点可以赋予相同的颜色。
而对于连接的节点,我们需要确保相邻的节点颜色不同。
基于这样的思想,我们可以使用贪心算法来给图的节点进行着色。
贪心算法的基本思路是从一个初始节点开始,每次选择一个尚未被上色的节点,并且给它赋予不同于相邻节点的颜色。
重复这个过程,直到所有的节点都被着色。
但是,通过贪心算法所得到的着色结果并不一定是最优解。
这引出了著名的四色定理。
四色定理是图论中一个重要的定理,指出任何平面图都可以使用不超过四种颜色进行着色,使得相邻节点的颜色不同。
该定理是由基姆和罗伯特森等人在1976年通过计算机模拟方法得到的,随后在1997年由托马斯·韦伦斯顿等人通过使用图论方法进行证明。
证明四色定理的过程非常复杂,但基本思想是从数学的角度证明了四色定理的逻辑正确性。
简单来说,四色定理的证明过程是通过构造方法,将平面图转化为一种特殊的图结构,即棋盘染色问题。
然后通过分析棋盘染色问题的特征和规律,进行推理和证明。
四色定理的证明不仅仅具有理论意义,也具有重要的实际应用。
例如,在地图着色中,四色定理可以用于保证地图上相邻地区的颜色不同。
此外,在计算机图像处理中,也可以采用四色定理的方法,有效地减少图像的颜色数量,从而节省存储空间和运算时间。
